Дополнительное занятие по теме Окружность в 8 классе

Дополнительное занятие по теме Окружность                 8 класс.

Цель: Повторить основные понятия по теме, решать задачи на  свойство вписанного угла и центрального; на свойство хорды.

Устно решить задачи:

а) R = 5см. Найти расстояние от центра окружности до прямой, содержащей хорду, равную 8 см.

б)  Найти расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса r, если 1) ОА = 12см, r = 8cм, 2) ОА = 6 см, r = 8 cм

Предложить учащимся ответить на вопрос: «Как может располагаться прямая относительно окружности?»  Далее объяснение нового материала в форме лекции (учебник, пункт 68). Слайд №3.

слайд 1.

·                     Закончите предложение.

1.            Центральный угол – это… (угол с вершиной в центре окружности).

2.            Градусная мера дуги – это… (градусная мера соответствующего центрального угла).

3.            Угол, вписанный в окружность, – это…(угол, вершина которого лежит на окружности, стороны пересекают ее).

4.            Угол, вписанный в окружность, равен…(половине соответствующего центрального угла).

5.            Вписанные углы, опирающиеся на одну и ту же дугу…(равны)

6.            Вписанные углы, опирающиеся на диаметр... (прямые).

·                     На доске на рисунке показать и назвать углы и дуги, на которые эти углы опираются.

Рисунок 1.

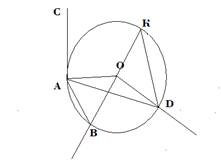
·                     центральный угол, ответ: ∠АОD, ∠АОВ, ∠ВОD, ∠КОD, ∠ВОК, ∠АОК.

·                     вписанный угол, ответ: ∠ВКD, ∠АDК, ∠ВАD

·                     вписанные углы, опирающиеся на одну и ту же дугу, ответ: ∠ВКD и ∠ВАD

·         №71. Начертите окружность и проведите ее радиусы ОА, ОВ и ОС так, чтобы углы АОВ, ВОС и СОА были равны. Вычислите градусные меры образовавшихся дуг АВ, ВС и СА.

·         Устно разобрать, чему равны градусные меры получившихся дуг.

·         АВ=ВС=  АС =120°.

·         №77. Точки М, К и Р делят окружность на дуги, градусные меры которых пропорциональны числам 3, 2 и 7 (считая от точки М к точке К). Вычислите градусные меры углов треугольника МКР.

·         В рабочей тетради в решении дается подсказка: принимаем градусные меры дуг за 3х°, 2х° и __, что подставили? (7х°).

·         Так как сумма их градусных мер равна 360°, составим уравнение ____________

·         Какое уравнение получили?

·         Проверили решение уравнения.

·         3х+2х+7х=360

·         12х=360

·         х=360:12

·         х=30

·         МК=3х=90, РК=2х=60, МР=7х=210

·         Используя свойство вписанных углов, находим величины углов треугольника МКР:

·         ∠ Р=45°, ∠ М=30°, ∠К=105°.

·         IV. Решение задач

·         1. Задачи по чертежам. слайд 3:

·                     Решите задачи устно найдите х:

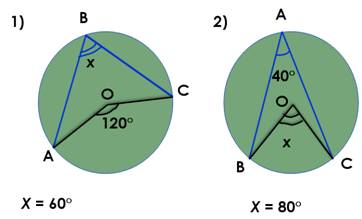
Разобрать, почему в задаче 1 x= 60°, а в задаче 2 x = 80°.

На основании какого свойства? ( свойство вписанного угла: угол, вписанный в окружность, равен половине соответствующего центрального угла).

Постройте в тетради четыре одинаковых окружности.

·                     Скопируйте задания с рисунков в тетрадь и по данным задач 3 и 4. Презентация слайд 4. См. рисунок 3, найдите х. 

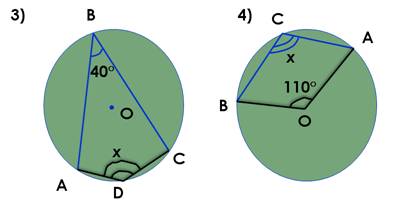
Решение задачи 3: 360° – 80° = 280°,

x = 280°:2 = 140°

Решение задачи 4: 360° – 110° = 250°,

x = 250°:2 = 125°

·                     Скопируйте задания с рисунков в тетрадь и по данным задач 5 и 6. слайд 5. См. рисунок 4 найдите х. 

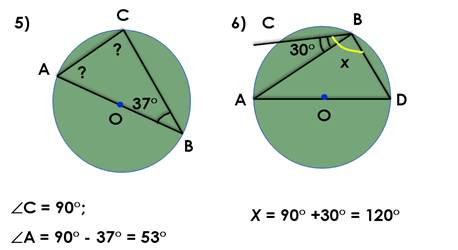
Решение задачи 5: ∠С = 90°,

Какое свойство вписанного угла применяем?

(Вписанные углы, опирающиеся на диаметр прямые)

∠А = 90° – 37°= 53°.

Решение задачи 6: в треугольнике АВD∠В = 90°, ∠CВD =30° + 90° = 120°.

2) Задача №79 в рабочей тетради.

Около равнобедренного треугольника АВС описана окружность. Его основание АС стягивает дугу, градусная мера которой равна 140°. Вычислите градусные меры всех углов треугольника АВС.

В рабочей тетради построили чертеж к задаче Рисунок 7.

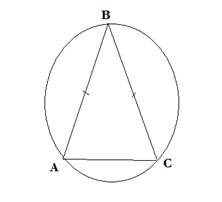
Решение.

Какой угол треугольника АВС можно найти?

Можно найти ∠B, т.к. это вписанный угол, который опирается на дугу АС.

∠В = 140°:2 = 70°,

Какое свойство равнобедренного треугольника можно применить?

В равнобедренном треугольнике углы при основании равны.

∠А = ∠С = (180° – 70°) : 2 = 110°:2 = 55°.

Ответ: ∠В = 70°, ∠А = ∠С = 55°.

V. Домашнее задание.

П.107, повторить теорию по теме «Углы, вписанные в окружность»

Решить задачи №80, 82 в рабочей тетради.

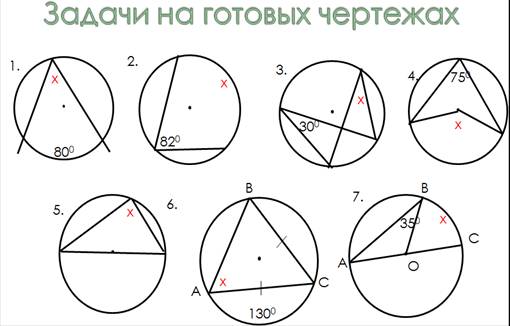
VI. Самостоятельная работа на карточках по готовым чертежам.

слайд 6.

Учащиеся получают карточки с заданиями. См. рисунок 5.

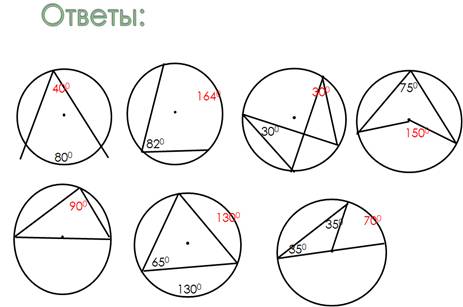
VII. Проверка самостоятельной работы.

слайд 7.