Электронное учебное пособие "Интеграл и его приложения"

Содержит краткий теоретический материал, большое количество типовых примеров, а также задачи для самостоятельного решения.

Департамент образования, науки и молодёжной политики Воронежской области

Государственное бюджетное профессиональное образовательное учреждение Воронежской области

«Воронежский техникум строительных технологий»

(ГБПОУ ВО «ВТСТ»)

МЕТОДИЧЕСКОЕ ПОСОБИЕ

по дисциплине МАТЕМАТИКА

Интеграл и его приложения

Воронеж

2017

Рассмотрено на заседании ПЦК математических дисциплин

Протокол № _____ от _____________

Председатель ПЦК _______ Болычева Т.В.

Разработана на основе Федерального государственного образовательного стандарта среднего профессионального образования для всех специальностей

1 курса

Настоящее пособие предназначено для студентов 1 курса всех специальностей и полностью соответствует программе по математике для СПО. Оно может быть использовано студентами для самостоятельного изучения раздела программы, а также преподавателем на уроке при изучении нового материала, для домашнего задания, при повторении и подготовке к контрольной работе.

Пособие включает в себя, помимо задач, краткие теоретические сведения и формулы, необходимые для решения задач указанного раздела математического анализа, подробные решения типовых примеров и задач, вопросы для самопроверки, а также упражнения для самостоятельного решения и примерный вариант контрольной работы по теме.

Автор - составитель: Сафонова Елена Артуровна, преподаватель ГБПОУ ВО

«Воронежский техникум строительных технологий»

СОДЕРЖАНИЕ

1. Введение……………………………………………………………………………...………4

2. Неопределенный интеграл и его свойства…………………………………………… 5

3. Упражнения к …………………………………………………………………………... 7

4. § 2. Нахождение неопределенных интегралов способом непосредственного……….. интегрирования……………………………………………………………………………...8

5. § 3. Выделение одной первообразной..............................................................................10

6. § 4. Интегрирование способом подстановки……………………………………...…....10

7. § 5. Определенный интеграл.……………………………………......................................12

8. 6. Вычисление площадей криволинейных фигур……………………………………….14

9. § 7. Вычисление объёма тела вращения.……………………………...............................16

10. Применение интеграла к решению технических задач.

8. Вычисление пути, пройденного телом.……………………………………………17

11. § 9. Вычисление работы, затраченной на растяжение пружины…………………...18

12. § 10. Сила давления жидкости на вертикально расположенную пластинку……18

13. Вопросы к зачёту по теме……………………………………………...………………….19

14. Задачи на повторение………………………………………………………………………20

15. Примерный вариант контрольной работы по теме «Интеграл и его приложения»…....22

16. Литература………………………………………………………………………………….23

Введение

В Концепции модернизации Российского образования подчеркивается: «Развивающемуся обществу нужны современно образованные, нравственные, предприимчивые люди, которые могут самостоятельно принимать ответственные решения в ситуации выбора, прогнозируя их возможные последствия, способные к сотрудничеству, отличаются мобильностью, динамизмом, конструктивностью, развитым чувством ответственности за судьбу страны».

Математика является фундаментальной общеобразовательной дисциплиной со сложившимся устойчивым содержанием и общими требованиями к подготовке обучающихся. В учреждениях СПО выбор целей смещается в практическом направлении, предусматривающем усиление и расширение прикладного характера изучения математики; преимущественной ориентации на алгоритмический стиль познавательной деятельности.

Раздел математики «Математический анализ» является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры современного специалиста. Этот раздел является базовым в математическом анализе, а изучение приложений производной позволяет студентам осмыслить возможность решения широкого спектра практических задач. Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке специалиста, выработку представления о роли и месте математики в современной цивилизации и в мировой культуре, умение логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.

С введением Федеральных государственных образовательных стандартов профессионального образования нового поколения меняется подход к преподаванию дисциплин общеобразовательного цикла, который предусматривает формирование новых ключевых компетенций, необходимых для современного специалиста, таких как экономическая (ориентация в современной рыночной экономике, участие в ней не только в качестве объекта – потребителя, но и субъекта – предпринимателя, менеджера, производителя товаров и услуг и т.д.) и профессиональная (ориентированность в профессии, профессиональная подготовка к выполнению в будущем социальных ролей «специалиста», «профессионала»).

В связи с этим, в данной методической разработке рассматривается большое количество примеров решения физических и технических задач, а также приёмы построения графиков различных функций. Оно может быть использовано студентами для самостоятельного изучения раздела программы, а также преподавателем на уроке при изучении нового материала, для домашнего задания, при повторении и подготовке к контрольной работе.

ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ

Неопределенный интеграл и его свойства

Актуализация изучаемого материала.

Мы знаем, что для данной функции по известным нам формулам можно найти производную, имеющую большое значение для исследования функции.

Но часто бывает необходимо решать и обратную задачу, т. е. по производной восстановить функцию, по угловому коэффициенту касательной к кривой составить уравнение самой кривой, по уравнению скорости движения найти уравнение самого движения и т.д.

Потребность отыскания функции по ее производной, а также потребность создавать общий метод для вычисления площадей, объёмов, работы и т. д. привели к созданию интегрального исчисления.

Возникновение интегрального исчисления, так же как и дифференциального относится ко II половине 17 века. И связывают его с именами английского математика и механика И. Ньютона и немецкого математика и философа Г. Лейбница. Дальнейшее развитие интегральное исчисление получило в трудах ученых различных стран. В России интегральное исчисление разрабатывали Л. Эйлер, М.В. Остроградский, П.А. Чебышев, а в последние десятилетия Н.Н. Лузин, А.Л. Хинчин, А.Н. Колмогоров и др.

1. Интегрирование и первообразная

Определение 1. Интегрированием называется действие нахождения функции по её призводной или по её дифференциалу.

Полученная при этом функция называется первообразной.

Определение 2. Первообразной функцией для данной функции f(x) называется такая функция F(x), производная (или дифференциал) которой равна f(x) (или f(x)dx), т.е. выполняется условие F′(х)=f(х).

Например: f(x)=3х², тогда F(x)=x³, т. к. F^’(x)=3x².

Но дифференциалу функции соответствует не единственная первообразная, а множество, причем они отличаются друг от друга постоянным слагаемым.

Действительно, функции F(x)= x³+5,

F(x)= x³-100

…………………

являются первообразными для функции f(x)=3x², где С - любое действительное число.

Определение 3. Совокупность всех первообразных функций F(x)+C для дифференциала f(x)dx называется неопределенным интегралом и записывается ,

где f(x) – подынтегральная функция;

f(x)dx – подынтегральное выражение;

F(x) – первообразная;

С- произвольная постоянная интегрирования.

Так, пользуясь определением неопределённого интеграла, можно записать .

Основные свойства неопределенного интеграла.

1. Дифференциал неопределенного интеграла равен подынтегральному выражению.

2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной С.

3. Постоянный множитель можно выносить за знак неопределённого интеграла.

, где ,

4. Неопределённый интеграл алгебраической суммы функций равен алгебраической сумме интегралов этих функций.

Основные формулы интегрирования

10.

11.

12.

13.

УПРАЖНЕНИЯ

1.1. Найдите первообразную функцию:

а) ;

в) ;

д)

б) ;

г);

е) .

1.2. Докажите, что F(x) является первообразной функции f(x) на указанном промежутке:

а) ;	, xR;
б) ;	, xR;
в) ;	, x(0;+∞);
г) ;	, x(0;+∞)

1.3. Для какой из данных функций f₁, f₂, f₃, f₄ функция F() является первообразной, если:

а) ;	б)

1.4. Какая из данных функций F₁, F₂, F₃, F₄ является первообразной для функции f(x):

а ) f(x)=	б)	в)

§ 2. Нахождение неопределенных интегралов способом непосредственного интегрирования

Способ непосредственного интегрирования применяется в том случае, когда для нахождения интеграла достаточно применить формулы интегрирования, свойства 3 и 4 неопределённого интеграла и простейшие алгебраические преобразования.

2.1. Проверьте справедливость равенства:

а)	в)
б)	г)

Найдите интегралы:

Пример 1. (по формуле 2 число)

Пример 2.

(свойства 1,2 и формулы 1,2)

Пример 3.

1. а) б) в) г) д)

2. а) ; б) в) г) д)

3. а) б) в) ; г) д)

4. а) б) в)

5. а)

б)

в) ;

г)

д)

е)

6. а)

б)

в)

г)

7. а) в)

г) д) е)

8. а) б) в)

9. а) б) в)

2.3. Найдите интегралы:

5. ;

10.

11.

*2.4. Найдите интегралы:

1.	5.
2.	6.
3.	7.
4.	8.

2.5. Найдите интегралы:

1.	3.	5.
2.	4.	6.

v 2.6. Найдите интегралы:

§ 3. ВЫДЕЛЕНИЕ ОДНОЙ ПЕРВООБРАЗНОЙ

Чтобы выделить из всей совокупности первообразных одну из них, нужно задать дополнительные данные или, так называемые, начальные условия, а затем:

1. Найти неопределенный интеграл от данной функции.

2. Подставив в полученную совокупность начальные условия, найти значение С.

3. Заменив в совокупности первообразных постоянную интегрирования С найденным значением, записать искомую функцию.

3.1. Найти функцию, производная которой равна , если известно, что при t=2 функция принимает значение, равное 25.

3.2. Найти функцию F(x),если и F(0)=1.

3.3. Найти , если при первообразная равна 6.

3.4. На промежутке найти такую первообразную функции , график которой проходит через точку А(1;3).

3.5. Найти уравнение линии, проходящей через точку А(2;1) и обладающей таким свойством, что угловой коэффициент касательной в каждой её точке равен абсциссе этой точки. Постройте эту линию.

3.6. Скорость тела задана уравнением . Найти уравнение пути, если к моменту отсчета времени точка прошла путь 5 м.

§ 4. ИНТЕГРИРОВАНИЕ СПОСОБОМ ПОДСТАНОВКИ

Если заданный интеграл с помощью алгебраических преобразований трудно или невозможно привести к одному или нескольким табличным интегралам, то для его нахождения применяют особые приёмы, одним из которых является способ подстановки.

Способ подстановки (замены переменной) заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя, на который всегда можно умножить или разделить подынтегральное выражение).

Пример 1. Найти интеграл:

1) Обозначим выражение через t, т.е. записываем

2) Продифференцируем (найдём дифференциалы) обе части этого выражения.

3) Выразим из этого выражения оставшуюся часть подынтегрального выражения: .

4) Подставим в интеграл и проинтегрируем.

5) Сделать обратную подстановку, т.е. вместо t подставить

Записывается следующим образом:

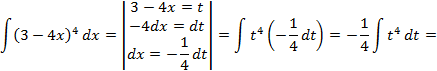
Пример 2. Найти интеграл:

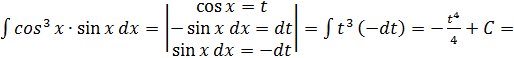
4.1. Найти интегралы способом подстановки:

1.	6.	11.
2.	7.	12.
3.	8.	13.
4.	9.	14.
5.	10.	15.

4.2. Найти интегралы:

1. ;

9. ;

10.

*4.3. Найти интегралы:

1.	3.	5.
2.	4.	6.

4.4. Найти интегралы:

1.	4.	7.
2.	5.	8.
3.	6.	9.

§ 5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Определение. Приращение любой из первообразных при изменении аргумента от до называется определенным интегралом и записывается

= ,

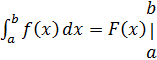где

Эта формула называется формулой Ньютона-Лейбница, и она даёт

правило вычисления определённого интеграла.

Чтобы вычислить определенный интеграл 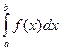нужно:

-найти соответствующий неопределенный интеграл;

-в полученное выражение вместо x подставить сначала верхний, а затем нижний пределы определенного интеграла;

-из первого результата подстановки вычесть второй, т.е. найти разность .

Основные свойства определённого интеграла

1. Постоянный множитель можно выносить за знак определённого интеграла.

2. Определённый интеграл алгебраической суммы функций равен алгебраической сумме интегралов этих функций с теми же пределами интегрирования.

3. Если пределы интегрирования определённого интеграла поменять местами, то его знак изменится на противоположный.

4. Определённый интеграл от непрерывной на отрезке

равен сумме интегралов от этой функции на отдельных частях отрезка.

Вычисление определённых интегралов

по формуле Ньютона-Лейбница

Пример. Вычислить интеграл:

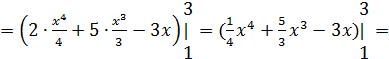
5.1. Вычислите определенный интеграл по формуле Ньютона-Лейбница:

1.	4.	7.
2.	5.	8.
3.	6.	9.

5.2. Вычислить определённые интегралы:

10.

5.3. Вычислите определённые интегралы способом подстановки:

1.	5.	9.
2.	6.	10.
3.	7.	11.
4.	8.	12.

*5.4. Вычислите интегралы:

1.	3.	5.
2.	4.	6.

6. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ КРИВОЛИНЕЙНЫХ ФИГУР.

Изобразим геометрически все элементы, входящие в определённый интеграл

y B

0 a b

где

и - прямые параллельные оси Ох;

- приращение аргумента.

Определение. Фигура ABB₁A_1,ограниченная графиком непрерывной функции , прямыми и и отрезком

оси Ох называется криволинейной трапецией.

Геометрический смысл определённого интеграла

Определённый интеграл 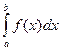геометрически даёт площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), слева и справа прямыми x=a, x=b и снизу отрезком оси OX, т. е.

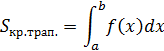
Пример. Вычислить площадь фигуры, ограниченной линиями

Решение. Изобразим графики всех перечисленных функций. Полученная фигура является криволинейной трапецией.

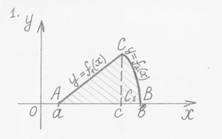
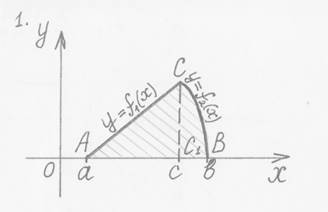
Поэтому её площадь можно найти как определённый интеграл

6.1. Вычислить площадь фигуры, ограниченной линиями:

Площадь любой плоской фигуры в прямоугольной системе координат может быть составлена из площадей криволинейных трапеций, прилегающих к оси OX (или OY).

Задачи на вычисление площадей плоских фигур решают по следующему плану:

1. Делают схематический чертёж по условию задачи.

2. Составляют формулу для вычисления площади полученной фигуры и находят пределы интегрирования из условия задачи.

3. Вычисляют площадь фигуры по составленной формуле.

6.2. Вычислить площадь фигуры, ограниченной линиями:

1. и

2 . и ,

3. и

4. и

5. и

6. и

9. и

10. ,

11. и

*6.3. Найдите площадь фигуры, ограниченной линиями:

1. ;

3. ,

§ 7. ВЫЧИСЛЕНИЕ ОБЪЁМА ТЕЛА ВРАЩЕНИЯ.

7.1. Вычислить объём тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями:

1. , , , ;

2 .

ПРИМЕНЕНИЕ ИНТЕГРАЛА К РЕШЕНИЮ ТЕХНИЧЕСКИХ ЗАДАЧ.

8. ВЫЧИСЛЕНИЕ ПУТИ, ПРОЙДЕННОГО ТЕЛОМ.

Как известно, путь, пройденный телом при равномерном движении за время , вычисляется по формуле

Если тело движется не равномерно в одном направлении и скорость его меняется в зависимости от времени , т.е. то для нахождения пути, пройденного телом за время от

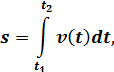
где

8.1. Скорость движения материальной точки задаётся формулой . Найти путь, пройденный точкой за первые четыре секунды движения.

8.2. Скорость движения изменяется по закону Найти путь, пройденный телом за третью секунду движения.

8.3. Скорость движения тела задана уравнением Определить путь, пройденным телом от начала движения до остановки.

8.4. Тело брошено вертикально вверх со скоростью Найдите наибольшую высоту подъёма тела.

8.5. Два тела выходят одновременно из одной точки: одно со скоростью другое – со скоростью На каком расстоянии друг от друга они окажутся через 20 секунд после начала движения, если движутся по прямой в одном направлении?

8.6. Два тела одновременно начали прямолинейное движение из одной точки в одном направлении со скоростями и Через сколько секунд после начала движения расстояние между нами будет равно 250 м?

§ 9. ВЫЧИСЛЕНИЕ РАБОТЫ, ЗАТРАЧЕННОЙ НА РАСТЯЖЕНИЕ ПРУЖИНЫ.

Согласно закону Гука, сила F необходимая для растяжения или сжатия пружины, пропорциональна величине растяжения или сжатия.

Пусть - величина растяжения или сжатия пружины. Тогда

где - коэффициент пропорциональности, зависящий от свойств пружины.

Для нахождения величины работы воспользуемся формулой:

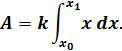
9.1. Какую работу совершает сила в 10 Н при растяжении пружины

на 0,02 м?

9.2. Сила в 60 Н достаточна для растяжения пружины на 2 см. Какую работу нужно совершить, чтобы растянуть эту пружину до длины 20 см, если первоначальная длина её равна 14 см.

9.3. Растягивая пружину на 0,04 м, произвели работу 100Дж. Какая работа будет затрачена при растяжении пружины на 0,1 м?

9.4. Для сжатия пружины на 0,03 м необходимо совершить работу 16Дж. На сколько сантиметров можно сжать эту пружину, совершив работу 144Дж?

9.5. Пружина в спокойном состоянии имеет длину 20 см. Сила в 100 Н растягивает её на 2,5 см. Какую работу надо совершить, чтобы растянуть её от длины в 25 см до 35 см?

§ 10. СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ВЕРТИКАЛЬНО РАСПОЛОЖЕННУЮ ПЛАСТИНКУ.

10.1. Определить силу давления воды на стенку шлюза, длина которой 20 м, а высота 5 м (считая шлюз доверху заполненным водой).

10.2. Вычислить силу давления воды на прямоугольную пластинку, погружённую вертикально в воду так, что верхнее основание пластинки находится на 10 см ниже поверхности воды. Если основание пластинки равно 16 см, а высота 24 см.

10.3. Цилиндрический стакан наполнен ртутью. Вычислить силу давления ртути на боковую поверхность стакана, если его высота равна 0,1 м, а радиус основания 0,04 м. (

10.4. Вычислить силу давления бензина на стенки цилиндрического бака высотой 3 м и радиусом основания 1 м (

Вопросы к зачёту по теме

1. Что такое интегрирование?

2. Что называется первообразной функцией для данной функции?

Какое при этом должно выполняться условие? Приведите примеры.

3. Сколько первообразных соответствует одному дифференциалу?

Почему?

4. Что называется неопределённым интегралом?

5. Сформулируйте и запишите свойства неопределённого интеграла, которые следуют из его определения.

6. Какие свойства необходимы для нахождения неопределённого интеграла?

7. Какие вы знаете способы нахождения неопределённого интеграла?

8. Что называется определённым интегралом?

9. Правило вычисления определённого интеграла.

10. Сформулируйте и запишите свойства определённого интеграла?

11. В чём заключается геометрический смысл определённого интеграла?

12. Какие геометрические задачи решаются с помощью интеграла?

13. Какие физические задачи решаются с помощью интеграла?

ЗАДАЧИ НА ПОВТОРЕНИЕ

1. Найти неопределенный интеграл:

1.	8.
2.	9.
3.	10.
4.	11.
5.	12.
6.	13.
7.	14.

2. Вычислить определённый интеграл:

1.	5.	9.
2.	6.	10.
3.	7.	11.
4.	8.	12.

3. Вычислите площадь фигуры, ограниченной линиями:

8 .

10.

11.

4. Вычислить объём тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями:

5. Скорость движения тела изменяется по закону Найти путь, пройденный телом за первые 4 секунды движения.

6. Найти путь, пройденный телом за 10-ю секунду, зная, что скорость его движения выражается формулой

7. Найти путь, пройденный точкой от начала движения до остановки, если его скорость

8. Два тела начали движение одновременно из одной точки в одном направлении со скоростями и На каком расстоянии друг от друга они будут через 5 секунд после начала движения?

9. Какую работу совершает сила в 8 Н при растяжении пружины на 0,06 м.

10. При растяжении пружины на 0,05 м затрачивается работа 29,43 Дж. На сколько растянется пружина, если затратить работу 9,81 Дж?

11. Пружина в спокойном состоянии имеет длину 0,15 м. Сила в 9,8 Н растягивает её на 0,02 м. Определить работу, затраченную на растяжение пружины от 0,3 м до 0,4 м.

Примерный вариант контрольной работы по теме

«Интеграл и его приложения»

1. Найти и вычислить интегралы: а) б)

2. Найти площадь фигуры, ограниченной линиями:

3. Тело движется прямолинейно со скоростью Найти путь, пройденный телом за пятую секунду.

----------------------------------------------------------------------------------------------------

4. Найти площадь фигуры, ограниченной линиями:

5. При сжатии пружины на 0,05 м затрачена работа 25 Дж. Какую работу необходимо совершить, чтобы сжать эту пружину на 0,1м?

Литература

1. Алимов Ш.А. Алгебра и начала математического анализа 10-11 классы: учебник для общеобразовательных учреждений (базовый уровень) – М.: Просвещение, 2012. – 464 с.

2. Башмаков М.И. Математика: учебник для учреждений нач. и сред.проф. образования. – М.: Издательский центр «Академия», 2010. – 256 с.

3. Валуцэ И.И., Дилигул В.Д. Математика для техникумов на базе средней школы. -М.Наука. Главная редакция физико-математической литературы, 1980. -496 с.

4. Мордкович А.Г. Алгебра и начала анализа 11 кл. в 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) – М.: Мнемозина, 2014 г. – 287 с.

5. Соловейчик И.Л., Лисичкин В.Т.Сборник задач по математике с решениями для техникумов – М.: ООО «Издательский дом «ОНИКС» 21 век» : ООО «Издательство «Мир и Образование».2011. – 462 с.

6. Математика для техникумов. Алгебра и начала анализа: Учебник. Под ред.

Г.Н. Яковлева. -3-е изд., перераб. –М.: Наука. Гл. ред. физ.-мат. лит., 1987.-464 с.

Электронное учебное пособие "Интеграл и его приложения"

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

17.12.2019