Электронное учебно-методическое пособие по математике.

Управление здравоохранения Липецкой области

Государственное автономное профессиональное образовательное учреждение

«Елецкий медицинский колледж»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Электронный образовательный ресурс.

 

Учебно – методическое пособие

по дисциплине «МАТЕМАТИКА»

для специальностей:

31. 02. 01 Лечебное дело, углубленная подготовка

34. 02. 01 Сестринское дело, базовая подготовка

33. 02. 01 Фармация, базовая подготовка

 

 

 

 

Автор:

А.А. Абреимова, преподаватель дисциплины «Математика» ГА ПОУ «Елецкий медицинский колледж»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2014 г.

МАТЕМАТИКА

 

Учебно – методическое пособие по дисциплине «Математика» для специальностей: 31. 02. 01 Лечебное дело, углубленная подготовка; 34. 02. 01 Сестринское дело, базовая подготовка; 33. 02. 01 Фармация, базовая подготовка.

 

Автор:

А.А. Абреимова, преподаватель математики ГА ПОУ «Елецкий медицинский колледж»

 

Учебно – методическое пособие по дисциплине «Математика» для специальностей: 31. 02. 01 Лечебное дело, углубленная подготовка; 34. 02. 01 Сестринское дело, базовая подготовка; 33. 02. 01 Фармация, базовая подготовка.

 

МАТЕМАТИКА: Учебно – методическое пособие по математике – ГА ПОУ «Елецкий медицинский колледж», 2014.

 

«Математика» - электронное учебно – методическое пособие для аудиторной и внеаудиторной работы по специальностям: 31. 02. 01 Лечебное дело, углубленная подготовка; 34. 02. 01 Сестринское дело, базовая подготовка; 33. 02. 01 Фармация, базовая подготовка. Содержит информацию по обучению теоретической части дисциплины «Математика».

Электронное учебно – методическое пособие составлено в соответствии с программой по математике и отвечает требованиям Федерального Государ­ственного образовательного стандарта специально­стей «Лечебное дело» углубленная подготовка, «Сестринское дело» базовая подготовка, «Фармация» базовая подготовка.

Цель пособия: оказать помощь студентам в подготовке к занятиям.

Задача сборника – дать студентам достаточный объем теоретических знаний по вопросам математики.

Материал изложен в доступной форме.

 

А.А. Абреимова, 2014

ГА ПОУ «Елецкий медицинский колледж», 2014

 

 

 

 

 

 

 

 

 

 СОДЕРЖАНИЕ ЭЛЕКТРОННОГО ОБРАЗОВАТЕЛЬНОГО РЕСУРСА.

 

№	Тема
1.	Роль и место математики в современном мире. Использование математических методов в будущей профессиональной деятельности.
2.	Производная функции, её геометрический и механический смысл. Формулы производных. Изучение производных суммы, произведения, частного функций. Обоснование производных элементарных и сложных функций, обратных функций.
3.	Изучение производных при исследовании функций и построения графиков. Определение функции нескольких переменных. Частные функции.
4.	Первообразная функция и неопределенный интеграл. Демонстрация основных свойств и формул неопределенных интегралов.  Методы интегрирования.
5.	Основные свойства определенных интегралов. Формула Ньютона – Лейбница для вычисления определенного интеграла. Вычисление определенных интегралов различными методами. Применение определенного интеграла к вычислению площади плоской фигуры, объемов тел.
6.	Составление дифференциальных уравнений на простых задачах. Решение дифференциальных уравнений с разделяющимися переменными, однородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
7.	Числовая последовательность. Пределы функций и последовательности. Обоснование сходимости и расходимости рядов. Разложение функций в ряд Маклорена. Нахождение пределов последовательности и функции в точке и на бесконечности.
8.	Числовые ряды. Сходимость и расходимость рядов. Признак Даламбера.
9.	Элементы и множества. Операции над множествами и их свойства. Графы. Элементы графов. Виды графов и операции над ними.
10.	Обоснование основных понятий комбинаторики: факториал, перестановки, размещения, сочетания.
11.	Определение вероятности события. Изложение основных теорем и формул вероятностей: теорема сложения, условная вероятность, теорема умножения, независимость событий, формула полной вероятности.
12.	Случайные величины. Дисперсия случайной величины.
13.	Математическая статистика и её связь с теорией вероятности. Основные задачи и понятия математической статистики. Определение выборки и выборочного распределения. Графическое изображение выборки. Определение понятия полигона и гистограммы.
14.	Санитарная (медицинская) статистика – отрасль статистической науки. Статистическая совокупность, её элементы, признаки.
15.	Обоснование методов обработки результатов медико – биологических исследований.
16.	Понятие о демографических показателях, расчет общих коэффициентов рождаемости, смертности. Естественный прирост населения.
17.	Определение процента. Решение трёх видов задач на проценты. Составление и решение пропорций, применяя их свойства. Расчёт процентной концентрации растворов. Газообмен в лёгких. Показатели сердечной деятельности.
18.	Расчёт прибавки роста и массы детей. Способы расчёта питания. Оценка пропорциональности развития ребенка, используя астрометрические индексы. Перевод одних единиц измерения в другие.

Тема: Роль и место математики в современном мире. Использование математических методов в будущей профессиональной деятельности.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме роль и место математики в современном мире. Использование математических методов в будущей профессиональной деятельности.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Развивать познавательный интерес к предмету на основных  достижениях науки и техники.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

·         Показать красоту математики, её роль в нашей жизни.

·         Подвести учащихся к пониманию сущности изучаемого материала.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать роль и место математики в современном мире, использование математических методов в будущей профессиональной деятельности.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Выдающийся  итальянский физик и астроном, один из основателей точного естествознания, Галилео Галилей (1564-1642) говорил, что "Книга природы написана на языке  математики". Почти через двести лет родоначальник немецкой классической философии Иммануил Кант (1742-1804) утверждал, что "Во всякой науке столько истины, сколько в ней математики". Наконец, ещё через почти сто  пятьдесят лет, практически уже  в наше время, немецкий математик  и логик Давид Гильберт (1862-1943) констатировал: "Математика - основа всего точного естествознания".

Приведенные высказывания великих  ученых дают полное представление о роли и значении математики  во всех областях жизни людей.

 

Леонардо Да Винчи –

итальянский художник, скульптор и учёный

(анатом, естествоиспытатель).

«Никакой достоверности нет в науках там,

где нельзя приложить ни одной

из математических наук, и в том,

что не имеет связи с математикой»

                                        Леонардо да Винчи

 

Пытаясь найти математическое обоснование законов природы, считая математику могучим средством познания, он применяет ее даже в такой науке, как анатомия. Леонардо изучал анатомию в ее обширном целом и со всей глубиной. С величайшей тщательностью он изучал каждую часть человеческого тела. И в этом превосходство его всеобъемлющего гения. Леонардо можно считать за лучшего и величайшего анатома своей эпохи. И, более того, он несомненно первый, положивший начало правильному анатомическому рисунку. Труды Леонардо в том виде, в каком мы имеем их в настоящее время, являются результатом огромной работы ученых, которые расшифровали их, подобрали по тематике и объединили в трактаты применительно к планам самого Леонардо.

Работа над изображением тел человека и животных в живописи и скульптуре пробудила в нем стремление познать строение и функции организма человека и животных, привела к обстоятельному изучению их анатомии.

 Во всех многообразных изысканиях Леонардо был исследователем нового в науке и искусстве. В частности, и анатомию он развил и обогатил новыми методами и исследованиями настолько, что его, несомненно, можно считать одним из зачинателей современной анатомии.

Один из современников, посетивший  Леонардо в 1517 г., писал: «Этот человек так детально разобрал анатомию человека, показав на рисунках части тела, мышцы, нервы, вены, связки и все остальное, как никто не сделал этого до него. Все это мы видели своими глазами» Преодолев все трудности, Леонардо сам занимался анатомированием и оставил подробное наставление, как производить его. Он изобрел модель из стекла для изучения клапанов сердца. Он первый стал делать распилы костей вдоль и поперек, для подробного изучения их структуры, ввел в практику зарисовку всех изучаемых им органов во время анатомирования. И этим объясняется необычайно правильное и реалистическое изображение людей и животных в его живописи и скульптуре. Точнее всего Леонардо изображает и описывает скелет, впервые совершенно правильно представляя и изображая его пропорции; он также первый точно определяет число позвонков крестца. Все анатомические изображения, сделанные до Леонардо, были условны, да и позднейшие художники не смогли превзойти Леонардо в этом искусстве. Все совершенное Леонардо в анатомии - грандиозно и явилось основой для новых величайших достижений. Леонардо стремился путем опыта выяснить функции отдельных частей человеческого тела. Изучая каждую часть, Леонардо воспринимал человеческий организм как нераздельное целое и называл его «прекрасным инструментом». Интересуясь движениями человеческого тела и тела животных, Леонардо изучал не только строение мышц, но и их двигательную способность, способы их прикрепления к скелету и особенности этих прикреплений.

Исследования Леонардо касаются  также функции мозга. Из органов чувств Леонардо наиболее подробно  занимался органом зрения, который он считал «повелителем и князем  прочих четырех чувств»; сначала  он заинтересовался зрением как  художник, вдохновенно видящий мир.  «Неужели не видишь ты, - пишет  Леонардо, - что глаз объемлет  красоту всего мира... Он направляет  и исправляет все искусства  человеческие, двигает человека  в разные части света. Он - начало  математики… Способности его несомненнейшие. Он измерил высоту и величину звезд. Он нашел элементы и их место. Он породил архитектуру и перспективу, он породил божественную живопись».

Витрувианский человек - рисунок, сделанный Леонардо Да Винчи примерно в 1490-92 годах, как иллюстрация для книги, посвященной трудам Витрувия. Рисунок сопровождается пояснительными надписями, в одном из его журналов. На нем изображена фигура обнаженного мужчины в двух наложенных одна на другую позициях: с разведенными в стороны руками, описывающими круг и квадрат. Рисунок и текст иногда называют каноническими пропорциями. При исследовании рисунка можно заметить, что комбинация рук и ног в действительности составляет четыре различных позы. Поза с разведенными в стороны руками и не разведенными ногами, вписывается в квадрат ("Квадрат Древних"). С другой стороны, поза с раскинутыми в стороны руками и ногами, вписывается в круг. И, хотя, при смене поз, кажется, что центр фигуры движется, на самом деле, пуп фигуры, который является настоящим её центром, остается неподвижным. Далее  идет описание соотношений между  различными частями человеческого  тела.

В сопроводительных записях Леонардо да Винчи указал, что рисунок был создан для  изучения пропорций (мужского) человеческого  тела, как оно описано в трактатах  античного римского архитектора  Витрувия, который написал следующее  о человеческом теле: "Природа  распорядилась в строении человеческого  тела следующими пропорциями:

- Длина четырёх пальцев равна длине  ладони.

- Четыре  ладони равны стопе.

- Шесть ладоней составляют один локоть.

- Четыре  локтя - рост человека.

- Четыре  локтя равны шагу, а двадцать четыре ладони равны росту человека.

- Если  вы расставите ноги так, чтобы расстояние между ними равнялось 1/14 человеческого  роста, и поднимите руки таким  образом, чтобы средние пальцы оказались  на уровне макушки, то центральной точкой тела, равноудаленной от всех конечностей, будет ваш пупок.

- Пространство  между расставленными ногами и полом  образует равносторонний треугольник.

- Длина вытянутых рук будет равна  росту.

- Расстояние  от корней волос до кончика подбородка равно одной десятой человеческого  роста.

- Расстояние  от верхней части груди до макушки  составляет 1/6 роста.

- Расстояние  же от верхней части груди до корней волос - 1/7.

- Расстояние  от сосков до макушки составляет ровно  четверть роста.

- Наибольшая  ширина плеч - восьмая часть роста.

- Расстояние  от локтя до кончиков пальцев - 1/5 роста, от локтя до подмышечной ямки - 1/8.

- Длина всей руки - это 1/10 роста.

- Стопа - 1/7 часть роста.

- Расстояние  от мыска ноги до коленной чашечки  равно четверти роста.

- Расстояние  от кончика подбородка до носа и  от корней волос до бровей будет  одинаково и, подобно длине уха, равно 1/3 лица."

Повторное открытие математических пропорций человеческого тела в XV веке, сделанное Леонардо Да Винчи и другими, стало одним из великих           достижений,     предшествующих итальянскому ренессансу.

Роль математического образования в профессиональной подготовке медицинских работников очень велика.

Математика  всем нужна. Наборы чисел, как ноты, могут быть мертвыми значками, а  могут звучать музыкой, симфоническим  оркестром... И медикам тоже. Хотя бы для того, чтобы грамотно прочитать  обычную кардиограмму. Без знания азов математики нельзя быть докой  в компьютерной технике, использовать возможности компьютерной томографии... Ведь современная медицина не может  обходиться без сложнейшей техники.

Процессы, происходящие в настоящее время во всех сферах жизни общества, предъявляют новые требования к профессиональным качествам специалистов. Современный этап развития общества характеризуется качественным изменением деятельности медицинского персонала, которое связано с широким применением математического моделирования, статистики и других важных явлений, имеющих место в медицинской практике.

Попытки использовать математическое моделирование  в биомедицинских  направлениях начались в 80-х гг. 19 в. Идея корреляционного анализа, выдвинутая английским психологом и антропологом  Гальтоном и усовершенствованная  английским биологом и математиком Пирсоном, возникла как результат  попыток обработки биомедицинских  данных. Начиная с 40-х гг. 20 в. математические методы проникают в медицину и биологию через кибернетику  и информатику.

Широко  применяются математические методы в биофизике, биохимии, генетике, физиологии, медицинском приборостроении, создании биотехнических  систем. Развитие математических моделей  и методов способствует: расширению области познания в медицине; появлению новых высокоэффективных методов диагностики и лечения, которые лежат в основе разработок  систем жизнеобеспечения; созданию медицинской  техники.

В последние  годы активное внедрение в медицину методов математического моделирования и создание автоматизированных, в том числе и компьютерных систем существенно  расширило возможности диагностики и терапии заболеваний. Одной из разновидностей медицинских компьютерных диагностических систем является диагностика с постановкой  конкретного диагноза  на основе имеющейся информации.

Самым активным сторонником использования статистики был основоположник военно-полевой хирургии Н. И. Пирогов (1810 – 1881). Еще в 1849г., говоря об успехах отечественной хирургии, он указывал: “Приложение статистики для определения диагностической важности симптомов и достоинства операций можно рассматривать как важное приобретение новейшей хирургии”.

Отличительная особенность статистического подхода состоит в том, что данные, характеризующие статистическую совокупность в целом, получаются в результате обобщения информации о составляющих ее объектах. Можно выделить следующие основные направления: методы сбора данных; методы измерения; методы обработки и анализа данных.

Примеры использования статистических  наблюдений в медицине. Два известных  профессора страсбургского медицинского  факультета Рамо и Саррю сделали  любопытное наблюдение относительно  скорости пульса. Сравнив наблюдения, они заметили, что между ростом  и числом пульса существует  зависимость. Возраст может влиять  на пульс только при изменении  роста, который играет в этом  случае роль регулирующего элемента. Число ударов пульса находится,  таким образом, в обратном отношении  с квадратным корнем роста.  Приняв за рост среднего человека  1,684 м, Рамо и Саррю полагают число ударов пульса равным 70. Имея эти данные, можно вычислить число ударов пульса у человека какого бы то ни было роста.

Медицинская статистика должна быть нацелена на решение наиболее выраженных современных проблем в здоровье населения. Основными проблемами здесь, как известно, являются необходимость снижения заболеваемости, смертности и увеличения продолжительности жизни населения.

Мое мнение твердо стоит на том, что медики не должны закрывать глаза хотя бы на элементарную математику, которая просто необходима для организации быстрой, четкой и качественной работы. Каждый студент должен с первого курса обучения отметить для себя значение математики. И понять, что не только в работе, но и в повседневной жизни эти знания важны и намного упрощают жизнь.

 

Контрольные вопросы:

1.     Какова роль математики в современном мире?

2.     Какие математические методы используются в  медицине?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Производная функции, её геометрический и физический смысл. Формулы производных. Производные суммы, произведения, частного функций. Производные элементарных и сложных функций, обратных функций.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме производная функции, её геометрический и физический смысл, производные суммы, произведения, частного функций, производные элементарных и сложных функций, обратных функций. 

·         Развить наглядно-образное мышление и внимание при работе с графиками функций.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятие производной функции, её геометрический и физический смысл.

 

План урока:

1.Ознакомление с темой урока и планом урока

2.Изучение нового материала.

 

Ход урока:

Пусть x – аргумент функции f(x) и ∆ х - малое число, отличное от нуля.

 

∆ х (читается «дельта икс») называют приращением аргумента функции. На рисунке красной линией показано изменение аргумента от значения x до значения х + ∆ х (отсюда видна суть названия «приращение» аргумента).

 

При переходе от значения аргумента х₀ к х₀ + ∆ х  значения функции изменяются соответственно от f(x₀)  до f(x₀+ ∆ х) при условии монотонности функции на отрезке [х₀; х₀ + ∆ х]. Разность f(x₀+ ∆ х) - f(x₀) = ∆ f(x)    называют приращением функции f(x), соответствующем данному приращению аргумента. На рисунке приращение функции показано синей линией.

 

 

 

 

 

 

 

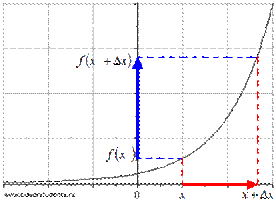
Определение производной функции в точке.

Пусть функция f(x) определена на промежутке (a; b), - х₀ и х₀ + ∆ х точки этого промежутка.

Производной функции f(x) в точке х₀ называется предел отношения приращения функции к приращению аргумента при ∆ х → 0 .

 Обозначается                .

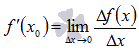Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.

Функцию f(x) называют дифференцируемой в точке х₀, когда она имеет в ней конечную производную.

Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке f '(x), то есть, мы имеем возможность определить новую функцию f '(x), которую называют производной функции f(x) на интервале (a; b).

Операция нахождения производной называется дифференцированием.

Проведем разграничения понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.

Пусть на некотором промежутке Х определена некоторая функция y =  f(x)_.

Вычисление производной функции y =  f(x) производится по общему правилу дифференцирования:

1.     Придавая аргументу Х приращение ∆ х и подставляя в выражение функции вместо аргумента  наращенное значение х + ∆ х, находим наращенное значение функции: y + ∆y = f (х + ∆ х).

2.     Вычитая из наращенного значения функции ее первоначальное значение, находим приращение функции:  ∆y = f (х + ∆ х) - f(x).

3.     Делим приращение функции ∆y на приращение аргумента ∆ х, т.е. составляем отношение:

.

4.     Находим предел этого отношения при ∆ х → 0:

.

Этот предел и есть производная от функции y =  f(x).

 

Итак: Производной функции f(x) в точке х=х₀ называется отношение приращения функции ∆f в этой точке к приращению ∆x аргумента, при стремлении последнего к нулю.

.

Нахождение производной называется дифференцированием.

 

 

 

 

 

 

 

 

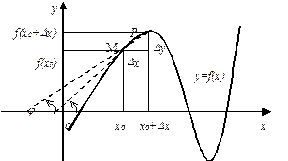
         Пусть f(x) определена на некотором промежутке (a, b). Тогда  тангенс угла наклона секущей МР к графику функции.

,

где a - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

         Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

         Уравнение касательной к кривой:  

         Уравнение нормали к кривой: .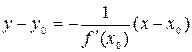

Фактически производная функции показывает скорость изменения функции, т.е. как изменяется функция при изменении переменной.

        

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

         Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение. 

 

Геометрический смысл производной.

Рассмотрим график функции  y = f (x):

 

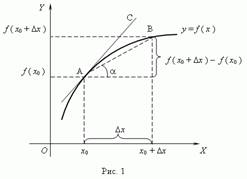
Из рисунка  видно, что для любых двух точек A и B графика функции:

 

                                             f (X₀ + ) - f (X₀)

                                            ________________ = tg α,

                                                          

 

где   - α угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то ∆x  неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

 

Контрольные вопросы:

1.     Сформулируйте определение производной.

2.     В чем заключается геометрический смысл производной?

3.     В чем заключается физический смысл производной?

 

 

 

 

 

 

Тема:  Изучение производных при исследовании функций и построения графиков. Определение функции нескольких переменных. Частные функции.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме изучение производных при исследовании функций и построения графиков, определение функции нескольких переменных, частные функции.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятие производных при исследовании функций и построения графиков, определение функции нескольких переменных, частных функции.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Схема полного исследования функции

Ниже приведена полная схема исследования функции (или алгоритм исследования функции) по пунктам. Часть из этих шагов обычно опускается при исследовании функции, в зависимости от вида функции и требований к решению (например, для многочлена можно не проверять наличие асимптот или точек разрыва и т.п.).

1)         Найти область определения функции.

2)         Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы.

3)         Исследовать непрерывность функции, выделить особые точки (точки разрыва).

4)         Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.

5)         Найти точки пересечения с осями координат.

6)         Найти нули функции. Найти интервалы знакопостоянства функции.

7)         Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.

8)         Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается.

9)         Найти первую производную. Найти точки экстремума (локального минимума и максимума) и интервалы монотонности (возрастания и убывания) функции.

10)     Найти вторую производную. Найти точки перегиба и интервалы выпуклости-вогнутости.

11)     Найти наклонные/горизонтальные асимптоты функции.

12)     Исследовать поведение функции на бесконечности.

13)     Построить график функции. Построить асимптоты.

14)     Отметить важные точки на графике.

 

Определение функции нескольких переменных.

Определение.  Если каждой совокупности значений "n" переменных  (х₁, х₂, …, х_n) из некоторого множества D этих совокупностей соответствует своё единственное значение переменной z, то говорят, что на множестве D задана функция z = f (х₁, х₂, …, х_n) "n" переменных.

 Множество D, указанное в определения, называется областью определения или областью существования этой функции.

 

 Если рассматривается функция двух переменных, то совокупности чисел (х₁, х₂) обозначаются, как правило, (x, y) и интерпретируются как точки координатной плоскости Oxy, а область определения функции z = f (x, y) двух переменных изобразится в виде некоторого множества точек на плоскости Oxy.

 

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δ_х z = f(x + Δх, y) - f(x,y)  – это частное приращение функции z по аргументу x; Δ_у z = f(x, y + Δу) - f(x,y)   – это частное приращение функции z по аргументу у.

Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:

Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

 

Контрольные вопросы:

1. Приведите схему полного исследования функции.

2. Сформулируйте определение функции нескольких переменных.

3. Сформулируйте определение частных функций.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Первообразная функция и неопределенный интеграл. Основные свойства неопределенных интегралов.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме первообразная функция и неопределенный интеграл, основные свойства неопределенных интегралов. 

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация.

 

Прогнозируемый результат:

·         Знать и понимать понятие первообразной функции и неопределенного интеграла.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала

 

Ход урока:

Определение: функция F(x), называется первообразной функцией для функции f(x), если

                                       F ' (x) = f (x).

Если F(x) есть первообразная для функции f(x), то все первообразные этой функции имеют вид F(x) + С и этот вид называется общим  выражением  первообразной.

 

 

 

 

 

 

 

 

 

 

Таблица первообразных.

Первообразная имеет простой геометрический смысл – первообразная есть функция, которая имеет заданный закон f(x) изменения тангенса угла наклона касательной к графику функции F(x).

 Определение: Отыскание первообразной функции – операция, обратная дифференцированию, ее называют также интегрированием.

Определение: Совокупность всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается

∫  f (x) dx = F(x) + C.

 ∫  - называется знаком интеграла,  f (x)dx – подынтегральным выражением, f (x) – подынтегральной функцией,  dx – дифференциал независимой переменной, переменная  х называется аргументом интегрирования.

Геометрически неопределённый интеграл представляет собой семейство графиков первообразных, получившихся друг из друга параллельным сдвигом вдоль оси ординат.

Основные свойства неопределённого интеграла.

1.Производная неопределённого интеграла равна подынтегральной функции:

(∫ f (x) dx)' = f(x).

2.Дифференциал неопределённого интеграла равен подынтегральному выражению:

d∫ f(x) dx = f(x) dx.

3. Неопределённый интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянной:

∫ d F(x)  = F(x) + С, или ∫ F'(x)  = F(x) + С.

4.Постоянный множитель можно выносить за знак неопределённого интеграла:

∫ a f(x) dx = a ∫ f(x) dx, где a- const.

5.Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов:

∫ [f(x) + g(x) - u(x)] dx = ∫ f(x) dx +  ∫ g(x) dx - ∫ u(x) dx.

6.Если f(x) есть первообразная функции f(x), то

∫ f (ax + b) dx = 1/ a · F(ax + b) + С.

На основании определения неопределённого интеграла, правил интегрирования и таблицы производных элементарных функций можно составить таблицу основных неопределённых интегралов.

Основные неопределенные интегралы.

 

Методы интегрирования.

1.Непосредственное интегрирование: способ вычисления неопределённых интегралов с помощью тождественных преобразований подынтегральной функции.

Пример: ∫ (4 х ³ ) dx = 4 ∫ х ³ dx = х ⁴ + С.

2.Интегрирование методом замены переменной (подстановки).

3.Интегрирование по частям.

 

Контрольные вопросы:

1. Сформулируйте определение первообразной.

2. Какие первообразные вы знаете?

3. Как называется операция, обратная дифференцированию?

4. Сформулируйте определение неопределенного интеграла.

5. Какие методы интегрирования вы знаете?

 

 

 

 

Тема: Основные свойства определенных интегралов. Формула Ньютона – Лейбница для вычисления определенного интеграла. Вычисление определенных интегралов различными методами. Применение определенного интеграла к вычислению площади плоской фигуры, объемов тел.

 

Цели урока:

·         Выработать у учащихся навыки использования теории нахождения площади криволинейной трапеции, объёмов тел при решении разнообразных задач.

·         Развить коммуникативные навыки при оперировании математическими понятиями сформулировать целостную систему полученных знаний.

·         Уметь вычислять площадь фигуры, ограниченной линиями, строить графики в координатной плоскости, выполняя их преобразования, находить конкретную первообразную в указанной точке.

·         Развитие познавательных интересов, самостоятельности, логической мыслительной деятельности, коммуникативных качеств.

·         Мотивировать к учебной деятельности, прививать любовь к предмету, через различные виды деятельности.

·         Воспитать аккуратность при записи в тетради.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать основные свойства определенных интегралов, формулу Ньютона – Лейбница для вычисления определенного интеграла, вычислять определенный интеграл различными методами, применять определенный интеграл к вычислению площади плоской фигуры, объемов тел.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала

 

Ход урока:

Определение. Если функция  F (x)  является первообразной для  f (x)    на отрезке    [a, b] , то число равное разности   F (a) – F (b)      называется определённым интегралом от функции    f (x)    на отрезке   [a, b]     и обозначается:

Числа a, b  называются, соответственно, нижним и верхним пределом интегрирования.

        Таким образом, по определению

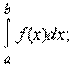
        Последняя формула носит название формулы Ньютона-Лейбница. Заметим, что значение определённого интеграла не зависит от выбора первообразной.

Основные свойства определённого интеграла.

1.Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

2.При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

3.Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

4.Постоянный множитель можно выносить за знак определенного интеграла.

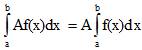
5.Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

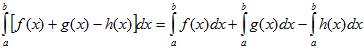
Вычисление площади криволинейной трапеции с помощью формулы Ньютона – Лейбница.

Рассмотрим непрерывную функцию  y = f (x), заданную на отрезке [ a, b ] и сохраняющую на этом отрезке свой знак.

 Фигура, ограниченная графиком этой функции, отрезком [a, b] и прямыми  x = a и x = b, называется криволинейной трапецией.

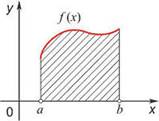
Если f – непрерывная, неотрицательная функция на отрезке [a, b], и F – её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a, b]:  S =  F (b) – F (a)

 

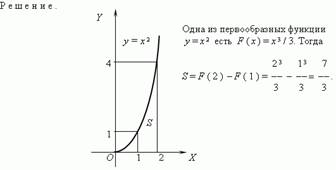
Пример. Найти площадь фигуры, ограниченной кривой  y = x² и прямыми  y = 0,  x = 1,  x = 2.

 

 

 

 

 

 

 

 

 

Вычислить объем тела вращения с помощью определенного интеграла.

Помимо нахождения площади плоской фигуры с помощью определенного интеграла важнейшим приложением темы является вычисление объема тела вращения.

Представьте некоторую плоскую фигуру на координатной плоскости. Данную фигуру можно вращать двумя способами:

– вокруг оси абсцисс;

– вокруг оси ординат.

 

Вычисление объема тела, образованного вращением плоской фигуры вокруг оси ОХ.

Пример 1

Вычислить объем тела, полученного вращением фигуры, ограниченной линиями y = 2x + x²,  y = 0, вокруг оси  ОХ.

 

Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости  необходимо построить фигуру, ограниченную линиями y = 2x + x²,  y = 0, при этом не забываем, что уравнение  задаёт ось ОХ.

 

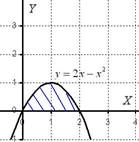
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси ОХ. В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси. Как вычислить объем тела вращения?

Объем тела вращения можно вычислить по формуле:

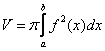
Объем тела вращения всегда неотрицателен.

Вычислим объем тела вращения, используя данную формулу:

 

 

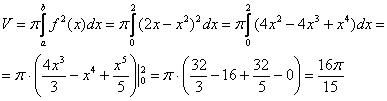
Ответ:

В ответе нужно обязательно указать размерность – кубические единицы.

 

Вычисление объема тела, образованного вращением плоской фигуры вокруг оси OY.

Пример 2

Дана плоская фигура, ограниченная линиями:

y = 3 + √x,  y = 3 -  √x,  y = x + 1.

Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси OY.

 

Решение: Выполним чертёж:

 

 

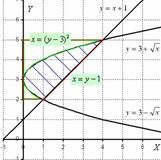
Фигура, заштрихованная синим цветом, вращается вокруг оси OY.

Для нахождения объема тела вращения будем интегрировать по оси OY.

Сначала нужно перейти к обратным функциям.

Как перейти к обратным функциям? Грубо говоря, нужно выразить «икс» через «игрек».

Разберемся с параболой:

Убедимся, что такую же  функцию можно вывести из нижней ветки:

С прямой всё проще:

Очевидно, что объем тела вращения, следует найти как разность объемов.

Вращаем фигуру, обведенную красным цветом, вокруг оси OY, в результате получается усеченный конус. Обозначим этот объем через V₁

Вращаем фигуру, обведенную зеленым цветом, вокруг оси OY и обозначаем через V₂ объем полученного тела вращения.

Объем фигуры равен разности объемов V =  V₁ - V₂.

Используем  формулу для нахождения объема тела вращения:

 

 

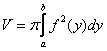
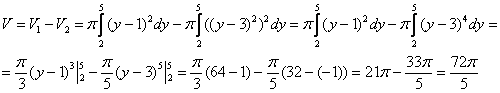
Ответ:

 

Контрольные вопросы:

1. Сформулируйте определение определенного интеграла.

2. Сформулируйте основные свойства определенного интеграла.

3. Определите алгоритм нахождения площади криволинейной трапеции с помощью определенного интеграла.

4. Определите алгоритм нахождения объема тел с помощью определенного интеграла.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Составление дифференциальных уравнений на простых задачах. Решение дифференциальных уравнений с разделяющимися переменными, однородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме составление дифференциальных уравнений на простых задачах, решение дифференциальных уравнений с разделяющимися переменными, однородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. 

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятие дифференциального уравнения.

 

План урока:

1.  Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Задачи, приводящие к понятию дифференциальных уравнений.

   Многие процессы в природе можно описать с помощью функции. Дифференциальное исчисление позволяет по данной функции исследовать ее свойства. Не менее важна и обратная задача: по данным свойствам функции найти эту функцию. Иными словами, исследуя процесс, найти функцию, которая его описывает.

   В алгебре для нахождения неизвестных величин пользуются уравнениями: по условию задачи составляют соотношение, связывающее неизвестную величину с данными и, решая его, находят неизвестную. Аналогично в анализе для нахождения неизвестной функции по данным ее свойствам составляют уравнение, связывающее неизвестную величину с величинами, задающими ее свойство. Поскольку свойства выражаются через производные или дифференциалы того или иного порядка, приходят к соотношению, связывающему функцию, ее производные или дифференциалы. Это соотношение называется дифференциальным уравнением, решая его, находят искомую функцию.

   Рассмотрим задачу, приводящую к понятию дифференциального уравнения.

Задача. На плоскости XOY найти кривую, которая в каждой своей точке имеет касательную, образующую с положительным направлением оси Ox угол, тангенс которого равен удвоенной абсциссе точки касания.

Решение. Пусть уравнение искомой кривой y = f (x).

 

 

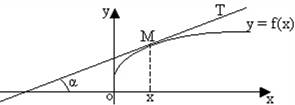
Обозначим через α угол, образованный касательной МТ с положительным направлением оси Ох. Как известно, угловой коэффициент касательной МТ есть tg α, и он равен производной от y по x, так что:  tg α = y '       (1.1)

С другой стороны, по условию задачи имеем: tg α = 2x.       (1.2)

Приравнивая значения tg α, определяемые формулами (1.1) и (1.2) получим: y ' = 2x.       (1.3)

Решением дифференциального уравнения (1.3) является любая первообразная для функции 2x. Например, решением будет: y = x².       (1.4)

Как известно из интегрального исчисления, все первообразные для функции 2x и, следовательно, все решения дифференциального уравнения (1.3) даются формулой: y = x² + С,       (1.5)

где С — произвольная постоянная.

Дифференциальное уравнение имеет бесчисленное множество решений, т.е. условию задачи удовлетворяет не одна кривая, а целое семейство кривых — парабол. Но если в условие задачи добавить точку M₀ (x₀, y₀), через которую проходит искомая кривая, то получим единственную кривую. Для этого достаточно заменить в уравнении (1.5) координаты x и y координатами точки M₀: y₀ = x² + С.       (1.6)

и, найдя из полученного уравнения значение произвольной постоянной С, подставить его в уравнение (1.5). Выполняя указанные выкладки, имеем:

            С = y₀ – x₀², y = x² – x₀² + y₀.

Таким образом, искомой кривой будет парабола: y = x² – x₀² + y₀.

 

Основные понятия и определения.

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

F (x,y,y') = 0, F (x,y,y") = 0, F (x,y,y',y",.., y(n)) = 0

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Решением дифференциального уравнения называется такая функция y = φ(x), которая обращает это уравнение в тождество.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.

Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.

Общим решением дифференциального уравнения называется функция вида y = φ (x, С₁, С₂, … С_n) в которую входит столько независимых произвольных постоянных, каков порядок уравнения.

Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

 

Дифференциальные уравнения первого порядка.

Основные понятия.

Дифференциальным уравнением первого порядка называется уравнение вида F (x,y,y') = 0.

В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.

Уравнение y' = f (x,y) называется уравнением первого порядка, разрешённым относительно производной.

Общим решением дифференциального уравнения первого порядка называется функция вида y = φ (x, С), которая содержит одну произвольную постоянную.

 

Дифференциальные уравнения с разделяющимися переменными.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y' = f(x)g(y) или через дифференциалы , где f(x)  и g(y)– заданные функции.

Для тех y, для которых , уравнение y'=f(x)g(y) равносильно уравнению,  в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y'=f(x)g(y) разделим переменные».

Уравнение вида  называется уравнением с разделёнными переменными.

Проинтегрировав обе части уравнения  по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций  и f(x), C произвольная постоянная.

 

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными:

1. Производную функции переписать через её дифференциалы  

2. Разделить переменные.

3. Проинтегрировать обе части равенства, найти общее решение.

4. Если заданы начальные условия, найти частное решение.

 

Линейные дифференциальные уравнения первого порядка.

Линейным дифференциальным уравнением первого порядка называется уравнение вида y' = f(x)y + g(x)

где f(x) и g(x) - некоторые заданные функции.

Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид:  y' = f(x)y

Если  то уравнение y' = f(x)y + g(x) называется неоднородным.

 

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y" + py' +qy = 0, где p и q - постоянные величины.

 

Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:

 

1. Записать дифференциальное уравнение в виде: y" + py' +qy = 0.

2. Составить его характеристическое уравнение, обозначив y" через r², y'  через r, y через 1: r² + pr +q = 0

3.Вычислить дискриминант  D = p² -4q и найти корни характеристического уравнения, при этом если:

а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня . Общее решение дифференциального уравнения выражается в виде , где C₁ и C₂ - произвольные постоянные.

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни . Общее решение дифференциального уравнения выражается в виде 

в) D < 0; следовательно, характеристическое уравнение имеет комплексные корни,  Общее решение дифференциального уравнения выражается, в виде

 

Контрольные вопросы:

1. Сформулируйте определение дифференциального уравнения.

2. Сформулируйте определение дифференциального уравнения первого порядка.

3. Сформулируйте определение дифференциального уравнения с разделяющимися переменными.

4. Определите алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными.

5. Сформулируйте определение линейного дифференциального уравнения первого порядка.

6. Сформулируйте определение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.

7. Определите алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Числовая последовательность. Пределы функций и последовательности. Обоснование сходимости и расходимости рядов. Разложение функций в ряд Маклорена. Нахождение пределов последовательности и функции в точке и на бесконечности.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме числовая последовательность, пределы функций и последовательности, сходимость и расходимость рядов, разложение функций в ряд Маклорена, нахождение пределов последовательности и функции в точке и на бесконечности.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятие числовой последовательности, предела функций и последовательности.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Рассмотрим ряд натуральных чисел: 1,  2,  3, … ,  n –1,  n, … .

Если заменить каждое натуральное число  n  в этом ряду некоторым числом  u_n , следуя некоторому закону, то мы получим новый ряд чисел:          

u₁ ,   u₂ ,   u₃ , …,   u _{n - 1} ,   u_n  , …,   кратко обозначаемый { u_n } и называемый числовой последовательностью. Величина  u_n называется общим членом  последовательности. Обычно числовая последовательность задаётся некоторой формулой  u_n = f (n), позволяющей найти любой член последовательности по его номеру  n - эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов.

 Примеры числовых последовательностей:

                         1,  2,  3,  4,  5, … -  ряд натуральных чисел;

                         2,  4,  6,  8,  10, … - ряд чётных чисел;

Последовательности могут быть конечными и бесконечными, возрастающими и убывающими.

 

Способы задания последовательностей.

1.     Аналитический способ: задаёт последовательность с помощью формулы n-ного члена. Это позволяет вычислить член с любым заданным номером.

2.     Рекуррентный способ: формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro– возвращаться).

 

Пределы функций и последовательности.

Определение: Предел функции (предельное значение функции) в заданной точке — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке:

                                                          

Свойства

(об арифметических действиях):

Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

 

Расширенное правило суммы

 

 

Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

 

 

Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

 

 

 Предел произведения

 Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):

 

 Расширенное правило произведения

 

 

Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

 

 

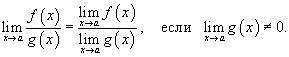
Предел степенной функции

 

 

 Предел показательной функции

 

 где основание a > 0.

 

 Предел логарифмической функции

 

 где основание a > 0.

 

Определение: Предел числовой последовательности — предел последовательности элементов числового пространства:

Свойства

(об арифметических действиях):

 

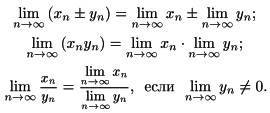
Сходимость и расходимость рядов.

Определение: Если  предел существует и конечен, то говорят, что числовой ряд сходится, а само значение предела, называют суммой числового ряда. Если этот предел не существует или бесконечен, то говорят, что числовой ряд расходится.

Разложение функций в ряд Маклорена.

Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора: 

 

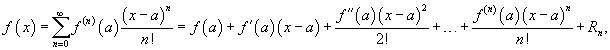
 где R_n − остаточный член. 

  Если приведенное разложение сходится в некотором интервале x, т.е.,

 

то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.

 

 Если a = 0, то такое разложение называется рядом Маклорена:

 

 

 

Примеры разложения функций в ряд Маклорена:

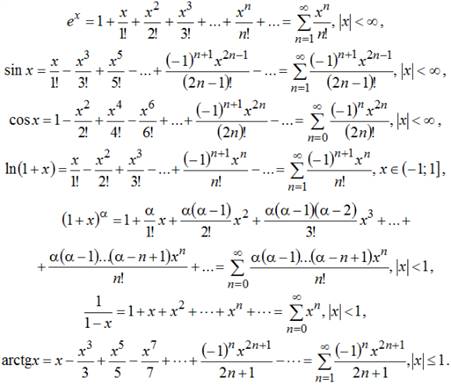
Нахождение пределов последовательности и функции

в точке и на бесконечности.

Общий алгоритм решения пределов.

1. Присвоить переменной в выражении после знака предела значение, к которому она стремится.

2. Если выражение после знака предела содержит сумму, произведение и/или частное – применить свойства о пределе суммы, произведения и частного.

3. Перейти к пункту 6.

4. Если выражение после знака предела представляет собой дробь и после присвоения переменной значения, к которому она стремится, знаменатель дроби обращается в нуль, преобразовать выражение, применив такие приёмы, как разложение выражений числителя и знаменателя на множители, формулам сокращенного умножения, сокращение дробей, умножение числителя и знаменателя на сопряженное выражение. После преобразования перейти к пункту 6.

5. Если выражение после знака предела после подстановки переменной значения, к которому она стремится, принимает неопределённость вида  или неопределённость вида , применить действия, перечисленные в пункте 4. Затем перейти к пункту 6.

6. Вычислить выражение и записать ответ.

 

Контрольные вопросы:

1. Сформулируйте определение предела функции.

2. Сформулируйте свойства предела функции.

3. Сформулируйте определение предела числовой последовательности.

4. Сформулируйте свойства предела числовой последовательности.

5. Сформулируйте общий алгоритм решения пределов.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Числовые ряды. Сходимость и расходимость рядов. Признак Даламбера.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме  числовые ряды, сходимость и расходимость рядов, признак Даламбера.

·         Развить наглядно-образное мышление и внимание.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятие числового ряда, сходимости и расходимости рядов, признак Даламбера.

 

План урока:

·                     Ознакомление с темой урока и планом урока.

·                     Изучение нового материала.

 

Ход урока:

Определение ряда и его сходимость.

Определение 1. Пусть задана бесконечная числовая последовательность u₁, u₂,…,u_n,…. Выражение:

    (1)

называется числовым рядом. Числа u₁, u₂,…,u_n,… называются первым, вторым, …, n-м, … членами ряда. u_n также называется общим членом ряда.

 

Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:

Определение 3. Если существует конечный предел  то он называется суммой ряда (1), а ряд (1) называется сходящимся. Если  не существует или равен бесконечности, то ряд (1) называется расходящимся и суммы не имеет.

 

Простейшие свойства числовых рядов.

Теорема 1. Если сходится ряд, полученный из ряда (1) отбрасыванием нескольких его членов, то сходится и ряд (1). Обратно, если сходится данный ряд (1), то сходится ряд, полученный из ряда (1) отбрасыванием нескольких членов.

Другими словами: на сходимость ряда не влияет отбрасывание конечного числа его членов.

 

Теорема 2. Если ряд (1) сходится и его сумма равна S, то ряд

,         (2)

где с – число, также сходится и его сумма равна c^.S.

 

Теорема 3. Если ряды

и

    (3)

сходятся и их суммы равны соответственно  и S, то ряды

   (4)

и

(u₁-v₁)+ (u₂-v₂)+…+ (u_n-v_n)+…        (5)

также сходятся и их суммы равны соответственно +S и  -S.

 

Теорема (необходимый признак сходимости ряда). Если ряд сходится, то  u_n=0.

Следствие. Если u_n≠0, то ряд u₁+u₂+…+u_n… расходится.

Пример.

Ряд  расходится, так как

u_n=.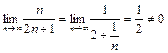

Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что u_n=0 не следует, что ряд сходится.

 

Достаточные признаки сходимости знакоположительных числовых рядов.

Определение 4. Числовой ряд называется знакоположительным, если u_n>0 при всех n=1,2,3… .

 

Теорема 4 (Признак сравнения).

Пусть даны два знакоположительных числовых ряда

       (6)

   (7)

причём u_n ≤ v_n при любых n=1,2,… .

Тогда:      Если ряд (7) сходится, то сходится и ряд (6);

                    Если ряд (6) расходится, то расходится и ряд (7).

 

Теорема 5 (Признак Даламбера).

Пусть дан знакоположительный числовой ряд

         (8)

и пусть существует предел  При p<1 ряд (8) сходится, при p>1 ряд (8) расходится.

 

Контрольные вопросы:

1. Сформулируйте определение числового ряда и его сходимости.

2. Сформулируйте свойства числового ряда.

3. Сформулируйте признак Даламбера.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Элементы и множества. Операции над множествами и их свойства. Графы. Элементы графов. Виды графов и операции над ними.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме элементы и множества, операции над множествами и их свойства, графы, элементы графов, виды графов и операции над ними.

·         Развить наглядно-образное мышление и внимание при работе с операциями над множествами.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятия  элементов и множеств, графов.

 

План урока:

1.                                         Ознакомление с темой урока и планом урока.

2.                                         Изучение нового материала.

 

Ход урока:

Элементы и множества. Операции над множествами и их свойства.

Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись  a  R  означает, что элемент  а  принадлежит множеству R , то есть  а  является элементом множества R . В противном случае, когда  а  не принадлежит множеству  R , пишут  a R .  

 

Два множества А и В называются  равными (А = В), если они состоят из одних и тех же элементов, то есть каждый элемент множества  А  является элементом множества  В  и наоборот, каждый элемент множества  В  является элементом множества  А.

 

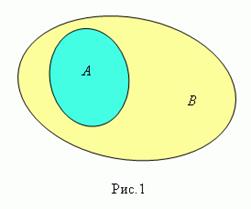
Говорят, что множество А содержится в множестве В ( рис.1 ) или  множество А  является подмножеством множества  В (в этом случае пишут А В), если каждый элемент множества  А одновременно является элементом множества  В. Эта зависимость между множествами называется  включением. Для любого множества  А имеют место включения:  А  и  А  А .

Сумма (объединение) множеств  А и В (пишется  А  В) есть множество элементов, каждый из которых принадлежит либо А, либо В. Таким образом,  е А  В  тогда и только тогда, когда либо  е А,  либо  е В.  

 

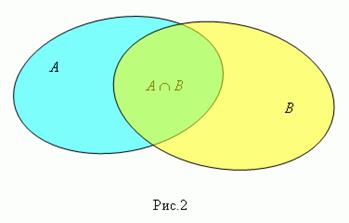
Произведение (пересечение) множеств  А и В (пишется  А  В, рис.2) есть множество элементов, каждый из которых принадлежит и А, и В. Таким образом,  е А В  тогда и только тогда, когда   е А  и  е В.

Разность множеств А и В (пишется  А – В, рис.3) есть множество элементов, которые принадлежат множеству А, но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

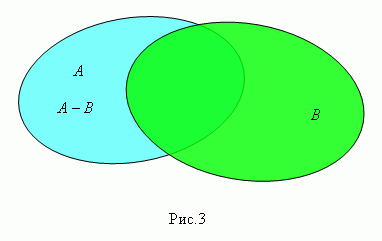
Симметричная разность множеств А и В (пишется  А \ В) есть множество: 

А \ В  = (А – В )   (В – А).

 

 Свойства операций над множествами:

Примеры: 

1. Множество детей является подмножеством всего населения.

2. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.

3. Объединением множества рациональных чисел с множеством иррациональных чисел является множество действительных чисел.

4. Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.

 

Графы. Элементы графов. Виды графов и операции над ними.

Введение.

Теория графов в качестве дисциплины может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами (изучение объектов).

 

Начальные понятия теории графов.

Графы являются существенным элементом математических моделей в самых разнообразных областях науки и практики. Они помогают наглядно представить взаимоотношения между объектами или событиями в сложных системах. Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.

 

Определение графа.

Для описания строения различных систем, состоящих из связанных между собой элементов, часто используют графические схемы, изображая элементы точками (кружками, прямоугольниками и т.д.), а связи между ними - линиями или стрелками, соединяющими элементы. При этом получаются диаграммы вроде тех, что показаны на рис. 1.1.

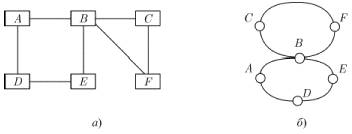
Рис. 1.1.

На таких диаграммах часто ни способ изображения элементов, ни форма или длина линий не имеют значения - важно лишь, какие именно пары элементов соединены линиями. Если посмотреть внимательно, то можно заметить, что рисунки (1.1 а) и (1.1 б) изображают одну и ту же структуру связей между элементами A, B,  C, D, Е, F.

Граф состоит из двух множеств - множества вершин и множества ребер, причем для каждого ребра указана пара вершин, которые это ребро соединяет. Вершины и ребра называются элементами графа. Конечные графы - графы, у которых оба множества конечны.

 

Операции над графами.

Для получения новых графов можно использовать разнообразные операции. Рассмотрим два вида операций:

1.) Локальные - заменяются, удаляются или добавляются отдельные элементы графа;

2.) Алгебраические - новый граф строится по определенным правилам из нескольких имеющихся.

 

Контрольные вопросы:

1. Сформулируйте определение операций над множествами и их свойства, приведите примеры.

2. Сформулируйте определение графа.

3. Сформулируйте определение операций над графами.

 

 

 

 

 

 

 

 

Тема:  Обоснование основных понятий комбинаторики: факториал, перестановки, размещения, сочетания.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме основные понятия комбинаторики: факториал, перестановки, размещения, сочетания.

·         Развить наглядно-образное мышление и внимание при работе с операциями над множествами.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Осуществить межпредметные связи с физикой, геометрией.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятия  комбинаторики: факториал, перестановки, размещения, сочетания.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Комбинаторикой называется раздел математики, в котором исследуется, сколько различных комбинаций (всевозможных объединений элементов), подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.

Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать».

Определение: Группы, составленные из каких – либо элементов, называются соединениями.

  Различают три основных вида соединений: размещения, перестановки и сочетания.

  Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными.

Определение: Размещениями из n элементов по k (k < или = n) называются такие соединения, которые отличаются друг от друга либо сами элементами (хотя бы одним), либо порядком их следования.

  Число размещений из n элементов по k обозначаются   А _n^k    (читается: «А из n по k»).

Формула вычисления:                

            А _n^k   = n · (n – 1) · (n – 2) · … · (n – (k – 1)).

 

Определение: комбинации из n-элементов, отличающихся друг от друга только порядком расположения в них элементов, называются перестановками из n элементов.

Перестановки из n элементов обозначают P_n и вычисляют по формуле: P_n=n!

n!=1 · 2 · 3 · 4 · … · n (n факториал)

Свойство: 0!=1

Задача: Сколькими способами могут разместиться 5 пассажиров в пятиместной каюте?

Решение: P₅ = 5! = 1 · 2 · 3 · 4 · 5 = 120

С использованием формулы Р_n = n! выражению А _n^k = n · (n – 1) · (n – 2) · … · (n – (k – 1)) можно придать вид:

 

Определение: Сочетаниями из n элементов по k называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.

 Число сочетаний из n элементов по k обозначают   С _n^k    (читается: «С из n по k»).

Число сочетаний из n элементов по k вычисляется по формуле:

                    n!

С _n^k    =

              k! (n – k)!

 

Контрольные вопросы:

1. Сформулируйте определение размещения.

2. Сформулируйте определение перестановки.

3. Сформулируйте определение сочетания

 

 

 

 

 

 

 

 

 

 

 

Тема:  Определение вероятности события. Изложение основных теорем и формул вероятностей: теорема сложения, условная вероятность, теорема умножения, независимость событий, формула полной вероятности.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме определение вероятности события, изложение основных теорем и формул вероятностей: теорема сложения, условная вероятность, теорема умножения, независимость событий, формула полной вероятности.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятия  вероятности события, основные теоремы и формулы вероятностей: теорема сложения, условная вероятность, теорема умножения, независимость событий, формула полной вероятности.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Случайные события, вероятность события.

Изучение каждого явления в порядке наблюдения или производства опыта связано с осуществлением некоторого комплекса условий (испытаний). Всякий результат или исход испытания называется СОБЫТИЕМ.

Если событие при заданных условиях может произойти или не произойти, то оно называется СЛУЧАЙНЫМ. В том случае, когда событие должно непременно произойти, его называют ДОСТОВЕРНЫМ,  а в том случае, когда оно заведомо не может произойти, - НЕВОЗМОЖНЫМ.

События называются НЕСОВМЕСТНЫМИ, если каждый раз возможно появление только одного из них. События называются СОВМЕСТНЫМИ, если в данных условиях появление одного из этих событий не исключает появления другого при том же испытании.

Вероятность события рассматривается как мера объективной возможности появления случайного события.

 

Классическое определение вероятности.

Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов, т.е.:

Р (А) = ^m/_n

 

Вероятность любого события не может быть меньше нуля и больше единицы. Невозможному событию соответствует вероятность Р (А) = 0, а достоверному – вероятность Р (А) = 1.

 

Теоремы сложения вероятностей.

ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ НЕСОВМЕСТНЫХ СОБЫТИЙ.

Вероятность одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А + В) = Р(А) + Р(В);

Р(А₁ + А₂ +…+ А_k) = Р(А₁) + Р(А₂) + … + Р(А_k).

 

ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ СОВМЕСТНЫХ СОБЫТИЙ.

Вероятность появлениях хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р(А + В) = Р(А) + Р(В) – Р(АВ).

Для трёх совместных событий имеет место формула:

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р (АС) – Р(ВС) + Р(АВС).

 

Сумма вероятностей двух противоположных событий равна единице.

 

Вероятность наступления события А, вычисленная в предположении, что событие В уже произошло, называется УСЛОВНОЙ ВЕРОЯТНОСТЬЮ события А при условии В и обозначается через РВ (А) или Р(А/В)*.

 

События А, В, С, … называются НЕЗАВИСИМЫМИ В СОВОКУПНОСТИ, если вероятность каждого из них не меняется в связи с наступлением или не наступлением других событий по отдельности или в любой их комбинации.

 

Теоремы умножения вероятностей.

ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ НЕЗАВИСИМЫХ СОБЫТИЙ.

Вероятность совместного появления (или произведения) двух независимых событий равна произведению вероятностей этих событий

Р(АВ) = Р(А) · Р(В).

Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле

Р(А₁ А₂…А_k) = Р(А₁) · Р(А₂) · … · Р(А_k).

 

ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ ЗАВИСИМЫХ СОБЫТИЙ.

   Вероятность совместного появления (или произведения) двух зависимых событий равна произведению одного из них на условную вероятность второго при условии первого:

Р(АВ) = Р(А) · Р(В/А) = Р(В) · Р(А/В).

 

Формула полной вероятности.

Пусть события (гипотезы) В₁, В₂, …,В_n образуют полную группу событий и при наступлении каждого из них, например, В_i, событие А может наступить с некоторой условной вероятностью Р(А/Вi). Тогда вероятность наступления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

Р(А) = Р(В₁) · Р(А/В₁) + Р(В₂) · Р(А/В₂) + … + Р(В_n) · Р(А/В_n)

 

Контрольные вопросы:

1. Сформулируйте определение события.

2. Сформулируйте определение вероятности.

3. Сформулируйте теоремы сложения вероятностей.

4. Сформулируйте теоремы умножения вероятностей.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Случайные величины. Дисперсия случайной величины.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме случайные величины, дисперсия случайных величин. 

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятие случайной величины, дисперсии случайной величины.

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Понятие случайной величины. Законы распределения случайных величин.

Определение. Случайной величиной, связанной  с данным опытом называется величина, которая при данном осуществлении данного опыта принимает то или иное числовое значение, заранее не известное какое именно.

Случайные величины обозначаются  Х, Y и т.д.

Примеры.

1) Опыт - бросается игральная кость один раз. Случайная величина Х - число выпавших очков. Множество значений случайной величины Х={1,2,3,4,5,6}.

2) Опыт стрельба по цели до первого попадания. Случайная величина Y  -  число израсходованных патронов – имеет множество значений {1,2,3,…}=N.

Определение. Случайная величина называется дискретной, если она принимает конечное или счетное множество значений.

В примерах 1, 2 случайные величины  являются дискретными.

Разные случайные величины могут иметь одно и тоже множество возможных значений.  Чтобы полностью охарактеризовать случайную величину,  кроме множества значений необходимо указать, с какой вероятностью случайная величина принимает то или иное своё значение.

Определение. Любое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.

 

        Для дискретной случайной величины Х закон распределения может быть задан  виде таблицы. В верхней строке перечисляются все возможные значения  случайной величины Х (обычно в порядке возрастания), а в нижней строке указываются  вероятности  соответствующих значений:  - это вероятность того, что случайная величина Х принимает значение.

Так как в результате каждого опыта  случайная величина Х обязательно  принимает только одно из значений, то события, образуют полную группу попарно несовместных событий.

Для наглядности закон распределения можно изобразить графически – на плоскости отмечаются точки с координатами  и соединяются отрезками. Полученная ломаная называется  многоугольником распределения СВ.

 

Математическое ожидание и дисперсия случайной величины.

Предположим теперь, что мы знаем закон распределения случайной величины x, то есть знаем, что случайная величина x может принимать значения x₁, x₂, ..., x_k с вероятностями p₁, p₂, ..., p_k.

Определение: Математическое ожидание M_x случайной величины x равно

M_x

 

Свойства математического ожидания:

1. Математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий: M _{x + y} = M_x + M_y.

2. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M _{x · y} = M_x · M_y.

 

Определение: Дисперсией случайной величины x называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

D_х = (х - M_x)² 

 

Свойства дисперсии:

1. Дисперсия суммы независимых случайных величин равно сумме дисперсий: D _{x + y} = D_x + D_y.

2. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D _{x - y} = D_x - D_y.

3. Постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат: D _Cх=C²D_X.

 

Контрольные вопросы:

1. Сформулируйте определение случайно величины.

2. Сформулируйте закон распределения случайной величины.

3. Сформулируйте определение математического ожидания и дисперсии случайной величины.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Математическая статистика и её связь с теорией вероятности. Основные задачи и понятия математической статистики. Определение выборки и выборочного распределения. Графическое изображение выборки. Определение понятия полигона и гистограммы.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме математическая статистика и её связь с теорией вероятности, основные задачи и понятия математической статистики, определение выборки и выборочного распределения, графическое изображение выборки, определение понятия полигона и гистограммы.

·         Развить наглядно-образное мышление и внимание при работе с графическими изображениями.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация.

 

Прогнозируемый результат:

·         Знать и понимать понятие математическая статистика, основные задачи математической статистики, определение выборки и выборочного распределения, графическое изображение выборки, определение понятия полигона и гистограммы.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Предметом математической статистики является изучение случайных величин по результатам наблюдений. Для получения опытных данных необходимо провести обследование соответствующих объектов. Совокупность, которая включает в себя все изучаемые объекты, называется генеральной.

Исходным материалом для любого статистического исследования являются статистические данные. Под статистическими данными понимаются сведения о числе объектов какой-либо обширной совокупности, обладающими теми или иными признаками (например, число студентов, родившихся в 1997 году).

На основании статистически данных можно сделать научно обоснованные выводы. Для этого статистические данные должны быть предварительно определенным образом систематизированы и обработаны.

   Одним из основных методов обработки статистических данных является выборочный метод. При выборочном исследовании из всей совокупности отбирают некоторым образом определенное число объектов и только их подвергают исследованию. Совокупность всех исследуемых объектов называют генеральной совокупностью.

Генеральную совокупность образуют, например, все больные с данным диагнозом, все новорожденные дети и т.д. Общую сумму членов генеральной совокупности называют её объёмом и обозначают буквой n. Теоретически объем генеральной совокупности ничем не ограничен (N —> ∞). Поэтому обычно изучается какая-то часть объектов генеральной совокупности - выборка.

Выборкой называют совокупность случайно отобранных объектов из генеральной совокупности.

Объем выборки будем обозначать буквой n.

Число объектов выборки называют объемом выборки (например, из 10000 студентов для контрольной флюорографии отобраны 100 студентов, то объем генеральной совокупности равен 10000, а объем выборки равен 100). Разность между наибольшим и наименьшим значениями числовой выборки называют размахом выборки.

    Выборку, представляющую собой неубывающую числовую последовательность, называют вариационным рядом. Любую числовую выборку можно записать в виде вариационного ряда.

Последовательность пар (x₁,n₁),(х₂,n₂),...,(х_к,n_к) называют статистическим рядом. Обычно статистический ряд записывают в виде таблицы, где х - значения выборки, a n — частоты значения выборки.

Для наглядного представления выборки часто используют различные графические изображения. Простейшими графическими изображениями выборки являются полигон и гистограмма. Пусть выборка задана статистическим рядом: (х₁,n₁),(х₂,n₂),…,(х_к,x_к). Полигоном выборки называется ломаная линия. Существует два вида полигонов выборки: полигон частот (n_i, (x_i)) и полигон относительных частот (n_i, (x_i)).

 

 

Пусть для изучения количественного признака X из генеральной совокупности извлечена выборка Х₁, Х₂,..., Х_n. Наблюдавшиеся значения признака X называют вариантами. Повторяемость признака X -  называется частотой п. Сумма всех частот равна n. Относительная частота - M_i = n_i/n -выборочный аналог вероятности: p_i появления значения X_i случайной величины X. Тогда выборочным аналогом ряда распределения естественно считать вариационный ряд.

Дискретным вариационным рядом распределения называется ранжированная (расположенная в порядке возрастания или убывания) совокупность вариантов X_i с соответствующими им частотами n, или относительными частотами pt.

Аналогично полигону распределения строится полигон относительных частот. Нецелесообразно построение дискретного ряда для непрерывной случайной величины или для дискретной, число возможных значений которой велико. В подобных случаях следует построить интервальный ряд.

Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины.

При большом объеме выборки более наглядное представление дает гистограмма.

Ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны относительной частоте или частоте.

Для построения гистограммы частот выборки промежуток от наименьшего значения выборки до наибольшего её значения разбивается на несколько частичных промежутков h. Для каждого частичного промежутка подсчитывают сумму S_k частот значений выборки, попавшей в этот промежуток. Затем на каждом интервале, как на основании, строится прямоугольник высотой равной S_k/h.

Построив вариационный ряд и изобразив его графически, можно получить первоначальное представление о закономерностях, имеющих место в ряду наблюдений. Однако на практике зачастую этого недостаточно. Такая ситуация возникает, например, когда имеется необходимость сравнить два ряда и более.

Сравниваемые распределения могут существенно отличаться друг от друга. Они могут иметь различные средние значения случайной величины, или различаться рассеиванием данных наблюдений вокруг указанных значений. Поэтому для дальнейшего изучения изменения значений случайной величины используют числовые характеристики вариационных рядов. Их обычно называют статистическими характеристиками или оценками

В математической статистике вводятся числовые характеристики выборки аналогично числовым характеристикам случайных величин в теории вероятности.

Пусть имеется выборка объема n:  х₁,х₂,...,х_n.

Выборочным математическим ожиданием (выборочным средним) называют среднее арифметическое выборки:

                            х₁ + х₂+ … + х_n

                                                         = Х

                                      n

 

Если выборка задана статистическим рядом, то

 

 

 

 

Контрольные вопросы:

1. Сформулируйте определение генеральной совокупности.

2. Сформулируйте определение выборки.

3. Сформулируйте определение статистического ряда.

4. Сформулируйте определение выборочного математического ожидания.

 

 

 

 

 

 

Тема:  Санитарная (медицинская) статистика – отрасль статистической науки. Статистическая совокупность, её элементы, признаки.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме санитарная (медицинская) статистика – отрасль статистической науки, статистическая совокупность, её элементы, признаки.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация.

 

Прогнозируемый результат:

·         Знать и понимать понятие санитарная (медицинская) статистика – отрасль статистической науки, статистическая совокупность, её элементы, признаки.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Медицинская статистика - отрасль статистики, изучающая явления и процессы в области здоровья населения и здравоохранения.

Основные задачи медицинской статистики.

•              Разработка специальных методов исследования массовых процессов и явлений в медицине и здравоохранении;

•              Выявление наиболее существенных закономерностей и тенденций в здоровье населения в целом и в различных его группах (возрастных, половых, профессиональных и др.) во взаимосвязи с конкретными условиями и образом жизни: изучение и оценка состояния и динамики развития сети, деятельности учреждений здравоохранения и медицинских кадров.

 

Основа медицинской статистики.

Основой медицинской статистики являются  общая теория статистики и математическая статистика. Важная роль в развитии теории и практики медицинской статистики принадлежит математике, кибернетике, информатике, вычислительной технике, автоматизированным системам обработки информации.

Практика медицинской статистики основывается на общегосударственной системе учета и отчетности, принятых в  России.

Важнейшими техническими средствами медицинской статистики являются: современная вычислительная техника. средства связи, передачи, хранения и отображения информации.

В медицинской статистике выделяют следующие основные разделы:

•              общая теория и методы;

•               статистика здоровья населения;

•              статистика здравоохранения;

•              применение методов медицинской статистики в управлении, в клинических, лабораторных, экспериментальных исследованиях.

Общая теория и методы медицинской статистики включают методологию медико-статистического исследования, т. е. совокупность специфических научных методов и приемов сбора, обработки, анализа и оценки медико-статистической информации.

Основными методами статистических исследований являются:

1.          статистическое наблюдение;

2.          группировка и сводка материалов наблюдения; методы первичной статистической обработки данных;

3.          метод выборочного медико-статистического исследования, включая оценку репрезентативности выборочных данных;

4.          методы математико-статистического анализа: статистическая оценка значимости различий сравниваемых показателей, исследование и оценка связей и взаимозависимостей, исследование динамики явлений и процессов, статистическое планирование эксперимента, прогнозирование, многомерный статистический анализ, графический анализ и др.

Медико-статистическое исследование включает пять самостоятельных, но взаимосвязанных этапов:

1) планирование исследования (формулировка цели, разработка задач, программы и плана исследования);

2) статистическое наблюдение (сбор материала для его последующей статистической обработки);

3) статистическая группировка и сводка материалов наблюдения;

4) первичная статистическая обработка данных;

5) научно-статистический анализ, графическое и литературное оформление результатов исследования.

Объектом медико-статистического исследования являются массовые процессы, происходящие среди населения, в сферах оказания медпомощи и проведения санитарно-противоэпидемических мероприятий, анализ которых позволяет вскрыть и охарактеризовать количественно закономерности и особенности здоровья населения в целом и составляющих его групп, развитие и течение болезней среди различных групп населения, деятельность органов и учреждений здравоохранения.

Важное место в медицинской статистике занимают фактические медико-статистические данные, регулярно собираемые, обрабатываемые, анализируемые и используемые в повседневной оперативной работе учреждениями и органами здравоохранения, а также направляемые в строго установленном порядке по подчиненности в виде специальных документов государственной медицинской отчетности.

С этой целью в системе здравоохранения создана медико-статистическая служба, звеном которой являются кабинеты медицинского учета и статистики медицинских учреждений.

Одним из важных направлений медицинской статистики служит разработка научно обоснованных критериев состояния здоровья населения и деятельности учреждений и органов здравоохранения, а также систем таких критериев, которые могут быть использованы в процессе управленческой работы с целью объективной оценки складывающихся конкретных ситуаций, их планирования и прогнозирования.

Важными медико-статистическими показателями являются показатели здоровья населения (смертность, заболеваемость и др.), показатели, характеризующие работу лечебно-профилактических учреждений.

Медико-статистические показатели периодически пересматриваются в соответствии с новыми задачами здравоохранения, развитием медицинской науки и практики, технической оснащенности служб здравоохранения.

 

Контрольные вопросы:

1. Сформулируйте определение и основные задачи медицинской статистики.

2. Определите основные разделы в медицинской статистике.

3. Сформулируйте основные методы статистических исследований.

4. Что является объектом медико-статистического исследования?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Обоснование методов обработки результатов медико – биологических исследований.

 

Цели урока:

·         Обобщить и систематизировать знания методов обработки результатов медико – биологических исследований.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятие методов обработки результатов медико – биологических исследований.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Развитие медицины невозможно без проведения медико-биологических экспериментов, эпидемиологического анализа, оценки эффективности фармакологических препаратов и других исследований как доклинического, так и клинического уровня.

Объектом научного исследования обычно выступает не просто отдельное явление, конкретная ситуация, а целый класс сходных явлений и ситуаций, их совокупность. Цель и непосредственные задачи научного исследования состоят в том, чтобы найти общее у ряда единичных явлений, выявить законы, по которым они возникают, развиваются и функционируют. Важнейшим обстоятельством, определившим необходимость применения математико-статистических методов, явилось установление факта, что многим биологическим системам свойственны статистические закономерности, обнаруживаемые при изучении совокупностей, но неприменимые к отдельным единицам этих совокупностей.

 Отличительными признаками научного исследования являются:

 -целенаправленность процесса (достижение поставленной цели, выполнение четко сформулированных задач)

-направленность на поиск, на творчество, на выдвижение идей

-систематичность как самого процесса исследования, так и его результатов

-строгая доказательность, обоснованность выводов.

 Развитие идей критической оценки медицинской информации привело к возникновению в конце 80-х годов XX века концепции доказательной медицины (ДМ).

 Основными постулатами ДМ являются следующие:

 — каждое решение врача должно основываться на научных данных;

 — вес каждого факта тем больше, чем строже методика научного исследования, в ходе которого он получен.

 ДМ является концепцией как для врачей, исследователей, руководителей учреждений и органов здравоохранения, так и для пациентов. Основная цель концепции ДМ состоит в том, чтобы постепенно превратить врачебную деятельность из искусства в науку.

 Любое исследование в зависимости от того, насколько надежны полученные в нем результаты и насколько они применимы в клинической практике, можно охарактеризовать с двух точек зрения:

 — достоверности (внутренней обоснованности)

 — о6общаемости (внешней обоснованности, применимости).

 Достоверность (внутренняя обоснованность) исследования определяется тем, в какой степени структура исследования соответствует поставленным задачам, а полученные результаты справедливы в отношении изучавшейся выборки.

Обобщаемость (внешняя обоснованность) результатов исследования отражает, в какой мере результаты данного исследования применимы к другим группам, например к больным другого пола, другой популяции и т.п.

 Достоверность и о6общаемость зависят от правильности проведения исследования на всех этапах, в том числе, от грамотной статистической обработки полученных данных.

 Широкая доступность вычислительной техники дает возможность обработки больших объемов данных, использования различных методов анализа. Кроме того, программа конкретного метода обработки позволяет многократно повторять вычисления с небольшими изменениями без дополнительных усилий. Для большинства стандартных статистических методов существуют пакеты программ, хотя им порой не хватает гибкости, которую в идеале они должны были бы допускать. Для большинства задач с небольшими объемами данных и с относительно простыми методами обработки вполне достаточно обычного калькулятора. Для данных среднего объема лучше пользоваться пакетами стандартных программ. Однако следует избегать использования сложных методов анализа только потому, что имеются соответствующие программы.

 Применение статистики в медицинских и биологических исследованиях не ограничивается анализом результатов. Статистические методы следует использовать также на этапе планирования биологического эксперимента или медицинского исследования. Следует подчеркнуть, что с точки зрения клинической эпидемиологии для получения надежных, научно обоснованных результатов необходимы 2 компонента:

 -правильное планирование структуры исследования (обеспечивающей возможность получения ответов на поставленные вопросы)

 -грамотный статистический анализ.

 

Статистика в медико-биологическом исследовании

 Всякое исследование должно удовлетворить следующим требованиям:

 

 - целеустремленность (конкретность задач). При анализе полученных данных могут быть выявлены и дополнительные результаты, не запланированные в исследовании (вторичные данные), однако обычно они представляют меньшую ценность, чем основные (соответствующие поставленной цели) результаты проводимого эксперимента.

 - эффективность, т. е. полученные выводы должны быть достоверны.

- экономность (минимальная затрата сил и средств, риску подвержено минимальное количество участников (как людей, так и животных)). Экономность может быть достигнута подбором минимальной численности групп, достаточной для получения достоверных результатов.

 

Формулирование целей

↓

Планирование

↓

Выполнение (сбор данных)

↓

Подготовка данных

↓

Анализ данных

↓

Интерпретация результатов

↓

Формулировка выводов

↓

Публикация

 

Контрольные вопросы:

1. Сформулируйте отличительные признаки научного исследования.

2. Определите роль статистики в медико – биологических исследованиях.

 

 

 

Тема:  Понятие о демографических показателях, расчет общих коэффициентов рождаемости, смертности. Естественный прирост населения.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме понятие о демографических показателях, расчет общих коэффициентов рождаемости, смертности, естественный прирост населения.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради.

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация

 

Прогнозируемый результат:

·         Знать и понимать понятия о демографических показателях, расчет общих коэффициентов рождаемости, смертности, естественный прирост населения.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Общие демографические коэффициенты — это отношение числа происшедших в населении событий к средней численности населения, продуцировавшей эти события в соответствующем периоде.

Общая численность населения:

P = P₀ + (N — M) + (V₊ — V_-) = P₀ + E + V_пр (уравнение демографического баланса)

 P — общая численность населения

 P₀ — численность населения на начало года

 N — общее число родившихся

 M — общее число умерших

 E — естественный прирост населения

 V₊ — число прибывших

 V_- — число выбывшиих, по каким либо причинам

 

Общий прирост населения: P₁ — P₀ = P_пр

Р₀ — численность населения на начало периода (обычно год)

Р₁ — на конец периода

 

Естественный прирост населения: N — M = E

N — общее число родившихся

M — общее число умерших

Значение показателя может быть отрицательным, если имеет место естественная убыль населения

 

Общие коэффициенты рождаемости и смертности – это отношение числа родившихся живыми и числа умерших в течение календарного года к среднегодовой численности населения, в промилле (‰).

 

Коэффициенты рождаемости и смертности:

M_x — число смертей за данный год

N_x — число рождений за данный год

P_x — средняя численность населения за год

 

Суммарный коэффициент рождаемости - это сумма возрастных коэффициентов рождаемости, рассчитанных для возрастных групп в интервале 15—49 лет. Этот коэффициент показывает, сколько в среднем детей родила бы одна женщина на протяжении всего репродуктивного периода (от 15 до 50 лет) при сохранении повозрастной рождаемости на уровне того года, для которого вычислен показатель.

Его величина, в отличие от общего коэффициента рождаемости, не зависит от возрастного состава населения и характеризует средний уровень рождаемости в данном календарном году.

Суммарный коэффициент рождаемости:

 

W _15-49 — средняя численность женщин репродуктивного возраста

 

Возрастные коэффициенты смертности — рассчитывают как отношение числа умерших в данном возрасте в течение календарного года к среднегодовой численности лиц данного возраста. (Эти коэффициенты характеризуют средний уровень смертности в каждой возрастной группе в календарном году.)

Коэффициент младенческой смертности - исчисляется как сумма из двух составляющих, первая из которых — отношение числа умерших в возрасте до одного года из родившихся в том году, для  которого исчисляется коэффициент, к общему числу родившихся в том же году, а вторая составляющая — отношение числа умерших в возрасте до одного года из родившихся в предыдущем году к общему числу родившихся в предыдущем году. Исчисляется на 1000 родившихся живыми, в промилле (‰).

Коэффициент младенческой смертности:

 

                                                                                (формула Ратса)

 

 

M₀ — число умерших в возрасте от 0 до 1 года

M _-1 — число детей, умерших в возрасте до года из числа родившихся в предыдущем году

N₀ — число родившихся в отчетном году

N_-1 — число родившихся в предыдущем году

 

Контрольные вопросы:

1. Сформулируйте определение общих демографических коэффициентов.

2. Определите общую численность населения.

3. Определите общий прирост населения.

4. Определите естественный прирост населения.

5. Определите коэффициенты рождаемости и смертности.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Определение процента. Решение трёх видов задач на проценты. Составление и решение пропорций, применяя их свойства. Расчёт процентной концентрации растворов. Газообмен в лёгких. Показатели сердечной деятельности.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме определение процента, решение трёх видов задач на проценты, составление и решение пропорций, применяя их свойства, расчёт процентной концентрации растворов, газообмен в лёгких, показатели сердечной деятельности. 

·         Развить наглядно-образное мышление и внимание при работе с графиками функций.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация.

 

Прогнозируемый результат:

·         Знать и понимать понятие процента, уметь составлять и решать пропорции, рассчитывать процентную концентрацию растворов, уметь вычислять газообмен в легких и показатели сердечной деятельности.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Процентом называется сотая часть. Запись 1 % означает 0, 01; 27 % = 0, 27; 100 % = 1; 150% = 1, 5 и т.д.

 

Чтобы найти процентное выражение данного числа, нужно умножить это число на 100 (или, что одно и то же, перенести в нем запятую на 2 знака вправо).

Примеры: Процентное выражение числа 2 есть 200 %; числа 0, 357 есть 35, 7%; числа 1, 753 есть 175, 3%.

 

Чтобы найти число по его процентному выражению, нужно разделить процентное выражение на 100 (или, что одно и то же, перенести в нем запятую на 2 знака влево).

Примеры: 13, 5% = 0, 135; 2, 3% = 0, 023; 145% = 1, 45.

 

Расчет процентной концентрации растворов

(в различных объемах жидкости)

Три основные математические задачи на проценты:

Задача 1. Найти указанный процент данного числа.

Данное число делится на 100, и полученный результат умножается на число процентов.

Пример: В отделении за сутки в среднем расходуется 0, 5 кг. хлорной извести. Во время генеральной уборки помещений было израсходовано 153% среднесуточного количества хлорной извести. Сколько хлорной извести израсходовал персонал отделения во время генеральной уборки помещения?

Решение:

1.) 0, 5 кг. : 100% = 0, 005

2.) 0, 005 · 153 % = 0, 765 кг.

     Ответ: За сутки во время генеральной уборки израсходовано 0, 765 кг. хлорной извести.

Задача 2. Найти число по данной величине указанного его процента.

Данная величина делится на число процентов, и результат умножается на 100.

Пример: Вес хлорной извести в растворе составляет 10 %. Сколько потребуется воды для разведения раствора, если известно, что хлорной извести взяли 0, 2 кг.?

Решение:

1.) 0, 2 : 10 = 0, 02

2.) 0, 02 · 100 = 2 л.

     Ответ: Потребуется 2 л. воды.

Задача 3. Найти выражение одного числа в процентах другого.

Умножаем первое число на 100 и результат делим на второе число.

Пример: За сутки в отделении израсходовано 765 г. хлорной извести вместо среднесуточной нормы расхода 500 г. На сколько процентов больше израсходовано хлорной извести?

Решение:

1.) 765 – 500 = 265

2.) 265 · 100 = 26500

3.) 26500 : 500 = 53

     Ответ: На 53 % больше израсходовано хлорной извести за сутки.

 

Расчет количества вещества.

По определению концентрации чистого вещества в растворе – это количество граммов в 100 мл. Следовательно, для расчета количества вещества в 1 мл. раствора необходимо имеющуюся массу чистого вещества в растворе разделить на 100.

Газообмен в легких.

При относительном покое взрослый человек совершает примерно 16 дыхательных движений в 1 мин. Жизненная емкость легких (ЖЕЛ): ЖЕЛ = ДО + РО _В + РО _ВЫД, где

ДО – дыхательный объём (0, 5 л.)

РО _В  - резервный объём вдоха (1, 5 л.)                 3 – 4 литра

РО _ВЫД - резервный объём выдоха (1, 5 л.)

Во вдыхаемом воздухе содержится:

- 20, 97 % кислорода,

- около 79 % азота,

- примерно 0, 03 % углекислого газа,

- небольшое количество водяных паров и инертных газов.

Процентный состав выдыхаемого воздуха иной:

- кислорода в нём остаётся 16 %,

- количество углекислого газа возрастает до 4 %.

 

Показатели сердечной деятельности.

Масса сердца взрослого человека составляет 1 / 220 части от массы тела (), 425 – 0, 570 кг.). Масса сердца новорождённого в среднем 0, 66 – 0, 80 % от массы тела (около 20 г.). Параметры сердца взрослого человека: длина h – 12 – 15 см, поперечный разрез d₁ – 8 – 10 см, передний – задний разрез d₂ – 5 – 8 см. Для вычисления объёма сердца используем формулу объёма конуса:

V = ⅓ Sh = ⅓ πR ² h = ¹ /₁₂ πd ² h.

 

Контрольные вопросы:

1. Сформулируйте три основные математические задачи на проценты.

2. Сформулируйте правило расчета количества вещества.

3. Сформулируйте формулу определения ЖЁЛ.

4. Сформулируйте формулу для вычисления объёма сердца.

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема:  Расчёт прибавки роста и массы детей. Способы расчёта питания. Оценка пропорциональности развития ребенка, используя астрометрические индексы. Перевод одних единиц измерения в другие.

 

Цели урока:

·         Обобщить и систематизировать знания, умения и навыки учащихся по теме расчёт прибавки и массы детей, способы расчета питания, оценка пропорциональности развития ребенка, используя астрометрические индексы, перевод одних единиц измерения в другие.

·         Развить коммуникативные навыки при оперировании математическими понятиями.

·         Воспитать аккуратность при записи в тетради. 

·         Повысить интерес учащихся к предмету.

 

Тип урока: изучение нового материала.

 

Оборудование:

·         компьютер

·         учебные материалы

·         научная литература

·         презентация.

 

Прогнозируемый результат:

·         Знать и понимать расчёт прибавки роста и массы детей, способы расчета питания, оценка пропорциональности развития ребенка, используя астрометрические индексы, перевод одних единиц измерения в другие.

 

План урока:

1.     Ознакомление с темой урока и планом урока.

2.     Изучение нового материала.

 

Ход урока:

Нормы роста и веса детей приблизительные, отклонения от нормы не значат патологию, но это повод понаблюдать за ребенком и его здоровьем.

Прибавка роста детей после 1 года жизни рассчитывается по формуле: Р = 75 + 5 · n, где n – количество лет.

Индивидуальность каждого отдельного человека начинает проявляться еще в тот момент, когда он только-только родился. Любой новорожденный наделен своими личными показателями, такими как рост, вес, окружность груди и головы. Они фиксируются еще в роддоме и пишутся рядом с именем младенца. И с этого момента начинается отсчет - как быстро и успешно будет ребенок расти, то есть набирать сантиметры в длину и увеличивать свой вес ежемесячно.

Средняя масса тела, с которой дети появляются на свет - от 2600 до 4000 г. Все, у кого вес ниже минимальной отметки, относятся к категории детей, имеющих дефицит веса (речь идет о рожденных точно в срок младенцах, а не о недоношенных детях). Новорожденные, перевалившие через отметку в 4 кг, считаются крупными.

Но помимо конкретных цифр, определяющих вес младенцев, врачи используют и так называемый индекс Кетле. Эта величина - частное от деления массы тела новорожденного ребенка на его длину. Допустимый диапазон индекса Кетле находится в границах от 60 до 70. Так, ребенок массой тела 3410 г при росте в 52 см имеет индекс 65, что полностью соответствует установленной норме. Детям, чей индекс ниже 60, ставится диагноз внутриутробная гипоксия. Это означает, что во время внутри утробного развития малыш не получал должного количества питательных веществ и кислорода.

Если ребенок имеет вес при рождении свыше 4 кг, о нем говорят "богатырь", а врачи нередко относят подобных младенцев к группе риска по развитию сахарного диабета. Но научные исследования, проведенные в течение последних лет, доказали, что у детей с повышенной массой тела риск развития сахарного диабета не выше, чем у "нормальных" младенцев. Более того, если малыш родился с весом 4300 г и выше, можно сказать, что данный диагноз ему совершенно не грозит - основные жизненно важные органы у подобных младенцев с самого рождения имеют высокую функциональную зрелость и сформировавшийся размер.

Большинство новорожденных детей на 3-4 день жизни несколько теряют в своем первоначальном весе - уходит лишняя жидкость и меконий, накопленный во внутриутробный период. Но уже со второй недели начинается нормальный, положенный по сроку набор массы тела, который и будет в дальнейшем фиксировать педиатр.

 

Прибавка в весе.

Существует несколько способов достоверно определить, правильно ли ребенок набирает вес. Вот один из них. Берем за основу, что масса тела полугодовалого ребенка равна 8200 г. Теперь для определения массы тела детей младше 6 месяцев будем отнимать от этой величины по 800 г за каждый предыдущий месяц. Для 4-х месячного младенца это будет - 8200 - (800х2)=7200 г. А для малышей старше полугода к 8200 г необходимо прибавлять по 400 г за каждый следующий месяц - годовалый ребенок должен иметь вес 8200+(400х6)=10600 г. Конечно, приведенная формула может давать лишь приблизительный результат, ведь вес младенцев при рождении сильно расходиться в ту или иную сторону.

 

Способы расчета питания.

В первые 7–10 дней жизни ребёнка его потребность в женском молоке или детской молочной смеси быстро возрастает. Для приблизительного расчёта суточного объёма питания можно пользоваться следующей формулой.

Объём молока за сутки (мл) = 2% от массы тела (г) при рождении х n,

где n — число дней жизни ребёнка.

 

Для определения количества детской молочной смеси, необходимого на одно кормление, следует разделить суточный объём на число кормлений. Разовый объём молока можно также подсчитать, умножив число дней жизни ребёнка на 10.

После 7–10-го дня жизни ребёнка при подсчёте объёма питания используют калорийный, объёмный способы или формулу Шкарина.

При расчёте питания калорийным способом учитываются энергетические потребности детей, которые в первом полугодии составляют 115 ккал/кг, а во втором полугодии – 110 ккал/кг. Зная массу тела ребёнка и приблизительную калорийность детской молочной смеси (680 ккал в 1 л), можно рассчитать его необходимый суточный объём.

Так, ребёнку в возрасте 2 мес с массой тела 4600 г требуется:

115 х 4,6 = 529 ккал в сутки.

Объём женского молока = (529 х 1000): 680 = 780 мл.

Объёмный метод заключается в определении суточного объёма питания в зависимости от массы тела и возраста ребёнка.

Возраст                            Суточный объём молока

10 дней - 2 мес                       1/5 массы тела

2–4 мес                                   1/6 массы тела

4–6 мес                                   1/7 массы тела

6–9 мес                                   1/8 массы тела

Использование формулы Шкарина предполагает, что ребёнок в возрасте 8 недель (2 месяца) должен получать 800 мл молока в сутки. На каждую неделю, недостающую до 8 недель – на 50 мл меньше смеси: 800–50 х (8 – n),

где n – число недель жизни ребёнка.

На каждый месяц после 2 мес – на 50 мл смеси больше:

800 + 50 х(n - 2),

где n — число месяцев жизни ребёнка.

 

При расчёте питания любым способом необходимо помнить, что его суточный объём питания у детей первого полугодия жизни не должен превышать 1000 мл, во втором полугодии — 1000–1100 мл.

 

Нормы развития ребенка.

Нормальные дети не только растут и активно набирают вес, но также постоянно двигаются и проявляют свои эмоции. Поэтому когда родители не обнаруживают присущую возрасту ребенка моторику или соответствующее психическое развитие, им следует незамедлительно выяснить, является ли эта задержка врожденным дефектом либо это следствие того, что они уделили занятиям с крохой слишком мало времени.

В развитии нервной системы малыша важную роль играют условия, в которых он находится. При хорошем уходе и постоянном общении с членами семьи закладывается надежный фундамент для гармоничного интеллектуального и физического развития крохи.

Интеллектуальное развитие ребенка зависит от родительского ухода и режима воспитания. Важно соблюдать определенный воспитательный кодекс, режим сна и питания. Ребенка необходимо снабдить развивающими игрушками, постоянно с ним разговаривать, следить за приобретением соответствующих возрасту навыков.

Пропорциональность развития – это правильное соотношение между ростом и весом ребенка. Массоростовый показатель рассчитывается как отношение массы тела малыша к его росту. У новорожденных детей нормативное значение показателя составляет 60-75 грамм.

Пропорциональность развития – это правильное соотношение между ростом и весом ребенка. Массоростовый показатель рассчитывается как отношение массы тела малыша к его росту. У новорожденных детей нормативное значение показателя составляет 60-75 грамм.

Кроме роста и веса для оценки физического развития ребенка важную роль играет пропорциональность его тела – окружность груди и головы. В момент появления на свет окружность головы доношенного малыша (33,0-37,5 см) больше окружности его груди. Однако следует отметить, что превышение должно быть не более 2 сантиметров. Дальнейший ежемесячный прирост окружности головы ребенка должен составлять в течение первых 6 месяцев от 1 до 1,6 сантиметров, а затем от 0,4 до 0,7 сантиметров. К первому году жизни окружность головы детей достигает 46-48 см, увеличившись на 10-12 сантиметров с момента рождения.

Основой для развития статических (двигательных) функций крохи являются врожденные рефлексы. Они помогают новорожденному адаптироваться к новой среде. Некоторые из рефлексов в течение нескольких месяцев исчезают, другие трансформируются в приобретенные рефлексы, становятся частью сознания и сопутствуют малышу на протяжении всей его жизни (чихание, моргание, вздрагивание, зевота, коленные рефлексы). В качестве основных рефлексов новорожденного младенца можно привести следующие:

• Хватательный рефлекс. Проявляется в момент легкого поглаживания детской ладошки – рефлекторно кроха схватывает и удерживает то, что прикасается к его ладони.

• Сосательный рефлекс (инстинкт питания). Если провести вокруг рта младенца соской, он делает губами заметные сосательные движения.

• Поисковый рефлекс. Если легко прикоснуться к щечке новорожденного, он будет поворачивать головку.

• Рефлекс Бабинского. Если провести пальцем по внешней части стопы ребенка, его пальчики разойдутся в разные стороны, а стопа повернется.

• Плавательный рефлекс. Если положить ребенка на живот, он будет совершать движения, похожие на плавательные.

• Рефлекс Мора. Реагируя на внезапный и громкий звук, младенец сводит и разводит руки и ноги.

• Рефлекс Бабкина. Если легко надавить ребенку на ладонь, он повернет головку и откроет рот.

• Рефлекс ходьбы. Если поддерживаемый под ручки малыш будет касаться ножками какой-нибудь поверхности, в своих движениях он будет имитировать ходьбу.

Нормы развития ребенка соблюдаются в том случае, если он усвоил большую часть навыков. В противном случае можно судить о нарушениях в развитии. Частичная задержка (опережение) свидетельствует о негармоничном развитии. Специфические или общие отклонения в развитии ребенка - это серьезный повод обратиться за помощью к специалистам.

 

Антропометрические индексы.

Антропометрические индексы - индексы, определяемые при сопоставлении двух или нескольких параметров физического развития, например, массы тела и роста, окружности грудной клетки и длины тела, длины туловища и длины конечностей. Для оценки физического развития детей используют чаще всего индексы Чулицкой, индекс Эрисмана, индекс Пирке, индекс Бругша.

Первый индекс Чулицкой характеризует упитанность ребёнка. У детей первых двух лет жизни он колеблется от 25 до 20 см и постепенно снижается к 7—8-му году жизни до 15—10 см. Второй индекс Чулицкой, т. наз. осевой, определяется разницей между длиной ноги и длиной туловища. У детей до 1 года он колеблется от 2 до 4 см, в 2—3 года — от 6 до 8 см. Уменьшение величины этого индекса указывает на отставание роста нижних конечностей.

Индекс Пирке выявляет соотношение между длиной туловища и конечностей. У грудных детей он равен 54—58 см, с возрастом увеличивается. Индекс Эрисмана характеризует развитие грудной клетки ребёнка и отчасти его упитанность. Чем лучше физически развит ребёнок, тем позднее у него окружность груди сравнивается с полуростом. Индекс Бругша, как и индекс Эрисмана, характеризует развитие грудной клетки. Для правильной оценки физического развития ребёнка необходимо пользоваться комбинацией, т. к. каждый индекс в отдельности не даёт полного представления о физическом развитии ребёнка.

 

Контрольные вопросы:

1. Сформулируйте формулу расчета прибавки роста детей.

2. Сформулируйте способы расчета питания.

3. Сформулируйте определение антропометрических индексов.

 

 

 

 

 

 

ЛИТЕРАТУРА:

 

1. И.Д. Пехлецкий. Математика: Учебник для средних специальных учебных заведений М., 2009.

2.  Алгебра и начала анализа, под ред. Г.Н. Яковлева в 2-х ч. М., 2011

3. Богомолов Н.В., Самойленко П.И. Математика: Учебник для средних специальных учебных заведений – М.: Дрофа, 2010.

4. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 5-е изд. – М.: Высшая школа, 2010.

5. Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений. / Е.В. Филимонова. – 2-е изд., доп. и перераб. – Ростов-на- Дону.: Феникс, 2009.

6. Михеев В.С., Стяжкина О.В., Шведова О.М. Математика: Учебное пособие для среднего профессионального образования. /  В.С.Михеев. – Ростов-на-Дону.: Феникс, 2009.

7. Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика. – Форум, 2011. – 240 с., 2011.

 

Интернет-ресурсы:

www.slovari.yandex.ru

www.wikiboks.org

revolution.allbest.ru

http://pedsovet.su

Скачано с www.znanio.ru