
Филиал бюджетного профессионального образовательного учреждения Чувашской Республики
«Чебоксарский медицинский колледж»
Министерства здравоохранения Чувашской Республики в городе Канаш
|
РАССМОТРЕНО и ОДОБРЕНО на заседании ЦМКОГСЭ Протокол № ____ «____» _______________ 20 ___ г. Председатель ЦМК ____________Л.М Иванова |
утверждено Зав. филиалом БПОУ «ЧМК» МЗ Чувашии в г. Канаш ____________ Т.Э Фадеева |
Методическая разработка теоретического занятия
Формула бинома ньютона.
Треугольник паскаля.
учебная дисциплина БД. 04 Математика
специальность 34.02.01Сестринское дело
(базовая подготовка)
Канаш, 2021
Составитель: Семенова А.М., преподаватель высшей квалификационной категории филиала БПОУ ЧР «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г. Канаш
|
|
Рецензент: Иванова Л.М., преподаватель, высшей квалификационной категории филиала БПОУ ЧР «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г. Канаш
|
Аннотация
Данная методическая разработка по теме «Формула бинома Ньютона. Треугольник Паскаля» является уроком изучения нового материала. Урок построен так, чтобы обучающиеся, опираясь на ранее полученные знания, могли вывести формулы сами. Материал урока направлен на нахождение биноминальных коэффициентов , используя треугольник Паскаля;
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. МЕТОДИЧЕСКИЙ БЛОК
1.1. Учебно-методическая карта
1.2. Технологическая карта
2.ИНФОРМАЦИОННЫЙ БЛОК
2.1. План лекции
2.2.Теоретическая часть.
2.3. Глоссарий
3. КОНТРОЛИРУЮЩИЙ БЛОК
Данная методическая разработка по теме «Формула бинома Ньютона. Треугольник
Паскаля» является уроком изучения нового материала. Урок построен так, чтобы обучающиеся,
опираясь на ранее полученные знания, могли вывести формулы сами. Материал урока
направлен на развитие логического мышления, алгоритмической культуры, интуиции,
навыков исследовательской деятельности, творческих способностей обучающихся.
Структура урока: постановка цели и задач урока; повторение умений и навыков,
являющихся опорой для восприятия новой темы; проведение проверочных упражнений
(устная работа); Упражнения
на закрепление данного алгоритма; тренировочные упражнения по образу и подобию
в виде самостоятельной работы; самоконтроль обучающихся. Урок направлен на нахождение
биноминальных коэффициентов, используя треугольник Паскаля;
Создание проблемных ситуаций на уроках математики повышает
интерес к предмету, вносит разнообразие и эмоциональную окраску
в учебную работу, снимает утомление, развивает внимание, сообразительность.
|
Тема занятия |
Целые и рациональные числа. |
||||||
|
Учебная дисциплина |
БД.04 Математика |
||||||
|
Специальность |
34.02.01 Сестринское дело (базовая подготовка) |
||||||
|
Курс |
I |
||||||
|
Группа |
9М-11-20, 9М-12-20, 9М-13-20,9М-14-20, 9М-15-20. |
||||||
|
Место проведения |
Кабинет № 5 |
||||||
|
Продолжительность занятия |
90 мин. |
||||||
|
Характеристика занятия |
Вид |
Вид занятия Лекция текущая, обзорная.
|
|||||
|
Тип |
Типы учебных занятий урок изучения нового материала; комбинированный урок
|
||||||
|
Форма |
Изложение, рассказ, объяснение с демонстрацией наглядных пособий. Формы деятельности Фронтальная.
|
||||||
|
Технологии обучения |
Традиционная (репродуктивная) технология обучения Технология развивающего обучения
|
||||||
|
Методы обучения |
Метод Репродуктивный: упражнения, действия по алгоритму. - практические (упражнение, тренинг, опыты, самостоятельная работа по алгоритму). Интерактивные методы – практическая отработка осваиваемых знаний, умений, навыков на уровне компетенций
|
||||||
|
Средства обучения |
1.По характеру воздействия на обучаемых: ИКТ - презентации; 2.По степени сложности: простые: учебники, печатные пособия.
|
||||||
|
Методическая цель |
Методическая цель - отрабатывать методику контроля результатов выполнения письменных упражнений. - реализовывать индивидуальный дифференцированный подход в процессе выполнения обучающимися заданий для самостоятельной работы; |
||||||
|
Цели и задачи занятия |
Воспитательная |
Формирование интеллектуальных, нравственных, эмоционально-волевых качеств у обучающихся.
|
Воспитывать положительное отношение к приобретению новых знаний; Воспитывать ответственность за свои действия и поступки; Вызвать заинтересованность новым для студентов подходом изучения математики. Пробудить чувства обучающихся удивления, гордости, уважения, сопричастности;
|
||||
|
Образовательная |
Решать задачи с помощью алгоритмов и методов; Логически и полно выстраивать ответ. Применять комбинаторики в практических целях и в жизни человека
|
Продолжить формировать обучающихся представления о комбинаторике и ее применении в жизни человека; Сформировать умение возводить двучлен в
натуральную степень;
|
|||||
|
Развивающая |
Развитие речи, мышления, сенсорной восприятие внешнего мира через органы чувств сферы;
|
Развитие комбинаторного мышления учащихся; Формировать навыки познавательного мышления. Формировать умения и навыки учебного труда. Продолжить развитие умения анализировать. Продолжить развитие умения сопоставлять. Продолжить развитие умения сравнивать. Выделять главное при работе с текстом задачи. Продолжить развитие умения выделять главное. Продолжить развитие умения устанавливать причинно-следственные связи.
|
|||||
|
Планируемый результат |
Уметь |
Решать комбинаторные задачи с использованием формул перестановок, размещений, сочетаний. Решать задачи с помощью алгоритмов и методов; Логически и полно выстраивать ответ. Формировать представление о биномиальных коэффициентах и их свойствах. Применять знания и умения студентов для решения комбинаторных задач.
|
|||||
|
Знать |
Формулы для вычисления соединений: перестановок, размещений, сочетаний |
||||||
|
Формирование компетенций у обучающихся |
Общие (ОК)
|
Л1. Сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики; Л5. Готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности; Л8. Отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;
|
|||||
|
Профессиональные (ПК) |
П1. Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке; П4. Владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств; |
||||||
|
Межпредметные связи |
Входящие |
История |
Комбинаторика |
||||
|
Литература |
|
||||||
|
|
|
||||||
|
Выходящие |
Перестановки |
Размещения |
|||||
|
Сочетания |
|
||||||
|
|
|
||||||
|
Внутрипредметные |
Комбинаторика. |
||||||
|
|
|||||||
|
Оснащение занятия |
Методическое |
Методическая разработка занятия. |
|||||
|
Материально-техническое |
Ручка, карандаш, тетрадь, линейка. |
||||||
|
Информационное |
Компьютер, интерактивная доска. |
||||||
|
Список литературы |
Основная |
1.Алимов, Ш. А. Алгебра и начала математического анализа (базовый и углубленный уровни)10—11 классы / Ш.А. Алимов — М., 2018. – с.455. 2.Колягин, Ю.М. Математика: алгебра и начала математического анализа. Алгебра и начала математического анализа (базовый и углубленный уровни). 11 класс / М. В Ткачева., Н. Е Федерова. — М., 2018. - 384 с. |
|||||
|
Дополнительная |
1 Александров А.Д., Геометрия / А.Л.Вернер, В.И. Рыжик (базовый и профильный уровни). 10—11 кл. – 2017. – 344 с. 2. Богомолов, И.Д. Математика: учебник / И.Д. Богомолов. – М., 2018. - 384 с.
|
||||||
|
Интернет-ресурсы |
1. Калашникова В.А. Методическое пособие: «Конспекты лекций по математике» [Электронный ресурс] /В.А. Калашникова. 2. Яковлев Г.Н. Алгебра и начала анализа (Математика для техникумов) [Электронный учебник] /Г.Н Яковлев. - Режим доступа: http://lib.mexmat.ru/books/78472. 3.www. fcior. edu. ru 4.www. school-collection. edu.
|
||||||
Структура комбинированного урока
|
Деятельность преподавателя |
Деятельность обучающихся |
Методическое обоснование |
Формируемые ОК и ПК |
|
1. Организационный этап -5 мин. |
|||
|
Проверяет готовность обучающихся к занятию.
|
Готовятся к началу занятия. |
Включение обучающихся в деятельность на личностно значимом уровне. |
ОК 1, ОК 4. П1. |
|
2. Этап всесторонней проверки домашнего задания - 10мин. |
|||
|
Выявляет правильность и осознанность выполнения всеми обучающимися домашнего задания; устранить в ходе проверки обнаруженные пробелы в знаниях. Режим работы: устная, письменная, фронтальная, индивидуальная. |
По очереди комментируют свои решения. Приводят примеры. Пишут под диктовку.
|
Повторение изученного материала, необходимого для открытия нового знания, и выявление затруднений в индивидуальной деятельности каждого обучающегося. |
ОК1, ПК 1, ПК4 |
|
3. Постановка цели и задач занятия. Мотивация учебной деятельности обучающихся - 5 мин. |
|||
|
Эмоциональный настроить и подготовить обучающихся на урок. Сообщение цели и задач.
|
Эмоциональный настрой и готовность обучающихся на урок.
|
Обсуждение затруднений; проговаривание цели урока в виде вопроса, на который предстоит ответить. Методы, приемы, средства обучения: побуждающий от проблемы диалог, подводящий к теме диалог. |
ОК 1, ОК 4. П1. |
|
4. Актуализация знаний - 30 мин. |
|||
|
Уточняет понимание обучающимися поставленных целей занятия. Выдвигает проблему.
|
Под диктовку, все выполняют задание, а один проговаривает вслух. Выполнить действия и записать результат в виде десятичной дроби:
|
Создание проблемной ситуации. Уч-ся- фиксируют индивидуальные затруднения . |
ОК 1, ОК 4. П1. |
|
5. Первичное усвоение новых знаний - 10 мин. |
|||
|
Создаёт эмоциональный настрой на усвоение новых знаний.
|
Внимательно слушают, записывают под диктовку в тетрадь. |
Создание условий, чтобы обучающийся смогли систематизировать знания о множестве натуральных, целых и рациональных чисел. |
ОК1, ПК 1, ПК4 |
|
6. Первичная проверка понимания - 10 мин. |
|||
|
Проводит параллель с ранее изученным материалом. Проводит беседу по уточнению и конкретизации первичных знаний;
|
Отвечают на заданные вопросы преподавателем. |
Осознание степени овладения полученными знаниями - каждый для себя должен сделать вывод о том, что он уже умеет. |
ОК1, ПК 1, ПК4 |
|
7. Первичное закрепление - 5 мин. |
|||
|
Контролирует выполнение работы. Осуществляет: индивидуальный контроль; выборочный контроль. Побуждает к высказыванию своего мнения. преподаватель показывает на доске решение, опираясь на алгоритм |
записывают решение, остальные решают на местах, потом проверяют друг друга;
|
Тренировка и активизация употребления новых знаний, включение нового в систему. Режим работы: устная, письменная, фронтальная, индивидуальная. |
ОК1, ПК 1, ПК4 |
|
8. Контроль усвоения, обсуждение допущенных ошибок и их коррекция (подведение итогов занятия 5 мин |
|||
|
Отмечает степень вовлечённости обучающихся в работу на занятии. |
под диктовку, все выполняют задание, а один проговаривает вслух; |
Оценивание работу обучающихся, делая акцент на тех, кто умело взаимодействовал при выполнении заданий. |
ОК 1, ОК 4. П1. |
|
9. Информация о домашнем задании, инструктаж по его выполнению5 мин |
|||
|
обсуждение способов решения;
|
Записывают номера заданий. Внимательно слушают преподавателя. |
Информация о домашнем задании, инструктаж по его выполнению
|
ОК 1, ОК 4. П1. |
|
10. Рефлексия (подведение итогов занятия), 5 мин |
|||
|
Акцентирует внимание на конечных результатах учебной деятельности обучающихся на занятии.
|
1. Проводят самоанализ: “Чему научились и что нового узнали?”
|
Осознание своей учебной деятельности; самооценка результатов деятельности своей. |
ОК1, ПК 1, ПК4 |
|
№ п/п |
Изучаемые вопросы |
Уровень усвоения |
|
1. |
Устная работа |
1 |
|
2. |
Объяснение темы «Формула бинома Ньютона. Треугольник Паскаля» |
|
|
|
1. Бином Ньютона;
|
2 |
|
|
2.Треугольник Паскаля.
|
2 |
|
3. |
Примеры и разбор решения заданий тренировочного модуля
|
|
|
|
Пример 1 |
3 |
|
|
Пример 2 |
3 |
|
4 |
Решение упражнений (нечетные пункты) на закрепление темы (№1092) |
3 |
|
5. |
Домашнее задание №1092 (четные). Подведение итогов. |
3 |
Устная работа.
Перечень вопросов, рассматриваемых в теме
1) Какое соединение зазывается перестановками?
2) Какое соединение называется размещением и сочетанием?
3) Правила подсчета числа сочетаний из n-элементов по m без повторений;
Теоретический материал
Сочетаниями из n элементов по m в каждом (m ≤ n) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.
Число всевозможных сочетаний из n различных
элементов по m элементов обозначают ![]()
Формула для подсчёта числа сочетаний:
![]()
Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.
Числа ![]() являются коэффициентами
в формуле бинома Ньютона:
являются коэффициентами
в формуле бинома Ньютона:
![]()
Общим термином «соединения» в комбинаторике называют три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству. Ранее уже рассматривались два вида комбинаций. Это перестановки и размещения. В данных соединениях важен порядок размещения элементов. В случае, когда этот порядок не важен, то мы имеем дело с сочетаниями.
Сочетаниями из n элементов по m в каждом (m ≤ n ) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.
Иногда такие сочетания называют сочетаниями без повторений.
Число всевозможных сочетаний из
из n элементов по m элементов обозначают ![]()
Формула для подсчёта числа сочетаний:
![]()
Используя данную формулу, можно отметить основные свойства сочетаний.
Простейшие свойства сочетаний:
1) ![]()
2) ![]()
3) ![]()
Доказательства свойства сочетаний
1) ![]()
![]()
2) ![]()
![]()
3) ![]()
![]()
![]()
При возведении суммы или разности двух чисел во вторую или третью степень мы пользовались формулами сокращенного умножения, которые являются частным случаем бинома Ньютона.
Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.
Числа ![]() являются коэффициентами
в формуле бинома Ньютона:
являются коэффициентами
в формуле бинома Ньютона:
![]()
Для более простого подсчета коэффициентов Бинома Ньютона для невысоких степеней удобно пользоваться треугольником Паскаля:
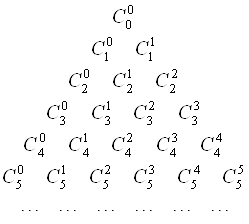

По бокам в каждой строчки имеется коэффициент, равный единице. Все средние коэффициенты считаются, как сумма верхних, которые находятся над ними.
Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.
Не трудно заметить, что строки треугольника симметричны относительно вертикальной оси. Это еще одно замечательное свойство треугольника Паскаля
Историческая справка
Исаак Ньютон (1642-1727 гг.) – выдающийся английский ученый, один из создателей классической физики. Биография Ньютона богата во всех смыслах этого слова. Он сделал немало открытий в области физики, астрономии, механике и математике. Ньютон является автором фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета, заложил основы современной физической оптики, создал многие другие математические и физические теории.
А при чем же здесь бином Ньютона и биномиальные коэффициенты? Формула
![]()
была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени произвольное рациональное число (возможно, отрицательное).
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
В вазе лежат двенадцать конфет, четыре из которых шоколадные, а остальные карамель. Вы хотите угоститься, выбрав две шоколадные и три карамельные конфеты. Сколькими способами вы можете это сделать?
Решение:
Мы имеем два события. Это выбор шоколадных и выбор
карамельных конфет. Порядок конфет не важен. Поэтому мы можем использовать
формулу сочетания для каждого из событий. Так, как шоколадных конфет всего
четыре, а выбрать мы хотим две, то это можно сделать способами ![]() .
.
1) ![]()
Теперь посчитаем количество выбора карамельных конфет. Их общее количество в вазе 12-4=8, а выбрать мы хотим три. Рассчитаем сочетание из восьми по три.
2) ![]()
События выбора разных видов конфет между собой независимы, поэтому по правилу умножения получаем
3) ![]()
Ответ: 336
Пример 2.
Представить разложение двучлена в n степени в виде многочлена, где n=0, 1, 2, …,5
Решение:
Первые четыре разложения мы хорошо умеем делать, используя формулы квадрата и куба разности.
![]()
![]()
![]()
![]()
А для представления бинома четвертой и пятой степени воспользуемся треугольником Паскаля.
![]()
![]()
4. Решение задач упражнения 1092 (не четные).

5. Домашнее задание. Решение 1092 – четные пункты.
|
Термин |
Значение |
|
Бином Ньютона |
– формула разложения произвольной натуральной степени двучлена в многочлен.
|
Тема: «Треугольник Паскаля. Формула бинома Ньютона»
Время 2 часа
Цель: студент должен уметь решать простейшие комбинаторные задачи.
|
Вариант №1 |
Вариант №2 |
|
|
№1. Раскройте скобки в выражении: |
||
|
|
|
|
|
№2. Найдите коэффициент при первой степени переменной х у многочлена Р(х):
|
||
|
|
|
|
|
№3.Найдите коэффициент при первой степени переменной х у многочлена Р(х):
|
||
|
|
|
|
|
№4. Найдите член разложения, не содержащий переменных: |
||
|
|
|
|
|
№5. В разложении по степеням переменной
х укажите: а) одночлен, содержащий х8; б) одночлен, содержащий х4; в) одночлен, содержащий х-2; г) свободный коэффициент (одночлен, не содержащий х). |
||
Максимальное количество баллов –11.
Критерии оценивания: оценка «5» - 9-11 баллов,
оценка «4» - 7-8 баллов,
оценка «3» - 4-6 баллов,
оценка «2» - 3 балла и менее.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.