Графический метод решения задач с параметрами

Конспект урока

Тема занятия: Графический метод решения задач с параметрами.

Тип занятия: занятие изучения нового.

Учебная задача занятия: В совместной деятельности с учащимися сформулировать условия, в которых используется графический метод решения задач с параметрами. Изучить КП-способ решения уравнений с параметром вида  и ; изучить метод частичных областей (МЧО) для решения неравенств на КП-плоскости.

Диагностируемые цели занятия:

В результате занятия ученик

знает:

- определение: КП-плоскости, КП-метода решений задач с параметрами, МЧО на КП-плоскости;

- алгоритм решения неравенств МЧО на КП-плоскости;

- формулировки теорем для уравнений вида  и ;

умеет:

- приводить уравнения к виду и  и соответственно выбирать разные координатно-параметрические плоскости;

- определять знак исходного выражения в каждой из полученных частичных областей;

понимает:

- что часто параметр а можно выразить через функцию координаты  и наоборот, отчего изменится рисунок, но не ответ;

- преимущества и недостатки графического метода решений задач с параметрами.

Учебные действия, формируемые на занятии:

•        Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом, должна осуществляться осмысленная организация собственной деятельности ученика.

•        Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно; планирование - определение последовательности промежуточных целей с учётом конечного результата; оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения; волевая саморегуляция как способность к мобилизации сил и энергии,  способность к волевому усилию к выбору в ситуации мотивационного конфликта и  к преодолению препятствий.

•        Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, в том числе совершенствование навыков работы в группе, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.

•        Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей, структурирование знаний, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

Методы обучения: репродуктивный, частично-поисковый, УДЕ.

Форма работы: фронтальная.

Средства обучения: традиционные.

Структура занятия:

•        Мотивационно-ориентировочная часть (8 минут).

- Актуализация знаний.

- Мотивация.

- Постановка учебной задачи (цели) урока.

•        Операционно-познавательная часть (35 минуты).

•        Рефлексивно-оценочная часть (2 минуты).

Ход занятия:

Мотивационно – ориентировочная часть.

Актуализация знаний.

- Задания 18 на ЕГЭ по математике – это одни из самых сложных заданий, задания с параметром. Их нужно учиться решать с самых лёгких, постепенно усложняя. Вы уже решали некоторые задания с параметром ранее. Давайте вспомним некоторый материал.

- Параметром называется независимая переменная величина, входящая в условие задачи или появляющаяся в процессе се решения, «управляющая» решением задачи.

- Решить задачу с параметрами — это значит, установив множество допустимых значений параметра, решить каждую частную задачу, получающуюся при каждом из таких значений.

Мотивация.

- Решите задачу №1.

Задача №1. Найти все значения параметра , при которых уравнение  имеет решение, принадлежащее промежутку .

Решение:

,

- Корни мы нашли, но на них накладывается дополнительное условие принадлежности к промежутку . Для того, чтобы уравнение имело хотя бы одно решение, необходимо, чтобы больший корень был меньше 1, т.к. условие, что он больше 0 и так выполняется.

Ответ: .

Из-за условия принадлежности корней к промежутку, вам пришлось дополнительно решать неравенство. А если бы сама задача содержала более сложные выражения, то и проверка создала большие трудности.

Постановка учебной задачи (цели) занятия.

Поэтому с текущего занятия вы начнете изучать графические способы решений задач с параметрами. А именно сегодня изучите координатно-параметрический метод.

Операционно-познавательная часть.

Пусть на плоскости даны две взаимно перпендикулярные с общим началом (точкой ) числовые оси. Одну из них () назовем координатой; другую () — параметрической, а плоскость ( или ) — координатно-параметрической, или КП-плоскостью.

Определение: Метод решения задач с параметрами, использующий КП-плоскость, назовём координатно-параметрическим, или КП-методом.

Он основан на нахождении множества всех точек КП-плоскости, значения координаты  и параметра  каж­дой из которых удовлетворяют заданному в условиях зада­чи условию (соотношению).

Если указанное множество точек найдено, то можно каждому допустимому значению параметра  поста­вить в соответствие координаты  точек этого множества, дающие искомое решение задачи, или указать те значения параметра, при которых задача не имеет решения.

Замечание: Если параметр а есть функция координаты : , неявно заданная уравнением , то можно рассматривать КП-плоскость  с вертикальной параметрической осью .

- Решим задачу №1 КП-методом.

Для начала упростим исходное выражение до вида, т.е. чтобы параметр а являлся функцией координаты :  

Т.к. , то можно рассматривать КП-плоскость  с вертикальной параметрической осью .

Изобразим КП-плоскость , параболу , ветви которой направлены вверх, ограничения - .

,

Закрашенной областью изобразим ограничение .

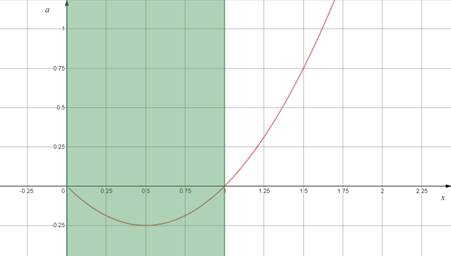
Рисунок 1

«Считывая» информацию с графика, видим, что .

Ответ: .

- В данном примере параметр а являлся функцией координаты , поэтому мы использовали КП-плоскость с вертикальной параметрической осью , однако есть и другой случай.

Замечание: Если координата  есть функция параметра :  неявно заданная уравнением , то на КП-плоскости  с горизонтальной параметриче­ской осью  множество всех точек, значения координаты  и параметр а каждой из которых удовлетворяют уравнению , представляет собой график функции , где роль аргумента функции играет параметр.

- Т.е. в зависимости от ситуации и рациональности решения, вы можете  выражать через параметр  или наоборот.

Задача №2. Для каждого значения параметра  решить уравнение  КП-методом.

Решение:

Для начала упростим исходное выражение до вида, т.е. чтобы координата  являлась функцией параметра :

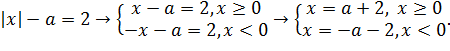
Т.к. , то можно рассматривать КП-плоскость  с горизонтальной параметриче­ской осью .

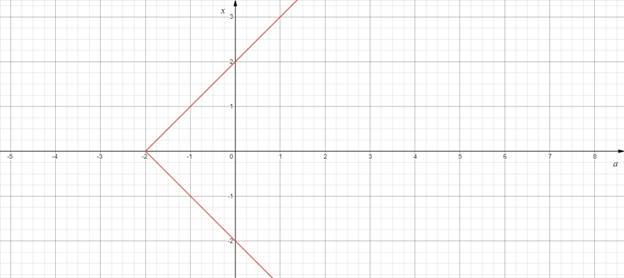
Рисунок 2

«Считывая» информацию с графика, получаем ответ.

Ответ: при ; при ; при .

- Очень часто встречаются не только уравнения с параметром, но и неравенства, для которых используется метод частичных областей.

Метод «частичных областей» - это метод, в котором реше­ние задачи в исходной области сводится к решению ее или совокупности более простых задач в каждой из «частичных областей», из которых составляется исходная область.

Применение МЧО при решении неравенств с парамет­рами во многом аналогично применению метода «интерва­лов» для решения неравенств с одной переменной.

Рассмотрим неравенство , где  — многочлен, аргументами которого являются переменная  и параметр .

Пусть уравнение  определяет некоторые линии  на КП-плоскости.

Разобьем этими линиями КП-плоскость на конечное число п «частичных областей» , ограниченных линиями .

В каждой из «частичных областей»  многочлен  отличен от нуля, так как точки, в кото­рых  принадлежат границе этих «частичных об­ластей» .

Справедлива теорема: В каждой из областей , на которые линии  делят КП-плоскость, мно­гочлен  либо положителен, либо отрицателен.

Таким образом, решение неравенства  — множест­во всех пар чисел , при которых неравенство выпол­няется, образует совокупность (объединение) тех областей , в которых значение многочлена  положительно.

Для установления, какое из неравенств  или  выполняется в данной области достаточно, например, вы­числить значение  в какой-нибудь определенной точ­ке этой области.

Сформулируем для неравенства , где  — некоторая функция пере­меной  и параметра  алгоритм МЧО на основе КП-метода.

1. Найдем на КП-плоскости ОДЗ (область допустимых значений переменной и параметра) — множество всех то­чек, при значениях координаты  и параметра  каждой из которых выражение  определено.

2. Построим на КП-плоскости линии, состоящие из всех точек, при значениях координаты  и параметра  каждой из которых выражение  обращается в нуль или не существует, и разобьем этими линиями найденную ОДЗ на «частичные области».

3. Исследуем знак выражения  в каждой из по­лученных «частичных областей». Для этого достаточно, на­пример, установить знак выражения  в какой-нибудь точке каждой из «частичных областей».

Решением рассматриваемого неравенства будут те из «частичных областей», в которых выражение  поло­жительно. Неравенство  решается аналогично.

Задача №3. Найти все значения параметра , при которых неравенство  выполняется при всех ,таких, что .

Решение: будем действовать по алгоритму

1. ОДЗ:

2.

Выразим координату  через функция параметра : ,

Изобразим данные линии на КП-плоскости с горизонтальной параметриче­ской осью , т.к. .

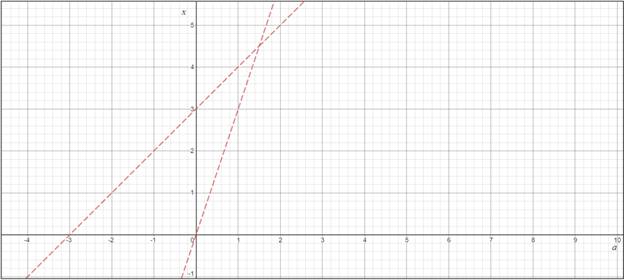
Рисунок 3

3. Исследуем знак выражения в каждой из по­лученных «частичных областей». Изобразим дополнительное условие .

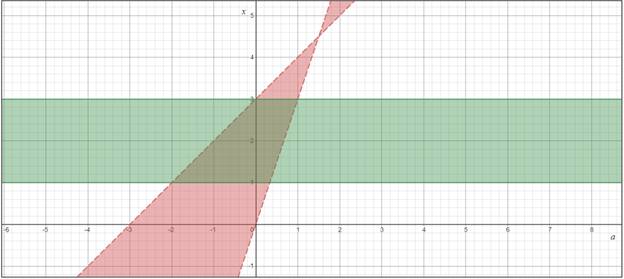
Рисунок 4

Искомыми будут значения параметра .

Ответ: .

- Замечание: Вы могли выразить параметр а через функцию координаты ,

тогда можно было рассматривать КП-плоскость  с вертикальной параметрической осью .

Задача №4. Найти все значения параметра , для каждого из которых выполняется неравенство  при всех  из отрезка .

Решение:

1. ОДЗ:

2.

Выразим параметр через функцию координаты :

.

Изобразим данные линии на КП-плоскости  с вертикальной параметрической осью , т.к. .

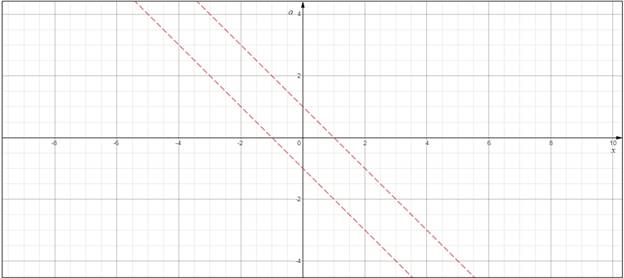
Рисунок 5

3. Исследуем знак выражения в каждой из по­лученных «частичных областей». Изобразим дополнительное условие .

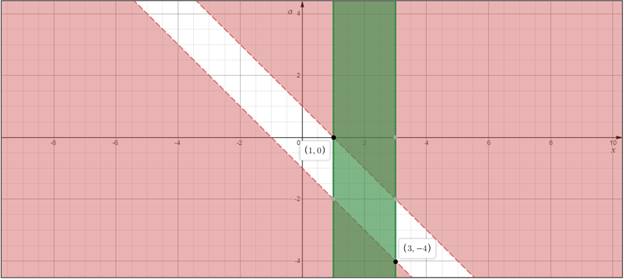
Рисунок 6

Искомыми будут значения параметра .

Ответ: .

Рефлексивно-оценочная часть.

- Какова была цель урока?

- (Изучить КП-способ решения уравнений с параметром вида  и ; изучить метод частичных областей (МЧО) для решения неравенств на КП-плоскости)

- Достигли мы её?

- (Да)

- Как мы её достигли?

- (Изучили определения КП-плоскости, КП-метода решений задач с параметрами, метода частичных областей на КП-плоскости; теоремы для выражений вида  и ; алгоритм решения неравенств МЧО на КП-плоскости).

Домашнее задание.

1. Найти все значения параметра , при которых уравнение  имеет решение.

Ответ: .

2. Найти все значения параметра , при которых неравенство  выполняется для всех  из промежутка .

Ответ: .

3. Найти все значения параметра , при которых неравенство  выполняется для всех .

Ответ:

Скачано с www.znanio.ru