Исследование функции с помощью производной, построение графика функции

Исследование функции с помощью производной, построение графиков функций. Общая схема исследования: 1. Найти область определения функции. 2. 3. Найти точки пересечения графика с осями координат (если это не вызывает  Выяснить является ли функция четной, нечетной или периодической. затруднений). 4. Найти асимптоты графика функции. 5. Найти промежутки монотонности функции и её экстремумы. 6. Найти промежутки выпуклости графика функции и точки перегиба. 7. Построить график. 9   6 2 х 3 х уD )( R . Пример.  Построить график функции  у  х 3 1. Функция определена на всей числовой прямой,  2. Функция не является ни четной, ни нечетной, ни периодической. 3. Найдем точки пересечения графика с осью Оу: полагая х=0, получим у=­3.  Точки пересечения графика с осью Ох найти затруднительно. График функции не имеет асимптот.  4. 5. Найдем производную:   3 2 х   делят область определения функции на 3 промежутка:  3 и   х 3 3 Решая уравнение  Точки  х 1 1х х , найдем   хи 1 ,  1 3 2 х  9  у 12 х х  х 12 0  3 х 1 1 9 . . .  2 2         __                             __  в промежутках  в промежутке  1                   1                 3 0у 0у   В точке  производная меняет знак с минуса на плюс , значит  у , т.е. функция убывает. 1х  х х 1 х 1  y  и   )3( 3 3 3 min . , т.е. функция возрастает, производная меняет знак с плюса на минус, а в точке  2 х 3   у max  y  1)1( , 6. Найдём вторую производную:  6  х у 12 . Решая уравнение  6 х 12 0 ,  найдем  Точка  и   2х 2х х .  делит область определения функции на 2 промежутка:  .  2 2 х           __                              2х                   2                  В промежутке   вверх, а в промежутке выпукла вниз. Таким образом получаем точку перегиба (2; ­1). 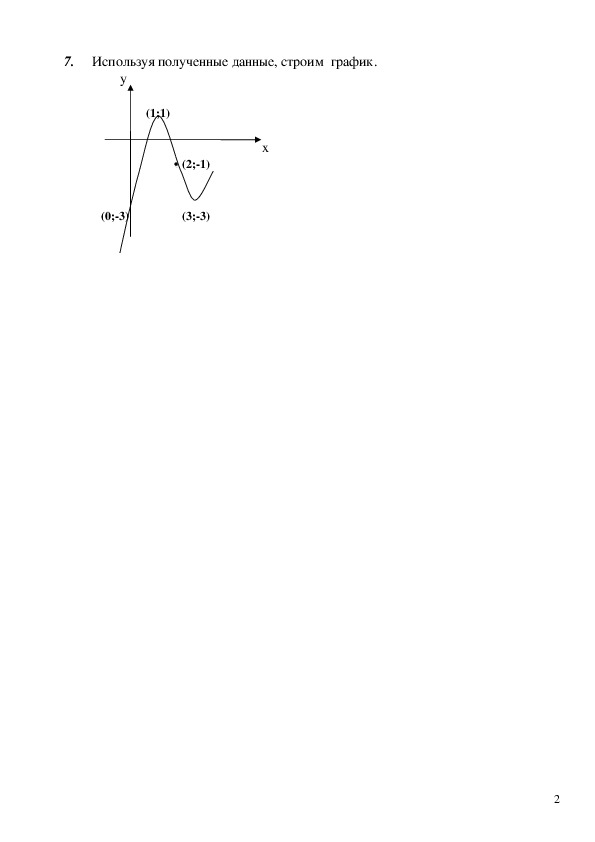0у    производная   производная  х 2 , следовательно, кривая выпукла  0у  , следовательно, кривая 7. Используя полученные данные, строим  график.                 у                   (1;1)       х     (2;­1)    (0;­3)     (3;­3) 2