Конспект урока геометрии в 10 классе Решение задач по теме Параллельность прямых, прямой и плоскости

10 класс геометрия                                           Урок № 11                                              Дата_______________

Тема: Решение задач по теме "Параллельность прямых, прямой и плоскости".

Цель урока: формировать умение решать задачи применяя признак параллельности прямой и плоскости. Воспитывать у учащихся точность, аккуратность. Развивать логическое мышление учащихся.

Планируемые результаты:

личностные: умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

метапредметные:

познавательные УУД: развивать основы логического и алгоритмического мышления; расширять кругозор учащихся; учить произвольно и осознанно владеть приемами решения задач, осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;

регулятивные УУД: формировать способность к мобилизации сил и энергии, к волевому усилию в преодолении препятствий, к осознанию уровня и качества усвоения результата.

коммуникативные УУД: учить строить высказывания, аргументировано доказывать свою точку зрения.

личностные: формировать устойчивую мотивацию к изучению и закреплению учебного материала; формировать навыки самоанализа и самоконтроля, взаимоконтроля.

предметные: повторить теоретический материал по теме «Параллельность прямой и плоскости»; закрепить умения: решать задачи на доказательство, опираясь  на точные аргументы(знания теоретического материала); при решении стереометрических задач применять знания, полученные при изучении планиметрии;

Формы работы: фронтальная, индивидуальная

Методы и приёмы: словесный, наглядный

Тип урока: формирование умений и навыков

Ход урока

1.       Организационный момент

2.       Проверка домашнего задания

Ответить на вопросы учащихся, сверить ответы. После выполнения самостоятельной работы в конце урока собрать тетради и проверить правильность решения.

3. Актуализация опорных знаний

Один ученик у доски доказывает признак параллельности прямой и плоскости.

Остальные отвечают на вопросы:

1. Какие две прямые в пространстве называются параллельными?
2. Сформулируйте теорему о параллельных прямых.
3. Какие возможны случаи взаимного расположение прямой и плоскости?
4. Какие прямая и плоскость называются параллельными?
5. Сформулируйте признак параллельности прямой и плоскости.
6. Дан куб А... D₁. Назовите четыре пары параллельных прямых и четыре пары пересекающихся прямых.

Выслушивается доказательство теоремы.

4. Формирование умений и навыков. Решение задач

1). Задача 1 (условие и рисунок к задаче записаны на доске)

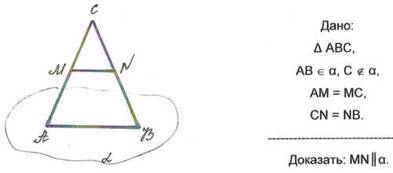
Доказательство

МN - средняя линия треугольника АВС, значит МN || АВ, АВ  a .

Таким образом, МN || a (по признаку параллельности прямой и плоскости). 

2). Задача 2 (условие и рисунок к задаче записаны на доске или на экране)

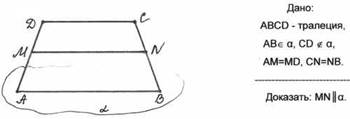
Доказательство

МN - средняя линия трапеции АВСD, значит МN || АВ; АВ  a (по условию),

Таким образом, МN || a (по признаку параллельности прямой и плоскости).

3). № 26 (Геометрия 10-11, Л.С. Атанасян и др.)

Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны.

Перед решением данной задачи необходимо вспомнить признаки подобия треугольников.

Доказательство

1. По утверждению 1° : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых).

2. угол В - общий.

З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN.

4). № 28 (Геометрия 10-11, Л.С. Атанасян и др.)

На сторонах АВ и АС треугольника АВС взяты соответственно точки D и E так, что ОE = 5 см и ВD = 2/3. Плоскость a проходит через точки B и С и параллельна отрезку ОE. Найдите длину отрезка ВС.

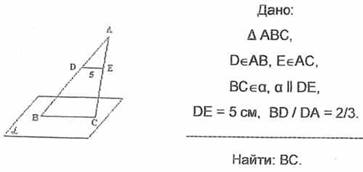
Решение:

Из условия задачи № 26: треугольник АВС подобен треугольнику АDЕ.

Тогда АВ/АD = ВС/DЕ, 5/3 = х/5, х = 25/3, х = 8¹/_3.

Ответ: 8¹/_3.

5.Подведение итогов урока

Самостоятельная работа

Вариант 1

1. В треугольнике АВС на стороне АВ выбрана точка D, такая, что BD : BA = 1 : 3. Плоскость, параллельная прямой АС и проходящая через точку D, пересекает отрезок ВС в точке D1.

а) Докажите, что треугольник DBD1 подобен треугольнику АВС

б) Найдите АС, если DD1 = 4 см.

Вариант 2

1. Точка D лежит на отрезке АВ, причем BD : BA = 1 : 4. Через точку А проведена плоскость α, через точку D – отрезок DD1, параллельный α. Прямая BD1, пересекает плоскость α в точке С.

а) Докажите, что треугольник DBD1 подобен треугольнику АВС

б) Найдите DD1, если АС =12 см

6. Домашнее задание: №27, № 30, № 31.