Конспект урока: "Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных"

Конспект  № 44

Тема: Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. 

Ход занятия

1. Организационный момент

Перед началом урока преподаватель проводит проверку подготовленности кабинета к занятию.

2. Мотивационный момент

В Америке несколько десятилетий назад была объявлена премия автору, который напишет книгу «Как человек без математики жил». Премия осталась невыданной. По-видимому, ни один из авторов не сумел изобразить жизнь человека без всяких математических знаний.

Вот и вы, наверняка, не представляете сейчас жизни без математики. Знания в области математики нужны нам как в обыденной жизни, так и для получения образования. Вы - выпускники и ваша задача на основе прочных математических знаний получить достойное образование. И цель сегодняшнего урока – максимально использовать все свои знания по  решению систем уравнений.

На доске плакаты с пословицами.

- Набирайся ума в ученье, храбрости в сраженье.

- Без муки нет науки.

- Была бы охота - заладится всякая работа.

- Математика – гимнастика ума.

- Ребята, прочитайте пословицы. Выберите наиболее понравившуюся народную мудрость. Скажите, почему вы выбрали именно эту пословицу? Чем она вам так понравилась, в чём её смысл? Может она помогла вам поставить перед собой цель на сегодняшний урок?

А мне нравится “ Математика – гимнастика ума”.

- Что такое гимнастика?

Гимнастика – это система упражнений для физического развития человека;

гимнаст – человек ловкий, стройный, сильный, пластичный, красивый.

Также много даёт математика для умственного развития человека - заставляет думать, соображать, искать простые и красивые решения, помогает развивать логическое мышление, умение правильно и последовательно рассуждать, тренирует память, внимание, закаляет характер.

3.  Актуализация опорных знаний

3.1. Устная работа.  

- Давайте мы с вами проведем небольшую математическую гимнастику. Для этого устно выполним упражнения.

3.2. Фронтальный опрос

- Разминку мы провели, а теперь перейдем к более сложным упражнениям.

- Что значит: решить систему уравнений? – Решить систему – это значит найти пару значений переменных, которая обращает каждое уравнение системы в верное равенство.

- Какие способы решения систем вы знаете? – подстановки, сложения и графический, замены переменных.

4.Изучение нового материала 

4.1. Определение системы уравнений.

Определение. Системой уравнений называют совокупность нескольких уравнений с несколькими неизвестными.

Определение. Решением системы уравнений называют совокупность значений этих неизвестных, обращающих каждое уравнение системы в тождество.

4.2. Основные методы решения систем уравнений

- Какой метод вы выберите для решения следующих систем? Суть метода подстановки?

1.        Способ подстановки:

Алгоритм использования метода подстановки:

1. Выразить из какого-нибудь уравнения системы одну переменную через другую.

2. Подставить в другое уравнение системы вместо этой переменной равное ему выражение.

3. Решить получившееся уравнение с одной переменной.

4. Найти соответствующее значение второй переменной

5. Записать ответ.

Из одного уравнений системы выражаем одно неизвестное через другие и подставляем в оставшиеся уравнения системы.

2.      Метод алгебраического сложения

- Суть метода алгебраического сложения. Решить систему методом алгебраического сложения:

Алгоритм использования метода алгебраического сложения:

1. Уравнять модули коэффициентов при какой-нибудь переменной.

2. Сложить или вычесть почленно левые и правые части уравнений системы.

3. Решить получившееся уравнение с одной переменной.

4. Найти соответствующее значение второй переменной

5. Записать ответ.

3m+2n=0,5,

2m+5n=4.

3.      Графический метод решения.

- Суть графического метода.

Алгоритм использования графического метода:

1.Построить графики уравнений в одной системе координат.

2. Найти координаты точки пересечения или указать, что таких точек нет.

3. Записать ответ.

4.      Метод введения новой переменной.

Алгоритм использования метода введения новых переменных:

1. Ввести одну или две новые переменные.

2. Записать новое уравнение или систему уравнений.

3. Решить новое уравнение или систему уравнений и найти значения введённых переменных.

4. Сделать обратную замену и найти значения переменных из условия.

5. Записать ответ.

5. Первичное применение приобретенных знаний

5.1. Работа у доски.

Решить систему уравнений тремя различными методами (графическим, подстановкой и сложением)

1 метод -графический

1)   Графиком этой функции является парабола, «ветви» направлены вверх, вершина в точке (0;-4)

2)     Графиком этой функции является прямая.

Точки пересечения (1;-3);(-3;5).               Ответ: (1;-3);(-3;5).

2 метод-подстановка.

Решение: Из второго уравнения выражаем у:  .

Подставляем в первое уравнение:

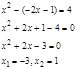
Если , то

Если , то                  Ответ: (1;-3);(-3;5).

3 метод - алгебраическое сложение

       Сложим уравнения системы, получим:

Если , то

Если , то               Ответ: (1;-3);(-3;5).

- Какой из способов решения системы вам понравился больше?

1. Решить системы уравнений методом подстановки.

 3                       

  4 

2. Решить системы уравнений методом сложения.

                                         3 

3. Решить системы уравнений графическим методом:

5.2. Тест по теме «Основные приемы решения систем уравнений»

Ответы: В1  -  2 2 1 3 2 4 3 4,            В2 – 3 3 4 2 1 1 4 3

6.      Подведение итогов. Рефлексия.

-  Чему мы научились на сегодняшнем уроке? (Решать системы уравнений способом замены переменной)

- Что необходимо сделать,  для того чтобы решить систему уравнений таким способом? (сделать замену переменной, решить новое уравнение, выполнить обратную замену)

- Что было наиболее сложным (трудным)?

- Какие вопросы остались после проведения занятия?

    7. Домашнее задание. Л 5.п.4.5 № 4.21 (а,б)

Тест по теме «Основные приемы решения систем уравнений»

Вариант 1

А1. Решите систему уравнений 
1)  2)  3)  4) 

А2. Пусть  - решение системы линейных уравнений  
Найдите . 1)  2)  3)  4) 
А3. Пусть  - решение системы линейных уравнений  
Найдите . 1)  2)  3)  4) 
А4. Пусть  - решение системы линейных уравнений  
Найдите . 1)  2)  3)  4) 
А5. На каком из рисунков изображено графическое решение системы линейных уравнений 

А6. Найдите координаты точки пересечения графиков уравнений  и .
1)  2)  3)  4) 
А7. Сколько точек пересечения имеют графики уравнений и ? 
1) 1       2) 2            3) бесчисленное количество               4) ни одной
А8. Сколько решений имеет система уравнений  
1) 1              2) 2               3) бесчисленное количество                    4) ни одного

Вариант 2

 А1. Решите систему уравнений 
1)  2)  3)  4) 
А2. Пусть  - решение системы линейных уравнений  
Найдите . 1)  2)  3)  4) 
А3. Пусть  - решение системы линейных уравнений  
Найдите . 1)  2)  3)  4) 
А4. Пусть  - решение системы линейных уравнений  
Найдите . 1)  2)  3)  4) 
А5. На каком из рисунков изображено графическое решение системы линейных уравнений 

А6. Найдите координаты точки пересечения графиков уравнений  и .
1)  2)  3)  4) 
А7. Сколько точек пересечения имеют графики уравнений и ? 
1) 1           2) 2                  3) бесчисленное количество                          4) ни одной
А8. Сколько решений имеет система уравнений  
1) 1                2) 2                     3) бесчисленное количество                          4) ни одного

Скачано с www.znanio.ru