Поделиться
Лекция 4.4.docx
Раздел 3. Введение в анализ. Дифференциальные исчисления.
Лекция № 4. Функции многих переменных. (Функции двух и нескольких переменных, способы задания, символика, область определения.) (2часа)
План лекции.
Литература:
1. Электронный ресурс. О3 Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440 - п.9.1 - 9.16, стр.10.
Формируемые знания, компетенции:
ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».
ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.
З2.Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;
З5.Структуру плана для решения задач;
З6.Порядок оценки результатов решения задач профессиональной деятельности.
Основные понятия:
Функция
двух переменных определяется следующим образом. Рассматривается множество 
пар чисел. При этом имеются в виду
упорядоченные пары, т.е. две пары чисел 
и 
считается равными (совпадающими) тогда и
только тогда, когда 
и 
. Если в силу некоторого закона f каждой паре 
ставится в соответствие одно и только одно
число z, то говорят, что
этим на множестве E определена функция 
от двух переменных x и y.
Линией
уровня
функции 
является такая кривая на плоскость XOY, в точках которой
функция 
сохраняет постоянное значение z=C, т.е. 
. При изменении значений C получается
семейство кривых.
Поверхностью
уровня
функции 
называется поверхность 
в пространстве XYZ, в точках которой
функция 
сохраняет постоянное значение C. Примером
поверхностей уровня могут служить эквипотенциальные поверхности, где земной
потенциал принимает постоянное значение. Например, эллипсоид Красовского,
используемый в геодезии и картографии.
Функция
имеет в точке 
предел, равный числу A, т.е. 
при стремлении к точке 
, если для любого сколь угодно малого
числа
существует число 
такое, что 
для всех точек M, удовлетворяющих
неравенству 
.
Пусть
точка 
принадлежит области E определения
функции и любая 
– окрестность точки 
содержит точки 
, отличные от 
. Функция
называется непрерывной в точке 
, если 
Функцию
двух переменных
можно дифференцировать по переменным x и y. Эти производные
называются частными производными и по определению
и 
, если эти пределы конечны.
Частными производными второго порядка от функции нескольких переменных называются первые частные производные от уже вычисленных первых частных производных.
Например,
для функции двух переменных 
частные производные 2-го порядка имеют
вид:
или 
или 
Смешанная
производная: 
; 
.
Главная
линейная относительность 
и 
часть полного
приращения 
называется дифференциалом 
функции 
. 
- бесконечно малая высшего порядка
относительно 
.
Пусть
функция 
дифференцируема, тогда производная
функции в точке 
в направлении 
, задаваемом, направляющими косинусами 
, имеет вид:
Градиентом функции 
в точке 
называется вектор с началом в точке 
и координатами 
и обозначается:
.
В предыдущих разделах курса высшей математики речь шла о функциях одной переменной. Но можно говорить также о функциях двух, трёх и вообще n переменных.
Функция
двух переменных определяется следующим образом. Рассматривается множество 
пар чисел. При этом имеются в виду
упорядоченные пары, т.е. две пары чисел 
и 
считается равными (совпадающими) тогда и
только тогда, когда 
и 
. Если в силу некоторого закона f каждой паре 
ставится в соответствие одно и только одно
число z, то говорят, что
этим на множестве E определена функция 
от двух переменных x и y.
Функцию 
от двух переменных можно изобразить в
трёхмерном пространстве, где введена прямоугольная система координат XYZ, в виде
геометрического места точек 
, проекция которых 
в плоскости XOY принадлежит
множеству определения E функции 
. Область определения функции 
в простейших случаях представляет собой
либо всю плоскость, либо часть плоскости, ограниченную замкнутой кривой, причём
точки этой кривой границы области – могут принадлежать или не принадлежать
области определения. Геометрическим изображением функции 
в прямоугольной системе координат, т.е.
графиком функции, является поверхность.
Пример 1:
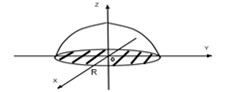
Функция 
геометрически представляет собой верхнюю
полусферу радиуса R с областью определения E: 
, являющуюся кругом радиуса R в плоскости XOY.
Аналогичным
образом можно определить функцию трёх переменных 
, определённую на множестве 
, представляющим собой некоторую область
в трёхмерном пространстве, её можно изобразить геометрически. А саму функцию 
геометрически интерпретировать невозможно.
Примером функции трёх переменных может служить, например, распределение плотности и температур на поверхности и внутри земного шара.
Если две функции f и 
определены на
одном и том же множестве E, то можно определить сумму 
, разность 
, произведение 
и частное 
. Естественным образом определяются также
сложные функции 
двух переменных и большего числа
переменных.
Частным значением
функции 
в точке
называется значение 
.
Пример 2: Найти частное
значение функции 
в точке 
.
Решение: 
Пример 3: Найти частное
значение функции 
в точке 
.
Решение: 
Линией уровня функции 
является такая кривая на плоскость XOY, в точках которой
функция 
сохраняет постоянное значение z=C, т.е. 
. При изменении значений C получается
семейство кривых. Например, на географических картах линиями уровня являются
линии равных высот рельефа.
Пример 4: Найти линии
уровня функции 
.
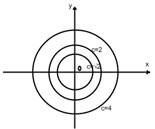
Решение: Семейство линий
уровня имеет вид 
и представляет концентрические окружности
с центром в начале координат, радиус которых 
изменяется в зависимости от задания C.
Поверхностью
уровня
функции 
называется поверхность 
в пространстве XYZ, в точках которой
функция 
сохраняет постоянное значение C. Примером
поверхностей уровня могут служить эквипотенциальные поверхности, где земной
потенциал принимает постоянное значение. Например, эллипсоид Красовского,
используемый в геодезии и картографии.
Определение 1. Функция 
имеет в точке 
предел, равный числу A, т.е. 
при стремлении к точке 
, если для любого сколь угодно малого
числа
существует число 
такое, что 
для всех точек M, удовлетворяющих
неравенству 
.
При этом функция 
определена в
некоторой окрестности точки 
, за исключением, быть может, самой точки 
.
Так,
например, для функции двух переменных 
пределом функции в предельной точке 
, называется число A, т.е.
, если для 
существует 
такое, что 
для всех точек 
, удовлетворяющих
условию 
.
Кстати,
стремление к точке 
плоскости XOY может
осуществляться по любому пути, а это означает, что предел функции двух или
большего числа переменных должен существовать при любых путях стремления к
предельной точке.
Определение
непрерывности функции 
нескольких переменных в точке 
аналогично определимо непрерывности
функции одной переменной.
Определение 2. Пусть точка 
принадлежит области E определения
функции и любая 
– окрестность точки 
содержит точки 
, отличные от 
. Функция
называется непрерывной в точке 
, если 
Точки в которых это не имеет места называются точками разрыва данной функции.
Функцию двух
переменных
можно дифференцировать по переменным x и y. Эти производные
называются частными производными и по определению
и 
,
если эти пределы конечны.
Частная
производная 
вычисляется по переменной x при фиксированном
y, а 
вычисляется по переменной y при фиксированном
x. При вычислении
производных справедливы обычные правила и формулы дифференцирования, потому
что, как видно из определения, техника вычисления проводится по правилу
дифференцирования функции одной переменной, а остальные переменные считаются
константами.
Совершенно
аналогично вычисляются частные производные 
функции трёх переменных 
.
Пример 1: Найти частные
производные 
функции 
.
Решение: При вычислении 
считаем x переменной
величиной, а y зафиксируем. Тогда 
Аналогично при
вычислении 
переменной считается 
, а – фиксированным,
тогда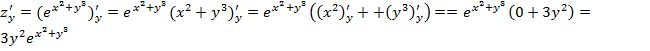 
Пример 2: Вычислить
производные 
в точке 
Функции 
.
Решение:
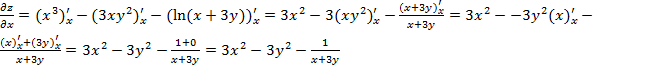
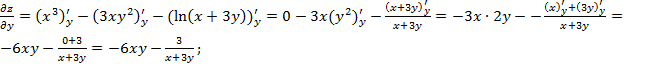
Вычисляем
производные в точке
Частными производными второго порядка от функции нескольких переменных называются первые частные производные от уже вычисленных первых частных производных.
Например, для
функции двух переменных 
частные производные 2-го порядка имеют
вид:
или 
или 
Смешанная производная:
; 
Другое обозначение
смешанной производной 
.
Существует
теорема: Если функция 
определена в некоторой окрестности точки 
и в самой точке смешанные производные 
и 
непрерывны, то они равны.
Подобная теорема имеет место для функция любого числа переменных и для смешанных производных более высокого порядка.
Дифференцирование
вторых производных даёт частные производные 3-го порядка: 
Последовательным многократным дифференцированием можно получить частные производные любого порядка.
Пример: Вычислить
частные производные второго порядка функции 
в точке 
.
Решение: Сначала найдём частные производные 1-го порядка:
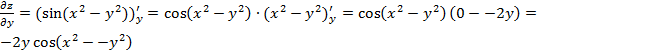
Частные производные 2-го порядка:
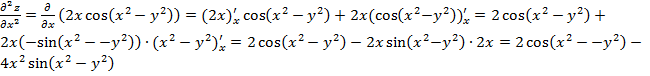
Вычислим эту
производную в заданной точке 
:
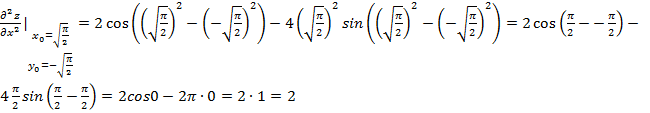
Далее: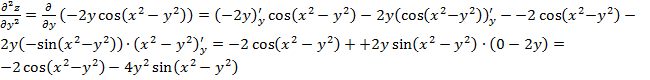 
Значение
производной в точке 
:
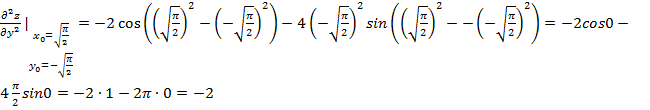
Смешанная производная:
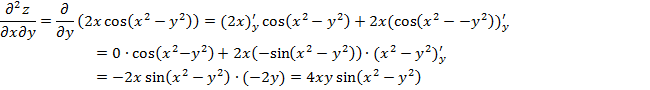
Её значение в точке:
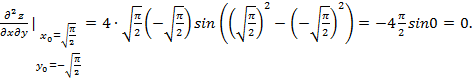
4. ДИФФЕРЕНЦИАЛЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Функция 
называется дифференцируемой в точке M если её полное
приращение 
в этой точке может быть представлено в
виде 
.
Главная линейная
относительность и часть полного
приращения 
называется дифференциалом 
функции 
. 
- бесконечно малая высшего порядка
относительно
.
Если функция
дифференцируема в точке M, то в этой точке существуют производные 
, и дифференциал функции имеет вид
.
Для
функции 
дифференциал I-го порядка имеет
вид:
Дифференциал I-го обладает
свойством инвариантности, т.е. его форма не меняется в случае, если переменные
сами являются функциями других переменных. Так, если 
и 
, то
.
2. Дифференциалы высших порядков.
Дифференциалом 2-го порядка называют дифференциал от дифференциала I-го порядка, т.е.
Аналогичным
образом определяются 
Имеет место символическая формула 
Например:
Пример 1: Найти 
и 
функции 
, вычислить их в точке 
Решение: Найдём частные производные I-го и 2-го порядков:
;
; 
(Кстати 
.
В общем виде дифференциалы имеют вид:
Вычислим
производные в точке 
: 
; 
;
; 
; 
;
И тогда 
Пример 2: Найти
дифференциал I-го порядка
функции 
Решение: 
Найдём частные производные:
И тогда: 
5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНЫХ ФУНКЦИЙ.
Задана функция 
, где переменные 
и
являются
функциями переменных 
и 
, т.e. 
и
, а 
Если функции 
дифференцируемы, то:
.
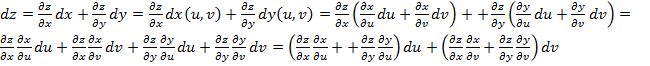Если воспользоваться свойством инвариантности дифференциала I-го порядка, то:
.
При дифференциалах
и 
стоят выражения
для частных производных сложной функции, а именно:
Пример: 
где 
Найти 
и 
. Вычислить их в точке 
.
Решение: 
Вычисление в точке
: 
Тогда: 
Пусть задана
функция 
, где 
и 
. В этом случае 
, т.е. функция z является функцией
одной переменной. Поэтому:
.
Отсюда можно получиться выражение для полной производной:
Пример: 
, где 
, 
. Найти 
. Вычислить при 
.
Решение:
; 
;
Тогда: 
;
Вычислим при 
: 
Пусть
задана функция 
, где 
, тогда 
- функция одной переменной. Полная
производная:
Пример: Найти частную
производную 
и полную производную 
, если 
, а 
Решение: 
; 
; 
;
.
Вычислим при 
; 
тогда:
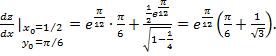
6. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ ФУНКЦИЙ.
Пусть
функция 
задана уравнением, не разрешенным
относительно символа функции, т.е. уравнением вида
. Будем считать, что функция 
– как функция трёх переменных,
дифференцируема. Тогда дифференциал
и имеет вид:
Выразив
отсюда 
, проучим 
. А так как, с другой стороны, 
, то выражения для частных производных
неявно заданной функции имеют вид:
; 
.
Если
неявно задана функция одной переменной 
уравнением 
, то производная 
определяется аналогичной формулой 
.
Пример 1: Найти значение
производной 
функции 
в точке 
Решение: В нашем случае 
Находим частные
производные 
и 
функции двух переменных 
:
Производная
функции 
Её значение в
точке 
: 
Пример 2: Вычислить
дифференциал 
в точке 
функции 
, заданной
уравнением 
Решение: Найдём 
Их значения в
точке 
соответственно 
;
И следовательно 
7. ПРОИЗВОДНАЯ ФУНКЦИИ В ДАННОМ НАПРАВЛЕНИИ. ГРАДИЕНТ ФУНКЦИИ.
Пусть функция 
дифференцируема,
тогда производная функции в точке 
в направлении 
, задаваемом, направляющими косинусами 
, имеет вид:
Градиентом
функции 
в точке 
называется вектор с началом в точке 
и координатами 
и обозначается:
Градиент функции
связан с производной по направлению в одной и той же точке очевидным
соотношением 
.
В
случае произвольного задания вектора направления 
его направляющие косинусы вычисляются по
формулам:
.
Для функции двух
переменных 
выражения для производной по направлению
и градиента имеют вид:
Производная
по направлению характеризует скорость возрастания функции в направлении вектора
. Градиент указывает направление
наибыстрейшего роста функции в данной точке. Производная 
в направлении градиента имеет наибольшее
значение, равное:
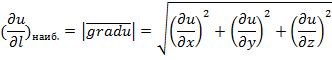
Вектор 
в данной точке 
ортогонален к той поверхности уровня
функции 
, которая проходит через точку 
.
Пример: Дана 
, точка 
и 
Найти производную по направлению в точке A в направлении
вектора 
, градиент функции в точке B и его модуль.
Решение: Найдём частные
производные функции 
и вычислим их в точках 
: 
; 
; 
;
; 
; 
;
; 
; 
;
Найдём
направляющие косинусы вектора 
Т.к. 
, то 
, 
, 
Тогда 
8. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.
Касательной
плоскостью
к поверхности в точке 
называется плоскость, содержащая в себе
касательные ко всем кривым, проведенным на поверхности через точку
.
Нормалью к
поверхности в точке 
называется прямая, проходящая через точку
перпендикулярно касательной плоскости в
этой точке.
Поверхность в
пространстве можно рассматривать как поверхность уровня функции 
, проходящую через точку 
Вектор 
в точке 
ортогонален поверхности, т.е. ортогонален
касательной плоскости, проходящей через эту точку. Тогда вектор нормали 
.
В случае задания
поверхности явным уравнением 
к предыдущему случаю легко перейти, записав
, и тогда вектор нормали 
=
.
Уравнение касательной плоскости в первом случае
или во втором случае
Уравнения нормальной прямой или нормали соответственно
или 
Примеры.
1. Написать уравнения
нормали и касательной плоскости в точке
к поверхности 
Решение. Частные
производные функции 
.
Их значения в точке
Уравнение
нормали 
Уравнение касательной плоскости
2. Написать уравнения нормали и касательной плоскости в точке c
к поверхности 
Решение. Аппликата 
точки касания 
. Частные производные 
,
их значения в
заданной точке 
.
Уравнение
нормали 
.
Касательная
плоскость 
или
9. ФОРМУЛА ТЕЙЛОРА.
Если функция 
дифференцируема в точке 
и ее окрестности n раз, то для
всякой точки 
из окрестности точки 
справедлива формула Тейлора
Где 
- остаточный член, который может быть
записан в различной форме.
Если 
, то формула называется формулой
Маклорена.
Формула 
называется формулой линеаризации
функции.
Так как 
а 
, то формула линеаризации имеет вид
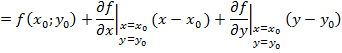
Пример. Функцию 
1) разложить по
формуле Тейлора в окрестности точки 
до членов 2го порядка
включительно;
2) линеаризовать ее в окрестности этой точки.
Решение. 1) Разложение до членов второго порядка включительно имеет вид
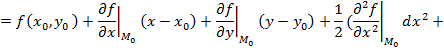
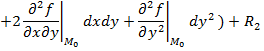
Вычислим частные производные 1ого порядка в точке (1; 1):
Дифференциал первого порядка в этой точке
Вычислим частные производные 2ого порядка в точке (1;1):
Дифференциал второго порядка в этой точке
Подставляем найденные значения дифференциалов в выражение формулы Тейлора
3. Линеаризованное
выражение функции 
в точке 
Функция 
имеет в точке 
, принадлежащей области определения
функции, максимум (минимум), если существует такая окрестность точки 
, что 
для любых точек 
из окрестности точки 
.
Если
дифференцируемая функция 
достигает в точке 
экстремума, то в этой точке 
или не существуют.
Такие точки называются стационарными или критическими.
Пусть 
- стационарная точка. Если функция 
дважды дифференцируема в окрестности точки
и вторые частные производные непрерывны,
то если
1) дискриминант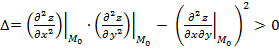 
в этой точке существует экстремум,
причем минимум, если 
, и максимум, если 
;
2) если 
, то экстремумов
нет;
3) если 
, то ответа на вопрос
нет, необходимо проделать более тонкие исследования, например геометрические.
Пример. Найти экстремумы
функции 
Решение.
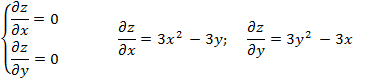
Решение системы 
и 
проверим выполнение достаточных
условий.Частные производные второго порядка
a) 
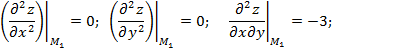
Тогда 
, следовательно, в точке 
экстремума нет.
b)
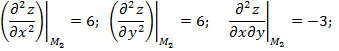
Тогда 
, следовательно, в точке 
экстремум есть. Причём минимум, т.к. 
.
Минимальное
значение функции 
-1.
Вопросы для закрепления:
1. Понятие функции нескольких переменных.
2. Предел и непрерывность функции двух переменных.
3. Дифференцирование функций.
4. Дифференциалы функций нескольких переменных.
5. Дифференцирование сложных функций.
6. Дифференцирование неявных функций.
7. Производная функции в данном направлении. Градиент функции.
8. Касательная плоскость и нормаль к поверхности.
9. Формула Тейлора.
10. Экстремумы функции двух переменных.
Для подготовки к самостоятельной работе:
1. Прочитать учебник О3: п. 9.1 – 9.11, стр. 10.
2. Выучить лекцию.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
