Конспект урока "Площадь ортогональной проекции"

Занятие № 25 (теоретическое)

Площадь ортогональной проекции

Изображение пространственных фигур

Решение прикладных задач

Цели урока:

ü обучающие: 

·          сформировать навыки нахождения ортогональной проекции многоугольника,

·          показать на конкретных примерах нахождение угла между плоскостями с помощью теоремы о площади ортогональной проекции многоугольника.

ü развивающие:

·        способствовать развитию логического мышления и пространственного воображения учащихся при решении задач;

ü воспитывающие:

·        воспитание познавательного интереса к предмету.

·        пробуждение устойчивого интереса к предмету и активизации познавательной деятельности обучающихся; 

·        воспитание интереса к своей профессии;

Тип урока: урок изучения нового материала

Время: 1 час 30 мин.                    

Средства обучения:

Компьютер на рабочем месте преподавателя, модели с геометрическими фигурами, маркерная доска.

Методы проведения: словесный, наглядный, деятельностный. 

Ход урока

1. Организационный момент.

Включает в себя приветствие преподавателем группы, подготовку помещения к уроку, проверку отсутствующих.

Проверка домашней работы.

2. Постановка цели урока.

Сегодня мы познакомимся с новой темой урока «Геометрические преобразования пространства».

3. Актуализация опорных знаний.

4 . Изучение нового материала.

Ортогональная проекция точки на прямую или на плоскость в стереометрии определяется так же, как проекция точки на прямую в планиметрии. А именно если точка не лежит на данной прямой (плоскости), то ортогональной проекцией точки на прямую (на плоскость) называется основание перпендикуляра, опущенного из этой точки на данную прямую (плоскость).

Если же точка лежит на прямой (на плоскости), то она и есть своя проекция на эту прямую (плоскость) (рис.1, а). Проекцией же фигуры F на плоскость α называется фигура F', состоящая из проекций всех точек фигуры F на эту плоскость (рис.1, б).

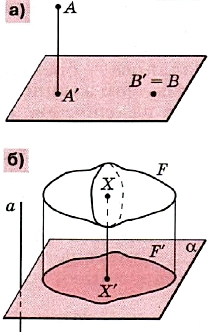
Рис. 1

Поскольку все прямые, перпендикулярные одной плоскости, параллельны друг другу, то ортогональное проектирование на плоскость является частным случаем параллельного проектирования и тем самым обладает всеми свойствами параллельного проектирования.

Кроме точек и отрезков, рисуя изображение сферы, цилиндра или конуса, мы будем встречаться с проекцией окружности на плоскость (когда плоскость окружности не перпендикулярна плоскости проекции). Кривая, которая является проекцией окружности в этом случае, называется эллипсом (рис.2, а). Эллипсом является и параллельная проекция окружности на плоскость (если направление проектирования не параллельно плоскости окружности). Если плоскость окружности параллельна плоскости проекции, то проекцией, очевидно, является равная ей окружность (рис.2, б). Поэтому окружность является частным случаем эллипса. Эллипсы обладают многими замечательными свойствами. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии.

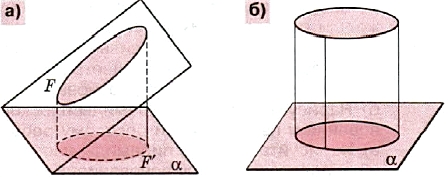
Рис. 2

Ортогональное проектирование на одну, две и три плоскости широко используется в технике, в черчении. Изображение предмета в проекциях позволяет судить о его устройстве, без чего невозможно ни конструирование предмета, ни его изготовление.

В дальнейшем, говоря «проекция» или «проектирование», мы имеем в виду ортогональное проектирование и ортогональную проекцию, если нет специальных оговорок.

На ортогональном проектировании основан такой важный для инженеров раздел прикладной математики, как «Начертательная геометрия».

Расстояние от точки до фигуры

Расстояние от точки до фигуры измеряется по кратчайшему пути. Поэтому расстоянием от данной точки А до фигуры F называется расстояние от этой точки до ближайшей к А точке фигуры F. Точка фигуры F, ближайшая к А, — это такая точка B ∈ F (рис.3), что для всех точек X фигуры F |АВ|≤ |АХ|.

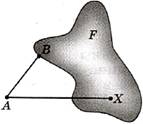
Рис. 3

Иначе говоря, если точка А не принадлежит фигуре F, то отрезок АВ — кратчайший из всех отрезков АХ, соединяющих точку А с точками фигуры F. (Если же A ∈ F, то ясно, что точка А оказывается ближайшей к самой себе. В дальнейшем случай, когда A ∈ F, мы не рассматриваем.)

Расстояние от точки А до фигуры F обозначаем | AF |.

Рассмотрим несколько простых примеров.

1.     Расстояние от точки А до прямой а равно длине перпендикуляра, опущенного из точки А на прямую а. Обозначаем его | Аа |.

2.     Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость, или, что то же, расстоянию от точки до её проекции на плоскость.

Эти два утверждения вытекают из того, что перпендикуляр короче наклонной.

3.     Расстояние от центра окружности до самой окружности равно радиусу. Все точки окружности находятся на одном расстоянии от центра, они все ближайшие к нему.

Понятие ближайшей точки даёт возможность получить интересное обобщение теоремы о трёх перпендикулярах.

Заменим в этой теореме прямую а на произвольную фигуру F в плоскости α (рис. 4).

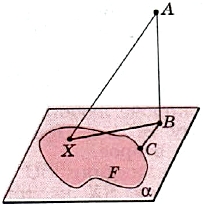
Рис.4

Замечание.

1.     Из теоремы о ближайшей точке следует такое утверждение: из данной точки А в ближайшую точку плоской фигуры F можно попасть так: сначала в ближайшую к А точку В самой плоскости, а потом из точки В в ближайшую к ней точку фигуры F.

Площадь проекции многоугольника

Вам хорошо известно, что длина с отрезка АВ и длина с' его проекции А'В' на некоторую прямую р (или плоскость α) связаны равенством

с' = с cos φ,

где φ — угол наклона прямой АВ к прямой р или к плоскости α (рис.5). Если φ ≠ 0° или φ ≠ 90°, то это равенство выражает длину катета с' прямоугольного треугольника через длину с его гипотенузы и косинус прилежащего к катету острого угла φ.

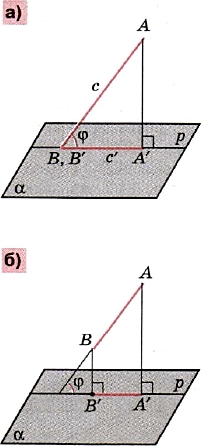
Рис. 5

Теорема о трёх перпендикулярах позволяет доказать аналогичную формулу

S' = S cos φ

для площади S некоторой фигуры F и площади S её проекции F' на некоторую плоскость α. Угол φ в равенстве— это угол наклона плоскости β, в которой лежит фигура F, к плоскости α (рис. 6).

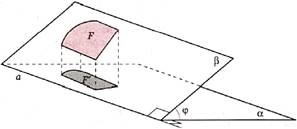
Рис.6

Равенство S' = S cos φ очевидно для случая, когда φ = 90° (в этом случае F' лежит на прямой и S' = 0, а также cos 90° = 0), и для случая, когда φ = 0° (в этом случае плоскости α и β параллельны или совпадают, фигура F' равна фигуре F и cos 0° = 1). Поэтому будем считать, что угол φ острый.

Докажем равенство для случая, когда фигура F — некоторый треугольник ABC. Прямую, по которой пересекаются плоскости α и β, обозначим через а. Если сторона АВ лежит на α, то высота С'Н треугольника ABC' является проекцией высоты СН треугольника ABC (по теореме о трёх перпендикулярах, рис.7, а).

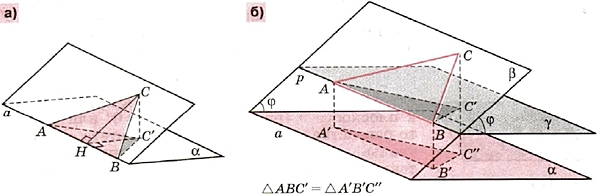
Рис.7

Тогда С'Н = СН cos φ и S' = 0,5АВ • C'H = 0,5ABC • CH cos φ = S cos φ.

Для случая, когда АВ лежит на а, равенство доказано.

Если сторона АВ параллельна прямой а, то проведём через прямую АВ плоскость γ, параллельную плоскости α, и сведём доказательство равенства к уже рассмотренному случаю (рис.7, б).

Пусть у треугольника ABC нет сторон, параллельных прямой а (или лежащих на α). Тогда через одну из его вершин (например, через вершину А) проходит прямая р, параллельная прямой а, которая разбивает треугольник ABC на два треугольника АВР и АСР, у которых уже есть такая сторона АР (рис.8). Тогда

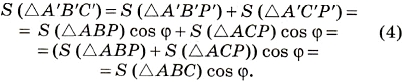
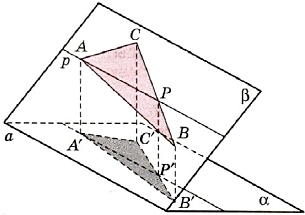
Рис. 8

Равенство S' = S cos φ доказано для любых треугольников.

Если фигура F — многоугольник, то, разбивая её на треугольники, доказываем равенство аналогично тому, как это было доказано в цепочке равенств  (рис.9).

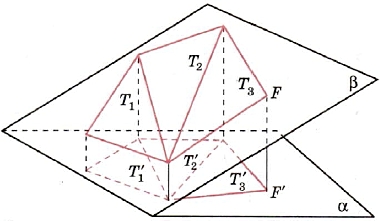
Рис. 9

Изображение пространственных фигур на плоскости

Изображения треугольной пирамиды при соответствующем выборе направления проектирования.

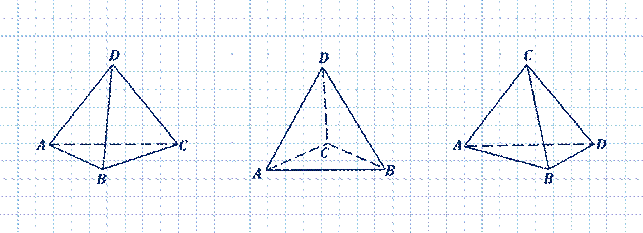
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.

При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.

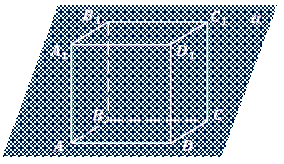
Аналогичным образом изображается прямоугольный параллелепипед.

Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.

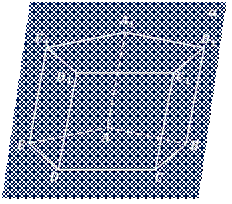
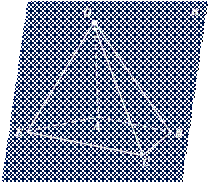
Для того чтобы построить изображение любой пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.

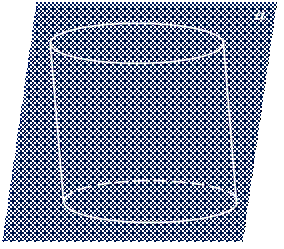
Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.

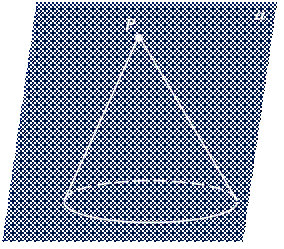
Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.