Конспект урока по алгебре и началам анализа. Решение логарифмических уравнений и неравенств

Тема. Логарифмическая функция. Логарифмические уравнения и неравенства

Цель: 1.Ввести алгоритм решения логарифмических уравнений, используя свойства логарифмов и логарифмической функции.

Научиться решать логарифмические уравнения, используя различные способы решения. Показать применение темы на итоговой аттестации.

2. Развивать умение обобщать учебный материал, выделять главное и применять в решении.

3. Воспитывать интерес к предмету.

I. Организационный момент.

Сегодня мы начнем изучать тему Логарифмические уравнения  и неравенства

 Мы научимся решать различные виды логарифмических уравнений, рассмотрим разные способы и алгоритмы их решения. начиная с элементарных, с которыми мы уже познакомились на прошлом уроке при изучении свойств логарифмической функции. Также посмотрим применение этой темы на едином государственном экзамене. Для того, чтобы хорошо усвоить эту тему, нужно хорошо знать свойства логарифмов и логарифмической функции. С этого и начнем.

Что из себя представляет логарифмическая функция?

 например, какие свойства имеет эта функция? ( убывающая, ооф)

Примеры возрастающих? Убывающих ? Что объединяет эти функции?  -точка (1;0), ооф, множество значений функции. Посмотрим на экран.

Используя свойства функций можно сравнивать значения логарифмов и решать неравенства ( примеры на доске)

В качестве аргумента может быть и не просто х, а буквенное выражение. Такую ф. мы в 11 классе назовем «сложная функция». Как найти ооф такой функции? – решить неравенство.

Дома вы находили ооф таких функций. № 831 – послушаем …

Проверим, все ли поняли? 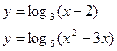                (на доске)

Найдем ооф еще 2 функций –

Теперь вспомним свойства логарифмов. ..Рассмотрим примеры их применения

Эти задания из базового варианта егэ:

Если можем устно, будут затруднения – письменно

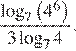
III. Объяснение новой темы.

Итак, вся эта теория нам пригодится в дальнейшем.

2. При решении логарифмического уравнения часто используются свойства логарифмов.

3. Рассмотрим несколько примеров. простейших уравнений несколько простейших из егэ.

, 

Поинтереснее

Теперь рассмотрим новый тип уравнений, сводящиеся к квадратным

Пример 2. Решить уравнение:

Решаем уравнение вида  . Решая это квадратное уравнение получаем корни х₁ = 2, х₂ = -3.   Так как, мы уже учли, что логарифмируемое выражение положительны это ответ

Проверим, как вы поняли. В каких уравнениях нужно ооу? Нужно ли рассматривать и правую и левую часть?                                  

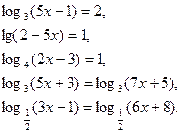
Теперь рассмотрим новый тип уравнений, сводящиеся к квадратным

Пример 2. Решить уравнение:

Решаем уравнение вида  . Решая это квадратное уравнение получаем корни х₁ = 2, х₂ = -3.  

Теперь решаем уравнения более сложного уровня. При решении мы будем применять свойства логарифмов:

1. Если в уравнении сумму логарифмов двух выражений заменить логарифмом их произведения, то полученное уравнение будет следствием данного.

2. Если в уравнении разность логарифмов двух выражений заменить логарифмом их частного, то полученное уравнение будет следствием данного.

                         будут ли равносильны эти уравнения? Почему нужна проверка? Можно также не делать проверку, но решать систему.

Рассмотрим примеры.

Что проще? Делить или умножать? Что нужно сделать, чтобы избавиться от деления, а получить уравнение с умножением?

Метод замены переменных

Теперь небольшая самостоятельная работа

1в

1. Сравните числа  log ₂ 3   и    log ₂ 0,2 .

2. Вычислите   log ₃₆ 84 – log ₃₆ 14

3. Решите уравнение    lg ( x-1 ) – lg ( 2x-11 ) = lg 2 .

4. Решите уравнение    log ₇ ( x² – 2x -8 ) = 1.

2в

1. Сравните числа   log _0,5 2,5  и    log _0,5 0,2 .

2. Вычислите  log _√2 12 – log ₂ 9.

3. Решите уравнение    log ₇ ( x² – 2x -8 ) = 1.

4. Решите уравнение    log ₂ ( x² – 4x + 4 ) = log ₄  x²

Чуть проще и чуть сложнее

. 

Итак, на протяжение  занятия мы рассматривали различные способы решения логарифмических уравнений. Неравенства будем решать позже Надеюсь, что вы хорошо усвоили этот материал и удачно примените теорию на экзамене. Желаю успеха!