Конспект урока по алгебре по теме: «Экстремумы функции» 11 класс

Урок № 69 (алгебра и начала мат. анализа)

Класс: 11

Тема урока: «Экстремумы функции § 50»

Цель урока: научиться применять производную к исследованию свойств функции.

Задачи урока:

1. Воспитательные: воспитание умения наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии; воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях; воспитание умения оценивать правильность выполнения учебной задачи, собственные возможности её решения. 

2. Развивающие: развитие логического мышления; развитие умений в применении знаний в конкретной ситуации; развитие навыков реализации теоретических навыков в практической деятельности; развитие коммуникативной компетентности в общении и сотрудничестве; развитие внимания, мышления, памяти, самостоятельности; расширение кругозора.

3. Образовательные: опираясь на знания учащихся по производной функции помочь сформулировать и осознать определение понятий критических, стационарных точек и точек экстремума; подвести к гипотезе: необходимое и достаточное условие существования экстремума функции; создать условие для первичного закрепления обучающимися умения аналитически и графически определять наличие у функции критических, стационарных точек и точек экстремума; подготовить учащихся к сдаче ЕГЭ.

Тип урока: урок изучения нового материала.

Форма проведения: классно-урочная.

Методы: эвристический; исследовательский; практический.

Формы работы: фронтальная, индивидуальная.

Оборудование урока: компьютер, презентация Microsoft Office PowerPoint, учебники.

Ход урока

1. Организационный момент.

Проверка подготовленности учащихся к занятию.

Приветствие учителя и учащихся.

2. Мотивация учебной деятельности учащихся, постановка темы, целей и задач урока, проверка домашнего задания.

3. Актуализация мыслительных процессов через организацию сопутствующего повторения.

Фронтальная работа с классом: Вычислить производную функции (дифференцированные задания): 

4. Изучение нового материала.

Постройте график функции: у = х2 –6х + 8;     

Ответьте на вопросы:

1.         Назовите промежутки возрастания и убывания полученного графика.

2.         Назовите точку, в которой функция принимает наименьшее значение.

Как ведет себя производная вблизи этой точки, при переходе через эту точку? А в самой этой точке?

Сформулируйте гипотезу.

(учащиеся выдвигают гипотезу)

Постройте график функции: у =  - х2 + 4х – 3.

Ответьте на вопросы:

1.         Назовите промежутки возрастания и убывания полученного графика.

2.         Назовите точку в которой функция принимает наибольшее значение.

3.         Как ведет себя производная вблизи этой точки, при переходе через эту точку? А в самой этой точке?

Сформулируйте гипотезу.

Работа с учебником.

Стр. 265 – 266. Найти в тексте сформулированную вами гипотезу.

Прочтите её.

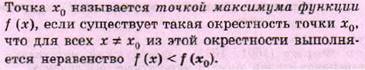
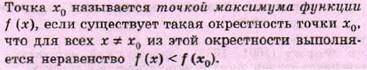
Точки минимума и точки максимума называются точками экстремума.

ТЕОРЕМА ФЕРМА

Работа с графиком (в левом столбце)

Доказательство через геометрический смысл производной.

Работа с рисунком (график функции у=х³ по центру)

Работа с книгой стр. 267

Найти какие точки называются стационарными, критическими.

Работа с графиком (в правом столбце)

Найти точки экстремума, стационарные и критические точки.

5. Здороровьесберегающие технологии.

Комплекс упражнений для снятия усталости глаз, профилактики близорукости и улучшения зрения –1 минута.

6. Закрепление изученного материала. 

Работа с материалами ЕГЭ.

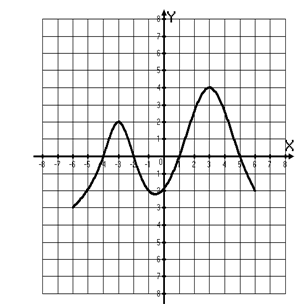
Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку минимума функции y = f(x)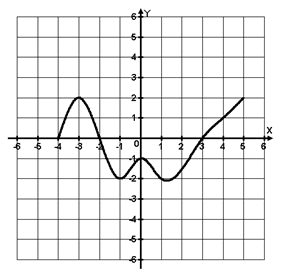

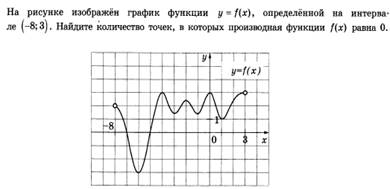
Функция y = f(x) определена на промежутке (- 6; 6). На рисунке изображён график её производной. Найдите точки, в которых производная функции равна нулю  (Ответ:  х = - 4;    х = - 2;    х = 1;     х = 5).

Просмотр видео:

https://www.youtube.com/watch?v=InPd07Ut23g

7. Подведение итогов урока. Информирование учащихся о домашнем задании и инструктаж по его выполнению.

Изучить §50 стр.265.

Решить №915(1; 2; 3); №920(1; 2; 3) письменно.

Великий философ Конфуций однажды сказал: “Три пути ведут к знанию: путь размышления - это путь самый благородный, путь подражания - это путь самый легкий и путь опыта - это путь самый горький”. Выполняя домашнее задание, каждый из вас пройдёт свой путь к знанию

8. Рефлексия.

Учитель задает вопросы, побуждая обучающихся к анализу своей деятельности на уроке.

Я умею …

Я знаю …

Хотелось бы лучше научиться …

Мне нравится …

Мне не нравится …

На уроке я чувствовала себя …

С домашней работой я …

Выражает удовлетворение от работы на уроке, оценивает работу, благодарит за работу на уроке.

Скачано с www.znanio.ru