Конспект урока по геометрии по теме «Скалярное произведение векторов. Угол между векторами»

Урок № 24 (геометрия)

Класс: 11

Тема урока: «Скалярное произведение векторов. Угол между векторами»

Цель урока: усвоение понятия угла между векторами и скалярного произведения векторов, формулы скалярного произведения в координатах; усвоение умений и навыков применения скалярного произведения векторов при решении задач, самостоятельно выбирая нужный метод решения; усвоение умений и навыков применения полученных знаний в нестандартных ситуациях.

Задачи урока:

1. Воспитательные: воспитание навыков самоконтроля и взаимоконтроля; воспитание культуры общения, умения работать в коллективе, взаимопомощи, умения организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях; воспитание умения оценивать правильность выполнения учебной задачи, собственные возможности её решения; умения анализировать свою деятельность, делать самостоятельные выводы. 

2. Развивающие: развитие пространственного мышления; развитие умений в применении знаний в конкретной ситуации; развитие навыков реализации теоретических навыков в практической деятельности; развитие умения сравнивать, обобщать, правильно формулировать и излагать мысли; развитие интереса к предмету через содержание учебного материала; развитие умений самостоятельно оценивать и принимать решения; развитие коммуникативной компетентности в общении и сотрудничестве; развитие внимания, мышления, памяти, самостоятельности; расширение кругозора.

3. Образовательные: ввести понятие угла между векторами и скалярного произведения векторов, рассмотреть формулу скалярного произведения в координатах; показать применение скалярного произведения векторов при решении задач; рассмотреть основные свойства скалярного произведения; сформировать умения вычислять скалярное произведение векторов и находить угол между векторами; показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя прямыми, а также между прямой и плоскостью.

Тип урока: комбинированный урок.

Методы: показательно-иллюстративные с применением мультимедийных технологий: словесный, практический, контролирующий.

Формы работы: фронтальная, индивидуальная, групповая, самостоятельная работа.

Оборудование урока: компьютер, учебники.

Ход урока

1. Организационный момент.

Проверка подготовленности учащихся к занятию.

Приветствие учителя и учащихся.

2. Мотивация учебной деятельности учащихся, постановка темы, целей и задач урока, проверка домашнего задания.

Тема «Скалярное произведение векторов. Угол между векторами» является важной темой в геометрии. Скалярное произведение векторов применяется для нахождения длины вектора, косинуса угла между векторами, проекции одного вектора на направление другого и установления перпендикулярности векторов.

3. Актуализация мыслительных процессов через организацию сопутствующего повторения.

Задача 1. (Демонстрация экрана рис.1).

Дано: О(0; 0; 0), А(4; 0; 0), В(0; 6; 0), ΔAОВ - прямоугольный.

Найти: 1) К(х; у; z) - центр окружности, описанной около ΔAОВ; 2) АК = R.

2. Устные упражнения

Решение задач с целью подготовить учащихся к восприятию нового материала.

Фронтальная работа с классом: отвечает один из учащихся, остальные при необходимости дополняют, исправляют ответ своего товарища.

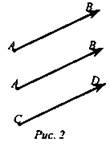Векторы в пространстве (Демонстрация экрана рис. 2).

1. Дано: А(-3; -2; 4), В(-4; 3; 2).

Найти: 

 2. Дано: А(2; -3; 1), В(4; -5; 0), С(5; 0; -4), D(7; -2;-3).

Равны ли векторы ?

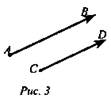
3. Коллинеарные ли векторы , если А(1; -3; 4), В(5; 1; -2), С(2; 0; 1), D(4; -2; 2) (Демонстрация экрана рис. 3).

4. Изучение нового материала.

Словесное объяснение нового материала с демонстрацией экрана и работа с учебником п.76; 77 стр.171-172.

Угол между векторами

Если векторы не являются сонаправленными, то лучи ОА и ОB образуют угол АОВ.

Определение: Два вектора называются перпендикулярными, если угол между ними равен 90°.

Скалярное произведение векторов:

Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Запишем формулу:

Доказательство утверждений:

Утверждение1. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Утверждение2. Скалярный квадрат вектора  равен квадрату его длины. 

Формула скалярного произведения двух векторов  и 

Через их координаты 

Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

Угол между векторами.

Косинус угла между векторами пространства  , заданными в ортонормированном базисе  , выражается формулой: 

Сформулируем основные свойства скалярного произведения векторов.

Для любых векторов  и любого числа k справедливы равенства:

1)  причем  при 

2)   (переместительный закон).

3)   (распределительный закон).

4)  (сочетательный закон).

Вычисление углов между прямыми и плоскостями.

Угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов.

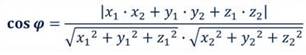
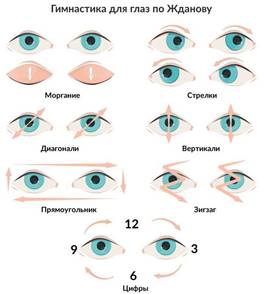
5. Здороровьесберегающие технологии.

Комплекс упражнений для снятия усталости глаз, профилактики близорукости и улучшения зрения –1 минута.

6. Первичное применение полученных знаний на практике. 

Демонстрация решения примера № 687 (а).

7. Формирование умений и навыков решения упражнений применение основного свойства дроби.

Практическое решение заданий.

1. Устно.

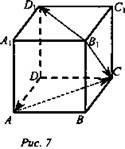
Дан куб ABCDA1B1C1D1 (рис. 7).

 Найдите угол между векторами

a) 

б) 

в) 

(Ответы: а) 45°; б) 45°; в) 135°.)

2. Решение задач № 687 (б).

Дополнительная задача

Вычислите угол между вектором  и координатным вектором 

 (Ответ: 48°11’.)

3. Решить самостоятельно (по группам, дифференцированные задания).

1 группа № 682 а); 2 группа № 684 а); 3 группа № 692 б).

Ответы: 

8. Закрепление изученного материала.

Ознакомиться с материалом:

https://resh.edu.ru/subject/lesson/5723/conspect/149166/

Просмотр видео:

https://www.youtube.com/watch?v=i0DXRtNdug8

9. Подведение итогов урока. Информирование учащихся о домашнем задании и инструктаж по его выполнению.

Учить п.76; 77 стр.171-172.

Дифференцированное домашнее задание.

I уровень: пройти онлайн тест по теме: 

https://onlinetestpad.com/ru/test/563942-skalyarnoe-proizvedenie-vektorov сделать screenshot результатов и прислать как д/з, подписав «Тест»;

II уровень: Решать №685; №692(а) письменно.

Желаю успехов!

10. Рефлексия.

Учитель задает вопросы, побуждая обучающихся к анализу своей деятельности на уроке. Выражает удовлетворение от работы на уроке, оценивает работу, благодарит за работу на уроке.

Скачано с www.znanio.ru