Конспект урока по геометрии теме: «Площадь круга, сектора, сегмента» 9 класс

Урок № 50 (геометрия)

Класс: 9

Тема урока: «Площадь круга, сектора, сегмента»

Цель урока: создать условия для доказательства теоремы косинусов; способствовать развитию умения применять формулы площади круга, сектора, сегмента при решении задач.

Задачи урока:

1. Воспитательные: воспитание аккуратности при выполнении чертежей; воспитание культуры умственного труда, коммуникативной культуры, рефлексивной культуры; воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях; воспитание умения оценивать правильность выполнения учебной задачи, собственные возможности её решения; умения анализировать свою деятельность, делать самостоятельные выводы;   мотивировать интерес обучающихся к предмету посредством вовлечения их в решение практических задач.

2. Развивающие: развитие качеств мышления – пространственного и функционального, характерных для математической деятельности и необходимых для продуктивной жизни в обществе; развитие памяти, внимания, устной и письменной математической речи; развитие умений в применении знаний в конкретной ситуации; развитие навыков реализации теоретических навыков в практической деятельности; формирование умений оформления решения задач; формирование интереса к изучению геометрии.

3. Образовательные: формирование знания формулировки формул площадь круга, сектора, сегмента, умения записывать формулы площади круга, сектора, сегмента в виде равенства; формирование умений решать задачи с использованием формул площадь круга, сектора, сегмента.

Тип урока: комбинированный урок.

Форма проведения: классно-урочная.

Методы: показательно-иллюстративные с применением мультимедийных технологий: словесный, практический, контролирующий.

Формы работы: фронтальная, индивидуальная, групповая, самостоятельная работа.

Оборудование урока: телевизор, компьютер, презентация Microsoft Office PowerPoint, чертежные принадлежности, карточки с задачами, учебники.

 

Ход урока

1. Организационный момент.

Проверка подготовленности учащихся к занятию.

Приветствие учителя и учащихся.

 

2. Мотивация учебной деятельности учащихся, постановка темы, целей и задач урока, проверка домашнего задания.

Тема «Площадь круга, сектора, сегмента» является важной темой в геометрии.

 

3. Актуализация мыслительных процессов через организацию сопутствующего повторения.

 

4. Изучение нового материала.

Создание проблемной ситуации.

Каждому учащемуся выданы карточки со следующими задачами:

Карточка с задачами.

1) Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 см и 12 см. (Рис.1)

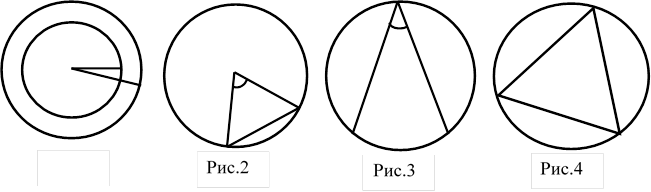2)Площадь кругового сектора равна  , а его центральный угол равен . Найти радиус сектора и площадь сегмента, опирающегося на центральный угол.(Рис.2)

3) Хорды АВ и АС равны между собой. Образованный ими угол вписан в окружность и равен . Найдите отношение площади той части круга, которая заключена в этом угле, к площади всего круга.(Рис.3)

4) Сторона равностороннего треугольника, вписанного в окружность, равна а. Вычислите площадь отсекаемого ею сегмента.(Рис.4)

5) Найдите длину дуги сектора, если его площадь , а периметр 28 см.(Рис.5)

6) Найти площадь круга, вписанного в круговой сектор с углом  и радиусом .(Рис.6)

7)Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого равна . Найти площадь квадрата.(Рис.7)

8) Определите площадь заштрихованной фигуры на рисунке, если  центр окружности с радиусом 4 см,      ,   центр окружности с диаметром АВ.(Рис.8)

Не получается справиться с решением задач. Возникает проблема с решением задачи на площадь круга и его частей. «Мозговой штурм». В итоге выбран план решения задач.

 

Чтобы решить задачи нам нужны формулы площади круга, сектора, сегмента.

 

 

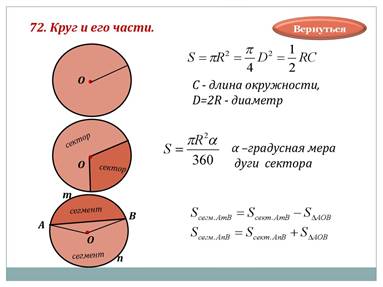
Вывод: дадим словесную формулировку, полученных равенств.

Итак, какая же тема урока? Какие цели вы перед собой поставите на уроке?  

Формулируют тему и цели урока. Записывают тему урока в тетрадях

 

5. Физкультминутка.

 

6. Усвоение умений и навыков.

Деятельность учителя:

Решаем первую задачу с карточки. (Вызываю ученика к доске). Рисунки переносить в тетрадь не нужно, все необходимые элементы дочерчиваем прямо на карточке. В тетради оформляем только решение.

Можно решать вперед задачи с листочка, только сверять при этом свое решение с решением на доске.

1)Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 см и 12 см.(Рис.1)

Деятельность ученика:

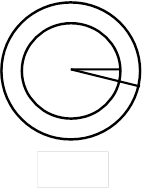Дано:  (радиус большего круга)

             (радиус меньшего круга)

Найти:

             (площадь кольца)

Решение:

Деятельность учителя:
Что для этого нужно сделать?

Деятельность ученика:

Из площади большего круга вычесть площадь меньшего круга, т.к. центры совпадают.

 

Но для этого мы вначале должны найти площади кругов, :

 

 

Теперь можем найти площадь кольца:

.

Ответ: .

Деятельность учителя:
Спасибо, можешь присесть. Решаем следующую задачу.

2)Площадь кругового сектора равна  , а его центральный угол равен . Найти радиус сектора и площадь сегмента, опирающегося на центральный угол.(Рис.2)

Деятельность ученика:

Дано:

           

           

Найти:

           

Решение:

Площадь сегмента находится по формуле , из нее мы можем выразить радиус сектора, зная площадь сектора и градусную меру дуги сектора:

 

 

 

 

 не удовлетворяет условию задачи.

 

Деятельность учителя:

Но это не полное решение задачи. Нам еще нужно найти площадь сегмента, опирающегося на угол в . Каким образом это можно осуществить?

Деятельность ученика:

Найдем площадь АОВ, а потом вычтем из площади сектора площадь

АОВ, тем самым найдем площадь искомого сегмента.

 

 (воспользуемся таблицей Брадиса)

 

 

Ответ:

             

             

Деятельность учителя:
Спасибо, можешь присесть. А сейчас решаем задачу из учебника №1117(а). 

(Вызываю ученика к доске). Кто решает вперед, обратите внимание на этот номер.

№ 1117(а)

Найдите площадь круга, вписанного в равносторонний треугольник со стороной .

№ 1117(а)

Деятельность ученика:

Дано:

             (сторона правильного треугольника)

Найти:

             (площадь вписанного круга)

Решение:

радиус вписанного круга находится как  радиус вписанной окружности по следующей формуле:

 

Теперь мы знаем радиус круга, можем найти площадь круга :

 

Ответ:

             

Деятельность учителя:
Есть ли еще способы решения данной задачи?

Деятельность ученика:

Например, по теореме Пифагора мы могли бы найти высоту равностороннего треугольника, зная, что биссектрисы, высоты и медианы в таком треугольнике совпадают и точкой пересечения делятся как 2:1, то могли бы найти радиус вписанного круга.

Деятельность учителя:

Но этот способ гораздо длиннее, и тем более мы уже знаем, как находить радиусы вписанных и описанных фигур в правильных многоугольниках.

Спасибо, можешь присесть.

Решаем третью задачу с карточки. (Вызываю ученика к доске)

 

3) Хорды АВ и АС равны между собой. Образованный ими угол вписан в окружность и равен . Найдите отношение площади той части круга, которая заключена в этом угле, к площади всего круга.(Рис.3)

 

 

 

 

Деятельность ученика:

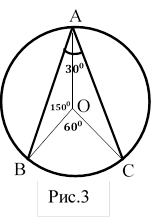Дано:

            АВ=АС

             ВАС=

Найти:

 

(отношение площади той части круга, которая заключена в угле  ВАС, к площади всего круга)

Решение:

Отметим центр круга, соединим точки, образующие радиусы ВО, ОС, ОА. Для начала найдем часть круга, заключенную в угле  ВАС, она складывается из следующих площадей фигур:

 

 ВОС=(как соответствующий центральный угол вписанному углу

 ВАС=)

Градусная мера всего круга равна .

АОВ=АОС (по трем сторонам: ВО=ОС как радиусы, АВ=АС по условию задачи, ОА общая сторона). Из равенства треугольников следует равенство соответствующих элементов:

 ВОА= СОА.

Достаточно найти площадь одного из равных треугольников:

 (т.к. синус второй четверти положителен)

составляет  часть от всего круга, значит, если площадь круга равна , то:

 

Теперь можем найти площадь части круга, заключенную в угле  ВАС:

 

Деятельность учителя:
Достаточно ли данных, чтобы найти отношение площадей? Нужно ли нам находить радиус, и можем ли мы это сделать?

Деятельность ученика:

Радиус мы найти не сможем, поскольку мало данных, и для нахождения отношения площадей он нам не потребуется, давайте убедимся в этом:

 

Ответ:

             

Деятельность учителя:
Есть ли вопросы по этой задаче? (Если есть, то ответить на них, можно еще раз пройтись по решению задачи)

Спасибо, можешь присесть.

А сейчас решаем 4 задачу с карточки. (Вызываю ученика к доске)

4) Сторона равностороннего треугольника, вписанного в окружность, равна а. Вычислите площадь отсекаемого ею сегмента.(Рис.4)

Деятельность ученика:

Дано:

             (сторона равностороннего треугольника)

Найти:

           

Решение:

радиус описанного круга находится как  радиус описанной окружности по следующей формуле:

 

 (площадь сегмента равна разности площади сектора, опирающего на угол

 АОС, и площади АОС)

 ,где площадь круга, т.к.  АОС=, поскольку треугольник АВС является равносторонним, т.е. правильным.

 

 

 (т.к. АВС является равносторонним, т.е. правильным)

А площадь правильного треугольника мы можем найти по известной нам формуле:

 

Следовательно, площадь треугольника АОС равна:

 

 (кв.ед.)

Деятельность учителя:

Сторона равностороннего треугольника отсекает только найденный сегмент?

Деятельность ученика:

Нет, еще один сегмент, который будет опираться на дугу АВС в .

Деятельность учителя:

Зная уже площадь маленького сегмента, как можно найти площадь большого сегмента?

Деятельность ученика:

Просто из площади всего круга вычесть площадь маленького сегмента:

 

 (кв.ед.)

Ответ:

            (кв.ед.)

             (кв.ед.)

Деятельность учителя:

Спасибо, можешь присесть.

Есть еще один более простой способ найти искомые сектора. Что можно сказать о маленьких секторах, которые получаются при отсечении от круга сторонами правильного треугольника?

Деятельность ученика:

Получаются три равных сектора, поскольку стороны треугольника равны.

Деятельность учителя:

Значит, как можно найти площадь сектора, зная площади круга и вписанного треугольника?

Деятельность ученика:

(Ученик диктует, а учитель записывает на доске краткое решение второго способа, также ученик может решить сам этим способом задачу, тогда учителю стоит спросить про первый способ ее решения, все зависит от выбора ученика решения задачи)

Три площади сектора равны разности всей площади круга и площади равностороннего треугольника:

 

 

 (кв.ед.)

А после по аналогии с решенной задачей найти площадь большого сегмента:

 (кв.ед.)

Деятельность учителя:

Как мы видим второй способ компактнее и удобнее.

Есть ли вопросы по этой задаче? (Если есть, то ответить на них, можно еще раз пройтись по решению задачи)

7. Закрепление изученного материала.

Просмотр видео: https://www.youtube.com/watch?v=MV_geY1l6eQ

https://www.youtube.com/watch?v=SbO9qdduf3k

 

8. Рефлексия. Итоги урока.

Теперь подведем итоги. Еще раз вспомним формулы площадей фигур, с которыми мы сегодня работали на уроке?

Деятельность ученика:

Круга, кругового сектора или просто сектора и сегмента.

Деятельность учителя:

Назовите эти формулы.

Деятельность ученика:

S=πR^2 (площадь круга, где R- радиус круга);

S=(πR^2)/360 α (площадь сектора, где R- радиус сектора, α-градусная мера дуги сектора);

S_сегмента=S_сектора±S_(треуг.)

9. Домашнее задание.

Откройте, пожалуйста, дневники и запишите домашнее задание:

1.      Изучить пп.115, 116 стр.280-281. Решить №1107; №1108;

2.      Пройти онлайн тест по теме:

https://onlinetestpad.com/ru/testview/2368911-proverka-teoreticheskikh-znanij-i-prakticheskikh-navykov-po-geometrii-9kl-g

 сделать screenshot результатов и прислать как д/з, подписав «Тест».

      3. Творческое задание: «Придумать жизненную задачу, при решении которой необходимо      применить площадь круга, сектора или сегмента»;

      4. Реферат на тему: «Площадь круга, сектора, сегмента» (выполняется по желанию обучающихся).

 

Комментарии по выполнению д/з.

Желаю успехов!

 

 

Скачано с www.znanio.ru