Конспект урока по математике ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПРЯМОУГОЛЬНИКА(4 класс)

Урок 105
 ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПРЯМОУГОЛЬНИКА

Цели: составить формулу вычисления площади прямоугольника; повторить соотношения единиц измерения площади; учить вычислять площадь прямоугольника с помощью умножения; совершенствовать умение решать задачи на определение площади; развивать логическое мышление и внимание.

Ход урока

I. Устный счет.

1. Заполните таблицы:

– Закончите выводы:

· Чтобы найти неизвестный множитель, надо...

· Чтобы найти неизвестное делимое, надо...

· Чтобы найти неизвестный делитель, надо...

2. Задача.

Составьте задачу, используя данные: «Сокол живет 170 лет, а жизнь дрозда в 17 раз короче».

3. Игра «Цепочка».

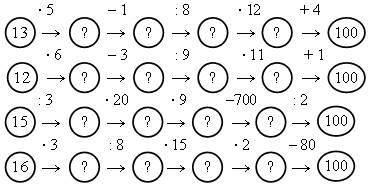
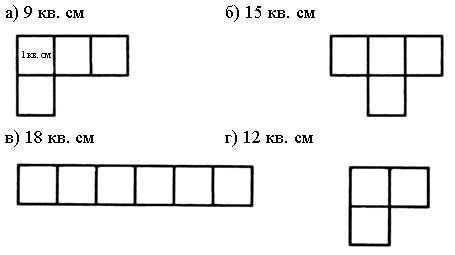
4. Дорисуйте фигуру так, чтобы получился прямоугольник, площадь которого равна:

II. Сообщение темы урока.

– Какие математические записи вы можете объяснить?

– Сегодня на уроке узнаем, что обозначает запись S = а · в.

III. Работа по теме урока.

1. Задание 276.

Учащиеся читают диалог Миши и Маши.

– Как найти площадь, если не получается ее измерить? (Надо умножить длину на ширину.)

– Площадь поля квадратной формы со сторонами 3 км и 2 км вычисляется следующим образом:

3 км · 2 км = 6 кв. км.

– Объясните, как можно вычислить площадь бассейна прямоугольной формы со сторонами 3 м и 5 м.

3 м · 5 м = 15 кв. м.

2. Задание 277.

– Если обозначить длину прямоугольника буквой а, а ширину – буквой в, то площадь прямоугольника (обозначается буквой S) можно вычислить по формуле

S = а · в.

– Вычислите площадь прямоугольника по этой формуле, если:

а) а = 7 см, в = 9 см;

S = 7 cм · 9 см = 63 кв. см;

б) а = 3 дм, в = 8 дм;

S = 3 дм · 8 дм = 24 кв. дм;

в) а = 5 м, в = 2 м

S = 5 м · 2 м = 10 кв. м.

– В каких единицах должны быть выражены длины сторон прямоугольника, для того чтобы площадь была выражена в квадратных сантиметрах? (В сантиметрах.)

– В квадратных дециметрах? (В дециметрах.)

– В квадратных метрах? (В метрах.)

– В квадратных километрах? (В километрах.)

– В квадратных миллиметрах? (В миллиметрах.)

IV. Продолжение работы по теме урока.

1. Задание 279.

– Прочитайте задачу.

– Что известно?

– Что требуется узнать?

– Решите задачу. Вычислите и запишите ответ.

Решение:

1) 9 · 2 = 18 (м) – длина площадки.

2) 18 · 9 = 162 (кв. м) – площадь.

Ответ: 162 кв. м.

2. Задание 280.

– Рассмотрите краткую запись задачи в виде таблицы.

– Сформулируйте задачу по данной краткой записи.

Задача. Чему равна площадь комнаты, если длина комнаты 6 м, что на 2 м больше ширины комнаты?

– Решите задачу. Вычислите и запишите ответ.

Решение:

1) 6 – 2 = 4 (м) – ширина комнаты.

2) 6 · 4 = 24 (кв. м) – площадь комнаты.

Ответ: 24 кв. м.

3. Практическая работа.

Задание 1.

Дорисуйте фигуру так, чтобы получился прямоугольник, площадь которого равна:

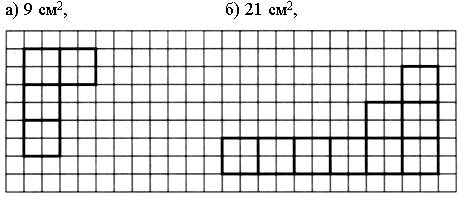
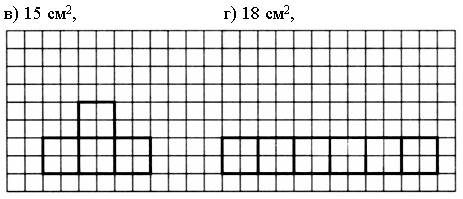
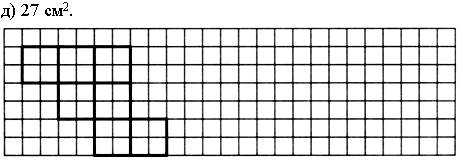
Задание 2.

Вычислите периметр и площадь фигуры удобным способом.

Задание 3.

Разделите фигуру на многоугольники площадью 4 см². Если сможете, найдите несколько решений.

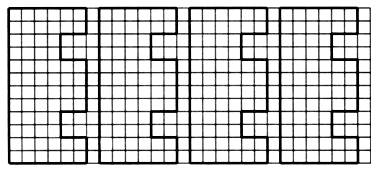
Чему равны у этой фигуры площадь

и периметр

Выберите любое из ваших решений и составьте из полученных четырех многоугольников другую фигуру, не выходящую за границу прямоугольника.

Чему равны площадь новой фигуры

и ее периметр

V. Итог урока.

– Что нового узнали на уроке?

– Как вычислить площадь прямоугольника с помощью умножения?

– Назовите единицы измерения площади в порядке увеличения.

Домашнее задание. № 278.

Скачано с www.znanio.ru