Конспект урока "Показательные уравнения"

Тема: «Методы решения показательных уравнений»

Показательные уравнения

Уравнения, содержащие неизвестные в показателе степени, называются показательными уравнениями. Простейшим из них является уравнение  а^x = b, где а > 0, а ≠ 1.

  1) При b < 0 и b = 0 это уравнение не имеет решения.

  2) При b > 0 уравнение имеет единственный корень. Для того, чтобы его найти, надо b представить в виде b = a^с,     а^x = b^с ó x = c или x = log_ab.

Показательные уравнения путем алгебраических преобразований  приводят к стандартным уравнениям, которые решаются, используя следующие методы:

1)                метод приведения к одному основанию ;

2)                метод введения новых переменных;

3)                метод разложения на множители;

4)                 показательно – степенные уравнения;

Метод приведения к одному основанию

Способ основан на следующем свойстве степеней: если равны две степени и равны их основания, то равны и их показатели, т.е. уравнение надо попытаться свести к виду

Примеры.  Решить уравнение:                   

                   1.  3^x = 81;

Представим правую часть уравнения в виде 81 = 3⁴ и запишем уравнение, равносильное исходному    3 ^x = 3⁴;  x = 4.  Ответ: 4.

                 2.   

Представим правую часть уравнения в виде и перейдем к уравнению для   показателей степеней 3x+1 = 3 – 5x; 8x = 4; x = 0,5. Ответ:  0,5.

                    3.

Представим правую часть данного уравнения в виде  1 = 5⁰ и перейдем к уравнению для показателей степеней  x²-3x+2 = 0, откуда легко получить решения x = 1 и x=2.

Ответ: 1 и 2.

                    4.        

Заметим, что числа 0,2 , 0,04 , √5 и 25 представляют собой степени числа 5. Воспользуемся этим и преобразуем исходное уравнение следующим образом:

, откуда 5^-x-1 = 5^-2x-2  ó - x – 1 = - 2x – 2, из которого находим решение  x = -1.  Ответ: -1.                                 

 Метод введения новых переменных

Введение новой переменной (подстановка) обычно производится после преобразований (упрощения) членов уравнения. Рассмотрим примеры.

Примеры. Решить уравнение:

 1.  .

Перепишем уравнение иначе: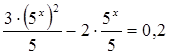  

Обозначим 5^x = t > 0, тогда   т.е. 3t² – 2t – 1 =0, отсюда t₁ = 1, -не удовлетворяет условию t > 0. Итак, 5^x = 1 = 5⁰ <=> x = 0. Ответ: 0.

 2.  .

 Решение.  Перепишем уравнение в виде 

и заметим, что оно является однородным уравнением второй степени.

Разделим уравнение на 4^2x, получим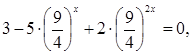         

Заменим            2t² – 5t +3 = 0 , где t₁ = 1,     t₂ =   .

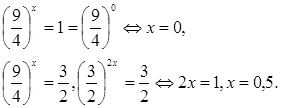
Ответ: 0; 0,5.

 Метод разложения на множители

1.   Решите уравнение:  5^x+1 - 5^x-1 = 24. 

Решение. Перепишем уравнение в виде    

Теперь в левой части уравнения вынесем за скобки общий множитель 5^x.

Получим 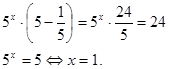  , откуда

Ответ:  1.

2.  6^x + 6^x+1 = 2^x + 2^x+1 + 2^x+2.                             

      Решение. Вынесем за скобки в левой части уравнения 6^x, а в правой части – 2^x. Получим уравнение  6^x(1+6) = 2^x(1+2+4) ó 6^x = 2^x.

Так как 2^x >0 при всех x, можно обе части этого уравнения разделить на 2^x, не опасаясь при этом потери решений. Получим  3^x = 1ó x = 0.

Ответ: 0.

3. 

Решение.  Решим уравнение методом разложения на множители.

Выделим квадрат двучлена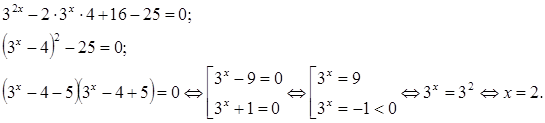 

Ответ: 2.

 Показательно – степенные уравнения

  К показательным уравнениям примыкают так называемые показательно – степенные уравнения, т.е. уравнения вида (f(x))^g(x) = (f(x))^h(x).

    Если известно, что f(x)>0 и f(x) ≠ 1, то уравнение, как и показательное, решается приравниванием показателей g(x) = f(x).

    Если условием не исключается возможность f(x)=0 и f(x)=1, то приходится рассматривать и эти случаи при решении показательно – степенного уравнения.

   1. Решить уравнение  

 Решение. Для нахождения корней уравнения следует рассмотреть четыре случая:

1)                x + 1=x² – 1 ( показатели равны);

2)                x = 1(основание равно единице);

3)                x = 0 (основание равно нулю);

4)                x = -1(основание равно -1).

Решим первое уравнение: x² – x – 2 = 0,  x = 2, x = -1.

Проверка:

x₁ = 2  => 2³ = 2³ – верно;

x₂ = -1 => (-1)⁰ =(-1)⁰ – верно;

x₃ = 1  => 1² = 1⁰ – верно;

x₄ = 0  =>  0¹ = 0^(-1) – не имеет смысла.

Ответ: -1; 1; 2.

  Уравнение вида f(x)^g(x) = 1 равносильно совокупности двух систем

         f(x)^g(x) = 1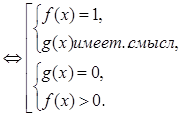

2. 

Решение. x² +2x-8 – имеет смысл при любых x , т.к. многочлен, значит уравнение равносильно совокупности

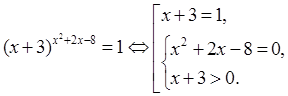
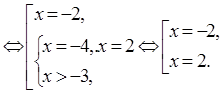
Ответ: -2; 2.

Домашнее задание.