Конспект урока "Производная. Правила и формулы дифференцирования"

Тема: Производная. Правила и формулы дифференцирования.

Вспомним определение производной функции.

Произво́дная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения прир5ащения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

Пример

Найти производную функции 

Решение: 

Это простейший пример, его можно найти в таблице производных элементарных функций. Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь: у нас была функция , которая в результате решения превратилась в функцию .

Говоря совсем просто, для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным исключением является экспоненциальная функция , которая превращается сама в себя. Операция нахождения производной называется дифференцированием.

Обозначения: Производную обозначают  или .

ВНИМАНИЕ, ВАЖНО! Забыть поставить штрих (там, где надо), либо нарисовать лишний штрих (там, где не надо) – ГРУБАЯ ОШИБКА! Функция и её производная – это две разные функции!

Вернемся к нашей таблице производных. Из данной таблицы желательно запомнить наизусть: правила дифференцирования и производные некоторых элементарных функций, особенно:

производную константы:
, где  – постоянное число;

производную степенной функции:
,  в частности: , , .

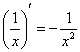В реальности простые табличные примеры – редкость, обычно при нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций.

В этой связи переходим к рассмотрению правил дифференцирования:

1) Постоянное число можно (и нужно) вынести за знак производной

, где  – постоянное число (константа)

Пример

Найти производную функции 

Смотрим в таблицу производных. Производная косинуса там есть, но у нас .

Решаем:

Самое время использовать правило, выносим постоянный множитель за знак производной:

А теперь превращаем наш косинус по таблице:

Ну и результат желательно преобразовать – ставим минус на первое место, заодно избавляясь от скобок:

Готово.

2) Производная суммы равна сумме производных

Пример

Найти производную функции 

Решаем. Как Вы, наверное, уже заметили, первое действие, которое всегда выполняется при нахождении производной, состоит в том, что мы заключаем в скобки всё выражение и ставим штрих справа вверху:

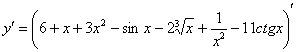
Применяем второе правило:

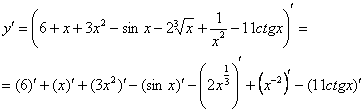
Обратите внимание, что для дифференцирования все корни, степени нужно представить в виде .

Теперь вспоминаем о первом правиле дифференцирования – постоянные множители (числа) выносим за знак производной:

Обычно в ходе решения эти два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).

Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:

Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:

Все степени вида  желательно снова представить в виде корней, степени с отрицательными показателями – сбросить в знаменатель.

3) Производная произведения функций

Вроде бы по аналогии напрашивается формула …., но неожиданность состоит в том, что:

Пример

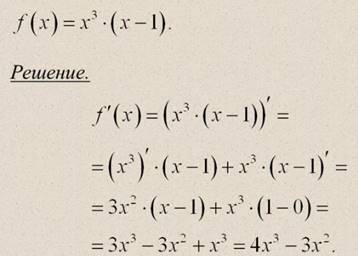
Пример

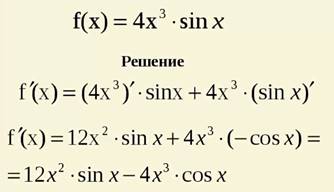
 4) Производная частного функций

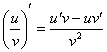
Пример

Найти производную функции 

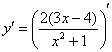
Теперь смотрим на выражение в скобках. В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной:

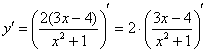
Заодно избавляемся от скобок в числителе, которые теперь не нужны.

Смотрим на наше выражение в скобках. У нас есть сложение, вычитание и деление. Со школы мы помним, что деление выполняется в первую очередь. И здесь – сначала применяем правило дифференцирования частного:

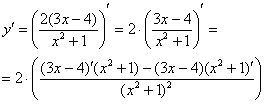
Применяем первое и второе правило:

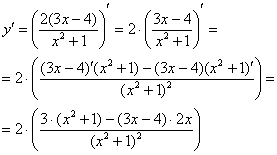
Штрихов больше нет, раскрываем скобки и упрощаем выражение.

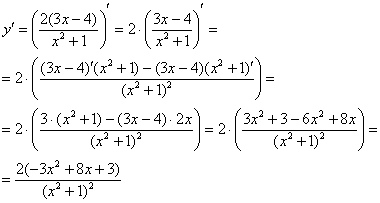
Пример

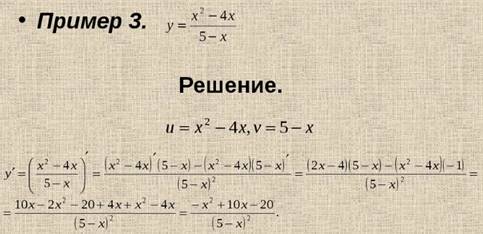
Задания для самостоятельной работы:

Найти производные функций:

1)

2)

3)