Конспект урока. Производная степенной функции

Конспект урока. Производная степенной функции

1. Этап мотивации к учебной деятельности. (1 мин)

Здравствуйте ребята. Я рада вас всех видеть на сегодняшнем уроке. Сейчас я озвучу вам высказывание великого математика Н.И. Лобачевского, а вы скажите, как его понимаете. (Слушают учителя. Думают над высказыванием, анализируют его и выражают свои мысли)

«Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира».

2. Этап актуализации и пробного учебного действия. (5 мин)

Повторим основные формулы и правила дифференцирования

Сформулировать понятие производной функции?

Ответ: Производной функции y = f(x) в данной точке x₀ называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю.

Обозначение производной:. Тогда .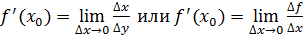

Как называется математическая операция нахождения производной функции?

Ответ: Операция нахождения производной называется дифференцированием.

В чем заключается геометрический смысл производной функции?

Ответ: Значение производной функции  в точке : .

А уравнение касательной к функции  в точке  имеет вид: .

Открыл геометрический смысл производной в 17-м в. Г. Ф. Лейбниц.

Какой знак имеет производная на интервале, если функция возрастает?

Ответ: Если функция возрастает, то f ′(x)>0 на этом интервале.

Какой знак имеет производная на интервале, если функция убывает?

Ответ: если функция убывает, то f ′(x)<0 на этом интервале.

В чем состоит физический (механический) смысл производной функции?

Ответ: Если тело движется по прямой согласно закону s(t), то формулы для нахождения скорости и ускорения тела в момент времени t: v (t)= s‘(t) и а(t) = v’(t).

Открыл механический смысл производной И. Ньютона.

Чтобы эффективно использовать производную при решении конкретных задач, необходимо, как таблицу умножения, знать таблицу производных элементарных функций и правила дифференцирования.

Убедимся в том, что вы эту таблицу знаете.

Учитель просит сформулировать правила нахождения производной.

Учащиеся называют основные правила нахождения производных.

Должны прозвучать ответы:

1. Производная суммы (u+v)'= u' + v';
2. О постоянном множителе (Cu)'=Cu';
3. Производная произведения (uv)'=u'v+uv';
4. Производная дроби (u/v)'=(u'v-uv')/v2;
5. Производная сложной функции  

3. Этап выявления места и причины затруднения. (3 мин). Теперь решим задачу.

Проблемная задача

Две материальные точки движутся прямолинейно

по законам

S₁(t)=2,5t² - 6t +1,

S₂(t)=0,5t² + 2t - 3

В какой момент времени скорости их равны, т.е.

V₁(t₀ )=V₂ (t₀ ), t₀ - ?

(Пытаются самостоятельно решить задачу. Приходя к выводу, что не хватает знаний, чтобы прийти к верному ответу)

Решение:

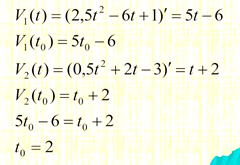
Мы столкнулись с задачей, для решения которой нам не хватает знаний о производной еще одной функции, которая называется степенной.

4. Построение проекта выхода из затруднения (3 мин).

Как вы думаете, о чем пойдет речь на уроке? Какие задачи перед нами стоят? (формулируют тему и задачи урока, ставят перед собой цель)

Тема урока: Производная степенной функции.

5. Реализация выбранного плана по разрешению затруднений (10 мин). Формула для вычисления производной степенной функции xⁿ, где n — произвольное натуральное число, большее 1, такова:

(xⁿ)’=nx^n-1 (1)

Формула производной функции х² уже известна: (х²)' = 2х. Пользуясь формулой дифференцирования произведения, получаем: 

(x³)’=( x²⋅x)’= (x²)’x+ x²(x)’= 2x⋅x + x²⋅1=3 x²;

(x⁴)’=( x³⋅x)’= (x³)’x+ x³(x)’= 3x²⋅x+ x³⋅1=4x³.

Заметим теперь, что 

(x²)’=2x^2-1, (x³)’=3x^3-1, (x⁴)’=4x^4-1,т.е. для n, равного 2, 3 и 4, формула (1) доказана. Продолжая аналогичные рассуждения, нетрудно убедиться в справедливости формулы (1) для n, равного 5, 6 и т. д. 

Докажем, что формула (1) верна для любого натурального n4. 

Допустим, что формула (1) верна при n = k, т. е. что (x^k)’=kx^k-1.

Покажем, что тогда формула (1) верна при n = k+1. Действительно, 

(x^k+1)’=(x^k⋅x)’=( x^k)’⋅x + x^k⋅(x)’= kx^k-1⋅x + x^k = (k+1) x^k

Поэтому из того, что формула (1) верна при п = 4, следует, что она верна и при n = 5, но тогда она верна и при n = 6, а, следовательно, и при n = 7 и т. д. до любого n∈ N (строгое доказательство основано на методе математической индукции). 

Если n = 1 или n = 0, то при х≠0 эта формула также справедлива. Действительно, по формуле (1) при х≠0 

(x¹)’=1⋅x^1-1 = 1⋅x⁰ =1,

(x⁰)’=0⋅x^0-1 = 0,что совпадает со значениями производных функций х и 1, уже известными из предыдущего пункта.

Пусть, наконец, п — целое отрицательное число, тогда n = —m, , где т — число натуральное. Применяя правило дифференцирования частного и пользуясь уже доказанной для натуральных т формулой (1), получаем при х≠0: 

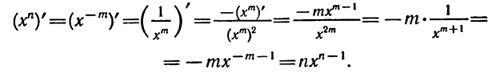
В результате можно сделать вывод:

 
Для любого целого n и любого x (x≠0 при n≤1) 

(xⁿ)'=nx^n-1

Из дифференцируемости степенной функции и основных правил вычисления производных вытекает, что целые рациональные функции (многочлены) и дробно-рациональные функции дифференцируемы в каждой точке своей области определения.

6. Этап первичного закрепления с проговариванием во внешней речи.

(15 мин).

Решим следующие задания. 46(1,3,5);47(1,3,5,7);48(1,3,5); 49 (1,3,5); 50(1,3).

7. Физ-минутка. Найти фигуры на стене (1 мин).

8. Самостоятельная работа с самопроверкой по эталону(5 мин).

Сверьте свои ответы с ответами на доске и поставьте оценку.

От 1-3 – «2»

От 4-6 – «3»

От 7-9 – «4»

10 – «5»

9. Этап включения в систему знаний и повторения. (1 мин)

Что мы делали сегодня на уроке?

Что узнали?

Какую функцию называют степенной?

Как найти производную степенной функции?

10. Рефлексия деятельности. (2 мин)

Записаны незаконченные фразы. Продолжите их.

Сегодня я вспомнил…

Сегодня я узнал…

Было интересно…

Было трудно…

11. Домашнее задание. (1 мин) 46(2,4,6);47(2,4,6,8);48(2,4,6); 49 (2,4,6); 50(2,4).