Конспект урока: "Разложении квадратного трехчлена на множители"

Учитель: Клименко Ольга Анатольевна                9 класс

Тема: разложении квадратного трехчлена на множители

У р о к № ___.

Тип урока: Изучение нового материала
Цели: изучить теорему о разложении квадратного трехчлена на множители и формировать умение ее применять.

Задачи:

1. Закрепить понятие квадратичного трехчлена и его корней; формировать умение находить корни квадратного трехчлена.

2. развивать умение и навыки решения уравнений объяснять, строить логические цепочки решения, записывать решение по формуле, образное и логическое мышление.

3. воспитывать аккуратность, ответственность, умение работать самостоятельно, интерес к изучению математики.

Оборудование: учебник, доска, цветные мелки.

ХОД УРОКА

I. ОРГМОМЕНТ. 1. Проверка отсутствующих и готовности класса к уроку.

2.Сообщение темы и цели урока, запись на доске и в тетради

I. Организационный момент.

II. Устная работа.

1. Какие из чисел: 1; 2; 3; –3 – являются корнями трехчлена х² + х – 6?

2. Сколько корней имеет квадратный трехчлен:

а) х² – 7; г) 5х² + 10;

б) 5х – 6х²; д) х² + 2х – 7;

в) х² + 2х + 1; е) х² + 2х + 10?

III. Объяснение нового материала.

Сначала необходимо актуализировать знания учащихся и создать у них мотивацию. Поэтому следует разобрать, как разложить на множители квадратный трехчлен методом группировки, рассмотрев несколько примеров:

а) х² + 3х – 4 = х² + 4х – х – 4 = х (х + 4) – (х + 4) = (х + 4) (х – 1);

б) –х² + 3х + 10 = –(х² – 3х – 10) = –(х² – 5х + 2х – 10) = –(х (х – 5) ++ 2 (х – 5)) = – (х – 5) (х + 2) = (5 – х) (х + 2);

в) 2х² + 6х + 4 = 2 (х² + 3х + 2) = 2 (х² + х + 2х + 2) = 2 (х (х + 1) + + 2 (х + 1)) = 2 (х + 1) (х + 2).

ax2 + bx + c = a (x – x1) (x – x2)

,

IV. Формирование умений и навыков.

На этом уроке учащиеся выполняют задания на непосредственное применение изученной теоремы. Использование теоремы для упрощения выражений лучше рассмотреть на следующем уроке.

Упражнения:

1. № 76, № 77 (а, б).

2. № 79 (а), № 80.

№ 82. Учащиеся могут подобрать такой трехчлен с конкретными коэффициентами и разложить его на множители. Н а п р и м е р: х² + 3х + 2 = 
= (х + 1) (х + 2). Однако доказательство факта, данного в задаче, необходимо провести в общем виде.

Пусть а = п, b = 2п, с = 3п. Тогда получим квадратный трехчлен пх² + 
+ 2пх + 3п. Его дискриминант равен –8п², то есть трехчлен такого вида корней не имеет, значит, не удовлетворяет условию задачи. Замечаем, что дискриминант будет отрицательным в тех трехчленах, в которых а = 3п или с = 3п.

Условию будут удовлетворять только два трехчлена:

пх² + 3пх + 2п и 2пх² + 3пх + п. Разложим их на множители:

пх² + 3пх + 2п = 0;

D = 9п² – 8п² = п^2;

х₁ = ; ;

пх² + 3пх + 2п = п (х + 1) (х + 2);

2пх² + 3пх + п = 0;

D = 9п² – 8п² = п^2;

х₁ = ; ;

2пх² + 3пх + п = 2п  (х + 1) = п (2х + 1) (х + 1).

Подставляя конкретные значения п, можно получить бесконечно много квадратных трехчленов указанного вида: х² + 3х + 2, 2х² + 3х + 1, 2х² + 6х + 4, 4х² + 6х + 2 и т. п.

V. Итоги урока.

– Что такое квадратный трехчлен?

– Как найти корни квадратного трехчлена?

– Сформулируйте теорему о разложении квадратного трехчлена на множители.

– Любой ли квадратный трехчлен можно разложить на множители? От чего это зависит?

Рефлексия:

Домашнее задание: № 77 (в, г), № 78, № 79 (б).

 

Учитель: Клименко Ольга Анатольевна                9 класс

Тема: разложении квадратного трехчлена на множители

У р о к № ___.

Тип урока: Изучение нового материала
Цель: продолжить формирование умения раскладывать на множители квадратный трехчлен, применяя это разложение для сокращения дробей и упрощения выражений.

Задачи: 1. Закрепить понятие квадратичного трехчлена и его корней; формировать умение находить корни квадратного трехчлена.

2. развивать умение и навыки решения уравнений объяснять, строить логические цепочки решения, записывать решение по формуле, образное и логическое мышление.

3. воспитывать аккуратность, ответственность, умение работать самостоятельно, интерес к изучению математики.

Оборудование: учебник, доска, цветные мелки.

ХОД УРОКА

I. ОРГМОМЕНТ. 1. Проверка отсутствующих и готовности класса к уроку.

2.Сообщение темы и цели урока, запись на доске и в тетради

I. Организационный момент.

II. Устная работа.

Определите, можно ли представить квадратный трехчлен в виде произведения многочленов первой степени:

а) 2х² + х – 5; г) х² – 2х + 8;

б) 2х² + х + 5; д) х² – 2х – 8;

в) х² – 4х + 4; е) 9х² + 6х + 1.

III. Формирование умений и навыков.

На этом уроке следует обобщить знания учащихся о различных способах разложения многочленов на множители. Особое внимание нужно уделить двум вопросам:

1) Сколько существует способов разложения многочленов на множители и в чем они заключаются?

2) При решении каких задач пригодится умение раскладывать многочлен на множители?

Поскольку для сокращения дробей и упрощения выражений учащимся потребуется знание всех способов разложения многочленов на множители, то для начала необходимо актуализировать эти знания.

Учитель сообщает учащимся, что теперь им известны все основные способы разложения многочленов на множители и просит перечислить эти способы. В тетрадях у учащихся должны быть записаны названия всех четырех способов и приведены примеры.

1. Вынос общего множителя за скобки:

а) 2х³ + 5х² – х = х (2х² + 5х – 1);

б) 9х⁵ + 15х³ = 3х³ (3х² + 5).

2. Применение формул сокращенного умножения:

а) 4х² – у² = (2х – у) (2х + у);

б) х² – 6х + 9 = (х – 3)²;

в) х³ + 8 = (х + 2) (х² – 2х + 4).

3. Метод группировки:

а) 6х³ – 8х² + 3х – 4 = 2х² (3х – 4) + (3х – 4) = (3х – 4) (2х² + 1);

б) 2х + у + у² – 4х² = 2х + у + (у – 2х) (у + 2х) = (у + 2х) (1 + у – 2х).

4. Разложение на множители квадратного трехчлена:

а) х² – 4х – 5 = (х + 1) (х + 5);

б) 3х² + х – 4 = 3 (x – 1) = (х – 1) (3х + 4).

Далее выделяются две основные группы заданий, при выполнении которых необходимо умение раскладывать многочлен на множители:

– сокращение дробей;

– упрощение выражений.

Упражнения:

1. № 83 (а, в, д), № 85 (а).

2. Сократите дробь:

а) ; б) .

Р е ш е н и е

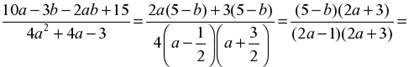
б) .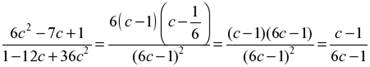

Упростите выражение:

а) ;

б) .

Р е ш е н и е

а) 

б) 

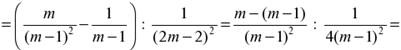
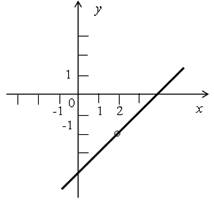
Если останется время, то можно предложить учащимся задание на построение графика функции .

Р е ш е н и е

Данная функция не является элементарной, и по точкам ее строить неудобно. Сократим дробь, задающую функцию:

Таким образом, график исходной функции совпадает с графиком функции у = х – 4, но точка х = 2 не входит в область определения данной функции, поэтому на графике эта точка будет выколотой.

IV. Проверочная работа.

В а р и а н т 1

1. Разложите на множители квадратный трехчлен:

а) х² – 7х + 12; б) 6х² + 5х – 4.

2. Сократите дробь:

а) ; б) .

3*. Упростите выражение:

.

В а р и а н т 2

1. Разложите на множители квадратный трехчлен:

а) х² + х – 72; б) 7х² + 20х – 3.

2. Сократите дробь:

а) ; б) .

3*. Упростите выражение:

.

V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Сформулируйте теорему о разложении квадратного трехчлена на множители.

– Всегда ли можно разложить на множители квадратный трехчлен? От чего это зависит?

– Какие существуют способы разложения многочлена на множители?

– При выполнении каких заданий пригодится умение раскладывать многочлен на множители?

– Как сократить алгебраическую дробь?

Рефлексия

Домашнее задание:

1. № 83 (б, г, е), № 84, № 85 (б).

2. Упростите выражение:

а) ;

б) .