Конспект урока: "умножение и деление дробей"

Учитель: Клименко О. А.

Урок № _____

Тема: Умножение и деление алгебраических дробей

Цели:

Обучающая: Формирование знаний и умений правил умножения и деления дробей дробей. Умение выполнять указанные действия. Повторить и обобщить полученные знания об обыкновенных дробях.

Развивающая: Развитие кругозора, мышления, любознательности, внимания, культуры математической речи, привитие интереса к изучению математики.

Воспитывающая: Воспитание аккуратности, чувство коллективизма, самоконтроля.

Форма урока: урок изучения нового материала.

Метод обучения: проблемный, с самостоятельным поиском решения.

Оборудование: Компьютер, проектор, раздаточный материал по уроку, таблица.

Ход урока

Урок проводится с использованием компьютерной презентации.

Ι. Организация урока.

1. Подготовка технической части.

2. Карточки для работы в парах и самостоятельной работы.

ΙΙ. Актуализация опорных знаний с целью подготовки  к изучению новой темы.

Устно: (Ответы  выводятся с помощью компьютера.)

1. Разложить на множители:

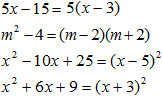
2. Сократить дробь:

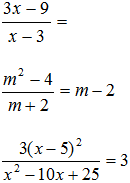
3. Умножить дроби:

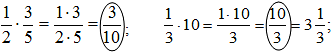
-    Как называются эти числа?    (Взаимообратные числа)

Найти число, обратное числу 

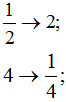
Какие два числа называются взаимообратными? (Два числа называются взаимообратными, если их произведение равно 1.)

Найти дробь обратную: 

Разделить дроби:

Проговариваем правила умножения и деления обыкновенных дробей. Плакат с правилами размещен на доске.

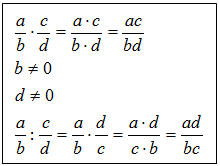
ΙΙΙ. Новая тема

Обращаясь к плакату, учитель говорит: a, b, c, d - в данном случае числа. А если это будут алгебраические выражения, как называются такие дроби? (Алгебраические дроби)

Правила их умножения и деления остаются теми же самыми.

Выполнить действия:

Первый и второй пример самостоятельно, с последующей записью решения учащимися на доске. Решение третьего примера учитель показывает на доске.

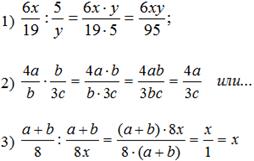
Арифметические действия с алгебраическими дробями выполняются также как и арифметические действия с обыкновенными дробями.

Сложение и вычитание арифметических дробей с общим знаменателем:

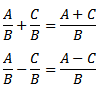
Сложение и вычитание арифметических дробей с разными знаменателями:

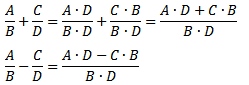
Умножение и деление алгебраических дробей:

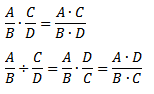
(С, B и D – ненулевой многочлен)

Примеры.

Сложение дробей с общим знаменателем, знаменатель оставляем без изменений, числители складываем.

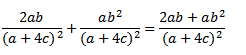
Вычитание дробей с общим знаменателем:

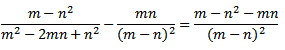
Умножение алгебраических дробей выполняется также как и умножение обыкновенных дробей:

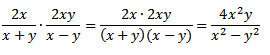
Деление выполняем при условии ненулевого значения многочленов

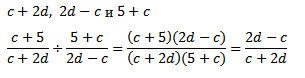
Рациональное выражение ˗ это выражение, в котором несколько алгебраических дробей соединены знаками арифметических действий.

Алгебраическая дробь – рациональное выражение.

Например, рациональное выражение:

Рациональное выражение 4ab : (a – a) не имеет смысла, так как содержит деление на нулевой многочлен.

Рациональные выражения можно упрощать:

Итак, алгебраические дроби можно складывать, вычитать, умножать и делить, при условии, что B, C и D ненулевые многочлены. Алгебраические дроби обладают рядом свойств, которые нужно запомнить. Алгебраическая дробь – это рациональное выражение.

Разбор заданий тренировочного модуля.

№1. Упростим рациональное выражение:

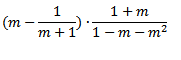
Выполним действие в скобках:

Выполним умножение алгебраических дробей:

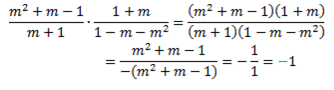
Ответ: -1.

№2. Тип задания: Выполним преобразование «цепочкой» равенств:

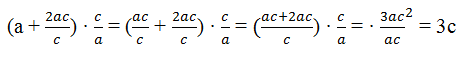
Ответ: 3с.

V.  Закрепление

1) №110,№111,№133,№137.

2) Работа в парах по карточкам:

6. Итог урока.

- Что нового узнали?

- Чему научились?

Выставление оценок

7. Домашнее задание.

П. , № 684 (а)