Конспект занятия вариативного курса по теме "Шкала"

ШКАЛА

Цель: ознакомление обучающихся со шкалой. Формирование умения определения цены деления, значения показаний приборов, имеющих шкалу.

Ход занятия

I.                Организационный момент.

Приветствие учащихся.

II.            Подготовка к восприятию нового материала.

Шкала измерений - основополагающее понятие метрологии (науки об измерениях), позволяющее количественно или как-либо другим способом определить свойство объекта. Шкала измерений является более общим понятием, чем единица физической величины, отсутствующая в некоторых видах измерений. .Шкалы необходимы как для количественных (длина, температуpa), так и для качественных (цвет) проявлений свойств объектов (тел, веществ, явлений, процессов). Уровень проявления свойства объектов, которые оцениваются с помощью шкалы измерений, позволяют установить между этими обьектами отношения типа «равенство», "больше", "меньше", возможность "суммирования" элементов или "деления" одного на другой. Вы уже встречались со шкалой, например, пятибальная шкала школьных отметок, пяти или девятибальная шкала для оценивания высоты вашей квартиры в доме (единицы измерения - этажи).

Примеры шкал (рис. 2.1)

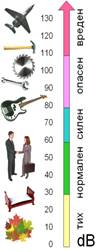
Рис 2.1. Примеры различных шкал

Шум измеряется в децибелах. Эта единица названа в честь изобретателя телефона Гоэхэма Белла и обозначается дБ (десятая часть Белла). В дБ проводится спектральный анализ шума. Для интегральной оценки служит единица измерений уровня звука — дБА

В теории измерений принято в основном различать 5 типов шкалы измерений: шкалы наименований, порядка, разностей (интервалов), отношений и абсолютные шкалы.

Шкала наименований характеризуется только отношением эквивалентности какого-либо качественного проявления свойства. Пример такой шкалы  измерений -  оценка цвета объекта по наименованиям (красный, белый, сине-зелёный). Измерения выполняются путём сравнения при определенном освещении образцов цвета из атласа с исследуемым цветом и установления ихравенства.

Шкала порядка описывает свойства, для которых имеют смысл не только отношение эквивалентности, но и отношение порядка по возрастанию или убыванию количественного проявления свойства. Характерный пример шкал порядка - шкалы чисел твёрдости тел, шкалы баллов землетрясений, шкалы баллов ветра и т. д. В такого рода шкалах в принципе нет возможности введения единицы измерений, также не имеют смысла суждения, во сколько раз больше или меньше проявления конкретных свойств. Разл. варианты шкал порядка для одного и того же свойства связаны между собой монотонными зависимостями. В шкалах порядка может быть (иметь смысл) нуль или его может не быть. Так, шкалы твёрдости начинаются с некоторого ненулевого значения, сейсмическая шкала начинается с одного балла, а шкала Бофорта для силы ветра - с нулевого значения.

Шкала разностей (интервалов) отличается от шкалы порядка тем, что для описываемого ею свойства имеют смысл не только отношения эквивалентности и порядка, но и пропорциональности или суммирования разностей между различными количественными проявлениями свойства. Характерный пример - шкалы времени; интервалы времени можно суммировать или вычитать, складывать же даты каких-либо событий бессмысленно. Шкалы разностей имеют условный нуль, измерения с помощью такой шкалы могут быть положительными или отрицательными (например, шкала Цельсия для измерения температуры воздуха).

Шкала отношений описывает свойства, ко множеству количественных проявлений которых применимы отношения равенства, порядка, пропорциональности или суммирования (а следовательно, и вычитания, и умножения). В шкале отношений существует естественный критерий нулевого количественного проявления свойства, т. е. нуль имеет не условное значение, а вполне определенный физический смысл. Примеры шкал отношений - шкала для измерения массы.

Абсолютные шкалы обладают всеми признаками шкал отношений, но дополнительно в них существует естественное однозначное определение единицы измерения. Такие шкалы измерений соответствуют относительным величинам - отношениям одноимённых физических величин, описываемых шкалами отношений. К таким величинам относятся коэфициент усиления, добротность колебательной системы, коэфициент ослабления, с которыми вы познакомитесь на уроках физики. Среди абсолютных шкал выделяются ограниченные по диапазону шкалы, значения которых находятся в пределах от 0 до 1 (например, КПД – кэффициент полезного действия).

Большинство свойств, которые рассматривают в практической метрологии, описывается одномерными шкалами измерений. Однако имеются свойства, которые можно описать только многомерными шкалами. Таковы, например, трёхмерные шкалы цвета в колориметрии. Шкалы сортности изделий и продуктов в общем случае являются многомерными шкалами наименований и опираются на ряд факторов, каждый из которых определяется по специализированным шкалам (например, вес , объем и процентной содержание отдельных составляющих).

Практическое создание шкалы с конкретными свойствами достигается путём точного копирования эталонов и средств измерений. Понятие единицы измерений, неизменной для любых участков шкалы, имеет смысл только для шкал отношений и разностей, а также для абсолютной шкалы. Поэтому единицы измерений, охватываемые международной системой единиц, соответствуют величинам, описываемым только шкалами отношений, разностей и абсолютной. Конкретные математические формулы в науке и технике могут связывать также только такие величины, которые измеряются шкалами отношений, разностей и абсолютными. Поэтому измерения в шкалах порядка и наименований иногда назвают оцениванием.

По мере развития метрологии наблюдается тенденция рассматривать в качестве объектов измерений все новые, и не только физические, свойства и соответствующие им величины. Так, например, формируется и описан метрологический подход к изучению и описанию свойств биологических, психологических, социальных. экономических систем, создаются новые и совершенствуются уже существующие шкалы  измерений.

III.         Основная часть.

1.                     Понятие штрихов. Делений, цены деления.

2.                     Решение задач по теме: «Шкала».

IV. Итог урока.

Учащимся предлагается придумать и изобразить в тетради шкалу настроения.

Информационный модуль к сценарию.

1. Итак, практически во всех измерительных приборах мы можем увидеть шкалу. Она состоит из штрихов и делений.

Штрихи – это название условное, так как они могут выглядеть как точки, кружочки или другие знаки, выделяющие конкретное место, точку на измерительной шкале. Каждому штриху шкалы соответствует определенное число единиц измерения той величины, для которой создан прибор с данной шкалой. Иногда крайнему штриху шкалы соответствует число нуль,  но это необязательно. Делениями называются расстояния между штрихами. Ценой деления – разность между двумя числами, соответствующими любым двум соседним штрихам.

Можно сравнить шкалу с отрезком пути, пройденным человеком при постоянной длине шага. Следы от ног – штрихи шкалы, неизменная длина шага – цена деления, число, стоящее около каждого отпечатка ноги – расстояние от нулевой точки (от начала движения).

Чтобы при измерении пользоваться шкалой правильно, нужно уметь определять число соответствующее каждом ее штриху.

2.Решение задач по теме: «Шкала».

Подписать числа, соответствующие каждому штриху шкалы.

1)   ----------------

       0     10

2)    ________________

       3      5

3)     ______________________

                         7       9

4)     9             15

5)  ___________________

      |     |     |     |     |     |     |

                            12        18

6)                                             

                              17                           23

7)      2                                            44

         |       |       |       |       |       |       |

 8) Утром работник приступил к распиловке бревен. Через час он подсчитал. Что за это время он сделал девять распилов, а получилось 13 чурок. Сколько бревен распилил работник?

Ответ: 4.