Конспект урока по геометрии в 8 классе «Применение подобия треугольников при решении практических задач».

Конспект урока по геометрии в 8 классе

«Применение подобия треугольников  при  решении практических задач».

Предмет: геометрия

Класс: 8

Тема: «Применение подобия треугольников  при  решении практических задач».

План урока

1.     Мотивационно-целевой этап.

2.     Актуализация усвоенных знаний учащихся.

3.     Применение теоретических основ при решении практических задач.

4.     Подведение итогов. Рефлексия.

1

Ход урока

1.     Мотивационно-целевой этап.

Учитель зачитывает отрывок из романа Жюля Верна  «Таинственный остров».     

-…Остановившись шагах в двадцати от кромки моря и шагах в пятистах от гранитного пляжа, Сайрес Смит воткнул жердь в песок и старательно выпрямил её, добившись путём выверки отвесом, чтобы она стояла перпендикулярно к плоскости горизонта.

     Сделав это, Сайрес Смит  отошел и лёг на землю на таком расстоянии, чтобы в поле его зрения находился и верхний конец жерди и гребень гранитной стены. Это место он отметил на песке колышком и, повернувшись к Герберту, спросил:

-Ты знаком с геометрией?

- Немножко, мистер Сайрес, - ответил Герберт, боясь попасть впросак.

- Помнишь свойства подобных треугольников?

- Да, - ответил юноша,- у подобных треугольников соответствующие стороны пропорциональны друг другу.

- Так вот, дитя моё, у меня тут два подобных треугольника, - один поменьше, в нём двумя сторонами будут: жердь, воткнутая перпендикулярно в песок, и прямая, равная расстоянию от нижнего конца жерди до колышка, а гипотенузой – мой луч зрения; у второго треугольника сторонами явятся: отвесная линия гранитной стены, высоту которой нам нужно измерить, расстояние от колышка до подошвы стены, а в качестве гипотенузы – мой луч зрения, то есть продолжение гипотенузы первого треугольника.

 - Понял, мистер Сайрес! Я всё понял!- воскликнул Герберт.

Учитель:

-Ребята, как вы думаете, о чем мы будем говорить на сегодняшнем уроке?

Учащиеся рассуждают, делают общий вывод:

- Об использовании  признаков подобия треугольников при решении практических задач.

2

Учитель:

-Какая будет цель нашего урока?

Учащиеся:

- Рассмотреть использование  подобия треугольников при решении практических задач.

Учитель:

- Великий П. Чебышев утверждал: «Сближение  теории и практики даёт самые благотворные результаты, и не одна только практика выигрывает: сама наука развивается под влиянием её».

Учитель:                                                                                                                                                                                                                             

- Но прежде чем решать практические задачи, проверим, как вы усвоили теоретические знания по данной теме.

2.Актуализация усвоенных знаний учащихся.

Учитель:

- К сегодняшнему уроку группа учащихся выполняла коллективный проект «Моя контрольная работа по теме «Подобные треугольники»».

Презентация проекта  «Моя  контрольная работа по теме «Подобные треугольники»».

Задание №1. Опишите конфигурацию, заданную рисунком, применив при этом имеющиеся знания.

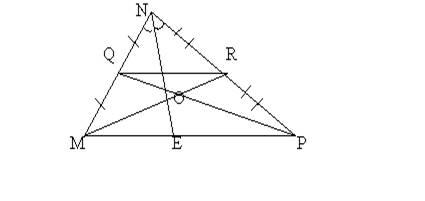
/Предполагается, что при описании конфигурации учащиеся должны увидеть среднюю линию, биссектрису и медианы треугольника, подобные треугольники, записать отношения, применив свойства биссектрисы и медиан треугольника/.

3

Задание №2 состоит из 10 предложений. Нужно установить их истинность.

Задание №3. Основания трапеции равны 5 см и 8 см. Боковые стороны, равные 3,6 см и 3,9 см, продолжены до пересечения в точке М. Найдите расстояние от точки М до концов меньшего основания.

4

Задание№4. В треугольник МNК вписан ромб МDEF так, что вершина D, Е и F лежат соответственно на сторонах MN, NK и MK. Найдите отрезки NE и EK, если MN=7 см, NK=6 cм, МК=5 см.

Задание №5. Даны два треугольника: произвольный  и прямоугольный. На одной из сторон отмечена точка М. Сколько можно получить треугольников, подобных треугольнику АВС, проведя через точку М различные прямые?

     Задания выполняются в группах (5 чел.). Решение и обсуждение задач в группах. Представление решений выполненных задач.                                                Учащиеся совместно с учителем подводят итог выполненных заданий проекта «Моя контрольная работа по теме «Подобные треугольники»»:

- Каков уровень сложности предложенных задач?

-Какая задача вызвала наибольшие затруднения?

-Какое задание вызвало наибольший интерес?

3.Применение теоретических основ при решении практических задач.

Учитель:

- Великий математик П.Рамус говорил: «Геометрия – это наука хорошо измерять». Геометрические знания широко применяются в жизни — в быту, на производстве, в науке. И на сегодняшнем уроке мы рассмотрим использование подобия треугольников для определения расстояния до недоступной точки, измерения высоты предмета.

Группа учащихся представляет проект «Использование признаков подобия треугольников для определения высоты предмета»

Проблема: недостаточно знаний по использованию  подобия треугольников при решении практических задач: определение высоты предмета (дерева, столба, здания, скалы и т.д.)                                                                                                             Цель проекта: рассмотреть использование  подобия треугольников для определения высоты предмета.                                                                                                                                             

5

Содержание проекта:

     1.Исторические задачи на определение высоты предмета.

     2.Определение высоты предмета с использованием  подобия   треугольников.

     3.Задачи на определение высоты предмета (дерева, столба, здания, скалы и т.д.)

Форма презентации: информационный справочник, компьютерная презентация

Результативность: составлен информационный справочник по использованию подобия   треугольников для определения высоты предмета;  составлены задачи  на определение высоты предмета.

Использование признаков подобия треугольников для определения высоты предмета

   Рассматриваются разные способы использования подобных треугольников для определения  высоты предмета (дерева, столба, здания, скалы и т.д.): с помощью вращающейся планки, с помощью тени, с помощью зеркала.

1 способ

Определение высоты предмета по его тени.

        21 июля 1798 г. генерал Бонапарт  произнес перед сражением  при   египетских пирамидах  такие красивые слова: «Сорок веков смотрят на вас с высоты этих пирамид».                                                                                                                 А как определить высоту  такого огромного сооружения?                                               Самый  легкий  и самый древний  способ без сомнения тот, которым  воспользовался греческий мудрец Фалес за шесть веков до нашей эры. Фараон и жрецы, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего высоту огромного сооружения.                                  – Знает ли кто- либо, какова её высота? – спросил он.                                                                              – Нет, сын мой, - ответил жрец,  – Древние папирусы не сохранили нам этого, а наши знания не дают возможности судить о ней даже приблизительно.    

6

 - Но ведь это можно сказать совсем точно и даже сейчас, - воскликнул Фалес.                                         - Вот смотри, мой рост 3 царских вавилонских локтя. А вот моя тень. Её длина такая же. И какой бы ты предмет ни взял именно в это время, тень от него, если ты поставишь его вертикально, точно равна длине предмета. Этот предмет и его тень образуют прямоугольный треугольник, знай же, что такие треугольники подобны.     

Фалес привёл в удивление жрецов, измерив высоту пирамиды без всяких приборов по отбрасываемой ею тени. Конечно, длину тени надо было  считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес  мог измерить  непосредственно.

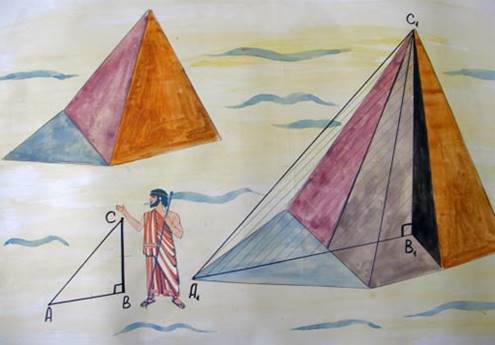
С₁В₁:СВ = А₁В₁:АВ, откуда

С₁В₁= (СВхА₁В₁)/АВ.

      Фалес определил высоту пирамиды  по ее тени.                                                                    Подобие прямоугольных треугольников помогло древнегреческому учёному Фалесу Милетскому измерить высоту Египетской пирамиды.

7

2 способ

     Предположим, что нам нужно определить высоту какого-нибудь предмета, например высоту телеграфного столба А₁В₁,   изображенного на рисунке.

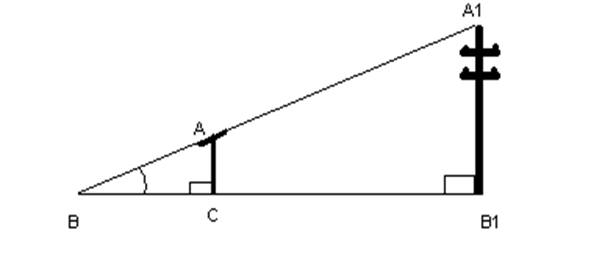
   Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку А₁ столба, как показано на рисунке. Отметим на поверхности земли точку В, в которой прямая А А₁ пересекается с поверхностью земли. Прямоугольные треугольники А₁ В₁В и АСВ подобны по первому признаку подобия треугольников ( ÐВ₁= Ð С= 90⁰,  Р В- общий).

Из подобия  треугольников следует:

А₁В₁ : АС = ВВ₁ : ВС, откуда

А₁В₁=(АСхВВ₁)/ВС.

Измерив расстояние ВВ₁ и ВС и зная длину АС шеста, по полученной формуле определяем высоту телеграфного столба А₁В₁.

Например, если  ВВ₁= 6,3 м., ВС= 2,1 м., АС= 1,7 м., то

А₁В₁=(1,7х6,3)/2,1 =  5,1 м.

8

3 способ

   Для определения высоты предмета можно использовать зеркало, расположенное на земле горизонтально. Луч света, отражаясь от зеркала, попадает в глаз человека. Используя подобие треугольников можно найти высоту предмета, зная рост человека (до глаз), расстояние от глаз до макушки человека и измеряя расстояние от человека до зеркала, расстояние от зеркала до предмета (учитывая, что угол падения луча равен углу отражения).

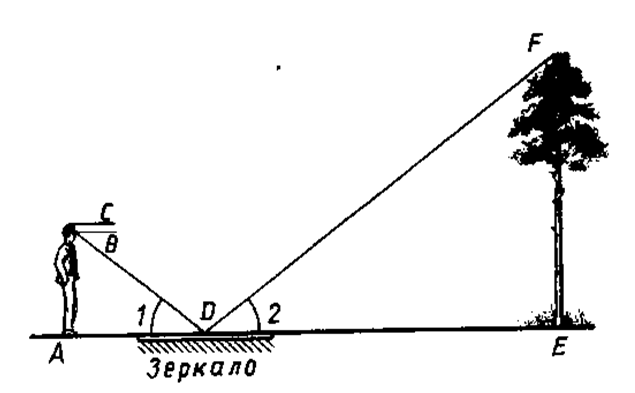
Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека -точку В. Треугольники FЕD, САD подобны по первому признаку подобия треугольников: Ð Е= Ð А= 90⁰,  Ð1= Ð2. Из подобия  треугольников следует:

FE : АС = ЕD : DA, откуда

FE= (АСхЕD)/DА

Обсуждение проекта.

Учитель:

- Ребята,  а как же справились с нахождением высоты скалы наши герои из романа

Жюля Верна  «Таинственный остров»?

9

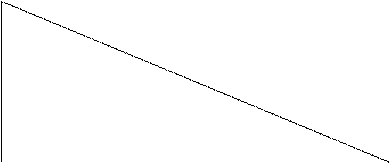
Учитель продолжает зачитывать отрывок из романа Жюля Верна «Таинственный остров»:

- …Основания обоих треугольников были измерены при помощи той же самой жерди, высота которой над поверхностью песка равнялась десяти футам; оказалось, что расстояние между колышком и жердью – пятнадцать футов, а расстояние между колышком и подошвой стены – пятьсот футов…

-Какой чертеж выполнил, какую пропорцию составил Сайрес Смит?

Ребята  выполняют чертеж, составляют пропорцию.

                  В

                                                   Н

                 А                                 D                                          С

CD=15 фут

АС= 500 фут

НD= 10 фут

СD : АС = НD : АВ

15: 500 = 10 : АВ

 АВ= (10х500)/15=333,33 фута.

Обсуждение решений.

Учитель доканчивает отрывок из произведения:

- …Следовательно, высота гранитной стены равнялась тремстам тридцати трем футам…

10

Группа учащихся представляет проект «Использование подобия треугольников для определения  расстояния до недоступной точки».

Проблема: недостаточно знаний по использованию  подобия треугольников при решении практических задач.

Цель проекта: рассмотреть использование  подобия треугольников для измерения расстояния до недоступной точки

Содержание проекта:

1.Определение расстояния до недоступной точки с использованием  подобия треугольников.

2. Рассмотрение жизненных ситуаций по измерению расстояния до недоступной точки.

3. Задачи на измерение расстояния до недоступной точки.

Форма презентации:  информационный справочник, компьютерная презентация

Результативность: составлен информационный справочник по использованию подобия треугольников для измерения  расстояния до недоступной точки; составлены задачи  на измерения расстояния до недоступной точки.

Измерение  расстояния до недоступной точки

   Треугольник является  основой многих практических измерений. Решение задач на измерение ширины реки, определение расстояния до недоступной точки  позволяют  увидеть масштаб применения геометрии в жизни человека.

Для измерения расстояния до недоступной точки рассматриваются следующие задачи:

- нахождение расстояния от пункта А до недоступного пункта В,  

-измерение расстояния между точками А и В, разделёнными препятствием (рекой, озером, болотом).

Определение расстояния до недоступной точки

    Предположим, что нам нужно найти расстояние от пункта A до недоступного пункта B.

11

                                                                                       В

                                                                                                                                     А                                                                                                                                          С

Для этого на местности выбираем точку C, провешиваем отрезок AC и измеряем его. Затем с помощью астролябии измеряем ÐA и ÐC. На листе бумаги строим  треугольник A₁B₁C₁, у которого    Ð A₁= ÐA,   ÐС₁=Ð С, и измеряем длины сторон A₁B₁ и A₁C₁ этого треугольника.

                                                              В₁

                    А₁                                                                            С₁

Так как треугольники ABC и A₁B₁ C₁ подобны (по первому признаку подобия треугольников), то                  

АВ /А₁В₁ = АС /А₁С₁.

Откуда получаем

AB=(АСхА₁В₁)/А₁С₁.

Эта формула позволяет по известным расстояниям AC, A₁C₁  и A₁B₁ найти расстояние AB.

12

Для упрощения вычислений удобно построить треугольник A₁B₁C₁ таким образом, чтобы

A₁C₁ :AC=1:1000.

В этом случае получаем:

AB= (АС/А₁С₁)хА₁ В₁=1000·A₁B₁

Например, если  AC=130м, то расстояние A₁ C₁ возьмем равным 130мм, отсюда получаем расстояние АВ в метрах.

Использование средней линии треугольника

для нахождения расстояния до недоступной точки

                                                        А

                                                                                      Е

                        В                                D                                         С

Выбрав точку С, находим середину D стороны ВС. Проводим DЕ параллельно АВ, тогда АВ=2 DЕ.

Определение ширины реки

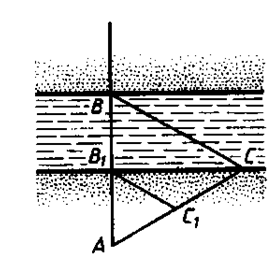
                              Как найти ширины реки ВВ₁?  Выбрав точку С₁, проводим В₁С_1.. Затем через точку А провешиваем АВ и АС таким образом, чтобы В₁С₁ была средней линий ∆ АВС, тогда ВВ₁=АВ₁.

13

                 Жизненные ситуации по измерению ширины реки                                                              Измерение ширины реки  при  помощи козырька

                                                                       Переправа, переправа!

                                                                       Берег левый, берег правый,

                                                                       Снег шершавый, кромка льда…

                                                                       Кому память, кому слава,

                                                                       Кому темная вода, –

                                                                       Ни приметы, ни следа.

                                                                                   «Василий Теркин»,  

                                                                                    А.Твардовский

     Вот так  этот  способ пригодился   старшему сержанту Куприянову во фронтовой  обстановке. Его отделению было  приказано измерить ширину  реки, через  которую  предстояло организовать  переправу …

 Подобравшись к кустарнику вблизи реки, отделение  Куприянова  залегло, а сам Куприянов вместе с солдатом  Карповым  выдвинулся  ближе  к реке, откуда  был  хорошо  виден  занятый фашистами берег. В таких  условиях  измерять  ширину реки  нужно было  на глаз.

 – Ну-ка, Карпов,  сколько? – спросил Куприянов.

 – По-моему, не больше  100-110 метров, – ответил Карпов. Куприянов был  согласен  со своим разведчиком, но для  контроля  решил  измерить  ширину  реки при помощи козырька.

Этот способ заключается  в следующем. Надо стать  лицом к реке  и надвинуть фуражку на глаза так, чтобы  нижний обрез  козырька точно совпал с линией  противоположного берега. (Козырек  можно заменить ладонью руки или записной книжкой, плотно  приложенной ребром ко лбу).

 Затем, не изменяя  положения  головы, надо повернуться  направо  или  налево, или даже назад  (в ту сторону, где  поровнее площадка,  доступная для  измерения  расстояния) и заметить  самую дальнюю точку, видимую  из-под козырька  (ладони, записной книжки).

 Расстояние до этой точки  и будет примерно равно  ширине реки. Этим способом  и  воспользовался Куприянов. Равные треугольники  подобны с k = 1

14

Обсуждение проекта.

Решение задачи: Одна из вершин земельного участка  треугольной формы недоступна. Как измерить периметр этого участка?

4.Домашнее задание. Задание: по конфигурации из задания №1 проекта «Моя контрольная работа по теме «Подобные треугольники»» составить различные задачи.

5.Подведение итогов. Рефлексия.

Учитель:

- Ребята, достигнута ли вами цель сегодняшнего урока?

- Что вы узнали нового на уроке?

-Оцените уровень представленных проектов.

Обсуждение.

Учитель:

-Ребята, на доске нарисован  треугольник. На столе лежат подобные и не подобные ему треугольники. Если вам понятна эта тема, то к  треугольнику, нарисованному на доске,  прикрепите подобные ему треугольники, если непонятна- то прикрепите неподобные.

    Вывод по уроку.

15