БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ «СОВЕТСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»

 

УТВЕРЖДАЮ

Заместитель директора

по учебной работе

____________/Куимова Г.Р./

«___»_______2019г.

 

 

 

 

Комплект контрольно-оценочных средств

для оценки результатов освоения

 

ОУД.03 «Математика»

 

  по профессии

15.01.09 Машинист лесозаготовительных и трелевочных машин

технический

 

 

 

 

 

 

 

 

г. Советский

2019 г.

 

Комплект контрольно-оценочных средств по учебной дисциплине ОУД.03  «Математика» разработан  на основе Федерального государственного образовательного стандарта среднего общего образования (утв. приказом Министерства образования и науки РФ от «17» мая 2012 г. № 413)  по профессии 15.01.09 Машинист лесозаготовительных и трелевочных машин

 

Организация-разработчик: бюджетное учреждение профессионального образования Ханты -Мансийского автономного округа-Югры «Советский политехнический колледж»

 

Разработчик:

Невенкина О.И.,   преподаватель бюджетного учреждения профессионального образования Ханты-Мансийского автономного округа-Югры «Советский политехнический колледж»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I.   ПАСПОРТ КОМПЛЕКТА ОЦЕНОЧНЫХ СРЕДСТВ

Общие положения

 

Учебная дисциплина ОУД.03 «Математика» изучается на 1 и 2 курсах.

Максимальное количество часов на реализацию программы УД -427 час.

Практикоориентированность учебной дисциплины составляет 59 %.

Учебная дисциплина ОУД.03 «Математика»  состоит из 4 разделов:

Раздел 1. Алгебра

Раздел 2. Геометрия

Раздел 3. Элементы комбинаторики, теории вероятностей и математической статистики

Раздел 4. Начала математического анализа

Профиль получаемого профессионального образования: технический.

Реализация программы учебной дисциплины способствует формированию у обучающихся:

Личностных результатов обучения:

1) сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;

2) понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;

3) развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;

4) овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественнонаучных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

5) готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;

6) готовность и способность к самостоятельной творческой и ответственной деятельности;

7) готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;

8) отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем.

 

Метапредметных результатов обучения:

1) умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

2) умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

3) владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;

4) готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;

5) умение использовать средства информационных и коммуникационных технологий (далее – ИКТ) в решении когнитивных, коммуникативных и организационных задач с соблюдением требований эргономики, техники безопасности, гигиены, ресурсосбережения, правовых и этических норм, норм информационной безопасности;

6) умение определять назначение и функции различных социальных институтов;

7) умение самостоятельно оценивать и принимать решения, определяющие стратегию поведения, с учётом гражданских и нравственных ценностей;

8) владение языковыми средствами – умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

9) владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения.

 

Предметных результатов:

1) сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;

2) сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

3) владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;

4) владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;

5) сформированность представлений об основных понятиях, идеях и методах математического анализа;

6) владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;

7) сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;

8) владение навыками использования готовых компьютерных программ при решении задач;  

9) сформированность представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений;

10) сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;

11) сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат;

12) сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

13) владение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.

 

Контроль формируемых знаний и умений проводится в процессе текущего контроля. Промежуточная аттестация предусмотрена в форме дифференцированного зачета на первом курсе во втором семестре и  экзамена на 2 курсе в 4 семестре.

Матрицы логических связей между объектами (предметами) контроля и разделами (темами) учебной дисциплины ОУД.03 «Математика»

 

Разделы (темы) программы УД

Объекты (предметы) контроля

Метапредметные результаты

Предметные результаты

МР 1

МР 2

МР 3

МР 4

МР 5

МР 6

МР 7

МР 8

МР 9

ПР 1

ПР 2

ПР 3

ПР 4

ПР 5

ПР 6

ПР 7

ПР 8

Раздел 1. Алгебра

Тема 1. Развитие понятия о числе

+

+

+

+

+

+

+

+

+

+

+

+

Тема 2  Корни, степени и логарифмы

+

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема 3  Основы тригонометрии

+

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема 4 Функции, их свойства и графики. Степенные, показательные, логарифмические и тригонометрические функции

+

+

+

+

+

+

+

+

+

+

+

+

+

+

Раздел 2.Начала математического анализа

Тема 5 Уравнения и неравенства

+

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема 6  Начала математического анализа

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

Раздел 3 Комбинаторика, статистика и теория вероятностей

Тема 7 Элементы комбинаторики

+

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема 8  Элементы теории вероятностей. Элементы математической статистики

+

+

+

+

+

+

+

+

+

+

+

+

+

+

Раздел 4  Геометрия

Тема 9 Прямые и плоскости в пространстве

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема  10 Многогранники

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема 11 Тела и поверхности вращения

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема  12  Измерения в геометрии

+

+

+

+

+

+

+

+

+

+

+

+

+

Тема  13 Координаты и векторы

+

+

+

+

+

+

+

+

+

+

+

+

+

 

 

II. Комплект оценочных средств

 

2.1. Комплект материалов для оценки сформированности личностных, метапредметных и предметных результатов по дисциплине ОУД.03 «Математика»

 

2.2.2 Задания к промежуточной аттестации по учебной дисциплине ОУД.03 «Математика» в форме дифференцированного зачета на первом курсе во втором семестре

 

 

Проверяемые  результаты	Показатели оценки	Критерии оценки
ЛР 1-10 МР 1-9 ПР 1-8	правильность решения тестового задания, рациональность распределения времени на выполнение задания.	-однозначность выбора ответа и соответствие эталону -совпадение с эталоном 70%  ответов
Условия выполнения задания На выполнение дифференцированного зачета по математике дается 2 часа (90 минут). Работа состоит из двух частей и содержит 10 заданий. Часть 1 содержит 7 заданий с кратким ответом (1-7) базового уровня по материалу курса математики. Часть 2 содержит 3 более сложных заданий (8-10) по материалу курса математики. При их выполнении заданий надо записать полное решение и ответ.

 

 

 Вариант 1

Часть 1

 

1. Решите уравнение log₂(4 - х) = 2.

 

2.  Используя график функции у = f(х) (см. рис. ниже), определите и запишите ответ:

 

 

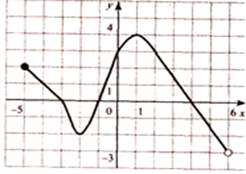
a.       Область определения функции;

b.      Область значения функции

c.       Промежутки возрастания и убывания;

d.      Нули функции;

e.       Наименьшее и наибольшее значения функции.

f.     При каких значениях  х , f(х) 0.

 

 

3. Найти область определения функции

 

 

4.  Решите  уравнение:     9^х + 2 3^х+1 – 7 = 0.

 

5. Решите неравенство

 

6. Из города A в город B ведут пять дорог, а из города B город C – три дороги. Сколько путей, проходящих через B, ведут из A в C?

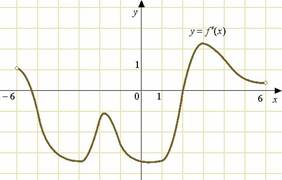
7. На рисунке изображён график  — производной функции , определенной на интервале . В какой точке отрезка функция  принимает наибольшее значение?

_______________________                                                                                                                                                               

8.Найдите промежутки возрастания и убывания функции и определите её точки экстремума  f(x)=3;

9. Решите систему уравнений

 

  .

10. Вычислить площадь фигуры, ограниченной линиями y=1-, y=0.

 

 

Вариант II

 

B1. Решите уравнение   = 5

B2. Используя график функции у = g(х) (см. рис. ниже), определите и запишите ответ:

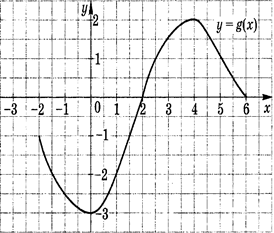
a.       Область определения функции;

b.      Область значения функции;

c.       Промежутки возрастания и убывания;

d.      Нули функции;                                 

e.       Наименьшее и наибольшее значения функции.

f.      При каких значениях  х , g(х)  0.

 

 

 

 

B3. Найти область определения функции

 

 

B4. Решите уравнение   2сos²x + 7cosx – 4 = 0

 

B5. Решите неравенство

 

B 6. Сколькими способами можно выбрать гласную и согласную буквы из слова «камзол»?

В 7. На рисунке изображен график  — производной функции , определенной на интервале . Найдите количество точек максимума функции , принадлежащих отрезку .

 

________________________________________

 

8.Найдите промежутки возрастания и убывания функции и определите её точки экстремума f(x)= ;

9. Решите систему уравнений

                                                               .

10. Вычислить площадь фигуры, ограниченной линиями y=,  x=-1, y=0.

 

Эталон ответов

1 вариант

 

Часть 1	1	2	3	4	5	6	7
	0	1. [-5;6) 2. (-3;4] 3.[-2;1] –возрастает; [-5;2][1;6)-убывает 4. -3;-1;4;         5. yнаиб=4; Yнаим=-2; 6.(-3;-1)	[-3;3]		[-3;0,5]	15	Наибольшее значение функции в точке x=3
Часть 2	8	9	10
	x max= -1; x min=1; возрастает на промежутке (1 [1;; убывает на промежутке [-1	x= 16 , y	1 кв.ед

 

2 вариант

 

Часть 1	1	2	3	4	5	6	7
	3	1.[-2;6] 2.[-3;2] [0;4]-возрастает [-2;0][4;6]-убывает 4.2;6 5.Yнаим= -3 Y наиб=2 6. (2;6)	(	n	(-1,5;2]	8	Одна точка максимума x=3
Часть 2	8	9	10
	x max= -;    x min=1; возрастает на промежутке ( [1;; убывает на промежутке [-	x= 4 ,            y	кв.ед

 

 

2.2.2 Задания к промежуточной аттестации по учебной дисциплине ОУД.03 «Математика» в форме экзамена в четвертом семестре на втором курсе

 

Проверяемые  результаты	Показатели оценки	Критерии оценки
ЛР 1-10 МР 1-9 ПР 1-8	правильность решения тестового задания, рациональность распределения времени на выполнение задания.	-однозначность выбора ответа и соответствие эталону -совпадение с эталоном  70%  ответов
Условия выполнения задания Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Работа состоит из двух частей и содержит 19 заданий. Часть 1 содержит 12 заданий (с кратким ответом базового уровня сложности и 4 задания с кратким ответом повышенного уровня сложности). Часть вторая содержит 7 заданий повышенного и высокого уровня сложности). На выполнение экзаменационной работы по математике дается 3 часа (235 минут). Ответы к заданиям 1-12 записываются в виде целого числа или конечной десятичной дроби. При выполнении заданий 13-19 требуется записать полное решение и ответ. При выполнении заданий можно пользоваться черновиком. Записи в черновике, а также в тексте контрольных измерительных материаловне учитываются при оценивании работы. Баллы, полученные Вами

 

 

Вариант 1

Часть 1

 

Ответом к заданиям В1–В 12 является целое число или конечная десятичная  дробь. Единицы измерений писать не нужно.

В1. Найдите значение выражения

В2. Найдите значение выражения ;

 

В3. В городе 180 000 жителей, причем 30 % - это пенсионеры. Сколько пенсионеров в этом городе?

В4. Площадь трапеции вычисляется по формуле S =, где   a и b – основания трапеции, h – её высота. Пользуясь этой формулой, найдите S, если a=3, b=8 и h=4.

В5. На день рождения полагается дарить букет из нечетного числа цветов. Хризантемы стоят 50 рублей за штуку. У Вани есть 510 рублей. Из какого наибольшего числа хризантем он может купить букет Маше на день рождения?

В6. Найдите корень уравнения .

 

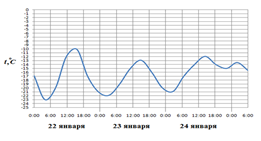
В7. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 22 января.

 

В8. Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены P  и оценок функциональности F, качества Q  и дизайна D . Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

 

R=8(F+Q)+4D-0,01P

Модель печи	Средняя цена	Функциональность	Качество	Дизайн
А	1900	1	1	1
Б	5900	4	1	2
В	3800	0	0	1
Г	4100	2	0	4

 

В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

 

В9. На экзамен вынесено 50 вопросов, Андрей не выучил 5 из них. Найдите вероятность того, что ему попадется выученный вопрос.

 

 

В10. Объем конуса равен 9π , а его высота равна 3. Найдите радиус основания конуса.

 

В11. В треугольнике АВС  угол С равен 90°, АС = 12,
АB = 20, Найдите sinA.

 

 

 

.

В12.На рисунке изображен график  — производной функции , определенной на интервале . Найдите количество точек максимума функции , принадлежащих отрезку .

 

Часть II

 

 

Запишите сначала номер выполняемого задания (С1,С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

 

С1. Найдите , если =0,8 и .

С2.Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.

 

С3.Найдите промежутки возрастания и убывания функции и определите её точки экстремума f(x)=;

С4. а) Решить уравнение 2cos2x + 4 cos (-x)+1=0;

б) Найдите все корни этого уравнения, принадлежащие промежутку [- -].

С5. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .

С6.Решите неравенство

С7. Сторона основания правильной треугольной призмы  равна 4, а высота этой призмы равна 3. Найдите площадь полной поверхности призмы .

 

 

Вариант 2

Часть 1

 

Ответом к заданиям В1–В 12 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно.

 

В1. Найдите значение выражения  ;

 

В2. Найдите значение выражения   ;

 

В3. Только 90% из 30 000 выпускников города правильно решили задачу № 1. Сколько выпускников из этого города правильно решили задачу №  1?

 

В4. Найдите m из равенства F=m, если F=84 иa=12.

 

 

В5. На день рождения полагается дарить букет из нечетного числа цветов. Чайные розы стоят 40 рублей за штуку. У Вани есть 190 рублей. Из какого наибольшего числа роз он может купить букет Маше на день рождения?

В6.  Найдите корень уравнения

В7.  Первый посев семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха не менее +6⁰ С. На рисунке показан прогноз дневной температуры воздуха в первых трех неделях апреля. Определите, в течение скольких дней за этот период можно производить посев петрушки.

 

 

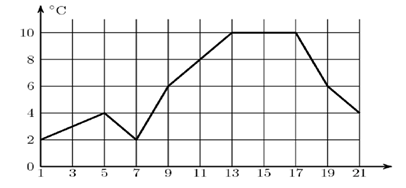
В8. Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены P  и оценок функциональности F, качества Q  и дизайна D . Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

R=8(F+Q)+4D-0,01P

Модель печи	Средняя цена	Функциональность	Качество	Дизайн
А	4600	2	4	4
Б	1600	2	2	0
В	4900	4	1	4
Г	5100	2	1	0

 

В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

 

В 9.На экзамен вынесено 50 вопросов, Алексей не выучил 5 из них. Найдите вероятность того, что ему попадется  не выученный вопрос.

 

В10. Радиус основания цилиндра равен 3, высота равна 2. Найдите объем цилиндра, деленный  на  π.

 

В11. В треугольнике АВС угол  Сравен 90°, АВ =10
АС =. Найдите sin

 

 

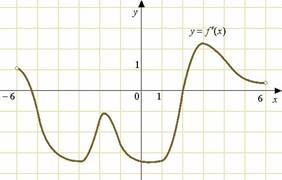
 В12.На рисунке изображён график  — производной функции , определенной на интервале . В какой точке отрезка функция  принимает наибольшее значение?

 

 

 

 

 

 

 

 

 

 

 

II часть

 

Запишите сначала номер выполняемого задания (С1,С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

 

С1. Найдите , если =;;

С2.Весной катер идёт против течения реки в 1 2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 1/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

С3.Найдите промежутки возрастания и убывания функции и определите её точки экстремума  f(x)=3;

С4. а) Решить уравнение sinx =;

б) Найдите все корни этого уравнения, принадлежащие промежутку [- -].

С5. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями:  ,осью Ох.

С6.Решите неравенство

С7. В прямоугольном параллелепипеде ребра CD, CB и диагональ боковой грани  равны соответственно 3, 4 и 5. Найдите площадь боковой поверхности параллелепипеда .

 

 

 

Вариант 3

 

Часть 1

 

Ответом к заданиям В1–В 12 является целое число или конечная десятичная  дробь. Единицы измерений писать не нужно.

 

^{В1. Вычислите значение выражения}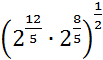

^В2. Найдите значение выражения    

В3.В сентябре 1 кг слив стоил 75 рублей. В октябре сливы подорожали на 40%. Сколько рублей стоил 1 кг слив после подорожания в октябре?

В4. Площадь треугольника вычисляется по формуле S=1/2bcsinα, где b и c — две стороны треугольника, а α — угол между ними. Пользуясь этой формулой, найдите площадь S, если b=18, c=16 и sinα=13.

В5. Для ремонта требуется 57 рулонов обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 5 рулонов?

В6.Решите уравнение .

В 7. На рисунке изображён график значений атмосферного давления в некотором городе за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба.Определите по рисунку наименьшее значение атмосферного давления 
за данные три дня (в миллиметрах ртутного столба).

 

 

 

 

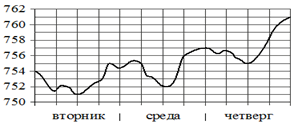
В8.Строительный подрядчик планирует купить 20 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича 
и условия доставки всей покупки приведены в таблице.

 

Поставщик	Цена кирпича (руб. за шт.)	Стоимость доставки (руб.)	Специальные условия
А	49	8000	Нет
Б	55	7000	Доставка бесплатно, если сумма заказа превышает 200 000 руб.
В	62	6000	Доставка со скидкой 50%, если сумма заказа превышает 240 000 руб.

 

Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?

 

В9. В среднем из 500 садовых насосов, поступивших в продажу, 25 подтекает. Найдите вероятность того, что случайно выбранный для контроля насос подтекает.

 

В 10.Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.

   В 11. В треугольнике АВС угол С равен 90°, АВ =10, ВС =6. Найдите sin

 

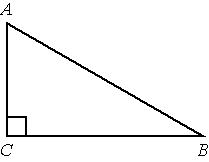
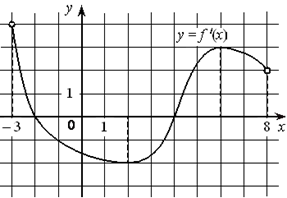
В12. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].

 

 

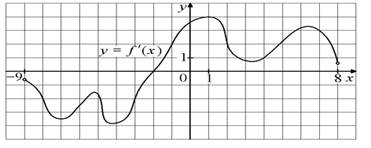
II часть

 

Запишите сначала номер выполняемого задания (С1, С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

 

С1 Найдите значение , если известно, что   и   <<

С2. Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.

С3. Напишите уравнение касательной к графику функции      

в точке с абсциссой     

С4.а) Решите уравнение cos2x+ =0,75.

б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 5π/2].

 

С5. Найдите площадь фигуры, ограниченной линиями у = 3х², у = 0,  х =  1 , х = 3.

 

С6. Решите неравенство  .

С7.ABCDA₁B₁C₁D₁ – прямоугольный параллелепипед, стороны основания которого 10 см и 15 см, а его боковое ребро равно 6 см. Найти   параллелепипеда.

 

Вариант 4

Часть 1

 

Ответом к заданиям В1–В 12 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно.

 

В1. Вычислите значение выражения.

В2. ^{Вычислите значение выражения}

В3. Городской бюджет составляет 67 млн рублей, а расходы на одну из его статей составили 15%. Сколько миллионов рублей потрачено на эту статью бюджета?

В4.В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6000+4100n, где n — число колец, установленных при копании колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 4 колец. Ответ дайте в рублях.

В5. Шоколадка стоит 31 рубль. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 170 рублей в воскресенье?

В6. Решите уравнение   .

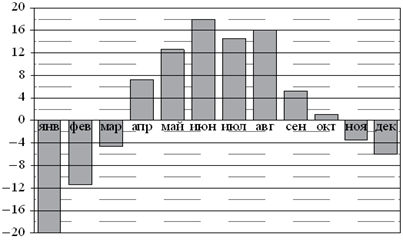
В7. На диаграмме показана среднемесячная температура воздуха 
в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали —температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.

.

В8. Для транспортировки 40 тонн груза на 1000 км можно воспользоваться услугами одной из трёх фирм-перевозчиков. Стоимость перевозки и грузоподъёмность автомобилей каждого перевозчика указаны в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант перевозки?

 

Перевозчик	Стоимость перевозки одним автомобилем (руб. на 100 км)	Грузоподъёмность одного автомобиля (тонн)
А	3200	3,5
Б	4100	5
В	9500	12

 

В9. На семинар приехали 7 учёных из Норвегии, 7 из России и 6 из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России.

В10. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?

В11.

На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.

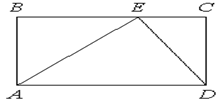
В12. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ; 8). Найдите точку минимума функции f(x).

 

 

II часть

 

Запишите сначала номер выполняемого задания (С1, С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

 

С1 Найдите значение, если известно, что и 0<<π/2.

С2.Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

С3. Найдите наименьшее значение функции y=x3−x2−8x+4 на отрезке [1; 7].

С4.а)Решите уравнение sin2x=sinx−2cosx+1.

б) Укажите корни этого уравнения, принадлежащие отрезку [3π/2; 3π].

С5. Найдите площадь фигуры (предварительно сделайте рисунок), ограниченную:

 а=1, b=3, f(x)=x+4 и осью Ох.

С6. Решите систему уравнений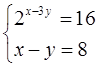

 

С7. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 8 см, а боковое ребро равно .

 

 

Эталон ответов

1 вариант

Часть В	В1	В2	В3	В4	В5	В6	В7
	2	16	54000	22	9	7	13
	В8	В9	В10	В11	В12
	А(1)	9/10	3	4/5	Наибольшее значение функции в точке x=3
Часть С	С1	С2	С3	С4	C5	С6	С7
	-0,6	90 км	xmax= -1; xmin=1; возрастает напромежутке (1 [1;; убывает на промежутке [-1	- ; -	16	[-3;0,5]	36+8

 

 

2 вариант

Часть В	В1	В2	В3	В4	В5	В6	В7
	2	4	27000	7	3	6	10
	В8	В9	В10	В11	В12	В13	В14
	A(18)	1/10	18	1/5	Одна точка максимума x=3	Место для формулы.
Часть С	С1	С2	С3	С4	C5	С6	С7
	-12/13	5 км/ч	xmax= -;    xmin=1; возрастает напромежутке ( [1;; убывает на промежутке [-	-	6	(-1,5;2]	42

 

3 вариант

 

Часть В	В1	В2	В3	В4	В5	В6	В7
	4	101	105	1872	12	-1	751 мл
	В8	В9	В10	В11	В12	В13	В14
	124000р.	1/20= 0,05	5	4/5=0,8	xmax=1
Часть С	С1	С2	С3	С4	C5	С6	С7
	-7/25	10 км/ч	9x+16	;	26 кв.ед.	(5/3;4)	600

 

4 вариант

 

Часть В	В1	В2	В3	В4	В5	В6	В7
	8	55	10.050.000	22400	7	725	16
	В8	В9	В10	В11	В12	В13	В14
	Б (328000)	0,3	В 6 раз	13	xmin=2
Часть С	С1	С2	С3	С4	C5	С6	С7
	4/5	8 км/ч	унаим=-8, унаиб=242	;	16кв.ед	х=10, у=2	64

 

 

Шкала оценки образовательных достижений

 

Каждое из заданий В1–В12 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Каждое верно выполненное задание оценивается 1 баллом.

Количество баллов, выставленных за выполнение заданий С1–С7, зависит от полноты решения и правильности ответа.

Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи иформы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.

 

Содержание критерия	Баллы
Обоснованно получены верные ответы	2
Обоснованно получен верный ответ в пункте а или пункте б, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения уравнения и отбора корней	1
Решение не соответствует ни одному из критериев, приведённых выше	0
Максимальный балл	2

 

 

 

Процент результативности (правильных ответов)	Оценка уровня подготовки
	балл (отметка)	вербальный аналог
90 ÷ 100	(24-26) 5	отлично
80 ÷ 89	(20-23) 4	хорошо
50 ÷ 79	(13-19) 3	удовлетворительно
менее 70	(менее 12) 2	неудовлетворительно

 

 

Перечень материалов, оборудования и информационных источников, используемых в аттестации

 

Основные источники:

1.  Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и др. Алгебра и начала математического анализа (базовый уровень) 10-11 Просвещение, 2012 г.

Интернет ресурсы:

1.     www.mathematics.ru

2. http://ege.edu.ru;

3.http://www.fipi.ru.

 4.http://www.itmathrepetitor.ru

 

 

 

 

 

 

 

 

Лист согласования

 

Дополнения и изменения к комплекту КОС на учебный год

 

Дополнения и изменения к комплекту КОСна __________ учебный год по дисциплине _________________________________________________________________ 

В комплект КОС внесены следующие изменения:

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

Дополнения и изменения в комплекте КОС обсуждены на заседании ЦМК _______________________________________________________

«_____» ____________ 20_____г. (протокол № _______ ). 

Председатель  ЦМК ________________ /___________________/

 

 

 

Скачано с www.znanio.ru