Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 1. Основные понятия комплексных чисел. Лекция № 1. Комплексные числа и действия над ними.

Раздел 1. Основные понятия комплексных чисел.

Лекция № 1. Комплексные числа и действия над ними. (2 часа)

План лекции.

1.    История появления комплексных чисел.

2.    Определение комплексного числа в алгебраической форме, действия над ними.

3.    Геометрическое изображение комплексных чисел.

4.    Модуль и аргументы комплексного числа. Формы комплексных чисел (алгебраическая, тригонометрическая, показательная).

5.    Решение алгебраических уравнений.

Литература: Электронный ресурс. О₃ Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440 - п.15.1 - 15.2, стр.356.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

З₂.Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₅.Структуру плана для решения задач.

Основные понятия:

Комплексными называются числа вида а + вi, где а и в – действительные числа, i – мнимая единица: i² = – 1, а называется действительной частью, вi – мнимой частью комплексного числа.

Два комплексных числа называются равными, если равны их действительные части и коэффициенты при мнимых частях, т.е. а + вi = с + di  a = c, b = d.

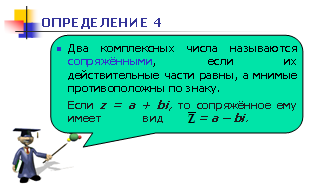
Два комплексных числа а + вi  и  а - вi называются сопряженными. Комплексные числа вида а + вi и - а - вi называются противоположным.

Корнем n-ой степени из комплексного числа z называется такое комплексное число  w, n-я степень которого равна z.

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Угол φ между положительным направлением действительной оси и радиус-вектора , соответствующим комплексному числу z=a+bi, называется аргументом этого числа и обозначается argz.

Запись комплексного числа в виде , где  и  - действительные числа, называется алгебраической формой комплексного числа.

Если  - модуль комплексного числа , а  - его аргумент, то тригонометрической формой комплексного числа  называется выражение:

Показательной формой комплексного числа  называется выражение:

1. История появления комплексных чисел.

Кардано называл такие величины “чисто отрицательными” и даже “софистически отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа  (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу. Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. образующих единое целое.

В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.

Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а за тем из любых комплексных чисел.

В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например,  в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов.

Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. Поэтому французский ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, - только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами.

“Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы иероглифы нелепых количеств” Л. Карно.

После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую систему вида , где , построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”.      Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.

                  

2. Определение комплексного числа в алгебраической форме, действия над ними.

Числа – один из основных математических объектов. Вам уже знакомы натуральные, целые, рациональные, иррациональные числа. Вместе они образуют множество действительных чисел. В математике нередко употребляют вместо понятия «множество» термин система чисел, который означает множество объектов вместе с некоторым выбором свойств и отношений.

Понятие числа развивалось и изменялось на протяжении всей истории человечества. С течением времени числовые системы расширялись, становились всё более сложными, включая как составные части ранее известные числовые системы. Каждая из числовых систем имела свои преимущества и свои недостатки. У более сложной больше различных возможностей по её использованию и применению, но при этом и само построение такой системы, и знание многочисленных деталей, очевидно, требуют больших усилий и большего времени. Рассмотрим «плюсы и «минусы» основных числовых систем.

               

Невозможно на множестве натуральных чисел выполнить действия: 45-210, 3:6, .

Приведите примеры действий невыполнимых в системе натуральных чисел.

                  

Невозможно на множестве целых чисел выполнить действия: 42:10, .

Приведите примеры действий невыполнимых в системе целых чисел.

                            

Невозможно на множестве рациональных чисел выполнить действие .

Приведите примеры действий невыполнимых в системе рациональных чисел.

Невозможно на множестве действительных чисел выполнить действие .

Приведите примеры действий невыполнимых в системе действительных чисел.

Частично допустимая операция извлечения корней из произвольных чисел становится допустимой в системе комплексных чисел.

Минимальные условия, которым удовлетворяют комплексные числа включают в себя:

·      Множество комплексных чисел содержит все действительные числа;

·      Существует комплексное число, квадрат которого равен -1;

·      Операции сложения, вычитания, умножения и деления комплексных чисел удовлетворяют обычным законам арифметических действий (сочетательному, переместительному, распределительному).

Произведения мнимой единицы и действительных чисел называют чисто мнимыми числами.

Введём понятие комплексного числа.

Определение. Комплексными называются числа вида а + вi, где а и в – действительные числа, i – мнимая единица: i² = – 1, а называется действительной частью, вi – мнимой частью комплексного числа.

Придумайте и запишите в тетрадях три комплексных числа.

Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.

Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0

Комплексное число a + bi при b = 0  считается совпадающим с действительным числом a: a + 0i = a.

Комплексное число a + bi при a = 0  называется чисто мнимым и обозначается bi: 0 + bi = bi.

Определение. Два комплексных числа называются равными, если равны их действительные части и коэффициенты при мнимых частях, т.е. а + вi = с + di  a = c, b = d.

Для комплексных чисел не существует соотношений «больше», «меньше».

Два комплексных числа  и  называются сопряженными. Комплексные числа вида  и называются противоположными.

Определение. Числа а + вi и – а – вi называются противоположными.

Действительно, (а + вi) + (– а – вi) = (а – а) + (в – в)i = 0 + 0i = 0.

Определение. Числа а + вi и а – вi называются сопряженными. Два комплексных числа z = a + bi  и  = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

(а + вi) + (а – вi) = 2а;

    

  

Действия над действительными числами.

Одним из условий, позволяющим определить всё множество комплексных чисел, являются выполнение следующих операций: 

Введём операции сложения и вычитания на множестве комплексных чисел и рассмотрим соответствующие примеры.

Введём операцию умножения на множестве комплексных чисел и рассмотрим соответствующий пример. Здесь формула получается более сложной.

Можно, конечно, выучить эту формулу, но гораздо надёжнее понимать, как она получена. В соответствии рассмотренными выше условиями, следует в произведении (а+bi)(c+di) раскрыть скобки и привести подобные члены. Проделайте это самостоятельно.

Рассмотрим операцию деления двух комплексных чисел.

Мы видим, что формула достаточно сложная для запоминания и для конкретных вычислений совсем необязательно её выучивать. Рассмотрим уравнение, где корнем как раз является частное двух комплексных чисел (а+bi) и  (c+di).

Т. о. получается формула для частного двух комплексных чисел.

Операции над комплексными числами в алгебраической форме.

1.                      Сложение (вычитание).

Пусть . Тогда

. Найти:  .

Решение.

.

Сложение комплексных чисел обладает следующими свойствами:

1)      Коммутативность: 

2)      Ассоциативность: 

.

Умножение производится по обычному правилу умножения многочленов.

Пусть     . Тогда

.

Найти:  .

Умножение комплексных чисел обладает свойствами:

1) Коммутативность:  

2) Ассоциативность:  

3) Дистрибутивность:  

3. Деление.

Пусть  . Тогда

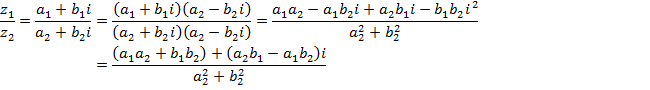
. Найти:  .

Решение. 

3.      Возведение комплексного числа в натуральную степень

Возводить в натуральную степень , если она достаточно велика, комплексные числа проще всего в тригонометрической форме, то есть если число  задано в алгебраической форме, то его изначально надо записать в тригонометрической.

Пусть число , тогда умножая его само на себя  раз (что эквивалентно тому, что мы его возводим в степень ), получим:

Таким образом, модуль степени комплексного числа равен той же степени модуля основания, а аргумент равен аргументу основания, умноженному на показатель степени.

Если , то получаем, что

Данная формула называется формулой Муавра (Абрахам де Муавр (1667 - 1754) - английский математик).

5. Извлечение корня из комплексного числа

Корнем n-ой степени из комплексного числа z называется такое комплексное число w, n-я степень которого равна z. 

Корень -ой степени из комплексного числа   обозначается символом  и на множестве комплексных чисел имеет ровно  значений.

Если комплексное число  задано в тригонометрической форме: , то все значения корня -ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):

Геометрически все значения корня лежат на окружности радиуса  с центром в начале координат и образуют правильный -угольник.

              

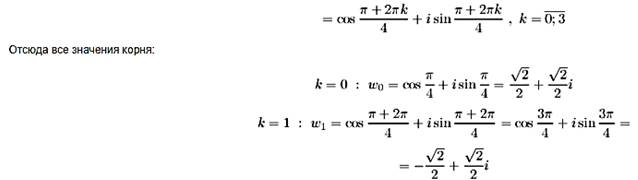
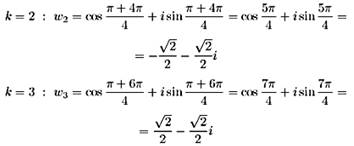
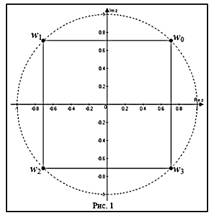
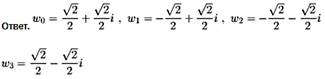
4. Геометрическое изображение комплексных чисел.

Как известно, действительные числа можно изображать точками числовой прямой. При этом каждому действительному числу соответствует единственная точка числовой прямой. Верно и обратное утверждение: каждой точке числовой прямой соответствует единственное действительное число. Значит, между точками числовой прямой и множеством всех действительных чисел установлено взаимно однозначное соответствие.

Подобно тому, как действительные числа изображаются точками числовой прямой, комплексные числа можно изображать геометрически точками плоскости. Каждому комплексному числу а + вi поставили в соответствие точку плоскости с координатами  А(а; в).

Множество всех комплексных чисел находится во взаимно-однозначном соответствии с множеством всех точек плоскости. К любой точке плоскости можно провести радиус-вектор.   Ось ОХ – действительная ось;    ОУ – мнимая ось.

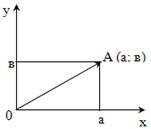
Пример. Постройте точки, изображающие комплексные числа: 1; - i; - 1 + i;     2 – 3i .

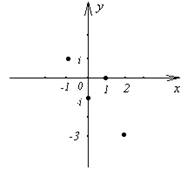
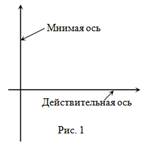
Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой системе координат оси абсцисс, называется действительной осью, а оси ординат - мнимой осью (рис. 1).

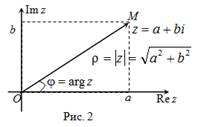
Комплексному числу  будет однозначно соответствовать на комплексной плоскости точка :  (рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.

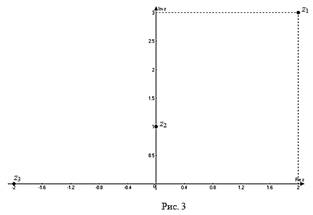
Например. На рисунке 3 на комплексной плоскости изображены числа ,  и .

5. Модуль и аргументы комплексного числа. Формы комплексных чисел (алгебраическая, тригонометрическая, показательная).

Комплексное число также можно изображать радиус-вектором  (рис. 2). Длина радиус-вектора, изображающего комплексное число , называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/ частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле: 

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Модулем комплексного числа называется неотрицательное число, равное  и обозначается .

Пример. Найти модуль комплексного числа

Решение. Так как , , то искомое значение

Ответ.

Замечание. Иногда еще модуль комплексного числа обозначается как  или .

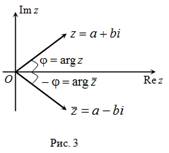
Угол  между положительным направлением действительной оси и радиус-вектора , соответствующим комплексному числу , называется аргументом этого числа и обозначается .

Аргумент  комплексного числа  связан с его действительной и мнимой частями соотношениями:

На практике для вычисления аргумента комплексного числа обычно пользуются формулой:

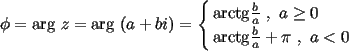
Пример. Найти аргумент комплексного числа

Решение. Так как , то в выше приведенной формуле будем рассматривать вторую строку, то есть

Ответ.

Аргумент действительного положительного числа равен , действительного отрицательного -  или . Чисто мнимые числа с положительной мнимой частью имеют аргумент равный , с отрицательной мнимой частью - .

У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).

Формы комплексных чисел.

Алгебраическая форма комплексного числа

Запись комплексного числа в виде , где  и  - действительные числа, называется алгебраической формой комплексного числа.

Например.

Тригонометрическая форма комплексного числа

Если  - модуль комплексного числа , а  - его аргумент, то тригонометрической формой комплексного числа  называется выражение

Задание 1. Записать число  в тригонометрической форме.

Решение. Для получения тригонометрической формы заданного комплексного числа найдем вначале его модуль и аргумент. Так как , , то

Тогда тригонометрическая форма заданного числа  имеет вид:

Ответ.

Пример 2. Представить в тригонометрической форме комплексное число 1– i.

a = 1, b = -1.

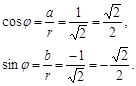
φ = .

1 – i = (cos  + i sin ).

Показательная форма комплексного числа

Показательной формой комплексного числа  называется выражение

Задание 2. Комплексное число  записать в показательной форме.

Решение. Найдем модуль и аргумент заданного комплексного числа:

А тогда имеем, что

Ответ.

Заметим, что показательную и тригонометрическую формы комплексного числа связывает формула Эйлера:

6.                      Решение алгебраических уравнений.

Квадратное уравнение с комплексными корнями и коэффициентами

Пусть задано квадратное уравнение , где коэффициенты ,   и  - в общем случае являются комплексными. Его решение находим с помощью дискриминанта тогда В общем случае и дискриминант, и корни уравнения являются комплексными числами. Задание. Составить квадратное уравнение, которое имеет корни   и . Решить его. Решение. Известно, что если  - корни квадратного уравнения , то указанное уравнение можно записать в виде . А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом: Раскрываем скобки и выполняем операции над комплексными числами:  - искомое квадратное уравнение. Решим полученное уравнение. Найдем дискриминант: Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде . То есть Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений  и : решив которую, имеем, что ,  или , . Рассматривая любую из полученных пар, например, первую, получаем, что , а тогда Ответ.

Вопросы для закрепления:

1. Дать определение модуля комплексного числа. Каков его геометрический смысл?

2. Комплексное число умножили на 2. изменился модуль этого числа?

3. Почему равны модули чисел: i; -i; 1; 1; 0?

4. Что такое аргумент комплексного числа?

5. Как определить главное значение аргумента числа z = a + bi?

6. Могут ли аргументом комплексного числа быть одновременно углы а и -а?

7. Найти геометрическое место точек плоскости, изображают комплексные числа с одинаковыми модулями.

8.Как размещаются на плоскости точки, изображающие комплексные числа с одинаковыми аргументами?

9. Как представить комплексное число вида а + bi в тригонометрической форме? Как найти модуль и аргумент этого числа?

10. Как перейти от тригонометрической формы комплексного числа в алгебраической?

11. Вывести правила умножения и деления комплексных чисел, записанных в тригонометрической форме.

12. По какому правилу выполняют действие возведения в степень комплексных чисел, записанных в тригонометрической форме?

 

Для подготовки к самостоятельной работе:

1.         Прочитать учебник О₃: п.15.1-15.2, стр.356.

2.         Выучить лекцию.

3.         Подготовиться к тестированию по пройденному материалу.

 

Скачано с www.znanio.ru