Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 2. Элементы линейной алгебры. Лекция № 2. Матрицы и определители.

Раздел 2. Элементы линейной алгебры.

Лекция № 2. Матрицы и определители. (2 часа)

План лекции.

1.        Матричные модели. Определение матрицы.

2.        Действия с матрицами: сложение, вычитание двух матриц, умножение матрицы на число, умножение матрицы на матрицу, возведение матрицы в степень, транспонирование матрицы.

3.        Определитель матрицы. Свойства определителя.

Литература: Электронный ресурс. О₁: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 1: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 276 с. — (Профессиональное образование). — ISBN 978-5-534-10174-4. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442438 -  п. 1.1 – 1.4, стр. 20.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

З₂.Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₃.Алгоритмы выполнения работ в профессиональной и смежных областях;

З₄.Методы работы в профессиональной и смежных сферах.

Основные понятия:

Матрицей размером m´n называется прямоугольная таблица, составленная из mn чисел и имеющая m строк и n столбцов. Числа a_ij, составляющие матрицу, называются элементами матрицы.

Горизонтальный ряд чисел называется строкой, а вертикальный – столбцом.

Если т = п, то матрица называется квадратной матрицей порядка n. Число ее строк или столбцов называется порядком матрицы.

Если же m ¹ n, то матрица называется прямоугольной матрицей.

Две матрицы считаются равными, если они имеют одинаковые размеры и их соответствующие элементы равны. Пусть А = (a_ij) размером т´ п, В = (b_ij) размером p´q. A = B, если m = p, n = q и a_ij = b_ij для i = 1, 2, …, m, j = 1, 2, …, n.

Последовательность элементов квадратной матрицы с одинаковыми индексами (i  =  j) называется главной диагональю матрицы  (a_11, a_22, a_33,…,a_nn).

Если в квадратной матрице все недиагональные элементы равны нулю (a_ij= 0, при i = j), то матрица называется диагональной.

Квадратная диагональная матрица, у которой элементы главной диагонали равны единице, называется единичной матрицей Е.

Матрица, все элементы которой равны нулю, называется нуль-матрицей.

Матрица, состоящая только из одной строки, называется матрицей-строкой.

Матрица, состоящая только из одного столбца, называется матрицей-столбцом.

Матрицу А^t называют транспонированной по отношению к матрице А, если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками.

Создание проблемной ситуации при постановке темы, цели и задач лекции.

В школьном курсе алгебры 7 – 9 классов рассматриваются различные способы решения систем линейных уравнений: метод подстановки, метод сложения, метод двойного сложения, графический метод, метод сравнения. Возникает вопрос, а существуют ли какие-либо другие способы решения данных систем. Действительно, кроме методов, изучаемых в школе, существуют и другие, доступные для обучающихся старших классов методы решения систем линейных уравнений: метод Крамера, метод Гаусса, матричный метод. Эти методы способствуют развитию внимания, памяти. При применении этих методов встречаются новые понятия: «матрица», «определитель», «минор», «дополнение». Возникает необходимость уметь вычислять определители, миноры, дополнения. При решении систем линейных уравнений методом Гаусса также нужно уметь выполнять преобразования над строками матриц.

Что же такое матрица, какие действия  с ними можно выполнять?

1.                  Матричные модели. Определение матрицы.

Среди разнообразных функциональных зависимостей, описывающих широкий круг природных и общественных явлений, линейная зависимость – самая простая и наиболее глубоко изученная. Линейная алгебра – ветвь математики, исследующая общие линейные функции конечного числа переменных. Ее идеи и методы пронизывают многие разделы математических знаний, а результаты широко используются в приложениях математики, в том числе экономических. Одним из традиционных методов изложения линейной алгебры как математической дисциплины для студентов прикладных профилей является обобщение хорошо известной со школьной скамьи одномерной линейной зависимости вида ax + b и соответствующего ей алгебраического уравнения 1-й степени (или линейного) ax + b = 0 . В основе этого обобщения лежит важное понятие матрицы. В простейшем случае матрицы «сделаны» из чисел и называются поэтому числовыми.

Определение матрицы. Совокупность чисел, расположенных в виде прямоугольной таблицы, состоящей из  строк и  столбцов, называют матрицей порядка  ( на ) и обозначают символом . В общем виде матрица выглядит так

.

Матрицей размером т´п называется прямоугольная таблица, составленная из тп чисел и имеющая т строк и п столбцов. Числа a_ij, составляющие матрицу, называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй – номер столбца, в котором расположен этот элемент.

Для изображения матрицы употребляют круглые скобки и часто обозначают ее одной буквой, например,

А=(a_ij)=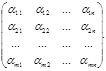

Первый индекс i  (i  = 1, 2, …m) обозначает номер строки, второй  j (j = 1, 2, …n) – столбец матрицы. Матрицу принято обозначать  заглавными буквами, например А, В, С и т.д.

Горизонтальный ряд чисел называется строкой, а вертикальный – столбцом.

Определение. Если т = п, то матрица называется квадратной матрицей порядка n. Число ее строк или столбцов называется порядком матрицы.

Определение. Если же m ¹ n, то матрица называется прямоугольной матрицей.

Определение. Две матрицы считаются равными, если они имеют одинаковые размеры и их соответствующие элементы равны. Пусть А = (a_ij) размером т´ п, В = (b_ij) размером p´q. A = B, если m = p, n = q и a_ij = b_ij для i = 1, 2, …, m, j = 1, 2, …, n.

Определение. Последовательность элементов квадратной матрицы с одинаковыми индексами (i  =  j) называется главной диагональю матрицы  (a_11, a_22, a_33,…,a_nn).

Определение. Если в квадратной матрице все недиагональные элементы равны нулю (a_ij= 0, при i = j), то матрица называется диагональной.

А =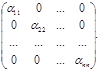

Определение. Квадратная диагональная матрица, у которой элементы главной диагонали равны единице, называется единичной матрицей Е.

А =

Определение. Матрица, все элементы которой равны нулю, называется нуль-матрицей.

Определение. Матрица, состоящая только из одной строки, называется матрицей-строкой.

Определение. Матрица, состоящая только из одного столбца, называется матрицей-столбцом.

2.                  Действия с матрицами.

1.Определение. Суммой двух матриц А = (a_ij) и В = (b_ij) одинаковых размеров т´ п называется матрица  С того же размера, элементы которых равны  сумме соответствующих элементов  матриц А и В.  С=А + В = (a_ij + b_ij) для        i = 1, 2, …, m, j = 1, 2, …, n. Ясно, что сложение матриц сводится к сложению всех пар соответствующих элементов. Для матриц разных размеров сумма не определена.

Сложение матриц подчиняется законам:

1.               А + В = В + А (переместительный закон)

2.               (А + В) + С = А + (В + С) (сочетательный закон)

3.               А + О = О + А = А.

Для любой матрицы А размеров т´ п существует матрица В тех же размеров такая, что А + В = В + А = О. При этом если  А = (a_ij) и В = (b_ij), то b_ij = - a_ij. Матрица В называется матрицей, противоположной матрице А и обозначается – А.

2.Определение. Произведением матрицы А = (a_ij) размером т´ п на число l называется матрица (la_ij) тех же размеров, которая обозначается lА.

Свойства  умножения матрицы на число:

1. a(bА) = (ab)А.

2. (a + b)А = aА + bА.

3. a(А + В) = aА + aВ.

4. 1×А = А.

3.Определение.Разность двух матриц  А и В одинаковых размеров определяется равенствами:

А – В = А + (- В) = А + (-1)В.

4.Определение. Произведением матрицы А = (a_ij) размеров т´ п на матрицу В = (b_ij) размеров n´k называется матрица С = (с_ij) размеров m´k, каждый элемент с_ij которой вычисляется по формуле

с_ij = a_i1b_1j + a_i2b_2j + … + a_inb_nj ,   i = 1,2,…,m; j = 1,2,…,n.         (2)      

Другими словами, элемент с_ij равняется сумме произведений элементов строки с номером i матрицы А на соответствующие элементы столбца с номером j матрицы В. Произведение матрицы А на матрицу В обозначается АВ.

Замечание: Операция умножения двух матриц выполнима лишь в том случае, когда число столбцов первой матрицы – сомножителя А должно равняться числу строк второй матрицы  сомножителя В. Если это условие не выполнено, произведение не существует.

Для запоминания формулы (2) пользуются мнемоническим правилом: «умножение i-той строки матрицы А на j-тый столбец матрицы В».

Приведем примеры сложения, вычитания и умножения матриц.

Пример 1:  Найти сумму матриц:  А = 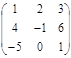 и  В  = .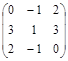

Решение: С = А + В           С =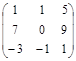

Чтобы вычесть из матрицы А матрицу В, надо к матрице А прибавить матрицу, противоположную матрице В.

А – В = А + (-В)

Пример 2:  Найти разность матриц А – В:  А =  и В = .

Решение: С = А – В      -В =       С =

Пример 3:  Дана матрица А =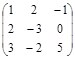.      Найти матрицу С = 2А.

Решение:   С = 2А =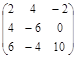

Пример 4:   Даны матрицы: А =  и  В = . Найти произведение матриц А и В.

Решение:   С = АВ     С =  С =

Пример 5:    Вычислить произведение АВ, где 

Число столбцов в первой матрице совпадает с числом строк во второй матрице, поэтому произведение АВ существует. Положим С = АВ. В матрице С столько же строк, сколько в матрице А, и столько же столбцов, сколько в матрице В, т.е. матрица С размеров 2´3. Пусть С = (с_ij), тогда по формуле (2) получаем

с₁₁ = 2×(-1) + 3×2 = 4,     с₁₂ = 2×2 + 3×1 = 7,      с₁₃ = 2×0 + 3×(-1) = - 3, 

с₂₁ =(-1)×(-1) + 4×2 = 9,               с₂₂ =(-1)×2 + 4×1 = 2,               с₂₃ = (-1)×0 + 4×(-1) =-4.

Записав эти числа в матрицу, получим 

Заметим, что произведение ВА не существует, поскольку число столбцов в матрице В не равно числу строк в матрице А.

Транспонирование матрицы.

Определение. Матрицу А^t называют транспонированной по отношению к матрице А ,если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками.

Например, пусть А - матрица размеров т´ п:

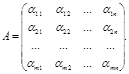      транспонированная ей матрица: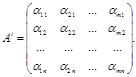   

Можно сказать, что транспонированная матрица получается переворачиванием матрицы вокруг главной диагонали.

Переход от матрицы А к матрице А^t  называют операцией транспонирования.

3. Определитель матрицы. Свойства определителя.

Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12.N = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.

Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.

Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ

обозначает подстановку, в которой 3 переходит в 4, 1 в 2, 2 в 1, 4 в 3. Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде

, т.е. с натуральным расположением чисел в верхней строке.

Пусть нам дана квадратная матрица порядка n

.                               (2.1)

Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида  ,                               (2.2)

где индексы q₁, q₂,..., q_n составляют некоторую перестановку из чисел 1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (2.2) равен (- 1)^q, где q - число инверсий в перестановке вторых индексов элементов.

Определителем n -го порядка, соответствующим матрице (2.1), называется алгебраическая сумма n! членов вида (2.2). Для записи определителя употребляется символ

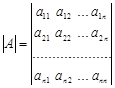                    или

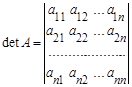
(детерминант, или определитель, матрицы А).

Квадратную матрицу  называют вырожденной (невырожденной), если  .

Виды и методы определения определителя матрицы.

1.Определитель матрицы первого порядка

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент  а₁₁:

.

2.Определитель матрицы второго порядка

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

.

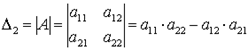Например, пусть  .

Рассмотрим квадратную матрицу второго порядка .

Определителем этой матрицы называют число, обозначаемое , или , или , полученное из элементов матрицы  по следующему правилу:

.

Например, если, то .

3.Определитель матрицы третьего порядка

Рассмотрим теперь квадратную матрицу третьего порядка 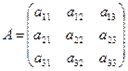. Определителем этой матрицы назовем число

.

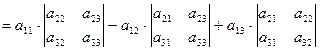 =, или

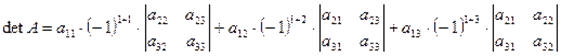 (1)

Равенство (1) называют разложением определителя по элементам первой строки.

Выражения ;  и  называют алгебраическими дополнениями элементов ,  и соответственно. Таким образом, разложение определителя третьего порядка по элементам первой строки может быть записано в виде:.

Нетрудно заметить, что аналогичным образом определитель третьего порядка может быть разложен по элементам второй и третьей строк, а также по элементам первого, второго или третьего столбца.

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

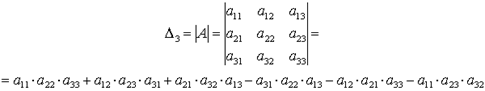
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

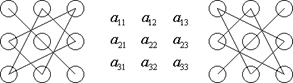
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Пример. Вычислить определитель третьего порядка:

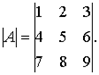
Решение.

Рассмотрим теперь квадратную матрицу  го порядка . Определителем такой матрицы, разложенным по  ой строке, назовем число

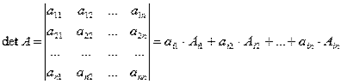, где  - элементы  ой строки, а  - их алгебраические дополнения.

Свойства определителей.

Свойство № 1: Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|^Т

Следствие: Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2: При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е:

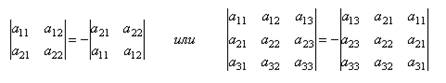
Свойство № 3: Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4: Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

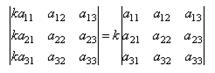
Следствия из свойств № 3 и № 4: Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
        Свойство № 5: Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.

Задания для решения:

1.      Вычислить произведение матриц:

.

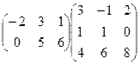Решение. Первая матрица имеет размеры 2´3, а вторая размеры 3´3, поэтому произведение существует. В результате умножения получится матрица С = (c_ij) размеров 2´3. Вычислим ее элементы.

с₁₁ = (-2)×3 + 3×1 + 1×4 = 1, с₁₂ = (-2)×(-1) + 3×1 + 1×6 = 11,

с₁₃ = (-2)×2+3×0+1×8 = 4, с₂₁ = 0×3 + 5×1 + 6×4 = 29,

с₂₂ = 0×(-1) + 5×1 + 6×6 = 41, с₂₃ = 0×2+5×0+6×8 = 48.

Ответ: .

2.      Вычислить произведение матриц:

.

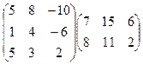Решение. Первая матрица имеет размеры 3´3, а вторая размеры 2´3. Число столбцов в первой матрице (3) не совпадает с числом строк во второй матрице (2), поэтому произведение не существует,

Ответ: произведение не существует.

3.      Вычислить произведение матриц и определитель новой матрицы:

.

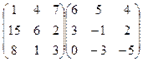Ответ: .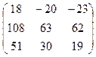

4. Найти сумму матриц и определитель новой матрицы: 

А = 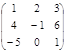 и  В  = .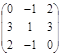

Решение: С = А + В           С =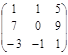

Вопросы для закрепления:

Определения:
- матрица, квадратная, единичная, диагональная, нулевая.

- определитель, виды определителей.
        Перечислить свойства:
- суммы и разности матриц, произведения матрицы на число, произведения матриц, возведения матрицы в степень, транспонирования матрицы;
- определителей.
        Записать формулы:
- для вычисления определителей второго, третьего и n-го порядка.

Для подготовки к самостоятельной работе:

1.         Прочитать учебник О.₁: п. 1.1 – 1.4, стр. 20.

2.         Выучить лекцию.

3.         Выполнить задания:

1.Найти , если .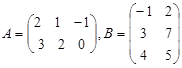

2.Даны матрицы .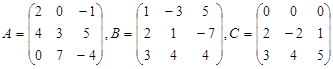

Найти:   а)     б)

Скачано с www.znanio.ru