Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 2. Элементы линейной алгебры. Лекция № 3. Методы решения систем линейных уравнений.

Раздел 2. Элементы линейной алгебры.

Лекция № 3. Методы решения систем линейных уравнений. (6 часов)

План лекции.

1.    Метод обратной матрицы.(2 часа)

- Ранг матрицы, минор матрицы, алгебраические дополнения матрицы.

- Обратная матрица и ее свойства. Алгоритм вычисления обратной матрицы.

- Решение систем линейных уравнений матричным методом.

2.    Правило Крамера.(2 часа)

- Понятие системы трех линейных уравнений с тремя переменными.

- Алгоритм решения системы трех линейных уравнений с тремя переменными методом определителей.

3.    Метод Гаусса.(2 часа)

Литература: Электронный ресурс. О₁: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 1: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 276 с. — (Профессиональное образование). — ISBN 978-5-534-10174-4. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442438 - п. 1.5 – 1.6, стр. 58; п. 2.1 – 2.5 – стр. 73.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

ОК 02. Использовать современные средства поиска,  анализа и интерпретации информации и информационные технологии для выполнения задач профессиональной деятельности

З₁.  Актуальный профессиональный и социальный контекст, в котором приходится работать и жить;

З₂.Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₃.Алгоритмы выполнения работ в профессиональной и смежных областях;

З₇.Номенклатуру информационных источников применяемых в профессиональной деятельности;

З₈.Приемы структурирования информации;

З₉. Формат оформления результатов поиска информации;

З₁₀. Современные средства и устройства информатизации; порядок их применения и программное обеспечение в профессиональной деятельности.

Основные понятия:

Минором M_i,j элемента a_i,j матрицы  n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы  А вычеркиванием  i-й строки и  j-го столбца.

Алгебраическим дополнением А_ij элемента а_ij матрицы  n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.

Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A называется союзной матрицей.

Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Решение системы уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.

Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.

Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной.

1. Метод обратной матрицы.

- Ранг матрицы, минор матрицы, алгебраические дополнения матрицы.

Минор матрицы.

Минором M_i,j элемента a_i,j матрицы  n-го порядка называется определитель матрицы  (n-1)-го порядка, полученный из матрицы  А вычеркиванием  i-й строки и  j-го столбца.

При выписывании определителя  (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.

Пример 1. Составить минор , полученный из исходной матрицы:

Решение:

.

Алгебраические дополнения матрицы.

Алгебраическим дополнением  А_ij элемента а_ij матрицы  n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.

Пример 1. Найти алгебраические дополнения всех элементов матрицы

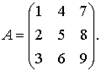
Решение:

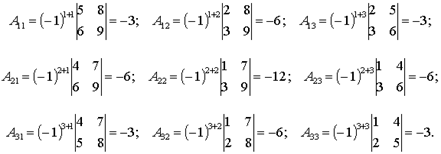
Ранг матрицы.

Определение ранга матрицы

Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение 

Вычисление ранга матрицы с помощью миноров

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

Пример 1. Найти методом окаймления миноров ранг матрицы

.

Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М₁ = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M₂ = , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М₂. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их: 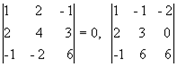 =0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

Вычисление ранга матрицы с помощью элементарных преобразований

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

.

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Пример 2. Найти ранг матрицы

А=  и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

;

из третьей строки вычтем первую; получим матрицу

В = , которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.

Ранг матрицы не изменяется от элементарных преобразований.
Под элементарными преобразованиями понимается:
А) замена строк столбцами, а столбцов - соответствующими строками;
Б) перестановка строк (столбцов) матрицы;
В) вычеркивание ряда (строки или столбца), все элементы которого равны нулю;
Г) умножение какого-либо ряда (строки или столбца) на число, отличное от нуля
Д) прибавление к элементам одного ряда соответствующих элементов другого параллельного ряда.

Как найти ранг матрицы с помощью метода Гаусса?

С технической точки зрения метод не отличается новизной:

1) с помощью элементарных преобразований приводим матрицу к ступенчатому виду;

2) ранг матрицы равен количеству строк.

Совершенно понятно, что использование метода Гаусса не меняет ранга матрицы, и суть здесь предельно проста: согласно алгоритму, в ходе элементарных преобразований выявляются и удаляются все лишние пропорциональные (линейно зависимые) строки, в результате чего остаётся «сухой остаток» – максимальное количество линейно независимых строк.

Преобразуем матрицу:

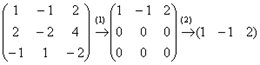
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку.

(2) Нулевые строки удаляем.

Таким образом, осталась одна строка, следовательно, . Что и говорить, это гораздо быстрее, чем рассчитать девять нулевых  миноров 2-го порядка и только потом сделать вывод.

Напоминаю, что в самой по себе алгебраической матрице ничего менять нельзя, и преобразования выполняются только с целью выяснения ранга! Кстати, остановимся ещё раз на вопросе, почему нельзя? Исходная матрица  несёт информацию, которая принципиально отлична от информации матрицы 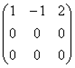 и строки . В некоторых  математических моделях (без преувеличения) разница в одном числе может быть вопросом жизни и смерти.

Перейдём к более содержательным заданиям, где помимо прочего познакомимся с важными вычислительными приёмами метода Гаусса:

Пример 1. Найти ранг матрицы с помощью элементарных преобразований

Решение: дана матрица «четыре на пять», значит, её ранг заведомо не больше, чем 4.

В первом столбце, отсутствует 1 или –1, следовательно, необходимы дополнительные действия, направленные на получение хотя бы одной единицы. За всё время существования сайта мне неоднократно задавали вопрос: «Можно ли в ходе элементарных преобразований переставлять столбцы?». Вот здесь – переставили первый-второй столбец, и всё отлично! В большинстве задач, где используется метод Гаусса, столбцы действительно переставлять можно. НО НЕ НУЖНО. И дело даже не в возможной путанице с переменными, дело в том, что в классическом курсе обучения высшей математике данное действие традиционно не рассматривается, поэтому на такой реверанс посмотрят ОЧЕНЬ криво (а то и заставят всё переделывать).

Второй момент касается чисел. В ходе решения полезно руководствоваться следующим эмпирическим правилом: элементарные преобразования по возможности должны уменьшать числа матрицы. Ведь с единицей-двойкой-тройкой работать значительно легче, чем, например, с 23, 45 и 97. И первое действие направлено не только на получение единицы в первом столбце, но и на ликвидацию чисел 7 и 11. Сначала полное решение, потом комментарии:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3. И до кучи: к 4-й строке прибавили 1-ю строку, умноженную на –1.

(2) Последние три строки пропорциональны. Удалили 3-ю и 4-ю строки, вторую строку переместили на первое место.

(3) Ко второй строке прибавили первую строку, умноженную на –3.

В приведённой к ступенчатому виду матрице две строки.

Ответ:

- Обратная матрица и ее свойства. Алгоритм вычисления обратной матрицы.

Теорема. Всякая невырожденная (т.е. определитель которой отличен от нуля) квадратная матрица A имеет обратную матрицу A^-1, которая находится по формуле:

Нахождение обратной матрицы является важной составляющей в разделе линейной алгебры. С помощью таких матриц, если они существуют, можно быстро найти решение системы линейных уравнений.

Матрицаназывается обратной к матрице, если выполняются следующие равенства:  .

Если определитель матрицыотличен от нуля, то матрицу называют не особой или невырожденной.

Для того, чтобы матрица имела обратную необходимо и достаточно, чтобы она была невырожденной

Алгоритм нахождения обратной матрицы

Пусть имеем квадратную матрицу и нужно найти обратную к ней. Для этого нужно выполнить следующие действия:

1. Найти определитель матрицы. Если он не равен нулю, то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной

2. Найти алгебраические дополнения элементов матрицы . Они равны минорам, умноженным на  в степени суммы строки и столбца, для которого ищем.

3. Составить матрицу из алгебраических дополнений элементов матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается .

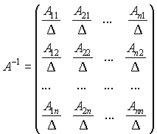
4. Разделить присоединенную матрицу на детерминант . Полученная матрица будет обратной и иметь свойства.

 Решение систем линейных уравнений матричным методом.

    Любую систему линейных уравнений можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.

Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .

Пусть нужно решить систему линейных уравнений:

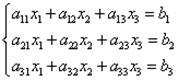
Запишем эту систему уравнений в матричном виде:

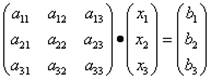
Если обозначим отдельно матрицу коэффициентов при неизвестных, матрицу неизвестных и матрицу свободных членов

,

тогда

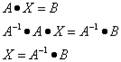
То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных  и приравнять соответствующие элементы полученных матриц.

Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере.

Пример 1. Решить матричным методом систему линейных уравнений:

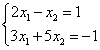
Решение состоит из следующих шагов.

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

Матрица неизвестных:

Матрица свободных членов:

Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:

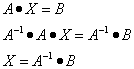
По выведенному выше последнему равенству и будем вычислять решения данной системы.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

Шаг 3. Находим матрицу неизвестных:

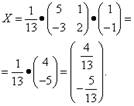
Итак, получили решение:

.

Сделаем проверку:

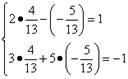
Следовательно, ответ правильный.

Для второго примера выберем систему линейных уравнений третьего порядка.

Пример 2. Решить матричным методом систему линейных уравнений:

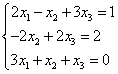
Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

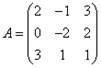
Матрица неизвестных:

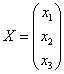
Матрица свободных членов:

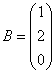
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

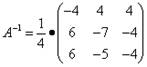Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

.

Сделаем проверку:

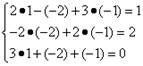
Следовательно, ответ правильный.

Вопросы для закрепления:

1. Определения: 

- Ранг и минор матрицы, алгебраическое дополнение, обратная матрица.
2. Записать формулы:

- для вычисления минора и алгебраического дополнения матрицы.

- для вычисления обратной матрицы.

Для подготовки к самостоятельной работе:

1.        Прочитать учебник О₁: п. 1.5 – 1.6, стр. 58; п.2.1 – 2.2 – стр. 73.

2.        Выучить лекцию.

3.        Выполнить задания:

1.Даны матрицы .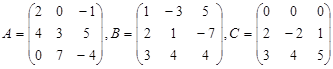

Найти:   а)     б)  Вычислить обратные матрицы полученных матриц.

2. Правило Крамера.

- Понятие системы трех линейных уравнений с тремя переменными.

Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

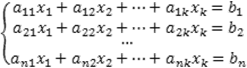
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Решение системы уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

1.        Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.

2.        Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.

3.        Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

- Алгоритм решения системы трех линейных уравнений с тремя переменными методом определителей.

Применим рассмотренную на прошлой лекции теорию определителей к решению систем линейных уравнений.
      Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;     .

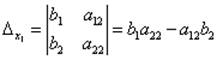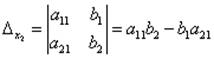Формулы Крамера для нахождения неизвестных:

.

Найти значения  и возможно только при условии, если .

Этот вывод следует из следующей теоремы.

Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

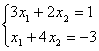.                         (1)

Согласно теореме Крамера имеем:

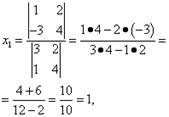
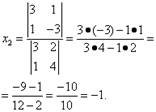
Итак, решение системы (1):

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера, при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение  (система совместна и определённа)

Условия:    * 

Второй случай: система линейных уравнений имеет бесчисленное множество решений (система совместна и неопределённа)

Условия:  * , ** , т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Условия:  * ** .

Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Система трёх линейных неоднородных уравнений с тремя неизвестными:

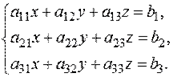
Составим и вычислим основной определитель  и вспомогательные определители ,

а) Если , то система имеет единственное решение, которое находится по формулам Крамера:

, ,  (2)

б) Если , то возможны случаи:

1) , тогда система будет иметь бесконечно много решений, она будет сводиться либо к системе состоящей из одного, либо из двух уравнений (одну неизвестную перенесём направо и решим систему двух уравнений с двумя неизвестными);

2) хотя бы один из определителей  отличен от нуля, система не имеет решения.

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

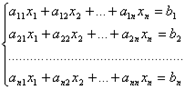На основании теоремы Крамера

где

-

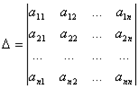определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

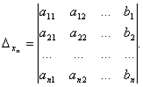
Пример 2. Решить систему линейных уравнений методом Крамера:

.

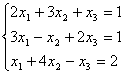Решение. Находим определитель системы:

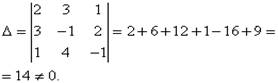
Следовательно, система является определённой. Для нахождения её решения вычисляем определители

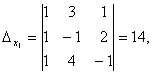
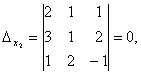
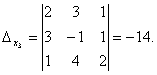
По формулам Крамера находим:
           
Итак, (1; 0; -1) – единственное решение системы.

Задания для решения

Пример 3. Решить систему линейных уравнений методом Крамера:

.

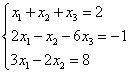Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

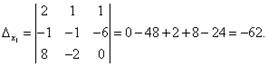
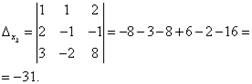
По формулам Крамера находим:

Итак, решение системы - (2; -1; 1).

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 4. Решить систему линейных уравнений методом Крамера:

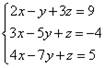
Решение. Находим определитель системы:

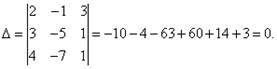
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

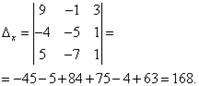
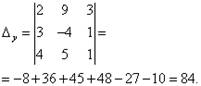
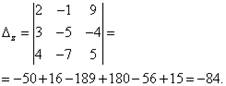
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко ходить не надо.

Пример 5. Решить систему линейных уравнений методом Крамера:

Здесь a - некоторое вещественное число. Решение. Находим определитель системы:

Находим определители при неизвестных

По формулам Крамера находим:

                                    ,     .

Следующий пример - на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 6. Найти решение системы трёх линейных уравнений с тремя неизвестными по формулам  Крамера:

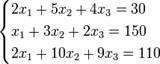
Решение. Находим определители третьего порядка, используя правило Сарруса или разложение по элементам первой строки:

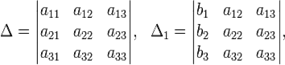
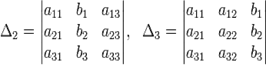
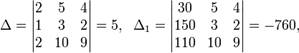
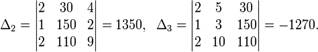
Находим решение системы по формулам:  

Ответ: (- 152; 270; -254)

Вопросы для закрепления:

1.      Правила вычисления определителей в зависимости от порядка определителя?

2.      Запишите формулы Крамера для решения системы трёх линейных уравнений с тремя переменными.

Для подготовки к самостоятельной работе:

1.   Прочитать учебник О₁: п. 2.1 – 2.2, стр. 73.

2.   Выучить лекцию.

3.   Выполнить задания:

I.  Вычислить определитель III порядка разложение по строке или столбцу.

II. Решить систему методом Крамера.      

Вариант 1.

1. 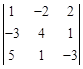 .       2.  

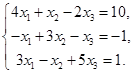
Вариант 2.

1.  .         2.   

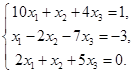
Вариант 3.

1. 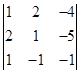 .        2.  

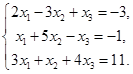
Вариант 4.

1. 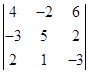 .      2.  

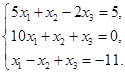
Вариант 5.

1. 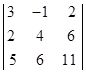 .       2.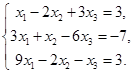  

3. Метод Гаусса или метод преобразований.

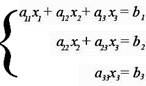
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной. Пример такой системы - на рисунке сверху.

В ней, как видим, третье уравнение уже не содержит переменных x₂ и x₁, а второе уравнение – переменной x₁.

После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.

Преимущества метода Гаусса:

1.    При решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера, поскольку при решении методом Гаусса необходимо меньше вычислений;

2.    Методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение, а, используя метод Крамера, можно лишь констатировать, что система неопределённа;

3.    Методом Гаусса можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений;

4.    Метод Гаусса основан на элементарных (школьных) методах - методе подстановки неизвестных и методе сложения уравнений.

Благодаря этим преимуществам, именно методом Гаусса чаще всего решаются прикладные задачи на сплавы и смеси, стоимость или удельный вес отдельных товаров в группе товаров и другие, в которых системы линейных уравнений применяются для моделирования реальных объектов физического мира.

Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение - один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.

Элементарные преобразования системы линейных уравнений

При решении методом Гаусса систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно:

1.      переставлять местами строки (это и было упомянуто в самом начале);

2.      если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;

3.      удалять "нулевые" строки, где все коэффициенты равны нулю;

4.      любую строку умножать или делить на некоторое число;

5.      к любой строке прибавлять другую строку, умноженное на некоторое число.

В результате преобразований получаем систему линейных уравнений, эквивалентную данной.

Алгоритм решения систем линейных уравнений методом преобразований или методом Гаусса.

Алгоритм решения системы линейных уравнений методом Гаусса с примером 3 на 3

Пусть дана система линейных уравнений

Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.

Для упрощения внешнего вида решения составим расширенную матрицу системы:

В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены.

Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:

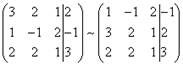
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую, умноженную на  (в нашем случае на ), к третьей – первую строку, умноженную на  (в нашем случае на ).

Это возможно, так как

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменную x:

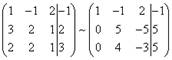
Для упрощения второй строки полученной системы умножим её на  и получим вновь матрицу системы уравнений, эквивалентной данной системе:

Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую, умноженную на  (в нашем случае на ).

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:

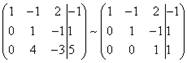
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:

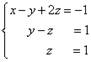
Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в примере.

Решение найдём "с конца" - это называется "обратный ход метода Гаусса". Для этого из последнего уравнения определим z:  .
Подставив это значение в предшествующее уравнение, найдём y:

Из первого уравнения найдём x:

Итак, решение данной системы - .

Проверить решение системы можно и методом Крамера: в этом случае будет выдан то же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ.

Пример решения методом Гаусса системы линейных уравнений 4 на 4

Перед нами вновь пример совместной и определённой системы линейных уравнений, в которой число уравнений равно числу неизвестных. Отличие от нашего примера из алгоритма - здесь уже четыре уравнения и четыре неизвестных.

Пример 1. Решить систему линейных уравнений методом Гаусса:

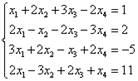
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную . Для этого ко второй строке прибавляем первую, умноженную на , к третьей строке - первую, умноженную на , к четвёртой - первую, умноженную на .

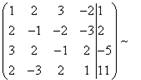
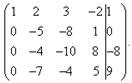
Теперь нужно с помощью второго уравнения исключить переменную  из последующих уравнений. Проведём подготовительные работы. Чтобы было удобнее с отношением коэффициентов, нужно получить единицу  во втором столбце второй строки. Для этого из второй строки вычтем третью, а полученную в результате вторую строку умножим на -1.

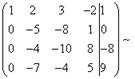
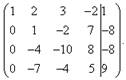
Проведём теперь собственно исключение переменной  из третьего и четвёртого уравнений. Для этого к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .

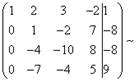
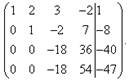
Теперь с помощью третьего уравнения исключим переменную  из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на . Получаем расширенную матрицу трапециевидной формы.

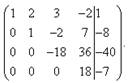
Заданная система эквивалентна, таким образом, следующей:

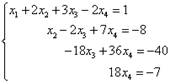
Следовательно, полученная и данная системы являются совместными и определёнными. Искомое решение находим «с конца». Из четвёртого уравнения имеем  .

Это значение подставляем в третье уравнение системы и получаем

, откуда  .

Далее, подставляем значения  и во второе уравнение системы:

, т.е. .

Наконец, подстановка значений  в первое уравнение даёт

, откуда  .

Итак, данная система уравнений имеет единственное решение

.

Решение методом Гаусса прикладных задач на примере задачи на сплавы

Системы линейных уравнений применяются для моделирования реальных объектов физического мира. Решим методом Гаусса одну из таких задач - на сплавы. Аналогичные задачи - задачи на смеси, стоимость или удельный вес отдельных товаров в группе товаров и тому подобные.

Пример 2. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй - 30%, третий - 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.

Решение. Составляем систему линейных уравнений:

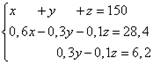
Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений: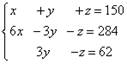

Составляем расширенную матрицу системы: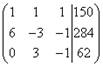

Внимание, прямой ход метода Гаусса. Путём сложения (в нашем случае - вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:

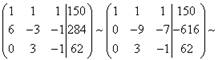
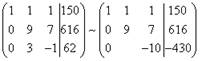
Прямой ход метода Гаусса завершился. Получили расширенную матрицу трапециевидной формы.

Применяем обратный ход метода Гаусса. Находим решение с конца. Видим, что.

Из второго уравнения находим . Из третьего уравнения - .

Во многих прикладных задачах может и не быть третьего ограничения, то есть, третьего уравнения, тогда приходится решать методом Гаусса систему двух уравнений с тремя неизвестными, или же, наоборот - неизвестных меньше, чем уравнений.

О простоте метода говорит хотя бы тот факт, что немецкому математику Карлу Фридриху Гауссу на его изобретение потребовалось лишь 15 минут. Кроме метода его имени из творчества Гаусса известно изречение "Не следует смешивать то, что нам кажется невероятным и неестественным, с абсолютно невозможным" - своего рода краткая инструкция по совершению открытий.

Задания для решения

Пример 3. Решить систему линейных уравнений методом Гаусса:

.

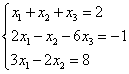Ответ: (2; -1; 1).

Пример 4. Решить систему линейных уравнений методом Крамера и методом Гаусса:

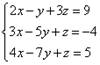
Пример 5. Найти решение системы трёх линейных уравнений с тремя неизвестными методом Гаусса:

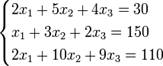
Ответ: (- 152; 270; -254)

Вопросы для закрепления:

1.      Правила вычисления определителей в зависимости от порядка определителя?

2.      Запишите формулы Крамера для решения системы трёх линейных уравнений с тремя переменными.

3.      Алгоритм решения систем линейных уравнений с тремя переменными методом Гаусса и матричным методом.

Для подготовки к самостоятельной работе:

1.   Прочитать учебник О₁: п. 2.3 – 2.5, стр. 80.

2.   Выучить лекцию.

3.   Подготовиться к тестированию по пройденному материалу.

4.   Выполнить задания:

I.  Вычислить определитель III порядка методом треугольников.

II. Решить систему методом Гаусса. 

Вариант 1.

1. 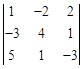 .       2.  

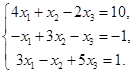
Вариант 2.

1. 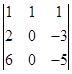 .         2.   

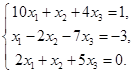
Вариант 3.

1. 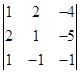 .        2.  

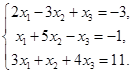
Вариант 4.

1. 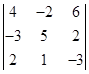 .      2.  

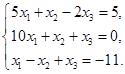
Вариант 5.

1. 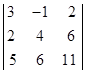 .       2.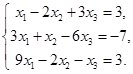

Скачано с www.znanio.ru