Тема 2. Векторная алгебра
Векторная алгебра - раздел математики, в котором изучаются вектора и операции с ними, а также свойства этих операций. Возникла в связи с потребностями механики и физики.Векторы и линейные операции над ними.
Векторы и линейные операции над ними
Величины, для определения которых достаточно задать одно число, называются скалярными (примерами скалярных величин могут служить площадь треугольника, длина окружности, масса материальной точки, время движения и т.д.). Но есть величины (скорость и ускорение материальной точки, сила и т.д.), которые характеризуются направлением, помимо численного значения. Такие величины называются векторными.
Опр. 1. Вектором называется направленный отрезок прямой, характеризующийся длиной и направлением.
На чертеже вектор обозначается стрелкой; над буквенным обозначением вектора также ста-
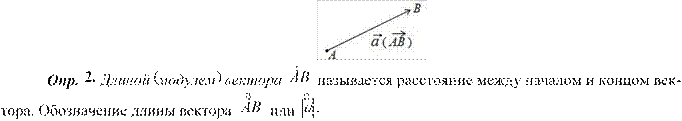
вится стрелка AB , a . Точка Α – начало a ,
точка Β – конец a .
Если Α =Β (начало вектора совпадает с концом), то он называется нулевым и обозначается0 .
По опр. 2
получим 0 0.
Вектор e
, у которого e 1,
назовем единичным.
Опр. 3. Коллинеарными называют векторы, расположенные на параллельных (в частности, на одной) прямых, а компланарными – векторы, расположенные в параллельных (в частности, в одной) плоскостях.
a || b– обозначение коллинеарных векторов. Нулевой вектор коллинеарен любому вектору:
0|| a .
Если a || b , то либо они направлены одинаково и тогда векторы a и b называются сонаправ-
ленными и обозначаются как a b , либо векторы a и b направлены противоположно и обознача-
ются как a b .
Опр. 4. Два вектора a и b называются равными, если они имеют одинаковую длину и сона-
правлены, пишут a b .
Отсюда следует, что вектор можно переносить параллельно самому себе, перемещая начало Α в любую другую точку на плоскости или в пространстве. Такие векторы называются свободными.
В дальнейшем будем рассматривать только свободные векторы.
Линейными операциями над векторами называют операцию сложения векторов и операцию умножения вектора на действительное число.
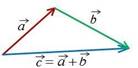
Суммой a bдвух векторов a и b называется вектор с a b , идущий
из начала вектора a в конец вектора b при условии, что начало вектора b
приложено к концу вектора a .
Это правило нахождения суммы двух неколлинеарных векторов называется правилом треугольника.
Данное определение справедливо для любых векторов.
AB BC AC
Кроме правила треугольника сумму двух векторов можно находить по правилу параллело-
грамма (если a и b не коллинеарны).
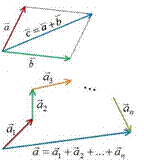
Если векторы a и b приложены к общему началу и на них постро-
ен параллелограмм, то сумма a b этих векторов представляет собой диа-
гональ параллелограмма, идущую из общего начала векторов a и b .
Сумму трех и более векторов можно находить по правилу многоугольника, при этом начало следующего вектора является концом предыдущего вектора.
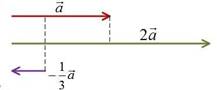
Произведением вектора a на действительное число α называется вектор b , удовлетворяющий следующим условиям:
1.
b a
2. b a при 0, то есть b и a сонаправлены,
b a при 0 , то есть b и a противоположно направлены.
Теорема. Два вектора a и b коллинеарны тогда и только тогда, когда существуют такое чис-
ло α, что b a .
Т.е. можно получить следующее
условие коллинеарности двух векторов: a || b 
b a
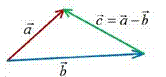
Разностью векторов a и b называется такой вектор с , который яв-
ляется суммой векторов a и -b , т.е. с a(-b) . Разность векторов a и b
будем обозначать с a-b . Если векторы a иb приложены к общему нача-
лу, то разностью векторов a и b будет вектор a-b, идущий из конца век-
тора b к концу вектора a .
Свойства линейных операций
|
Свойства операции сложения векторов |
Свойства операции умножения вектора на число |
|
1. ab b a (коммутативность сложения) 2. a b c a b c(ассоциативность сло- жения) 3. Для любого вектора a существует вектор (-a ) (противоположный) такой, что a(a) 0 (свойство противоположного вектора) 4. Для любого вектора a выполняетсяa 0 a (свойство нулевого вектора) |
1. ab ab (дистрибутивность умножения относительно сложения векторов) 2. a aa (дистрибутивность умножения относительно сложения чисел) 3. a a (ассоциативность числовых сомножителей)
|
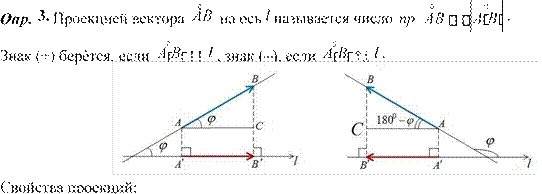
Проекция вектора на ось и еѐ свойства Под осью l будем понимать направленную прямую.
Опр. 1. Проекцией точки A на ось l называется основание перпендикуляра АА, опущенного из точки A на l. Обозначение прl А А .
Опр. 2. Составляющей вектора AB по оси l называется вектор AB , где А прl А , В прl В .
1) прl АВ
АВ cosАВ
,l;
2) проекция суммы векторов на ось l равна сумме проекций векторов на l
прl a b прl a прl b ;
3) прl АВпрl AB , = const. Разложение вектора по базису.
Множество всех векторов пространства с введенными над ними операциями сложения векторов и умножения вектора на число образует векторное (или линейное) пространство. Будем обозначать егоV3. Соответственно на плоскости получим векторное пространство V2 , а на прямой -V1.
Опр. 1. Любой ненулевой вектор e1 0 в пространстве V1 (множестве всех коллинеарных между собой векторов) называется базисом этого пространстваV1.
Для любого вектора aV1 существует такое число x∈R, что a x e1. Число x называется ко-
ординатой вектора a в базисе ⟨ e1⟩.
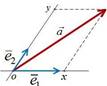Опр. 2. Базисом
на плоскости (пространство V2 )
назовем любые два не-
коллинеарных вектора e1,e2 этой плоскости, взятые в определенном порядке.
Для любого вектора aV2 существуют такие два числа x,y ∈R, что
a x e1 ye2.
Эти числа называются координатами вектора a в базисе ⟨ e1,e2 ⟩, то есть a (x, y).
Опр. 3. Базисом в пространстве (пространство V3) назовем любые три некомпланарных вектора, взятые в определенном порядке.
Для любого вектора a V3 существуют такие три числа x,y,z ∈R, что a x e1 y e2 z e3.
Эти числа называются координатами вектора a в базисе ⟨ e1,e2,e3 ⟩, то есть a (x, y,z). При сложении двух векторов, заданных в одном базисе, их соответственные координаты складываются. При умножении вектора на число все его координаты умножаются на это число.
Декартова прямоугольная система координат (ДПСК)
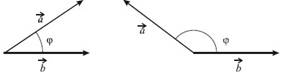
Опр. 1. Углом между ненулевыми векторами a и b (обозначается a,b ) называется
наименьший угол, на который надо повернуть вектор a до совмещения с вектором b (направления должны совпасть).
Очевидно, что 0 1800 (0).
Если угол между векторами прямой, то они называются ортогональными (перпендикулярны-
ми) и обозначаются a
b .
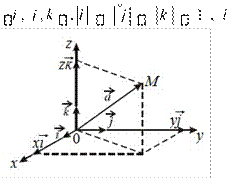
Пусть в качестве базиса в пространстве выбраны три взаимноперпендикулярных вектора с длинами, равными единице. Обозначение:
j
, ik
, jk
.
Такой базис называется ортонормированным. Векторы
i, j,k называются базисными ортами.
Зафиксируем точку O– начало координат и отложим от нее век-
торы i, j,k . Полученная система координат называется ПДСК.
Координаты любого вектора в этом базисе называются декартовыми координатами вектора:
а OA x i y j zk , a = (x, y, z),
x – абсцисса, y – ордината, z – аппликата.
Обычно рассматривается правая система координат (правая тройка векторов i, j,k ), то есть
такая, что из конца вектора k (последний в тройке) кратчайший поворот от i к j виден совершающимся против хода часовой стрелки.
В противном случае система векторов левая.
0 a x , y , z представляет собой вектор единичной длины или орт данного
Вектор а a
a a a
направления.
Если началом вектора a является точка A (x1, y1,z1), концом – точка B (x2, y2,z2) , то век-
тор аAB имеет координаты a (x2 x1, y2 y1,z2 z1) и a (x2 x1)2 (y2 y1)2 (z2 z1)2 .
Деление отрезка в данном отношении
Координаты точки M (x, y), делящей вектор АВ в соотношении λ (λ≠ -1), то есть АМ МВ, находятся по формулам:
хА хВ уА уВ zА zВ
х
1
, у 1
, z 1
в частности, при λ =1 ( АММВ, M – середина АВ )
х хА хВ , у уА уВ , z zА zВ .
2 2 2
Действие над векторами, заданными своими координатами
Если а (ах ,аy ,аz ) и b (bх ,by ,bz ), то:
1) аb (ах bx ,аy by ,аz bz );
2) а (ах ,аy ,аz );
3)
а ах2 ау2 аz2 , т.е. в
ортонормированном базисе длина вектора есть корень квадратный из суммы
квадратов его координат.
4) аb т. и т. т., когда ах bx ,аy by ,аz bz
a ay az
5)
a || b т. и т. т., когда a b 
bx
by
bz
(1), то есть координаты векторов a иb пропор-
циональны. Условие (1) считается выполненным, если числитель и знаменатель одной из трех дробей равны нулю, а две другие дроби образуют верное равенство. Выполнено оно и в случае, когда числители и знаменатели двух дробей равны нулю.
Скалярное произведение векторов
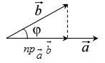
Скалярным произведением двух ненулевых векторов a иb называется число, равное произведению модулей векторов на косинус угла между ними
ab a bcos,
где
угол между векторами a и b
Обозначение ab или (a,b).
Так как пр
a
a cos
и пр
bb cos, то для
скалярного произвеba
дения справедливо ab bпрa a прb .
b a
Свойства скалярного произведения
1. Переместительный закон ab ba
2. Сочетательный закон(a)b (ab)
3. Распределительный закон a(b с) ab aс
2
4. 
a2 a (скалярный квадрат
вектора равен квадрату его длины)
5. a ⊥b a 0, b 0 ⇔ab 0.
Скалярное произведение в координатах
Если векторы a и b заданы своими координатами а (ах ,аy ,аz ) и b (bх ,by ,bz ), то для определения скалярного произведения и угла между векторами справедливы следующие соотношения:
ab axbx ayby azbz ,
т.е. в ортонормированном базисе скалярное произведение есть сумма произведений соответствующих координат.
cos(a,b) ab axbx ayby azbz , a
b ах2 ау2 аz2 bх2 bу2 bz2
т.е. в ортонормированном базисе длина вектора есть корень квадратный из суммы квадратов его координат.
Условие ортогональности векторов в координатной форме a ⊥b ⇔axbx ayby azbz 0.
Векторное произведение векторов
Векторным произведением векторов a иb называется вектор с такой, что:
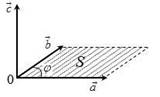
1) 
с a bsin,
где
угол между векторами a
и b ;
2) с a, с b,т.е. он перпендикулярен двум данным векторам;
3) векторыa , b и с образуют правую тройку векторов.
Обозначение a b или [a,b]
Замечание. Если векторы a и b неколлинеарны, т.е. непараллельны, то модуль векторного
произведения равен площади параллелограмма, построенного на векторах a и b (геометрический смысл векторного произведения):
1
Sпаралма ab a bsin.
Тогда площадь треугольника Sтреуг.
Sпаралма . 2
Свойства векторного произведения
1. Антипереместительный закон [a,b] [b,a]
2. Сочетательный закон [a,b][a,b][a,b], т.е. постоянный множитель можно выносить за знак векторного произведения векторов.
3.
Распределительный закон [a,bс] [a,b][a,с] 4. a
|| b
a
0, b
0
[a,b] 0 .
В частности 
.
Векторное произведение в координатах
Если векторы a иb заданы своими координатами а (ах,аy,аz ) и b (bх,by ,bz ) в ортонор-
мированном базисе i, j,k , то
i j k
ay azax azax ay
ab ax ay azk aybz byaz iaxbz bxaz j axby bxay k by bzbx bzbx b bx by bzy
Смешанное произведение векторов
Смешанным произведением трех векторов a , b и с называется скалярное произведение
векторного произведения векторов a иb и вектора с , которое обозначают abc или (ab)c. Свойства смешанного произведения
1. Смешанное произведение не изменится при перестановке знаков скалярного и векторно-
го произведений [a,b]с а[b,с]
2. При перестановке в смешанном произведении двух векторов его знак меняется на про-
тивоположный:abc bac acb cba
3. Смешанное произведение не меняется при круговой перестановке векторов:
abc bca cab
Смешанное произведение в координатах
Если известны координаты всех трех векторов а (ах ,аy ,аz )
|
их смешанное произведение находится по формуле: abc bx cx |
ay by cy |
Применение смешанного произведения
1. Установление компланарности векторов: abc 0 одной плоскости.
, b (bх ,by ,bz ), с (сх ,сy ,сz ),то az bz. cz
a,b,c
компланарны, т.е. лежат в
2. Определение взаимной ориентации векторов a,b,c : если смешанное произведение
abc 0, то векторы a,b,c образуют правую тройку, если abc 0, то тройка векторовa,b,c – левая.
3.
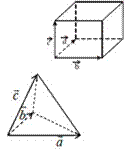
Определение объемов параллелепипеда и тетраэдра,
построенного
на векторахa,b,c : Vпаралда ab c
1
Объѐм треугольной пирамиды
Vпирамиды Vпаралда
6
Тема 2. Векторная алгебра
Линейными операциями над векторами называют операцию сложения векторов и операцию умножения вектора на действительное число
Разностью векторов a и b называется такой вектор с , который яв- ляется суммой векторов a и -b…
АВ АВ cos АВ , l ; 2) проекция суммы векторов на ось l равна сумме проекций векторов на l…
Опр. 1. Углом между ненулевыми векторами a и b (обозначается a , b ) называется…
А х В у
Сочетательный закон ( a ) b ( a b ) 2
Свойства векторного произведения 1
Определение взаимной ориентации векторов a , b , c : если смешанное произведение a b c 0, то…
© ООО «Знанио»
С вами с 2009 года.
