Лекционно-практическое занятие 15 Перпендикулярность прямых и плоскостей в пространстве

 

 

 

Тема. Расстояние от точки к плоскости. Теорема о трех перпендикулярах.  

Цель: сформулировать определения: перпендикуляр к плоскости, наклонная, основа наклонной, проекции наклонной на плоскость, расстояние от точки к плоскости; сформировать представление о том, где используется перпендикулярность в реальной жизни, понятие перпендикулярности как основного принципа архитектуры; формировать умения представлять прямую, перпендикулярную к плоскости и решать задачи, применяя знания о перпендикулярности прямой и плоскости; формировать умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач по данной теме; формировать умение видеть математическую задачу в контексте проблемной ситуации в окружающей жизни; развивать пространственное мышление студентов, воспитывать математическую культуру. 

Оборудование: стереометрический набор, презентация PowerPoint к теме.

 

План

1.   Перпендикуляр и наклонная.

2.   Расстояние от прямой до параллельной плоскости. 3. Теорема о трех перпендикулярах.

 

Литература

 

1.     Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10 – 11 классы: учеб. для общеоразоват. организаций: базовый и углубл. уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 3 – е изд. – М.: Просвещение, 2016. – 255 с.

2.     Чекова А.М. Агебра и начала анализа. 7 – 11 классы. Учеб. пособие. – Изд. 4-е, испр. и доп. – Х.: Країна мрій^тм, 2008. – 200 с.

3.     Генденштейн Л.Э., Ершова А.П. Математика. Наглядный справочник с примерами для школьников и абитуриентов. – Х.: «Гимназия», - 2002. 

4.     А.М. Колмогоров, О.М. Абрамов та др. Алгебра и начала анализа: Учеб. для 10-11 кл. серед шк. – М.: Просвещение, 1993. 

5.     Пособие по математике для поступающих в вузы: Учеб. Пособ. Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х.; под ред. Г.Н. Яковлева. – М.: Наука, 1985. – 480с.

6.     Погорєлов О.В. Геометрія. Стереометрія. Підручник за 10-11 кл. Київ : Освіта, 1994 – 128с.  

7.     Афанасьєва О.М., Бродский Я.С., Павлов О.Л. Геометрія 10 -11кл. : Пробний підручник. – Тернопіль: Навчальна книга – Богдан, 2004

 

Ход занятия

 

1. Актуализация опорных знаний студентов, мотивация обучения

 

1.1. Самостоятельное повторение предыдущей темы в конспекте

 

1.2. Фронтальный опрос

 

•      Прямые в пространстве называются перпендикулярными?

•      Какие свойства прямой и плоскости, перпендикулярных между собой, вы знаете?

•      Сформулируйте признак перпендикулярности прямой и плоскости.

•      Сколько прямых, перпендикулярных к данной плоскости, можно провести через данную точку?

•      Сколько плоскостей, перпендикулярных к данной прямой, можно провести через данную точку?

        

1.3.   Проверка выполнения домашнего задания

 

1.4.   Минутка каллиграфии

 

1.5.   Устный счет. Игра

 

1.6. Математический диктант

 

1.             Какие прямые в пространстве называются перпендикулярными?

2.             Сформулируйте признак перпендикулярности прямой и плоскости.

3.             Сколько прямых, перпендикулярных к данной плоскости, можно провести через данную точку?

4.             Дайте определение прямой, перпендикулярной плоскости.

5.             Сколько плоскостей, перпендикулярных к данной прямой, можно провести через данную точку?

6.             Даны плоскость и точка А на ней. Проведите через точку А прямую, которая была перпендикулярна к плоскости_.

 

Ответы:

1)                     Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

2)                     Если прямая перпендикулярна к двум прямым, лежащим в плоскости и пересекающихся, то она перпендикулярна данной плоскости.

3)                     Только одну.

4)                     Прямая называется перпендикулярной к плоскости, если она пересекает эту плоскость и перпендикулярна к любой прямой, лежащей в этой плоскости и проходит через точку пересечения.

5)                     Только одну.

 

2. Сообщение темы и задач занятия

 

На центральной площади Донецка, рядом с памятником В. И. Ленину находится трехгранный        пилон, выполненный из нержавеющей стали высотой сорок два метра. Постамент и пилон находятся на гранитном стилобате,   на      который     ведет лестница. На пилоне размещена цитата Ленина: «Донбасс, это — не случайный район, а это — район, без которого      социалистическое строительство останется простым, добрым пожеланием».

Спрашивается, вертикально ли установлен пилон, или это искажение при фотосъемке, ведь угол постамента вождя выглядит вполне вертикально, да и столб уличного освещения на дальнем плане на фоне деревьев вполне вертикален? Как нам, пользуясь

вторым фото, доказать, что пилон установлен строго перпендикулярно?  

Обратим внимание на полуколонны дома на пересечении проспекта Ильича и улицы Постышева. Пилон параллелен очертаниям полуколонн, а они, в свою очередь, архитектурно перпендикулярны плоскости площади. Воспользуемся прямой теоремой о двух параллельных прямых, одна из которых (полуколонна) перпендикулярна к плоскости, значит и другая прямая (пилон) перпендикулярна к плоскости площади.

А есть ли другой способ утверждать перпендикулярность прямой и плоскости?

 

3. Первичное восприятие и осознание нового материала

 

3.1. Перпендикуляр и наклонная

 

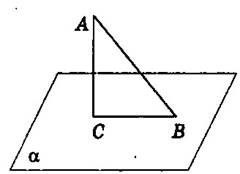
Пусть дана плоскость и точка, не лежащая на ней (рис.1).

Перпендикуляром, опущенным из данной точки на одну плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежит на прямой, перпендикулярной плоскости (АС).

Конец этого отрезка, лежащий в плоскости, называется основой перпендикуляра (С).

Расстоянием от точки к плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость (АС).

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости и не является перпендикуляром к плоскости (АВ).

Конец отрезка, лежащий в плоскости, называется основой наклонной

(В).

Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной (ВС).

 

Рис.1

 

3.2. Расстояние от прямой до параллельной плоскости

 

Определение. Расстоянием от прямой к параллельной ей плоскости называется расстояние от любой точки этой прямой к плоскости.

 

Определение. Расстоянием между параллельными плоскостями называется расстояние от любой точки одной плоскости к другой плоскости.

 

3.2. Теорема о трех перпендикулярах

 

Как должна быть установлена мачта относительно палубы яхты? (Перпендикулярно плоскости палубы). Каким образом мачта закреплена вертикально? (Закреплена вантами – растяжками к бортам и носу судна)

 

В современной круизной парусной яхте управление парусами производится с помощью правой и левой лебедок, которые натягивают паруса и изменяют их угол наклона. Ширина судна на миделе 4,5 м (в самой широкой части), высота мачты 21 м от ватерлинии, высота миделя (поперечного сечения от киля до палубы) 4,5 м, осадка яхты 2 м. Как установить крепления лебедочных растяжек перпендикулярно теоретической основной линии судна?

Одна из целей нашего занятия – выяснить, как связаны наклонная, проекция и перпендикулярная прямая к проекции между собой; как применяется на практике эта теорема с собственным названием

«Теорема о трех перпендикулярах»  

 

 

 

 

Теорема 7. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она

перпендикулярна наклонной.

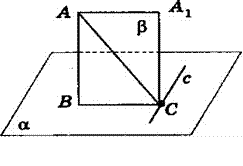
Дано:

AB;C,c;c^BC . Доказать: cAC . 

 

Доказательство

Через точку С и прямую АВ проводим ^ и  в ней ^{A1C : A1CAB} . Поскольку A1CAB и AB , то A1C, A1Cc . 

Поскольку  ^cBC,cA₁^C, то ^c, и, с АС .

 

Теорема 8. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

 

 

 

 

 

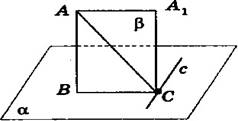
Дано:

AB;C,c;c^AC

Доказать: с  ВС . 

 

 

Доказательство

Через точку С и прямую АВ проводим ^ и в ней А₁С : А₁С  АВ . Поскольку A1CAB и AB ,то A1C, A1Cc .  Поскольку АС с , ^A1^Cc, то ^c, и, BC^c .

 

4. Закрепление и осмысление изученного материала

 

4.1. Решение задач (фронтально)

 

1.                      Найти длину наклонной, если длина перпендикуляра равна 4 см, а проекция наклонной на плоскость - 3 см.

 

2.                      Найти проекцию наклонной на плоскость, если наклонная равна 13 см, а перпендикуляр, проведенный с той же точки - 12 см. Найти длину перпендикуляра, если наклонная равна 10 см, а ее проекция на плоскость - 8 см.

 

3.                      Сколько перпендикуляров можно опустить с данной точки к данной плоскости? Почему?

 

4.                      Сколько наклонных можно провести с данной точки к данной плоскости? Как следует установить на крестовине елку, чтобы она была перпендикулярна к плоскости пола?

 

5.                      Как на практике с помощью отвеса проверить вертикальность установленного столба?

 

7.                      С точки^S проведен перпендикуляр^SOк плоскости^ и наклонные SА и SВ. Длины наклонных соответственно равны 13 и 20 см. Длина проекции наклонной АS равна 5 см (рис. 2). Найти расстояние от точки S до плоскости и длину проекции наклонной SВ.

Ответ: ОВ=16см, SO= 12см

S

 

Рис.2

 

8.                      Найти расстояние от точки А к граням куба, если ребро куба равно 10 см.

 

4.2. Решение задач (работа в группах)

 

Первая группа – это те, кто сидит за партой слева, а вторая группа– те, кто сидит за партой справа

1-я группа – рассматривает решение в учебнике стр.37, записывает себе в тетрадь, а затем объясняет соседу. 

2-я группа – пока сосед разбирается решение задания со стр. 37, разбирает решение задания № 133 стр. 40 (доказательство единственности решения), затем объясняет соседу.

 

3.3. Решение задач (самостоятельная работа)

 

Задача № 129. Прямая АМ перпендикулярна к  плоскости квадрата АВСD, диагонали которого пересекаются в точке О. Докажите, что: 1) прямая  ВD АМО; 2) МОВD. Доказательство.

Прямая АМ  к плоскости квадрата, а значит и к любой прямой из плоскости квадрата, например, к его диагонали ВD. АМ  ВD. Диагонали квадрата пересекаются под прямым углом, значит ВDАО. АМ и АО пересекаются в точке А плоскости АМО, значит по признаку перпендикулярности прямой к плоскости ВD АМО. Ч.т.д.

Рассмотрим треугольник ВМD, ВМ=МD как диагонали граней, построенных на равных сторонах, ВО=ОD по свойству диагоналей квадрата, значит МО – медиана в равнобедренном треугольнике, а, следовательно, и высота. МОВD. Ч.т.д.

 

Рефлексия

 

•      Что такое перпендикуляр, опущенный из данной точки к плоскости?

•      Что такое наклонная, опущенная с данной точки к плоскости?

•      Дайте определение расстояния от прямой к параллельной ей плоскости.

•      Сформулируйте теорему о трех перпендикулярах.

 

Самооценивание

 

Если представить все, что мы сегодня выучили, в форме коробки, выберите картинку, которая соответствует вашим ощущениям.

Рисунок 1  

                                                                                         Рисунок 2                      Рисунок 3

Рисунок 1 «Много всего, нужно навести порядок».

Рисунок 2 «Мне помогли получить знания»

Рисунок 3 «Меня нагрузили по полной, не вижу, куда бы это сложить»

 

Домашнее задание

 

1) [1] §19, 20   №   142, 143, 144