
Утверждаю
и.о. директора Добровольская Е.Н.________
21.04.2020 г
Дата урока: 21.04.2020 г
Срок сдачи материала: 21.04.2020
Преподаватель: Синявская Анна Федоровна
Лекционный материал для группы 19 ТМ по теме: «Понятие многогранника. Призма. Параллелепипед. Площадь и объем поверхности призмы».
1.
 Переписать конспект (списываем и срисовываем ВСЁ!!! это уже
готовый конспект)
Переписать конспект (списываем и срисовываем ВСЁ!!! это уже
готовый конспект)
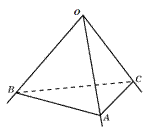
Фигура, состоящая из трех углов и части пространства, называется трехгранным углом
 Рассмотрим фигуру, составленную из углов А1ОА2,
А2ОА3, и так далее до АпОА1 и их внутренних областей так, что
смежные углы не лежат в одной плоскости, а несмежные углы не имеют общих точек.
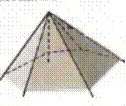
Такая фигура называется многогранным углом. Фигура,
состоящая из
Рассмотрим фигуру, составленную из углов А1ОА2,
А2ОА3, и так далее до АпОА1 и их внутренних областей так, что
смежные углы не лежат в одной плоскости, а несмежные углы не имеют общих точек.
Такая фигура называется многогранным углом. Фигура,
состоящая из ![]() углов и части пространства,
называется многогранным углом
углов и части пространства,
называется многогранным углом
Свойства плоских углов
Свойство 1: Сумма плоских углов трехгранного угла больше третьего плоского угла, поэтому каждая сумма углов в скобках не больше, чем соответствующий им третий плоский угол. Поэтому искомая сумма не превышает 360 градусов.
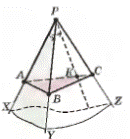 Свойство 2:
Каждый плоский угол трехгранного угла меньше суммы двух других плоских углов.
Свойство 2:
Каждый плоский угол трехгранного угла меньше суммы двух других плоских углов.
Геометрическое тело, ограниченное плоскими многоугольниками, называется многогранником, а многоугольники — его гранями и их общие стороны — ребрами.
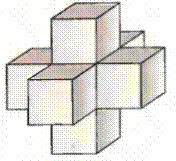
Многогранник называется выпуклым, если он расположен целиком по одну сторону от любой из плоскостей, содержащих его грани
. 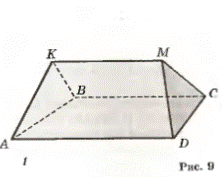
Призмой (n-угольной) называется многогранник, у которого две грани равные n-угольники А1 А2…Аn и В1 В2…В (называемые основаниями), с соответственно параллельными сторонами, а остальные n граней – параллелограммы, у каждого из которых две стороны являются соответственными сторонами оснований.
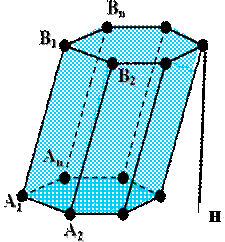 Делаем описание фигуры
Делаем описание фигуры
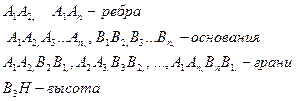
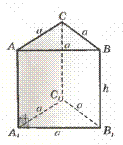
Призма называется прямой, если все её боковые грани являются прямоугольниками.
![]()
![]()
![]()
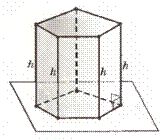
Призма называется правильной, если основаниями её служат правильные многоугольники и боковые рёбра перпендикулярны к основаниям.
Параллелепипед— призма, основаниями которой являются параллелограммы.
![]()
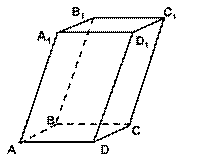
2. Сделать описание фигуры (строим фигуру, справа делаем описание)
Диагональ параллелепипеда – это отрезок, соединяющий две вершины
параллелепипеда, не лежащие в одной грани их 8
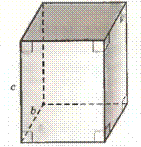 Прямоугольный параллелепипед — это прямой параллелепипед, в основании
которого лежит прямоугольник. Т.к. это прямой параллелепипед, то боковые грани
представляют собой прямоугольники. Значит, вообще все грани прямоугольного
параллелепипеда – прямоугольники.
Прямоугольный параллелепипед — это прямой параллелепипед, в основании
которого лежит прямоугольник. Т.к. это прямой параллелепипед, то боковые грани
представляют собой прямоугольники. Значит, вообще все грани прямоугольного
параллелепипеда – прямоугольники.
![]()
![]()
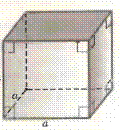 Куб — это прямоугольный параллелепипед, все грани которого – равные
квадраты.
Куб — это прямоугольный параллелепипед, все грани которого – равные
квадраты.
![]()
![]()
![]()
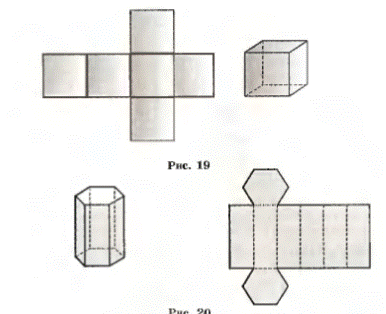
Развертка призмы (развертка должна соответствовать фигуре)
3. Решить задачу:

Домашнее задание: Построить
параллелепипед ![]() . Выписать все
ребра параллельные
. Выписать все
ребра параллельные ![]() , скрещивающиеся с
, скрещивающиеся с ![]() .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.