
Министерство образования Новосибирской области
Государственное автономное профессиональное образовательное учреждение Новосибирской области
«НОВОСИБИРСКИЙ
КОЛЛЕДЖ ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ
И ПЕРЕРАБОТКИ»
|
|
|
Лекция по теме «Комбинаторика»
Математика: алгебра и начала анализа, геометрия.
19.01.04 Пекарь; 19.01.14 Оператор процессов колбасного производства;
1курс
Составитель: преподаватель Загурская А.А.
Лекция 1. Перестановки. (Сделать конспект)
Цель работы:
1. Познакомиться с историей возникновения раздела теории вероятности – комбинаторики
2. Выяснить области применения комбинаторики.
3. Узнать правила решения комбинаторных задач.
4. Познакомиться с примерами решения комбинаторных задач.
В комбинаторике различают три вида различных соединений (комбинаций) элементов фиксированного (конечного) множества. Это перестановки, размещения и сочетания.
Перестановками из n элементов называются соединения, которые состоят из одних и тех же n элементов и отличаются одно от другого только порядком их расположения.
Кстати, перестановки – это простейшие комбинации, которые можно составить из элементов конечного множества.
Перестановка без повторений. Выборки, имеющие одинаковый состав и отличающиеся друг от друга только порядком элементов, называются перестановками без повторений. Количество перестановок из n элементов находится по формуле Pn=n!. (буква P, видимо, ассоциируется с первой буквой английского слова permute (permutation) – переставлять (перестановка)
Факториа́л натурального числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л, n!= 1·2·3·4·…· (n-1) ·n. )
Перестановки
с повторениями. Пусть
множество X состоит из k различных элементов: X ={x1, x2,…xk}
Перестановкой с повторениями
состава (r1, r2, …rk) называется упорядоченный набор длины n=r1+r2+…+rk , в котором элемент xi встречается ri раз (i=1,
2,… k). Количество таких перестановок находится
по формуле Pn (r1, r2, …rk) = 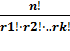
Решим задачу.
Сколько слов можно получить, переставляя буквы в слове «гора» и
«институт»?
Решение.
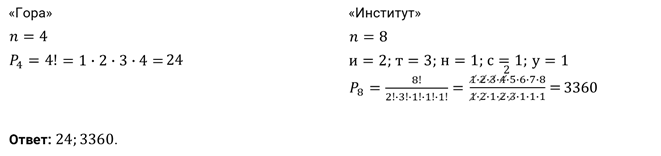
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.