
Министерство образования Новосибирской области
Государственное автономное профессиональное образовательное учреждение Новосибирской области
«НОВОСИБИРСКИЙ
КОЛЛЕДЖ ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ
И ПЕРЕРАБОТКИ»
|
|
|
Лекция по теме «Размещение. Сочетание»
Математика: алгебра и начала анализа, геометрия.
19.01.04 Пекарь; 19.01.14 Оператор процессов колбасного производства;
1курс
Составитель: преподаватель Загурская А.А.
Лекция 1. Размещение. Сочетание. (Сделать конспект)
Цель работы:
1. Познакомиться с историей возникновения раздела теории вероятности – комбинаторики
2. Выяснить области применения комбинаторики.
3. Узнать правила решения комбинаторных задач.
4. Познакомиться с примерами решения комбинаторных задач.
Итак, в комбинаторике различают три вида различных соединений (комбинаций) элементов фиксированного (конечного) множества. Это перестановки, размещения и сочетания.
Размещениями из m элементов по n элементов (![]() ) называются такие соединения, каждое из которых
содержит n элементов, взятых из данных m разных элементов, и которые
отличаются одно от другого либо самими элементами, либо порядком их
расположения.
) называются такие соединения, каждое из которых
содержит n элементов, взятых из данных m разных элементов, и которые
отличаются одно от другого либо самими элементами, либо порядком их
расположения.
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по n различным местам n из m различных предметов?
Число всевозможных размещений из m элементов по n элементов обозначают ![]() .
.
Формула числа размещений m элементов по n имеет следующий вид:
![]() .
.
В случае, когда нужно найти число размещений из n элементов по n элементов, оно равно числу перестановок из этих элементов.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по n различным местам n из m предметов, среди которых есть одинаковые?
Формула числа размещений с повторениями имеет следующий вид:
![]() .
.
Решим задачу.
В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
Решение.
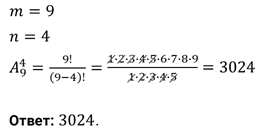
Решим ещё одну задачу.
В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Решение.
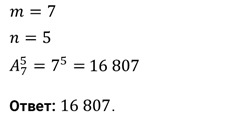
Ну а теперь давайте поговорим о последнем виде комбинаций элементов, о сочетаниях.
Сочетаниями из m элементов по n в каждом (![]() ) называются соединения, каждое из которых содержит n элементов, взятых из данных m разных элементов, и которые
отличаются одно от другого по крайней мере одним элементом.
) называются соединения, каждое из которых содержит n элементов, взятых из данных m разных элементов, и которые
отличаются одно от другого по крайней мере одним элементом.
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать n из m различных предметов?
Число всевозможных размещений из m различных элементов по n элементов обозначают ![]() .
.
Формула числа сочетаний из m элементов по n имеет следующий вид:
![]() , или
, или ![]() .
.
Задачу о числе сочетаний с повторениями можно выразить вопросом: имеется по m одинаковых предметов каждого из различных типов; сколькими способами можно выбрать n из этих m предметов?
Формула числа сочетаний с повторениями имеет следующий вид:
![]() .
.
Решим задачу.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение.
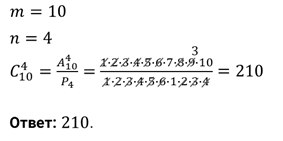
И решим ещё одну задачу. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоёные. Сколькими способами можно купить 7 пирожных?
Решение.
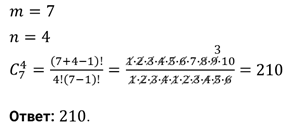
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.