Лекция по теме "Преобразования графиков функций"

Исследование и построение графиков степенной функции различными преобразованиями.

Цель занятия: формировать у обучающихся способность к рефлексии, научить находить причину своих затруднений, самостоятельно строить алгоритм действий по устранению затруднений, научить самоанализу действий и способам нахождения разрешения конфликта; закрепить усвоенные знания, понятия, способы действия.

Порядок работы:

1) Изучить теоретическую часть (устно).

2) Записать примеры и выполнить задания (письменно, все графики начертить с помощью таблиц значений, которые составить самостоятельно. Функции на графике необходимо подписать, где какая).

Преобразование графиков элементарных функций

В чистом виде основные элементарные функции встречаются, к сожалению, не так часто. Гораздо чаще приходится иметь дело с элементарными функциями, полученными из основных элементарных при помощи добавления констант и коэффициентов. Графики таких функций можно строить, применяя геометрические преобразования к графикам соответствующих основных элементарных функций (или переходить к новой системе координат). К примеру, квадратичная функция   представляет собой квадратичную параболу  , сжатую втрое относительно оси ординат, симметрично отображенную относительно оси абсцисс, сдвинутую против направления этой оси на 2/3 единицы и сдвинутую по направлению оси ординат на 2 единицы.

Таким образом, различают три вида геометрических преобразований графика функции:

·  Первый вид - масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.

На необходимость масштабирования указывают коэффициенты   и  отличные от единицы, если  , то происходит сжатие графика относительно oy и растяжение относительно ox , если  , то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.

·  Второй вид - симметричное (зеркальное) отображение относительно координатных осей.

На необходимость этого преобразования указывают знаки «минус» перед коэффициентами  (в этом случае симметрично отображаем график относительно оси ox ) и   (в этом случае симметрично отображаем график относительно оси oy ). Если знаков «минус» нет, то этот шаг пропускается.

·  Третий вид - параллельный перенос (сдвиг) вдоль осей ox и oy.

Это преобразование производится В ПОСЛЕДНЮЮ ОЧЕРЕДЬ при наличии коэффициентов a и b, отличных от нуля. При положительном а график сдвигается влево на |а| единиц, при отрицательных а – вправо на |а| единиц. При положительном b график функции параллельно переносим вверх на |b| единиц, при отрицательном b – вниз на |b| единиц.

Пример.

Постройте график функции f(x) = x²+2.

Решение:

Построим график функции f(x) = x². Затем перенесём его вверх на 2 единицы:

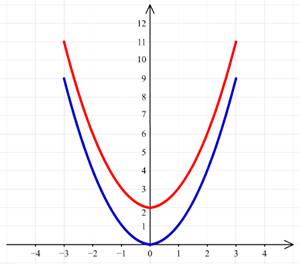
В результате получим график функции f(x) = x²+2.

Для построения графика функции y=f(x)+a, где a≠0 можно перенести ось абсцисс Ox на |a| единиц вверх (если a>0) или вниз (если a<0). При этом точка (0;0) перейдёт в точку (0;a). Затем перенесём его вверх на 2 единицы:

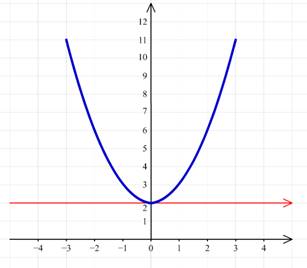
Для построения графика функции y = f(x+b) график функции f(x) следует перенести параллельно относительно оси абсцисс Ox на |b| единиц влево (если b>0) или вправо (если b<0).

Пример.

Постройте график функции y=(x+2)².

Решение:

Построим график функции y=x². График функции y = (x+2)² получается из графика y=x² перемещением его влево на 2 единицы.

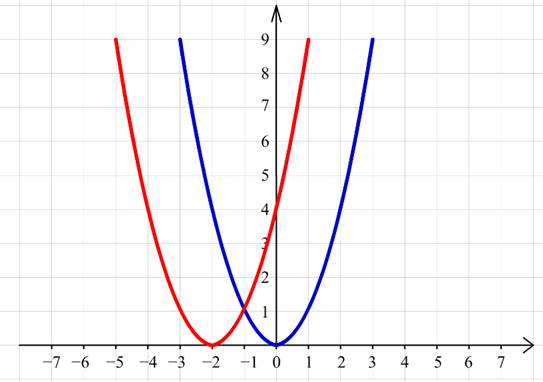
Для построения графика функции y=f(x+b)+a график функции f(x) следует перенести параллельно относительно оси абсцисс Ox на |b| единиц влево (если b>0) или вправо (если b<0) и параллельно относительно оси ординат Oy на |a| единиц вниз (если a<0) или вверх (если a>0).

Выполните следующие задания

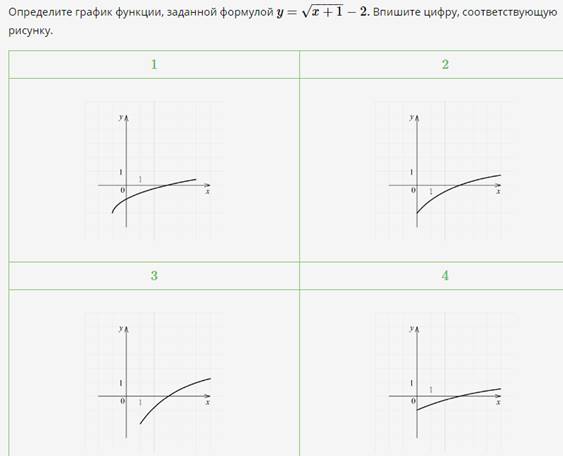
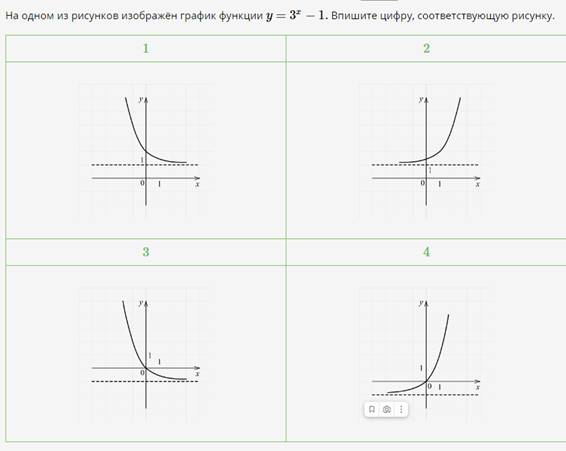
Для построения графика функции y=mf(x), где m≠0 следует каждую ординату графика f(x) увеличить в m раз, если m>1 (произвести растяжение от оси Ox), или уменьшить в 1m раз, если 0<m<1(произвести сжатие к оси Ox). Нули функций остаются на месте. Если m<0, то к преобразованию сжатия (растяжения) присоединяется симметрия относительно оси Ox.

Пример.

Постройте графики функций y=2x² и y=0,5x².

Решение.

Для построения графика функции y=2x² следует каждую ординату графика функции y=x² увеличить в два раза:

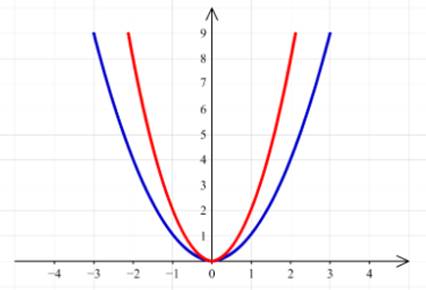
Для построения графика функции y=0,5x² следует каждую ординату графика функции y=x²  уменьшить в два раза:

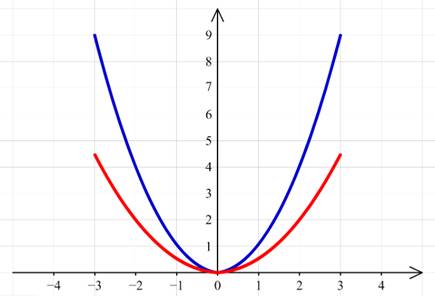
Для построения графика функции y=f(nx), где n≠0 следует каждую абсциссу графика f(x) уменьшить в n раз, если n>1 (произвести сжатие от оси Oy), или увеличить в 1n раз, если 0<n<1 (произвести растяжение к оси Oy). Нули функций остаются на месте. Если n<0, то преобразованию сжатия (растяжения) присоединяется симметрия относительно оси Oy.

Пример.

Постройте график функции y=(2x)².

Решение.

Для построения этого графика следует каждую абсциссу графика функции уменьшить в два раза.

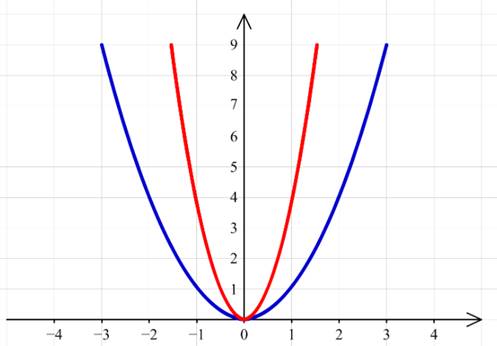
Для построения графика функции y=f(−x) следует график функции f(x) симметрично отобразить относительно оси Oy.

Пример.

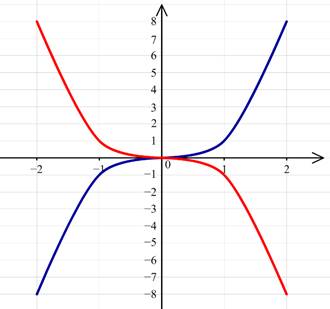
Постройте график функции y=(−x)³.

Решение.

Для построения этого графика следует график функции y=x³ симметрично отобразить относительно оси Oy.

Для построения графика функции y=−f(x) следует график функции f(x) симметрично отобразить относительно оси Ox.

Пример.

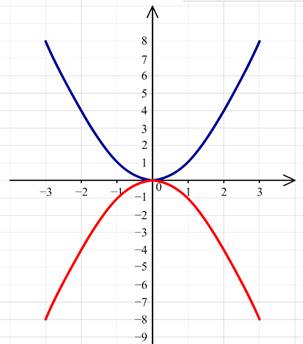
Постройте график функции y=−x².

Решение:

Для построения этого графика следует график функции y=x²

 симметрично отобразить относительно оси Ox.

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x — симметрично отражаются относительно этой оси (вверх).

Примеры

Постройте график функции y=|2x+3| и y=∣x²−2x−3∣.

Решение:

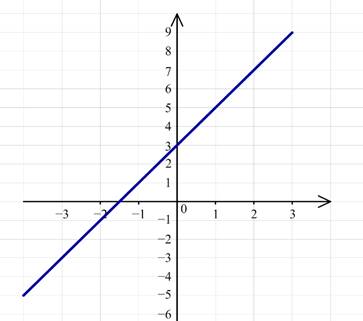
1) Графиком функции является прямая y=2x+3.

Для построения графика y=|2x+3| следует симметрично отобразить часть прямой для всех x∈(−∞;0).

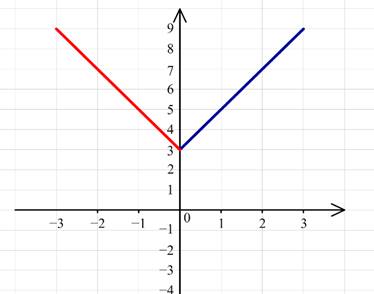
2) Графиком функции y=x²−2x−3 является парабола.

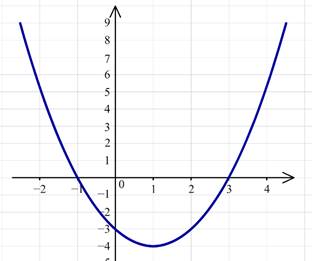
Для построения графика функции y=∣x²−2x−3∣ часть графика, лежащего ниже оси Ox следует симметрично отобразить относительно оси Ox.

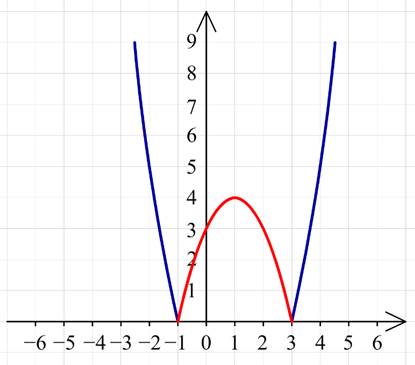
Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси Oy, остаётся без изменения и, кроме того, симметрично отражается относительно оси Oy (влево). Точка графика, лежащая на оси Oy, остаётся неизменной.

Примеры.

Постройте график функции y=2|x|+3 и y=x²−2|x|−3.

Решение:

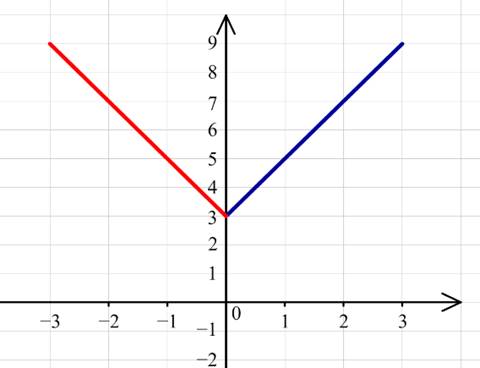
1) Графиком функции является прямая y=2x+3.

Для построения графика y=2|x|+3 следует симметрично отобразить относительно Oy часть прямой для всех x∈(0;+∞).

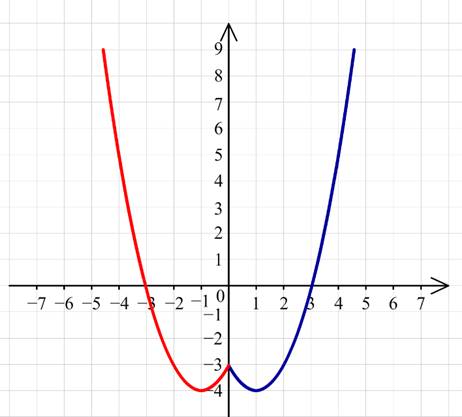
2) Графиком функции y=x²−2x−3 является парабола.

Для построения графика функции часть графика y=x²−2|x|−3, лежащего справа от оси Oy, следует симметрично отобразить относительно оси Oy.