Методическая разработка урока по алгебре в 7 классе по теме Решение систем линейных уравнений

Этап

Деятельность учителя

Деятельность учащихся

Универсальные действия

1. Мотивационный этап.

Самоопределение к деятельности.

Организационный момент.

Добрый день. Эпиграф нашего урока «Ум заключается н только в знании, и в умении прилагать знания на деле.» Аристотель. Попробуем проанализировать слова Аристотеля.

  Ребята кто знает: «Кто такой Аристотель, может к его словам нет смысла прислушиваться?» (слайд2)

-Как вы думаете, чем мы будем заниматься на уроке?

 Ребята анализируют цитату.

- один из учащихся передает информацию об Аристотеле.

«Будем прилагать усилия при решении систем уравнений», «Искать пробелы в умении решать системы»

Личностные: - самоопределение;

Регулятивные: - целеполагание;

Коммуникативные: - планирование учебного сотрудничества с учителем и сверстниками

2. Актуализация знаний и осуществление первичного действия.

 А начнем с теста. (слайд3).

1. Какие из перечисленных уравнений являются линейными?

п) х – 2у = 1;                      м) ху + 3у = - 18

в) х² + 2у = 5;                    о) – х – у =  - 11.

2. Какая из перечисленных пар чисел является решением системы уравнений

 2х + у = 12,

 х – 2у = 2?

р) (2; 0);                             к) (1; -2);

с) (4; 4);                             б) (5,2; 1,6).

3. Какая из перечисленных систем не имеет решения?

н)    2х + у = 5,   к)  2х + 3у = 8,   е) х – у = 6

       4х +2у = 10,    3х – у = - 9         х – у = - 3.                                       

4. Какая из перечисленных систем имеет одно решение?

и)    2х + у = 5   д)     2х + 3у = 8,   в) х – у = 6,

      4х +2у = 10         3х – у = - 9         х – у = - 3.

5. Укажите значение х + у, где х и у – решение системы уравнений

         х – 2у = 2,

        2х + у = 1

а) -0,2;        б) 1;          в) – 3;                    г) 0.

Решают тест.

Познавательные:

-выделение и формирование познавательной цели,

- анализ объектов и понятий;

-поиск и выделение необходимой информации; применение методов информационного поиска

Коммуникативные:

-сотрудничество с учителем и сверстниками;

-умение слушать и вступать в диалог;

-учет позиции других учеников.

Личностные:

-постановка учебной задачи;

Регулятивные:

-выдвижение гипотез;

- целеполагание.

3. Выявление индивидуальных затруднений в реализации полученных знаний и умений.

 В результате должно получиться «ПОБЕДА»

Разбираем тест.

 Ребята оцените свою работу.

В 1 задании в) и м) не являются линейными уравнениями. В задании 2 можно найти решение подставить каждую пару в систему, а можно решить систему. № 3в пункте е)коэффициенты при х и у одинаковые, а ответы различные. В 4 задании те же системы. Последнее не имеет решения. В первой системе умножим коэффициенты первого уравнения и они совпадут с коэффициентами второго значит решения совпадут. Остается пункт д).

В последнем задании решим  систему любым способом и полученные результаты сложим.

Регулятивные:

- планирование, прогнозирование;

Познавательные:

- моделирование,

 - логические решение проблемы, построение логической цепи рассуждений,доказательство,

- выдвижение гипотез и их обоснование; Коммуникативные :

- инициативное сотрудничество в поиске и выборе информации

4. Построение плана по разрешению возникших затруднений

Какой вывод сделаем из полученных результатов?

Какой составим план по ликвидации затруднений?

Еще не все умеют определять имеет ли система решение. Возникают трудности при решении системы.

5. Реализация на практике выбранного плана, стратегии по разрешению проблемы

Вопросы:

1. Какими способами  можно решить систему  двух линейных уравнений  с двумя  переменными?

2. В чем заключается  способ  подстановки решения  системы двух линейных уравнений с двумя переменными?

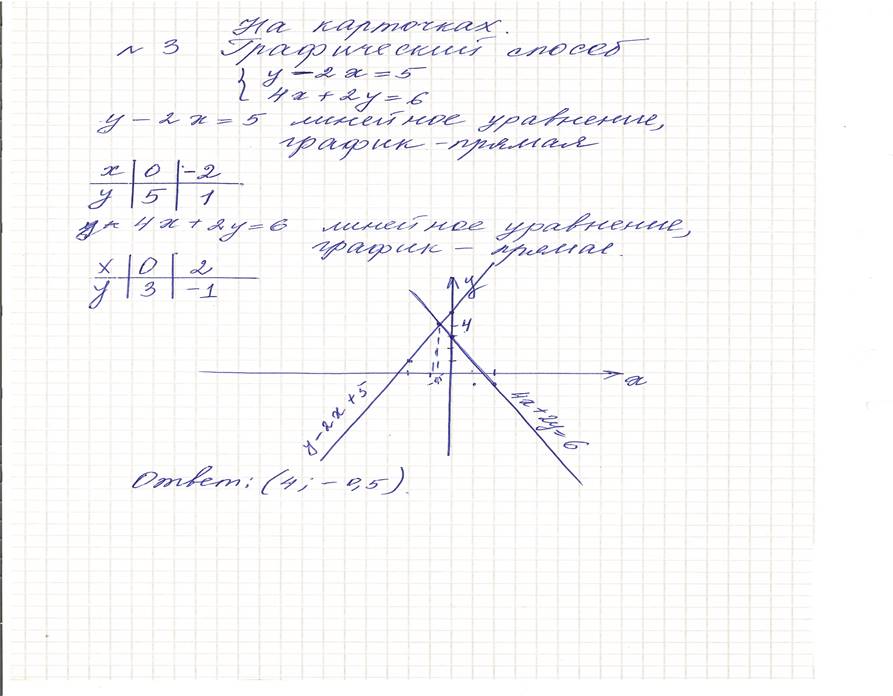
-Применяя этот способ, решить систему  уравнений: (задание дано на карточках)

 №1.         2х + у = 2

                6х – 2у = 1    

3. В чем заключается  способ  сложения? Решить систему  уравнений  способом  сложения

№2.           2х + 2у = 10

                 3х - 4у= 1  

4. В чем заключается  графический  способ   решения  системы  уравнений  с двумя  переменными? Решить графическим  способом систему уравнений:

№3.      у – 2х = 5

          4х + 2у = 6

 №4. Докажите, что данная  система уравнений  не имеет  решений:

     у = 3х - 2

     3х – у = 0  (на  доске) 

- На ваш взгляд, каким  способом легче  решаются системы?

- Но, решая графическим  способом, мы  наглядно можем  увидеть,  имеет ли  система  уравнений  решение  или нет. Поэтому этот  способ служит  геометрической  иллюстрацией  наличия  или  отсутствия   решения системы уравнений.

- А как еще   можно  выяснить, имеет система уравнений  решение  или нет?

Для чего нам нужны системы уравнений? Умение их решать?

Задача. Слайд 6.

Найдите два числа, если их разность равна 23, а сумма удвоенного большего из этих чисел и второго числа равна 22.

РЕШЕНИЕ: Пусть х-первое большее число, тогда у- второе число. Известно, что их разность равна 23. т.е. х-у=23. По условию задачи, сумма удвоенного большего из этих чисел и второго числа равна 22 т.е. Значит получим систему

х-у=23,

2х+у=22.

 Решаем любым удобным для вас способом.

Ответ: 15 и -8

 Ответы. Способ подстановки, способ сложения и графический способ.

(решают на доске)

(способом подстановки, способом сложения)

(выразить  из  каждого уравнения у  через х и сравнить угловые  коэффициенты). Для решения задач.

 Учащиеся решают самостоятельно.

Регулятивные:

- контроль, оценка, коррекция; Познавательные:

- общеучебные- умение структурировать знания,

- умение осознанно и произвольно строить речевое высказывание,

Коммуникативные:

- умение слушать;

- обосновывать свою точку зрения;

 Физкультминутка

6. Осуществление самостоятельной работы и самопроверки по эталонному образцу

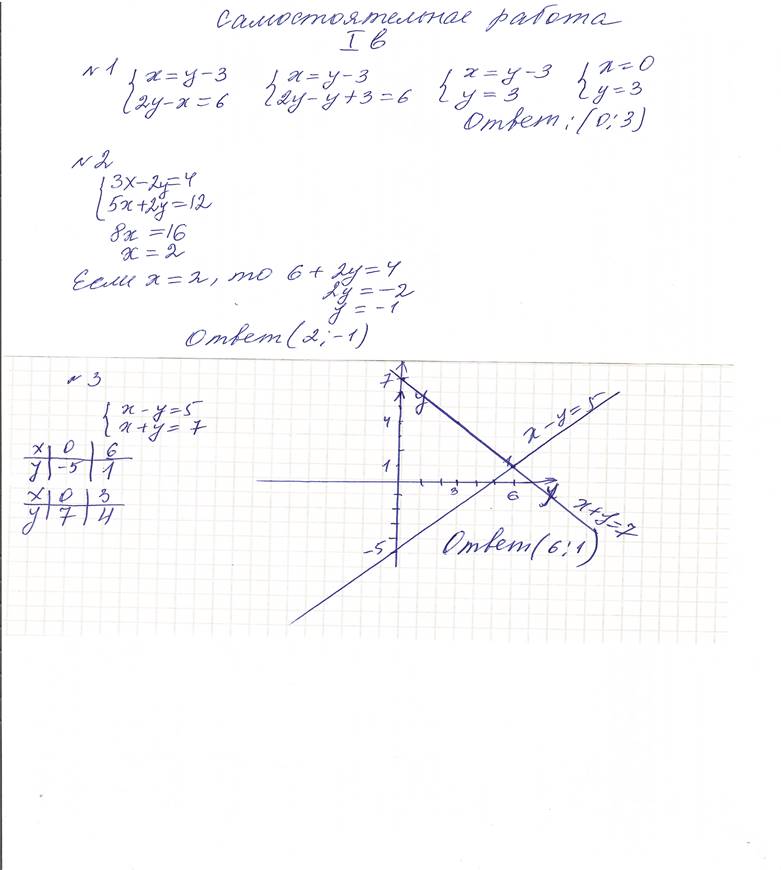
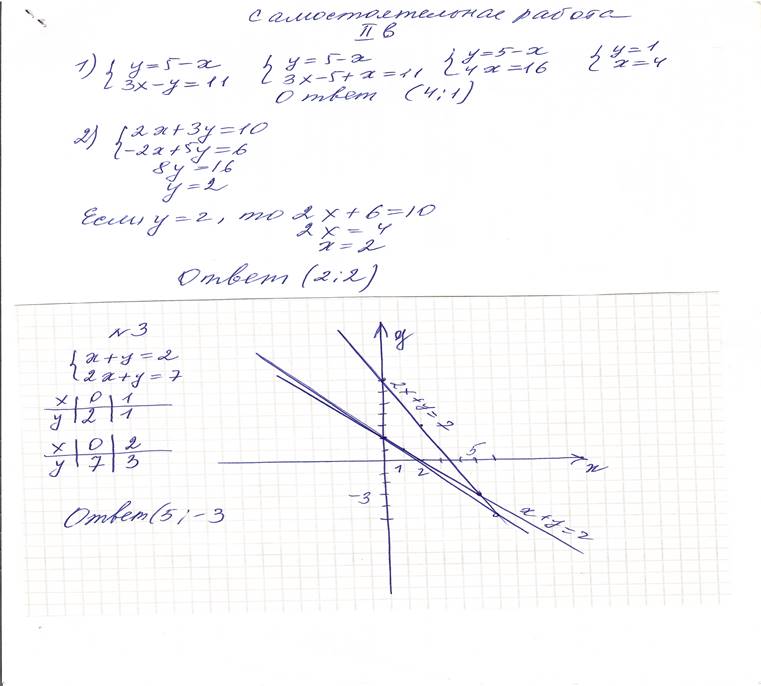
Приступим к самостоятельной работе. Убедимся, что все затруднения у нас ликвидированы. Самостоятельная работа

Вариант 1.

№1. Решить систему способом подстановки.

x = y - 3,

2у – х = 6

№2. Решить систему способом сложения.

 3x - 2y = 4,

5x + 2y = 12

№3. Решить систему графическим способом.

 x - y = 5,

 x + y = 7.

Вариант 2.

№1. Решить систему способом подстановки.

  y = 5 - х,

  3x – y = 11

№2. Решить систему способом сложения.

   2x + 3y = 10,

   -2x + 5y = 6

№3. Решить систему графическим способом.

  x + y = 2,

  2x + y = 7

На столах памятка по решению различными способами. Решают и выполняют самопроверку. Оценивают свою работу.

Личностные: самоопределение

Регулятивные:

-контроль, коррекция, оценка,осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества усвоения.

Познавательные:

-выполнение универсальных логических действий (сравнение, анализ, синтез);

-выстраивание логической цепи рассуждений;

-ориентация в своей системе знаний, сопоставление и отбор информации.

7. Включение в систему знаний и умений

Найдите решение системы уравнений

1) (х-3)²-4у=(х+2)(х+1)-6

     (х-4)(у+6)=( х+3)(у-7)+3

2)  (х-у)(х+у)-х(х+10)=у(5-у)+15

     (х+1)²+(у-1)²=(х+4)²+(у+2)²-12.

Мы можем сказать, что это система линейных уравнений? Попробуем упростить данные уравнения. Какие правила применим?

Формулы сокращенного умножения, умножение многочлена на одночлен и многочлен, приведем подобные слагаемые.

2 ученика работают у доски. Остальные на местах

Ученики выставляют оценки отвечающим. Комментируют их ответы

Личностные: самоопределение

Регулятивные:

-контроль, коррекция, оценка, осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества усвоения.

Познавательные:

-выполнение универсальных логических действий (сравнение, анализ, синтез);

-выстраивание логической цепи рассуждений;

-ориентация в своей системе знаний, сопоставление и отбор информации.

Домашнее задание

№ 1050 (4–6), 1052, № 1079 задача

Просматривают домашнее задание. Задают вопросы

Коммуникативные:

-  умение с достаточной полнотой и. точностью выражать свои мысли;

8. Осуществление рефлексии.

Закончите предложения.

Я сегодня узнал на уроке…

Мне запомнилось на уроке…

Я хочу узнать больше о…

Как вы думаете, мы в полной мере выполнили наказ Аристотеля? Кто может сказать: Я сегодня одержал маленькую победу над системой уравнений. Поставьте оценку себе.

Отвечают.

Коммуникативные:

-  умение с достаточной полнотой и. точностью выражать свои мысли;

Познавательные:

-  рефлексия;

Личностные:

-смыслообразование