
Методическая разработка занятия
по дисциплине «Математика»
по специальностям 060110 Лабораторная диагностика-51
и 060109 Сестринское дело-51(базовая подготовка)
из раздела «Функции их свойства и графики»,
по теме «Логарифмическая функция»
преподавателя математики первой категории
ГБПОУ ДЗМ «МК№1» г. Москвы
Захаровой Виктории Викторовны
Пояснительная записка
Внедрение Федерального государственного образовательного стандарта среднего профессионального образования и постоянное обновление его содержания, появление новых эффективных педагогических технологий и методов обучения диктует необходимость создания методического обеспечения каждого раздела, каждой темы, каждого занятия.
Данное методическое пособие представляет собой разработку занятия по дисциплине «Математика» по специальностям 060110 Лабораторная диагностика-51 и 060109 Сестринское дело-51(базовая подготовка) из раздела «Функции их свойства и графики», по теме «Логарифмическая функция» и предназначено для преподавателей математики медицинских колледжей. Может быть полезно другим преподавателям математики.
Основной целью создания данной методической разработки является оптимизация учебного процесса за счет обогащения современными методиками преподавания и улучшение качества подготовки обучающихся по вышеуказанным учебным специальностям в соответствии с требованиями Государственного образовательного стандарта.
Основная часть пособия состоит из 3 блоков: методического, информационного и блока контроля знаний и сформированных компетенций.
Методический блок – содержит методические рекомендации по проведению занятия и технологическую карту занятия.
Информационный блок – содержит теоретический материал к занятию и описание применяемых методов обучения.
Блок контроля знаний и сформированных компетенций –содержит все включенные в данную методическую разработку контролирующие материалы с подробными инструкциями для преподавателя и для студентов, эталонами ответов и критериями оценки.
В конце пособия приведен список использованной литературы и компьютерных презентаций. [5]
Содержание работы
1. Введение………………………………………………………………4
2. Основная часть
2.1. Методический блок.
2.1.1. Методические рекомендации по проведению занятия….5
2.1.2. Технологическая карта занятия…………………………...7
2.2. Информационный блок
2.2.1. Теоретический материал к занятию………………………13
2.2.2. Описание применяемых методов обучения……………....16
2.3. Блок контроля знаний и сформированных компетенций…...22
3. Заключение…………………………………………………………....24
4. Список литературы
5. Список компьютерных презентаций……………………………..…25
1. ВВЕДЕНИЕ
Новый образовательный стандарт среднего профессионального образования ставит перед преподавателями математики колледжей весьма сложную задачу: при минимуме времени, отводимом на изучение математики, сформировать у обучающихся множество компетенций, определенных стандартом. В данном методическом пособии я попробую на примере разработки занятия по теме «Логарифмическая функция» показать, как с помощью новых эффективных педагогических технологий и методов обучения можно справиться с поставленной задачей.
Согласно программе, в разделе «Функции, их свойства и графики» на изучение логарифмической функции отводится одно занятие (90 минут). За это время требуется повторить свойства логарифмов, проверить сформированность у обучающихся основных компетенций по этой теме, объяснить новый материал, закрепить его, проверить у обучающихся уровень усвоения нового материала и провести необходимую коррекцию. Стараясь сэкономить время, преподаватели готовят лекцию, где в сжатой форме излагают весь необходимый теоретический материал. Студентам при этом достается роль пассивных слушателей, а уровень эффективности усвоения учебного материала составляет, по мнению психологов, лишь 5% [2] . После лекции, решив на доске несколько заданий по новой теме, студентам дают самостоятельную работу, которая проверяется преподавателем в конце занятия, пока студенты списывают с доски записанное там домашнее задание.
Коррекция ошибок в основном сводится к сообщению правильных ответов.
Такой традиционный подход, как правило, дает очень низкий результат, не соответствуетствующий новым образовательным стандартам. [7]
Я предлагаю, не меняя традиционную структуру комбинированного занятия, использовать компьютерные технологии и эффективные методы обучения, что позволит повысить интерес обучающихся к изучаемому предмету, создаст условия для активности студентов, а значит более глубокому усвоению материала.
2. ОСНОВНАЯ ЧАСТЬ
2.1. Методический блок
Скажи мне, я забуду.
Покажи мне, и, может быть, я буду помнить.
Позволь мне сделать это, и это станет моим навсегда.
(Китайская пословица)
2.1.1. Методические рекомендации по проведению занятия.
Главный секрет успешности занятия - в применении интерактивных методов обучения, сущность которых состоит во взаимодействии и сотрудничестве всех обучающихся, включая педагога. Педагог должен выступать лишь в роли организатора процесса обучения, создателя условий для инициативы обучающихся. Важно не просто дать студентам готовый набор фактов, а опираясь на предыдущие знания, умения и навыки подвести их к открытию нового, ранее не изученного.
Даже объявление темы урока можно сделать интересным событием, если предложить учащимся разгадать ребус (рис. 1), а затем предложить студентам самостоятельно сформулировать цели и задачи занятия.

Рис.1. Название темы (электронное приложение №1)
На этапе актуализации знаний можно организовать устную работу по повторению основных понятий и способов задания функции, свойств функции и свойств логарифма. Причем повторению свойств функции и свойств логарифмов следует уделить особое внимание. При этом можно провести фронтальный опрос с фиксированием на доске основных свойств функции и небольшую самостоятельную работу на повторение свойств логарифма с последующей самопроверкой (электронное приложение №2).
Работу по изучению нового материала можно организовать в форме исследования логарифмических функций с разными основаниями (электронное приложение №3). При этом студенты самостоятельно должны сделать выводы по обобщению свойств логарифмической функции в зависимости от основания. Подводя итоги исследования, предложить учащимся ответить на вопросы, которые высвечиваются на экране. (электронное приложение №1). Для экономии времени к началу урока на столах уже должны лежать бланки ответов, которые учащиеся после заполнения сдают преподавателю. Пока преподаватель проверяет работы, один из учащихся делает сообщение о практическом применении логарифмов. (Приложение №1)
Закреплении материала рекомендуется провести традиционно разбором заданий с записью их на доске и в тетрадях студентов. При объяснении заданий важно, чтобы учащиеся четко представляли себе, что от них требуется.
Для контроля знаний и сформированных компетенций рекомендуется провести самостоятельную работу с последующей самопроверкой. При этом хорошо использовать листы, проложенные копировальной бумагой, с тем, чтобы первый лист сдать на проверку преподавателю, а копию оставить себе для последующей самопроверки. Такие листы и конверты с вариантами самостоятельной работы так же следует приготовить заранее и положить на середину стола перед занятием. Варианты самостоятельной работы должны быть разно уровневыми и содержать критерий выставления оценки.
Подводя итоги самостоятельной работы по каждому заданию преподавателю рекомендуется спросить у студентов: кто выполнил задание без ошибок, кто допустил ошибку, в чем состояла ошибка, у кого была такая же ошибка, у кого другая, довольны ли студенты своими результатами, какие были проблемы при выполнении работы. Как вариант, облегчающий подведение итогов самостоятельной работы: для самооценки студенты поднимают смайлики (зеленые - без ошибок, синие - 1 ошибка, желтые - 2 ошибки, красные - 3 ошибки и более).
При подведении итогов занятия важно вспомнить какие цели и задачи были поставлены в начале занятия, обсудить со студентами удалось ли решить поставленные задачи и достигнуть цели. Выявить причины возникших затруднений, наметить дальнейшие пути решения проблем.
Для закрепления полученных результатов предложить студентам задание на дом, указать имеющиеся электронные образовательные ресурсы по данной теме.
2.1.2. Технологическая карта занятия
1. Дисциплина (УД, ПМ, МДК): Математика
2. Курс 1 Семестр
3. Тема: Функции, их свойства и графики
4. Тема занятия: Логарифмическая функция, ее свойства и график
5. Вид занятия: урок
6. Тип урока: комбинированный
7. Место проведения занятия: учебная аудитория время проведения занятия: 2 часа (90 минут)
8. Мотивация темы: Актуализация знаний по предыдущему материалу по темам «Функции и их свойства», «Логарифм числа. Свойства логарифмов». Сообщение по теме «Практическое применение логарифмов».
9. ЦЕЛИ ЗАНЯТИЯ:
Общая цель: способствовать формированию общих и профессиональных компетенций будущего выпускника:
|
Код/шифр компетенции |
Содержание компетенции |
Пути формирования компетенции |
|
Общие компетенции |
||
|
ОК 2. |
Организовывать собственную деятельность, выбирать типовые методы и способы выполнения задач, оценивать их выполнение и качество. |
Выполнение аудиторной и внеаудиторной работы |
|
ОК 3. |
Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. |
Решение задач |
|
ОК 4. |
Осуществлять поиск и использование информации, необходимой для эффективного выполнения задач, профессионального и личностного развития. |
Выполнение внеаудиторной работы, работа с информацией на занятии |
|
ОК 6.
|
Работать
в коллективе и команде, эффективно общаться |
Обсуждение решения задач, |
|
ОК 8.
|
Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием |
Анализ выполненной работы. Выполнение домашнего задания |
|
ОК 12. |
Организовывать рабочее место с соблюдением требований охраны труда, производственной санитарии, инфекционной и противопожарной безопасности. |
Подготовка рабочего места в аудитории и дома, содержание его в чистоте и порядке |
|
Профессиональные компетенции |
||
|
ПК 2.1. СД |
Представлять информацию в понятном для пациента виде |
Развитие речи: подготовка устных ответов |
Конкретные цели (задачи):
Дидактические цели:
с целью формирования вышеуказанных компетенций обучающийся в итоге занятия должен знать:
- основные понятия и способы задания функции
- основные свойства функции
- иметь наглядное представление об основных свойствах логарифмической функции
с целью формирования вышеуказанных компетенций обучающийся в итоге занятия должен уметь:
- определять значение функции по значению аргумента при различных способах задания функции
- изображать график логарифмической функции
- описывать свойства логарифмической функции, опираясь на график
- использовать свойства функции для сравнения и оценки ее значений
- ясно, точно и грамотно выражать свои мысли в устной и письменной речи, использовать различные языки математики (словесный, символический) и свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства
Развивающие цели:
- способствовать развитию умений учащихся обобщать полученные знания, проводить анализ, синтез, сравнения, делать необходимые выводы
- содействовать развитию умений применять полученные знания в типовых условиях
- способствовать развитию абстрактного, логического, мышления
- обеспечить условия для овладения учащимися алгоритмом решения проблемных и исследовательских задач
Воспитательные цели:
-создание на уроке условий, обеспечивающих воспитание аккуратности и внимательности при выполнении работ с применением чертежных инструментов, способствование развитию творческого отношения к учебной деятельности, организация ситуаций, акцентирующих формирование сознательной дисциплины при работе, способствовать овладению необходимыми навыками самостоятельной учебной деятельности
10. Уровень освоения 1-2
11. Междисциплинарные и внутридисциплинарные связи.
Междисциплинарные связи(с указанием разделов, тем):
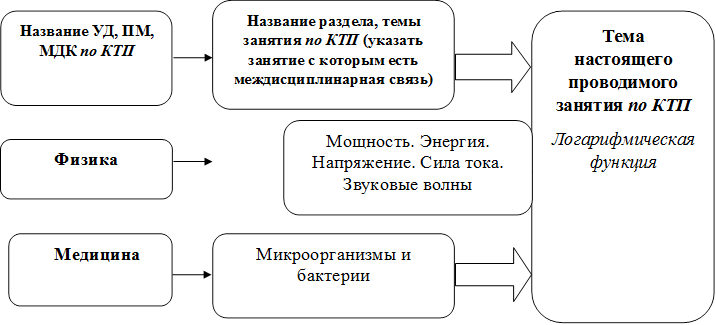
 Внутридисциплинарные
связи (с указанием разделов, тем):
Внутридисциплинарные
связи (с указанием разделов, тем):




12. Обеспечение занятия:
А. Методическое обеспечение:
Технологическая карта урока, демонстрационные материалы (компьютерные презентации)
Б. Материально- техническое обеспечение:
компьютер, медиапроектор, экран
В. Раздаточный материал:
карточки для проведения самостоятельной работы и бланки ответов, смайлики
13. Литература:
Основная:
Дополнительная литература
1. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П., Ивлев Б.М., Шварцбурд С.И. Алгебра и начала анализа: учебник для 10-11 классов общеобразоват. учреждений, М.: Просвещение, 2007 – 384 с.;
2. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика: учебное пособие: в 2 кн. Книга 1, М.: ООО «Издательство Новая Волна», 2004 – 656 с.;
3. Средняя математическая интернет-школа. [Электронный ресурс]. Режим доступа: http://www.bymath.net/
14. Ход занятия
|
№ п/п |
Этап занятия |
Время (мин) |
Дидактические задачи |
Деятельность преподавателя |
Деятельность студента |
|
1. |
Оргмомент |
5 |
Создание психологического настроя студентов на предстоящую работу Создание проблемной ситуации. Сообщение темы, цели и задач урока. |
Предлагает решить ребус, чтобы узнать тему занятия, исходя из темы определить цели и задачи занятия. |
Решают ребус, определяя тему. Ставят цели и задачи. Записывают тему и цели занятия в тетрадь |
|
2. |
Актуализация знаний |
10 |
Создание ситуации успеха путем проверки владения ранее изученным материалом. Мотивация студентов на изучение нового материала |
Актуализирует знания по предыдущему материалу по теме "Логарифм числа. Свойства логарифмов", используя задания устного счета |
Отвечают на вопросы преподавателя. Выполняют задания по теме «Свойства логарифмов с последующей самопроверкой» |
|
3. |
Изучение нового материала |
10 |
Получение новых знаний |
Объясняет новый материал, опираясь на знания студентов по теме свойства логарифма. используя демонстрационный материал. Подводит студентов к самостоятельному обобщению свойств логарифмической функции. |
Записывают определение логарифмической функции, отвечают на вопросы преподавателя при нахождении значений логарифмических функций. Делают выводы при обобщении свойств логарифмической функции. |
|
4. |
Первичная проверка усвоения нового материала |
5 |
Установление правильности и осознанности усвоения нового материала. |
Демонстрирует на экране и зачитывает вопросы по теме |
Заполняют бланк ответов и сдают его преподавателю |
|
5. |
Историческая справка |
5 |
Осознание практического применения изучаемого материала |
Проверяет работы студентов |
Знакомятся с презентацией творческой работы по теме « Применение логарифмов» одного из студентов
|
|
6. |
Закрепление материала |
25 |
Использование нового содержания совместно с ранее изученным при решении задач и выполнении упражнений |
Инструктирует студентов, наблюдает за их работой, корректирует ее. Задает вопросы по материалу. |
Выполняют построение графиков логарифмических функций, объясняют их свойства, решают графически уравнения и неравенства, отвечают на вопросы преподавателя. |
|
7. |
Самостоятельное творческое использование сформированных умений и навыков |
20 |
Установление правильности и осознанности усвоения нового материала. |
Организует самостоятельную работу студентов. Контролирует её выполнение. По окончании работы организует проверку. |
Выполняют задания самостоятельной работы по теме «Логарифмическая функция», под капирку. Сдав работу преподавателю, совместно проверяют ее выполнение по копии |
|
8. |
Подведение итогов занятия. |
5 |
Анализ и оценка успешности достижения цели. |
Предлагает студентам обобщить изученное на занятии, проанализировать допущенные ошибки, причины затруднений и успехов, оценить степень достижения целей. Оценивает работу группы, выставляет отметки за занятие и комментирует их |
Обобщают изученное на занятии, анализируют допущенные ошибки, оценивают индивидуальную степень достижения целей, причины возникших затруднений и достигнутых успехов. |
|
9. |
Информация о домашнем задании |
2-3 |
Обеспечение понимания содержания домашнего задания |
Предлагает дифференцированное домашнее задание |
Каждый студент выбирает себе по лепесточек с заданием в зависимости от уровня сложности.. |
|
10. |
Рефлексия |
2-3 |
|
Предлагает студентам оценить занятие с помощью смайликов |
Поднимают соответствующий смайлик |
|
Общее время занятия (мин.) |
90 |
|
|
|
|
14. Задание на дом: №№ 321(1,3); 322; 327(1,3,5), 325(1,3)
2.2 Информационный блок
2.2.1. Теоретический материал к занятию
Функции и их свойства.
Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y=f(x). (Читают: у равно f от х.) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х.
Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Способы задания функции:
1. аналитический способ (функция задается с помощью математической формулы;
2. табличный способ (функция задается с помощью таблицы)
3. описательный способ (функция задается словесным описанием)
4. графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
1. Нули функции Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
2. Промежутки знакопостоянства функции Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
3. Возрастание (убывание) функции. Функция у = f (x) называется возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е. для любых x1 и x2 из этого промежутка, таких, что x1> x2, справедливо неравенство f(x1)>f(x2).
Функция у = f (x) называется убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е. для любых x1 и x2 из этого промежутка таких, что x1 > x2 , справедливо неравенство f(x1) <f(x2).
4. Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Например, у = х2 - четная функция. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат. Например: у = х3 - нечетная функция. Функция общего вида не является четной или нечетной
(у = х 2+х).
Логарифм. Свойства логарифмов.
loga b - Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует только у положительных чисел).
logab = x означает что ax = b
· loga b - логарифм числа b по основанию a (a > 0, a ≠ 1, b > 0)
· lg b - десятичный логарифм (логарифм по основанию 10, a = 10).
· ln b - натуральный логарифм (логарифм по основанию e, a = e).
Для любых a;
a > 0; a ≠ 1 и для любых x; y > 0.
1. alogab = b - основное логарифмическое тождество
2. loga 1 = 0
3. loga a = 1
4. loga(x · y) = logax + logay
5. loga (x/y) = logax - logay
6. loga (1/х) = -logax
7. loga xp = p logax
8. logak x = 1/k ·loga x, при k ≠ 0
9. logax = logac xc
10. loga x = logb x/logb a - формула перехода к новому основанию
11. loga x = 1/logx a
Логарифмическая функция и ее свойства
Функцию, заданную формулой y = logаx, называют логарифмической функцией с основанием a. (a>0, a≠1)
1. Область определения логарифмической функции - множество всех положительных чисел.
D(f)=(0;+∞);
2. Множество значений логарифмической функции - множество R всех действительных чисел.
E(f)=(−∞;+∞);
3.Логарифмическая функция на всей области определения возрастает при a>1 или убывает при 0<a<1. (рис. 2а, 2б)
а) б)
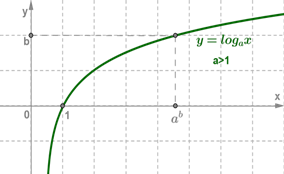
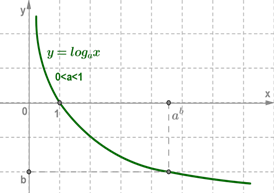
Рис. 2 Возрастание (убывание) логарифмической функции.
4. Логарифмическая функция:
-
не является ни четной, ни нечетной;
- не имеет ни наибольшего, ни наименьшего значений;
- не ограничена сверху, не ограничена
снизу;
График любой логарифмической функции y=logа x проходит через точку (1;0).
2.2.2. Описание применяемых методов обучения
Хороших методов существует столько,
сколько существует хороших учителей.
( Д. Пойя)
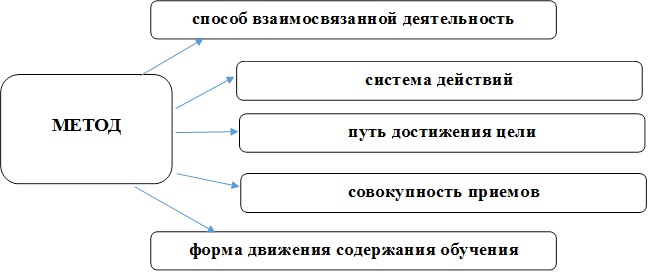 |
§ объяснительно-иллюстративные;
§ репродуктивные;
§ проблемные;
§ частично-поисковые;
§ исследовательские.
§ организационно-действенные (методы организации и осуществления учебно-познавательной деятельности);
§ стимулирования (методы влияния на мотивацию учебно-познавательной деятельности);
§ контрольно-оценочные (методы, определяющие эффективность учебно- познавательной деятельности).
§ подготовки к восприятию;
§ изучения нового материала;
§ закрепления изученного
§ контроля за усвоением;
§ организации повторения и т.п.
§ монологические;
§ диалогические.
§ коллективные;
§ групповые;
§ индивидуальные.
§ словесные;
§ наглядные;
§ практические.
§ изложения;
§ беседы;
§ самостоятельная работа
§ аналитический,
§ синтетический;
§ сравнительный;
§ обобщающий;
§ классификационный.
§ индуктивный;
§ дедуктивны
§ методы, направленные на организацию деятельности учащихся для получения знаний и формирование умений;
§ методы, направленные на организацию деятельности учащихся по применению знаний и развитию умений.
Классификация методов обучения математике по характеру
учебно–познавательной деятельности и организации содержания учебного материала (по Г.И. Саранцеву) [6]
· Эмпирические методы познания (наблюдение, опыт, измерение и др.);
· Логические методы познания (анализ, синтез, индукция, дедукция, сравнение, аналогия, абстрагирование, конкретизация, классификация и др.);
· Математические методы познания (метод математического моделирования, аксиоматический метод и др.).
Классификация в зависимости от роли
обучающегося в процессе обучения
· Пассивные,
· Активные
· Интерактивные.
На сегодняшний день актуальны два последних метода, которые я и применяю на своих занятиях
· Использование таких методов, которые адекватны возрасту учащихся и их опыту работы с интерактивными методами;
· Использование заданий для предварительной подготовки обучающихся: прочитать, продумать, выполнить самостоятельные подготовительные задания;
· Отбор для занятия таких интерактивных упражнений, которые давали бы обучающемуся «ключ» к освоению темы;
· При выполнении самих интерактивных упражнений выделение времени для обдумывания обучающимися задания, чтобы они восприняли его серьезно, а не механически или «понарошку» исполнили его;
· Учет темпа работы каждого учащегося и его способностей;
· Использование на одном занятии одного (максимум – двух) интерактивных метода, а не их калейдоскоп;
· Проведение неторопливого обсуждения по итогам выполнения интерактивного упражнения, в том числе актуализация ранее изученного материала; при возможности акцентирование внимания и на другом материале темы, прямо не затронутом в интерактивном упражнении;
· Проведение эскпресс-опросов, самостоятельных домашних работ по различным темам, которые не были затронуты интерактивными заданиями.
Рациональное применение методов обучения зависит от знаний об условиях эффективности их применения. Для этого необходимо ответить на 4 основных вопроса: При каком содержании материала рационально применять метод? При решении каких дидактических задач этот метод применяется наиболее успешно? При каких особенностях, учащихся рационально применять метод? Какие возможности должен иметь учитель для использования данного метода? [ ]
2.2. Блок контроля знаний и сформированных компетенций
Подведение итогов при исследовании логарифмической функции
Прочитайте утверждение. Если оно верно, вы в бланке ответов ставите знак «+», не верно – знак «–». За каждый правильный ответ вы получаете – 1 балл. Материал усвоен, если вы набрали более 14 баллов.
|
1. Логарифмическая функция у =
logax определена при любом х |
|
Бланк ответов по теме «Свойства логарифмической функции»
ФИО студента:_____________________________________________________
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правильные ответы:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
- |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
- |
Самостоятельная работа по теме
Логарифмическая функция, ее свойства и график
Вариант 1
А1. Постройте график функции ![]() . Используя график функции
решите неравенство log3
x ≤ 2.
. Используя график функции
решите неравенство log3
x ≤ 2.
А2. Найдите область определения функции: ![]() .
.
А3. Найдите нули функции ![]()
В1. Решите графически уравнение 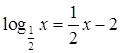 .
.
Ответы: А1. (-∞; 9]. А2. а) (2; ∞); б) (-∞; 3)U(3; ∞). А3. 1; 3. В1. 2.
Вариант 2
А1. Постройте график функции ![]() . Используя график функции
решите неравенство
. Используя график функции
решите неравенство ![]() ≤ 2.
≤ 2.
А2. Найдите область определения функции: ![]() .
.
А3. Найдите нули функции ![]()
В1. Решите графически уравнение ![]() .
.
Ответы: А1. [![]() ; ∞).
А2. а) (0; 1); б) (-∞; 4)U(4;
∞). А3. 2; 4. В1. 3.
; ∞).
А2. а) (0; 1); б) (-∞; 4)U(4;
∞). А3. 2; 4. В1. 3.
Критерий выставления оценок:
«5»- верно выполнено все 4 задания; «4» - верно выполнено 3 задания;
«3» - верно выполнено 2 задания; «2» - верно выполнено менее 2 заданий.
3. ЗАКЛЮЧЕНИЕ
Подводя итоги, посмотрим, как применение интерактивных методов на данном занятии сказалось на его результатах. Прежде всего надо отметить, что обучающиеся принимали активное участие на каждом этапе занятия, решая поставленные задачи и предлагая свои варианты ответа, мобилизуя все силы для совместной работы. Внутри группы сложилась благоприятная рабочая атмосфера, основанная на взаимном уважении и дружелюбии. Результаты самостоятельных работ показали, что применение интерактивных методов на данном занятии позволило поднять уровень усвоение материала до 75%.
Все выше изложенное свидетельствует о решении поставленных задач и формировании таких компетенций как:
ОК2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения задач, оценивать их эффективность и качество;
ОК3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность;
ОК4. Осуществлять поиск и использование информации, необходимой для личностного развития;
ОК5. Использовать информационно-коммуникационные;
ОК6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями;
ОК7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
Следовательно, можно сделать общий вывод: применение на занятиях интерактивных методов в полной мере реализует обучающие, развивающие и воспитательные цели образовательного процесса; является интересным и необходимым элементом математического воспитания. Это значит, что интерактивное обучение обладает большими потенциальными возможностями для выполнения социального заказа современного общества.
4. СПИСОК ЛИТЕРАТУРЫ
1. Бабанский Ю. К. Методы обучения в современной общеобразовательной школе. - М.: Просвещение, 1985.
2. Блинова Т.Л. Современные аспекты методики обучения математике: учебное пособие / Т.Л. Блинова, Э.А. Власова, И.Н. Семенова, А.В. Слепухин. – ГОУ ВПО «Урал. гос. пед. ун-т». – Екатеринбург, 2007.
3. Малый академический словарь. — М.: Институт русского языка Академии наук СССР/ под ред. Евгеньева А. П. , 1984.
4. Манвелов С. Г. «Конструирование современного урока математики» Москва «Просвещение», 2005.
5. Рябчикова А.М. Методические рекомендации для преподавателей по созданию методической разработки занятия.- М. ГБПОУ ДЗМ «МК №1», 2015.
6. Саранцев, Г.И. Методика обучения математике в средней школе: Учеб. пособие для студентов мат. спец. пед. вузов и ин-тов / Г.И. Саранцев.– М.: Просвещение, 2002.
7. Семенова И.Н., Слепухин А.В. Модернизация школьного российского образования: проблемы и пути реализации в процессе обучения математике: Сборник публицистических, научных статей и методических материалов практико-ориентированного характера. – Екатеринбург, 2007.
8. Суворова Н. «Интерактивное обучение: Новые подходы» / Н. Суворова. М., 2005
5. СПИСОК КОМПЬЮТЕРНЫХ ПРЕЗЕНТАЦИЙ
1. Презентация к уроку.
2. Устный счет по свойствам логарифма
3. Демонстрационный материал по теме «Логарифмическая функция и ее свойства»
4. Презентация на тему «Применение логарифмов»
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.