
Тема: Дифференциация в обучении математике.
Л.И. Семыкина
Учитель математики
Гимназия №20 им.Титова
Г. Шымкент
«Мне мудрость не чужда была земная,
Разгадки тайн ища, не ведал сна я.
За семьдесят перевалило мне,
Что ж я узнал! –
Что ничего не знаю».
Выдающийся арабский поэт математик
Омар Хайям.
Важнейшей особенностью современного этапа развития школы является дифференциация в обучении. Дифференциацию обучения можно истолковывать как направленность всего учебно-воспитательного процесса на личность учащегося, т.е. максимальный учет интересов, склонностей, способностей и возможностей ребенка. Учитель, составляя планы, придумывая содержание учебного материала и ход урока, должен заботиться о комфортном психологическом состоянии учащихся. Это означает, что дети не должны работать в чрезмерно сложных условиях, испытывать беспомощность, ущемленность, разочарование от непонимания и неумения выполнить требование учителя.
Дифференциация математического образования означает, что в обучении математике акцент ставится на общее развитие учащегося, а именно развитие логического мышления, математической речи, пространственного воображения, интуиции и т.п.
Важнейшими чертами дифференциации в обучении является ориентация на активное освоение учеником способов познавательной деятельности, личностную значимость образования, а также ориентация обучения на личность ученика, обеспечение возможности его самораскрытия, самореализации.
Проблема дифференцированного подхода к учащимся исследуется давно, в педагогике и методике, ей всегда уделялось значительное внимание. Однако в выдвижении и развитии в последние годы новых концептуальных идей, в частности идей планирования обязательных результатов обучение математике, приводит к постепенной перестройке всей методической системы, в том числе позволяет по- новому взглянуть на проблему дифференцированного обучения.
На мой взгляд, качество знаний среди некоторой группы учащихся не повышается, количество успевающих на «4» и «5» даже сокращается, несмотря на проведение консультаций, дополнительных занятий, работу с тетрадями. Возникает вопрос: «В чем же причина? Почему те же усилия дали давать меньший эффект?»
На мой взгляд, дело в том, что теряется интерес к знаниям, потребность в них. Это связанно, я думаю, с резким изменением условия жизни, происходящими в последние годы. Если раньше полученное в школе образование помогало чувствовать себя социально защищенным, то теперь этого нет. Зачастую те, кто учился слабо, преуспевают гораздо больше тех, кто добросовестно и упорно грыз гранит науки. Если полученные в школе знания не помогают адаптироваться в современных условиях жизни, нужны ли они? Стоит ли прикладывать столько усилий для овладения ими? Вот и падает интерес к знаниям.
Некоторая сумма знаний, умений, навыков должна быть освоена учеником в любом случае. Может быть, надо учить применять и использовать полученные знания?
В школе считается «успешным» ученик, который внимательно слушает учителя, выполняет его указания, «неуспешный» ученик ловчит, приспосабливается, чтобы тем или иным способом получить вожделенную «тройку». Оказывается, что в современном быстроменяющимся мире, где никто не может указать, что и как надо делать, в лучшем положении оказались те, кто в школе, помимо воли учителя, научился приспосабливаться к внешним обстоятельствам. Значит, менять надо не содержание материала, а способы овладения им и его применения. Но овладение способами действия возможны только в деятельности, т.е. когда ученик становится субъектом в учебном процессе. Возникает следующий вопрос: «А как сделать его субъектом? Можно ли добиться результата, применяя традиционные методы обучения? Если нет, то какие новые подходы надо использовать?»
Функция учителя состоит не только в том, что правильно, грамотно, интересно, понятно изложить материал, а в том, как организовать работу для получения новых знаний в процессе деятельности самих учащихся. Одна из трудностей заключается в придумывании такой ситуации, при которой перед учащимися возникает проблема, для решения которой, имеющегося запаса знаний не хватило и было необходимо искать новые подходы, тем самым расширяя и пополняя их объем.
Учитель здесь выступает не только как носитель, но и как организатор совместной деятельности. Моя задача как учителя, при конструировании учебного материала, состояла из следующих шагов:
1. выявление обязательных знаний, умений, навыков;
2. вычленение ключевых понятий, несущих основную смысловую нагрузку по данной теме;
3. составление опорных схем, конспектов по всей теме;
4. составление заданий, блока вопросов (разрабатывались задания трех уровневой сложности);
5. продумывается форма организации урока.
Я старалась разбирать новые упражнения и задания для учащихся, выполнение которых направлено на реализацию вышеизложенных идей. Новизна упражнений заключается в использовании нематематической информации, в разнообразии форм подачи условия (таблицы, схемы). Еще одной особенностью предлагаемых заданий являлось то, что они содержат вопросы, направленные на развитие логического мышления математической речи, умение объяснить «что, почему, как».
В преподавании очень важно добиваться от учащихся сознательного и обоснованного решения задач, побуждать школьников опираться в решении на изучаемые определения, теоремы, законы, чтобы приобретенные ими знания неразрывно связывались с практическими навыками. Понимая важность этой проблемы, многие учителя требуют от вызываемых к доске учащихся, чтобы они обосновывали решаемые задачи, а остальные слушали их. Но это требование чисто внешне, оно далеко не всегда соответствует внутренним процессам, протекающим в сознании учащихся. Поэтому многие ребята не вникают в суть обоснований, не прислушиваются к ним и решают задачи механически, несознательно. В своей работе я старалась выявить методические подходы, побуждающие учащихся к обоснованию решаемых задач.
Так, например, при изучении действий над действительными числами предлагалась такая группа заданий:
Решите уравнения, каждому корню уравнения соответствует слово из пословицы, расшифруй пословицу и объясни ее смысл
а)![]()
![]() отвори – 41
отвори – 41
б) ![]()
![]() себя – 3,21
себя – 3,21
в) ![]()
![]() вставай – 77,26
вставай – 77,26
г) ![]()
![]() не – 0,8
не – 0,8
д) ![]()
![]() кто – 5,95
кто – 5,95
е) ![]()
![]() смотрит – 7,432
смотрит – 7,432
ключ других – 3,11
|
3,21 |
14,76 |
5,95 |
3,11 |
0,8 |
7,726 |
|
себя |
губит |
кто |
других |
не |
любит |
любит – 7,726
губит – 14,76
плохих – 9,14
Очень часто в работе я применяла блок-схемы, решив которые и найдя правильные ответы мы находили много интересной информации , например при изучении действий над обыкновенными дробями использовалась следующая схема :
|
А |
|
|
|
|
|
|
|
а |
б |
в |
г |
д |
е |


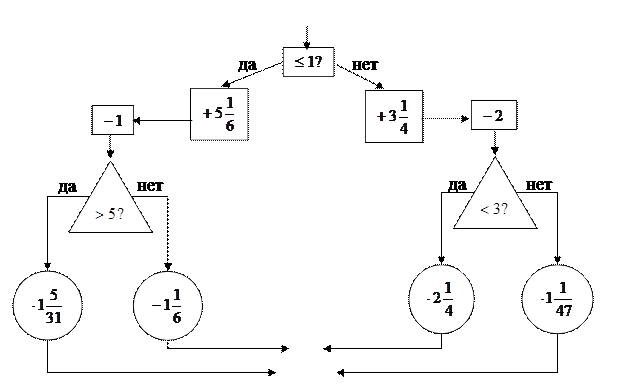
|
магний |
натрий |
олень |
литий |
портрет |
титан |
пародия |
сайгак |
|
4 |
|
1 |
6 |
|
|
|
|
|
Х |
|||||||
а) металл, который горит (магний)
б) металл, который плавает в воде как пробка (литий)
в) самый прочный металл (титан)
г) мягкий металл, который можно сплющить пальцами (натрий)
д) быстроногие антилопы, живущие в южных степях (сайгак)
е) литературный термин (объясни его)
ключ
|
А |
|
|
|
|
|
|
|
Х |
4 |
6 |
|
|
|
|
|
|
магний |
литий |
титан |
натрий |
сайгак |
пародия |
Чтобы у школьника была должным образом сформирована учебная деятельность, необходимо в каждый этап работы включать самооценку. Ученик должен уметь реально оценивать свои силы, видеть, что в теме он пока еще не смог усвоить, над чем ему нужно работать. Очень полезна в этом отношении игра «Тяжеловесы», она является необычным конкурсом по решению задач различных трудностей. Делался планшет с кармашками. В каждый кармашек кладется набор карточек – заданий одинаковой трудности, в разные – различной трудности. Сложность задач оценивается в килограммах, поэтому на каждом кармашке пишется «вес содержащих задач». Эта игра ясно показывает учащимся с какими заданиями из пройденной темы они справляются легко, а какие им оказываются еще не по силам. В процессе обучения я использовала такие методы и формы, которые делают урок богаче, разнообразнее. Все это оказывает эмоциональное воздействие на учащихся, способствует лучшему запоминанию материала, повышает их интерес к предмету, обеспечивает прочность знаний. Часто в классе я использовала работу по группам, где ученики не только воспроизводят некоторый объем знаний, а получают знания самостоятельно, при этом у них вырабатываются способы деятельности, позволяющие получать результаты.
Сущность дифференциации состоит в поиске приемов и способов обучения, которые индивидуальными путями ведут всех школьников к одинаковому овладению программой. Уравнивая, дифференциация основывается на явном выделении уровня обязательной подготовки и формировании на этой основе повышенных умений овладения материалом. Сообразуясь с ними и учитывая свои способности, интересы, потребности, ученик получает право, и возможность выбирать объем и глубину усвоения учебного материала. Проработка материала на уровнях воспроизведения, элементарных умений и навыков и переноса знаний производятся по всем темам. Неоднократное возвращение к содержанию по «нарастающей» - от простого к сложному, от репродуктивных заданий к творческому поиску, дает возможность каждому ученику усвоить учебный материал на уровне «понимания» до уровня «переноса заданий».
При оценке результатов учебного труда учащихся я использовала принципы «сладкого лимона» (повышения ценности совершенного учеником действия) и «зеленого винограда» (обесценивание его отрицательного аспекта). Отрицательные оценки, нужны в определенных случаях, являются все же при частом их применении, основой для скрытого или явного конфликта между учителем и учеником. Конфликт же вреден для учения. Чтобы избежать явного конфликта, психологи предлагают способ, называемый изживанием – это игнорирование нежелательного поведения ученика, отсутствие негативного подкрепления в случае его ошибочных ответных реакций.
В психологии установлен интересный факт: если учитель ожидает, что ученики достигнут определенного уровня, успехов и будут вести себя определенным образом, то это, вероятно, всего, так и происходит.
В заключении отметим, что изученное знает хорошо тот, кто может его объяснить другим. Древние говорили так: ученик может превзойти своего учителя, если он много спрашивает, спрашиваемое усваивает и усвоенное передает другим. Великий Конфуций говорил: три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький.
Используемая литература:
1. Учебно – методическая газета «МАТЕМАТИКА». (издательский дом первое сентября).
2. Научно – методический журнал «Математика и физика в школах Казахстана».
3. От игры к знаниям. Е.М. Минскин (пособие для учителя, Москва «Просвещение» 1987г.
Резюме:
В своей статье я рассмотрела проблемы дифференцированного обучения учащихся и в поиске приемов и способов ее реализации.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.