Методические приёмы решения задач в начальной школе

Методические приемы обучения младших школьников решению задач на движение.

 Текстовые задачи в начальной школе принято условно делить на простые и составные. Простая задача характеризуется тем, что для ответа на поставленный вопрос нужно выполнить одно арифметическое действие, а для ответа на вопрос составной задачи нужно выполнить два и более арифметических действий. Таким образом, решение любой арифметической задачи связано с выбором арифметических действий, в результате выполнения которых ученики могут дать ответ на поставленный вопрос. Математической основой выбора арифметических действий для решения задач являются определения сложения, вычитания, умножения и деления в количественной теории.

Обоснование выбора действий для решения простых задач позволяет сформулировать методическое положение, которое лежит в основе процесса обучения решению простых задач в начальных классах, а именно: решение простых задач тесно связано с осознанием школьниками смысла арифметических действий. Выделяют несколько методических подходов:

1)                          формирование у учащихся того или иного механизма решения простых задач есть одновременно и формирование у них той или иной трактовки арифметических действий.

Представляя определенную познавательную ценность, такой подход имеет один существенный недостаток: решая простые задачи на уровне предметных действий, ученик не осознает, что он производит то или иное арифметическое действие. Кроме того, задача выступает для него как определенное упражнение, суть которого сводится сначала к выполнению предметных действий, а затем к записи их в виде операций с числами. Детям трудно осознать выбор арифметических действий. Многое зависит от количества тренировочных упражнений, выполняемых учащимися, но при этом операция выбора арифметического действия довольно долгое время не осознается или выполняется формально.

2)                          другой подход, реализующий положение о тесной взаимосвязи решения простых задач и смысла арифметических действий заключается в том, что смысл арифметических действий осознается школьниками до решения простых задач.

Задачи на движение выделяются среди других типов задач по сюжету. По структуре они бывают самыми разнообразными: простыми, составными, задачами с пропорциональными величинами и т.д.

Задачи на движение можно разделить на виды по разным основаниям:

1. В зависимости от того, во сколько действий задача, она может быть простой и составной. Простая задача: «Турист прошел в первый день 8 км, а во второй 10 км. Какое расстояние турист прошел за два дня?» Составная задача: «Турист в первый день прошел 8 км, а во второй на 2 км больше, чем в первый день. Какое расстояние турист прошел за два дня?»

2. В зависимости от того, сколько тел движутся, задачи могут быть на движение одного тела или на движение двух тел. Так, в предыдущем пункте приведены примеры задач на движение одного тела. Пример задачи на движение двух тел: «Из города и деревни навстречу друг другу выехали два автомобиля. Первый автомобиль проехал до встречи 25 км, а второй - на 7 км больше, чем первый автомобиль. Найдите расстояние от города до деревни».

3. В зависимости от того, сколько мерок разного рода используется для измерения расстояния, задачи могут быть только с одной величиной - расстоянием (измеряется только в метрах, километрах или других однородных мерках) или с тремя величинами - скоростью, временем, расстоянием (расстояние измеряется двумя мерками разного рода: мерами длины и мерами времени).

С задачами на движение учащиеся начальных классов знакомятся уже в 3 классе (по традиционной программе 1-4). Подготовительная работа к решению задач, связанных с движением предусматривает обобщение представлений детей о движении, знакомство с новой величиной – скорость, раскрытие связей между величинами: скорость, время, расстояние. Учащиеся учатся составлять чертеж к задачам после предварительного анализа ее текста. Расстояние принято обозначать отрезком, место отправления, встречи, прибытия обозначают по выбору точками, буквами, флажком, черточками и т.д., направление движения указывают стрелками. Например,

                _____________________________

  А                                                       В

Важным результатом ознакомления учащихся 3 класса с задачами на движение является усвоение простейших формул, связывающих такие величины, как скорость, время и расстояние ( V, t, S ).

Рассмотрим основные пути усвоения зависимости между этими величинами, характеризующими равномерное движение.

На рассмотрение связи между скоростью, временем и расстоянием выделяется 4-5 уроков в начале изучения умножения и деления многозначных чисел. Полученные сведения систематически используются в дальнейшем при решении задач на движение в течение всего учебного года.

В результате рассмотрения этих вопросов ученик должен получить представление о новой величине – скорости, которая характеризуется расстоянием, проходимым в единицу времени. Подчеркивается, что речь идет о таком движении, при котором скорость не изменяется.  Раскрывается связь между скоростью, расстоянием и временем (при равномерном движении) в виде формулы  V= S : t, где   S – пройденное расстояние,  V – скорость движения,  t – затраченное время. Дети учатся решать задачи, в которых по времени и скорости находится путь; по времени и пути находится скорость; по скорости и пути находится время.

В ходе решения этих задач у учащихся формируются представления о некоторых средних скоростях (пешехода, велосипедиста, автомобиля, теплохода, самолета), представления о встречном движении и о движении в одном и том же направлении. На этой основе дети должны уметь решать простые и несложные составные задачи.

На первом из уроков необходимо, опираясь на жизненный опыт и наблюдения учащихся обратить внимание детей на то, что некоторые предметы могут двигаться быстрее и медленнее. Например, велосипедист может обогнать пешехода, автомобиль – велосипедиста, самолет – автомобиль и т.д. Предметы могут двигаться равномерно. Так, например, пешеход может проходить за каждый час по 3 км; автомобиль может проезжать за каждый час по 100 км; бегун может пробегать за каждую секунду по 8 м и т.д. В этом случае говорят, что скорость (соответственно) пешехода – 3 км в час (записывают 3км/ч), автомобиля 100 км/ч, бегуна – 8 м/с.

Таким образом, скорость движения – это расстояние, которое проходит движущийся предмет за единицу времени. Затем рассматриваются простые задачи, на основании которых делается вывод, что для того, чтобы найти скорость движения предмета, нужно расстояние, которое прошел предмет, разделить на затраченное для этого время. Коротко этот вывод можно сформулировать так: скорость равна расстоянию, деленному на время. Если скорость обозначить буквой V, путь S, а время буквой t, то можно  записать этот вывод в виде формулы: V= S : t.

На последующих уроках с помощью соответствующих простых задач устанавливается, что расстояние равно скорости, умноженной на время:        S =V*t.

Например, в задаче «Пассажир проехал в автобусе 90 км. Скорость автобуса 45 км/ч. Сколько времени ехал пассажир?» устанавливается, что время равно расстоянию, деленному на скорость. Можно обратить внимание учащихся на связь между этими тремя формулами (например, последняя формула может быть выведена из первой: t = S : V),  на основе правила нахождения неизвестного делителя V, когда известно частное t  и делимое S.

  Основной методический аппарат, с помощью которого происходит ознакомление учащихся со взаимосвязью между величинами, представляет собой подбор задач и примеров, которые их раскрывают. Для определения соответствующей методики следует также иметь в виду указания, что «первоначальное ознакомление детей с разного рода зависимостями очень важно для установления причинной связи между явлениями окружающей действительности и имеет большое значение для подведения детей к идее функциональной зависимости». Заметим, что в этом случае речь идет о зависимости между двумя (а не тремя) величинами, например, между путем, пройденным телом, и временем, затраченным на прохождение этого пути (здесь скорость – величина постоянная). В этом случае мы имеем дело с тремя множествами: 1) множество значений такой величины, как время движения; 2) множеством значений длины (пути, пройденного за различные промежутки времени) и 3) множеством пар, в которых на первом месте стоит значение времени, а на втором соответствующее одно значение пути. В таком случае, действительно, формируются определенные функциональные представления.

Большую роль в развитии учащихся играет прием обобщения. Формированию у младших школьников умения пользоваться этим приемом способствует решение задач на одновременное движение двух тел. В традиционной программе рассматриваются задачи на встречное движение и задачи на движение в противоположных направлениях. По сути, это задачи одного вида - на движение двух тел в противоположных направлениях. Задача второго вида в реальной жизни является как бы продолжением задачи первого вида. Если между двумя телами есть какое-то расстояние, то они, двигаясь навстречу друг другу, перемешаются в противоположных направлениях - сначала сближаются, а после встречи удаляются.

Используя формулы: Sсбл./уд. = S1 + S2, Vсбл./уд. = V1 + V2, tсбл./уд.=t1=t2=t, S = V • t - школьники легко находят разные арифметические способы решения задач данного вида. Особое внимание следует обращать при этом на то, что данные рассуждения справедливы с момента начала одновременного движения двух тел.

Аналогичный подход можно применить к решению задач на одновременное движение двух тел в одном направлении. Такие задачи рассматриваются в начальной школе по альтернативным программам, а по традиционной программе они встречаются в V классе. К сожалению, часто приходится наблюдать, что при решении этих задач арифметическим способом трудности испытывают не только учащиеся, но и учителя.

Таким образом, в начальной школе рассматриваются следующие виды задач на движение: задачи на встречное движение и движение в противоположных направлениях. Каждая из этих задач имеет 3 вида в зависимости от данных и искомого:

1. в задаче даны скорость каждого из тел и время движения, необходимо найти пройденный путь;

2. в задаче даны скорость каждого из тел и пройденный путь, искомое – время движения;

3. в задаче даны пройденный путь, время движения и скорость одного из тел, искомое – скорость другого тела.

Оба вида задач на движение – в одном и противоположных направлениях – целесообразно решать одновременно, начиная с простейших задач.

  В условии одной задачи даются два направления движения: над чертой записывается одно направление, а под чертой – другое, тем самым разбивая задачу на две задачи. Например, расстояние между точками A и B 140 м.

                   навстречу друг другу                                                                                                                                              

 Из A в B  в разные стороны             едут велосипедисты со скоростями 8м/сек и             6 м/сек         съезжаются

                               разъезжаются  .

Можно обсудить следующие вопросы и вывести общий способ решения:

- на сколько метров они сближаются/удаляются за 1 сек? (4 + 3 = 7 (м)- но в первом случае велосипедисты сближаются за 1 сек на 7 м, а во втором удаляются на 7 м)

- какое расстояние будет между ними через 1 сек? (140 – 7 = 133(м)-расстояние уменьшается, 140 + 7 = 147(м)-расстояние увеличивается) через 3 сек?(за 3 сек в первом случае расстояние уменьшается на 7 * 3 = 21(м), а во втором на столько же метров увеличится) через 10 сек? (формулы расстояний будут такие: 140 – 7*10, 140 + 7*10) через x сек? (в общем виде расстояния через x сек будут представлены выражениями: 140 + 7x, 140 - 7x).

Рассмотрим еще один пример решения задач на встречное движение и движение в противоположных направлениях:

«Два велосипедиста выехали одно­временно навстречу друг другу из двух поселков и встретились через 2 ч. Ско­рость одного из них 11 км/ч, а другого 13 км/ч. Найти расстояние между поселка­ми». После чтения задачи выполняется под руководством учителя чертеж:

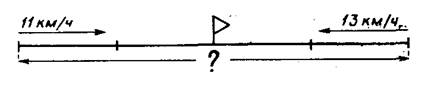Для разбора решения этой задачи другим способом можно проиллюстрировать движе­ние, вызвав к чертежу двух учеников. Учи­тель ведет объяснение: «Вы будете велоси­педистами. Покажите указкой, откуда вы на­чали движение. Вы начали двигаться одно­временно и ехали 1 ч. Сколько километ­ров проехал за это время каждый из вас? (11 км и 13 км.) Подпишем 11 км и 13 км на чертеже. На сколько километров вы сблизились за 1 ч? (На 24 км.) прошел еще 1 ч. На сколько километров вы еще сбли­зились? (На 24 км.) Встретились ли вело­сипедисты? (Да.) Составьте план решения. (Сначала узнаем, на сколько километров сближались велосипедисты в час, выпол­нив сложение; затем найдем расстояние меж­ду поселками, выполнив умножение.)» Эти два способа решения надо сравнить и. оце­нить, какой из них рациональнее.

Задачи, обратные данной, ученики могут составить сами по преобразованным чер­тежам, которые выполняет учитель. Снача­ла искомым становится время движения до встречи, а затем

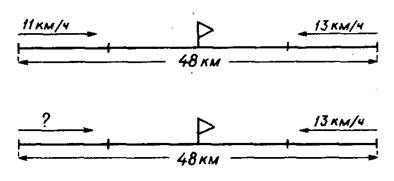План решения той и другой задачи уче­ники могут составить сами. Решение лучше записать отдельными действиями. Затрудне­ние обычно вызывает один из способов решения последней задачи (48:2=24, 24-13= 11). В этом случае, обращаясь к иллю­страции, надо показать, что в каждый час велосипедисты сближались на одинаковое расстояние, поэтому легко узнать, на сколько километров они сближались в час, выпол­нив деление (48:2=24), зная это и скорость одного из них, можно найти скорость дру­гого (24—13=11).

На другом уроке решаются задачи на движение навстречу и вдогонку. Условия обеих задач целесообразно написать вместе.

В целях подготовки к введению задач на встречное движение очень важно сформировать правильные представления об одновременном движении двух тел. Дети должны хорошо уяснить, что если два тела вышли одновременно навстречу друг другу, то до встречи они будут находиться в пути одинаковое время и при этом пройдут все расстояние между пунктами, из которых они вышли. Можно предложить учащимся следующие задачи:

1) Из двух городов отплыли навстречу друг другу два теплохода и встретились через 3 часа. Сколько времени был в пути каждый теплоход?

2) Из деревни вышел в город пешеход и в это время из города навстречу ему выехал велосипедист, который встретил пешехода через 40 минут. Сколько времени был в пути до встречи пешеход?

После этого можно ознакомить детей с решением задач на встречное движение, причем целесообразно на одном уроке ввести все 3 вида, получая новые путем преобразования данной в обратные. Н.Г.Чеботарев говорил, что «для того чтобы каждая задача могла считаться вполне решенной, необходимо решить или, по крайней мере, точно формулировать сущность задачи, ей обратной».  [50;46]

Такой прием позволяет детям самостоятельно найти решение, поскольку задача нового вида будет получена из задачи, уже решенной детьми.

  Рассмотрим особенности решения основных видов задач на движение:

1. Задачи на встречное движение двух тел.

Пусть движение первого тела характеризуется величинами s1, v1, t1; движение второго - s2, v2 ,t2. Такое движение можно представить на схематическом чертеже:

                     v1                                                                        v2

                __ t1_____________________ t2___

  А                                                       В

                                           s

Если два тела начинают движение одновременно навстречу друг другу, то каждое из них с момента выхода и до встречи затрачивает одинаковое время, т.е. t = t1 = tвстр. Расстояние, на которое сближаются движущиеся объекты за единицу времени, называется скоростью сближения, т.е. vсбл  = v1 + v2. Все расстояние, пройденное движущимися телами при встречном движении, может быть подсчитано по формуле: s = vсбл. * tсбл. Например, «Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного их них 5 км/ч, а другого 4 км/ч. Через сколько часов они встретились?» Поиск плана решения удобно вести, рассуждая от данных к вопросу. Так как скорости пешеходов известны, можно найти их скорость сближения. Зная скорость сближения пешеходов и все расстояние, которое им надо пройти, можем найти время, через которое пешеходы встретятся.

2. Задачи на движение двух тел в одном направлении.

Среди них следует различать два типа задач:

1)                                                                                                                движение начинается одновременно из разных пунктов;

2)                                                                                                                движение начинается в разное время из одного пункта.

Рассмотрим случай, когда движение двух тел начинается одновременно в одном направлении из разных пунктов, лежащих на одной прямой.

Пусть движение первого тела характеризуется величинами s1, v1, t1; движение второго - s2, v2 ,t2. Такое движение можно представить на схематическом чертеже:

                 v1                   v2

                t1                                    t2

           А      s                                                       s2

                         s1

Если при движении в одном направлении первое тело догоняет второе, то v1 >  v2. Кроме того, за единицу времени первый объект приближается к другому на расстояние v1 – v2. Это расстояние называют скоростью сближения: vсбл  = v1  -  v2. Расстояние s, представляющее длину отрезка АВ, находят по формулам: s = s1 – s2 и s = vсбл *  tвстр.

Например, Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном направлении два мотоциклиста. Скорость одного- 40 км/ч, другого – 50 км/ч. Через сколько часов второй мотоциклист догонит первого?

Текстовые задачи на движение в одном направлении (движение вдогонку) включены в программы и учебники развивающего обучения. Однако решение задач такого типа вызывает большие затруднения в практике обучения. Рассмотрим пример, «Собака погналась за лисицей, которая была от нее на расстоянии 30 м. Скачок собаки 2м, скачок лисицы 1 м. В то время как лисица делает 3 скачка, собака делает только 2 скачка. Догонит ли собака лисицу? Сколько скачков она должна сделать? Какое расстояние пробежит собака?»

При решении данной задачи большинство учащихся испытывает затруднения, которые обусловлены тем, что в ней не определен промежуток времени, за который собака делает два скачка (4м), а лисица 3 скачка (3м). Учащимся трудно осознать, что 3м и 4м – это скорости лисицы и собаки. Совместно составляется чертеж к задаче:

                 4 м                 3 м

                               30 м                                                                                                              

                                    х

Затем учитель подводит учащихся к составлению уравнения, рассуждая так: «Обозначим за х – число промежутков времени, за которое собака догонит лисицу. Собака делает за один промежуток времени 2 скачка, а каждый скачок равен 2 м, т.е. собака за некоторый промежуток времени пробегает 4 м – это скорость движения собаки. За такой же промежуток времени лиса пробегает 3 м – это скорость лисицы. Время одинаковое, поэтому 4х – расстояние, которое пробегает собака, а лисица за это время пробегает 3х. Согласно условию задачи, собака пробегает на 30 м больше, поэтому можно составить уравнение:4х - 3х= 30

Решив его, получим х = 30 (за 30 промежутков времени собака догонит лисицу). Так как в задаче сказано, что собака в каждый промежуток времени делала 2 скачка, то можно найти число скачков, для чего 2 * 30 = 60. А так как скачок равен 2м, то можно найти расстояние, которое пробежит собака – 2 * 60 = 120 (м).

Этот способ решения вполне доступен детям.

Лучшему усвоению приемов и методов решения задач на движение «вдогонку» способствует решение специально подобранных пар взаимообратных задач, например:

1. Из пункта А в одном направлении вышли два пешехода. Скорость первого 7 км/ч, а скорость второго 5 км/ч. Какое расстояние будет между ними через 3 ч после выхода? На сколько километров первый пройдет больше, чем второй?

2. Из двух пунктов, расстояние между которыми 6 км, вышли одновременно два пешехода и идут в одном направлении. Через сколько часов первый догонит второго, если первый идет со скоростью 7 км/ч, а второй – 5 км/ч?

Сравнивая пары задач, их чертежи и решения, учащиеся осознают выбор действий и правильно его обосновывают.

Не следует забывать о том, что задачи на движение в одном направлении должны вводиться с нарастающей трудностью. Причем введение каждого нового типа задач должно сопровождаться такой наглядной интерпретацией, которая обеспечивала бы более качественный анализ задачи и помогала бы осознавать и обосновывать выбор действий, необходимых для решения.

Умение же решать задачи отрабатывается в процессе развития специально подобранных заданий. Конечно, здесь речь не должна идти о разучивании способов решения, но и «не следует отказываться от обобщения решения нескольких задач в тот или иной метод (алгоритм, правило) решения задач определенного типа» [22;38]

3. Задачи на движение двух тел в противоположных направлениях.

В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки: а) одновременно, б) в разное время. А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.

Общим теоретическим положением для них будет следующее: vудал. = v1 + v2, где v1 и v2 соответственно скорости первого и второго тел, а vудал – это скорость удаления, т.е. расстояние, на которое удаляются друг от друга движущиеся тела за единицу времени.

Например, Два поезда отошли одновременно от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70 км/ч. На каком расстоянии друг от друга будут эти поезда через 3 часа после выхода?

4. Задачи на движение по реке.

При решении таких задач различают: собственную скорость движущегося тела, скорость течения реки, скорость движения тела по течению и скорость движения тела против течения. Зависимость между ними выражается формулами:

Vпо теч. = vсоб. + vтеч. р.

Vпр теч. = vсоб. - vтеч. р.

                  vпо теч. + vпр. теч.

Vсоб. =  

                               2

Например, Расстояние 360 км катер проходит за 15 ч, если двигается против течения реки, и за 12 ч, если двигается по течению. Сколько времени потребуется катеру, чтобы проплыть 135 км по озеру?

Как уже отмечалось, задачи на движение выделяются среди других только по сюжету. Поэтому никаких отличий в обучении решению задач этого вида нет. Исключение составляют лишь задачи на движение двух тел.

Задачи на движение, рассматриваемые в начальных классах, включают в себя описание процесса движения одного или двух тел. Эти задачи по существу математических зависимостей между величинами, входящими в задачу, структуре и их моделей нельзя отнести к особому виду задач. В качестве примера рассмотрим пары задач и их решения:

1. а) За 6 часов рабочий изготовил 120 одинаковых деталей. Сколько деталей он изготовит за 3 часа?

б) Пароход прошел 120 км за 6 ч. Сколько километров он пройдет за 3 ч, если будет идти с той же скоростью?

Эту пару задач можно решить тремя способами:

1-й способ                      2-й способ                     3-й способ

1)120:6=20                      1)6:3=2                          6 ч =360 мин

2)20 * 3=60            2)120:2=60                    3ч =180 мин

1)360:180=2

2)120:2=60

2. а) Из двух городов, находящихся на расстоянии 280 км, выехали одновременно две машины. Через сколько часов машины встретятся, если скорость первой машины 60 км/ч, второй - 80 км/ч?

б) Двум мастерам нужно изготовить 280 одинаковых деталей. За сколько часов они могут это сделать вместе, если первый за 1 ч изготавливает 60 деталей, а второй 80 деталей?

Приведем арифметический и алгебраический способы решения:

280 : (80 + 60) = 2                     (80 + 60) • х = 280

Как видим, структура, модели и способы решения как арифметические, так и алгебраические полностью совпадают. Однако в методической литературе задачи, связанные с движением тел, традиционно принято выделять в особый тип, так как эти задачи имеют свою особенность. Особенность состоит в том, что они построены на основе функциональной зависимости между величинами: скорость, время, расстояние. Методика обучения решению таких задач зачастую связана с использованием чертежа и построена на основе четких представлений о скорости равномерного движения тел и на основе понятий двигаться навстречу друг другу, двигаться вдогонку, выехали одновременно и встретились, скорость сближения. Чтобы подготовить детей к восприятию этих понятий, необходимо проводить определенную предварительную работу, которая должна сводиться к формированию умения работать с чертежом, к осознанию понятия «скорость движения» и взаимосвязи между величинами, включенными в задачу.

Однако, как показывает практика обучения, умение решать задачи на движение у учащихся сформировано недостаточно. Например, учащимся были предложены две задачи, одинаковые по структуре, но различные по фабуле. В первой задаче речь шла о покупке тетрадей, во второй о движении тел. С первой задачей справилось значительное большинство учащихся, в то время как с задачей на движение - лишь незначительная часть. Некоторые дети вообще отказались от решения, обосновывая это тем, что задачи на движение они решать не умеют. Думается, что причина этого заключается в том, что дети недостаточно подготовлены к восприятию этих задач.

С задачами, где встречаются величины «скорость», «время», «расстояние» ученики встречаются лишь после знакомства с величиной «скорость». Анализ задач на движение осуществляется с помощью таблицы или чертежа (в зависимости от вида задачи), где рассматриваются все задачные ситуации. Существуют определенные требования по оформлению чертежа к задаче: величины скоростей указываются обычно над соответствующими стрелками, время указывается на чертеже либо над флажком, либо пройденные расстояния делятся на соответствующее число единиц времени. При решении таких задач целесообразно подвести детей к выводу о том, что при движении тел в противоположных направлениях общая скорость (скорость сближения или скорость удаления) находится сложением скоростей, а при движении тел в одном направлении - вычитанием скоростей. Этот вывод ученики могут получить при решении нескольких задач и сравнении их решения (индуктивным путем).