МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Вычисление и сравнение корней. Выполнение расчетов с радикалами.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Вычисление и сравнение корней. Выполнение расчетов с радикалами.

Цель работы: 

- применить умения по выполнению расчетов с радикалами.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Степень с натуральным показателем

      Пусть - действительное число, а - натуральное число, больше единицы. - й степенью числа называют произведение множителей, каждый из которых равен :

Если , то полагают .

Справедливы следующие свойства степени с натуральным показателем:

Если ,

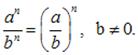
По определению: если , то

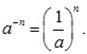
Арифметический корень

Если - натуральное число, больше единицы, то существует, и только одно, неотрицательное число такое, что выполняется равенство . Это число называется арифметическим корнем - й степени из неотрицательного числа и обозначается .

Если , то справедливы следующие свойства:

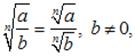
Полагают по определению: если - натуральные числа, , то

.

Нецелая степень отрицательного числа не имеет смысла.

Полезно знать свойства

,

.

Для рациональных показателей свойства степеней остаются теми же.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

2. Величина корня не изменится, если показатель степени уменьшить в n раз и одновременно извлечь корень n-й степени из подкоренного количества:

Пример 2.

Замечание. Это свойство останется в силе и в том случае, когда число m/n не будет целым; точно так же оба вышеуказанных свойства сохранят силу и для n дробного. Но для этого нужно сначала расширить понятие степени и корня, введя дробные показатели.

3. Корень из произведения нескольких сомножителей равен произведению корней той же степени из этих сомножителей:

Пример 3.

Последнее преобразование основывается на свойстве 2.

Пример 4.

Обратно, произведение корней одной и той же степени равно корню той же степени из произведения подкоренных количеств:

Пример 5.

4. Корень от частного равен частному от деления корня из делимого на корень из делителя (показатели корней разумеются одинаковыми):

Обратно:

Пример 6.

5. Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное количество:

Обратно, чтобы извлечь корень из степени, достаточна, возвести в эту степень корень из основания степени:

Пример 7.

.

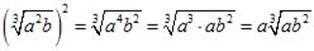
Вопросы для закрепления теоретического материала к практическому занятию:

1.Перечислите свойства степени с натуральным показателем?

2.Перечислите свойства арифметического корня?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.

Скачано с www.znanio.ru