
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ»
филиал ФГБОУ ВО «КГМТУ» в г. Феодосия
Цикловая комиссия гуманитарных и фундаментальных дисциплин
МАТЕМАТИКА:
алгебра, начала математического анализа, геометрия
(часть I, алгебра)
Методические указания
к практическим занятиям для студентов 1 курса
специалистов среднего звена по специальности:
26.02.02 Судостроение
22.02.060 Сварочное производство
Профиль обучения: технический
Форма обучения: очная
Сидорова Людмила Валентиновна
Феодосия, 2018
Составитель: преподаватель высшей категории дисциплины «Математика» председатель цикловой комиссии филиала ФГБОУ ВО «КГМТУ» в г. Феодосия ____________________ Сидорова Л.В.
Рецензент: Зубрилин К.М., кандидат физико-математических наук, доцент кафедры математических и естественно-научных дисциплин филиала ФГБОУ ВО «КГМТУ» в г. Феодосия __________________
Методические указания рассмотрены и одобрены на заседании цикловой комиссии гуманитарных и фундаментальных дисциплин филиала ФГБОУ ВО «КГМТУ» в г. Феодосия,
протокол № ____ от ____________2018 г.
Председатель цикловой комиссии________________ Л.В. Сидорова
Методические указания утверждены на заседании методической комиссии СПО филиала ФГБОУ ВО «КГМТУ» в г. Феодосия,
протокол № от ______________2018 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1 ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН ПРАКТИЧЕСКИХ ЗАНЯТИЙ
2 ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
2.1 Практическое занятие № 1 «Целые и рациональные числа. Действительные числа»
2.2 Практическое занятие № 2 «Линейные уравнения, неравенства и их системы»
2.3 Практическое занятие № 3 «Квадратные уравнения, неравенства и их системы»
2.4Практическое занятие № 4 «Свойства и графики элементарных функций»
2.5 Практическое занятие № 5 «Построение графиков функций с помощью геометрических преобразований»
2.6 Практическое занятие № 6 «Промежуточная аттестация»
2.7 Практическое занятие № 7 «Преобразование выражений, содержащих радикалы»
2.8 Практическое занятие № 8 «Иррациональные уравнения»
2.9 Практическое занятие № 9 «Иррациональные неравенства»
2.10 Практическое занятие № 10 «Иррациональные уравнения и их системы»
2.11 Практическое занятие № 11 «Преобразование выражений содержащих степени»
2.12 Практическое занятие № 12 «Преобразование выражений, содержащих логарифмы»
2.13 Практическое занятие № 13 «Построение графиков показательной функции с помощью преобразований»
2.14 Практическое занятие № 14 «Построение графиков логарифмической функции с помощью преобразований»
2.15 Практическое занятие № 15 «Решение показательных уравнений и неравенств» 52
2.16 Практическое занятие № 16 «Решение логарифмических уравнений и неравенств»
2.17 Практическое занятие № 17 «Радианная мера угла»
2.18 Практическое занятие № 18 «Тригонометрические функции угла и числового аргумента»
2.19 Практическое занятие № 19 «Свойства тригонометрических функций»
2.20 Практическое занятие № 20 «Основные формулы»
2.21 Практическое занятие № 21 «Формулы суммы и разности аргументов»
2.22 Практическое занятие № 22 «Формулы двойных и половинных углов»
2.23 Практическое занятие № 23 «Формулы приведения»
2.24 Практическое занятие № 24 «Формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму»
2.25 Практическое занятие № 25 «Преобразование тригонометрических выражений. Доказательство тождеств»
2.26 Практическое занятие № 26 «Построение графиков функций синуса и косинуса с помощью преобразований»
2.27 Практическое занятие № 27 «Построение графиков функций тангенса и котангенса с помощью преобразований»
2.28 Практическое занятие № 28 «Обратные тригонометрические функции, Решение простейших тригонометрических уравнений»
2.29 Практическое занятие № 29 "Решение простых тригонометрических уравнений"
84
2.30 Практическое занятие № 30 «Решение тригономтрических уравнений методом замены переменной»
2.31 Практическое занятие № 31 Решение однородных тригонометрических уравнений»
2.32 Практическое занятие № 32 «Решение тригонометрических уравнений приведением к одной функции (с одинаковым аргументом)»
2.33 Практическое занятие № 33«Решение тригонометрических неравенств»
2.34 Контрольная работа № 1 96
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Математика является одной из обязательных дисциплин математического и общего естественнонаучного учебного цикла подготовки специалистов среднего звена по специальностям 26.02.02 Судостроение, 22.02.06 Сварочное производство.
Знания, которые студент должен приобрести в результате изучения математики, необходимы для успешного изучения других общеобразовательных и специальных дисциплин (физики, информатики, статистики).
Настоящие методические указания содержат краткие сведения из теории по каждому разделу алгебры, изучаемому в первом семестре.
Методические указания включают следующие разделы математики: развитие понятия о числе, корни, степени и логарифмы, показательная, логарифмическая и степенная функции, основы тригонометрии. Каждое практическое занятие содержит тему, краткие теоретические сведения, примеры решения задач, задания для самостоятельной работы.
В конце изучения алгебры проводится зачетная контрольная работа, которая оценивается по пятибалльной системе. Примерные задания контрольной работы приведены в данных методических указаниях.
Студенты очной формы обучения могут использовать данные указания для самостоятельного изучения материала, при выполнении домашнего задания, при подготовке к контрольной работе и экзамену. Студенты заочной формы обучения могут использовать данные указания для самостоятельного изучения математики, для подготовки к семестровому контролю.
Учебная дисциплина математика является образовательной учебной дисциплиной в цикле математических и общих естественно-научных дисциплин, формулирующей базовые знания для освоения общепрофессиональных и специальных дисциплин.
Методические рекомендации к практическим занятиям по дисциплине «Математика» (алгебра) разработаны в соответствии с рабочей программой дисциплины «Математика».
Содержание методических рекомендаций к практическим занятиям по дисциплине «Математика» (алгебра) соответствует требованиям Государственного стандарта среднего профессионального образования.
Целью изучения дисциплины «Математика» является формирование у студентов вычислительных навыков, получение студентами необходимых знаний и приобретение практических умений в области математики, усвоение внутрипредметных и межпредметных связей с физикой, информатикой, экономикой, а также воспитание достаточно высокой математической культуры.
Задачи дисциплины «Математика» (алгебра):
- расширение и систематизация общих сведений о функциях, изучение новых классов элементарных функций;
- расширение и совершенствование математического аппарата, сформированного в основной школе;
- формирование практических навыков решения уравнений, неравенств и их систем, применяя общие методы решения;
- расширение и углубление представлений о математике как элементе человеческой культуры, о применении её в практике;
- совершенствование интеллектуальных и речевых умений путём развития логического мышления, обогащение математического языка;
- использование математических методов и основ математического моделирования в практической деятельности.
В результате освоения учебной дисциплины обучающийся должен знать:
- значение математики в профессиональной деятельности и при освоении ППССЗ;
- основные математические методы решения прикладных задач в области профессиональной деятельности.
В результате освоения учебной дисциплины обучающийся должен уметь:
- выполнять арифметические действия над числами, сочетая устные и письменные приёмы, применения вычислительных устройств; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения;
- находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах;
- выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций;
- строить графики изученных функций, иллюстрировать по графику свойства элементарных функций;
- решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;
- решать прикладные задачи в области профессиональной деятельности.
Рекомендуемое количество часов на освоение программы дисциплины:
- максимальной учебной нагрузки обучающегося 351 часов, в том числе:
обязательной аудиторной учебной нагрузки обучающегося 234 часов; самостоятельной работы обучающегося 117 часа
Распределение часов на изучение раздела «Алгебра»
|
№ |
Содержание раздела |
Кол-во часов |
Теоретических |
Практических |
Самостоятельная работа |
|
1 |
Раздел 1. Развитие понятия о числе |
25 |
2 |
12 |
11 |
|
2 |
Раздел 2. Корни, степени и логарифмы. |
28 |
4 |
14 |
10 |
|
3 |
Раздел 3. Показательная, логарифмическая и степенная функции |
32 |
10 |
10 |
12 |
|
4 |
Раздел 4. Основы тригонометрии |
53 |
8 |
32 |
13 |
|
|
Итого: |
138 |
24 |
68 |
46 |
Содержание методических указаний направлено на достижение следующих целей:
Самостоятельная работа по дисциплине «Математика: (алгебра) направлено на достижение следующих результатов:
· овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественнонаучных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;
· готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
· готовность и способность к самостоятельной, творческой и ответственной деятельности;
· готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
· отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;
· умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
· умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
· владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;
· готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
· владение языковыми средствами – умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
· владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения;
· целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;
С целью обеспечения успешного обучения студент должен готовиться к практическим занятиям, поскольку они являются важнейшей формой организации учебного процесса и выполняют следующие функции:
Ø способствуют расширению теоретических знаний, полученных на лекциях;
Ø систематизируют полученные знания;
Ø ориентируют в учебном процессе;
Ø формируют практические умения и навыки;
Ø учат применять теоретические знания для решения практических задач;
Ø помогают установить межпредметные связи.
Подготовка к практическим занятиям заключается в следующем:
- внимательно прочитайте материал лекций относящихся к данному практическому занятию, ознакомьтесь с учебным материалом по учебнику и учебным пособиям;
- постарайтесь уяснить место изучаемой темы в своей профессиональной подготовке;
- запишите возможные вопросы, которые вы зададите преподавателю на практическом занятии по теории;
- выпишите основные термины, определения, формулы;
- ответьте на контрольные вопросы по теме занятия, готовьтесь дать развёрнутый ответ на каждый из вопросов;
- уясните, какие учебные элементы остались для вас неясными и постарайтесь получить на них ответ до занятия;
- изучите примеры решения типовых задач , приведённые в ходе лекций;
- готовиться можно индивидуально, парами, в составе малой группы, последние являются эффективными формами работы;
- рабочая программа дисциплины, методические указания, разработанные преподавателем, могут быть использованы вами в качестве ориентира в организации обучения.
Практические занятия - одна из форм аудиторной работы по дисциплине, которые проводятся под руководством преподавателя. После выполнения заданий на практических занятиях у студентов должно сформироваться чёткое представление об объёме и характере знаний и умений, которыми необходимо овладеть при изучении дисциплины. Систе6матическое выполнение учебной работы на практических занятиях позволит успешно освоить дисциплину и создать хорошую базу для сдачи экзамена или зачёта.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Раздел I. Развитие понятия о числе.
Тема: «Целые и рациональные числа. Действительные числа».
План.
1. Числовые множества.
2. Изображение действительных чисел на координатной прямой.
3. Модуль действительного числа.
Цель: систематизация и обобщение знаний студентов о числе, научиться записывать действительные числа в виде бесконечной десятичной дроби, изображать действительные числа, применять понятие модуля действительного числа к решению уравнений; развитие математического мышления обучающихся.
Рациональные
числа - Q. Можно
записать в виде несократимой дроби Записывают
в виде бесконечной периодической дроби ( Иррациональные
числа Нельзя записать
в виде несократимой дроби Записывают
в виде бесконечной непериодической дроби ( Действительные
числа - R. Числа, которые можно
представить в виде бесконечной десятичной дроби
![]() , где m – целое, n-
натуральное число.
, где m – целое, n-
натуральное число.![]() = 0,3333… = 0,(3) )
= 0,3333… = 0,(3) )
![]() , где m – целое, n-
натуральное число.
, где m – целое, n-
натуральное число.![]() )
)![]()
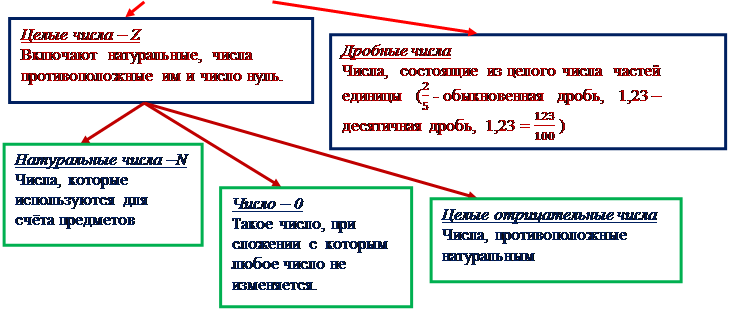
Числовые множества.
![]()
Практическая часть:
Упражнение 1. Представить каждую обыкновенную дробь в виде
периодической десятичной дроби: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Образец. Представить
![]() в виде
периодической десятичной дроби.
в виде
периодической десятичной дроби.
1. Разделить 3 на 22.
2.
Записать ![]() = 0,136363636… = 0,1(36).
= 0,136363636… = 0,1(36).
Упражнение 2. Представить каждую бесконечную периодическую дробь в виде обыкновенной дроби: 0,(3); 0,(13); 0,(27); 0,(128); 0,0(3); 0,2(3); 2,(14); 0,12(0)
Образец №1.
Бесконечная десятичная дробь может быть записана в виде суммы бесконечно убывающей геометрической прогрессии
0,(7) = 0,7777777… = ![]() +
+ ![]() +
+ ![]() + … , у которой первый член
+ … , у которой первый член ![]() =
=![]() , а знаменатель q=
, а знаменатель q=![]() . Сумма членов бесконечно убывающей
геометрической прогрессии вычисляется по формуле S =
. Сумма членов бесконечно убывающей
геометрической прогрессии вычисляется по формуле S = ![]() .
.
S = ![]() =
= ![]() =
= ![]() =
= ![]() . 0,(7) =
. 0,(7) =![]() .
.
Ответ: 0,(7) =![]() .
.
Образец № 2. 0,2(9) = ![]() +
+ ![]() +
+ ![]() +
+ ![]() + … =
+ … = ![]() +
+ ![]() =
= ![]() +
+ ![]() = 0,3 = 0,3(0).
= 0,3 = 0,3(0).
1.
2,5 2 0 1 -0,5 X
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Изображение
действительных чисел на координатной прямой.
Изображение
действительных чисел на координатной прямой.
2. Модуль действительного числа.
|
Определение |
Геометрический смысл модуля |
||||||||||||||
|
Модулем положительного числа называется само это число, модулем отрицательного числа называется число ему противоположное, модуль нуля равен нулю.
|
0 O B A a b Х На координатной прямой модуль – это расстояние от начала координат до точки, изображающей это число. Модуль разности двух чисел a и b - это расстояние между точками a и b на координатной прямой. |
Практическая часть.
Упражнение
№3. Решить уравнения: а) ![]() = 4; б)
= 4; б) ![]() = 6; в)
= 6; в) ![]() = 7; г)
= 7; г) ![]() = 7.
= 7.
Образец. Решить уравнение ![]() = 4;
= 4;
1. Заменить по определению уравнение с модулем совокупностью двух уравнений, не содержащих модуль
![]()
2. Решить каждое уравнение совокупности
![]()
![]()
![]()
![]()
![]()
Ответ: 0,8; 2,4.
Упражнение № 4. Решить неравенства а) ![]() >7; б)
>7; б) ![]()
![]() 5; в)
5; в) ![]() < 3; г)
< 3; г) ![]()
![]() 4;
4;
1 -1
Образец: Решить неравенство
![]()
![]() 1;
1;
2х-7 Х
Решение.
1.
![]()
![]()
![]()
![]() Внимание на знак неравенства
Внимание на знак неравенства
2. Заменяется системой неравенств, не содержащих знак модуля
![]()
Решается
составленная система неравенств:
![]()
![]() Ответ: х
Ответ: х ![]()
3 -3
Образец: Решить неравенство
![]()
![]() 3;
3;
2х-7 2х-7 Х
Решение.
3.
![]()
![]()
![]()
![]()
![]() Внимание на знак неравенства
Внимание на знак неравенства
4. Заменяется совокупностью неравенств, не содержащих знак модуля
![]()
Решается
составленная система неравенств:
![]()
![]()
![]() х
х ![]() .
.
Вопросы для контроля:
- Какие числа называются а) натуральными; б) целыми; в) рациональными; г) иррациональными; д) действительными?
- Как обозначаются множества: а) натуральных чисел; б) целых чисел; в) рациональных чисел; г) действительных чисел?
- Может ли разность двух отрицательных чисел быть положительным числом?
- Может ли сумма двух иррациональных чисел быть рациональным числом?
- Может ли произведение иррациональных чисел быть рациональным числом?
- В каком случае несократимую обыкновенную дробь можно представить в виде конечной десятичной дроби?
- Верно ли, что каждой точке координатной оси соответствует действительное число и каждому действительному числу соответствует точка координатной оси?
Домашнее задание: Учебник Гл. I, §11.1 – 1.2,
1.
Решить уравнения: а) ![]() = 11; б)
= 11; б) ![]() = 7;
= 7;
2.
Решить неравенства: а) ![]()
![]() 11; б)
11; б) ![]()
![]() 6.
6.
3. Представьте каждую дробь в виде обыкновенной: а) 0,(54); б) 0,5(3); в) 2, 4(5); г) 7, 008 (0).
Тема: «Линейные уравнения, неравенства и их системы»
План.
4. Определение линейного уравнения.
5. Теоремы о равносильности уравнений. Решение линейных уравнений.
6. Системы линейных уравнений и их методы их решения.
7. Линейные неравенства и их решение.
8. Системы линейных неравенств и их решение.
Цель: систематизация и обобщение знаний студентов о линейных уравнениях , неравенствах и их системах, научиться решать линейные уравнения, неравенства и их системы; развитие математического мышления обучающихся.
1. ОПРЕДЕЛЕНИЕ ЛИНЕЙНОГО УРАВНЕНИЯ.
Уравнение вида ax + b = 0, где х – неизвестная величина, а а и b - некоторые числа, называется линейным уравнением с одним неизвестным.
х =
Линейное уравнение
![]()
имеет один корень, который вычисляется по формуле
2. Теоремы о равносильности уравнений
|
Теорема |
Пример |
|
1. Для любого числа равносильны уравнения F(x) = G(x)
и F(x) |
х + 1 = 2 х + 1 = 2 |
|
2.
Для любого числа а F(x) = G(x)
и F(x) (каждый член уравнения можно умножить на одно и тоже число не равное нулю) |
3х +6 = -9 |
|
3. Равносильны уравнения F(x) + P(x) = G(x), F(x) = G(x) - P(x) , P(x) = G(x) - F(x) и F(x) + P(x) - G(x) = 0 (члены уравнения можно переносить из одной части уравнения в другую, меняя их знаки на противоположные) |
х + 1 = 2 6 – х = х
|
Алгоритм решения линейных уравнений.
1. Если уравнение имеет дробные коэффициенты, его надо привести к уравнению с целыми коэффициентами, умножив каждый член уравнения на число, равное наименьшему общему кратному знаменателей (теорема 2).
2. Если в уравнении есть скобки их надо раскрыть ( правило раскрытия скобок, перед которыми стоит знак «+» или знак «-«; правило умножения одночлена на многочлен; правило умножения многочленов; формулы сокращённого умножения).
3. Перенести (теорема 3) члены содержащие неизвестные в левую часть уравнения, а члены, не содержащие неизвестное в правую часть уравнения.
4. Привести подобные слагаемые в левой и правой частях уравнения.
5.
Из уравнения ах = b найти
корень по формуле X
= ![]() .
.
6. Записать ответ ( в ответе записать число).
Пример 1
(образец). Решить уравнение ![]() =
= ![]() .
.
|
№ |
Алгоритм решения |
Пример |
|
1 |
Найти наименьшее общее кратное знаменателей |
НОК (2; 7) = 14 |
|
2. |
Каждый член уравнения умножить на НОК |
|
|
3. |
Сократить полученные дроби |
|
|
4. |
Раскрыть скобки |
35х – 28 = 32х + 2 |
|
5. |
Перенести члены содержащие неизвестное в левую часть уравнения, не содержащие неизвестное в правую часть уравнения. |
35х -32х = 2 + 28 |
|
6. |
Привести подобные слагаемые в каждой части уравнения. |
3х = 30 |
|
7. |
Из полученного уравнения найти х |
Х = 30 : 3; х = 10. |
|
8. |
Записать ответ |
Ответ: 10. |
Упражнение № 1 Решить уравнения:
а) ![]() =
= ![]() б)
б) ![]() =
= ![]() .
.
Системы линейных уравнений и их методы их решения.
Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений обращается в верное равенство. Системы уравнений были известны в древности. В древневавилонских текстах, написанных в III – II тысячелетиях до н.э., содержится немало задач, решаемых с помощью составления систем уравнений.
|
Графический способ решения систем уравнений |
||||||||||||||||||
|
Решить систему |
||||||||||||||||||
|
1. |
Выполнить равносильные преобразования в системе так чтобы удобно было построить график |
|
||||||||||||||||
|
2.
|
Построить в одной системе координат график каждого уравнения
|
4x + y = 6 X + y = 0 0 2 2 А X Y |
||||||||||||||||
|
3. |
Найти точку пересечения графиков уравнений |
Точка А |
||||||||||||||||
|
4. |
Найти координаты точки пересечения графиков функций |
А( |
||||||||||||||||
|
5. |
Записать ответ |
Ответ: ( |
||||||||||||||||
Решить систему уравнений графическим способом:
![]()
|
Решение систем уравнений методом подстановки |
||
|
Решить систему |
||
|
1. |
Из одного уравнения выразить одну переменную через другую и известные величины. |
|
|
2. |
Найденное значение переменной подставить во второе уравнение |
|
|
3. |
Решить второе уравнение |
|
|
4. |
Найденное значение переменной подставить в первое уравнение и вычислить значение второй переменной |
|
|
5 . |
Записать ответ |
Ответ: (1; 0). |
Упражнение № 3 Решить систему уравнений ![]()
|
Решение систем уравнений методом сложения |
||
|
Решить систему |
||
|
1. |
Уравнять коэффициенты при одной переменной путём почленного умножения на специально подобранные множители |
|
|
2. |
Сложить (вычесть) почленно уравнения системы, исключая одну из переменных |
|
|
3. |
Решив первое уравнение, найдём одно из неизвестных |
|
|
4. |
Найденное значение переменной подставляем во второе уравнение |
|
|
5. |
Решив второе уравнение находим второе неизвестное |
|
|
6. |
Записать ответ. |
Ответ: ( |
Упражнение № 4. Решить систему уравнений способом сложения ![]()
Линейные неравенства и их решение.
3. Теоремы о равносильности неравенств
|
Теорема |
Пример |
|
1. Для любого числа равносильны уравнения F(x) > (<) G(x)
и F(x) |
х + 1 < 2 х + 1 >2 |
|
2.
Для любого числа а F(x)>G(x)
и F(x) (каждый член неравенства можно умножить на одно и тоже положительное число) |
|
|
3.
Для любого числа а F(x)>G(x)
и F(x) 4. (каждый член неравенства можно умножить на одно и тоже отрицательное число, при этом знак неравенства поменяется на противоположный) |
3х +6 > -9 |
|
5. Равносильны уравнения F(x) + P(x) < G(x), F(x) <G(x) - P(x) , P(x) = G(x) - F(x) и F(x) + P(x) - G(x) < 0 (члены неравенства можно переносить из одной части неравенства в другую, меняя их знаки на противоположные) |
х + 1 > 2 6 – х > х
|
|
Решение неравенств |
||||
|
Решить неравенство |
||||
|
1 |
Найти наименьшее общее кратное знаменателей |
НОК (2; 7) = 14 |
||
|
2 |
Каждый член неравенства умножить на НОК |
|
||
|
3 |
Сократить полученные дроби |
|
||
|
4 |
Раскрыть скобки |
35х – 28 |
||
|
5 |
Перенести члены содержащие неизвестное в левую часть уравнения, не содержащие неизвестное в правую часть уравнения. |
35х -32х |
||
|
6 |
Привести подобные слагаемые в каждой части уравнения. |
10 |
||
|
7 |
Найти числовой промежуток, которому принадлежит переменная |
|
||
|
8 |
Записать ответ |
Ответ: [10; + |
||
Упражнение 5. Решить неравенство 5(х – 1) + 7![]() 1 – 3 (х + 2)
1 – 3 (х + 2)
Системы и совокупности неравенств с одной переменной.
|
Решение систем неравенств |
Решение совокупности неравенств |
|||||||||
|
Отдельно решить каждое уравнение |
|
Отдельно решить каждое уравнение |
|
|||||||
|
Найти пересечение найденных решений |
Ответ: нет решенияя |
Найти объединение найденных решений |
2 -2 |
|||||||
Упражнение 6. Решить систему неравенств ![]()
Упражнение № 7 Решить
совокупность неравенств ![]() .
.
Домашнее задание.
1. Решить уравнение ![]() –
– ![]() =
= ![]() .
.
2. Решить систему уравнений 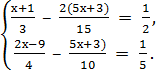
Тема: «Решение квадратных уравнений и неравенств. Решение систем уравнений, в которых одно из уравнений квадратное»
План.
1. Квадратное уравнение и его решение.
2. Квадратное неравенство и его решение
3. Решение систем уравнений, в которых одно уравнение квадратное
Цель: систематизация и обобщение знаний студентов о квадратных уравнениях и способах их решения; формирование навыка решения квадратных уравнений, неравенств и их систем; развитие логического мышления и математической культуры.
Квадратное уравнение и его решение.
Квадратным
уравнением называется уравнение вида а![]() +bx
+ c = 0,
где a
+bx
+ c = 0,
где a![]() , b, c
- некоторые числа, х – переменная.
, b, c
- некоторые числа, х – переменная.
|
РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ |
||||||||
|
Полное квадратное уравнение |
Приведённое квадратное уравнение |
Уравнение с чётным вторым коэффициентом |
||||||
|
а b |
а
|
а |
||||||
|
D
= |
D
= |
|
||||||
|
D > 0 |
D = 0 |
D < 0 |
D > 0 |
D = 0 |
D < 0 |
D > 0 |
D = 0 |
D < 0 |
|
|
|
Нет корней |
|
|
Нет корней |
|
|
Нет корней |
Упражнение
1. Решить уравнения: а) 3![]() -7х + 4 = 0; б) 5
-7х + 4 = 0; б) 5![]() -8х + 3 = 0 в)
-8х + 3 = 0 в) ![]() -10х - 24 = 0 г)
-10х - 24 = 0 г) ![]() =
= ![]()
|
НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ |
||
|
а b |
а b |
а b |
|
а |
а |
а |
|
Если коэффициенты а и с разных знаков, то уравнение имеет два различных корня. |
При любых допустимых значениях коэффициентов а и b уравнение имеет два различных корня |
При любом допустимом значении коэффициента а уравнение имеет корень |
|
|
|
|
Упражнение
№ 2. Решить уравнения: а) ![]() - 50 = 0 б)
- 50 = 0 б) ![]() + 10х = 0 в)
+ 10х = 0 в) ![]() - 30 = 0 г)
- 30 = 0 г) ![]() + 81 = 0 д)
+ 81 = 0 д) ![]() - 42х = 0
- 42х = 0
Квадратное неравенство и его решение
Пусть
дано неравенство ![]() . Всякое значение
переменной, при котором данное неравенство с одной переменной обращается
в верное числовое неравенство, называется решением неравенства с одной
переменной. Решить неравенство с переменной - значит найти все его решения или
доказать, что их нет.
. Всякое значение
переменной, при котором данное неравенство с одной переменной обращается
в верное числовое неравенство, называется решением неравенства с одной
переменной. Решить неравенство с переменной - значит найти все его решения или
доказать, что их нет.
|
|
|||||||||||||
|
С помощью графика квадратичной функции |
Методом интервалов |
||||||||||||
|
|
а |
||||||||||||
|
|
|
Найти корни квадратного трёхчлена |
|
||||||||||
|
Внимание на знак неравенства |
Если знак неравенства «меньше», то в качестве ответа выбирается числовой промежуток (
|
Отметить их на координатной прямой и определить знаки на каждом числовом промежутке |
- + + В соответствии с знаком неравенства выбрать числовой промежуток |
||||||||||
Упражнение
№ 3 Решить неравенства: а) 3![]() - 7x + 4 < 0 методом интервалов;
- 7x + 4 < 0 методом интервалов;
Б) 2![]() - 9x + 10 < 0 с помощью графика квадратичной функции
- 9x + 10 < 0 с помощью графика квадратичной функции
Упражнение
4. Решить систему уравнений ![]()
Домашнее задание:
1. Решить уравнения а) (х – 4)(4х – 3) + 3 = 0;
б) ![]() + 1 –
+ 1 – ![]() =
= ![]()
2.
Решить систему ![]()
Тема: «Свойства и графики элементарных функций».
План.
1.Линейная функция y = kx + b
2. Функция y = ![]() (k
(k![]() 0)
0)
3. Функция
y = a![]() (a
(a![]() 0)
0)
4. Практическая часть: построение графиков функций.
Цель: повторение и обобщение свойств элементарных функций; построение графиков; развитие логического мышления и умения обобщать и систематизировать имеющиеся знания.
Повторение и обобщение свойств основных видов функций.
1) Самостоятельная работа студентов: закончить предложения.
a)
Областью определения функции y = ![]() является … (ответ: (-
является … (ответ: (- ![]() ; 1)
; 1) ![]() (1;
(1; ![]() ))
))
b)
Областью определения функции y = ![]() является … (ответ: x
является … (ответ: x ![]() 1).
1).
c)
Областью значений функции y = ![]() +1 является … ( числовой промежуток [1;
+1 является … ( числовой промежуток [1; ![]() ) ).
) ).
d)
Если для функции y = f(x)
выполняется равенство f(-x) = f(x) для всех x ![]() D(f), то функция … (называется чётной).
D(f), то функция … (называется чётной).
e) График нечётной функции симметричен относительно …. (начала координат).
f) Если для некоторых значений х1 и х2 из области определения функции y = f(x) при условии х1 < х2 выполняется неравенство y1 < y2, то функция … (называется возрастающей).
Свойства изученных в основной школе функций записаны в таблице:
|
Функция |
|
D(y) |
E(y) |
Чётн. нечётн. |
Возрастание убывание |
||||||||||||||||
|
Линейная y =kx+b |
k> 0

|
R |
R
b |
Не чётная, не нечётная |
возрастает |
||||||||||||||||
|
Y
|
убывает |
||||||||||||||||||||
|
b =
0
|
Не чётная |
Возраст. или убыв. в завис–ти от k. |
|||||||||||||||||||
|
O |
чётная |
постоянная |
|||||||||||||||||||
|
Обратная пропорциональность
y = |
|
х |
х |
нечётная |
Убывает на каждом из промежутков (- (0;
|
||||||||||||||||
|
|
Y
|
х |
х |
нечётная |
Возрастает на каждом из промежутков (- (0; |
||||||||||||||||
|
X
y = a
|
a>
X Y |
R |
[0, |
чётная |
(- (0;
|
||||||||||||||||
|
y = a
|
a>
O X Y |
R |
[0, |
чётная |
(-
(0;
|
||||||||||||||||
|
|
O X Y |
|
(- |
|
(- (0; |
||||||||||||||||
|
y =
|
O |
R
|
R |
нечётная |
возрастает
|
||||||||||||||||
|
|
убывает |
||||||||||||||||||||
|
y =
|
O |
R |
[0, |
чётная |
(-
[0; |
||||||||||||||||
|
y =
|
X O Y |
[0; |
[0; |
Не чётная, не нечётная |
[0;
|
||||||||||||||||
|
Y (a
|
O X Y |
R |
[
|
Не чётная, не нечётная |
[
( - |
||||||||||||||||
|
O X Y |
(- |
( -
[ |
|||||||||||||||||||
|
y = [x]
|
Y X |
R |
Z |
Не чётная, не нечётная |
Постоянная х n |
||||||||||||||||
|
y = {x}
|
Y X |
R |
[0; 1) |
Не чётная, не нечётная |
Возрастает х n |
||||||||||||||||
Практическая часть: построить графики функций
a) y = x-2,
b) y = 3-x
c)
y = ![]() -2x
-2x
d)
y = ![]() -4x + 3
-4x + 3
e)
y = 4x - ![]() .
.
Домашнее задание: §3, п. 3.1, № 3.2, № 3.5 (а, б, д) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Построение графиков функций с помощью геометрических преобразований».
План.
1.Решение упражнений на свойства функций
2.Систематизация знаний о геометрических преобразованиях графиков функций.
Цель: формирование умений строить графики функций с помощью геометрических преобразований, развитие логического мышления, формирование математической культуры.
1.
Найти область определения
функций y = ![]() , y =
, y = ![]() , y =
, y = ![]() +
+ ![]() .
.
3 2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Решение:
Решение:
y
= ![]() ,
,
![]()
![]() 0. Корни трёхчлена х1 = 3, х2
= 2.
0. Корни трёхчлена х1 = 3, х2
= 2.
D(y) = ( - ![]() ; 2]
; 2] ![]() [3,
[3, ![]() )
)
y
= ![]() Знаменатель дроби не равен 0. х – 2
Знаменатель дроби не равен 0. х – 2 ![]() 0; х
0; х ![]() 2.
2.
D(y) =
( - ![]() ; 2)
; 2)
![]() (2,
(2,
![]() ).
).
y = ![]() +
+ ![]() . Область определения функции является решением
системы
. Область определения функции является решением
системы
0 1![]()
![]()
![]()
![]()
![]()
![]()
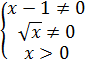 < = >
< = > ![]()
D(y) = (0; 1) ![]() (1,
(1, ![]() ).
).
3.
Исследовать функции на чётность
и нечётность функции f(x) = ![]() (2x -
(2x - ![]() ), f(x) =
), f(x) = ![]() .
.
Область определения функции f(x) = ![]() (2x -
(2x - ![]() ) – всё множество действительных чисел.
) – всё множество действительных чисел.
f(-x) = ![]() (2(-х) –
(2(-х) – ![]() ) =
) = ![]() (- 2x +
(- 2x + ![]() ) = -
) = - ![]() (2x -
(2x - ![]() ) = - f(x) - нечётная.
) = - f(x) - нечётная.
Область определения функции f(x) = ![]() – всё множество действительных чисел.
– всё множество действительных чисел.
f(-x) = ![]() =
= ![]() = f(x) - чётная.
= f(x) - чётная.
Повторение и систематизация знаний студентов о геометрических преобразованиях графиков функций.
Запас функций, графики которых мы умеем строить пока не велик. Но используя свойства с курса геометрии и алгебры о преобразовании фигур, этот список можно значительно расширить.
I. Сдвиг графика элементарной функции по осям координат.
y = f(x +a) - график функции y = f(a) сдвинуть по оси Ох на а единиц влево, если а положительное число, и на а единиц вправо, если а отрицательное число.
y = f(x) +a - график функции y = f(a) сдвинуть по оси Оy на а единиц вверх, если а положительное число, и на а единиц вниз, если а отрицательное число.
Построить графики функций:
a)
y = ![]()
b) y = ![]()
c)
y = ![]()
d)
y = ![]() – 2.
– 2.
e)
y = ![]() + 1
+ 1
f)
y = ![]() + 2
+ 2
II. Построение графиков функций с использованием симметрии.
y = - f(x) - график функции y = f(x) отобразить симметрично оси Ох;
y = f(- x) - график функции y = f(x) отобразить симметрично оси Оy;
y = ![]() - часть графика функции y = f(x)
в верхней полуплоскости и на оси Ох оставить без изменений, а часть
графика расположенную под осью Ох отобразить относительно оси Ох в
верхнюю полуплоскость.
- часть графика функции y = f(x)
в верхней полуплоскости и на оси Ох оставить без изменений, а часть
графика расположенную под осью Ох отобразить относительно оси Ох в
верхнюю полуплоскость.
y = f(![]() ) - часть графика функции y = f(x)
в правой полуплоскости и на оси Оy оставить
без изменений; часть графика функции y = f(x),
расположенную в левой полуплоскости удалить; сохранённую часть графика
функции y = f(x) в правой полуплоскости и на оси Оy
отобразить симметрично оси Оy в левую полуплоскость.
) - часть графика функции y = f(x)
в правой полуплоскости и на оси Оy оставить
без изменений; часть графика функции y = f(x),
расположенную в левой полуплоскости удалить; сохранённую часть графика
функции y = f(x) в правой полуплоскости и на оси Оy
отобразить симметрично оси Оy в левую полуплоскость.
Построить графики функций:
a)
y = ![]()
b) y = - ![]()
c)
y = ![]()
d) y = - ![]()
e)
y = ![]() .
.
Выполняя
последовательно построение графиков функций y = f(![]() ) и y =
) и y = ![]() построить
графики функций:
построить
графики функций:
y = ![]()
y = ![]()
Домашнее задание: §3, п. 3.1, № 3.4, № 3.5 (в, г) , № 3.6 (а-г) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Промежуточная аттестация»
План.
1. Математический диктант
2. Построение графиков с помощью геометрических преобразований.
3. Самостоятельная работа.
Цель: формирование умения строить графики функций с помощью геометрических преобразований; контроль усвоения знаний и сформированность умений по теме; развитие логического мышления.
1.Математический диктант.
Запишите формулой функцию, график которой получен в результате:
-
Параллельного переноса графика
функции y = ![]() на 3 единицы вправо вдоль оси Ох;
на 3 единицы вправо вдоль оси Ох;
-
Параллельного переноса графика
функции y = ![]() на 3 единицы влево вдоль оси Ох;
на 3 единицы влево вдоль оси Ох;
-
Параллельного переноса графика
функции y = ![]() на 3 единицы вверх по оси Oy;
на 3 единицы вверх по оси Oy;
-
Параллельного переноса графика
функции y = ![]() на 3 единицы вниз по оси Oy;
на 3 единицы вниз по оси Oy;
-
Растяжения графика функции y = ![]() от точки О(0; 0) вдоль оси ординат в 3 раза;
от точки О(0; 0) вдоль оси ординат в 3 раза;
-
Сжатия графика функции y = ![]() до точки О (0; 0) вдоль оси абсцисс в 3 раза.
до точки О (0; 0) вдоль оси абсцисс в 3 раза.
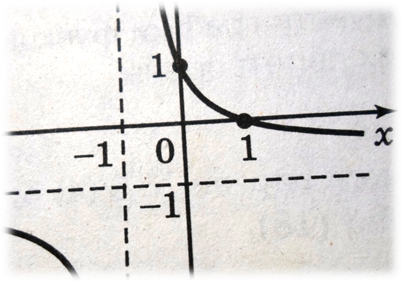 (рис.а)
(рис.а)
2.Построить графики функций;
Ø
y = ![]() –1 (рис. а)
–1 (рис. а)
Ø
y =![]() – 1
(рис.б)
– 1
(рис.б)
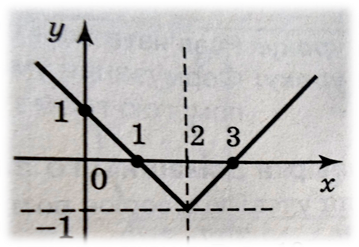 (рис.б)
(рис.б)
Ø y = 1
– ![]() (рис.в)
(рис.в)
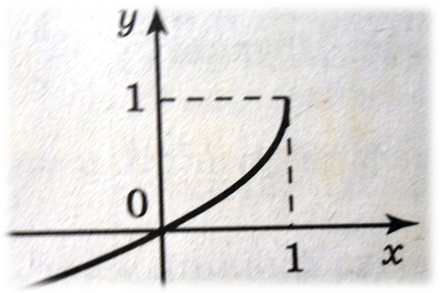 (рис.
в)
(рис.
в)
Ø y = ![]() (рис. г)
(рис. г)
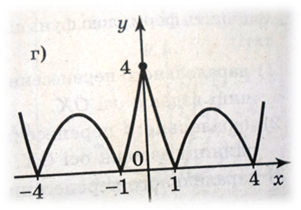 (рис.
г)
(рис.
г)
3.Самостоятельная работа
Вариант 1.
1.
Найдите область определения
функции y = ![]() .
.
2.
Исследовать на чётность и
нечётность функцию y = ![]() - х.
- х.
3.
Постройте график функции: а) y = ![]() - 2; б) y =
- 2; б) y = ![]()
Ответы: 1) D(e) =
(- ![]() (-3; 3)
(-3; 3) ![]() (3;
(3; ![]() ); 2) нечётная; 3)
); 2) нечётная; 3)
а) 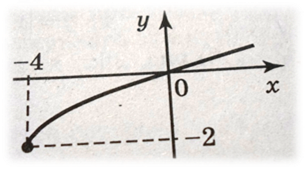
 б)
б)
Вариант 2.
1.
Найдите область определения
функции y = ![]() .
.
2.
Исследовать на чётность и
нечётность функцию y = ![]() -
- ![]() .
.
3.
Постройте график функции: а) y = ![]() + 2; б) y =
+ 2; б) y = ![]()
Ответы: 1) D(e) =
(- ![]() (-2; 2)
(-2; 2) ![]() (2;
(2; ![]() ); 2) чётная; 3)
); 2) чётная; 3)
а)

б) 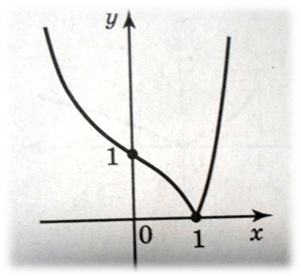
Домашнее задание: §3, п. 3.1, № 3.7 учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Преобразование выражений, содержащих радикалы»
План.
1.Преобразовапние корней.
2.Сравнение радикалов.
3.Действия над радикалами
Цель: познакомить студентов с простейшими преобразованиями радикалов: вынесение множителя из под знака радикала, внесенение множителя под знак радикала; приведение радикалов к простейшему виду; дать понятие подобных радикалов; сформировать умение сравнивать радикалы; познакомить студентов с действиями над радикалами; развитие практических умений и навыков, логического мышления и математической культуры.
Ответить на вопросы:
Ø
Что называют арифметическим
корнем степени n (n ![]() 2) из числа а?
2) из числа а?
Ø
Для каких чисел а ![]() R введено понятие арифметического корня степени n (n
R введено понятие арифметического корня степени n (n ![]() 2)
из данного числа а?
2)
из данного числа а?
Ø
Сколько существует арифметических
корней степени n (n ![]() 2) из данного числа а?
2) из данного числа а?
Ø
Верны ли для любого
неотрицательного числа а и любого натурального числа n (n ![]() 2)
равенства
2)
равенства ![]() =
= ![]() = a?
= a?
Ø
Если ![]() =
= ![]() , то всегда ли a = b? (n
, то всегда ли a = b? (n ![]() N, n
N, n ![]() 2)
2)
Ø
Чему равен корень степени n (n ![]() 2)
из произведения неотрицательных чисел?
2)
из произведения неотрицательных чисел?
Ø
Чему равен корень степени n (n ![]() 2)
из частного положительных чисел?
2)
из частного положительных чисел?
Ø
Чему равен ![]() , если a
, если a![]() R?
R?
Ø
Чему равен ![]() , если a - любое действительное
число?
, если a - любое действительное
число?
Ø Какие свойства корней n-ой степен6и вам известны?
Изученные свойства корней дают возможность выполнять преобразования корней.
Вынесение множителя из - под знака корня.
В некоторых случаях подкоренное выражение раскладывается на множители так, что из одного или нескольких из них можно точно вычислить корень. Вычислив корни, можно полученные результаты записать перед корнем в качестве множителей. Множители из которых корень точно не извлекается остаются под знаком корня. Такое преобразование называется вынесением множителя за знак корня.
Например:
![]() =
= ![]() =
= ![]() ·
·![]() = 2
= 2![]() ;
;
![]() =
= ![]() =
= ![]() ·
· ![]() = 2
= 2![]() ;
;
![]() =
= ![]() =
= ![]() ·
· ![]() $
$
![]() =
= ![]() =
= ![]() ·
· ![]() =
= ![]() .
.
Решить упражнения:
Вынести множитель за знак радикала: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Вынести множитель за знак корня, если a>
0, b > 0: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Вынесите множитель за знак корня: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Внесение множителя под знак корня.
Преобразование обратное вынесению множителя из-под знака корня называется внесением множителя под корень.
Чтобы внести множитель под знак корня надо записать его множителем под корнем в степени равной степени корня.
Например:
2![]() =
= ![]() =
= ![]() =
= ![]() ;
;
3![]() =
= ![]() =
= ![]() =
= ![]() ;
;
а![]() =
= ![]() =
= ![]() ;
;
a![]() =
= 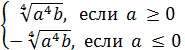
Решить упражнения:
Внести множитель под знак корня: а) 3![]() б) -2
б) -2![]() ,
в)
,
в) ![]()
![]() , г)
, г) ![]() .
.
Внести множитель под знак корня, если a>
0, b > 0: а) -b![]() б) ab
б) ab ![]() в) a
в) a![]() г) -ab
г) -ab![]()
Внести множитель под знак корня: а) a![]() ;
б) a
;
б) a![]() ;
в) -ab
;
в) -ab![]() .
.
Приведение радикалов к простейшему виду, понятие подобных радикалов.
Будем считать, что радикал приведён к простейшему виду, если: подкоренное выражение не содержит дробей; рациональные множители вынесены за знак корня; показатель корня и пок5азатель подкоренного выражения разделены на их наибольший общий множитель.
Например. Приведём радикалы к простейшему виду:
а) ![]() =
= ![]() =
= ![]() ; б)
; б) ![]() = 2
= 2![]() .
.
Радикалы называются подобными, если после
приведения их к простейшему виду они имеют равные подкоренные
выражения и равные показатели корня. Например, подобными являются
радикалы: а) 3![]() ; а
; а![]() ;
; ![]() ; б) 5
; б) 5![]() ,
, ![]() , (a-1)
, (a-1)![]() .
.
Рациональный множитель, который стоит
перед корнем, называется коэффициентом. Например, 3![]() . В этом выражении 3- коэффициент. Чтобы
утверждать, подобны радикалы или нет, их надо привести к простейшему
виду.
. В этом выражении 3- коэффициент. Чтобы
утверждать, подобны радикалы или нет, их надо привести к простейшему
виду.
Например,
![]() и
и ![]() подобные, так как
подобные, так как ![]() =
= ![]() = 3
= 3![]() , а
, а ![]() =
= ![]() = 2
= 2![]() .
.
Решить упражнения:
а) упростить: ![]() ;
; ![]() , где b>0;
, где b>0;
б) подобны ли радикалы: ![]() и
и ![]() ;
; ![]() и
и ![]() ?
?
Сравнение радикалов.
Для сравнения радикалов применяется
теорема: если a > b ![]() 0 то
0 то ![]() >
> ![]() , то есть большему положительному подкоренному
выражению соответствует и большее значение корня.
, то есть большему положительному подкоренному
выражению соответствует и большее значение корня.
Например, сравнить ![]() и
и ![]() . Представим
. Представим ![]() и
и ![]() в виде корней с одинаковым показателем.
в виде корней с одинаковым показателем.
![]() =
= ![]() =
= ![]()
![]() =
= ![]() =
= ![]() .
.
Согласно теоремы, 32 > 27 < = > ![]() >
> ![]() < = >
< = > ![]() >
> ![]() .
.
Решить упражнения:
а) Сравнить числа: ![]() и
и ![]() ;
; ![]() и
и ![]() ;
;
б) Что больше ![]() или
или ![]() ;
; ![]() или
или ![]() ;
; ![]() или
или ![]() ?
?
в) Что меньше ![]() или
или ![]() ;
; ![]() или
или ![]() ?
?
Действия над радикалами.
Сложение и вычитание радикалов выполняется как и сложение и вычитание рациональных одночленов (многочленов).
Примеры:
а) 3![]() -5
-5![]() + 12
+ 12![]() = (привести радикалы к
простейшему виду)
= (привести радикалы к
простейшему виду)
= 3![]() -5
-5![]() + 12
+ 12![]() = 6
= 6![]() -15
-15![]() + 60
+ 60![]() = (6-15+60)
= (6-15+60)![]() = 51
= 51![]() ;
;
б) ![]() - (2
- (2![]() - 3
- 3![]() ) =
) = ![]() - 2
- 2![]() + 3
+ 3![]() =4
=4 ![]() - 6
- 6![]() + 6
+ 6![]() = 4
= 4 ![]()
При умножении (делении) радикалов с разными показателями сначала их надо привести к одинаковому показателю, а затем перемножить (разделить) подкоренные выражения и записать произведение (частное) под знак корня с тем же показателем.
Примеры:
а) ![]() ·
· ![]() =
= ![]() ·
· ![]() =
= ![]() =
= ![]() =
= ![]() ;
;
б) ![]() :
: ![]() =
= ![]() :
: ![]() =
= ![]() =
= ![]()
Домашнее задание: §3, п. 3.1, № 3.74-3.77 (в, г), №3.79 (в-е) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Иррациональные уравнения»
План.
1. Понятие иррационального уравнения. Область решения иррационального уравнения
2. Решение иррационального уравнения
3. Способы решения иррациональных уравнений.
Цель: углубление знаний студентов об иррациональных уравнениях ; ввести понятия область решения уравнения, решение уравнения, что значит решить уравнение; рассмотреть способы решения иррациональных уравнений; развитие логического мышления и математической культуры студентов.
Уравнения, в которых переменная находится под знаком корня, называются иррациональными.
Например,
![]() = 8,
= 8, ![]() = 2.
= 2.
Корнем иррационального уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.
Решить иррациональное уравнение - значит найти его корни.
Область решения уравнения - множество значений среди которых могут быть решения уравнения.
Все корни чётной степени, входящие в уравнение, являются арифметическими. Другими словами, если подкоренное выражение отрицательно, то корень лишён смысла (уравнение не имеет решения; если подкоренное выражение равно нулю, то корень также равен нулю; если подкоренное выражение положительно, то и значение корня положительно.
Все корни нечётной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения. При этом корень отрицателен, если подкоренное выражение отрицательно; равен нулю, если подкоренное выражение равно нулю; положителен, если подкоренное выражение положительно.
Функции
y = ![]() и y =
и y = ![]() являются возрастающими на всей области определения.
являются возрастающими на всей области определения.
Используя эти свойства, в некоторых случаях, можно установить, имеет ли уравнение корни, не прибегая ни к каким преобразованиям.
Например, доказать, что уравнение не имеет корней:
1.
![]() = -2 (арифметический корень не может равняться
отрицательному числу). Ответ: нет решения.
= -2 (арифметический корень не может равняться
отрицательному числу). Ответ: нет решения.
2.
![]() +
+ ![]() = 0 (область решения уравнения
= 0 (область решения уравнения ![]()
![]() Значит
Значит ![]() . При каждом таком х величина
. При каждом таком х величина ![]() неотрицательна, а величина
неотрицательна, а величина ![]() положительна. Следовательно их сумма всегда
больше нуля). Ответ: нет решения.
положительна. Следовательно их сумма всегда
больше нуля). Ответ: нет решения.
3. ![]() –
– ![]() = 2 (область решения уравнения
= 2 (область решения уравнения ![]()
![]()
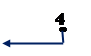 |
![]()
![]()
Следовательно, не существует таких значений х, при которых оба корня существуют). Ответ: нет решения.
4.
![]() =
= ![]() ( выражение
( выражение ![]() определено при х
определено при х![]() . При таких значениях х верно неравенство х -
5<0. Поэтому выражение
. При таких значениях х верно неравенство х -
5<0. Поэтому выражение ![]() отрицательно. Левая часть уравнения
неотрицательна, а правая - отрицательна, чего быть не может) Ответ: нет
решения.
отрицательно. Левая часть уравнения
неотрицательна, а правая - отрицательна, чего быть не может) Ответ: нет
решения.
5.
5![]() - 3
- 3![]() +
+ ![]() = 4 (выражение
= 4 (выражение ![]() имеет смысл при х
имеет смысл при х![]() , выражение
, выражение ![]() имеет смысл при х
имеет смысл при х![]() но дробь
но дробь ![]() при х = 0 не существует) Ответ: нет решения
при х = 0 не существует) Ответ: нет решения
6.
![]() –
– ![]() =
= ![]() ( область решения данного уравнения определяется
системой
( область решения данного уравнения определяется
системой 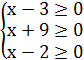 из которой х
из которой х![]() . При любом х верно неравенство х-3<х+9;
поэтому
. При любом х верно неравенство х-3<х+9;
поэтому ![]() <
< ![]() , значит разность
, значит разность ![]() –
– ![]() < 0 –отрицательное число. В то же время на
области решения уравнения
< 0 –отрицательное число. В то же время на
области решения уравнения ![]()
![]() ) Ответ: нет решения.
) Ответ: нет решения.
 Решение иррациональных уравнений основывается на
приведении данного уравнения с помощью некоторых преобразований к
рациональному уравнению.
Решение иррациональных уравнений основывается на
приведении данного уравнения с помощью некоторых преобразований к
рациональному уравнению.
Способ возведения левой и правой части уравнения в одну и ту же степень.
Иррациональное уравнение приводится к рациональному уравнению возведением левой и правой части уравнения в одну и ту же степень (степень равную показателю степени корня).
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель корня - четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным (определение корня с четным показателем степени);
2) если показатель корня - нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения
Пример 1. Решить уравнение ![]()
Решение. Возведем обе части
уравнения в квадрат.
x2 - 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных
слагаемых x2 = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.
Произведем проверку
полученных корней, для этого произведем подстановку значений переменной x в
исходное уравнение.
Проверка.
При x1 = -2 ![]() -
истинно:
-
истинно:
При x2 = -2 ![]() -
истинно.
-
истинно.
Отсюда следует, что исходное иррациональное
уравнение имеет два корня -2 и 2.
При возведении обеих частей уравнения в нечётную степень всегда получаем уравнение равносильное данному на его области решения.
Например, ![]() = 3;
= 3;
![]() =
= ![]() ;
;
![]() х+7 = 27;
х+7 = 27;
х=20. Ответ: 20.
Решить уравнения. ![]() =2, (Ответ: 9);
=2, (Ответ: 9); ![]() = 3;
= 3; ![]() = - 3
= - 3
Если для решения иррационального уравнения обе части уравнения необходимо возвести в чётную степень, то получим уравнение-следствие. Получение уравнения-следствия гарантирует нахождение корней, но при этом возможно появление посторонних корней. Если все найденные корни входят в область решения уравнения, то необходимо делать проверку каждого корня. Если среди найденных корней есть такие, которые не входят в область решения уравнения, то это посторонний корень, а остальные проверять.
Например, ![]() = 2-х;
= 2-х;
![]() =
= ![]() ;
;
![]() х = 4 – 4х +
х = 4 – 4х + ![]() ;
;
![]() -5х + 4 =0;
-5х + 4 =0;
х1 = 1 и х2 = 4.
Оба корня входят в область решения уравнения (х![]() .
.
Выполняем проверку: если х = 1, то ![]() = 2-1 - верное равенство;
= 2-1 - верное равенство;
если х = 4, то ![]() = 2-4; 2=-2 - неверное равенство. Значит х = 4
посторонний корень.
= 2-4; 2=-2 - неверное равенство. Значит х = 4
посторонний корень.
Ответ: 1.
Решить уравнения. ![]() = х-5;
= х-5; ![]() + х = 4;
+ х = 4;
Способ уединения корня.
В иррациональном уравнении сначала перенести один из радикалов в правую часть уравнения. Тогда в левой части уравнения останется один радикал и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональная функция. Такой прием (уединение радикала) довольно часто применяется при решении иррациональных уравнений.
Пример. Решить уравнение ![]() -
- ![]() = 3.
= 3.
Решение.
Уединив первый радикал,
получаем уравнение
![]() =
= ![]() + 3, равносильное исходному.
+ 3, равносильное исходному.
Возводя обе части этого уравнения в квадрат, получаем уравнение
x2 + 5x + 2 = x2
- 3x + 3 + 6![]() ,
равносильное уравнению
,
равносильное уравнению
4x - 5 = 3![]() (1). Это уравнение является следствием
исходного уравнения.
(1). Это уравнение является следствием
исходного уравнения.
Возводя обе части
уравнения в квадрат, приходим к уравнению
16x2 - 40x + 25 = 9(x2 - Зх + 3), или
7x2 - 13x - 2 = 0.
Это уравнение является
следствием уравнения (1) (а значит, и исходного уравнения) и имеет корни.
Первый корень x1 = 2 удовлетворяет исходному уравнению, а второй x2
= ![]() - не
удовлетворяет.
- не
удовлетворяет.
Ответ: x = 2.
Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе части исходного уравнения в квадрат нам бы пришлось выполнить довольно громоздкие преобразования.
Решить уравнения. ![]() +
+![]() =3;
=3; ![]() +
+ ![]() = 5;
= 5; ![]() –
– ![]() = 2.
= 2.
Способ подстановки (замены переменной)
При решении иррациональных уравнений, кроме уединения радикалов используют и другие методы. Рассмотрим пример использования метода замены неизвестного (метод введения вспомогательной переменной).
|
Методы решения иррациональных уравнений |
|
|
Определение: Уравнения, в которых переменная находится под знаком корня, называются иррациональными. Например,
|
|
|
Способ возведения левой и правой части уравнения в одну и ту же степень.
|
Пример 1. Решить уравнение Ответ: -2; 2. |
|
Способ уединения корня.
|
Пример. Решить уравнение Решение. Уединив первый радикал,
получаем уравнение Возводя обе части этого уравнения в квадрат, получаем уравнение x2 + 5x + 2 = x2
- 3x + 3 + 6 4x - 5 = 3 Возводя обе части
уравнения в квадрат, приходим к уравнению 7x2 - 13x - 2 = 0. Это уравнение
является следствием уравнения (1) (а значит, и исходного уравнения) и имеет
корни. Первый корень x1 = 2 удовлетворяет исходному уравнению, а
второй x2 = Ответ: x = 2. |
|
Способ подстановки (замены переменной)
|
Пример. Решить уравнение 2x2 - 6x + Решение. Введем вспомогательную
переменную. Пусть y = Подставив новую переменную в данное уравнение, получим уравнение 2y2 + y - 10 = 0, корни которого y1 = 2и y2 = - 2,5. Второй корень не
удовлетворяет условию y |
Уравнения для
самостоятельного решения:
Решить уравнения: а) ![]() +3
+3![]() = 4 (Замена:
= 4 (Замена: ![]() = t,
= t, ![]() =
= ![]() =
= ![]() );
);
б) ![]() + 2
+ 2![]() = 3;
= 3;
Домашнее задание: Гл. II, §8, п. 8.1, 8.2 № 8.8 (а, б), № 8.9 (в-е) учебник «Алгебра и начала математического анализа» 11 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Иррациональные неравенства».
План
1. Понятие иррационального неравенства
2. Равносильные преобразования иррациональных неравенств
3. Метод интервалов для решения иррациональных неравенств
Неравенства
вида ![]() > g (x),
> g (x),
![]() < g (x),
< g (x),
![]() g (x),
g (x), ![]()
![]() g (x) называются иррациональными
неравенствами.
g (x) называются иррациональными
неравенствами.
Решением иррационального неравенства называют все значения переменной, которые обращают его в верное неравенство.
Решить иррациональное
неравенство, значит найти все значения переменной, которые обращаю его в
верное числовое неравенство. Когда для решения
иррационального неравенства используются равносильные преобразования, то
чаще всего с помощью возведения обеих частей неравенства в одну и ту же
степень данное неравенство приводится к рациональному неравенству. При
этом необходимо помнить следующие свойства:

Ø
из неравенства ![]() > g(x) следует неравенство f(x)
>
> g(x) следует неравенство f(x)
> ![]()
Ø ![]() < g(x) следует
< g(x) следует 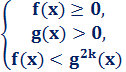 .
.
Пример. ![]() < х-2 < = >
< х-2 < = > 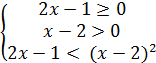 < = >
< = > 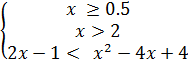 < = >
< = > ![]()
D(f)
Корни трёхчлена х1 =
1, х2=5 f(x) =
![]()
![]()
Ответ:
(5; +![]() )
)
Ø
![]() > g(x) следует
> g(x) следует ![]() или
или ![]() .
.
Пример. ![]() > х-2 < = >
> х-2 < = > ![]() < = >
< = >![]()
![]()
![]()
![]()
Ответ: (0,5; 2)
Решить неравенства:
а)
![]() < х; б)
< х; б) ![]() > 2x+3;
> 2x+3; ![]()
![]() x+1 г)
x+1 г) ![]()
![]() х+1
х+1
Решение неравенств методом интервалов.
Решение неравенств методом интервалов опирается на свойства функций, связанные с изменением знаков функций.
Функция может изменить свой знак только в двух случаях:
ü
Если график функции
разрывается в некоторой точке х0. Например, график функции
y = ![]() разрывается в точке х0 = 0 и знак функции в этой точке
меняется.
разрывается в точке х0 = 0 и знак функции в этой точке
меняется.
ü Если график функции без разрыва переходит из нижней полуплоскости в верхнюю (или наоборот), то есть при переходе через нуль функции.
Точки, в которых разрывается график функции, определяют при нахождении области решения уравнения. Если на каком – нибудь промежутке области определения график функции не разрывается и функция не равна нулю, то она не может на этом промежутке поменять свой знак.
Чтобы найти нули функции, надо приравнять её к нулю и решить полученное уравнение. Нули функции разбивают её область определения на промежутки, внутри которых функция не может менять свой знак.
План решения неравенства методом интервалов
|
Пример |
Комментарий |
План решения |
||||||||
|
О.Д.З. х + 4 |
Данное неравенство
равносильно неравенству
|
Найти ОДЗ неравенства |
||||||||
|
Нули функции
х + 4 = (х+2)2; х + 4 = х2 +4х+4; х2 +3х = 0; х=0 и х= -3 – посторонний корень |
Функция y = |
Найти нули функции y = 0. |
||||||||
|
0 - 4 - + |
Отметим нули на области
определения функции y = |
Отметить нули на ОДЗ и найти знак функции в каждом промежутке, на которые разбивается ОДЗ. |
||||||||
|
Ответ: [- 4; 0] |
На рисунке видно, что решением является отрезок [- 4; 0] |
Записать ответ, учитывая знак неравенства |
Пример №1
![]() >
>![]()
1.
ОДЗ: ![]() ;
; ![]() ;
; ![]() .
.
2.
Находим корни: ![]() =
= ![]() ,
,
х+3 = 2х-5,
-х = -8,
х = 8.
-
![]()
3.
3
![]()
![]()
![]()
![]()
![]() Выполняем рисунок:
Выполняем рисунок:
Определяем
знаки на числовых промежутках: ![]() -
- ![]() =
= ![]() -
- ![]() >0.
>0.
4.
Ответ: х ![]()
Пример №2 Решить неравенство методом интервалов.
. 
Решить неравенства
методом интервалов. а) ![]() >
> ![]() ;
;
б) ![]() <
< ![]() ; в)
; в) ![]()
![]()
![]()
Рассмотрим метод помогающий решать сложные иррациональные неравенства. Это метод замены функций (замены множителей). Суть метода замены заключается в том, что разность значений монотонных функций можно заменить разностью значений их аргументов.
Рассмотрим иррациональное
неравенство вида ![]() <
<![]() ,
,
то есть ![]() –
– ![]() < 0.
< 0.
По теореме, если p(x) возрастает на некотором промежутке, которому принадлежат a и b, причем a>b, то неравенства p(a) – p(b) > 0 и a – b > 0 равносильны на D(p), то есть
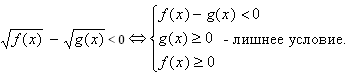
Решим методом замены множителей неравенство.
Пример 1. Решить
неравенство ![]() >
> ![]() методом замены функций.
методом замены функций.
Решение.
Знак неравенства совпадает
со знаком разности 4 – х2 – х – 5 при условии, х принадлежит
области определения функции. Значит данное неравенство равносильно
системе 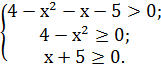 Второе и третье неравенства системы позволяют
найти ОДЗ как [-2; 2]
Второе и третье неравенства системы позволяют
найти ОДЗ как [-2; 2]![]() . Значит, х принадлежит отрезку [-2; 2].
. Значит, х принадлежит отрезку [-2; 2].
Первое неравенство после выполнения тождественных преобразований примет вид
х2 + х +1 < 0, дискриминант которого меньше нуля. При положительном а=1 неравенство не имеет решения. Значит и данное неравенство не имеет решения.
Ответ: х![]() ø.
ø.
Решить неравенства. ![]() >
> ![]() ;
;
![]()
![]()
![]() ;
;
Домашнее задание: Конспект, Алгебра и начала анализа, 11 класс, учебник для общеобразовательных организаций: базовый и углублённый уровень - С.М. Никольский, М, Просвещение, 2014 Глава II, § 9, № 9.45(б), 9.44(б), 9.46(б).
Тема: Иррациональные уравнения и их системы.
План.
1. Устное решение иррациональных уравнений ( по таблице )
2. Коллективное решение иррациональных уравнений.
3. Решение систем иррациональных уравнений.
1) Устно решить уравнения
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
|
|
|
3 + |
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
2) Коллективное решение уравнений.
![]() +3х-18+4
+3х-18+4![]() = 0.
= 0.
Замена: ![]() = t, t
= t, t![]() 0, тогда
0, тогда ![]() +3х-18 =
+3х-18 = ![]() -12.
-12.
Получим уравнение ![]() -12 + 4t = 0 из которого t1 = - 6, t2 = 2.
-12 + 4t = 0 из которого t1 = - 6, t2 = 2.
Возвращаемся к замене.
Уравнение ![]() = - 6 не имеет корней.
= - 6 не имеет корней.
Уравнение ![]() = 2 < = >
= 2 < = > ![]() +3х- 6 = 4 < = >
+3х- 6 = 4 < = > ![]() +3х- 10 = 0 < = >
+3х- 10 = 0 < = > ![]()
Проверка показывает, что - 5 и 2 - корни уравнения.
Ответ: -5; 2.
![]() =
= ![]() .
.
Ø
Помножим числитель и знаменатель дроби на выражение
сопряжённое знаменателю ![]() .
.
![]() =
= ![]() < = >
< = > ![]() =
= ![]() Из этого уравнения 21+ х = 0 или 21- х = 0.
Следовательно корни -21, 21.
Из этого уравнения 21+ х = 0 или 21- х = 0.
Следовательно корни -21, 21.
Ответ: -21; 21.
3) Решить системы с иррациональными уравнениями.
а) 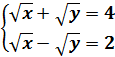
Сложим почленно левые и правые части уравнений и получим уравнение
2![]() = 6 < = >
= 6 < = > ![]() = 3 < = > х = 9.
= 3 < = > х = 9.
Вычтем почленно левые и правые части уравнений и получим уравнение
2![]() = 2 < = >
= 2 < = > ![]() = 1 < = > y = 1.
= 1 < = > y = 1.
Ответ: (9; 1).
б) 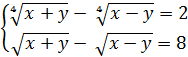
Введём новые переменные: ![]() = u,
= u, ![]() = v
= v
Получим систему рациональных уравнений: ![]() < = >
< = > ![]() < = >
< = > ![]() < = >
< = > ![]()
Сложив почленно левые и правые части уравнений, получим 2u = 6 < = > u = 3.
Вычтем почленно левые и правые части уравнений и получим уравнение
2v = 2 < = > v = 1.
Возвращаемся к замене: 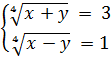 < = >
< = > ![]()
Сложив почленно левые и правые части уравнений, получим 2x = 82 < = > x = 41.
Вычтем почленно левые и правые части уравнений и получим уравнение
2y = 80 < = > y = 40.
Ответ: (41; 40).
№ 14.21 (а) 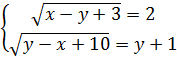 .
.
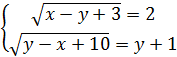 < = >
< = > ![]() < = >
< = > ![]()
Сложив почленно левые и правые части уравнений,
получим ![]() . Из этого уравнения находим y1 = - 4, y2 = 2.
. Из этого уравнения находим y1 = - 4, y2 = 2.
Из уравнения ![]() находим х1 + 4 = 1 < = > х1
= - 3;
находим х1 + 4 = 1 < = > х1
= - 3;
х2 - 2 = 1 < = > х2 = 3.
Решениями системы могут быть пары чисел (- 3; - 4) и (3; 2).
Проверка.
Проверим пару (- 3; - 4):
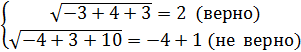 Пара чисел (- 3; - 4) решением не является.
Пара чисел (- 3; - 4) решением не является.
Проверим пару ( 3; 2):
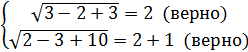 Пара чисел ( 3; 2) решением является.
Пара чисел ( 3; 2) решением является.
Ответ: ( 3; 2) .
Домашнее задание: Гл. II, §14, п. 14.2(пример 2), № 14.21(б, в), № 14.22 (а) учебник «Алгебра и начала математического анализа» 11 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Преобразование выражений содержащих степени»
1. Обобщение понятия степени.
2. Свойства степеней с рациональным показателем
3. Решение упражнений на преобразование выражений с рациональным показателем.
Цель: обобщение понятия степени; формирование понятия степени с рациональным показателем; рассмотреть свойства степени с рациональным показателем; сформировать умение применять свойства степени с рациональным показателем для преобразования выражений; развитие логического мышления и практических умений и навыков студентов.
Повторение сведений о степени, полученные в основной школе.
1) Что называют n-ой степенью
числа а, если n ![]() N?
N?
2) Что называют n-ой степенью числа а, если n = 1?
3) Что называют n-ой степенью числа а, если n = 0?
4) Что называют степенью? Основанием степени? Показателем степени?
5) Что называют n-ой степенью
числа а, если n ![]() Z?
Z?
6) Сформулируйте основные свойства степени.
|
СТПЕНИ |
|
|
С натуральным показателем:
|
С целым показателем:
|
|
СВОЙСТВА:
|
|
Степень с дробным показателем.
Введём понятие степени с дробным показателем, причём это понятие должно иметь те же свойства, что и степень с натуральным и целым показателем.
То есть, n- ая степень числа ![]() должна равняться
должна равняться ![]() . Если это свойство выполняется, то
. Если это свойство выполняется, то ![]() =
= ![]() =
= ![]() - а это означает по определению корня n-ой
степени, что
- а это означает по определению корня n-ой
степени, что ![]() должно быть корнем n-ой степени
из числа
должно быть корнем n-ой степени
из числа ![]() .
.
Определение: степенью ![]() числа, а > 0 с рациональным показателем
числа, а > 0 с рациональным показателем ![]() , где n
, где n ![]() N, m
N, m ![]() Z (n
Z (n ![]() 1) называется число
1) называется число ![]() .
.
Степень числа 0 определена только для
положительных показателей, по определению ![]() = 0 для любого r > 0.
= 0 для любого r > 0.
Выполнить упражнения.
1)
Представить выражение в виде
степени с рациональным показателем: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
2)
Представить выражения в виде
корня из числа или выражения: а) ![]() ; б) 5
; б) 5![]() в) 6
в) 6![]() г) 3
г) 3![]() д)
д) ![]() : е)
: е) ![]() ;
;
3) Вычислить: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() .
.
4) Выполнить № 4.2 (д, е); № 4.4; № 4.6 (в, г)
Домашнее задание: Гл. I, §4, п. 4.1; 4.2 № 4.2 (а-г); № 4.3 ; № 4.6 (а, б) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Преобразование выражений, содержащих логарифмы»
План.
1. Логарифмическая единица и логарифмический ноль.
2. Основное логарифмическое тождество
3. Вынесение показателя степени за знак логарифма.
4. Формулы перехода к новому основанию и следствия из них.
Логарифмом
положительного числа b по основанию а (a . 0, a ![]() называется показатель степени, в которую
необходимо возвести а, чтобы получить число b.
называется показатель степени, в которую
необходимо возвести а, чтобы получить число b.
Логарифмическая единица и логарифмический ноль.
Рассмотрим два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма.
1. log a a = 1 — это логарифмическая единица.
Запомнить! Логарифм по любому основанию a от самого этого основания равен единице.
2. log a 1 = 0 — это логарифмический ноль.
Запомнить! Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! ( a 0 = 1 — это прямое следствие из определения).
Основное логарифмическое тождество
Рассмотрим
показательное равенство ![]() = N. (1)
= N. (1)
По определению логарифма x = loga N (2). Подставив в равенство (1) значение х из равенства (2), получаем
![]() = N
(3).
= N
(3).
![]()
Это тождество является краткой записью определения логарифма: loga N - это показатель степени, в которую надо возвести основание а, чтобы получить число N.
Например, 5log5125 = 125, 10lg1000
= 1000, ![]() = 9.
= 9.
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
1. n = log a a n
2.
![]()
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.
Вторая формула — это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество.
В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a? Правильно: получится это самое число a.
Вынесение показателя степени за знак логарифма.
Если в основании или аргументе логарифма стоит степень, то показатель этой степени можно вынести за знак логарифма по следующим правилам:
1. log a x n = n · log a x;
2.
![]()
3.
![]()
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.
Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма:
a > 0, a ≠ 1, x > 0.
Все формулы являются тождествами и их можно применять не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.
Задача. Найдите значение выражения: log7 496.
Избавимся от степени в
аргументе по первой формуле:
log7 496 = 6 · log7 49 = 6 · 2 = 12
Задача. Найдите значение выражения:
![]()
Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 24; 49 = 72. Имеем:
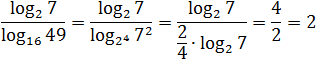
Так как log2 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.
Практическое применение логарифмов базируется на основных свойствах:
1.
Из определения логарифма
получаем log a 1 = 0, так как ![]() = 1.
= 1.
2.
Так как ![]() = а, то log
a а = 1.
= а, то log
a а = 1.
|
|
Формула |
Пример |
|
Произведение |
loga(xy) = logax+ logay |
log3243= log3(9 ∙27) = log39 + log327 = 2 + 3 = 5 |
|
Частное |
loga( |
lg |
|
Степень |
loga |
log264 = log2 |
|
Корень |
loga |
lg |
3.
logax
=
Логарифм положительного числа х
по одному основанию а равен логарифму этого же числа х по новому
основанию b, делённому на логарифм прежнего основания а по новому
основанию b.
![]()
4.
logab
=
logab
=
![]()
![]() . Учитывая, что
. Учитывая, что ![]() , имеем
, имеем
5. Аналогично, учитывая формулу перехода к новому основанию и формулу логарифма степени получаем формулу
logab =
![]()
Например, log827 = ![]() = log23
= log23
Решение упражнений на применение свойств логарифмов:
1) Вычислить: а) ![]() +
+ ![]() ; б)
; б) ![]() -
- ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
2)
Действие нахождения
логарифма числа (выражения) называется логарифмированием. Прологарифмируйте
выражение y = ![]() .
.
3)
Потенцирование - нахождения
числа (выражения) по его логарифму. Пропотенцировать выражение lg x = ![]() lg5a – 3lg b + 4lg c/.
lg5a – 3lg b + 4lg c/.
4) Выполнить упражнения: № 5.4, № 5.6, № 5.8, 5.16,№5.18, № 5.20.
Домашнее задание: Гл. I, §5, п. 5.1; 5.2 № 5.11, № 5.12 ; № 5.13, № 5.17 учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Построение графиков показательной функции с помощью преобразований»
План
1. Определение показательной функции, её свойства и график.
2. Построение графиков показательной функции.
Если
а положительное, то для любого числа х степень ![]() имеет вполне определённое положительное
значение. Поэтому
имеет вполне определённое положительное
значение. Поэтому ![]() является функцией переменной х, которая
определена на всей числовой оси, то есть х
является функцией переменной х, которая
определена на всей числовой оси, то есть х ![]() (-
(-![]() ).
).
Функция
y = ![]() , где a > 0
и a
, где a > 0
и a ![]() 1 называется показательной с основанием а.
1 называется показательной с основанием а.
Так
функции y = ![]() , y =
, y = ![]() , y =
, y = ![]() - показательные. Выясним сущность ограничений a
> 0 и a
- показательные. Выясним сущность ограничений a
> 0 и a ![]() 1.
1.
1) Требование
a > 0. Если а = 0 и х ![]() 0, то выражение
0, то выражение ![]() не имеет смысла. Например, выражение
не имеет смысла. Например, выражение ![]() ,
, ![]() ,
, ![]() лишены смысла.
лишены смысла.
Если
а <0 и х – несократимая дробь, знаменатель которой чётный, то
выражение ![]() не имеет смысла. Например, степень
не имеет смысла. Например, степень ![]() =
= ![]() =
= ![]() не может быть выражена действительным числом.
не может быть выражена действительным числом.
2) Требование а ![]() . Если а = 1, то каждое значение
. Если а = 1, то каждое значение ![]() равно 1, то есть функция сводится к постоянной.
Этот случай ничего нового не добавляет к определению показательной
функции, поэтому его исключают.
равно 1, то есть функция сводится к постоянной.
Этот случай ничего нового не добавляет к определению показательной
функции, поэтому его исключают.
Рассмотрим
функцию y = ![]() . Составим таблицу значений функции
. Составим таблицу значений функции
|
х |
-4 |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
1 |
2 |
4 |
8 |
16 |
Построим в
координатной плоскости точки по координатам, взятым из этой таблицы: (-
4; ![]() ); (- 3;
); (- 3; ![]() ); (- 2;
); (- 2; ![]() ); (- 1;
); (- 1; ![]() ); (0; 1); (1; 2); (2; 4); (3;8); (4; 16).
); (0; 1); (1; 2); (2; 4); (3;8); (4; 16).
Построенные точки соединим
плавной линией, так как функция определена для всех х ![]() (-
(-![]() ) и является непрерывной.
) и является непрерывной.
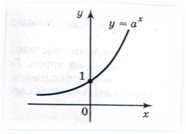
Построенную линию называют
графиком функции y = ![]() . Как видим из графика, функция принимает
только неотрицательные значения Е(y)
= (0;
. Как видим из графика, функция принимает
только неотрицательные значения Е(y)
= (0; ![]() ),
является возрастающей.
),
является возрастающей.
Составим
аналогичную таблицу для функции y = ![]() .
.
|
х |
-4 |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
4 |
|
|
16 |
8 |
4 |
2 |
1 |
|
|
|
|
Построим в координатной
плоскости точки по координатам, взятым из этой таблицы: (- 4; ![]() ); (- 3;
); (- 3; ![]() ); (- 2;
); (- 2; ![]() ); (- 1;
); (- 1; ![]() ); (0; 1); (1;
); (0; 1); (1; ![]() ); (2;
); (2; ![]() ); (3;
); (3;![]() ); (4;
); (4; ![]() ).
).
Построенные, точки соединим
плавной линией, так как функция определена для всех х ![]() (-
(-![]() ) и является непрерывной.
) и является непрерывной.
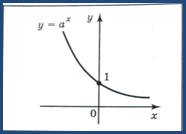
Построенную линию называют графиком функции y
= ![]() . Как
видим из графика, функция принимает только неотрицательные значения Е(y) = (0;
. Как
видим из графика, функция принимает только неотрицательные значения Е(y) = (0; ![]() ), является убывающей.
), является убывающей.
Свойства показательной функции:
|
|
y = |
y = |
|
|
Область определения |
R, х
|
||
|
Область значений |
Е(y) = (0;
|
||
|
Чётность, нечётность |
Общего вида
|
||
|
Точки пересечения с осями координат |
Аy (0; 1), ось Ох не пересекает, ось Ох называется горизонтальная асимптота |
||
|
Промежутки знакопостоянства |
Принимает только неотрицательные значения |
||
|
Промежутки возрастания и убывания |
Возрастающая |
Убывающая |
|
|
Экстремумы, особые точки |
Нет |
||
|
Наибольшее и наименьшее значения |
Нет |
||
|
Поведение при сколь угодно больших по модулю значениях аргумента |
Если х Если х |
Если х Если х |
|
Построенную линию, которая является графиком показательной функции, называют ЭКСПОНЕНТА.
Свойства показательной функции, рассмотренные ранее:
![]() ∙
∙ ![]() =
= ![]()
![]() :
: ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() ∙
∙ ![]()
![]() =
= ![]()
![]() =
= ![]()
Отметим
ещё одно свойство показательной функции , которое выделяет её из ряда
других функций: если f(x) = ![]() ( a>0,
a
( a>0,
a ![]() 1), то при любых действительных значениях
аргументов x1 и x2 выполняется равенство f(x1) ∙ f(x2) = f(x1 + x2).
1), то при любых действительных значениях
аргументов x1 и x2 выполняется равенство f(x1) ∙ f(x2) = f(x1 + x2).
Кроме общих свойств показательной функции отметим некоторые особенности поведения графиков функции при различных значениях а.
Чем больше
основание а (а > 1) тем круче поднимается график функции y = ![]() при движении точки х вправо и тем быстрее
приближается к оси Ох при движении точки х влево;
при движении точки х вправо и тем быстрее
приближается к оси Ох при движении точки х влево;
чем меньше основание а (0<
а <1), тем круче поднимается график функции y = ![]() при движении точки х влево и тем быстрее
приближается к оси Ох при движении точки х вправо.
при движении точки х влево и тем быстрее
приближается к оси Ох при движении точки х вправо.
Изобразить
схематически график функции y = ![]()
Последовате6льность построения графика:
1)
Строим график функции y = ![]()

2)
Строим график функции y = ![]()
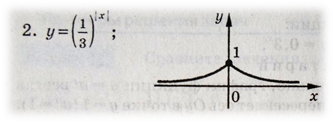
3)
Строим график функции y = ![]() - 3
- 3 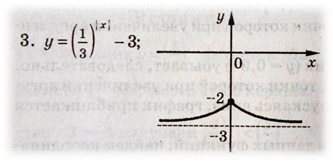
4) Строим график функции y = ![]()
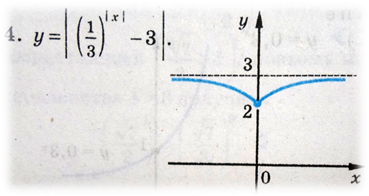
Постройте
графики функций: а) y = - ![]() ; б) y =
; б) y = ![]() в) y =
в) y = ![]() г) y =
г) y = ![]() д) y =
д) y = ![]()
Домашнее задание: Гл. I, §4, п. 4.8; № 4.60, № 4.61 ; учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Построение графиков логарифмической функции с помощью преобразований»
План.
1. Понятие логарифмической функции. Свойства и график логарифмической функции.
2. Построение графиков функций
Цель: систематизировать знания о логарифмической функции, её свойствах и графике; расположением графиков логарифмической функции при различных основаниях а; научиться строить графики логарифмической функции с помощью геометрических преобразований; развитие логического мышления и математической культуры обучающихся.
Определение.
Логарифмической называется функция y = loga x, где а > 0, а ![]() 1, обратная показательной функции.
1, обратная показательной функции.
График
функции y = loga x можно получить, отобразив
график функции y = ![]() , симметрично относительно прямой y =
х.
, симметрично относительно прямой y =
х.
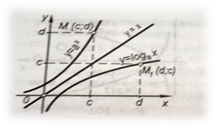
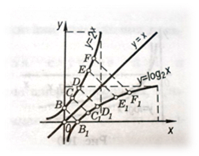
Графики показательной и логарифмической функций, которые имеют одинаковые основания, симметричны относительно прямой y = х, так как функции
![]() y =
y = ![]() и y =
и y = ![]() являются взаимно обратными:
являются взаимно обратными:
Функция y
= ![]() , где а
- заданное число
, где а
- заданное число
а > 0, а ![]() 1 имеет следующие свойства:
1 имеет следующие свойства:
Свойства логарифмической функции
|
Свойства |
y = loga x, где а > 1 |
y = loga x, где (0< а <1) |
|
Область определения |
(0; |
|
|
Область значений |
R, х
|
|
|
Чётность, нечётность |
Общего вида |
|
|
Точки пересечения с осями координат |
Ах (1; 0), ось Оу не пересекает, ось Оу называется вертикальная асимптота |
|
|
Промежутки знакопостоянства |
На числовом
промежутке от 0 до 1 – отрицательные значения, от 1 до |
На числовом
промежутке от 0 до 1 – положительные значения, от 1 до |
|
Промежутки возрастания и убывания |
возрастающая |
убывающая |
|
Экстремумы, особые точки |
нет |
|
|
Наибольшее и наименьшее значения |
нет |
|
|
Поведение при сколь угодно больших по модулю значениях аргумента |
При х При х
стремящемся от 1 к + |
При х При х
стремящемся от 1 к + |
Из этих свойств вытекает,
что функция y = ![]() имеет следующие графики:
имеет следующие графики:
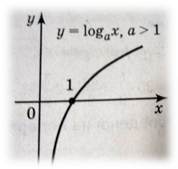
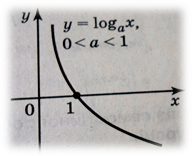
Решение упражнений на применение свойств логарифмической функции:
Найти область определения
функции y = ![]() .
.
Решение. (использовать опорный конспект «Ограничения на область определения функций»).
![]() > 0. Решить это неравенство методом
интервалов: а) 2х-6 = 0; 2х = 6; х = 3 - корень; х+2 = 0; х = - 2
– точка, в которой функция не существует.
> 0. Решить это неравенство методом
интервалов: а) 2х-6 = 0; 2х = 6; х = 3 - корень; х+2 = 0; х = - 2
– точка, в которой функция не существует.
- 2 - 3 +
+
Ответ: D(y)
= (- ![]() ; -2)
; -2) ![]() [3;
[3; ![]() )
)
Определяем знаки функции y
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() на каждом
из числовых промежутков.
на каждом
из числовых промежутков.
Пример № 1. Найти область определения функции: а) y = ![]() б) y =
б) y = ![]() в) y =
в) y = ![]() .
.
Пример 2. Построить
схематически график функции
y =
![]()
Последовательность построения графика функции :
1.
y = ![]()
2. y = ![]()
3. y = ![]()
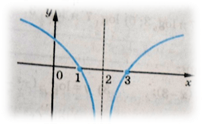
Построить графики функций; № 5.35 (учебник).
Домашнее задание: Гл. I, §5, п. 5.3; № 5.36, учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Решение показательных уравнений и неравенств».
План.
1. Основные формулы и соотношения
2. Решение простейших показательных уравнений.
3. Некоторые методы решения показательных уравнений.
4. Решение показательных неравенств.
Цель: рассмотреть основные формулы и соотношения, применяемые при решении показательных уравнений и неравенств; сформировать умение решать простейшие показательные уравнения; сформировать умение решать показательные уравнения методом сведения к общему основанию, методом вынесения за скобки общего множителя, способом приведения к общему показателю; познакомить студентов со способами решения показательных неравенств; развитие логического мышления и математической культуры.
Показательными уравнениями обычно называют уравнения, в которых переменная входит в показатель степени (основание этой степени переменной не содержит).
|
Основные формулы и соотношения |
|||
|
|
Графики функции y = |
||
|
a > 1 |
0 < a < 1 |
a = 1 |
|
|
|
|
|
|
Рассмотрим простейшее показательное уравнение вида
![]() = b,
= b,
где
а > 0, а ![]() 1.
Поскольку при этих значениях а, функция y =
1.
Поскольку при этих значениях а, функция y = ![]() строго
монотонная ( а
строго
монотонная ( а ![]() строго возрастает, при 0< а <1 - строго
убывает), то каждое своё значение она принимает только при одном
значении аргумента. Это означает, что уравнение,
строго возрастает, при 0< а <1 - строго
убывает), то каждое своё значение она принимает только при одном
значении аргумента. Это означает, что уравнение, ![]() = b при b > 0
имеет единственный корень. Чтобы его найти достаточно представить b в
виде b =
= b при b > 0
имеет единственный корень. Чтобы его найти достаточно представить b в
виде b = ![]() .
.
Очевидно,
что х = с является корнем уравнения, ![]() =
= ![]() . Например, решить уравнение
. Например, решить уравнение ![]() = 121, достаточно представить это уравнение в
виде
= 121, достаточно представить это уравнение в
виде ![]() =
= ![]() и записать его единственный корень х = 2.
и записать его единственный корень х = 2.
Если
b ![]() 0, то уравнение,
0, то уравнение, ![]() = b (при
а
= b (при
а ![]() корней не имеет, поскольку функция y =
корней не имеет, поскольку функция y = ![]() всегда
принимает только положительные значения.
всегда
принимает только положительные значения.
Например,
уравнение ![]() = - 121 не имеет корней.
= - 121 не имеет корней.
Решить уравнения:
а) ![]() = 125; б)
= 125; б) ![]() = 49; в)
= 49; в) ![]() = 1 (Указание. Любое число в нулевой степени
равно 1: 1 =
= 1 (Указание. Любое число в нулевой степени
равно 1: 1 = ![]() ); г)
); г) ![]() = - 2; д)
= - 2; д) ![]() = 32; е)
= 32; е) ![]() =
= ![]() ; ж)
; ж) ![]() = 1; з)
= 1; з) ![]() = 5;
= 5;
Решить уравнения, применив свойства:
а) ![]() ·
· ![]() б)
б) ![]() ·
· ![]() = 36; в)
= 36; в) ![]() = 4; г)
= 4; г) ![]() = 4
= 4![]() .
.
МЕТОДЫ РЕШЕНИЯ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ.
Способ приведения уравнения к общему основанию.
Обобщая приведённые выше рассуждения относительно решения простейших показательных уравнений, отметим, что
при а ![]() и а
и а ![]() 1 уравнение вида
1 уравнение вида
![]() =
= ![]()
равносильно уравнению
f(x) = g(x).
Коротко это утверждение можно записать так:
при а ![]() и а
и а ![]() 1
1
![]() =
= ![]()
![]() f(x) = g(x).
f(x) = g(x).
Пример
1. Решить уравнение ![]() = 1.
= 1.
Решение.
![]() = 1; приведём уравнение к виду
= 1; приведём уравнение к виду ![]() =
= ![]() , где а
, где а ![]() и а
и а ![]() 1 и перейдём к равносильному.
1 и перейдём к равносильному.
f(x) = g(x).
![]() =
= ![]() ;
;
![]() = 0;
= 0;
х = 2 или х = - 2;
Ответ: -2; 2.
Чтобы привести
уравнение к виду ![]() =
= ![]() применяют
свойства степени (см. таблицу)
применяют
свойства степени (см. таблицу)
Решить уравнения: Решить уравнения, применив свойства:
а) ![]() ·
· ![]() б)
б) ![]() ·
· ![]() = 36; в)
= 36; в) ![]() = 4; г)
= 4; г) ![]() = 4
= 4![]() .
.
д) ![]() = 0,125; е)
= 0,125; е) ![]() - 1 = 0; з)
- 1 = 0; з) ![]() =
= ![]() ; и)
; и) ![]() = 1; к)
= 1; к) ![]() ·
· ![]() = 0,1
= 0,1![]()
Способ вынесения общего множителя за скобки.
Пример 1. Решить уравнение ![]() -2 ·
-2 · ![]() = 63.
= 63.
Решение.
![]() -2 ·
-2 · ![]() = 63;
= 63;
![]() (
(![]() - 2) = 63 - в левой части уравнения выносим за
скобки 3 в наименьшей степени;
- 2) = 63 - в левой части уравнения выносим за
скобки 3 в наименьшей степени;
![]() · 7 = 63 - делим обе части уравнения на 7;
· 7 = 63 - делим обе части уравнения на 7;
![]() = 9;
= 9;
![]() =
= ![]() < = > х-2 = 2 < = > х
= 4.
< = > х-2 = 2 < = > х
= 4.
Ответ: 4.
Пример 2. Решить уравнение ![]() -
- ![]() +
+ ![]() +
+ ![]() = 0.
= 0.
Решение.
![]() -
- ![]() +
+ ![]() +
+ ![]() = 0 - группируем члены в левой части уравнения;
= 0 - группируем члены в левой части уравнения;
![]() -
- ![]() ) +(
) +( ![]() +
+ ![]() = 0 - в каждой группе выносим общий множитель;
= 0 - в каждой группе выносим общий множитель;
![]() (
(![]() - 1) +
- 1) + ![]() (1+
(1+ ![]() = 0;
= 0;
![]() ·
· ![]() +
+ ![]() · 5 = 0;
· 5 = 0;
![]() · 5 =
· 5 = ![]() ·
· ![]() - делим обе части уравнения на
- делим обе части уравнения на ![]() ·
· ![]() ;
;
![]() = 1 < = >
= 1 < = > ![]() ·
· ![]() = 1 < = >
= 1 < = > ![]() =
= ![]() < = >
< = > ![]() =
= ![]() < = > 2х = 2 < = > х=1.
< = > 2х = 2 < = > х=1.
Ответ: 1.
Решить уравнения: а) ![]() -
- ![]() =
= ![]() -
- ![]() ; б)
; б) ![]() + 4 ·
+ 4 · ![]() =
= ![]() -
- ![]()
Способ приведения уравнения к квадратному.
Пример 1. Решить уравнение ![]() - 8 ·
- 8 · ![]() + 7 = 0.
+ 7 = 0.
Решение.
![]() - 8 ·
- 8 · ![]() + 7 = 0;
+ 7 = 0;
![]() - 8 ·
- 8 · ![]() + 7 = 0;
+ 7 = 0;
![]() - 8 ·
- 8 · ![]() + 7 = 0 - замена t =
+ 7 = 0 - замена t = ![]() ;
;
![]() - 8t + 7 = 0 < = > t1 = 7 и t2 = 1;
- 8t + 7 = 0 < = > t1 = 7 и t2 = 1;
Возвращаемся к замене ![]() = 7 или
= 7 или ![]() = 1. Тогда х1 = 1 и х2 =
0.
= 1. Тогда х1 = 1 и х2 =
0.
Ответ: 0; 1.
Решить уравнения: а) ![]() + 4 ·
+ 4 · ![]() - 5 = 0; б)
- 5 = 0; б) ![]() - 5 ·
- 5 · ![]() - 6 = 0;
- 6 = 0;
РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ НЕРАВЕНСТВ.
|
График показательной функции |
|
|
a > 1 |
0 < a < 1 |
|
|
|
|
|
|
|
Схема равносильных преобразований |
|
|
Знак неравенства сохраняется |
Знак неравенства меняется на противоположный
|
|
Примеры |
|
|
x > 6 ответ : (6; |
Ответ: (- |
Решение более сложных показательных неравенств.
|
Пример 1. |
Пояснение |
||||||
|
4 · 4
Первое неравенство не имеет решения. Из второго неравенства х > - 2. Ответ: (- 2;
|
С помощью равносильных преобразований (по схеме решения показательных уравнений) данное неравенство приводят к неравенству известного вида (квадратному, дробному и т. д.)
Возвращаемся к замене и получаем два простейших показательных неравенства |
||||||
|
Пример 2. |
|
||||||
|
1.ОДЗ . х 2.Нули функции f(x)
=
- + 1
4.Ответ: (1; |
Применяем общий метод интервалов, приведя неравенство к виду f(x) > 0 и используя схему: 1.Найти ОДЗ. 2.Найти нули функции f(x). 3.отметить нули на ОДЗ и найти знак функции f(x) на каждом из промежутков, на которые разбивается ОДЗ. 4.Записать ответ, учитывая знак неравенства. |
Решить неравенства: а) ![]() + 8 ·
+ 8 · ![]() - 3
- 3 ![]() 0; б)
0; б) ![]() - 12 ·
- 12 · ![]() + 27
+ 27 ![]() 0.
0.
Домашнее задание: Гл. I, §6, п. 6.1; 6.3; 6.4; 6.6 № 6.6 (1 ст.), № 6.21(1 ст), № 6.34(а, б) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Решение логарифмических уравнений и неравенств»
План.
1.Основные формулы и соотношения
2.Решение простейших логарифмических уравнений.
3.Некоторые методы решения логарифмических уравнений.
4.Решение логарифмических неравенств.
Цель: рассмотреть основные формулы и соотношения, применяемые при решении логарифмических уравнений и неравенств; сформировать умение решать простейшие логарифмические уравнения; сформировать умение решать логарифмические уравнения различными методами; развитие логического мышления и математической культуры.
Логарифмическими уравнениями называют уравнения, которые содержат переменную под знаком логарифма.
Например, ![]() = 9,
= 9, ![]() = lg
= lg![]() , lgx = 1+
, lgx = 1+ ![]() .
.
Решить логарифмическое уравнение - это значит найти все его корни или доказать , что уравнение не имеет корней.
|
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И СООТНОШЕНИЯ |
|
|
ОПРЕДЕЛЕНИЕ:
логарифмом положительного числа b по основанию а (а >
0, a
|
|
|
a > 1 |
0 < a < 1 |
|
|
|
|
РЕШЕНИЕ ПРОСТЕЙШИХ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ |
|
|
Пример |
Обоснование |
|
х-1 = х = 10. |
Если число а (а > 0, a
|
|
РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ |
|
|
2х + 1 = 9 < = > х= 4. |
Используем свойство логарифма Используем свойство n Используем свойство если |
|
t1 = 3 t2 = - 1 lgx = 3 или lgx= - 1 x1
= x1 = 1000 или x2 = 0.1 |
Если в уравнение (неравенство) переменная входит в одном и том же виде, то удобно соответствующее выражение обозначить новой переменной. |
|
Ответ: 1; 3. |
Уравнение вида
(учитываем ОДЗ и приравниваем выражения, стоящие под знаком логарифма) |
|
ОДЗ: На ОДЗ уравнение равносильно уравнениям:
(х+1)(х+3) = 8
х1 = 1 – удовлетворяет ОДЗ; х2 = - 5 посторонний корень ( не удовлетворяет условию ОДЗ) Ответ: 1. |
1. Учитываем ОДЗ данного уравнения и избегаем преобразований, приводящих к сужению ОДЗ. 2. Следим за тем, чтобы на ОДЗ каждое преобразование можно было выполнить как в прямом, так и в обратном направлениях с сохранением верного равенства. |
Решить уравнения:
1)
![]() =2; lg(3-x) = - 1;
=2; lg(3-x) = - 1; ![]()
2)
lg(x+9) + lg(2x+8) =
2; ![]() +
+ ![]() = 1;
= 1;
3)
![]() x - 4
x - 4![]() + 3 = 0;
+ 3 = 0; ![]() x +
x + ![]() = 8;
= 8;
4)
lg(2![]() lg(2
lg(2![]()
Решение логарифмических неравенств.
Простейшими логарифмическими неравенствами считают неравенства вида
![]() >
> ![]() (а > 0, a
(а > 0, a ![]() ).
).
Для решения такого неравенства можно применять равносильные преобразования.
Для этого необходимо учесть ОДЗ: ![]() и рассмотреть два случая: 1) a
> 1; 2) 0 < a < 1.
и рассмотреть два случая: 1) a
> 1; 2) 0 < a < 1.
Если a > 1, то функция y = ![]() возрастает на всей области определения.
возрастает на всей области определения.
![]() Следовательно,
Следовательно,
Пример 1. ![]() > 3.
> 3.
ОДЗ: х-5 > 0 < = > x > 5
![]() > 3
> 3 ![]() < = >
< = > ![]() >
> ![]() <
= >
<
= > ![]() >
> ![]() .
.
При a> 1 x-5 > 8 < = > x > 13.
Ответ: (13; ![]() ).
).
Пример 2.
![]() > 3.
> 3.
![]() > 3
> 3 ![]() < = >
< = > ![]() >
> ![]() < = >
< = > ![]() >
> ![]() .
.
При 0 < a < 1 x-5
< ![]() < = > x < 5
< = > x < 5![]() .
.
Учитывая ОДЗ, можно записать ответ.
Ответ: (5; 5![]() ).
).
Пример 3. Решение неравенства приводимого к квадратному.
Решить неравенство ![]() – lg x
– lg x ![]() 3.
3.
ОДЗ: х > 0. На этой области определения неравенство равносильно неравенствам:
![]()
![]()
![]() - lg x
- lg x ![]() 3 < = >
3 < = > ![]() - lg x
- lg x ![]() 3; замена lg x = t/
3; замена lg x = t/
-2 1
![]() -t
-t ![]() 3 < = >
3 < = > ![]() + t – 2
+ t – 2 ![]() 0
0
![]()
Следовательно, t ![]() -2 и t
-2 и t ![]() 1. Обратная замена даёт lg x
1. Обратная замена даёт lg x ![]() -2 и
lg x
-2 и
lg x ![]() 1.
1.
lg x ![]() lg
lg ![]() и lg x
и lg x ![]() lg 10 < = > x
lg 10 < = > x![]() 0,01 и x
0,01 и x ![]() 10. С учётом ОДЗ записываем ответ.
10. С учётом ОДЗ записываем ответ.
Ответ: (0; 0,01] ![]() [10;
[10; ![]() ).
).
Домашнее задание: Гл. I, §6, п. 6.2; 6.11 (а,б); 6.22(а,в); 6.20 (б) № 6.41 (1 стр.) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Радианная мера угла»
План .
1.Понятие угла.
2.Измерение углов.
3.Радианная мера угла.
Цель: обобщение и систематизация знаний учащихся о радианном измерении углов; формирование умения переводить градусную меру угла в радианную и радианную меру в градусную; развитие логического мышления.
|
ПОНЯТИЕ УГЛА |
||||||||||||||||
|
В геометрии |
В тригонометрии |
|||||||||||||||
|
А
|
В А |
|||||||||||||||
|
ИЗМЕРЕНИЕ УГЛОВ |
||||||||||||||||
|
Градусная мера угла (1 ̊ = |
||||||||||||||||
|
В
|
В
|
|||||||||||||||
Радианная мера угла |
||||||||||||||||
|
|
|
|||||||||||||||
1.
Выразить в радианах величины
углов: 30 ̊; 45 ̊; 60 ̊; 90 ̊; 270 ̊; 360 ̊; 540 ̊ Пример. Выразить в радианах угол 225 ̊. Решение: 225 ̊· ![]() =
= ![]() =
= ![]() .
.
2.
Выразите в градусах величины
углов: ![]() ;
; ![]() ;
; ![]() ; 5; 3π; -
; 5; 3π; -![]() ;
; ![]() ; Пример. Выразить в градусах величину угла
; Пример. Выразить в градусах величину угла ![]() . Решение:
. Решение: ![]() ·
· ![]() =
= ![]() = 210 ̊.
= 210 ̊.
Вопросы для контроля.
1) Объясните, как можно определить угол с помощью поворота луча? Как при таком определении измеряются углы?
2) Как вы понимаете такие утверждения: «Величина угла равна 450 ̊?», «Величина угла равна (- 225) ̊»? Изобразите эти углы.
3) Как определить угол в 1 ̊?
4) Дайте определение угла в 1 радиан.
5) Чему равна градусная мера угла в π радиан?
6) Объясните на примерах, как по радианной мере угла найти его градусную меру и наоборот - по градусной мере угла найти его радианную меру.
Домашнее задание: Гл.I I, §7, п. 7.1, 7.2; № 7.16, 7.17 учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Тригонометрические функции угла и числового аргумента».
План.
1. Определение тригонометрических функций.
2. Тригонометрические функции числового аргумента.
3. Линии тангенсов и котангенсов.
4. Решение типовых упражнений.
Цель: формирование понятия тригонометрических функций числового аргумента, изучение значений тригонометрических функций некоторых чисел (углов); изменение знаков тригонометрических функций в координатных углах.
Решить упражнения.
1) Представьте в радианной мере углы: 5 ̊; 1140 ̊; - 765 ̊.
2) Представьте в градусной мере углы: ![]() 1,25π; 1; 10.
1,25π; 1; 10.
3) Найдите длину дуги, если на неё опирается
центральный угол ![]() =
= ![]() , а радиус круга равен 10 м. Решение. По
определению радианного измерения углов
, а радиус круга равен 10 м. Решение. По
определению радианного измерения углов ![]() (рад.) =
(рад.) = ![]() . Следовательно,
. Следовательно, ![]() =
= ![]() (рад.) ·
(рад.) · ![]() .
. ![]() =
= ![]() · 10 =
· 10 = ![]() (м).
(м).
|
ОПРЕДЕЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ |
||||||||||||||||||||||||||
|
Через единичную
окружность ( |
Через произвольную окружность |
B |
||||||||||||||||||||||||
|
|
O x y |
C A c b a |
||||||||||||||||||||||||
|
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА |
||||||||||||||||||||||||||
|
sin (числа
cos (числа
tg (числа ctg (числа |
||||||||||||||||||||||||||
|
Y
Ось Оy - называется линией синусов. Синус угла (числа) это ордината соответствующей точки на линии синусов. Ось Ох - называется линией косинусов. Косинус угла (числа) это абсцисса соответствующей точки на линии косинусов. |
A(1,
Y
АС – линия тангенсов (АС |
Линия котангенсов
C B( Y
ВС – линия котангенсов (ВС |
||||||||||||||||||||||||
|
ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ |
||||||||||||||||||||||||||
|
III четверть II четверть Y
|
||||||||||||||||||||||||||
Введённые определения тригонометрических функций и их некоторых
свойств, позволяют вычислять значения тригонометрических функций углов. Для
этого удобно пользоваться таблицей значений тригонометрических функций
некоторых углов:
|
|
В градусах |
0 ̊ |
30 ̊ |
45 ̊ |
60 ̊ |
90 ̊ |
180 ̊ |
270 ̊ |
360 ̊ |
|
В радианах |
0 |
|
|
|
|
π |
|
2π |
|
|
sin |
0 |
|
|
|
1 |
0 |
|
0 |
|
|
cos |
1 |
|
|
|
0 |
|
0 |
1 |
|
|
tg |
0 |
|
1 |
|
― |
0 |
― |
0 |
|
|
ctg |
― |
|
1 |
|
0 |
― |
0 |
― |
|
1)
S L К М N Р 1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Каким числам соответствуют точки
Каким числам соответствуют точки ![]() K, L, S если известно, что точка N середина
дуги
K, L, S если известно, что точка N середина
дуги ![]() , а дуги
, а дуги ![]() , РМ, МК равны.
, РМ, МК равны.
2) Обозначьте на одной окружности точки, которые соответствуют числам:
![]() + 2πn, -
+ 2πn, - ![]() + 2πn,
+ 2πn,
![]() +2πn, -
+2πn, - ![]() +2πn,
+2πn, ![]() + 2πn,
+ 2πn, ![]() + 2πn,
+ 2πn, ![]() + 2πn,
+ 2πn, ![]() + 2πn.
+ 2πn.
3)Вычислить: cos 7π,
sin 7π, cos ![]() , sin
, sin ![]() ,
,
4) Вычислить: : sin ![]() + sin
+ sin ![]() , sin(-
, sin(- ![]() ) + cos
) + cos ![]() , sin π + sin 1,5 π, cos 0
+ cos 3,5 π – cos 3π.
, sin π + sin 1,5 π, cos 0
+ cos 3,5 π – cos 3π.
5) Вычислить: tg π, tg (-π), tg 4π,
tg ![]() .
.
6)Определите знак числа: tg ![]() ; tg(-
; tg(- ![]() ; tg
; tg ![]() ; сtg(-
; сtg(- ![]() ;
;
7) Вычислить:
3 sin ![]() + 2 cos
+ 2 cos![]() - tg
- tg ![]() ; 5 sin
; 5 sin ![]() + 3 tg
+ 3 tg ![]() - 5 cos
- 5 cos ![]() - 10 сtg
- 10 сtg ![]() ;
;
![]() : cos
: cos ![]() ; sin
; sin ![]() · cos
· cos![]() - tg
- tg ![]() .
.
8)В какой четверти находится точка ![]() , если sin α > 0 и cos α> 0; если sin α < 0 и cos α> 0; если sin α > 0 и cos α < 0; если sin α < 0 и cos α < 0;
, если sin α > 0 и cos α> 0; если sin α < 0 и cos α> 0; если sin α > 0 и cos α < 0; если sin α < 0 и cos α < 0;
9) В какой четверти находится точка ![]() , если sin α ·cos α
> 0; если sin α
· cos α <
0; если tg α
· cos α >
0; если ctg α
· sin α <
0;
, если sin α ·cos α
> 0; если sin α
· cos α <
0; если tg α
· cos α >
0; если ctg α
· sin α <
0;
10) Определите знак выражения: sin 105 ̊ · cos 105 ̊; tg 127 ̊ · ctg 200 ̊; cos 155 ̊ · sin 225 ̊; tg 351 ̊ · ctg 220 ̊;
11) Определите знак произведения:
tg 2 · tg 3 · ctg 3 · cos 1; sin 1 · cos 2 ·tg 3 · ctg 4.
Домашнее задание: Гл.I I, §7, 8, п. 7.3, 8.1; № 7.32, 7.45, 7.47
(в,г), 8.5 учебник «Алгебра и начала математического анализа» 10 класс,
С.М. Никольский, М, Просвещение, 2014
Тема: «Свойства тригонометрических функций»
y
|
|
|
|
|
|
|
|
|
|
f(x) = f(x + T) = f(x- T) |
|
|
|
|
|
|
|
|
(A, k, b - некоторые числа и k |
|
Учитывая, что значение функции
π) = = 1.
2)
Среди данных функций найдите
периодические и укажите наименьший положительный период для каждой из
них: а) f(x) = ![]() б) f(x) = sin 2x в) f(x) =
б) f(x) = sin 2x в) f(x) = ![]() г) f(x) = tg 3x
д) f(x) = 3.
г) f(x) = tg 3x
д) f(x) = 3.
3)
Найдите период каждой из
данных функций: а) y = cos 2x б) y = tg 5x
в) y = sin ![]() г) y = ctg 3x
д) y = cos
г) y = ctg 3x
д) y = cos ![]() . Пример.
Найти период функции y = ctg
. Пример.
Найти период функции y = ctg ![]() .
Решение. Наименьший положительный период функции y = ctg x равен =
.
Решение. Наименьший положительный период функции y = ctg x равен = ![]() .
.
4) На каждом из рисунков (рис.1 - рис.4) приведена часть графика некоторой периодической функции с периодом Т. Продолжите график на отрезке [-2T, 3T].
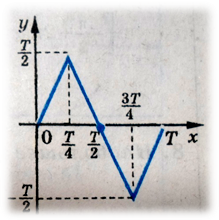
Домашнее задание: Гл.I I, §7, 8, п. 7.3, 8.1; № 7.31, 7.47(г), 7.46 , 8.5 учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Основные формулы».
Цель: изучить соотношения между тригонометрическими функциями одного аргумента сформировать умение применять эти соотношения для тождественных преобразований (упрощения) выражений; нахождения значений тригонометрических функций угла, если известна одна из них.
План .
1. Соотношения между тригонометрическими функциями одного аргумента.
2. Решение типовых задач на применение соотношений между тригонометрическими функциями одного аргумента.
|
O y α 1 1 x |
Основное тригонометрическое тождество
|
||||||||||||||||
|
Задача 1. Зная значение одной из тригонометрических функций и интервал,
в котором находится ![]() , найти значение трёх остальных тригонометрических
функций.
, найти значение трёх остальных тригонометрических
функций.
Дано: sin α = ![]() и 90 ̊< α < 180 ̊. Найти: cos α,
tg α, ctg α.
и 90 ̊< α < 180 ̊. Найти: cos α,
tg α, ctg α.
Решение .
1) Из равенства ![]() +
+ ![]() = 1 получаем:
= 1 получаем:
![]() = 1 -
= 1 - ![]() . Из
которого
. Из
которого ![]() = 1-
= 1- ![]() = 1 -
= 1 - ![]() =
= ![]() ; поскольку
90 ̊< α < 180 ̊(вторая четверть), то cos x = -
; поскольку
90 ̊< α < 180 ̊(вторая четверть), то cos x = -
![]() = -
= - ![]() .
.
2)
Из равенства tgx = ![]() находим tgx =
находим tgx = ![]() : (-
: (-![]() ) = -
) = - ![]() .
.
3)
Из равенства сtgx = ![]() находим ctgx
= -
находим ctgx
= - ![]() :
: ![]() = -
= - ![]() .
.
Задачи для самостоятельного решения.
а) дано: sin x = - ![]() ,
, ![]() ̊< x < 2π. Найти: cos α,
tg α, ctg α.
̊< x < 2π. Найти: cos α,
tg α, ctg α.
б) дано: cos x = - 0.8, ![]() ̊< x < π. Найти: sin α,
tg α, ctg α.
̊< x < π. Найти: sin α,
tg α, ctg α.
Задача 2.
Упростить выражение ![]() .
.
Решение. Для преобразования числителя дроби из основного
тригонометрического тождества ![]() +
+ ![]() = 1 находим
= 1 находим
![]() = 1 -
= 1 - ![]() . Затем
в знаменателе применяем формулу tgx =
. Затем
в знаменателе применяем формулу tgx = ![]() и упрощаем выражение.
и упрощаем выражение.
![]() =
= ![]() =
= ![]() .
.
Задача 3.
Упростить выражение ![]() -
- ![]() +
+ ![]() .
.
Решение . для преобразования тригонометрических выражений наряду с
тригонометрическими формулами (пример 1) используются также формулы
сокращённого умножения. Выражение ![]() -
- ![]() можно рассматривать как разность квадратов:
можно рассматривать как разность квадратов: ![]() -
- ![]() =
= ![]() -
- ![]() . Тогда его можно разложить на множители
(сумма квадратов синуса и косинуса и их разность) и применить основное
тригонометрическое тождество
. Тогда его можно разложить на множители
(сумма квадратов синуса и косинуса и их разность) и применить основное
тригонометрическое тождество ![]() +
+ ![]() = 1.
= 1.
![]() -
- ![]() +
+ ![]() =
= ![]() -
- ![]() +
+ ![]() = (
= (![]() ) (
) (![]() +
+ ![]() = (
= (![]() ) · 1 +
) · 1 + ![]() =
= ![]() +
+ ![]() =
= ![]() .
.
Задачи для самостоятельного решения.
Упростить выражения: а) 1 - ![]() б) (1 – cos α)
(1 +cos α); в)
б) (1 – cos α)
(1 +cos α); в)
![]() - tg α · ctg α,
г)
- tg α · ctg α,
г) ![]() + 2
+ 2 ![]() +
+ ![]() ,
,
д) (![]() + ctg α) (
+ ctg α) (![]() - ctg α).
- ctg α).
Задача 4.
Доказать тождество ![]() = 2.
= 2.
Доказательство.
Тождеством называется равенство верное
при всех допустимых значениях букв, входящих в него. Поэтому данное
равенство является тождеством при условии tgxα ![]() и cos α
и cos α ![]() 0.
0.
Докажем, что левая часть равна правой.
Для этого преобразуем левую часть, заменив tgxα = ![]() ,
а в числителе применяем формулу
сокращённого умножения и тождество
,
а в числителе применяем формулу
сокращённого умножения и тождество ![]() +
+ ![]() = 1.
= 1.
![]() =
= ![]() =
= ![]() = 2.
= 2.
2 = 2 что и требовалось доказать.
Задачи для самостоятельного решения.
Докажите тождества: а) ![]() +
+ ![]() = 2; б)
= 2; б) ![]() =
= ![]() в)
в) ![]() +
+ ![]() =
= ![]() .
.
Домашнее задание: Гл.I I, §7, 8, п. 7.4, 8.2; № 7.55, 7.59 8.22(д, е) , 8.25 учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Формулы суммы и разности аргументов»
План.
1. Формулы сложения.
2. Решение типовых задач с применением формул сложения.
Цель: изучение формул тригонометрических функций суммы и разности двух чисел;
формирование умен6ий применять изученные формулы для упрощения тригонометрических выражений и вычислений.
|
Косинус разности и суммы |
|||||||||
|
|
|||||||||
Синус суммы и разности |
|||||||||
|
|
|||||||||
Тангенс суммы и разности |
|||||||||
|
|
|
||||||||
Задача 1. Вычислите: sin 15 ̊, cos 15 ̊, tg 15 ̊/
Решение. Представим 15 ̊как разность 15 ̊= 45 ̊-30 ̊, значения тригонометрических функций 45 ̊и 30 ̊смотреть в таблице «Значения тригонометрических функций некоторых углов».
sin 15 ̊= sin (45 ̊-30
̊) = sin 45 ̊cos 30 ̊- cos 45 ̊sin 30 ̊ = ![]() ·
· ![]() -
- ![]() ·
· ![]() =
= ![]() .
.
cos 15 ̊= cos (45 ̊-30
̊) = cos 45 ̊cos 30 + sin
45 ̊sin
30 ̊ = ![]() ·
· ![]() +
+ ![]() ·
· ![]() =
= ![]() .
.
tg 15 ̊= tg (45 ̊-30 ̊) = ![]() =
= ![]() =
= ![]() .
.
Задачи для самостоятельного решения.
1) С помощью формул сложения вычислите: sin 75 ̊; cos 75 ̊; sin 105 ̊; cos 105 ̊.
Задача 2. Вычислите cos 18 ̊ cos 12 ̊ - sin 18 ̊ sin 12 ̊.
Решение.
cos
18 ̊ cos 12 ̊
- sin 18 ̊ sin
12 ̊ = cos (18 ̊+
12 ̊)= cos 30 ̊=
![]() .
.
Задачи для самостоятельного решения.
С помощью формул сложения вычислите: sin 13 ̊ cos 17 ̊ + cos 13 ̊ sin 17 ̊,
sin 78 ̊ cos 18 ̊ + cos 78 ̊ sin 18 ̊, cos 66 ̊ cos 6 ̊ + sin 66 ̊ sin 6 ̊ ,
cos 20 ̊ cos 25 ̊ - sin 20 ̊ sin 25. ̊
Задача 3. Упростить
выражение ![]() .
.
Решение.
Для преобразования числителя и знаменателя дроби применим формулы сложения косинуса суммы и косинуса разности и приведём подобные слагаемые.
![]() =
= ![]() =
= ![]() = tg α · tg β = 1.
= tg α · tg β = 1.
Задачи для самостоятельного решения.
Упростить выражения: а) sin 5α
cos 3α – cos 5α sin 3α,
б) ![]() , в)
, в) ![]() г)
г) ![]() д)
д) ![]() .
.
![]() При решении тригонометрических уравнений
применяются тождества:
При решении тригонометрических уравнений
применяются тождества:
Доказать самостоятельно.
Домашнее задание: Гл.I I, §9, п. 9.1, 9.3, 9.7;
№ 9.3, 9.10, 9.11, 9.12 учебник «Алгебра и начала математического
анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Формулы двойных и половинных углов»
План.
1. Теоретическая часть: формулы двойного и половинного аргумента.
2. Применение формул двойного и половинного аргумента.
3. Формулы понижения степени.
Цель: изучение формул тригонометрических функций двойного и половинного аргументов; формирование умения применять изученные формулы.
Рассмотрим некоторые формулы сложения при условии, что аргумент α = β.
Используем формулу sin (α + β) = sins α cos β+ cos α sin β. Имеем sin (α + α) = sins α cos α+ cos α sin α. Упростив полученную формулу, получим sin 2α= 2 sin α cos α.
Анологично, Cos (α
+ β) = cos α cos β - sin α sin
< = > Cos (α + α) = cos α cos α - sin α sinα < = > cos 2α = ![]() -
- ![]()
Анологично, tg (α
+ β)= ![]() < = > tg (α
+ α)=
< = > tg (α
+ α)= ![]() < = > tg2α
=
< = > tg2α
= ![]() .
.
![]()
![]()
![]()
![]() При выполнении преобразований
тригонометрических выражений удобно пользоваться вместо основной
формулы косинуса двойного угла, формулами в которых косинус двойного угла
выражен только через синус аргумента или только через косинус:
При выполнении преобразований
тригонометрических выражений удобно пользоваться вместо основной
формулы косинуса двойного угла, формулами в которых косинус двойного угла
выражен только через синус аргумента или только через косинус:
![]() Формулы
Формулы
называют формулами синуса и косинуса половинного аргумента или формулами
понижения степени.
Пример 1. Вычислить : а) ![]() -
- ![]() , б) sin 15 ̊cos
15 ̊, в) 2
, б) sin 15 ̊cos
15 ̊, в) 2![]()
![]() – 1 г)
– 1 г) ![]() + 2
+ 2 ![]() .
.
Решение.
а) достаточно «узнать» в левой части равенства правую часть формулы косинуса двойного угла и записать результат:
![]() -
- ![]() = cos (2 ·
= cos (2 · ![]() ) = cos
) = cos ![]() =
= ![]()
б) во втором задании следует обратить внимание
на то, заданное выражение отличается от правой части формулы синуса
двойного аргумента только отсутствием двойки. Поэтому если выражение
умножить на 2 и умножить одновременно на ![]() , то оно не изменится:
, то оно не изменится:
sin 15 ̊cos 15 = ![]() · 2 sin 15 ̊cos 15 =
· 2 sin 15 ̊cos 15 = ![]() sin (2 · 15 ̊) =
sin (2 · 15 ̊) = ![]() sin 30 ̊=
sin 30 ̊= ![]() ·
· ![]() =
= ![]()
Упражнения для самостоятельного решения.
Вычислить: а) ![]() -
- ![]() б) 2 sin
б) 2 sin ![]() cos
cos![]() в)
в) ![]() г)
г) ![]() д)
д) ![]() , е) -
, е) - ![]() + 2
+ 2 ![]() .
.
Задача 2.
Сократить дробь ![]() .
.
Решение.
Чтобы сократить дробь надо числитель и знаменатель разложить на множители:
-
В знаменателе дроби заменить
по формуле косинуса двойного угла и полученную разность квадратов
косинуса угла и синуса разложить по формуле сокращённого умножения
(разность квадратов ![]() =
= ![]() , где а = cos α, b = sin α);
, где а = cos α, b = sin α);
-
В числителе дроби заменить 1,
применив основное тригонометрическое тождество, ![]() заменить по формуле синуса двойного аргумента
и полученный трёхчлен разложить на множители по формуле сокращённого
умножения (
заменить по формуле синуса двойного аргумента
и полученный трёхчлен разложить на множители по формуле сокращённого
умножения ( ![]() + 2 ab) =
+ 2 ab) = ![]() , где а = cos α, b = sin α);
, где а = cos α, b = sin α);
![]() =
= ![]() =
= ![]() =
= ![]() .
.
![]()
Упростить выражения: а) ![]() б) 2
б) 2
![]() – 1
– 1![]() в) 1 - 2
в) 1 - 2 ![]() г) cos 4α
г) cos 4α ![]()
Задача 3.
Доказать тождество ![]() = tg α
= tg α
Доказательство.
Докажем, что левая часть тождества равна правой.
- В числителе дроби находится выражение, которое можно преобразовать по формуле синуса двойного аргумента и полученное выражение разложить на множители.
-
В знаменателе дроби заменить
1, применив основное тригонометрическое тождество, ![]() заменить по формуле косинуса двойного
аргумента, привести подобные слагаемые и, полученное выражение
разложить на множители;
заменить по формуле косинуса двойного
аргумента, привести подобные слагаемые и, полученное выражение
разложить на множители;
- Сократить полученную дробь.
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() = tg α
= tg α
tg α = tg α, что и требовалось доказать.
Упражнения для самостоятельной работы.
а) ![]() = tg α б)
= tg α б) ![]() = ctg 2α. в) 2
= ctg 2α. в) 2 ![]() - cos 2α = 1 г)
- cos 2α = 1 г) ![]() = tg α
= tg α
Домашнее задание: Гл.I I, §9, п. 9.5, № 9.49, 9.54, 9.55, учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Формулы приведения».
План.
1. Формулы приведения.
2. Алгоритм составления формул приведения.
3. Формулы дополнительных аргументов.
4. Применение формул приведения.
Цель: изучить формулы приведения; сформировать у4мение студентов применять изученные формулы для преобразования тригонометрических выражений и вычислений.
Тригонометрические функции чисел вида ![]() ∓ α;
π ∓ α;
∓ α;
π ∓ α; ![]() ∓ α;
2π ∓ α могут быть выражены через функции угла
α с помощью формул, которые называются формулами приведения.
∓ α;
2π ∓ α могут быть выражены через функции угла
α с помощью формул, которые называются формулами приведения.
Пользуясь формулами сложения можно доказать следующие формулы:
![]() для функции синуса
для функции синуса
![]()
для косинуса
![]() для тангенса и котангенса
для тангенса и котангенса
Формулы приведения запоминать необязательно. Для того чтобы
записать какую – нибудь из них, можно пользоваться таким правилом:
если отсчёт угла ведётся от вертикального
диаметра единичной окружности (![]() ∓ α;
∓ α; ![]() ∓ α), то наименование функции меняется на противоположное
(синус на косинус; косинус на синус; тангенс на котангенс; котангенс
на тангенс);
∓ α), то наименование функции меняется на противоположное
(синус на косинус; косинус на синус; тангенс на котангенс; котангенс
на тангенс);
если отсчет угла ведётся от горизонтального диаметра (π ∓ α; 2π ∓ α ), то наименование функции не меняется;
знак полученного выражения определяется знаком исходной функции.
Согласно этому правилу запись какой-либо формулы приведения выполняется по алгоритму:
1. Определить от какого диаметра ведётся отсчёт угла и поменять или нет наименование функции.
2. Определить какой четверти данный угол
3. Выяснить какой знак имеет исходная функция в данной четверти.
Пример 1.
Записать формулу приведения cos (![]() + α).
+ α).
1.
Угол ![]() + α отсчитывается от вертикального диаметра,
значит наименование функции косинус надо поменять на синус.
+ α отсчитывается от вертикального диаметра,
значит наименование функции косинус надо поменять на синус.
2.
Угол ![]() + α является углом четвёртой четверти.
Значит полученное выражение будет со знаком «+», так исходная функция
косинус в четвёртой четверти со знаком «+».
+ α является углом четвёртой четверти.
Значит полученное выражение будет со знаком «+», так исходная функция
косинус в четвёртой четверти со знаком «+».
3.
Ответ: cos (![]() + α) = sin α.
+ α) = sin α.
Задача 1. Привести к тригонометрическ5ой функции
угла α: а) sin (![]() + α) б)
cos (
+ α) б)
cos (![]() - α
в) ctg (π
– α) г) tg (π
+ α) д) sin (π
+ α) е) tg (
- α
в) ctg (π
– α) г) tg (π
+ α) д) sin (π
+ α) е) tg (![]() - α)
- α)
Дополнительными углами называются углы,
сумма которых равна ![]() .
.
![]() Для таких углов справедливы формулы приведения,
которые называются формулами дополнительных аргументов
Для таких углов справедливы формулы приведения,
которые называются формулами дополнительных аргументов
Пример 2. Найти значение sin ![]() , cos210 ̊.
, cos210 ̊.
Решение. представим заданные
аргументы так, чтобы можно было применить формулы приведения, то есть
выделим в аргументе такие части, которые изображаются на вертикальном
или горизонтальном диаметре единичной окружности. Например, ![]() = (3-
= (3- ![]() )π = 3π -
)π = 3π - ![]() ; 210 ̊= 270 ̊- 60 ̊.
; 210 ̊= 270 ̊- 60 ̊.
Sin (3π - ![]() ) - с учётом периодичности функции синуса
можно записать Sin (3π -
) - с учётом периодичности функции синуса
можно записать Sin (3π - ![]() ) = Sin (π -
) = Sin (π - ![]() ) и применить формулу приведения
) и применить формулу приведения
sin ![]() = Sin (3π -
= Sin (3π - ![]() ) = Sin (π -
) = Sin (π - ![]() ) = Sin
) = Sin ![]() =
= ![]() ;
;
cos 210 ̊=
cos (270 ̊- 60 ̊) = cos 60 ̊= ![]()
Упражнения для самостоятельного решения.
Найти значение выражения: а) sin ![]() б) cos
б) cos ![]() в) tg
в) tg ![]() г) sin
г) sin ![]()
Пример 3.Упростить
выражение ![]() .
.
Решение. В числителе и знаменателе дроби применим формулы приведения, приведём подобные слагаемые, сократим полученную дробь:
![]() =
= ![]() =
= ![]() = 1.
= 1.
Упражнения для самостоятельного решения.
а) 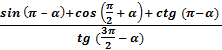 , б)
, б) ![]() , в)
, в) ![]() .
.
Пример 4.
Доказать тождество ![]() ·
· ![]() -
- ![]() = cos 2α.
= cos 2α.
Доказательство. Докажем, что левая часть тождества равна правой. Для преобразования левой части тождества используем формулы приведения
![]() ·
· ![]() -
- ![]() =
= ![]() ·
· ![]() -
- ![]() .
.
Упростим полученные выражения, применив формулы tg α · ctg α = 1, ![]() -
- ![]() = cos 2α.
= cos 2α.
![]() ·
· ![]() -
- ![]() =
= ![]() ·
· ![]() -
- ![]() =
= ![]() -
- ![]() =
= ![]() -
- ![]() = cos 2α.
= cos 2α.
cos 2α = cos 2α, что и требовалось доказать.
Упражнения для самостоятельного решения.
Доказать тождества: а) 2sin(90
̊+ α) sin (180 ̊+ α) = - sin 2α б)
ctg 20 ̊·
ctg 70 ̊=
1 в) ![]()
Домашнее задание: Гл.I I, §9, п. 9.5, № 9.26, 9.19, 7.69, учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение, 2014
Тема: «Формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму».
План .
1. Формулы преобразования суммы (разности) одноимённых тригонометрических функций в произведение.
2. Преобразование произведения тригонометрических функций в сумму.
3. Решение типовых задач на применение изученных формул.
Цель: изучить формулы преобразования суммы и разности одноимённых тригонометрических функций в произведение и формулы преобразования произведения тригонометрических функций в сумму; формирование умений студентов применять изученные формулы для преобразования тригонометрических выражений.
Используя формулы сложения можно получить формулы преобразования суммы и разности одноимённых тригонометрических функций в произведение:
![]()
![]()
![]() В процессе обоснования формул
преобразования суммы и разности одноимённых тригонометрических функций
в произведение, как следствие, получают формулы преобразования
произведения тригонометрических функций в сумму:
В процессе обоснования формул
преобразования суммы и разности одноимённых тригонометрических функций
в произведение, как следствие, получают формулы преобразования
произведения тригонометрических функций в сумму:
Пример 1. Преобразуйте заданную сумму или разность в произведение и,
если возможно, упростите: а) sin 75 ̊+ sin 15 ̊
б) ![]() -
- ![]() .
.
Решение.
В первом задании
можно непосредственно применить формулу sin α
+ sin β = 2 sin ![]() cos
cos ![]() , затем использовать табличные значения синусов и
косинусов углов.
, затем использовать табличные значения синусов и
косинусов углов.
sin 75 ̊+ sin 15 ̊= 2
sin ![]() cos
cos ![]() = 2 sin 45 ̊cos 30 ̊= 2 ·
= 2 sin 45 ̊cos 30 ̊= 2 · ![]() ·
· ![]() =
= ![]() .
.
Во втором задании выражение
![]() -
- ![]() можно рассматривать как разность квадратов.
Разложить разность квадратов в произведение суммы и разности
тригонометрических функций и применить формулы преобразования суммы и
разности синусов в произведение. Для дальнейшего преобразования
полученного выражения используем формулу синуса двойного угла.
можно рассматривать как разность квадратов.
Разложить разность квадратов в произведение суммы и разности
тригонометрических функций и применить формулы преобразования суммы и
разности синусов в произведение. Для дальнейшего преобразования
полученного выражения используем формулу синуса двойного угла.
![]() -
- ![]() =
= ![]() = - 2 sin
= - 2 sin ![]() sin
sin ![]() 2 cos
2 cos ![]() cos
cos ![]() = - sin
(α + β) sin (α - β).
= - sin
(α + β) sin (α - β).
Пример 2. Преобразовать в произведение ![]() .
.
Решение.
Заменим косинус угла по
формуле дополнительных углов: cos β
= sin (![]() - β) и применим формулу для преобразования
суммы синусов в произведение:
- β) и применим формулу для преобразования
суммы синусов в произведение:
![]() =
= ![]() sin (
sin (![]() - β) = 2 sin
- β) = 2 sin ![]() · cos
· cos ![]() = 2 sin (
= 2 sin (![]() +
+ ![]() ) cos (
) cos (![]() -
- ![]() ).
).
Пример 3. Упростить выражение ![]() .
.
Решение. Для упрощения
данной дроби её надо сократить. Разложим числитель и знаменатель
дроби в произведение. В числителе применим формулы преобразования
разности тригонометрических функций в произведение, а в знаменателе
формулу 1 - cos α = 2 ![]()
![]() .
.
![]() =
= ![]() = 2 cos 5α sin 5α = x sin
10α.
= 2 cos 5α sin 5α = x sin
10α.
Пример 4. Докажите тождество 4 sin 70 ̊ - ![]() = -2.
= -2.
Доказательство. Докажем, что левая часть тождества равна
правой. После приведения к общему знаменателю преобразуем произведение
синусов в разность косинусов, а затем с учтём, что cos 60 ̊= ![]() и cos 80 ̊=
sin 10 ̊(по
формуле приведения для дополнительных углов).
и cos 80 ̊=
sin 10 ̊(по
формуле приведения для дополнительных углов).
4 sin 70 ̊ - ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() = - 2, что и требовалось доказать.
= - 2, что и требовалось доказать.
Упражнения для самостоятельного решения.
1.
Преобразуйте сумму (разность)
в произведение и упростите: а) cos 152 ̊+ cos 28 ̊,
б) cos 48 ̊
- cos 12 ̊
в) ![]() г) sin α + sin
2α + sin 3α + sin 4α.
г) sin α + sin
2α + sin 3α + sin 4α.
2.
Докажите тождество: а) ![]() = -
= - ![]() б)
б) ![]() = 2 sin 2α в)
= 2 sin 2α в) ![]() = tg
= tg ![]() .
.
3.
Преобразуйте в
сумму: а) cos 45 ̊cos 15 ̊; б) sin ![]() cos
cos ![]() ; в) sin 20 ̊sin
10 ̊; г) cos
; в) sin 20 ̊sin
10 ̊; г) cos ![]() cos
cos ![]() .
.
4. Вычислить: а) 2 cos 20 ̊· cos 40 ̊-cos 20 ̊; б) 4 sin 10 ̊· sin 50 ̊· sin 70 ̊.
Домашнее задание: Гл.I I, §9, п. 9.4, 9.6, № 9.35, 9.39, 9.67, учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение.
Тема: «Преобразование тригонометрических выражений. Доказательство тождеств»
План.
1. Систематизация теоретических знаний.
2. Преобразование тригонометрических выражений.
3. Доказательство тождеств.
4. Текущий контроль.
Цель: систематизация знаний студентов по изученной теме; отработка практических умений и знаний; проверка уровня усвоения знаний и сформированности практических умений студентов.
Вопросы для контроля теоретических знаний:
1) Запишите соотношения между тригонометрическими функциями одного аргумента.
2) Запишите формулы сложения: а) для косинуса суммы и косинуса разности; б) для синуса суммы и синуса разности; в) тангенса суммы и тангенса разности.
3) Запишите формулы синуса, косинуса и тангенса двойного аргумента.
4) Проиллюстрируйте на на примерах применение формул приведения.
5) Запишите несколько формул приведения пользуясь правилом записи формул.
6) Запишите формулы преобразования суммы и разности синусов или суммы и разности косинусов в произведение.
7) Запишите формулы преобразования суммы и разности тангенсов.
Примеры.
а) упростить выражение cos 2α + cos 14α cos 6α + cos 10α
б) упростить выражение ![]()
в) доказать тождество 2 ![]() = 1 + sin α.
= 1 + sin α.
Самостоятельная работа.
Вариант 1.
1.
Найти sin α
ctg α = ![]() π < α <
π < α < ![]()
2.
Найти значение выражения cos ![]() cos
cos ![]() - sin
- sin ![]() sin
sin ![]() .
.
3.
Упростить выражение ![]() -
- ![]() и вычислить его значение если α = -
и вычислить его значение если α = - ![]() .
.
4. Вычислить sin 75 ̊ не пользуясь таблицей и калькулятором.
5. Вычислить 4 sin 15 ̊sin 75 ̊ - 1.
Вариант 2.
1.
Найти cos α
tg α = - ![]()
![]() < α < π
< α < π
2.
Найти значение выражения sin ![]() sin
sin ![]() - cos
- cos ![]() cos
cos ![]()
3.
Упростить выражение ![]() -
- ![]() и вычислить его значение если α = -
и вычислить его значение если α = - ![]() .
.
4. Вычислить cos 105 ̊ не пользуясь таблицей и калькулятором.
5.
Вычислить sin ![]() cos
cos ![]() .
.
Ответы:
вариант 1: 1) - ![]() ; 2) 0; 3)
; 2) 0; 3) ![]() ;
; ![]() ; 4)
; 4) ![]() ; 5) 0.
; 5) 0.
Вариант
2: 1) - ![]() ; 2) 0; 3)
; 2) 0; 3) ![]() ;
; ![]() ; 4)
; 4) ![]() ; 5) 0,25.
; 5) 0,25.
Домашнее задание: Гл.I I, §9, п. 9.4, 9.6, № 9.66 (б), 9.63 (г), 9.59 (а), учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение.
Тема: «Построение графиков функций синуса и косинуса с помощью преобразований»
План.
1. Построение графиков функций y = sin x с помощью единичного круга .
2. Построение графика функции y = cos x применив формулу дополнительного угла.
3. Построение графиков функций синуса и косинуса с помощью геометрических преобразований.
Цель: построение графиков элементарных
функций y = sin x и y = cos x; с помощью геометрических преобразований научится
строить графики функций y = Аsin ![]() y = Аcos
y = Аcos![]() и с модулями.
и с модулями.
Построение графика функции y = sin x пользуясь единичным кругом:
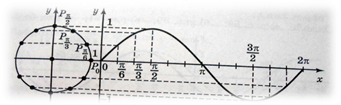
График функции y = sin x имеет вид

Для построения графика функции y = cos x применяем формулу дополнительного угла: cos x = sin (90 ̊-x). Значит график функции y = sin x надо сдвинуть в системе координат по оси Ох на 90 ̊влево:
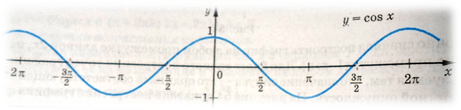
Выполнение упражнений.
1) Построить график функции y = sin (x- ![]()
Чтобы построить график функции y = sin (x- ![]() , надо построить график функции y = sin x и сдвинуть его по оси Ох вправо на
, надо построить график функции y = sin x и сдвинуть его по оси Ох вправо на ![]()
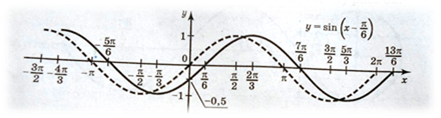
2)
Построить график функции y = sin 2x
. Период данной функции вычисляется по формуле Т = ![]() = π. Следовательно график данной функции
сжат по оси Ох в 2 раза:
= π. Следовательно график данной функции
сжат по оси Ох в 2 раза:
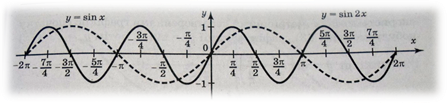
3) Построить график функции y = 2sin x . Для построения графика данной функции надо построить график функции y = sin x и вытянуть его по оси ординат в 2 раза:
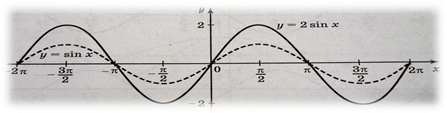
4) Построить график функции y = sin (- x). Для построения графика данной функции надо построить график функции y = sin x и отобразить его симметрично оси Ох:
Упражнения для самостоятельной работы студентов.
1. Объяснить построение графиков функций:
а) y = cos (x+ ![]()
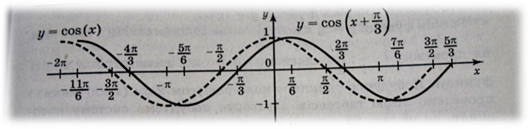
б) y = cos ![]()
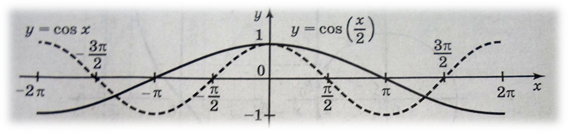
в) y = ![]() cos x
cos x

г) y
= ![]()
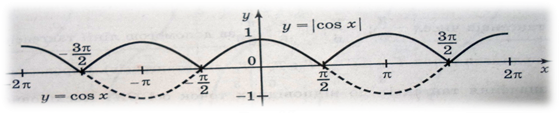
2.
Построить графики
функций: а) y = ![]() б) y = sin (x-
б) y = sin (x- ![]() в) y = cos (2x +
в) y = cos (2x + ![]() ) г) y = 2sin
) г) y = 2sin ![]() .
.
Домашнее задание: Гл.I I, §10, п. 10.1, 10.2, № 10.8 (а, г, е), 10.17 (а, б, г, д), учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение.
Тема: «Построение графиков функций тангенса и котангенса с помощью преобразований»
1. Построение графиков функций y = tg x и y = ctg x.
2. Построение графиков с помощью геометрических преобразований
Цель: построение графиков элементарных
функций y = tg x и y = ctg x; с помощью геометрических преобразований
научится строить графики функций y = Аtg ![]() y = Аctg
y = Аctg![]() и с модулями.
и с модулями.
График функции y = tg x строят с помощью линии тангенсов на числовом
промежутке ( - ![]() ,
, ![]() π этой функции:
π этой функции:
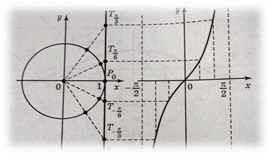
Так как функция y = tg x периодическая с периодом π, для построения графика функции на всей прямой Ох достаточно параллельно перенести построенный график вдоль оси Ох на π, 2 π, 3 π единиц влево и вправо:
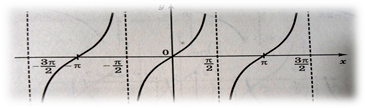
График функции y = tg x называется тангенсоидой.
График функции y = сtg x легко
получить воспользовавшись формулой ctg x = tg
(90 ̊-x) и двумя геометрическими преобразованиями:
симметрия относительно оси ординат и параллельное перемещение вдоль
оси абсцисс на - ![]() .
.
а) построили график y = tg x

б) построили ему симметричный относительно оси ординат
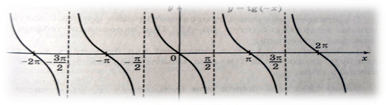
в) перенесли построенный график вдоль оси
абсцисс на - ![]() .
.
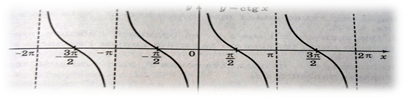
Выполнение упражнений.
Построить графики функций:
а) y = tg 2x.
Период данной тригонометрической функции вычисляется по формуле Т = ![]() , учитывая, что период функции тангенса
π:
, учитывая, что период функции тангенса
π:
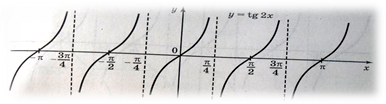
б) y = tg ![]() . Период данной функции вычисляется по формуле
Т = π :
. Период данной функции вычисляется по формуле
Т = π : ![]() = 2π, учитывая, что период функции тангенса
равен π:
= 2π, учитывая, что период функции тангенса
равен π:
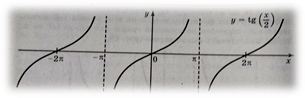
в) y = tg ![]() .
Для построения графика данной функции надо последовательно выполнить два
построения: построить график y = tg
.
Для построения графика данной функции надо последовательно выполнить два
построения: построить график y = tg ![]() и сдвинуть его по оси ординат вверх на 2
единицы:
и сдвинуть его по оси ординат вверх на 2
единицы:

г) y = tg ![]() Для построения графика данной функции надо
последовательно выполнить два построения: построить график y = tg
Для построения графика данной функции надо
последовательно выполнить два построения: построить график y = tg ![]() и отобразить его симметрично относительно оси ординат:
и отобразить его симметрично относительно оси ординат:
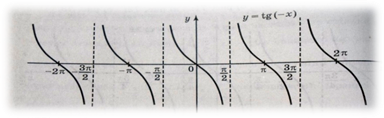
Задания для самостоятельной работы.
Построить графики функций и объяснить
построение: а) y = ctg ( ![]() ) + 1 б) y =
) + 1 б) y = ![]() в) y = ctg
в) y = ctg ![]() г) y =ctg
г) y =ctg ![]() .
.
Домашнее задание: Гл.I I, §10, п. 10.1, 10.2, № 10.25 (а, б.г, д), 10.33 (а, б, д, е), учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение.
Тема: «Обратные тригонометрические функции. Решение простейших тригонометрических уравнений» .
План.
1. Обратные тригонометрические функции.
2. Решение простейших тригонометрических уравнений.
3. Примеры решения тригонометрических уравнений.
Цель: систематизация знаний студентов об обратных тригонометрических функциях; применение обратных тригонометрических функций для записи решения простейших тригонометрических уравнений; формирование умения решать простейшие тригонометрические уравнения.
Для получения обратных тригонометрических функций для каждой тригонометрической функции выделяется промежуток, на котором она возрастает (убывает). Для обозначения обратных тригонометрических функций перед каждой соответствующей функцией ставится буквосочетание «arc» (читается: «арк).
|
Значение arc sin a ( |
|
|
arc sin a - это
такое число из промежутка
Нечётность функции y = arc sin x
|
arc
sin
так как |
|
Значение arc cos
a ( |
|
|
arc cos a - это
такое число из промежутка
Чётность функции y = arc cos x
|
arc
cos
так как |
|
Значение arc tg a |
|
|
arc tg a - это
такое число из промежутка
Нечётность функции y = arc tg x
|
arc
tg
так как |
|
Значение arc ctg a |
|
|
arc ctg a - это
такое число из промежутка
Нечётность функции y = arc ctg x
|
arc
ctg
так как |
Задания для самостоятельного решения.
а) Вычислить: а) arc sin
1 б) arcsin ![]() в) arccos
в) arccos
![]() г) arc sin
г) arc sin ![]() д) arc cos
(-
д) arc cos
(-![]() ) е) arcos 1 ж)
arctg (-
) е) arcos 1 ж)
arctg (- ![]() ) з) arc sin 0.
) з) arc sin 0.
б) Найти значение выражения: а) arcsin1
– 2 arc cos (-![]() ) б) 2 arccos 0.5 – 3 arcsin
) б) 2 arccos 0.5 – 3 arcsin ![]() в) 2 arccos
в) 2 arccos
![]() + arc sin
+ arc sin ![]()
Простейшими тригонометрическими уравнениями называются уравнения вида cos x = a, sin x = a, tg x = a, ctg x =a.
|
Уравнение |
Формулы корней |
Частные случаи решения |
|
cos x = а |
х = x
= |
cos x = 0 x = |
|
cos x = 1 x = 2 |
||
|
cos x = - 1 x =
|
||
|
sin x = a. |
х = х =
|
sin
x = 0 x = |
|
sin
x = 1 x = |
||
|
sin
x = - 1 x = |
||
|
tg x = a |
х = arc tg a + х = - arc tg a +
|
tg x = 0
х = |
|
|
||
|
ctg x = a |
х =
arc сtg a + x
= ( |
сtg x = 0 х = |
Примеры решения простейших тригонометрических уравнений.
Пример
1. Решить уравнение cos x = - ![]() .
.
Поскольку
![]() < 1, то данное уравнение вида cos x = а имеет корни, которые можно найти по
формуле х =
< 1, то данное уравнение вида cos x = а имеет корни, которые можно найти по
формуле х = ![]() arc cos a + 2
arc cos a + 2![]() Z.
Z.
Для вычисления ![]() arc cos (-
arc cos (-![]() ) можно воспользоваться
формулой arc cos(-
a) =
) можно воспользоваться
формулой arc cos(-
a) = ![]() - arc cos a
- arc cos a
Тогда arc cos (-![]() ) =
) = ![]() - arc cos
- arc cos ![]() =
= ![]() -
- ![]() =
= ![]()
Решение.
cos x = - ![]() ,
,
х = ![]() arc cos a + 2
arc cos a + 2![]() Z,
Z,
х = ![]() arc cos (
arc cos (![]() + 2
+ 2![]() Z,
Z,
х = ![]() ) + 2
) + 2![]() Z,
Z,
х = ![]() + 2
+ 2![]() Z.
Z.
Ответ: х = ![]() + 2
+ 2![]() Z.
Z.
Пример 2. Решить уравнение sin
x = - ![]() .
.
Решение.
Поскольку ![]() < 1, то данное уравнение вида sin x = а при
< 1, то данное уравнение вида sin x = а при ![]()
![]() 1 имеет корни, которые можно найти по формуле х =
1 имеет корни, которые можно найти по формуле х =
![]() arc sin a +
arc sin a + ![]() Z. Для вычисления arc sin (-
Z. Для вычисления arc sin (- ![]() ) можно воспользоваться формулой arc sin (-a) = - arc sin a.
Тогда arc sin (-
) можно воспользоваться формулой arc sin (-a) = - arc sin a.
Тогда arc sin (- ![]() ) = - arc sin
) = - arc sin ![]() = -
= - ![]()
sin x = - ![]() ,
,
х = ![]() arc sin(- a )+
arc sin(- a )+ ![]() Z,
Z,
х = ![]() arc sin a +
arc sin a + ![]() Z,
Z,
х = ![]() arc sin
arc sin ![]() +
+ ![]() Z,
Z,
х
= ![]()
![]() +
+ ![]() Z.
Z.
Ответ:
х = ![]()
![]() +
+ ![]() Z.
Z.
Пример
3. Решить уравнение tg x = - ![]() .
.
Решение.
Уравнение tg x = a
имеет корни при любом значении а, поэтому всегда можно воспользоваться
формулой х = arc tg a + ![]()
Для нахождения arc tg (- ![]() ) можно воспользоваться формулой arc tg (-a) = - arc tg a.
Тогда arc tg (-
) можно воспользоваться формулой arc tg (-a) = - arc tg a.
Тогда arc tg (- ![]() ) = - arc tg
) = - arc tg ![]() = -
= - ![]() .
.
tg x = - ![]() ,
,
х = arc tg a
+ ![]()
х = arc tg (- ![]() ) +
) + ![]()
х = - arc tg ![]() +
+ ![]()
х = - ![]() +
+ ![]()
Ответ: х = - ![]() +
+ ![]()
Пример 4.
Решить уравнение cos x = ![]()
Решение.
Так как ![]() >
1, то уравнение не имеет корней.
>
1, то уравнение не имеет корней.
Ответ: ![]() .
.
Пример 5. Решить уравнение cos x = 0,37.
Решение. согласно формулы корней имеем
х = ![]() arc cos 0,37 + 2πn,
n
arc cos 0,37 + 2πn,
n![]() N.
N.
Ответ: х = ![]() arc cos 0,37 + 2πn,
n
arc cos 0,37 + 2πn,
n![]() N.
N.
Задания для самостоятельного решения.
Решить
уравнения: а) cos x = -1; б) tg x = ![]() ; в) сtg x = -
; в) сtg x = -
![]() ; г) sin
x =
; г) sin
x = ![]() ; д) sin
x = -
; д) sin
x = - ![]() ; е) cos x = 0;
ж) sin x
= -1; з) sin x = -
; е) cos x = 0;
ж) sin x
= -1; з) sin x = - ![]() .
.
Домашнее задание: Гл.I I, §11, п. 11.1( стр. 295, )№ 11.2, №11.3 (1 столб.)учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение.
Тема: "Решение простых тригонометрических уравнений"
План.
1.
Решение тригонометрических
уравнений вида A sin x = b, A cos x = b (![]()
![]() 1), A tg x = c, A ctg x = c
1), A tg x = c, A ctg x = c
2.
Решение тригонометрических
уравнений вида sin ![]() = b, cos
= b, cos ![]() = b (
= b (![]()
![]() 1), tg
1), tg ![]() = c, ctg
= c, ctg ![]() = c
= c
3.
Решение тригонометрических
уравнений вида Asin ![]() = b, Acos
= b, Acos ![]() = b (
= b (![]()
![]() 1), Atg
1), Atg ![]() = c, Actg
= c, Actg ![]() = c
= c
Цель: научиться решать простые тригонометрические уравнения, применяя не более двух равносильных преобразований и формулы записи решения простейших тригонометрических уравнений.
Математический диктант.
Запишите решения уравнений:
1) sin x = 0; 2) sin x = 1; 3) sin x = -1;
4) cos x = 0; 5) cos x = 1; 6) cos x = - 1;
7) tg x = 1; 8) tg x = -1; 9) ctg x = - 1;
10) sin x = π; 11) ctg
x = π; 12) cos x = - ![]() .
.
Какие тригонометрические уравнения являются простейшими?
Как определить, что данное уравнение простейшее?
Решить уравнения: а) sin x =
- ![]() б) sin x = 𝒆; в) cos x = 0,25; д) tg x = - 1; е) ctg x =
-
б) sin x = 𝒆; в) cos x = 0,25; д) tg x = - 1; е) ctg x =
- ![]() ; ж) tg x =
5.
; ж) tg x =
5.
Простыми тригонометрическими уравнениями считаются уравнения, в которых надо выполнить не более двух равносильных преобразований и, применив формулы записи решения простейших тригонометрических уравнений записать ответ.
Пример 1. Решить уравнение 2 cos x = - 1.
Решение. Данное уравнение приводится к простейшему делением левой и правой части на 2
2 cos x = - 1;
cos x = - ![]() ;
;
x = ![]() (
(![]() - arc cos
- arc cos ![]() ) + 2πn,
) + 2πn, ![]() Z;
Z;
х = ![]() (
(![]() -
- ![]() ) + 2πn,
) + 2πn, ![]() Z;
Z;
х = ![]()
![]() + 2πn,
+ 2πn, ![]() Z;
Z;
Ответ: ![]()
![]() + 2πn,
+ 2πn, ![]() Z;
Z;
Задания для самостоятельного решения.
Решить
уравнения: а) 2 sin x
= ![]() ; б) 3 sin
x = 1 в)
; б) 3 sin
x = 1 в) ![]() tg x = - 1; г) 2 sin x = π
д) 3 ctg x = π;
tg x = - 1; г) 2 sin x = π
д) 3 ctg x = π;
Пример 2. Решить уравнение cos 4х = - 1.
Решение. Для решения данного уравнения можно сразу воспользоваться особой формой записи ответа, так как а = - 1.
cos 4х = - 1;
4х
= π + 2πn, ![]() Z - разделить каждый член выражения на 4;
Z - разделить каждый член выражения на 4;
х
= ![]() +
+ ![]() ,
, ![]() Z.
Z.
Ответ:
![]() +
+ ![]() ,
, ![]() Z.
Z.
Пример
3. Решить уравнение sin (2x + ![]() = -1
= -1
Решение. Для решения данного уравнения можно сразу воспользоваться особой формой записи ответа, так как а = - 1.
sin (2x + ![]() = -1;
= -1;
2x + ![]() =
= ![]() +
+ ![]() -
- ![]() перенести
в правую часть равенства, поменяв знак на противоположный;
перенести
в правую часть равенства, поменяв знак на противоположный;
2x = (
![]() -
- ![]() ) +
) + ![]() - выполнить в скобках сложение;
- выполнить в скобках сложение;
2x = ![]() +
+ ![]() - разделить каждый член выражения на 2;
- разделить каждый член выражения на 2;
x = ![]() +
+ ![]()
Ответ: ![]() +
+ ![]()
Задания для самостоятельного решения.
Решить уравнения: а) tg ![]() = - 1;
б) sin
= - 1;
б) sin ![]() = -1;
в) cos
= -1;
в) cos ![]() =
= ![]() ; г) tg
; г) tg ![]() =
= ![]() .
.
Пример 4.
Решить уравнение 2 cos ![]() =
= ![]() .
.
Решение.
2 cos ![]() =
= ![]() - используя свойство чётности функции
косинуса заменили аргумент на противоположный;
- используя свойство чётности функции
косинуса заменили аргумент на противоположный;
cos ![]() =
= ![]() - разделить каждый член выражения на 2;
- разделить каждый член выражения на 2;
![]() =
= ![]() arc cos
arc cos ![]() + 2
+ 2![]() Z - воспользоваться формой записи ответа для
простейшего уравнения;
Z - воспользоваться формой записи ответа для
простейшего уравнения;
![]() =
= ![]()
![]() + 2
+ 2![]() Z -
Z - ![]() перенести в правую часть равенства, поменяв
знак на противоположный;
перенести в правую часть равенства, поменяв
знак на противоположный;
![]() =
= ![]()
![]() +
+ ![]() + 2
+ 2![]() Z - выполнять сложение нельзя, так как первое
слагаемое в правой части равенства имеет двойной смысл «- « и «+»;
разделить каждый член выражения на 3;
Z - выполнять сложение нельзя, так как первое
слагаемое в правой части равенства имеет двойной смысл «- « и «+»;
разделить каждый член выражения на 3;
![]() =
= ![]()
![]() +
+ ![]() +
+ ![]() Z.
Z.
Ответ:
![]()
![]() +
+ ![]() +
+ ![]() Z.
Z.
Задания для самостоятельного решения.
Решить уравнения: а) ![]() tg
tg ![]() = - 1;
б) 2sin
= - 1;
б) 2sin ![]() = -1;
в) 2cos
= -1;
в) 2cos ![]() =
= ![]() ; г) 3 tg
; г) 3 tg ![]() = -
= - ![]()
Пример 5. Найти корни уравнения sin 3x = ![]() на заданном отрезке
на заданном отрезке ![]() .
.
Решение .
1)
Решить уравнение sin
3x = ![]() .
.
sin
3x = ![]() < = > 3х =
< = > 3х = ![]() arc sin
arc sin ![]() +
+ ![]() Z < = > 3х =
Z < = > 3х = ![]()
![]() +
+ ![]() Z < =
> х =
Z < =
> х = ![]()
![]() +
+ ![]() Z .
Z .
2) Вычисляем корни для некоторых значений ![]() и выбираем те, которые принадлежат отрезку
и выбираем те, которые принадлежат отрезку ![]() :
:
![]() = 0 < =
> х =
= 0 < =
> х = ![]()
![]() +
+ ![]() =
= ![]()
![]()
![]() ;
;
![]() = 1 < =
> х =
= 1 < =
> х = ![]()
![]() +
+ ![]() = -
= - ![]() +
+ ![]() =
= ![]()
![]()
![]() ;
;
![]() = 2 < =
> х =
= 2 < =
> х = ![]()
![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]()
![]()
![]() ;
;
![]() = 3 < =
> х =
= 3 < =
> х = ![]()
![]() +
+ ![]() = -
= - ![]() + π =
+ π = ![]()
![]()
![]() ;
;
![]() = 4 < =
> х =
= 4 < =
> х = ![]()
![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]()
![]()
![]() ;
;
![]() = 5 < =
> х =
= 5 < =
> х = ![]()
![]() +
+ ![]() = -
= - ![]() +
+ ![]() =
= ![]()
![]()
![]() .
.
Ответ: отрезку ![]() принадлежит шесть корней уравнения:
принадлежит шесть корней уравнения: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Задания для самостоятельного решения.
Найти корни уравнения на заданном отрезке:
а) cos3 x = ![]() ,
, ![]() ; б) sin
3x = -
; б) sin
3x = - ![]() ,
, ![]() ; в) ctg4 x = - 1,
; в) ctg4 x = - 1, ![]() .
.
Домашнее задание: Гл.I I, §11, п. 11.2 № 11.12 (3 ст.), №11.13 (3 столб.)учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение.
Тема: «Решение тригонометрических уравнений методом замены переменной».
План.
1. Решение тригонометрических уравнений способом приведения к одной тригонометрической функции.
2. Примеры решения тригонометрических уравнений.
Цель: формирование умения решать тригонометрические уравнения способом замены переменной, содействовать развитию познавательного интереса и личной активности студентов.
Методы решения тригонометрических уравнений разрабатывались математиками долгие годы. Ими выделены классы тригонометрических уравнений, для которых известны алгоритмы решения. Рассмотрим один из них - «Метод замены переменной». Этот метод решения уравнений вам хорошо известен, вы не раз применяли его при решении алгебраических уравнений.
Покажем, как он применяется при решении тригонометрических уравнений.
Пример 1.
Решить уравнение tg ![]() = -
= - ![]() .
.
Решение .
Введя замену t = ![]() , получим простейшее тригонометрическое
уравнение tg t = -
, получим простейшее тригонометрическое
уравнение tg t = - ![]() , ре5шением которого будет t = -
arc tg
, ре5шением которого будет t = -
arc tg ![]() + πk, k
+ πk, k ![]() N.
N.
Вернёмся к замене ![]() = - arc tg
= - arc tg ![]() + πk, k
+ πk, k ![]() N < = >
N < = > ![]() = -
= - ![]() + πk, k
+ πk, k ![]() N.
N.
Выполним тождественные преобразования: ![]() перенести в правую часть уравнения, поменяв
знак на противоположный; каждый член полученного выражения умножаем на
3.
перенести в правую часть уравнения, поменяв
знак на противоположный; каждый член полученного выражения умножаем на
3.
![]() = -
= - ![]() + πk, k
+ πk, k ![]() N;
N;
![]() = -
= - ![]() -
- ![]() + πk, k
+ πk, k ![]() N;
N;
![]() = -
= - ![]() + πk, k
+ πk, k ![]() N;
N;
х = -
π + 3 πk, k ![]() N;
N;
Ответ:
- π + 3 πk, k ![]() N;
N;
Уравнения для самостоятельного решения: а) sin (3x - ![]() = -1
б) tg
= -1
б) tg ![]() =
= ![]() .
в) 2cos
.
в) 2cos ![]() = -
= - ![]() ;
;
Рассмотрим уравнения A ![]() x + B sin x + C = 0 и A
x + B sin x + C = 0 и A ![]() x + B sin x + C = 0.
x + B sin x + C = 0.
Чем отличаются эти уравнения?
Какое из них сложнее? Почему?
Второе уравнение можно привести к такому же виду как первое, применив основное тригонометрическое тождество:
![]() x +
x + ![]() x =
1 < = >
x =
1 < = > ![]() x = 1
-
x = 1
- ![]() x.
x.
Во второе уравнение подставить найденное значение квадрата косинуса, раскрыть скобки и привести подобные слагаемые.
После этого оба уравнения решаются одним методом - «Методом замены переменной».
Пример 2.
Решить уравнение 2 ![]() x + 7
sin x + 3 = 0.
x + 7
sin x + 3 = 0.
Решение.
Анализируем вид данного уравнения, замечаем, что в его запись входит
только одна тригонометрическая функция sin x.
Следовательно, для решения данного уравнения надо ввести новую
переменную t = sin x, где ![]() < 1.
< 1.
2 ![]() + 7 t + 3 = 0 - решаем данное уравнение;
+ 7 t + 3 = 0 - решаем данное уравнение;
D = ![]() - 4 ac; D =
- 4 ac; D = ![]() - 4·2 · 3 = 49 – 24 = 25;
- 4·2 · 3 = 49 – 24 = 25; ![]() =
= ![]() ;
;
![]() =
= ![]() ; х1=3
и х2 =
; х1=3
и х2 = ![]() .
.
После решения квадратного уравнения необходимо выполнить обратную замену и решить полученные простейшие тригонометрические уравнения.
Учитывая, что ![]() < 1, обратную замену выполняем только для х2
=
< 1, обратную замену выполняем только для х2
= ![]() .
.
sin x = ![]() ;
;
х = ![]() arc sin a +
arc sin a + ![]() Z;
Z;
х = ![]()
![]() +
+ ![]() Z.
Z.
Ответ: ![]()
![]() +
+ ![]() Z.
Z.
Пример 3.
Решить уравнение 2 ![]() x + 3
cos x = 0.
x + 3
cos x = 0.
Решение.
Для решения приводим все тригонометрические функции к одной функции, применив основное тригонометрическое тождество
![]() x +
x + ![]() x =
1 < = >
x =
1 < = > ![]() x = 1
-
x = 1
- ![]() x.
x.
2(1 - ![]() x) + 3
cos x = 0 - раскрываем скобки и приводим подобные
слагаемые.
x) + 3
cos x = 0 - раскрываем скобки и приводим подобные
слагаемые.
2 - 2![]() x + 3 cos x = 0;
x + 3 cos x = 0;
2![]() x -3 cos x -2 = 0;
x -3 cos x -2 = 0;
В запись
входит только одна тригонометрическая функция cos x.
Следовательно, для решения данного уравнения надо ввести новую
переменную t = cosx, где ![]() < 1.
< 1.
2 ![]() - 3 t
- 2 = 0 - решаем данное уравнение;
- 3 t
- 2 = 0 - решаем данное уравнение;
D = ![]() - 4 ac; D =
- 4 ac; D = ![]() +4·2
· 2 = 9 +16 = 25;
+4·2
· 2 = 9 +16 = 25; ![]() =
= ![]() ;
; ![]() =
= ![]() ; х1=2
и х2 = -
; х1=2
и х2 = - ![]()
После решения квадратного уравнения необходимо выполнить обратную замену и решить полученные простейшие тригонометрические уравнения.
Учитывая, что ![]() < 1, обратную замену выполняем только для х2
=
< 1, обратную замену выполняем только для х2
= ![]() .
.
cos x = - ![]() ;
;
x = ![]() (
(![]() - arc cos a) + 2πn,
- arc cos a) + 2πn, ![]() Z;
Z;
x = ![]() (
(![]() - arc cos
- arc cos![]() ) + 2πn,
) + 2πn, ![]() Z;
Z;
x = ![]() (
(![]() -
- ![]() ) + 2πn,
) + 2πn, ![]() Z;
Z;
x = ![]()
![]() + 2πn,
+ 2πn, ![]() Z.
Z.
Ответ: ![]()
![]() + 2πn,
+ 2πn, ![]() Z.
Z.
Уравнения для самостоятельного решения:
Решить уравнения: а) 3 ![]() x - 5 sin x - 2 = 0; б) 3
x - 5 sin x - 2 = 0; б) 3 ![]() x + 10sin 2x + 3
= 0;
x + 10sin 2x + 3
= 0;
в) 4 ![]() x + 11
sin x -3 =
0; г) 6
x + 11
sin x -3 =
0; г) 6 ![]() x + cos x - 1
= 0;
x + cos x - 1
= 0;
д)
2 ![]() x + 5 cos 3x - 3 = 0; е)
8
x + 5 cos 3x - 3 = 0; е)
8 ![]() x + cos 2x + 1= 0.
x + cos 2x + 1= 0.
ж) 3 ![]() x + 2
tg x - 1 = 0; з) c
x + 2
tg x - 1 = 0; з) c![]() x – 6
ctg 2x +5 = 0; и) 4 sin 3x +
x – 6
ctg 2x +5 = 0; и) 4 sin 3x + ![]() x =
4.
x =
4.
Домашнее задание: Гл.I I, §11, п. 11.2 № 11.10 ( а, б, е, з, к) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение.
Тема: «Решение однородных тригонометрических уравнений»
План.
1. Понятие однородного уравнения.
2. Метод решение однородных тригонометрических уравнений
3. Примеры решения однородных тригонометрических уравнений.
Цель: формирование умения решать однородные тригонометрические уравнения; способствовать формированию умения использовать приёмы сравнения, переноса знаний в новую ситуацию; содействовать воспитанию интереса к дисциплине «математика», активности, умению общаться, пониманию значимости дисциплины в в дальнейшей жизни и профессиональной деятельности.
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело. Чтобы переваривать знания, нужно поглощать их с аппетитом». Давайте следовать совету писателя, будем активны, внимательны, поглощать знания с желанием ведь они пригодятся вам в дальнейшей жизни и профессиональной деятельности.
Если все члены уравнения, в левой и правой частях которого стоят многочлены от двух переменных (или от двух функций одной переменной), имеют одинаковую степень, то уравнение называется однородным.
Отличительными признаками однородного уравнения являются:
1) Все одночлены имеют одинаковую степень;
2) Свободный член равен 0;
3) В уравнении присутствуют степени с разными основаниями.
Однородное уравнение имеет вид A ![]() (x) + B f(x) · g(x) + C
(x) + B f(x) · g(x) + C ![]() (x) = 0.
(x) = 0.
Решается однородное уравнение делением
на наивысшую степень одной из переменных. Например, делим на ![]() (x). Можно делить на
(x). Можно делить на ![]() (x) или на f(x) · g(x).
(x) или на f(x) · g(x).
При делении левой и правой частей уравнения на выражение с переменной можно потерять корни. Поэтому необходимо проверить не являются ли корни того выражения на которое делим обе части уравнения, корнями данного уравнения. Если являются, то их надо записать, чтобы потом не забыть включить в решения.
При решении любого уравнения, в правой части которого ноль, нужно попытаться разложить левую часть на множители любым доступным способом. Затем каждый множитель приравнять к нулю и решить полученную систему. В этом случае точно не произойдёт потеря корней.
При решении однородных тригонометрических уравнений следует помнить:
1)
Свободный член можно
преобразовывать в сумму квадратов синуса и косинуса, применяя основное
тригонометрическое тождество ![]() x +
x + ![]() x =
1. Например, 5 = 5 · 1 = 5 · (
x =
1. Например, 5 = 5 · 1 = 5 · (![]() x +
x + ![]() x) =
5
x) =
5 ![]() x +
x + ![]() x.
x.
2)
Синус и косинус двойного
аргумента являются выражениями второй степени sin 2x = 2sin x cos x и
cos 2x = ![]() x -
x - ![]() x.
x.
Рассмотрим примеры решения однородных тригонометрических уравнений.
Пример 1. Решить уравнение sin x + 2 cos x = 0.
Решение . sin x + 2 cos x = 0 - однородное уравнение
первой степени, решается делением на cos x. Согласно
основного тригонометрического тождества, ![]() x +
x + ![]() x =
1. Поэтому sin x и cos x
одновременно не могут равняться 0. Поэтому при деление на cos x не происходит потеря корней.
x =
1. Поэтому sin x и cos x
одновременно не могут равняться 0. Поэтому при деление на cos x не происходит потеря корней.
![]() +
+ ![]() = 0 < = > tg x + 2 = 0 < =
> tg x = - 2 < = > x = - arc tg( - 2) + πk, k
= 0 < = > tg x + 2 = 0 < =
> tg x = - 2 < = > x = - arc tg( - 2) + πk, k ![]() N.
N.
Ответ
: - arc tg( - 2) + πk, k ![]() N.
N.
Пример 2.
Решить уравнение ![]() x + sin x cos x =
0.
x + sin x cos x =
0.
Решение.
Разложить левую часть уравнения на множители способом вынесения общего множителя cos x:
![]() x + sin x cos x = 0;
x + sin x cos x = 0;
cos x (![]() cos x + sin x) = 0.
cos x + sin x) = 0.
Составляем
совокупность двух уравнений cos x = 0 или ![]() cos x + sin x =
0.
cos x + sin x =
0.
Решаем первое уравнение: cos x = 0 - простейшее тригонометрическое уравнение,
решение которого х = ![]() + πn, n
+ πn, n ![]() N.
N.
Второе уравнение ![]() cos x + sin x =
0 - однородное тригонометрическое уравнение первой степени (пример 1).
cos x + sin x =
0 - однородное тригонометрическое уравнение первой степени (пример 1).
![]() cos x + sin x = 0
cos x + sin x = 0
![]() +
+ ![]() = 0 < = >
= 0 < = > ![]() + tg x = 0 < = > tg
x = -
+ tg x = 0 < = > tg
x = - ![]() < = > x = - arc tg
< = > x = - arc tg ![]() + πk, k
+ πk, k ![]() N < = > x = -
N < = > x = - ![]() + πk, k
+ πk, k ![]() N.
N.
Так как уравнения образуют совокупность, то в ответе должны быть записаны все корни каждого из этих уравнений.
Ответ: ![]() + πn, n
+ πn, n ![]() N; -
N; - ![]() + πk, k
+ πk, k ![]() N.
N.
Пример 3.
Решить уравнение ![]() x – sin x cos x - 2
x – sin x cos x - 2![]() x = 0.
x = 0.
Решение.
Данное уравнение однородное, так как все его члены имеют одинаковую
степень, в уравнении присутствуют степени с разными основаниями,
свободный член равен нулю. Его можно решить делением на ![]() x.
Если мы будем делить на
x.
Если мы будем делить на ![]() x,
то потели корней не произойдет, так как если cos x =
0 подставим в данное уравнение, то получим, что и sin x так же должен равняться нулю. Это невозможно,
так как
x,
то потели корней не произойдет, так как если cos x =
0 подставим в данное уравнение, то получим, что и sin x так же должен равняться нулю. Это невозможно,
так как ![]() x +
x + ![]() x =
1 (основное тригонометрическое тождество). Следовательно корни
уравнения cos x = 0 не являются корнями
данного уравнения.
x =
1 (основное тригонометрическое тождество). Следовательно корни
уравнения cos x = 0 не являются корнями
данного уравнения.
![]() x – sin x cos x - 2
x – sin x cos x - 2![]() x = 0.
x = 0.
![]() -
- ![]() -
- ![]() = 0 < =
>
= 0 < =
> ![]() x -
x - ![]() - 2 = 0.
- 2 = 0.
В
полученное уравнение переменная входит в одном и том же виде ![]() . Поэтому можно сделать замену
. Поэтому можно сделать замену ![]() = t и получим уравнение
= t и получим уравнение ![]() –
– ![]() - 2 = 0, корни которого
- 2 = 0, корни которого ![]() 1 = - 1
и
1 = - 1
и ![]() 2 = 2.
2 = 2.
Возвращаемся к замене и решаем два простейших тригоном5трических уравнения:
1) ![]() = - 1 < = > х = - arc tg
= - 1 < = > х = - arc tg ![]() + πk, k
+ πk, k ![]() N < = > х = -
N < = > х = - ![]() + πk, k
+ πk, k ![]() N ;
N ;
2)
![]() = 2 < = > х = arc
tg
= 2 < = > х = arc
tg ![]() + πn, n
+ πn, n ![]() N.
N.
Ответ:
- ![]() + πk, k
+ πk, k ![]() N ; arc tg
N ; arc tg ![]() + πn, n
+ πn, n ![]() N.
N.
Пример 4.
Решить уравнение 4![]() x +
0,5 sin 2x + 3
x +
0,5 sin 2x + 3![]() x = 3.
x = 3.
Решение. Привести данное уравнен6ие к однородному. Для этого надо:
1)
привести все члены уравнения
к одному аргументу применив формулу синуса двойного аргумента: 4![]() x + sin x cos x +
+ 3
x + sin x cos x +
+ 3![]() x = 3;
x = 3;
2)
свободный член 3 умножить на
1, а 1 расписать применив основное тригонометрическое тождество: 4![]() x + sin x cos x +
+ 3
x + sin x cos x +
+ 3![]() x = 3·
1;
x = 3·
1;
4![]() x + sin x cos x + + 3
x + sin x cos x + + 3![]() x = 3(
x = 3(![]() x +
x + ![]() x);
x);
3)
раскрыть скобки, перенести все
члены в левую часть уравнения и привести подобные слагаемые: 4![]() x + sin x cos x +
+ 3
x + sin x cos x +
+ 3![]() x = 3
x = 3![]() x +
x + ![]() x;
x;
4![]() x + sin x cos x + 3
x + sin x cos x + 3![]() x - 3
x - 3![]() x -
x - ![]() x = 0;
x = 0;
![]() x + sin x cos x = 0;
x + sin x cos x = 0;
4) разложить левую часть уравнения на множители; cos x (cos x + sin x) = 0;
5) Составляем совокупность двух уравнений cos x = 0 или cos x + sin x = 0.
Решаем первое уравнение: cos x = 0 - простейшее тригонометрическое уравнение,
решение которого х = ![]() + πn, n
+ πn, n ![]() N.
N.
Второе уравнение cos x + sin x = 0 - однородное тригонометрическое уравнение первой степени (пример 1).
cos x + sin x = 0
![]() +
+ ![]() = 0 < = > 1 + tg x = 0 < = > tg x = - 1 < = > х = - arc tg
= 0 < = > 1 + tg x = 0 < = > tg x = - 1 < = > х = - arc tg ![]() + πk, k
+ πk, k ![]() N < = > х = -
N < = > х = - ![]() + πm, m
+ πm, m ![]() N .
N .
Ответ:
![]() + πn, n
+ πn, n ![]() N; -
N; - ![]() + πm, m
+ πm, m ![]() N.
N.
Уравнения для самостоятельного решения: а) ![]() x + 2
sin x cos x - 3
x + 2
sin x cos x - 3![]() x = 0;
б)
x = 0;
б) ![]() x – 4
sin x cos x + 3
x – 4
sin x cos x + 3![]() x = 0;
в)
x = 0;
в) ![]() x +sin x cos x - 2
x +sin x cos x - 2![]() x = 0
г)
x = 0
г) ![]() x – 3 sin x cos x = - 1; д)
x – 3 sin x cos x = - 1; д) ![]() x – 7 sin 2x = 2.
x – 7 sin 2x = 2.
Вопросы для контроля.
1. Какие уравнения называются однородными?
2. Перечислите отличительные признаки однородного уравнения?
3. Какие формулы тригонометрии позволяют уравнение привести к однородному?
4.
Почему деление левой и правой
части однородного уравнения на ![]() x
не приводит к потере корней?
x
не приводит к потере корней?
Домашнее задание: Гл.I I, §11, п. 11.4 № 11.26 ( а, б, в,), 11. 29((б, в, г) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение .
Тема: «Решение тригонометрических уравнений приведением к одной функции (с одинаковым аргументом)»
План.
1. План поиска решения тригонометрического уравнения.
2. Примеры решения тригонометрических уравнений приведением к одной функции (с одинаковым аргументом).
Цель: формирование умения студентов решать тригонометрические уравнения методом приведением к одной функции; способствовать формированию умения ранее полученные знания; содействовать воспитанию интереса к предмету, активности, умения общаться.
При поиске решения более сложных тригонометрических уравнений модно воспользоваться следующими рассуждениями:
1) Пробуем привести тригонометрические функции к одному аргументу;
2) Если удалось привести к одному аргументу, то пробуем все тригонометрические функции привести к одной функции.
3) Если к одному аргументу удалось привести, а к одной функции нет, то пробуем привести к однородному уравнению.
4) В других случаях переносим все члены в одну часть уравнения и пробуем разложить на множители или используем специальные приёмы решения.
Следует помнить три «закона» тригонометрии.
Закон 1. «Увидел сумму - делай произведение».
Закон 2. «Увидел произведение - делай сумму».
Закон 3. «Увидел квадрат - понижай степен6ь».
В некоторых тригонометрических уравнениях можно используя тождества одного аргумента привести все функции к одной. Рассмотрим примеры.
Пример 1. Решить уравнение сos 2x – 5 sin x – 3 = 0.
|
Решение |
Пояснение |
|
|
сos 2x – 5 sin x – 3 = 0. |
||
|
|
Все тригонометрические функции приводим к
одному аргументу х, используя формулу cos 2x
= |
|
|
1 - |
Используя основное тригонометрическое тождество
приводим все тригонометрические функции к одной |
|
|
2 |
Приводим подобные слагаемые и меняем знаки всех членов уравнения на противоположные. |
|
|
2 |
Замена sin x = t |
|
|
|
Решаем уравнение |
|
|
sin x = - х =
х = |
Выполняем обратную замену и решаем полученные простейшие тригонометрические уравнения. |
|
|
sin x = - 2 - нет решения |
||
Ответ: ![]()
![]() +
+ ![]() Z;
Z;
Пример 2. Решить уравнение sin x + sin 7x = sin 3x + sin 5x.
Решение. Применив первый «закон» тригонометрии, заменим сумму произведением и разделим левую и правую части уравнения на 2.
sin x + sin 7x = sin 3x + sin 5x < = > sin ![]() · cos
· cos ![]() = sin
= sin ![]() · cos
· cos ![]() < = >
< = >
< = > sin 4x cos 3x = sin 4x cos x.
Перенесём все члены в левую часть уравнения и разложим левую часть уравнения на множители.
sin 4x cos 3x - sin 4x cos x = 0 < = > sin 4x ( cos 3x - cos x) = 0.
В полученном уравнении заменим разность произведением и разделим левую и правую части уравнения на - 2.
sin 4x sin 2x sin x = 0.
Составляем совокупность двух уравнений sin 4x = 0, sin 2x = 0, sin x = 0. Решаем каждое уравнение .
а) sin 4x = 0 < = > х = ![]() , k
, k ![]() N
N
б) sin 2x = 0 < = > х = ![]() , m
, m ![]() N
N
в) sin x = 0 < = > х =
πn, n ![]() N.
N.
![]()
![]()
![]() Ответ должен включать решения всех трёх уравнений. Однако,
запись ответа может быть сокращена. Изобразим решения всех уравнений
на единичной окружности.
Ответ должен включать решения всех трёх уравнений. Однако,
запись ответа может быть сокращена. Изобразим решения всех уравнений
на единичной окружности.
*
![]()
![]()
![]() - решения первого уравнения
- решения первого уравнения
![]()
![]()
*
![]()
![]()
Из рисунка видно, что решения второго и третьего уравнений не внесли ничего нового в решения первого уравнения. Значит, ответ может содержать только решения первого уравнения.
Ответ: ![]() , k
, k ![]() N.
N.
Уравнения для самостоятельного решения: а) 1 – cos x = 2
sin ![]() ; б) cos 2x = 2
; б) cos 2x = 2 ![]() sin x;
в)
sin x;
в) ![]() x - 3
sinx cosx = - 1; г) sin 5x – sin x = 0; д) cos 4x + cos 2x = 0.
x - 3
sinx cosx = - 1; г) sin 5x – sin x = 0; д) cos 4x + cos 2x = 0.
Ответы:
а) 2πn, π + 4πn, n ![]() N;
б)
N;
б) ![]() arcsin
arcsin ![]() + πn, n
+ πn, n ![]() N; в)
N; в) ![]() + πn, arctg
2 + πn, n
+ πn, arctg
2 + πn, n ![]() N;
г) πn,
N;
г) πn, ![]() +
+ ![]() n
n ![]() N; д)
N; д) ![]() +
+ ![]() n
n ![]() N.
N.
Домашнее задание: Гл.I I, §11, п. 11.4 № 11.31 (в, г,), 11. 29((д) учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение .
Тема: «Решение тригонометрических неравенств»
План.
1. Решение простейших тригонометрических неравенств с помощью е5диничной окружности.
2. Способы решения более сложных тригонометрических неравенств.
3. Примеры решения неравенств.
Цель: формирование умения студентов решать простейшие тригонометрические неравенства: sin x > 0, sin x < 0, cos x > 0, cos x < 0, tg x > 0, tg x < 0, ctg > 0, ctg x < 0; рассмотреть примеры решения более сложных тригонометрических неравенств: содействовать воспитанию интереса к предмету, активности, умения общаться.
|
Примеры решения простейших тригонометрических неравенств |
|
|
|
Sin x – это ордината соответствующей точки
значениях х, удовлетворяющих данному неравенству,
ордината точки
|
|
|
cos x― это абсцисса соответствующей точки
значениях х, удовлетворяющих данному неравенству, абсцисса
точки С учётом периодичности функции синус записываем ответ:
|
Рассмотрим решение простейших тригонометрических неравенств, содержащих функции тангенса и котангенса.
|
Примеры решения простейших тригонометрических неравенств |
|
|
|
полуокружности на промежутке (- значения х которых удовлетворяют данному неравенству, воспользуемся линией
тангенсов. Выделим на линии тангенсов значения тангенсов большие или
равные - 1, а затем для каждой точки линии тангенсов на правой
полуокружности найдём соответствующую точку
|
|
|
Для выделения всех точек
значения х которых удовлетворяют данному неравенству, воспользуемся линией котангенсов.
Выделим на линии котангенсов значения котангенсов меньшие
|
Неравенства для
самостоятельного решения:
а) cos x <
- ![]() ; б)
Sin x <
; б)
Sin x < ![]() ;
;
в) Sin x < - ![]() ; г) ctg x >
; г) ctg x > ![]() д) ctg x
> -
д) ctg x
> - ![]() ;
е) tg x > -
;
е) tg x > - ![]() .
.
Пример 1. Решить
неравенство 2 cos ![]() <
< ![]() .
.
Решение.
2 cos ![]() <
< ![]() - используя свойство чётности функции
косинуса заменили аргумент на противоположный;
- используя свойство чётности функции
косинуса заменили аргумент на противоположный;
cos ![]() <
< ![]() - разделили каждый член неравенства на 2;
- разделили каждый член неравенства на 2;
введём замену ![]() = t;
= t;
получим простейшее неравенство cos t <
![]() ;
;
![]()
![]()
![]()
![]()
cos t― это абсцисса соответствующей точки
![]() единичной окружности, то при всех
единичной окружности, то при всех
значениях х, удовлетворяющих данному
неравенству, абсцисса точки ![]() меньше
меньше ![]() .
.
Все точки на единичной окружности лежат левее прямой х =
![]() (без крайних точек, так как неравенство
строгое).
(без крайних точек, так как неравенство
строгое).
Если двигаться против часовой стрелки по окружности, то точка ![]() будет её началом, а точка
будет её началом, а точка ![]() ― её концом
― её концом
С учётом периодичности функции синус записываем ответ:
![]() + 2πk < t <
+ 2πk < t < ![]() + 2πk, k
+ 2πk, k![]() N.
N.
Возвращаемся к замене и преобразуем полученное двойное неравенство:
![]() + 2πk <
+ 2πk < ![]() <
< ![]() + 2πk, k
+ 2πk, k![]() N;
N;
![]() +
+ ![]() 2πk <
2πk < ![]() <
< ![]()
![]() + 2πk, k
+ 2πk, k![]() N;
N;
![]()
![]() 2πk <
2πk < ![]() <
< ![]() + 2πk, k
+ 2πk, k![]() N;
N;
![]() <
< ![]() <
< ![]() +
+![]() , k
, k![]() N.
N.
Ответ: (![]()
![]() +
+![]() ), k
), k![]() N.
N.
Неравенства для самостоятельного решения: а)
sin (3x - ![]() > -1
б) tg
> -1
б) tg ![]() <
<
![]() .
в) 2cos
.
в) 2cos ![]() > -
> - ![]() ;
;
Решая более сложные тригонометрические неравенства, можно применять метод интервалов. Тригонометрические функции на своей области определения имеют бесчисленное множество нулей. Поэтому можно решить тригонометрическое неравенство на одном периоде, а затем записать ответ с учётом периодичности данной функции.
Алгоритм решения:
1) Найти ОДЗ неравенства.
2) Найти период.
3) Найти нули на одном периоде.
4) Отметить нули на ОДЗ внутри одного периода и найти знак функции на в каждом из промежутков, на которые разбивается ОДЗ одного периода.
5) Записать ответ, учитывая знак данного неравенства и период функции.
Пример 2. Решить неравенство cos 2x + 5cos x + 3 > 0.
Решение.
1)
Привести все члены неравенства к
одному аргументу, применив тождество cos 2x
= 2![]() x – 1
x – 1
2![]() x – 1 + 5cos x + 3
> 0;
x – 1 + 5cos x + 3
> 0;
2)
Привести подобные слагаемые 2![]() x + 5cos x + 2
> 0;
x + 5cos x + 2
> 0;
3)
Замена cos x = t; получаем неравенство 2![]() + 5 t + 2 > 0;
+ 5 t + 2 > 0;
4)
решаем методом интервалов;
находим нули 2![]() + 5 t + 2 = 0, t1 = - 2, t2
= -
+ 5 t + 2 = 0, t1 = - 2, t2
= - ![]()
![]()
![]()
– + + • •
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решаем каждое неравенство:
а) cos x
< - 2 б)
cos x
> -
![]()
![]()
![]()
![]()
Нет
решения – ![]() + 2πk < x <
+ 2πk < x < ![]() + 2πk, k
+ 2πk, k ![]() N.
N.
Ответ: ( – ![]() + 2πk;
+ 2πk; ![]() + 2πk), k
+ 2πk), k ![]() N.
N.
Неравенства для самостоятельного решения: а) sin x < cos x б) ![]() x -
x - ![]() x >
sin 2x в) sin x > 1 +
x >
sin 2x в) sin x > 1 + ![]() x.
x.
Домашнее задание: Гл.I I, §11, п. 11.5, 11.6, 11.7, № 11.34 (и,м) 11. 36((и,м), 11.39 (и,м), 11.41 (и,м), 11.45 учебник «Алгебра и начала математического анализа» 10 класс, С.М. Никольский, М, Просвещение .
Тема: Контрольная работа № 1.
Цель: проверить знания, умения и навыки студентов полученные при изучении раздела «Алгебра».
Контрольная работа № 1. Вариант 1.
1. Выберите уравнение, которое задаёт множество точек, наиболее точно соответствующее графику, изображённому на рисунке.
|
А |
Б |
В |
Г |
Д |
|
y = |
y = - |
y = - x - 1 |
y = |
y = 2x + 1 |
X Y O
![]()
![]()
![]()
2.
Установите соответствие между
геометрическим преобразованием графика функции y = ![]() (1 – 4) и функциями, графики которых получены
в результате этих преобразований (А – Д).
(1 – 4) и функциями, графики которых получены
в результате этих преобразований (А – Д).
|
1 |
Графика функции y = |
А |
y = |
|
2 |
Графика функции y = |
Б |
y = |
|
3 |
Графика функции y = |
В |
y = |
|
4 |
Графика функции y = |
Г |
y = |
|
Д |
y = |
3.
Укажите верное равенство, если
для каждого из них ![]() принимает все допустимые значения.
принимает все допустимые значения.
|
А |
Б |
В |
Г |
Д |
|
|
1+ |
tg
|
Sinα · cosα=1 |
|
4. Укажите уравнение, к которому
можно привести уравнение ![]() - 3sin x – 3 = 0
- 3sin x – 3 = 0
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
5. Решить уравнения: а) ![]() - 3sinx +2 = 0;
- 3sinx +2 = 0;
Контрольная работа № 1. Вариант 2.
1. Выберите уравнение, которое задаёт множество точек, наиболее точно соответствующее графику, изображённому на рисунке.
|
А |
Б |
В |
Г |
Д |
|
y = - x +1 |
y = x + 1 |
y = |
y = |
y =- |
X Y O![]()
![]()
![]()
2.
Установите соответствие между
геометрическим преобразованием графика функции y = ![]() (1 – 4) и функциями, графики которых получены
в результате этих преобразований (А – Д).
(1 – 4) и функциями, графики которых получены
в результате этих преобразований (А – Д).
|
1 |
Графика функции y = |
А |
y = |
|
2 |
Графика функции y = |
Б |
y = |
|
3 |
Графика функции y = |
В |
y
= |
|
4 |
Графика функции y = |
Г |
y =
|
|
Д |
y = |
3.
Укажите неверное равенство,
если для каждого из них ![]() принимает все допустимые значения.
принимает все допустимые значения.
|
А |
Б |
В |
Г |
Д |
|
|
tg
|
|
tg |
ctg |
4. Укажите уравнение, к которому
можно привести уравнение 3 ![]() + 7 cos x – 3 = 0
+ 7 cos x – 3 = 0
|
А |
Б |
В |
Г |
Д |
|
3 |
3 |
3 |
3 |
10 |
5. Решить уравнения: а) Cos 2x (sinx +2) = 0;
Контрольная работа № 1. Вариант 3.
1.
Найти область определения
функции y = ![]() .
.
2.
Построить график функции y = ![]() .
.
3.
Упростить выражение ![]() -
- ![]() и вычислить его значение, если β = –
и вычислить его значение, если β = – ![]() .
.
4.
Решить уравнение ![]() x
- 4
x
- 4![]() + 3 = 0;
+ 3 = 0;
5. Решить уравнение cos 2 x – cos x = cos 3x.
Контрольная работа № 1. Вариант 4.
1.
Найти область определения
функции y = ![]()
2.
Построить график функции y = ![]() - 1
- 1
3.
Упростить выражение ![]() и вычислить его значение, если β = –
и вычислить его значение, если β = – ![]() .
.
4.
Решить уравнение ![]() + х = 4;;
+ х = 4;;
5.
Решить уравнение 4![]()
Контрольная работа № 1. Вариант 5.
1.
Исследовать функцию y = ![]() на чётность и нечётность
на чётность и нечётность
2.
Построить график функции y = ![]() -1
-1
3.
Доказать тождество ![]() = tg β
= tg β
4.
Решить уравнение ![]() = 4
= 4![]()
5.
Решить уравнение 4![]()
Контрольная работа № 1. Вариант 6.
1.
Исследовать функцию y = ![]() на чётность и нечётность
на чётность и нечётность
2.
Построить график функции y = ![]() .
.
3.
Доказать тождество ![]() · ctg β
= 1
· ctg β
= 1![]()
4.
Решить уравнение ![]() +
+ ![]() = 1;
= 1;
5.
Решить уравнение ![]() x - 3
sinx cosx = - 1
x - 3
sinx cosx = - 1
Рекомендованная литература:
ü Алгебра и начала анализа, 10 класс, учебник для общеобразовательных организаций: базовый и углублённый уровень - С.М. Никольский, М, Просвещение, 2014.
ü 3 000 конкурсных задач по математике (пособие для абитуриентов) Е.Д. Куланин, М, 1997.
ü Элементарная математика (повторительный курс) М.И. Сканави, М, Наука, 1976.
ü Устные упражнения по алгебре и началам анализа Р.Д. Лукин, Т.К. Лукина, М.С. Якунина, М, Просвещение, 1999
ü Математика (тематические тренировочные задания) И.ПИ. Кочагин, М.Н. Кочагина, М, ЭКСМО, 2014
ü Уравнения и неравенства М.И. Башмаков, М, Наука, 1991
ü Неравенства (популярные лекции по математике) П.П. Коровкин, М, Наука, 1993
ü Интернет-ресурсы.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.