Определение синуса

Определение синуса, косинуса и тангенса угла

Сегодня на лекции мы узнаем, как по-другому называются абсцисса и ордината точки, лежащей на единичной окружности.

Цели и задачи

Цель:

·         познакомиться с понятиями синус, косинус, тангенс и котангенс угла.

Задачи:

·         научиться определять синус, косинус, тангенс, котангенс угла;

·         рассмотреть решение задач на применение знаний о синусе, косинусе, тангенсе и котангенсе;

·         контролировать свои успехи на занятии.

знаем, научимся, сможем

На занятии

мы узнаем:

·         что такое синус, косинус, тангенс угла;

·         что такое линия тангенсов;

мы научимся:

·         решать простейшие тригонометрические уравнения;

·         определять линию тангенсов, котангенсов;

мы сможем:

·         понимать связь между синусом, косинусом, тангенсом углов.

·         Определение синуса, косинуса и тангенса угла

·         Найдите координаты точек А, В, С и D, лежащих на единичной окружности. Установите соответствие.

Конспект урока

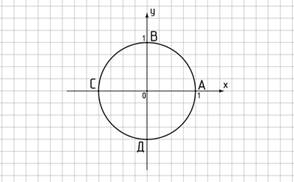
Алгебра и начала математического анализа

Урок №____. Определение синуса, косинуса и тангенса угла

Перечень вопросов, рассматриваемых в теме:

·         Ввод понятий синуса, косинуса, тангенса и котангенса угла

·         Определение синуса, косинуса, тангенса и котангенса угла

·         Решение простейших тригонометрических уравнений

·         Решение задач на применение знаний о синусе, косинусе, тангенсе и котангенсе;

Глоссарий по теме

Синус угла– ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Косинус угла – абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Тангенс угла  – отношение синуса угла к его косинусу.

Обозначается tg

Котангенс угла  отношение косинуса угла к его синусу.

Обозначается сtg

На единичной окружности касательная, проведенная к точке (1; 0) называется линией тангенсов.

Касательная, проведенная к точке (0; 1) - линия котангенсов.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Историческая справка

Зарождение тригонометрии относится к глубокой древности. Слово «тригонометрия» греческое: тригоно — треугольник, метрити — мера. Иными словами, тригонометрия — наука об измерении треугольников. Длительную историю имеет понятие синуса. Различные отношения отрезков треугольника и окружности встречаются уже в III в. до н. э. в работах великих математиков Древней Греции — Евклида, Архимеда, Аполлония Пергского. В IV—V вв. появился специальный термин в трудах по астрономии великого индийского ученого Ариабхаты (476 — ок.550). Отрезок он назвал ардхаджива, или более кратко джива. Арабскими математиками в IX в. слово джива было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в XII в. это слово было заменено латинским синус (sinus — изгиб, кривизна).

Косинус — это сокращение латинского выражения complementysinus, т. е. «дополнительный синус» или иначе «синус дополнительной дуги».

Название «тангенс» происходит от латинского tanger (касаться). Tangens переводится как «касающийся» (линия тангенсов — это касательная к единичной окружности).

Несмотря на то, что тригонометрия зародилась в древние времена, сегодня она охватывает практически все естественные науки и технику.

Актуализация знаний

1.Найдите координаты точек А, В, С и D, лежащих на единичной окружности (рис. 1)

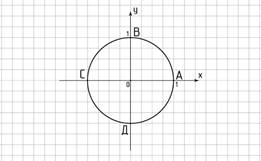
Рисунок 1 – единичная окружность

Поставьте в соответствие точке её координаты

А (0; 1)

В (-1; 0)

С (1; 0)

D (0; -1)

Ответ: А(1; 0); В(0; 1); С(-1; 0); D(0; -1)

Сегодня на уроке мы узнаем, как по-другому называются абсцисса и ордината точки, лежащей на единичной окружности.

1.Рассмотрим окружность радиуса, равного 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют

единичной или тригонометрической.

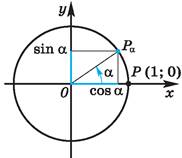
Рисунок 2 – точка Р на единичной окружности

Точка Р (1; 0) при повороте вокруг начала координат на угол  переместилась в точку Рₐ. Определим её координаты. (рис. 2).

Определения.

Синусом угла называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол.

Обозначается

Косинусом угланазывается абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается 

Угол  может выражаться и в градусах и в радианах.

Пример 1.

Точка А(1; 0) при повороте на угол 90 (рис. 1)

Ордината точки В равна 1, значит или

Абсцисса точки В равна 0, значит 

Пример 2.

Точка А(1; 0) при повороте на угол  переместилась в точку ( рис. 1)

Найдите  и 

Ответ: = 0; 

Пример 3.

Точка А(1; 0) при повороте на угол  переместилась в точку  (рис. 1)

Найдите  и 

Ответ: =1= 0.

Рассмотрим ещё два понятия.

Определение. Тангенсом угла  называется отношение синуса угла к его косинусу.

Обозначается tg

tg, 

Пример 4.

Найти tg 0. Вычислим по формуле tg  = = 0.

Определение. Котангенсом угла  называется отношение косинуса угла к его синусу.

Обозначается сtg

сtg

Пример 5.

Найти сtg .

Вычислим по формуле сtg  = 

2. Меру угла(в радианах) можно рассматривать как действительное число, поэтому  и  – это числовые выражения. А так как каждая точка единичной окружности имеет координаты х и у такие, что выполняются неравенства -1 ≤ х ≤ 1; -1 ≤ у ≤ 1,то синус и косинус не могут превышать значения, больше .

Чтобы решить уравнения = а,  нужно считать х неизвестным, число а – заданным.

Пример 6.

Решить уравнение  = 1.

Найдем точку с ординатой 1 и запишем, каким числам х она соответствует. На окружности мы видим эту точку: В (0; 1). Она соответствуют числу  и всем числам вида 

Решением уравнения  = 1 являются х =.

3. Полезно знать синусы, косинусы, тангенсы некоторых углов. Для этого рассмотрим дугу единичной окружности в I четверти координатной плоскости (рис. 3).

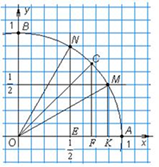
Рисунок 3 – 1 четверть единичной окружности

Точки А (1; 0) и В (0; 1) нам знакомы. Рассмотрим ещё несколько точек на окружности и найдем их координаты. Точка С является серединой дуги АВ, значит угол АОС равен половине прямого угла, 45 или . Ордината точки С равна её абсциссе. Их значения нетрудно найти по теореме Пифагора из прямоугольного треугольника ОСF, оно равно  А значит, 

,

tg 45

Дуга АМ составляет третью часть прямого угла, . Ордината точки М равна , значит

, tg30.

Дуга АNсоставляет  прямого угла, . Абсцисса точки N равна , поэтому

,  tg 60.

Чтобы легче запомнить эти значения, придумали мнемоническое правило- правило на ладони (рис. 4).

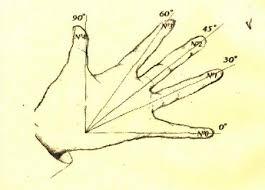
Рисунок 4 - мнемоническое правило- правило на ладони

Расположим ладонь так, как на рисунке, пусть мизинцу соответствует угол 0, следующим пальцам– 30, 45, 60 и 90. Так же присвоим им номера: мизинец №0, следующие №1, №2, №3, №4. Чтобы найти синус, используем формулу: =. А для косинуса нумерацию будем вести от большого пальца, выполняя вычисления по той же формуле. =.

Например, =, = = .

А тангенс можно вычислить по формуле: tg = .

Тангенсы и котангенсы, также как и синусы, косинусы, можно определить по единичной окружности. Для этого познакомимся с ещё одним понятием.

На единичной окружности касательная, проведенная к точке (1; 0) называется линией тангенсов. Касательная, проведенная к точке (0; 1) - линия котангенсов (рис. 5).

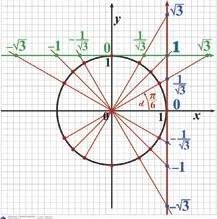
Рисунок 5 – линия тангенсов и линия котангенсов

Например, чтобы найти tg, находим пересечение радиус-вектора под углом  с линией тангеса. Это число , или .

Чтобы найти ctg , радиус-вектор под углом  должен пересечь линию котангенсов.

Это число .

Примеры и разбор решения заданий тренировочного модуля

Пример 6.

Решить уравнение =0.

Синусом угла является ордината точки, поэтому значения синусов находим по оси Оу.

Найдем точки А (1; 0) и С (-1; 0) с ординатой 0 и запишем, каким числам х они соответствуют. Они соответствуют числам 0 (точка А), (точка С), 2

Решением уравнения = 0 являются х =.

Z- множество целых чисел.

Пример 6.

Решить уравнение=1.

Найдем точки с абсциссой 1 и запишем, каким числам х они соответствуют. На рис.3 мы видим эту точку: А (1; 0) Она соответствуют числу  и всем числам вида 

Решением уравнения= 1. являются х = , где .

Скачано с www.znanio.ru