КОНСПЕКТ ОТКРЫТОГО УРОКА

«ОБОБЩЕНИЕ ТЕМЫ «ТРЕУГОЛЬНИКИ»

(геометрия, 9 класс)

«Вс)охновение нужно в геометрии

как и в поэзии»

                                                                                                                                                              А. С. П) '?нкин          

Цели и задачи Урока:

-  обобщить и закрепить основные понятия. свойства и теоремы по данной теме при решении задач;

-  воспитать навыки коллективной работы;

-  продолжить развитие логического мышления, вычислительных навыков.

Подготовительная работа к уроку (теоретические вопросы).

1. Определение треугольника.

Условие су^гществования треугольника (неравенство треугольника). З. Определение. свойства и признак равнобедренного треугольника.

4.       Признаки равенства треугольников.

5.       Признаки подобия треугольников.

6.       Отношения периметров и площадей подобных треугольников.

7.       Определение и свойство внешнего угла треугольника.

8.       Определение м свойство средней линии треугольника,

9.       Теорема о сумме углов треугольника.

10.   Теорема Фалеса.

1 . Замечательные точки треугольника.

12. Теорема Пифагора.

13. Все формулы для вычисления площади треугольника.

[4. Определение треугольника, вписанного в окружность.

15.  Определение треугольника, описанного около окружности.

16.  Положение центра окружности, описанной около треугольника.

17.  Тригонометрические ф\'нкции ос грого угла ПРЯМОУТОЛЬНОГО треугольника.

18.  Теорема синусов.

19.  Теорема косинусов.

ПЛАН ПРОВЕДЕНИЯ УРОКА.

       1.         Устная работа с теоретической частью темы.

       П.         Практическая работа (решение задач).

ш. Подведение итогов урока.

       lV,       Домашнее задание.

ОРГАНИЗАЦИЯ РАБОТЫ НА УРОКЕ.

При проведении устной работы ученики выполняют задания индивидуально. Решение задач проводится в группах. Задания дифференцированные и содержат 2 уровня сложности: уровень А — для слабых учеников. уровень В — для более подготовленных учащихся. Все ответы учеников комментируются и обсуждаются.

Т. УСТНАЯ РАБОТА.

(индивидуальная деятельность)

Ученики. из группы А соотносят некоторые утверждения с их названиями или формулами, ученики из группы В находят ОШЛОкИ в тексте.

А. СООТНЕСИТЕ ВЫСКАЗЫВАНИЕ С ЕГО НАЗВАНИЕМ ИЛИ формулой.

В. НАЙДИТЕ ОШИБКИ В ТЕКСТЕ.

«Некий ученик написал сочинение по теме «Треугольники». Вот некоторые фрагменты его сочинения.

         Треугольник это геометрическая фигура, состоящая из трех точек, соединенньпх попарно отрезками.

         Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.

 Площадь любого треугольника можно вычислить по формулам,

(* ) и S = ab •sinZC (**)

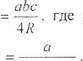
Если в треугольник вписана окружность, то его площадь можно найти по формуле S где радиус этой окрх:жности вычисляется по теореме

КОСИНУСОВ: R =

2 cos ZA

         А если около треугольника описать окружность, то для нахождения

площади треугольника справедлива формула S = (а + Ь + с) ,

         Прямая, параллельная стороне треугольника, является его средней линией.  Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.

Все ли верно в сочинении ученика?»

П. РЕШЕНИЕ ЗАДАЧ.

(рабо 1 а в группах)

УРОВЕНЬ А.

В треугольнике АВС АВ = 10, АС 12. Периметр треугольника АВС равен 32.

 . Определите вид треугольника по длинам его сторон.

2. Найдите высоту, опущенную из вершины В.

3. Найдите площадь треугольника.

4.   Найдите sinB

5.   Найдите радиус описанной около треугольника окружности.

6.   Найдите радиус вписанной в треугольник окружности.

7.   Подобны ли треугольник АВС и треугольник, вершинами которого являются середины сторон треугольника АВС? Найди] е перимегр и площадь получившегося треугольника.

Если при решении задач хченики ИСПЫТЫВЕ{ЮТ затруднения, они могч:т ВОСПОЛЬЗОГзаТЬСЯ шпаргалкой.

ШПАРГАЛКА К РЕШЕНИЮ ЗАДА Ч.

К пункту ]. Воспользуйтесь определением периметра треугольника и найс)ите сторону вс.

К пункту 2. Используйте своЙст60 равнобедренного треугольника и теорему Пифагора.

Испоиьзуйте формулу S = —ah .

К пункту 4. ВОСПОЛЬЗУЙТЕСЬ формулой S — —с“) •sin  ZC и результатами

2

АС

К ПУНКТУ 5.Используйте слеДствне к теореме синусов     sin В

пункту 6.Воспользуйтесь формулой S = — Рг- .

2

К пункту 7. Используйте свойство средней ЛИНИИ треугольника и Докажите поДобие треуголДников. Затем найДите коэффициент поДобия и воспользуйтесь теоремами об отношении периметров и риощаДей поДобных треугольников. УРОВЕНЬ В.

1. Даны треугольники АВС и MNk. Верно ли, что если дт =42 ⁰ , ZN=63 ⁰

       0=75 ⁰ , ZA:ZC      ЛК=З, ВС    то

2. Верно ли, что если треугольник АВС со сторонами АВ —-3, ВС=5, АС = 2 вписан в окружность, то центр окружности лежит во внешней области треугольника? Найдите радиус окружности.

З. Верно ли, что в треугольник со сторонами, равными 5, 6, 7 можно вписать окружность с радиусом — ?

4.       В четырехчгольнике АВГ)С сторона ВГ) равна 5, диагональ ВС равна 8, = а ДВЕ) = 60 ⁰ „на. ШОВ = 120 ⁰ - внешний угол треугольника АВС. Верно ли, что периметр треугольника АВС равен 24?

5.       Существует ли треугольник, стороны которого равны 2, 5, 8? Если нет, то какой должна быть меньшая сторона этого треугольника? Можно ли задать длину этой стороны целым числом?

6.       Треугольник АВС — прямоугольный (ZB = 90 ⁰ ). Во внешней области этого треугольника построен прямоугольный треугольник АШ), в котором АВ гипотенуза. АС = 6, ВС = 343 , Г)В 1. Найдите cigZDAB, S cosZDAC' и угол между прямыми АВ и СГ).

Ш. ПОДВЕДЕНИЕ ИТОГОВ УРОКА

Ученики вместе с учителем обсуждают успехи и недостатки работы на уроке. Дают оценку деятельности учащихся и качества предложенных заданий.

W. ДОМАШНЕЕ ЗАДАНИЕ.