Открытый урок по математике на тему: " Построение графика квадратичной функции"

Гонодинская СОШ

Урок по алгебре

Построение графика квадратичной функции (9класс)

Тип урока: урок закрепления знаний

Цели урока:

- повторение свойств  и особенности графика квадратичной функции вида  y = ax²;

- закрепление навыков построения графиков квадратичной функции, умения  указывать             координаты вершины параболы, её оси симметрии, направление ветвей;

- отработка приёмов построения графика функции  на конкретных примерах; 

- обучение способам самоконтроля;

- развитие речи, пространственного абстрактного мышления, мелкой моторики;

-  развитие культуры выполнения графических работ.

План и ход урока.

I. Организационный момент. Сообщение темы и постановка целей урока.

II. Проверка домашнего задания.

III. Актуализация опорных знаний.

1) - Что называют функцией?

    - Что называется графиком функции?

    - Что называется областью определения и областью значений функции?

    - Какая функция называется квадратичной?

    - Как из графика функции  y = ax² получить график функции y = - ax² ? Показать на модели.

    - Как изменится при этом область значений функции?

    - Каким образом из графика функции y = ax²  получить график функции                                                                                     ?

    - Перечислите свойства квадратичной функции  при a>0, при a<0 (Таблица с изображением графиков на доске). Учащиеся подробно проговаривают все свойства функции (Область определения и область значений, нули, ось симметрии, промежутки возрастания и убывания, наибольшее и наименьшее значения функции).

2) a) Работа по карточкам (4 человека возле доски):

 - На координатной плоскости, используя шаблон графика функции y = x ² ,  построить графики:

б) Остальные – устно.

1) Укажите координаты вершины и направление ветвей параболы:

а) у = 3(х + 2)²  - 8;

б) у = - (х – 4)²;

в) у = х ² + 6;

г) у = - 3х²  - 0,1.

                    2) определите нули функции у = ах² + вх + с  и ось симметрии параболы:

а) у = (х - 3) ∙ (х + 5);

б) у = х ∙ (х + 4);

в) у = - 3 ∙ (х - 1) ∙ (х - 6);

г) у = - х ∙ (х + 7).

                                                                                (m = (х₁ + х₂) / 2, где х₁ и  х₂  - нули функции).

IV. Построение графика квадратичной функции.

                           - План построения?

(1 ученик у доски, остальные в тетрадях)

            3) Точки     пересечения с осью абсцисс (-5;0); (-1;0), с осью ординат (0;-5).

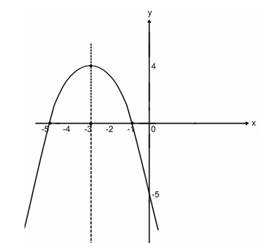
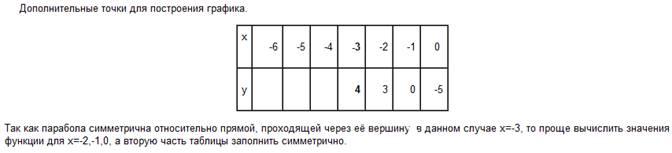         4) Строим график.

V.

VI. Домашнее задание.

                          п.7, № 126, 133(а).