ПЛАН-КОНСПЕКТ ЗАНЯТИЯ Тема: "ПИД регуляция"

МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ УЧРЕЖДЕНИЕ

ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ

МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОД КРАСНОДАР

«МЕЖШКОЛЬНЫЙ ЭСТЕТИЧЕСКИЙ ЦЕНТР»-

АССОЦИИРОВАННАЯ ШКОЛА ЮНЕСКО

 

 

 

 

 

ПЛАН-КОНСПЕКТ ЗАНЯТИЯ

 

Тема: "ПИД регуляция"

 

 

 

 

 

 

 

 

Автор: Никита Олегович Шевцов,

педагог дополнительного образования

 

 

 

 

 

 

 

 

 

 

Краснодар, 2021

 

ПЛАН-КОНСПЕКТ

Тема: "ПИД регуляция"

Вопросы для рассмотрения:

1.                 Формула PID регулятора

2.                 Пропорциональная составляющая

3.                 Интегральная составляющая

4.                 Дифференциальная составляющая

5.                 Реакция на помехи

6.                 Настройка

7.                 Частота опроса

8.                 Настройка пропорционального коэффициента

9.                 Настройка интегрального коэффициента

10.             Настройка дифференционального коэффициента

11.            Заключение

12.            Задание для детей

 

ХОД ЗАНЯТИЯ

В начале занятия необходимо проверить наличие у детей тетрадок, ручек.

Дать под запись дату. Озвучить тему занятия, что она подразумевает. Дети включают компьютеры, начало рассмотрения вопросов.

 

Формула ПИД-регулятора

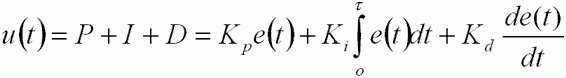
·                   u (t) — наша Функция;

·                   P — пропорциональная составляющая;

·                   I — интегральная составляющая;

·                   D — дифференциальная составляющая;

·                   e (t) – текущая ошибка;

·                   Kp — пропорциональный коэффициент;

·                   Ki — интегральный коэффициент;

·                   Kd — дифференциальный коэффициент

У нас есть воздействие, наша Функция (u (t)). Она состоит из трех составляющих – Пропорциональной, Интегральной и Дифференциальной (отсюда и ПИД-регулятор).

·                   Формула в вышеприведенном виде хороша для изучения, но неудобна для расчетов (хотя бы потому, что в вычислительной технике надо переходить к численным методам). В программной реализации, переходят к дискретной реализации

u(t) = P (t) + I (t) + D (t);

P (t) = Kp * e (t);

I (t) = I (t — 1) + Ki * e (t);

D (t) = Kd * {e (t) — e (t — 1)};

Вот это уже выглядит куда реальнее и понятнее! Мы вычисляем сумму трех составляющих. Каждая из них определяется своими коэффициентами. Если данный коэффициент нулевой, то составляющая в вычислении не участвует. С этой формулой мы и будем работать далее, ее я и реализую.

Впрочем, есть еще и другая, рекуррентная реализация:

u(t) = u(t — 1) + P (t) + I (t) + D (t);

P (t) = Kp * {e (t) — e (t — 1)};

I (t) = I * e (t);

D (t) = Kd * {e (t) — 2 * e (t — 1) + e (t — 2)};

Какая из них лучше/правильней? Математика, в общем-то, одинаковая. Коэффициенты тоже. Говорят, что есть разные подводные булыжники при реализации.

Обратите внимание! Коэффициенты тут – обязательно дробные числа! В языке программирования Си – как минимум float, а лучше бы и double.

Вся магия ПИД-регуляторов – именно в этих коэффициентах. Как их подбирать – посмотрим в конце. А сейчас переведем дух от математики и поедем к изучению поведения этой формулы.

Пропорциональная составляющая

Название пропорциональный коэффициент идет из-за прямо пропорционального воздействия на результат. Он самый очевидный и понятный. Рассмотрим его -пропорционального коэффициента -влияние на результат.

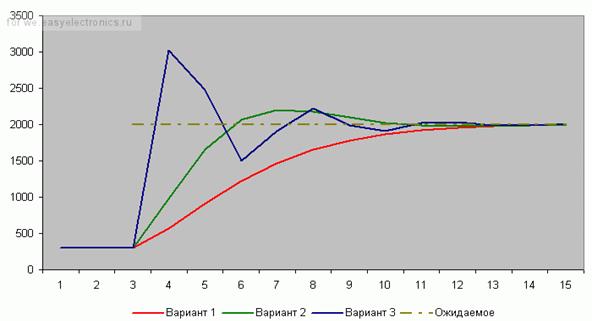
«Ожидаемое» – это то, что мы хотим получить. Вначале оно равно какому-то низкому значению

Сделаем первый вариант: Kp = 2. Посмотрим на красную линию. Что мы видим? По ходу дела обороты начали расти – ошибка стала снижаться – значение коррекции постепенно растет — красная линия растет

Попробуем другой коэффициент: Kp = 5. Что видим? Зеленая линия. Достигла результата шустро .

А что если коэффициент сделать еще больше? Kp = 20. Синяя линия – бух! За один шаг! Но – сразу перелет. Потом падаем вниз – ошибка стала отрицательной. Опять сильно вниз! Рывок вверх! Опять вниз! Что видим? Пошли колебания. Они, слава Богу, затухающие.

Если увеличивать коэффициент больше, то такие колебания могут стать незатухающими. Система начнет колебаться все больше и больше, пока не … ну-у, тут уже все зависит от конкретной системы.

Какова природа колебаний? Система, на которую воздействуют, всегда (в реальной жизни) инерционна. Обороты повышаются – коэффициент падает к нулю. И вот – достигли нужной точки. Коэффициент ошибки (и регулирования) достиг нуля. Но ведь процесс поднятия оборотов инерционен!

Отсюда вывод подбирать коэффициент необходимо, экспериментально в зависимости от системы в которой ведется расчет.

 

 

 

Интегральная составляющая

Эта составляющая накапливает ошибку. Т. е. постепенно накапливается эта самая ошибка, интегратор «наполняется» и его воздействие увеличивается. Эффект от такого накопления не мгновенен — ибо ошибка должна накопиться, на что уходит некоторое количество шагов алгоритма.

Рассмотрим случай, когда Kp = 5, а Ki будем менять:


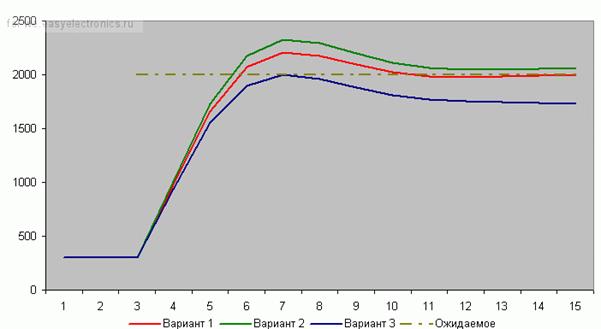
Вариант 1 (красный) – Ki = 0.

Вариант 2 (зеленый) – Ki = 0.2.

Вариант 3 (синий) – Ki = -0.3.

Использование положительного коэффициента (зеленая линия) в данном случае, пожалуй, ничего нам не дало. А вот отрицательный коэффициент (синяя линия) очень даже неплохо помог! Но вот только линяя пошла вниз, и потом она приведет к раскачиванию системы… (но на практике раскачивания системы, как правило, не происходит, т. к. постоянно будут коррекции текущего состояния)

Итак, интегральная составляющая позволила нам сгладить резкий эффект пропорциональной составляющей. Это неплохо!

Но вы погодите – сейчас нам покажет всю свою мощь

 

 

 

 

 

Дифференциальная составляющая

Эта составляющая пропорциональна темпу изменений. Как и ранее, Kp = 5, а Kd будем менять:

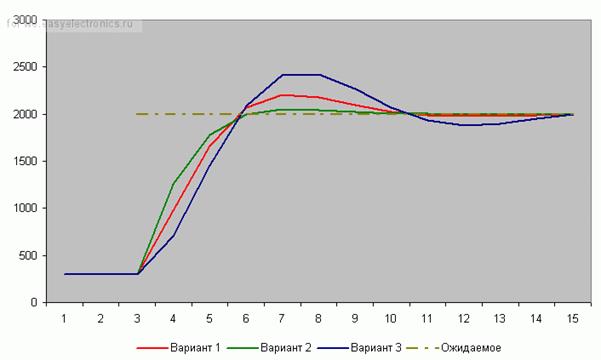
Вариант 1 (красный) – Kd = 0.
Вариант 2 (зеленый) – Kd = 0.2.
Вариант 3 (синий) – Kd = -0.2.
Каково? И сглаживает, и не дает раскачиваться в будущем!

Реакция на помехи

Надо еще не забывать об одной такой малоприятной вещи – о помехах. Они будут раскачивать лодку нашей системы.

Вот картинка, когда у нас стоит задача поддерживать одно и то же значение ошибок:

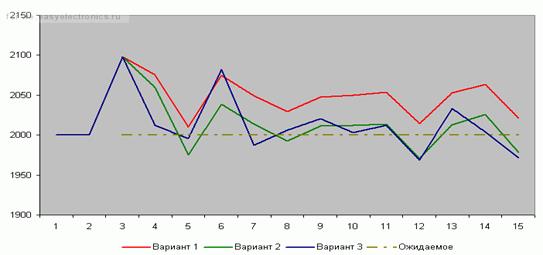
Шумовое (случайное) воздействие – одинаковое для всех вариантов.

Вариант 1 (красный) – Kp = 10, Ki = 0, Kd = 10.

Вариант 2 (зеленый) – Kp = 10, Ki = 2, Kd = 0.

Вариант 3 (синий) – Kp = 10, Ki = 2, Kd = 6.

Как видно, с добавлением составляющих стабильность (немного) увеличивается.

Настройка

Я думаю, общее представление о формуле ПИД-регулирования вы получили. Программируется легко, эффект красивый. И следующий вопрос у вас будет – «а как получит коэффициенты»? И вот тут все становится кисло… Потому что, если до этих пор шла строгая математика, то дальше начинаются танцы с бубнами, шаманство и шайтанство.

Прежде всего, вы должны иметь четкое представление о своей системе регулирования – насколько она инерционна? какие шумы на нее могут воздействовать? какие воздействия (результаты функции ПИД-регулятора) для нее недопустимы?

Следующий вопрос – насколько вашу систему можно погонять в разные стороны? Все методы, что я нашел, базируются на тестовых воздействиях на систему и анализе результатов. Нужно пробовать, пробовать, считать, считать, считать (ну или по науке — строить модель)… А температура двигателя-то растет, и воздействие через полчаса работы уже будет совсем не таким, как при начале.

⁃                увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;

⁃                с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;

⁃                уменьшение постоянной интегрирования уменьшает запас устойчивости;

⁃                увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие

Частота опроса/воздействия

Есть очень важный момент работы при разработке ПИД-регулятора: воздействие должно быть строго периодичным, т. е. производиться через равные промежутки времени! Аналогично, ошибка должна вычисляться также периодически.

Какой должен быть период измерений/воздействий? Для начала определите время стабилизации системы – за сколько должно быть достигнуто устойчивое состояние. Потом разделите это время на 10 … 100 – и вы получите длительность шага (в моем случае хватит и 10 мсек). А вообще – чем выше частота, тем лучше! Но надо помнить, что операции с дробными числами весьма медленны. Фактически, они и зададут вам период работы.

Посмотрим, как период опроса (и воздействия) влияет на качество результата:


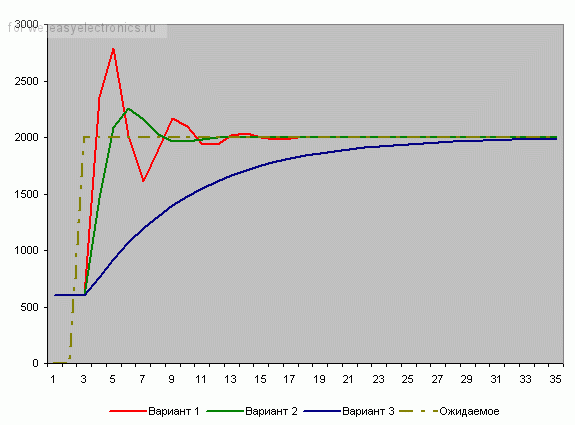
Коэффициенты ПИД-регулятора: – Kp = 10, Ki = 0, Kd = 0.

Вариант 1 (красный) – период опроса 0.5 у.е.

Вариант 2 (зеленый) – период опроса 0.35 у.е.

Вариант 3 (синий) – период опроса 0.15 у.е.

Как видим, в первом случае есть мощные выбросы. Во втором случае (70% от первого периода) они стали слабее, а в третьем (30%) – преобразование вообще получилось гладким! Т. е. для первых двух вариантов нужны дополнительно интегральная или дифференциальная составляющие, а для последнего мы обошлись только пропорциональной. А это существенная разница в вычислениях!

Так что вопросу выбора периода надо уделить первостепенное внимание. В микроконтроллерах Arduino Uno присутствует присутствует кристал atmega 328, с частотой 16  Мгц

Настройка пропорционального коэффициента Kp

Для начала я устанавливаю коэффициент Kp в 1 и смотрю, что будет. Растет слишком медленно – увеличиваю. В какой-то момент начнутся перелеты и колебания. Значит, многовато – уменьшаем. Исчезли – немного увеличиваем. Начались – немного уменьшаем. Исчезли — … И так далее, пока не надоест. В итоге получили достаточно устойчивый пропорциональный регулятор, который надо немного скорректировать (надо ли? Если все работает вполне качественно, то не морочим себе голову и считаем, что все настроено)

Настройка дифференциального коэффициента Kd

Понемногу наращиваю коэффициент Kd — 0.5, 1,… Колебания системы уменьшаются, все работает красивее… Пока не происходит обратное – начинаются мощные выбросы. Все, перерегулировали, уменьшаем.
Итак, имеем выбросы – уже меньше, но все равно имеем. Самое то сгладить, притормозить воздействие!

Настройка интегрально го коэффициента Ki

Шаманим дальше. Берем совсем немного – 0.1 для начала. Можно попробовать и небольшое отрицательное значение. Смотрим, пробуем, крутим.

Процесс этот – настройки – итерационный. Стоит пробовать разные варианты, начинать сначала. Для меня он по-прежнему туманен и шайтанен.

В заключение – о реализации

С теорией вроде бы разобрались. Теперь – о реализации.

Сердце регулятора – формула. Она оперирует с дробными числами. Учтите, что такие операции и на 32-хбитным контроллерах выполняются не моментально, что тут говорить о 8-битках. Вычисление отдельных частей формулы – П-, И-, Д- лучше написать не одной строкой на Cи, а разбить на части. И делать между ними что-нибудь полезное.

 

Заключительная часть занятия

Рефлексия. Итоговый опрос.

Задание: Совместное задание с детьми создать программу с ПИД регулятором для езды по линии.