План-конспект урока "Комплексные числа. Арифметические операции над ними"

Комплексные числа.

Арифметические операции над комплексными числами

(разработка урока по математике)

ЦЕЛЬ УРОКА:

добиться понимания обучающимися необходимости введения новой числовой системы – системы комплексных чисел и научить их выполнять арифметические операции в новой системе.

ЗАДАЧИ УРОКА:

Образовательные:

·          познакомиться с новой числовой системой, системой комплексных чисел, с историей её возникновения;

·          ввести понятия: комплексного числа, чисто мнимого числа; противоположных, равных, сопряжённых чисел на  множестве С;

·          познакомить обучающихся с устной и письменной символикой введённых понятий;

·          ввести операции сложения, вычитания, умножения, деления и перехода к сопряжённому числу на множестве комплексных чисел;

·          сформировать у обучающихся умение выполнять арифметические операции над комплексными числами.

Воспитательные:

·          подвести обучающихся к выводу о необходимости введения новой числовой системы – системы комплексных чисел;

·          формировать научное мировоззрение;

·          расширить  кругозор обучающихся.

Развивающие:

·          активизировать познавательную деятельность обучающихся;

·          развивать навыки самостоятельной работы.

ТИП УРОКА: комбинированный

Структура урока

I.         Актуализация знаний (3-5 мин.)

- проверка готовности к уроку

- объявление темы урока;

- постановка целей урока.

II.      Подготовка к изучению нового материала (5-7 мин.)

Устный работа (3-5 мин.)

- понятие числа

- числовые множества: натуральные, целые, рациональные, действительные числа

ü допустимые операции в числовых множествах

ü частично допустимые операции в числовых множествах

ü недопустимые операции в числовых множествах

Историческая справка в форме доклада обучающегося (3-4 мин.)

III.   Изучение нового материала (10-15 мин.)

Новый материал

- необходимость "пополнить"  множество  действительных  чисел

- определение комплексного числа

- определение мнимой и действительной части комплексного числа

- комплексно сопряженные числа

- равные комплексные числа

- противоположные комплексные числа

- обозначения в множестве комплексных чисел

Историческая справка, подготовленная обучающимися.

Алгебраическая формула комплексного числа

Действия над комплексными числами

Минимальные условия, которым удовлетворяют комплексные числа

IV.   Закрепление нового материала (6-10 мин.)

- устная работа:

назовите пары равных между собой комплексных чисел

назовите пары противоположных комплексных чисел

- решение задач на закрепление нового материала

решение тренировочных задач

- обучающая самостоятельная работа

V. Итог урока (2-3 мин.)

- объявление оценок

- итог урока по вопросам «Сегодня на уроке…», «Мне запомнилось…»,  «Хотелось бы отметить…»

Ход урока

                  I.     Организационный момент. Формулировка целей урока.

Сегодня на уроке мы познакомимся с новой числовой системой – системой комплексных чисел. Рассмотрим историю её возникновения, введём арифметические операции на множестве комплексных чисел и их свойства.

                   II.Подготовка к изучению нового материала.

1.        Устная работа

Числа – один из основных математических объектов.

Понятие числа развивалось и изменялось на протяжении всей истории человечества. С течением времени числовые системы расширялись, становились всё более сложными, включая как составные части ранее известные числовые системы. Каждая из числовых систем имела свои преимущества и свои недостатки. У более сложной больше различных возможностей по её использованию и применению, но при этом и само построение такой системы, и знание многочисленных деталей, очевидно, требуют больших усилий и большего времени. Рассмотрим основные числовые системы. 

Вам уже знакомы натуральные, целые, рациональные, иррациональные числа. В математике нередко употребляют вместо понятия «множество» термин система чисел, который означает множество объектов вместе с некоторым выбором свойств и отношений. Вместе они образуют множество действительных чисел.

.

Невозможно на множестве натуральных чисел выполнить действия: 45-210, 3:6, .

Приведите примеры действий невыполнимых в системе натуральных чисел.

Невозможно на множестве целых чисел выполнить действия: 42:10, .

Приведите примеры действий невыполнимых в системе целых чисел.

Невозможно на множестве рациональных чисел выполнить действие .

Приведите примеры действий невыполнимых в системе рациональных чисел.

Невозможно на множестве действительных чисел выполнить действие .

Приведите примеры действий невыполнимых в системе действительных чисел.

2.      Историческая справка

Число – одно из основных понятий математики, позволяющее выразить результаты счета или измерения. Понятие числа служит исходным для многих математических теорий. Числа находят широкое применение в физике, механике, астрономии, химии и многих других науках. Числами постоянно пользуются в повседневной жизни.

Магические свойства чисел волновали людей еще в глубокой древности. Хотим мы этого или нет, но где-то глубоко в нас сидит какая-то симпатия к одним числам и осторожность, а порой и совсем неприятные чувства к другим. Особым почитанием окружены были числа в Древней Греции. Философ и математик Пифагор утверждал, что «числа правят миром». Он создал школу единомышленников, которые верили в магию чисел и думали, что за каждым предметом стоит какое-то число. Числа, считали они, несут с собой добро и зло, счастье и несчастье.

Число 0. Это символ абсолюта, бесконечности и является числом непроявленного мира. Это начало всех вещей, это сон или смерть. Графически изображается как кольцо или круг.

Единица. Пифагор и его единомышленники ставили единицу выше всех других чисел, считая, что именно она – начало всех начал, что именно от нее пошел весь мир. Без единицы не состоялось бы самое простое счисление. Графически изображается как вертикальная линия.

Двойка. Это число является символом любви, непостоянства и равновесия. Число 2 – это мягкость и тактичность, стремление сгладить острые углы. Оно находится между добром и злом, теплом и холодом, светом и мраком, богатством и нищетой.

Тройка. У многих народов весьма продолжительное время пределом счета было число 3. Его считали символом полноты, совершенства. Так, у древних греков это число считалось счастливым, а в Древнем Вавилоне стали поклоняться трем божествам: Солнцу, Луне и Венере. Число три стало самым излюбленным числом и в мифах, и в сказках. Еще его магия заключалась в том, что оно складывалось из суммы предыдущих чисел (3=1+2), символизировалось треугольником, который представляет прошлое, настоящее и будущее.

Четвёрка. Древние считали это число символом устойчивости и прочности. Ведь оно представлено квадратом, четыре стороны которого означают четыре стороны света, четыре времени года, четыре стихии- Огонь, Земля, Воздух и Воду. Геометрическая правильность: квадрат или ромб; в славянской символике - символ Земли.

Тоже очень знаменательное число, как и три.

В японо-китайском мире 4-роковое число.

Числу 5 Пифагор отводил особое место, считая его самым счастливым из всех чисел. Древние же считали число «пять» символом риска, приписывали ему непредсказуемость, энергичность и независимость. Числовая правильность: 5-простое число; 5 пальцев - пятеричная система счисление; 5- конечная звезда; 5 чувств ( зрение, слух, обоняние, осязание, равновесие). 5 главных признаков в православие: Обрезание Господне, Рождество Иоанна, Праздник святых Петра и Павла, Усекновение главы Иоанна-Крестителя, Покров пресвятой Богородицы. 5 заветов буддизма; мусульманин молится 5 раз в день.

Число 6. Пифагор считал его удивительным числом, так как оно обладает замечательным свойством: получается в результате сложения или перемножения всех чисел, на которые делится.

Шестёрка делится на 1, 2, 3 и если сложить или перемножить эти числа, то вновь получиться 6 (1 + 2 + 3 = 1 х 2 х 3 = 6). Таким свойством не обладает ни одно другое число. 6 - «число творения», Бог создал мир за 6 дней.

Геометрическая правильность: правильная, плоская, выпуклая фигура – правильный 6 - угольник.

В славянской символике – символ солнца.

Числовая правильность: 6 – совершенное число.

6 – число предметов в чайных и столовых сервизах.

Семь. В египетской и вавилонской философии и астрономии оно рассматривалось как сумма двух «жизненных» чисел: три и четыре. Три человека – отец, мать, ребёнок составляют основу жизни; а четыре – это число стран света и направлений ветра, откуда приходит дождь, живительная влага которого делает землю плодоносящей.

По утверждению Пифагора, сумма чисел 3 и 4 (символизирующих собой треугольник и квадрат) считалось проявлением законченности и совершенства. Поэтому-то число 7, сумма тройки и четвёрки, воспринималось как священное.

Семь считали магическим, возможно, ещё и потому, что человек воспринимает окружающий мир (свет, звуки, запахи, вкус) через семь «отверстий» в голове (два глаза, два уха, две ноздри, рот).

Свято почитали число и древние евреи. В Священном писании говорится: «…В шесть дней создал Господь небо и землю, море и всё, что в них, а в день седьмой почил». С тех пор евреи, а затем и все христиане, воспринявшие от них Ветхий Завет, считают 7 священным числом.

С давних пор число 7 имело разное символическое значение. Так, древние греки ежегодно выбирали 7 лучших актёров (комических и трагических), древние римляне почитали семерых мудрецов. В христианстве говориться о семи грехах и семи таинствах. У мусульман местом «высшего просветления» считается седьмое небо, куда, якобы, попадают все угодные аллаху.

Это волшебное число широко использовалось в сказках, мифах древнего мира.

А вообще-то особой геометрической правильностью семёрка не обладает, да и очень неудобное для расчётов это число, но испокон веков почиталось оно как священное число.

Число 8. Древние считали воплощением надежности, доведенным до совершенства. Символизировалось двойным квадратом. Разделенное пополам, оно имеет равные части. Если его еще разделить, то части тоже будут равными(2, 2, 2, 2).

Девятка. Таинственную силу приписывали древние и числу 9, причем в одни времена добрую, в другие – злую. У древних римлян за этим числом установилась добрая слава. Монголы считали девятку совершенством. В японо-китайском мире 9 – несчастливое число; воспринимается как «болезнь».

Десять. Символом гармонии и полноты выступало число 10. Этим числом, выражающимся суммой 1+2+3+4, символизировался философский камень. Десяток стал основой десятичной системы счета, которую используют во всем мире.

Одиннадцать. Наши предки относили к нехорошим числам, число 11. Как теперь установлено, изменения активности Солнца влияют на здоровье людей, а такие изменения совершаются периодически через каждые 11 лет. Но это совсем не значит, что число 11 имеет мистическое значение.

Число 12. Очень почиталось число 12, «дюжина». 12 месяцев в году, 12 знаков Зодиака, 12 делений на циферблатах часов, сервизы на 12 персон. Число 12 замыкало свет, поэтому его считали символом полноты, богатства, счастливым числом. Число 12 имеет собственные делители 2, 3, 4, 6, что при низком уровне вычислений в древности давало большие преимущества.

Число 13. А вот с числом 13 были одни неприятности. Оно простое и делится только на себя и единицу. Суеверия, связанные с числом 13, оказались наиболее устойчивыми и получили наибольшее распространение. Люди многих стран (Англия, Франция, Польша и др.) считают это число несчастливым, испытывают перед ним панический страх и стараются избегать его. Но интересно заметить, что у наших предков – славян не было суеверий, связанных с числом 13.

Число 40. Оно играет в преданиях многих восточных народов особую роль. Выступая на определенной стадии предельным при счете, число 40 попадает в категорию счастливых. С числом 40 связан ряд религиозных обычаев и народных поверий.

Число 60. Во многих вавилонских, персидских и греческих легендах синонимом самого большого представлялось 60. Это число вавилоняне считали «божьим».

Число 1001. Это число считалось мистическим. Получается оно последовательным умножением трех простых чисел: 7, 11 и 13. А если умножить на него любое трехзначное число, то результат будет состоять из умноженного числа, записанного дважды.

Число 666. Число 666- число зверя. В разных странах христиане обозначали этим числом неугодных церкви правителей, общественных деятелей, выдавая их за антихристов.

Вот такая история чисел. Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют и понимают во всем мире.

           III.     Объяснение нового материала.

Как известно не всякий многочлен с действительными  коэффициентами имеет корни среди действительных чисел, например, многочлен x² + 1 не имеет действительных корней. Поэтому возникла необходимость "пополнить"  множество  действительных  чисел таким  образом,  чтобы, по крайней мере, любой квадратный трехчлен,  а еще лучше,  любой многочлен имел корни. С этой целью и ввели, так называемые комплексные числа.

Если дано комплексное число z = (x, y),  то комплексное число z = (x, –y) называется комплексно сопряженным комплексному числу z и обозначается .

Будем обозначать само комплексное число буквой z,  то есть положим z = (x, y), действительную часть – x обозначим  Rez ("Re"– начало латинского  слова  "realis"– действительный), мнимую часть y – Imz ("Im" – начало латинского слова "imajinarius"– мнимый), а модуль комплексного числа – ½z½. Заметим, что и действительная и мнимая части комплексного числа это действительные числа. Если Rez = 0, то число называют чисто мнимым.

Все множество комплексных чисел обозначают обычно С. Заметим, что это множество совпадает с R².

Историческая справка, подготовленная обучающимися.

На пути к комплексным числам

В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида  кубические и квадратные корни: .

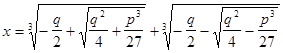 Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень ( x=1), а если оно имеет  три действительных корня ( x₁=1 x_2,3 =), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени  нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень,  извлечение корня).

 В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически.        Тем не менее, всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены еще в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.

Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений , не имеющая решений во множестве действительных чисел, имеет решения вида , , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что .

Кардано называл такие величины “чисто отрицательными” и даже “софистически отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа  (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу .  Термин “комплексные числа”  так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. образующих единое целое.

 В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование. 

 Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а за тем из любых комплексных чисел.

В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например,  в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов.

 Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел.  После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую систему вида , где , построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”.

Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.

Алгебраическая формула комплексного числа

Действия над комплексными числами

Обозначают сумму и произведение обычным образом: соответственно z₁ + z₂ и z₁z₂.

Правило сложения  здесь вполне естественное. Очевидно, все свойства операции сложения действительных чисел сохраняются и  для  комплексных чисел.

Операция умножения комплексных чисел на первый взгляд определена несколько искусственно. Однако легко проверить, что и для нее сохраняются все свойства операции умножения действительных чисел,  а также распределительный закон.

Чтобы удобнее было выполнять арифметические операции над комплексными  числами, введем новую форму их записи.  Для этого,  во-первых,  заметим, что, при сложении и умножении комплексных чисел,  у которых мнимые  части равны нулю, снова получаются комплексные числа с мнимой частью, равной нулю, то есть (x₁, 0) + (x₂, 0) = (x₁ + x₂, 0) и (x₁, 0)(x₂, 0)=(x₁x₂, 0). Это следует непосредственно из определений. 

Таким образом, комплексные числа вида (x, 0) можно отождествить с действительными числами  и вместо (x, 0) писать просто x. Во-вторых, среди комплексных чисел особую роль играет число (0, 1).  Его называют мнимой единицей и обозначают буквой i. 

Это число замечательно тем,  что i×i = (–1, 0), то есть i² = – 1.

Кроме того (0, 1)×(y, 0) = (0, y), то есть iy = (0, y) и, следовательно,   любое  комплексное  число  z = (x, y)  можно  представить  в  виде: z = (x, y) = (x, 0) + (0, y) = x + iy. 

Таким образом мы пришли к новой форме записи комплексного числа z = (x, y): z = x + iy, которая называется алгебраической (иногда пишут x + yi).

 Такая форма записи комплексного числа удобна тем, что арифметические операции над комплексными числами теперь можно формально выполнять так, как это делается с обычными алгебраическими выражениями, только надо помнить, что i² = – 1.

Например,

(2 + 3i) + (–5 + 6i) = – 3 + 9i; (2+3i)(–5+6i) = – 10 – 15i + 12i + 18i² = 28 – 3i.

В частности, при этом сохраняются формулы сокращенного умножения. Например,

если  z = x + iy, то z² = x² + 2ixy + (iy)² =x² –y² + 2xyi;

если  z = x + iy  и  = x – iy , то = x² – (iy)² = x² + y² = ½z½².

Отметим, что комплексное число 0 + i0 = 0 играет ту же роль среди комплексных чисел, что и обычный 0 среди действительных чисел, то есть

(x + iy) + (0 + i0) = x + iy,

 и для любого комплексного числа z = x + iy существует противоположное комплексное число –z  =  – x – iy такое, что z + (–z) = 0. Это позволяет естественным образом определить операцию   вычитания    комплексных чисел:

z₁ – z₂ = z₁ + (– z₂).

Например, (2 + 3i) – (5 + i) = –3 + 2i.

Точно так же комплексное число 1 + i0 = 1 играет  среди комплексных чисел роль единицы, то есть

(x + iy)×(1 + i0) = x + iy,

 и для любого комплексного числа z = x + iy ¹ 0 существует обратное число 1/z такое, что z×(1/z) = 1. Можно непосредственно проверить, что

.

Это   позволяет определить операцию деления комплексных чисел, положив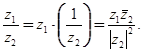

Минимальные условия, которым удовлетворяют комплексные числа включают в себя:

·      Множество комплексных чисел содержит все действительные числа;

·      Существует комплексное число, квадрат которого равен -1;

·      Операции сложения, вычитания, умножения и деления комплексных чисел удовлетворяют обычным законам арифметических действий (сочетательному, переместительному, распределительному).

            IV.     Закрепление нового материала

1.   Устная работа

2.     Решение задач на закрепление нового материала.

3.   Обучающая самостоятельная работа.

Учащиеся выполняют задания самостоятельно с последующим обсуждением решений и комментариями учителя.

V. Подведение итогов урока.

Сегодня на уроке мы ввели новую числовую систему – систему комплексных чисел, рассмотрели историю развития и возникновения комплексного числа. На конкретных примерах, показали необходимость введения нового множества чисел.

Познакомились с новыми понятиями (перечисляют) и арифметическими операциями над ними.