Пятое ноября Деление нацело

(Делаем запись в тетрадочке)

Видеоматериал по уроку:

https://www.youtube.com/watch?v=DD5jpr_FSNM

Учебник: страница 41-43;

Здравствуйте, ребята! Перед началом занятия предлагаю вам, как обычно, размять наши мозги. Переходим по ссылочкам и устно выполняем задания:

https://learningapps.org/8066055 https://learningapps.org/382771

Справились? Молодчинки!

Мы уже знакомы с операцией деления – это операция, обратная умножению. Она обозначается двоеточием «:» или знаком «÷». Подобно тому, как умножение заменяет многократно повторенные слагаемые, деление заменяет многократно повторяющиеся вычитаемые. Сейчас нам предстоит повторить операцию деления и рассмотреть основные свойства деления.

Давайте вспомним, что нам уже известно об операции деления. 

Пусть у нас есть натуральные числа a и b, причѐм а больше b или

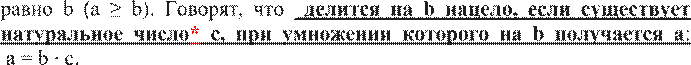
 *  - вы ведь помните, что натуральное число – это число, возникающие естественным образом при счёте (например, 1, 2, 3, 4, …).  

Обычно слово «нацело» в этой фразе опускается. При этом записывают: a : b = с и называют а – делимым, b – делителем, с – частным.

(Делаем запись в тетрадочке)

Любое натуральное число а делится на 1 и само на себя: а : 1 = а,   а : а = 1

так как а ∙ 1 = а, 1 ∙ а = а.

Например, 14 делится на 1 и на 14.

14 : 1 = 14, 14 : 14 = 1

При делении ноля на любое натуральное число получается ноль: 

0 : а = 0, потому что 0 ∙ а = 0.

Запомните: делить на нуль нельзя!

(Делаем запись в тетрадочке)

Для деления чисел из двух и более цифр (знаков) применяют деление уголком.

Вспомним, как делить уголком, на примере. Вычислим 392 : 28 = ?

Для начала запишем делимое и делитель уголком:

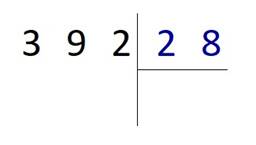
Начнѐм делить 392 на 28 следующим образом.

Во-первых, определим неполное частное. Для этого слева направо сравниваем цифры делимого и делителя.

Рассмотрим цифру 3. Она меньше 28 – значит, нужно взять ещѐ одну цифру из делимого. 39 больше 28, следовательно, это неполное частное.

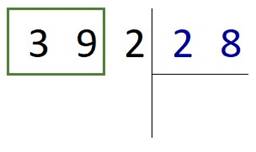
Приступаем к делению: 28 помещается в 39 только один раз, поэтому ставим первой цифрой ответа единицу и вычитаем 28 из 39.

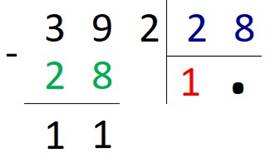
После вычитания в остатке получилось 11, это меньше, чем 28, поэтому к 11 дописываем 2.

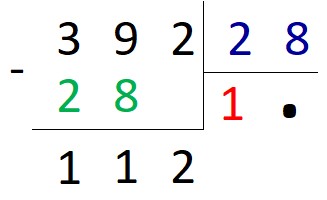
112 делится на 28. Получаем 4. Записываем полученный результат второй цифрой в ответе.

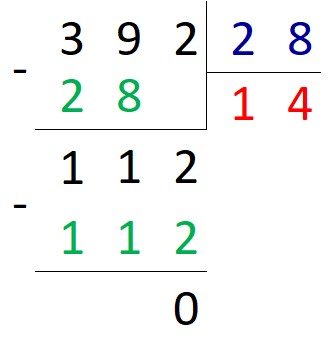
В остатке получился нуль – значит, числа разделились нацело. Таким образом, 392 : 28 = 14.

(Делаем запись в тетрадочке)

Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число - частное от этого не изменится.

Вычислим 50 : 25 = ?

Сначала одновременно умножим 50 и 25 на 2. Получим: 100 : 50 = 2.

Теперь разделим 50 и 25 на 5. Получим:

10 : 5 = 2.

В обоих случаях ответ оказался одинаковым. Значит, свойство частного верно.

(Делаем запись в тетрадочке)

Если каждое из натуральных чисел a и b делится на натуральное число с, то верно равенство:

(a+b) : c = a : c + b : c.

Убедимся в правдивости данного свойства на примере.

Вычислим выражение: 124 : 4 + 36 : 4.

Рассмотрим два способа решения. 1 способ. Выполним деление и сложим результаты.

124 : 4 + 36 : 4 = 31 + 9 = 40.

2 способ. Заметим, что у нас есть общий делитель – 4. Вынесем его за скобки. Получим:

(124 + 36) : 4 = 160 : 4 = 40.

В обоих случаях у нас получился один и тот же ответ. Значит, свойство верно.

(Делаем запись в тетрадочке)

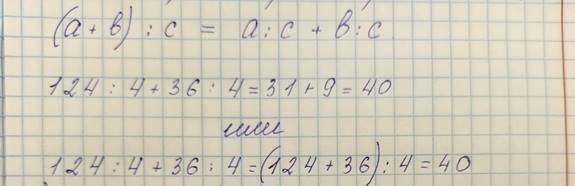
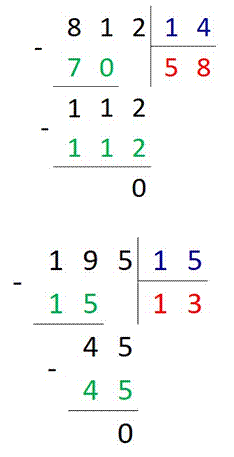№ 1. Вычислите 812 : 14 = _____. Решение: выполним деление уголком.

Ответ: 58.

№ 2. Найдите неизвестный множитель х из равенства: 15 ∙ х = 195.

Решение: чтобы найти неизвестный множитель, надо произведение поделить на известный множитель, то есть:

15 ∙ х = 195 х = 195 : 15

Выполнив деление уголком, получим:

Ответ: х = 13.

(Делаем запись в тетрадочке)

Итак, мы с вами повторили тему «Деление нацело», вспомнили основные свойства деления.

Проверить свои знания вы сможете, перейдя в свой кабинет на ЯндексУчебнике, как мы делали на прошлых уроках.

Успехов!