«Построение графиков тригонометрических функций»

Муниципальное бюджетное

Общеобразовательное учреждение

«Средняя школа №15»

 

 

 

 

ПРОЕКТ

по направлению: математика

«Построение графиков тригонометрических функций»

Тип проекта: исследовательский

 

 

                                      Автор проекта:

Бамматова Аида           

Класс: 10 а

Руководитель:

                                             Злобова Людмила Викторовна,

                              учитель математики

 

 

 

 

 

 

 

 

 

 

 

 

г. Новый Уренгой, 2021

ОГЛАВЛЕНИЕ

 

ВВЕДЕНИЕ …………………………………………………………………3 стр.

I РАЗДЕЛ (теоретический) …………………………………….……..…4-9 стр.

II РАЗДЕЛ (практический) ………………………………………….….10-12стр.

ЗАКЛЮЧЕНИЕ ……………………………………………………………13 стр.

СПИСОК ЛИТЕРАТУРЫ ………………………………………………..13 стр.

ПРИЛОЖЕНИЯ ………………………………………………….…….14-17 стр.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

Тема проекта и ее актуальность:

данная тема непосредственно связана с изучением технологии построения и редактирования различных видов графиков тригонометрических функций, с использованием полученных в процессе работы над проектом знаний для более глубокого  изучения свойств тригонометрических функций,  а также со сдачей ЕГЭ. Рассматриваемая тема имеет теоретическую и практическую значимость. Она находит широкое применение в разных разделах математики и других областях науки, и тесно связана с практической  деятельностью человека.

 

Цель проекта:

Ø Научиться строить графики тригонометрических функций.

Ø Установить закономерности построения графиков тригонометрических функций в зависимости от коэффициентов, изменения значения аргумента и значения функции.

Ø Узнать о практическом применении тригонометрических функций в жизни человека.

Задачи:

1.     Изучить историю возникновения тригонометрии.

2.     Повторить: определение графика функции, области определения и области значения функции; определения синуса, косинуса, тангенса и  котангенса в прямоугольном треугольнике; повторить табличные значения синусов, косинусов, тангенсов и котангенсов.  

3.     Изучить теорию: познакомиться с новым понятием - радианная мера угла, с формулами перевода градусной меры угла в радианную и обратно,  вывести и выучить новые табличные значения синусов, косинусов, тангенсов, котангенсов, арксинусов, арккосинусов, арктангенсов и арккотангенсов. 

4.     Научиться строить графики различных тригонометрических функций.

5.     Рассмотреть методы построения графиков сложных тригонометрических функций.

6.     Рассмотреть задания с применением графиков тригонометрических функций на ЕГЭ.

7.     Найти подтверждение применения графиков тригонометрических функций в окружающем нас мире и различных отраслях практической деятельности человека.

 

РАЗДЕЛ I.

ТЕОРИЯ.

          Тригонометрия - это раздел математики, изучающий тригонометрические функции, которые применяются в геометрии (в переводе с греческого языка  τρίγωνον - «треугольник», а  μετρέω - «измеряю», т.е. «измерение треугольников»). В 1595 г. данный термин впервые появился как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии.

            Тригонометрия или тригонометрические функции используются в астрономии, в морской и воздушной навигации, в машиностроении, в теории музыки, в акустике, в оптике, в архитектуре, в метеорологии, в сейсмологии, в океанографии, в медицинской визуализации (компьютерная томография, ультразвук), в анализе финансовых рынков, в электронике, в компьютерной графике, в разработке компьютерных игр, а также во многих науках: в теории вероятностей, в статистике, в биологии, в химии, в теории чисел, в физике и т.д. Синус и косинус имеют фундаментальное значение для теории периодических функций, например, при описании звуковых и световых волн.     

Определение синуса и косинуса:

          Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Синус индийские математики обозначали словом «джива» (перев. «тетива лука»). Этот термин арабы переделали в «джиба», который в последствии превратился в «джайо»- означающий изгиб, пазуха, складка одежды, и соответствует латинскому слову «sinus». Косинусом (новолат. cosinus, сокращение от complementi sinus - дополнение синуса) острого угла прямоугольного треугольнике называется отношение прилежащего катета к гипотенузе. Тангенсом (лат. tangens - касающийся) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Котангенсом (новолат. cotangens, сокращение от complementi tangens – «дополнение тангенса») острого угла прямоугольного треугольника называется отношение катета прилежащего к противолежащему катету.

Дополнительно:

ü секансом α называется отношение гипотенузы к прилежащему катету;

ü косекансом α называется отношение гипотенузы к противолежащему катету.

Из истории возникновения тригонометрии.

          Начала тригонометрии обнаружены в сохранившихся документах Древнего Вавилона. Сведения тригонометрического характера встречаются ив старинных памятниках других народов древности. Хорда, соответствующая своей дуге, была самой первой тригонометрической функцией. Еще во II в. до н. э. Гиппархом и Птолемеем были построены «тригонометрические таблицы», которые впоследствии использовались в астрономии. Впервые в истории науки индийские математики и астрономы в период V-XII века вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали «архиджива», что означало «половина тетивы лука».
         Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин «тангенс» (с латинского «касательная») был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин «секанс». В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название «косинус» и «котангенс», где приставка «ко» (co) обозначает дополнение (complementum).

          И все-таки, к началу 18 века тригонометрия была еще недостаточно разработана. Не было условных обозначений, формулы записывались словами, поэтому усваивать их было трудно. Неясным был и вопрос о знаках тригонометрических функций в разных четвертях круга. Современные обозначения синуса и косинуса знаками sinx и cosx были впервые введены в 1739 году И. Бернулли, что упоминается в письме к петербургскому математику Л. Эйлеру И только в трудах Эйлера, крупнейшего математика 18-го столетия, тригонометрия получила современный вид. Именно он, стал рассматривать тригонометрическую функцию числа. То есть под аргументом стали понимать не только дуги или градусы, но и числа. Эйлер вывел все тригонометрические формулы из нескольких основных, упорядочил вопрос о знаках тригонометрической функции в разных четвертях круга. Для обозначения тригонометрических функций он ввел следующую символику: tang x, cot x, sec x, сosec x. В развитии тригонометрии на пороге 18-го века появилось новое направление - аналитическое. До этого решение треугольников считалось главной целью тригонометрии, а Леонард Эйлер стал рассматривать тригонометрию как науку о тригонометрических функциях. Учение о функции стало частью общего учения о функциях, которое изучается в математическом анализе, а решение треугольников стало главой геометрии. Вот такие нововведения были сделаны Леонардом Эйлером (Эйлер родился в Швейцарии, но долгие годы жил и работал в России, член Петербургской академии). Мы изучаем свойства тригонометрических функций, пользуемся формулами  тригонометрии, решаем уравнения, неравенства и поэтому должны помнить имя этого великого ученого.

              В 1770 г. появилось название «тригонометрические функции» и удерживается до наших дней. Его ввел Г. С. Клюгель, немецкий математик и физик; почётный член Петербургской Академии, в работе «Аналитическая тригонометрия» (Прил.№1). По мере развития математики определение тригонометрических функций было расширено. В современном понимании аргументом тригонометрических функций может быть произвольное вещественное или комплексное число.

 К тригонометрическим функциям традиционно относят:

прямые тригонометрические функции: синус (sin x) и косинус ({\displaystyle \cos x}cos x);

производные тригонометрические функции: тангенс ({\displaystyle \mathrm {tg} \,x}tg x) и котангенс ({\displaystyle \mathrm {ctg} \,x}ctg x);

другие тригонометрические функции: секанс (sec x) и косеканс{\displaystyle \mathrm {cosec} \,x} (сosec x)

обратные тригонометрические функции: арксинус (arcsin х), арккосинус (arccos х), арктангенс (arctg х), арккотангенс (arcctg х).

Что касается свойств тригонометрических функций, то особое внимание нужно обратить на:

ü область определения и область значений функций, т.к. для синуса и косинуса есть ограничения в области значений, а для тангенса и котангенса ограничения в области определения;

ü периодичность всех тригонометрических функций, значения которых не изменяются при добавлении к значениям их аргумента некоторого числа T (отличного от нуля). Такой аргумент называют периодом функции и обозначают буквой T. Для синуса и косинуса T = 2, а  тангенса и котангенса.

 

Тригонометрические функции числового аргумента.

Функция y = sin х.

Если каждому действительному числу х поставлено в соответствие число у, равное синусу угла в х радиан, то говорят, что этим определена функция        y = sin х, называемая синусом числового аргумента х.

D(y)=R; E(y) = [−1;1]

Свойства функции y = sin х: 

1.       Функция y=sinх  нечетная, так как  sin(−х) = − sin х.

2. Функция y=sin х  периодическая с главным периодом  T= 2π, т.е.

 sin (х+2π)= sin х.

3. Функция y = sin х   непрерывна на промежутке (- ∞ ; + ∞).
4. График функции пересекает ось Ох при х = πk, k ∈ Z.
5. Промежутки знакопостоянства:

y > 0 при (0+2πk; π+2πk), k ∈ Z и y < 0 при (π+2πk; 2π+2πk), k ∈ Z.

6. Функция y=sinх возрастает на каждом из промежутков [− +2πk;  +2πk], k ∈ Z  и убывает на каждом из промежутков [ +2πk; +2πk],

 k ∈ Z.

7. Минимум функции при х = − + 2πk, k∈Z, а максимум при х= + 2πk, k∈Z.

  График функции  y = sinх   - синусоида:

 

 

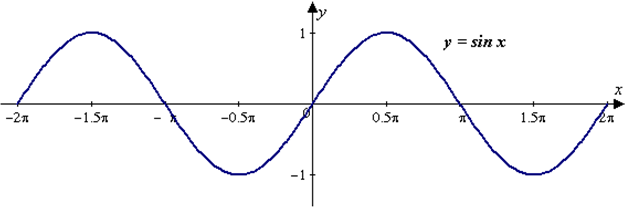
Функция y = cos х.

Если каждому действительному числу х поставлено в соответствие число у, равное косинусу угла в х радиан, то говорят, что этим определена функция    y = cos х называемая косинусом числового аргумента х.

D(y)=R; E(y) = [−1;1].

Свойства функции y = cos х:

1. Функция y= cos х  четная, так как cos(−х) = cos х.
2. Функция y=cosх  периодическая с главным периодом T= 2π, т.е. cos(х+2π)= cosх.
3. Функция y=cosх непрерывна на промежутке (- ∞ ; + ∞).
4. График функции пересекает ось Ох при х=+πk, k∈Z.
5. Промежутки знакопостоянства: 

y > 0 при (−+2πk; +2πk), k ∈ Z и y < 0 при (+2πk; +2πk), k ∈ Z.

6. Функция y=cosх возрастает на каждом из промежутков [−π+2πk;2πk], k∈ Z, и убывает на каждом из промежутков [2πk;π+2πk], k∈ Z.
7. Минимум функции при х=π+2πk, k ∈ Z, а максимум при х=2πk, k∈ Z.

График функции y = cos α - косинусоида:

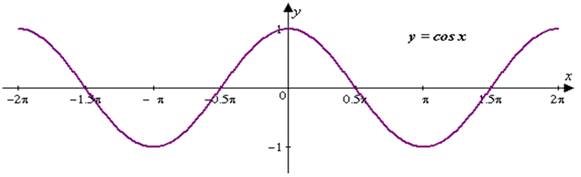
Функция y = tg х.

 Если каждому действительному числу х, отличному от х=+πk, где k-любое целое число, поставлено в соответствие число у, равное тангенсу угла в х радиан, то говорят, что этим определена функция y = tg х, называемая тангенсом числового аргумента х.

 D(y)=R,  исключая числа х=  + πk, где k ∈ Z; E(y) = (- ∞ ; + ∞).

Свойства функции y = tg х:

1. Функция y= tgх  нечетная, так как tg(−х)=−tg х.
2. Функция y=tgх  периодическая с главным периодом равным  T= π, т.е.  tg(х+π)=tg(х).
3. Функция y=tg х   непрерывна на каждом интервале (−+πk; +πk), k ∈ Z
4. График функции пересекает ось Ох при х=πk, k ∈ Z.
5. Промежутки знакопостоянства: 

y > 0 при (πk; +πk), k ∈ Z и y < 0 при (−+πk; πk), k ∈Z.

6. Функция y=tg х возрастает на каждом интервале (−+πk; +πk), k ∈ Z.

График функции y=  tgх  - тангенсоида:

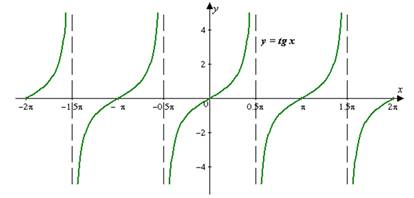
Функция y = сtg х.

 Если каждому действительному числу х, отличному от х=πk, где k ∈ Z, поставлено в соответствие число у, равное котангенсу угла в х радиан, то говорят, что этим определена функция y = сtg х, называемая котангенсом числового аргумента х.

 D(y)=R,  исключая числа х= πk, где k ∈ Z; E(y) = (- ∞ ; + ∞).

Свойства функции y = сtg х:

1. Функция y=ctgх  нечетная, так как  ctg(−х)=−ctg х.
2. Функция y=ctgх  периодическая с главным периодом равным  T= π,  т.е.  ctg(х+π)=ctg(х).
3. Функция y=ctgх  непрерывна на каждом интервале (πn; π+πk), где k∈Z..
4. График функции пересекает ось Ох при х=+πk, k ∈ Z.
5. Промежутки знакопостоянства: 

y > 0 при (πk;+ πk), k ∈ Z и y < 0 при (+πk; π+πk), k ∈Z.

6. Функция y=ctg x убывает на каждом интервале (0+πk; π+πk), k ∈Z.

График функции y=  сtgх  - котангенсоида:

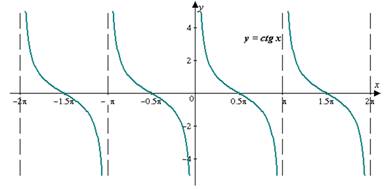
РАЗДЕЛ  II

ПРАКТИЧЕСКИЙ.

Рассмотрим построение графика тригонометрической функции на примере  построения синусоиды:

Аналогично построению любого графика функции в системе координат, график синусоиды строится по точкам, полученным путем подстановки значений х в формулу y= sinх. Алгоритм построения графика синусоиды:

1.     Строим особую систему координат.

2.     Выбираем масштаб по оси Ох, который равен 2π , что  приближенно равно 12 клеточкам, а по оси Оу 2 клеточки=1единичный отрезок.

3.    Находим значение функции, если вместо аргумента х подставить 0; ; п; ; 2п и т.д. (в принципе, можно сразу использовать соответствующие табличные значения). Затем, наносим основные точки на координатную плоскость. При этом помним, что функция нечетная и график симметричен началу отсчета. Последовательно соединяем точки плавной линией. Получаем кривую, которая является «синусоидой». Для исследования свойств этой кривой полученного отрезка [0;2п], в принципе, вполне достаточно.

4.     Так как функция y= sinх периодическая и Т=2π , то через интервал 2π значения функции повторяются и можно продолжать волну синусоиды до бесконечности.

5.   Если нужно построить более точный график, то можно взять больше точек, например, ;  ;  и т.д.

 

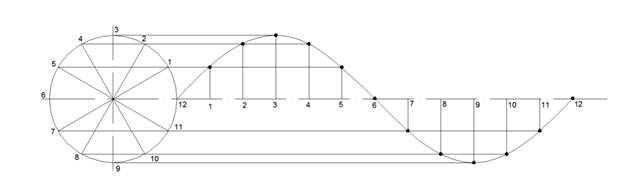
В интернете я увидела еще один метод построения синусоиды. Опишу построение, как алгоритм:

ü Окружность разделим на 12 частей.

ü   Пронумеруем точки указанным способом, т.е. 1 соответствует ; 2 соответствует ; 3 соответствует  и т.д.

ü Измерим длину дуги на окружности. Отложим на прямой между точками 1 и 2 соответствующее расстояние. Затем отметим  точку на пересечении соответствующих чисел, т.е. точка находится под таким же номером, как и на окружности.

ü      Все полученные точки последовательно соединяем плавной   сплошной линией.

ü      Получим искомую синусоиду.

 

ОБЩИЙ ВИД ПРЕОБРАЗОВАНИЯ ФУНКЦИИ (Прил.№2)

 

I) Параллельный перенос графика вдоль оси абсцисс на  |a|  единиц:

 

 

 

II) Параллельный перенос графика вдоль оси ординат на  |n|  единиц:

 

 

III) Симметричное отражение графика относительно оси абсцисс:

 

 

IV) Симметричное отражение графика относительно оси ординат:

 

 

 

V) Сжатие и растяжение графика: y = kf(x)

 

а) при  k ˃ 1 – растяжение графика от оси абсцисс в  k  раз,

б)  при  0 < k < 1 – сжатие графика к оси абсцисс в  k  раз.

 

VI) Сжатие и растяжение графика: y = f(kx):

 

а) при  k ˃ 1 – сжатие графика к оси ординат в  k  раз,

б) при  0 < k < 1 – растяжение графика от оси ординат в  k  раз,

 

VII) Преобразования графика с модулем: у = | f(x)|:

а) При  f(x) ˃ 0 – график остаётся без изменений,

б) при  f(x) < 0 – график симметрично отражается относительно оси абсцисс.

 

 

Практическое применение

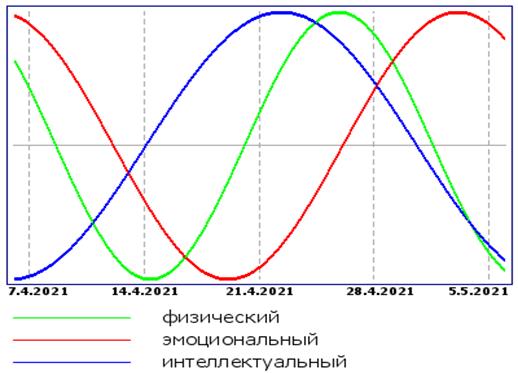
1.     С самого рождения человека включаются его биологические  часы, определяющие его состояние, самочувствие и работоспособность. Эти часы (биологические ритмы) определяют циклическое изменение состояния всей жизни человека. Существуют  различные биоритмы. Например, суточные. Они определяют самочувствие и  работоспособность человека в течении суток. Если научиться  планировать свою деятельность в течении дня, в соответствии с этими ритмами, то уверена наша продуктивность и эффективность резко возрастет. На сайте Bio-Ritm.Ru мы можем быстро, в режиме   онлайн, получить расчет наших биоритмов (Прил.№3).

2.     Наверняка, многие  видели изображение траектории полёта какого-либо космического корабля по телевидению или хотя бы на карте, например МКС. Оно напоминает синусоиду (косинусоиду). Но почему? Ведь, казалось бы, что корабль летит прямо. Попробуем разобраться. Действительно, МКС вращается по круговой орбите. Ось вращения Земли имеет наклон, примерно 24 градуса. Именно благодаря этому наклону, меняются времена года. МКС запускают так, чтобы получать максимум солнечной энергии. А эта орбита не совпадает с экватором. Таким образом, орбита МКС проходит частично по южному, а частично по северному полушарию. В сутки международная станция делает 16 оборотов вокруг Земли, поэтому южное полушарие меняется на серверное и наоборот. Отсюда и получается траектория, напоминающая синусоиду.(Прил.4).

 

 

Заключение.

В данном проекте, опираясь на научные источники, рассмотрен вопрос о зарождении и развитии тригонометрии как о самостоятельном разделе математики, даны определения тригонометрических функций, а также представлены способы построения графиков различных тригонометрических функций, в которых используются данные методы.

Работа над проектом способствовала развитию моих познавательных навыков, расширила умение строить графики тригонометрических функций и наблюдать за их преобразованием в зависимости от линейных преобразований самой функции. Также укрепило мое мнение о математике как универсальном языке науки. В проекте рассматривалось построение различных графиков средствами элементарной математики, что станет хорошей подготовкой к дальнейшему усвоению методов построения других тригонометрических функций, которые мы будем изучать в 11 классе. Таким образом, цель моей работы:  представить способы построения графиков тригонометрических функций, рассмотреть вопросы о практическом применении тригонометрических функций в жизни человека, выполнена. Построение графиков имеет важное значение в тригонометрии, а так же важное самостоятельное прикладное значение в изучении математики.

 

 

ЛИТЕРАТУРА:

1.     Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К. Потапов, Н.Н.Решетников и др.]- М.: Просвещение, 2017.

2. Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов,  Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова- М. Просвещение, 2018.

 

 

Дополнительные источники:

1.     https://ru.wikipedia.org/wiki/Абу-ль-Вафа_аль-Бузджани

2.     https://krasavtsev.blogspot.com/2018/10/3algebray30.html

3.     http://bio-ritm.ru/Расчет биоритмов человека онлайн по дате рождения | Bio-Ritm.Ru

4.     contenton.ru/geo-mks-tracking

5.     https://ru.wikipedia.org/wiki/Тригонометрия

6.     https://ru.wikipedia.org/wiki/ Преобразования_графиков_функций Преобразования графиков функций — Википедия

 

 

 

Приложение №1

Абуль-Вафа Мухаммад ибн Мухаммад аль-Бузджани (Бузган, 10 июня 940 - Багдад, 998) - персидский учёный X века, один из крупнейших математиков и астрономов средневекового Востока.	Я́коб Берну́лли (1655 - 1705) -  швейцарский математик. Один из основателей теории вероятностей и  математического  анализа.
Георг Симон Клюгель   (1739-1812) -           немецкий математик и физик.	Леона́рд Э́йлер (1707- 1783) -   швейцарский математик и       механик.

                                                                                           

                                                                                            

 

 

 

  Приложение №2

Построим график функции  y=sinx и параллельно перенесём его вниз на  5  единиц вдоль Оу  (так как  –5 < 0), получим график функции y=sinx-5. Аналогично рассуждаем, выполняя построение графика функции y=sinx+6. Строим график функции  y=sinx и параллельно перенесём его вверх на  6  единиц вдоль Оу  (т. к. как  6 > 0), получим график функции y=sinx-5.	Построим график функции y=cosx и параллельно перенесем его вправо на  единиц вдоль Ох (так как -  < 0). получим график функции y=cos(x -). Затем, параллельно перенесем график функции вверх на  4  единицы вдоль Оу  и получим график функции y=cos(x - )+4.	Построим график функции y=sinx. Выполним сжатие графика функции  в пять раз до Oу  и получим график функции y=5sinx. Затем отобразим  его симметрично относительно Oх и получим график функции y = - 5sinx.
Построим график функции  y=sinx. Выполним сжатие графика функции в три раза до Oу . Отобразим симметрично относительно Oх  ту часть графика, которая находится под осью, и получим график функции     y=|3sinx|.	Построим график функции  y=tgx.  Отобразим симметрично относительно Oх  ту часть графика, которая находится под осью, и получим график функции y=|tgx|.

                                                             Приложение №3

Состояние	Значение
Физическое	40%
Эмоциональное	90%
Интеллектуальное	-97%
Общее	11%

Приложение №4

Изображение траектории полёта  космического корабля на карте

 

 

 

 

 

 

 

 

ПАСПОРТ  ПРОЕКТА

№	параметры	характеристика
1	Тема проекта	«Построение графиков тригонометрических функций»
2	Направление(предмет)	Математика
3	Тип проекта	Исследовательский
4	Цель проекта	Научиться строить графики тригонометрических функций. Установить закономерности построения графиков тригонометрических функций в зависимости от коэффициентов, изменения значения аргумента и значения функции. Узнать о практическом применении тригонометрических функций в жизни человека
5	Задачи проекта	Изучить историю возникновения тригонометрии. Научиться строить графики различных тригонометрических функций. Рассмотреть методы построения графиков сложных тригонометрических функций. Рассмотреть задания с применением графиков тригонометрических функций на ЕГЭ.
6	Аннотация проекта (актуальность проекта, краткое обоснование выбора, личностная значимость), содержание (кратко)	Актуальность заключается в том, что знания тригонометрии откроют новые способы решения различных задач во многих областях науки и упростят понимание некоторых аспектов различных наук.
7	Планируемые результаты	Овладеть теоретическими и практическими навыками построения графиков тригонометрических функций
8	Предполагаемый продукт	Раскрыть сущность методов построения графиков сложных тригонометрических функций
9	Оборудование, ИКТ	Линейка, карандаш
10	Разработчик проекта	Бамматова Аида
	ФИ, класс	Бамматова Аида, 10 класс
11	Руководитель (ФИО, должность)	Злобова Людмила Викторовна, преподователь математики

 

 

Скачано с www.znanio.ru