
Линейные и квадратные неравенства
(повторение) (3 ч)
У р о к 1
Цели: повторить формулы сокращенного умножения, научить применять их при упрощении выражений и разложении на множители; повторить определение линейного неравенства с одной переменной; вспомнить определение равносильных неравенств и правила преобразования неравенств и закрепить их знание в ходе выполнения упражнений.
Ход урока
I. Повторение изученного материала.
1. Повторить формулы сокращенного умножения и записать эти формулы на доске и в тетрадях.
2. Решить устно № 1.5 (а; б) и № 1.6 (а; б) из задачника.
3. Решить письменно с комментированием на месте № 1.5 (в; г) и № 1.6 (в; г) из задачника.
4. На доске и в тетрадях решить № 1.7 (в; г) из задачника.
Р е ш е н и е
в) (а – 3)(а + 4) – (а + 2)(а + 5) = а2 + 4а – 3а – 12 – а2 – 5а – 2а – 10 = = – 6а – 22
При а = –![]() имеем – 6 · (–
имеем – 6 · (–![]() ) – 22 = 1 – 22 = – 21.
) – 22 = 1 – 22 = – 21.
г) (с + 2)2 – (с + 4)(с – 4) = с2 + 4с + 4 – с2 + 16 = 4с + 20
При с = – 0,25 имеем 4 · (– 0,25) + 20 = – 1 + 20 = 19.
5. Вспомнить способы разложения многочлена на множители. Решить № 8 (а) и № 13 устно на с. 6 задачника.
II. Работа с учебником.
1. Вспомнить определение линейного неравенства с одной переменной; записать в тетради: ах + в > 0 или ах + в < 0, где а и в – действительные числа (а ≠ 0).
2. Что называют решением неравенства f(х) > 0?
3. Решить устно № 1.1 (а; б) из задачника.
4. Повторить определение равносильных неравенств: два неравенства f(х) < q(x) и r(х) < s(х) называют равносильными, если они имеют одинаковые решения или оба неравенства не имеют решений.
5. По учебнику на с. 6–7 повторить правила 1; 2; 3, выражающие равносильные преобразования неравенств.
6. Разобрать по учебнику решение примера 1 на с. 8–9.
III. Выполнение упражнений.
1. Решить № 1.2 (а; в) на с. 13 задачника самостоятельно, а затем проверить решение.
|
а) 4а – 11 < а + 13 4а – а < 13 + 11 3а < 24 а < 24 : 3 а < 8 О т в е т: а < 8, или (–∞; +8). |
в) 8b + 3 < 9 b – 2 8b – 9b < – 2 – 3 – b < – 5 b > – 5 : (–1) b > 5 О т в е т: (5; ∞). |
2. Решить № 3 (а; в) на доске и в тетрадях.
|
а) 15 × 5(5 – а) – 3(3 – 2а) < 0 25 – 5а – 9 + 6а < 0 а < – 16 О т в е т: а < – 16. |
в) 3(х + 7) > 4(5 + 4х) 3х + 21 > 20 + 16х 3х – 16х > 20 – 21 – 13х > – 1 х
< О т в е т: х < |
3. Решить № 1.4 (в; г). Двое учащихся самостоятельно решают на доске, остальные в тетрадях; затем проверяется решение.
|
в) 3х(3х – 1) – 9х2 ≤ 2х + 6 9х2– 3х – 9х2 ≤ 2х + 6 – 3х – 2х ≤ 6 – 5х ≤ 6 х ≥ х ≥ – 1,2 О т в е т: х ≥ – 1,2 или [– 1,2; ∞). |
г) 7с(с – 2) – с(7с + 1) < 3 7с2 – 14с – 7с2 – с < 3 – 15с < 3 с > – 3 : 15 с > О т в е т: с > |
4. Повторение ранее изученного материала. Решить задачу № 42 на с. 10 задачника.
Пусть запланированная скорость пешехода равна х км/ч, тогда за 1,2 ч пешеход пройдет 1,2х км. Пешеход же шел со скоростью (х + 1) км/ч и за 1 ч прошел путь (х + 1) · 1 км. Длина пути пешехода одинакова. Составим и решим уравнение:
1,2х = (х + 1) · 1;
1,2х – х = 1;
0,2х = 1;
х = 1 : 0,2 = 5.
Длина пути равна 1,2 · 5 = 6 (км).
О т в е т: 6 км.
IV. Итог урока.
Домашнее задание: изучить по учебнику страницы 12–14; решить № 1.1 (в; г), № 1.2 (б; г), № 1.4 (а; б); № 1.3 (б; г).
У р о к 2
Цели: повторить определение квадратного неравенства и его решения; напомнить еще один способ рассуждений, который можно применять при решении неравенств, – это метод интервалов; упражнять учащихся в решении квадратных неравенств; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Что называется квадратным неравенством с одной переменной х? Что называется решением неравенства f(х) > 0?
2. Разобрать решение примера 2 по учебнику на с. 9–10 (рис. 1).
3. Сформулировать два утверждения, применяемые при решении квадратных неравенств (при дискриминанте D < 0).
4. Записать в тетрадях теорему: квадратный трехчлен ах2 + bх + с с отрицательным дискриминантом при всех значениях х имеет знак старшего коэффициента а.
5. Разобрать решение примера 3 на с. 10 учебника и записать в тетради решение.
а) 2х2 – х + 4 > 0; D = – 31 < 0; а = 2, а > 0; значит, по теореме, при всех х выполняется неравенство 2х2 – х + 4 > 0.
О т в е т: (– ∞; + ∞).
б) – х2 + 3х – 8 ≥ 0; D = – 23 < 0; а = – 1, то есть а < 0. Тогда по теореме – х2 + 3х – 8 < 0. Значит, данное неравенство не имеет решений.
О т в е т: нет решений.
II. Выполнение упражнений.
1. Решить № 1.5 (а; б) на доске и в тетрадях.
|
а) х2 – 6х – 7 ≥ 0 х2 – 6х – 7 = 0 D = (– 6)2 – 4 · 1 · (– 7) = 64 х1 = х2 =
О т в е т: х ≤ – 1, х ≥ 7. |
б) – х2 + 6х – 5 < 0 – х2 + 6х – 5 = 0 D
= 62 – 4 · (– 1) · (– 5) = х1 = х2 =
О т в е т: х < 1, х > 5. |
2. Решить № 1.6 (в; г). Двое учащихся решают самостоятельно на доске, остальные – в тетрадях, затем проверяется решение.
|
в) 6х2 – 7х – 20 ≤ 0 6х2– 7х – 20 = 0 D = (– 7)2 – 4 · 6 · (– 20) = 529 х1 = х2 = О т в е т: |
г) 15х2 – 29х – 2 > 0 15х2 – 29х – 2 = 0 D = (– 29)2 – 4 · 15 · (– 2) = 961 х1 = х2 =
О т в е т: х < |
3. Решить № 1.7 (в; г) с комментированием на месте.
|
в) 5х2 – 2х + 1 < 0 5х2 – 2х + 1 = 0 D = (– 2)2 – 4 · 5 · 1 = – 16 < 0 а = 5 > 0; по теореме не имеет решений. О т в е т: нет решений. |
г) – 7х2 + 5х – 2 ≤ 0 – 7х2 + 5х – 2 = 0 D
= 52 – 4 · (– 5) · (– 2) = а = – 7 < 0, тогда по теореме х – любое число. О т в е т: (– ∞; + ∞). |
III. Работа по учебнику.
1. Вспомним еще один способ рассуждений, который можно использовать при решении неравенств. Разберем решение неравенства х2 – 6х + + 8 > 0 по учебнику на с. 10 (пример 4) по рис. 2.
2. Метод рассуждений, который мы применили в примере 4, называют обычно методом интервалов (или методом промежутков). Он активно используется в математике для решения рациональных неравенств.
3. Решить № 1.14 (а) и 1.10 (б) методом интервалов. Решение объясняет учитель.
1.14 (а) ![]() . Выражение имеет смысл, если подкоренное
выражение неотрицательно, то есть (3 – х)(х + 7) ≥ 0.
Отметим на числовой прямой числа 3 и – 7.
. Выражение имеет смысл, если подкоренное
выражение неотрицательно, то есть (3 – х)(х + 7) ≥ 0.
Отметим на числовой прямой числа 3 и – 7.
|
|
Если х < – 7, то 3 – х > 0 и х + 7 < 0. Если – 7 ≤ х ≤ 3, то 3 – х > 0 и х + 7 > 0. Если х > 3, то 3 – х < 0 и х + 7 > 0. |
О т в е т: – 7 ≤ х ≤ 3, или [– 7; 3].
1.10 (б) ![]() Выражение
имеет смысл, если 5х – х2 + 6 ≥ 0; – х2 + 5х + 6 = 0; D = 52 – 4 · (– 1) · 6 = 49; х1 = – 1; х2 = 6; тогда – (х + + 1)(х
– 6) ≥ 0.
Выражение
имеет смысл, если 5х – х2 + 6 ≥ 0; – х2 + 5х + 6 = 0; D = 52 – 4 · (– 1) · 6 = 49; х1 = – 1; х2 = 6; тогда – (х + + 1)(х
– 6) ≥ 0.
![]()
О т в е т: – 1 ≤ х ≤ 6.
4. Повторение ранее изученного материала.
1) Решить № 8 (в; г) на с. 6 самостоятельно с проверкой.
в) 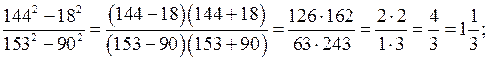
г) 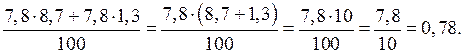
2) Решить № 11 (в; г) на с. 6 на доске и в тетрадях.
в) 428 + 427 = 427 · (42 + 1) = 427 · 43 кратно 43;
г) 223 + 220 = 220 · (23 + 1) = 220 · 9 = 217 · (23 · 9) = 217 ·72 кратно 72.
IV. Итог урока. Выставление отметок.
Домашнее задание: решить № 8 (б) на с. 6 и № 1.15 на с. 14 задачника; решить № 1.5 (в; г), № 1.6 (а; б), № 1.7 (а; б).
У р о к 3
Цели: выработать навыки решения квадратных неравенств; рассмотреть на примерах решение неравенств с модулями; повторить и закрепить навык разложения многочлена на множители способом группировки.
Ход урока
I. Проверка домашнего задания.
1. Выборочно проверить домашние задания у некоторых учащихся.
2. Трое учащихся решают на доске задания по карточкам (с последующей проверкой):
1) решить неравенство х2 – 4х – 5 ≤ 0;
2) решить № 8 (в) на с. 6;
3) решить неравенство 3х2 – 6х + 8 ≤ 0.
II. Выполнение упражнений.
1. Решить на доске и в тетрадях.
б) f(х) = 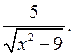 Областью определения выражения f(х)
являются все значения х, при которых х2 – 9 > 0. Применим метод интервалов:
Областью определения выражения f(х)
являются все значения х, при которых х2 – 9 > 0. Применим метод интервалов:
(х – 3)(х + 3) > 0; х = 3; х = – 3.
![]()
О т в е т: х < – 3; х > 3.
в) f(х) = 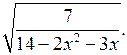
14 – 2х2 – 3х > 0;
– 2х2 – 3х + 14 = 0;
D = (– 3)2 – 4 · (– 2) · 14 = 9 + 112 = 121;
х1 = – 3,5;
х2 = 2.
– 2(х + 3,5)(х – 2) > 0
![]()
О т в е т: – 3,5 < х < 2.
2. Решить № 1.20 (а; б).
|
а) 2х2 + х < 2 2х2 + х – 2 < 0 2х2 + х – 2 = 0 D = 1 – 4 · 2 · (– 2) = 17 х1 = х2 = О т в
е т: |
б) 3 – х2 ≤ х – х2 – х + 3 ≤ 0 – х2 – х + 3 = 0 D = (– 1)2 – 4 · (– 1) · 3 = 13 х1 = х2 =
О т в е т: х
≤ х
≥ |
3. Решить № 1.21 (б).
|
б) х2 – 5 + 2х + 2 – 12 ≥ 0; х2 + 2х – 15 ≥ 0; х2 + 2х – 15 = 0; х1 = – 5; х2 = 3. О т в е т: х ≤ – 5; х ≥ 3. |
|
III. Изучение нового материала.
1. Напомним геометрическое истолкование выражения | х – а | – это расстояние на координатной (числовой) прямой между точками х и а, которое обозначают ρ(х; а). Применим это к решению неравенств с модулями.
2. Решить № 1.17 (б) и 1.19 (а). Решение объясняет учитель.
1.17 (б) | х – 2 | ≤ 3. Нужно найти на координатной прямой такие точки х, которые удалены от точки 2 на расстояние, меньшее или равное 5. Это все точки, принадлежащие отрезку [– 3; 7]:
![]()
1.19 (а) | 1 – х | > 2. Нужно найти на координатной прямой такие точки х, которые удалены от точки 1 на расстояние, большее 2.
![]()
О т в е т: х < – 1; х > 3.
3. Решить № 1.22 (а). Объясняет учитель.
а) | 4х + 3 | > 5
Р е ш е н и е
Имеем: 4 | х + ![]() | > 5; | х +
| > 5; | х + ![]() | >
| > ![]() Надо найти на числовой прямой все такие
точки, которые удалены от точки (
Надо найти на числовой прямой все такие
точки, которые удалены от точки (![]() ) более чем на
) более чем на ![]() Получаем:
Получаем:
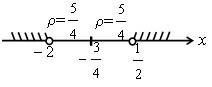
О т в е т: х < – 2; х > ![]()
4. Решить № 1.22 (б) на доске и в тетрадях.
б) 6 – | 3х + 1 | > 0;
– | 3х + 1 | > – 6;
| 3х + 1 | < 6;
3 | х + ![]() | < 6;
| < 6;
| х + ![]() | < 2.
| < 2.
Надо найти на числовой прямой все точки, которые
удалены от точки (![]() )
на расстояние, меньшее 2.
)
на расстояние, меньшее 2.
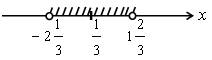
О т в е т: ![]() < х <
< х < ![]() .
.
IV. Повторение пройденного материала.
Вспомнить, в чем заключается способ группировки при разложении многочлена на множители.
1) Решить № 10 (в; г) на с. 6 задачника.
в) 9m2 – 9mn – 5m + 5n
= (9m2 – 9mn)
– (5m – 5n) = 9m(m – n) –
– 5(m – n) = (m – n)(9m – 5);
г) 16ab2 + 5b2c + 10c3 + 32ac2 = (16ab2 + 32ac2) + (5b2c + 10c3) =
= 16a(b2 + + 2c2) + 5c(b2 + 2c2) = (b2 + 2c2)·(16a + 5c).
2) Решить № 12 (а) на с. 6 на доске и в тетрадях; № 12 (б) на с. 6 самостоятельно с проверкой.
а) 2,7 · 6,2 – 9,3 · 1,2 + 6,2 · 9,3
– 1,2 · 2,7 = (2,7 · 6,2 + 6,2 · 9,3) –
– (9,3 · 1,2 + 1,2 · 2,7) = 6,2(2,7 + 9,3) – 1,2 · (9,3 + 2,7) = (2,7 +
9,3) ×
× (6,2 – 1,2) = 12 · 5 = 60;
б) 125 · 48 – 31 · 82 – 31 · 43 + 125
· 83 = (125 · 48 + 125 · 83) –
– (31 · 82 + 31 · 43) = 125 · 131 – 31 · 125 = 125(131 – 31) = 125 × 100 =
= 12500.
V. Итоги урока.
Домашнее задание: по учебнику изучить материал § 1 и записать в тетради решение примера 5 на с. 11; решить по задачнику № 10 (а; б) и № 12 (в; г) на с. 6; решить № 1.12; 1.22 (в; г) на с. 14–15.
Рациональные
неравенства
(4 ч)
У р о к 1
Цели: ввести понятие рационального неравенства с одной переменной; закрепить знание трех правил (из § 1) при решении рациональных неравенств; научить применять метод интервалов к решению рациональных неравенств.
Ход урока
I. Проверочная работа (10–12 минут).
|
В а р и а н т I 1. Решите неравенство: а) х2 – 8х + 15 > 0; б) 3х2 + 2х + 4 < 0; в) х2 – 9 ≥ 0. |
В а р и а н т II 1. Решите неравенство: а) х2 – 10х + 21 > 0; б) – 4х2 + 3х – 5 < 0; в) х2 – 16 ≥ 0. |
2. Найдите область определения выражения f(х):
|
f(х) = |
f(х) = |
|
3. Решите неравенство: а) | х – 4 | ≤ 3; б) | х + 2 | > 1. |
3. Решите неравенство: а) | х + 5 | ≤ 2; б) | х – 3 | > 4. |
II. Объяснение нового материала.
1. Определение рационального неравенства с одной переменной.
Рациональное неравенство с одной переменной х – это неравенство вида h(х) > q(х), где h(х) и q(х) – рациональные выражения.
2. При решении рациональных неравенств используются те три правила, которые были сформулированы выше в § 1 (повторить эти правила).
3. При решении рациональных неравенств используют метод интервалов.
4. Учитель объясняет решение № 2.1 (а; б).
а) (х + 2)(х + 3) > 0. Рассмотрим выражение f(х) = (х + 2)(х + 3). Оно обращается в 0 в точках – 2; – 3; отметим эти точки на числовой прямой:
![]()
Числовая прямая разбивается указанными точками на три промежутка, на каждом из которых выражение f(х) сохраняет постоянный знак. Найдем знаки выражения на каждом промежутке: на промежутке (–∞; –3) f(х) > 0; на промежутке (– 3; – 2) f(х) < 0; на промежутке (– 2; ∞) f(х) > 0. Неравенство f(х) > 0 выполняется на промежутках (–∞; – 3) и (– 2; +∞).
О т в е т: х < – 3; х > – 2.
б) (х – 0,5)(х + 3) < 0.
Выражение f(х) = (х + 3)·(х – 0,5) обращается в нуль в точках – 3 и 0,5:
![]()
На промежутке (–∞; – 3) выражение f(х) > 0; на промежутке (– 3; 0,5) выражение f(х) < 0; на промежутке (0,5; + ∞) f(х) > 0. Выбираем промежуток, на котором выражение отрицательно.
О т в е т: – 3 < х < 0,5.
III. Закрепление изученного материала.
1. Решить № 2.2 (а; б) на доске и в тетрадях.
а) t(t – 1) < 0; t = 0; t = 1
![]()
О т в е т: 0 < t < 1.
б) t(t – ![]() )(t – 12) ≥ 0; t
= 0; t =
)(t – 12) ≥ 0; t
= 0; t = ![]() ;
t = 12
;
t = 12
О т в е т: 0 ≤ t ≤ ![]() ; t ≥ 12.
; t ≥ 12.
2. Решить № 2.3 (в; г) с комментированием на месте.
в) х2 – 3х ≥ 0; х(х – 3) ≥ 0; х = 0; х = 3
![]()
О т в е т: х ≤ 0; х ≥ 3.
г) 5х + х2 < 0; х(5 + х) < 0; х = 0; х = – 5
![]()
О т в е т: (– 5; 0).
3. Решить № 2.4 (в; г), используя формулу а2 – b2 = (а – b)(a + b).
4. Решить № 2.6 (в; г). Учитель объясняет решение № 2.6 (в).
в) (х – 2)(х + 3)(х + 1) < 0. Нули выражения f(х) = (х – 2)(х + 3) × (х + 1) равны 2; – 3 и – 1. Отметим эти числа на числовой прямой:
![]()
О т в е т: (– ∞; – 3); (– 1; 2).
г) (х + 5)(х + 1)(х – 3) > 0; х = – 5; – 1; 3.
![]()
О т в е т: – 5 < х < – 1; х > 3.
5. Решить № 1.15, закрепляя ранее изученный материал.
3х2 – 2рх – р + 6 = 0
а) Квадратное уравнение имеет два различных корня, если D > 0.
D = (– 2р)2 – 4 · 3(– р + 6) = 4р2 + 12р – 72;
4р2 + 12р – 72 > 0;
4р2 + 12р – 72 = 0;
р2 + 3р – 18 = 0;
р1 = 3;
р2 = – 6
4р2 + 12р – 72 = 4(р – 3)(р + 6); с помощью метода интервалов решим неравенство 4(р – 3)(р + 6) > 0:
![]()
О т в е т: при р < – 6 и р > 3.
б) Квадратное уравнение имеет один корень, если D = 0:
4р2 + 12р – 72 = 0;
р1 = – 6;
р2 = 3.
О т в е т: при р = – 6 и р = 3.
в) Квадратное уравнение не имеет корней, если D < 0:
![]()
О т в е т: при – 6 < р < 3.
IV. Итоги урока. Выставление отметок.
Домашнее задание: изучить материал на с. 12–15 учебника и записать в тетради решение примеров 1 и 2; решить № 2.1 (в; г), № 2.2 (в; г), № 2.3 (а; б); № 2.4 (а; б), № 2.5 (а; б).
У р о к 2
Цели: способствовать выработке навыка решения неравенств методом
интервалов; научить решать рациональные неравенства вида ![]() > 0 и
> 0 и ![]() < 0.
< 0.
Ход урока
I. Анализ проверочной работы.
1. Указать ошибки, сделанные учащимися при решении квадратных неравенств.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Выполнение упражнений.
1. Решить № 2.5 (б; в) с комментированием на месте.
2. Решить № 2.7 (а; б) на доске и в тетрадях.
|
а) (х – 4)(3х + 1)(х + 1) > 0 (х – 4) · 3(х + (х – 4)(х + х = 4; х = –
О т в е т: (– 1; – |
б) (2х + 3)(х + 1)(х – 1) < 0 2(х + 1,5)(х + 1)(х – 1) < 0 | : 2 (х + 1,5)(х + 1)(х – 1) < 0 х = – 1,5; х = – 1; х = 1
О т в е т: х < – 1,5; – 1 < х < 1. |
3. Решить № 2.8 (а; б). Решение объясняет учитель.
|
а) (2 – х)(3х + 1)(2х – 3) > 0 – 1·(х–2)·3(х+ (х – 2)( х
+ |
б) (2х + 3)(1 – 2х)(х – 1) < 0 2(х+1,5)·(–2)(х– (х + 1,5)(х – |
|
х = 2; х
= –
О т в е т: х < – |
х = – 1,5; х =
О т в е т: (– 1,5; |
4. После решения квадратных неравенств сделать в ы в о д: при решении неравенств вида f(х) > 0 или f(х) < 0, где f(х) = (х – а)(х – b)(х – с), на самом правом из выделенных промежутков выполняется неравенство f(х) > 0, а далее по промежуткам знаки выражения f(х) чередуются.
III. Изучение нового материала.
1. Разобрать по учебнику решение примеров 3 и 4 на страницах 15–18. Обратить внимание учащихся на рисунки 16а, 16б (с. 18).
2. Учитель объясняет решение № 2.9 (б; г), обращая внимание учащихся на то, что дробь равна нулю, если числитель дроби равен нулю, а знаменатель не равен нулю.
б) ![]() Числитель дроби равен нулю при х =
0 и х = – 1; знаменатель не равен нулю при всех значениях х,
кроме х = 9. Учитываем чередование знаков справа (ставим «+») налево на
числовой прямой и чертим кривую знаков.
Числитель дроби равен нулю при х =
0 и х = – 1; знаменатель не равен нулю при всех значениях х,
кроме х = 9. Учитываем чередование знаков справа (ставим «+») налево на
числовой прямой и чертим кривую знаков.
О т в е т: – 1 ≤ х ≤ 0; х > 9.
г)  Числитель дроби обращается в нуль при х
= 5, а знаменатель – в точках 0 и – 7.
Числитель дроби обращается в нуль при х
= 5, а знаменатель – в точках 0 и – 7.
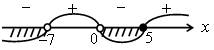
О т в е т: х < – 7; 0 < х ≤ 5.
IV. Закрепление изученного материала.
1. Решить № 2.10 (в; г) на доске и в тетрадях.
|
в)
Отмечаем точки х = 1 и х = – 2
О т в е т: х < – 2; х ≥ 1. |
г) Отмечаем точки х = 14 и х = 5 на числовой прямой и чертим кривую знаков:
О т в е т: х < 5; х > 14. |
2. Самостоятельно решить № 2.11 (в; а).
О т в е т ы: в) х ≤ – 5; х ≥ – 2; а) – 3 ≤ х ≤ – 1.
V. Итоги урока.
На примере неравенства (3х – 12)(х + 7)(9 – х) < 0 расскажите, как решают неравенства методом интервалов.
Домашнее задание: прочитать по учебнику материал на с. 14–19; решить № 2.7 (в; г), № 2.8 (в; г), № 2.9 (а; в), № 2.10 (а; б), № 2.11 (б; г); решить задачу № 44 на с. 10.
У р о к 3
Цели: упражнять в решении более сложных квадратных неравенств методом интервалов; закреплять навыки разложения квадратного трехчлена на множители; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Двое учащихся решают на доске задания № 2.13 (а) и № 2.14 (а), используя теорему о квадратном трехчлене с отрицательным дискриминантом.
2. Двое учащихся решают на доске задания № 2.10 (а) и № 2.10 (б) из домашней работы.
О т в е т ы: а) ![]() < х <
< х < ![]() ; б) х < 2.
; б) х < 2.
3. Со всем классом разбирается решение неравенств методом интервалов:
а) (х – 3)(х + 1)(х – 8) < 0;
б) х2 – 81 ≤ 0;
в) ![]() > 0;
> 0;
г) 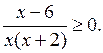
При решении используется чередование знаков с помощью кривой знаков.
II. Решение более сложных квадратных неравенств.
1. Решить № 2.15 (в; г) на доске и в тетрадях; учащиеся решают самостоятельно, а учитель при необходимости помогает в решении.
|
в) (3х – 2)(5 – х)(х + 1)(2 – х) < 0; 3(х – (х – х =
О т в е т: (– 1; |
г) (2х + 5)(4х + 3)(7 – 2х)(х – 3) < 0 2(х +
2,5)·4(х + (х +
2,5)(х + х
= – 2,5; х = –
О т в е т: х
< –2,5; – |
2. Решить № 2.16 (в) с комментированием на месте.
в) 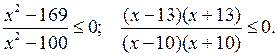
Отмечаем на числовой прямой точки х = 13, х = – 13, х = 10 и х = – 10.
![]()
О т в е т: [– 13; – 10)![]() (10; 13] или – 13 ≤ х <
– 10; 10 < х ≤ 13.
(10; 13] или – 13 ≤ х <
– 10; 10 < х ≤ 13.
3. Решить № 2.16 (г). Решение объясняет учитель.
г) 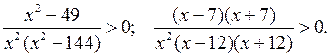
Отмечаем на числовой прямой точки 7; – 7; 0; 12; –
12. Так как в знаменателе есть множитель х2, то нельзя пользоваться «кривой знаков», а надо определять
знаки выражения f(х) = 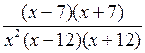 в каждом из выделенных промежутков по
отдельности:
в каждом из выделенных промежутков по
отдельности:
![]()
О т в е т: х < – 12; – 7 < х < 0; 0 < х < 7; х > 12.
4. Решить № 2.17 (а; б). Учитель объясняет начало решения неравенства с помощью разложения на множители левой части, а заканчивают решение учащиеся самостоятельно.
|
а) х3 – 64х > 0 х(х2 – 64) > 0 х(х – 8)(х + 8) > 0 х = 0; х = 8; х = – 8
О т в е т: – 8 < х < 0; х > 8. |
б) х3 ≤ 2х х3 – 2х ≤ 0 х(х2 – 2) ≤ 0 х(х – х = 0; х =
О т в е т: х ≤ – |
5. Решить № 2.18 (а; в). Двое учащихся самостоятельно решают на доске, остальные в тетрадях. Учитель при необходимости помогает.
|
а)
|
в)
|
|
О т в е т: х < |
О т в е т: х
< – 4; – 3 ≤ х ≤ – 2; |
6. Решить неравенство № 2.22 (а). Объясняет учитель.
а) (х – 1)2(х2 +
4х – 12) < 0. Разложим на множители квадратный трехчлен х2 + 4х – 12 = (х +
6)(х – 2) и решим неравенство (х –1)2(х + 6)(х –2) <
< 0. Рассмотрим выражение f(х) = (х –1)2(х +6)(х –2),
отметим точки 1; – 6 и 2 на числовой прямой и определим знаки f(х)
на каждом из полученных промежутков. Пользоваться «кривой знаков»
нельзя из-за множителя (х – 1)2.
![]()
О т в е т: – 6 < х < 1, 1 < х
< 2 или (– 6; 1)![]() (1; 2).
(1; 2).
7. Повторение ранее пройденного материала. Решить самостоятельно № 38 (а; б) и № 39 (а) на с. 9 учебника.
III. Итоги урока. Выставление отметок.
Домашнее задание: изучить по учебнику материал на с. 18–21 и коротко записать в тетради решение примеров 5 и 6; решить № 2.15 (а; б), № 2.16 (а; б), № 2.17 (в; г), 2.18 (б; г) и № 2.22 (в).
У р о к 4
Цели: закрепить знания и умения учащихся в решении квадратных неравенств; развивать логическое мышление учащихся; закрепить навыки разложения квадратного трехчлена на множители и разложения многочлена с помощью формул сокращенного умножения.
Ход урока
I. Устная работа.
1. Пояснить решение заданий из домашней работы, вызвавших затруднения у учащихся.
2. Повторить разложение квадратного трехчлена на множители по формуле ах2 + bх + с = а(х – х1)(х – х2) и разложение многочлена на множители с помощью формул сокращенного умножения.
3. На примере неравенств 3х2 + 5х – 2 < 0 и х2 + 2х + 6 > 0 расскажите, как можно решить неравенство второй степени, используя график квадратной функции.
4. На примере неравенств (х + 11)(х
– 8)(х + 16) > 0 и ![]() расскажите, как решают неравенства
методом интервалов, используя «кривую знаков».
расскажите, как решают неравенства
методом интервалов, используя «кривую знаков».
II. Тренировочные упражнения.
1. Решить № 2.22 (б) на доске и в тетрадях.
|
б) (х + 2)(х2 – 6х – 16) > 0 х2 – 6х – 16 = 0 D = 36 + 64 = 100 х1 = – 2; х2 = 8
О т в е т: х > 8. |
(х + 2) · (х + 2)(х – 8) > 0 (х + 2)2(х – 8) > 0 х = – 2; х = 8
|
2. Решить № 2.19 (в; г). Сначала объясняет учитель, а потом решение каждого несложного неравенства учащиеся заканчивают сами.
|
в) х + х + х = – 3; х = – 1; х = 0
О т в е т: х ≤ – 3; – 1 ≤ х < 0. |
г) х – х – х = 4; х = – 2; х = 0
О т в е т: – 2 < х < 0; х > 4. |
3. Решить № 2.24 (б; в). Решение № 2.24 (б) объясняет учитель.
б) 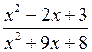 < 0;
< 0;
х2 – 2х + 3 = 0
D = 4 – 12 = – 8 < 0,
Корней нет, а потому формула ах2 + bх + с = а(х – х1)(х – х2) здесь неприменима.
Применяем теорему о квадратном трехчлене с отрицательным дискриминантом и положительным старшим коэффициентом, по ней трехчлен х2 – 2х + 3 положителен при всех значениях х. Тогда на него можно разделить обе части неравенства, не меняя знаки неравенства х2 + 9х + 8 = 0; D = 81 – 32 = 49; х1 = – 8; х2 = – 1; х2 + 9х + 8 = (х + 8)(х + 1).
Решим равносильное данному неравенство 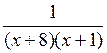 < 0.
< 0.
![]()
О т в е т: – 8 < х < – 1.
в) 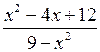 < 0;
< 0;
х2 – 4х + 12 = 0;
D = 16 – 48 = – 32 < 0.
Значит, по теореме х2 – 4х + 12 > 0 при всех значениях х.
Решим равносильное данному неравенство: 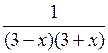 < 0;
< 0;
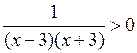
![]()
О т в е т: х < – 3; х > 3.
4. Решить № 2.25 (в) самостоятельно. Один учащийся решает на доске, другие в тетрадях, затем проверяется решение.
в) 
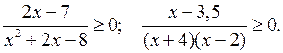
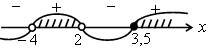
О т в е т: – 4 < х < 2; х ≥ 3,5.
5. Разобрать по учебнику решение неравенства 3х2 – 2х – 2 < 0 (пример 8 на с. 23).
6. Решить № 2.37. Решение объясняет учитель.
Преобразуем неравенство к виду х2(х + 2)(х – р) ≤ 0 и рассмотрим следующие возможности:
р = – 2; р < – 2; – 2 < р < 0; р = 0; р > 0.
1) Если р = – 2, то неравенство примет вид х2(х + 2)2 ≤ 0. Решение неравенства состоит из двух точек: х = – 2, х = 0.
![]()
2) Если р < – 2, то решения неравенства:
![]()
3) Если – 2 < р < 0, то решения неравенства:
![]()
4) Если р = 0, то решения:
![]()
5) Если р > 0, то решения неравенства:
![]()
О т в е т:
а) два целых числа при р = – 2 (случай 1);
б) четыре целых числа при р = – 4 (случай 2) и при р = 1 (случай 5);
в) три целых числа при р = – 3 (случай 2), при р = – 1 (случай 3) и при р = 0 (случай 4);
г) пять целых чисел при р = – 5 (случай 2) и при р = 2 (случай 5).
III. Итоги урока. Выставление отметок.
Домашнее задание: рассмотреть по учебнику решение примера 7 на с. 21–22 и записать его в тетрадь; на отдельных листочках решить домашнюю контрольную работу № 1 на с. 31–32 с № 1 по № 6.
МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
(3 ч)
У р о к 1
Цели: познакомить учащихся с понятием множества, способами задания и описания множеств; учить задавать множества различными способами; развивать логическое мышление учащихся.
Ход урока
I. Изучение нового материала.
1. Знакомство с новым понятием начнем с рассмотрения становления и развития языка математики со времен Галилео Галилея (1564–1642) до наших дней.
2. Современный математический язык более краток и в первую очередь заменяет естественный, разговорный язык специальными буквенными и символьными выражениями. Он более формализован и унифицирован, то есть подходит к рассмотрению сразу многих однотипных случаев. Более 100 лет фундаментом современного математического языка являются простейшие понятия и обозначения языка теории множеств.
3. Множество состоит из элементов. Если этих элементов немного, то удобно все элементы просто перечислить в каком-нибудь порядке. Чтобы не забыть, что перечисляемые элементы объединены вместе в некоторое множество, такое перечисление производят внутри скобок { , }. Словесное, поэлементное описание множества, задание множества перечислением его элементов можно рассмотреть в таблице на с. 25 учебника.
4. Замечание 1 на с. 25 (прочитать в учебнике).
5. Множество, элементами которого являются числа, называется числовым. Для числовых множеств есть естественный порядок перечисления их элементов от меньшего числа к большему числу.
6. Рассмотреть решение примера 1 на с. 25–26 учебника.
7. Множество, не содержащее ни одного элемента, называется пустым. Обозначается символом – Ø.
8. Если число элементов множества достаточно велико (например, несколько десятков, сотен и т. д.) или если множество бесконечно (например, множество всех натуральных или множество всех целых чисел), то явное перечисление элементов такого множества невозможно. Способы задания, описания таких множеств весьма разнообразны.
9. Рассмотреть примеры в таблице на с. 26–27 учебника.
10. Рассмотреть примеры 2–3 на с. 28–29 учебника.
11. Такие словесные обороты, как «элемент х
принадлежит множеству А» или «х является элементом множества А»
в математике более кратко записывают так: x ![]() A. Смысл знака принадлежности
A. Смысл знака принадлежности ![]() легко запомнить:
легко запомнить: ![]() – это перевернутая
буква «Э», то есть буква, с которой начинается слово элемент. Знак
– это перевернутая
буква «Э», то есть буква, с которой начинается слово элемент. Знак ![]() – это отрицание знака
принадлежности
– это отрицание знака
принадлежности ![]() .
Запись x
.
Запись x ![]() A
означает, что х не является элементом множества А.
A
означает, что х не является элементом множества А.
12. Рассмотреть примеры использования этих знаков на с. 30 учебника.
13. Рассмотреть пример 4, с. 30 учебника.
14. Замечание 2 на с. 30 (прочитать в учебнике).
II. Закрепление изученного материала.
1. Решить № 3.1 (a; б) на с. 21 задачника.
a) {6; 7; 8; …}, б) {–6; –5; –4; –3; –2; –1}.
2. Решить № 3.2 на с. 21 задачника.
а) множество всех четных цифр.
б) все числа вида х + 1, где х ненулевая цифра.
в) множество натуральных чисел, кратных трем, которые меньше 31.
г) заглавные буквы английского алфавита.
3. Решить письменно № 3.3 (а, б) на с. 21.
a) ![]()
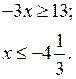
О т в е т: ![]()
б) ![]()
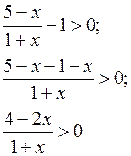
![]()
О т в е т: (–1; 2).
4. Решить устно № 3.4 на с. 21.
а) нет, б) да, в) нет, г) да.
|
5. Решить № 3.5 (а, б) на с. 21. а) Следует найти множество всех х таких, что является решением неравенства x2 ≤ 0, то есть надо решить данное неравенство. Его решением является одно число х = 0. О т в е т: {0}. |
|
б) Следует найти множество всех х таких, что являются решением неравенства x2 + 18x ≤ –81, то есть надо решить данное неравенство
|
x2 + 18x ≤ –81; x2 + 18x + 81 ≤ 0; y = x2 + 18x + 81 x2 + 18x + 81 = 0 D = 182 – 4 × 1 × 81 = 324 – 324 = 0
|
|
Решением данного неравенства является одно число х = –9.
О т в е т: {–9}.
5. Решить № 3.6 (б, г) на с. 21.
б) Нет. Подставим х = 0,7 в неравенство x2 + 16x ≤ –64. Получим неверное числовое неравенство 11,69 ≤ –64.
г) Да. Подставим х = 1,001. Получим верное
числовое неравенство 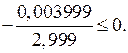
О т в е т: б) нет; г) да.
6. Решить № 3.7 на с. 22.
a) x(x2 + 19) + 6 = (2x + 3)(3x + 2) – x2
x3 + 19x + 6 = 6x2 + 9x + 4x + 6 – x2
x3 + 19x + 6 – 6x2 – 9x – 4x – 6 + x2 = 0
x3 – 5x2 + 6x = 0
x1 = 0
D = 25 – 24 = 1
x2 = 3, x3 = 2.
О т в е т: 0; 2; 3.
б) M = {0; 2; 3}.
в) {0; 2; 3}, {0; 3; 2}, {2; 0; 3}, {2; 3; 0}, {3; 2; 0}, {3; 0; 2}.
г) 6.
О т в е т: а) 0, 2, 3; б) M = {0; 2; 3}; в) {0; 2; 3}, {0; 3; 2}, {2; 0; 3}, {2; 3; 0}, {3; 2; 0}, {3; 0; 2}; г) 6.
III. Итоги урока.
Перечислить способы задания и описания множеств.
Домашнее задание: изучить материал § 3.1 на с. 23–30 учебника; решить № 3.3 (в, г); № 3.5 (в, г); № 3. 6 (а, г); № 3.17 (б) на с. 21–23 задачника.
У р о к 2
Цели: познакомить учащихся с понятием подмножества, учить перечислять подмножества данного множества; развивать логическое мышление.
Ход урока
I. Актуализация опорных знаний.
1. Решить на доске задания из домашней работы, вызвавшие затруднения у учащихся.
2. Какое множество называется числовым? Приведите примеры числовых множеств.
3. Какое множество называется пустым?
4. Перечислите способы задания и описания множеств.
5. Решить задачу № 3.16 на с. 23 задачника.
а) Наименьшее натуральное число, куб которого есть трехзначное число, – это 5. То есть 53 = 125. Так же 63 = 216, 73 = 343, 83 = 512, 93 = 729.
б) Наименьшее натуральное число из 125; 216; 343; 512 и 729 – это 125, а наибольшее число – 729, так как требуется перечислить числа в порядке убывания от большего числа к меньшему числу, то множество М равно M = {729; 512; 343; 216; 125}.
в) Так как требуется записать множество А последних цифр элементов множества М, то надо выписать последнюю цифру каждого из чисел. Например, последней цифрой числа 729 является цифра 9, 512 – цифра 2, 343 – цифра 3, 216 – цифра 6, 125 – цифра 5. Перечислить их в порядке возрастания. Тогда A = {2; 3; 5; 6; 9}.
г) Вторых цифр из множества М всего 3 – это 2; 1; 4. Если на I место поставить 2, то для двух оставшихся чисел и двух оставшихся мест есть два варианта – {2; 1; 4} и {2; 4; 1}. Если на I месте стоит 1, то также имеется два варианта {1; 2; 4} и {1; 4; 2}. Если на первом месте стоит 4, то так же имеется два варианта {4; 2; 1} и {4; 1; 2}. Всего способов – 6.
О т в е т: а) 5, 6, 7, 8, 9; б) M = {729; 512; 343; 216; 125}; в) A = {2; 3; 5; 6; 9}; г) 6.
6. Решить задачу № 3.17 (а) на с. 23 задачника.
а) Следует найти множество таких х, что 3(x + 1) – x2 > 5, то есть решить это неравенство
3(x + 1) – x2 > 5;
3x + 3 – x2 > 5;
–x2 + 3x – 2 > 0;
x1 = 2, x2 = 1.
Множество решений неравенства 3(x + 1) – x2 > 5 – это интервал между корнями x1 = 2 и x2 = 1.
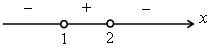
О т в е т: (1; 2).
II. Объяснение нового материала.
1. Элементы множества А можно объединять не сразу все вместе, а группируя их в разных комбинациях. Так можно получать различные подмножества.
2. Рассмотреть пример 5 на с. 30–31 учебника.
3. Определение 1.
Если каждый элемент множества В является элементом множества А,
то множество В называют подмножеством множества А. Обозначается: B
![]() A. Знак «
A. Знак «![]() » называется знаком
включения.
» называется знаком
включения.
4. Рассмотреть пример 6 на с. 32–33 учебника.
5. Замечание 3 (прочитать в учебнике на с. 33–34).
III. Выполнение упражнений.
1. Решить № 3.8 на с. 22 задачника.
![]() – это множество, из которого выбираются
различные двухэлементные подмножества. Перечислим их –
– это множество, из которого выбираются
различные двухэлементные подмножества. Перечислим их –
![]()
а) Выберем из них подмножества, состоящие из двух
чисел разного знака – это ![]()
б) Выберем из них подмножества, состоящие из двух
положительных чисел – это ![]()
в) Выберем из них подмножества, состоящие из
рациональных чисел – это ![]()
г) Выберем из них подмножества, среди которых есть
иррациональные числа – это ![]()
О т в е т: а) ![]() , б)
, б) ![]() , в)
, в) ![]() ,
,
г) ![]()
2. Решить устно № 3.10 на с. 22 задачника.
а) Включение A ![]() B – не верно, так как множество А
– это множество натуральных чисел, а множество В – множество четных
натуральных чисел.
B – не верно, так как множество А
– это множество натуральных чисел, а множество В – множество четных
натуральных чисел.
б) Включение B ![]() C – не верно, так как множество В
– множество четных натуральных чисел, а множество С – множество четных
натуральных чисел, кратных 4.
C – не верно, так как множество В
– множество четных натуральных чисел, а множество С – множество четных
натуральных чисел, кратных 4.
в) Включение C ![]() A – верно так как А –
множество натуральных чисел, а С – множество четных натуральных чисел, кратных
четырем.
A – верно так как А –
множество натуральных чисел, а С – множество четных натуральных чисел, кратных
четырем.
г) Включение C ![]() B – верно, так как С –
множество четных натуральных чисел, кратных четырем, В – множество
натуральных четных чисел.
B – верно, так как С –
множество четных натуральных чисел, кратных четырем, В – множество
натуральных четных чисел.
3. Решить № 3.11 на с. 22 задачника.
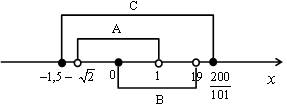
а) A ![]() B не верно.
B не верно.
б) B ![]() C верно.
C верно.
в) C ![]() A не верно.
A не верно.
г) A ![]() C верно.
C верно.
4. Решить № 3.18 на с. 23 задачника.
а) Получится 3 утверждения –
![]()
б) Таких утверждений получится 6 –
![]()
![]()
в) Получится 9 утверждений
![]()
![]()
![]()
г) Верные утверждения составляют ![]() всех утверждений.
всех утверждений.
О т в е т: а) 3; б) 6; в) 9; г) ![]()
IV. Итоги урока.
Сформулировать понятие подмножества.
Домашнее задание: изучить материал § 3.2 на с. 30–34 учебника; решить № 3.9, № 3.19 на с. 22–23 задачника.
У р о к 3
Цели: познакомить учащихся с операциями над множествами – пересечением и объединением, учить находить пересечение и объединение множеств; развивать логическое мышление.
Ход урока
I. Проверка выполнения домашнего задания.
1. Решить на доске задания из домашней работы, вызывающие затруднения у учащихся.
2. Дать определение подмножества.
II. Объяснение нового материала.
1. Изображение множеств в виде плоских фигур очень удобно для наглядного объяснения различных операций над множествами. Обычно множества при этом изображают в виде некоторых кругов. Такие круги называют кругами Эйлера в честь великого швейцарского математика Леонарда Эйлера (1707–1783), который долгое время работал в России.
2. Определение 2. Пересечением множеств А и В называют множество, состоящее из всех общих элементов множества А и В, то есть из всех элементов, которые принадлежат и множеству А и множеству В.
3. Рассмотреть рис. 30 на с. 34 учебника.
4. Пересечение множеств А и В обозначается так: А ![]() В.
В.
5. Познакомиться с формульной записью определения пересечения множеств А
и В: А ![]() В = {x | x
В = {x | x ![]() A и x
A и x ![]() B}.
B}.
6. Рассмотреть пример 7 на с. 35 учебника.
7. Часто рассматривается пересечение не только двух, но и трех, четырех и
т. д. множеств. Пересечением множеств А, В и С
называют множество, состоящее из всех элементов, которые принадлежат и
множеству А, и множеству В, и множеству С. Обозначают так: А ![]() В
В ![]() C. Рассмотреть
рис. 32 на с. 36 учебника.
C. Рассмотреть
рис. 32 на с. 36 учебника.
8. Замечание 4 на с. 36 учебника прочитать.
9. Определение 3. Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В.
10. Рассмотреть рис. 33 на с. 37 учебника.
11. Объединение множеств А и В обозначают так: А ![]() В.
В.
12. Познакомиться с формульной записью определения объединения множеств А
и В: А ![]() В {x | x
В {x | x ![]() A или x
A или x ![]() B}.
B}.
13. Рассмотреть пример 8 на с. 37–38 учебника.
14. Часто рассматривается объединение не только двух, но и трех, четырех
и т. д. множеств. Объединением множеств А, В и С называют
множество, состоящее из всех элементов, которые принадлежат или множеству А,
или множеству В, или множеству С. Обозначают так: А ![]() В
В ![]() C. Рассмотреть
рис. 39 на с. 39 учебника.
C. Рассмотреть
рис. 39 на с. 39 учебника.
15. Замечание 5 на с. 40 прочитать в учебнике.
III. Выполнение упражнений.
1. Решить № 3.12 (а, б) на с. 22 задачника.
а) А – множество всех натуральных чисел, кратных 10; В – множество натуральных чисел от 1 до 41 включительно. Число х принадлежит и множеству А, и множеству В, если это одно из натуральных чисел, больше либо равных 1 и меньше, либо равных 41, кратных 10. Таких чисел имеется ровно четыре: 10; 20; 30; 40.
Итак, А ![]() В = {10; 20; 30; 40}.
В = {10; 20; 30; 40}.
б) А – множество всех нечетных целых чисел, В – множество всех целых чисел от 0 до 21, кратных 3. Число х принадлежит и множеству А, и множеству В, если оно нечетное целое число от 0 до 21 включительно, кратное 3. Таких чисе л имеется ровно четыре: 3; 9; 15; 21.
Итак, А ![]() В = {3; 9; 15; 21}.
В = {3; 9; 15; 21}.
в) {–10; 0}.
г) {2}.
О т в е т: а) А ![]() В = {10; 20; 30; 40}; б) А
В = {10; 20; 30; 40}; б) А ![]() В = {3; 9; 15;
21}; в) {–10; 0}; г) {2}.
В = {3; 9; 15;
21}; в) {–10; 0}; г) {2}.
2. Решить № 3.13 на с. 23 задачника.
№ 3. 13 (в) объясняет учитель.
а) А ![]() В = (0; 0,9].
В = (0; 0,9].
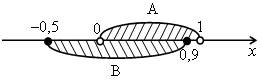
б) В ![]() С = [–0,5; 0,9].
С = [–0,5; 0,9].

в) А ![]() В
В ![]() D = (0,1; 0,9].
D = (0,1; 0,9].
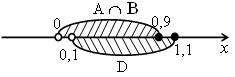
3. Решить № 3.14 (а, б, в) на с. 23 задачника.
а) А ![]() В = [–0,5; 1).
В = [–0,5; 1).
б) А ![]() D = (0; 1,1].
D = (0; 1,1].
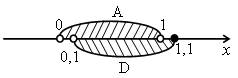
в) В ![]() D = [–0,5; 1,1].
D = [–0,5; 1,1].
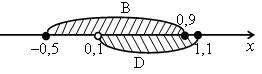
4. Решить № 3.15 на с. 23 задачника.
а) {c}, б) {c, d, e, g, k}, в) {c, e}, г) {a, b, c, d, e, f, g, k}.
5. Решить № 3.20 (а; б) на с. 24 задачника.
а) ![]()
![]()
б) ![]()
Ответ: а) ![]() б)
б) ![]()
6. Решить № 3.22 на с. 24 задачника.
а) 18; б) 14; в) 7.
7. Решить № 3.23 на с. 24 задачника.
а) 900 + 700 = 1600 (м2) – площадь участка застройки, если бы она состояла из двух непересекающихся участков.
1600 – 1500 = 100 (м2) – площадь участка, отведенного под гараж.
б) 900 – 100 = 800 (м2) – площадь части первого прямоугольника, не отведенная под гараж.
в) Аналогично б) 700 – 100 = 600 (м2) – площадь части второго прямоугольника, не отведенная под гараж.
г) 600 + 800 = 1400 (м2) – площадь части застройки без учета гаража.
Ответ: 100 м2, 800 м2, 600 м2, 1400 м2.
IV. Итоги урока.
Перечислить основные операции, выполняемые над множествами.
Домашнее задание: изучить материал § 3.3 на с. 34–40 учебника; решить № 3.20 (в; г), 3.24, 3.21, 3.25 на с. 24 задачника.
Системы неравенств
(4 ч)
У р о к 1
Цели: ввести понятие системы неравенств, решения системы неравенств; повторить и закрепить знания решения неравенств.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Собрать у учащихся домашние контрольные работы.
2. Вспомнить, как найти область определения выражения
f(х) = ![]()
3. Рассмотреть нахождение области определения выражения
f(х) = ![]()
Сделать в ы в о д: задача сводится к решению системы неравенств
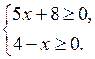
II. Изучение нового материала.
1. Определение системы неравенств.
2. Определение решения системы неравенств.
3. Решить систему неравенств – значит найти все ее частные решения.
4. Устно решить № 4.1 (а; б).
5. Учитель объясняет решение № 4.3 (а–г) и показывает с помощью штриховки нахождение общего решения.
6. Повторить правила для решения неравенств и объяснить решение № 4.6 (в; г).
|
в)
О т в е т: (– ∞; – 2] или х ≤ – 2. |
г)
О т в е т: [2; ∞) или х ≥ 2. |
III. Закрепление изученного материала.
1. Решить № 4.5 (в; г) на доске и в тетрадях.
2. Решить № 4.7 (в; г) с комментированием на месте.
|
в)
О т в е т: нет решений. |
г)
О т в е т: х ≤ |
3. Решить № 4.8 (в; г). Двое учащихся самостоятельно решают на доске, остальные в тетрадях. Учитель при необходимости помогает в решении.
|
в)
О т в е т: нет решений. |
г)
О т в е т: – 5 < х ≤ – 1 или (– 5; – 1]. |
4. Решить № 4.21 (б) на доске и в тетрадях.
б) 
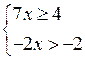
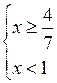

О т в е т: ![]()
5. Решить № 4.22 (в; г).
Сначала решение объясняет учитель, затем несложную систему неравенств решают учащиеся самостоятельно.
|
в) |
г)
О т в е т: 1 < х < 15. |
|
|
О т в е т: х ≥ |
|
|
IV. Итоги урока.
1. Что называется системой неравенств? Решением системы неравенств?
2. Что значит решить систему неравенств?
Домашнее задание: изучить материал учебника на с. 28–33; решить № 4.6 (а; б); № 4.7 (а; б), № 4.8 (а; б), № 4.21 (а); № 4.22(а; б), № 16 (на с. 7).
У р о к 2
Цели: способствовать развитию навыков решения систем неравенств; учить находить общее решение системы неравенств; научить решать систему, содержащую квадратные неравенства; повторить метод интервалов.
Ход урока
I. Анализ домашней контрольной работы.
1. Указать ошибки, допущенные в работе.
2. Решить на доске задания, вызвавшие затруднения у учащихся.
II. Выполнение упражнений.
1. Вспомнить формулу разложения квадратного трехчлена на множители.
2. Повторить, в чем заключается метод интервалов при решении квадратных неравенств.
3. Решить № 4.9 (г). Решение объясняет учитель.
г) 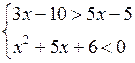
1) Решим неравенство 3х – 10 > 5х –
5; 3х – 5х > – 5 + 10; – 2х > 5;
х < – 2,5.
2) Решим неравенство х2 + 5х + 6 < 0; х2 + 5х + 6 = 0; D =
1; х1 = – 3;
х2 = – 2; тогда (х
+ 3)(х + 2) < 0.
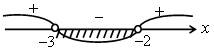
Имеем – 3 < х < – 2.
3) Найдем решение системы неравенств 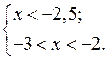
![]() О т в е
т: – 3 < х < – 2,5.
О т в е
т: – 3 < х < – 2,5.
4. Решить № 4.9 (в) самостоятельно с проверкой.
О т в е т: нет решений.
5. Решить № 4.10 (г). Объясняет учитель. Предварительно повторить теорему о квадратном трехчлене с отрицательным дискриминантом.
г) 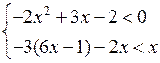
1) Решим неравенство – 2х2 + 3х – 2 < 0; – 2х2 + 3х – 2 = 0; D = 9 – 16 = = – 7 < 0. По теореме неравенство верно при любых значениях х.
2) Решим неравенство –3(6х – 1) – 2х
< х; – 18х + 3 – 2х < х; – 20х – х
< < – 3; – 21х <– 3; х > ![]() Решение данной системы неравенств х
>
Решение данной системы неравенств х
> ![]()
О т в е т: х > ![]()
6. Решить № 4.10 (в) на доске и в тетрадях.
в) 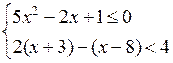
Решим неравенство 5х2 – 2х + 1 ≤ 0. 5х2–2х + 1 = 0; D = 4 – 20 = –16 < 0.
По теореме неравенство не имеет решений, а это значит, что данная система не имеет решений.
О т в е т: нет решений.
7. Решить № 4.11 (в) самостоятельно. Один учащийся решает на доске, другие в тетрадях, потом проверяется решение.
в) 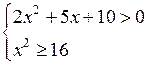
1) Решим неравенство 2х2 + 5х + 10 > 0. 2х2 + 5х + 10 = 0; D = –55 < 0.
По теореме неравенство верно при всех значениях х.
2) Решим неравенство х2 ≥ 16; х2 – 16 ≥ 0; (х – 4)(х + 4) ≥
0; х = 4;
х = – 4.
![]()
Решение х ≤ –4 и х ≥ 4.
3) Решение системы неравенств 
О т в е т: х ≤ – 4; х ≥ 4.
8. Решить № 4.32 (б) на доске и в тетрадях.
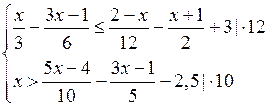

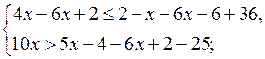
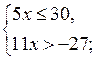
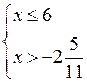
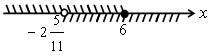
Решение ![]()
Наименьшее целое число равно –2; наибольшее целое число равно 6.
О т в е т: –2; 6.
9. Повторение ранее изученного материала.
1) Решить № 4.11 (а; б) на с. 12 устно.
2) Решить № 4.12 (б), построив графики функций (с. 12).
б) ![]()
Строим графики функций ![]() и y = –1 – x.
и y = –1 – x.
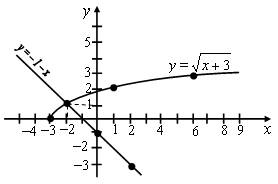
О т в е т: –2.
III. Итоги урока.
1. В курсе алгебры 9 класса мы будем рассматривать только системы из двух неравенств.
2. Если в системе из нескольких неравенств с одной переменной одно неравенство не имеет решений, то и система не имеет решений.
3. Если в системе из двух неравенств с одной переменной одно неравенство выполняется при любых значениях переменной, то решением системы служит решение второго неравенства системы.
Домашнее задание: рассмотреть по учебнику решение примеров 4 и 5 на с. 44–47 и записать решение в тетрадь; решить № 4.9 (а; б), № 4.10 (а; б), № 4.11 (а; б), № 4.32 (а).
У р о к 3
Цели: закрепить навыки решения неравенств и систем неравенств; учить решать более сложные системы неравенств; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Двое учащихся работают на доске, решая № 4.10 (б) и № 4.11 (б) из домашнего задания.
2. С остальными учащимися устно решить № 4.1 (в), № 4.2 (а) и № 4.5 (а; б).
II. Решение более сложных систем неравенств.
1. Решить № 4.12 (в; г) на доске и в тетрадях.
|
в) |
г) |
|
1) х = 5; х = – 5; х = 0
Решение – 5 ≤ х < 0; х ≥ 5. 2) 5х – 10 ≥ 35 5х ≥ 45 х ≥ 9 3)
О т в е т: [9; + ∞) или х ≥ 9. |
1) Отметим точки х = 2, х = – 3, х = 0, х = – 7
Решение –7 < х < –3 и 0 < х < 2. 2) 20х ≥ 20 х ≥ 1 3)
О т в е т: 1 ≤ х < 2 или [1; 2). |
2. Решить № 4.13 (в; г). Двое учащихся самостоятельно решают на доске, остальные в тетрадях, затем проверяется решение.
|
в) 1) х2 – 6х + 8 < 0 (х – 4)(х – 2) < 0
Решение 2 < х < 4 2) х2 – 36 ≥ 0 (х – 6)(х + 6) ≥ 0
Решение х ≤ – 6; х ≥ 6 3)
О т в е т: нет решений. |
г) 1) 49х2 – 1 < 0 (7х – 1)(7х + 1) < 0 7(х – (х –
Решение – 2) х2 + 5х + 6 ≥ 0 (х + 2)(х + 3) ≥ 0
Решение х ≤ – 3 и х ≥ – 2 |
|
|
3)
О т в е т: – |
3. Решить № 4.20 (б; в).
|
б) Функция определена, если
О т в е т: – 4 ≤ х ≤ 5. |
в) Областью определения являются все значения х, для которых выполняется условие
О т в е т: 2 ≤ х ≤ 4. |
4. Решить № 4.24 (в; г). Решение одной системы объясняет учитель.
в) 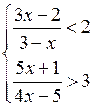
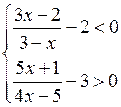
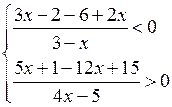
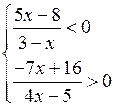
1) 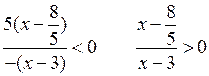
Решение
х < ![]() х
> 3
х
> 3 
2) 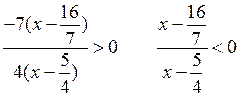

Решение ![]() < х <
< х < ![]()
3) 
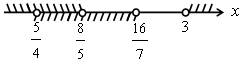
О т в е т: ![]() < х <
< х < ![]()
5. Решить № 4.33 (в; г) на доске и в тетрадях.
в) 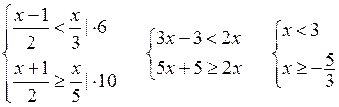
Решение системы ![]()
О т в е т: целые числа –1; 0; 1; 2.
г) 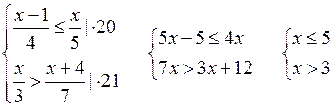
Решение системы 3 < х ≤ 5.
О т в е т: целые числа 4; 5.
6. Решить № 4.27* (в). Учитель объясняет решение.
в) 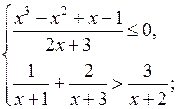
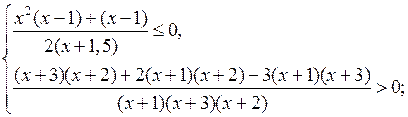


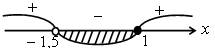
![]()
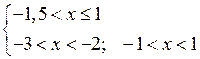
![]()
О т в е т: – 1 < х < 1.
III. Итоги урока. Выставление отметок.
Домашнее задание: решить № 4.12 (а; б), № 4.13 (а; б), № 4.20 (а; г), № 4.24 (а; б), № 4.33 (а; б).
У р о к 4
Цели: упражнять учащихся в решении двойных неравенств и нахождении области определения выражения; научить решать системы неравенств, содержащих модули; развивать логическое мышление учащихся.
Ход урока
I. Проверка домашнего задания.
1. Проверить выборочно у нескольких учащихся выполнение ими домашнего задания.
2. Решить на доске задания, вызвавшие затруднения у учащихся.
3. Устно решить № 4.2 (б) и № 4.1 (г).
II. Объяснение нового материала.
1. Двойное неравенство можно решить двумя способами:
а) сведением к системе двух неравенств;
б) без системы неравенств с помощью преобразований.
2. Решить двойное неравенство № 4.15 (в) двумя способами.
I с п о с о б 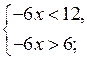
 Решение – 2 < х <
– 1.
Решение – 2 < х <
– 1.
II с п о с о б 6 < – 6х < 12 | : (– 6)
– 1 > х > – 2, тогда – 2 < х < – 1.
О т в е т: (– 2; – 1).
3. Решить № 4.16 (б; в).
I с п о с о б
б) – 2 ≤ 1 – 2х ≤ 2. Решим систему неравенств:
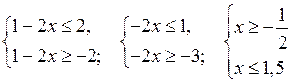 О т в е т:
О т в е т: ![]()
II с п о с о б
– 2 ≤ 1 – 2х ≤ 2; прибавим к
каждой части неравенства число (– 1), получим – 3 ≤ – 2х ≤
1; разделим на (– 2), тогда ![]()
в) – 3 < ![]() < 1. Умножим каждую часть неравенства
на 2, получим – 6 < 5х + 2 < 2. Решим систему неравенств:
< 1. Умножим каждую часть неравенства
на 2, получим – 6 < 5х + 2 < 2. Решим систему неравенств:

О т в е т: – 1,6 < х < 0.
III. Выполнение упражнений.
1. Решить № 4.18 (б) и № 4.19 (б) на доске и в тетрадях.
2. Решить № 4.14 (в) методом интервалов.
в) 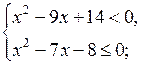
1) х2 – 9х + 14 < 0; (х – 7)(х – 2) < 0; х = 7; х = 2
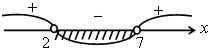
Решение 2 < х < 7.
2) х2 – 7х – 8 ≤ 0; (х – 8)(х + 1) ≤ 0; х = 8; х = – 1
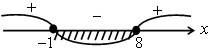
Решение – 1 ≤ х ≤ 8.
3) 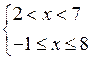
![]()
О т в е т: 2 < х < 7.
4) Решить № 4.28 (в) самостоятельно с проверкой.
в) ![]() Решим систему неравенств
Решим систему неравенств
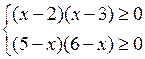
1) (х – 2)(х – 3) ≥ 0; х = 2; х = 3
![]()
Решение х ≤ 2 и х ≥ 3.
2) (5 – х)(6 – х) ≥ 0; – 1(х – 5) · (– 1)(х – 6) ≥ 0; (х – 5)(х – 6) ≥ 0
х = 5; х = 6
![]()
Решение х ≤ 5 и х ≥ 6.
3) 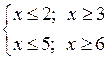
![]()
О т в е т: х ≤ 2, 3 ≤ х ≤ 5, х ≥ 6.
5. Решение систем неравенств, содержащих переменную под знаком модуля.
Решить № 4.34 (в; г). Учитель объясняет решение № 4.34 (в).
в) 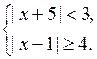
1) | х + 5 | < 3
![]()
Решение – 8 < х < – 2.
2) | х – 1 | ≥ 4
![]()
Решение х ≤ – 3 и х ≥ 5.
3) 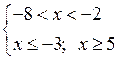
![]()
О т в е т: – 8 < х ≤ 3.
г) 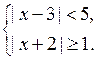
1) | х – 3 | < 5;
![]()
Решение – 2 < х < 8.
2) | х + 2 | ≥ 1
![]()
Решение х ≤ – 3 и х ≥ – 1.
3) 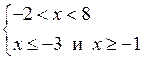
![]()
О т в е т: –1 ≤ х < 8.
6. Решить № 4.31 (б). Учащиеся решают самостоятельно. Один ученик решает на доске, остальные в тетрадях, затем проверяется решение.
б) 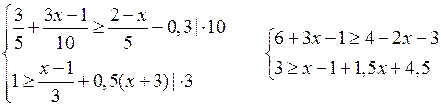
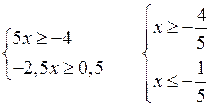
Решение ![]() Середина промежутка
Середина промежутка ![]()
О т в е т: ![]()
7. Решить № 4.38 (а; б). Учитель на доске с помощью числовой прямой показывает решение данного упражнения, привлекая к рассуждениям учащихся.
О т в е т: а) р < 3; р ≥ 3; б) р ≤ 7; р > 7.
8. Повторение ранее изученного материала.
Решить № 2.33.
Пусть первоначальная скорость велосипедиста х км/ч, после уменьшения стала (х – 3) км/ч.
![]()
15x – 45 + 6x = 1,5x(x – 3);
21x – 45 = 1,5x2 – 4,5x;
1,5x2 – 25,5x + 45 = 0 | : 1,5; тогда х2 – 17х + 30 = 0; D = 169;
х1 = 15; х2 = 2 не удовлетворяет смыслу задачи.
О т в е т: 15 км/ч; 12 км/ч.
IV. Итоги урока. Выставление отметок.
Домашнее задание: выполнить на отдельных листочках домашнюю контрольную работу № 1 с № 7 по № 10 на с. 32–33 и еще № 4.34 (а; б), № 4.35 (а; б).
Подготовка к контрольной работе
Цели: обобщить и систематизировать изученный материал; подготовить учащихся к контрольной работе.
Ход урока
I. Повторение изученного материала.
1. Собрать листочки с выполненной домашней контрольной работой.
2. Какие правила применяют при решении неравенств? Объясните решение неравенств:
а) 3х – 8 < х + 2; б) 7(х – 1) ≥ 9х + 3.
3. Сформулируйте теорему для квадратного трехчлена с отрицательным дискриминантом. Устно решите неравенства:
а) х2 + 2х + 11 > 0; б) – 2х2 + х – 5 > 0; в) 3х2 – х + 4 ≤ 0.
4. Сформулируйте определение системы неравенств с двумя переменными. Что значит решить систему неравенств?
5. В чем заключается метод интервалов, активно используемый при решении рациональных неравенств? Объясните это на примере решения неравенства:
а) (2x – 4)(3 – x) ≥ 0;
б) 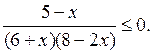
II. Тренировочные упражнения.
1. Решить неравенство:
а) 12(1 – х) ≥ 5х – (8х + 2); б) – 3х2 + 17х + 6 < 0;
в) 
2. Найдите область определения выражения.
|
а) f(х) = 12 + 4х – х2 ≥ 0; – х2 + 4х + 12 ≥ 0 | · (– 1); х2 – 4х – 12 ≤ 0; D = 64; х1 = 6; х2 = – 2; (х – 6)(х + 2) ≤ 0
О т в е т: – 2 ≤ х ≤ 6 или [– 2; 6]. |
б) f(х) = х2 + 2х + 14 ≥ 0; D < 0. По теореме о квадратном трехчлене с отрицательным дискриминантом имеем х – любое число. О т в е т: множество решений или (– ∞; ∞). |
3. Решите двойное неравенство и укажите,
если возможно, наибольшее и наименьшее целое решение неравенства ![]()
Р е ш е н и е
Умножим каждую часть неравенства на 5, получим 0 – 5 < 3 – 8х ≤ 15; – 8 < – 8х ≤ 12; – 1,5 ≤ х < 1.
Наибольшее целое число 0, наименьшее целое число (– 1).
О т в е т: 0; – 1.
4. Решить № 76 (б) на доске и в тетрадях.
б) 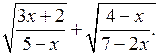
Р е ш е н и е
Для нахождения области определения выражения решим
систему неравенств 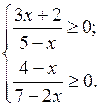
1) 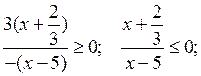 х =
х = ![]() х = 5.
х = 5.
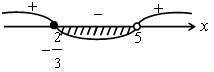
Решение ![]() ≤ х < 5.
≤ х < 5.
2) 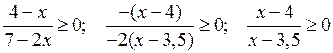

Решение х < 3,5 и х ≥ 4.
3) 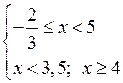

О т в е т: ![]() ≤ х < 3,5 и 4 ≤ х
< 5.
≤ х < 3,5 и 4 ≤ х
< 5.
5. Найти область определения выражения.
а) f(х) = 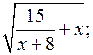 б) f(х) =
б) f(х) = 
а) 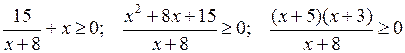
![]()
О т в е т: – 8 < х ≤ – 5; х ≥ – 3.
б) 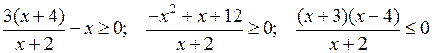
![]()
О т в е т: х ≤ – 3; – 2 < х ≤ 4.
6. Решить систему неравенств (самостоятельно).
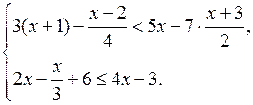
Р е ш е н и е
Выполнив преобразования каждого из неравенств системы, получим:
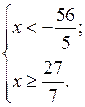
О т в е т: нет решений.
7. Решить № 4.40*. Решение объясняет учитель.
Если р = 2, то неравенство примет вид 2х + 4 > 0, х > – 2. Это не соответствует ни заданию а), ни заданию б).
Значит, можно считать, что р ≠ 2, то есть заданное неравенство является квадратным.
а) Квадратное неравенство вида ах2 + bх + с > 0 не имеет решений, если а < 0, D < 0. Имеем D = (р – 4)2 – 4(р – 2)(3р – 2) = – 11р2 + 24р. Значит, задача сводится к решению системы неравенств
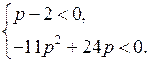
Решив эту систему, получим р < 0.
б) Квадратное неравенство вида ах2 + bх + с > 0
выполняется при любых значениях х, если а > 0 и D <
0. Значит, задача сводится к решению системы неравенств 
Решив эту систему, получим р > ![]()
III. Итоги урока.
Необходимо дома просмотреть весь изученный материал и подготовиться к контрольной работе.
Домашнее задание: решить № 1.21 (б; г), № 2.15 (в; г); № 4.14 (г), № 4.28 (г); № 4.19 (а), № 4.33 (г).
Основные понятия
(3 ч)
У р о к 1
Цели: повторить определенные представления о
системах уравнений, имеющиеся у учащихся, уточнить их; ввести определение
рационального уравнения с двумя переменными и определение решения
уравнения
р(х; у) = 0; научить строить график уравнения.
Ход урока
I. Анализ контрольной работы.
1. Указать основные ошибки, допущенные учащимися в ходе выполнения работы.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Изучение нового материала.
1. Разобрать решение примера 1 на с. 49–50 учебника.
2. Ввести определение 1 рационального уравнения с двумя переменными х, у.
3. Решить № 5.1 устно.
4. Ввести определение 2 решения уравнения р(х; у) = 0.
5. Решить № 5.2 устно.
6. Ввести понятие равносильности уравнений (определение 3).
7. При решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения.
8. Два основных равносильных преобразования:
1) Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.
2) Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число или выражение.
9. Неравносильными преобразованиями уравнения являются:
1) Освобождение от знаменателей, содержащих переменные.
2) Возведение обеих частей уравнения в квадрат.
10. Иногда удается перейти к геометрической (графической) модели уравнения с двумя переменными, то есть построить график уравнения.
11. Рассмотреть по учебнику на с. 57 решение примеров 8 и 9 (рисунки 53 и 54).
III. Закрепление изученного материала.
1. Решить № 5.4 (а; б) на доске и в тетрадях.
а) 2х + 3у = 6; 3у = 6
– 2х; у = ![]()
б) 4х – 5у = 20; 5у = 4х
– 20; у = ![]()
2. Решить № 5.5 (в; г).
в) у + 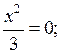 у =
у = 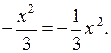
Графиком является парабола с вершиной в начале координат. Ветви параболы опущены вниз.
г) ![]() при х ≠ 0.
при х ≠ 0.
Графиком уравнения является гипербола, расположенная в I и III координатных четвертях.
3. Решить № 5.28 (а; б). Учитель объясняет решение № 5.28 (б).
а) (3х + у + 9)(5х + у – 5) = 0.
3х + у + 9 = 0 или 5х + у – 5 = 0
у = – 3х – 9 или у = – 5х + 5.
Строим в одной системе координат две прямые.
б) (2х – 5у – 10)(7х – 3у – 21) = 0.
2х – 5у – 10 = 0 или 7х – 3у – 21 = 0.
5у = 2х – 10 или 3у = 7х – 21
у = ![]() или
или ![]()
Строим две прямые.
4. Повторение ранее изученного материала.
Решить № 24 (а; в) на с. 8 задачника.
Повторить решение системы уравнений способом сложения.
а) 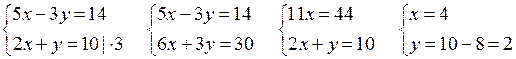
О т в е т: (4; 2).
в) 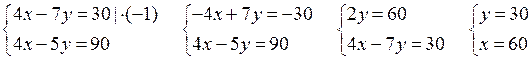
О т в е т: (60; 30).
IV. Итоги урока. Выставление отметок.
Домашнее задание: изучить материал на с. 50–57 учебника; решить № 5.4 (в; г); № 5.5 (а; б), № 5.28 (в; г) и № 24 (б; г) на с. 8.
У р о к 2
Цели: изучить теорему о графике уравнения – окружности; научить строить окружности и записывать уравнение окружности по координатам центра и радиусу; в ходе упражнений закрепить полученные знания.
Ход урока
I. Устная работа.
1. Сформулируйте определение рационального уравнения с двумя переменными. Приведите примеры.
2. Что называется решением уравнения р(х; у) = 0?
3. Устно решить № 5.2 (а; б).
4. Какие уравнения называются равносильными? Сформулируйте два основных равносильных преобразования.
II. Объяснение нового материала.
1. Записать в тетрадях теорему:
«Графиком уравнения (х – а)2 + (у – b)2 = r2 является окружность с центром в точке (а; b) и радиусом r». (Рис. 36.)
2. Частный случай теоремы:
Если а = 0, b = 0, то х2 + у2 = r2. Графиком этого уравнения является окружность с центром в начале координат и радиусом r, где r – положительное число.
3. Рассмотреть решение примера 10 (рис. 57) на с. 59 учебника.
4. Работа по учебнику: на с. 60 изучить таблицу аналитической, геометрической и словесной модели окружности.
III. Закрепление изученного материала.
1. Решить № 5.6 (в; г). Построить графики окружностей на доске и в тетрадях:
в) х2 + у2 = 4. Центр О (0; 0), радиус r = 2.
г) х2 + у2 = 1. Центр окружности О (0; 0), радиус r = 1.
2. Решить № 5.7 (в; г) с комментированием на месте.
в) (х – 10)2 + (у + 1)2 =
17. Центр в точке А (10; – 1) и радиус ![]()
г) (х – 4)2 + (у – 5)2 = 144. Центр в точке В (4; 5) и радиус 12.
3. Решить № 5.8 (в; г).
в) (х – 4)2 + (у – 1)2 = 9. Построим окружность с центром в точке В (4; 1) и радиусом 3.
г) (х + 1)2 + (у – 3)2 = 4. Строим окружность с центром D (– 1; 3) и радиусом 2.
4. Решить № 5.10, записывая решение только на доске, а ученики устно дают о т в е т:
а) х2 + у2 = 25;
б) х2 +
у2 = ![]()
в) х2 +
у2 = ![]()
г) х2 + у2 = 1.
5. Решить № 5.11 (в; г) на доске и в тетрадях.
(х – а)2 + (у – b)2 = r2 уравнение окружности.
в) (х – 0)2 + (у + 10)2 = 72; х2 + (у + 10)2 = 49;
г) (х + 5)2 + (у + 2)2 = 42; (х + 5)2 + (у + 2)2 = 16.
6. Решить № 5.12 (устно) по рис. 1; 2; 3; 4 на с. 35–36 задачника.
7. Решить № 5.13 (в; г) по рис. 7 и рис. 8 на с. 36, записывая в тетради координаты центра окружности, ее радиус, а затем уравнение окружности.
в) Центр в точке А (1; 4), радиус окружности r
= 2; тогда (х – 1)2 +
(у –
– 4)2 = 4.
г) Центр окружности В (–3; – 2), радиус равен 1; уравнение окружности (х + 3)2 + (у + 2)2 = 1.
8. Решить № 5.14 (а; б), используя рис. 9 и рис. 10 на с. 37 задачника.
а) Центр окружности М (0; –2) и радиус r
= 2; уравнение окружности
х2 + (у + 2)2 = 4.
б) Центр окружности D (–3; 0) и радиус r = 3, тогда (х + 3)2 + у2 = 9.
9. Повторение ранее изученного материала.
1) Решить № 25 (а; б) на с. 8, вызывая по одному учащемуся к доске.
а) 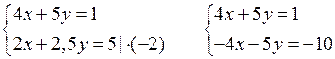
0 · х + 0 · у = – 9
О т в е т: нет решений.
б) 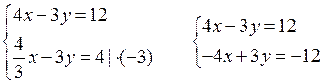
0 · х + 0 · у = 0 верно при любом значении х.
О т в е т: бесконечное множество решений.
2) Решить задачу № 46 на с. 10.
Пусть х м ткани требуется на одно платье, у м ткани на один сарафан.

О т в е т: 3 м и 2 м.
IV. Итоги урока.
1. Записать уравнение окружности с центром в начале координат.
2. Записать уравнение окружности в общем виде.
Домашнее задание: разобрать по учебнику решение примера 11 на с. 59 и записать решение в тетрадь; решить № 5.6 (а; б); № 5.7 (а; б), № 5.8 (а; б); № 5.11 (а; б), № 5.13 (а; б), № 5.14 (в; г).
У р о к 3
Цели: ввести определение системы уравнений, ее решения; показать графический метод решения системы уравнений; упражнять учащихся в построении графиков функций; способствовать выработке навыка построения графиков функций.
Ход урока
I. Проверка усвоения изученного материала.
1. Решить устно № 5.2 (в; г).
2. Найдите координаты центра и радиус окружности (устно):
а) (х – 7)2 + (у + 4)2 = 16; в) (х + 5)2 + у2 = 7;
б) х2 + (у – 9)2 = 100; г) х2 + у2 = 13.
3. Назовите уравнение окружности с центром в точке О (0; 0) и радиусом:
а) 8; б) ![]() в)
в) ![]() г) 1.
г) 1.
4. Изобразив схематически графики уравнений на доске, решить № 5.9 (в; г).
5. Проверить домашнее задание № 5.13 (а; б) и № 5.14 (в; г).
II. Работа по учебнику.
1. Ввести определение 4 системы уравнений 
2. Определение решения системы уравнений.
3. Решить систему уравнений – это значит найти все ее решения или установить, что решений нет.
4. Устно решить № 5.16 (а; б) и № 5.17.
5. Иногда удается решить систему уравнений графическим методом: надо построить графики каждого из уравнений, найти точки пересечения графиков; координаты каждой точки пересечения служат решением системы уравнений.
6. Рассмотреть по учебнику решение примеров 12 и 13 на с. 62–63 (рис. 60 и рис. 61).
III. Решение систем уравнений графическим способом.
1. Решить № 5.18 (в; г) на доске и в тетрадях.
в) 
О т в е т: (3; 6); (– 3; 6).
г) 
Строим параболу у = х2 – 4 и прямую у = – 2х – 1 и находим координаты их точек пересечения.
О т в е т: (1; – 3); (– 3; 5).
2. Решить № 5.19 (г). Строим гиперболу ху
= 6, то у = ![]() при
х ≠ 0 и прямую 3х – 2у = 0, у =
при
х ≠ 0 и прямую 3х – 2у = 0, у = ![]() и находим координаты
точек пересечения графиков функций.
и находим координаты
точек пересечения графиков функций.
О т в е т: (2; 3); (– 2; – 3).
3. Решить № 5.20 (г), построив окружность
(х + 2)2 + (у –
2)2 = 1 с центром D (–
2; 2) и радиусом 1 и кривую у = ![]() при х ≥ – 1.
при х ≥ – 1.
Графики не пересекаются, значит, решений нет.
О т в е т: 0.
4. Решить № 5.21 (в; г), вызвав сразу двух учащихся к доске, остальные решают самостоятельно.
в) г)
О т в е т: (0; – 1); (6; – 1). О т в е т: (2; 2).
5. Решить № 5.34 (а) самостоятельно. О т в е т: (0; 0); (1; 1).
№ 5.34 (б) на доске и в тетрадях. О т в е т: (0; 2).
6. Решить задание на доске и в тетрадях.
а) 1) (х – 2)2 + (у – 3)2 = 4.
Строим окружность с центром (2; 3) и радиусом 2.
2) 2у = 6 – 2х; у = ![]() – прямая.
– прямая.
О т в е т: (0; 3); (2; 1).
7. Решить № 5.35 (а; б). Решение объясняет учитель.
а) 
О т в е т: (– 1; 1); (1; 1).
б) 
О т в е т: (– 1; 0); (0; – 1); (1; 0).
IV. Итоги урока.
Прочитать по учебнику на с. 46 рубрику «Обратите внимание».
Домашнее задание: решить на отдельных листочках домашнюю контрольную № 2 на с. 53–56 номера 1, 2 и 3 и к ним еще по вариантам решить № 5.21 (а; б), № 5.28 (а; б), № 5.35 (в; г).
Методы решения систем уравнений
(5 ч)
У р о к 1
Цели: повторить алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х и у, применяемый в седьмом классе; научить применять метод подстановки при решении систем, содержащих уравнение второй степени; развивать логическое мышление учащихся.
Ход урока
I. Повторение ранее изученного материала.
1. Вспомнить способы решения систем уравнений с двумя переменными:
а) Графический способ – решить № 5.34 (г).
О т в е т: нет решений.
б) Способ сложения – решить систему уравнений 
О т в е т: (11; – 9).
в) Способ подстановки – решить систему уравнений

О т в е т: (3; – 1).
2. Уточнить, в чем состоит способ подстановки при решении систем уравнений.
(Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными прочитать на с. 47 учебника.)
II. Изучение нового материала.
1. Разобрать решение примера 1 на с. 69 учебника.
2. Решение способом подстановки системы уравнений (объясняет учитель): № 6.1 (в).
в) 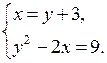
1) Подставим выражение х = у + 3 во второе уравнение вместо х:
у2 – 2(у + 3) = 9.
2) Решим полученное уравнение у2 – 2у – 6 – 9 = 0, у2 – 2у – 15 = 0;
у1 = 5; у2 = – 3.
3) Подставим поочередно каждое из найденных значений
у в формулу
х = у + 3.
Если у = 5, то х = 5 + 3 = 8; если у = – 3, то х = – 3 + 3 = 0.
О т в е т: (8; 5); (0; – 3).
3. Учитель объясняет решение № 6.3 (в).
в) 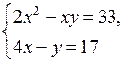
1) 4х – у = 17; у = 4х – 17;
2) 2х2 – х(4х – 17) = 33;
2х2 – 4х2 + 17х – 33 = 0;
– 2х2 + 17х – 33 = 0;
2х2 – 17х + 33 = 0;
D = 289 – 264 = 25;
х1 = ![]() х2 =
х2 = ![]()
3) Если х = 3, то у = 4 · 3 – 17 = – 5;
Если х = 5,5, то у = 4 · 5,5 – 17 = 5.
О т в е т: (3; – 5); (5,5; 5).
III. Выполнение упражнений.
1. Решить № 6.2 (б; г) на доске и в тетрадях.
б) 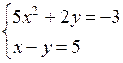
1) х – у = 5; у = х – 5
2) 5х2 + 2(х – 5) = – 3; 5х2 + 2х – 10 + 3 = 0;
5х2 + 2х – 7 = 0;
D = 144; х1 = – 1,4; х2 = 1.
3) Если х = – 1,4, то у = – 1,4 – 5 = – 6,4;
Если х = 1, то у = 1 – 5 = – 4.
О т в е т: (– 1,4; – 6,4); (1; – 4).
г) 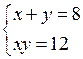
1) х + у = 8; х = 8 – у
2) (8 – у)у = 12; – у2 + 8у – 12 = 0; у2 – 8у + 12 = 0
у1 = 6; у2 = 2.
3) Если у = 6, то х = 8 – 6 = 2; если у = 2, то х = 8 – 2 = 6.
О т в е т: (2; 6); (6; 2).
2. Решить № 6.5 (г). Решение объясняет учитель.
г) 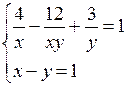
Преобразуем первое уравнение:
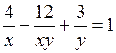
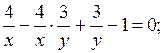 применим способ группировки:
применим способ группировки:

 или
или ![]()
![]() или
или ![]()
у = 3 х = 4.
Значения х = 4 и у = 3 являются решениями уравнения х – у = 1.
О т в е т: (4; 3).
3. Решить № 6.5 (в).
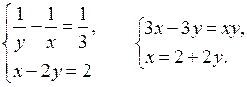
Решим уравнение 3(2 + 2у) – 3у = (2 + 2у) · у;
6 + 6у – 3у = 2у + 2у2; 2у2 – у – 6 = 0; D = 49; у1 = – 1,5; у2 = 2.
Если у = – 1,5, то х = 2 + 2 · (– 1,5) = – 1;
если у = 2, то х = 2 + 2 · 2 = 6.
О т в е т: (6; 2); (– 1; – 1,5).
4. Повторение пройденного материала.
Решить № 5.29* (а). Построить график уравнения х2 + у2 + 8х = 0. Воспользуемся методом
выделения полного квадрата. Имеем х2 + у2 +
8х =
= (х2 + 8х +
16) + у2 – 16 = (х
+ 4)2 + у2 – 16. Значит, заданное уравнение
можно переписать в виде (х + 4)2 + у2 =
16. Это – уравнение окружности с центром в точке (– 4; 0) и радиусом 4.
IV. Итоги урока.
Повторить алгоритм решения системы уравнений способом подстановки.
Домашнее задание: решить № 6.1 (а; б), № 6.2 (а), № 6.3 (а; б), № 6.5 (а; б).
У р о к 2
Цели: повторить способ алгебраического сложения, известный учащимся из седьмого класса; научить применять этот способ при решении систем уравнений второй степени; закрепить знание решения систем уравнений второй степени способом подстановки.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Решить на доске задания, вызвавшие затруднения у учащихся в домашней работе.
2. Решите № 6.6 (а; б) устно. Расскажите, в чем состоит метод алгебраического сложения.
3. Решить № 6.7 (а; б) на доске и в тетрадях методом алгебраического сложения; № 6.7 (в) решить самостоятельно.
|
а)
О т в е т: (– |
б) О т в е т: (– 0,5; 1). |
в) О т в е т: ( |
II. Объяснение нового материала.
1. Если система уравнений состоит из двух уравнений второй степени с двумя переменными, то найти ее решения обычно бывает трудно. В отдельных случаях такие системы удается решить, используя способ сложения.
2. Решение № 6.8 (в) объясняет учитель.
в) 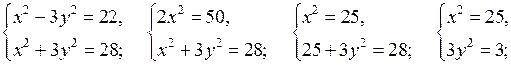
 или
или 
Отсюда 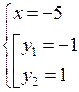 или
или 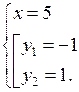
О т в е т: (– 5; – 1); (– 5; 1); (5; – 1); (5; 1).
3. Решение системы объясняет учитель:
а) 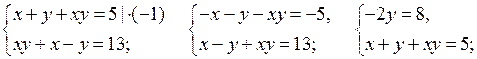
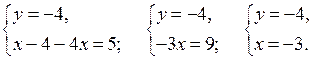
О т в е т: (– 3; – 4).
б) № 6.17 (б). 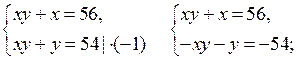

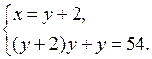
Решим уравнение у2 + 3у – 54 = 0; у1 = – 9; у2 = 6.
 или
или 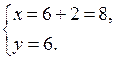
О т в е т: (– 7; – 9); (8; 6).
III. Закрепление изученного материала.
1. Решить № 6.8 (б) на доске и в тетрадях.
б) 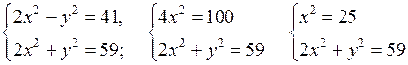
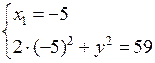 или
или 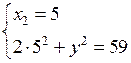
 или
или 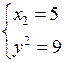
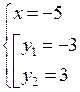 или
или 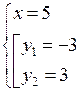
О т в е т: (– 5; – 3); (– 5; 3); (5; – 3); (5; 3).
2. Решить № 6.17 (в). Один ученик самостоятельно решает на доске, остальные в тетрадях. Учитель при необходимости помогает.
в) 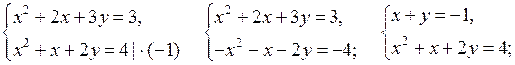
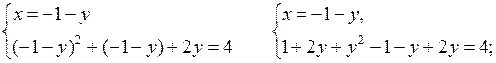
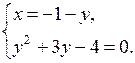
у2 + 3у – 4 = 0; у1 = – 4; у2 = 1.
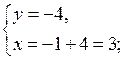 или
или 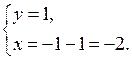
О т в е т: (3; – 4); (– 2; 1).
3. Повторение пройденного материала.
а) Решить № 6.4 (а) способом подстановки.
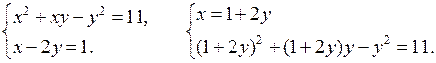
1 + 4у + 4у2 + у + 2у2 – у2 – 11 = 0;
5у2 + 5у – 10 = 0 | : 5;
у2 + у – 2 = 0; у1 = – 2; у2 = 1.
 и
и 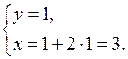
О т в е т: (– 3; – 2); (3; 1).
б) Решить № 5.37*. Решение объясняет учитель, привлекая учащихся к обсуждению решения.
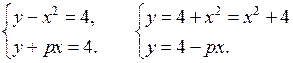
Графиком функции у = х2 + 4 является парабола с вершиной в точке (0; 4) и ветвями вверх; у = 4 – рх – прямая, проходящая через точку (0; 4).
Если прямая параллельна оси х (это будет при р = 0), то она касается параболы и имеет с ней лишь одну общую точку; это значит, что заданная система уравнений имеет одно решение. Если р ≠ 0, то прямая пересекает параболу в ее вершине и еще в одной точке, то есть заданная система имеет два решения.
О т в е т: р = 0.
IV. Итоги урока.
Домашнее задание: изучить решение примера 2 по учебнику на с. 69–70 и записать решение в тетрадь; решить № 6.7(в; г), № 6.8 (а; г), № 6.17 (г).
У р о к 3
Цели: показать способ решения систем уравнений методом введения новых переменных; научить решать системы уравнений методом введения новых переменных; закреплять способы подстановки и алгебраического сложения при решении систем уравнений.
Ход урока
I. Проверочная работа (10–15 мин).
В а р и а н т I
1. Решите систему уравнений:
а) 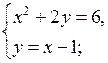 б)
б) 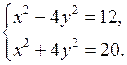
2. Решите графически систему уравнений 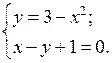
В а р и а н т II
1. Решите систему уравнений:
а) 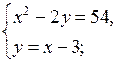 б)
б) 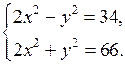
2. Решите графически систему уравнений 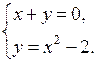
II. Изучение нового материала.
1. С методом введения новой переменной при решении рациональных уравнений с одной переменной мы познакомились в курсе алгебры 8 класса. Суть этого метода при решении систем уравнений та же самая. Метод введения новых переменных применяется при решении систем двух уравнений с двумя переменными одним из следующих способов:
1) вводится одна новая переменная только для одного уравнения системы;
2) вводятся две новые переменные сразу для обоих уравнений. Рассмотрим эти способы при решении систем уравнений.
2. Решение № 6.9 (в; г) объясняет учитель.
в) 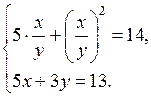
Введем новую переменную t = ![]() тогда 5t + t2 = 14; t2 + 5t – 14 = 0;
тогда 5t + t2 = 14; t2 + 5t – 14 = 0;
t1 = – 7; t2 = 2.
Значит, ![]() = – 7, х = – 7у; либо
= – 7, х = – 7у; либо ![]() = 2, х = 2у.
= 2, х = 2у.
Решим две системы уравнений:
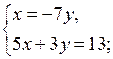
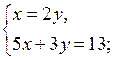

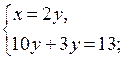
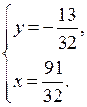
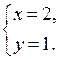
О т в е т: 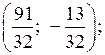 (2; 1).
(2; 1).
г) 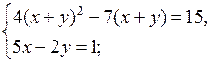
Обозначим х + у = t, тогда 4t2 – 7t – 15 = 0; D =
289; t1 = –![]() t2 = 3.
t2 = 3.
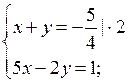 и
и 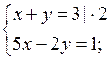
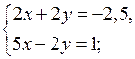
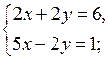
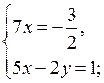
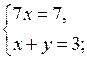
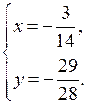

О т в е т: 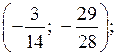 (1; 2).
(1; 2).
3. Решение № 6.10 (в; г) объясняет сначала учитель, а потом вызванные к доске ученики заканчивают решение.
в) 
Введем две новые переменные: а = х + у; b = ху. Решаем систему:
Решим уравнение ![]() D = 4; а1 =
D = 4; а1 = ![]() а2 = 4, тогда
а2 = 4, тогда
b1 = 5; b2 = 3.
Возвращаясь к переменным х и у, получаем две системы уравнений:
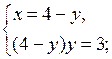
у2 – 2,4у + 5 = 0 у2 – 4у + 3 = 0; D = 4;
D < 0, нет корней. у1 = 3; у2 = 1. Тогда
 и
и 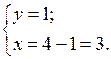
О т в е т: (1; 3); (3; 1).
г) 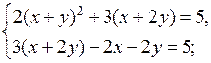
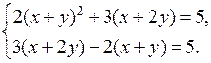
Обозначим х + у = а, х + 2у = b.
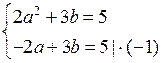
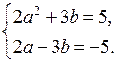
2а2 + 2а = 0,
2а(а + 1) = 0;
а = 0 или а = – 1.
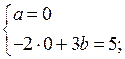

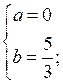
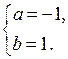
Возвращаясь к переменным х и у, получаем две системы уравнений:
1) 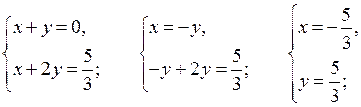
2) 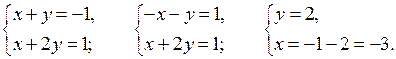
О т в е т: 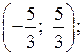 (– 3; 2).
(– 3; 2).
III. Итоги урока.
Домашнее задание: изучить по учебнику решение примера 3 на с. 71–72 и записать решение в тетрадь; решить № 6.9 (а; б) и № 6.10 (а; б).
У р о к 4
Цели: способствовать выработке у учащихся умений и навыков в решении систем уравнений различными способами; развивать логическое мышление учащихся.
Ход урока
I. Анализ проверочной работы.
1. Указать ошибки, сделанные учащимися в работе.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Выполнение упражнений.
1. Решим системы уравнений, используя разные методы:
№ 6.11 (в; г). Учитель объясняет решение в).
в) 
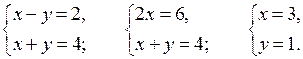
О т в е т: (3; 1).
г) 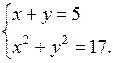
Учащиеся решают способом подстановки самостоятельно.
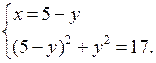
25 – 10у + у2 + у2 – 17 = 0;
2у2 – 10у + 8 = 0 | : 2
у2 – 5у + 4 = 0; у1 = 4; у2 = 1.
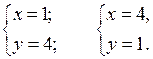
О т в е т: (1; 4); (4; 1).
2. Решение № 6.12 (а; г) объясняет сначала учитель, применяя для решения формулы сокращенного умножения а2 – b2 = (а – b) × (а + b) и (а + + b)2 = а2 + 2аb + b2, а потом решают вызванные к доске ученики.
а) 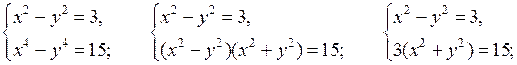
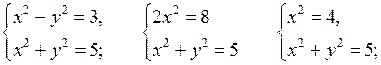
Отсюда  и
и 
Тогда 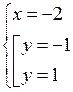 и
и 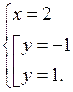
О т в е т: (– 2; – 1); (– 2; 1); (2; – 1); (2; 1).
г) 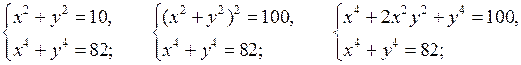

Решаем две системы уравнений:
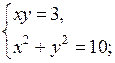 и
и 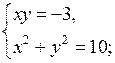
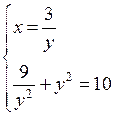 и
и 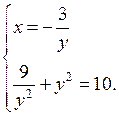
Решим уравнение:
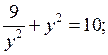
у4 – 10у2 + 9 = 0;
у2 = 9 и у2 = 1.
Если у2 = 9, то у = ± 3, тогда х = ± 1;
если у2 = 1, то у = ± 1, тогда х = ± 3.
О т в е т: (± 1; ± 3); (± 3; ± 1).
3. Решить № 6.13 (в). Учитель объясняет использование формулы (а + + b)2 = а2 + 2аb + b2 при решении данной системы.
в) 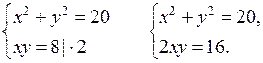
Сложим почленно оба уравнения, получим х2 + 2ху + у2 = 36, отсюда
(х + у)2 = 36,
значит, х + у = 6 или х + у = – 6.
Решаем две системы способом подстановки:
1) 
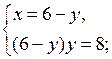
у2 – 6у + 8 = 0
у1 = 4; у2 = 2
 и
и 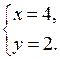
2) 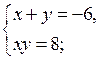
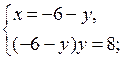
– у2 – 6у – 8 = 0
у2 + 6у + 8 = 0;
у1 = – 4; у2 = – 2
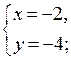
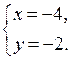
О т в е т: (2; 4); (4; 2); (– 2; – 4); (– 4; – 2).
4. Решить № 6.15 (б), вычитая из первого уравнения системы второе:
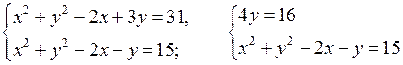

О т в е т: (3; 4); (– 1; 4).
5. Решить № 6.16 (г) методом введения новой переменной.
г) 
Обозначим ![]() тогда
тогда ![]()
![]() 4t2 – 17t + 4 = 0; D = 225; t1 =
4t2 – 17t + 4 = 0; D = 225; t1 = ![]() ; t2 = 4.
; t2 = 4.
Если t = ![]() , то
, то  отсюда у = 4х.
отсюда у = 4х.
Если t = 4, то 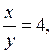 отсюда х = 4у.
отсюда х = 4у.
1) 
2) 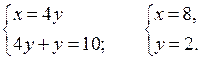
О т в е т: (2; 8); (8; 2).
6. Повторение ранее изученного материала.
Решить № 5.38.
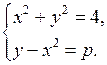
Графиком первого уравнения х2 + у2 = 4 является окружность с центром в начале координат и радиусом 2. Графиком у = х2 + р является парабола с ветвями вверх и вершиной в точке (0; р).
При р = 2 кривые имеют лишь одну общую, одно решение системы уравнений. При р = – 2 графики пересекаются в трех точках, система имеет три решения.
О т в е т: а) р = – 2; б) р = 2.
III. Итоги урока.
Какими способами можно решить систему двух уравнений?
Домашнее задание: выполнить на отдельных листочках домашнюю контрольную № 2 номера 4; 5; 6; 7 на страницах 54–55 задачника.
У р о к 5
Цели: закрепить и развить имеющиеся у учащихся навыки решения систем уравнений, научить решать более сложные системы уравнений различными способами.
Ход урока
I. Проверка домашнего задания.
1. Двое учащихся работают у доски по карточкам.
К а р т о ч к а № 1
1) Решите неравенство х2 – 6х > 0.
2) Изобразив схематически графики уравнений, определите, имеет ли решения
система уравнений и сколько: 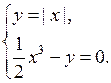
К а р т о ч к а № 2
1) Решите систему уравнений 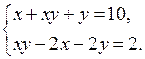
2) Решите неравенство х2 ≤ 4.
2. Учитель собирает листочки с домашней контрольной работой.
3. Решить № 6.6 (в; г) устно с остальными учащимися.
II. Решение систем уравнений.
1. Решить № 6.14 (в) способом подстановки.
в) 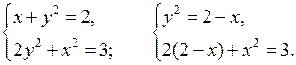
Решим уравнение 4 – 2х + х2 = 3, х2 – 2х + 1 = 0
(х – 1)2 = 0; х = 1. Тогда:
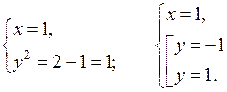
О т в е т: (1; – 1); (1; 1).
2. Решить № 6.14 (б) на доске и в тетрадях способом подстановки.
б) 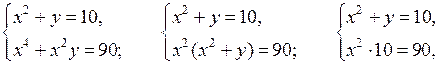
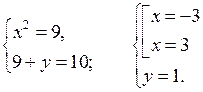
О т в е т: (– 3; 1); (3; 1).
3. Решить № 6.15 (в) методом алгебраического сложения.
в) 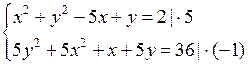

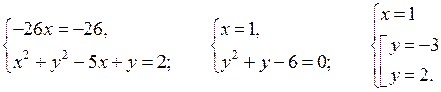
О т в е т: (1; – 3); (1; 2).
4. Решить № 6.16 (в) методом замены переменных.
в) 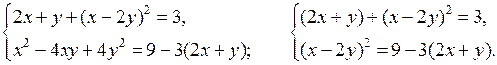
Обозначим 2х + у = а, х – 2у = b, тогда решаем систему


О т в е т: (1,2; 0,6).
5. Решить № 6.18 (б).
б) 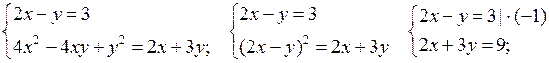
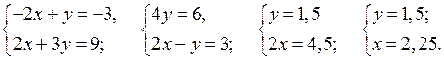
О т в е т: (2,25; 1,5).
6. Решить № 6.22 (а). Решение объясняет учитель.
а) 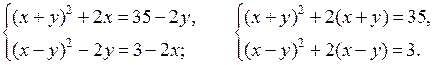
Обозначим х + у = а, х –
у = b, получим 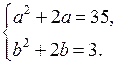
Из первого уравнения а2 + 2а – 35 = 0 находим а1 = 5; а2 = – 7.
Из второго уравнения b2 + 2b – 3 = 0 находим b1 = 1; b2 = – 3.
Решаем совокупность четырех систем уравнений:
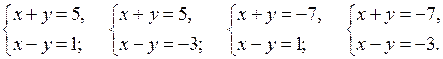
О т в е т: (3; 2); (1; 4); (– 3; – 4); (– 5; – 2).
7. Решить № 6.23 (а). Решение объясняет учитель.
а) Обозначим х2 – ху = а, у2 – ху = b, тогда
Возвращаясь к переменным х, у, решим систему:
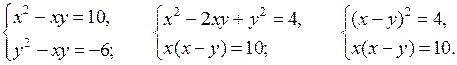
Решаем две системы уравнений.
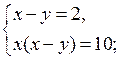 и
и 

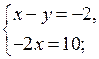
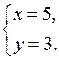
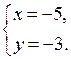
О т в е т: (5; 3); (– 5; – 3).
III. Итоги урока.
1. Записать в тетрадях определение равносильных систем: «Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений».
2. Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые мы рассмотрели, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.
Домашнее задание: рассмотреть по учебнику на с. 73–74 решение примера 4 и записать в тетрадь; решить № 6.15 (а; г), № 6.16 (а), № 6.18 (г).
Системы уравнений как математические
модели реальных ситуаций
(5 ч)
У р о к 1
Цели: показать способ решения задач с помощью составления систем уравнений второй степени; способствовать развитию навыков и умений при решении систем уравнений.
Ход урока
I. Повторение ранее изученного материала.
Решить задачу № 55 на с. 11 задачника.
Пусть скорость второго велосипедиста х км/ч,
тогда скорость первого (х + 3) км/ч. ![]() ч время движения второго велосипедиста,
ч время движения второго велосипедиста, ![]() ч время движения
первого велосипедиста.
ч время движения
первого велосипедиста. ![]() = 2.
= 2.
По смыслу задачи х > 0.
120(х + 3) – 120х = 2х(х + 3)
120х + 360 – 120х = 2х2 + 6х
2х2 + 6х – 360 = 0 | : 2
х2 + 3х – 180 = 0;
D = 729; х1 = 12; х2 = – 15 не удовлетворяет смыслу задачи.
О т в е т: 15 км/ч; 12 км/ч.
II. Объяснение нового материала.
1. При решении задач можно вводить две переменные и составлять систему уравнений.
2. Решим задачу № 7.1 с помощью введения двух переменных.
Пусть скорость первого поезда х км/ч, а скорость второго поезда у км/ч.
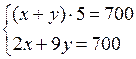

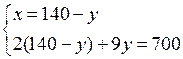
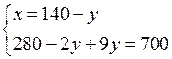

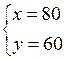
О т в е т: 80 км/ч; 60 км/ч.
3. Решить задачу № 7.5. Объясняет учитель.
Пусть первое число равно х, второе число у.
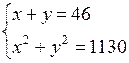
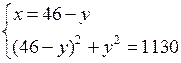
Решим уравнение:
(46 – у)2 + у2 = 1130
2116 – 92у + у2 + у2 – 1130 = 0
2у2 – 92у + 986 = 0
у2 – 46у + 493 = 0
D = 144; у1 = 17; у2 = 29.
Если у = 17, то х = 46 – 17 = 29;
если у = 29, то х = 46 – 29 = 17.
О т в е т: 29 и 17.
III. Закрепление изученного материала.
1. Решить задачу № 7.2 на доске и в тетрадях.
Пусть х км/ч собственная скорость лодки, у км/ч скорость течения реки. Тогда (х + у) км/ч скорость по течению реки; (х – у) км/ч скорость лодки против течения реки.
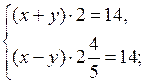
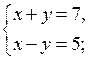
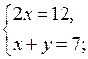

О т в е т: 6 км/ч; 1 км/ч.
2. Решить № 7.6 самостоятельно с проверкой.
Пусть первое натуральное число равно х, второе число равно у.


Решим уравнение:
у2 + 24у – 481 = 0
D = 2500; у1 = 13; у2 = – 37
у = – 37 не удовлетворяет условию задачи, что у – натуральное число.
Если у = 13, то х = 24 + 13 = 37.
О т в е т: 37 и 13.
3. Решить № 7.8. Учащиеся самостоятельно решают задачу. Один ученик самостоятельно решает на доске задачу. Учитель при необходимости помогает в решении.
Пусть первое натуральное число равно х, второе – у. Составим и решим систему уравнений.
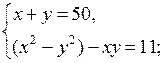
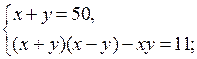

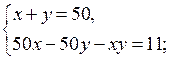
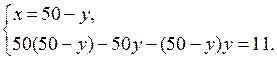
2500 – 50у – 50у – 50у + у2 – 11 = 0;
у2 – 150у + 2489 = 0;
D = 12544 = 1122; у1 = 19; у2 = 131 не удовлетворяет условию задачи (сумма двух натуральных чисел равна 50).
Если у = 19, то х = 50 – 19 = 31.
О т в е т: 31 и 19.
4. Повторение пройденного материала.
Изобразив схематически графики уравнений, определите, сколько решений имеет система уравнений:
а) 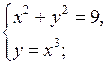 б)
б) 
IV. Итоги урока.
Домашнее задание: по учебнику на с. 75–77 изучить пример 1; решить № 7.3; № 7.4; № 7.7; № 6.21 (а).
У р о к 2
Цели: упражнять учащихся в составлении систем уравнений как математических моделей реальных ситуаций при решении задач; способствовать выработке навыков и умений при решении систем уравнений различными способами.
Ход урока
I. Проверка домашней работы.
1. Двое учащихся на доске решают задачи № 7.3 и № 7.7 из домашней работы.
2. Учитель выборочно проверяет по тетрадям выполнение учащимися домашней работы.
3. Решить с остальными учащимися № 40 (а) на с. 10 на доске и в тетрадях.
а) 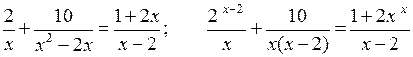
2х – 4 + 10 = х + 2х2; 2х2 – х – 6 = 0;
D = 49; х1 = – 1,5; х2 = 2.
Проверка показывает, что х = 2 не является корнем.
О т в е т: – 1,5.
II. Выполнение упражнений. Решение задач.
1. Решить задачу на доске и в тетрадях. Двузначное число в 6 раз больше суммы его цифр. Если из этого числа вычесть произведение его цифр, то получится 34. Найдите исходное число.
Пусть х – число десятков двузначного числа, у – число единиц двузначного числа. Тогда 10х + у данное двузначное число.
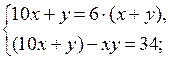
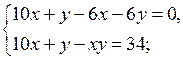
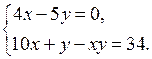
Подстановка у = 0,8х; тогда 10х + 0,8х – х · 0,8х = 34;
0,8х2 – 10,8х + 34 = 0 | : 0,2; 4х2 – 54х + 170 = 0 | : 2;
2х2 – 27х + 85 = 0;
D = 729 – 680 = 49; х1 = 5; х2 = 8,5 не удовлетворяет условию задачи.
Если х = 5, то у = 0,8х = 0,8 · 5 = 4. Число 54.
О т в е т: 54.
2. Решить задачу № 7.11 самостоятельно.
Учитель помогает учащимся при составлении системы уравнений.
Пусть х числитель дроби, у знаменатель
дроби, тогда ![]() исходная
дробь.
исходная
дробь.
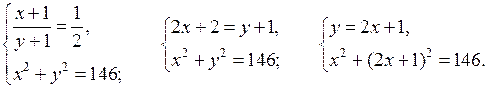
х2 + 4х2 + 4х + 1 – 146 = 0; 5х2 + 4х – 145 = 0;
D = 16 + 2900 = 2916 = 542; х1 = – 5,8; х2 = 5.
Условию задачи удовлетворяет х = 5, тогда у
= 2 · 5 + 1 = 11. Исходная дробь ![]()
Ответ: ![]()
3. Решить задачу № 7.12. Повторить формулу периметра прямоугольника Р = (а + b) · 2 и теорему Пифагора с2 = а2 + b2.
Пусть стороны прямоугольника равны х см и у см. Тогда периметр (х + у) · 2 = 28; по теореме Пифагора х2 + у2 = 102 = 100.
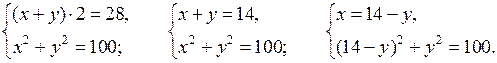
Решим уравнение:
196 – 28у + у2 + у2 = 100; 2у2 – 28у + 96 = 0; у2 – 14у + 48 = 0; у1 = 6;
у2 = 8.
Если у = 6, то х = 14 – 6 = 8;
если у = 8, то х = 14 – 8 = 6.
О т в е т: 6 см и 8 см.
4. Решить задачу № 7.15. Вспомнить
формулу площади прямоугольного треугольника S = ![]()
Пусть х и у – катеты прямоугольного
треугольника, тогда ![]() по
теореме Пифагора х2 + у2 = 372. Составим и решим систему уравнений:
по
теореме Пифагора х2 + у2 = 372. Составим и решим систему уравнений:
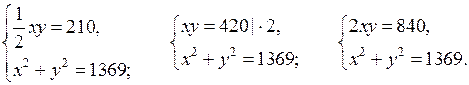
Складывая оба уравнения почленно, получим х2 + 2ху + у2 = 2209;
(х + у)2 = 472. Решим две системы уравнений,
используя способ подстановки.
 и
и 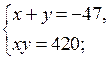
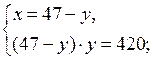 и
и 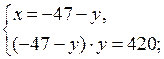
у2 – 47у + 420 = 0; у2 + 47у + 420 = 0;
D = 2209 – 1680 = 529 = 232; D = 529 = 232;
у1 = 12; у2 = 35. у1 = – 35; у2 = – 12.
Оба корня не удовлетворяют смыслу (условию) задачи.
Если у = 12, то х = 47 – 12 = 35;
если у = 35, то х = 47 – 35 = 12.
Р∆ = 35 + 12 + 37 = 84 (см).
О т в е т: 84 см.
5. Решение задачи № 7.48 объясняет учитель, используя геометрические модели состояния процесса движения.
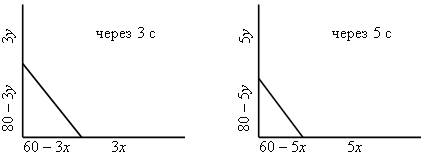
Р е ш е н и е
х м/с – скорость первого тела;
у м/с – скорость второго тела.
По теореме Пифагора
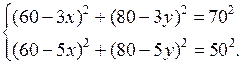
После упрощений получим:
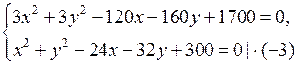
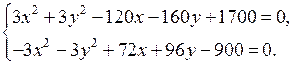
Сложим два уравнения почленно, получим – 48х
– 64у = 800, отсюда
3х + 4у = 50; найдем у = ![]() и подставим во второе уравнение системы:
и подставим во второе уравнение системы: ![]()
О т в е т: 6 м/с; 8 м/с.
III. Итоги урока.
Домашнее задание: решить задачи № 7.9, № 7.13, № 7.14; из повторения на с. 10 решить № 40 (г).
У р о к 3
Цели: научить учащихся решать задачи на совместную работу с помощью составления систем уравнений; закреплять знания и умения учащихся в решении систем уравнений различными методами; развивать логическое мышление учащихся.
Ход урока
I. Самостоятельная работа (15–20 мин).
В а р и а н т I
1. Прямоугольный участок земли площадью 3250 м2 обнесен изгородью, длина которой 230 м. Найдите длину и ширину участка.
2. Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.
В а р и а н т II
1. Разность двух числе равна 5, а их произведение равно 84. Найдите эти числа.
2. Прямоугольный участок земли площадью 2080 м2 обнесен изгородью, длина которой равна 184 м. Найдите длину и ширину участка.
II. Решение задач на совместную работу.
1. Решение задачи № 7.22 объясняет учитель.
Примем объем работы (задания) за 1. х ч
работает первая бригада одна; у ч в одиночку выполнит все задание вторая
бригада; ![]() часть
работы, выполненная первой бригадой за 1 ч;
часть
работы, выполненная первой бригадой за 1 ч; ![]() производительность второй бригады за 1 ч;
производительность второй бригады за 1 ч;
![]() производительность
обеих бригад за 1 ч.
производительность
обеих бригад за 1 ч.
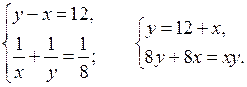
8(12 + х) + 8х = х(12 + х)
96 + 8х + 8х = 12х + х2
х2 – 4х – 96 = 0
D = 400; х1 = 12; х2 = – 8 не удовлетворяет условию задачи.
Если х = 12, то у = 12 + 12 = 24.
О т в е т: 12 ч.
2. Решить задачу № 7.23 самостоятельно.
Один учащийся самостоятельно решает на доске, остальные в тетрадях, затем проверяется решение.
Р е ш е н и е
Примем объем всей работы за 1. Пусть первый
экскаватор один работает х ч, второй в одиночку выполнит всю работу за у
ч, тогда у – х = 4; ![]() часть работы, выполненная первым
экскаватором за 1 ч,
часть работы, выполненная первым
экскаватором за 1 ч, ![]() производительность второго за 1 ч;
производительность второго за 1 ч; 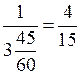 производительность
обоих экскаваторов за 1 ч. Составим и решим систему уравнений:
производительность
обоих экскаваторов за 1 ч. Составим и решим систему уравнений:
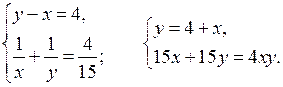
15(4 + х) + 15х = 4х(4 + х)
60 + 15х + 15х = 16х + 4х2
4х2 – 14х – 60 = 0 | : 2
2х2 – 7х – 30 = 0
D = 289; х1 = ![]() = 6; х2 = – 2,5 не удовлетворяет условию задачи
= 6; х2 = – 2,5 не удовлетворяет условию задачи
х > 0.
Если х = 6, то у = 4 + 6 = 10.
О т в е т: 6 ч; 10 ч.
3. Решить задачу № 7.26.
Примем площадь всего поля за 1. Пусть один тракторист
половину поля вспахал за х ч, а второй половину поля вспахал за у
ч, тогда оба они поле вспахали за 100 ч, значит, х + у = 100. ![]() часть поля вспашет
один тракторист отдельно за 1 ч;
часть поля вспашет
один тракторист отдельно за 1 ч; ![]() часть поля вспашет отдельно второй
тракторист за 1 ч;
часть поля вспашет отдельно второй
тракторист за 1 ч; ![]() производительность
обоих трактористов за 1 ч.
производительность
обоих трактористов за 1 ч.
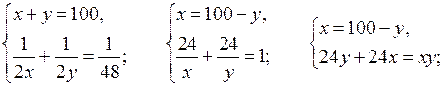
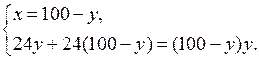
у2 – 100у + 2400 = 0;
у1 = 40; у2 = 60.
Если у = 40, то х = 100 – 40 = 60;
если у = 60, то х = 100 – 60 = 40.
Все поле один тракторист вспахал бы за 60 · 2 = 120 (ч), а другой за 40 · 2 = 80 (ч), если каждый тракторист работал бы отдельно.
О т в е т: 120 ч; 80 ч.
4. Решение задачи № 7.47 объясняет учитель.
Примем за 1 объем воды в бассейне. Если первая труба
наполняет бассейн за х ч, а вторая опорожняет его за у ч, то к
имеющемуся количеству воды, равному ![]() емкости бассейна, за 8 ч нальется
емкости бассейна, за 8 ч нальется ![]() а выльется
а выльется ![]() емкости бассейна.
Поскольку бассейн в итоге оказывается пустым, то это значит, что
емкости бассейна.
Поскольку бассейн в итоге оказывается пустым, то это значит, что 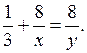 Второе уравнение х – у
= 2.
Второе уравнение х – у
= 2.

у2 + 2у + 24у – 24у – 48 = 0;
у2 + 2у – 48 = 0;
у1 = – 8 не удовлетворяет условию задачи; у2 = 6.
Если у = 6, то х = 6 + 2 = 8.
О т в е т: 8 ч; 6 ч.
III. Итоги урока.
Домашнее задание: разобрать по учебнику на с. 79–81 решение примера 3 и записать в тетрадь; решить № 7.21; № 7.24 и № 6.16 (б).
У р о к 4
Цели: закрепить у учащихся навыки и умения решения задач с помощью систем уравнений второй степени; развивать логическое мышление учащихся.
Ход урока
I. Анализ самостоятельной работы.
1. Указать ошибки, допущенные учащимися в работе.
2. Решить на доске задачи, вызвавшие затруднения у учащихся.
II. Решение задач с помощью составления систем уравнений.
1. Решить задачу № 7.19 на доске и в тетрадях.
Пусть х – число рядов в синем зале кинотеатра;
у – число мест в каждом ряду синего зала.
Тогда х + 2 число рядов в красном зале,
у – 4 число мест в каждом ряду красного зала.
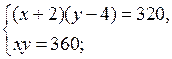
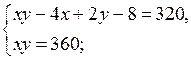
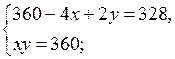
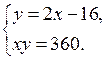
х(2х – 16) = 360
2х2 – 16х – 360 = 0
х2 – 8х – 180 = 0
D = 784 = 282
х1 = 18; х2 = – 10 не удовлетворяет условию задачи х > 0.
Если х = 18, то у = 2 · 18 – 16 = 20.
В синем зале 18 рядов, в красном зале 20 рядов.
О т в е т: 20 рядов; 18 рядов.
2. Решить задачу № 7.20 самостоятельно, предварительно обсудив составление системы уравнений.
Пусть х – число учеников, собирающихся сдавать экзамены для поступления в колледж; у – число листов, предполагаемых для каждого ученика. Тогда х – 20 учеников сдавали экзамен по математике; у + 1 лист дали каждому ученику на экзамене по математике.
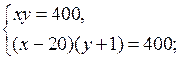
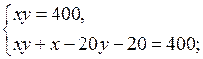
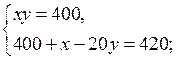
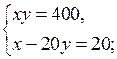
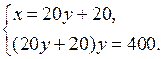
Решим уравнение:
20у2 + 20у – 400 = 0;
у2 + у – 20 = 0;
у1 = 4; у2 = – 5 не удовлетворяет у > 0.
Если у = 4, то х = 20 × 4 + 20 = 100.
Поступало в колледж 100 человек, а по математике сдавало экзамен 80 человек.
О т в е т: 80 человек.
3. Решить задачу № 7.16 на доске и в тетрадях.
Решение задачи объясняет учитель, привлекая к обсуждению учащихся.
Р е ш е н и е
Пусть х км/ч – собственная скорость лодки;
у км/ч – скорость течения реки.
Тогда (х + у) км/ч – скорость лодки по течению реки;
(х – у) км/ч – скорость лодки против течения реки.
![]() ч время движения лодки по течению
реки;
ч время движения лодки по течению
реки; ![]() ч время
движения лодки против течения реки. Всего затрачено 7 ч, тогда
ч время
движения лодки против течения реки. Всего затрачено 7 ч, тогда ![]() + +
+ + ![]() = 7.
= 7.
![]() ч время движения лодки против течения
реки;
ч время движения лодки против течения
реки; ![]() ч турист
затратил время на движение по течению реки. Время движения одинаковое, тогда
ч турист
затратил время на движение по течению реки. Время движения одинаковое, тогда ![]() =
= ![]() .
.
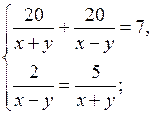
Обозначим ![]() = а,
= а, ![]() = b.
= b.

![]() =
= ![]() то есть х – у = 4;
то есть х – у = 4;
![]() =
= ![]() то есть х + у = 10.
то есть х + у = 10.
Решим систему уравнений 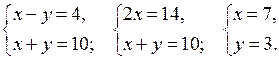
О т в е т: 3 км/ч.
4. Решить задачу № 7.42.
Один ученик самостоятельно решает на доске, остальные самостоятельно решают в тетрадях. Совместно обсуждается ответ на вопрос задачи.
Р е ш е н и е
Пусть х км/ч – скорость катера в стоячей воде,
у км/ч – скорость течения.

Ответим на вопрос задачи.
96 км по течению катер прошел за 6 ч (скорость катера по течению 16 км/ч). Плот за это время прошел 12 км. Расстояние между катером и плотом в этот момент составило 84 км. Они пошли навстречу друг другу, один со скоростью 2 км/ч, другой со скоростью 12 км/ч, следовательно, сближались они со скоростью 14 км/ч, поэтому шли до встречи 6 ч. За эти 6 ч плот пройдет еще 12 км, а в итоге он будет находиться от пристани А на расстоянии 24 км.
О т в е т: 24 км.
5. Повторение пройденного материала.
Решить графически систему уравнений 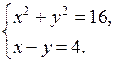
О т в е т: (4; 0); (0; – 4).
III. Итоги урока. Выставление отметок.
Домашнее задание: изучить по учебнику решение примеров 1 и 2 на с. 75–79; решить № 7.18, № 7.17, № 6.19 (а).
У р о к 5
Цели: способствовать выработке навыков и умений решать задачи и системы уравнений различными методами; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Прочитать по учебнику «Основные результаты» на с. 82.
2. Ответить на в о п р о с ы:
а) Какие методы решения систем двух уравнений с двумя переменными вы знаете?
б) Назвать варианты при решении систем уравнений методом введения новых переменных.
в) Назвать уравнение окружности с центром в начале координат и радиусом r.
г) Сформулировать теорему об уравнении окружности.
3. Решить задачи из домашнего задания, вызвавшие затруднения у учащихся.
II. Решение задач.
1. Решить задачу № 7.28.
Учитель помогает в составлении системы уравнений, а систему решают самостоятельно учащиеся.
Р е ш е н и е
Пусть х – число десятков двузначного числа,
у – число единиц.
Тогда исходное двузначное число равно 10х + у.

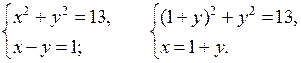
1 + 2у + у2 + у2 = 13;
2у2 + 2у – 12 = 0;
у2 + у – 6 = 0;
у1 = 2; у2 = – 3 не удовлетворяет условию задачи.
Если у = 2, то х = 3. Число было 32.
О т в е т: 32.
2. Решить задачу № 7.32.
Решение объясняет учитель.
Р е ш е н и е
Пусть х – число десятков исходного числа,
у – число его единиц.
Исходное двузначное число равно 10х + у.

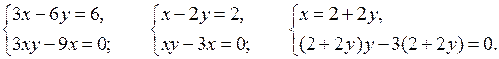
Решим уравнение:
2у + 2у2 – 6 – 6у = 0,
у2 – 2у – 3 = 0.
у1 = 3, у2 = – 1 не удовлетворяет у > 0.
Если у = 3, то х = 2 + 2 · 3 = 8.
Исходное число 83.
О т в е т: 83.
3. Решить № 7.34 самостоятельно.
Р е ш е н и е
Пусть х км/ч – скорость велосипедиста,
у км/ч – скорость мотоциклиста.
600 м/мин = 36 км/ч.
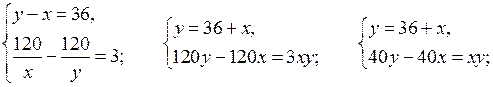
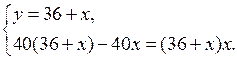
х2 + 36х – 1440 = 0;
D = 7056 = 842;
х1 = – 60 не удовлетворяет условию задачи х > 0; х2 = 24.
Если х = 24, то у = 36 + 24 = 60.
О т в е т: 24 км/ч и 60 км/ч.
4. Решить задачу № 7.43 на совместную работу. Обратить внимание учащихся на то, что в домашней контрольной работе будет аналогичная задача.
Р е ш е н и е
Объем всей работы примем за 1. Пусть первая наборщица сделала половину всей работы за х ч, а вторая остальную половину работы сделала за у часов.


Решим уравнение:
(12,5 – у)у = 37,5;
у2 – 12,5у + 37,5 = 0 | · 2;
2у2 – 25у + 75 = 0;
D = 25; у1 = 5; у2 = 7,5.
Если у = 5, то х = 12,5 – 5 = 7,5;
если у = 7,5 то х = 12,5 – 7,5 = 5.
Половина работы одной наборщицей сделана за 5 ч, значит, вся работа ею будет выполнена отдельно за 10 ч, а вторая наборщица в одиночку выполнит работу за 15 ч.
О т в е т: 10 ч; 15 ч.
5. Решить задачу 7.39.
Учитель объясняет решение задачи, привлекая к обсуждению учащихся.
Р е ш е н и е
Пусть х км/ч – скорость первого поезда; тогда (х + 40) км/ч – скорость второго поезда. 2у км – расстояние между А и В.
Время 3 ч 45 мин = ![]() ч =
ч = ![]() =
= ![]() ч.
ч.
![]() х км пройдет первый поезд до
встречи;
х км пройдет первый поезд до
встречи; ![]() (х
+ 40) км пройдет второй поезд до встречи; вместе до встречи они пройдут
2у км, значит,
(х
+ 40) км пройдет второй поезд до встречи; вместе до встречи они пройдут
2у км, значит,
![]() х +
х + ![]() (х + 40) = 2у.
(х + 40) = 2у.
Если встреча поездов произойдет на середине пути, то
каждый поезд до встречи пройдет у км. ![]() ч затратит время первый поезд до встречи;
ч затратит время первый поезд до встречи;
![]() ч время,
затраченное вторым поездом до встречи. Поезд из А выйдет на 2 ч раньше,
чем из В, значит,
ч время,
затраченное вторым поездом до встречи. Поезд из А выйдет на 2 ч раньше,
чем из В, значит, ![]() –
–
![]() = 2. Составим и
решим систему уравнений:
= 2. Составим и
решим систему уравнений: 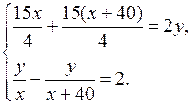
О т в е т: 60 км/ч; 100 км/ч.
III. Итоги урока.
Домашнее задание: на отдельных листах решить домашнюю контрольную работу № 2 на с. 54 номера 8, 9 и 10 (по вариантам).
Подготовка к контрольной работе
Цели: повторить и закрепить методы решения систем уравнений в ходе выполнения упражнений; подготовиться к контрольной работе.
Ход урока
I. Проверка усвоения изученного материала.
1. Собрать у учащихся листочки с домашней контрольной работой.
2. Объяснить на доске решение заданий, вызвавших затруднения у учащихся.
3. Повторить методы решения систем уравнений.
4. Устно: что является графиком данных уравнений:
а) 6х + у = 4; г) у = ![]() ж)
у – х2 = – 3;
ж)
у – х2 = – 3;
б) х2 + у2 = 9; д) х2 + у = 5; з) у – х = 0?
в) ху = 6; е) (х – 2)2 + (у + 7)2 = 16;
5. Устно: решить систему уравнений методом алгебраического сложения:
а) 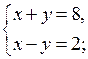 б)
б)  в)
в) 
II. Решение систем уравнений и задач.
1. Решите систему уравнений методом подстановки:
а)  б)
б)  в)
в) 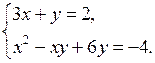
О т в е т ы: а) (3; 4); (4; 3); б) (5; 1); (– 1; – 5).
в) 
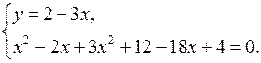
4х2 – 20х + 16 = 0 | : 4;
х2 – 5х + 4 = 0; х1 = 1; х2 = 4.
Если х = 1, то у = 2 – 3 · 1 = – 1;
если х = 4, то у = 2 – 3 · 4 = – 10.
О т в е т: (1; – 1); (4; – 10).
2. Решите систему уравнений методом алгебраического сложения:
а) 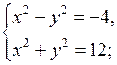 б)
б) 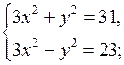 в)
в) 
а) 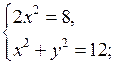
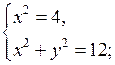
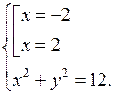
Тогда 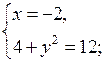 и
и 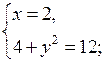
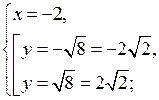 и
и 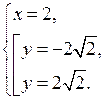
О т в е т: (– 2; ![]() ); (– 2;
); (– 2; ![]() ); (2;
); (2; ![]() ); (2;
); (2; ![]() ).
).
б) 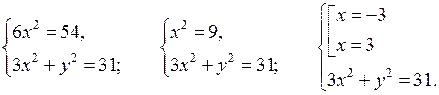
Решим две системы уравнений:
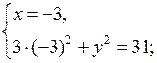 и
и 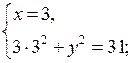
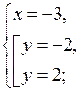 и
и 
О т в е т: (– 3; – 2); (– 3; 2); (3; – 2); (3; 2).
в) 
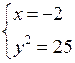 и
и 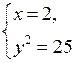
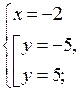 и
и 
О т в е т: (– 2; – 5); (– 2; 5); (2; – 5); (2; 5).
3. Решите графически систему уравнений:
а) 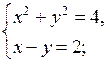 б)
б) 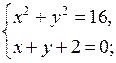 в)
в) 
4. Решите задачу: «Отношение двузначного числа к сумме его цифр равно 4, а отношение этого числа к произведению его цифр равно 2. Найдите это число».
Р е ш е н и е
Пусть х – число десятков двузначного числа;
у – число единиц двузначного числа.
Тогда (10х + у) – данное двузначное число.
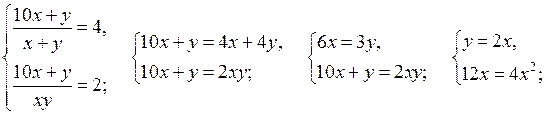
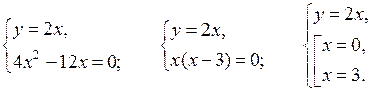
Корень х = 0 не удовлетворяет условию задачи; тогда при х = 3 имеем у = 6. Данное число 36.
О т в е т: 36.
5. При каком значении параметра b система уравнений имеет
а) одно решение;
б) два решения;
в) три решения:
1)  2)
2) 
О т в е т:
1) 
а) система имеет одно решение при ![]() и при
и при ![]()
б) два решения при ![]() < b <
< b < ![]()
III. Итоги урока.
Домашнее задание: № 6.11 (б); № 6.8 (г); № 6.2 (а; г); № 5.34 (г). Повторить решение данных заданий для подготовки к контрольной работе.
Определение числовой функции.
Область определения, область
значений функции (4 ч)
У р о к 1
Цели: ввести определение функции и области определения; учить находить область определения функции; повторить решение неравенств второй степени методом интервалов.
Ход урока
I. Анализ контрольной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Выполнить работу над ошибками.
II. Беседа по ранее изученному материалу.
1. За два года изучения школьного курса алгебры вы уже привыкли к тому, что термин «функция» используется практически постоянно. Но в математике действует закон: если используется какой-то термин, то его надо точно определить.
2. Учитель проводит беседу по прочитанному дома
учащимися материалу на с. 83–86. Учащиеся вспоминают, какие функции они изучили
ранее:
у = kх + m, у = х2, у = kх2; у = ![]() у = ах2 + bх + с, у
=
у = ах2 + bх + с, у
= ![]() у = | х
|.
у = | х
|.
3. Работа по рис. 68–70 учебника. Повторяют, как можно построить графики, изображенные на этих рисунках.
III. Объяснение нового материала.
1. Что же такое функция? Формулируется определение 1 и записывается в тетрадь.
О п р е д е л е н и е 1. Если даны числовое
множество Х и правило f, позволяющее поставить в с о о т в е т
с т в и е каждому элементу х из множества Х определенное
число у, то говорят, что задана функция у = f(х)
с областью определения Х; пишут у = f(х), х ![]() Х.
Х.
При этом переменную х называют независимой переменной или аргументом; а переменную у – зависимой переменной.
2. Для области определения функции у
= f(х), х ![]() Х, иногда удобно использовать
обозначение D(f). Например:
Х, иногда удобно использовать
обозначение D(f). Например:
для функции у = ![]() х ≥ 0 (рис. 68) имеем D(f)
= [0; + ∞);
х ≥ 0 (рис. 68) имеем D(f)
= [0; + ∞);
для функции у = ![]() х
х ![]() [0; 4] (рис. 69) имеем D(f)
= [0; 4];
[0; 4] (рис. 69) имеем D(f)
= [0; 4];
для функции у = g(х) (рис. 70) имеем D(g) = (– ∞; + ∞).
3. Нельзя говорить о функции у = f(х) без указания ее области определения, которая или указывается явно, или подразумевается – в случае, если область определения функции у = f(х) совпадает с областью определения выражения f(х) (такую область определения иногда называют естественной).
IV. Закрепление изученного материала.
1. Устно решить с № 8.1 (в; г) по № 8.3 (в; г).
2. Решить № 8.4 (в; г) на доске и в тетрадях.
в) Функция определена в любой точке х, за исключением тех точек, при которых знаменатель дроби обращается в 0.
О т в е т: D(f): х ≠ – 3
или D(f) = (–∞; – 3)![]() (– 3; + ∞).
(– 3; + ∞).
г) D(f) = (–∞; – 1,6)![]() (– 1,6; + ∞).
(– 1,6; + ∞).
3. Решить № 8.5 (в; г) самостоятельно с проверкой.
4. Решить № 8.6 (в; г) с комментированием на месте.
в) D(f) = (–∞; 0)![]() (0; 7)
(0; 7)![]() (7; ∞);
(7; ∞);
г) D(f): х ≠ 0; х ≠ – 6.
5. Решить № 8.9 (в; г). Вспоминают учащиеся сначала, что под знаком квадратного корня может находиться только неотрицательное число.
в) у = ![]() х + 4 ≥ 0; х ≥
– 4; D(f) = [– 4; + ∞);
х + 4 ≥ 0; х ≥
– 4; D(f) = [– 4; + ∞);
г) у = ![]() 2 – х ≥ 0; х ≤
2; D(f) = (– ∞; 2].
2 – х ≥ 0; х ≤
2; D(f) = (– ∞; 2].
6. Решить № 8.10 (в; г) устно.
О т в е т: D(f) = (– ∞; + ∞).
7. Повторение пройденного материала.
1. Решить № 37 (а; б) на с. 9 из раздела «Задачи на повторение».
а) (а2 – 5)2 – (2а + 3)2 = 0.
Воспользуемся формулой а2 – b2 = (а – b)(а + b).
(а2 – 5 – 2а – 3)(а2 – 5 + 2а + 3) = 0;
(а2 – 2а – 8) · (а2 + 2а – 2) = 0;
а2 – 2а – 8 = 0 или а2 + 2а – 3 = 0;
а1 =
4; а2 = – 2; а1 = – 1 – ![]() ; а2 = –1 +
; а2 = –1 + ![]() .
.
О т в е т: 4; – 2; – 1 ± ![]() .
.
2. Рассказать, как решаются неравенства методом интервалов
(х – 8)(х + 3) > 0.
IV. Итоги урока.
Сформулировать определение функции.
Домашнее задание: по учебнику рассмотреть решение примера 1 на с. 87–89 и записать решение в тетрадь; решить № 8.4 (а; б); № 8.5 (а; б); № 8.6 (а; б), № 8.9 (а; б), № 7.35.
У р о к 2
Цели: способствовать выработке навыков и умений учащихся в нахождении области определения функций; закрепить знания учащихся при решении неравенств методом интервалов.
Ход урока
I. Устная работа.
1. Сформулируйте определение функции.
2. Как называют переменную х? переменную у?
3. Приведите примеры функций, которые уже изучили. Что является их графиками?
4. Что такое область определения Х функции? Как обозначают область определения?
5. Устно решите № 8.1 (а; б) – № 8.3 (а; б).
II. Нахождение области определения функции. Выполнение упражнений.
1. Решить № 8.7 (в; г) на доске и в тетрадях.
в) Функция у = 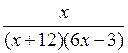 определена в любой точке х, при
которой знаменатель дроби не равен нулю.
определена в любой точке х, при
которой знаменатель дроби не равен нулю.
х + 12 ≠ 0; х ≠ – 12 и 6х – 3 ≠ 0, х ≠ – 0,5.
О т в е т: D(f) : х ≠ – 12; х ≠ – 0,5.
г) D(f) = (– ∞; 0,8)![]() (0,8; 13)
(0,8; 13)![]() (13; + ∞).
(13; + ∞).
2. Решить № 8.8 (б; г) самостоятельно с проверкой.
б) 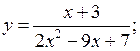
2х2 – 9х + 7 ≠ 0;
2х2 – 9х + 7 = 0
D = 25; х1 = ![]() х2 =
х2 = ![]()
О т в е т: D(f) = (– ∞; 1)![]() (1; 3,5)
(1; 3,5)![]() (3,5; + ∞).
(3,5; + ∞).
г) 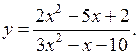
Функция определена, если 3х2 – х – 10 ≠ 0, то
есть при х ≠ ![]() и х ≠ 2.
и х ≠ 2.
О т в е т: D(f): х ≠ 2; х
≠ ![]()
3. Решить № 8.10 (а; б) устно.
4. Решить № 8.11 (в) методом интервалов.
в) ![]() Под знаком квадратного корня может
находиться только неотрицательное число, значит, х2 – 144 ≥ 0, (х – 12)(х
+ 12) ≥ 0.
Под знаком квадратного корня может
находиться только неотрицательное число, значит, х2 – 144 ≥ 0, (х – 12)(х
+ 12) ≥ 0.
![]()
О т в е т: D(f) = (– ∞; – 12]![]() [12; ∞).
[12; ∞).
5. Решить № 8.12 (в) самостоятельно, используя метод интервалов.
6. Решить № 8.13 (в; б), используя построение (схематически) параболы.
в) ![]()
Функция определена, если х2 – 5х + 6 ≥ 0; х1 = 2; х2 = 3.
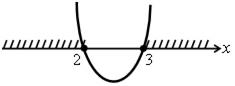
О т в е т: D(f) = (– ∞; 2]![]() [3; ∞).
[3; ∞).
б) ![]()
– х2 + 3х + 4 ≥ 0; х1 = – 1; х2 = 4.
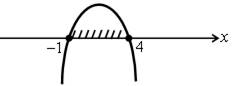
О т в е т: D(f) = [– 1; 4].
7. Решить № 8.18 (в; г) самостоятельно.
8. Решить № 8.16 (в; г).
Решение № 213 (в) объясняет на доске учитель.
в) 
Функция определена для всех значений х, при
которых выполняется условие 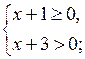
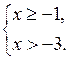
Общее решение х ≥ – 1.
О т в е т: х ≥ – 1.
г) 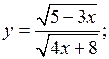
Решим систему неравенств 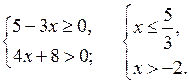
Общее решение – 2 < х ≤ ![]()
О т в е т: D(f) = (– 2; ![]() ].
].
9. Решить № 8.25 (в) на доске и в тетрадях.
в) 
(х2 – 1)(х2 – 2х – 15) ≠ 0
х2 – 1 ≠ 0 или х2 – 2х – 15 ≠ 0
х ≠ ± 1 или х1 ≠ – 3; х2 ≠ 5.
О т в е т: х ≠ 1; – 1; – 3; 5.
10. Решить № 8.26 (г).
г) 
Решим систему 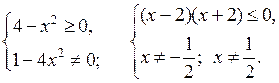
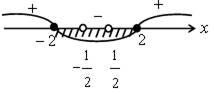
О т в е т: D(f) = [– 2; –![]() )
)![]() (–
(–![]() ;
; ![]() )
)![]() (
(![]() ; 2].
; 2].
11. Повторение ранее изученного материала.
Решить № 6.21 (г).
г) 
Обозначим  тогда
тогда 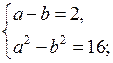

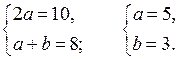
Тогда 
О т в е т: 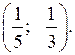
III. Итоги урока.
Домашнее задание: решить № 8.7 (а; б), № 8.8 (а; б), № 8.11 (а), № 8.12 (а), № 8.13 (а; г), № 8.16 (а; б), № 8.25 (а), № 8.26 (в).
У р о к 3
Цели: ввести понятие области значений функции и научить учащихся ее находить; упражнять учащихся в нахождении области определения функции и решении неравенств и систем неравенств.
Ход урока
I. Проверка пройденного материала.
1. Проверить домашнее задание выборочно у учащихся.
2. Двое учащихся решают на доске № 8.25 (а) и № 8.26 (в) из домашнего задания.
3. Устно решить № 8.18 (а; б) и № 8.14 (а; в) с остальными учащимися.
II. Изучение нового материала.
1. Ввести определение области значений функции и ее обозначения.
О п р е д е л е н и е 2. Множество всех значений
функции у = f(х), ![]() называют областью значений функции
и обозначают Е(f).
называют областью значений функции
и обозначают Е(f).
2. Если известен график функции, то область значений функции найти сравнительно нетрудно.
Для этого достаточно спроецировать график на ось
ординат. То числовое множество, геометрическая модель которого получится на оси
ординат в результате указанного проецирования, и будет представлять собой
Е(f).
3. Найти области значений для функций по рис. 68–69 на с. 85 учебника.
III. Закрепление изученного материала.
1. Решить № 8.20 (а; б) и № 8.21 (а; б).
2. Решить № 8.17 (в; г) на доске и в тетрадях.
в) 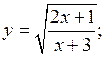
Функция определена, если подкоренное выражение
неотрицательно, то есть 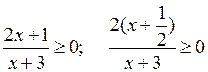
О т в е т: х ≥ –![]() х < – 3.
х < – 3.
г) 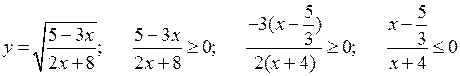
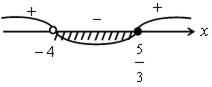
О т в е т: D(f) = (– 4; ![]() ].
].
3. Решить № 8.27 (в; г) устно.
Обратить внимание учащихся на то, что на числитель дроби никаких условий не накладывается, а только на знаменатель.
в) 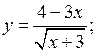 х + 3 > 0; х > –
3.
х + 3 > 0; х > –
3.
О т в е т: D(f) = (– 3; + ∞).
г)  4 – х > 0; х < 4.
4 – х > 0; х < 4.
О т в е т: D(f) = (– ∞; 4).
4. Решить № 8.29 (г) самостоятельно с проверкой. Учитель при необходимости помогает в решении.
г) 
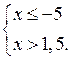 и х ≥ 5,
и х ≥ 5,
Общее решение х ≥ 5.
О т в е т: D(f) = [5; + ∞).
5. Решить № 8.31 (в) с комментированием на месте.
в) 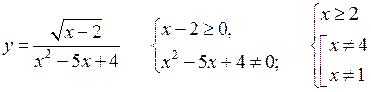
![]()
О т в е т: 2 ≤ х < 4; х > 4.
6. Решить № 8.37. Построить график
функции ![]()
Р е ш е н и е. Здесь область определения функции состоит из одной точки х = 3. В этой точке функция принимает значение 3. Следовательно, график функции состоит из одной точки (3; 3).
7. Решить № 8.32 (б; г). Учитель обращает внимание учащихся на то, чем отличается нахождение области определения заданных функций.
б) 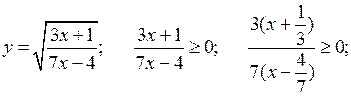
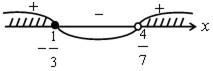
О т в е т: D(f) = (– ∞; –![]() ]
]![]() (
(![]() ; + ∞).
; + ∞).
г) 
Общее решение х > ![]() .
.
О т в е т: D(f) = (![]() ;∞).
;∞).
8. Повторение ранее изученного материала.
Решить № 41 (а) на с. 10 («Задачи на повторение»).
а) х4 – 17х2 + 16 = 0.
Обозначим х2 = у, тогда
у2 – 17у + 16 = 0, у1 = 16; у2 = 1.
Если у = 16, то х2 = 16; х = ± 4;
если у = 1, то х2 = 1, х = ± 1.
О т в е т: ± 4; ± 1.
IV. Итоги урока.
Домашнее задание: решить № 41 (в) на с. 10; решить № 8.21 (в; г), № 8.17 (а; б), № 8.29 (а; б), № 8.31 (а), № 8.32 (а; в).
У р о к 4
Цели: закрепить знания учащихся по изученному материалу; проверить степень усвоения ими материала; развивать логическое мышление.
Ход урока
I. Самостоятельная работа (15 мин).
В а р и а н т I
1. Найдите область определения функции:
а) ![]() б)
б)  в)
в) 
г) 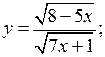 д)
д) 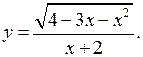
2. Начертите график какой-либо
функции у = f(х), для которой
D(f) = [– 3; 5], Е(f) = [– 4; 4].
В а р и а н т II
1. Найдите область определения функции:
а) ![]() б)
б) 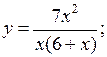 в)
в) 
г) 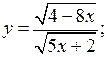 д)
д) 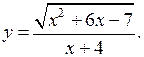
2. Начертите график какой-либо
функции у = f(х), для которой
D(f) = [– 3; 0], Е(f) = [2; 5].
II. Работа по учебнику.
1. Рассмотреть решение примера 2 на с. 89–91 учебника.
2. Область значений функции удобнее всего находить с помощью графика функции.
3. Решить № 8.22.
Решение объясняет учитель.
а) D(f) = (– ∞; 3];
б) f(– 2) = –![]() = –
= –![]() = 1; f(– 1) = –
= 1; f(– 1) = –![]() = 2; f(0) = х
– 1 = 0 – 1 = – 1;
= 2; f(0) = х
– 1 = 0 – 1 = – 1;
f(3) = х – 1 = 3 – 1 = 2; f(7) не существует;
в)
г) Е(f) = (– 2; 2].
III. Тренировочные упражнения.
1. Решить № 8.34 на доске и в тетрадях.
а) D(f) = (– ∞; 4];
б) f(– 2) = х = – 2; f(0) = х = 0; f(2) = 4; f(4) = 4; f(8) не существует;
в)

г) Е(f) = (– ∞; 4].
2. Решить № 8.36.
а) D(f) = [– 3; + ∞);
б) f(– 5) не существует; f(–
2) = х + 1 = – 2 + 1 = – 1; f(0) = х + 1 = 1;
f(2) = х2 – 4х
+ 1 = 22 – 4 · 2 + 1 = –
3; f(4) = ![]()
в)
г) Е(f) = [– 3; 1].
3. Решить № 8.30 (в; г) на доске и в тетрадях.
в) 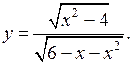
Решим систему неравенств 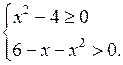
1) х2 – 4 ≥ 0, (х – 2)(х + 2) ≥ 0
![]()
Решение х ≤ – 2 и х ≥ 2.
2) 6 – х – х2 > 0; х2 + х – 6 < 0; (х + 3)(х – 2) < 0

Решение – 3 < х < 2.
3) 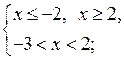
![]()
О т в е т: – 3 < х ≤ – 2.
г) 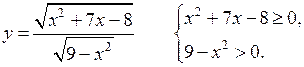
1) х2 + 7х – 8 ≥ 0, (х + 8)(х – 1) ≥ 0
![]()
Решение х ≤ – 8 и х ≥ 1.
2) 9 – х2 > 0, х2 – 9 < 0; (х – 3)(х + 3) < 0

Решение – 3 < х < 3.
3) 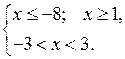
![]()
О т в е т: 1 ≤ х < 3.
IV. Итоги урока.
Домашнее задание: решить № 8.23, № 8.24, № 8.30 (а; б), № 8.31 (б).
Способы задания функции
(2 ч)
У р о к 1
Цели: изучить способы задания функции, научить применять эти способы при выполнении упражнений; способствовать развитию навыков чтения графиков и построения графиков функций.
Ход урока
I. Проверка домашнего задания.
1. Учитель выборочно проверяет выполнение домашнего задания у отдельных учащихся.
2. Решить на доске задания, вызвавшие затруднения у учащихся.
3. Решить устно № 60 (в; г) и № 62 (а) на с. 12.
4. Решить № 41 (б) на с. 10. Один ученик самостоятельно решает на доске, другие в тетрадях.
б) х6 – 9х3 + 8 = 0.
Обозначим х3 = у, тогда у2 – 9у + 8 = 0;
у1 = 8; у2 = 1.
Если у = 8, то х3 = 8; х = 2;
если у = 1, то х3 = 1, х = 1.
О т в е т: 1; 2.
II. Работа по учебнику.
1. Все функции, рассмотренные нами на предыдущих уроках, были заданы аналитическим способом, то есть с помощью формулы или нескольких формул.
2. Между тем есть другие способы задания функции. Рассмотрим рис. 76 на с. 92 учебника.
На отрезке [а; b] задана функция у = f(х).
Такой способ задания функции называют графическим, а линию F – графиком функции.
3. Если функция была задана аналитически и нам удалось построить график функции, то мы фактически перешли от аналитического способа задания функции к графическому. Обратный же переход удается осуществить далеко не всегда.
4. Не всякая линия на координатной плоскости может рассматриваться как график некоторой функции. Разобрать примеры по рис. 77–79.
5. Кроме аналитического и графического, на практике применяют табличный способ задания функции. При этом способе приводится таблица, в которой указаны значения функции (иногда точные, иногда приближенные) для конечного множества значений аргумента. Примерами табличного задания функции могут служить таблицы квадратов чисел, кубов чисел, квадратных корней и т. д. Во многих случаях табличное задание функции является удобным.
6. Аналитический, графический, табличный – наиболее простые, а потому наиболее популярные способы задания функции.
III. Закрепление изученного материала.
1. Решить № 9.1 устно по рис. 13–16.
2. Решить № 9.3 по рис. 21–24.
О т в е т: а) да; у = х + 2; б) да;
у = 2 | х | – 2; в) нет; г) да; 
3. Решить № 9.5 по рис. 29–32.
а) да; у = – 2х – 2; б) у = (х + 2)2 – 2; в) у = 1,5х + 2; г) у = – (х – 2)2 + 4.
4. Решить № 9.8 на доске и в тетрадях.
t = ![]()
а) t(36) = ![]() t(2,7)
=
t(2,7)
= ![]() t(144) =
t(144) = ![]()
б) S = 12t; t = 4,5 ч, то S = 12 · 4,5 = 54 (км);
в) S = 150
м = 0,15 км; t = ![]() (ч);
(ч);
г) t = 45 с = ![]() ч =
ч = ![]() ч; S = 12 ·
ч; S = 12 · ![]() =
= ![]() (км) =
(км) = ![]() · 1000
м =
· 1000
м =
= 150 (м).
5. Решить № 9.9 (б; г) на доске и в тетрадях.
б) х + 1 = (х – 1)2. Строим графики функций у = (х – 1)2 парабола с вершиной в точке (1; 0), ветви которой направлены вверх, и у = х + 1 – прямая.
О т в е т: х = 0; х = 3.
г) х2 –
3 = ![]() строим
графики функций у = х2 –
3 и у =
строим
графики функций у = х2 –
3 и у = ![]() Находим
координаты точки пересечения графиков.
Находим
координаты точки пересечения графиков.
О т в е т: х = 2.
6. Повторение пройденного материала.
Учитель объясняет решение задачи № 7.54.
Р е ш е н и е
Пусть х л – объем 40%-го раствора;
у л – объем 60%-го раствора;
(х + у + 5) л – объем 20%-го раствора.
Поскольку в первом растворе было 0,4х
кг соли, во втором 0,6у кг соли, а в третьем (х + у + 5)
· 0,2 кг соли, получим уравнение 0,4х + 0,6у =
= 0,2(х + у + 5).
Далее, (х + у + 5) л – объем 70%-го раствора, соли в нем 0,7(х + у + + 5) кг. Она складывается из трех частей: 0,4х кг соли из первого раствора; 0,6у кг соли из второго раствора; 5 · 0,8 = 4 кг соли из 5 л 80%-го раствора. Значит, 0,4х + 0,6у + 4 = 0,7(х + у + 5). Получим систему двух линейных уравнений с двумя переменными:
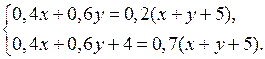
О т в е т: 1 л; 2 л.
IV. Итоги урока.
Назвать способы задания функции.
Домашнее задание: решить № 41 (г) на с. 10; решить № 9.2, № 9.4, № 9.6, № 9.7, № 9.9 (а; в).
У р о к 2
Цели: закрепить знания учащихся о способах задания функции; рассмотреть словесный способ задания функции; в ходе упражнений развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Проверить решение № 9.2 по рис. 17–20 и № 9.4 по рис. 25–28.
2. Назовите способы задания функции. Расскажите, в чем заключается каждый способ.
3. Решить № 8.24 (а; в) устно.
О т в е т: а) нет; в) да.
II. Изучение нового материала.
1. В математике имеется довольно много различных способов задания функции, но мы познакомимся еще только с одним способом, который используется в весьма своеобразных ситуациях. Речь идет о словесном способе, когда правило задания функции описывается словами.
2. По учебнику на с. 93–95 рассмотреть решение примеров 1 и 2.
3. Функцию, о которой шла речь в примере 2, называют целой частью числа; для целой части числа х используется обозначение [х]. Например, [3,451] = 3; [89] = 89; [– 0,(23)] = – 1. Очень своеобразно выглядит график функции у = [х] (рис. 54).
III. Выполнение упражнений.
1. Решить № 9.14 (в; г) на доске и в тетрадях.
в) ![]()
г) ![]()
О т в е т: в) 3; г) 4.
2. Решить № 9.15 (в; г).
Учитель объясняет, что сначала надо заданное число возвести в квадрат, а потом взять цифру единиц этого числа.
в) ![]() Цифра единиц равна 9.
Цифра единиц равна 9.
г) ![]() Цифра единиц равна 4.
Цифра единиц равна 4.
О т в е т: в) 9; г) 4.
3. Решить № 9.16.
02 = 0; 12 = 1; 22 = 4; 32 = 9; 42 = 16; 52 = 25; 62 = 36; 72 = 49; 82 = 64; 92 = 81; 102 = 100; 112 = 121; 122 = 144 и т. д.
Замечаем, что цифры единиц квадрата числа х равны 0; 1; 4; 5; 6; 9. Значит, область значений этой функции Е(f) = {0; 1; 4; 5; 6; 9}.
4. Решить № 9.17 по рис. 42 (б).
О т в е т: 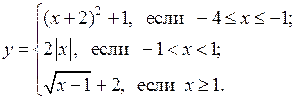
5. Решить № 9.19. Учитель объясняет решение.
а) у = ![]()
Если 0 ≤ х < 1, то [х] = 0, значит, у = 0.
Если 1 ≤ х < 2, то [х] = 1, значит, у = 1.
Если 2 ≤ х < 3, то [х] = 2,
значит, у = ![]()
Если 3 ≤ х < 4, то [х] = 3,
значит, у = ![]()
Если 4 ≤ х < 5, то [х] = 4,
значит, у = ![]() =
2 и так далее.
=
2 и так далее.
б) у = [![]() ].
].
Если 0 ≤ х < 1, то 0 ≤ ![]() < 1, [
< 1, [![]() ] = 0, значит, у
= 0.
] = 0, значит, у
= 0.
Если 1 ≤ х < 4, то 1 ≤ ![]() < 2, [
< 2, [![]() ] = 1, значит, у
= 1.
] = 1, значит, у
= 1.
Если 4 ≤ х < 9, то 2 ≤ ![]() < 3, [
< 3, [![]() ] = 2, значит, у
= 2.
] = 2, значит, у
= 2.
Если 9 ≤ х < 16, то 3 ≤ ![]() < 4, [
< 4, [![]() ] = 3, значит, у
= 3.
] = 3, значит, у
= 3.
Если 16 ≤ х < 25, то 4 ≤ ![]() < 5, [
< 5, [![]() ] = 4, значит, у
= 4 и т. д.
] = 4, значит, у
= 4 и т. д.
IV. Итоги урока.
Какие способы задания функции мы изучили?
Домашнее задание: решить № 9.11, № 9.13, № 9.14 (а; б), № 9.15 (а; б), № 9.18 (а).
Свойства функций
(3 ч)
У р о к 1
Цели: изучить свойства функции; научить исследовать на монотонность функцию, ограниченность функции снизу, сверху; развивать логическое мышление учащихся.
Ход урока
I. Объяснение нового материала.
1. В 7 и 8 классах мы изучали
некоторые свойства функций. Сейчас мы их соберем вместе. Во всех
определениях будет фигурировать числовое множество Х, являющееся
частью области определения функции:
Х ![]() D(f).
D(f).
2. О п р е д е л е н и е 1.
Функцию у = f(х) называют возрастающей на
множестве Х ![]() D(f), если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство f(х1) < f(х2).
D(f), если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство f(х1) < f(х2).
3. О п р е д е л е н и е 2.
Функцию у = f(х) называют убывающей на
множестве х ![]() D(f), если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство f(х1) > f(х2).
D(f), если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство f(х1) > f(х2).
4. Формулировка правила, которым пользуемся на практике. Рассмотреть рис. 84–85 на с. 98 учебника.
5. Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
6. Разобрать по учебнику на с. 98 пример 1.
7. Определение 3. Функцию у
= f(х) называют ограниченной снизу на множестве Х
![]() D(f),
если все значения функции на множестве Х больше некоторого числа. Рис.
86 на с. 99.
D(f),
если все значения функции на множестве Х больше некоторого числа. Рис.
86 на с. 99.
8. Определение 4. Функцию у
= f(х) называют ограниченной сверху на множестве Х
![]() D(f),
если все значения функции меньше некоторого числа. Рассмотреть рис. 87.
D(f),
если все значения функции меньше некоторого числа. Рассмотреть рис. 87.
9. Если функция ограничена и снизу, и сверху, то ее называют ограниченной.
10. Рассмотреть решение примера 2 по учебнику на с. 99–100.
II. Закрепление изученного материала.
1. Решить № 10.1 (в) – № 10.3 (в) на доске и в тетрадях.
2. Решить № 10.4 (в) – № 10.6 (в) с комментированием на месте.
3. Решить № 10.7 (в) – № 10.9 (в), построив графики соответствующих функций.
4. Решить № 10.18 (в; г) на доске и в тетрадях.
5. Решить № 10.19● (а).
Учитель объясняет решение.
а) Доказать, что функция ![]() х > –3
возрастает.
х > –3
возрастает.
Р е ш е н и е
Пусть х1 > х2 > – 3. Тогда
f(х1) = 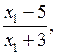 f(х2) =
f(х2) = 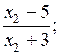
f(х1) – f(х2) = 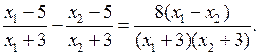
Здесь все множители положительны, значит, f(х1) > f(х2), а это и означает возрастание функции на заданном промежутке (– 3; + ∞).
6. Решить № 10.20 (в; г).
7. Повторение ранее изученного материала.
Решить № 40 (б) на с. 10 из темы «Задачи на повторение».
б) 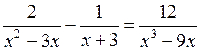

2(х + 3) – х(х – 3) = 12
2х + 6 – х2 + 3х – 12 = 0;
х2 – 5х + 6 = 0;
х1 = 3; х2 = 2.
х = 3 не является корнем уравнения, так как знаменатель дроби обращается в нуль при этом значении.
О т в е т: 2.
III. Итоги урока.
Домашнее задание: выучить определения 1–4 на с. 97–98 учебника; решить № 10.1 (а) – 10.6 (а); № 10.7 (а) – № 10.9 (а); № 10.18 (а), № 10.20 (а), № 10.19 (б).
У р о к 2
Цели: закрепить изученные свойства функции в ходе выполнения упражнений; научить находить наименьшее и наибольшее значения функции.
Ход урока
I. Проверка изученного материала.
1. Сформулируйте определение возрастающей функции, убывающей функции.
2. Какими формулировками пользуемся на практике при определении возрастания или убывания функции?
3. Устно решить № 10.1 (б), № 10.2 (б), № 10.5 (б), № 10.6 (б).
4. Определение функции, ограниченной снизу, ограниченной сверху.
5. Устно решить № 10.7 (б), № 10.8 (б), № 10.9 (б), схематично построив на доске графики функций.
II. Изучение нового материала.
1. О п р е д е л е н и е 5. Число m называют наименьшим
значением функции у = f(х) на множестве Х ![]() D(f), если:
D(f), если:
1) в Х существует такая точка х0, что f(х0) = m;
2) для всех х из Х выполняется
неравенство f(х) ≥ f(х0). Обозначение
унаим.
2. О п р е д е л е н и е 6. Число М
называют наибольшим значением функции у = f(х)
на множестве Х ![]() D(f),
если:
D(f),
если:
1) в Х существует такая точка х0, что f(х0) = М;
2) для всех х из Х выполняется
неравенство f(х) ≤ f(х0). Обозначение
унаиб.
3. Если множество Х не указано, то подразумевается, что речь идет об отыскании наименьшего или наибольшего значения функции во всей области определения.
4. Рассмотреть решение примера 3 на с. 101 учебника.
5. Рассмотреть понятия «функция выпукла вниз» и «функция выпукла вверх», используя рис. 88 и рис. 89 на с. 102.
6. Непрерывность функции на промежутке Х означает, что график функции на промежутке Х – сплошной, то есть не имеет проколов и скачков.
7. Запись в тетрадях учениками свойств функции:
1) область определения функции;
2) монотонность;
3) ограниченность;
4) наименьшее и наибольшее значения функции;
5) непрерывность функции;
6) область значений;
7) выпуклость.
III. Закрепление изученного материала.
1. Решить № 10.11 (б; в) на доске и в тетрадях.
б) у = – 2х2, х ![]() [– 1; 1].
[– 1; 1].
у(– 1) = – 2 · (– 1)2 = – 2 · 1 = – 2;
у(1) = – 2 · 12 = – 2.
у(0) = – 2 · 02 = 0
унаим = – 2; унаиб = 0.
в) у = – 4х + 1; х ![]() (– ∞; 0].
(– ∞; 0].
у(0) = – 4 · 0 + 1 = 1.
При отрицательных значениях х значения у будут положительными и больше 1.
Значит, унаим = 1, унаиб – не существует.
2. Решить № 10.12 (а; б) с комментированием на месте.
а) у = ![]() , если х
, если х ![]() [0; + ∞).
[0; + ∞).
у(0) = ![]() унаим = 0; унаиб –
не существует.
унаим = 0; унаиб –
не существует.
б) у = ![]() , если х
, если х ![]() [0; 3].
[0; 3].
у(0) = ![]() у(3) =
у(3) = ![]() унаим = 0; унаиб =
унаим = 0; унаиб =
![]()
3. Решить № 10.13 (а; б) на доске и в тетрадях.
а) ![]() D(f) = [4; + ∞);
D(f) = [4; + ∞);
у(4) = ![]() унаим = 0; унаиб –
не существует.
унаим = 0; унаиб –
не существует.
б) ![]() D(f) = [0; + ∞).
D(f) = [0; + ∞).
у(0) = ![]() унаиб = 3; унаим –
не существует.
унаиб = 3; унаим –
не существует.
4. Решить № 10.14 на доске и в тетрадях.

Свойства функции:
1) D(f) = (– ∞; ∞);
2) убывает на луче (– ∞; 0) и возрастает на луче [0; + ∞);
|
3) ограничена сверху и снизу; 4) унаим не существует, унаиб не существует; 5) непрерывна; 6) Е(f) = (– ∞; + ∞); 7) выпукла вверх. |
|
5. Решить № 8.25 (б) самостоятельно.
IV. Итоги урока. Выставление отметок.
Домашнее задание: по учебнику на с. 103–109
изучить свойства функций; решить № 10.11 (а; г), № 10.12 (в; г), №
10.13 (в; г); № 10.15,
№ 8.25 (г).
У р о к 3
Цели: в ходе выполнения упражнений закрепить знание свойств функций; способствовать выработке навыков и умений в построении и прочтении графиков функций; развивать логическое мышление учащихся.
Ход урока
I. Проверка домашнего задания.
1. Перечислите свойства функции.
2. Рассмотреть постоянную функцию у = С (рис. 90) на с. 103 учебника.
3. Перечислите свойства линейной функции у = kх + m (k ≠ 0) по рис. 91; 92 на с. 104.
4. Используя рис. 93 и рис. 94,
перечислите свойства функции у = kх2
(k ≠ 0).
5. Назовите свойства функции у = ![]() по рис. 95 и 96.
по рис. 95 и 96.
6. Какими свойствами обладает функция ![]() (рис. 97)?
(рис. 97)?
7. Сформулируйте свойства функции y = | x |, используя рис. 98.
8. Назовите свойства функции у = ах2 + bх + с (рис. 99 и рис. 100).
II. Выполнение упражнений.
1. Решить № 10.7 (г) и № 10.8 (г), используя графики функции.
2. Решить № 10.18 (б) и № 10.20 (б) на доске и в тетрадях.
3. Решить № 10.21 (б; в). Решение № 10.21 (б) объясняет учитель.
б) у = – 4х2 – 12х + 1. Графиком функции является парабола, ветви которой направлены вниз. Наибольшего значения функция достигает в вершине параболы (х0; у0):
х0 =
–![]()
у0(–![]() ) = – 4 ·
) = – 4 · ![]() – 12 · (–
– 12 · (–![]() ) + 1 = – 9 + 18 + 1 =
10;
) + 1 = – 9 + 18 + 1 =
10;
унаиб = 10, унаим – не существует;
в) у = 9х2 + 6х – 5.
Графиком функции является парабола, ветви которой
направлены вверх. Наименьшее значение функция имеет в вершине параболы (х0; у0). Найдем х0 = ![]()
у0 = 9 · (–![]() )2 + 6 · (–
)2 + 6 · (–![]() ) – 5 = 1 – 2 – 5 = – 6.
) – 5 = 1 – 2 – 5 = – 6.
унаим = – 6; унаиб – не существует.
4. Решить № 10.22 (а; в).
а) у = | х | + 3; х ![]() [– 5; 1].
[– 5; 1].
у(– 5) = | – 5 | + 3 = 5 + 3 = 8;
у(0) = | 0 | + 3 = 3;
у(1) = | 1 | + 3 = 4
унаим = 3; унаиб = 8.
в) у = – | 2х | – 1; х ![]() [– 1; 1].
[– 1; 1].
у(– 1) = – | – 2 | – 1 = – 2 – 1 = – 3;
у(1) = – | 2 | – 1 = – 2 – 1 = – 3;
у(0) = – | 0 | – 1 = – 1;
унаим = – 3; унаиб = – 1.
5. Решить № 10.26 на доске и в тетрадях.
Учитель при необходимости помогает в решении задания.
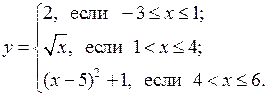
Свойства функции:
1) D(f) = [– 3; 6];
2) возрастает на (1; 4] и [5; 6];
убывает на отрезке [4; 5];
постоянна на отрезке [– 3; 1];
3) ограничена и снизу и сверху;
4) унаим = 1; унаиб = 2;
5) непрерывна;
6) Е(f) = [1; 2];
7) выпукла и вверх и вниз.
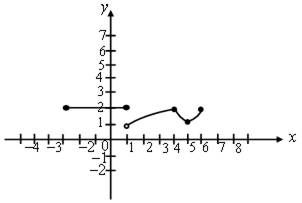
6. Повторение ранее изученного материала.
1) Решить № 8.31 (г) самостоятельно.
г) 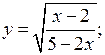
Функция определена, если
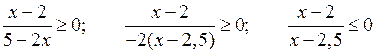
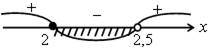
О т в е т: 2 ≤ х < 2,5.
2) Найдите область определения функции.
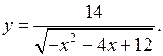
Решим неравенство:
– х2 – 4х + 12 > 0,
х2 + 4х – 12 < 0;
(х + 6)(х – 2) < 0.

О т в е т: (– 6; 2) или – 6 < х < 2.
III. Итоги урока.
1. Повторить способы задания функции.
2. Назвать свойства функции.
Домашнее задание: решить из домашней контрольной работы № 3 на с. 91–92 номера № 1 – № 4 на два варианта на отдельных листочках; к этим заданиям добавить еще № 10.21 (а; г) и № 10.22 (б; г) соответственно по вариантам.
Свойства функций
(3 ч)
У р о к 1
Цели: изучить свойства функции; научить исследовать на монотонность функцию, ограниченность функции снизу, сверху; развивать логическое мышление учащихся.
Ход урока
I. Объяснение нового материала.
1. В 7 и 8 классах мы изучали
некоторые свойства функций. Сейчас мы их соберем вместе. Во всех
определениях будет фигурировать числовое множество Х, являющееся
частью области определения функции:
Х ![]() D(f).
D(f).
2. О п р е д е л е н и е 1. Функцию
у = f(х) называют возрастающей на множестве
Х ![]() D(f),
если для любых двух точек х1 и
х2 множества Х,
таких, что х1 < х2, выполняется неравенство f(х1) < f(х2).
D(f),
если для любых двух точек х1 и
х2 множества Х,
таких, что х1 < х2, выполняется неравенство f(х1) < f(х2).
3. О п р е д е л е н и е 2.
Функцию у = f(х) называют убывающей на
множестве х ![]() D(f), если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство f(х1) > f(х2).
D(f), если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство f(х1) > f(х2).
4. Формулировка правила, которым пользуемся на практике. Рассмотреть рис. 84–85 на с. 98 учебника.
5. Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
6. Разобрать по учебнику на с. 98 пример 1.
7. Определение 3. Функцию у
= f(х) называют ограниченной снизу на множестве Х
![]() D(f),
если все значения функции на множестве Х больше некоторого числа. Рис.
86 на с. 99.
D(f),
если все значения функции на множестве Х больше некоторого числа. Рис.
86 на с. 99.
8. Определение 4. Функцию у
= f(х) называют ограниченной сверху на множестве Х
![]() D(f),
если все значения функции меньше некоторого числа. Рассмотреть рис. 87.
D(f),
если все значения функции меньше некоторого числа. Рассмотреть рис. 87.
9. Если функция ограничена и снизу, и сверху, то ее называют ограниченной.
10. Рассмотреть решение примера 2 по учебнику на с. 99–100.
II. Закрепление изученного материала.
1. Решить № 10.1 (в) – № 10.3 (в) на доске и в тетрадях.
2. Решить № 10.4 (в) – № 10.6 (в) с комментированием на месте.
3. Решить № 10.7 (в) – № 10.9 (в), построив графики соответствующих функций.
4. Решить № 10.18 (в; г) на доске и в тетрадях.
5. Решить № 10.19● (а).
Учитель объясняет решение.
а) Доказать, что функция ![]() х > –3
возрастает.
х > –3
возрастает.
Р е ш е н и е
Пусть х1 > х2 > – 3. Тогда
f(х1) = 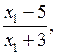 f(х2) =
f(х2) = 
f(х1) – f(х2) = 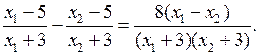
Здесь все множители положительны, значит, f(х1) > f(х2), а это и означает возрастание функции на заданном промежутке (– 3; + ∞).
6. Решить № 10.20 (в; г).
7. Повторение ранее изученного материала.
Решить № 40 (б) на с. 10 из темы «Задачи на повторение».
б) 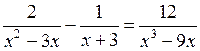
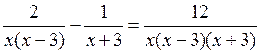
2(х + 3) – х(х – 3) = 12
2х + 6 – х2 + 3х – 12 = 0;
х2 – 5х + 6 = 0;
х1 = 3; х2 = 2.
х = 3 не является корнем уравнения, так как знаменатель дроби обращается в нуль при этом значении.
О т в е т: 2.
III. Итоги урока.
Домашнее задание: выучить определения 1–4 на с. 97–98 учебника; решить № 10.1 (а) – 10.6 (а); № 10.7 (а) – № 10.9 (а); № 10.18 (а), № 10.20 (а), № 10.19 (б).
У р о к 2
Цели: закрепить изученные свойства функции в ходе выполнения упражнений; научить находить наименьшее и наибольшее значения функции.
Ход урока
I. Проверка изученного материала.
1. Сформулируйте определение возрастающей функции, убывающей функции.
2. Какими формулировками пользуемся на практике при определении возрастания или убывания функции?
3. Устно решить № 10.1 (б), № 10.2 (б), № 10.5 (б), № 10.6 (б).
4. Определение функции, ограниченной снизу, ограниченной сверху.
5. Устно решить № 10.7 (б), № 10.8 (б), № 10.9 (б), схематично построив на доске графики функций.
II. Изучение нового материала.
1. О п р е д е л е н и е 5. Число m называют наименьшим
значением функции у = f(х) на множестве Х ![]() D(f), если:
D(f), если:
1) в Х существует такая точка х0, что f(х0) = m;
2) для всех х из Х выполняется
неравенство f(х) ≥ f(х0). Обозначение
унаим.
2. О п р е д е л е н и е 6. Число М
называют наибольшим значением функции у = f(х)
на множестве Х ![]() D(f),
если:
D(f),
если:
1) в Х существует такая точка х0, что f(х0) = М;
2) для всех х из Х выполняется неравенство
f(х) ≤ f(х0). Обозначение
унаиб.
3. Если множество Х не указано, то подразумевается, что речь идет об отыскании наименьшего или наибольшего значения функции во всей области определения.
4. Рассмотреть решение примера 3 на с. 101 учебника.
5. Рассмотреть понятия «функция выпукла вниз» и «функция выпукла вверх», используя рис. 88 и рис. 89 на с. 102.
6. Непрерывность функции на промежутке Х означает, что график функции на промежутке Х – сплошной, то есть не имеет проколов и скачков.
7. Запись в тетрадях учениками свойств функции:
1) область определения функции;
2) монотонность;
3) ограниченность;
4) наименьшее и наибольшее значения функции;
5) непрерывность функции;
6) область значений;
7) выпуклость.
III. Закрепление изученного материала.
1. Решить № 10.11 (б; в) на доске и в тетрадях.
б) у = – 2х2, х ![]() [– 1; 1].
[– 1; 1].
у(– 1) = – 2 · (– 1)2 = – 2 · 1 = – 2;
у(1) = – 2 · 12 = – 2.
у(0) = – 2 · 02 = 0
унаим = – 2; унаиб = 0.
в) у = – 4х + 1; х ![]() (– ∞; 0].
(– ∞; 0].
у(0) = – 4 · 0 + 1 = 1.
При отрицательных значениях х значения у будут положительными и больше 1.
Значит, унаим = 1, унаиб – не существует.
2. Решить № 10.12 (а; б) с комментированием на месте.
а) у = ![]() , если х
, если х ![]() [0; + ∞).
[0; + ∞).
у(0) = ![]() унаим = 0; унаиб –
не существует.
унаим = 0; унаиб –
не существует.
б) у = ![]() , если х
, если х ![]() [0; 3].
[0; 3].
у(0) = ![]() у(3) =
у(3) = ![]() унаим = 0; унаиб =
унаим = 0; унаиб =
![]()
3. Решить № 10.13 (а; б) на доске и в тетрадях.
а) ![]() D(f) = [4; + ∞);
D(f) = [4; + ∞);
у(4) = ![]() унаим = 0; унаиб –
не существует.
унаим = 0; унаиб –
не существует.
б) ![]() D(f) = [0; + ∞).
D(f) = [0; + ∞).
у(0) = ![]() унаиб = 3; унаим –
не существует.
унаиб = 3; унаим –
не существует.
4. Решить № 10.14 на доске и в тетрадях.
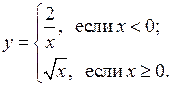
Свойства функции:
1) D(f) = (– ∞; ∞);
2) убывает на луче (– ∞; 0) и возрастает на луче [0; + ∞);
|
3) ограничена сверху и снизу; 4) унаим не существует, унаиб не существует; 5) непрерывна; 6) Е(f) = (– ∞; + ∞); 7) выпукла вверх. |
|
5. Решить № 8.25 (б) самостоятельно.
IV. Итоги урока. Выставление отметок.
Домашнее задание: по учебнику на с. 103–109
изучить свойства функций; решить № 10.11 (а; г), № 10.12 (в; г), №
10.13 (в; г); № 10.15,
№ 8.25 (г).
У р о к 3
Цели: в ходе выполнения упражнений закрепить знание свойств функций; способствовать выработке навыков и умений в построении и прочтении графиков функций; развивать логическое мышление учащихся.
Ход урока
I. Проверка домашнего задания.
1. Перечислите свойства функции.
2. Рассмотреть постоянную функцию у = С (рис. 90) на с. 103 учебника.
3. Перечислите свойства линейной функции у = kх + m (k ≠ 0) по рис. 91; 92 на с. 104.
4. Используя рис. 93 и рис. 94,
перечислите свойства функции у = kх2
(k ≠ 0).
5. Назовите свойства функции у = ![]() по рис. 95 и 96.
по рис. 95 и 96.
6. Какими свойствами обладает функция ![]() (рис. 97)?
(рис. 97)?
7. Сформулируйте свойства функции y = | x |, используя рис. 98.
8. Назовите свойства функции у = ах2 + bх + с (рис. 99 и рис. 100).
II. Выполнение упражнений.
1. Решить № 10.7 (г) и № 10.8 (г), используя графики функции.
2. Решить № 10.18 (б) и № 10.20 (б) на доске и в тетрадях.
3. Решить № 10.21 (б; в). Решение № 10.21 (б) объясняет учитель.
б) у = – 4х2 – 12х + 1. Графиком функции является парабола, ветви которой направлены вниз. Наибольшего значения функция достигает в вершине параболы (х0; у0):
х0 =
–![]()
у0(–![]() ) = – 4 ·
) = – 4 · ![]() – 12 · (–
– 12 · (–![]() ) + 1 = – 9 + 18 + 1 =
10;
) + 1 = – 9 + 18 + 1 =
10;
унаиб = 10, унаим – не существует;
в) у = 9х2 + 6х – 5.
Графиком функции является парабола, ветви которой
направлены вверх. Наименьшее значение функция имеет в вершине параболы (х0; у0). Найдем х0 = ![]()
у0 = 9 · (–![]() )2 + 6 · (–
)2 + 6 · (–![]() ) – 5 = 1 – 2 – 5 = – 6.
) – 5 = 1 – 2 – 5 = – 6.
унаим = – 6; унаиб – не существует.
4. Решить № 10.22 (а; в).
а) у = | х | + 3; х ![]() [– 5; 1].
[– 5; 1].
у(– 5) = | – 5 | + 3 = 5 + 3 = 8;
у(0) = | 0 | + 3 = 3;
у(1) = | 1 | + 3 = 4
унаим = 3; унаиб = 8.
в) у = – | 2х | – 1; х ![]() [– 1; 1].
[– 1; 1].
у(– 1) = – | – 2 | – 1 = – 2 – 1 = – 3;
у(1) = – | 2 | – 1 = – 2 – 1 = – 3;
у(0) = – | 0 | – 1 = – 1;
унаим = – 3; унаиб = – 1.
5. Решить № 10.26 на доске и в тетрадях.
Учитель при необходимости помогает в решении задания.
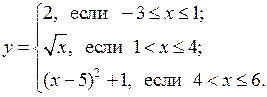
Свойства функции:
1) D(f) = [– 3; 6];
2) возрастает на (1; 4] и [5; 6];
убывает на отрезке [4; 5];
постоянна на отрезке [– 3; 1];
3) ограничена и снизу и сверху;
4) унаим = 1; унаиб = 2;
5) непрерывна;
6) Е(f) = [1; 2];
7) выпукла и вверх и вниз.
6. Повторение ранее изученного материала.
1) Решить № 8.31 (г) самостоятельно.
г) 
Функция определена, если
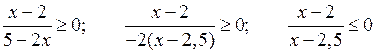
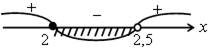
О т в е т: 2 ≤ х < 2,5.
2) Найдите область определения функции.
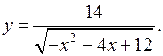
Решим неравенство:
– х2 – 4х + 12 > 0,
х2 + 4х – 12 < 0;
(х + 6)(х – 2) < 0.

О т в е т: (– 6; 2) или – 6 < х < 2.
III. Итоги урока.
1. Повторить способы задания функции.
2. Назвать свойства функции.
Домашнее задание: решить из домашней контрольной работы № 3 на с. 91–92 номера № 1 – № 4 на два варианта на отдельных листочках; к этим заданиям добавить еще № 10.21 (а; г) и № 10.22 (б; г) соответственно по вариантам.
Функции у = хn (n Î N),
их свойства и графики (3 ч)
У р о к 1
Цели: изучить свойства степенной функции с натуральным показателем, ее график; закрепить знание свойств функции у = хn (при n – четном числе) в ходе упражнений.
Ход урока
I. Анализ контрольной работы.
1. Указать основные ошибки, допущенные учащимися в ходе выполнения работы.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Изучение нового материала.
1. Определение степенной функции у = хn с натуральным показателем.
2. Две степенные функции мы уже изучили: у = х (n = 1) и у = х2 (n = 2). Как выглядят графики функций у = х3, у = х4, у = х5, у = х6 и т. д.? Каковы свойства этих функций?
3. Рассмотреть функцию у = х4, х ≥ 0, составив таблицу значений и построив точки по соответствующим координатам: рис. 104a и рис. 104б на с. 116 учебника.
4. Построить график функции у = х4 (рис. 105) и записать в тетрадях свойства функции у = х4:
1) D(f) = (– ∞; ∞);
2) четная функция;
3) убывает на луче (– ∞; 0], возрастает на луче [0; + ∞);
4) ограничена снизу, не ограничена сверху;
5) унаим = 0, унаиб – не существует;
6) непрерывна;
7) Е(f) = [0; + ∞);
8) выпукла вниз.
5. Функция у = х2n (2n – четное
число). Речь идет о функциях у = х6,
у = х8 и вообще
о степенной функции с четным показателем степени.
График любой такой функции похож на график функции у = х4 (рис. 105), только его ветви более круто направлены вверх.
Кривая у = х2n касается оси х в точке (0; 0), то есть одна ветвь кривой плавно переходит в другую, как бы прижимаясь к оси х.
III. Закрепление изученного материала.
1. Решить № 12.1 (б; в) и на доске и в тетрадях.
2. Решить № 12.9 (а) и № 12.10 (б) на доске и в тетрадях.
3. Решить № 12.11 (а; в).
а) у = х6 на отрезке [– 1; 1].
у = f(х) = f(0) = х6 = 06 = 0; унаим = 0;
у = f(– 1) = f(1) = (– 1)6 = (1)6 = 1; унаиб = 1;
в) у = х6 на полуинтервале (– 2; 2].
у = f(0) = 0; унаим = 0;
у = f(2) = 26 = 64; унаиб = 64.
4. Решить № 12.13 (в) с комментированием на месте.
в) у = х6 и у = – 2х2. Решим уравнение х6 = – 2х2;
х6 + 2х2 = 0; х2(х4 + 2) = 0; х = 0; х4 = – 2 – нет решений.
х = 0, то у = 0.
О т в е т: (0; 0).
5. Решить № 12.14 (а), построив графики функций у
= х6 и ![]() и найдя координаты точки их
пересечения.
и найдя координаты точки их
пересечения.
О т в е т: х = – 1.
6. Решить № 12.19 (а) на доске и в тетрадях.
а) 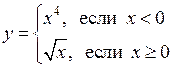
Свойства:
1) D(f) = (– ∞; + ∞);
2) функция ни четная, ни нечетная;
3) убывает на луче (– ∞; 0], возрастает на луче [0; + ∞);
4) ограничена снизу, не ограничена сверху;
|
5) унаим = 0, унаиб – не существует; 6) непрерывна; 7) Е(f) = [0; + ∞); 8) выпукла вниз на луче (–∞; 0); выпукла вверх на луче [0; + ∞). |
|
7. Решить № 12.33● (а; в). Решение объясняет учитель.
а) х4 + х2 + 1 = 0.
Левая часть уравнения положительна при всех значениях х, значит, уравнение не имеет корней.
в) х4 + х2 – 2х + 3 = 0.
I способ.
Преобразуем уравнение к виду х4 = – х2 + 2х – 3. Графики
функций
у = х4 и у
= – х2 + 2х – 3
не пересекаются, следовательно, уравнение не имеет корней.
II способ.
Преобразуем уравнение к виду х4 + (х – 1)2 + 2 = 0. Левая часть уравнения положительна при всех значениях х, значит, уравнение не имеет корней.
IV. Итоги урока. Выставление отметок.
Домашнее задание: изучить по учебнику материал на с. 115–119; решить № 12.1 (а; г); № 12.9 (в); № 12.10 (г); № 12.13 (а); № 12.14 (в); № 12.19 (в).
У р о к 2
Цели: изучить свойства степенной функции у = хn при нечетном показателе, ее график; закрепить знание свойств функции у = х2n + 1 в ходе выполнения упражнений; развивать у учащихся навыки построения графиков функций.
Ход урока
I. Устная работа.
1. Дайте определение четной и нечетной функции. Сформулируйте свойства графика четной функции и нечетной функции.
2. Какую функцию называют степенной функцией с натуральным показателем?
3. Сформулируйте свойства степенной функции с четным показателем. Покажите схематически, как выглядит график этой функции.
II. Объяснение нового материала.
1. Функция у = х3 – нечетная, значит, ее график симметричен относительно начала координат. Разобрать построение графика по рис. 107 на с. 118 учебника. Кривую называют кубической параболой.
2. Свойства функции у = х3 (записать в тетради):
1) D(f) = (– ∞; + ∞);
2) нечетная функция;
3) возрастает;
4) не ограничена ни снизу, ни сверху;
5) нет ни наименьшего, ни наибольшего значений;
6) непрерывна;
7) Е(f) = (– ∞; + ∞);
8) выпукла вверх при х < 0, выпукла вниз при х > 0.
3. Функция у = х2n + 1 (2n + 1 – нечетное число).
Речь идет о функциях у = х3, у = х5, у = х7 и вообще о степенной функции с нечетным показателем степени (3; 5; 7; 9 и т. д.).
График любой такой функции похож на график функции у = х3 (рис. 107), только чем больше показатель, тем более круто направлены вверх (и вниз) ветви графика. Кривая у = х2n + 1 касается оси х в точке (0; 0).
III. Закрепление изученного материала.
1. Решить № 12.8 (в; г) на доске и в тетрадях.
2. Решить № 12.9 (б) и № 12.10 (а).
3. Решить № 12.12 (а; в) с комментированием на месте.
а) у = х5 на отрезке [– 1; 1];
у = f(– 1) = (– 1)5 = – 1; унаим = – 1;
у = f(1) = 15 = 1; унаиб = 1.
в) у = х5 на полуинтервале (1; 3].
унаим – нет, унаиб = 35 = 243.
4. Решить № 12.13 (г) на доске и в тетрадях.
г) у = х7 и у = ![]() решим уравнение х7 =
решим уравнение х7 = ![]() при х ≥ 0;
при х ≥ 0;
(х7)2 = (![]() )2; х14 =
х; х14 – х
= 0;
)2; х14 =
х; х14 – х
= 0;
х(х14 – 1) = 0; х = 0 или х14 – 1 = 0, х14 = 1, х = 1.
Если х = 0, то у = 0;
если х = 1, то у = 1.
О т в е т: (0; 0); (1; 1).
5. Решить № 12.14 (б). О т в е т: 1; – 1.
6. Решить № 12.17 (в; г), изобразив графики функций.
б) 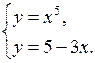
О т в е т: одно решение.
в) 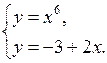
О т в е т: нет решений, то есть 0 решений.
7. Решить № 12.19 (г). Построить и прочитать график функции.

Свойства:
1) D(f) = (– ∞; 2];
2) функция ни четная, ни нечетная;
3) возрастает на (– ∞; – 1], убывает на [– 1; 2];
4) ограничена сверху;
5) наименьшего значения нет; унаиб = – 1;
6) непрерывна;
7) Е(f) = (– ∞; – 1];
8) выпукла вверх при х < – 1.
8. Решить № 12.37●.
Решение объясняет учитель.
f(х) = – х3; f(–![]() ) = – (–
) = – (–![]() )3 =
)3 = ![]() ;
;
f(2х5) = – (2х5)3 = – 8х15;
Значит, (f(х))9 : f(–![]() ) = (– х3)9 :
) = (– х3)9 : ![]() = – 8х15 = f(2х5).
= – 8х15 = f(2х5).
9. Решить № 12.35●.
Решают учащиеся с помощью учителя.
Р е ш е н и е
f(х) = – х4; f(4х) = – (4х)4 = – 256х4; f(–![]() ) = – (–
) = – (–![]() )4 = –
)4 = –![]()
(f(х))2 = (– х4)2 = х8; значит, f(4х)
· f(–![]() ) =
– 256х4 · (–
) =
– 256х4 · (–![]() ) = х8 =
) = х8 =
= (f(х))2.
IV. Итоги урока.
Повторить свойства функции у = хn при нечетном показателе.
Домашнее задание: изучить по учебнику на с. 119–122 материал и решение примеров 1 и 2, записать в тетрадь; решить № 12.13 (б); № 12.14 (г), № 12.17 (а; г), № 12.19 (б) и № 12.34●.
У р о к 3
Цели: развивать и закреплять знания учащихся в построении и чтении графиков функций; использовать свойства степенной функции с натуральным показателем при решении систем уравнений и графическом решении неравенств; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Построить на доске график функции у = х2n. Используя этот график, решить устно задание:
Дана функция у = f(х), где f(х) = х8. Сравните числа:
а) f(16,8) и f(16,2); б) f(– 3,1) и f(– 2,9);
в) f(– 8,3) и f(8,3).
2. Построить на доске график функции у = х2n + 1. По этому графику устно решить упражнение:
Дана функция у = f(х), где f(х) = х11. Сравните числа:
а) f(13,4) и f(13,6); б) f(– 7,2) и f(– 4,1);
в) f(– 2,7) и f(2,7).
3. Обратить внимание учащихся на то, что при решении уравнения х5 = 3 – 2х (пример 1, рис. 108 на с. 120 учебника) геометрическая модель наглядно иллюстрирует следующее утверждение, которое иногда позволяет изящно решить уравнение: «Если функция у = f(х) возрастает, а функция у = g(х) убывает и если уравнение f(х) = g(х) имеет корень, то только один».
II. Выполнение упражнений.
1. Решить № 12.18 (б; в), построив графики функций.
О т в е т: б) одно; в) два решения.
2. Решить № 12.20 на доске и в тетрадях.
а) у = хn; точка (2; 256), тогда х = 2, у =
256; имеем 256 = 2n;
28 = 2n,
n = 8.
б) Точка (– 2; – 128); х = – 2; у
= – 128. Значит, – 128 = (– 2)n;
(– 2)7 =
= (– 2)n; отсюда n
= 7.
в) Самостоятельно решить: точка (3; 243), тогда х = 3, у = 243. Получим 3n = 243; 3n = 35; n = 5.
г) Самостоятельно: точка (– 4; 256);
отсюда х = – 4, у = 256. Получим
(– 4)n = 256 = (– 4)4; n = 4.
О т в е т: а) 8; б) 7; в) 5; г) 4.
3. Решить № 12.25 (в; г).
Учитель объясняет решение, привлекая учащихся к обсуждению построения графиков функций.
в) х3 ≥ | х | – 2; строим графики функций у = х3 и у = | х | – 2.
При х ≥ – 1 график функции у = х3 расположен выше графика у
= | х | –
– 2, значит, х3 ≥
| х | – 2.
О т в е т: х ≥ – 1.
г) – х4 < ![]() + 1.
+ 1.
Строим графики функций у = – х4 и у = ![]() + 1.
+ 1.
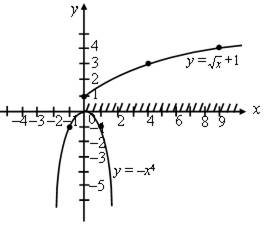
При х ≥ 0 график функции у =
– х4 расположен
ниже графика
у = ![]() + 1,
значит, значения меньше, то есть выполняется неравенство
+ 1,
значит, значения меньше, то есть выполняется неравенство
– х4 < ![]() + 1.
+ 1.
О т в е т: х ≥ 0.
4. Решить № 12.27 и № 12.28 на доске и в тетрадях, построив и прочитав графики функций.
5. Повторение ранее изученного материала.
Решить № 30 на с. 8 из «Задачи на повторение».
а) ![]()
![]()
б) ![]()
![]()
![]()
О т в е т: а) 1; б) 0.
III. Итоги урока.
Домашнее задание: решить № 12.18 (а; г); № 12.25 (а; б), № 12.30, № 12.36●.
Функции у = х–n (n Î N),
их свойства и графики (3 ч)
У р о к 1
Цели: ввести определение степенной функции с целым отрицательным показателем; изучить графики и свойства функций вида у = х–2n, научить строить графики и с их помощью графически решать уравнения.
Ход урока
I. Самостоятельная работа (10–15 мин).
В а р и а н т I
1. Постройте график функции:
а) y = –x4; б) y = (x – 3)5 – 2.
2. Найдите наименьшее и наибольшее значения функции y = x6 на отрезке [– 2; 1].
3. Определите число решений системы уравнений: 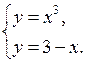
В а р и а н т II
1. Постройте график функции:
а) y = –x5; б) y = (x – 2)4 – 3.
2. Найдите наименьшее и наибольшее значения функции y = x8 на отрезке [– 1; 2].
3. Определите число решений системы уравнений: 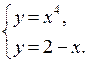
II. Изучение нового материала.
1. О п р е д е л е н и е. Функции вида у = х–n, где n – натуральное число, называют степенными функциями с отрицательным целым показателем.
2. По определению степени с отрицательным
показателем, х–n = ![]()
Поэтому вместо записи у = х–n можно использовать запись 
3. В курсе алгебры 8 класса мы изучили функцию ![]() ее свойства и график
(рис. 110 на с. 123 учебника). График
ее свойства и график
(рис. 110 на с. 123 учебника). График ![]() – гипербола.
– гипербола.
4. Рассмотрим функцию у = х–2 = ![]() при х ≠ 0, ее график и
свойства.
при х ≠ 0, ее график и
свойства.
Рассмотрим таблицу значений функции у = ![]() , х > 0 (с.
101) и построение точек по координатам (рис. 111a и рис. 111б на с. 125
учебника).
, х > 0 (с.
101) и построение точек по координатам (рис. 111a и рис. 111б на с. 125
учебника).
Затем изучим построение графика у = х–2 по рис. 112 на с. 126.
5. Записать в тетрадь свойства функции у = х–2:
1) D(f) = (– ∞; 0) ![]() (0; + ∞);
(0; + ∞);
2) четная функция;
3) убывает на открытом луче (0; + ∞),
возрастает на открытом луче
(– ∞; 0);
4) ограничена снизу, не ограничена сверху;
5) нет ни наименьшего, ни наибольшего значений;
6) непрерывна при х < 0 и при х > 0;
7) Е(f) = (0; + ∞);
8) выпукла вниз и при х < 0, и при х > 0.
6. Рассмотреть функцию у = х–2n.
Речь идет о функциях у = ![]() у =
у = ![]() у =
у = ![]() и т. д.
и т. д.
График такой функции похож на график функции у
= ![]() (рис. 112).
(рис. 112).
Кривая у = ![]() асимптотически приближается к осям
координат. Ось х (прямая у = 0) является горизонтальной
асимптотой графика функции
асимптотически приближается к осям
координат. Ось х (прямая у = 0) является горизонтальной
асимптотой графика функции
у =![]() , а ось у
(прямая х = 0) вертикальной асимптотой этого графика.
, а ось у
(прямая х = 0) вертикальной асимптотой этого графика.
III. Закрепление изученного материала.
1. Решить № 13.1 (а) устно.
2. Решить № 13.2 (в) на доске и в тетрадях.
3. Решить № 13.7 (а; б), используя график
у = ![]() или
график рис. 112 учебника.
или
график рис. 112 учебника.
а) у = х–4 на отрезке [![]() 1].
1].
у = 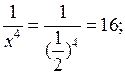 у(1) =
у(1) = 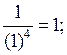 значит, унаим = 1; унаиб = 16.
значит, унаим = 1; унаиб = 16.
б) на луче (– ∞; – 2]; унаим не существует; унаиб = 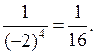
4. Решить № 13.9 (б; г) на доске и в тетрадях.
б) у = х–4 и у = – 2; решим уравнение х–4 = – 2; ![]() = – 2 – нет решений.
= – 2 – нет решений.
г) у = ![]() и у = | х |; решим
уравнение
и у = | х |; решим
уравнение ![]() = | х
|.
= | х
|.
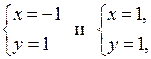 тогда точки (– 1; 1) и (1; 1).
тогда точки (– 1; 1) и (1; 1).
О т в е т: б) нет точек пересечения графиков функций; г) точки (– 1; 1) и (1; 1).
5. Решить № 13.15 (а; г).
Объясняет учитель.
а) у = х–n; т очка (2; ![]() ); х = 2; у =
); х = 2; у = ![]() ;
;
![]() = 2–n; 2–8 =
2–n; n = 8.
= 2–n; 2–8 =
2–n; n = 8.
г) у = х–n; точка (![]() ; 625), тогда (
; 625), тогда (![]() )–n = 625; 5n = 54;
n = 4.
)–n = 625; 5n = 54;
n = 4.
IV. Итоги урока.
Домашнее задание: изучить материал на с. 122–127 учебника; решить № 13.2 (а), № 13.7 (в; г); № 13.12, № 12.33● (б).
У р о к 2
Цели: изучить функцию у = х–(2n + 1), ее свойства и график; закрепить знания учащихся в ходе выполнения упражнений; развивать умения в построении и прочтении графиков функции.
Ход урока
I. Анализ самостоятельной работы.
1. Сообщить учащимся результаты самостоятельной работы, ошибки, сделанные ими в ходе работы.
2. Объяснить на доске решение заданий, вызвавших затруднения.
3. Проверить выборочно по тетрадям выполнение домашнего задания.
4. Решить устно № 13.1 (в).
II. Объяснение нового материала.
1. Рассмотрим функцию у = х–(2n + 1) = 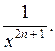
Речь идет о функциях 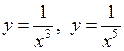 и т. д. График любой такой функции похож
на график функции
и т. д. График любой такой функции похож
на график функции ![]() рассмотреть
по учебнику рис. 110 на с. 123.
рассмотреть
по учебнику рис. 110 на с. 123.
2. Отметим, что ось х является горизонтальной
асимптотой графика функции у = 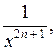 а ось у является вертикальной
асимптотой этого графика.
а ось у является вертикальной
асимптотой этого графика.
3. Записать в тетради свойства функции у = х–(2n + 1):
1) D(f) = (– ∞; 0) ![]() (0; + ∞);
(0; + ∞);
2) нечетная функция;
3) убывает на открытом луче (0; + ∞) и на открытом луче (– ∞; 0);
4) не ограничена ни снизу, ни сверху;
5) нет ни наименьшего, ни наибольшего значений;
6) непрерывна при х < 0 и при х > 0;
7) Е(f) = (– ∞; 0) ![]() (0; + ∞);
(0; + ∞);
8) выпукла вверх при х < 0, выпукла вниз при х > 0.
III. Выполнение упражнений.
1. Решить устно № 13.1 (б).
2. Решить № 13.2 (г) на доске и в тетрадях.
3. Решить № 13.3 (в; г); напомнить учащимся построение графиков таких функций.
4. Решить № 13.8 (а; в) с комментированием на месте.
а) 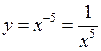 на отрезке [– 2; – 1]. Используем график
функции на рис. 110 с. 123 учебника.
на отрезке [– 2; – 1]. Используем график
функции на рис. 110 с. 123 учебника.
у(– 2) = 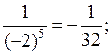 у(– 1) =
у(– 1) = 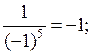
унаим =
– 1; унаиб = ![]()
в) y = x–5 на полуинтервале (![]() 4];
4];
у(4) = 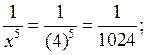
унаиб –
не существует; унаим =
![]()
5. Решить № 13.9 (в).
в) y = x–7 и y = –x; решим уравнение х–7 = – х;
 х ≠ 0, тогда 1 + х8 = 0;
х ≠ 0, тогда 1 + х8 = 0;
х8 = – 1 нет решений, значит, нет точек пересечения графиков функций.
6. Решить № 13.10 (а; г), построив графики функций.
а) х–5 = х.
|
Строим графики |
|
О т в е т: х = – 1; х = 1.
г) х–4 =
![]()
Строим графики 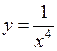 и у =
и у = ![]()
О т в е т: х = 1.
7. Решить № 13.11 (а; б) только на доске, схематично построив графики функций.
|
а) |
|
О т в е т: а) одно решение.
|
б) |
|
О т в е т: б) четыре решения.
8. Учитель объясняет решение № 13.25●.
Р е ш е н и е
f(х2) = (х2)2 = х4; 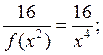
g(![]() ) =
) = 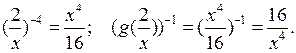
Значит, 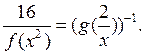
III. Итоги урока.
Повторить свойства функции у = х–n.
Домашнее задание: изучить материал § 13, записать в тетради решение примеров 1 и 2 на с. 127–128; решить № 13.2 (б), № 13.8 (б; г); № 13.9 (а), № 13.10 (б; в); № 13.23●.
У р о к 3
Цели: способствовать выработке умений и
навыков в построении графиков функций и их прочтении; закрепить знание
свойств функции
у = х–n;
научить решать графически неравенство; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Сформулируйте свойства функции у = х–2n и на доске постройте ее график.
2. Сформулируйте свойства функции у = х–(2n + 1) и постройте ее график.
3. Решите № 13.1 (г) устно.
II. Выполнение упражнений.
1. Решить № 13.4 (а; б) на доске и в тетрадях.
2. Решить № 13.15 (б; в).
б) у = х–n, точка (– 2; –![]() ); тогда х = – 2, у = –
); тогда х = – 2, у = –![]()
(– 2)–n =
(–![]() ); (– 2)–n = (– 2)–5, значит, n = 5.
); (– 2)–n = (– 2)–5, значит, n = 5.
в) (7; ![]() ); (7)–n =
); (7)–n = ![]() ; (7)–n = (7)–3; значит, n = 3.
; (7)–n = (7)–3; значит, n = 3.
О т в е т ы: б) 5; в) 3.
3. Решить № 13.18 (в; г), изобразив схематично графики функций.
|
в) |
|
О т в е т: четыре решения.
|
г)
О т в е т: два решения. |
|
4. Решить № 13.22 (в; г), построив графики функций.
в) х–2 ≤ 2х – 1;
Строим графики функций у = х–2 = ![]() и у = 2х – 1.
и у = 2х – 1.
При х ≥ 1 график у = 2х – 1 (прямая) расположена выше кривой графика функции у = х–2.
О т в е т: х ≥ 1.
г) х–3 >
![]()
Строим графики функций у = х–3 = ![]() и у =
и у = ![]() при х ≥ 0.
при х ≥ 0.
Значения функции у = х–3 больше значений функции у
= ![]() (кривая
(кривая
у = х–3 выше)
при 0 < х < 1.

О т в е т: 0 < х < 1.
5. Решить № 13.24●.
Учитель помогает при решении, один ученик решает у доски, остальные самостоятельно в тетрадях.
f(х) = х–3; f(х2) = (х–3)2 = х–6; (f(х2))2 = (х–6)2 = х–12;
g(х) = х4; (g(х))–3 = (х4)–3 = х–12.
Значит, (f(х2))2 = (g(х))–3.
6. Повторение ранее изученного материала.
Решить № 19 (в; г) на доске и в тетрадях (с. 7 «Задачи на повторение»).
в) 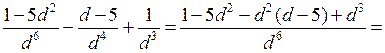
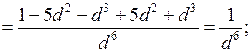
г) 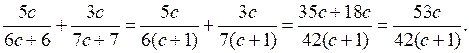
7. Решить № 13.21 (б).
III. Итоги урока. Выставление отметок.
Домашнее задание: повторить изученный материал § 13; решить № 13.4 (в; г); № 13.13; № 13.18 (а; б); № 13.22 (а; б).
Функция у = ![]() ее
свойства и график (3 ч)
ее
свойства и график (3 ч)
У р о к 1
Цели: познакомить учащихся с понятием кубического корня; учить вычислять кубический корень из числа; развивать вычислительные навыки учащихся.
Ход урока
I. Проверка домашнего задания.
1. Решить на доске задачи из домашней работы, вызвавшие затруднения у учащихся.
2. Объяснение нового материала.
1. Определение 1. Число b называют кубическим корнем (или корнем третьей степени) из числа a, если выполняется равенство b3 = a.
Пишут: ![]() ; а – подкоренное число, 3 –
показатель корня.
; а – подкоренное число, 3 –
показатель корня.
2. Равенства ![]() , b3 = a и
, b3 = a и ![]() эквивалентны, то есть выражают одну и ту
же зависимость между действительными числами а и b. Короче это
записывается с помощью знака эквивалентности «
эквивалентны, то есть выражают одну и ту
же зависимость между действительными числами а и b. Короче это
записывается с помощью знака эквивалентности «![]() », т. е.
», т. е. ![]()
3. Рассмотреть примеры вычисления кубического корня из числа на с. 128 учебника.
4. Кубический корень ![]() существует для любого числа а. Это
утверждение доказывается в курсе высшей математики. Мы будем пользоваться им
без доказательства. Результат извлечения кубического корня сравнительно редко
оказывается рациональным числом. Чаще получается иррациональное число, для
которого можно найти лишь приближенное значение.
существует для любого числа а. Это
утверждение доказывается в курсе высшей математики. Мы будем пользоваться им
без доказательства. Результат извлечения кубического корня сравнительно редко
оказывается рациональным числом. Чаще получается иррациональное число, для
которого можно найти лишь приближенное значение.
5. Рассмотреть как пример доказательство того, что ![]() – иррациональное число
на с. 129 учебника.
– иррациональное число
на с. 129 учебника.
6. Корень третьей степени из положительного числа –
положительное число, а корень третьей степени из отрицательного числа –
отрицательное число. Это следует из того, что при возведении в куб знак числа
не меняется. Справедливо тождество ![]()
7. Рассмотреть пример 1 на с. 129 учебника.
II. Выполнение упражнений.
1. Решить устно № 14.1 на с. 88 задачника.
О т в е т: а) 4; б) –5; в) 6; г) –7.
2. Решить № 14.2 на с. 88 задачника на доске и в тетрадях.
а) ![]()
б) ![]()
в) ![]()
г) ![]()
О т в е т: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
3. Решить № 14.3, с. 88 задачника на доске и в тетрадях.
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Ответ: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
4. Решить № 14.4, с. 88 задачника на доске и в тетрадях.
О т в е т: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
5. Решить № 14.5 (а, б), с. 88 задачника на доске и в тетрадях.
а) ![]()
б) ![]()
О т в е т: а) ![]() б)
б) ![]()
6. Решить № 14.6 (а, б), с. 88 задачника на доске и в тетрадях.
a) ![]()
б) ![]()
О т в е т: a) ![]() б)
б) ![]()
7. Решить № 14.7 (а, б), с. 88 задачника на доске и в тетрадях.
О т в е т: а) ![]() б)
б) ![]()
8. Решить № 14.8, с. 88 задачника на доске и в тетрадях.
О т в е т: a) a2; б) –3b; в) 2a3b4.
9. Решить № 14.9, с. 88 задачника на доске и в тетрадях.
а) 
б) 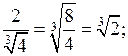
в) 
г) 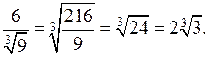
О т в е т: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
10. Решить № 14.10 (а, б), с. 88 задачника на доске и в тетрадях.
О т в е т: а) ![]() б)
б) ![]()
11. Решить № 14. 11 (а, б, в), с. 88 задачника на доске и в тетрадях.
а) ![]()
О т в е т: а) ![]() б)
б) ![]() в)
в) ![]()
12. Решить № 14. 12 (а, б, в), с. 88 задачника на доске и в тетрадях.
а) ![]()
О т в е т: а) ![]() б)
б) ![]() в)
в) ![]()
III. Итог урока.
Сформулировать определение кубического корня из числа.
Домашнее задание: изучить материал учебника § 14 на с. 128–129; решить № 14.4 (в, г); № 14.5 (в; г); № 14.6 (в, г); № 14.7 (в; г); № 14.10 (в, г) на с. 88 задачника.
У р о к 2
Цели: изучить свойства функции ![]() , ее график; закрепить знания
свойств функции
, ее график; закрепить знания
свойств функции ![]() в
ходе выполнения упражнений, развивать логическое мышление.
в
ходе выполнения упражнений, развивать логическое мышление.
Ход урока
I. Повторение изученного материала.
1. Дать определение кубического корня.
2. Решить № 14.11 (г) на с. 88 задачника у доски.
г) ![]()
О т в е т: г) ![]()
3. Решить № 14. 12 (г) на с. 88 задачника у доски.
г) ![]()
О т в е т: г) ![]()
II. Изучение нового материала.
1. Рассмотреть функцию ![]() , отметить некоторые ее свойства,
разобрать построение графика функции по рис . 114 а и 114 б на с. 131 учебника.
, отметить некоторые ее свойства,
разобрать построение графика функции по рис . 114 а и 114 б на с. 131 учебника.
2. Сделать выводы.
Свойства функции ![]()
1) D(f) = (–∞; +∞);
2) ![]() – нечетная функция;
– нечетная функция;
3) функция ![]() возрастает на всей числовой
прямой;
возрастает на всей числовой
прямой;
4) функция ![]() не ограничена ни снизу, ни сверху;
не ограничена ни снизу, ни сверху;
5) у функции нет ни наименьшего, ни наибольшего значений;
6) функция непрерывна на всей числовой прямой;
7) Е(f) = (–∞; +∞);
8) функция выпукла вниз на (–∞; 0] и выпукла вверх на [0; +∞).
График функции

3. Рассмотреть примеры 2 и 3 на с. 116–117 учебника.
III. Закрепление изученного материала.
1. Решить устно № 14.14, с. 89 задачника.
О т в е т: а) да; б) нет; в) да; г) да.
2. Решить № 14.16 на с. 89 задачника.
О т в е т: а) 1; 2, б) унаим не существует, унаиб = 0, в) –3; 4,
г) унаим = 0,5,
унаиб не существует.
3. Решить № 14.17 (б) на с. 89 задачника.
Построив в одной системе координат графики
функций ![]()
и у = | x | (рис. 1), мы убеждаемся, что они
пересекаются в точках (1; 1)
и (0; 0). Так как функция ![]() – возрастающая функция, а у
= | x |
– возрастающая функция, а у
= | x |
биссектрисы I и II координатных четвертей, то больше точек нет.
Рис. 1
4. Решить № 14.18 (а) на с. 89 задачника.
Введем привычное для нас обозначение ![]()
![]() следовательно, функция
следовательно, функция ![]() – нечетная.
– нечетная.
5. Решить № 14.20 (а) на с. 89 задачника.
Построив в одной системе координат графики функций y
= 4 – x2 и ![]() (рис. 2), мы
убеждаемся, что они пересекаются в двух точках.
(рис. 2), мы
убеждаемся, что они пересекаются в двух точках.
Рис. 2
6. Решить № 14.21 (а, б) на с. 89 задачника.
а) Перейдем к вспомогательной системе координат с
началом
в точке (3; 2) (пунктирные прямые х = 3, у = 2 на рис. 3) и
привяжем функцию ![]() к
новой системе координат. Получим требуемый рисунок.
к
новой системе координат. Получим требуемый рисунок.
Рис. 3
Прочитаем построенный график.
1) D(f) = (–∞; +∞);
2) функция не является ни четной, ни нечетной;
3) функция возрастает на всей числовой прямой;
4) функция не ограничена ни снизу, ни сверху;
5) у функции нет ни наименьшего, ни наибольшего значений;
6) функция непрерывна на всей числовой прямой;
7) E(f) = (–∞; +∞);
8) функция выпукла вниз на (–∞; 3] и выпукла вверх на [3; +∞).
б) Построим вначале график функции ![]() и отразим его симметрично
относительно оси Оу. Получим требуемый рисунок (см. рис. 4).
и отразим его симметрично
относительно оси Оу. Получим требуемый рисунок (см. рис. 4).
Рис. 4
Прочитаем построенный график
1) D(f) = (–∞; +∞);
2) функция нечетная;
3) функция убывает на всей числовой прямой;
4) функция не ограничена ни снизу, ни сверху;
5) у функции нет ни наименьшего, ни наибольшего значений;
6) функция непрерывна на всей числовой прямой;
7) E(f) = (–∞; +∞);
8) функция выпукла вверх на (–∞; 0] и выпукла вниз на [0; +∞).
IV. Итоги урока.
Перечислить свойства функции ![]() .
.
Домашнее задание: изучить материал учебника, § 14 на с. 130–133; решить № 14.12 (в, г); № 14.13 (в, г), № 14.18 (б); № 14.21 (в; г) на с. 88–89 задачника.
У р о к 3
Цели: закрепить навыки и умения учащихся в построении и чтении графиков функции; подготовить учащихся к контрольной работе.
Ход урока
I. Проверка усвоения знаний учащимися.
1. Решить задания, вызвавшие затруднения у учащихся.
2. Указать ошибки, сделанные учащимися при решении заданий.
3. Построить график функции ![]() (только на доске)
(только на доске)
4. Решить № 14.20 (б), с. 142 задачника.
О т в е т: б) 2.
II. Изучение нового материала.
1. Разобрать по учебнику решение примера 4 на с. 133–134 учебника.
2. Рассмотреть еще одно свойство, которое полезно при исследовании функции, при построении ее графика, при решении неравенств графическим методом – промежутки знакопостоянства функции, то есть те промежутки оси х, на которых функция сохраняет свой знак. Рассмотреть график функции, который изображен на рис. 120 учебника.
III. Закрепление изученного материала.
1. Решить № 14.15 (а, б), с. 89 задачника на доске и в тетради.
а) Перейдем к вспомогательной системе координат с
началом в точке (0; –1) (пунктирные прямые х = 0, у = –1 на рис.
1) и привяжем функцию ![]() к новой системе координат. Получим
требуемый рисунок (см. рис. 1).
к новой системе координат. Получим
требуемый рисунок (см. рис. 1).
Рис. 1
Промежутками знакопостоянства для этой функции будут: открытый луч (–∞; 1) – здесь функция принимает отрицательные значения, (1; +∞) – на этом открытом луче функция принимает положительные значения.
б) Перейдем к вспомогательной системе координат с
началом в точке (–2; 0) (пунктирные прямые х = –2, у = 0 на рис.
2) и привяжем функцию ![]() к новой системе координат. Получим
требуемый рисунок (см. рис. 2).
к новой системе координат. Получим
требуемый рисунок (см. рис. 2).
Рис. 2
Промежутками знакопостоянства для этой функции будут: открытый луч (–∞; –2) – здесь функция принимает отрицательные значения, (–2; +∞) – на этом открытом луче функция принимает положительные значения.
2. Решить № 14.19 (а) на с. 89 задачника. Учитель при необходимости помогает в решении учащимся.
Построим прямую y = –2x и возьмем ее
часть при x ≤ 0 (рис. 3). Построим график функции ![]() и возьмем ее часть при x
> 0 (рис. 4). А теперь обе построенные линии расположим в одной системе
координат (рис. 5) – это и будет требуемый график.
и возьмем ее часть при x
> 0 (рис. 4). А теперь обе построенные линии расположим в одной системе
координат (рис. 5) – это и будет требуемый график.
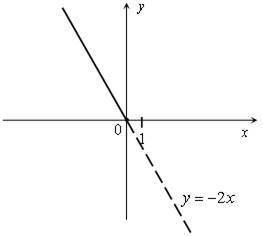
Рис. 3

Рис. 4
Рис. 5
Прочитаем построенный график.
1) D(f) = (–∞; +∞);
2) функция не является ни четной, ни нечетной;
3) функция убывает на (–∞; 0] и возрастает [0; +∞);
4) функция ограничена снизу нулем;
5) у функции есть наименьшее значение у = 0, наибольшего значения нет;
6) функция непрерывна на всей числовой прямой;
7) E(f) = (0; +∞);
8) функция выпукла вверх на [0; +∞).
3. Решить № 14.22 (а) на с. 90 задачника. Учитель при необходимости помогает в решении учащимся.
4. Решить № 14.23 (а) на с. 90 задачника. Учитель объясняет у доски № 14.23 (а).
Введем замену переменной ![]() тогда уравнение примет вид z2 +
тогда уравнение примет вид z2 +
+ z – 6 = 0. Решив уравнение, получим z1 = 2 и z2 = –3. Тогда х1 = 8 и
х2 = –27.
О т в е т: 8; –27.
5. № 14.23 (б) на доске и в тетрадях выполняют самостоятельно ученики. Учитель при необходимости помогает в решении учащимся.
6. Решить № 14.24 (а) на с. 90 задачника.
7. Решить № 14.25 на с. 90 задачника. Учитель объясняет решение, привлекая учащихся к обсуждению построения графика функции.
Построим график функции ![]() и возьмем его
часть при x ≤ –1
и возьмем его
часть при x ≤ –1
(рис. 7). Построим график функции y = x5 и возьмем ее часть при
–1 < x < 1 (рис. 7). Построим график функции ![]() и возьмем его часть при x
≥ 1 (рис. 6). А теперь все три построенные линии расположим в одной
системе координат (рис. 8) – это и будет требуемый график.
и возьмем его часть при x
≥ 1 (рис. 6). А теперь все три построенные линии расположим в одной
системе координат (рис. 8) – это и будет требуемый график.
|
|
|
|
Рис. 6 |
Рис. 7 |
|
|
|
|
Рис. 8 |
Рис. 9 |
Прочитаем построенный график.
1) D(f) = (–∞; +∞);
2) функция является нечетной;
3) функция возрастает на всей числовой прямой;
4) функция не ограничена ни снизу, ни сверху;
5) у функции нет ни наименьшего, ни наибольшего значений;
6) функция непрерывна на всей числовой прямой;
7) E(f) = (–∞; +∞);
8) функция выпукла вверх на [–1; 0] и [1; +∞) выпукла вниз на (–∞; –1) и [0; 1].
8. Решить № 14.27 (а) на с. 90 задачника.
Построив в одной системе координат график функции ![]() и график функции y
= x3 (рис. 9), мы
убеждаемся, что они пересекаются в точке (0; 0).
и график функции y
= x3 (рис. 9), мы
убеждаемся, что они пересекаются в точке (0; 0).
IV. Итоги урока.
Повторить свойства функции ![]() .
.
Домашнее задание: повторить § 4 на с. 128–135 учебника; решить № 14.15 (в, г); № 14.19 (б); № 14.26, № 14.27 (б; в; г) на с. 89–90 задачника.
Числовые последовательности
(3 ч)
У р о к 1
Цели: ввести понятие числовой последовательности и членов последовательности; рассмотреть аналитическое задание числовой последовательности.
Ход урока
I. Анализ контрольной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Выполнить работу над ошибками.
II. Объяснение нового материала.
1. Рассмотрим четыре функции:
1) у = х2, х ![]() [0; 1]; 3) у = х2;
[0; 1]; 3) у = х2;
2) у = х2, х ![]() [0; +∞); 4) у = х2, х
[0; +∞); 4) у = х2, х ![]() N.
N.
Они заданы одной и той же формулой у = х2, но области определения функций различны.
В третьем случае D(f) = (–∞; +∞), в четвертом случае область определения – множество N натуральных чисел D(f) = N.
Графики этих функций изображены на рис. 121–124 (с. 137 учебника).
График четвертой функции состоит из отдельных точек.
2. Прочитать по учебнику на с. 112 две
задачи из учебника «Алгебра–7» и сделать вывод, что функции, заданные на
множестве натуральных чисел (у = f(x), x ![]() N), нужно изучать.
N), нужно изучать.
3. Математики как-то задумались: зачем
писать у = f(x), x ![]() N, не проще ли в таких случаях
писать у = f(n), договорившись раз и навсегда подразумевать в
этой записи, что аргумента n – натуральное число (n
N, не проще ли в таких случаях
писать у = f(n), договорившись раз и навсегда подразумевать в
этой записи, что аргумента n – натуральное число (n ![]() N). Так и
сделали: например, вместо записи у = х2, х
N). Так и
сделали: например, вместо записи у = х2, х ![]() N, решили использовать запись у
= n2.
N, решили использовать запись у
= n2.
И еще об одном обстоятельстве они договорились:
вместо f(1) писать
у1, вместо f(2)
– у2, вместо f(3)
– у3 и т. д.; вместо f(n)
– yn.
Значения функции у = f(n) можно записать последовательно одно за другим: f(1); f(2); f(3), …, f(n), … или же y1, y2, y3, …, yn, … Например, для функции у = n2 имеем: у1 = 1; у2 = 4; у3 = 9;… Полученные значения можно записать последовательно одно за другим: 1; 4; 9; 16; … n2, …
Число 1 в этой записи находится на первом месте, 4 – на втором, 9 – на третьем, 16 – на четвертом, а n2 – на n-ом месте.
4. Подчеркнем еще раз, что три математические модели:
1) у = f(x), х ![]() N;
N;
2) у = f(n);
3) f(1), f(2), f(3), …, f(n), … или y1, y2, y3, …, yn, …
(уn = f(n)) – различны по форме, но одинаковы по содержанию.
5. О п р е д е л е н и е 1. Функцию вида
у = f(x), x ![]() N, называют функцией натурального
аргумента или числовой последовательностью и обозначают у = f(n)
или y1, y2, y3, …, yn,
… .
N, называют функцией натурального
аргумента или числовой последовательностью и обозначают у = f(n)
или y1, y2, y3, …, yn,
… .
6. Значения y1, y2, y3 (и т. д.) называют соответственно первым, вторым, третьим (и т. д.) членами последовательности.
В символе уn число n называют индексом, который характеризует порядковый номер того или иного члена последовательности (уn).
7. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, словесный и рекуррентный.
8. Аналитическое задание числовой последовательности:
Говорят, что последовательность задана аналитически, если указана формула ее n-го члена уn = f(n).
Рассмотреть примеры 1–10 на с. 139–142 учебника.
III. Закрепление изученного материала.
1. Решить № 15.1 устно.
2. Решить № 15.4 на доске и в тетрадях.
3. Решить № 15.10 и 15.11 устно.
4. Решить № 15.12 (в; г) и 15.13 (в; г) с комментированием на месте.
5. Решить № 15.15 (в; г).
О т в е т: в) уn = n + 5; г) уn = – n.
6. Решить № 15.16 (в; г).
О т в е т: уn = 2n + 2; г) уn = 4n.
7. Решить № 15.17 (в; г).
О т в е т: в) уn = n2 + 1; г) уn = n3.
8. Решить № 15.38 (а; в).
Построить графики функций ![]() и у = х2 – 4.
и у = х2 – 4.
|
а) |
|
График состоит из точек прямой с абсциссами х = 1; х = 2; х = 3 и т. д.
|
в) yn = n2 – 4. |
|
График состоит из точек параболы с абсциссами х = 1; х = 2 и т. д.
IV. Итоги урока.
Домашнее задание: изучить материал на с. 136–142 учебника; решить № 15.12 (а; б); № 15.13 (а; б); № 15.15 (а; б); № 15.16 (а; б); № 15.17 (а; б); № 15.38 (б; г).
У р о к 2
Цели: расмотреть словесный и рекуррентный способы задания последовательности и закрепить их знание в ходе выполнения упражнений; вырабатывать навыки и умения при нахождении членов числовой последовательности по формуле.
Ход урока
I. Устная работа.
1. Сформулируйте определение числовой последовательности.
2. Назовите способы задания числовой последовательности.
3. Приведите пример последовательности, заданной формулой n-го члена. Найдите пять первых членов этой последовательности.
4. Последовательность (уn) задана формулой уn = 6n –1. Найдите y1; y4;
y20; y100; уk.
5. Решить № 15.2 устно.
II. Изучение нового материала.
1. Рассмотрим словесное задание последовательности.
Известно, что ![]() = 1,41421… С этим иррациональным числом
можно связать две последовательности:
= 1,41421… С этим иррациональным числом
можно связать две последовательности:
1) последовательность десятичных приближений числа ![]() по недостатку 1; 1,4;
1,41; 1,414; 1,4142,…
по недостатку 1; 1,4;
1,41; 1,414; 1,4142,…
2) последовательность десятичных приближений числа ![]() по избытку 2; 1,5;
1,42; 1,415; 1,4143,…
по избытку 2; 1,5;
1,42; 1,415; 1,4143,…
В обоих случаях правило составления последовательности описано словами (не формулой).
2. Решить № 15.6 и № 15.8 устно.
3. Важный для приложений способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Такой способ задания последовательности называют рекуррентным (от лат. слова recurrere – возвращаться).
4. Рассмотреть примеры 11–13 на с. 142–144 учебника.
III. Закрепление изученного материала.
1. Решить № 15.20 (в; г) на доске и в тетрадях.
в) х1 = 1; xn = 2 + xn – 1;
х2 = 2 + 1 = 3;
х3 = 2 + 3 = 5;
х4 = 2 + 5 = 7;
х5 = 2 + 7 = 9;
х6 = 2 + 9 = 11.
О т в е т: 1; 3; 5; 7; 9; 11.
г) х1 = –3;
хn = –xn – 1 – 2;
х2 = –(–3) – 2 = 3 – 2 = 1;
х3 = –1 – 2 = –3;
х4 = –(–3) – 2 = 3 – 2 = 1;
х5 = –1 – 2 = –3;
х6 = –(–3) – 2 = 1.
О т в е т: –3; 1; –3; 1; –3; 1.
2. Решить № 15.21 (в; г) с комментированием на месте.
в) х1 = –512;
хn = 0,5 × xn – 1;
х2 = –512 × 0,5 = –256;
х3 = –256 × 0,5 = –128;
х4 = –128 × 0,5 = –64;
х5 = –64 × 0,5 = –32;
х6 = –32 × 0,5 = –16.
О т в е т: –512; –256; –128; –64; –32; –16.
г) х1 = 1;
хn = xn – 1 : 0,1;
х2 = 1 : 0,1 = 10;
х3 = 10 : 0,1 = 100;
х4 = 100 : 0,1 = 1000;
х5 = 1000 : 0,1 = 10000;
х6 = 10000 : 0,1 = 1000000.
3. Решить № 15.30.
х1 = –3;
х2 = –2;
х3 = (–3 + (–2)) × 2 = –5 × 2 = –10;
х4 = (–2 – 10) × 2 = –24;
х5 = (–10 – 24) × 2 = –68;
х6 = (–24 – 68) × 2 = –92 × 2 = –184;
xn = 2 × (xn – 2 + xn – 1).
О т в е т: –3; –2; –10; –24; –68; –184.
4. Решить № 15.31 (в; г).
Р е ш е н и е
Объясняет учитель.
в) 9; 7; 5; 3; 1; …
О т в е т: х1 = 9; хn = xn – 1 –2.
г) 5; –5; 5; –5; 5; –5; …
О т в е т: х1 = 5; хn = –xn – 1.
5. Решить № 15.33. Словесное задание последовательности.
![]() …
…
а) по недостатку: 1; 1,7; 1,73; 1,732;
б) по избытку: 2; 1,8; 1,74; 1,733.
6. Решить № 15.28. В ходе рассуждений учащиеся записывают формулу n-го члена:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) 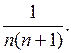
7. Повторение ранее изученного материала:
1) Решить № 13.3 (а; б), построив графики функций.
2) Решить № 19 (а; б) на с. 7 самостоятельно.
О т в е т ы: а) 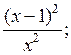 б)
б) 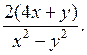
IV. Итог урока.
Домашнее задание: изучить материал учебника на с. 142–144; решить № 15.9; № 15.20 (а; б); № 15.21 (а; б); № 15.14; № 15.31 (а; б); № 9.12.
У р о к 3
Цели: закрепить знание учащимися способов задания числовой последовательности; изучить свойства числовых последовательностей и научить применять их в ходе выполнения упражнений; развивать логическое мышление учащихся.
Ход урока
I. Проверка усвоения изученного материала.
1. Назовите способы задания числовой последовательности и опишите каждый из способов.
2. Приведите примеры числовой последовательности, заданной:
а) формулой n-го члена;
б) словесно;
в) рекуррентный формулой. Это № 15.5.
3. Решить устно № 15.3 и № 15.4 (а; г).
4. Решить устно № 15.7.
хn = 7 × n; х1 = 7; х2 = 14; х3 = 21; х4 = 28.
х8 = 56; х10 = 70; х37 = 7 × 37 = 259.
II. Изучение нового материала.
1. Числовая последовательность – частный случай числовой функции, а потому некоторые свойства функций рассматривают и для последовательностей. Ограничимся свойством монотонности.
1. О п р е д е л е н и е 2. Последовательность (yn) называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:
y1 < y2 < y3 < y4 < … < yn < yn + 1 < …
3. Рассмотреть решение примеров 14 и 17 на с. 145 учебника.
4. О п р е д е л е н и е 3. Последовательность (yn) называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:
y1 > y2 > y3 > y4 > … > yn > yn + 1 > …
5. Рассмотреть решение примеров 15 и 18 учебника на с. 145.
6. Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
7. Разобрать решение примера 16 на с. 145 учебника.
8. Записать в тетрадях вывод:
1) Если а > 1, то последовательность уn = an возрастает.
2) Если 0 < a < 1, то последовательность уn = an убывает.
III. Выполнение упражнений.
1. Решить № 15.24 на доске и в тетрадях.
Простые числа: 2; 3; 5; 7; 11; 13; 17.
Квадраты простых числе: 4; 9; 25; 49; 121; 169; 289.
2. Решить № 15.22 (а; в).
а) yn = 3n + 4;
у1 = 3 × 1 + 4 = 7;
у2 = 3 × 2 + 4 = 10;
у3 = 3 × 3 + 4 = 13;
у4 = 3 × 4 + 4 = 16;
у5 = 19.
Имеем 7; 10; 13; 16; 19… возрастающая последовательность.
в) yn = 7n – 2;
у1 = 7 × 1 – 2 = 5;
у2 = 7 × 2 – 2 = 12;
у3 = 7 × 3 – 2 = 19;
у4 = 26, …
Получим 5; 12; 19; 26; 33… возрастающая.
3. Решить № 15.23 (а; в) самостоятельно с проверкой.
а) yn = –2n – 3; у1 = –5; у2 = –7; у3 = –9; у4 = –11…
значит, –5; –7; –9; –11; –13; … убывающая.
в) yn = 4 – 5n; у1 = –1; у2 = –6; у3 = –11; у4 = –16…
Имеем, –1; –6; –11; –16; … убывающая.
4. Решить № 15.35 (в; г).
Учитель объясняет решение.
№ 15.35 (в), задание № 15.35 (г) решают самостоятельно.
в) ![]()
13(n + 1) = 6(3n + 2);
13n + 13 = 18n + 12;
5n = 1;
![]()
О т в е т: не существует.
г) ![]()
23(n + 1) = 8(3n + 2);
23n + 23 = 24n + 16;
n = 7.
О т в е т: 7.
5. Решить № 15.41 (а) и № 15.42 (а) устно.
6. Решить № 15.36 (в; г) на доске и в тетрадях.
в) (2n – 1)(3n + 2) = 153;
6n2 + n – 155 = 0;
D = 3721 = 612;
n1 =
5; n2 = ![]() не удовлетворяет.
не удовлетворяет.
О т в е т: является n = 5.
г) (2n – 1)(3n + 2) = –2;
6n2 + n = 0;
n(6n + 1) = 0;
n = 0 или ![]()
Эти значения n не натуральные числа.
О т в е т: нет.
7. Решить № 15.37 (в; г) с комментированием на месте.
О т в е т: в) xn = 15 – 4n; г) 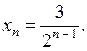
IV. Итог урока.
Домашнее задание: на отдельных листочках решить из домашней контрольной работы № 4 на с. 118–119 № 1, № 2 и № 3; к ним добавить по вариантам № 15.35 (а; б); № 15.36 (а; б); № 15.37 (а; б).
Арифметическая прогрессия
(4 ч)
У р о к 1
Цели: дать определение арифметической прогрессии; вывести формулу n-го члена арифметической прогрессии.
Ход урока
I. Проверка домашнего задания.
1. Собрать листочки с домашней контрольной работой.
2. Решить на доске задания, вызвавшие затруднения у учащихся в домашней работе.
II. Изложение нового материала (лекция).
1. З а д а ч а. Бригада стеклодувов изготовила в январе 80 изделий, а в каждый следующий месяц изготовляла на 17 изделий больше, чем в предыдущий. Сколько изделий изготовила бригада в июне?
2. Определение арифметической прогрессии.
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.
3. Таким образом, арифметическая прогрессия – это числовая последовательность (an), заданная рекуррентно соотношениями:
a1 = a, an = an – 1 + d (n = 2; 3; 4; …)
4. Решить № 16.1 и № 16.3 устно. Формула разности арифметической прогрессии d = a2 – a1 = a3 – a2 = a4 – a3 = …
5. Арифметическая прогрессия является возрастающей последовательностью, если d > 0, и убывающей, если d < 0. Рассмотреть решение примеров 1 и 2 на с. 146 учебника.
6. Обозначение арифметической прогрессии: ¸ а1, а2, а3, … аn …
7. Решить № 16.4 (в; г) и № 16.5 (в; г).
8. Задание арифметической прогрессии, о котором идет речь в определении, является рекуррентным. Во многих случаях оно неудобно: чтобы вычислить, например, а100, надо предварительно найти предшествующие 99 членов последовательности. Эту вычислительную работу можно существенно упростить, если удастся найти формулу n-го члена, то есть перейти к аналитическому заданию арифметической прогрессии.
9. Вывод формулы n-го члена арифметической прогрессии:
an = a1 + (n – 1)d.
Разобрать решение примеров 1, 2 на с. 148–149 учебника.
10. Формулу n-го члена арифметической прогрессии
an = a1 + (n – 1)d
можно записать иначе:
an = dn + (a1 – d).
Введем обозначения:
аn = y, a1 – d = m.
Получим y = dn + m, или y = dx + m, x
![]() N.
N.
Значит, арифметическую прогрессию можно рассматривать как линейную функцию (у = dx + m), заданную на множестве N натуральных чисел.
Рассмотреть график арифметической прогрессии – рис. 126 на с. 148 учебника.
III. Закрепление изученного материала.
1. Решить № 16.7 (в; г).
в) 100; 90; 80; 70; … Найти d и а10.
а1 = 10; а2 = 90; d = а2 – а1 = 90 – 100 = –10; d = –10;
а10 = а1 + 9d = 100 + 9 × (–10) = 100 – 90 = 10; а10 = 10.
г) 3; ![]()
![]()
![]() … Найти d и а10.
… Найти d и а10.
![]()
2. Решить № 6.14 (в; г) с комментированием на месте.
в) 7; 5; 3; 1; … Найти аn.
а1 =
7; а2 = 5; d = 5
– 7 = –2; аn = a1 + d(n – 1) = 7 – 2(n
– 1) = 7 – 2n +
+ 2 = 9 – 2n.
О т в е т: аn = 9 – 2n.
г) –1; ![]()
![]()
![]() … d =
… d = ![]() аn = –1 –
аn = –1 – ![]() (n – 1) = – 1 –
(n – 1) = – 1 – ![]()
![]()
О т в е т: аn = ![]()
3. Решить № 16.16 (в; г) самостоятельно.
в) a17 = a1 + 16d = –12 + 16 × 2 = –12 + 32 = 20; a17 = 20.
г) a9 =
a1 + 8d = 101 +
8 ×
![]() = 105.
= 105.
О т в е т: а9 = 105.
IV. Итог урока.
1. Сформулируйте определение арифметической прогрессии.
2. Какой функцией можно рассматривать арифметическую прогрессию.
Домашнее задание: изучить материал на с. 145–149 учебника; решить № 16.4 (а; б); №; 16.6; № 16.7 (а; б); № 16.14 (а; б); № 16.16 (а; б).
У р о к 2
Цели: учить учащихся решать задачи, используя формулу n-го члена арифметической прогрессии.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Сформулируйте определение арифметической прогрессии. Какое число называют разностью арифметической прогрессии?
2. Решить № 16.2 устно.
3. Один учащийся на доске выводит формулу n-го члена арифметической прогрессии.
4. Решить № 16.24 (а) и № 16.5 (а; б), записывая решение только на доске, обсуждая решение со всем классом.
II. Выполнение упражнений. Решение задач.
1. Решить № 16.8 на доске и в тетрадях.
хn = 5n + 3; х1 = 5 × 1 + 3 = 8; х2 = 13; х3 = 18; х4 = 23; х5 = 28…
Имеем: 8; 13; 18; 23; 28; … арифметическая прогрессия. Первый член равен 8, разность 5.
2. Решить № 16.17 (в; г). Найти разность d.
в) а1 = –8; а11 = –28; а11 = а1 + 10d; –28 = – 8 + 10d; –20 = 10d; d = –2.
О т в е т: –2.
г) а11 = 4,6; а36 = 54, 6.
Решим систему уравнений:
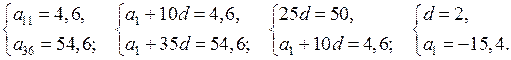
О т в е т: 2.
3. Решить № 16.18 (в; г). Найти первый член а1.
в) а26 =
–71; d = –3; а26 =
а1 + 25d; –71 =
а1 + 25 × (–3); –71 = а1 – 75;
а1 = 4.
О т в е т: 4.
г) а14 =
![]() d =
d = ![]()
а14 =
а1 + 13d; ![]()
![]()
О т в е т: ![]()
4. Решить с комментированием на месте.
an = –0,1n + 3;
а1 = –0,1 × 1 + 3 = 2,9; а2 = –0,1 × 2 + 3 = 2,8;
d = а2 – а1 = 2,8 – 2,9 = –0,1; d = –0,1.
О т в е т: а1 = 2,9; d = –0,1.
аn = 5 – 2n;
а1 = 5 – 2 × 1 = 3; а2 = 5 – 2 × 2 = 1; d = 1 – 3= –2; d = –2.
О т в е т: а1 = 3; d = –2.
5. Решить № 16.19 (б) на доске и в тетрадях.
¸ 3; 7; 11; …
аn = 43.
Найти номер n.
аn = а1 + d(n – 1); 43 = 3 + 4(n – 1);
d = 7 – 3 = 4; d = 4; 43 = 3 + 4n – 4; 4 n = 44; n = 11.
О т в е т: 11.
6. Решить № 16.20 (б) с комментированием на месте.
¸ 7,5; 11; 14,5; …
Является ли аn = 43,5?
а1 = 7,5; а2 = 11; d = 11 – 7,5 = 3,5;
аn = а1 + d(n – 1); 43,5 = 7,5 + 3,5(n – 1);
43,5 – 7,5 + 3,5 = 3,5n; 39,5 = 3,5n; ![]()
О т в е т: не является.
7. Решить № 16.21 (б) самостоятельно с проверкой.
б) а1 = 3; d = –6; аn = – 33?
an = a1 + (n – 1)d; –33 = 3 – 6 × (n – 1); –33 = 3 – 6n + 6;
– 42 = –6n; n = 7.
О т в е т: является.
8. Решить задачу № 16.31. Решение объясняет учитель.
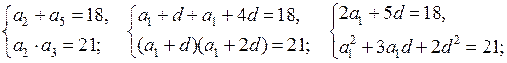
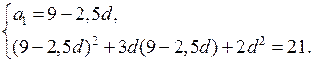
Решим уравнение 0,75d2 – 18d + 60 = 0 | × ![]()
d2 – 24d + 80 = 0; d1 = 20; d2 = 4.
Если d = 20, то а1 = 9 – 50 = –41; а2 = –41 + 20 = –21 ![]() N, но по условию а2 – натуральное число.
N, но по условию а2 – натуральное число.
Если d = 4, то а1 = 9 – 10 = – 1; а2 = –1 + 4 = 3; а2 ![]() N.
N.
Найдем прогрессию: –1; 3; 7; 11; 15; …
9. Повторение ранее изученного материала.
Решить № 21 (а; б) на с. 7 из «Задачи на повторение». Вспомнить правило умножения и деления дробей.
III. Итог урока.
Домашнее задание: изучить по учебнику на с.
149–151 решение при-
меров 4 и 5 и записать решения в тетрадь; решить № 16.9; № 16.17 (а; б);
№ 16.19 (а); № 16.21 (а); № 16.30.
У р о к 3
Цели: вывести формулу суммы n первых членов арифметической прогрессии и научить применять ее при решении упражнений.
Ход урока
I. Самостоятельная работа (15 мин).
В а р и а н т I
1. В арифметической прогрессии известны а1 = –1,2 и d = 3. Найдите
а4; а8; а21.
2. Найдите разность арифметической
прогрессии (аn),
если а1 = 2;
а11 = –5.
3. В арифметической прогрессии известны а1 = –12 и d = 3. Найти номер члена прогрессии, равного 9.
4. Выписали двадцать членов арифметической прогрессии 6,5; 8; … Встретится ли среди них число 36?
В а р и а н т II
1. В арифметической прогрессии (аn) известны а1 = –0,8 и d = 4. Найдите а3; а7; а24.
2. Найдите разность арифметической
прогрессии (аn),
если а1 = 4;
а18 = –11.
3. В арифметической прогрессии известны а1 = 14 и d = 0,5. Найти номер члена прогрессии, равного 34.
4. Выписали двадцать членов арифметической прогрессии 18; 4; … Встретится ли среди них число –38?
II. Объяснение нового материала (лекция).
1. Рассказать предание о маленьком Карле Гауссе, будущем немецком короле математики XIX века, решившем в возрасте 5 лет очень быстро задачу о нахождении суммы первых ста натуральных чисел.
2. Предложить учащимся найти сумму первых ста натуральных чисел; решить на доске эту задачу.
3. С помощью аналогичных рассуждений можно найти сумму первых членов любой арифметической прогрессии.
4. Вывод формулы суммы n первых членов арифметической прогрессии (аn):
(I) ![]()
(II) ![]()
5. Разобрать решение примера 6 на с. 152–153 учебника.
III. Закрепление изученного материала.
1. Решить № 16.33 (в; г) с комментированием на месте.
в) ![]() S10 = –90.
S10 = –90.
г) ![]() S25 = 600.
S25 = 600.
2. Решить № 16.34 (в; г) самостоятельно.
в) ![]() S50 = 3175.
S50 = 3175.
г) ![]() S50 = –245.
S50 = –245.
3. Решить № 16.35 (в; г) по формуле (II):
в) ![]()
г) ![]()
О т в е т: в) 2350; г) –6175.
4. Решить № 16.37 (в; г) на доске и в тетрадях.
в) аn = –2n + 8; а1 = –2 × 1 + 8 = 6; а30 = –2 × 30 + 8 = –52;
![]()
г) аn = –2,5n – 6; а1 = –8,5; а30 = –2,5 × 30 – 6 = –81;
![]()
О т в е т: в) –690; г) –1342,5.
5. Решить № 16.39. Решение объясняет учитель.

![]()
О т в е т: 122,5.
6. Решить задачу № 16.65. Учитель помогает ученикам при решении задачи.
а1 = 30 см; d = 5 см; S = 5,25 м = 525 см. Найдем n.
![]()
1050 = (55 + 5n) × n; 5n2 + 55n – 1050 = 0; n2 + 11n – 210 = 0;
n1 =
10, n2 = –21 ![]() N.
N.
О т в е т: 10 минут.
IV. Итог урока. Выставление отметок.
Домашнее задание: изучить по учебнику материал на с. 151–154 и записать в тетради решение примеров 7 и 8; решить № 16.33 (а; б) – 16.35 (а; б); № 16.37 (а; б); № 16.66.
У р о к 4
Цели: изучить характеристическое свойство арифметической прогрессии; способствовать выработке навыков и умений решения задач с использованием формул суммы n первых членов арифметической прогрессии; закрепить изученный материал.
Ход урока
I. Анализ самостоятельной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Решить на доске задания, вызвавшие затруднения у учащихся.
3. Проверить решение домашней задачи № 16.66.
Р е ш е н и е
а1 = 1400; d = –100; S = 5000. Найдем n.
![]() 10000 = 2900n – 100n2;
10000 = 2900n – 100n2;
n2 – 29n + 100 = 0; n1 = 4; n2 = 25.
По смыслу задачи из двух найденных значений n выбираем n = 4.
О т в е т: 4 дня.
II. Работа по учебнику.
1. Пусть дана арифметическая прогрессия (аn). Рассмотрим три ее члена, следующие друг за другом: аn – 1; аn; аn + 1. Известно, что аn – d = аn – 1; аn + d = an + 1.
Сложив эти равенства, получим  при любом n >1.
при любом n >1.
2. Прочитать по учебнику формулировку этого утверждения и ему обратного (с. 155).
3. Формулировка теоремы, выражающей характеристическое свойство арифметической прогрессии.
4. Разобрать по учебнику на с. 155–156 решение примера 9.
III. Выполнение упражнений.
1. Решить № 16.40 устно, используя характеристическое свойство арифметической прогрессии:
а) ![]() тогда
тогда ![]()
б) ![]() тогда а18 + а20 = 2 × а19 =
2 × 5 = 10;
тогда а18 + а20 = 2 × а19 =
2 × 5 = 10;
в) а6 + а8 = 2 × а7 = 2 × 4 = 8;
г) ![]()
О т в е т: а) 61; б) 10; в) 8; г) –1.
2. Решить № 16.42 (б) с комментированием на месте.
Если а14 + а16 = –20, то а15 = –20 : 2 = –10;
Если а29 + а31 = 40, то а30 = 40 : 2 = 20;
Найдем а15 + а30 = –10 + 20 = 10.
О т в е т: 10.
3. Решить № 16.44 на доске и в тетрадях.
Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению
![]() 2у = 5у – 3; 3у =
3; у = 1.
2у = 5у – 3; 3у =
3; у = 1.
О т в е т: 1.
4. Решить № 16.46. Решение объясняет учитель.
а) Речь идет о сумме членов конечной арифметической прогрессии 104; 112; 120; … 992. У этой прогрессии а1 = 104; аn = 992; d = 8. Сначала найдем n (количество членов прогрессии):
аn = а1 + (n –1)d; 992 = 104 + (n – 1) × 8;
992 = 8n + 96; n = 112.
Имеем 
О т в е т: 61376.
б) Речь идет о сумме членов конечной арифметической прогрессии 101; 113; 125; 137; …; 989.
а1 = 101; d = 12; аn = 989. Найдем n.
аn = а1 + (n – 1)d; 989 = 101 + (n –1) × 12; 12n = 900; n = 75.
Найдем ![]()
О т в е т: 40875.
5. Решить № 16.48 (б; г) на доске и в тетрадях.
б) а9 = –30; а19 = –45. Найдем аn.
аn = а1 + (n – 1)d = –18 + (n – 1)(–1,5) = –1,5n – 16,5.
г) а5 = 0,2; а16 = –7,5. Найдем an.
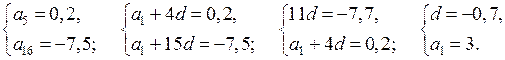
аn = 3 – 0,7(n – 1).
О т в е т: б) –18 – 1,5(n – 1); г) 3 – 0,7(n – 1).
6. Решить № 16.68·. Решение объясняет учитель.
Используя характеристическое свойство арифметической
прогрессии, получаем уравнение ![]()
![]() х – 3 =
х – 3 =
= (х – 5)2; х2 – 11х + 28 = 0; х1 = 7; х2 = 4 – посторонний корень, не
удовлетворяющий иррациональному уравнению ![]()
О т в е т: 7.
IV. Итог урока.
Домашнее задание: повторить материал на
с. 145–156; решить
№ 16.42 (а); 16.43; № 16.48 (а; в); 16.36 (а; б); 16.47 (в).
Геометрическая прогрессия
(5 ч)
У р о к 1
Цели: ввести понятие геометрической прогрессии; вывести формулу n-го члена геометрической прогрессии; развивать логическое мышление учащихся и вычислительные навыки.
Ход урока
I. Проверочная работа (10 мин).
В а р и а н т I
1. Выведите формулу n-го члена арифметической прогрессии.
2. Найдите сумму первых шестнадцати членов арифметической прогрессии –16; –13; …
В а р и а н т II
1. Выведите формулу суммы n первых членов арифметической прогрессии.
2. Найдите сумму первых двенадцати членов арифметической прогрессии.
II. Объяснение нового материала.
1. Сформулировать определение геометрической прогрессии. Знаменатель геометрической прогрессии
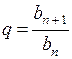 при bn ≠ 0, q ≠ 0.
при bn ≠ 0, q ≠ 0.
2. Геометрическая прогрессия – это числовая последовательность (bn), заданная рекуррентно соотношениями
b1 = b, bn = bn – 1 × q
(n = 2; 3; 4; …)
b и q – заданные числа, b ≠ 0, q ≠ 0.
3. Рассмотреть решение примеров 1–5 по
учебнику на с. 157. Геометрическая прогрессия является возрастающей
последовательностью, если
b1 > 0, q > 1 (см. пример
1), и убывающей, если b1 > 0, 0
< q < 1 (см. пример 2).
4. Обозначение геометрической прогрессии ![]() b1, b2, b3, …, bn,
…
b1, b2, b3, …, bn,
…
5. Решить устно № 17.1 (а; в) и № 17.2.
6. Решить устно № 17.4 (б; в) и № 17.6 (а; в).
7. Вывод формулы n-го члена геометрической прогрессии
bn = b1 × qn – 1.
8. Разобрать решение примеров 1–5 на с. 159–160 учебника.
9. Геометрическую прогрессию можно рассматривать как показательную функцию у = mqх, заданную на множестве N натуральных чисел.
На рис. 127а и рис. 127б изображены графики
геометрической прогрессии у = 2х и 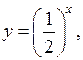 где х
где х ![]() N.
N.
III. Закрепление изученного материала.
1. Решить № 17.8 (в; г) с комментированием на месте.
в) 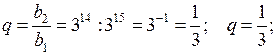
г) 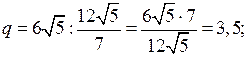 q = 3,5.
q = 3,5.
2. Решить № 17.12 (в; б) на доске и в тетрадях.
в) q = b3 : b2 =
![]()
![]() b1 = b2 : q =
b1 = b2 : q = ![]()
б) q = b5 : b4 =
![]() b4 = b1 × q3,
отсюда
b4 = b1 × q3,
отсюда
b1 =
b4 : q3 = 1 : 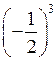 = –8; b1 = –8.
= –8; b1 = –8.
О т в е т: б) –8; –0,5; в) 3; 0,5.
3. Решить № 17.13 (б; г). Учащиеся решают самостоятельно на доске и в тетрадях. Учитель при необходимости помогает в решении.
б) ![]()
г) ![]()
![]()
О т в е т: б) ![]() г)
г) ![]()
4. Решить № 17.15 (в; г). Решение объясняет учитель.
в)  bn = b1 × qn – 1; тогда
bn = b1 × qn – 1; тогда 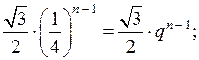 отсюда
отсюда  значит,
значит, ![]()
г) 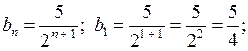 найдем q из равенства
найдем q из равенства
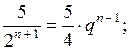 умножим обе части на
умножим обе части на ![]() получим
получим 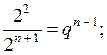
21 – n =
qn – 1; 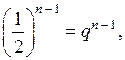 отсюда
отсюда ![]()
О т в е т: в) 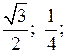 г)
г) ![]()
5. Решить. Учитель помогает в решении, если учащиеся затрудняются решить самостоятельно.
a) ![]() А = –1250; найдем номер n:
–1250 =
А = –1250; найдем номер n:
–1250 = ![]() отсюда
отсюда
![]() = 625 = 54, значит,
= 625 = 54, значит, ![]() n = 8
n = 8 ![]() N.
N.
О т в е т: да.
в) 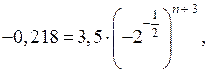 отсюда
отсюда 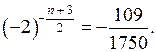
О т в е т: нет.
IV. Итог урока.
Домашнее задание: изучить материал учебника на с. 156–161; решить № 17.8 (а; б); № 17.12 (а; г); 17.13 (а; в); № 17.15 (а; б).
У р о к 2
Цели: закрепить знание формулы n-го члена геометрической прогрессии в ходе решения задач; способствовать выработке навыков и умений решения систем уравнений.
Ход урока
I. Повторение изученного материала.
1. Сформулируйте определение геометрической прогрессии. Что называют знаменателем геометрической прогрессии?
2. Приведите примеры геометрической прогрессии.
3. Решить устно № 17.1 (б; г), № 17.3, № 17.4 (а; г).
4. Записать на доске формулу n-го члена геометрической прогрессии.
5. Решите устно:
а) зная первые два члена геометрической прогрессии 1,6; 0,8; …, найдите следующие за ними четыре числа;
б) в геометрической прогрессии (bn) известны b1 = 3,2 и q = 2; найдите b2, b3, b4.
II. Выполнение упражнений и решение задач.
1. Решить № 17.13 (в; г) с комментированием на месте.
в) b1 = 2,5; q = –0,2; bn = b1qn – 1 = 2,5 × (–0,2)n – 1;
г) 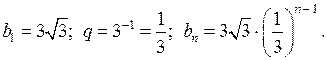
2. Решить № 17.14 (в; г).
в) 4; 1; ![]() … b1 = 4; b2 =
1; q = b2 : b1 =
… b1 = 4; b2 =
1; q = b2 : b1 = ![]() bn = 4
bn = 4 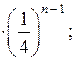
г) ![]() ; 2;
; 2; ![]() ; b2 = 2;
; b2 = 2; ![]() ; q = b3 : b2 =
; q = b3 : b2 = ![]() ;
; ![]()
3. Решить № 17.9 устно.
4. Решить № 17.10 (б; г) самостоятельно с проверкой.
б) b1 =
270; ![]() ; b5 = b1 × q4 =
; b5 = b1 × q4 =
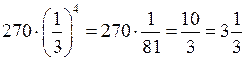 ;
;
г) b1 =
![]() b8 = b1 × q7 =
b8 = b1 × q7 =
![]()
5. Решить № 17.21 (в; г). Решение объясняет учитель.
в) bn = b1 × qn – 1; по условию bn = 4 × 10–3, тогда
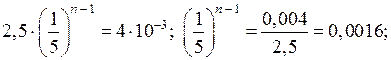 отсюда
отсюда
(0,2)n – 1 = (0,2)4; n – 1 = 4; n = 5.
г) bn =
–2401; ![]()
(–7)n – 1 = (–7)7; n – 1 = 7; n = 8.
О т в е т: в) 5; г) 8.
6. Решить № 17.22 (в; г) на доске и в тетрадях.
Решение № 17.22 (в) объясняет учитель.
в) ![]() Найти b1 и q.
Найти b1 и q.
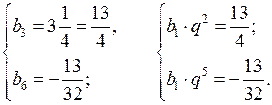
Разделим почленно второе уравнение на первое уравнение, получим:
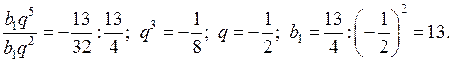
г) b3 = 12; b5 = 48 (q < 0). Найти b1 и q.
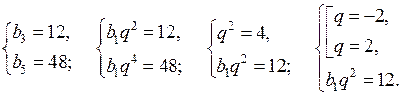
По условию q < 0, значит, q = –2; b1 = 12 : 4 = 3.
О т в е т: в) –0,5; 13; г) –2; 3.
7. Решить задачу № 17.42.
Дано: b1 = 4; b3 + b5 = 80. Найти q и b10 (q > 1).
b3 +
b5 = 80; b1 × q2 + b1 × q4 =
80; b1(q2 + q4) = 80; 4 × (q2 +
q4) = 80;
q2 + q4 = 20; q4 + q2 – 20 = 0; q2 = y; y2 + y
– 20 = 0; y1 = –5; y2 = 4; то q2 =
= –5 нет решений; q2 =
4; q1 = 2 и q2 = –2 не удовлетворяет условию q
> 1.
Если q = 2, то b10 = b1 × q9 = 4 × 29 = 4 × 512 = 2048.
О т в е т: q = 2; b10 = 2048.
8. Решить № 17.44. Учитель помогает в решении задачи.
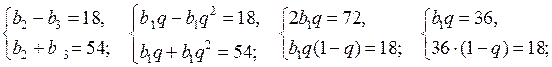

О т в е т: b1 = 72; q = ![]()
9. Решить № 17.45 на доске и в тетрадях.

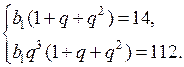
Делим второе уравнение на первое уравнение, получим
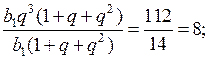 q3 = 8; q = 2.
q3 = 8; q = 2.
b1 =
14 : (1 + 2 + 22) = 14 : 7 =
2; b1 = 2; b2 = 4; b3 = 8; b4 = 16; b5 = 32;
b6 = 64.
О т в е т: 2; 4; 8; 16; 32; 64.
III. Итог урока.
Домашнее задание: на отдельных листочках выполнить номера с 4 по 7 из домашней контрольной работы, № 4 на с. 118–119 на два варианта, к ним еще решить по 2 вариантам № 17.14 (а; б), № 17.21 (а; б) и № 17.22 (а; б).
У р о к 3
Цели: вывести формулу суммы n первых членов геометрической прогрессии; вырабатывать навыки нахождения суммы n первых членов геометрической прогрессии.
Ход урока
I. Проверка домашнего задания.
1. Собрать листочки с домашней контрольной работой.
2. Сообщение учащимися исторического материала.
1) Доклад «О прогрессиях».
2) Пересказ древней индийской легенды об изобретателе шахмат.
II. Объяснение нового материала.
1. Вывод формулы суммы n первых членов геометрической прогрессии.
(I) 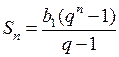 при q ≠ 1; (II)
при q ≠ 1; (II) 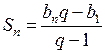 при q ≠
1.
при q ≠
1.
2. Разобрать решение примера 8 на с. 162–164 учебника.
III. Закрепление изученного материала.
1. Решить № 17.25 (г) (объясняет решение учитель).
г) b1 =
4; q = ![]() n
= 4;
n
= 4; 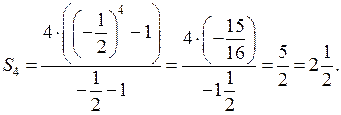
2. Самостоятельно решить № 17.25 (б).
3. Решить № 17.27 (в; г) на доске и в тетрадях.
в) b1 =
–4; q = ![]() n
= 13;
n
= 13;
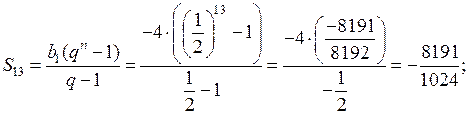
г) b1 =
4,5; ![]() n =
8;
n =
8; 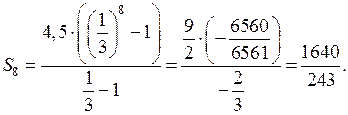
4. Решить № 17.47 (в). Решение объясняет учитель.
в) 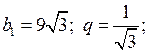 n = 6. Найти сумму квадратов ее
членов. Воспользуемся формулой
n = 6. Найти сумму квадратов ее
членов. Воспользуемся формулой 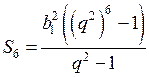 на с. 165 учебника.
на с. 165 учебника.
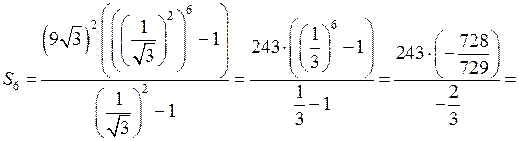
![]()
О т в е т: 364.
5. Решить № 17.28 (в; г) на доске и в тетрадях.
в) –3; ![]() … Найти S5.
… Найти S5.
b1 =
–3; b2 = 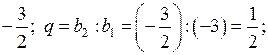 n = 5.
n = 5.
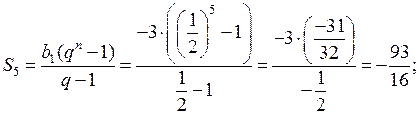
г) ![]() … q = 3;
… q = 3; ![]() n = 5, тогда
n = 5, тогда
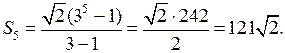
О т в е т: а) ![]() г)
г) ![]()
6. Решить № 17.39 (г). Учитель объясняет решение.
г) b1 =
3; ![]() Найти n.
Найти n.
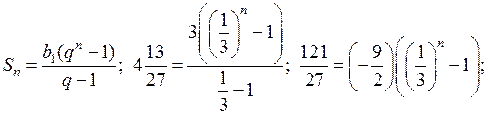
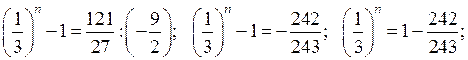
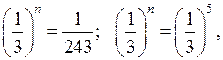 отсюда n = 5.
отсюда n = 5.
О т в е т: 5.
7. Решить задачу № 17.50·.
Дана характеристическая прогрессия b1; b2; b3; b4;
… b2n – 1; b2n. Обозначим S
сумму членов прогрессии, находящихся на четных местах:
S = b2 + b4 + … + b2n.
Имеем S = b1q + b1q3 + … b1q2n – 1 = b1q(1 + q2 + … + q2n – 2).
Обозначим Р сумму членов прогрессии, находящихся на нечетных местах:
Р = b1 + b3 + … + b2n – 1.
Имеем Р = b1 + b1q2 + … b1q2n – 2 = b1(1 + q2 + … + q2n – 2).
Разделив S на Р, получим q, что и требовалось доказать.
IV. Итог урока.
1. Запишите на доске формулу n-го члена геометрической прогрессии.
2. Запишите формулу суммы n членов геометрической прогрессии.
Домашнее задание: изучить по учебнику материал на с. 164–166; решить № 17.26 (а; в); № 17.27 (а; б); № 17.28 (а; б); № 17.47 (а); № 17.39 (а).
У р о к 4
Цели: закрепить в ходе упражнений знание формул n-го члена геометрической прогрессии и суммы членов конечной геометрической прогрессии; доказать теорему, выражающую характеристическое свойство геометрической прогрессии; научить учащихся применять характеристическое свойство геометрической прогрессии при решении задач.
Ход урока
I. Проверка домашнего задания.
1. Двое учащихся решают на доске № 17.47 (а) и № 17.39 (а) из домашнего задания.
2. Учитель выборочно проверяет домашние работы у некоторых учащихся.
3. Решить устно № 17.13 (а); № 17.6 (б); № 17.7 (а; в); № 17.25 (а; в).
II. Изучение нового материала.
1. Провести доказательство теоремы, выражающей характеристическое свойство геометрической прогрессии; записать вывод:
![]()
2. Выполним преобразования равенства
![]()
Число ![]() называют средним геометрическим чисел
а и b.
называют средним геометрическим чисел
а и b.
Таким образом, последнее равенство означает, что модуль любого члена геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов.
3. Рассмотреть решение примера 11 на с. 167–168 учебника.
III. Выполнение упражнений.
1. Решить № 17.31 (а; б) с комментированием на месте.
а) b2 =
4; b4 = 16; b3 = ![]() (b3 >
0).
(b3 >
0).
b3 = 8; q = b3 : b2 = 8 : 4 = 2; q = 2.
б) b5 = 12; b7 = 3; по условию b6 < 0, тогда
![]() q = b7 : b6 = 3 : (–6) =
q = b7 : b6 = 3 : (–6) = ![]()
О т в е т: а) 2; 8; б) ![]() –6.
–6.
2. Решить № 17.34 на доске и в тетрадях. Согласно характеристическому свойству
![]() 3х = 6х2 – 6х; 6х2 – 9х = 0; 3х(2х
– 3) = 0; 3х = 0 или 2х – 3 = 0; х = 0 или х = 1,5.
3х = 6х2 – 6х; 6х2 – 9х = 0; 3х(2х
– 3) = 0; 3х = 0 или 2х – 3 = 0; х = 0 или х = 1,5.
Подставляя х = 0 в заданные выражения х
– 1, ![]() 6х,
находим соответственно –1; 0; 0 – это не геометрическая прогрессия.
6х,
находим соответственно –1; 0; 0 – это не геометрическая прогрессия.
Подставляя х = 1,5 в заданные выражения
находим 0,5; ![]() 9 –
это конечная геометрическая прогрессия со знаменателем
9 –
это конечная геометрическая прогрессия со знаменателем ![]()
О т в е т: 1,5.
3. Самостоятельно решить № 17.33 (с проверкой).
Согласно характеристическому свойству (3у)2 = –81 ×
(–1); 9у2 = 81;
у2 = 9; у1 = –3; у2 = 3.
О т в е т: –3; 3.
4. Решить № 17.43 на доске и в тетрадях.
1; b2; b3; b4; 81. Отсюда b1 = 1; b5 = 81; найдем q.
b5 = b1 × q4; 81 = 1 × q4; q4 = 34 или q4 = (–3)4;
тогда q = 3 или q = –3.
1) Если q = 3, то 1; 3; 9; 27; 81.
2) Если q = –3, то 1; –3; 9; –27; 81.
О т в е т: 1; 3; 9; 27; 81 или 1; –3; 9; –27; 81.
5. Решить № 17.29 (в; г). Решение № 17.29 (г) объясняет учитель.
в) b3 =
1; b5 = ![]() (q > 0). Найти S5.
(q > 0). Найти S5.
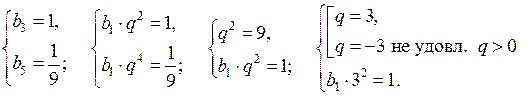
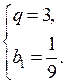

г) ![]() b7 = 27. Найти S5.
b7 = 27. Найти S5.
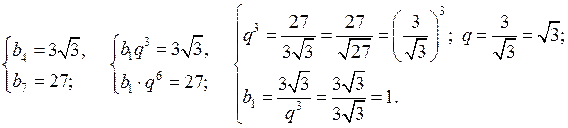
Найдем b5 = b4 × q
= ![]() Применим
формулу (II).
Применим
формулу (II).
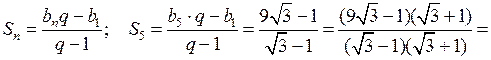
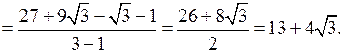
О т в е т: в) ![]() г)
г) ![]()
6. Решить № 17.29 (а) самостоятельно.
IV. Итог урока.
Домашнее задание: изучить материал на с. 166–167 учебника; решить № 17.31 (в; г); № 17.32, № 17.23; № 17.29 (б); № 17.35.
У р о к 5
Цели: способствовать выработке навыков и умений учащихся при решении заданий геометрической прогрессии, нахождении суммы членов конечной геометрической прогрессии; учить решать более сложные задачи, связанные с геометрической и арифметической прогрессией.
Ход урока
I. Самостоятельная работа (15 мин).
В а р и а н т I
1. Сформулируйте определение геометрической прогрессии. Выведите формулу n-го члена геометрической прогрессии.
2. Найдите сумму пяти первых членов геометрической
прогрессии (bn), в
которой b1 = 27; q =
![]()
В а р и а н т II
1. Выведите формулу суммы n первых членов геометрической прогрессии.
2. Найдите сумму шести первых членов
геометрической прогрессии
–4; 8; …
II. Выполнение упражнений.
1. Решить № 17.26 (г). Один ученик самостоятельно решает на доске, остальные в тетрадях.
г) b1 =
–9; q = ![]() n
= 6. Найти S6.
n
= 6. Найти S6.

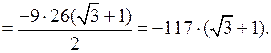
О т в е т: ![]()
2. Решить № 17.39 (в) на доске и в тетрадях.
в) b1 = 3; q = 2; Sn = 189. Найти n.
 189 = 3 × (2n –1); 2n –
1 = 63;
189 = 3 × (2n –1); 2n –
1 = 63;
2n = 64; 2n = 26; n = 6.
О т в е т: 6.
3. Решить № 17.48 (а; в). Решение № 17.48 (а) объясняет учитель.
а) 1 +2 + 22 + … + 28. Найти Sn.
Воспользуемся формулой (II) 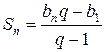 при q ≠ 1; b1 = 1; b2 = 2;
при q ≠ 1; b1 = 1; b2 = 2;
q = 2 : 1 = 2; q = 2; bn = 28 =
256; ![]() S =
511.
S =
511.
в) 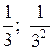 + … +
+ … + ![]() Найти S.
Найти S.
b1 =
![]() b2 =
b2 = ![]() q =
q = ![]()
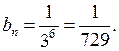

![]()
О т в е т: а) 511; в) ![]()
4. Решить задачу № 17.53·. Решение объясняет учитель.
Имеем:
![]() b1; b2;
b3;
b1; b2;
b3;
![]() b1; b2;
b3 – 16; b1 = 9.
b1; b2;
b3 – 16; b1 = 9.
Опираясь на характеристическое свойство арифметической прогрессии, получаем соотношение:
2b2 = b1 + (b3 – 16); 2b1q = b1 +b1q2 – 16;
18q = 9 + 9q2 – 16; 9q2 –
18q – 7 = 0; q1 =
![]() q2 =
q2 = ![]()
Если ![]() то b2 = b1q
=
то b2 = b1q
= ![]() b3 = b2q =
b3 = b2q = ![]()
Если ![]() то b2 = b1q
=
то b2 = b1q
= 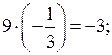 b3 = b2q =
b3 = b2q = 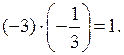
О т в е т: 21 и 49 или –3 и 1.
5. Решить задачу № 17.54·. Учитель помогает учащимся в решении задачи.
По условию ![]() а1; а2;
а3;
а1; а2;
а3;
![]() а1; а2 +
1; а3 + 14;
а1; а2 +
1; а3 + 14;
а1 + а2 + а3 = 24.
Опираясь на характеристическое свойство геометрической прогрессии, получаем соотношение:
(а2 + 1)2 = а1 × (а3 + 14); (а1 + d + 1)2 = а1 × (а1 + 2d + 14);
d2 + 2d + 1 = 12a1.
По третьему условию задачи а1 + а2 + а3 = 24;
а1 + (а1 + d) + (а1 + 2d) = 24; a1 + d = 8.
В итоге имеем систему уравнений:
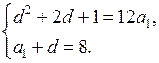
О т в е т: 27; 8 и –11 или 3; 8; 13.
6. Повторение ранее изученного материала. Решить № 15.36 (в; г) самостоятельно с проверкой.
III. Итог урока.
Домашнее задание: повторить материал на с. 156–171 учебника; на отдельных листочках решить домашнюю контрольную работу № 4 номера 8, 9 и 10 на с. 118–119 задачника.
Подготовка к контрольной работе
Цели: повторить и закрепить изученный материал об арифметической и геометрической прогрессии; подготовить учащихся к контрольной работе.
Ход урока
I. Повторение изученного материала.
1. Сообщить учащимся результаты самостоятельной работы. Устранить ошибки, сделанные в ходе работы.
2. Собрать листочки с домашней контрольной работой. Решить на доске задания, вызвавшие затруднения у учащихся.
3. Записать на доске формулы n-го члена арифметической и геометрической прогрессии; формулы суммы членов конечной арифметической и геометрической прогрессии.
II. Подготовка к контрольной работе.
1. Найдите девятый член арифметической прогрессии 8,4; 8; 7,6… Вычислите сумму первых девяти ее членов.
2. Найдите седьмой член геометрической
прогрессии ![]() 2; …
2; …
3. Найдите девятый член геометрической
прогрессии ![]() …
…
4. Сумма второго и пятого членов арифметической прогрессии равна 11. Третий ее член на 6 больше первого. Найдите второй и четвертый члены этой прогрессии.
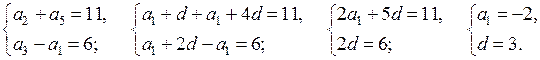
a2 = a1 + d = –2 + 3 = 1; a4 = a1 + 3d = –2 + 9 = 7.
О т в е т: а2 = 1; а4 = 7.
5. Сумма третьего и шестого членов арифметической прогрессии равна 2. Четвертый ее член на 6 меньше первого. Найдите первый и пятый члены этой прогрессии.

a1 = 8; a5 = a1 + 4d = 8 + 4 × (–2) = 8 – 8 = 0.
О т в е т: а1 = 8; а5 = 0.
6. Найдите все значения х, при
которых значения выражений ![]()
![]() являются тремя последовательными членами
геометрической прогрессии.
являются тремя последовательными членами
геометрической прогрессии.
Р е ш е н и е
По характеристическому свойству геометрической прогрессии имеем:
![]()
![]()
![]()
36 – 12х + х2 = 3х2 + 7х – 10;
2х2 + 19х – 46 = 0;
D = 361 + 368 = 729 = 272
![]()
Если х = –11,5, то ![]() не существует.
не существует.
Если х = 2, то ![]()
Числа 4; 2; 1 – члены убывающей геометрической прогрессии.
О т в е т: х = 2.
7. Найдите сумму всех двузначных чисел, дающих при делении на 4 в остатке 3.
Р е ш е н и е
Числа имеют вид 4 × у + 3, тогда двузначные числа 11; 15; 19; 23; …; 99.
d = a2 – a1 = 15 – 11 = 4; d = 4. Найдем количество двузначных чисел n, если аn = 99:
аn = a1 + d(n – 1); 99 = 11 + 4(n – 1); 88 = 4n – 4; 4n = 92; n = 23.
Найдем сумму:
![]()
О т в е т: 1265.
8. Решить № 17.56.
Р е ш е н и е
Имеем ![]() а1; а2;
а7 и а1 + а2 + а7 = 31.
а1; а2;
а7 и а1 + а2 + а7 = 31.
Первое условие перепишем в виде ![]() (a1 + d)2 = a1(a1 +
6d).
(a1 + d)2 = a1(a1 +
6d).
Второе условие можно переписать в виде a1 + (a1 + d) + (a1 + 6d) = 31;
3a1 + 7d = 31.
Получим систему уравнений:

3d2 – 124d + 28d2 = 0; 31d2 – 124d = 0; d(31d – 124) = 0;
d = 0 или 31d – 124 = 0; d = 4.
Если d = 0, то ![]()
Если d = 4, то а1 = 1; а2 = 5; а3 = 25.
О т в е т: ![]() или 1; 5; 25.
или 1; 5; 25.
III. Итог урока.
Домашнее задание: подготовиться к контрольной работе, повторив материал § 16 и § 17; решить № 16.23 (б; в); № 16.34 (а; б); № 16.45; № 17.18 (а; в); № 17.26 (б).
Комбинаторные задачи
(3 ч)
У р о к 1
Цели: познакомить учащихся с комбинаторными задачами и их решением; ввести правило умножения и его геометрическую модель – дерево возможных вариантов; учить учащихся решению комбинаторных задач.
Ход урока
I. Анализ контрольной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Выполнить работу над ошибками.
II. Изучение нового материала. Работа по учебнику.
1. Знакомство с новыми понятиями начнем с составления из цифр 1, 5, 9 трехзначных чисел без повторяющихся цифр. В этой задаче был осуществлен полный перебор всех возможных вариантов, или комбинаций. Поэтому подобные задачи называют комбинаторными. Рассмотреть решение примера 1 на с. 174 учебника.
2. Рассмотреть еще один вариант решения примера 1 (в) на с. 174–175 учебника.
Построенная схема действительно напоминает дерево, только перевернутое. Видимо поэтому его и называют деревом возможных вариантов (рис. 128 на с. 175 учебника).
3. Рассмотреть решение примеров 2 и 3 на с. 175 учебника.
Такого рода диаграммы, как на рис. 130–131 учебника, удобно рисовать только для сравнительно небольшого числа вариантов, а например, для сотен комбинаций дерево вариантов целиком не нарисуешь. Тогда приходится действовать по-другому. Чаще всего при различных подсчетах используют правило умножения.
Правило умножения
Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
4. Рассмотреть объяснение правила умножения на примере дерева вариантов на с. 177–178 учебника.
5. Правило умножения можно объяснять и по-другому, с использованием таблицы возможных результатов проведения двух испытаний. Рассмотреть пример 4 на с. 179 учебника.
6. Замечания 1 и 2 прочитать на с. 178–179 учебника.
7. Для следующего примера мы приведем три способа решения: перебором, с помощью дерева вариантов и по правилу умножения. Рассмотреть пример 5 на с. 179–180 учебника.
III. Закрепление изученного материала.
1. Решить только на доске № 18.1, с. 120 задачника.
О т в е т: а) 90; б) 81; в) 5 – это 79, 97, 89, 98, 99; г) 10 – это 10, 11, 20, 30, 40, 50, 60, 70, 80, 90.
2. Решить устно задачу № 18.2 на с. 120 задачника.
а) наибольшим числом будет 764, ведь если на первое место поставить цифру 7, то на второе место лучше поставить 6, так как 6 > 4, на последнее место поставить 4;
б) рассуждая аналогично, найдем наименьшее число – это 467;
в) таких чисел ровно два – это 467, 647;
г) всего можно составить шесть чисел – это 467, 476, 647, 674, 746, 764.
О т в е т: а) 764; б) 467; в) 2; г) 6.
3. Решить задачу № 18.3 (а, б) на с. 120 задачника.
а) 99;
б) Число кратно 9, если сумма его цифр делится на 9, так как число с цифры 0 начинаться не может, то на I позицию поставим наименьшую цифру из оставшихся цифр – 1 и начнем складывать ее с 1, 4, 8, 9. Из полученных сумм на 9 делится только сумма цифр 1 и 8. Т. е. наименьшее число, кратное 9 – 18.
О т в е т: а) 99; б) 18.
4. Решить задачу № 18.4 (а, б), с. 120 задачника на доске и в тетрадях.
а) Завтрак

б) 12.
О т в е т: б) 12.
5. Решить задачу № 18.5 (а; б; в), с. 121 задачника на доске и в тетрадях.
а)
б) 4;
в) 1.
О т в е т: б) 4; в) 1.
5. Решить задачу № 18.8 (а; б; в), с. 121 задачника на доске и в тетрадях.
а) Треугольник можно раскрасить в любой
из семи цветов радуги, для раскрашивания квадрата останется 7 – 1 = 6 цветов, а
для раскрашивания круга 6 – 1 = 5 цветов. Тогда всего существует ![]() способов
раскрашивания треугольника, квадрата и круга.
способов
раскрашивания треугольника, квадрата и круга.
б) 210 : 7 = 30 способов раскрашивания, в которых круг будет оранжевым.
в) 210 : 7 = 30 способов раскрашивания, в которых треугольник будет красным. Тогда 210 – 30 = 180 способов раскрашивания, в которых треугольник не будет красным.
О т в е т: а) 210; б) 30; в) 180.
IV. Итоги урока.
Перечислите способы решения комбинаторных задач.
Сформулировать правило умножения.
Домашнее задание: изучить материал § 18 на с. 173–180 учебника; решить № 18.3 (в, г), 18.4 (в, г), 18.5 (г), 18.6, 18.7, 18.18 на с. 120–123 задачника.
У р о к 2
Цели: учить решать учащихся комбинаторные задачи в ходе выполнения упражнений; развивать логическое мышление.
Ход урока
I. Актуализация опорных знаний.
1. Решить на доске задачи из домашней работы, вызвавшие затруднения учащихся.
2. Перечислите способы решения комбинаторных задач.
3. Сформулируйте правило умножения.
4. Решить задачу № 18.17, с. 123 задачника только на доске.
а) 200;
б) так как на первой позиции в числе стоит цифра 2 и она наименьшая из цифр, которые могут занимать I позицию, то на II позицию фиксируем либо цифру 0, либо цифру 2, так как 0 < 5 и 2 < 5. На III позицию можно поставить любую из цифр 0, 2, 8, 9. Получим 8 чисел – это 200, 202, 208, 209, 220, 222, 228, 229.
в) 909; 929; 989; 999.
г) 200; 280; 800; 880; 920.
О т в е т: а) 200, б) 200, 202, 208, 209, 220, 222, 228, 229; в) 909, 929, 989, 999; г) 200, 280, 8000, 880, 920.
II. Выполнение упражнений.
1. Решить задачу № 18.9, с. 122 задачника на доске и в тетрадях.
а) Всего таких точек на координатной
плоскости – ![]()
б) таких точек на координатной
плоскости всего 10 – это (–3; 1),
(–3; 2), (–3; 7), (–3; –1), (–1; 1), (–1; 2), (–1; 7), (–1; –1), (–3; –3),
(–1; – 3),
или 2 · 5 = 10.
в) таких точек на координатной
плоскости всего 15 – это (–3; 1),
(–3; 2), (–3; 7), (1; 1), (1; 2), (1; 7), (–1; 1), (–1; 2), (–1; 7),
(2; 1), (2; 2),
(2; 7) (7; 1), (7; 2), (7; 7), или 5 · 3 = 15.
г) таких точек на координатной
плоскости всего 16 – это (–3; 1),
(–3; 2), (–3; –1), (–3; –3), (1; 1), (1; 2), (1; –1), (1; –3), (–1;
–1), (–1; 1),
(–1; 2), (–1; –3), (2; 1), (2; 2), (2; –1), (2; –3), или 4 · 4 = 16.
О т в е т: а) 25; б) 10; в) 15; г) 16.
2. Решить № 18.10 (а; б), с. 122 задачника на доске и в тетрадях.
а) наименьшее значение ![]() а наибольшее число
а наибольшее число ![]()
б) ![]() числа всего можно составить.
числа всего можно составить.
О т в е т: а) 1 и 27000; б) 64.
3. Решить задачу № 18.20, с. 124 задачника на доске и в тетрадях.
а) ![]() вариантов контрольной работы возможно
составить.
вариантов контрольной работы возможно
составить.
б) ![]() вариантов контрольной работы, в которых
встретится задача на движение.
вариантов контрольной работы, в которых
встретится задача на движение.
в) ![]() вариантов контрольной работы, в которых
у квадратного уравнения будет хотя бы один корень.
вариантов контрольной работы, в которых
у квадратного уравнения будет хотя бы один корень.
г) ![]() варианта, в которых встретится одновременно
задача на работу и квадратное уравнение, не имеющее корней.
варианта, в которых встретится одновременно
задача на работу и квадратное уравнение, не имеющее корней.
120 – 24 = 96 вариантов, в которых не встретится одновременно задача на работу и квадратное уравнение, не имеющее корней.
О т в е т: а) 120; б) 48; в) 80; г) 96.
4. Решить задачу № 18.23, с. 124 задачника на доске и в тетрадях.
а) Точку с координатами (0; 0) можно обозначить тремя
способами А, В и С, тогда точку (2; 0) можно обозначить
любой из двух оставшихся букв, тогда для точки (3; 2) останется только одна
буква. То есть всего существует ![]() способов.
способов.
б) Точку с координатами (0; 0) можно обозначить любой
из четырех букв, тогда точку (2; 0) можно обозначить любой из трех оставшихся
букв, точку (3; 0) – 2 оставшимися буквами, тогда для точки (3; 7) останется
одна буква. То есть обозначить точки в данном случае можно ![]() способами.
способами.
в) ![]() способов обозначения вершин буквами P,
R, S, T и Q.
способов обозначения вершин буквами P,
R, S, T и Q.
г) ![]() – случаев в задании в) PR будут
одной из сторон.
– случаев в задании в) PR будут
одной из сторон.
О т в е т: а) 6; б) 24; в) 120; г) 60.
III. Итоги урока.
Сформулировать правило умножения.
Домашнее задание: повторить материал § 18 на с. 173–180 учебника; решить № 18.10 (в; г), 18.21, 18.22 на с. 124–125 задачника.
У р о к 3
Цели: ввести понятие факториала и перестановки, учить находить их в ходе упражнений; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний.
1. Решить на доске задания из домашней работы, вызывающие затруднения у учащихся.
2. Сформулируйте правило умножения.
3. Какими способами можно решать комбинаторные задачи?
4. Решить задачу № 18.8 (г), с. 121 задачника (устно).
г) Холодных цветов всего 4, поэтому всего способов ![]()
II. Объяснение нового материала.
1. Правило умножения позволяет в один шаг решать самые разнообразные задачи. Например, оно приводит к крайне важному в математике понятию факториала.
2. Рассмотреть пример 6 на с. 180 учебника.
3. Определение. Произведение подряд идущих первых n – натуральных чисел обозначают n! и называют «эн факториал»
![]()
Одно из значений английского слова factor – «множитель». Так что эн факториал примерно переводится как «Состоящий из n множителей».
4. Записать в тетрадь значения 1!, 2!, 3!, 4!, 5!, 6!.
5. Рассмотреть и записать в тетрадь формулу для подсчета, связанных с n! на с. 181 учебника.
6. Рассмотреть пример 7 на с. 181 учебника.
7. Теорема. n различных элементов можно расставить по одному на n различных мест ровно n! способами.
8. Исторически сложилось так, что более употребителен не термин «расстановка», а «перестановка», и потому эту теорему чаще формулируют так: «Число всех перестановок множества из n элементов равно n!». Сокращенно это записывается в виде формулы Pn = n!.
В этом сокращении буква P соответствует первой
букве английского глагола (существительного) permute (permutation),
который и переводится как «переставлять» («перестановка»). Например, P3 = 3! = 6, P7 = 7! =
= 5040 и т. д.
III. Выполнение упражнений.
1. Решить № 18.11 на с. 122 задачника.
а) 7! = 5040;
б) 8! = 5040 ![]()
в) 6! – 5! = 720 – 120 = 600;
г) ![]()
О т в е т: а) 5040, б) 40320, в) 600, г) 24.
2. Решить № 18.12 на с. 122 задачника.
а) ![]()
б) ![]()
в) ![]()
г) ![]()
О т в е т: а) 30240; б) 462; в) 2550; г) 120120.
3. Решить № 18.13. на с. 122 задачника на месте с комментированием.
Число 11! Делится на такое число, в разложении которого содержатся только множители, входящие в 11!
а) ![]() поэтому 11! делится на 64;
поэтому 11! делится на 64;
б) ![]() поэтому 11! делится на 25 (вторая
пятерка содержится в множителе 10);
поэтому 11! делится на 25 (вторая
пятерка содержится в множителе 10);
в) ![]() поэтому 11! делится на 81 (вторая тройка
содержится в множителе 6);
поэтому 11! делится на 81 (вторая тройка
содержится в множителе 6);
г) ![]() число 11! Содержит только один множитель
7, поэтому 11! Не делится на 49.
число 11! Содержит только один множитель
7, поэтому 11! Не делится на 49.
4. Решить № 18.14 (в; г) на с. 122 задачника.
в) 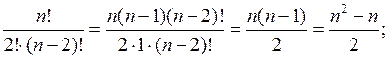
г) 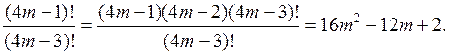
5. Решить № 18.15 (а; б; в) на с. 122 задачника. Решение № 18.15 (б) объясняет учитель.
a) n! = 7(n – 1)!
n(n – 1)! = 7(n – 1)!
n = 7;
б) (m + 17)! =
420(m + 15)!; m ![]() N
N
(m + 17) (m + 16) (m + 15)! = 420(m + 15)!
m2 + 33m – 148 = 0
![]()
m = 4;
в) (k – 10)! = 77(k – 11)!
(k – 10) (k – 11)! = 77(k – 11)!
k – 10 = 77
k = 87.
О т в е т: а) 7, б) 4, в) 87.
6. Решить № 18.25 (а; б) на с. 125 задачника.
а) 
б) 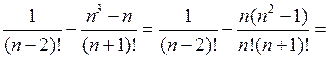

7. Решить № 18.16 на с. 122 задачника.
а) Общее число способов рассаживания равно: ![]()
б) Хозяин сразу займет свое конкретное место. Гость А
может занять одно из 4 мест, гость В – одно из 3, гость С – одно
из 2, а гость D – займет оставшееся место. Общее число способов
рассаживания по местам равно ![]()
в) Гость А может занять любое из 5 мест,
тогда гость С займет любое из двух мест рядом с А, гость В
займет любое из трех оставшихся мест, гость D любое из двух оставшихся
мест, хозяин займет последнее место. Общее число возможных вариантов равно: ![]()
г) Аналогично г), если бы гость А и D сидели вместе, то существовало бы 60 возможных вариантов. Поэтому способов рассаживания гостей А и D врозь существует 120 – 60 = 60.
О т в е т: а)120; б) 24; в) 60; г) 60.
IV. Итоги урока.
Дать определение n-факториала.
Домашнее задание: изучить § 18 на с. 180–182 учебника; решить № 18.14 (а; б), 18.15 (г), 18.25 (в; г), 18.24 на с. 122–125 задачника
Статистика – дизайн информации (3 ч)
Урок 1
Цели: познакомить учащихся с элементами статистики на конкретных примерах; ввести понятие варианты, кратности варианты, частоты варианты; развивать логическое мышление учащихся.
Ход урока
I. Изучение нового материала.
1. Рассмотреть пример на с. 182 учебника и сделать вывод, что основная задача статистики – обработка информации.
2. Рассмотреть порядок преобразований первоначально, полученной информации:
1) сначала данные измерений упорядочивают и группируют;
2) затем составляют таблицы распределения данных;
3) таблицы распределения переводят в графики распределения;
4) наконец, получают своего рода паспорт данных измерения в которых собрано небольшое количество основных числовых характеристик полученной информации.
3. Зафиксируем конкретное измерение и проследим шаг за шагом, как его данные преобразовываются. Рассмотреть измерение (И) на с. 183 учебника.
4. Группировка информации:
1) Оценить рамки, в которых вообще могут находиться данные измерения;
2) Составить общий ряд данных. Данные располагают в порядке возрастания (рассмотреть таблицу в учебнике на с. 184).
5. Разобрать пример 1 на с. 184 учебника.
6. При проведении конкретного измерения вполне может случиться. Значит, надо отличать реально полученные результаты измерения от общего ряда данных. Например, в измерении (И) нам встретилось только такие результаты: 10, 20, 30, 40, 50, 60, 80, 90, 100, 120. Каждое из этих чисел называют вариантой измерения.
Варианта измерения – один из результатов этого измерения; ряд данных измерения – это все варианты измерения, перечисленные по порядку (рассмотреть таблицу в учебнике на с. 185).
Если все варианты измерения перечислить по порядку (и без повторений), то получится ряд данных измерения.
В измерении (И) ряд данных – это 10, 20, 30, 40, 50, 60, 80, 90, 100, 120.
Рассмотреть таблицу на с. 185 учебника.
7. Разобрать решение примера 2 на с. 185 учебника.
8. Определение. Если среди всех данных конкретного измерения одна из вариант встретилась ровно k раз, то число k называют кратностью этой варианты измерения.
9. Разобрать группировку данных измерения (И) на с. 186–187 учебника.
10. Внесем в таблицу ряд данных измерения и кратности соответствующих вариант. Получим таблицу распределения данных. Разобрать пример таблицы в измерении (И).
11. Если сложить все кратности, то получится количество всех данных измерения – объем измерения. Выяснить объем измерения для измерения (И).
12. 
Частоты всех вариант удобно приписывать следующей строкой к уже составленной таблице. Полученную таблицу называют таблицей распределения частот измерения. Рассмотреть пример таблицы распределения частот измерения (И), с. 188 учебника.
13. Сумма всех частот всегда равна 1 – ведь это сумма дробей с одинаковыми знаменателями, у которых сумма всех числителей как раз и равна знаменателю. Для удобства счета и построения графиков частоты переводят в проценты от объема измерения. Тогда таблицу распределения дополняют еще строкой частот в процентах. Она получается из предыдущей строки умножением на 100 %.
Процентная частота варианты = частота варианты · 100 %
(п. ч. в. = ч. в. · 100 %)
Рассмотреть пример таблицы распределения частот в процентах для измерения (И) на с. 188 учебника.
14. Сумма всех частот в процентах равна 100 %.
II. Закрепление изученного материала.
1. Решить задачу № 19.1 на с. 125 задачника на доске и в тетрадях.
а) Вряд ли взрослый человек будет весить менее 45 кг и более 120 кг. Значит, общий ряд данных выглядит так: 45, 50, 57, …, 89, 90, 120.
б) Длина слова русского языка может состоять из одной и более букв, но количество букв не превосходит 35. Значит, общий ряд данных выглядит так: 1, 2, 3, …, 32, 35.
в) Число страниц в ежедневной газете не менее 4 и не более 8. Значит, общий ряд данных выглядит так: 4, 6, 8.
г) В школьном дневнике могут стоять отметки от 1 до 5. Поэтому, общий ряд данных выглядит так: 1, 2, 3, 4, 5.
2. Решить задачу № 19.3 на с. 126 задачника на доске и в тетрадях.
а) 15 · 4 = 60 арбузов продал продавец.
б) От 4 до 25 кг с шагом 0,5.
в) Наименьшая варианта этого измерения – 5 кг.
Наибольшая варианта этого измерения – 12 кг.
г) 2 арбуза по 5 кг было продано, т. е. кратность варианты 5–2, 14 арбузов по 8 кг, то есть кратность варианты 8–13, 3 арбуза – по 12 кг, то есть кратность варианты 12–3.
д) Таким числом может быть число 5,5; 7,5; 9,5.
О т в е т: а) 60; б) от 4 до 25 кг с шагом 0,5; в) 5 и 12; г) 5,5; 7,5; 9,5.
3. Решить № 19.10 на с.128 задачника на доске и в тетрадях.
а) Так как 22 = 4,23 = 8,24 = 16,25 = 32,26 = 64,27 = 128 и т. д., то общий ряд данных – 2, 4, 6, 8.
б) 22 = 4,23 = 8,25 = 32,27 = 128,28 = 256,210 = 1024,211 = 2048.
Ряд данных этого измерения выглядит таким образом – 4, 8, 2, 8, 6, 4, 8.
О т в е т: а) 2, 4, 6, 8; б) 4, 8, 2, 8, 6, 4, 8.
4. Решить № 19.11 на с. 128 задачника на доске и в тетрадях.
а) 12, 13, 14, 16, 17, 18, 19, 20, то есть общий ряд данных от 12 до 20 баллов.
б) 19, 13, 17, 14, 20, 19, 20, 13, 14, 17, 14, 17, 17, 17, 17.
в) Кратность варианты 13 – 2, кратность варианты 14 – 3, кратность варианты 15 – 0.
г) 13, 13, 14, 14, 14, 17, 17, 17, 17, 17, 17, 19, 19, 20, 20.
О т в е т: а) от 12 до 20 баллов; б) 19, 13, 17, 14, 20, 19, 20, 13, 14, 17, 14, 17, 17, 17, 17; в) 2, 3 и 0; г) 13, 13, 14, 14, 14, 17, 17, 17, 17, 17, 17, 19, 19, 20, 20.
5. Решить задачу № 19.13 на с. 129 задачника. Учитель при необходимости помогает в решении учащимся.
Процентная частота варианты получается умножением
частоты варианты на 100 % – п. ч. в. = ч. в. · 100 %. Выразим из
этой формулы частоту варианты –  то есть
то есть 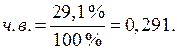
Частота варианты равна частному кратности варианты и
объема измерения  выразим
из этой формулы объем измерения, получим
выразим
из этой формулы объем измерения, получим 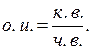 Объем измерения равен
Объем измерения равен 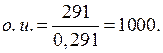
Зная основные данные, можно заполнить всю таблицу.
|
|
Варианта |
Сумма |
|||||
|
№ 1 |
№ 2 |
№ 3 |
№ 4 |
№ 5 |
№ 6 |
||
|
Кратность |
291 |
122 |
113 |
202 |
79 |
193 |
1000 |
|
Частота |
0,291 |
0,122 |
0,113 |
0,202 |
0,079 |
0,193 |
1 |
|
Частота (%) |
29,1 |
12,2 |
11,3 |
20,2 |
7,9 |
19,3 |
100 |
III. Итоги урока.
Сформулировать понятие общего ряда данных, варианты, кратности варианты, частоты варианты, процентной частоты варианты.
Рассказать как составляются таблицы распределения частот и процентных частот измерения.
Домашнее задание: изучить § 19 на с. 182–183 учебника; решить № 19.2, №19.4, № 19.10 (в, г), № 19.12, с. 125–126 задачника.
У р о к 2
Цели: изучить графическое представление информации, ввести понятие многоугольника распределения данных; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний.
1. Проверить выборочно по тетрадям нескольких учащихся выполнение ими домашнего задания.
2. Решить на доске задачи, вызвавшие затруднения.
3. Решить задачу № 19.4 на с. 126 задачника.
а) от 140 см до 210 см.
б) 157 и 190.
в) Кратность варианты 168 – 4, кратность варианты 179 – 4.
г) 161.
II. Объяснение нового материала.
1. Распределение данных измерения удобно задавать с помощью таблиц. Но мы знаем, что и для функций есть табличный способ их задания. Таблицы образуют «мостик», по которому от распределения данных можно пройти к функциям и графикам.
2. Разобрать построение графика распределения выборки на с. 189 учебника (рис. 134) для данных в измерении (И).
3. Ломаную линию, которая является графиком некоторой кусочно-линейной функции, называют многоугольником или полигоном распределения данных (polygon – «многоугольник»). Составленные таблицы распределения частот и распределения частот в процентах позволяют построить многоугольник частот и многоугольник частот в процентах. Для наглядности в практических приложениях удобнее использовать многоугольник частот в процентах.
4. Разобрать построение многоугольника частот в процентах для измерения (И) на с. 190, рис. 135 учебника.
5. При оперировании с большими объемами информации используют методы приближенной группировки данных. В таких случаях вариантой измерения является не одно число, а числовой промежуток. Разобрать приближенную группировку данных на примере измерения (И).
6. При графическом представлении больших объемов информации многоугольника распределения заменяют гистограммами, или столбчатыми диаграммами, которые будут изучаться в старшей школе.
III. Закрепление изученного материала.
1. Решить задачу № 19.14 (а; в; г), с. 129 на доске и в тетрадях.
а) 26 + 18 + 44 + 54 + 22 + 36 = 200 – объем измерения.
в) Рассчитаем частоту каждой варианты, для этого разделим кратность варианты на объем измерения.
Частота варианты:
![]()
Сумма всех частот должна быть равна 1, проверим
это 0,13 + 0,09 +
+ 0,22 + 0,27 + 0,11 + 0,18 = 1.
Заполним строку «Частота, %». Умножим результаты, полученные в предыдущей строке на 100 %.
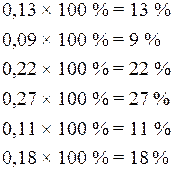
Найдем сумму частот в
процентах ![]() или
13 % +
или
13 % +
+ 9 % + 22 % + 27 % + 11 % + 18 % = 100 %.
|
|
Варианта |
Сумма |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
Кратность |
26 |
18 |
44 |
54 |
22 |
36 |
200 |
|
Частота |
0,13 |
0,09 |
0,22 |
0,27 |
0,11 |
0,18 |
1 |
|
Частота, % |
13 |
9 |
22 |
27 |
11 |
18 |
100 |
г) Отложим по оси абсцисс значения первой строки таблицы, по оси ординат значения четвертой строки таблицы. Построим соответствующие точки, соединим отрезками.
|
по оси абсцисс |
1 |
2 |
3 |
4 |
5 |
6 |
|
по оси ординат |
19 |
9 |
22 |
27 |
11 |
18 |
Получим многоугольник процентных частот.

2. Решить задачу № 19.5 на с. 126 задачника.
а) 31 + 52 + 47 + 38 + 19 + 13 = 200 – распределенных ценников.
б) ![]() – частота варианты «от 100 до 150 р.».
– частота варианты «от 100 до 150 р.».
в) ![]() – частота варианты «больше или равно 200
р.».
– частота варианты «больше или равно 200
р.».
![]() – процентная частота варианты «больше
или равно 200 р.».
– процентная частота варианты «больше
или равно 200 р.».
г)
|
|
Ценовая категория, р. |
|||||
|
0–20 |
20–50 |
50–100 |
100–150 |
150–200 |
≥ 200 |
|
|
Количество ценников |
31 |
52 |
47 |
38 |
19 |
13 |
|
Частота |
0,155 |
0,26 |
0,235 |
0,19 |
0,095 |
0,065 |
|
Частота, % |
15,5 |
26 |
23,5 |
19 |
9,5 |
6,5 |
3. Решить задачу № 19.8 (а; б; г) на с. 127 задачника.
а) вариант ровно 7 – это 2, 3, 5, 6, 7, 9, 10.
б) Объем измерения равен сумме всех кратностей измерений, поэтому найдем кратности всех вариант:
варианты 2–9;
варианты 3–8;
варианты 5–10;
варианты 6–5;
варианты 7–4;
варианты 9–5;
варианты 10–9
и сложим их 9 + 8 + 10 + 5 + 4 + 5 + 9 = 50.
г) найдем частоты вариант
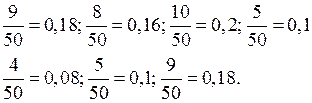
Найдем процентные частоты вариант 18 %, 16 %, 20 %,
10 %, 10 %,
8 %, 10 %, 18 %.
Наименьшая процентная частота – 8 %.
IV. Итоги урока.
Сформулировать понятие многоугольника или полигона распределения данных.
Рассказать алгоритм построения многоугольника частот и многоугольника процентных частот измерения.
Домашнее задание: изучить §
19 на с. 188–191; решить задачу
№ 19.15 (в; г), 19.6 (а; б; в), 19.7 на с. 126–127 задачника.
У р о к 3
Цели: изучить числовые характеристики, или «паспорт» выборки; учить учащихся решать задачи, развивать логическое мышление.
Ход урока
I. Проверка домашнего задания.
1. Проверить выборочно по тетрадям нескольких учащихся выполнение ими домашнего задания.
2. Решить на доске задачи, вызвавшие затруднения.
II. Объяснение нового материала.
1. У измерений есть краткий паспорт, состоящий из набора основных числовых характеристик. Рассмотреть основные числовые характеристики на примере измерения (И).
2. Разность между максимальной и минимальной вариантами называют размахом измерения.
3. Ту варианту, которая в измерении встретилась чаще других, называют модой измерения. Если данные измерения уже собраны в двустрочную таблицу распределения, то для нахождения моды следует:
§ во второй строке (кратности) выбрать наибольшее число;
§ от найденного числа подняться на клетку выше: полученное число и будет модой.
Если данные измерения представлены графически в виде многоугольника распределения, то мода – это точка, в которой достигается максимум многоугольника распределения.
4. Наиболее важная характеристика числового ряда данных – среднее значение (среднее арифметическое, или просто среднее).
Для нахождения среднего значения следует:
§ просуммировать все данные измерения;
§ полученную сумму разделить на количество данных.
5. Рассмотреть подсчет среднего значения для измерения (И) на с. 193. Сформулировать общее правило:
1) каждую варианту умножить на ее частоту;
2) cложить все полученные произведения.
6. Рассмотреть пример 3, с. 194–196, повторив для него все шаги 1) – 4) обработки данных.
III. Закрепление изученного материала.
1. Решить № 19.8 (в), с. 127 задачника (устно).
в) Точка, в которой достигается максимум многоугольника распределения, – это 10, то есть точка 5 – это мода.
О т в е т: в) 5.
2. Решить задачу № 19.9, с. 128 задачника на доске и в тетрадях.
а) Размах измерения равен 4 – 0 = 4.
б) Мода равна 2.
в) ![]() ч.
ч.
О т в е т: а) 4; б) 2; в) 1,8 ч.
3. Решить задачу № 19.15, с. 130 задачника на доске и в тетрадях.
а) мода равна 431.
б) 220 + 360 + 610 + 430 + 200 = 1820 – количество деталей, вес которых отличается от планового на два грамма.
![]() – деталей, вес которых отличается от
планового на два грамма.
– деталей, вес которых отличается от
планового на два грамма.
О т в е т: а) 431; б) 91 %.
4. Решить № 19.17, с. 130 задачника на доске и в тетрадях.
a) ![]()
4 · 5 + 7 · 2 + 3x = 100;
34 + 3x = 100;
3x = 66;
x = 22.
|
Варианта |
4 |
7 |
22 |
|
Кратность |
5 |
2 |
3 |
б) Размах измерения равен 22 – 4 = 18. Мода измерения равна 4.
в) Нет.
г) ![]()
4 · 5 + 7 · 3 + 3y = 10x;
34 + 3y = 10x;
3y = 10x – 34;
![]()
О т в е т: а) 22; б) 18 и 4; в) нет; г) ![]()
5. Решить № 19.19, с. 131 задачника на доске и в тетрадях.
a) ![]()
![]()
в) 
Так как решение системы интервал (–∞; ![]() ), то х может
быть равным 3, 4, 5, 6.
), то х может
быть равным 3, 4, 5, 6.
г) 3x – 1 > 19;
3x > 20;
x > ![]() .
.
Мода распределения может равняться трем при х = 7.
О т в е т: а) ![]() в) 3, 4, 5, 6; г) 3; при х = 7.
в) 3, 4, 5, 6; г) 3; при х = 7.
IV. Итоги урока.
Перечислить основные числовые характеристики выборки.
Домашнее задание: изучить § 19 на с. 192–196, решить № 19.18, № 19.14 (в), № 19.20, с. 127–130 задачника.
Простейшие вероятностные задачи
(3 ч)
У р о к 1
Цели: ввести понятия событий достоверных, невозможных и случайных; дать классическое определение вероятности, закрепить его в ходе решения задач; развивать логическое мышление.
Ход урока
I. Проверка домашнего задания.
1. Проверить выборочно по тетрадям нескольких учеников выполнение ими домашнего задания.
2. Решить на доске задачи из домашней работы, вызвавшие затруднения у учащихся.
II. Изучение нового материала.
1. С некоторыми комбинаторными задачами мы уже встречались. В каждой из них мы подсчитывали количество всевозможных комбинаций, которые тем или иным способом можно составить, исходя из условия конкретной задачи. Например, из цифр 1, 5, 9 можно составить ровно шесть трехзначных чисел без повторяющихся цифр: 159, 195, 519, 591, 915, 951. А какую часть из них составляют, например, числа, кратные пяти?
2. Делается вывод: ![]() часть. В теории вероятностей
говорят в этом случае так:
часть. В теории вероятностей
говорят в этом случае так: ![]() – это вероятность того, что трехзначное
число, составленное из неповторяющихся цифр 1, 5 и 9, будет кратно пяти.
– это вероятность того, что трехзначное
число, составленное из неповторяющихся цифр 1, 5 и 9, будет кратно пяти.
3. Рассмотреть решение примера 1 на с. 197 учебника.
4. Проанализировать решение примера 1 на с. 198 учебника. Ввести понятия достоверного, невозможного и случайного событий.
5. Рассмотреть решение примера 2 на с. 198–199 учебника.
6. Равновозможные между собой события и вероятностная модель (прочитать на с. 199–200 учебника).
7. Классическая вероятностная схема, прочитать на с. 200 учебника.
Принято вероятность события А обозначать P(A) (объяснение такого обозначения очень простое: «вероятность» по-французски – probabilite, по-английски «вероятно» – probably).
Итак, ![]()
8. Классическое определение вероятности:
Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания.
В частности, если событие А невозможно при
проведении некоторого испытания, то N(A) = 0 и поэтому ![]() Напротив,
достоверность события А при проведении некоторого испытания означает, что N(A)
= N, поэтому
Напротив,
достоверность события А при проведении некоторого испытания означает, что N(A)
= N, поэтому ![]()
9. Рассмотреть решение примера 3 на с. 201–202 учебника.
III. Закрепление изученного материала.
1. Решить № 20.1, с. 131 задачника на доске и в тетрадях.
Из цифр 4, 6, 7 можно составить ровно шесть трехзначных чисел без повторяющихся цифр: 467, 476, 647, 674, 746, 764, то есть N = 6.
а) Событие А – получится
наибольшее из всех таких чисел. Тогда
N(A) = 1, так как наибольшее из шести таких чисел одно – 764.
Тогда искомая вероятность – ![]()
б) Событие В – получится число,
у которого вторая цифра 7. Тогда
N(В) = 2, так как таких чисел ровно 2 из шести – это 476, 674.
Значит, искомая вероятность ![]()
в) Событие С – получится
число, заканчивающееся на 6. Тогда
N(С) = 2, так как таких чисел ровно 2 из шести – это 476, 746.
Значит, искомая вероятность ![]()
г) Событие D – получится число,
кратное 5. Тогда N(D) = 0, так как среди этих шести чисел таких
нет. Поэтому искомая вероятность равна ![]()
О т в е т: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г) 0.
; г) 0.
2. Решить № 20.2, с. 131 задачника на доске и в тетрадях.
Составим дерево вариантов, обозначим О – выпадение «орла» и Р – выпадение «решки». Мы видим, что всего возможно восемь исходов: ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР, то есть N = 8.
а) Событие А – «решка»
выпадет в последний раз. Тогда N(A) = 4. Значит, искомая
вероятность интересующего нас события равна P(A) = ![]()
б) Событие В – ни разу не
выпадет орел. Тогда N(В) = 1. Значит, искомая вероятность равна ![]()
в) Событие С – число
выпадений «орла» в два раза больше числа выпадений «решки». Тогда N(С)
= 3. Значит, искомая вероятность равна ![]()
г) Событие D – при первых
двух подбрасываниях результаты будут одинаковыми. N(D) = 4. Тогда
искомая вероятность равна P(D) =![]()
О т в е т: а) 0,5; б) 0,125; в) 0,375; г) 0,5.
3. Решить задачу № 20.3 (а; в) на с. 132 задачника на доске и в тетрадях.
Число не может начинаться с нуля, поэтому первую позицию в двузначном числе могут занимать 9 цифр – 1, 2, 3, 4, 5, 6, 7, 8, 9, а вторую позицию перечисленные девять цифр и нуль. Поэтому общее количество двузначных чисел N, которое можно составить из этих цифр 9 · 10 = 90, то есть N = 90.
а) Событие А – двузначное число
оканчивается нулем. N(A) = 9 – это 10, 20, 30, 40, 50, 60, 70,
80, 90. Значит, искомая вероятность равна ![]()
в) Событие В – двузначное число
больше 27 и меньше 46. N(В) = 18 – это 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45. Значит, искомая вероятность
равна ![]()
О т в е т: а) ![]() в) 0,2.
в) 0,2.
4. Решить задачу № 20.4 (а; б) на с. 132 задачника. Учитель при необходимости помогает в решении учащимся.
Составим дерево вариантов. Всего возможно исходов случайных выборов двух кандидатов 4 · 4 = 16, но надо учесть, что из них исключаются пары с одинаковыми кандидатами, таких – 4 и пары, в которых имена просто поменяли местами. Например: (Владимир Владимирович; Василий Всеволодович) и (Василий Всеволодович; Владимир Владимирович). Таких пар – 6. Поэтому 16 – 4 – 6 = 6, то есть N = 6.
а) Событие А – выбран Владимир Венедиктович. N(A)
= 3. Тогда ![]()
в) Событие В – выбраны кандидаты с одинаковыми
именами. N(В) = 1. Тогда ![]()
5. Решить задачу № 20.13 (а; в), с. 133 задачника на доске и в тетрадях.
Число не может начинаться с нуля, поэтому первую позицию в двузначном числе могут занимать 4 цифры – 1, 4, 8, 9, а вторую позицию перечисленные четыре цифры и нуль. Поэтому общее количество двузначных чисел N, которое можно составить из этих цифр, 4 · 5 = 20 – это 10, 11, 14, 18, 19, 40, 41, 44, 48, 49, 80, 81, 84, 88, 89, 90, 91, 94, 98, 99, то есть N = 20.
а) Событие А – получится наименьшее из всех
таких чисел. N(A) = 1 – это 10. Значит, искомая вероятность равна
![]()
в) Событие В – получится число, кратное 9. N(В)
= 4 – это 18, 81, 90, 99. Значит, искомая вероятность равна ![]()
О т в е т: а) 0,05; б) 0,2.
6. Решить № 20.18 на с. 134 задачника.
Изобразив дерево возможных вариантов, увидим, что всего исходов возможно 12, то есть N = 12.
а) Событие А – обе карты – тузы черной масти. N(A)
= 2. Тогда искомая вероятность равна ![]()
б) Событие В – вторая карта – пиковый туз. N(В)
= 3. Значит, искомая вероятность равна ![]()
О т в е т: а) ![]() б) 0,25.
б) 0,25.
IV. Итог урока.
Сформулировать понятия достоверных, невозможных и случайных событий. Дать классическое определение вероятности.
Домашнее задание: изучить материал § 20 на с. 196–202 учебника; решить № 20.3 (б; г); № 20.13 (б; г); № 20.14; № 20.16 на с. 132–134 задачника.
У р о к 2
Цели: ввести определение противоположного события, изучить теорему для нахождения вероятности противоположного события, ввести определение несовместных событий, изучить вероятность суммы несовместных событий; развивать логическое мышление учащихся.
Ход урока
I. Изучение нового материала.
1. Имеется тесная связь между, с одной стороны, множествами, их элементами и подмножествами и, с другой стороны, испытаниями (опытами, экспериментами), их исходными и случайными событиями.
Допустим, перечислены все N возможных исходов некоторого опыта, испытания, эксперимента. Все N исходов рассматриваются как единое множество, перечисленное поэлементно (рис. 144а) на с. 203 учебника.
2. Теперь нас интересует вероятность некоторого случайного события А, которое может произойти, а может и не произойти в результате проведенного испытания. Это означает, что событие А происходит при наступлении только некоторых из всех возможных N исходов. Тогда в списке всех исходов возникает некоторое подмножество, состоящее из N(А) элементов.
3. Сделать вывод: случайное событие А –
просто подмножество подмножества всех исходов, благоприятствующих А,
среди множества всех N возможных исходов. Вероятность каждого отдельного
исхода равна ![]() то
есть все они равновероятны.
то
есть все они равновероятны.
4. Рассмотреть связь между терминами теории вероятностей и теории множеств в таблице, приведенной на с. 203 учебника.
5. Разобрать решение примера 4, на с. 204 учебника.
6. Определение.
Событие В называют противоположным событию А, если событие
В происходит тогда и только тогда, когда не происходит событие А;
обозначение: ![]() Событие
А и В называют несовместными, если они не могут
происходить одновременно.
Событие
А и В называют несовместными, если они не могут
происходить одновременно.
Рассмотреть примеры несовместных событий А и В на рис. 145, с. 204 учебника.
7. Т е о р е м а 1. Если событие А и В несовместны, то вероятность того, что наступит или А, или В, равна Р(А) + Р(В).
Рассмотреть доказательство теоремы 1 на с. 205 учебника.
8. Сумма событий А и В – это событие состоящее в наступлении хотя бы одного из двух данных событий А и В. На языке теории множеств получается операция объединения множеств. Ввести краткую формулировку теоремы 1. Если А и В несовместны, то Р(А + В) = Р(А) + Р(В).
9. Т е о р е м а 2. Для нахождения вероятности противоположного события следует из единицы вычесть вероятность самого события:
Р(![]() ) = 1 – Р(А).
) = 1 – Р(А).
Разобрать доказательство теоремы 2 на с. 205 учебника.
Довольно часто удобно использовать и симметричную
формулу ![]() Это
бывает в тех случаях, когда посчитать вероятность противоположного события
проще, чем найти вероятность самого события. Типичной ситуацией являются
события, описание которых использует оборот «хотя бы один раз» или аналогичный
ему.
Это
бывает в тех случаях, когда посчитать вероятность противоположного события
проще, чем найти вероятность самого события. Типичной ситуацией являются
события, описание которых использует оборот «хотя бы один раз» или аналогичный
ему.
II. Выполнение упражнений.
1. Решить № 20.18 (в, г), с. 132.
в) Событие С – первая карта – туз красной
масти. N = 4, а N(A) = 2. Значит, искомая вероятность
равна ![]()
г) Событие D – среди выбранных карт есть бубновый туз. Оно наступит тогда и только тогда, когда бубновый туз выпадет или при первом вытаскивании или при втором.
Событие Е – бубновый туз выпал при первом
вытаскивании ![]()
Событие F – бубновый туз выпал при втором
вытаскивании ![]()
Так как события Е и F несовместны, то
Р(D) = P(E) + P(F). Поэтому
Р(D) = 0,25 + 0,25 = 0,5.
О т в е т: в) 0,5; г) 0,5.
2. Решить задачу № 20.7 (а; в) на с. 132 на доске и в тетрадях.
Общее число исходов расстановки крестика и нолика в
каждую клетку таблицы ![]() равно 16 = 4 · 4 – это ХХХХ, ХХХО,
ХХОО, ХООО, ОООО, ОООХ, ООХХ, ОХХХ, ХООХ,
ХОХО, ОХХО, ОХОХ, ООХО, ОХОО, ХХОХ, ХОХХ,
то есть N = 16.
равно 16 = 4 · 4 – это ХХХХ, ХХХО,
ХХОО, ХООО, ОООО, ОООХ, ООХХ, ОХХХ, ХООХ,
ХОХО, ОХХО, ОХОХ, ООХО, ОХОО, ХХОХ, ХОХХ,
то есть N = 16.
а) Событие А – будет поставлен ровно один
крестик. N(A) = 4. Значит, ![]()
б) Событие В – будет поставлено ровно два
нолика. N(В) = 6. Значит, искомая вероятность равна ![]()
в) Событие С – будет поставлен крестик в левой
нижней клетке таблицы N(С) = 8. Значит, искомая вероятность равна
![]()
г) Событие D – будут поставлены в верхней
левой и нижней правой клетках разные значки. N(D) = 8. Значит,
искомая вероятность равна ![]()
О т в е т: а) 0,25; б) 0,375; в) 0,5; г) 0,5.
3. Решить задачу № 20.5, с. 132 задачника на доске и в тетрадях.
Общее количество двузначных чисел N = 90.
а) Событие А – цифры числа различаются больше чем на 8. N(A) = 1.
![]()
в) Событие В – при перестановке цифр местами получится двузначное число, меньшее исходного. N(В) = 36.
![]()
О т в е т: а) ![]() б) 0,4.
б) 0,4.
4. Решить устно № 20.9, с. 133 задачника на доске и в тетрадях.
Общее число возможных исходов при бросании игрального кубика равно 6, то есть N = 6.
а) Событие А – выпадет четверка. N(A)
= 1. Значит, искомая вероятность равна ![]()
б) Событие В – выпадет четное число очков. N(В)
= 3 (это 2, 4, 6). Значит, искомая вероятность равна ![]()
в) Событие С – выпадет число очков, большее
четырех. N(С) = 2 (это 5; 6). Значит, искомая вероятность равна ![]()
г) Событие D – выпадет число очков, не кратное
трем. N(D) = 4 (это 1; 2; 4; 5). Значит, искомая вероятность
равна ![]()
О т в е т: а) ![]() б) 0,5; в)
б) 0,5; в) ![]() г)
г) ![]()
5. Решить задачу № 20.14 (б) на с. 134. Учитель при необходимости помогает в решении учащимся.
При одном бросании монеты равновозможны выпадения «орла» и «решки». При втором бросании, вне зависимости от исхода предыдущего бросания, возможны те же результаты. Для четырех бросаний по правилу умножения получаем, что возможно N = 2 · 2 · 2 · 2 = 16 исходов.
б) При первом бросании возможен 1 исход – «решка»,
аналогично при втором и третьем бросании, а при четвертом бросании – 2 исхода –
«орел» и «решка». Применим правило умножения и найдем N(A)
=
= 1 · 1 · 1 · 2 = 2. Тогда ![]()
6. Решить № 20.15 на с. 134 задачника.
Всего в квадратное уравнение можно подставить
10 чисел, то есть
N = 10.
а) Событие А – у полученного
квадратного уравнения будут два различных корня. Это возможно только при
подстановке четырех чисел, таких как 8, 9, 10, 11. Поэтому N(A) =
4. Значит, искомая вероятность равна ![]()
б) Событие В – у полученного
квадратного уравнения не будет корней. N(В) = 6. Значит, искомая
вероятность равна ![]()
в) Событие С – у полученного квадратного уравнения будет хотя бы один отрицательный корень. Это произойдет в четырех случаях, так как корень из полученных дискриминантов в сумме с – b дает только отрицательное число (так как – b по модулю больше, чем корень из каждого дискриминанта). Значит, N(С) = 4.
Искомая вероятность равна ![]()
г) Событие D – у полученного
квадратного уравнения будет хотя бы один положительный корень. Так как корни
получаются только отрицательные, то N(D) = 0. Искомая вероятность
равна ![]()
О т в е т: а) 0,4; б) 0,6; в) 0,4; г) 0.
7. Решить № 20.20 на с. 135 на доске и в тетрадях.
Всего в промежутке [100; 200) содержится 100 чисел. Значит, общее число возможных исходов равно 100. N = 100.
а) Событие А – число не
оканчивается нулем. Событие ![]() – число оканчивается нулем. Таких чисел
ровно 10 – это 100, 110, 120, 130, 140, 150, 160, 170, 180, 190. Поэтому N(
– число оканчивается нулем. Таких чисел
ровно 10 – это 100, 110, 120, 130, 140, 150, 160, 170, 180, 190. Поэтому N(![]() ) = 10. Найдем
вероятность того, что число, выбранное случайным образом, оканчивается нулем,
то есть
) = 10. Найдем
вероятность того, что число, выбранное случайным образом, оканчивается нулем,
то есть 
Применим симметричную формулу для теоремы о нахождении вероятности противоположного события. Получим Р(А) = 1 – 0,1 = = 0,9.
б) Событие В – число, среди цифр
которого хотя бы одна больше двух. Событие ![]() – число, все цифры которого меньше или
равны 2. Таких чисел ровно 9 – это 100, 101, 102, 110, 111, 112, 121,
120, 122. Поэтому
– число, все цифры которого меньше или
равны 2. Таких чисел ровно 9 – это 100, 101, 102, 110, 111, 112, 121,
120, 122. Поэтому
N(![]() ) = 9.
) = 9. 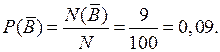
Применим симметричную формулу для теоремы о нахождении вероятности противоположного события. Получим Р(В) = 1 – 0,09 = 0,91.
в) Событие С – число не является
квадратом другого числа. Событие ![]() – число является квадратом другого
целого числа. Таких чисел ровно 5 – это 100, 121, 144, 169, 196.
Поэтому N(
– число является квадратом другого
целого числа. Таких чисел ровно 5 – это 100, 121, 144, 169, 196.
Поэтому N(![]() )
= 5.
)
= 5.
Тогда 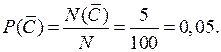 Найдем Р(С) = 1 – 0,05 =
0,95.
Найдем Р(С) = 1 – 0,05 =
0,95.
г) Событие D – сумма цифр числа меньше либо
равна 17. Событие ![]() –
сумма цифр числа больше либо равна 17. Таких чисел ровно 6 – это 179, 188,
189, 197, 198, 199. Поэтому N(
–
сумма цифр числа больше либо равна 17. Таких чисел ровно 6 – это 179, 188,
189, 197, 198, 199. Поэтому N(![]() ) = 6.
) = 6.
Тогда 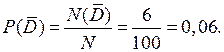 Найдем Р(D) = 1 – 0,06 =
0,94.
Найдем Р(D) = 1 – 0,06 =
0,94.
О т в е т: а) 0,9; б) 0, 91; в) 0,95; г) 0,94.
III. Итоги урока.
Дать определение противоположного события.
Сформулировать теорему для нахождения вероятности противоположного события.
Дать определение несовместных событий.
Рассказать, как рассчитывается вероятность суммы несовместных событий.
Домашнее задание: изучить § 20 на с. 200–207; решить № 20.4 (б; г); № 20.5 (б; г); № 20.6; № 20.7 (б; г); № 20.16 на с. 132–134 задачника.
У р о к 3
Цели: упражнять в решении более сложных вероятностных задач; развивать логическое мышление.
Ход урока
I. Актуализация опорных знаний.
1. Проверить выборочно по тетрадям нескольких учеников выполнение ими домашнего задания.
2. Решить на доске задачи из домашней работы, вызвавшие затруднения у учащихся.
3. Какие события называются несовместными?
4. Сформулировать теорему о вероятности наступления хотя бы одного из двух несовместных событий.
5. Какие события называются противоположными?
6. Сформулировать теорему для нахождения вероятности противоположного события.
7. Решить задачу № 20.8 на с. 132 задачника (решение записывается только на доске).
а) ![]()
б) ![]()
в) ![]()
г) ![]()
О т в е т: а) 0,23; б) 0,63; в) 0,6; г) 0,4.
II. Отработка навыков.
1. Разобрать решение примера 6 на с. 206 учебника на доске и в тетради.
2. Решить задачу № 20.11 (а; в) на с. 133 задачника.
Решим неравенство:
x2 + 4x – 21 ≤ 0,
y = x2 + 4x – 21,
x2 + 4x – 21 = 0,
D = 16 – 4 · (–21) = 16 + 84 = 100,
![]()
[–7; 3] – решение неравенства x2 + 4x – 21 ≤ 0.
Отметим этот отрезок длиной 10 штриховкой. Нанесем решение обоих неравенств на одну координатную прямую.
В пересечении получится отрезок [–7; 1].
а) Мы видим, что из всех решений неравенства x2 + 4x – 21 ≤ 0 только
![]() составляют
решение неравенства –8 ≤ x ≤ 1. Значит, искомая вероятность
0,8.
составляют
решение неравенства –8 ≤ x ≤ 1. Значит, искомая вероятность
0,8.
в) Решим неравенство
![]()
[–5; 2) – решение неравенства ![]() .
.
![]()
Нанесем решение обоих неравенств на одну координатную
прямую. В пересечении получится [–5; 2). Мы видим, что из всех решений
неравенства x2 + 4x
– 21 ≤ 0 только ![]() составляет решение неравенства
составляет решение неравенства ![]() . Значит, искомая
вероятность – 0,7.
. Значит, искомая
вероятность – 0,7.
3. Разобрать решение примера 7 на с. 207 задачника.
4. Решить задачу № 20.12 (а; в) на с. 133 задачника. Учитель при необходимости помогает в решении учащимся.
а) Найдем площадь всего прямоугольника SABCD = BC · CD. Найдем площадь ΔKCN, для этого выразим сторону СК и NC.
![]()
Тогда ![]()
Искомая вероятность равна 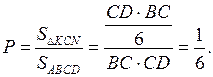
б) Найдем вначале вероятность того, что точка попадет в ΔAMC.
SΔAMC = SΔABC – SΔBMC.
![]()
Тогда ![]()
Вероятность того, что точка окажется в треугольнике АМС,
равна 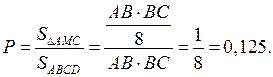
Применим теорему для нахождения вероятности
противоположного события. Получим вероятность того, что точка окажется вне
треугольника
ΔAMC, равна 1 – 0,125 = 0,875.
О т в е т: а) ![]() в) 0,875.
в) 0,875.
3. Решить задачу № 20.17 на с. 134. Учитель при необходимости помогает в решении учащимся.
Так как к некоторое число из множества {–5;
–2; 1; 3; 4}, то можно составить пять гипербол – ![]() из которых две гиперболы будут
расположены во II и IV координатных четвертях, – это
из которых две гиперболы будут
расположены во II и IV координатных четвертях, – это ![]() и три гиперболы будут расположены в I и
III координатных четвертях.
и три гиперболы будут расположены в I и
III координатных четвертях.
а) Среди этих гипербол ни одна не пройдет через
начало координат. Поэтому Р = ![]() то искомая вероятность равна 0.
то искомая вероятность равна 0.
б) График прямой у = х проходит через начало
координат и располагается в I и III координатных четвертях. Тогда прямую у
= х будут пересекать только те гиперболы, которые расположены в I и III
координатных четвертях. Таких гипербол всего 3 – это ![]() Искомая вероятность равна
Искомая вероятность равна ![]()
в) Точка с координатами (–5; 0,4) расположена во II
координатной четверти, следовательно, возможность пройти через нее есть только
у гипербол, расположенных во II и IV координатных четвертях. Таких гипербол
ровно 2 – это ![]()
Проверим, какая из них пройдет через точку с координатами (–5; 0,4).
|
Гипербола через точку с координатами (–5; 0,4). |
Гипербола |
Тогда искомая вероятность равна ![]()
г) ![]()
III. Итог урока.
Домашнее задание: повторить § 20 на с. 196–209; решить № 20.11 (б; г); № 20.22; № 20.10; № 20.19; № 20.21 (а; г) на с. 133–135 задачника.
Экспериментальные
данные
и вероятности событий (2 ч)
У р о к 1
Цели: показать связь между вероятностями случайных событий и экспериментальными статическими данными; ввести понятие статической устойчивости; научить рассчитывать статическую вероятность события, развивать логическое мышление учащихся.
Ход урока
I. Изучение нового материала.
1. Статические данные, как правило, представляют собой данные какого-либо конкретного измерения, проведенного в реальности, а при вычислении вероятностей случайных событий мы имеем дело с той или иной моделью реальности. Как же связаны между собой реальность и модель реальности? Насколько точно наши теоретические представления об окружающем мире соответствуют тому, что происходит на практике?
2. Рассмотреть пример 1 на с. 210–211 учебника.
3. Определение. При неограниченном увеличении числа независимых повторений одного и того же опыта в неизменных условиях практически достоверно, что частота появления фиксированного случайного события сближается с некоторым постоянным числом. Это явление называют статической устойчивостью, а указанное число – статической вероятностью события.
4. Явление статической устойчивости соединяет реально проводимые эмпирические испытания с теоретическими моделями этих испытаний.
5. Рассмотреть пример 2 на с. 212 учебника на доске и в тетради.
II. Выполнение упражнений.
1. Решить задачу № 21.1 на с. 135.
а) Таких чисел 4 – это 4, 8, 12, 16.
б) Кратность варианты равна 4, объем измерения равен
17, тогда частота варианты равна ![]()
в)
|
n |
17 |
18 |
19 |
20 |
27 |
28 |
29 |
30 |
40 |
60 |
80 |
100 |
|
Кол-во чисел, кратных 4, от 1 до n |
4 |
4 |
4 |
5 |
6 |
7 |
7 |
7 |
10 |
15 |
20 |
25 |
|
Частота |
0,235 |
0,222 |
0,21 |
0,25 |
0,222 |
0,25 |
0,24 |
0,23 |
0,25 |
0,25 |
0,25 |
0,25 |
г) 0,25.
О т в е т: а) 4, 8, 12, 16; б) ![]() г) 0,25.
г) 0,25.
2. Решить задачу № 21.7, с. 137 задачника на доске и в тетради.
а) такое число ровно одно – это 4;
б) кратность варианты равна 1, объем измерения равен 17, тогда
частота варианты равна ![]()
|
n |
17 |
57 |
100 |
400 |
500 |
1000 |
4000 |
5000 |
10000 |
|
Кол-во начинаю-щихся с 4 |
1 |
11 |
11 |
12 |
111 |
111 |
112 |
1111 |
1111 |
|
Частота |
0,06 |
0,19 |
0,11 |
0,03 |
0,222 |
0,111 |
0,028 |
0,2222 |
0,1111 |
в) нет,
от ![]() до
до ![]()
О т в е т: а) 4; б) 0,06; в) нет, от ![]() до
до ![]()
3. Решить задачу № 21.2 (а; в) на с. 136 задачника на доске и в тетради.
а) Так как из 1000 экземпляров некоторой детали, выпущенной на предприятии, в среднем оказывается 4 бракованные детали, то в 4000 бракованных деталей будет в 4 раза больше – 16 бракованных деталей.
в) в 11000 экземплярах будет содержаться 44
бракованные детали и еще одна вероятно содержится в оставшихся 250 деталях,
так как 250 =
= ![]() от 1 тысячи, а
одна четвертая от четырех равна 1, поэтому в 11250 деталях будет содержаться 45
деталей.
от 1 тысячи, а
одна четвертая от четырех равна 1, поэтому в 11250 деталях будет содержаться 45
деталей.
О т в е т: а) 16; в) 45.
4. Решить задачу № 21.3 (а; в) на с. 137 задачника на доске и в тетради.
|
а) 405 аб – 100 % x аб – 1,5 % |
|
|
в) 534 аб – 100 % x аб – 1,5 % |
|
О т в е т: а) 6; в) 8.
IV. Итоги урока.
Домашнее задание: изучить материал § 21; решить № 21.2 (в; г); 21.3 (б; г); 21.4 (а; б); 21.6; принести игральные кубики.
У р о к 2
Цели: показать на примере 3, с. 213 учебника, что явление статической устойчивости позволяет приблизительно оценивать вероятность даже в тех случаях, когда эти вероятности мы не знаем; развивать логическое мышление.
Ход урока
I. Проверка домашнего задания.
1. Решить на доске из домашней работы задания, вызвавшие затруднения.
2. Дать определение статической устойчивости и статической вероятности.
II. Повторение ранее изученного материала.
1. Решить задачу № 21.4 (в; г) на с. 136 задачника на доске и в тетради.
|
в) 9785 чек. – 100 % x чек. – 9 % |
|
|
9785 чек. – 100 % x чек. – 11 % |
|
О т в е т: от 880 до 1076.
г) x чек. – 100 %
4017 чек. – 9 %
![]()
x чек. – 100 %
4017 чек. – 11 %

О т в е т: около 40000: от 36520 до 44630.
2. Решить задачу № 21.5 на с. 137 задачника на доске и в тетради.
a) x бил. – 100 %
12153 бил. – 38 %
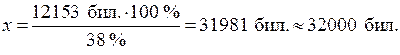
|
б) 32000 бил. – 100 % x бил. – 17 % |
|
О т в е т: а) около 32000; б) 5440.
3. Решить задачу № 21.8 на с. 138 задачника на доске и в тетради.
а) 700000 чел. – 100 %
x чел. – 73 %
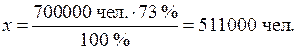 – решали задачу,
– решали задачу,
700000 – 511000 = 189000 (чел.) – не решали задачу.
О т в е т: 189000.
в) 113586 чел. – 100 %
x чел. – 66 %
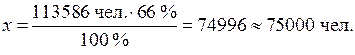
О т в е т: около 75000.
III. Объяснение нового материала.
1. Статическая устойчивость означает, что при проведении большого числа повторения испытаний подсчитанная частота практически совпадает с неизвестной вероятностью наступления события А. Значит, найденная частота приблизительно равна вероятности события А. Следует только точно понимать, что частота наступления подсчитывается для реальных событий, а вероятность – для теоретической модели этих событий.
2. Рассмотреть пример 3 на с. 136 учебника.
IV. Решение задач.
Решить задачу № 21.9 на с. 138 учебника самостоятельно. Учитель при необходимости помогает в решении учащимся.
V. Итоги урока.
Домашнее задание: изучить § 21 на с. 209–215 учебника; решить № 21.8 (б; г); № 21.10; № 21.5 (в; г) на с. 138–139 задачника.
Контрольная работа
Рациональные неравенства и их системы
Цели: выявить знания и умения учащихся и степень усвоения ими изученного материала.
Ход урока
I. Организация учащихся на выполнение контрольной работы.
II. Выполнение работы по четырем вариантам.
В а р и а н т I
1. Решите неравенство:
а) 2(1 – x) ≥ 5x – (3x + 2);
б) 3x2 + 5x – 8 ≥ 0;
в) 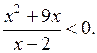
2. Решите двойное неравенство и укажите, если возможно,
наибольшее и наименьшее целое решение неравенства ![]()
|
3. Найдите область определения выражения f(х)
= |
4. От дачного поселка до станции 10 км. Дачник идет сначала со скоростью 4 км/ч, а затем увеличивает скорость на 2 км/ч. Какое расстояние он может идти со скоростью 4 км/ч, чтобы не опоздать на поезд, который отправляется через 2 ч после выхода дачника из поселка?
В а р и а н т II
1. Решите неравенство:
а) 7x + 3 > 5(x – 4) + 1;
б) 2x2 + 13x – 7 > 0;
в) 
2. Решите двойное неравенство и укажите, если возможно,
наибольшее и наименьшее целое решение неравенства ![]()
|
3. Найдите область определения выражения f(х)
= |
4. Мастер и его ученик получили заказ на изготовление 140 деталей. Мастер делает за 1 мин 3 детали, а ученик – две детали. К выполнению заказа приступает сначала ученик, а затем его сменяет мастер. Сколько деталей может изготовить ученик, чтобы на выполнение заказа было затрачено не более 1 часа?
В а р и а н т III
1. Решите неравенство:
а) 4x + 1 ≤ 43 – 3(7 + x);
б) 2x2 + 5x – 18 ≤ 0;
в) 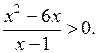
2. Решите двойное неравенство и укажите, если возможно,
наибольшее и наименьшее целое решение неравенства ![]()
|
3. Найдите область определения выражения f(х)
= |
4. Группу туристов из 48 человек размещают в гостинице сначала в двухместные, а затем в трехместные номера. Сколько двухместных номеров можно занять, чтобы всего было использовано не более 18 номеров?
В а р и а н т IV
1. Решите неравенство:
а) 5(x + 1) – x > 2x + 13;
б) 5x2 – 11x + 6 ≥ 0;
в) 
2. Решите двойное неравенство и укажите, если возможно,
наибольшее и наименьшее целое решение неравенства ![]()
|
3. Найдите область определения выражения f(х)
= |
4. Девятиклассники собрали в саду 100 кг черной смородины. Затем они разложили ее в ящики, вмещающие по 3 кг и по 5 кг ягод.
Сначала использовались меньшие ящики, а затем большие. Сколько потребуется меньших ящиков, чтобы использовать всего не более 24 ящиков?
П р и м е ч а н и е. Каждый вариант состоит из трех частей. Первая часть (до первой черты) включает материал, соответствующий базовому уровню математической подготовки учащихся.
Выполнение этой части контрольной работы гарантирует ученику получение удовлетворительной оценки. Вторая часть (от первой до второй черты) содержит задания, несколько более сложные с технической точки зрения.
Третья часть (после второй черты) включает задания, которые в определенном смысле можно охарактеризовать как творческие.
Чтобы получить хорошую оценку, учащийся должен выполнить, кроме базовой части, вторую или третью часть работы. Чтобы получить отличную оценку, ученику необходимо выполнить все три части работы.
Контрольная работа
Системы уравнений
Цель: выявление степени усвоения учащимися изученного материала.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение контрольной работы по вариантам.
В а р и а н т I
1. Решите систему уравнений методом подстановки:
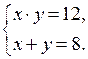
2. Решите систему уравнений методом алгебраического сложения:
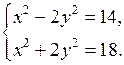
3. Решите графически систему уравнений: 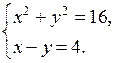
|
4. Сумма цифр двузначного числа равна 10. Если поменять местами его цифры, то получится число, большее данного на 36. Найдите данное число. |
5. При каком значении параметра а
система уравнений 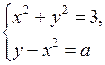 имеет:
а) одно решение; б) три решения?
имеет:
а) одно решение; б) три решения?
В а р и а н т II
1. Решите систему уравнений методом подстановки:
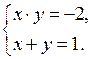
2. Решите систему уравнений методом алгебраического сложения:

3. Решите графически систему уравнений: 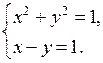
|
4. Если двузначное число разделить на число, записанное теми же цифрами, но в обратном порядке, то в частном получится 4, а в остатке 3. Если же это число разделить на сумму его цифр, то в частном получится 8, а в остатке 7. Найдите эти числа. |
5. При каком значении параметра m система уравнений
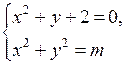 имеет: а) одно решение; б) три
решения?
имеет: а) одно решение; б) три
решения?
В а р и а н т III
1. Решите систему уравнений методом подстановки:
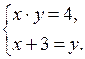
2. Решите систему уравнений методом алгебраического сложения:
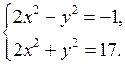
3. Решите графически систему уравнений: 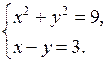
|
4. Отношение двузначного числа к сумме его цифр равно 4, а отношение этого числа к произведению его цифр равно 2. Найдите это число. |
5. При каком значении параметра b
система уравнений 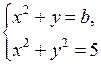 имеет:
а) одно решение; б) три решения?
имеет:
а) одно решение; б) три решения?
В а р и а н т IV
1. Решите систему уравнений методом подстановки:
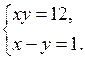
2. Решите систему уравнений методом алгебраического сложения:
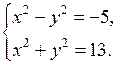
3. Решите графически систему уравнений: 
|
4. Разность квадратов двух чисел равна 100. Если из утроенного первого числа вычесть удвоенное второе число, то получится 30. Найдите эти числа. |
5. При каком значении параметра k
система уравнений 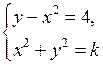 имеет:
а) одно решение; б) три решения?
имеет:
а) одно решение; б) три решения?
III. Итоги урока.
Домашнее задание: решить № 27 (а; б), № 28 (а; б), № 29 на с. 8 из темы «Задачи на повторение»; изучить по учебнику материал § 7 на с. 75–81.
Контрольная работа
Числовые функции
Цели: выявление знаний учащихся и степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение контрольной работы по вариантам.
В а р и а н т I
1. Найдите область определения функции 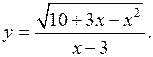
2. Постройте и прочитайте график функции
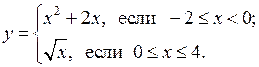
3. На рисунке изображена часть графика нечетной функции. Достройте график этой функции.
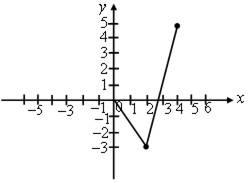
|
4. Какая из данных функций является четной, а какая – нечетной: а) у = 2 + Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 4. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 7) ≤ 0.
В а р и а н т II
1. Найдите область определения функции 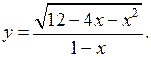
2. Постройте и прочитайте график функции
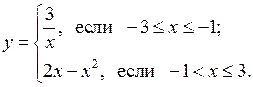
3. На рисунке изображена часть графика четной функции. Достройте график этой функции.
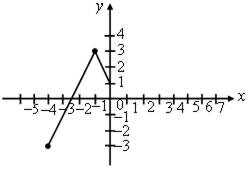
|
4. Какая из данных функций является четной, а какая – нечетной: а) у = Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 1. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 5) ≥ 0.
В а р и а н т III
1. Найдите область определения функции 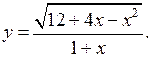
2. Постройте и прочитайте график функции
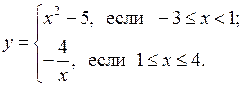
3. На рисунке изображена часть графика нечетной функции. Достройте график этой функции.
|
4. Какая из данных функций является четной, а какая – нечетной: а) у = х(х4 + 1); б) у = Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 4. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 5) ≥ 0.
В а р и а н т IV
1. Найдите область определения функции 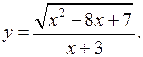
2. Постройте и прочитайте график функции
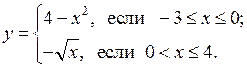
3. На рисунке изображена часть графика четной функции. Достройте график этой функции.

|
4. Какая из данных функций является четной, а какая – нечетной: а) у = | х | (1 – х2); б) у = Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 4. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 18) ≤ 0.
Контрольная работа
Степенная функция
Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
Ход урока
I. Организация учащихся на проведение работы.
II. Выполнение работы по вариантам.
В а р и а н т I
1. Найдите наибольшее и наименьшее значения функции у = х6 на отрезке [–1; 2].
2. Сколько корней имеет уравнение –0,5х4 = х – 4?
3. Постройте и прочитайте график функции:

|
4. Найдите наибольшее и наименьшее значения функции у
= (х – 2)3 + |
5. Дана функция f(х), где f(х)
= х–3. Найдите все
значения х, при которых выполняется неравенство 
В а р и а н т II
1. Найдите наибольшее и наименьшее значения функции у = х8 на отрезке [–2; 1].
2. Сколько корней имеет уравнение 0,5х3 = 2 – х?
3. Постройте и прочитайте график функции:
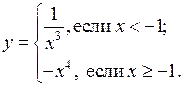
|
4. Найдите наибольшее и наименьшее значения функции у
= (х + 3)4 – |
5. Дана функция f(х), где f(х)
= х–5. Найдите все
значения х, при которых выполняется неравенство 
В а р и а н т III
1. Найдите наибольшее и наименьшее значения функции у = х8 на отрезке [–1; 2].
2. Сколько корней имеет уравнение 2х4 = х – 3?
3. Постройте и прочитайте график функции:
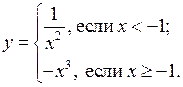
|
4. Найдите наибольшее и наименьшее значения функции у
= (х + 3)3 – |
5. Дана функция f(х), где f(х)
= х–4. Найдите все
значения х, при которых выполняется неравенство 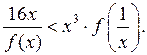
В а р и а н т IV
1. Найдите наибольшее и наименьшее значения функции у = х6 на отрезке [–2; 1].
2. Сколько корней имеет уравнение –0,5х3 = х – 3?
3. Постройте и прочитайте график функции:
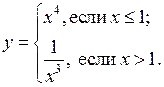
|
4. Найдите наибольшее и наименьшее значения функции у
= (х – 2)4 – |
5. Дана функция f(х), где f(х)
= х–6. Найдите все
значения х, при которых выполняется неравенство 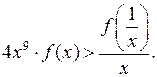
III. Итоги урока.
Домашнее задание: прочитать по учебнику на с. 108–109 «Основные результаты».
Контрольная работа
Прогрессии
Цели: выявить степень усвоения учащимися изученного материала; развитие навыков самостоятельной работы.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
В а р и а н т I
1. Найдите десятый член арифметической прогрессии –8; –6,5; –5; … . Вычислите сумму первых десяти ее членов.
2. Найдите восьмой член геометрической
прогрессии ![]() …
…
3. Сумма третьего и шестого членов арифметической прогрессии равна 3. Второй ее член на 15 больше седьмого. Найдите первый и второй члены этой прогрессии.
|
4. Найдите все значения х, при которых значения
выражений |
5. Найдите сумму всех трехзначных чисел от 100 до 550, которые при делении на 7 дают в остатке 5.
В а р и а н т II
1. Найдите двенадцатый член арифметической прогрессии 26; 23; 20; … . Вычислите сумму первых двенадцати ее членов.
2. Найдите восьмой член
геометрической прогрессии ![]()
![]()
![]() …
…
3. Третий член арифметической прогрессии на 12 меньше шестого. Сумма восьмого и второго членов равна 4. Найдите второй и третий члены этой прогрессии.
|
4. Найдите все значения х, при которых значения
выражений |
5. Найдите сумму всех двузначных чисел, дающих при делении на 4 в остатке 3.
В а р и а н т III
1. Найдите одиннадцатый член арифметической прогрессии – 4,2; –2; 0,2; … . Вычислите сумму первых одиннадцати ее членов.
2. Найдите десятый член геометрической
прогрессии ![]() …
…
3. Сумма седьмого и четвертого членов арифметической прогрессии равна 6. Пятый ее член на 12 больше второго. Найдите первый и третий члены этой прогрессии.
|
4. Найдите все значения х, при которых значения
выражений |
5. Найдите сумму всех трехзначных чисел от 100 до 450, которые при делении на 8 дают в остатке 5.
В а р и а н т IV
1. Найдите тринадцатый член арифметической прогрессии 5,2; 3,7; 2,2; … . Вычислите сумму первых тринадцати ее членов.
2. Найдите восьмой член геометрической
прогрессии ![]() …
…
3. Пятый член арифметической прогрессии на 15 меньше второго. Сумма третьего и седьмого ее членов равна –6. Найдите третий и четвертый члены этой прогрессии.
|
4. Найдите все значения х, при которых значения
выражений |
5. Найдите сумму всех двузначных чисел, которые при делении на 5 дают в остатке 4.
Домашнее задание: прочитать тему «Основные результаты» по учебнику на с. 172.
Итоговая контрольная работа по алгебре
за курс основной школы
В а р и а н т I
Часть 1
1. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки:
а) (а2)3 а2;
б) (а2а3)2; в) 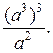
1) а12; 2) а10; 3) а8; 4) а7.
|
О т в е т: |
а |
б |
в |
|
|
|
|
|
2. Упростите выражение 4у(у – 4) – (у – 8)2.
О т в е т: ____________________.
3. Сократите
дробь 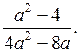
О т в е т: ____________________.
4. При каком значении х значение
выражения ![]() является
числом рациональным?
является
числом рациональным?
А. При х = 6. В. При х = –3.
Б. При х = 0. Г. При х = –2.
|
5. В спортивном зале выделили помещение для раздевалки (на рисунке оно показано штриховкой). Какова площадь S оставшейся части зала? A. S = a2 + аb + b2. Б. S = a2 + ab – b2. B. S = a2 – ab – b2. Г. S = a2 – ab + b2. |
|
6. Укажите наибольшее из чисел:
–1,5; –0,5; (–0,5)3; (–1,5)3.
О т в е т: ____________________.
7. Какое из указанных чисел не делится на 3?
А. 12852. Б. 1143. В. 20293. Г. 7239.
8. В начале года число абонентов интернет-компании «Север» составляло 200 тыс. человек, в течение года 50 тыс. абонентов перешли в другие компании, а 60 тыс. новых абонентов присоединились к компании «Север». На сколько процентов увеличилось за год число абонентов этой компании?
А. На 5 %. В. На 0,05 %.
Б. На 10 %. Г. На 105 %.
9. Решите уравнение 5х2 + 3х – 2 = 0.
О т в е т: ____________________.
10. От одного города до другого автобус доехал за 3 ч, а автомобиль – за 2 ч. Скорость автомобиля на 25 км/ч больше скорости автобуса. Чему равно расстояние между городами?
Пусть расстояние между городами равно х км. Составьте уравнение по условию задачи.
О т в е т: ____________________.
|
11. На координатной плоскости отмечены точки С и D и через них проведена прямая. Какое уравнение задает прямую CD? A. х + у = 24. Б. х + у = 34. B. х – у = 4. Г. х – у = 5. |
|
12. Решите неравенство 3 – х ³ 3х + 5.
А. [–0,5; +∞). Б. (–∞; –0,5]. В. [–2; –∞). Г. (–∞; –2].
13. На координатной прямой отмечены числа а, b и с. Какая из разностей отрицательна?
|
А. b – а. В. с – а. В. b – с. Г. с – b. |
|
14.
Последовательность задана формулой ![]() Сколько членов этой
последовательности больше 1?
Сколько членов этой
последовательности больше 1?
А. 12. Б. 11. В. 10. Г. 9.
15. Функции заданы формулами:
1) у = х2 + 1; 3) у = –х2 +1;
2) у = х2 – 1; 4) у = –х2 – 1.
Графики каких из этих функций не пересекают ось х?
А. 1 и 4. Б. 2 и 4. В. 1 и 3. Г. 2 и 3.
16. Из пункта А в пункт В вышел пешеход, и через некоторое время вслед за ним выехал велосипедист. На рисунке изображены графики пути пешехода и велосипедиста. Определите, на сколько меньше времени затратил на путь из пункта А в пункт В велосипедист, чем пешеход.
А. На 10 мин. Б. На 30 мин.
В. На 50 мин. Г. На 20 мин.
Часть 2*
1. Решите
систему уравнений 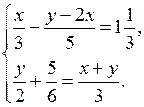
2. Лодка проплывает 15 км по течению реки и еще 6 км против течения за то же самое время, за которое плот проплывает по этой реке 5 км. Найдите скорость течения реки, если известно, что собственная скорость лодки равна 8 км/ч.
3. Парабола с вершиной в точке А(0; –3) проходит через точку В(6; 15). В каких точках эта парабола пересекает ось х?
4. При каких значениях параметра р система неравенств
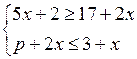 имеет решения?
имеет решения?
5. В арифметической прогрессии среднее арифметическое первых десяти ее членов равно 20. Найдите первый член и разность этой прогрессии, если известно, что они являются натуральными числами.
В а р и а н т II
Часть 1
1. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки:
а)  б) (b4b3)2;
в) b4(b3)2.
б) (b4b3)2;
в) b4(b3)2.
1) b14; 2) b12; 3) b10; 4) b9.
|
О т в е т: |
а |
б |
в |
|
|
|
|
|
2. Упростите выражение 6а(а + 1) – (3 + а)2.
О т в е т: ____________________.
3. Сократите
дробь 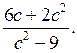
О т в е т: ____________________.
4. При каком
значении х значение выражения ![]() является числом иррациональным?
является числом иррациональным?
A. При х = 3.
Б. При х = 0.
В. При х = 1.
Г. При х = –1.
|
5. В гараже выделили помещение для мойки машин (на рисунке оно показано штриховкой). Какова площадь S оставшейся части гаража? А. S = c2 + ac – a. Б. S = c2 – ac + a2. В. S = c2 + ac + a2. Г. S = c2 – ac – a2. |
|
6. Укажите наименьшее из чисел:
–0,2; –1,2; (–0,2)3; (–1,2)3.
О т в е т: ____________________.
7. Какое из указанных чисел не делится на 9?
А. 81234. Б. 8883. В. 30159. Г. 3219.
8. В начале года в городской библиотеке было 50 тыс. книг. В течение года библиотечный фонд обновлялся. В связи с этим 10 тыс. книг списали и купили 16 тыс. новых. На сколько процентов увеличился за год библиотечный фонд?
А. На 6 %. В. На 15 %.
Б. На 12 %. Г. На 40 %.
9. Решите уравнение 3х2 – 4х – 4 = 0.
О т в е т: ____________________.
10. От турбазы до станции турист доехал на велосипеде за 3 ч. Пешком он смог бы пройти это расстояние за 7 ч. Известно, что идет он со скоростью, на 8 км/ч меньшей, чем едет на велосипеде. Чему равно расстояние от турбазы до станции?
Пусть расстояние от турбазы до станции равно х км. Составьте уравнение по условию задачи.
О т в е т: ____________________.
|
11. На координатной плоскости отмечены точки М и N и через них проведена прямая. Какое уравнение задает прямую MN? A. х + у = 20. Б. х + у = 26. B. х – у = 3. Г. х – у = 2. |
|
12. Решите неравенство 2 + х £ 5х – 8.
А. (–∞; 1,5]. В. (–∞; 2,5].
Б. [1,5; +∞). Г. [2,5; +∞).
13. На координатной прямой отмечены числа х, у и z. Какая из разностей положительна?
|
А. х – у. В. z – у. Б. у – z. Г. х – z. |
|
14.
Последовательность задана формулой ![]() Сколько членов этой
последовательности меньше 1?
Сколько членов этой
последовательности меньше 1?
А. 8. Б. 9. В. 10. Г. 11.
15. Функции заданы формулами:
1) у = х2 + 2;
2) у = х2 – 2;
3) у = –х2 + 2;
4) у = –х2 – 2.
Графики каких из этих функций пересекают ось х?
А. 1 и 4. В. 1 и 3.
Б. 2 и 3. Г. 2 и 4.
16. Из пункта А в пункт В вышел пешеход, через некоторое время навстречу ему из пункта В в пункт А выехал велосипедист. Используя графики пути пешехода и велосипедиста, определите, на сколько больше времени затратил на весь путь пешеход, чем велосипедист.

А. На 10 мин. Б. На 30 мин.
В. На 40 мин Г. На 60 мин.
Часть 2*
1. Решите
систему уравнений 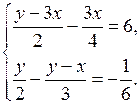
2. Катер проплывает 20 км против течения реки и еще 24 км по течению за то же самое время, за которое плот проплывает по этой реке 9 км. Скорость катера в стоячей воде равна 15 км/ч. Найдите скорость течения реки.
3. Парабола с вершиной в точке С (0; 5) проходит через точку В (4; –3). В каких точках эта парабола пересекает ось x?
4. При каких значениях параметра а система неравенств
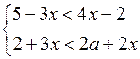 не имеет решений?
не имеет решений?
5. В арифметической прогрессии среднее арифметическое первых восьми ее членов равно 23. Найдите первый член и разность этой прогрессии, если известно, что они являются натуральными числами.
П р и м е ч а н и е:
*Задания этой части выполняются с записью решения.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.