
Подобие фигур (15 часов)
Цель: усвоить признаки подобия треугольников.
В результате изучения темы учащиеся должны:
|
знать |
уметь |
|
– определение гомотетии, подобия, коэффициентов гомотетии и подобия; – определение подобных фигур; – формулировку признаков подобия треугольников; – определение центрального угла; – определение угла, вписанного в окружность |
– доказывать свойство о сохранении углов при преобразованиях подобия; – воспроизводить доказательства признаков подобия; – применять признаки подобия при решении задач; – доказывать теорему о вписанном угле; – доказывать свойства отрезков хорд и секущих окружности; – решать задачи на применение свойства вписанного угла |
Урок 1
Понятие о гомотетии
и подобии ФИГУР
Цели: повторить понятие о «преобразовании фигур», движении и его свойствах; ввести понятия «преобразование подобия», «гомотетия и ее свойства»; познакомить учащихся с практическим применением гомотетии и подобия.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
На доске подготовлена таблица, которая заполняется по ходу повторения и изучения материала.
1. Вопросы для учащихся:
– Ввести понятие преобразования фигур.
– Какое преобразование фигур называется движением?
– Какие виды движения вам известны?
– Каковы способы их задания? Показать на конкретных примерах.
После ответов на вопросы заполняется левая часть таблицы.
|
Преобразование фигур |
|||
|
движение |
преобразование подобия |
||
|
способы задания |
|||
|
Центральная симметрия Осевая симметрия Поворот Параллельный перенос |
Точка – центр симметрии Ось симметрии Центр, угол поворота Направление, расстояние Центр, коэффициент гомотетии |
Гомотетия |
|
2. Построение образов отрезка.
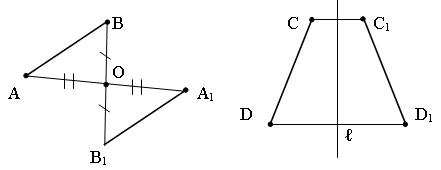
ZО (АВ) = А1В1 Sе(СD) = С1D1
![]()
– Во что переходят при движении точки, лежащие на прямой; сохраняется ли при этом порядок их взаимного расположения?
– Во что переходят при движении прямые, полупрямые, отрезки?
– Сохраняются ли при движении углы?
III. Изучение нового материала.
Задание.
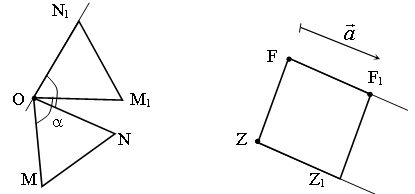
Построить отрезок, полученный преобразованием, при котором для каждой точки
выполняется равенство ![]() где О – заданная точка. Решение оформляется на доске с
комментарием.
где О – заданная точка. Решение оформляется на доске с
комментарием.
– Чем заданное преобразование отличается от предыдущих?
План
1. Определение преобразования подобия.
2. Понятие коэффициента подобия.
3. Условие, при котором преобразование подобия является движением.
4. Определение гомотетии относительно центра.
5. Свойство гомотетии.
После ответов на вопросы заполняется правая часть таблицы.
IV. Закрепление изученного материала.
1. решение задач.
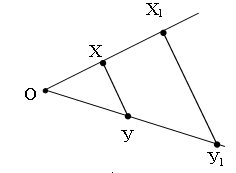
1) При гомотетии точка Х переходит в точку Х1, а точка У – в У1. Как найти центр гомотетии, если точки Х, Х1, У, У1 не лежат на одной прямой?
Решение.
Так как при гомотетии ![]() то
точку О – центр гомотетии получим при пересечении лучей У, У1
и хх1.
то
точку О – центр гомотетии получим при пересечении лучей У, У1
и хх1.
2) На плоскости даны точки А, В, О, где О
– центр гомотетии. Постройте точки А1В1, в
которые перейдут заданные точки, если k1 = 3, k2
= ![]() (k
– коэффициент гомотетии).
(k
– коэффициент гомотетии).
2. Выполнение заданий.
– Познакомьтесь с практическим применением гомотетии и подобия.
– Вспомните определение масштаба.
– Дайте новое определение: коэффициент подобия – это масштаб (М = 1 : 10). Это значит, что одному сантиметру на плане соответствует один метр на местности.
– Решите задачу 4, с. 156.
V. Итог урока.
– С каким новым преобразованием познакомились на уроке? При каких условиях гомотетия будет движением?
Домашнее задание: п. 100; вопросы 1–3; задачи 2, 3; повторить п. 83, 19.
Урок 2
Свойства преобразования
Цели: познакомить со свойствами преобразования подобия, формировать умение доказывать теоремы, повторить алгоритм доказательства теорем методом от противного.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
1. Индивидуальная работа.
Карточка 1.
Доказать теорему о том, что гомотетия есть преобразование подобия (передняя часть доски).
Карточка 2.
Доказать теорему о том, что точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения (передняя часть доски).
Карточка 3.
Доказать, что при движении сохраняются углы между полупрямыми (задняя часть доски).
Карточка 4.
Сформулировать и записать свойства движения (задняя часть доски).
Примечание: карточки 1, 2, 3 предназначены для наиболее подготовленных учащихся.
2. Фронтальный опрос (вопросы сформулированы в уроке 1).
3. Практическое задание.
Начертите треугольник ABC. Постройте гомотетичный ему треугольник, приняв за центр гомотетии одну из его вершин и коэффициент гомотетии, равный:
|
I вариант |
II вариант |
III вариант |
|
Центр А |
Центр В |
Центр С |
|
k = 3 |
|
k = 3 |
Выполнение работы проверяют учащиеся с высоким уровнем подготовки.
II. Изучение нового материала.
– В чем заключается алгоритм доказательства теоремы методом от противного?
Делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и теоремы, приходим к выводу, противоречащему либо условию, либо одной из аксиом, либо доказанной ранее теореме.
Делаем вывод: наше предположение неверно, а значит, верно утверждение теоремы.
Учитель обращает внимание учащихся на выполнение задания по карточке 2.
– Выполняется ли данное свойство при преобразовании подобия?
Доказательство свойств преобразования подобия (самостоятельно).
Свойство 1. Точки, лежащие на прямой, при преобразовании подобия переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Следствие 1. Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки.
Следствие 2. Преобразование подобия сохраняет углы между полупрямыми.
Доказательство:
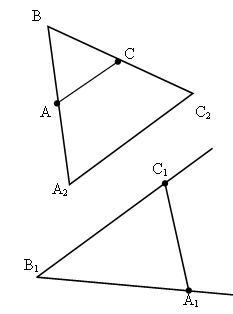
1) Преобразованием подобия с коэффициентом k.
ÐАВС ® А1В1С1, т. е.
1) В1А1 = k BA,
2) В1С1 = k BC,
3) В1А1 = k АС.
2) Подвергнем угол ABC преобразованию гомотетии относительно его вершины В с коэффициентом k, т. е.
ВА2 = k BA,
ВС2 = k ВС,
A2C2 = kAC.
3) Получим, что В1С1 = ВС2, В1А1= ВА2, А1С1 = А2С2.
Следовательно, DА1В1С1 = DА2ВС2 (по третьему признаку равенства треугольников).
Значит, ÐA2BC2 = ÐA1B1Cl, что и требовалось доказать.
III. Закрепление изученного материала.
Решение задач.
Постройте четырехугольник ABCD. Отметьте вне его
точку А1 и постройте образ четырехугольника ABCD при гомотетии с
коэффициентом k = ![]() ,
отображающей точку А на точку А1.
,
отображающей точку А на точку А1.
IV. Итог урока.
– Что происходит с фигурой, если k > 1?
– Где расположен центр гомотетии?
– Что происходит с фигурой, если 0 < k < 1?
– Где расположен центр гомотетии?
Анализируется выполнение практической работы, проведенной в начале урока. Ответы демонстрируются на доске.
Домашнее задание: повторить п. 42, п. 101, в. 4.
Дополнительные задачи
1. Постройте образ данной прямой ℓ при гомотетии с центром О(О Ï ℓ) и k = 3. Возьмите на прямой ℓ произвольную точку С, а на прямой ℓ1(ℓ1 = H(ℓ)) – точку М1 и постройте с помощью одной линейки:
a) точку С1, такую, что С1 = ![]()
б) точку М, если M1 = 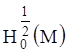 .
.
2. Постройте окружность с центром в данной точке Р
радиусом 2 см и ее образ при гомотетии с центром О и k =![]() .
Отметьте точку С (С Î окр. (Р, 2 см) и точку М (М Ï
окр. (Р, 2 см). Найдите с помощью линейки:
.
Отметьте точку С (С Î окр. (Р, 2 см) и точку М (М Ï
окр. (Р, 2 см). Найдите с помощью линейки:
а) С1 = ![]()
б) М1 = ![]() .
.
3. Постройте прямую а и отметьте вне ее точки А и О. Каково должно быть взаимное расположение прямой а, точки О и точки А, чтобы гомотетия с центром О отобразила прямую а на прямую, содержащую точку А?
4. Можно ли задать гомотетию:
а) центром и парой соответствующих точек?
б) двумя парами соответствующих точек?
5. Гомотетия задана центром и парой соответствующих точек. Как построить образ произвольной точки М?
6. Гомотетия задана двумя парами соответствующих точек. Как построить образ произвольной точки М?
7. Дан угол ABC и точка Р внутри его. Провести прямую ℓ через точку Р так, чтобы отрезок MN, являющийся пересечением угла и прямой ℓ, делился точкой Р в отношении 1 : 2.
8. Доказать, что прямая, содержащая середину оснований трапеции, проходит через точку пересечения ее диагоналей и точку пересечения продолжений ее боковых сторон. Верно ли обратное утверждение?
Указание: воспользуйтесь тем, что точка пересечения продолжений боковых сторон трапеции, точка пересечения ее диагоналей являются центрами гомотетий, при которых одно основание трапеции отображается на другое.
9. Пересечением двух окружностей является точка М. Через точку М проведены две прямые АС и BD, которые пересекают окружности, кроме точки М, соответственно в точках А и С, В и D. Доказать, что АВ || CD.
Указание: рассмотрите гомотетию с центром М, при которой окружность отображается на другую.
Урок 3
Подобие фигур.
Первый признак подобия треугольников
Цели: повторить алгоритм решения задач на построение, познакомить с понятием подобия фигур, доказать первый признак подобия треугольников.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
1. Индивидуальная работа.
Карточка 1.
Докажите, что преобразование подобия сохраняет углы между полупрямыми.
Карточка 2.
Построить треугольник, гомотетичный данному, взяв за центр гомотетии точку, лежащую вне треугольника, и k = 2.(Передняя часть доски.)
Карточка 3.
Построить треугольник, гомотетичный данному, взяв за
центр гомотетии точку, лежащую внутри треугольника, и k = ![]() .
(передняя часть доски.)
.
(передняя часть доски.)
2. Фронтальный опрос.
– Закончите предложения.
При преобразовании подобия переходят прямые в ... (прямые); полупрямые в ... (полупрямые); отрезки в ... (отрезки); угол в ... (равный угол).
– Сформулируйте общую схему решения задач на построение.
Решить задачу на построение при помощи циркуля и линейки – значит свести ее к конечному числу элементарных построений, которые считаются всегда выполнимыми.
Решение задач на построение проводится по классической схеме, которая состоит из следующих этапов:
1. Анализ. Это очень важный, первый, этап, на котором намечается план решения. Построение предполагается выполненным. На этом этапе делается гипотетический рисунок, исследуется условие задачи, ищутся связи между данными искомыми элементами.
2. Построение. Это основной этап решения задачи, на котором конечные результаты проделанного анализа используются для заданного изначально построения (т. е. действия выполняются в обратной последовательности). На основании этого второй этап можно назвать синтезом, так как в ходе его осуществляется фактическое построение требуемой фигуры, т. е. делается чертеж.
3. Доказательство. Целью этого этапа является выяснение того, отвечает ли построенная фигура требованиям задачи, справедливы ли рассуждения, проведенные на первом этапе решения.
4. Исследование. На этом завершающем этапе необходимо выяснить, всегда ли проводимые построения возможны и сколько решений существует.
III. Изучение нового материала.
План
1. Определение подобия, обозначение.
2. Свойство транзитивности: «Если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то F1 подобна фигуре F3».
3. Определение подобных треугольников.
Треугольники называются подобными, если они переводятся друг в друга преобразованием подобия.
4. Проверка задания, выполненного учащимися на доске.
– Можно ли сказать, что полученные фигуры подобны?
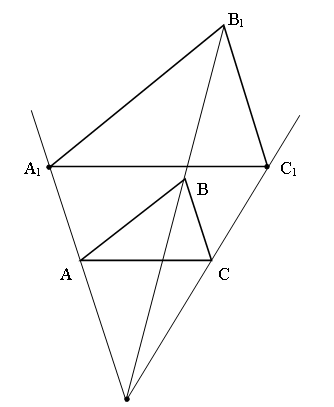
Акцентировать внимание учащихся на том, что если DАВС ~ DА1В1С1, то А переходит в А1, В – в В1, С – в С1, ÐА = ÐА1, ÐВ = ÐВ1, ÐС = ÐС1;
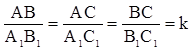 – коэффициент подобия.
– коэффициент подобия.
Самостоятельно сделать запись.
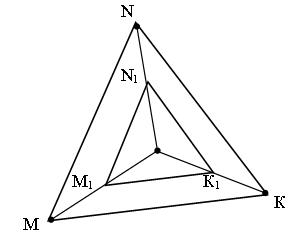
5. Устно решить задачи 5, 6, 7 (п. 102).
6. Доказать первый признак подобия треугольников по двум углам.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство.
|
Что делаем |
Что получаем |
|
1) Подвергаем DА1В1С1
преобразованию подобия с коэффициентом
2) Сравниваем DА2В2С2 и DАВС.
3) Сравниваем DА2В2С2 ~ DА1В1С1, DА2В2С2 = DАВС |
Получаем DА2В2С2: DА2В2С2 ~ DА1В1С1, причем ÐА2
= ÐА1,
ÐВ2
= ÐВ1
Следовательно,
ÐА2
= ÐА,
ÐВ2
= |
IV. Закрепление изученного материала.
Решение задач по готовым чертежам:
– найдите подобные треугольники;
– докажите их подобие;
– запишите пропорциональность сторон.
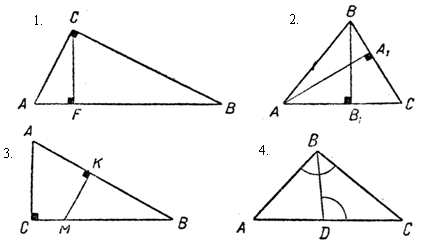
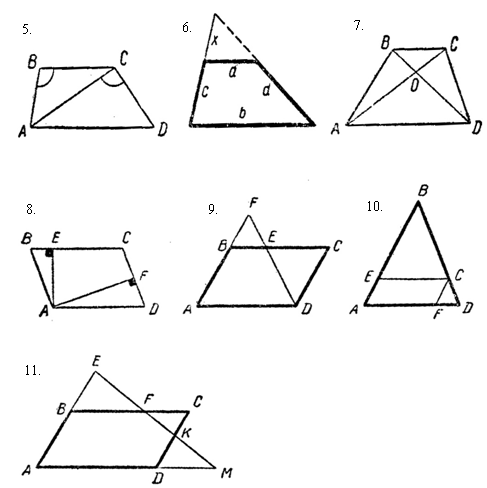
V. Итог урока.
1. Что значит DАВС ~ DА1В1С1?
2. DАВС ~ DА1В1С1, ÐА = 30°, ÐВ = 85°, ÐС = 65°. Чему равны ÐА1, ÐВ1, ÐС1?
3. DАВС ~ DС1А1В1.
АВ = 3 см, ВС = 4 см, АС = 6 см, А1В1 = 12 см.
Вычислить В1С1 и А1С.
Домашнее задание: п. 102, № 8; п. 103, № 14, 15; дополнительно решить задание № 9 (для учащихся с высоким уровнем подготовки).
Задача № 8 (для учащихся с высоким уровнем подготовки).
Даны угол и внутри него точка А. Постройте окружность, касающуюся сторон угла и проходящую через точку А.
Анализ.
1) Если такая окружность найдена, то ее центр лежит на биссектрисе угла.
2) Окружности гомотетичны.
Центр гомотетии N, k = ![]() .
.
При заданной гомотетии А1 переходит в A, О1![]() в
O.
в
O.
Таким способом найдется точка O.
Построение.
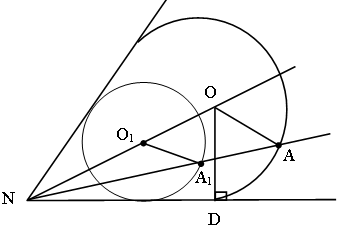
1. Строим биссектрису угла.
2. Строим любую окружность, центр которой лежит на биссектрисе, окружность касается сторон угла.
3. Соединяем точки A и N.
Прямая AN пересекает окружность в точке А1.
4. Проводим прямую d, параллельную О1А1.
(теорема. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.)
5. Прямая d пересекает биссектрису в точке O – центр искомой окружности.
6. Строим искомую окружность. Радиус окружности равен ОD.
Задача № 9.
Впишите в данный треугольник квадрат, у которого две вершины лежат на одной стороне, а две другие вершины – на двух других сторонах.
Решение:
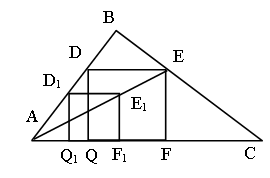
1) Построим квадрат D1E1F1Q1, такой, чтобы вершины F1 и Q1 лежали на стороне АС, а вершина D1 на стороне АВ.
2) Гомотетия относительно вершины А, переводящая точку E1 в точку Е, лежащую на стороне ВС, переводит точки D1 в D, F1 – в F, Q1 – в Q.
3) ЕF ^ АС, длина отрезка ЕF – сторона искомого квадрата.
4) Четырехугольник DEFQ – квадрат, так как гомотетия переводит фигуру в подобную фигуру.
Урок 4
Первый признак подобия треугольников.
Решение задач
Цели: закрепить полученные знания в ходе решения задач.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
Двое учащихся показывают решение на доске, так как эти задачи ключевые; остальные учащиеся решают самостоятельно по вариантам: вариант I – № 10, 12; вариант II – № 11, 13; затем проверяется решение задач № 14 и 15.
задача 14.
Докажите, что высота прямоугольного треугольника, опущенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
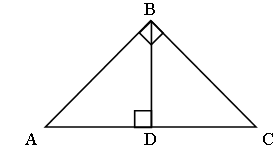
Дано:DАВС , ÐВ = 90°, BD – высота.
Доказать:DАВD ~ DВDС.
Доказательство:
1) DАВD~ DАВС,
так как ÐА
– общий, ÐАВС = ÐВDА = 90°, потому что BD – высота,
значит, ![]() .
.
2) DВDС ~ DАВС, так как ÐС – общий, ÐВDС = ÐАВС =90°.
3) DАВD ~ DАВС, DАВС ~DВDС по свойству подобия фигур: DАВD ~ DВDС и т. д.
Задача 15.
Дано: DАВС, А1В1 || АВ.
Доказать: DА1В1С ~ DАВС.
Доказательство:
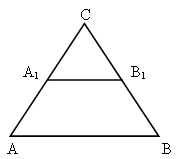
1) Прямые А1В1 || АВ, значит, ÐА1 = ÐА как соответственные (по свойству параллельных прямых).
2) ÐА1 = ÐА, ÐС – общий, следовательно, DА1В1С ~ DАВС по первому признаку подобия треугольников.
III. решение задач.
№ 21.
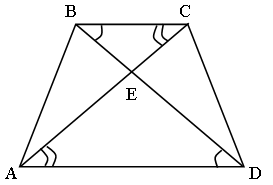
Дано: ABCD – трапеция; AC, BD – диагонали.
Доказать: DВСЕ ~ DАDE.
Доказательство:
1) так как ABCD – трапеция, значит, AD || BC.
2) AD || BC, ![]() как
накрест лежащие при секущей BD,
как
накрест лежащие при секущей BD, ![]() как
накрест лежащие при секущей AC.
как
накрест лежащие при секущей AC.
3) DВСЕ ~ DАDE по первому признаку подобия, по двум углам.
Для решения задачи повторяется материал:
1) Определение трапеции.
2) Свойство углов, полученных при пересечении двух параллельных прямых третьей.
3) первый признак подобия.
4) свойство вертикальных углов (для второго варианта доказательства).
№ 27.
Дано: ABCD – трапеция.
AB![]() CD
= E.
CD
= E.
EM – высота, BC = 7 см, AD = 15 см, NM = 3 см.
Найти: EM.
Решение:
1) ![]()
2) DВЕN ~ DАEМ,
так как ![]() как
соответственные,
как
соответственные, ![]() (EM – высота);
(EM – высота);
3) 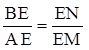 .
.
Пусть EN = x.
![]() , x + 3 = 3x,
2x = 3, x = 1,5.
, x + 3 = 3x,
2x = 3, x = 1,5.
Ответ: EM = 4,5 см.
IV. Итог урока.
– Какие задачи можно отнести к ключевым?
Домашнее задание: вариант I – № 18, 22; вариант II – № 20 (1), 23; вариант III – № 26, 24; наиболее подготовленные учащиеся – № 28, 29.
№ 29.
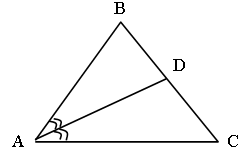
Дано: ![]() ABC; AB = BC, ÐB = 36°,
AD – биссектриса.
ABC; AB = BC, ÐB = 36°,
AD – биссектриса.
Доказать: DАDС ~ DАВС.
Найти: AC, если AB = c.
Решение:
1) ![]() ABC
– равнобедренный, так как AB = BC.
ABC
– равнобедренный, так как AB = BC.
По свойству углов при основании в равнобедренном треугольнике ÐA = ÐC = (180° – 36°) : 2 = 72°.
2) AD – биссектриса, следовательно, ÐBAD =ÐDAC = 36°.
3) Рассмотрим ![]() ADC
и
ADC
и ![]() ABC.
ABC.
ÐC = 72° – общий; ÐB = ÐDAC = 36°.
Значит, DАDС ~ DАВС по первому признаку подобия.
4) DABD – равнобедренный, BD = AD, так как ÐB = ÐDAB;
DADC – равнобедренный, так ÐADC =ÐDCA = 72°, т. е. AD = AC.
![]() .
.
Пусть АС = х, х > 0.
5) ![]() так
как х > 0, то
так
как х > 0, то
![]() .
.
![]() .
.
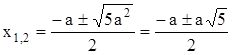 .
.
Вывод: все задачи к пункту можно разбить на группы:
I группа – № 10, 11 (равнобедренный треугольник); II группа – № 12, 13 (свойство подобия); III группа – № 14, 15; IV группа – № 18, 19, 20, 26, 27 (свойство углов при параллельных прямых, пересеченных третьей); V группа – № 21, 22, 23, 24 (трапеция). Все задачи объединяет первый признак подобия треугольников.
Необходимо повторить и включить в теоретический зачет темы:
1. Определение и свойства равнобедренных треугольников.
2. Свойства углов, образованных при пересечении параллельных прямых секущей.
3. Определение трапеции.
Урок 5
Признак подобия треугольников
по двум сторонам и углу между ними
Цели: изучить второй признак подобия треугольников.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
Каждый учащийся получает карточку с задачей.
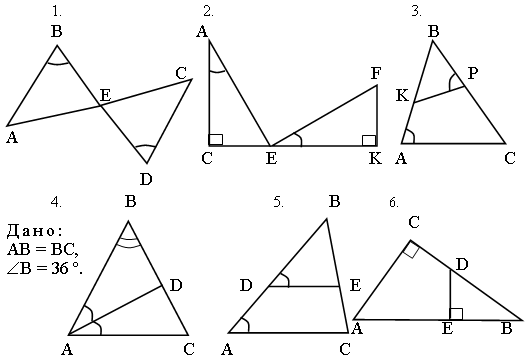
найти на рисунке подобные треугольники и доказать их подобие.
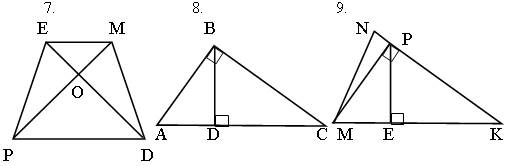
Дано: PEMD – трапеция.
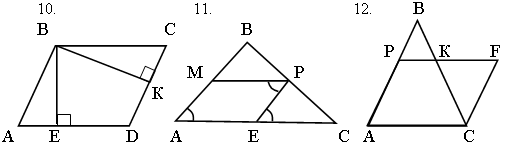
Дано: АВСD – параллелограмм. Дано: АPFC – параллелограмм.
Решите задачу и сверьте ответы с записями на доске.

Требования к оформлению решенияВ
|
1-я сторона |
2-я сторона |
|
Доказательство подобия |
Теоретические вопросы, которые использованы при решении |
Образец решения карточки № 11
|
2) 3) ( 4) |
1) первый признак подобия; 2) свойство подобия (транзитивность); 3) признак параллельности прямых; 4) свойство углов, полученных при пересечении двух параллельных прямых секущей |
III. Изучение нового материала. Второй признак подобия.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Дано: ![]()
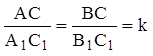 .
.
Доказать: ![]()
Доказательство:
1) Подвергнем ![]() преобразованию
подобия с коэффициентом k (гомотетии с центром в точке O).
преобразованию
подобия с коэффициентом k (гомотетии с центром в точке O).
![]() ;
;
![]() .
.
2) AC = ![]()
BC = ![]() =
=![]()
![]()
Значит, ![]() (по
первому признаку равенства треугольников).
(по
первому признаку равенства треугольников).
3) ![]() –
гомотетичны, следовательно,
–
гомотетичны, следовательно,
![]()
4) ![]()
Значит, ![]() что
и требовалось доказать.
что
и требовалось доказать.
Так как доказательство производится по той же схеме,
что и доказательство первого признака, можно для наиболее подготовленного
ученика обозначить этапы
доказательства: I – подвергнуть ![]() преобразованию
подобия – гомотетии; II – доказать, что
преобразованию
подобия – гомотетии; II – доказать, что ![]() ;
III – доказать, что
;
III – доказать, что ![]() IV – доказать, что
IV – доказать, что ![]() .
.
Менее подготовленные ученики доказывают поэтапно.
IV. Решение задач.
№ 31 (ключевая).
Дано:DАВС; BD, AE – высоты.
Доказать: ![]() .
.
Доказательство:
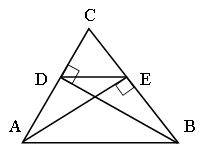
Пусть ÐС = a°.
1) Рассмотрим ![]() –
прямоугольный; cos a =
–
прямоугольный; cos a = ![]() .
.
2) Рассмотрим ![]() –
прямоугольный, cos a =
–
прямоугольный, cos a =![]() .
.
3) ![]() =
=![]() ,
,
![]() –
общий, следовательно,
–
общий, следовательно, ![]() по второму признаку
подобия.
по второму признаку
подобия.
Назовите равные углы. (ÐСЕD = ÐА, ÐСDЕ = ÐВ.)
Повторение:
1) определение косинуса острого угла прямоугольного треугольника; 2) признак подобия.
V. Итог урока.
– Сформулируйте известные признаки подобия.
– Какие элементы в треугольниках сравнивались?
– Какие еще возможны признаки подобия?
Домашнее задание: п. 104, № 30, 32–33 (для учащихся с высоким уровнем подготовки).
Задача № 32.
Дано: DАВС, АD, ВЕ, СF – высоты.
Найти: углы DFDE.
Решение: углы DАВС известны.
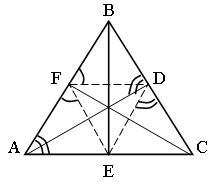
1) ![]()
![]()
(ключевая задача № 31).
2) ÐВFD = ÐC, ÐВDF = ÐA;
ÐAFE = ÐC, ÐFEA = ÐB; ÐЕDС = ÐА, ÐDЕС = ÐВ.
3) ÐF = 180° – 2ÐС; ÐD = 180° – 2ÐA; ÐE = 180° – 2Ð B.
Задача № 33.
Доказать, что FC, DA, ЕB – биссектрисы.
Ð1 = 90° – ÐС, Ð2 = 90° – ÐС, значит, Ð1 = Ð2, т. е. FC – биссектриса.
Ð3 = 90° – ÐА, Ð4 = 90° – ÐА, значит, Ð3 = Ð4, т. е. DА – биссектриса.
Ð5 = 90° – ÐВ, Ð6 = 90° – ÐВ, значит, Ð5 = Ð6, т. е. ЕD – биссектриса.
Урок 6
Решение задач
Цели: проверить уровень усвоения первого и второго признака треугольников; закрепить умения учащихся применять изученные теоремы при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
Решение задач по готовым чертежам.
Найти подобные треугольники, доказать их подобие.
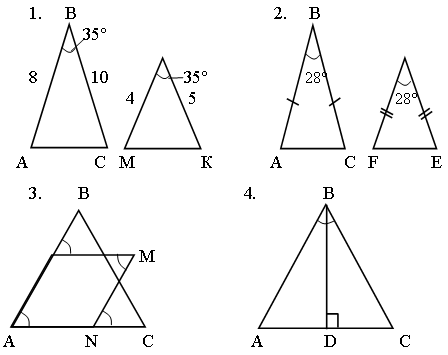
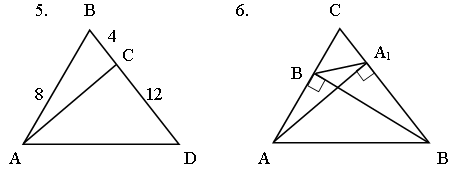
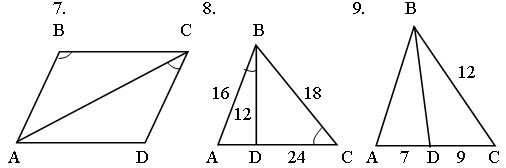
Дано: АВСD – трапеция.
III. Самостоятельная работа.
Вариант I.
1. Точка О является точкой пересечения отрезков AC и
BD. Докажите подобие треугольников ABO и CDO, если ![]() .
.
2. В треугольниках ABC и EDF углы при вершинах B и D равны, а стороны AB и BC, соответственно, больше сторон ED и DF в три раза. Определите, подобны ли эти треугольники. (Да.)
3. Биссектриса угла при основании равнобедренного треугольника делит его на два треугольника, один из которых подобен данному. Найдите углы исходного треугольника. (36°, 72°, 72°.)
Вариант II.
1. Точка О является точкой пересечения отрезков AC и
BD. Докажите подобие ![]()
2. Определите, подобны ли равнобедренные треугольники, если угол при вершине одного из них равен 54°, а угол при основании другого 63°. (Да.)
3. В произвольном треугольнике один из углов равен 40°. Биссектриса этого угла делит данный треугольник на два треугольника, один из которых подобен данному. Найдите наибольший угол исходного треугольника.
IV. Итог урока.
Какие задания вызвали трудности при решении?
Домашнее задание:
|
1. Дано: DАВС, ÐА = ÐN, ВС = 12 см, СМ = 6 см, CN = 4 см. Найдите: АС. Ответ: 8 см. |
|
|
2. Дано: DАВС, Ð3 = Ð1 + Ð2, СD = 4 см, ВС = 9 см. Найдите: АС. Ответ: 6 см. |
|
Урок 7
Третий признак подобия
треугольников
Цели: изучить третий признак подобия треугольников, формировать навык применения всех признаков подобия при решении задач.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Рассмотреть типичные ошибки, показать правильное решение. Учащимся, которые не справились с заданиями, предложить дифференцированную домашнюю самостоятельную работу.
Вариант I Вариант II
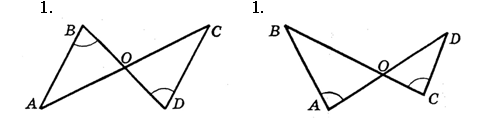
|
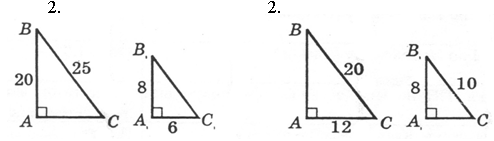
Дано: ÐВ = ÐD. Доказать: |
Дано: ÐА = ÐС. Доказать: |
|
Подобны ли треугольники, изображенные на рисунке? Почему? |
Подобны ли треугольники, изображенные на рисунке? Почему? |
|
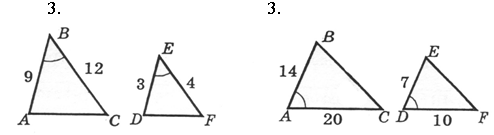
Дано: ÐВ = ÐЕ. Доказать: ÐА = ÐD. |
Дано: ÐА = ÐD. Доказать: ÐC = ÐF. |
Вариант III Вариант IV
|
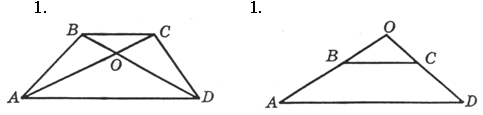
Дано: АВСD – трапеция. Найдите на рисунке подобные треугольники и докажите их подобие. |
Дано: АВСD – трапеция. Найдите на рисунке подобные треугольники и докажите их подобие. |
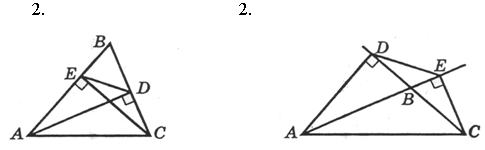
|
Дано: АD ^ ВС; СЕ ^ АВ. Доказать: 3. Докажите подобие двух прямоугольных трапеций, у которых острые углы равны, а диагонали являются биссектрисами этих углов. |
Дано: АD ^ ВС; СЕ ^ АВ. Доказать: 3. Докажите подобие двух прямоугольных трапеций, у которых тупые углы равны, а диагонали являются биссектрисами этих углов. |
III. Изучение нового материала.
Фронтальная работа с классом.
– какие фигуры называются подобными?
– в чем заключается смысл подобия треугольников?
– сформулируйте первый и второй признаки подобия треугольников; признаки равенства треугольников.
– Запишите схему доказательства признаков подобия треугольников.
– Сформулируйте и запишите свойство транзитивности для подобия фигур.
– Сформулируйте третий признак подобия треугольников (по трем сторонам).
Теорема: если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Дано:
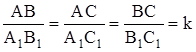 .
.
Доказать:
![]()
Доказательство:
1) По условию ![]() (1).
(1).
2) подвергнем
преобразованию подобия ![]() с коэффициентом k
(гомотетии)
с коэффициентом k
(гомотетии) ![]() .
.
![]() (2).
(2).
3) Рассмотрев (1) и (2), получаем ![]()
![]() по
третьему признаку треугольника.
по
третьему признаку треугольника.
Значит, ![]() .
.
4) ![]() следовательно,
следовательно,
![]()
IV. Закрепление изученного материала.
Устное решение задач.
№ 34. Подобны ли два равнобедренных треугольника?
№ 35. Подобны ли треугольники ABC и ![]() ,
если:
,
если:
1) AB = 1 м, AC = 1,5 м, BC = 2 м;
![]() = 10 см,
= 10 см, ![]() (Да.)
(Да.)
2) AB = 1 м, AC = 2 м, BC = 1,5 м;
![]() = 8 дм,
= 8 дм,![]() (Нет.)
(Нет.)
3) AB = 1 м, AC = 2 м, BC = 1,25 м;
![]() = 10 см,
= 10 см, ![]() .
(Нет.)
.
(Нет.)
№ 36 (ключевая задача).
Докажите, что у подобных треугольников периметры относятся как соответствующие стороны.
V. Итог урока.
– Сформулируйте три признака подобия треугольников, сделав на доске краткую запись.
– Сколько элементов должно быть равно или пропорционально для того, чтобы треугольники были подобны?
Домашнее задание.
1. Приготовить тематическую таблицу (черновой вариант) «Подобие треугольников».
Рекомендации для составления таблицы: кратко изложить теорию конкретного вопроса (определение, теоремы, следствия, формулы); привести рисунки; примеры решений ключевых задач.
2. Задачи № 37, 38.
Урок 8
третий Признак подобия треугольников.
Решение задач
Цели: закрепить умение применять признаки при решении задач, показать практическое применение знаний о подобии треугольников.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
1. Проверка самостоятельной работы учащимися-консультантами.
2. Индивидуальная работа.
Карточка 1. Решить задачу № 38.
Дано: DАВС ~ DА1В1С1,
![]()
![]() .
.
Найти:![]() .
.
Решение:
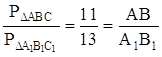 ;
;
![]() ,
,
![]() , 13AB = 11 + 11AB,
, 13AB = 11 + 11AB,
2AB = 11; AB = 5,5; А1С1 = 6,5.
Ответ:5,5 см; 6,5 см.
Карточка 2. Решить задачу № 37.
Карточка 3. Доказать третий признак подобия треугольников.
Карточка 4. Доказать, что периметры подобных треугольников относятся как соответствующие стороны.
При проверке выполнения заданий внимание учащихся всего класса акцентируется на карточке 4, так как эта задача будет внесена в таблицу «Подобие тругольников».
3. Составление тематической таблицы.
|
Подобие треугольников |
|
|
Определение |
|
|
1 |
2 |
|
|
|
|
Признаки подобия треугольников |
|
|
По двум углам (первый признак) |
|
|
По двум сторонам и углу между ними (второй признак) |
|
|
По трем сторонам |
|
|
Ключевые задачи |
|
|
Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному |
А1С1 || AC, следовательно,
|
Окончание табл.
|
1 |
2 |
|
Периметры подобных треугольников относятся как соответствующие стороны |
=
|
|
Высоты подобных треу- |
∆ABC ~ ∆A1B1C1, значит, ÐА = ÐА1, ∆АВD ~ ∆A1B1D1, так как ÐА = ÐА1, ÐD = ÐD1 = 90°. Следовательно,
|
III. Решение задач по готовым чертежам.
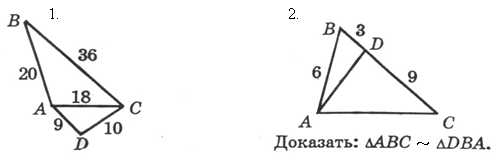
Найдите на рисунке равные углы и докажите их равенство.
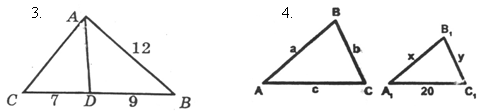
Доказать: DАВС ~ DDВА. Дано: а : b : с = 4 : 3 : 5.
DАВС ~ Dа1В1С1.
Найти: х, у.
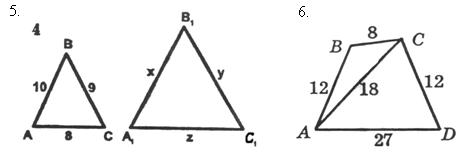
Дано: ![]() Найдите
на рисунке равные
Найдите
на рисунке равные
DАВС ~ Dа1В1С1. углы и докажите их равенство.
Найти: х, у.
IV. Практическое приложение подобия треугольников.
1. Задачи на построение.
При решении многих задач на построение треугольников применяется метод подобия. Он состоит в том, что сначала на основании некоторых данных строят треугольник, подобный искомому, а затем, используя остальные данные, строят искомый треугольник.
Построить треугольник по двум углам и биссектрисе при вершине третьего угла.
Решение:
Повторим алгоритм решения задач на построение, который состоит из следующих этапов: анализ; построение; доказательство; исследование.
Дано:

Анализ:
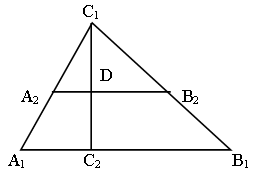
Если построить Dа1В1С1, подобный искомому (по двум углам), провести в нем любую прямую, параллельную а1В1, то получим Dа2В2С1 ~ Dа1В1С1.
Построение:
1) Строим Dа1В1С1, ÐА = ÐА1, ÐВ = ÐВ1, получим Dа1В1С1, подобный данному.
2) Проведем биссектрису С1С2, на ней отложим отрезок, равный данной биссектрисе: С1D = с.
3) Через точку D проведем прямую А2В2 || А1В1.
4) DА2С1В2 – искомый треугольник.
Доказательство: DА2В2С1 – искомый треугольник, так как ÐА2 = ÐА1 = ÐА, ÐВ2 = ÐВ1 = ÐВ, С1D = с – биссектриса угла.
Исследование:
Задача имеет решение, если сумма двух данных углов меньше 180°. Так как отрезок а1С1 выбран произвольно, то таких треугольников существует бесконечно много, все они подобны искомому.
Отложив на биссектрисе отрезок, равный заданному, получим треугольник, равный заданному и причем единственный.
2. Измерительные работы на местности.
Свойства подобных треугольников могут быть использованы для проведения измерительных работ на местности.
Задача № 1.
Найти расстояние от пункта A до недоступного пункта B.
Решение:
Для этого на местности выбираем точку C, зрительно проведем отрезок AC и измеряем его. Затем с помощью астролябии (астролябия – простейший прибор для измерения углов. Он состоит из двух частей: диска, разделенного на градусы, и вращающейся вокруг центра диска линейки (алидады). На концах алидады находятся два узких «окошечка», которые используются для установки ее в определенном направлении) измеряем углы.
На листе бумаги строим какой-нибудь треугольник Dа1В1С1,
у которого ÐА = ÐА1, ÐС = ÐС1, измеряем длины сторон а1В1 и а1С1. Эти
треугольники подобны по первому признаку. Значит, 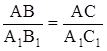 ,
откуда
,
откуда 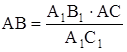 .
.
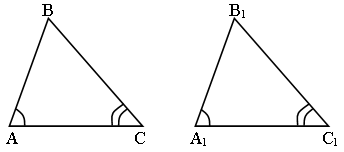
Для упрощения вычислений удобно построить треугольник а1В1С1 так, чтобы а1С1 : AC = 1 : 1000. Поэтому, измерив расстояние а1В1 в миллиметрах, получим AB в метрах.
Задача № 2.
Измерить ширину реки.
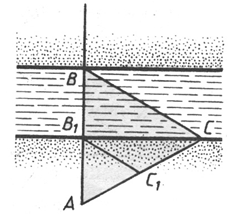
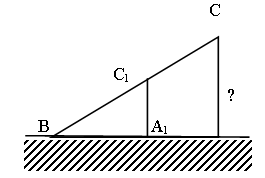
Задача № 3.
Определить высоту предмета.
V. Итог урока.
– Имеют ли знания о подобных треугольниках практическое применение?
Домашнее задание: практическая работа по решению задач (например, найти высоту дерева).
Урок 9
Подобие прямоугольных
треугольников
Цели: сформулировать признак подобия прямоугольных треугольников, свойства катетов, высоты и биссектрисы прямоугольного треугольника.
Ход урока
I. Организационный момент.
II. Анализ практической работы.
1) Лучшие работы демонстрируются всем учащимся.
2) Рассматривается задача на определение высоты предмета.
Вопросы:
– Какие треугольники рассматриваются в этом случае?
– Какой признак подобия треугольников используется в этом случае? Нужно ли измерять углы? сколько углов придется измерить?
– Сформулируйте признак подобия прямоугольных треугольников и обоснуйте его.
III. Изучение нового материала.
Если острый угол одного прямоугольника треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны.
|
Соотношения в прямоугольном треугольнике |
|
|
1 |
2 |
|
катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу |
так
как ÐВ
– общий, ÐСАВ = ÐВСD, Следовательно,
Значит, |
|
Высота прямоугольного треугольника, проведенная из вершины прямого угла, |
(по свойству транзитивности). |
Окончание табл.
|
1 |
2 |
|
есть среднее пропорциональное между проекциями катетов на гипотенузу |
|
Эти свойства учащиеся доказывают самостоятельно с последующей проверкой. Двое учащихся выполняют доказательство на доске (задняя часть доски).
Формулируется свойство биссектрисы угла треугольника: биссектриса треугольника делит противоположные стороны на отрезки, пропорциональные двум другим отрезкам.
В классе только делается чертеж, записываются предложенные задачи. Наиболее подготовленным учащимся дома предлагается доказать это свойство, а менее подготовленным – выучить формулировку.
Дано:![]() ; CD – биссектриса.
; CD – биссектриса.
Доказать: ![]() .
.
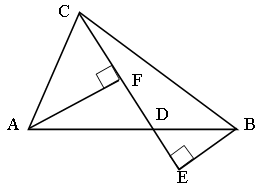
Доказательство:
Выполним дополнительное построение: AF![]() CD,
BE
CD,
BE![]() CD.
CD.
1) ![]() (CD
– биссектриса.)
(CD
– биссектриса.)
Значит, ![]() ,
а по условию
,
а по условию ![]() . Следовательно,
. Следовательно, ![]() (по
свойству транзитивности), что и требовалось доказать.
(по
свойству транзитивности), что и требовалось доказать.
IV. Закрепление изученного материала.
Cамостоятельное решение задач № 39, 40, 41, 42, 43.
Задача № 42 (ключевая, решается коллективно).
Докажите, что высоты подобных треугольников относятся как соответственные стороны.
V. Итог урока.
– Где понадобятся знания об изученных свойствах прямоугольного треугольника?
Домашнее задание: повторить п. 100–106; вопросы 1–12; выписать новые слова, со значениями которых познакомились; задачи 44, 45; для наиболее подготовленных учащихся – задания № 46, 47.
Урок
10
Подобие прямоугольных треугольников.
Решение задач
Цели: закрепить знания учащихся о подобии треугольников в ходе решения задач, проверить уровень этих знаний и умений.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
1. Индивидуальная работа.
Карточка 1. Докажите, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Карточка 2. Докажите, что высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Карточка 3. Докажите, что биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.
2. Фронтальный опрос (вопросы 1–12).
III. Самостоятельная работа.
Вариант 1.
1. Докажите, что два прямоугольных треугольника подобны, если их катеты пропорциональны.
2. Докажите, что если основание и боковая сторона одного равнобедренного треугольника пропорциональны основанию и боковой стороне другого равнобедренного треугольника, то такие треугольники подобны.
3. Два ромба имеют равные острые углы. Докажите, что эти ромбы подобны.
Вариант 2.
1. На сторонах AB, BC, AC равностороннего треугольника ABC соответственно отмечены точки P, R, Q так, что отрезки AP, BR и CQ равны. Докажите, что треугольник PRQ подобен треугольнику ABC.
2. Докажите, что высота прямоугольного треугольника, проведенная из вершины прямого угла, делит его на два подобных треугольника.
3. В равнобедренный треугольник, у которого боковая сторона равна 10 см, а основание 6 см, вписана окружность. Определите расстояние между точками касания, находящимися на его боковых сторонах.
IV. Итог урока.
Какие задания вызвали затруднения при решении?
Домашнее задание: повторить п. 38–41; принести тематическую таблицу «Окружность» (7 класс).
1. Дано: АВСD – параллелограмм; ВЕ ^ АD; BF ^ CD.
Доказать: ![]()
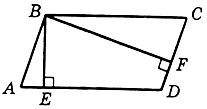
2. Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 15 см и 20 см. Найдите длины отрезков гипотенузы, на которые ее делит высота треугольника.
3. Высота прямоугольного треугольника делит гипотенузу на отрезки 12,6 см и 22,4 см. Найдите длины отрезков гипотенузы, на которые ее делит биссектриса прямого угла.
Урок 11
Углы, вписанные в окружность
Цели: ввести понятия градусной меры дуги окружности, центрального и вписанного углов.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Рассмотреть типичные ошибки, показать правильное решение. Учащимся, которые не справились с заданиями, предложить домашнюю самостоятельную работу.
Вариант I Вариант II
|
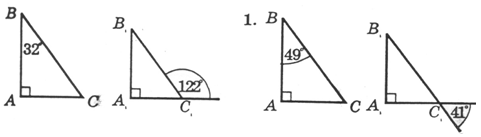
Докажите подобие прямоугольных треугольников, изображенных на рисунке. |
Докажите подобие прямоугольных треугольников, изображенных на рисунке. |

|
Дано: ÐАВС = 90°; BD ^ АС; АВ = 15 см; ВС = 20 см. Найти: ВD. 3. В треугольнике со сторонами 25 см и 40 см проведена биссектриса угла между данными сторонами. Она делит третью сторону на отрезки, меньший из которых равен 15 см. Найдите периметр треугольника. |
Дано: ÐАВС = 90°; BD ^ АС; АD = 9 см; DС = 16 см. Найти: ВD. 3. В треугольнике АВС наибольшая сторона АВ равна 40 см. Биссектриса ВD делит сторону АС на отрезки длиной 15 см и 24 см. Найдите периметр треугольника АВС. |
Вариант III Вариант IV
|
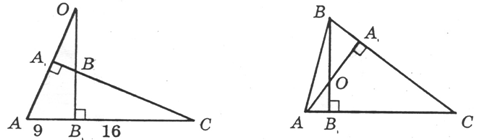
Дано: АА1 ^ ВС; ВВ1 ^ АС. Найдите на рисунке все пары подобных прямоугольных треугольников и докажите их подобие. |
Дано: АА1 ^ ВС; ВВ1 ^ АС. Найдите на рисунке все пары подобных прямоугольных треугольников и докажите их подобие. |
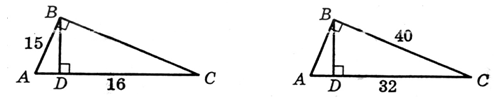
|
Дано: ÐАВС = 90°; BD ^ АС; АВ = 15 см; DС = 16 см. Найти: РDАВС 3. Катет прямоугольного треугольника равен 18 см. Точка, принадлежащая данному катету, удалена от гипотенузы и от второго катета на 8 см. Найдите периметр треугольника. |
Дано: ÐАВС = 90°; BD ^ АС; ВС = 40 см; DС = 32 см. Найти: РDАВС 3. Катет прямоугольного треугольника равен 28 см. Точка, принадлежащая гипотенузе, удалена от каждого из катетов на 12 см. Найдите периметр треугольника. |
III. Изучение нового материала.
Работа по тематическим таблицам, составленным в 7 классе.
|
Окружность |
|
|
Окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром |
|
|
Расстояние от точек окружности до ее центра называется радиусом окружности |
|
|
Отрезок, соединяющий две точки окружности, называется хордой |
|
Окончание табл.
|
Хорда, проходящая через центр окружности, называется диаметром |
Обозначение: окр. (О, R), ОА = R – радиус, ВС – хорда, АD – диаметр |
|
Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведенному в эту точку, называется касательной |
а ^ ОА, а – касательная, А – точка касания, МN – секущая |
|
Точка окружности называется точкой касания |
|
|
Прямая, имеющая с окружностью две общих точки, называется секущей |
план
– определение плоского угла;
– градусная мера плоского угла;
– определение угла, дополнительного данному плоскому;
– определение центрального угла;
– градусная мера центрального угла;
– определение дуги окружности;
– определение вписанного угла;
– теорема об измерении вписанных углов;
– свойство вписанного угла, опирающегося на диаметр;
– свойство вписанных углов, опирающихся на одну и ту же дугу.
IV. Закрепление изученного материала.
Устно решить задачу.
1. вписанный угол ABC равен 48°. Как расположены точки O и B относительно прямой AC? О – центр окружности.
2. Вписанный угол ADC равен 150°. Как расположены точки O и D относительно прямой AC?
3. а)![]() .
.
Найти:![]()
б)![]() .
.
Найти:![]() .
.
4. Решить письменно задачи № 48 (по вариантам), 49, 51, 52.
Домашнее задание: п. 107; подготовить материал тематической таблицы «Углы в окружности»; задачи № 50, 54, 56 (наиболее подготовленным учащимся), 59.
Задача № 50.
Точки A, B, C лежат на окружности. Чему равен угол ABC, если хорда AC равна радиусу окружности?
Случай 1.
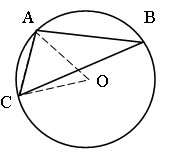
1) ÐАВС – вписанный, опирается на хорду AC.
ÐАОС – соответствующий ему центральный угол (острый).
2) Рассмотрим DАОС – равносторонний, так как AC = OC = OA. Значит, ÐАОС = 60°.
3) По теореме о вписанном угле ÐАВС
= ![]() ÐАОС
= 30°.
ÐАОС
= 30°.
Случай 2.
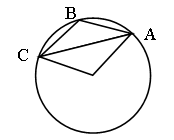
1) ÐАВС – вписанный, ему соответствующий центральный угол (тупой). ÐАОС = 360° – 60° = 300°.
2) по
теореме о вписанном угле ÐАВС = ![]() ÐАОС
= 150°.
ÐАОС
= 150°.
Задача № 56 (ключевая).
Докажите, что у четырехугольника, вписанного в окружность, сумма противолежащих углов равна 180°.
Дано: ABCD – вписанный, окр. (O, r).
Доказать: ![]()
![]() .
.
Доказательство:
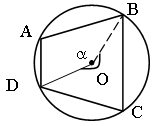
1) ÐBAD – вписанный, ему соответствующий центральный ÐDOB = a.
ÐBCD – вписанный, ему соответствующий центральный является дополнительным к ÐDOB = 360° – a.
![]() a +
a + ![]() (360°
– a)
=
(360°
– a)
= ![]() a
+ 180°–
a
+ 180°– ![]() a
= 180°.
a
= 180°.
2) Аналогично доказывается, что ![]() .
.
Задача № 59 (ключевая).
Докажите, что острый угол между хордой окружности и касательной к окружности в конце хорды равен половине угла между радиусами, проведенными к концам хорды.
Дано: Окр. (O, r),
AB – хорда, BC – касательная.
Доказать: ![]()
Доказательство:
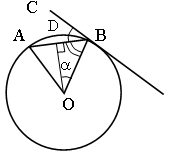
1) Рассмотрим ![]() –
равнобедренный, так как AO = OB, DO – высота, а значит, и биссектриса,
–
равнобедренный, так как AO = OB, DO – высота, а значит, и биссектриса, ![]() Пусть
ÐDOB
= l°.
Пусть
ÐDOB
= l°.
2) ![]() DOB
– прямоугольный, ÐDBО =
90° – a.
DOB
– прямоугольный, ÐDBО =
90° – a.
3) OB – радиус, проведенный в точку касания,
значит, OB![]() BC,
BC, ![]() ABC
= 90° – ÐDBO
= 90° – (90° – l) = 90° – 90° + l°
= l°.
ABC
= 90° – ÐDBO
= 90° – (90° – l) = 90° – 90° + l°
= l°.
4) Получили ÐABC = ![]() что
и требовалось доказать.
что
и требовалось доказать.
Урок 12
Пропорциональность отрезков окружности,
хорд и секущих
Цели: изучить свойство отрезков пересекающихся хорд и секущих окружности и показать применение этих свойств при решении задач.
Ход урока
I. Проверка домашнего задания.
II. Актуализация опорных знаний.
Решение задач по готовым чертежам.
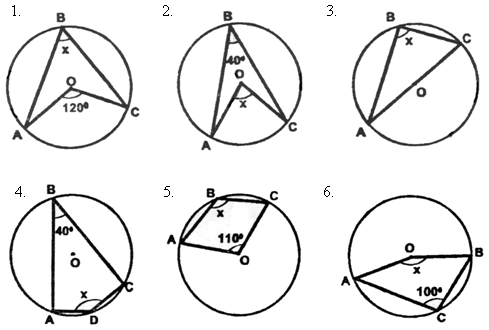
|
|
Ответы: 1. х = 60º 5. х = 125º 2. х = 80º 6. х = 160º 3. х = 90º 7. х = 30º 4. х = 140º |
III. Изучение нового материала.
1. Сформулировать и доказать свойство отрезков пересекающихся хорд.
Если хорды AB и CD окружности пересекаются в точке S, то AS · BS = CS · DS.
2. Сформулировать и доказать свойство секущих окружности.
Если из точки P к окружности проведены две секущие, пересекающие окружность в точках A, B и C, D соответственно, то AP · BP = CP · DP.
IV. Закрепление изученного материала.
1. Решение задач по готовым чертежам.
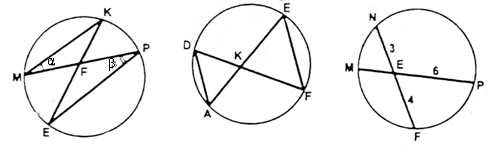
Найти: ÐКFP. Доказать: DADK ~ DFEK. Найти: МЕ.
Ответ: α + β. АК · КЕ = DК · KF. Ответ: 8.
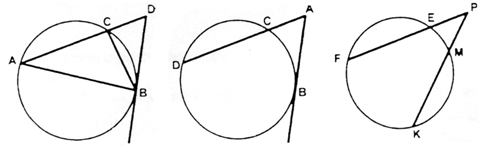
Доказать: Доказать: Доказать:
DABD ~ DBCD. АВ2 = АD · AC. РЕ · РF = PM · PK.
2. Письменное решение задач.
Задача № 61.
Из точки C окружности проведен перпендикуляр CD к диаметру AB. Докажите, что CD = AD · BD.
Дано: окр.
(O r). AB – диаметр, CD![]() AB.
AB.
Доказать: CD2 = AD · BD.
Доказательство:
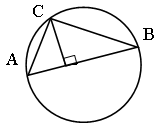
DAСB – прямоугольный, так как AB – диаметр, ÐAСB – вписанный. Значит, CD2 = AD · BD (по свойству высоты прямоугольного треугольника).
V. Итог урока.
Расскажите обо всех фигурах, которые можно получить, имея окружность.
Домашнее задание: составить тематическую таблицу «Углы в окружности»; задачи № 62, 63.
Урок 13
ВПИСАННЫЕ УГЛЫ. Пропорциональность
отрезков хорд и секущих окружности
Цели: проверить уровень усвоения темы.
Ход урока
I. Актуализация опорных теоретических знаний.
Работа с тематической таблицей.
|
Углы в окружности |
|
|
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность. Центральным углом в окружности называется плоский угол с вершиной в ее центре |
ÐАОВ – центральный ÐАСВ – вписанный |
|
Угол, вписанный в окружность, равен половине соответствующего центрального угла |
ÐАОВ = ÐАСВ =
|
|
Если хорды окружности
пересекаются в точке M, то АМ · ВМ = |
|
|
Ключевые задачи |
|
ÐАРВ
=
АР = АQ MA · MB = MC2
ÐAPB
= |
II. Самостоятельная работа.
Вариант 1.
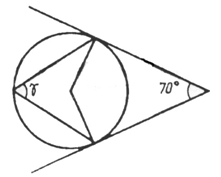
1. найдите градусную меру центральных углов, обозначенных буквами: a, b и φ.
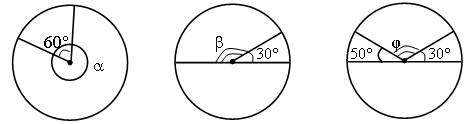
Ответ: a = 300º, b = 150º и φ = 100º.
2. угол, образованный двумя касательными, проведенными из одной точки к окружности, равен 42º. Найдите градусную меру дуг, заключенных между точками касания.
Ответ: 138º, 222º.
3. Докажите, что градусная мера угла, вершина которого лежит внутри окружности, равна полусумме градусных мер дуг, из которых одна заключена между его сторонами, а другая – между продолжениями сторон.
Вариант II.
1. найдите градусную меру угла, обозначенного буквой γ.
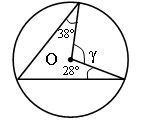
Ответ: 128º.
2. Вписанный угол на 25° меньше центрального, опирающегося на ту же дугу. Найдите градусную меру этих углов.
Ответ: 25º, 50º.
3. Докажите, что градусная мера угла, вершина которого лежит вне окружности, равна полуразности градусных мер дуг, заключенных между его сторонами.
Решение задач.
Вариант 1.
Дано: окр.
(O, r), ![]()
Доказать:![]()
Доказательство:
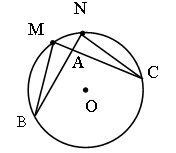
1) ![]() –
внешний угол треугольника ABM. По свойству внешнего угла:
–
внешний угол треугольника ABM. По свойству внешнего угла: ![]()
2) ![]() –
вписанный, значит,
–
вписанный, значит, ![]() ;
;
![]()
![]()
Вариант II.
Дано: окр.
(O, r); ![]() ,
где AB, AC – секущие.
,
где AB, AC – секущие.
Доказать:![]() .
.
Доказательство:
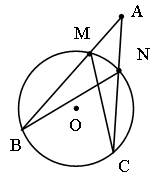
Рассмотрим ![]()
![]()
![]() ;
;
![]() – смежный с углом BNC, значит,
– смежный с углом BNC, значит, ![]() = 180º –
= 180º – ![]()
Следовательно, ![]() =
180º – (
=
180º – (![]() ) =
) =
= ![]()
![]() – вписанные углы,
– вписанные углы, ![]()
![]() . Значит,
. Значит, ![]() .
.
III. Итог урока.
Какие задания вызвали затруднения при решении?
Домашнее задание: повторить п. 11; ответить на контрольные вопросы 1–17, с. 155–156.
Урок 14
Зачет по теме «Подобие фигур»
Цели: обобщить и систематизировать теоретические знания учащихся.
Ход урока
I. Работа в группах.
Карточка 1.
1. Докажите, что вписанный в окружность угол равен половине соответствующего центрального угла.
2. Что такое преобразование подобия?
Карточка 2.
1. Докажите свойства отрезков пересекающихся хорд и свойства отрезков секущих.
2. Что такое гомотетия (центр гомотетии, коэффициент гомотетии)?
Карточка 3.
1. Сформулируйте и докажите признак подобия треугольников по двум сторонам.
2. Что такое плоский угол?
Карточка 4.
1. Сформулируйте и докажите признак подобия треугольников по двум сторонам и углу между ними.
2. Что такое центральный угол?
Карточка 5.
1. Сформулируйте и докажите признак подобия треугольников по трем сторонам.
2. Какой угол называется вписанным в окружность?
Карточка 6.
1. Докажите, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
2. Какие фигуры называются подобными?
Карточка 7.
1. Докажите, что высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.
2. Каким знаком обозначается подобие? Как записывается подобие треугольника?
Карточка 8.
1. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.
2. Что такое движение?
Карточка 9.
1. Какие свойства преобразования подобия вы знаете? Докажите, что преобразование подобия сохраняет углы между полупрямыми.
2. Какие виды движения вы знаете?
II. Тест «Подобие фигур».
Вариант I.
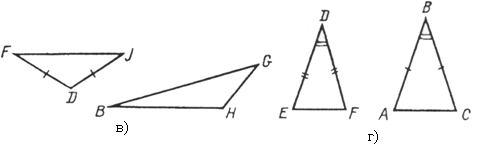
1. Укажите, на каком из рисунков есть подобные треугольники.
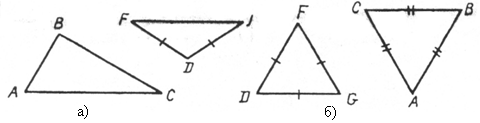
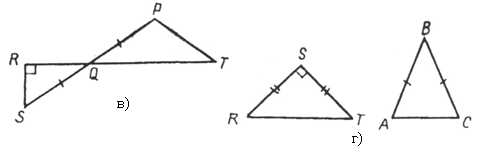
2. В трапеции АВСD проведены диагонали АС и ВD. Тогда DСОВ ~ DАОD:
а) по двум углам;
б) двум пропорциональным сторонам и углу между ними;
в) трем пропорциональным сторонам и углу.
3. В прямоугольном треугольнике АВС со стороной АВ, равной 13 см, проведена высота СD. Найдите катет АС, если коэффициент подобия треугольников АВС и АСD равен 2,6.
Ответ: АС = ____ см.
4. Найдите градусную меру центральных углов, обозначенных буквами: a, b и φ.
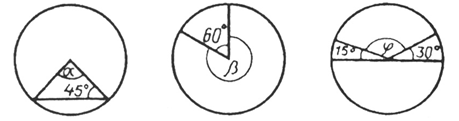
Ответ: Ða = ____ ; Ðb = ____; Ðφ = ____.
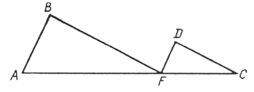
5. Треугольники АFC и DFB подобны. Запишите отношения соответствующих сторон.

Ответ: AF : ___ = FC : ___ = АС: ____.
6. Равнобедренные треугольники ABF и СDF подобны. Известно, что AF = 15 см, АВ = 12 см, DC = 3 см. Определите коэффициент подобия.
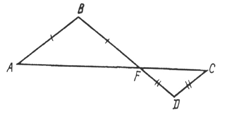
Ответ: ________ .
7. В треугольнике АВС отрезок NM параллелен стороне АС. Известно, что ВС = 21 см. Если AN : NB = 4 : 3, то отрезок МС равен:
а) 3 см; б) 9 см; в) 12 см; г) 18 см.
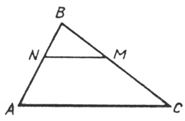
8. Найдите градусную меру углов, обозначенных буквами: a, обозначенных a, b и g.
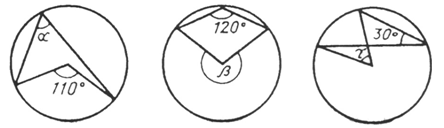
Ответ: Ða= ____; Ðb= ____; Ðg= ____.
9. Найдите градусную меру дуги окружности, соответствующей углу, обозначенному буквой g.
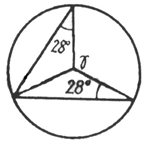
Ответ: Ðg = ____ .
Вариант II.
1. Укажите, на каком из рисунков есть подобные треугольники.
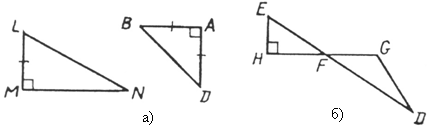
2. В прямоугольном треугольнике АВС отрезок FG перпендикулярен гипотенузе АВ.
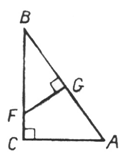
Тогда DАВС ~ DFBC:
а) по двум углам;
б) двум пропорциональным сторонам и углу между ними;
в) трем пропорциональным сторонам.
3. В трапеции АВСD проведены диагонали АС и ВD. Треугольники АОD и СОВ подобны. Известно, что ВС = 28 см, АD = 40 см, ОD = 24 см. Определите коэффициент подобия.
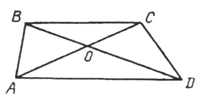
Ответ: _________ .
4. Найдите градусную меру центральных углов, обозначенных буквами: φ, σ и x.
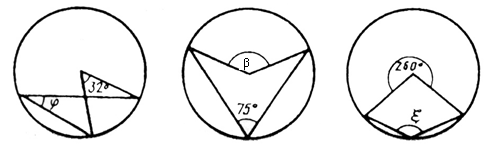
Ответ: Ðφ = ______ ; Ðb = ______; Ðx = ______ .
5. В треугольнике АВC отрезок NM параллелен стороне АС. Известно, что АВ = 18 см. Если СМ : МВ = 7 : 2, то отрезок BN равен:
а) 4 см; б) 2 см; в) 14 см; г) 16 см.
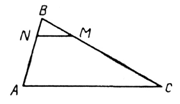
6. Треугольники ABF и СDF подобны. Запишите отношения соответствующих сторон.
Ответ: АВ : ____ = BF : ____ = AF : ____ .
7. В параллелограмме АВСD проведены диагональ АС и отрезок DG так, что AG = 14 см. Найдите сторону параллелограмма, если коэффициент подобия треугольников АОG и СOG равен 0,7.
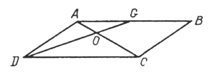
Ответ: ______
8. Найдите градусную меру углов, обозначенных буквами: x, d и τ.
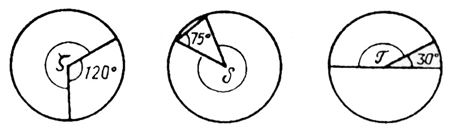
Ответ: Ðx= ______; Ðd= ______; Ð τ = ______.
9. Найдите градусную меру дуги окружности, соответствующей углу, обозначенному буквой g.
Ответ: Ðg = ______.
Ключ к тесту
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
I |
б |
а |
5 |
90º 300º 135º |
DF BF BD |
|
в) |
55º 240º 30º |
112º |
|
II |
г |
а |
0,7 |
16º 150º 130º |
а |
DF DC FC |
20 |
240º 330º 150º |
55º |
Урок 15
Контрольная работа № 1
по теме «Подобие фигур»
Цель: проверить уровень знаний и умений учащихся.
Ход урока
I. Организационный момент.
II. Выполнение работы.
Вариант I.
1. На сторонах АВ и ВС треугольника АВС отмечены точки N и M так, что NM || АС. Докажите, что DNBM ~ DАВС.
2. Прямоугольные треугольники ABF (ÐА = 90°) и СDF (ÐC = 90°) подобны. Известно, что AF = 18 см, АВ = 6 см, DC = 12 см. Определите коэффициент подобия.
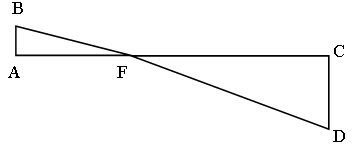
3. Основание ВС трапеции АВСD равно 9 см. О – точка пересечения диагоналей трапеции. Найдите основание АD, если АО : ОС = 4 : 3.
4. На рисунке ÐСВА = 37°. Найдите угол GEF.
5. В треугольнике АВС проведены высоты АD и BF, которые пересекаются в точке G. Докажите, что DAGF ~ DВСF.
Вариант II.
1. В прямоугольном треугольнике АВС (ÐС – прямой) проведена высота СD. Докажите, что DACD ~ DAВС.
2. Равнобедренные треугольники АBF и СDF подобны, причем АВ = BF и АВ || DC. Известно, что AF = 20 см, AB = 12 cм, DC = 4 см. Определите коэффициент подобия.
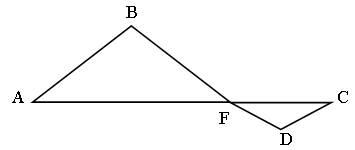
3. Из вершины D параллелограмма АВСD проведены прямая, пересекающая сторону ВС в точке G, и диагональ АС. О – точка их пересечения, GC = 14 см. Найдите сторону AD, если GO : OD = 7 : 10.
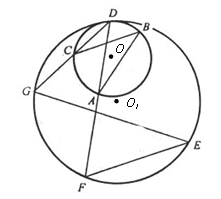
4. На рисунке точки О и О1 – центры окружностей. Найдите угол DBC.
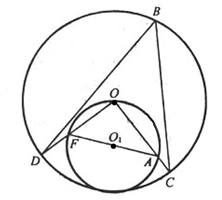
5. Сумма углов при основании трапеции равна 90°. Докажите, что высота трапеции есть среднее пропорциональное между проекциями ее боковых сторон на основание.
Оформление решения задач.
Вариант II.
1. Дано:
![]() высота.
высота.
Доказать: ∆АСD ~ ∆АВС.
Доказательство:
1) CD – высота, значит, прямая CD перпендикулярна
прямой AB, ![]() .
.
2) ∆АСD ~ ∆АВС,
так как ![]() –
общий, что и требовалось доказать.
–
общий, что и требовалось доказать.
2. Дано:
![]() –
равнобедренный,
–
равнобедренный,
∆CDF – равнобедренный,
AB || DC, AF = 20 см, AB = 12 см, DC = 4 см.
Найти:FC.
Решение:
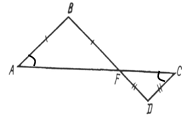
1) AB || DC, значит,![]() как накрест лежащие при секущей AC.
как накрест лежащие при секущей AC.
![]() как вертикальные.
как вертикальные.
2) ÐВАF = ÐВFA, так как ∆АВF – равнобедренный. Значит, ÐCFD = ÐFCD.
3) ∆АВF ~ ∆CDF, следовательно:
![]()
Ответ:
FC = 6![]() см.
см.
3. Дано:
ABCD – параллелограмм,
GC = 14 см, GO : OD = 7 : 10.
Найти: AD.
Решение:
1) ABCD – параллелограмм, AD || BC, значит, ![]() как
накрест лежащие при секущей AC,
как
накрест лежащие при секущей AC, ![]() как
вертикальные.
как
вертикальные.
2) ∆ AOD ~ ∆GOC по двум углам.
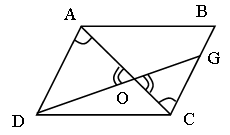
Следовательно,![]() ,
,
![]() .
.
Ответ: AD = 20 см.
4. 1) Рассмотрим окружность с центром в точке О1,
![]() ,
так как
,
так как ![]() –
вписанный, а FA – диаметр.
–
вписанный, а FA – диаметр.
2) Для окружности с центром в точке О ![]() –
центральный, следовательно,
–
центральный, следовательно, ![]() .
.
3) ÐDBC – вписанный, ![]() .
.
Ответ: ![]() .
.
5. Дано:
ABCD – трапеция, ![]() =
90º, AM – высота.
=
90º, AM – высота.
Доказать:![]() .
.
Доказательство:
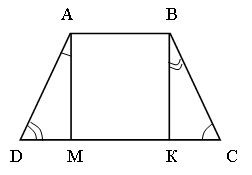
1) DM и KC – проекции боковых сторон на основании.
![]()
![]() = 90º, значит,
= 90º, значит, ![]() .
.
2)![]() –
прямоугольные, следовательно, ÐD = ÐKBC.
–
прямоугольные, следовательно, ÐD = ÐKBC.
3) ∆DAM ~ ∆ВКС по второму признаку подобия.
4)![]()
Вариант 1.
1. Дано: DАВС, MN || AC.
Доказать: ∆NBM ~ ∆ABС.
Доказательство:
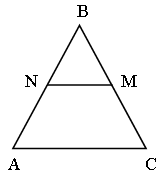
1) ![]() как
соответственные при параллельных прямых MN и AC и секущей
AB, ÐB – общий.
как
соответственные при параллельных прямых MN и AC и секущей
AB, ÐB – общий.
2) Рассмотрим ∆NBM и ∆ABС,
они подобны по первому признаку подобия: ÐB – общий, ![]() .
.
2. Дано:![]() ,
AF = 18 см, AB = 6 см, DC = 12 см.
,
AF = 18 см, AB = 6 см, DC = 12 см.
Найти: k.
Решение:
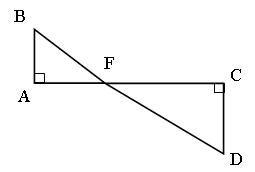
1) Рассмотрим ∆ABF и ∆CFD,
так как ![]() ,
,
![]() как
вертикальные, то ∆ABF ~ ∆CFD.
как
вертикальные, то ∆ABF ~ ∆CFD.
2) ∆ABF ~ ∆CFD,
значит, ![]()
![]() ,
,
![]() .
.
3) ∆ABF – прямоугольный, AF = 18 см, AB = 6 см.
Ответ:![]() .
.
3. Дано: ABCD – трапеция, AО : OC = 4 : 3, BC = 9.
Найти: AD.
Решение:
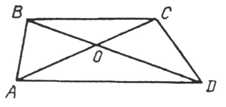
ABCD – трапеция, значит, BC || AD. Следовательно, ÐВСА = ÐСАD как накрест лежащие при секущей AC, ÐCBD = ÐBDA – при секущей DB.
2) ÐВСА = ÐСАD, ÐCBD = ÐBDA, значит, ∆ВОС ~ ∆DОА по первому признаку подобия:
![]()
3) ![]() (см).
(см).
Ответ: AD = 12 см.
4. Дано:![]() .
.
Найти:![]()
Решение:
1) Рассмотрим окружность с центром в точке O,
![]() (вписанные),
(вписанные), ![]() .
.
2) Рассмотрим окружность с центром в точке О, ÐGEF = ÐGDF = ÐCDA.
Значит, ![]() .
.
Ответ: ![]() =
37º.
=
37º.
5. Дано: DABC, AD, BF – высоты.
Доказать: ∆AGF ~ ∆BCF.
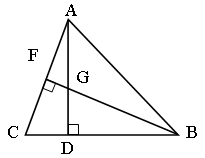
Доказательство: 1) ∆ACD ~ ∆AGF, так как они прямоугольные, ÐA – общий.
2) ∆ACD ~ ∆ВСF, треугольники прямоугольные и ÐС – общий.
3) ∆AGF ~ ∆BCF по свойству транзитивности.
Тема: РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
Цель: сформировать алгоритм решения произвольных треугольников.
В результате изучения темы (11 часов) учащиеся должны
|
знать: – формулировку теоремы косинусов и следствия из нее; – утверждения о свойствах диагоналей параллелограмма; – формулировки теоремы синусов и следствия из нее о соотношении между сторонами и углами треугольника; – что значит решить треугольник; – четыре типа задач: по данной стороне и двум углам; по двум сторонам и углу между ними; по двум сторонам и углу, противолежащему одной из них; по трем сторонам |
уметь: – доказывать теорему косинусов; – записывать в виде
равенства теорему косинусов применительно – применять теорему косинусов; – доказывать теорему синусов; – записывать ее
формулировку – составлять пропорции для сторон и углов данного треугольника; – применять ее при решении задач; – решать задачи четырех типов; – для каждой из трех основных задач проводить решение в общем виде и для конкретных треугольников (III тип) |
Визитная карточка темы «решение треугольников»
|
Теория |
Домашнее |
Самостоятельная работа |
Тест |
Контрольная |
|
Теорема косинусов. Следствие из теоремы. Теорема синусов. Соотношение между углами и противолежащими сторонами |
Урок 1 – № 1, 7 |
№ 1, 2 |
|
|
Урок 1
ТЕОРЕМА КОСИНУСОВ
Цели: доказать теорему косинусов, формировать умение применять ее при решении задач.
Ход урока
I. Организационный момент.
Сообщение темы и цели всего блока уроков, а также темы и цели данного урока.
II. Актуализация опорных знаний.
1. Вопросы:
– Что значит «решить треугольник»?
– Каковы основные задачи по решению треугольников?
– Какими они становятся для прямоугольного треугольника?
– Какие известные вам теоремы, определения, следствия из теорем могут помочь решить треугольник?
Предполагаемые ответы.
· Решить треугольник – это значит вычислить все элементы треугольника по трем данным независимым элементам.
· Основные задачи по решению треугольников:
– по двум сторонам и углу между ними;
– по стороне и двум углам;
– по трем сторонам;
– по двум сторонам и углу, противолежащему одной из них.
· Для прямоугольного треугольника достаточно знать два независимых элемента, так как один элемент известен: это угол, равный 90°.
· Теорема о сумме углов треугольника.
· Теорема Пифагора.
· Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника.
2. Решите устно.
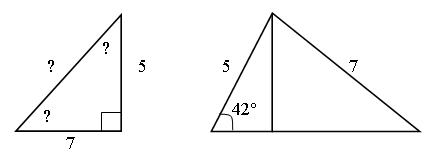
Итак, возникла проблема: мы не можем решить произвольный треугольник, не разделив его на прямоугольник. Почему?
Цель урока: дополнить наш багаж новыми сведениями, познакомить с теоремой косинусов и синусов.
Необходимо повторить:
· Понятие суммы (разности) векторов.
· Понятие скалярного произведения векторов.
· Понятие проекции наклонной проекции стороны треугольника на другую его сторону для различных углов между ними.
· Определение синуса, косинуса, острого угла прямоугольного треугольника.
· Основные тригонометрические тождества.
· Знак косинуса угла для острого и тупого углов.
III. Изучение нового материала.
1. Доказать теорему.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2. Изучить следствие.
Квадрат стороны треугольника равен сумме квадратов двух других сторон ± удвоенное произведение одной из них на проекцию другой. Знак «+» надо брать, когда противолежащий угол тупой, а знак «–», когда угол острый.
в2 = а2 + с2 – 2авс
с2 = а2 + в2 + 2асв
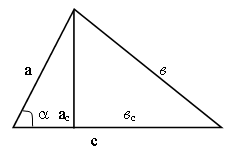
IV. Закрепление: решение задач.
Задача 1.
Стороны треугольника 5 м, 6 м, 7 м. Найдите косинусы углов треугольника.
Задача 2.
Стороны треугольника равны а, в, с.
Докажите, что если а2 + в2 > с2, то угол, противолежащий стороне с, острый.
Если а2 + в2 < с2, то угол, противолежащий стороне с, тупой.
Задача 3 (устно). При каких значениях угла a квадрат стороны треугольника, лежащей против этого угла: 1) меньше суммы квадратов двух других сторон; 2) равен сумме квадратов двух других сторон; 3) больше суммы квадратов двух других сторон?
Задача 4 (устно). Не вычисляя величины углов треугольника, укажите вид каждого из треугольников (относительно углов), если его стороны равны: 1) 7, 8, 12; 2) 8, 10, 12; 3) 3,3; 5,6; 6,5.
V. Итог урока.
Что значит решить треугольник?
Домашнее задание: п. 109, вопросы 1, 2; задачи 2, 7.
Урок 2
ТЕОРЕМА КОСИНУСОВ. РЕШЕНИЕ ЗАДАЧ
Цели: сформировать у учащихся умение применять теорему и следствие из нее в решении задач при нахождении углов треугольника по трем данным сторонам, нахождении третьей стороны по данным двум сторонам и углу между ними.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
1. Индивидуальная работа по карточкам, предназначенным для наиболее подготовленных учащихся.
Карточка 1.
Докажите теорему косинусов.
Карточка 2.
Докажите, что квадрат стороны треугольника равен сумме квадратов двух других сторон ± удвоенное произведение одной из этих сторон на проекцию другой.
Карточка 3.
Как изменятся стороны АВ треугольника АВС, если угол С возрастает, а длины сторон АС и ВС остаются без изменения?
2. Фронтальная беседа.
– Пользуясь формулой а2 = в2 + с2 – 2вс cos a, исследуйте, как изменяется сторона а при возрастании угла от 0° до 180° (при постоянных значениях в и с).
В результате решения этой задачи с учащимися повторяется зависимость косинуса угла от его величины: при возрастании угла от 0° до 90°, косинус угла при этом убывает.
– По таблицам Брадиса найдите косинусы некоторых углов: a = 57° 23΄; 131° 57΄, 32° 15΄.
3. Проверочная работа.
Вычислить неизвестную сторону треугольника АВС по следующим данным:
вариант I: а = 7, в = 10, g = 56° 29΄;
вариант II: а = 2, с = 3, u = 123° 17΄;
вариант III: в = 0,4 с = 1,2; a = 23° 28΄.
Ответ: 1) с » 8,5; 2) в » 4,4; 3) а » 0,8.
Проводится анализ допущенных ошибок: в формуле; при нахождении косинуса; при вычислении.
III. Решение задач.
1. Задача (ключевая).
Доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Доказательство:
|
по теореме косинусов
|
|
2. Задача 9 (из учебника).
Двое учащихся решают задачу у доски, остальные – в тетради.
Самостоятельно решаются задачи 4 (вариант I), 5 (вариант II), 6 (вариант III). Тетради сдаются на проверку учителю.
IV. Итог урока.
Выполняется ли теорема косинусов для прямоугольного треугольника?
Домашнее задание: п. 109, задачи 8, 10 (для наиболее подготовленных учащихся).
Задача. Найдите медианы треугольника, в котором стороны равны 5 м, 6 м, 7 м.
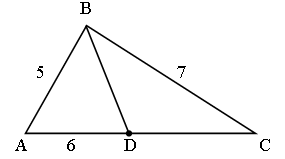
Решение:
1) Рассмотрим DАВС. По теореме косинусов ВС2 = АВ2 + АС2 – 2АВ · АС cos А;
72 = 52 + 62 – 2 · 5 · 6 сos A;
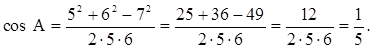
2) Рассмотрим DАВD,
в котором АВ = 5 м, АD = 3 м (так как ВД – медиана), соs А = ![]() .
.
ВD2 = АВ2 + АD2 – 2АВ · АD cos А;
ВD2 = 52 + 32 – 2 · 5
· 3 · ![]() =
25 + 9 – 6 = 28;
=
25 + 9 – 6 = 28;
ВD = ![]() (м).
(м).
Аналогично находятся остальные медианы.
Задача № 10.
Найти биссектрису треугольника, у которого стороны равны 5 м, 6 м, 7 м.
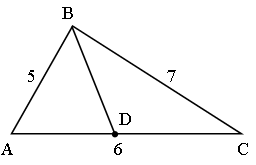
Решение:
1) По свойству биссектрисы угла треугольника ![]() 5
DС = 7 АD,
5
DС = 7 АD, ![]()
Так как AD + DC = AC, то AD + 1,4AD = 6, 2, 4AD = 6.
Значит, DС = 3,5 м, АD = 2,5 м.
2) соs А = ![]() .
.
ВD2 = АВ2 + АD2 – 2АВ · АD cos А;
ВD2 = 52 + 2,52 – 2 ·
5 · 2,5 · ![]() ;
;
ВD2= 25 + 6,25 – 5 = 26,25 = ![]() ;
;
ВD = 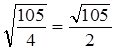 (м).
(м).
Аналогично находятся остальные биссектрисы.
Урок 3
ТЕОРЕМА СИНУСОВ
Цели: доказать теорему синусов, формировать умение применять ее при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
Повторить:
– Определение синуса острого угла прямоугольного треугольника.
– Формулы приведения.
– Определение окружности, вписанной в треугольник.
– Определение окружности, описанной около треугольника.
– Где лежит центр вписанной и описанной окружностей?
Все ответы должны сопровождаться рисунками.
III. Изучение нового материала.
Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство.
1-й случай.
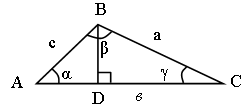
Угол a – острый.
1) Проведем высоту ВD и выразим ее из DАВD и DВDС, используя определение синуса острого угла прямоугольного треугольника.

Приравнивая (1) и (2), получим с sina
= a sin g
или 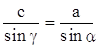 .
.
2) Если провести высоту АМ и проделать ту же операцию,
получим 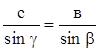 .
.
3) Объединив два равенства, получаем: 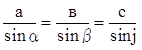 (теорема
синусов).
(теорема
синусов).
2-й случай.
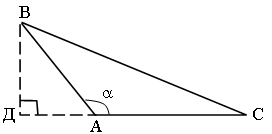
Угол a – тупой.
В этом случае ВD = АВ sin (180° – a) = АВ sin a.
Запись доказательства теоремы нужно сделать на доске и в тетради. Доказать теорему может учитель или хорошо подготовленный ученик.
IV. Закрепление изученного материала.
1. По данным рисункам найдите х.
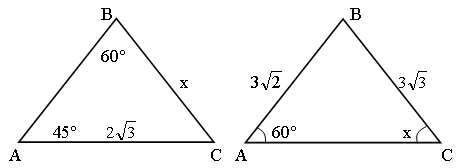
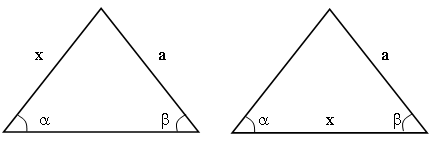
2. Вычислите стороны и углы треугольника, если а = 37, с = 59, g = 23° 20΄.
Ответ: α » 14° 23΄, b » 142° 17΄; в » 91,3.
V. Итог урока.
Назовите всю теоретическую базу, которую необходимо знать для решения треугольников.
Домашнее задание: п. 110. Вопросы 3, задача 12.
Дополнительные задачи:
1. В DАВС АВ = ВС = 8, АС = 4. Найдите косинус угла А.
2. В DВСD ВС = 6, ÐВ = 75°, ÐС = 45°. Найдите сторону ВD.
Урок 4
ТЕОРЕМА СИНУСОВ.
СООТНОШЕНИЕ МЕЖДУ УГЛАМИ ТРЕУГОЛЬНИКА
И ПРОТИВОЛЕЖАЩИМИ СТОРОНАМИ
Цели: познакомить учащихся со следствием из теоремы синусов, формировать навыки применения этих теорем при решении задач, показать практическое применение теоремы синусов.
Ход урока
I. Организационный момент.
II. Изучение нового материала.
Следствие из теоремы синусов.
В треугольнике против большого угла лежит большая сторона, против большей стороны лежит больший угол.
Прежде чем приступить к доказательству, нужно выяснить, что данное следствие содержит две теоремы: прямую и обратную; сформулировать прямую, обратную теоремы; какова зависимость между величиной угла и его синусом.
Прямая теорема.
В треугольнике против большего угла лежит большая сторона.
Дано: a > b.
Доказать: а > в.
Доказательство:
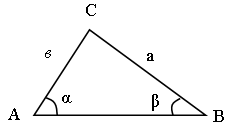
1) Пусть α, β – острые.
Если a > b, то sin a > sin b.
По теореме синусов
![]() , так как sin a > sin b, значит, а > в.
, так как sin a > sin b, значит, а > в.
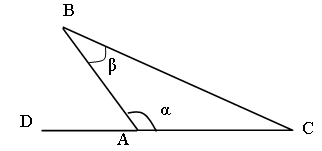
a – тупой.
Если a – тупой, то ÐDАВ = (180° – a) – острый.
Причем, ÐDАВ > Ðb, так как он внешний для DАВС.
sin a = sin (180° – a) > sin b.
Следовательно, ![]()
Обратная теорема. В треугольнике против большей стороны лежит больший угол.
Доказательство этой теоремы предлагается сделать дома. Предварительно нужно еще раз повторить метод доказательства от противного (см. урок 2).
III. Закрепление изученного материала.
1. Решить устно задачи 17, 18, 19, 20.
2. Решить письменно задачу 13 (ключевая задача).
3. Показать практическое применение теоремы синусов. Задача 15.
IV. Итог урока.
– Опишите алгоритм доказательства методом от противного.
– Как связаны между собой прямая и обратная теоремы?
– Как связаны стороны и углы треугольника с радиусом
описанной окружности? 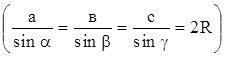
Домашнее задание: повторить п. 109, 110, 111; задачи 14, 16, 23; 25 – для более подготовленных учащихся.
Урок 5
ТЕОРЕМА КоСИНУСОВ. РЕШЕНИЕ ЗАДАЧ
Цели: проверить уровень усвоения учащимися теорем синусов и косинусов и умение использовать их при решении задач.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
Задача 14.
Как найти радиус окружности, описанной около треугольника, зная его стороны?
Найдите радиус окружности, описанной около треугольника со сторонами 5 м, 6 м, 7 м.
Решение:
1) ![]() (из
предыдущей ключевой задачи 13).
(из
предыдущей ключевой задачи 13).
а2 = в2 + с2 – 2вс
cos a;
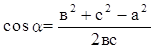 ,
sinα
=
,
sinα
=
![]() ;
;
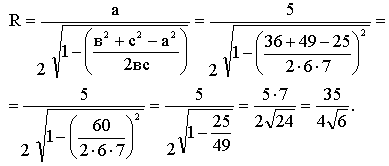
Ответ:
R = ![]() .
.
III. Решение (устно).
· Можно ли решить треугольник по трем углам? По трем сторонам?
· Верно ли, что теорема косинусов позволяет найти углы треугольника с данными сторонами?
· Определить, есть ли в треугольнике с данными сторонами тупой угол.
· Верно ли, что если для треугольника со сторонами а, в, с выполняется условие а2 > в2 + с2, то данный треугольник – тупоугольный? Если а2 < в2 + с2 – остроугольный?
· Из четырех перечисленных величин: стороны треугольника а, градусной меры противолежащего ей угла a, синуса этого угла sin a и диаметра d окружности, описанной около треугольника, – выберите две пары величин, между которыми существует прямая пропорциональная зависимость.
IV. Самостоятельная работа.
Вариант I.
1. Основание треугольника равно 10 см, один из углов при основании равен 45°, а угол, противолежащий основанию, равен 60°. Найдите сторону, лежащую против угла в 45°.
2. Докажите, что диагональ, соединяющая вершины тупых углов параллелограмма, меньшая.
3. Докажите, что биссектриса треугольника не больше его медианы, проведенной из той же вершины.
Вариант II.
1. Основание треугольника равно 10 см, один из углов при основании равен 45º, а угол, противолежащий основанию, равен 60º. Найдите сторону, лежащую против угла в 45º.
2. Докажите, что диагональ, соединяющая вершины острых углов параллелограмма, большая.
3. В треугольнике АВС проведена биссектриса ВD. Докажите, что если ВС > AB, то…
V. Итог урока.
Какие задания вызвали наибольшую трудность при решении задач?
Домашнее задание: п. 111, № 18, 19.
Урок 6
РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
Цели: повторить методы решения прямоугольных треугольников, познакомить учащихся с основными алгоритмами решения произвольных треугольников.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Рассмотреть типичные ошибки, показать правильное решение.
Учащимся, которые не справились с самостоятельной работой, предложить домашнюю самостоятельную работу.
III. Актуализация опорных знаний.
Составление тематической таблицы «Решение треугольников».
|
Решение треугольников |
|
|
1. Сумма углов треугольника равна 180°
|
a + b + j = 180° |
|
2. Сумма острых углов прямоугольного треугольника равна 90° |
a + b = 90° |
|
Теоремы косинусов а2 = в2 + с2 – 2вс cos a в2 = а2 + с2 – 2вс cos b с2 = в2 + а2 – 2aв cos g |
|
|
Следствие: а2 = в2 + с2 ± 2ввс и т. д. (вс – проекция на с) |
|
|
Теорема синусов
Следствие: против большего угла лежит и большая сторона, против большей стороны лежит и больший угол |
|
|
Ключевые задачи |
|
|
Сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон |
|
|
Докажите, что в теореме синусов каждое из трех соотношений:
где R – радиус окружности, описанной около треугольника |
|
IV. Изучение нового материала.
|
Основные задачи |
|
|
I тип – по стороне и двум углам
|
Дано: а, a, b. Найти: a, в, с. Решение: a = 180° – (a + b);
|
|
II тип – по двум сторонам и углу между ними |
Дано: а, в, j. Найти: a, b, с. Решение: с2 = в2 + а2 – 2aв cos j Þ
а2 = c2 + в2 – 2вс cos a Þ
в2 = а2 + с2 – 2ас cos b Þ
Угол b можно найти из равенства a + b + j = 180°
в2 = а2 + с2 – 2ас cos b Þ
Угол b можно найти из равенства a + b + j = 180° |
|
III тип – по трем сторонам |
Дано: а, в, с. Найти: a, b, j. Решение: a2 = в2 + c2 – 2вc cos a Þ
с2 = в2 + а2 – 2aв cos j Þ
в2 = а2 + с2 – 2ас cos b Þ
|
Рекомендации. При рассмотрении задач на решение треугольников полезно обратить внимание учащихся на то, что при вычислении углов треугольника предпочтительно использовать теорему косинусов, а не синусов. Поскольку синус угла равен синусу смежного с ним угла, то нахождение синуса угла еще не позволяет определить сам угол – он может быть острым или тупым. Если же вычислить косинус угла, то по его знаку и величине угол определяется однозначно.
V. Закрепление изученного материала.
Учащиеся самостоятельно решают задание № 26 (1), 27 (1), 29 (1), используя таблицу.
VI. Итог урока.
Любой ли треугольник сможем решить, если знаем только теорему косинусов? Только теорему синусов?
Домашнее задание: повторить теорию по таблице, задачи № 26 (2), 27 (2), 29 (2).
Теорема синусов и ее следствия
|
Вариант А-1 |
Вариант А-2 |
|
По данным рисунка найдите х. |
По данным рисунка найдите х. |
|
2. В треугольнике ABC ÐВ = 30°, ÐС = 25°. Укажите наибольшую сторону треугольника. Ответ объясните. |
2. В треугольнике ABC ÐА = 110°, ÐB = 55°. Укажите наименьшую сторону треугольника. Ответ объясните. |
|
3. Один из углов треугольника равен 30°, а диаметр окружности, описанной около треугольника, равен 14 см. Найдите сторону, противолежащую данному углу.
|
3. В треугольнике АВС ÐB = 45°, АС= Найдите диаметр окружности, описанной около окружности. |
|
Вариант Б-1 |
Вариант Б-2 |
|
По данным рисунка выразите АВ. |
По данным рисунка выразите АВ. |
|
2. Дан равнобедренный треугольник ABC с основанием АС. Известно, что АС – наименьшая сторона треугольника. В каких пределах может изменяться величина угла А? |
2. Дан равнобедренный треугольник ABC с основанием АС. Известно, что АВ = ВС = а и ÐB – наименьший угол треугольника. В каких пределах может изменяться длина основания АС? |
|
3. Радиус окружности, описанной около треугольника, равен одной из его сторон. Найдите угол треугольника, противолежащий данной стороне. Сколько решений имеет задача? |
3. Сторона треугольника
а и радиус описанной окружности R связаны соотношением а = R |
|
Вариант В-1 |
Вариант В-2 |
|
Дано: AD – биссектриса треугольника ABC; BD = a; ÐB = b; ÐBAD = a. Найти: DC. |
Дано: Aс = в; ÐА = a; ÐB = g. Найти: ВD. |
|
2. В параллелограмме ABCD точка М – середина стороны ВС. Известно, что ÐB – тупой. Сравните углы MAD и MDA. |
2. В параллелограмме ABCD точка М – середина стороны ВС. Известно, что ÐMDA > ÐMAD. Определите, какие из углов параллелограмма острые. |
|
3. Две стороны
треугольника равны 4 см и |
3. Две стороны
треугольника равны 4 см и |
Теорема косинусов.
соотношение диагоналей и сторон
параллелограмма
|
Вариант А-1 |
Вариант А-2 |
|
1. Две стороны треугольника равны 3 см и 8 см, а угол между ними равен 60°. Найдите периметр треугольника. |
1. Две стороны треугольника равны 3 см и 5 см, а угол между ними равен 120°. Найдите периметр треугольника. |
|
2. Стороны треугольника равны 3 см, 5 см и 7 см. Найдите угол треугольника, противолежащий стороне, равной 7 см. |
2. Стороны треугольника равны 3 см, 7 см и 8 см. Найдите угол треугольника, противолежащий стороне, равной 7 см. |
|
3. Стороны параллелограмма равны 7 см и 9 см, а диагонали относятся как 4 : 7. Найдите диагонали параллелограмма. |
3. Диагонали параллелограмма равны 7 см и 11 см, а стороны относятся как 6 : 7. Найдите стороны параллелограмма. |
|
Вариант Б-1 |
Вариант Б-2 |
|
1. На сторонах угла,
равного 45°, отмечены две точки, удаленные от вершины угла на 17 см и |
1. На сторонах угла,
равного 30°, отмечены две точки, удаленные от вершины угла на |
|
2. Две стороны треугольника равны 3 см и 7 см, а угол, противолежащий большей из них, равен 60°. а) Найдите третью сторону треугольника. б) Докажите, что угол, противолежащий третьей стороне, – острый. |
2. Две стороны треугольника равны 5 см и 7 см, а угол, противолежащий большей из них, равен 60°. а) Найдите третью сторону треугольника. б) Докажите, что угол, противолежащий третьей стороне, – острый. |
|
3. Диагонали параллелограмма равны 19 см и 23 см, а его периметр равен 58 см. Найдите стороны параллелограмма. |
Сумма диагоналей параллелограмма равна 22 см, а его стороны равны 7 см и 9 см. Найдите диагонали параллелограмма. |
|
Вариант В-1 |
Вариант В-2 |
|
1. Две стороны
треугольника равны 7 см и 8 см, а синус угла между ними равен |
1.
Две стороны треугольника равны 4 см и 8 см, а синус угла между ними равен |
|
2. Треугольник со сторонами 6 см, 10 см и 14 см вписан в окружность. Найдите центральный угол, соответствующий вписанному углу, образованному двумя меньшими сторонами треугольника. |
2. Треугольник со сторонами 6 см, 14 см и 16 см вписан в окружность. Найдите центральный угол, соответствующий вписанному углу, образованному наибольшей и наименьшей сторонами треугольника. |
|
3. Две стороны треугольника равны 7 см и 9 см. Медиана, проведенная к третьей стороне, на 1 см меньше этой стороны. Найдите периметр треугольника. |
3. Разность двух сторон треугольника равна 2 см, а медиана, проведенная к третьей стороне, – 4 см. Найдите периметр треугольника, если третья сторона равна 14 см. |
Урок 7
РЕШЕНИЕ задач
Цели: познакомить с IV типом задач на решение треугольников по двум сторонам и углу, противолежащему одной из сторон.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
Рассмотрим варианты решения задачи 29 (2) с применением теоремы косинусов и теоремы синусов.
Учитывая то, что sin α = sin (180° – a), а задача должна иметь единственное решение, должны помочь следующие факты:
· против большей стороны лежит больший угол;
· сумма углов равна 180°.
Возможны следующие случаи:
1) если сторона с наибольшая, то a и b – острые;
2) если сторона с наибольшая, то сначала находим тот из углов, который лежит против меньшей стороны и, следовательно, является острым. Третий угол находится из равенства a + b + j = 180°.
№ 29 (2).
Дано: а = 7, в = 2, с = 8.
Найти: a, b, j.
Решение:
с = 8, то a и b – острые;
а2 = в2 + с2 – 2в cos a Þ
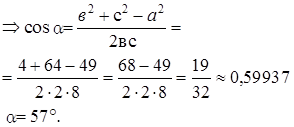 ;
;
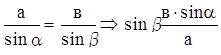 ;
;
b = 19°.
j = 180° – (a + b) = 102°.
Ответ: 57°, 13°, 102°.
III. Изучение нового материала.
IV тип задач: решение треугольника по двум сторонам и углу, противолежащему одной из сторон.
Дано: а = 12, в = 5, a = 120°.
Решение:
Если a = 120°, то углы b и j – острые.
sin 120° = sin (180° – 60°) = sin 60° = ![]() ;
;
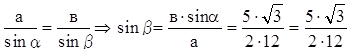 »
0,3541;
»
0,3541;
b » 21°.
j = 180° – (a + b) = 180° – 141° = 39°.
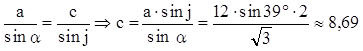 .
.
Ответ: b = 21°, j = 39°, c = 8,69.
№ 28 (4).
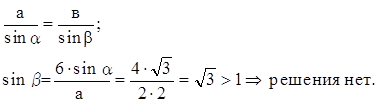
В общем виде задачи этого типа со всем классом не рассматриваются. Такое задание предлагается хорошо подготовленным учащимся в качестве домашнего задания.
IV. Закрепление изученного материала.
Вариант I: № 26 (3), 27 (3), 29 (3).
Вариант II: № 26 (4), 27 (4), 29 (4).
Вариант III: № 26 (5), 27 (5), 29 (5).
Домашнее задание: п. 112, задачи 28 (2, 5).
Урок 8
решение треугольников
Цели: провести промежуточный контроль знаний, умений и навыков учащихся с целью их корректировки и подготовки к контрольной работе.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
1. Индивидуальная работа.
Карточка 1.
Решить треугольник по стороне и двум углам (в общем виде).
Карточка 2.
Решить треугольник по трем сторонам.
Карточка 3.
Решить треугольник по двум сторонам и углу между ними.
Карточка 4 (для наиболее подготовленных учащихся).
Решить треугольник по двум сторонам и углу, противолежащему одной из них.
2. Фронтальная беседа, в ходе которой повторяются основные типы задач на решение треугольника и способы их решения.
III. Самостоятельная работа.
Вариант I.
1. Найдите синус и косинус наибольшего угла треугольника, стороны которого равны 40 см, 75 см и 105 см.
2. Найдите синусы и косинусы углов треугольника, две стороны которых равны 10 см и 8 см, а угол между ними 60°.
3. В треугольнике одна сторона равна 58 см, а косинус противолежащего ей угла равен 0,6. Другая сторона треугольника равна 50 см. Найдите третью сторону и косинус двух других углов.
Вариант II.
1. Найдите синус и косинус наименьшего угла треугольника, сторона которого равна 45 см, 70 см и 95 см.
2. В треугольнике две стороны равны 14 см и 16 см, а
косинус угла между ними ![]() . Найдите третью сторону
и синусы двух других углов.
. Найдите третью сторону
и синусы двух других углов.
3. В треугольнике одна
сторона равна 30 см, а косинус противолежащего ей угла равен ![]() .
Другая сторона треугольника равна 26 см. Найдите третью сторону и синусы всех
углов.
.
Другая сторона треугольника равна 26 см. Найдите третью сторону и синусы всех
углов.
Оформление решения задач.
Вариант I.
1. Дано: а = 40 см, в = 75 см, с = 105 см.
Найти: sin j, cos j.
Решение:
с = 105 см – наибольшая сторона, значит, j – наибольший угол,
c2 = а2 + в2 –
2авcosj Þ 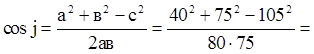
![]() .
.
Значит, угол j – тупой.
По таблицам Брадиса находится сразу угол и его синус.
g = 129º18; sin g ≈ 0,7738.
2. Дано: а = 10 см, в = 8 см, Ðg = 60º.
Найти: sin α, cos α, sin β, cos β.
Решение:
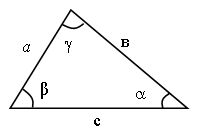
с2 = а2 + в2 – 2ав соs g;
с2 = 102 + 82 – 2 ·
10 · 8 · ![]() = 84, с ≈ 9 см.
= 84, с ≈ 9 см.
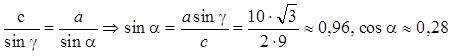 .
.
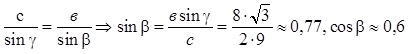 .
.
Ответ: sin a ≈ 0,96; cos a ≈ 0, 28; sin β ≈ 0,77, cos β ≈ 0,6.
3. Дано: АВ = 58 см, cos C = 0,6; ВС = 50 см.
Найти: АС, cos A, cоs B.
Решение:
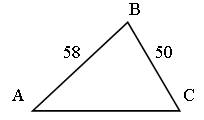
cos C = 0,6, ÐС – острый.
По таблицам Брадиса находим ÐС и его синус: ÐС = 53º12';
sin C = 0,8.
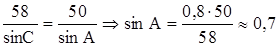 .
.
IV. Итог урока.
– Что значит решить треугольник?
– Какие возможны типы задач?
– Какие трудности возникли при решении задач?
Домашнее задание: обобщающий тест, с. 80.
Урок 9
РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
Цели: обобщить и систематизировать знания по теме, подготовиться к контрольной работе.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Анализ ошибок проводится по образцам решения. Выслушиваются выводы, где допущены ошибки: при использовании формул; при работе с таблицами Брадиса; при вычислении.
III. Решение задач.
Решение задач по готовым чертежам (по одной задаче на выбор из каждого типа):
I тип – по стороне и двум углам – № 3, 4, 5, 7.
II тип – по двум сторонам и углу между ними – № 1, 2.
III тип – по трем сторонам – № 9.
IV тип – по двум сторонам и углу, противолежащему одной из сторон – № 6, 10, 12.
Таблица 1
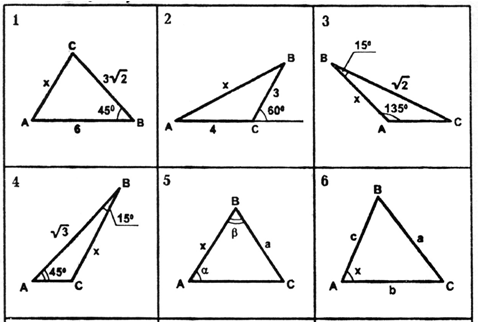
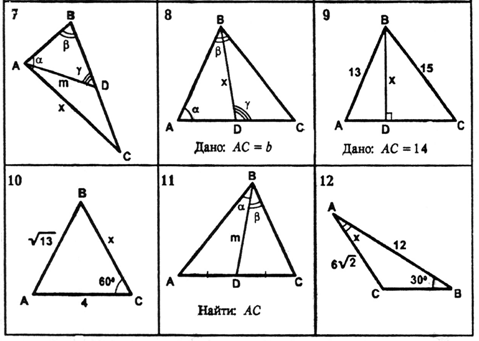
Ответ:
1. ![]() 2.
2.
![]() 3.
1; 4. х =
3.
1; 4. х = ![]() 5.
5. 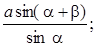
6. 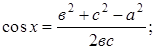 7.
7.
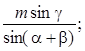 8.
8.
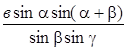 ;
;
9. 12; 10. 1 и 3; 11. 2m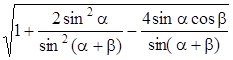 ;
;
12. 15º или 105º.
Для хорошо подготовленных учащихся таблица 2.
Таблица 2
Найти: х, y.
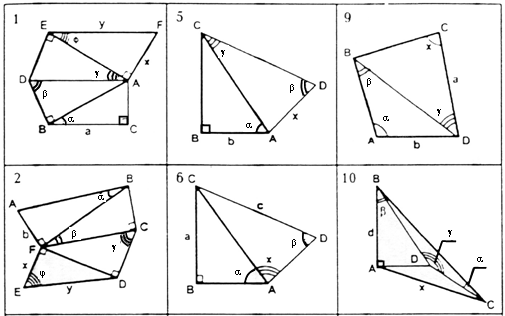
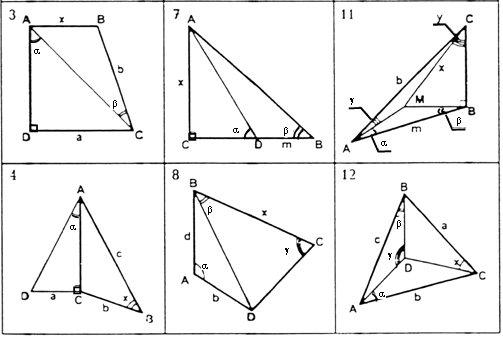
Ответ:
1. 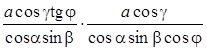 ;
2.
;
2. 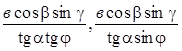 ;
;
3. ![]() ,
где
,
где ![]() ;
;
4. cosx = 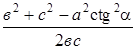 ;
5.
;
5. 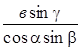 ;
6. sinx
;
6. sinx ![]() ;
;
7. 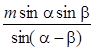 ;
;
8. x
= 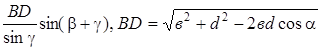 ;
;
9. sin
x = 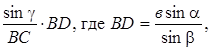
![]() ;
;
10. ![]()
![]() ;
;
11. x
= 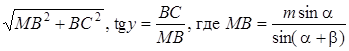 ,
,
![]() ;
;
12. cos
x = 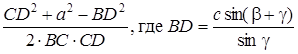 ,
,
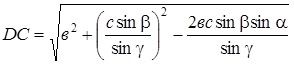 .
.
Домашнее задание: решить задачи.
1. Решите треугольник АВС, если ВС = ![]() см,
АС = 2 см, ÐС= 135°.
см,
АС = 2 см, ÐС= 135°.
2. Большая диагональ прямоугольной трапеции равна d и образует с меньшим основанием угол a. Острый угол трапеции равен b.
Найдите основания трапеции.
3. Средние линии треугольника АВС, вписанного в
окружность, равны 3 см, ![]() см и 6 см. Найдите углы
треугольника АВС и радиус окружности.
см и 6 см. Найдите углы
треугольника АВС и радиус окружности.
Урок 10
ТЕОРЕТИЧЕСКИЙ ЗАЧЕТ ПО ТЕМЕ
«РЕШЕНИЕ ТРЕУГОЛЬНИКОВ»
Цель: систематизировать и обобщить теоретические знания учащихся.
Ход урока
I. Организационный момент.
II. Работа в группах.
Карточка 1.
1. Докажите теорему косинусов.
2. Решите треугольник, если известны а, a, b.
Карточка 2.
1. Докажите, что квадрат стороны треугольника равен сумме квадратов двух других сторон ± удвоенное произведение одной из этих сторон на проекцию другой. От чего зависит «+» или «–»?
2. Решите треугольник, если известны две стороны и угол между ними.
Карточка 3.
1. Докажите, что в любом треугольнике против большей стороны лежит и больший угол и против большего угла лежит большая сторона.
2. Решите треугольник, если известны три стороны.
Карточка 4.
1. Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
2. Решите треугольник, если известны а, b, j.
Карточка 5.
1. Докажите, что в теореме синусов каждое из трех
соотношений 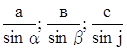 равны 2R, где R – радиус
окружности, описанной около треугольника.
равны 2R, где R – радиус
окружности, описанной около треугольника.
2. Как найти углы треугольника, если известны стороны?
III. Итог урока.
– Сформулирована ли база для решения треугольников?
– Обозначьте все необходимые теоретические положения.
– Какие вопросы возникли при выполнении домашней работы?
Домашнее задание: повторить теорию, используя тематические таблицы; решить задачи:
1) Решите треугольник АВС, если ÐА
= 45°, ÐВ
= 75°, АВ = ![]() см.
см.
2) Диагонали параллелограмма равны 12 см и 20 см, а угол между ними 60°. Найдите стороны параллелограмма.
3) В прямоугольном треугольнике один из углов равен a, а катет, прилежащий к данному углу, равен а. Выразите через а и a биссектрису прямого угла треугольника.
Урок 11
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
«РЕШЕНИЕ ТРЕУГОЛЬНИКОВ»
Цель: проверить уровень знаний, умений и навыков учащихся по теме.
Ход урока
I. Организационный момент.
II. Содержание контрольной работы.
Вариант I.
1. В треугольнике АВС сторона АВ равна 11 см, ÐВАС = 45°, ÐАСВ = 30°. Найдите сторону ВС.
2. Найдите сторону треугольника, лежащую против угла в
135°, если две другие стороны равны ![]() см
и 3 см.
см
и 3 см.
3. Докажите, что если точка К лежит на стороне СВ прямоугольного треугольника АВС (ÐС = 90°), то АК > АС.
4. Сторона параллелограмма равна ![]() см.
Найдите его углы, если диагональ, образующая с другой стороной угол в 30°,
равна 6 см.
см.
Найдите его углы, если диагональ, образующая с другой стороной угол в 30°,
равна 6 см.
5*. Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Вариант II.
1. В треугольнике GED сторона GF равна 13 см, ÐFDG = 45°, ÐDGF = 60°. Найдите сторону FD.
2. Найдите сторону треугольника, лежащую против угла в
150°, если две другие стороны равны ![]() и
7 см.
и
7 см.
3. Докажите, что если точка N лежит на стороне СВ равностороннего треугольника АВС (ÐС = 90°), то AN < AC.
4. Найдите углы равнобокой трапеции, в которой боковая
сторона равна ![]() см, а диагональ, равная 4
см, образует с основанием угол в 30°.
см, а диагональ, равная 4
см, образует с основанием угол в 30°.
5*. Диагональ параллелограмма делит один из его углов на два угла, равные 45° и 30°. Найдите отношение сторон параллелограмма.
Оформление решения задач.
Вариант I.
1. Дано: АВ = 11 см,
ÐА = 45°, ÐС = 30°.
Найти: ВС.
Решение:
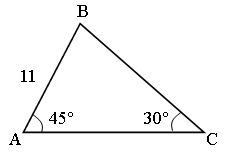
По теореме синусов
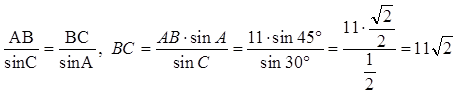 .
.
Ответ:
ВС = ![]()
2. Дано:
АВ = ![]() см,
см,
ВС = 3 см; ÐАВС = 135°.
Найти: АС.
Решение:
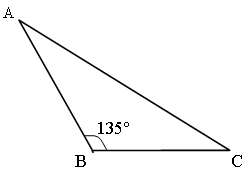
АС2 = АВ2 + ВС2 – 2АВ · ВС · сos B;
АС2
= ![]() 2
+ 32 – 2 ·
2
+ 32 – 2 · ![]() · 3 · сos
135° = 50 + 9 – 2 ·
· 3 · сos
135° = 50 + 9 – 2 · ![]()
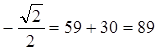 ;
;
сos 135°= cos (180° – 45°)
= cos 45° =![]() .
.
АС ≈ 9 см.
Ответ: АС = 9 см.
3. Дано: DАВС – прямоугольный, ÐС = 90°, К Î ВС.
Доказать: АК > АС.
Доказательство:
Рассмотрим DАКС, ÐС = 90°.
В треугольнике может быть только один прямой угол. Значит, он наибольший. Следовательно, АК > АС.
4. Дано:
АD = ![]() см,
ВD = 6 см, ÐАВD = 30°.
см,
ВD = 6 см, ÐАВD = 30°.
Найти: ÐА, ÐС, ÐВ, ÐD.
Решение:
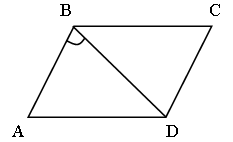
B ∆ABD
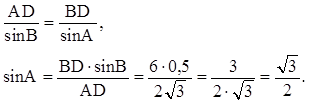
а) Если угол а – острый, то ÐА = 60°.
По свойству параллелограмма ÐС = ÐА = 60°,
ÐВ = ÐD = 120°.
б) Если угол а – тупой, то ÐА = 120°, ÐВ = 60°.
Ответ: 60°, 60°, 120°, 120°.
5*. Дано: АВСD – прямоугольник, ÐВАС : ÐСАD = 1 : 2.
Найти:
![]() .
.
Решение:
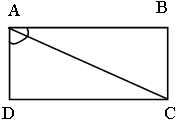
1) Пусть ÐВАС = αº, тогда ÐСАD = 2αº.
Так как АВСD – прямоугольник, то ÐА = 90º.
Значит, αº + 2αº = 90º, 3αº = 90º, α = 30º.
ÐВАС = 30º, ÐСАD = 60º.
2) Рассмотрим ∆ABС, в котором ÐВАС = 30º, ÐВСА = 60º.
По теореме синусов ![]()
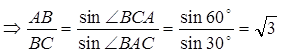 .
.
Ответ:
![]() .
.
Тема: МНОГОУГОЛЬНИКИ (13 часов)
Цель: расширить и систематизировать знания учащихся о многоугольнике и окружностях.
В результате изучения темы учащиеся должны
|
знать: – что длина ломаной не меньше длины отрезка, соединяющего ее концы; – сумма углов выпуклого n-угольника равна 180°(n – 2), а сумма внешних углов – 360°; – для каждого правильного многоугольника существует окружность, вписанная в него, и окружность, описанная около него; – существуют формулы, связывающие радиус описанной окружности и радиус вписанной окружности со стороной а правильного n-угольника для n = 3, n = 4, n = 6; –
периметры правильных n-угольников относятся как радиусы описанных (вписанных)
окружностей, |
уметь: – изображать ломаную, называть по рисунку ее элементы, проводить доказательство теоремы; – чертить многоугольник (выпуклый), строить его диагонали, внешние углы, уметь доказывать теорему о сумме углов выпуклого многоугольника; – выводить формулу
– применять формулу длины окружности для решения задач. |
ПЛАН-СЕТКА ПО ТЕМЕ
|
Ломаная, п. 113 |
Выпуклые многоугольники, п. 114 |
Правильные
многоугольники, |
Формула для радиусов вписанных и описанных окружностей, п. 116 |
|
Формула для радиусов вписанных и описанных окружностей; решение задач, п. 116 |
Формулы для радиусов
вписанных и описанных окружностей; решение задач, |
Построение правильных многоугольников, п. 117; практическая работа |
Подобие правильных выпуклых многоугольников, п. 118; тематическая таблица «Правильные многоугольники» |
|
Длина окружности;
радианная мера угла; п. 119– |
Длина окружности; радианная мера угла; решение задач, п. 119–120; самостоятельная работа |
Длина окружности;
радианная мера угла; п. 119– |
Урок-зачет |
|
|
Контрольная работа |
|
|
Урок 1
ЛОМАНАЯ
Цели: подготовить учащихся к введению понятия многоугольник, сформировать умение изображать ломаную, называть по рисунку ее элементы, выработать понимание того, что длина ломаной не меньше длины отрезка, соединяющего его концы.
Ход урока
I. Организационный момент.
Сообщается тема и цель всего блока уроков и данного урока.
II. Изучение нового материала.
1. Ввести понятия: ломаная; элементы ломаной (вершины, звенья); простая ломаная (незамкнутая); длина ломаной.
2. Доказать теорему.Длина ломаной не меньше длины отрезка, соединяющего его концы.
III. Закрепление изученного материала.
1. Решить устно задачу.
У ломаной АВСD АВ = 3 см, ВС = 4 см, СD = 2 см. Может ли длина отрезка АD быть равной:
а) 10 см; б) 7 см; в) 9 см?
2. Решить задачи 3, 4, 5, 6 (устно).
3. Разобрать или решить самостоятельно задачу 1.
IV. Итоги урока.
· Сформулируйте теорему о длине ломаной.
· Какая теорема использовалась при ее доказательстве?
В любом треугольнике каждая сторона меньше суммы двух других сторон.
(Неравенство треугольника.)
Домашнее задание: п. 13; вопросы 1, 2; задачи 2, 7.
Урок 2
ВЫПУКЛЫЕ МНОГОУГОЛЬНИКИ
Цели: ввести понятие выпуклый многоугольник, сформировать умения изображать его и называть все его элементы, доказывать теорему о сумме углов выпуклого многоугольника.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Решить устно задачи по чертежам.
а) Найти: длину ломаной АВСDОМ, где А, В, С, D – вершины квадрата со стороной 2 см, О – точка пересечения его диагоналей, М – середина стороны АD.
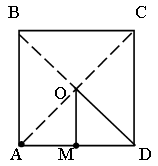
Ответ:
![]() .
.
б) Какая из трех ломаных АВСDМН (1), АВСЕМН (2), АКNН (3) имеет наименьшую длину, какая – наибольшую? Ответ обосновать.
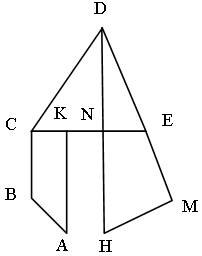
Ответ: АКNH – наименьшая длина; ABCDMN – наибольшая длина.
III. Изучение новой темы.
1. Постройте:
1) простую ломаную линию;
2) простую замкнутую ломаную.
На какие группы их можно разбить?
|
I группа Соседние вершины лежат на одной прямой. |
II группа Соседние вершины не лежат на одной прямой. |

Многоугольники
I группа II группа
|
Лежат в разных полуплоскостях относительно прямой, содержащей сторону. Невыпуклые. |
Лежат в одной полуплоскости относительно любой прямой, содержащей сторону. Выпуклые. |
2. Учащиеся дают определения многоугольника; плоского многоугольника; выпуклого многоугольника; называют виды известных выпуклых многоугольников (квадрат, параллелограмм, ромб, прямоугольник, трапеция).
3. Формулировка и доказательство теоремы о сумме углов выпуклого n-угольника.
Сумма углов выпуклого n-угольника равна 180° (n-2).
Вопросы:
– На сколько треугольников можно разбить любой выпуклый n-угольник?
– Чему равна сумма углов треугольника?
4. Введение понятий «внешний угол выпуклого многоугольника, вписанные и описанные многоугольники».
IV. Закрепление изученного материала.
1. Устно решить задачи.
1) Может ли пятиугольник иметь стороны длиной 3 см, 4 см, 6 см, 8 см, 25 см?
2) Вычислите сумму углов выпуклого: а) пятиугольника; б) девятиугольника.
2. Письменно решить задачи 9 (самостоятельно), 11.
Задача 11 (ключевая).
Докажите, что у четырехугольника, описанного около окружности, суммы длин противоположных сторон равны.
Дано: DАВСD – описанный четырехугольник.
Доказать:
АВ + DС = АD + ВС.
Доказательство:
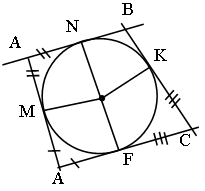
1) АВ, ВС, DС, АD – касательные,
N, K, F, M – точки касания.
AN = АМ, NB = BK, КС = FC, DF = MD – отрезки касательных, проведенные из одной точки.
2) АВ + DС = AN + NB + FC + DF = AM + BK + KC + МD = АD + ВС,
АВ + DС = АD + ВС, что и требовалось доказать.
V. Итог урока.
· В чем отличие выпуклого многоугольника от невыпуклого ?
· Чему равна сумма углов многоугольника?
Домашнее задание: п. 114; вопросы 3–7; задачи 8, 10.
Урок 3
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Цели: сформулировать понятие правильные многоугольники, многоугольник, вписанный в окружность и описанный около окружности.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
Какие из фигур являются многоугольниками?
Что называется многоугольником?
Что такое плоский многоугольник?
Какие из многоугольников, изображенных на рисунке, являются выпуклыми? Обозначьте вершины одного из выпуклых многоугольников буквами и назовите его углы.
Что такое угол выпуклого многоугольника при данной вершине?
Что такое внешний угол выпуклого многоугольника?
3. Начертите выпуклый восьмиугольник и проведите в нем все диагонали из какой-нибудь вершины. Сколько при этом образовалось треугольников? Найдите сумму углов восьмиугольника.
Чему равна сумма углов многоугольника?
Назовите выпуклый четырехугольник, у которого все внешние углы прямые.
Сколько сторон имеет выпуклый многоугольник, если сумма его внутренних углов равна сумме внешних?
Сколько сторон имеет выпуклый многоугольник, если его внешние углы тупые?
III. Изучение нового материала.
1. Повторение.
Какой треугольник называется равносторонним?
Какой треугольник называется вписанным в окружность?
Какой треугольник называется описанным около окружности?
Какой многоугольник называется правильным?
Какой многоугольник называется описанным около окружности? (Ответы сопровождаются рисунками.)
· Можно ли вписать в окружность треугольник и описать около окружности треугольник?
· Где находится центр вписанной и описанной около равностороннего треугольника окружности?
· Что называется окружностью?
2. Формулировка и доказательство теоремы.
Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.
Вывод. Точка О – равноудалена от вершин А, В, С, D…, так как АО = ОВ = ОС = ОD = … (стороны равных равнобедренных треугольников). Значит, О – центр описанной окружности. Точка O равноудалена от Н, Н1, Н2 … Нn, так как ОН = ОН1 = ОН2 = … ОНn. (Высоты равных треугольников.)
Значит, О – центр вписанной окружности.
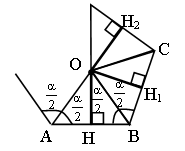
Правила нахождения для заданного правильного многоугольника общего центра описанной и вписанной окружностей.
1. Центром окружности, описанной около правильного многоугольника, является точка пересечения серединных перпендикуляров к сторонам многоугольника.
Радиусом является отрезок биссектрисы угла многоугольника, соединяющий его вершину с центром.
2. Центром окружности, вписанной в многоугольник, является точка пересечения биссектрис двух соседних углов. Радиусом является перпендикуляр, опущенный из этой точки на соответствующую сторону многоугольника.
3. Практическая работа.
Вариант I. Начертить правильный треугольник, построить окружность, вписанную в этот треугольник (описанную около этого треугольника).
Вариант II. Начертить квадрат, построить окружность, описанную около квадрата (вписанную в этот квадрат.)
III. Закрепление изученного материала.
1. Решение задач 12 (2), 13 (2), 14 (самостоятельно).
Задача 14.
Докажите, что взятые через одну вершины правильного 2n-угольника являются вершинами правильного n-угольника.
Доказательство.
1) DАА1А2 = DА2А3А4 = DА4А5А6 = …DАn – 2Аn –1Аn по двум сторонам и углу между ними.
Значит, АА2 = А2А4 = А4А6 = … = Аn–2An.
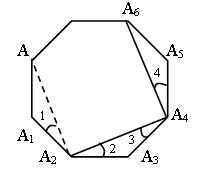
Ð1 = Ð2 = Ð3 = Ð4 = …
ÐА = ÐА2 = ÐА4 = … , Ð1 = Ð2 = Ð3 = Ð4 … , так как углы полученного многоугольника равны. Следовательно, многоугольник АА2А4А6А2n – 2 – правильный.
2. Самостоятельная работа.
– Найдите сумму углов выпуклого а) пятиугольника; б) шестиугольника; в) десятиугольника.
– Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен: а) 90°; б) 60°; в) 120°; г) 108°?
IV. Итог урока.
Домашнее задание. п. 115, вопросы 8, 9. Задачи 12 (1), 13 (1), 15.
Дополнительные задачи.
1. На рисунке изображен квадрат, вписанный в окружность радиуса R.
Заполните пустые клетки в таблице (а4 – сторона квадрата, r – радиус вписанной окружности, Р – периметр).
|
N |
R |
r |
a4 |
P |
|
1 |
|
|
6 |
|
|
2 |
|
2 |
|
|
|
3 |
4 |
|
|
|
|
4 |
|
|
|
28 |
2. На рисунке изображен правильный треугольник, вписанный в окружность радиуса R.
Заполните пустые клетки в таблице (а3 – сторона треугольника, Р – периметр треугольника, r – радиус вписанной окружности).
|
N |
R |
r |
a3 |
P |
|
1 |
3 |
|
|
|
|
2 |
|
2 |
|
|
|
3 |
|
|
5 |
|
|
4 |
|
|
|
6 |
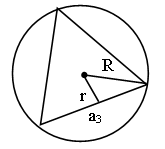
Урок 4
ФОРМУЛЫ ДЛЯ РАДИУСОВ ВПИСАННЫХ
И ОПИСАННЫХ ОКРУЖНОСТЕЙ
Цели: ввести формулы, связывающие радиусы вписанной и описанной окружностей, формировать умение применять полученные знания при решении задач.
Ход урока
I. Организационный момент.
II. Изучение нового материала.
1. задача.
Дано: n – число сторон правильного многоугольника, an – сторона. Выразить R и r через аn и n.
Решение:
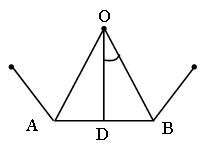
1) Рассмотрим DАОВ, АО = ОВ = R, ОD = r, ОD – биссектриса и медиана равнобедренного треугольника.
![]()
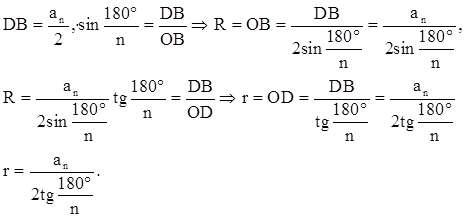
2. Повторение.
1) Свойство биссектрисы равнобедренного треугольника.
2) Определение синуса и тангенса острого угла прямоугольного треугольника.
3. Найти: R и r, при n = 3 (правильный треугольник).
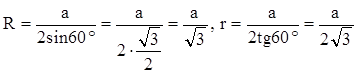 .
.
n = 4 (правильный четырехугольник);
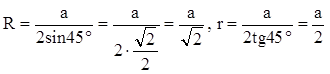 .
.
n = 6.
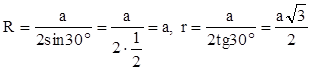 .
.
4. Задача 16. Выразить сторону правильного многоугольника через R и r.
Учащиеся самостоятельно могут получить формулы:
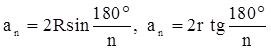 ,
,
при n = 3;
аn = 2Rsin 60° = 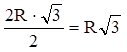 а3
= 2rtg 60° = 2
а3
= 2rtg 60° = 2![]() r,
r,
при n = 4;
а4 = 2Rsin 45° =  а4
= 2r tg 45° = 2r,
а4
= 2r tg 45° = 2r,
при n = 6;
а6 = 2Rsin 30° = R,
а6 = 2rtg 30° = ![]() .
.
Выведенные формулы можно проиллюстрировать рисунками.
III. Закрепление изученного материала.
Решение задач по готовым чертежам.
Правильные многоугольники
а – сторона многоугольника, R (r) – радиус описанной (вписанной) окружности, О – центр многоугольника.
Найти количество сторон многоугольника.
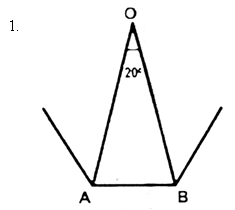
Ответ: n = 18.
Зная один из элементов (а, R или r), найти два других.
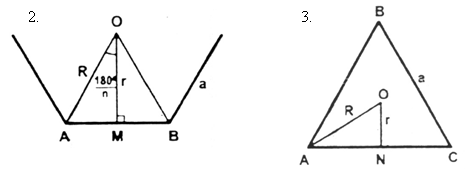
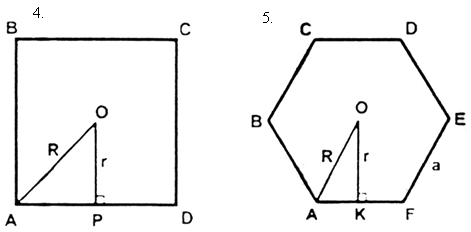
Решение (№ 2).
а) Дано: а.
Найти: R, r.
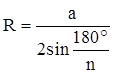 ,
, 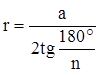 .
.
б)Дано: R.
Найти: а, r.
![]()
в) Дано: r.
Найти: а, R.
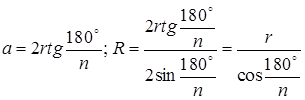
IV. Итог урока.
– Какие правильные многоугольники уже рассматривались в курсе геометрии?
– Приведите пример такого выпуклого многоугольника, у которых все стороны равны, но он не является правильным.
– Назовите выпуклый многоугольник, у которого все внешние углы прямые.
Домашнее задание: подготовить тематическую таблицу «Правильный многоугольник»; п. 116, вопросы 10, 12; задачи 18, 26.
Урок 5
РЕШЕНИЕ ЗАДАЧ
Цель: формировать навык применения полученных знаний при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний
1. Индивидуальная работа.
Карточка 1.
Выведите формулы для радиусов вписанной и описанной окружности правильного n-угольника.
Карточка 2.
Найдите радиусы вписанной и описанной окружностей для правильного треугольника, четырехугольника, шестиугольника. Сделайте рисунок.
Карточка 3.
Найдите выражение для стороны аn правильного n-угольника через радиус R описанной около него окружности и радиус r вписанной окружности. Вычислите аn при n = 3, 4, 6.
2. Фронтальная работа по таблице «Правильные многоугольники».
Правильные многоугольники
Выпуклый многоугольник называется правильным, если у него все углы и стороны равны. Существуют правильные многоугольники с любым числом сторон n, где n ³ 3. Правильный n-угольник имеет одни и те же углы,
![]()
![]() .
.
Вокруг всякого правильного n-угольника можно описать окружность. Центр окружности – точка пересечения биссектрис углов.
В каждый правильный многоугольник можно описать окружность. Центр окружности – точка пересечения биссектрис углов.
Вписанная и описанная окружности правильного многоугольника имеют общий центр. Он называется центром данного правильного многоугольника.
|
Число сторон многоугольника, n |
Выражение стороны
правильного |
|
|
R |
r |
|
|
3 |
|
|
|
4 |
|
a4 = 2 r |
|
6 |
a6 = R |
|
|
n |
an
= 2Rsin |
an
= 2r tg |
C помощью таблицы можно увидеть решение задач 18, 26.
III. Решение задач.
1. Решение задач по готовым чертежам.
Найти количество сторон.
|
1) 180°n – 360° = 150°n. 30°n = 360°. n = 12. |
|
|
2) a = 140°.
180°n – 360° = 140°n. 40°n = 360°. n = 9. |
|
|
3) a + 2a + 2a = 180°. 5a = 180°. a = 36°.
n = 10. |
|
|
4) |
Дано: а |
|
|
|
R |
|
||
|
r |
|
2. Решение задач.
№ 17.
Сторона правильного вписанного треугольника ![]() .
.
Рассмотрим DАОВ – равнобедренный, ОD
– высота, а значит, медиана АD = DВ, АО = R, ОD = ![]() (по
условию).
(по
условию).
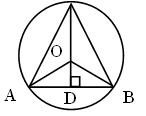
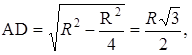
АВ = R![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
№ 19.
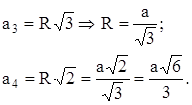
№ 20.
Дано: окр. (О, R1), R1 = 4 дм,
∆АВС – вписанный, правильный.
BCMN – квадрат.
Найти: О, В = R2.
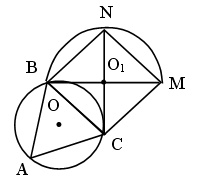
![]() .
.
![]() – сторона квадрата.
– сторона квадрата.
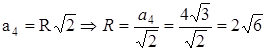 .
.
IV. Итог урока.
Тест «Правильные многоугольники»
В каждой строке таблицы необходимо поставить один или несколько знаков «+», указывающих, при каких значениях n правильные n-угольники обладают описанным свойством.
(1) n = 3,
(2) n = 4,
(3) n = 6.
|
Т-13 |
Свойство |
(1) |
(2) |
(3) |
|
1 |
2 |
3 |
4 |
5 |
|
Образец |
В таком правильном n-угольнике внешние углы – не острые |
+ |
+ |
|
|
Вариант I |
1. В таком правильном n-угольнике все углы – тупые |
|
|
|
Окончание табл.
|
1 |
2 |
3 |
4 |
5 |
|
|
2. В таком правильном n-угольнике радиус вписанной окружности равен половине стороны |
|
|
|
|
3. В таком правильном n-угольнике радиус вписанной окружности вдвое больше радиуса вписанной окружности |
|
|
|
|
|
4. В таком правильном n-угольнике количество осей симметрии меньше пяти |
|
|
|
|
|
5. В таком правильном n-угольнике радиус описанной окружности равен половине диагонали |
|
|
|
|
|
Вариант II |
1. В таком правильном n-угольнике все углы – острые |
|
|
|
|
2. В таком правильном n-угольнике радиус описанной окружности равен стороне |
|
|
|
|
|
3. В таком правильном n-угольнике радиус вписанной окружности в восемь раз меньше периметра |
|
|
|
|
|
4. В таком правильном n-угольнике есть центр симметрии |
|
|
|
|
|
5. Такой правильный n-угольник можно осью симметрии разделить на два треугольника |
|
|
|
Ответы:
|
Т-13 |
№ |
(1) |
(2) |
(3) |
|
Вариант I |
1 |
|
|
+ |
|
2 |
|
+ |
|
|
|
3 |
+ |
|
|
|
|
4 |
+ |
+ |
|
|
|
5 |
|
+ |
+ |
|
|
Вариант II |
1 |
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
Домашнее задание: п. 116, задачи 21, 22.
Урок 6
РЕШЕНИЕ ЗАДАЧ
Цель: закрепить знания в ходе решения задач.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
Задача № 21.
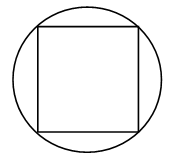
Наибольший размер будет иметь сторона квадрата, вписанного в данную окружность, R = 2 cм.
а4 = R![]() см.
см.
Задача № 22.
Сечение конуса винта имеет наибольший размер, если оно представляет собой правильный треугольник, вписанный в окружность заданного радиуса R = 1 cм.
а3 = R![]() см.
см.
III. Решение задач № 26, 27, 28.
IV. Самостоятельная работа.
Вариант I.
1. Дана ломаная А1А2А3А4, у которой звенья А1А2 = 3 см, А2А3 = 4 см и А3А4 = 2 см. Может ли длина отрезка A1A4 быть равной 10 см?
2. Сумма углов выпуклого многоугольника в 2 раза меньше суммы внешних углов, взятых по одному при каждой вершине. Найдите число сторон этого многоугольника.
3. Расстояния от точки А до точек В и С равны 3 см и 7 см соответственно, а расстояния от точки D до точек В и С равны 11 см и 1 см соответственно. Докажите, что точки А, В, С и D лежат на одной прямой.
Вариант II.
1. Точки А1, А2, А3 и А4 – вершины равнобокой трапеции, одно из оснований которой равно 8 см, а боковая сторона – 12 см. Может ли длина второго основания быть равной 36 см?
2. Сумма углов выпуклого многоугольника равна сумме его внешних углов, взятых по одному при каждой вершине. Найдите число сторон этого многоугольника.
3. Докажите, что в выпуклом четырехугольнике биссектрисы двух углов, прилежащих к одной стороне, образуют угол, равный полусумме двух других углов четырехугольника.
V. Итог урока.
– Какие задания вызвали затруднения при решении?
Домашнее задание: п. 116, № 29, 25 (наиболее подготовленным учащимся).
Урок 7
ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Цель: сформировать умение строить некоторые правильные многоугольники.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Рассматриваются типичные ошибки, показывается правильное решение.
III. Изучение нового материала.
– Какую задачу на построение комбинации окружности и многоугольника мы умеем решать? Какой будет задача, обратная этой?
Задача. Дана окружность, построить вписанный или описанный правильный многоугольник.
Указание. Для построения правильных n-угольников обычно используется окружность, описанная около этого многоугольника. Решение этой задачи дает нам способ построения правильных многоугольников.
Анализ.
– Как найти вершины многоугольника?
Достаточно найти величину центрального угла: ![]()
(Для этого разделить окружность на n равных частей.)
Алгоритм построения правильного n-угольника
1) Найдите центральный угол: ![]()
2) Постройте полученный центральный угол.
3) Разделите окружность на части, равные величине дуги, соответствующей этому центральному углу.
4) Соедините полученные точки отрезками: получаем правильный n-угольник.
|
Вариант I |
Вариант II |
Вариант III |
|
Построить правильный треугольник |
Построить правильный четырехугольник |
Построить правильный шестиугольник |
Если имеем только циркуль и линейку, как построить правильный шестиугольник?
Можно ли не использовать транспортир при построении?
Как построить восьмиугольник?
Как получить правильный треугольник? Ответ обосновать.
Чтобы из n-угольника получить правильный 2n-угольник, необходимо провести серединные перпендикуляры. Точки пересечения этих перпендикуляров с окружностью – это вершины … 2n-угольника.
– Как вы думаете, любой ли многоугольник можно построить таким образом с помощью циркуля и линейки?
Ответ на этот вопрос мы получим, познакомившись с исторической справкой.
– Как построить описанный многоугольник?
Вывод: для построения правильного описанного многоугольника достаточно провести касательные к окружности в вершинах правильного вписанного многоугольника.
IV. Самостоятельная работа.
Задача.
Построить правильный многоугольник.
|
Вариант I |
Вариант II |
|
четырехугольник |
шестиугольник |
V. Итог урока.
1) Что может помочь построить правильный выпуклый многоугольник?
2) Сформулируйте алгоритм построения правильных n-угольников с использованием окружности.
Дополнительный материал.
Деление окружности
на пять и десять равных частей
с помощью циркуля
1. Проводим окружность О радиусом R и делим ее циркулем на шесть равных частей. Получаем точки 1, 2, 3, 4, 5, 6 (рис. 1).
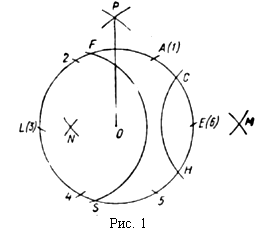
2. Из точек 3 и 6,
как из центров, проводим дуги окружностей радиусом R1, – R![]() до пересечения их
в точке R1, OP – a4 – R
до пересечения их
в точке R1, OP – a4 – R![]() .
.
3. Из точек 1 и 5
окружности О, как из центров, проводим дуги окружности радиусом R2 –
R![]() до их пересечения
в точках М и N.
до их пересечения
в точках М и N.
4. а) Из М, как из центра, проводим дугу окружности радиусом R до пересечения ее с данной окружностью О в точках С и Н;
б) из N, как из центра, проводим дугу окружности радиусом R до пересечения ее с данной окружностью О в точках F и S.
Обозначим точки 1, 3, 6 окружности О через А, L, E соответственно. Тогда дуга СЕ равна дуге ЕН и равна 1/10 окружности О, а дуга СН равна 1/5 окружности О; дуга LF равна дуге LS и равна 1/5 окружности О, а ON – а10.
Доказательство.
1) Для точки М.
Делаем дополнительное построение: проведем LM, AO, CO, AM, CM, CE, AB ^ LM, CH ^ LM (рис. 2).
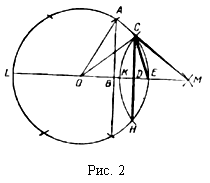
а) Из прямоугольного треугольника АВМ
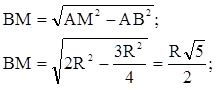
б) ОМ = ОВ + ВМ; ОМ = 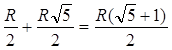 ;
;
в) ОD = DM = ![]() OM;
OD = DM =
OM;
OD = DM = 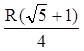 ;
;
г) DM + DK = R; DK = R – 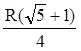 =
=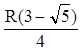 ;
;
DK = DE = 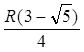 ;
;
д) из прямоугольного треугольника ОСD
CD = ![]() ;
;
CD = 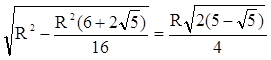 ;
;
e) CH = 2CD = 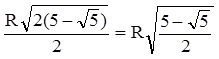 ;
;
ж) из прямоугольного треугольника CDE
CE = ![]() ;
;
CE = 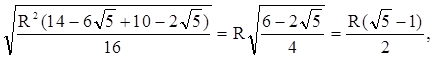
следовательно, СЕ = а10.
2) Для точки N.
Дополнительное построение: проведем LE, FL, NF, AN, OF, FD ^ LE, AB ^ LE (рис. 3).
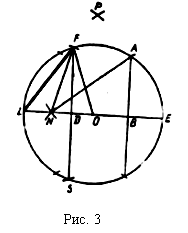
а) Из прямоугольного треугольника ANB
![]() ;
;
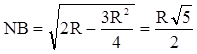 ;
;
б)
ON = NB – OB; ON = 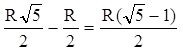 ;
;
следовательно, ON = a10.
в)
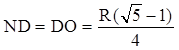 ;
;
г)
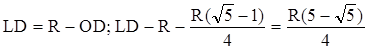 ;
;
д) из прямоугольного треугольника NDF
![]() ;
;
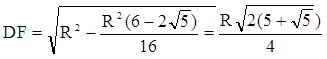 ;
;
е) Из прямоугольного треугольника LFD
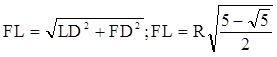 ,
,
следовательно, FL = a5.
Домашнее задание: п. 117, задачи 30, 31 (8-угольник).
Урок 8
подобие ПРАВИЛЬНЫХ
выпуклых МНОГОУГОЛЬНИКОВ
Цели: доказать теорему о подобии правильных выпуклых n-угольников, свойство о том, что отношение периметров правильных n-угольников равно отношению радиусов вписанных (описанных) окружностей.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
· Какое преобразование фигуры называется движением?
· Какими свойствами обладает движение?
· Что такое преобразования подобия?
· Что такое гомотетия?
· Какие фигуры называются равными?
· Какие фигуры называются подобными?
III. Изучение нового материала.
Докажем теорему.
Правильные выпуклые n-угольники подобны (I ч). В частности, если у них стороны одинаковы, то они равны (II ч).
Дано:
Р1: А1А2А3…Аn
Р2: В1В2В3…Вn – правильные n-угольники.
А1А2 = В1В2 = …
Доказать: Р1 = Р2
Доказательство:
Две фигуры называются равными, если они движением переводятся одна в другую. Следовательно, нужно доказать, что эти многоугольники совмещаются движением.
DА1А2А3 = DВ1В2В3 по первому признаку (А1А2 = В1В2, А2А3 = В2В3, ÐА1А2А3 = ÐВ1В2В3). Значит, существует движение, при котором А1 ® В1, А2 ® В2, А3 ® В3.
Подвергнем Р1 движению: А1 ® В1, А2 ® В2, А3 ® В3, А4 ® С.
Точки С и В4 лежат по одну сторону от прямой В2В3.
Движение сохраняет углы и расстояние: ÐВ2В3С = ÐВ2В3В4 и В3С = В3В4. А значит, точка С совпадает с В4 и т. д.
А4 ® В4, А5 ® В5 … Аn ® Вn.
То есть Р1 ® Р2 при движении, следовательно, Р1 = Р2.
I часть. Докажем, что Р1 ® Р2.
Подвергнем Р1 преобразованию подобия:
гомотетии с коэффициентом k = 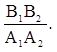
Р1 ® Р¢ (стороны Р¢ равны сторонам Р2).
Значит, Р¢ ® Р2 ( в результате движения).
Р1 ® Р´, Р´ ® Р2. Следовательно, Р1 ® Р2 и т. д.
У подобных фигур
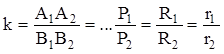 , где P1, P2
– периметры, R1, R2, r1, r2 –
радиусы.
, где P1, P2
– периметры, R1, R2, r1, r2 –
радиусы.
IV. Закрепление изученного материала.
Решение задач 33, 32.
Задача 1. Сторона одного квадрата в 3 раза больше стороны другого квадрата. Как относятся радиусы окружностей, описанных около них и вписанных в них? Ответ объясните.
Ответ: 3 : 1.
Задача 2. Дан равносторонний треугольник. Как относятся радиусы окружностей, вписанных в данный треугольник, и треугольник, вершинами которого является середина сторон данного равностороннего треугольника?
Ответ: 2 : 1.
V. Итог урока.
Что нового мы можем добавить в тематическую таблицу «Правильные многоугольники»?
Домашнее задание: п. 118. Вопрос 13.
Задача 1. Дан квадрат, докажите, что середины его сторон являются вершинами другого квадрата. Как относятся радиусы окружностей, вписанных в эти квадраты и описанных около них?
Задача 2. Найдите радиусы
окружностей, вписанной в квадрат и описанной около него, если их произведение
равно ![]() см2.
см2.
Задача 3. Центральные углы двух правильных многоугольников отличаются на 20°, а суммы внутренних углов этих многоугольников отличаются на 540°. Найдите количество сторон каждого многоугольника.
Урок 9
длина окружности. радианная мера угла
Цели: вывести формулу длины окружности, длины дуги, сформировать умение применять эту формулу при решении задач, дать понятие радианной меры.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
Учитель должен четко понимать, что вывод формулы длины окружностей основан на интуитивном представлении о пределе: при неограниченном увеличении числа сторон правильного многоугольника, вписанного в окружность, его периметр стремится к длине окружности.
Для формирования этого понятия необходимо:
– построить вписанные в окружность правильные n-угольники: n = 3, 4, 6, 12, 24;
– проиллюстрировать длину окружности с использованием нити, сложенной в виде окружности.
– Как измерить длину окружности?
– Какой величиной характеризуется окружность?
– Значит, и длина окружности должна характеризоваться длиной радиуса. Чем больше радиус, тем больше длина окружности.
Теорема. Отношение длины
окружности к ее диаметру не зависит от окружности для любых двух окружностей: 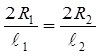 .
.
Доказательство.
– Вспомните, в чем заключаются способы доказательства методом от противного. (Можно обратиться к памятке.)
Итак, нам нужно доказать, что
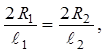 где R1, R2
– радиусы; ℓ1, ℓ2 – длина окружности.
где R1, R2
– радиусы; ℓ1, ℓ2 – длина окружности.
Допустим, что 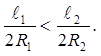
Впишем в окружности правильные n-угольники. если n – величина бесконечно большая,
то Р1 » ℓ1, Р2 »
ℓ2, 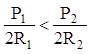 ,
получено противоречие с тем, что известно
,
получено противоречие с тем, что известно 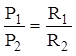 или
или
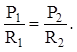
Следовательно, наше допущение неверно и 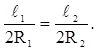
Принято обозначать это отношение – π.
Значит,
![]() .
.
– Как найти длину дуги?
Длина окружности: 2pR.
Какова длина дуги, соответствующей центральному углу,
равному 1º: ![]() ?
?
Какова длина дуги, соответствующей центральному углу в
n°: 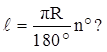
Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности.
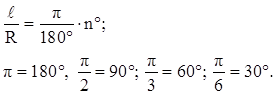
Единица измерения – радиан.
1 рад. = ![]()
III. Закрепление изученного материала.
Решение задач 34 (1), 35, 43 (1, 3), 51 (1, 3).
IV. Итог урока.
Домашнее задание: подготовить тематическую таблицу, п. 119–120, Вопросы 14–18, задачи 34 (2), 43 (2, 4), 51 (2, 4).
Таблица
|
Длина окружности. Радианная мера угла |
|
|
Отношение длины окружности к ее диаметру есть величина постоянная
Длина дуги окружности, соответствующей центральному углу в n°
Радианная мера угла – это отношение длины соответствующей дуги к радиусу окружности:
Единица измерения – радиан. 1 радиан – это угол, у которого длина дуги равна радиусу. 1 радиан = 1 град = |
|
Урок 10
длина окружности. радианная мера угла
Цель: формировать умения применять формулы при решении задач.
Ход урока
I. Организационный момент.
II. Самостоятельная работа с взаимопроверкой.
|
Вариант I |
Вариант II |
|
1. Вычислите длину окружности: |
|
|
если R = 15 cм |
R = 20 м |
|
2. Найдите длину дуги радиуса 1 см, отвечающей центральному углу: |
|
|
120° |
30° |
|
3. Найдите градусную меру угла, если его радианная мера равна: |
|
|
|
|
III. Решение задач 35, 36, 44 (1, 2), 47 (1), 48 (2).
№ 36.
– По какой формуле находится сторона правильного восьмиугольника?
![]() (задача 23).
(задача 23).
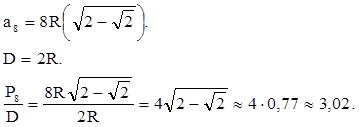
№ 44.
– Сколько градусов содержит центральный угол, если соответствующая ему дуга составляет
1) ![]() окружности?
окружности?
Решение:
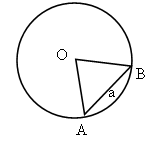
Градусная мера окружности – 360°.
1) ![]() ·
360° = 120°;
·
360° = 120°;
2) ![]() ·
360° = 90°.
·
360° = 90°.
Градусная мера дуги равна градусной мере центрального угла: a1 = 120°; a2 = 90°.
№ 47.
По данной хорде а найдите длину ее дуги, если градусная мера дуги равна 60°.
Решение:
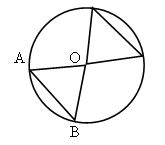
ÈАВ![]() ,
значит, ÐАОВ
= 60°.
,
значит, ÐАОВ
= 60°.
Так как DАОВ – равнобедренный (АО = ОВ = R) и ÐАОВ = 60°, то это треугольник будет равносторонним: АО = ОВ = АВ = а.
Длина дуги:
![]()
Ответ: ![]()
№ 48 (2).
По данной длине дуги ℓ найдите ее хорду, если дуга содержит 90°.
Решение:
1) ÈАВ![]() ,
Þ ÐАОВ
(центральный) = 90°.
,
Þ ÐАОВ
(центральный) = 90°.
Значит, DАОВ – прямоугольный и АВ2 = АО2 + ОВ2;
АВ2 = 2R2 (по теореме Пифагора).
2) Найдем радиус из формулы длины дуги ℓ = ![]()
ℓ = 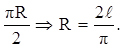
Итак, АВ2 = 2 · 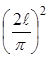 ;
АВ =
;
АВ = 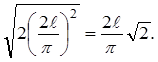
IV. Итог урока.
– Какие задания вызвали трудность при решении?
Домашнее задание: № 37, 45, 50.
Урок 11
длина окружности. радианная мера угла
Цель: проверить уровень усвоения обозначенной темы.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Фронтальный опрос.
· Какой угол называется центральным?
· По какой формуле находится длина окружности?
· По какой формуле находится длина дуги окружности, соответствующей центральному углу в 1°, 180°, n°?
· Что называется радианной мерой угла?
· Какова связь радианной и градусной меры угла?
· Подобны ли правильные многоугольники?
· Какими отношениями связаны стороны, периметры, радиусы вписанных и описанных окружностей правильных подобных многоугольников?
· Чему равна сумма внутренних углов правильного n-угольника?
· Чему равен центральный угол правильного n-угольника?
· Скольким градусам равен 1 радиан, p радиан, 2p радиан?
2. Решите устно:
1) Чему равна градусная мера дуги окружности, если соответствующий центральный угол равен: а) 45; б) 120°; в) 270°?
2) Чему равна градусная и радианная мера дуги, равной:
а) ![]() окружности;
б)
окружности;
б) ![]() окружности;
в)
окружности;
в) ![]() окружности;
окружности;
г) ![]() окружности;
д)
окружности;
д) ![]() части
окружности?
части
окружности?
III. Самостоятельная работа.
Вариант I.
1. Дуга,
соответствующая данному центральному
углу, составляет
![]() окружности.
окружности.
а) Найдите градусную и радианную меры центрального угла.
б) Найдите длину дуги, если радиус окружности равен 4 см.
2. Найдите количество сторон выпуклого многоугольника, сумма углов которого равна 3p радиан.
3. Хорда
длиной ![]() см
стягивает дугу 90°. Найдите длину окружности.
см
стягивает дугу 90°. Найдите длину окружности.
Вариант II.
1. В окружности радиусом ![]() см
выбрана дуга длиной 9 см.
см
выбрана дуга длиной 9 см.
а) Найдите градусную и радианную меры дуги.
б) Найдите длину дуги данной окружности, соответствующей центральному углу, равному 2 рад.
2. Найдите количество сторон и сумму внутренних углов
правильного многоугольника, если его центральный угол равен ![]() .
.
3. Хорда длиной ![]() см
делит дугу окружности в отношении 1 : 2. Найдите длину большей из двух
образовавшихся дуг.
см
делит дугу окружности в отношении 1 : 2. Найдите длину большей из двух
образовавшихся дуг.
Вариант III.
1. Длина дуги окружности paдиусом 12 см составляет ![]() длины окружности.
длины окружности.
а) Найдите градусную и радианную меры данной дуги.
б) Найдите радиус окружности, длина которой равна длине данной дуги.
2. Найдите радианную меру центрального угла
правильного многоугольника, если сумма его внешних углов с одним из внутренних
равна ![]()
3. На высоте равностороннего треугольника, как на
диаметре, построена окружность. Найдите длину дуги окружности, заключенной
внутри треугольника, если сторона треугольника равна ![]() см.
см.
Домашнее задание: самостоятельная работа.
Самостоятельная работа.
Правильные многоугольники. Длина окружности
Вариант I.
1. Докажите, что в правильном восьмиугольнике существуют по крайней мере три параллельные диагонали.
2. Используя данные рисунка, найдите длину границы заштрихованной фигуры.
3. В окружности радиуса 1 см проведены две хорды, равные ![]() см
и
см
и ![]() см.
Определите отношение длин меньших дуг, стягиваемых этими хордами.
см.
Определите отношение длин меньших дуг, стягиваемых этими хордами.
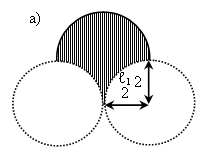
Вариант II.
1. Докажите, что в правильном шестиугольнике A1A2A3A4A5A6 стороны А1А2 и А4А5 параллельны.
2°. Используя данные рисунка, найдите длину границы заштрихованной фигуры.
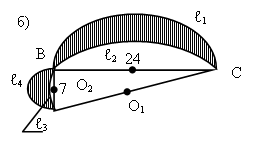
3. Сторона правильного вписанного в окружность
многоугольника равна 6 см, а его угол равен 135°. Найдите сторону подобного ему
многоугольника, вписанного
в окружность радиусом 12![]() см.
см.
Решение:
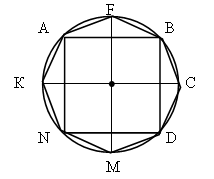
1. АВDN – квадрат, КС, FM – оси симметрии. АВ || КС || ND.
2. а) ℓ =![]() ;
R = 2,
;
R = 2,
n° = 90°; 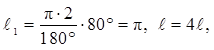
![]()
б) 1) ℓ1 – длина дуги окружности с центром в точке О и радиусом – 12.
2) ℓ4 – длина дуги окружности с центром в точке О2 и радиусом – 3,5.
3) (ℓ3 + ℓ2) – длина дуги окружности с центром в точке О1. Найдем ее радиус ÐАВС – вписанный, ему соответствует полуокружность, ÐАВС = 90°.
По теореме Пифагора АС2 = АВ2 + ВС2 = 72 + 242 = 625.
АС = 25, значит, радиус равен 12,5.
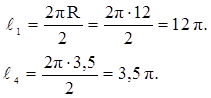
ℓ3 + ℓ2 =![]() .
.
L = 228p.
3. ![]()
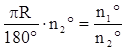 .
.
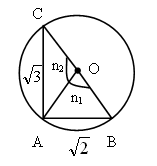
Рассмотрим DАОВ и DАОС – равнобедренные, применим формулу косинусов: АВ2 = АО2 + ОВ2 – 2АО ∙ ОВcosn1 = 2R2 – 2R2cosn2 = 2R2(1 – cosn1).
2 = 2R2(1 – cosn1), 1 = 1 – cosn1, cosn1 = 0, n1 = 90º.
AC2 = 2R2 – 2R2cosn2,
3 = 2R2(1 – cosn2), ![]() =
1 – cosn2,
=
1 – cosn2,
cosn2 = – ![]() ,
n2 = 120º;
,
n2 = 120º; ![]() .
.
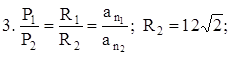
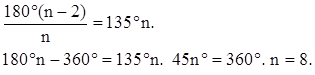
Значит, задан правильный восьмиугольник.
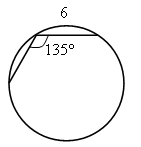
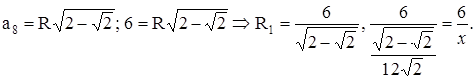
Урок 12
ТЕОРЕТИЧЕСКИЙ ЗАЧЕТ ПО ТЕМЕ
«МногоугольникИ»
Цель: обобщить, систематизировать и проверить знания.
Ход урока
I. Организационный момент.
II. Работа в группах.
Группа состоит из 6 учащихся. Один ученик – консультант. Оценки выставляются в зачетный лист по каждому вопросу. Итоговая оценка выставляется в визитную карточку.
Карточка 1.
1. Докажите, что длина ломаной не меньше длины отрезка, соединяющего его концы.
2. Что такое радианная мера угла? Чему равны радианные меры углов в 180° и 90°?
Карточка 2.
1. Выведите формулу для суммы углов выпуклого многоугольника.
2. По какой формуле вычисляется длина окружности? По какой формуле вычисляется длина дуги окружности?
Карточка 3.
Докажите, что правильный многоугольник является вписанным в окружность и описанным около окружности.
2. Как построить правильный выпуклый шестиугольник?
Карточка 4.
1. Выведите формулу для радиусов вписанной и описанной окружностей правильного n-угольника.
2. Что называется центром многоугольника, центральным углом многоугольника?
Карточка 5.
1. Докажите, что правильные выпуклые n-угольники подобны. В частности, если у них стороны одинаковы, то они равны.
2. Что такое ломаная, длина ломаной? Что такое внешний угол выпуклого многоугольника.
Карточка 6.
1. Докажите, что отношение длины окружности к ее диаметру не зависит от окружности, то есть одно и то же для всех окружностей.
2. Что такое многоугольник, выпуклый многоугольник, плоский многоугольник?
Контрольная
работа № 3
по теме «Многоугольники»
Цели: проверить уровень усвоения знаний и умений.
Вариант I.
1. Сколько сторон имеет многоугольник, если сумма его углов равна 1620°?
Ответ: 11.
2. В окружность вписан правильный шестиугольник со стороной, равной 9 см. Найдите длину дуги окружности, стягиваемой стороной шестиугольника.
Ответ: 3π.
3. Найдите длину окружности, описанной около правильного треугольника, если радиус вписанной в этот треугольник окружности равен 7 см.
Ответ: 14 см.
4. В правильном шестиугольнике ABCDFG проведены диагонали ВС и CF. Докажите, что четырехугольник BCFG – прямоугольник, и выразите его стороны через сторону шестиугольника.
5. Около окружности описан многоугольник, все углы которого равны. Является ли данный многоугольник правильным?
II вариант.
1. Сколько сторон имеет многоугольник, если сумма его углов равна 1980°?
Ответ: 13.
2. В окружность вписан квадрат со стороной, равной 8 см. Найдите длину дуги окружности, стягиваемой стороной квадрата.
Ответ: 4π.
3. Найдите длину окружности, вписанной в правильный треугольник, если радиус описанной около этого треугольника окружности равен 8 см.
Ответ: 2p.
4. В правильном восьмиугольнике ABCDEFGH проведены диагонали СН и DG. Докажите, что четырехугольник CDGH – прямоугольник, и выразите его стороны через сторону восьмиугольника.
5. Около окружности описан многоугольник, все стороны которого равны. Является ли данный многоугольник правильным?
Оформление решения задач
Вариант I.
4.Дано: АВСDFG – правильный, АВ = а.
Доказать: ВСFG – прямоугольник и выразить ВС и BG через а.
Доказательство:
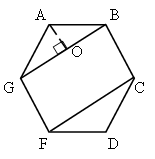
АВСDFG – правильный, значит,
ÐА = ÐВ = ÐС = ÐD = ÐF = ÐG = 120°.
DGAB, DFDC – равнобедренный, следовательно, ÐАВG = ÐAGB = ÐDCF = ÐCFD = 30°.
2) ÐGBC = ÐВСF = ÐCFG = ÐFGB = 120° – 30° = 90°.
Следовательно, ВСFG – прямоугольник, ВС = GF = а.
3) Рассмотрим DGAB – равнобедренный, АО – высота, медиана: GO = OB, GB = 2GO.
DАОG – прямоугольный, ÐG = 30°;
![]() GO = a cos
30° =
GO = a cos
30° = ![]() ;
GB =
;
GB = 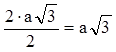 .
.
Ответ: ВСFG
– прямоугольник, ВС = GF = а, BG = FC = а![]() .
.
Вариант II.
4. Доказательство аналогично.
ПЛОЩАДИ ФИГУР (13 часов)
Цель: сформировать у учащихся общее представление о площади и умение вычислять площади фигур.
В результате изучения темы учащиеся должны
|
знать: |
уметь: |
|
– свойства площади; – формулу площади прямоугольника, треугольника, параллелограмма, трапеции; – формулы, связывающие площадь треугольника и радиусы вписанных и описанных окружностей; – что площади подобных фигур относятся как квадраты линейных размеров; – определение круга кругового сектора и кругового сегмента; – формулу площади круга, кругового сектора и кругового сегмента. |
– выводить формулу площади прямоугольника; – проводить доказательство справедливости формул площадей фигур; – находить отношение площадей подобных фигур по известным длинам пары соответствующих элементов этих фигур; – находить площадь круга, распознавать и изображать круговой сектор и круговой сегмент, вычислять их площади; – применять все известные формулы при решении задач. |
Урок 1
ПОНЯТИЕ ПЛОЩАДИ.
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Цели: дать представление об измерении площадей многоугольника, вывести формулу для вычисления площади прямоугольника, закрепить усвоение определения площади в процессе решения задач.
Ход урока
I. Организационный момент.
Сообщаются общая тема, ее основная цель, дается визитная карточка темы, объявляются тема урока и его цель. Анализируются ошибки, допущенные в контрольной работе.
II. Изучение нового материала.
1. Самостоятельное изучение п. 121 по памятке.
Памятка
Самостоятельная работа с математическим текстом
· Прочти внимательно текст учебника. Его надо читать не спеша, по предложениям, не переходя к следующему предложению, не поняв смысл предыдущего.
· Выдели в тексте все определения и теоремы, которые необходимо знать.
· Если требуется дать определение какой-либо фигуры, мысленно дай такое определение.
· Если речь идет о теореме, сформулируй ее, уясни себе, в чем условие и значение этой теоремы.
· Сделай чертеж, иллюстрирующий содержание теоремы.
После прочтения текста обозначился план повторения и изучения темы:
1) Определение:
– простой фигуры (m);
– плоского треугольника (n);
– выпуклого плоского многоугольника (n);
– площади простой фигуры;
– свойства площадей простых (n-) фигур;
– единицы измерения площади, их связь.
2) Дополнительные вопросы:
· С какими величинами вы уже знакомы?
· Привести примеры, связанные с практической необходимостью измерения площади.
2. Выполнение практической работы.
Из двух равных прямоугольных треугольников (модели учащиеся заранее подготовили дома) составить:
а) равнобедренный треугольник;
б) прямоугольник;
в) параллелограмм, не являющийся прямоугольником.
– Что можно сказать о площади этих фигур? Ответ объяснить.
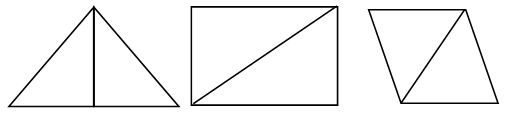
– Дайте понятие равновеликих фигур.
3. Сформулировать и записать свойства площади.
1) Если F1 = F2, то S (F1) = S (F2);
2) Если F = F1 + F2 + … Fn, то S(F) = S(F1) + S(F2) + … S(Fn).
3) Sкв = 1 мм2,
Sв = 100 м · 100 м = 1000 м2 = 1 га,
Sкв = 1 см2,
Sв = 10 м · 10 м = 100 м2 = 1 ар,
Sкв = 1 дм2, Sкв = 1 м ´ 1 м = 1 м2.

4. Выводится формула для вычисления площади прямоугольника.
S = ab, где а, в – стороны прямоугольника;
S – его площадь.
III. Закрепление изученного материала.
1. Земельный участок имеет площадь 2700000 м2. Чему равна площадь этого участка, если за единицу измерения принять 1) квадратный километр; 2) гектар; 3) ар?
2. Стороны двух квадратов равны 8 см и 16 см. Найдите сторону квадрата, площадь которого равна сумма площадей данных квадратов. (Устно. Используется таблица квадратов.)
3. На рисунке четырехугольник АВСD – параллелограмм, точка Е – симметрична точке А относительно точки В. Докажите, что SАВСD = SADЕ.
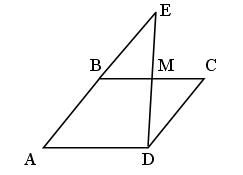
4. Решение задач 1, 2 из учебника.
IV. Итоги урока.
– С какой новой величиной познакомились сегодня на уроке?
– Какими свойствами обладает эта величина?
– Каковы единицы измерения площади?
Домашнее задание: п. 121, 122, вопросы 1, 2. Задачи 3, 5, 6.
Урок 2
ПОНЯТИЕ ПЛОЩАДИ.
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА.
РЕШЕНИЕ ЗАДАЧ
Цель: закрепить умение решать задачи на применение свойств площадей и формулы площади прямоугольника.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Проверка домашнего задания (особо обратить внимание на ключевую задачу 3).
Найти площадь квадрата S по его диагонали d.
Решение:
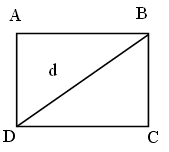
АВСD – квадрат, значит, АВD – прямоугольный равнобедренный треугольник.
По теореме Пифагора
DВ2 = АВ2 + АD2 = 2АВ2.
d2 = 2АВ2, значит, ![]()
Sкв. = 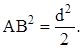
Ответ:
S = ![]()
2. Решение задачи 3 (из предыдущего урока).
Запишем доказательство:
1) DВЕМ = DМСD по второму признаку равенства треугольников.
(DС = АВ, ÐВЕD = ÐМDС – внутренние накрест лежащие при АЕ || DС и секущей DE, ÐЕВС = ÐМСD – накрест лежащие при ÐAE || DC, секущей ВС.)
Значит, SDВЕМ = SDМСD.
2) SАВСD = SАВМD + SМСD, SАDE = SАВМD + S∆BEM, следовательно, SАВСD = SАDЕ.
III. Решение задач по готовым чертежам.
|
1. а) SАВСD = 48, CD = 3. Найти: АD. б) РАВСD = 40, АD = 3 СD. Найти: SАВСD. в) SАВСD = 32, АD = 2АВ. Найти: РАВСD. |
|
|
2. а) Доказать, что SАОD = SBОС. б) АD = 20, SDОС = 60. Найти: СD. в) SАСD = 28, АВ = АD + 1. Найти: РАВСD. |
|
|
3. а) Ð1 = Ð2, ВМ = 5, МС = 4. Найти: SАВСD. б) Ð1 = Ð2, АВ = МС, РАВСD = 48. Найти: SАВСD. в) Ð1 = Ð2, АВ : МС = 1 : 2, РАВСD = 40. Найти: SАВСД. |
|
Задача 7 (п. 122).
Чему равны стороны прямоугольника, если они относятся как 4 : 9, а его площадь 144 м2?
Ответ: a = 8 м, в = 18 м.
Задача 8.
Чему равна стророна прямоугольника, если его периметр 74 дм, а площадь 3 м2?
Решение:
Пусть АВ = DС = а, АD = в.
Получим Р = 2 (а + в) = 74 дм = 7, 4 м.
S = ав = 3 м2.
Решим систему:
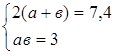
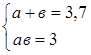
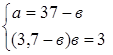
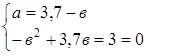
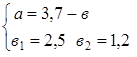
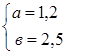
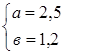
Ответ: 1,2 м; 2,5 м.
IV. Самостоятельная работа «Площадь прямоугольника. Площадь параллелограмма».
Вариант I.
1. Стороны двух квадратов равны 8 см и 15 см. Найдите сторону квадрата, площадь которого равна сумме площадей данных квадратов.
2. На стороне AD прямоугольника ABCD постройте треугольник ADE так, чтобы точка пересечения отрезков ВС и АЕ была серединой стороны АЕ. Докажите, что площади прямоугольника АВСD и треугольника AED равны.
Вариант II.
1. Площадь прямоугольника равна 36 см2, а стороны относятся как 1 : 4. Найдите площадь квадрата, периметр которого равен периметру данного прямоугольника.
2. Постройте точку м, симметричную точке D относительно точки С параллелограмма ABCD. Докажите, что площади параллелограмма АВСD и треугольника AMD равны.
V. Итог урока.
· Что называется площадью?
· С какими еще величинами знакомы?
Домашнее задание.
1. Сторона квадрата равна 4 см. На его диагонали построен новый квадрат. Его площадь равна…
2. Практическая работа: произведите необходимые измерения и вычислите световую площадь своей комнаты (площадь окон). Вычислите отношение световой площади к площади пола и выразите ее в процентах.
Нормально ли освещение комнаты? Освещенность считается нормальной, если световая площадь окон составляет 20 % от площади пола.
Урок 3
площадь параллелограмма
Цели: повторить определение и свойства параллелограмма, вывести формулу площади параллелограмма.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Повторить классификацию выпуклых четырехугольников по схеме. Желательно, чтобы ученики формулировали определение.
2. Повторить признаки равенства треугольников.
3. Устно решить задачи:
1) АВСD – прямоугольник, ДD = CF = ![]() EF.
EF.
Докажите, что SDКЕF = 2SDBCF.
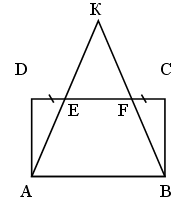
2) Отрезки ВН и СК – высоты параллелограмма АВСD.
Найдите площадь параллелограмма, если АВ = 6 см, ВС = 8 см, ÐВАН = 30°.
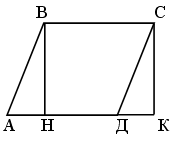
III. Изучение нового материала.
Дано: АВСD – параллелограмм,
ВН – высота.
Доказать: SАВСD = АD · ВК.
Учитель предлагает доказать теорему желающему учащемуся.
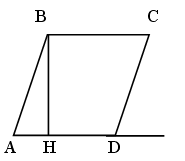
IV. Решение задач.
Задача 9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.
Задача 13 (ключевая).
Докажите, что площадь ромба равна половине произведения диагоналей.
Доказательство.
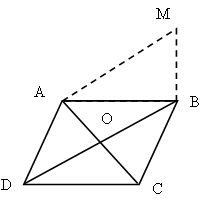
Дополнительное построение: АМ || DВ, АМВD параллелограмм (AM || DB, AD || MB).
АС ^ DВ.
SАМВD = DВ · АО.
DАМВ = DАВD = DDВС.
Значит, SАВСD
= SАМВD = DВ · АО = ![]() DВ · АС.
DВ · АС.
V. Итог урока.
Выпишите основные формулы по нахождению площади четырехугольника.
S = a2,
Sкв. = ![]() где d – диагональ
квадрата.
где d – диагональ
квадрата.
Sn = ab, Sпар-ма = ah, где а – сторона, h – высота.
![]() где d1,
d2 – диагонали.
где d1,
d2 – диагонали.
Домашнее задание: п. 123. Вопросы 3. Задачи 11, 14.
Домашняя самостоятельная работа.
Вариант I.
1. Стороны параллелограмма равны 5 см и 12 см, а один из его углов равен 150°. Найдите площадь параллелограмма.
2. Периметр прямоугольника равен 52 см, а его стороны относятся как 4 : 9.
а) Найдите площадь прямоугольника.
б) Найдите сторону квадрата, площадь которого равна площади прямоугольника.
3. Высоты параллелограмма равны 3 см и 4 см, а его площадь равна 48 см2. Найдите периметр параллелограмма.
Вариант II.
1. Периметр параллелограмма равен 66 см. Два угла параллелограмма относятся как 1 : 5, а две стороны – как 2 : 9. Найдите площадь этого параллелограмма.
2. Диагональ прямоугольника больше его сторон на 2 см и 16 см соответственно.
а) Найдите площадь прямоугольника.
б) Найдите площадь квадрата, периметр которого равен периметру прямоугольника.
3. Высоты параллелограмма равны 4 см и 6 см, а одна из его сторон на 4 см больше другой. Найдите периметр параллелограмма.
Вариант III.
1. Стороны параллелограмма равны 12 см и 9 см, а угол между его высотами равен 30°. Найдите площадь параллелограмма.
2. В квадрат, площадь которого равна 81 см2, вписан прямоугольник так, что вершины прямоугольника делят стороны квадрата в отношении 2 : 1. Найдите площадь прямоугольника.
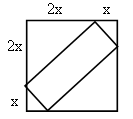
3. Стороны параллелограмма равны 12 см и 18 см, а одна из его высот – 15 см. Найдите вторую высоту параллелограмма.
Урок 4
площадь ТРЕУГОЛЬНИКА
Цель: вывести формулы для вычисления площади треугольника.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Индивидуальная работа.
Карточка 1.
Докажите, что площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Карточка 2.
Докажите, что площадь ромба равна половине произведения диагонали.
Карточка 3.
Стороны параллелограмма равны 10 см и 6 см, а угол между ними равен 150°. Найдите площадь этого параллелограмма.
Карточка 4.
Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны 4 см и 3 см. Найдите площадь этого параллелограмма.
2. Решение задач по готовым чертежам.
Найти площадь АВСD.
Прямоугольник параллелограмм ромб
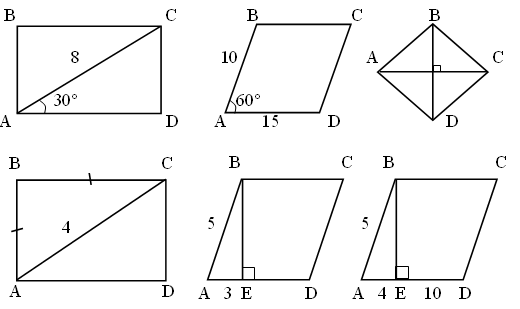
III. Изучение нового материала.
1. Площадь треугольника равна половине произведения
его стороны на проведенную к ней высоту: ![]()
2. Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними.
Доказательства:
1-й случай.

1. SDАВС
= ![]() АС
· ВD, a
– острый.
АС
· ВD, a
– острый.
2. DАВD – прямоугольный, значит, sina
= ![]() Þ
ВD = АВ sina.
Þ
ВD = АВ sina.
Следовательно, SDАВС
= ![]() АС
· АВ sin a.
АС
· АВ sin a.
2-й случай.
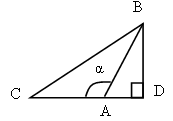
1) SDАВС
= ![]() АС
· ВD, α – тупой.
АС
· ВD, α – тупой.
2) DАВD – прямоугольный, значит,
sin (180° – a) = ![]()
sin (180° – a) = sina.
Следовательно, SDАВС
= ![]() АС
· АВ sin a.
АС
· АВ sin a.
Какие вопросы по теории нам пришлось повторить? (Площадь параллелограмма; признаки равенства треугольников; свойства параллелограмма; определение синуса острого угла прямоугольного треугольника; формулы приведения.)
Дополнительные вопросы для повторения: теорема косинусов; основное тригонометрическое тождество; формулы сокращенного умножения.
3. Вывести формулу Герона для площади треугольника:
![]() а, в, с – длины сторон
треугольника.
а, в, с – длины сторон
треугольника.
Вопросы для учащихся:
– Имея формулу S = ![]() только
стороны а, в, с треугольника, что необходимо найти? (sin j.)
только
стороны а, в, с треугольника, что необходимо найти? (sin j.)
– Какая существует теорема, связывающая стороны и углы?
Теорема косинусов: с2 = а2 + в2 – 2ав cos j.
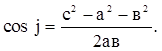
– Каким соотношением связаны sin a и cos a?
sin2a + cos2a = 1; sin2a = 1 – cos2a
– Чему равна разность квадратов? (а2 – в2 = (а – в) (а + в).)
Наиболее подготовленному учащемуся предлагается вывести формулу Герона, используя вспомогательную таблицу.
|
S = По теореме косинусов с2 = а2 + в2 – 2ав cosγ |
sinγ – ?
cosγ
= |
|
Основное тригонометрическое тождество sin2α + cos2α = 1 Формулы сокращенного умножения: а2 – в2 = (а – в)(а + в) (а + в)2 = а2 + 2ав + в2 (а – в)2 = а2 – 2ав + в2 |
sin2α = 1 – cos2α = (1 – cosα) (1 + cosα) = = = = = = = = sinγ
= SD
= S
= |
|
Периметр треугольника Р = а + в + с, если р – полупериметр, то а + в + с = 2р с + в – а = 2р – 2а а + в – с = 2р – 2с а + с – в = 2р – 2в |
IV. Итог урока.
– Какие формулы для площади треугольника вам известны?
– Чему равна площадь прямоугольного треугольника?
Домашнее задание: п. 124, № 15; п. 125, № 30 (1).
Урок 5
площадь ТРЕУГОЛЬНИКА. РЕШЕНИЕ ЗАДАЧ
Цель: выработать умение применять формулы площадей при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Записать все известные формулы для нахождения
площади фигур S = ab, ![]()
Sð = ![]() где а, b – катеты.
где а, b – катеты.
2. Каким свойством обладает диагональ ВD?
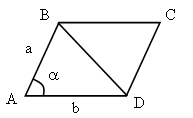
– Чему равна площадь прямоугольника, выраженная через известную величину S = ab sina?
3. Найти площадь равностороннего треугольника.
ÐА = ÐВ = ÐС = 60°, sin 60° = ![]()
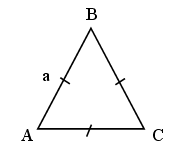
SD = ![]() .
.
4. Что можно сказать о площади одного треугольника, найденной по различным формулам?
![]()
5. Какие задачи могут создаваться на основе этого вывода?
III. Решение задач.
Работа в группах.
1-я группа – № 17 (без формулы Герона).
Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м?
Ответ: S = 4800 м2.
№ 30 (2). Найдите площадь треугольника по трем сторонам: 17, 65, 80.
Ответ: 288.
2-я группа – № 26.
Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними 70°.
Ответ: S = 0,47 м2.
№ 34. Найдите высоты треугольника, у которого стороны равна 13 см, 14 см и 15 см.
Ответ:12
см; 11,2 см; ![]()
3-я группа (наиболее подготовленные учащиеся) – № 18.
Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а.
Ответ:
S = ![]() м2.
м2.
№ 39. Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную на боковую сторону.
Ответ: 13,44 см.
4-я группа (наиболее подготовленные учащиеся) – № 28.
Найдите площадь треугольника по стороне а и прилежащим к ней углам a и b.
Решение:
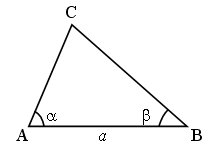
1) Используем формулу
S = 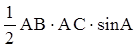 .
.
АВ = а, sin А = sin a.
2) ÐC = 180° – (a + b).
По теореме синусов
![]()
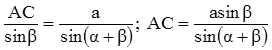 .
.
3. SDАВС =
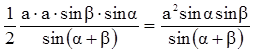 .
.
Ответ: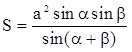 .
.
№ 31. Стороны треугольника а, в, с. Найдите высоту треугольника, опущенную на сторону с.
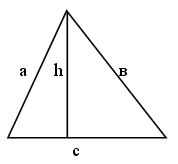
Решение:
![]()
где ![]() .
.
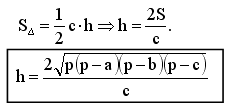
На проверку учитель берет только одну тетрадь из группы. Оценка будет выставлена учащимся всей группы. Каждый учащийся должен выписать все теоретические вопросы, которые необходимо было повторить, для того чтобы решить задачи.
IV. Итог урока.
– Какие новые формулы пополнили наш банк данных?
Домашнее задание: № 27, 24, 36 (1).
Урок 6
площадь ТРАПЕЦИИ
Цели: ввести формулу площади трапеции, закрепить навыки при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Индивидуальная работа.
Карточка 1.
Доказать, что SD
= ![]() .
.
Карточка 2.
Доказать, что SD
= ![]()
Карточка 3 (для наиболее подготовленных учащихся).
Доказать, что ![]()
2. Решение задач по готовым чертежам.
Найти площадь АВСD.
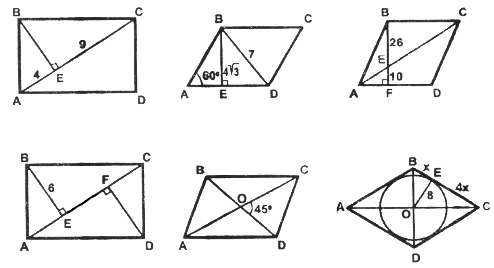
Дано: EF = 16. Дано: АС = 8, BD = 6.
III. Изучение новой темы.
Теорема.
Площадь трапеции равна произведению полусуммы ее оснований на высоту
![]() .
.
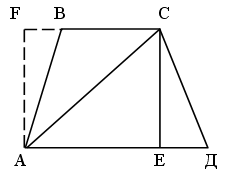
Теоретические вопросы, которые необходимо повторить: свойства площади; определение трапеции; высота трапеции; расстояние между параллельными прямыми.
IV. Закрепление изученного материала.
1. Решение задач 38 (коллективно), 37, 39 (индивидаульно).
V. Итог урока.
– Что наывается высотой трапеции?
– Какая трапеция называется равнобокой?
– Что называется средней линией трапеции?
Вывод: Sтрапеции = mh, где ![]() –
средняя линия трапеции.
–
средняя линия трапеции.
Домашнее задание: п. 126, вопрос 6, задачи 40 (ключевая), 41 (наиболее подготовленным учащимся).
Урок 7
ФОРМУЛА ДЛЯ РАДИУСОВ
ВПИСАННОЙ И ОПИСАННОЙ ОКРУЖНОСТЕЙ
Цели: проверить уровень усвоения знаний и умений нахождения площадей треугольника и трапеции, вывести формулы, связывающие площадь треугольника с радиусами вписанной и описанной окружностей.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
1. Записать все известные формулы площадей.
2. Решение задач по готовым чертежам.
1) Найти площадь трапеции АВСD.
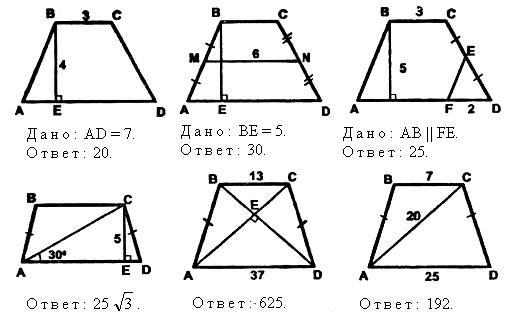
2) Найти площадь треугольника.
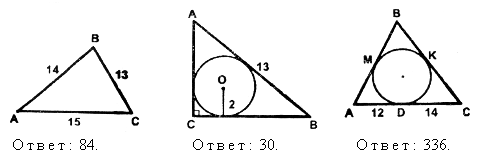
III. Самостоятельная работа по теме «Площадь треугольника. Площадь трапеции».
Вариант I.
1. Докажите, что сумма расстояний от любой точки внутри правильного треугольника до всех его сторон равна высоте треугольника.
2. Диагонали параллелограмма, равные ![]() см
и 7 см, пересекаются под углом 45°. Найдите площадь параллелограмма.
см
и 7 см, пересекаются под углом 45°. Найдите площадь параллелограмма.
3. Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делится на отрезки 4 см и 9 см. Найдите площадь трапеции.
Вариант II.
1. Докажите, что сумма расстояний от любой точки основания равнобедренного треугольника до его боковых сторон равна высоте треугольника, проведенной к его боковой стороне.
2. Боковая сторона равнобедренного треугольника равна 29 см, а его основание – 40 см. Найдите радиусы вписанной и описанной окружностей данного треугольника.
3. Диагонали трапеции, равные 14 см и 8 см, взаимно перпендикулярны. Найдите площадь трапеции.
IV. Изучение новой темы.
– Каким свойством обладают площади?
– Как построить окружность и в нее вписать треугольник?
– Как связаны между собой радиус описанной окружности и сторона треугольника?
– Какова формула площади треугольника, выраженная через две стороны и синус угла между ними?
– Запишите теорему синусов.
Задача № 42.
Выведите следующие формулы для радиусов описанной (R)
и вписанной (r) окружностей треугольника а: ![]()
Решение.
1) 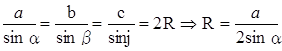 .
(Умножим на bc.)
.
(Умножим на bc.)
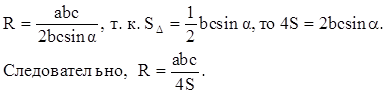
2) SDABC = SDAOB + SDAOC + SDBOC.
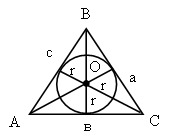
SDABC
=![]()
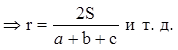
V. Закрепление изученного материала.
Решить задачу 43 (1). Площадь найти по формуле Герона.
Ответ:
![]()
VI. Итог урока.
– Площади каких фигур известны? Записать все формулы площадей.
Домашнее задание: п. 127; задачи 44, 48, подготовить черновой вариант тематической таблицы «Площади фигур».
Урок 8
площадИ ПОДОБНЫХ ФИГУР
Цели: рассмотреть зависимость отношений площадей подобных фигур от отношения их линейных размеров, выработать умение находить отношение площадей подобных фигур по известным длинам пары соответствующих элементов.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
· Какие фигуры называются подобными?
· Какими свойствами обладают подобные фигуры?
· Какие треугольники называются подобными?
· Каким свойством обладают площади фигур?
· Что можно сказать о соответствующих высотах подобных треугольников?
III. Изучение новой темы.
Задача 1.
Треугольник А¢В¢С¢ подобен треугольнику АВС с коэффициентом подобия k. Выразите площадь треугольника через площадь треугольника АВС.
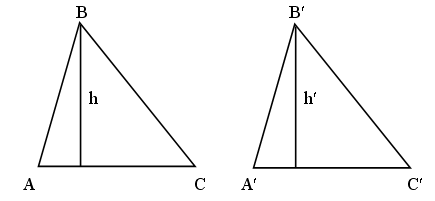
Решение:
1. Так как DА¢В¢С¢ DАВС Þ а¢ = ka, h¢ = kh.
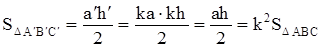
Замечание. Если k > 1, то площадь треугольника А¢В¢С¢ в k2 раз больше площади треугольника АВС, а если k < 1, то площадь треугольника А¢В¢С¢ в k2 раза меньше площади треугольника АВС.
Задача 2. Найдите отношение площадей подобных простых фигур F¢ и F¢¢, если коэффициент подобия, при котором фигура F¢ переходит в фигуру F¢¢, равен k.
Решение:
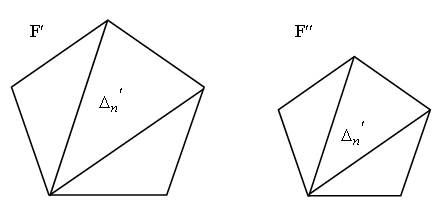
1) Разобьем фигуру F¢
на треугольники ![]() ,
, ![]() ,
… ,
,
… ,![]() .
.
2) Преобразование подобия, переводящее F¢ ®
F¢¢,
переводит треугольники ![]() ®
® ![]() ,
,
![]() ®
® ![]() ,
… ,
,
… , ![]() ®
® ![]() ;
;
3) S(F¢)
= S![]() + S
+ S![]() + … S
+ … S![]() .
.
Но S![]() = k2 S
= k2 S![]() … S
… S![]() = k2S
= k2S![]() (по предыдущей задаче).
(по предыдущей задаче).
4) S(F¢¢)
= k2 S![]() + k2S
+ k2S![]() + … k2S
+ … k2S![]() .
.
S(F¢¢) = k2 S(F¢).
Следовательно, 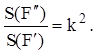
Но коэффициент подобия равен отношению соответствующих линейных размеров.
Вывод: площади подобных фигур относятся как квадраты их соответствующих линейных размеров.
IV. Закрепление нового материала.
1. решить устно.
1) DАВС ~ DА¢В¢С¢. Найдите отношение площадей этих треугольников, если АВ = 2 см, А¢В¢ = 6 см.
2) Найдите отношение площадей двух квадратов, если их стороны относятся как а) 1 : 3; б) р : q.
3) Соответствующие стороны подобных многоугольников относятся как 2 : 1. Найдите площадь меньшего многоугольника, если площадь большего равна 35 см2.
2. Решить письменно.
Через середину высоты треугольника проведена перпендикулярная ей прямая. В каком отношении она делит площадь треугольника?
Решение:
1) А¢С¢ ^ ВD, АС ^ ВD, значит, А¢С¢ || АС.
2) А¢С¢ || АС Þ ÐА¢ = ÐА как соответственные при секущей АВ.
3) ÐВ – общий, ÐА¢ = ÐВ Þ DА¢В¢С¢ ~ DАВС.
В¢D¢ = ![]()
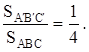
Домашнее задание: п. 128. Вопрос 7. Задачи 51, 52.
Домашняя самостоятельная работа.
Вариант I.
1. Дано: АВ = ВС = 4 см;
ÐС = 75°.
Найти: SDАВС.
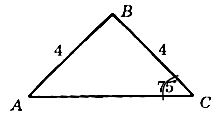
2. Найдите наибольшую высоту треугольника со сторонами 11 см, 25 см и 30 см.
3. Высота прямоугольного треугольника делит гипотенузу на отрезки длиной 18 см и 32 см. Найдите площадь треугольника.
Вариант II.
1. По данным рисунка найдите площадь трапеции ABCD'.
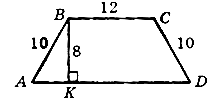
2. Найдите площадь ромба, если сумма его диагоналей равна 14 см, а периметр – 20 см.
3. Меньшая боковая сторона прямоугольной трапеции равна 4 см. Найдите среднюю линию трапеции, если ее площадь равна 36 см2.
Вариант II.
1. По данным рисунка найдите площадь трапеции ABCD.
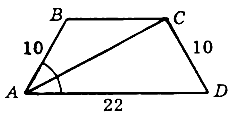
Разность диагоналей ромба равна 14 см, а его площадь – 120 см2. Найдите периметр ромба.
3. Диагональ разнобокой трапеции перпендикулярна боковой стороне. Найдите площадь трапеции, если ее высота равна 12 см, а диагональ – 20 см.
Вариант III.
1. Дано: AD = 18 см; ВС = 2 см; АС = 15 см; ВD = 7 см.
Найдите площадь трапеции ABCD.
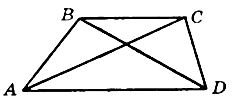
2. Высота и диагонали ромба относятся как 12 : 15 : 20, а его периметр равен 100 см. Найдите площадь ромба.
3. Диагонали равнобокой трапеции взаимно перпендикулярны. Найдите площадь трапеции, если точка пересечения диагоналей удалена от оснований на 5 см и 6 см.
Урок 9
ПЛОЩАДЬ КРУГА И ЕГО ЧАСТЕЙ
Цели: ввести понятия «круг», «круговой сектор», «круговой сегмент»; учить распознавать и изображать эти фигуры, вывести формулы для нахождения площади этих фигур.
Ход урока
I. Организационный момент.
II. Актуализация опорных знаний.
– Какая фигура называется простой?
– Каким свойством обладает площадь?
– Является ли круг простой фигурой?
– Предложите, как определить площадь произвольной фигуры.
III. Изучение нового материала.
1. Определение. Данная фигура имеет площадь S, если существуют содержащие ее простые фигуры и содержащиеся в ней простые фигуры.
– Найдутся ли такие фигуры для круга? (Да, выписанные и описанные многоугольники.)
Теорема. Площадь круга равна половине произведения длины окружности на радиус.
Доказательство.
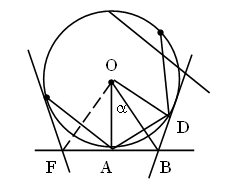
Р1 – вписанный правильный многоугольник (простая фигура);
Р2 – описанный (простая фигура).
|
1) SP1 = h · SАОD, SАОD = = АС · ОС = АС · АО cos a
= 2) SВОF = = АB · ОA =
= |
DАОС – прямоугольный
сos a
=
DАBС – прямоугольный
сos a
= |
3) Если n ® ¥, то Р ® ℓ (периметры стремятся к длине окружности).
Если a ® 0, то cosa ® 1.
Значит, по определению 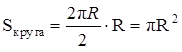 .
.
2. Определение. Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла:
Sсект = 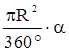
3. Определение. Круговым сегментом называется общая часть круга и полуплоскости.
Сколько сегментов получено на рисунке? В чем их отличие?
1-й случай. a1 < 180°
2-й случай. a2 > 180°
Как найти площадь для первого случая?
Sсегм= 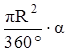 º–
SD
º–
SD
Как найти площадь для второго случая?
Sсегм= 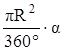 º+
SD
º+
SD
В общем случае: Sсегм = 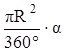 ±
SD
±
SD
IV. Закрепление изученного материала.
Решение задач 53, 54, 55, 59.
V. Итог урока.
· С какими фигурами познакомились?
· Как находятся их площади?
· Покажите возможные комбинации фигур в круге.

Домашнее задание: п. 129, вопросы 8, 9; задачи 56 (по вариантам), 59.
Урок 10
ПЛОЩАДЬ КРУГА И ЕГО ЧАСТЕЙ.
РЕШЕНИЕ ЗАДАЧ
Цель: закрепить полученные знания в ходе решения задач.
Ход урока
I. Организационный момент.
II. Решение задач.
1. Решение задач по готовым чертежам.
Найти площадь заштрихованной фигуры.
Дано: R1 = 5; R2 = 3. Дано: R1 = 10; R2 = 6; R3 = 2. Дано: R = 3.
Дано: R = 6.
Дано: АВСD – прямо- Дано: R1 = R2 = R3 = Дано: R1 = R2 = R3 =
угольник; R1 = R2 = 1. = R4 = 2, R5 = 3. = R4 = 4.
Дано: R1 = 10. Дано: R1 = R2 = R3 = Дано: R1 = R2 = R3 = 4.
= R4 = 2.
Ответы:1. 25π – 9π = 16π; 2. 60π; 3. 3π; 4. 24π;
5. 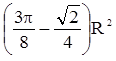 ;
6.
;
6. 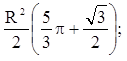 7.
8 – π; 8. 300 – 13π;
7.
8 – π; 8. 300 – 13π;
9. 64 – 16π; 10. 12,5π; 11. 16
– 4π; 12. 16![]() – 8.
– 8.
2. Решить задачи 57, 58, 62.
№ 62.
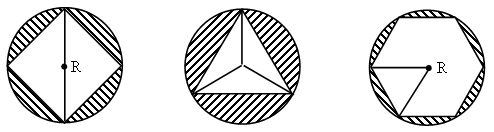

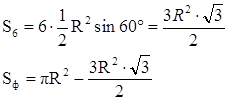
III. Итог урока. Выставление оценок.
Домашняя самостоятельная работа.
Вариант I.
1. Площади подобных треугольников относятся как 4 : 9.
Сторона первого треугольника равна 8 см. Найдите соответствующую сторону второго треугольника.
2. Найдите площадь круга, вписанного в квадрат со стороной 4 см.
3. Площадь кругового сектора равна 9p см. Найдите радиус круга, если соответствующий этому сектору центральный угол равен 90°.
Вариант II.
1. Соответствующие стороны подобных треугольников равны 15 см и 25 см. Найдите отношение площадей данных треугольников.
2. Найдите
площадь круга, описанного около равностороннего треугольника со стороной 3![]() см.
см.
3. Радиус круга равен 6 см. Найдите центральный угол, соответствующий круговому сектору, площадь которого равна 12 см2.
Вариант III.
1. Средняя линия отсекает от данного треугольника треугольник, площадь которого равна 15 см2. Найдите площадь данного треугольника.
2. Найдите площадь круга, вписанного в треугольник со сторонами 18 см, 24 см и 30 см.
3. Радиус круга равен 6 см. Найдите площадь кругового сегмента, если соответствующий ему центральный угол равен 60°.
Вариант IV.
1. В треугольнике, площадь которого равна 48 см2, проведена средняя линия. Найдите площади частей, на которые она делит треугольник.
2. Найдите площадь круга, описанного около треугольника со сторонами 16 см, 30 см и 34 см.
3. Радиус круга равен 6 см. Найдите площадь кругового сегмента, если соответствующий ему центральный угол равен 300°.
Урок 11
ЗАЧЕТ ПО ТЕМЕ «ПЛОЩАДИ»
Цель:обобщить и систематизировать теоретические знания.
I. Организационный момент.
II. Работа в группах.
Карточка 1.
1. Cформулируйте свойства площади для простых фигур.
2. Дайте определение кругового спектра, запишите формулу, по которой вычисляется площадь кругового спектра.
Карточка 2.
1. Докажите, что площадь прямоугольника равна произведению его сторон.
2. Дайте определение кругового сегмента. по какой формуле вычисляется площадь кругового сегмента?
Карточка 3.
1. Докажите, что площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
2. Как относятся площади подобных фигур?
Карточка 4.
1. Докажите, что площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
2. Дайте определение круга. По какой формуле находится площадь круга?
Карточка 5.
1. Докажите, что площадь трапеции равна произведению полусуммы оснований на высоту.
2. Запишите формулы, связывающие площадь треугольника и радиусы вписанной и описанной окружности.
Карточка 6.
1. Докажите, что если диагонали пересекаются, то площадь четырехугольника равна половине произведения диагоналей на синус угла между ними.
2. Запишите формулу Герона для нахождения площади треугольника.
Карточка 7.
1. Докажите, что площадь ромба равна половине произведения диагоналей.
2. Выпишите все формулы, по которым находится площадь треугольника.
Домашнее задание: а) используя тематические таблицы, повторить курс геометрии за 9 класс; б) выполнить домашнюю контрольную работу.
Домашняя контрольная работа.
Вариант I.
1. Две стороны треугольника равны 6 см и 10 см, а угол между ними – 120є.
а) Найдите периметр треугольника.
б) Найдите площадь треугольника.
2. Длина окружности, вписанной в правильный четырехугольник, равна 8 см. Найдите сторону и площадь четырехугольника.
3. Биссектриса прямоугольного треугольника делит гипотенузу на отрезки 20 см и 15 см. Найдите площадь треугольника.
Вариант II.
1. Стороны треугольника равны 3 см и 7 см, а угол, противолежащий большей из них, равен 60є.
а) Найдите периметр треугольника.
б) Найдите площадь треугольника.
2. Площадь правильного треугольника равна 12![]() см2. Найдите площадь круга, вписанного в треугольник, и площадь
квадрата, описанного около этого круга.
см2. Найдите площадь круга, вписанного в треугольник, и площадь
квадрата, описанного около этого круга.
3. Диагональ прямоугольной трапеции делит острый угол пополам, а вторую диагональ – в отношении 8 : 6. Найдите площадь трапеции, если ее высота равна 12 см.
Вариант III.
1. Одна из сторон треугольника равна 7 см, разность двух других сторон – 5 см; а угол между ними – 60є.
а) Найдите периметр треугольника.
б) Найдите площадь треугольника.
2. Сумма площадей правильных шестиугольников, вписанного
и описанного около одной окружности, равна 12![]() см2.
Найдите площадь круга, ограниченного данной окружностью.
см2.
Найдите площадь круга, ограниченного данной окружностью.
3. Меньшее основание разнобокой трапеции равно боковой стороне, а диагонали делятся точкой пересечения в отношении 5 : 11. Найдите площадь трапеции, если ее высота равна 20 см.
Урок 12
контрольная работа № 4 по теме
«площади фигур»
Цель: проверить уровень знаний, умений и навыков.
Ход урока
I. Организационный момент.
II. Повторение изученного материала по тематической таблице.
Тематическая таблица
|
Площади фигур |
|
|
Площадь – это положительная величина, численное значение которой обладает следующими свойствами: 1. Равные фигуры имеют равные площади. 2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей. 3. Площадь квадрата со стороной, равной единице измерения, равна единице |
|
|
Фигуры, имеющие равные площади, называются равновеликими |
|
|
Площадь треугольника |
|
|
S∆ABC
= S∆ABC
= Формула Герона: S = ВС = а, АС = в, АВ = с Р = S∆ABC = ∆АВС – прямоугольный S∆ABC = ∆АВС – равносторонний |
|
|
Ключевые задачи |
|
|
S∆AOM = S∆BOM = S∆BON = S∆CON = = S∆AOK = S∆CON
|
|
|
Площади четырехугольников |
|
|
Параллелограмм S = DC · AE S = AD · DC sinA
|
|
|
Прямоугольник S = AD · AB
|
|
|
Ромб SABCD
= SABCD = AD · BH |
|
|
Квадрат S
= a2, S =
|
|
|
Трапеция SABCD = SABCD = MN · BH MN – средняя линия |
|
|
Выпуклый четырехугольник SABCD =
|
|
III. Содержание контрольной работы.
Вариант I.
1. Найдите площадь параллелограмма, если одна из его сторон равна 6 см, а высота, проведенная к этой стороне, равна 9 см.
2. Найдите площадь правильного треугольника со стороной 8 см.
3. В равнобокой трапеции с боковой стороной, равной ![]() см,
меньшее основание равно 4 см, угол при большем основании составляет 45°.
Найдите площадь трапеции.
см,
меньшее основание равно 4 см, угол при большем основании составляет 45°.
Найдите площадь трапеции.
4. На стороне АВ параллелограмма ABCD отмечена произвольная точка G. Докажите, что сумма площадей треугольников ACG и BDG равна половине площади этого параллелограмма.
5. Найдите площадь описанного около окружности
правильного треугольника, если площадь вписанного в эту окружность квадрата
равна ![]() см2.
см2.
Вариант II.
1. Найдите площадь трапеции, если ее основания равны 7 см и 11 см, а высота равна 4 см.
2. Найдите площадь равнобедренного прямоугольного треугольника, если его катет равен 8 см.
3. Меньшая диагональ ромба равна ![]() см,
один из углов равен 60°. Найдите площадь ромба.
см,
один из углов равен 60°. Найдите площадь ромба.
4. Внутри параллелограмма ABCD отмечена произвольная точка G. Докажите, что сумма площадей треугольников CGD и АGВ равна половине площади этого параллелограмма.
5. Найдите площадь описанного около окружности
квадрата, если площадь вписанного в эту окружность правильного шестиугольника
равна ![]() см2.
см2.
Оформление решения.
Вариант I.
1. Ответ: S = ah = 6 · 9 = 54 (cм2).
2. Ответ: SD
= 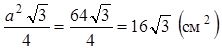 .
.
3. Дано: АD
= ![]() см,
см,
ABCD – трапеция,
АВ = 4 см, ÐD = 45°, AD = BC.
Найти: SАВСD.
Решение:
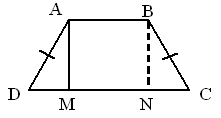
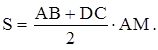
1) Проведем высоту трапеции АМ.
Рассмотрим DАDМ – прямоугольный; равнобедренный, так как ÐD = 45°. Следовательно, DМ = АМ.
По теореме Пифагора АD2 = DМ2 + АМ2 = 2АМ2;
![]() АМ2 = 9; АМ =
3.
АМ2 = 9; АМ =
3.
DМ = АМ = 3.
2) Так как трапеция равнобокая, то DАДМ = DNBC (по гипотенузе и катету).
Значит, DМ = NC = 3.
DС = DМ + MN + NC = 3 + 4 + 3 = 10 (см).
3) 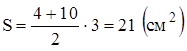 .
.
Ответ: 21 см2.
4. Дано: АВСD – параллелограмм.
Доказать:
SDАСG
+ SDВDЕ
= ![]() SАВСD.
SАВСD.
Доказательство:
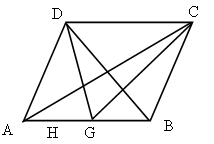
Проведем высоту параллелограмма DН.
1) SАВСD = АВ · DН
SDАСG
= ![]()
SDDВG
= ![]()
SDАСG
+ SDDВG
= 
=![]()
5. Дано:
∆АВС – правильный описанный, MNKZ – вписанный квадрат Sкв = 4![]() cм2.
cм2.
Найти: SDАBС
Решение:
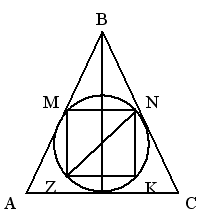
1) Если S— = 4![]() cм2, то акв =
cм2, то акв = ![]() .
.
MN – средняя линия. Значит, АС = ![]() .
.
2) SD = 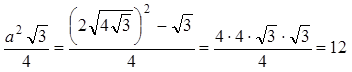 .
.
Ответ: 12.
Вариант II.
1. S—
= 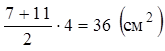 .
.
2. SD
= 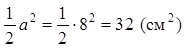 .
.
3. Дано:
АВСD – ромб; АС = ![]() см, ÐВ
= 60°.
см, ÐВ
= 60°.
Найти: SАBСD.
Решение:
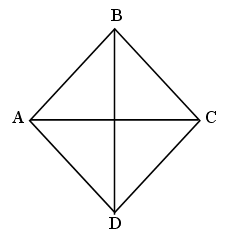
1) DАВС – равнобедренный (АВ = ВС), ÐВ = 60°.
Значит, DАВС – равносторонний, то
есть ВС = АВ = АС = ![]() см.
см.
2) SАВСD = АВ · ВС · sinB = ![]() ·
·![]() ·
sin 60° =
·
sin 60° =
= 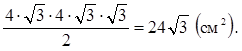
Ответ: 21 см2.
4. Дано: АВСD – параллелограмм.
Доказать:
SDАСG
+ SDDGC
= ![]() SАВСD.
SАВСD.
Доказательство:
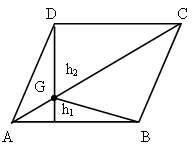
1) h = h1 + h2, где h – высота параллелограмма, h1, h2 – высоты треугольников, АВ = DС (по свойству параллелограмма).
2) SDDСG
= 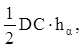
SDАВG
= ![]() ,
,
SDDВС
+ SDАGВ
= ![]()
=![]()
5. Дано:
АВСD – описанный квадрат, S6 = 9![]() cм2.
cм2.
Решение:
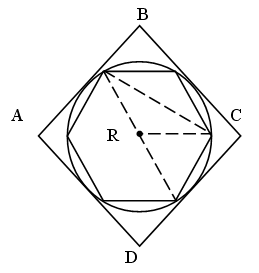
1. SАВСD = (2R)2 = 4R2.
2. Найдем радиус.
S6 = 6 · ![]() R
· R · sin 60° = 3R2 ·
R
· R · sin 60° = 3R2 · 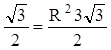 ;
;
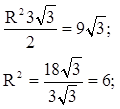
S = 4 · 6 = 24 (см2).
Ответ: 24 см2.
Итоговый тест
Вариант I.
1. Средняя линия трапеции АBCD равна 13 см, а сторона АВ, равная 12 см, образует с основанием AD угол в 30°. Найдите площадь трапеции.
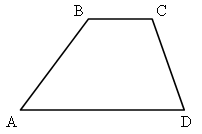
Ответ: 78 см2.
2. В прямоугольнике одна из сторон равна 6 см, а диагональ – 10 см, тогда его площадь равна:
а) 24 см2; б) 60 см2;
в) 48 см2; г) 30 см2.
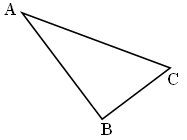
3. В прямоугольном тpeyгольникe АВС: ас = 17 cм, Вс = 8 см, АВ = 15 см.
Найдите cos С.
Ответ: cos С =
4. Из точки D к окружности с центром в точке О проведена касательная DF. Если OD = 17 cм, а FD = 15 см, то радиус окружности равен:
a) ![]() см;
б) 8 см;
см;
б) 8 см;
в) 32 см; г) 4![]() см.
см.
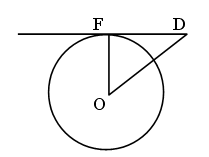
5. В разнобокой трапеции ABCD сумма двух углов равна 212°. Определите градусную меру углов трапеции.
Ответ: ÐAВС = 106º; ÐBCD = 106º; ÐDAB = 74º; ÐCDA = 74º.
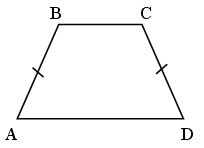
6. В равностороннем треугольнике ABC проведены средние линии FG и DF. Найдите периметр четырехугольника ADFG, если периметр треугольника FBD равен 27 см.
Ответ: PADFC = _____ см.
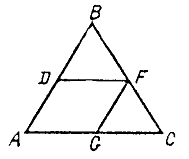
7. В трапеции АВСD проведены диагонали АС и ВD. Треугольники АОD и СОВ подобны. Известно, что ВС = 28 см, АD = 40 см, ОD = 24 см. Определите коэффициент подобия.
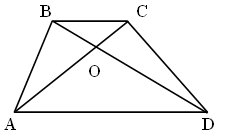
8. В треугольнике АВС отрезок NM параллелен стороне АС. Известно, что АВ = 18 см. Если СМ : МВ = 7 : 2, то отрезок BN равен:
а) 4 см; б) 2 см;
в) 14 см; г) 16 см.
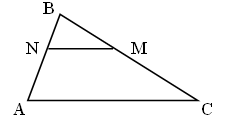
9. Радиус окружности с центром в точке О равен 8 см, ÐAOB = 60°. Найдите хорду АВ.
Ответ: АВ = _____ см.
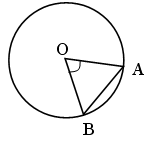
10. Дана окружность с центром в точке О. Медиана ОС треугольника АВС равна 6 см. Найдите диаметр окружности.
Ответ: АВ = _____ см.
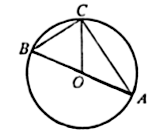
Вариант II.
1. Основания трапеции АВСД равны 17 см и 9 см, а высота – 4 см. Найдите площадь трапеции.
2. Если в равнобедренном треугольнике ABC (АВ = ВС) АВ = 5 см и АС = 8 см, то его площадь равна:
а) 40 см2; б) 48 см2; в) 24 см2; г) 12 см2.
3. В прямоугольном треугольнике АВС АС = 13 см, АВ = 12 см, ВС = 5 см. Найдите sin С.

4. Из точки А к окружности с центром в точке О проведена касательная АС. Отрезок ОА равен 20 см, а ОС – 16 см, тогда длина отрезка СА равна:
а) 2 см; б) ![]() см;
см;
в) 12 см; г) 6 см.
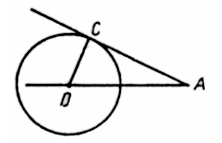
5. В параллелограмме ABCD сумма двух углов равна 132°. Oпределите градусную меру углов параллелограмма.
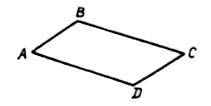
Ответ: ÐABC = _____ ; ÐBCD = _____ ; ÐDAB = _____ ; ÐCDA = _____ .
6. Из точки К к окружности с центром в точке О проведены касательная КМ и секущая KN. ÐNKM = 28°. Найдите другие углы треугольника ОМК.
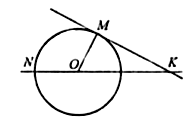
Ответ: ÐMOK = _____ ; ÐOMK = _____ .
7. Радиус окружности с центром в точке О равен 7 см, ÐBAO = 60°. Найдите хорду АВ.
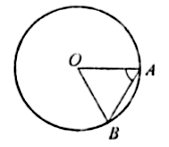
Ответ: АВ = _____ см.
8. Равнобедренные треугольники АВF и CDF подобны. Известно, что AF = 15 см, АВ = 12 см, DC = 3 см. Определите коэффициент подобия.
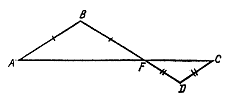
9. В треугольнике ABC отрезок NM параллелен стороне АC. Известно, что BC = 21 см. Если AN : NB = 4 : 3, то отрезок МС равен:
а) 3 см; б) 9 см; в) 12 см; г) 18 см.
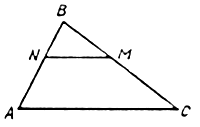
10. В равностороннем треугольнике ABC проведена средняя линия DF. Вычислите периметр четырехугольника ADFC, если периметр DFBD равен 27 см.
Ответ: РADFC = _____ см.
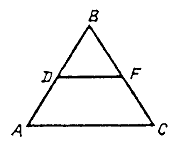
Ключ к тесту
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Вариант I |
78 |
в |
|
б |
106º 106º 74º 74º |
36 |
0,7 |
а |
8 |
12 |
|
Вариант II |
52 |
г |
|
в |
114º 66º 66º 114º |
62º 90º |
7 |
4 |
в |
45 |
ВИЗИТНАЯ КАРТОЧКА
ПО ОБОБЩАЮЩЕМУ ПОВТОРЕНИЮ ГЕОМЕТРИИ
(7–9 классы)
|
Тема |
Количество часов |
Практическая |
Тест |
Проверочная |
Теория |
|
Углы. Параллельные прямые. перпендикулярные прямые |
2 |
|
|
|
|
|
Треугольники |
3 |
|
|
|
|
|
Четырехугольники |
2 |
|
|
|
|
|
Многоугольники. Окружность. Круг |
2 |
|
|
|
|
|
Преобразование фигур |
2 |
|
|
|
|
|
Векторы на плоскости |
1 |
|
|
|
|
|
Итоговый тест по всему курсу геометрии |
2 |
|
|
|
|
|
Итоговая контрольная работа |
2 |
|
|
|
|
|
Всего |
15 |
|
|
|
|
I. Углы. Параллельные прямые. Перпендикулярные прямые (2 часа).
1. Угол. Градусная и радианная мера углов. Построение угла, равного данному. Построение биссектрисы угла. Смежные углы и их свойства.
Вертикальные углы и их свойства.
2. Параллельные прямые. Существование и единственность прямой, параллельной данной и проходящей через точку вне ее (аксиома).
Признаки параллельности прямых.
Теоремы об углах, полученных при пересечении двух параллельных прямых третьей.
3. Перпендикулярные прямые. Существование и единственность перпендикуляра к прямой, проведенного через данную точку.
Построение прямой, перпендикулярной данной.
Геометрическое место точек, равноудаленных от двух данных. Деление отрезка пополам.
4. Расстояния: между двумя точками; от точки до прямой; между параллельными прямыми.
Уравнение прямой.
Теорема Фалеса.
II. Треугольники (3 часа).
1. Соотношение между сторонами и углами треугольника.
Неравенство треугольника.
Средняя линия треугольника.
Биссектриса угла треугольника и ее свойства.
Равные треугольники. Признаки равенства треугольников.
Подобные треугольники. Признаки подобия треугольников.
2. Равнобедренный треугольник. Теорема об углах при основании равнобедренного треугольника и теорема, обратная ей. Свойства медианы, биссектрисы и высоты равнобедренного треугольника, проведенных к его основанию. Сумма углов треугольника. Свойства внешнего угла треугольника.
3. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников. Признаки подобия прямоугольных треугольников.
Теорема Пифагора.
Перпендикуляр, наклонная и ее проекция.
Средние пропорциональные в прямоугольном треугольнике.
4. Синус, косинус и тангенс острого угла в прямоугольном треугольнике.
Значение синуса, косинуса и тангенса некоторых углов.
Решение прямоугольных треугольников. Основные тригонометрические тождества.
5. Теорема косинусов.
Теорема синусов.
Площадь треугольников.
Решение треугольников.
III. Четырехугольники (2 часа).
1. Параллелограмм. Прямоугольник. Ромб. Квадрат. Определение. Признаки параллелограмма. Свойства параллелограмма. Свойства прямоугольника, ромба, квадрата. Площадь параллелограмма, прямоугольника, ромба, квадрата.
2. Трапеция. Свойства средней линии трапеции, площадь трапеции.
IV. Многоугольник. Окружность. Круг (2 часа).
1. Выпуклый многоугольник, сумма углов выпуклого многоугольника. Внешний угол выпуклого многоугольника.
2. окружность, круг. Уравнение окружности. Касательная к окружности и ее свойства. Длина окружности.
Центральный угол и дуга окружности.
3. Вписанный и описанный многоугольник.
Расположение центров окружностей, описанной около треугольника и вписанной в треугольник.
Формулы, выражающие радиус окружности, описанной около треугольника, и радиус окружности, вписанной в треугольник, через длины сторон и площадь.
Правильный многоугольник. Теорема о существовании для правильного многоугольника окружности, описанной около него, и окружности, вписанной в него. Совпадение центров окружностей, описанной около правильного многоугольника и вписанной в него.
Формулы, связывающие сторону правильного многоугольника с радиусом описанной около него окружности и радиусом вписанной в него окружности, их частные случаи для n = 3, 4, 6.
4. Площадь круга и его частей.
5. Углы, вписанные в окружность.
V. Преобразование фигур (1 час).
1. Движение. Виды движений: симметрии относительно точки, симметрия относительно прямой, поворот, параллельный перенос.
2. Преобразование подобия. Гомотетия. Подобие фигур. Отношение площадей подобных фигур. Отношение периметров подобных фигур.
VI. Векторы на плоскости (1 час).
1. Векторы и его окружность. Равные векторы. Условие равенства векторов, заданных геометрически, условие равенства векторов, заданных координатами. Откладывание вектора, равного данному, от заданной точки.
2. Сложение и вычитание векторов в координатной и геометрической формах. Умножение вектора на число в координатной и геометрической формах.
Коллинеарные векторы, условие коллинеарности векторов, заданных координатами. Выражение вектора через … .
3. Скалярное произведение векторов, заданных в координатной и геометрической формах, нахождение угла между векторами, заданными координатами. Условие перпендикулярности векторов.
Уроки 1–2
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
Цели: обобщить и систематизировать знания и умения, усвоить системы опорных знаний и умений, углубить знания в пределах темы.
Ход урока
I. Актуализация опорных теоретических знаний.
Учащиеся работают в группах из 4 человек. Учебные группы сформированы из учащихся с неравными возможностями.
На каждом столе имеются: вопросы по обозначенной теме (раздел I); тематические таблицы, составленные в 7 классе; предметный указатель из учебника (желательно ксерокопии).
Из учащихся с высокими учебными возможностями можно создать отдельную группу, они могут самостоятельно повторить теорию, составить опорную таблицу и приступить к решению задач.
Таблица 1
Углы.
Параллельные прямые.
Перпендикулярные прямые
Углы. Определение.
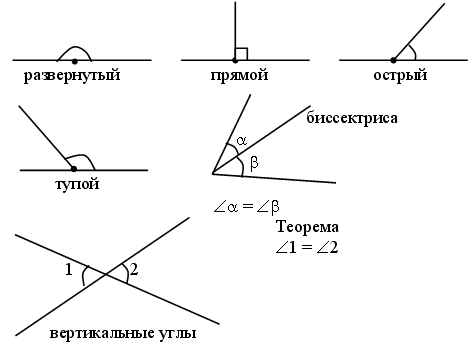
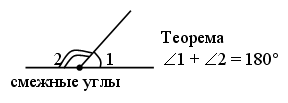
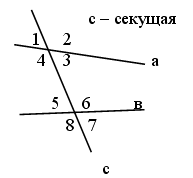
Внутренние накрест лежащие углы – 3 и 5, 4 и 6, односторонние углы – 4 и 5, 3 и 6, соответственные углы – 1 и 5, 4 и 8, 2 и 6, 3 и 2.
Задачи на построение: угла, равного данному; биссектрисы угла; перпендикулярной прямой; деление отрезка пополам.
Таблица 2
Параллельные прямые
Определение:
а и в не пересекаются. 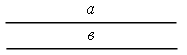
|
Признаки |
Рисунок |
Свойства |
|
1. Если Ð1 = Ð2, то а || в. Следствие: если а ^ с, в ^ с, то а || в |
|
1. Если а || в,
то Следствие: если
а || в и с ^ а, то |
|
2. Если Ð1 = Ð2, то а || в |
|
2. Если а || в , то Ð1 = Ð2
|
|
3.
Если Ð1
+ Ð2
= |
|
2. Если а || в , то Ð1 + Ð2 = 180°
|
Таблица 3
Перпендикулярные прямые
Определение: АВ ^ СD: ÐАОD = ÐСОВ = ÐАОС = ÐDОВ = 90°.
АВ – наклонная,
АН – перпендикуляр;
ВН – проекция;
Н – основание перпендикуляра;
В – основание наклонной.
АН – расстояние от точки А до прямой а.
Свойство:
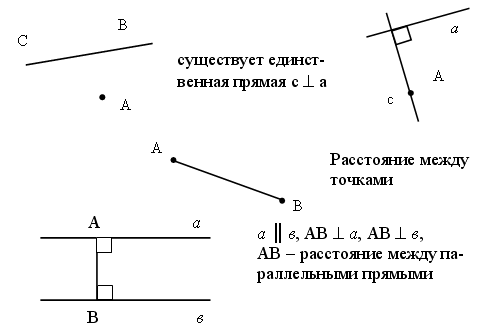
II. задачи для устного решения.
1. Верно ли,
– что угол, смежный с тупым углом, – тупой;
– угол, смежный с прямым углом, прямой;
– если два угла сложные, то они прямые;
– если два угла смежны с одним тем же углом, то они равны?
2. Если две параллельные прямые пересечены секущей,
– то сумма односторонних углов равна 180°;
– сумма накрест лежащих углов равна 180°;
– соответственные углы могут быть тупыми;
– односторонние углы могут быть острыми;
– среди образовавшихся углов есть не менее четырех равных;
– среди образовавшихся углов есть ровно четыре равных угла.
3. Может ли при пересечении двух прямых образоваться:
– четыре прямых угла;
– четыре острых угла;
– три тупых и один острый угол;
– два прямых и два тупых угла?
4. Могут ли:
– две прямые, имеющие общую точку, быть параллельными третьей прямой;
– две прямые, параллельные третьей, иметь общую точку;
– две прямые, перпендикулярные третьей, быть перпендикулярными;
– две прямые, перпендикулярные третьей, быть параллельными?
III. Задачи на готовых чертежах.
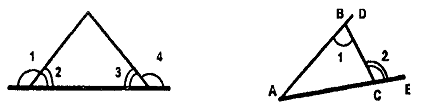
Дано: Ð1 = Ð4. Дано: Ð1 + Ð2 = 180°.
Доказать: Ð2 = Ð3. Доказать: 1) ÐАВС = ÐАСЕ;
2) ÐDВС = ÐВСЕ.
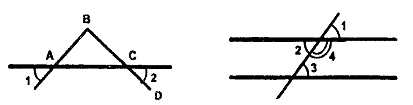
Дано: Ð1 = Ð2. Дано: Ð2 = Ð3.
Доказать: ÐВАС + ÐАСD = Доказать: 1) Ð1 = Ð3;
= 180°. 2) Ð3 + Ð4 = 180°.
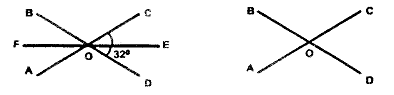
Найти:
ÐВОС Дано: ÐАОВ = ![]() (ÐВОС
+
(ÐВОС
+
ÐСОD + ÐDОА).
Найти: 1) ÐАОВ, ÐВОС,
ÐСОD, ÐDОА
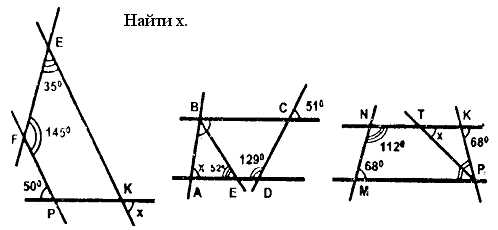
Дано: ÐАВЕ = ÐСВЕ.
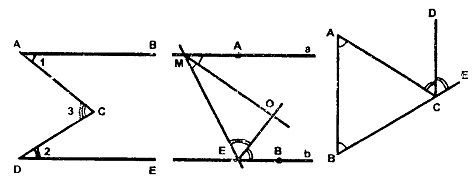
Дано: АВ || DЕ. Дано: а || в. Доказать: АВ || СD.
Доказать: Ð1 + Доказать:
+ Ð2 = Ð3. ÐМОЕ = 90°.
III. Тест по теме «Углы. Параллельные прямые. перпендикулярные прямые».
Вариант I.
1. Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами.
а) 24°; б) 30°; в) 36°; г) 40°.
2. Разность между двумя односторонними углами при параллельных а и в и секущей с равна 24°. Найдите больший из этих углов.
3. Прямые АВ и СD пересекаются в точке Е, причем сумма углов ВЕС и АЕD равна 194°. Найдите угол АЕС.
а) 97°; б) 83°; в) 117°; г) 73°.
4. Углы ВОD и СОD – смежные. ОЕ – биссектриса угла ВОD, причем угол СОD на 21° больше угла DОЕ. Найти угол ВОЕ.
а) 67°; б) 74°; в) 46°; г) 56°.
5. Прямые MN и РК пересекаются в точке Е, ЕС – биссектриса угла МЕР, ÐСЕК = 137°. Найдите угол КЕМ.
а) 108°; б) 84°; в) 94°; г) 82°.
а) 114°; б) 112°; в) 102°; г) 124°.
6. Дано: СД ^ АК, MN ^ АК, ÐAMN = 28°, CЕ – биссектриса ÐВСD.
Найти: ÐAСЕ.
а) 92°; б) 104°; в) 114°; г) 98°.
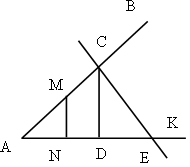
Вариант II.
1. Величины смежных углов пропорциональны числам 4 и 11. Найдите разность между этими углами.
а) 84°; б) 76°; в) 96°; г) 68°.
2. Разность между двумя внутренними односторонними углами при параллельных прямых а и в с секущей с равна 46°. Найдите больший из этих углов.
а) 126°; б) 123°; в) 113°; г) 136°.
3. Прямые MN и КР пересекаются в точке О, причем сумма углов КОМ и NOP равна 134°. Найдите величину угла КОN.
а) 44°; б) 46°; в) 113°; г) 67°.
4. Углы АОМ и СОМ – смежные. ОК – биссектриса угла АОМ, причем угол АОК в 4 раза меньше, чем угол СОМ. Найдите угол КОМ.
а) 45°; б) 30°; в) 36°; г) 40°.
5. Прямые АВ и СD пересекаются в точке О, ОК – биссектриса угла АОD, ÐСОК = 118°. Найдите угол ВОD.
а) 59°; б) 64°; в) 68°; 56°.
6. Дано: АВ ^ ЕD, КМ ^ ЕD, ÐАВЕ = 34°. MN – биссектриса ÐКМС.
Найти: ÐЕMN.
а) 107°; б) 117°;
в) 97°; г) 113°.
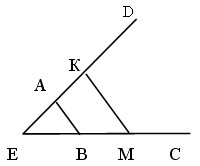
Ключ к тесту.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
I |
б |
в |
б |
г |
в |
б |
|
II |
а |
в |
в |
б |
г |
а |
Уроки 3–5
ТреугольникИ
Ход урока
I. Изучение нового материала.
Опорные таблицы
Соотношения между сторонами и углами треугольника:
с < a < b, ÐC < ÐA < ÐB
Неравенство треугольника:
b < a + c
Свойство биссектрисы угла треугольника:
l – биссектриса
![]()
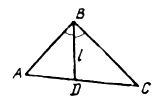
Средняя линия треугольника:
DЕ || АС
![]()
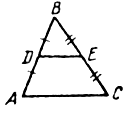
Равные треугольники:
DАВС = DА´В´С´
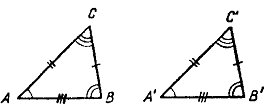
Признаки равенства треугольников:
I. II. III.
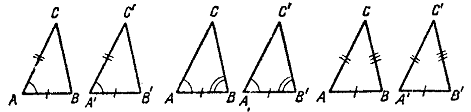
Подобные треугольники:
DАВС ~ DА´В´С´
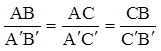
Признаки подобия треугольников:
I II III
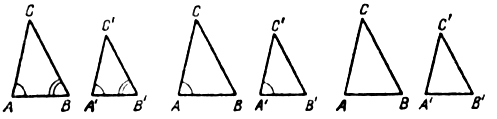
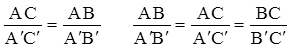
Равнобедренный треугольник
![]()
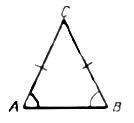
m ³ ℓ ³ h AD = m = h = l
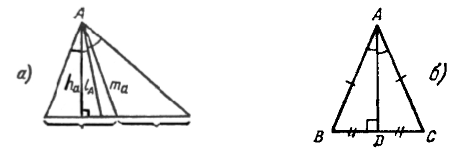
![]()
Сумма углов треугольника.
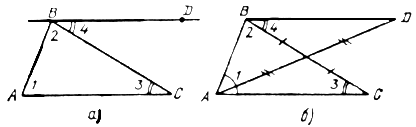
Ð1 + Ð2 + Ð3 = Ð1 + Ð2 + Ð4 = 180°.
Свойства внешнего угла треугольника.
ÐВСD = ÐА + ÐВ;
ÐВСD > ÐА;
ÐВСD > ÐВ.
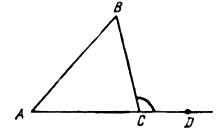
S = ![]()
![]() – формула Герона.
– формула Герона.
S = 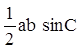 .
.
S = rp, где r – радиус вписанной окружности, р – полупериметр.
r = ![]() S
=
S
= 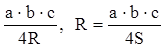 .
.
|
Решение треугольников |
|||
|
|
Дано |
Найти |
Решение |
|
|
1. а, ÐВ,
|
ÐА, b, с |
ÐА = 180° – (ÐВ + ÐС)
|
|
|
Дано |
Найти |
Решение |
|
|
2. b, с, ÐА |
а, ÐВ, ÐС |
ÐВ и ÐС – по таблицам |
|
|
3. а, b, с |
ÐА, ÐВ, ÐС |
а2 = b2+ с2– 2bс cos A
ÐA – по таблицам
ÐВ – по таблицам ÐС = 180° – (ÐА + ÐВ) |
|
|
4. а, с, ÐА |
b, ÐВ, ÐС |
ÐВ = 180° – (ÐА + ÐС)
|
Прямоугольный треугольник.
1. Теорема Пифагора с2 = а2 + b2.
2. b2 = с · сb, са, сb – проекции катетов на гипотенузу.
3. h2 = cb · ca
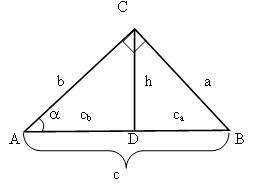
4.
Если a
= 30°, то ![]()
5.
Радиус описанной окружности R: 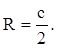
6.
Радиус вписанной окружности: ![]()
7.
Площадь 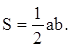
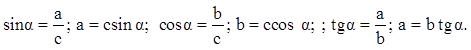
Произвольный треугольник.
1. Теорема косинусов
с2 = а2 + b2 – 2аb cos C
с2 = а2 + b2 – 2bbа
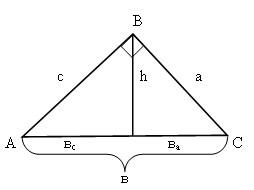
2. Теорема синусов
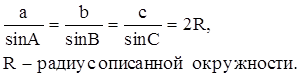
3. Площадь треугольника.
![]()
II. Решение задач по готовым чертежам.
1. Найти равные треугольники.
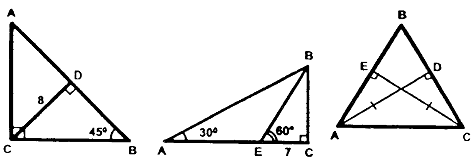
2. Найти: АВ. Найти: АЕ. Дано: АВ = ВС.
Доказать: АD = СЕ.
3. Найдите неизвестные углы треугольника.
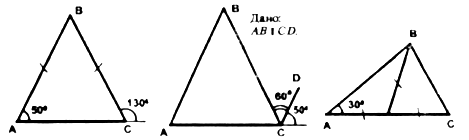
4. Дано: DАВС ~ DА1В1С1.
Найти: х, у, z.
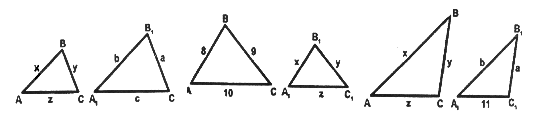
Дано: а : в : с = 5 :
6 : 7, Дано: ![]() = 9. Дано: РАВС = 39
= 9. Дано: РАВС = 39
Р∆АВС = 108.
![]() = 26, а : в = 2 :
3
= 26, а : в = 2 :
3
5. Указать подобные треугольники, доказать их подобие.
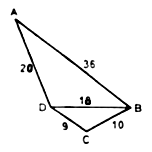
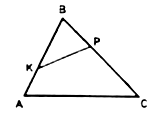
Дано: АВ ∙ ВК = СВ ∙ ВР
Доказать, что ∆АВС ~ ∆А1В1С1
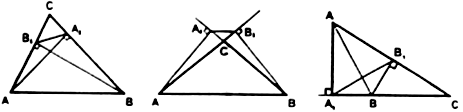
6. Решить треугольники (для учащихся с высоким уровнем подготовки).
Найти: х, у.
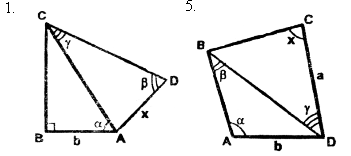
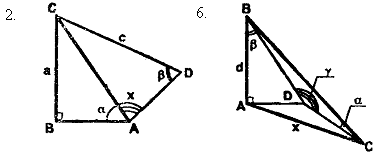
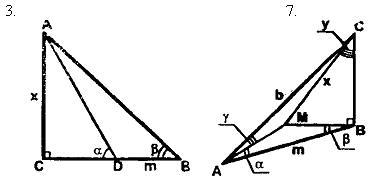
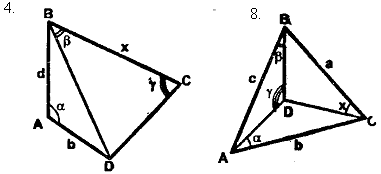
Ответы: Рис.
1. 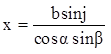 ;
рис. 2.
;
рис. 2. ![]() ;
;
рис. 3. 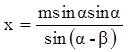 ;
рис. 4.
;
рис. 4. 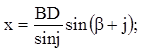
![]()
рис. 5. 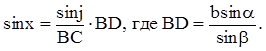
ВС = ![]() ;
;
рис. 6. ![]() где
АD = d tgb,
где
АD = d tgb,
DС = ![]() ;
;
рис. 7. х = ![]() tg
J =
tg
J = ![]() где
МВ =
где
МВ = 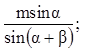
![]() ;
;
рис. 8. 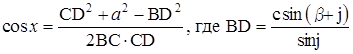 ;
;
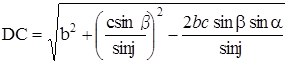 .
.
Тест 1 «Признаки равенства треугольников»
Вариант I.
1. Укажите, на каком из рисунков есть равные треугольники.
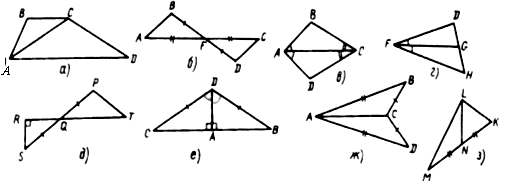
2. Так как АС – биссектриса ÐBAD и АВ = АD, то ΔВАС = ΔСАD:
а) по двум сторонам и углу между ними;
б) по стороне и прилежащим к ней углам;
в) по трем сторонам.
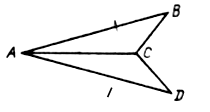
3. ΔАВС – равнобедренный. АД и СF – биссектрисы углов CAB и АСВ coответственно. Тогда ΔАДС = ΔСFA: а) по двум сторонам и углу между ними; б) по стороне и прилежащим к ней углам; в) по трем сторонам.
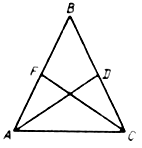
4. ΔDEA = ΔFEB. Тогда ΔAKB
а) разносторонний; б) paвносторонний; в) равнобедренный.
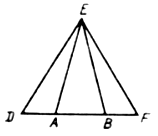
5. В треугольнике ABC ÐАВС = 90°, AD = BD = DC, ÐBCD = 64°.
Найдите: ÐDAB.
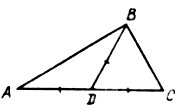
6. В равнобедренном треугольнике АВС проведена медиана АД. Если периметр ΔABC равен 50 см, а периметр ΔABD – 30 см, то длина AD равна: а) 10 см: б) 5 см; в) 20 см; г) 35 см.
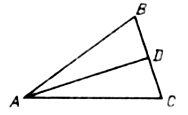
7. Периметр треугольника RQP равен 34 см, а сторона RQ – 12 см. Если Ða = Ðb, то сторона RP равна: а) 11 см; б) 10 см; в) 12 см; г) 23 см.
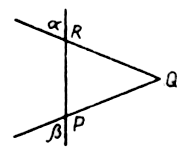
8. Треугольник RST – равнобедренный. Определите Ð1, если Ð2 = 112°.
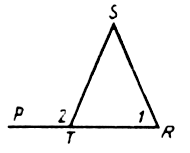
9. DA – медиана равнобедренного треугольника ВDC с основанием СВ: ÐD = 120°.
Найдите углы ΔADС.
Вариант II.
1. Укажите, на каком из рисунков есть равные треугольники.
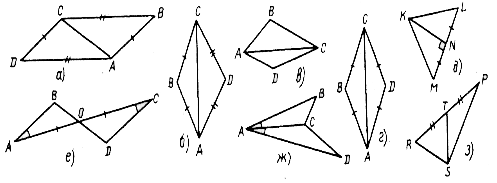
2. Так как AD = АВ и ВС = DC, то ΔВAС = ΔDAС:
а) по двум сторонам и углу между ними;
б) по стороне и прилежащим к ней углам;
в) по трем сторонам.
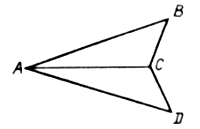
3. ΔВAС – равнобедренный. АD и CF – медианы. Тогда ΔADC = ΔCFA:
а) по двум сторонам и углу между ними;
б) по стороне и прилежащим к ней углам;
в) по трем сторонам.
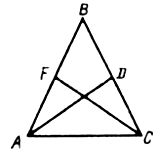
4. Треугольник DGH – равнобедренный. Определите Ð2, если Ð1 = 67°.
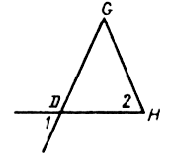
5. ΔAВC – равносторонний, АF = BG = CD.
Тогда ΔFGD: а) разносторонний; б) равносторонний; в) равнобедренный.
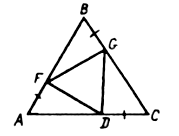
6. В равнобедренном треугольнике AВС медиана ВD = 8 см. Если периметр ΔABD равен 28 см, то периметр треугольника ABC равен: а) 40 см; б) 50 см; в) 20 см; г) 36 см.
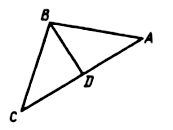
7. Периметр треугольника АBG равен 38 см, а сторона FB – 14 см. Если ÐBFA = ÐBGD, то сторона FG равна: а) 14 см; б) 10 см; в) 12 см; г) 26 см.
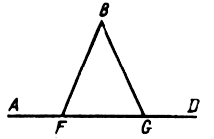
8. В треугольнике ABC AD = BD = DC, ÐA = 37°, ÐC = 53°.
Найдите ÐABC.
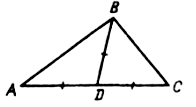
9. ΔADB – равносторонний, сторона DB является медианой треутольника ABC; ÐВСА = 30°.
Определите углы ΔBDC.
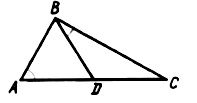
Ключ к тесту 1
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
I |
б, в, с, ж |
а |
б |
в |
26° |
5 |
б |
69° |
30°, 60°, 90° |
|
II |
а, г, д, е |
в |
а |
67° |
б |
а |
б |
90° |
30°, 120°, 30° |
Тест 2 «Сумма углов треугольника»
Вариант I.
1. Прямые ВС и AD параллельны. Угол ВСА в треугольнике ADС равен 34°. Чему равен угол DAС в треугольнике ADC?
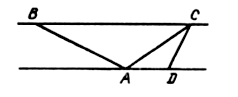
2. Треугольник ABC – равносторонний.
Найдите его углы.
3. Определите взаимное расположение биссектрис внешних углов DBA и FAB равнобедренного прямоугольного треугольника ABC. Они: а) перпендикулярны; б) параллельны; в) пересекаются под углом, не равным 90°.
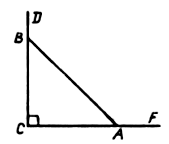
4. Ð1+ Ð2 = 180°, Ð3 > Ð4. Какие из прямых с, d и е параллельны?
Ответ: а) с || е; б) с || d; в) e || d.
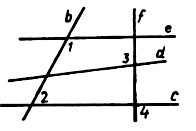
5. В тупоугольном треугольнике ABC (ÐABC = 105°) высота BD = 10 см отсекает равнобедренный треугольник ABD, тогда сторона ВС равна: а) 20 см; б) 10 см; в) 5 см; г) 30 см.
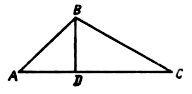
6. Могут ли в треугольнике два угла быть прямыми?
7. Треугольник СDЕ – равнобедренный, АВ || CD. Укажите, какие углы треугольника FDC равны соответствующим углам треугольника ABF.
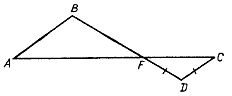
8. Если у треугольника два внешних угла равны, то он является: а) равносторонним; б) равнобедренным; в) произвольным.
9. Какой из рисунков содержит равные треугольники?
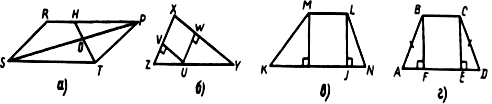
Вариант II.
1. Определите взаимное расположение биссектрисы внешнего угла DBC равнобедренного треугольника ABC и его основания АС. Они:
а) перпендикулярны;
б) параллельны;
в) пересекаются под углом, не равным 90°.
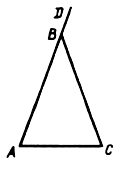
2. Ð1 = Ð2, Ð3 ¹Ð4.
Какие из прямых с, d и е параллельны?
Ответ: а) с || е; б) с || d; в) е || d.
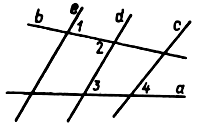
3. Прямые ВС и AD параллельны. Угол CBD в треугольнике BCD paвен 31°. Чему равен ÐBDА в треугольнике ABD?
4. Треугольник ABC – прямоугольный равнобедренный (АВ = ВС). Найдите его углы.
5. В прямоугольном треугольнике ABC медиана CD отсекает равносторонний треугольник CBD. Расстояние от точки D до катета АС равно 10 см, тогда гипотенуза АВ равна: а) 10 см; б) 20 см; в) 30 см; г) 40 см.
6. Могут ли в треугольнике два угла быть тупыми?
7. DF – высота прямоугольного треугольника ADB. Укажите, какие углы треугольника ADF равны соответствующим углам треугольника ABD.
8. Если у треугольника один из внешних углов острый, то треугольник: а) остроугольный; б) прямоугольный; в) тупоугольный.
9. Какой из рисунков содержит равные треугольники?
Ключ к тесту 2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
I |
34° |
60° |
в |
а |
а |
нет |
ÐFCD ÐDFC ÐFDC |
б |
г, а |
|
II |
б |
в |
31° |
45°, 90°, 45° |
г |
нет |
ÐАFD ÐDАF ÐАDF |
в |
a, в |
Тест 3 «Теорема Пифагора»
Вариант I.
1. Укажите, какой из рисунков содержит треугольники, к которым применима теорема Пифагора.

2. Диагонали ромба равны 12 см и 16 см, тогда его
сторона равна: а) 10 см; б) ![]() см; в) 2 см; г)
см; в) 2 см; г) ![]() см.
см.
3. В прямоугольном треугольнике ABC: АС = 13 см, АВ = 12см, ВС = 5см.
Найдите sin С.
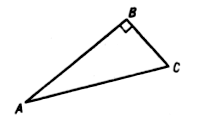
4. Из точки А к окружности с центром в точке О проведена касательная АС. Отрезок ОА равен 20 см, а ОС – 16 см, тогда длина отрезка СА равна:
а) 2 см; б) ![]() см;
см;
в) 12 см; г) 6 см.
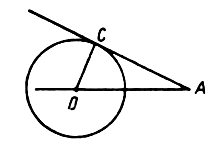
5. Из одной точки на прямую опущены перпендикуляр и наклонная. Если проекция наклонной равна 12 см, а перпендикуляр – 5 см, то длина наклонной равна:
а) ![]() см;
б)
см;
б) ![]() см;
в) 13 см; г)
см;
в) 13 см; г) ![]() см.
см.
6. Сторона равностороннего треугольника равна 8 см, а его медиана равна:
а) 4 см; б) ![]() см;
в) 2 см; г)
см;
в) 2 см; г) ![]() см.
см.
7. Две окружности равных радиусов с центрами в точках О и О1 пересекаются в точках А и В. Одна сторона треугольника АОВ равна 13 см, другая – 6 см. Определите расстояние между центрами окружностей.
8. В окружности с центром в точке О и радиусом, равным
10 см, проведена хорда GС. Если хорда GС = 16 см, то расстояние от центра
окружности до нее равно: а) ![]() см;
б) 6 см; в)
см;
б) 6 см; в) ![]() см; г)
см; г) ![]() см.
см.
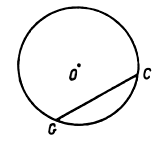
9. Дан прямоугольный треугольник ABC. В нем гипотенуза АС = 10 см, cos С = 0,25. Найдите катет ВС.
Вариант II.
1. Укажите, какой из рисунков содержит треугольники, к которым применима теорема Пифагора.
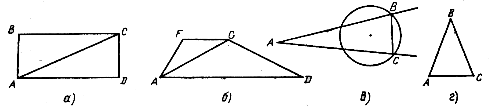
2. Сторона квадрата равна 3 см, тогда его диагональ равна:
а) 9 см; б) ![]() см;
в)
см;
в) ![]() см;
г)
см;
г) ![]() см.
см.
3. В равнобедренном треугольнике боковая сторона равна
10 см, а основание – 16 см, тогда высота, опущенная на основание, равна: а) 2![]() см;
б) 6 см; в)
см;
б) 6 см; в) ![]() см; г)
см; г) ![]() см.
см.
4. Из одной точки на прямую опущены перпендикуляр и наклонная. Если перпендикуляр равен 9 см, а наклонная – 15 см, то длина проекции наклонной равна:
а) 12 см; б) ![]() см;
в)
см;
в) ![]() см;
г)
см;
г) ![]() см.
см.
5. Из точки D к окружности с центром в точке О проведена касательная DF. Если OD = 17 см, a FD = 15 см, то радиус окружности равен:
а) ![]() см;
б) 8 см;
см;
б) 8 см;
в) 32 см; г) ![]() см.
см.
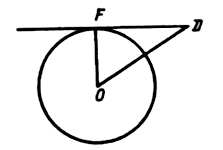
6. Дан прямоугольный треугольник ABC. Гипотенуза АС = 10 см, sin С = 0,3. Найдите катет АВ.
7. В равнобедренном треугольнике одна сторона равна 11 см, а вторая – 4 см. Найдите третью сторону.
8. В прямоугольном треугольнике ABC: АС = 17см, ВС = 8 см, АВ = 15 см.
Найдите cos С.
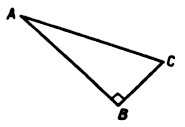
9. В окружности с центром в точке О проведена хорда АВ, равная 18 см. Если расстояние от центра окружности до хорды равно 12 см, то радиус окружности равен:
а) 15 см; б) ![]() см;
см;
в) ![]() см;
г)
см;
г) ![]() см.
см.
Ключ к тесту 3
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
I |
в |
а |
|
в |
в |
б |
|
б |
2,5 |
|
II |
а |
г |
б |
а |
б |
3 |
11 |
|
15 |
Уроки 6–7
ЧЕТЫРЕХУГОЛЬНИКИ
Цель: систематизировать, обобщить и расширить знания.
I. Актуализация опорных теоретических знаний.
Опорная таблица
|
Определения |
||||
|
Параллелограмм
АВ || DС, АД || ВС |
Прямоугольник
ÐА = ÐВ = 90° |
Ромб
АВ = ВС= СD = АD |
Квадрат
|
|
|
Свойства |
||||
|
1) Диагонали в точке пересечения делятся пополам. 2) Диагонали делят на два равных треугольника. 3) Противоположные стороны и углы равны |
Диагонали равны |
Диагонали перпендикулярны и являются биссектрисами углов |
|
|
|
Ключевая задача АС2 + ВD2 = = 2 (АD2 + АВ2) |
Признаки |
|
|
|
|
1. Если АD = ВС, АD = DС, то АВСD – параллелограмм |
Если у паралеллограмма диагонали равны, то АВСD – прямоугольник |
1. Если у параллелограмма диагонали перпендикулярны, то АВСD – ромб |
|
|
|
2. Если АD = ВС, АD || ВС, то АВСD – параллелограмм |
|
2. Если у параллелограмма диагонали являются биссектрисами, то АВСD – ромб |
|
|
|
3. Если АО = ОС, DО = ОВ, то АВСD – параллелограмм |
|
|
|
|
|
Площади S = ah, где а – основание, h – высота. S = aв sin a |
S = aв |
|
S = a2, где а – сторона |
|
Трапеция
ВС, АD – основание, АВ, СD – боковые стороны, СН – высота.
MN – средняя линия.
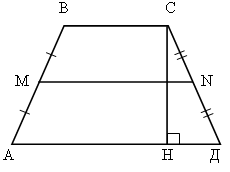
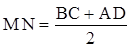 .
.
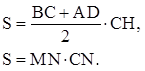
Ключевая задача.
а + в = d + c
Виды:
прямоугольная равнобокая
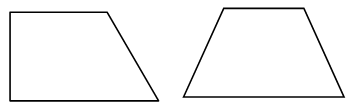
II. Решение задач по готовым чертежам.
1. Найти площадь х.
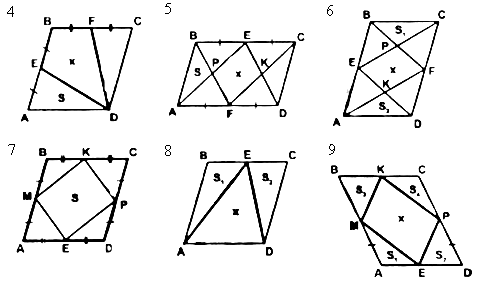
Ответы: 1. 7; 2. 12; 3. 2; 4. 2S; 5. 2S; 6. S1 + S2; 7. 2S; 8. S1 + S2; 9. S1 + S2 + S3 + S4.
2. Найти площадь трапеции.
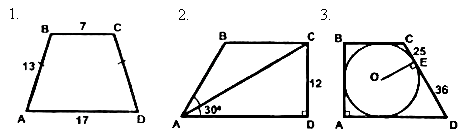
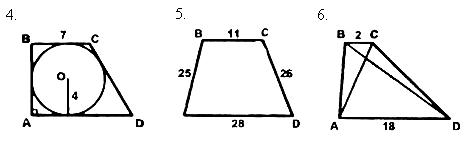
Дано: АС = 7, ВD = 15.
Ответы: 1.
144; 2. 120![]() ; 3. 3630; 4. 65
; 3. 3630; 4. 65![]() ;
5. 468; 6. 42.
;
5. 468; 6. 42.
3. Найти отношение площадей: ![]() .
.
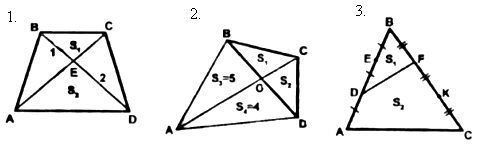
Дано: АВСD –
трапеция
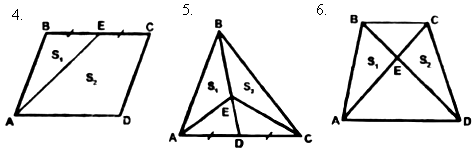
Дано: АВСD – Дано: АВСD –
параллелограмм. трапеция.
Ответы:
1. ![]() ;
2.
;
2. ![]() ;
3.
;
3. ![]() ;
4.
;
4. ![]() ;
5. 1; 6. 1.
;
5. 1; 6. 1.
III. Выполнение тестов.
Тест 1 «Четырехугольники»
Вариант I.
1. Периметр параллелограмма ABCD равен 30 см, а его диагональ BD – 9 см. Найдите периметр DABD.
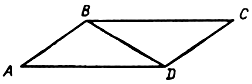
2. Периметр квадрата равен 24 см. Найдите его сторону.
3. Отрезки BF и DC перпендикулярны и точкой пересечения делятся пополам. Тогда четырехугольник BDFC является:
а) прямоугольником;
б) трапецией;
в) ромбом;
г) параллелограммом.
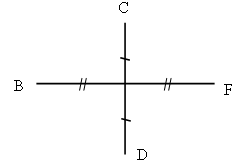
4. Отрезки АВ и CD – диаметры окружности. Тогда четырехугольник BDAC является:
а) прямоугольником;
б) квадратом;
в) ромбом;
г) параллелограммом.
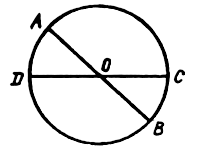
5. В параллелограмме ABCD сумма двух углов равна 132°. Определите градусную меру углов параллелограмма.
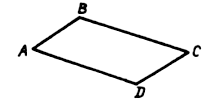
6. Дана равнобокая трапеция ABCD, О – точка пересечения ее диагоналей. Укажите хотя бы одну пару равных треугольников.
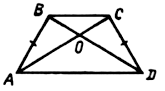
7. В равностороннем треугольнике ABC проведена средняя линия DF. Вычислите периметр четырехугольника ADFC, если периметр DFBD равен 27 см.
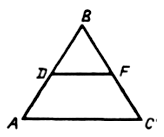
8. В трапеции ABCD средняя линия FG равна 8 см, а основание AD – 12 см. Она пересекает диагональ BD в точке К, тогда отрезок КG равен:
а) 6 см; б) 4 см;
в) 2 см; г) 10 см.
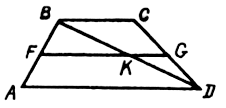
9. Большая диагональ ромба делит его на два равных треугольника. Эти треугольники являются по сторонам: а) разносторонними; б) равносторонними; в) равнобедренными; по углам: а) остроугольными; б) прямоугольными; в) тупоугольными.
Вариант II.
1. Периметр прямоугольника ABCD равен 34 см, а его диагональ АС – 13 см. Найдите периметр DABD.
2. Периметр ромба равен 36 см. Найдите его сторону.
3. Отрезки BF и DC точкой пересечения делятся пополам. Тогда четырехугольник BDFC является: а) прямоугольником; в) ромбом; г) параллелограммом.
4. Отрезки BF и CD – диаметры окружности, пересекающиеся под прямым углом. Тогда четырехугольник BDFC является: а) прямоугольником; б) квадратом; в) ромбом; г) параллелограммом.
5. В равнобокой трапеции ABCD сумма двух углов равна 212°. Определите градусную меру углов трапеции.
6. Дан параллелограмм ABCD, О – точка пересечения его диагоналей. Укажите хотя бы одну пару равных треугольников.
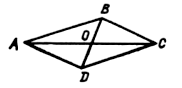
7. В равностороннем треугольнике ABC проведены средние линии FG и DF. Найдите периметр четырехугольника ADFG, если периметр треугольника FBD равен 27 см.
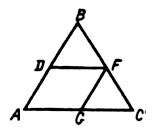
8. В трапеции ABCD с основанием АD = 12 см и ВС = 4 см проведена средняя линия FG. Она пересекает диагональ ВD в точке К, а диагональ АС в точке L, тогда отрезок KL равен: а) 16 см; б) 4 см; в) 8 см; г) 2 см.
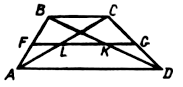
9. Диагональ квадрата делит его на два равных треугольника. Эти треугольники являются: по сторонам: а) разносторонними; б) равносторонними; в) равнобедренными; по углам: а) остроугольными; б) прямоугольными; в) тупоугольными.
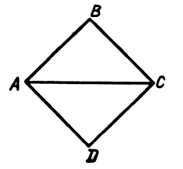
Ключ к тесту «Четырехугольники»
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
I |
24 |
6 |
в |
а |
114°, 66°, 66°, 114° |
DАВD = DАDС |
45 см |
2 |
в, в |
|
II |
30 |
6 |
г |
в |
106°, 106°, 74°, 74° |
DАDВ= DDОС |
36 |
4 |
в, б |
Тест 2 «Площади фигур»
Вариант I.
1. В треугольнике ABC основание АС равно 8 см, а высота, опущенная на АС, равна 7 см. Найдите площадь треугольника ABC.
2. Если в равнобедренном треугольнике АВС (АВ = ВС) АВ = 5 см и АС = 8 см, то его площадь равна:
а) 40 см2; б) 48 см2; в) 24 см2; г) 12 см2.
3. Если диагональ квадрата равна 8 см, то его площадь равна:
а) 64 см2; б) 256 см2; в) 32 см2; г) 128 см2.
4. В трапеции ABCD проведены диагонали АС и BD. Площадь треугольника АВD равна 57 см2. Определите площадь треугольника ACD.
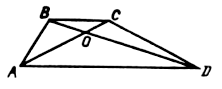
5. Основания трапеции ABCD равны 17 см и 9 см, а высота 4 см. Найдите площадь трапеции.
6. В параллелограмме АВСD стороны равны 4 см и 7 см, а угол между ними составляет 45°, тогда его площадь равна:
а) 7![]() см2;
б) 14
см2;
б) 14![]() см2;
см2;
в) 28 см2; г) 28![]() см2.
см2.
7. Площадь круга, вписанного в квадрат со стороной 12 см, равна:
а) 36p см2; б) 12p см2;
в) 72p см2; г) 18p см2.
8. Дан равносторонний треугольник. Найдите площадь заштрихованной фигуры, используя данные рисунка.
9. В треугольнике ABC проведена средняя линия FG. Тогда:
а) площади DАВС и DFBG равны;
б) площадь DFBG равна половине площади DАВС;
в) площадь DFBG равна одной четвертой площади DАВС.
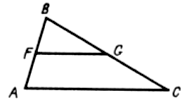
Вариант II.
1. В треугольнике ABC сторона АС равна 6 см, а высота, опущенная на АС, равна 9 см. Найдите площадь треугольника ABC.
2. Если в равностороннем треугольнике АВС сторона АВ =
12 см, то его площадь равна: а) 36![]() см2;
б) 72
см2;
б) 72![]() см2;
в) 72 см2; г) 144 см2.
см2;
в) 72 см2; г) 144 см2.
3. Площадь круга, описанного около правильного шестиугольника со стороной 6 см, равна:
а) 12p см2; б) 36p см2; в) 72p см2; г) 18p см2.
4. Средняя линия трапеции АВСD равна 13 см, а сторона АВ, равная 12 см, образует с основанием AD угол в 30°. Найдите площадь трапеции.
5. В прямоугольнике одна из сторон равна 6 см, а диагональ – 10 см, тогда его площадь равна:
а) 24 см2; б) 60 см2; в) 48 см2; г) 30 см2.
6. Если диагонали ромба равны 10 см и 24 см, то его площадь равна: а) 240 см2; б) 30 см2; в) 60 см2; г) 120 см2.
7. Дан квадрат; найдите площадь заштрихованной фигуры, используя данные рисунка.

8. В параллелограмме ABCD проведены диагонали АС и ВD.
Площадь треугольника ABD равна 72 см2. Найдите площадь треугольника ACD.
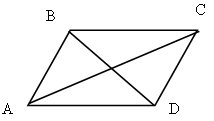
9. В треугольнике ABC проведены средние линии FG и ДF. Тогда: а) площади четырехугольника ADFG и треугольника FBG равны;
б) площадь четырехугольника ADFG равна половине площади треугольника АВС;
в) площадь четырехугольника ADFG равна одной четвертой площади треугольника ABC.
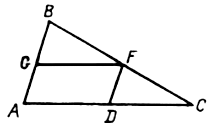
Ключ к тесту
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
I |
28 |
г |
в |
57 см2 |
52 см2 |
б |
а |
|
в |
|
II |
27 |
а |
б |
78 см2 |
в |
г |
16–4p |
72 см2 |
б |
Домашняя контрольная работа.
Вариант I.
1. В треугольнике ABC проведена высота BD (точка D лежит на отрезке АС). Найдите площадь треугольника ABC, если АВ = 25 см, БС = 26 см, BD = 24 см.
2. Диагонали ромба относятся как 8 : 15, а его площадь равна 240 см2. Найдите диагонали ромба.
3. Площадь треугольника равна 18 см2, а радиус окружности, вписанной в треугольник, – 4 см. Найдите периметр треугольника.
4. Найдите площадь прямоугольной трапеции, основания которой равны 4 см и 9 см, а одна из боковых сторон на 1 см больше другой.
Вариант II.
Боковая сторона равнобедренного треугольника равна 17 см, а его периметр – 50 см. Найдите площадь треугольника.
2. В ромбе с площадью 98 см2 один из углов равен 150°. Найдите периметр ромба.
3. Боковая сторона равнобедренного треугольника равна 40 см, а высота, проведенная к основанию, – 32 см.
Найдите радиус окружности, описанной около треугольника.
4. Найдите площадь равнобокой трапеции, основания которой равны 11 см и 25 см, а диагонали являются биссектрисами тупых углов.
Вариант III.
1. Высота равностороннего треугольника равна 12 см. Найдите площадь треугольника, для которого стороны данного треугольника являются средними линиями.
2. Точка касания окружности, вписанной в ромб, делит его сторону на отрезки 9 см и 16 см. Найдите его диагонали.
3. Периметр прямоугольного треугольника равен 24 см, а радиус вписанной окружности – 2 см. Найдите радиус окружности, описанной около треугольника.
4. Боковые стороны и высота трапеции соответственно равны 30 см, 25 см и 24 см. Найдите площадь трапеции, если биссектрисы ее тупых углов пересекаются на большем основании.
Уроки 8–9
многоугольники
Цель: систематизировать, обобщить и расширить знания.
Ход урока
I. Беседа по опорной таблице.
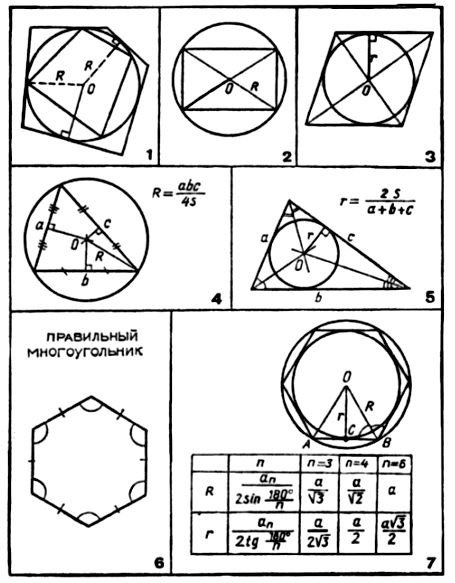
Вопросы для учащихся:
– Что значит многоугольник вписан в окружность (или окружность описана около многоугольника)?
– Что значит многоугольник описан около окружности (окружность вписана в многоугольник) (по рис. 1)?
– Во всякий ли многоугольник можно вписать окружность?
– Около всякого ли многоугольника можно описать окружность (рис. 2, 3)?
– Что можно сказать о комбинации окружности и треугольника (рис. 4, 5)?
– Совпадают ли центры вписанной и описанной окружностей для треугольника?
–
Где расположен центр описанной окружности около прямоугольного треугольника? (![]() где С – гипотенуза.)
где С – гипотенуза.)
– По каким формулам можно найти R и r, если известны стороны треугольника (рис. 4, 5)?
– Что можно сказать о комбинации окружностей и правильных многоугольников (рис. 6, 7)?
II. Практическая работа.
– Как вписать и описать окружность в многоугольник?
|
I вариант |
II вариант |
|
1. Вписать окружность
|
1. Описать окружность
|
|
2. Описать окружность
|
2. Вписать окружность
|
|
3. Построить правильный многоугольник |
|
|
|
|
III. Устное решение задач по готовым чертежам.
1. Найти х, у (О – центр окружности).
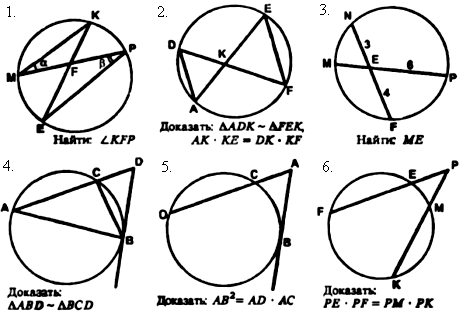
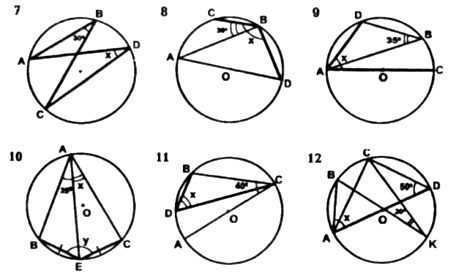
2. Доказать.
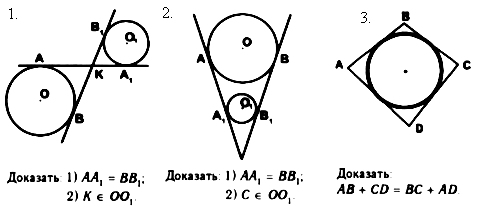
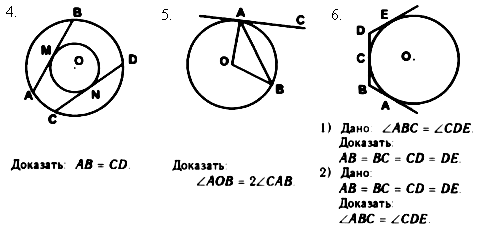
Окружность и круг
S(O, r) – обозначение окружности,
D = AB – диаметр, R = OC – радиус,
D = 2R, MN – хорда, ÈMN – дуга,
С = 2pR = pD, где p » 3,14 длина окружностей.
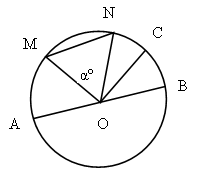
![]()
Свойства.
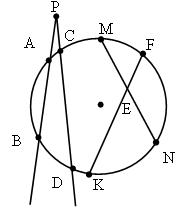
АВ, ВД – касательные,
1) АВ = ВD, ВО – биссектриса угла АВD.
2) ОА ^ АВ.
(MN, KF – хорды, РВ, РD – секущие)
3) МЕ · ЕN = FE · EK.
4) FH · HD = CP · DP.
Sкруга = pR2 = ![]() ,
,
С – длина окружности,
D – диаметр.
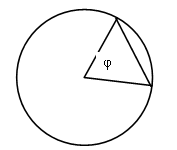
Sсектора = ![]()
Sсегмента = 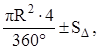
если φ < 180°, то берем знак «–»,
если φ > 180°, то знак «+».
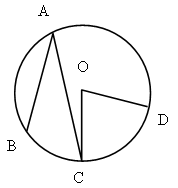
ÐВАС – вписанный,
ÐСОD – центральный.
ÐСОD = È СD,
ÐВАС = ![]() È
ВС.
È
ВС.
Тест «Окружность»
Вариант I.
1. На каком из рисунков есть равные треугольники?
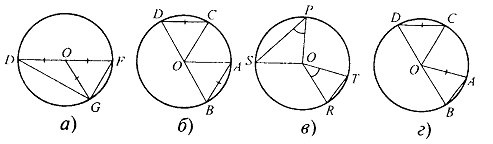
2. Дана окружность с центром в точке О. Тогда треугольник ВОА:
а) разносторонний;
б) равносторонний;
в) равнобедренный (но не равносторонний).
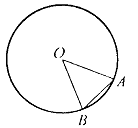
3. В окружности с центром в точке О отрезок ОС перпендикулярен диаметру АВ. Определите углы треугольника воС.
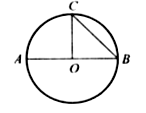
4. Радиус окружности с центром в точке О равен 7 см, ÐBAO = 60°. Найдите хорду АВ.
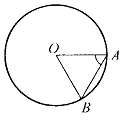
5. DB – касательная к окружности с центром в точке О, В – точка касания, треугольник BOA – равносторонний. Найдите угол ABD.
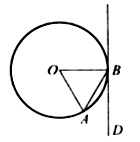
6. Из точки К к окружности с центром в точке О проведены касательная КМ и секущая KN. ÐNKM = 28°. Найдите другие углы треугольника ОМК.
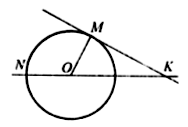
7. Дана окружность с центром в точке О, медиана ОС треугольника ABC равна 6 см. Найдите диаметр окружности.
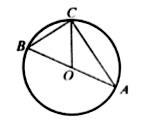
8. Треугольник ABC описан около окружности с центром в
точке О,
ÐСАО
= 27°. Найдите угол ВАО.
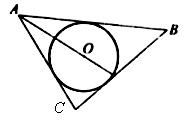
9. Даны две концентрические окружности. АС и BD – их диаметры. Треугольники АВО и CDO равны:
а) по двум сторонам и углу между ними; б) по стороне и прилежащим к ней углам; в) по трем сторонам.
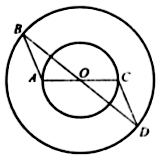
Вариант II.
1. На каком из рисунков есть равные треугольники?
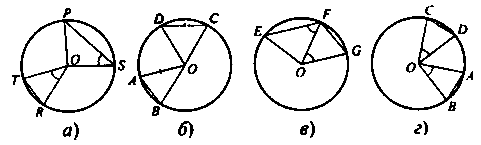
2. Дана окружность с центром в точке О. Хорда АВ равна радиусу. Тогда треугольник BOA:
а) разносторонний;
б) равносторонний;
в) равнобедренный (но не равносторонний).
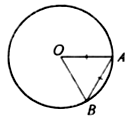
3. АС – диаметр окружности с центром в точке О, ÐAOB = 24°. Определите углы треугольника ВОС.
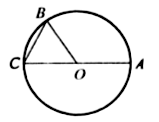
4. Радиус окружности с центром в точке О равен 8 см, ÐAOB = 60°. Найдите хорду АВ.
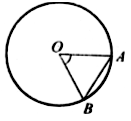
5. DB – касательная к окружности с центром в точке О, В – точка касания, треугольник BOA – прямоугольный. Найдите угол ABD.
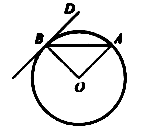
6. Из точки С к окружности с центром в точке О проведены касательная СА и секущая СВ. ÐACB = 39°. Найдите другие углы треугольника CAB.
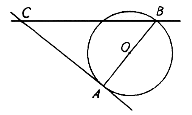
7. АВ – диаметр окружности с центром в точке О, высота СF треугольника ABC равна 9 см. Найдите хорду CG.
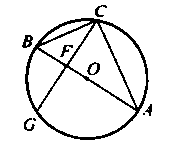
8. Треугольник ABC описан около окружности с центром в точке О. Тогда:
а) ÐCAO > ÐBAO;
б) ÐCAO < ÐBAO;
в) ÐCAO = ÐBAO.
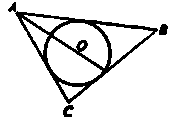
9. АВ и CD – диаметры окружности с центром в точке О. Треугольники DOА и СОВ равны:
а) по двум сторонам и углу между ними; б) по стороне и прилежащим к ней углам; в) по трем сторонам.
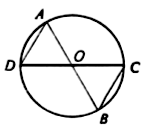
Ключ к тесту
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
I |
б |
в |
90°, 45°, 45 |
7 см |
30° |
90°, 62° |
12 |
27 |
а |
|
II |
г |
б |
56°, 62°, 62° |
8 с м |
45° |
90°, 51° |
18 |
в |
а |
Домашняя самостоятельная работа.
Окружность и многоугольник
Вариант I.
1. Высота треугольника равна 15 см и делит его сторону на отрезки длиной 8 см и 20 см. Найдите радиусы описанной и вписанной окружностей треугольника.
2. Высота равнобедренного треугольника, проведенная к основанию, равна 32 см, а радиус окружности, вписанной в треугольник, равен 12 см. Найдите радиус окружности, описанной около треугольника.
3. Центр окружности, описанной около равнобедренного треугольника, делит медиану, проведенную к основанию, в отношении 25 : 7. Боковая сторона треугольника равна 40 см. Найдите радиус окружности, вписанной в треугольник.
4. Точка касания вписанной окружности делит гипотенузу прямоугольного треугольника на отрезки 4 см и 6 см. Найдите радиусы описанной и вписанной окружностей.
5. В прямоугольном треугольнике радиусы описанной и вписанной окружностей соответственно равны 10 см и 4 см. Найдите периметр треугольника.
6. Периметр прямоугольника равен 46 см. Биссектриса прямого угла делит диагональ в отношении 8 : 15. Найдите длину окружности, описанной около прямоугольника.
7. Высота ромба, проведенная из вершины тупого угла, делит его сторону на отрезки 7 см и 18 см. Найдите радиус окружности, вписанной в ромб.
8. Основания прямоугольной трапеции равны 21 см и 14 см. Найдите радиус окружности, вписанной в трапецию.
9. Центр окружности, описанной около трапеции, лежит на большем основании. Найдите радиус окружности, если высота и диагональ трапеции соответсенно равны 24 см и 40 см.
10. Около трапеции со средней линией 6 см описана окружность. Угол между радиусами окружности, проведенными к концам боковой стороны, равен 120°. Найдите площадь трапеции.
Вариант II.
1. Две стороны остроугольного треугольника равны 13 см и 15 см, а высота, проведенная к третьей стороне, – 12 см. Найдите радиусы описанной и вписанной окружностей треугольника.
2. Центр окружности, вписанной в равнобедренный треугольник с основанием 48 см, делит высоту, проведенную к основанию, в отношении 3 : 5, считая от основания. Найдите радиус окружности, описанной около треугольника.
3. Высота равнобедренного треугольника, проведенная к основанию, равна 64 см, а диаметр вписанной окружности равен 48 см. Найдите радиус окружности, описанной около треугольника.
4. Точка касания вписанной окружности делит катет прямоугольного треугольника на отрезки 2 см и 6 см, считая от вершины прямого угла. Найдите радиусы описанной и вписанной окружностей.
5. Радиус окружности, вписанной в прямоугольный треугольник с периметром 72 см, равен 6 см. Найдите радиус описанной окружности.
6. Разность сторон прямоугольника равна 14 см. Биссектриса прямого угла делит диагональ в отношении 5 : 12. Найдите длину окружности, описанной около прямоугольника.
7. Точка касания окружности, вписанной в ромб, делит его сторону на отрезки 9 см и 16 см. Найдите высоту ромба.
8. Основания равнобокой трапеции равны 8 см и 18 см. Найдите радиус окружности, вписанной в трапецию.
9. В полукруг вписана трапеция с меньшим основанием 14 см, параллельным диаметру, и высотой 24 см. Найдите радиус полукруга.
10*. Около трапеции с высотой 6 см описана окружность. Угол между радиусами окружности, проведенными к концам боковой стороны, равен 60°. Найдите площадь трапеции.
Урок 10
Преобразование фигур
Цели: систематизировать знания и умения учащихся по теме, закрепить навыки построения образа фигуры при любом преобразовании.
I. Актуализация опорных теоретических знаний.
Преобразование фигур
(Смещение каждой точки фигуры каким-нибудь способом)
|
Движение
|
Подобие
в k раз)
|
Такое преобразование фигуры Ф в Ф1, при котором каждая точка Х переходит в точку Х1 следующим образом:
![]()
Свойства преобразования:
1. Точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок расположения.
2. Прямая переходит в прямую.
3. Отрезок переходит в отрезок.
4. Луч переходит в луч.
5. Сохраняется величина углов.
6. Результат последовательного выполнения движения является движением.
7. Преобразование, обратное движению, является движением.
II. Задачи для устного решения.
Осевая симметрия.
1. Точка А симметрична точке В относительно оси L. Как расположен отрезок АВ по отношению к прямой l?
2. Точки А и A1 принадлежат одному перпендикуляру к прямой l. Можно ли утверждать, что они симметричны относительно прямой L?
3. Как располагаются по отношению к оси симметрии вершины треугольника, симметричного треугольнику ABC относительно оси АВ?
4. Даны полуплоскость с границей а, ось симметрии l, причем а ¹ 1, а Ç l = А. Как построить образ данной полуплоскости при заданной осевой симметрии?
5. Некоторая точка А (х, у) координатной плоскости отображается при осевой симметрии с осью Ох на точку А1. Запишите координаты точки А1.
6. Точки В(c; …) и В1(…; d) симметричны относительно оси Оу. Восстановите пропущенные координаты точек.
7. Ученик строил треугольник А1В1С1, симметричный треугольнику АВС относительно оси l. Верно ли выполнено построение?
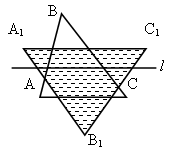
8. На берегу канала требуется построить водонапорную башню для снабжения водой двух селений А и В. Выберите места для башни с таким расчетом, чтобы общая длина труб от нее до обоих селений была наименьшей.
Симметрия фигур
1. Сколько осей симметрии имеет фигура, которая является объединением: а) двух точек, б) трех точек?
2. Фигура Ф является объединением прямой а и окружности с. Имеет ли фигура Ф оси симметрии?
3. Треугольник имеет ось симметрии. Какой отсюда можно сделать вывод о положении вершин данного треугольника относительно этой оси? Каким по виду может быть треугольник?
4. Нарисуйте фигуру, которая имела бы: а) две, б) три, в) четыре оси симметрии.
5. Приведите примеры фигур, каждая из которых имеет бесконечное множество осей симметрии.

6. На рисунке все фигуры, кроме одной, обладают одним общим свойством. Какое это свойство и какая из фигур этим свойством не обладает?
Центр симметрии фигуры
1. Нарисуйте несколько фигур, каждая из которых имеет центр симметрии.
2. Имеет ли центр симметрии фигура, составленная из а) двух точек, б) трех точек, в) четырех точек?
3. Истинно ли высказывание: треугольник не может иметь центра симметрии?
4. Почему многоугольник с нечетным числом вершин не имеет центра симметрии?
5. Имеет ли центр симметрии фигура, представляющая собой объединение а) вертикальных углов, б) смежных углов?
6. Дана прямая и точка вне ее. Дополните данное множество точек только одной точкой так, чтобы получилась центрально-симметричная фигура. Сколькими способами можно это сделать?
7. Имеет ли центр симметрии а) плоскость, б) полуплоскость, в) полосу?
8. Данную фигуру дополните так, чтобы получилась фигура, имеющая центр симметрии в точке О.
9. Укажите общее свойство всех фигур на рисунке.
Центральная симметрия
1. Найдите образ полуплоскости с границей а при симметрии относительно центра А, если известно, что А Î а.
2. Существуют ли а) лучи, б) отрезки, в) точки, отображающиеся центральной симметрией сами на себя?
3. Ученик утверждает, что фигура Ф1 получена из фигуры Ф с помощью центральной симметрии. Верен ли ответ ученика?
4. Точка А имеет координаты (а; b). Какие координаты имеет точка А1, симметричная точке А относительно начала координат?
5. Запишите уравнение прямой, симметричной прямой у = х + 1 относительно начала координат.
6. Расстояние между пунктами В и С нельзя измерить непосредственно. На рисунке показан один из способов косвенного измерения, при котором вместо ½ВС½ измеряют ½МК½. Укажите условия, при которых правомерно так поступать. Какие теоретические сведения при этом используются?
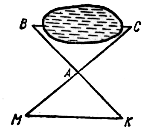
Многоугольники
1. Сколько осей симметрии имеет а) параллелограмм, отличный от ромба, прямоугольника и квадрата, б) ромб, отличный от квадрата, в) прямоугольник, отличный от квадрата, г) квадрат?
2. Изобразите четырехугольник, у которого только одна ось симметрии и одна из его диагоналей принадлежит этой оси.
3. Диагонали параллелограмма принадлежат его осям симметрии. Каким по виду может быть параллелограмм?
4. В параллелограмме прямые, проходящие через середины противоположных сторон, являются его осями симметрии. Каким по виду может быть параллелограмм?
5. В параллелограмме диагональные прямые и прямые, проходящие через середины противоположных сторон, являются его осями симметрии. Каким по виду должен быть параллелограмм?
6. Истинны ли высказывания:
а) Если четырехугольник имеет одну ось симметрии, то он обязательно имеет и другую ось, перпендикулярную первой;
б) Если параллелограмм имеет одну ось симметрии, то он обязательно имеет и другую ось, перпендикулярную первой?
7. Даны три точки А, В и С. Дополните это множество точек четвертой точкой D так, чтобы фигура Ф = {А, В, С, D} имела центр симметрии. Рассмотрите все возможные случаи.
8. Всякий ли четырехугольник (параллелограмм) имеет центр симметрии?
9. Фигуры, изображенные на рисунке, достройте так, чтобы точка О была их центром симметрии. Как быстрее выполнить задание?
10. Фигура, состоящая из отрезков, симметрична относительно центра О. Какие отрезки можно убрать, чтобы оставшаяся фигура тоже была симметрична относительно точки О?
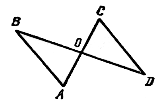
Преобразование
1. На плоскости даны две точки А и А1, причем точка А1 получена из точки А в результате некоторого преобразования. Какие преобразования вполне определяются двумя данными точками?
2. Известно, что в результате некоторого преобразования полуплоскость с границей а отобразилась на другую полуплоскость с той же границей а. Можно ли утверждать, что это перемещение является осевой симметрией?
3. При некотором преобразовании луч ℓ переходит в луч ℓ1, а точка А – в точку A1. Как найти образ точки В при данном преобразовании?
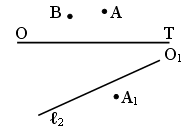
4. Какие из букв, изображенных на рисунке, имеют а) только одну ось симметрии, б) две взаимно перпендикулярные оси симметрии, в) центр симметрии?
А В Г Ж И Н
5. Известно, что фигура имеет две перпендикулярные оси симметрии. Следует ли из этого, что фигура имеет и центр симметрии? Истинно ли обратное предложение?
6. На рисунке изображены фигуры и их образы при некотором преобразовании. Укажите, какие преобразования могут быть использованы в каждом из случаев.
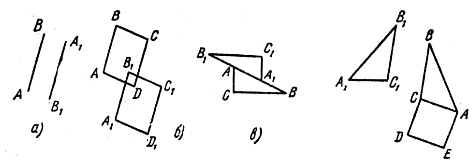
7. При некотором преобразовании треугольник ABC отобразился на треугольник А1В1С1. Постройте фигуру, на которую отобразится при этом преобразовании квадрат ACDE.
III. Задачи повышенного уровня усложности.
Метод симметрии
Иногда, производя анализ задачи, бывает удобно для всей фигуры или ее части построить фигуру, ей симметричную относительно какой-либо оси. После такого построения иногда обнаруживается такая зависимость между элементами фигур, которую раньше трудно было заметить.
Задача. Дана прямая l и две точки А и В по одну сторону от нее. Найти на прямой такую точку X, чтобы сумма расстояний АХ + ВХ была наименьшей.
Решение.
Построим точку В', симметричную точке В относительно прямой l.
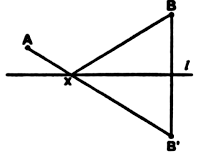
Пусть X – искомая точка, тогда ВХ = В'Х и АХ + ХВ = АХ + ХВ'; следовательно, задача сводится к нахождению точки X такой, что сумма АХ + ХВ' имеет наименьшую величину.
Этому условию, очевидно, удовлетворяет X – точка пересечения данной прямой l прямой АВ'.
Метод подобия
Во многих задачах на построение условие задачи удается разделить на две такие части, что одна часть условий вполне определяет форму искомой фигуры, а другая определяет ее размер.
Применение метода подобия состоит в том, что сначала по тем элементам, которые определяют форму фигуры, строят фигуру, подобную искомой, а затем при помощи подобного преобразования придают ей тот размер, который соответствует второй части задачи.
Задача. Построить треугольник по двум углам А и В и медиане mc.
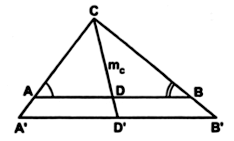
Решение.
По двум углам А и В можно построить треугольник А'В'С, подобный данному. Если за центр подобия взять вершину С, то подобное преобразование можно выполнить так: на медиане CD построенного треугольника откладываем отрезок СД, равный заданной длине mс, и через точку D проведем прямую, параллельную А'В', пересекающую прямые СА' и СВ' в точках А и В. Треугольник АСВ – искомый.
Задача. Построить треугольник, если даны а : b, ÐC и hc.
Решение.
Первые два данных условия а : b и ÐC вполне определяют форму искомого треугольника. Возьмем какие-либо два отрезка а1 и b, отношение которых равно а : b, и построим треугольник А'В'С по двум сторонам а1 и b1 и углу между ними С. Этот треугольник будет подобен искомому.
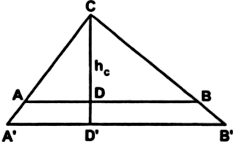
За центр подобия удобно взять вершину С. На высоте CD' треугольника А'В'С или на ее продолжении откладываем отрезок CD = h и через точку D проводим прямую, параллельную А'В' до пересечения со сторонами СА' и СВ' (или их продолжениями) в некоторых точках А и В. Треугольник ABC – искомый.
Задача. В данный треугольник вписать квадрат так, чтобы две его вершины лежали на основании треугольника, а две другие – на его боковых сторонах.
Решение.
В данном треугольнике ABC проводим отрезок MN || АС и на отрезке MN строим квадрат MNPQ. Приняв за центр подобия вершину В, проводим прямые ВР и BQ и продолжаем их до пересечения в точках Р' и Q' со стороной АС. Квадрат M'N'Q'P' – искомый.
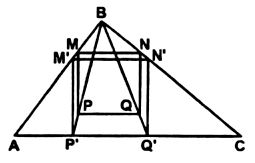
Метод параллельного перемещения
Сущность параллельного перемещения заключается в следующем: после перемещения какого-либо отрезка параллельно своему первоначальному положению его новое положение вместе с первоначальным будет составлять пару противоположных сторон параллелограмма, чем удобно пользоваться при решении некоторых задач.
Задача. Построить трапецию по четырем сторонам а, b, с, d.
Анализ.
Пусть ABCD – искомая трапеция. Перенесем CD параллельно самой себе в BE.
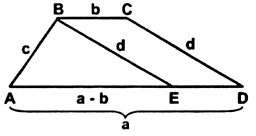
В полученном после перемещения треугольнике ABE
АЕ = а – b, ВЕ = d, AB = с.
Следовательно, этот треугольник может быть построен по трем сторонам. Построив его, легко найти оставшиеся точки С и D.
Задача. Построить равнобедренную трапецию по двум основаниям и диагонали.
Анализ.
Пусть ABCD – искомая трапеция. Перенесем BD параллельно самой себе в СЕ.
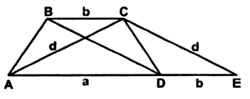
В полученном после перемещения треугольнике АСЕ АЕ = а + b, СЕ = BD = d, AC = d.
Следовательно, этот треугольник может быть построен по трем сторонам. Построив его, легко найти оставшиеся точки D и В.
Тест «виды движений»
В каждой строке таблицы необходимо поставить один или несколько знаков «+», указывающих, какие из видов движений обладают описанным свойством. Предполагается, что параллельный перенос задается ненулевым вектором, а поворот осуществляется на угол а такой, что 0° < a < 180°.
Осевая симметрия.
‚ Центральная симметрия.
ƒ Параллельный перенос.
„ Поворот.
|
Т-14 |
Свойство |
|
‚ |
ƒ |
„ |
|||||
|
Обра- зец |
При таком движении нельзя отобразить квадрат на себя |
|
+ |
+ |
+ |
|||||
|
Вариант I |
1. При таком движении нельзя отобразить квадрат на себя |
|
|
|
|
|||||
|
2. При таком движении можно отобразить одну боковую сторону равнобедренного треугольника на другую |
|
|
|
|
||||||
|
3. При таком движении можно отобразить угол параллелограмма на противолежащий угол |
|
|
|
|
||||||
|
4. При таком движении нельзя отобразить равнобедренную трапецию на себя |
|
|
|
|
||||||
|
5. При таком движении можно отобразить окружность на себя |
|
|
|
|
||||||
|
Вариант II |
1. При таком движении нельзя отобразить отрезок на себя |
|
|
|
|
|||||
|
2. При таком движении можно отобразить одну диагональ прямоугольника на другую |
|
|
|
|
||||||
|
3. При таком движении можно отобразить один из накрест лежащих углов при двух параллельных прямых и секущей на другой |
|
|
|
|
||||||
|
4. При таком движении нельзя отобразить равнобедренный треугольник на себя |
|
|
|
|
||||||
|
5. При таком движении нельзя отобразить полукруг на себя |
|
|
|
|
||||||
|
|
||||||||||
|
|
№ п/п |
|
‚ |
ƒ |
„ |
|
|
|
|
|
|
Вариант I |
1 |
|
|
+ |
|
|
|
|
|
|
|
2 |
+ |
|
|
+ |
|
|
|
|
|
|
|
3 |
|
+ |
|
+ |
|
|
|
|
|
|
|
4 |
|
+ |
+ |
+ |
|
|
|
|
|
|
|
5 |
+ |
+ |
|
+ |
|
|
|
|
|
|
|
Вариант II |
1 |
|
|
+ |
|
|
|
|
|
|
|
2 |
+ |
|
|
+ |
|
|
|
|
|
|
|
3 |
|
+ |
|
+ |
|
|
|
|
|
|
|
4 |
|
+ |
+ |
+ |
|
|
|
|
|
|
|
5 |
|
+ |
+ |
+ |
|
|
|
|
|
|
Тест «Преобразования плоскости»
Вариант I.
1. Какое из высказываний верное?
А: Прямоугольник имеет две оси симметрии, это две его диагонали.
В: Прямоугольник имеет две оси симметрии, это два серединных перпендикуляра к его сторонам.
С: Прямоугольник имеет четыре оси симметрии.
D: Все высказывания А, В и С – неверные.
а) А; б) В; в) С; г) D.
2. Любой отрезок имеет осей симметрии:
а) 0; в) 2; б) 1; г) бесконечно много.
3. Известно, что при некоторой центральной симметрии точка А переходит в точку С, а В – в D (центр симметрии не принадлежит АВ). Назовите верные высказывания:
А: Длина отрезка AD равна длине отрезка ВС.
В: Фигура, составленная из отрезков АВ, ВС, CD и AD, является параллелограммом.
С: Величина угла ABC равна величине угла CBD.
D: Длина отрезка АВ равна длине CD.
а) А, С; б) В, С, D; в) В, D; г) А, В, D.
4. Назовите верные высказывания:
А: При осевой симметрии два соответственных отрезка параллельны.
В: При центральной симметрии два соответственных луча сонаправлены.
С: Центр поворота, при котором точка А переходит в точку В, лежит на серединном перпендикуляре к отрезку АВ.
D: Любой пятиугольник не имеет центра симметрии.
а) С, D; б) В, С, D; в) А, В; г) A, D.
5. Сторона равностороннего треугольника ABC равна 12 см, BD – медиана. При параллельном переносе k на направленный отрезок AD треугольник ABC отобразился на треугольник DB1C1. Найдите периметр фигуры СКВ1С1, где К – точка пересечения ВС и DB1.
а) 28 см; б) 24 см; в) 30 см; г) 36 см.
6. При параллельном переносе точка А(–3; 4) переходит в А1(1; –1). Найдите координаты точки B1, в которую переходит точка В(2; –3).
а) (4; –5); б) (–2; 2); в) (6; –8); г) (–2; 0).
7. А(–2,4; 3,7), А1 – симметричная ей точка относительно оси Ох, точка А2 – симметричная точке А1 относительно оси Оу. Найдите координаты точки А2.
а) (2,4; –3,7);
б) (–2,4; –3,7);
в) (2,4; 3,7);
г) правильного ответа нет.
8. ÐАВC = 38°. При гомотетии с коэффициентом, равным a, угол АВС переходит в угол А1В1С1. Найдите величину угла А1В1С1.
а) 76°; в) 19°;
б) 38°; г) правильного ответа нет.
Вариант II.
1. Какое из высказываний верное?
А: Ромб имеет две оси симметрии, это две его диагонали.
В: Ромб имеет две оси симметрии, это два серединных перпендикуляра к его сторонам.
C: Ромб имеет четыре оси симметрии.
D: Высказывания А, В, С – неверные.
а) А; б) В; в) С; r) D.
2. Любой угол имеет осей симметрии:
а) 0; в) 2;
б) 1; г) бесконечно много.
3. Известно, что при некоторой центральной симметрии точка М переходит в точку К, а N в точку Е (центр симметрии не принадлежит отрезку MN). Назовите верные высказывания:
А: Отрезок МК равен отрезку NE.
В: Угол EMN равен углу NKE.
С: Фигура, составленная из отрезков MN, NK, КЕ и ME, является прямоугольником.
D: Отрезок ME равен отрезку NK.
a) C, D; б) А, В; в) А, С; г) В, D.
4. Назовите верные высказывания:
А: При центральной симметрии два соответственных отрезка параллельны.
В: При осевой симметрии два соответственных луча сонаправлены.
С: Центр поворота, при котором А ® А1, а В ® В1 является пересечением отрезков АА1 и ВВ1.
D: Некоторые шестиугольники имеют центр симметрии.
а) В, С; б) С, D; в) А, В; г) A, D.
5. Сторона равностороннего треугольника СКР равна 14 см, КЕ – высота треугольника. При параллельном переносе на направленный отрезок СЕ треугольник СКР отобразился на треугольник ЕК1Р1. Найдите периметр фигуры РМК1Р1, где М – точка пересечения ЕК1 и КР.
а) 49 см; б) 28 см; в) 35 см; г) 42 см.
6. При параллельном переносе точка С(2; –3) переходит в точку C1(–1; 1). Найдите координаты точки F1, в которую переходит точка F(–4; –1).
а) (3; – 5); б) (–7; 3); в) (–1; –5); г) (–1; 3).
7. В (5,6; –3,8), В1 – симметричная ей точка относительно оси Оу, а В2 – точка, симметричная В1 относительно оси Ох. Найдите координаты точки В2.
а) (5,6; 3,8); в) (–5,6; 3,8);
б) (–5,6; –3,8); г) правильного ответа нет.
8. При гомотетии угол CDE, равный 56°, переходит в угол С1Д1. Найдите величину угла C1D1E1, если коэффициент гомотетии равен 0,5.
а) 28°; в) 112°;
б) 56°; г) правильного ответа нет.
Ключ к тесту
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
I |
б |
в |
г |
а |
в |
в |
в |
б |
|
II |
а |
б |
г |
г |
в |
б |
в |
б |
Урок 11
ВЕКТОРЫ НА ПЛОСКОСТИ
Цель: овладеть всеми операциями над векторами.
Ход урока
I. Актуализация опорных теоретических знаний.
Векторы на плоскости
Вектор и его координаты.
а1 = х2 – х1, а2 = у2 – у1
![]()
![]()
Равные векторы.
Сумма векторов.
![]() +
+ ![]()
Правило треугольника. Правило параллелограмма
![]()
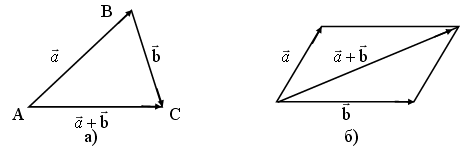
Разность векторов.
![]() –
– ![]()
Умножение вектора на число. Коллинеарные векторы.
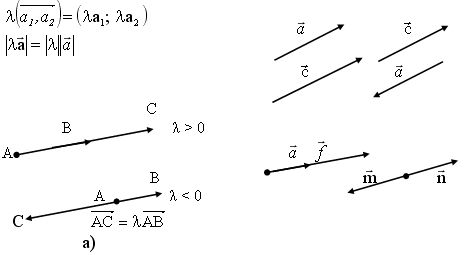
![]() и
и ![]() коллинеарны Û
коллинеарны Û 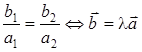
Представление вектора через одинаковые векторы.
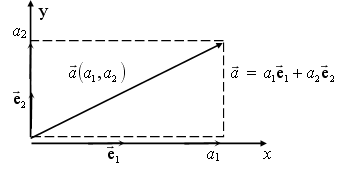
Скалярные произведения векторов.
![]() а1b1 – а2b2
=
а1b1 – а2b2
= ![]()
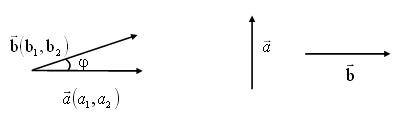
При ![]() ¹
¹ ![]() и
и ![]() ¹
¹ ![]()
![]()
II. Решение задач (устно).
1. Верно ли, что:
– длина вектора ![]() равна
длине вектора
равна
длине вектора ![]() ?
?
– если длины векторов равны, то векторы равны?
– равные векторы имеют равные длины?
– разность двух векторов может равняться нулевому вектору?
– разность двух векторов может равняться нулю?
– чем больше число k, тем больше длина вектора k![]() ?
?
– от одной точки можно отложить два различных не нулевых равных вектора?
2*. Могут ли... Может ли... Верно ли, что...
– коллинеарные векторы не лежать на одной прямой?
– векторы, лежащие на параллельных прямых, не являются коллинеарными?
– противоположные векторы не являются коллинеарными?
– противолежащие векторы не лежат на одной прямой?
– скалярное произведение двух векторов равняться произведению их длин?
– скалярное произведение двух сонаправленных векторов быть отрицательным?
– скалярное произведение векторов является вектором?
– если скалярное произведение двух векторов равно нулю, то один из векторов – нулевой?
– если скалярное произведение двух векторов равно нулю, то данные векторы перпендикулярны?
3. Фронтальная работа по решению задач.
1) Дано: ![]() b,
b,
![]()
![]()
![]()
Укажите: а) коллинеарные векторы; б) сонаправленные векторы; в) противоположно направленные векторы, г) равные векторы; д) нулевые векторы.
2) Дано:

Найдите:
длины векторов ![]()
Постройте векторы:
а) ![]() правилом
треугольника;
правилом
треугольника;
б) ![]() правилом
параллелограмма;
правилом
параллелограмма;
в) ![]()
г) 2![]()
3) Дано: АВСD – параллелограмм. К Î ВС, ВК : КС = 2 : 1, М – середина СD.
Разложите векторы ![]() и
и ![]() через векторы
через векторы ![]() и
и ![]()
4) Дано: А (3; –2), 5 (–5; 4), С (–1; –3).
Найдите:
а) координаты
вектора ![]()
б) длину вектора ![]() ;
;
в) координаты середины отрезка АС;
г) расстояние между точками А и В.
5) Дано: ![]() {3; –4},
{3; –4}, ![]() {–2; 4}.
{–2; 4}.
Найдите:
а) ![]() б)
б) ![]()
в) ![]() ; г)
; г) ![]()
д) найдите косинус
угла между векторами ![]() и
и ![]() .
.
6) Даны ![]() {2; –5} и
{2; –5} и ![]() {–10; у}.
{–10; у}.
При каком значении
векторы ![]() и
и ![]() перпендикулярны?
перпендикулярны?
7) Дан треугольник АВС. Постройте его образ:
а) при осевой симметрии относительно прямой АВ;
б) при центральной симметрии относительно точки С;
в) при параллельном переносе на вектор АМ, где М – середина стороны ВС;
г) при повороте вокруг точки А на 45° по часовой стрелке.
III. Самостоятельное решение задач.
1. АВСD и АDЕF – параллелограммы, имеющие общую сторону.
Постройте вектор ![]() такой, что:
такой, что:
а) ![]()
б) ![]()
2. На стороне СD и
диагонали АС параллелограмма АВСD лежат точки Р и Е так, что DР : РС = 3 : 2,
АЕ : ЕС = 4 : 3. Выразите вектор ![]() через векторы
через векторы ![]()
3. В треугольнике МNК О –
точка пересечения медиан, ![]() =
=
![]() ,
,
![]() =
=
![]() ,
,
![]() =
k ×
(
=
k ×
(![]() +
+![]() ).
Найдите число k.
).
Найдите число k.
4. Докажите, что если для четырехугольника АВСD и
произвольной точки О выполняется равенство ![]() то
этот четырехугольник – параллелограмм.
то
этот четырехугольник – параллелограмм.
5. Докажите, что четырехугольник МNКР, заданный координатами своих вершин М (2; 2), N (5; 3), К (6; 6), Р (3; 5), является ромбом, и вычислите его площадь.
6. Найдите координаты точки N, лежащей на оси абсцисс и равноудаленной от точек Р (–1; 3) и К (0; 2).
7. В равнобедренном треугольнике основание равно 12 см, а высота, проведенная к основанию, равна 8 см. Найдите медиану, проведенную к боковой стороне.
8. Определите значение х, при котором вектор ![]() {2
– х; 2х + 3} и вектор
{2
– х; 2х + 3} и вектор ![]() {–2; 5}:
{–2; 5}:
а) коллинеарны;
б) перпендикулярны.
9. В четырехугольнике АВСD АВ = АD = 5, ВС = СD = 3![]() ,
АС = 7. Используя метод координат, найдите расстояние между серединами
противолежащих сторон четырехугольника.
,
АС = 7. Используя метод координат, найдите расстояние между серединами
противолежащих сторон четырехугольника.
Ответы к текстовым задачам.
1. а) ![]() б)
б)
![]()
2. ![]() 3.
3.
![]() 4.
S = 8; 6. N (–3; 0); 7.
4.
S = 8; 6. N (–3; 0); 7.![]() ;
;
8. а) х = 16; б) х = ![]() 9.
9.
![]() .
.
Домашнее задание: подготовиться к итоговой контрольной работе.
Ключевые задачи для домашнего задания.
№ 48. Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Даны три точки О, А, В. Точка Х делит отрезок АВ в
отношении l : m, считая от точки А. Выразите ![]() через
векторы
через
векторы ![]() и
и
![]() .
.
Решение:
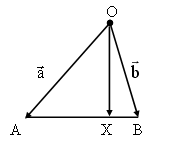
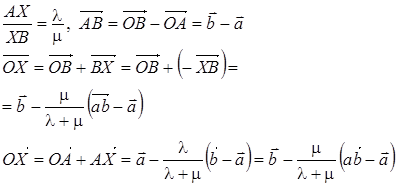
2) Докажите, что медианы треугольника пересекаются в одной точке, которая делит их в отношении 2 : 1, считая от соответствующих вершин.
Тест «угол между векторами»
В каждой строке таблицы необходимо поставить ровно один знак «+», указывающий, является ли угол a между ненулевыми векторами а и b острым, прямым или тупым (с учетом описанного свойства данных векторов).
Острый.
‚ Прямой.
ƒ Тупой.
|
Т-12 |
Свойство |
|
‚ |
ƒ |
||||
|
Обра- зец |
|
+ |
|
|
||||
|
Вариант I |
1.
Скалярное произведение векторов |
|
|
|
||||
|
2. cos a < 0 |
|
|
|
|||||
|
3. векторы ВС2 < АВ2 + АС2 |
|
|
|
|||||
|
|
4.
Обе координаты каждого из векторов |
|
|
|
||||
|
5. |
|
|
|
|||||
|
Вариант II |
1.
Скалярное произведение векторов |
|
|
|
||||
|
2. cos a = 0 |
|
|
|
|||||
|
3. векторы |
|
|
|
|||||
|
4.
Обе координаты каждого из векторов |
|
|
|
|||||
|
5. |
|
|
|
|||||
|
|
||||||||
|
|
№ |
|
‚ |
ƒ |
|
|
|
|
|
Вариант I |
1 |
|
+ |
|
|
|
|
|
|
2 |
|
|
+ |
|
|
|
|
|
|
3 |
+ |
|
|
|
|
|
|
|
|
4 |
+ |
|
|
|
|
|
|
|
|
5 |
|
|
+ |
|
|
|
|
|
|
Вариант II |
1 |
|
|
+ |
|
|
|
|
|
2 |
|
|
+ |
|
|
|
|
|
|
3 |
|
|
+ |
|
|
|
|
|
|
4 |
+ |
|
|
|
|
|
|
|
|
5 |
|
+ |
|
|
|
|
|
|
Уроки 12–13
ИТОГОВЫЙ ТЕСТ
Цель: проверить уровень усвоения знания и умения учащихся по геометрии за курс основной школы.
Часть А.
l. B трапеции ABCD DM = 12, MB = 6, АB = 8. Найдите CD.
1) 4; 2) 10; 3) 24; 4) 16.
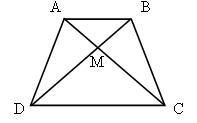
2. Внутренний угол треугольника равен 135°, а один из внешних его углов – 170°. Найдите острый угол треугольника, не смежный с данным внешним.
1) 10°; 2) 35°; 3) 45°; 4) 65°.
3. Используя данные, указанные на рисунке, найдите АС, если ВК = 6.
1) 12; 2) 4![]() ;
;
3) 3![]() ;
4) 6
;
4) 6![]() .
.
4. В треугольнике МРТ РТ = 12, МТ = 8, sin ÐM
= ![]() .
.
Найдите угол Р.
1) 150°; 2) 120°; 3) 60°; 4) 30°.
5. Используя данные, указанные на рисунке, найдите площадь треугольника АВС, если СН = 13 м.
1) 126 м2; 2) 78 м2;
3) 63 м2; 4) 60 м2.
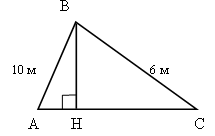
6. Окружность с центром Р и прямая КТ касаются в точке К. Найдите РТ, если ТК = 12, а диаметр окружности – 10.
1) 12; 2) 5; 3) 13; 4) 7.
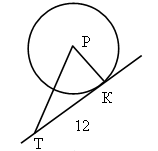
7. Точка О – центр окружности радиусом 5. Найдите ВС.
1) 5![]() ;
2) 5; 3) 10; 4) 7,5.
;
2) 5; 3) 10; 4) 7,5.
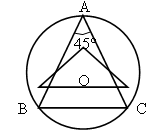
8. В четырехугольнике ABCD ÐCBD = 35°, ÐBAC = 45°. Найдите угол BAD.
1) 80°; 2) 100°; 3) 135°; 4) 90°.
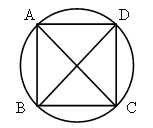
9. Сторона квадрата равна 6 м. Найдите площадь вписанного в него круга.
1) 36p м2; 2) 12p м2; 3) 9p м2; 4) 18p м2.
10. Какая из следующих фигур имеет центр симметрии?

1) равнобокая 2) правильный 3) правильный 4) паралле-
трапеция треугольник пятиугольник лограмм
11. Точки М и К – середины сторон правильного
треугольника ABC. Укажите вектор, равный вектору ![]() :
:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() .
.
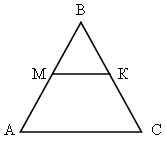
12. КСТР – ромб. Найдите сумму векторов ![]()
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() .
.
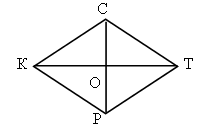
Часть В.
1. Боковая сторона равнобедренного треугольника равна 15, а биссектриса, проведенная к основанию, равна 9. Найдите периметр треугольника.
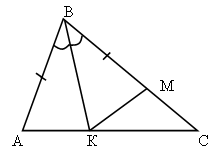
2. Отрезок ВК – биссектриса треугольника ABC, AB = BM, ÐAKB = 50". Найдите угол скм.
3. Диагонали прямоугольника АВСD пересекаются в точке О, ÐСDО = 60°, АС = 10. Найдите периметр треугольника ОСD.
4. Основания равнобокой трапеции равны 14 м и 8 м, а один из углов равен 45°. Найдите площадь трапеции.
5. В параллелограмме ABCD BD = 17 м. Найдите плошадь параллелограмма, если СН = 2 м и ВН = 15 м.
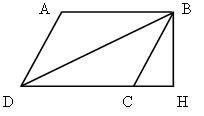
Часть С.
1. Стороны параллелограмма равны 7 и 6. Биссектрисы углов, прилежащих к большей стороне, делят противолежащую сторону на три части. Найдите длину большей из этих частей.
2. В треугольнике ABC АВ = ВС = 10, АС = 8. Окружность, вписанная в треугольник, касается стороны АВ в точке М. Найдите ВМ.
3. Отрезок АО – биссектриса треугольника АВС. АС = 16, ВС = 20. Найдите ОС, если ÐВАС = 2ÐАВС.
Вариант II.
Часть А.
1. В трапеции ABCD DP = 9, ВР = 3, ВС = 6. Найдите AD.
1) 2; 2) 10; 3) 12; 4) 18.
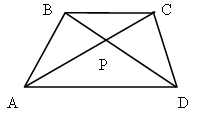
2. Внутренний угол треугольника равен 145°, а один из внешних его углов – 165°. Найдите острый угол треугольника, не смежный с данным внешним.
1) 5°; 2) 20°; 3) 15°; 4) 35°.
3. Используя данные, указанные на рисунке, найдите МК, если НT = 12.
1) 12![]() ;
2) 24; 3) 6
;
2) 24; 3) 6![]() ; 4) 8
; 4) 8![]() .
.
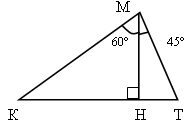
4. В треугольнике СЕК КС = 8, ЕС = 6, sinÐЕ
= ![]() .
Найдите угол К.
.
Найдите угол К.
1) 45°; 2) 60°; 3) 120°; 4) 135°.
5. Используя данные, указанные на рисунке, найдите плошадь треугольника СКР, если МР = 9 м.
1) 24 м2; 2) 48 м2;
3) 18 м2; 4) 30 м2.
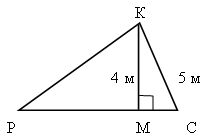
6. Окружность с центром С и прямая АВ касаются в точке В. Найдите АВ, если АС = 17, а диаметр окружности – 16.
1) ![]() ;
2) 8; 3) 15; 4) 12.
;
2) 8; 3) 15; 4) 12.
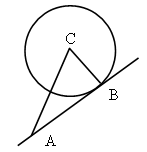
7. Угол ВАС опирается на дугу в 120°, АВ = АС = 6. Найдите ВС.
1) 3; 2) 6; 3) ![]() ;
4) 12.
;
4) 12.
8. В трапеции ABCD ÐACB = 25°, ÐABD = 80°. Найдите угол BCD.
1) 55°; 2) 75°; 3) 90°; 4) 105°.
9. Стороны прямоугольника равны 6 м и 8 м. Найдите площадь описанного около него круга.
1) 25p м2; 2) 50p м2; 3) 100p м2; 4) 20p м2.
10. Какая из следующих фигур не имеет центра симметрии?

1) параллелограмм; 2) правильный 3) отрезок 4) правильный
треугольник шестиугольник
11. Точки А и В – середины сторон равнобокой трапеции
KLMN. Укажите вектор, равный вектору ![]() .
.
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() .
.
12. КСТР – ромб. Найдите сумму вектора ![]()
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() .
.
Часть В.
1. Основание равнобедренного треугольника равно 18, а проведенная к нему медиана равна 12. Найдите периметр треугольника.
2. В треугольнике ABC АС = 5, ВС = 13, ÐAMC = ÐKMC, отрезок СМ – биссектриса треугольника. Найдите ВК.
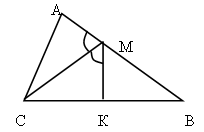
3. Диагонали прямоугольника ABCD пересекаются в точке О, ÐABO = 60°, АВ = 8. Найдите диагональ BD.
4. Основания прямоугольной трапеции равны 12 м и 8 м, а один из углов равен 135°. Найдите площадь трапеции.
5. В параллелограмме KLMP PL = 17 м. Найдите площадь параллелограмма, если РТ = 15 м и MТ = 3 м.
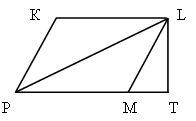
Часть С.
1. Биссектриса угла А прямоугольника ABCD пересекает сторону ВС в точке М. Найдите периметр прямоугольника, если ВМ = 8 и СМ = 5.
2. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки, равные 2 и 3, считая от основания. Найдите периметр треугольника.
3. В треугольнике ABC точка М лежит на стороне АС, ВС = 6 и АС =18. Найдите СМ, если ÐAMB = ÐBAC + ÐACВ.
Ключ к итоговому тесту
Часть А.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
I |
4 |
2 |
2 |
4 |
3 |
3 |
1 |
1 |
1 |
4 |
2 |
3 |
|
II |
4 |
2 |
2 |
1 |
1 |
3 |
2 |
4 |
1 |
2 |
3 |
2 |
Часть В.
|
|
1 |
2 |
3 |
4 |
5 |
|
I |
54 |
80° |
15 |
33 |
90 |
|
II |
48 |
8 |
16 |
40 |
96 |
Часть С.
|
|
1 |
2 |
3 |
|
I |
12,8 |
2 |
5 |
|
II |
104 |
14 |
2 |
ВВЕДЕНИЕ В СТЕРЕОМЕТРИЮ
Цели: познакомить учащихся с историей возникновения и развития геометрии, основными понятиями стереометрии; основными положениями, которыми нужно руководствоваться при изображении пространственных фигур на плоскости; с формулами нахождения площадей поверхности и объемов; стереометрической задачей; начать формировать умение анализировать ее; устанавливать связь с планиметрической задачей.
Урок 1
Строение геометрии.
Аксиомы стереометрии
Ход урока
I. Изучение нового материала.
Геометрия – это наука о свойствах геометрических фигур: треугольника, квадрата, круга, пирамиды, сферы и др. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Своеобразие геометрии, выделяющее ее среди других разделов математики, да и всех наук вообще, заключается в неразрывном органическом соединении живого воображения со строгой логикой. Геометрия в своей сути и есть пространственное воображение, пронизанное и организованное строгой логикой.
В геометрическом предложении, будь то аксиома, теорема или определение, неразрывно присутствуют эти два элемента: наглядная картина и строгая формулировка, строгий логический вывод. Там, где нет одной из двух сторон, нет и подлинной геометрии.
Наглядность, воображение принадлежат больше искусству, строгая логика – привилегия науки. Сухость точного вывода и живость наглядной картины: «лед и пламень не столь различны меж собой». Так геометрия соединяет в себе эти две противоположности. Так ее и надо изучать: соединяя живость воображения с логикой, наглядные картины – со строгими формулировками и доказательствами.
Поэтому основное правило состоит в том, что, обращаясь к определению, теореме или задаче, нужно, прежде всего, представить и понять их содержание: представить наглядно, нарисовать или, еще лучше, хотя и труднее, вообразить то, о чем идет речь, и одновременно понять, как это точно выражается.
Приступая к изучению доказательства теоремы или к решению задачи, следуйте такому принципу: старайтесь видеть – нарисовать, вообразить – и одновременно следить за логикой рассуждения; карандаш должен набрасывать или аккуратно рисовать соответствующие картинки и тут же выписывать кратко в словах и формулах основные ходы рассуждения.
Геометрия, которая изучается в школе, называется Евклидова по имени древнегреческого ученого Евклида, жившего в III в. до нашей эры.
Школьная геометрия состоит из двух частей: планиметрии и стереометрии. Планиметрия – это раздел геометрии, в котором изучаются геометрические фигуры на плоскости.
Стереометрией называют геометрию в пространстве – от греческих слов: «стереос» – темный, пространственный, «метрео» – измеряю.
Планиметрия:
Стереометрия:
Строение курса геометрии можно охарактеризовать так:
1. Перечисляются основные геометрические понятия, они вводятся без определения.
2. На основе введенных понятий даются определения всем остальным геометрическим понятиям.
3. Формулируются аксиомы.
4. На основе аксиом и определений доказываются теоремы, которые, в свою очередь, используются для доказательства других теорем курса геометрии. Построение геометрии с учетом выполнения всех этих пунктов называется аксиоматическим.
Рассмотрим строение планиметрии и стереометрии.
|
Общепринятые обозначения: |
|
|
Фигура |
Обозначение |
|
Точки |
А, В, С, D… |
|
Прямые |
а, b, с или АВ, СD, MN |
|
Плоскости |
a, b, j |
|
Точка А принадлежит прямой а |
А Î а |
|
Прямая а не принадлежит плоскости a |
а Ï a |
|
|
Планеметрия |
Стереометрия |
|
Основные геометрические фигуры |
Точка, прямая |
Плоскость, прямая, точка |
|
Аксиомы |
I–IX |
Система аксиом стереометрии состоит из аксиом планиметрии I–IX и трех аксиом пространства (С1 – С3) |
|
Формулировка |
Чертеж |
Запись на
математическом |
|
С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей |
|
А Î a, b Ï a, С Î a |
|
С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой |
|
А Î a, А Î b, А Î a Ç b = а, где А Î a |
|
С3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну |
|
а Ç b = A a Ì a, b Ì a |
Примером доказательства теорем, опирающихся на эти аксиомы, будут следующие теоремы, которые мы будем называть следствием.
Теорема. Через три точки, не лежащие на одной прямой, можно провести плоскость.
Доказательство.
1. Проведем прямые АВ, АС на основание аксиомы А1, они различны, так как А, В, С не лежат на одной прямой.
2. Проведем плоскость a, проходящую через эти прямые (С3).
3. Эта плоскость содержит точки А1в1С, так как
|
А Î а Ì a, значит, А Î a В Î а Ì a, значит, В Î a С Î b Ì a, значит, C Î a |
|
Теорема. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.
Доказательство.
1. Отметим точку С Ï a (С1).
2. Построим b, проходящую через А, В, С.
4. Плоскости пересекаются по прямой, содержащей общие точки А и В, а эта прямая – единственная (аксиома). Значит, АВ – единственная.
Повторение аксиом.
Сколько известно аксиом планиметрии, которые вы изучали?
I (аксиома принадлежности).
|
Формулировка Какова бы ни была прямая, существуют точки, принадлежащие этой прямой. Через любые две точки можно провести прямую, и притом только одну. |
Чертеж
|
II. Итог урока.
– Составьте опорную схему.
Строение геометрии
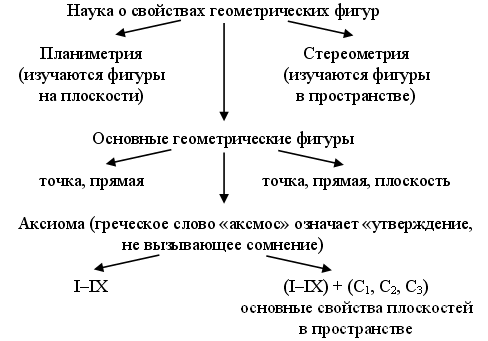
Домашнее задание: п. 130–132.
Урок 2
МНОГОГРАННИКИ
Ход урока
I. Изучение нового материала.
Рассказ учителя.
Выпуклые и невыпуклые многогранники. С одним из самых простейших многогранников – прямоугольным параллелепипедом – вы познакомились еще в начальной школе. На рисунке 1 показаны и некоторые другие многогранники: куб (это прямоугольный параллелепипед, у которого все шесть граней – квадраты), тетраэдр, октаэдр.
Можно сказать, что многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Это геометрическое тело также называют многогранником.
Многоугольники, из которых составлен многогранник, называют его гранями. Стороны граней – ребра многогранника, а концы ребер – вершины многогранника.
Многогранники бывают выпуклые и невыпуклые. Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани. На рис. 1 изображены выпуклые многогранники, а на рис. 2 – невыпуклый многогранник.
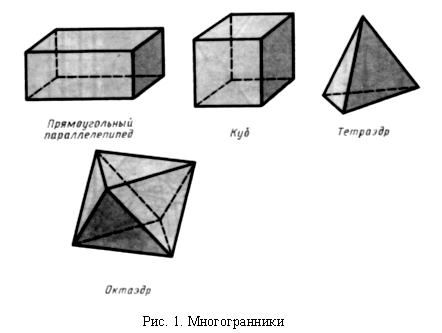
|
|
Рис. 2. Невыпуклый
многогранник, составленный из квадратов. |
Призмы. Призма получается так: в параллельных плоскостях a и b берутся два равных многоугольника А1…Аn и В1...Вn, у которых равные стороны А1А2 и В1В2, … , АnА1 и BnB1 попарно параллельны (рис. 3), затем вершины А1 и В1, ... , Аn и Вn соединяются отрезками. В результате получается n-угольная призма – многогранник А1...АnВ1...Вn, гранями которого служат многоугольники А1...Аn и В1...Вn (основания призмы) и параллелограммы А1А2В2В1, ... , АnА1В1Вn (боковые грани). Отрезки А1В1, ... , АnВn называют боковыми ребрами призмы. Боковые грани призмы образуют ее боковую поверхность.
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. Другие призмы называют наклонными.
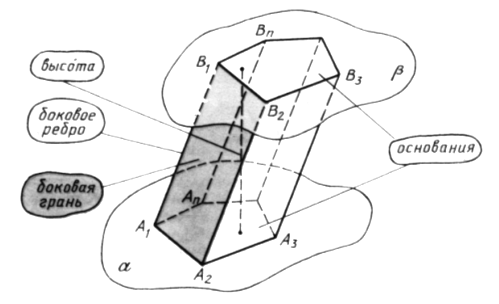
Рис. 3. Призма А1А2…АnВ1В2…Вn:
Основания – многоугольники А1А2…аn и В1В2…Вn;
Общий перпендикуляр к паралелльным плоскостям a и b – высота призмы
Прямая призма называется правильной, если ее основаниями служат правильные многоугольники (рис. 4).
Четырехугольная призма, основаниями которой служат параллелограммы, называется параллелепипедом (рис. 4). Очевидно, параллелепипед будет прямоугольным, если он прямой и его основаниями являются прямоугольники.
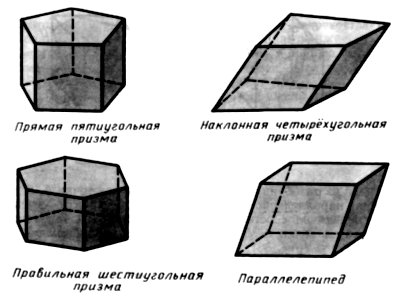
Рис. 4. Правильные многоугольники
Построение сечений параллелепипеда. Для решения многих геометрических задач, связанных с призмами и другими многогранниками, полезно уметь строить их сечения различными плоскостями. Это важно для инженера, имеющего дело с чертежами различных конструкций, а также для других специалистов.
Мы рассмотрим задачи на построение сечений параллелепипеда. Нетрудно сообразить, что в сечении параллелепипеда плоскостью может получиться треугольник, четырехугольник (рис. 5, а), пятиугольник (рис. 5, б) или шестиугольник (рис 5, в). А вот многоугольник с большим числом сторон получиться не может. Подумайте почему.
Важным правилом построения сечений параллелепипеда является следующее (попробуйте его обосновать).
Так, на рис. 5, б АВ || СО и также ВС || АЕ, а на рисунке 5, в имеются три пары параллельных отрезков (назовите их).
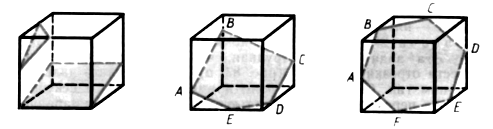
Рис. 5. Построение сечений параллелепипеда
Пирамиды. На рис. 6 изображены пирамиды. Такую форму имеют знаменитые египетские пирамиды-усыпальницы, форму пирамид имели также ритуальные здания в Древней Мексике. Шатровые купола православных церквей – пирамиды. В словацком городе Братиславе есть здание в виде перевернутой пирамиды. Все башни Московского Кремля увенчаны пирамидами.
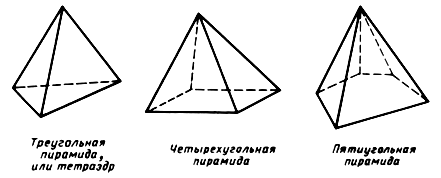
Рис. 6. Пирамиды
Пирамида фараона Хеопса (XXVIII в. до н. э.) – это самая большая из древнегреческих пирамид, ее высота 147 м. Вплоть до XIX в. это самое высокое из рукотворных сооружений.
Желая прославить своего фараона в веках, древнегреческие зодчие из всех геометрических тел выбрали именно пирамиду. Выбор этот не случаен, ибо в условиях земного тяготения пирамида является наиболее устойчивой конструкцией.
Как получается пирамида? Берутся многоугольник А1А2…Аn и точка Р вне плоскости этого многоугольника (рис. 7). Эта точка соединяется с вершинами А1, А2, ... , Аn отрезками. В результате получается n-угольная пирамида – многогранник РА1А2...Аn. На рисунке 7 указаны вершина, основание, боковые ребра, боковые грани и высота пирамиды – перпендикуляр, опущенный из вершины на основание. Боковые грани пирамиды образуют ее боковую поверхность.
Если основание пирамиды – правильный многоугольник, а ее высота проходит через центр основания, то пирамида называется правильной. Высота боковой грани такой пирамиды называется апофемой.
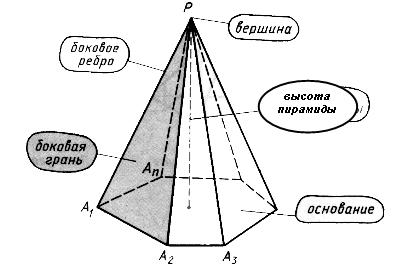
Рис. 7. n-угольная пирамида РА1А2…Аn
Площади поверхностей призмы, пирамиды.
Зачем нужно уметь вычислять площади. Вычисление площадей геометрически фигур – задача, тесно связанная с практикой.
Под площадью Sбок поверхности призмы понимается сумма площадей всех ее боковых граней, а площадь S всей поверхности призмы равна сумме площади ее боковой поверхности и площадей двух оснований:
S = Sбок + 2Sосн (1)
Эта формула не очень удобна для вычислений. Для прямой призмы можно получить более удобную формулу. Поступим так: развернем боковую поверхность призмы (рис. 8). Получим прямоугольник, одна сторона которого равна высоте h призмы, а другая – периметру Р ее основания.
Поэтому Sбок = Рh (2)
и формула (1) примет вид:
S = Рh + 2Sосн (3)
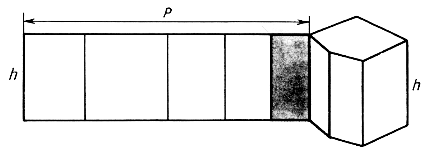
Рис. 8. Боковая поверхность призмы
Площадь S всей поверхности пирамиды равна сумме площади ее боковой поверхности и площади основания.
II. Практическая работа (в группах).
Каждой группе выдается модель многогранника (желательно иметь и каркасную модель), карточка.
Образец карточки
|
Призма (прямая) |
Развертка |
Элементы |
Виды сечений |
Формулы площадей поверхности, объем |
|
|
|
Грани:
Основания:
Вершины:
Ребра:
Высота:
Диагонали: |
|
Sп.п. = = 2Sосн. + V = Sосн. · Н |
Домашнее задание: п. 133; ответить на вопросы.
– Что такое многогранник?
– Что такое грани, ребра и вершины многогранника?
– Какие многогранники называются выпуклыми и какие невыпуклыми? Изобразите выпуклый и невыпуклый многогранники.
– Объясните, что такое призма. Какие грани призмы называют ее основаниями, а какие – боковыми гранями?
– Что такое боковая поверхность призмы?
– Какая призма называется прямой, какая наклонной и какая правильной?
– Что такое высота призмы? Может ли боковое ребро призмы быть меньше ее высоты?
– Что представляют собой боковые грани наклонной призмы? Прямой призмы?
– Докажите, что высота прямой призмы равна ее боковому ребру.
– Что такое параллелепипед?
– Чем отличается прямой параллелепипед от прямоугольного?
– Объясните, что такое пирамида.
– Изобразите пирамиду и покажите ее основание, вершину, боковые ребра, боковые грани.
– Какая пирамида называется правильной?
– Что такое боковая поверхность пирамиды?
Урок 3
ТЕЛА ВРАЩЕНИЯ
Ход урока
I. Изучение нового материала.
Рассказ учителя.
Тела и поверхности вращения в нашей жизни.
Представьте себе, что имеется плоская фигура F и прямая а – ось вращения, расположенная в плоскости фигуры (рис. 1). Будем вращать фигуру F вокруг оси а. После завершения полного оборота в пространстве образуется тело. Его поверхность называется поверхностью вращения.

Рис. 1. Плоскости фигур Рис. 2. Тела и поверхности вращения
Что такое цилиндр и цилиндрическая поверхность?
Цилиндр получается путем вращения в пространстве прямоугольника вокруг прямой, содержащей одну из его сторон (рис. 3). Эта прямая называется осью цилиндра. На рисунке указаны основания цилиндра, его боковая поверхность и образующие. Длина образующей цилиндра называется его высотой, радиус основания цилиндра – радиусом цилиндра. Боковая поверхность цилиндра называется цилиндрической поверхностью.
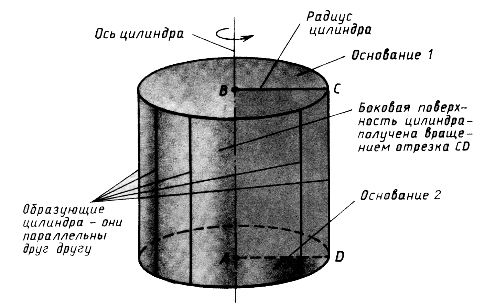
Рис. 3. Цилиндр
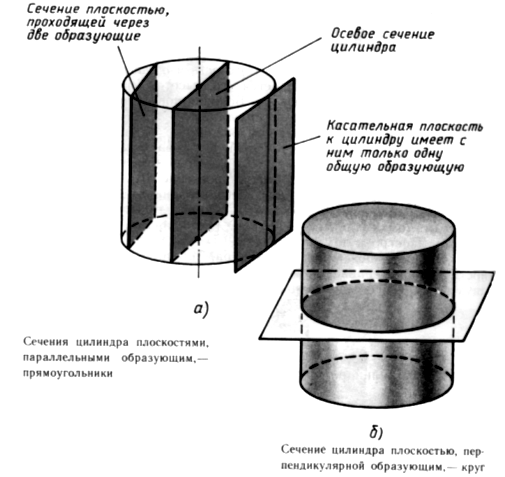
Рис. 4. Сечение цилиндра
Площадь поверхности цилиндра.
Площадь S всей поверхности цилиндра равна сумме площади его боковой поверхности и двух площадей его оснований:
S = Sбок. + 2Sосн. (1)
Рис. 5. Развертка боковой поверхности цилиндра
Площадь S может быть найдена так. Разрежем боковую поверхность цилиндра по образующей и развернем ее на плоскости. Получится прямоугольник, стороны которого равны h – высоте цилиндра и 2πr – длине окружности основания цилиндра. По формуле площади прямоугольника находим:
Sбок = 2πrh
Площадь Sосн равна площади круга радиуса г:
Sосн = πr2
Подставляя выражения для Sбок и Sосн в правую часть формулы (1), получаем:
S = 2πr(r + h).
Что такое конус и коническая поверхность?
Конус получася путем вращения в пространстве прямоугольного треугольника вокруг прямой, содержащей один из его катетов. Эта прямая называется осью конуса. На рисунке указаны вершина, основание конуса, его боковая поверхность, образующие и высота. Боковая поверхность конуса называется конической поверхностью.
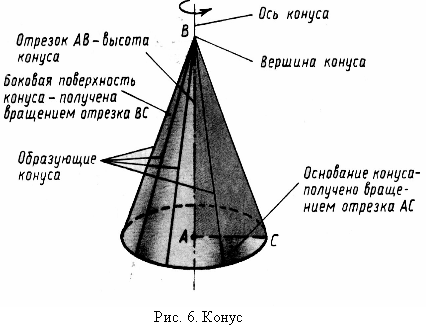
Конус получен вращением прямоугольного треугольника АВС вокруг прямой АВ.
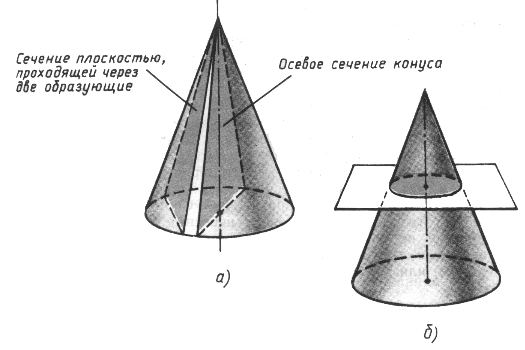
Рис. 7. Виды сечений
Площадь поверхности конуса.
Площадь S всей поверхности конуса равна сумме площадей его боковой поверхности и основания:
S = Sбок + Sосн (1)
Площадь Sбок может быть найдена так. Разрежем боковую поверхность конуса по образующей и развернем ее на плоскости. Получится круговой сектор, радиус которого равен длине l образующей конуса, а длина дуги этого сектора равна длине окружности основания конуса. Градусную меру центрального угла сектора обозначим буквой a.
Вы знаете, что площадь кругового сектора радиуса l
с центральным углом a равна 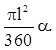
Поэтому
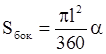 (2)
(2)
Рис. 8. Развертка боковой поверхности конуса – круговой сектор радиуса l
Выразим a через l и радиус r окружности основания конуса.
Длина дуги сектора равна ![]() ,
а длина окружности основания конуса равна 2π.
Приравнивая
эти выражения, получаем
,
а длина окружности основания конуса равна 2π.
Приравнивая
эти выражения, получаем
2πr
=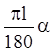 ,
откуда
,
откуда 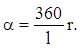
Подставив это выражение для a в правую часть формулы (2), выходим к формуле для Sбок:
Sбок = πrl.
Площадь Sосн. основания конуса равна πr2, поэтому из равенства (1) получается следующая формула для площади S всей поверхности конуса:
Sбок = πrl + πr2 = πr(l + r).
II. Решение задач.
Алгоритм решения стереометрической задачи.
1. Внимательно прочитать условие задачи. (Для некоторых учащихся это необходимо сделать не один раз.)
2. Выяснить, что означает каждая заданная величина. Например, в задаче 45: цилиндр; основание и высота цилиндра; радиус основания; осевое сечение; диагональ.
Желательно на модели найти все эти элементы. (При необходимости обратиться к записям в тетради или учебнике.)
3. Попытаться построить изображение цилиндра и указать на нем все заданные элементы.
При построении цилиндра необходимо правильно чертить видимые и невидимые линии, так как изображение должно быть наглядным.
4. Определить, элементами каких планиметрических фигур являются элементы. (На примере задачи 45. АВСD – прямоугольник, ВС – диагональ.)
5. В задаче необходимо решить прямоугольный треугольник.
Появилась обычная задача по планиметрии.
– Какие теоретические знания необходимы для решения прямоугольных треугольников?
Теорема Пифагора
№ 45.
Дано: цилиндр, ОС = 2 м, АВ = 3 м.
Найти: ВС.
Решение:
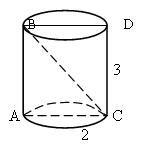
1) ΔАВС – прямоугольный, по теореме Пифагора найдем
ВС = ![]()
Ответ: 5 м.
Домашнее задание: п. 134, изготовить модель фигуры, заполнить таблицы, проиллюстрировав рисунками.
|
Цилиндр |
Элементы |
Развертка |
Виды |
Формулы поверхности |
|
|
|
|
|
|
|
Конус |
Элементы |
Развертка |
Виды |
Формулы |
|
|
|
|
|
|
РЕКОМЕНДАЦИИ К
ЗАКЛЮЧИТЕЛЬНОМУ
ПОВТОРЕНИЮ КУРСА ГЕОМЕТРИИ
Повторение курса геометрии в конце учебного года имеет большое и учебное, и воспитательное значение, приводя знания учащихся в целостную систему, подводит их к более широким обобщениям и пониманию сущности и смысла пройденного курса геометрии; ученик как бы воспроизводит весь изученный материал, чувствует и осознает свой рост в продвижении, его знания приводятся в систему.
Главная особенность курса – в установлении более глубоких связей как между отдельными темами геометрии, так и между геометрией и другими предметами.
Чтобы составить план заключительного повторения, учителю необходимо проанализировать знания учащихся по каждой теме программы на основании результатов итоговых контрольных работ и их устных ответов. Планы повторения и количество часов, отводимых на тот или иной раздел программы, могут быть различными, в разных по своим знаниям классах.
Характер заключительного повторения (расстановка акцентов, степень, глубина рассмотрения тех или иных вопросов, соотношение теории и практики, логики и интуиции и т. д.) определяется требованиями к уровню подготовки учащихся по геометрии за курс 7–10 классов, изложенных в стандартах.
В целях обобщения и систематизации знаний учащихся повторение целесообразно проводить по содержательным линиям (темам), каждая из которых объединяет материал из разных разделов курса по принципу внутрипредметных связей.
В помощь учителю предлагается примерная схема повторения курса планиметрии. При отборе теоретического материала и задач для повторения нужно учитывать и содержание экзаменационных билетов.
Теоретический материал повторяется на уроках в обзорном порядке, обсуждаются доказательства тех теорем, которые включены в первые вопросы экзаменационных билетов; наиболее трудоемкие из них предлагаются учащимся для дополнительной проработки дома. Ведущая роль при повторении отводится решению задач.
Предлагается один из вариантов повторения курса планиметрии. Учитель может по своему усмотрению, наличию времени использовать этот материал или на уроках, или на консультациях.
проведение урока-зачета
На зачетном уроке сочетаются индивидуальные, коллективные и групповые формы работы.
К зачету каждый ученик заранее готовит лист учета знаний, в который ему будут выставляться оценки за определенный вид деятельности.
|
Вид деятельности |
Оценка |
Подпись |
|
Теория (без доказательств) Терминологический диктант |
|
|
|
Теория (с доказательством) |
|
|
|
Решение устных задач |
|
|
|
Решение задач |
|
|
|
Итоговая оценка |
|
|
Урок будет иметь следующую структуру:
1-й этап. Разминка (5–7 мин).
2-й этап. Опрос первой группы ассистентов (без предварительной подгтовки (10–12 мин).
3-й этап. Опрос второй группы ассистентов ассистентами первой группы (10 мин).
4-й этап. Первая группа ассистентов решает задачи (до конца урока).
5-й этап. Вторая группа ассистентов ведет опрос. Ответившие на оценку не ниже «4» присоединяются ко второй группе ассистентов.
Первую группу ассистентов можно опросить заранее.
Разминка представляет собой фронтальный опрос учащихся по теоретическому материалу (без доказательств) и решению устных задач, можно включить треминологический диктант. За разминку учитель может выставить две оценки в лист учета знаний.
Затем каждый ученик получает карточку, в которой указаны два задания: теоретический вопрос (с доказательством) и вопрос (без доказательства). Дается устная задача на повторение материала.
Устные задачи по геометрии
Решение устных задач придает уроку геометрии необходимую глубину и живость, открывает широкие возможности для выявления и формирования у учащихся склонностей и интересов к математике. Никакая другая форма занятия не может обеспечить широкого фронта активной и творческой работы учащихся, а значит, и не будет столь эффективной.
Успех указанной работы в значительной степени зависит от подбора задач.
Устные задачи должны отвечать общим требованиям, предъявляемым к задачам школьного курса математики, но в то же время обладать и некоторой спецификой. Они должны быть краткими по содержанию, побуждать учащихся к проявлению сообразительности и находчивости. Эти задачи должны развивать у учащихся геометрические представления и умения быстро читать чертежи.
Для устной работы подбираются, как правило, задачи на применение уже изученного теоретического материала, требующие хотя бы небольшой трансформации знаний. Они предлагаются в определенной последовательности и, как правило, являются доступными для всех учащихся.
Для большей четкости и быстроты ознакомления учащихся с текстами задач целесообразно проектировать их на доску с помощью кодоскопа или подготовить демонстрационные плакаты с текстами, чертежами, рисунками и т. п.
Рекомендации по использованию исторического
материала на уроках математики
Знакомство учеников с фрагментами истории математики на уроках имеет вполне определенные цели, а именно:
1) Сведения из истории повышают интерес учащихся к изучению математики и углубляют понимание ими изучаемого раздела;
2) Ознакомление с историческими фактами расширяет умственный кругозор учащихся и повышает их общую культуру, позволяет лучше понять роль математики в современном обществе.
Знакомство учеников с развитием математики означает продуманное, планомерное ознакомление из истории науки в органической связи с систематическим изучением программного материала. Лишь такое тесное сплетение истории и теории обеспечит достижение указанных целей.
На первый взгляд кажется трудным найти на уроке время, необходимое для ознакомления с историческим материалом.
Какая бы ни была форма сообщения исторических фактов – краткая беседа, экскурс, лаконичная справка, решение задачи, показ и разъяснение рисунка, в любом случае использованное время (5–12 мин) нельзя считать потерянным напрасно, если учитель сумел преподнести исторический факт в тесной связи с изученным на уроке теоретическим материалом.
Исторический материал предполагается вводить в том порядке, в котором он может быть применен на уроках:
1. о подобии.
2. о построении подобных фигур. Пропорциональный циркуль. Галилей.
3. теорема косинусов и теорема синусов.
4. о вписанных углах. Гиппократ.
5. о правильных многоугольниках.
6. о длине окружности и площади круга. Архимед.
7. о числе p.
8. вычисление площадей в древности.
9. измерение площадей в Древней Греции.
10. Герон Александрийский. Формула площади треугольника.
11. начальные сведения по стереометрии.
12. краткий обзор развития геометрии.
О подобии
Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.
Пропорциональность отрезков, образующихся на прямых, пересеченных несколькими параллельными прямыми, была известна еще вавилонским ученым, хотя некоторые приписывают это открытие Фалесу Милетскому. До наших дней сохранилась клинописная табличка, в которой речь идет о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов.
Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V–IV вв. до н. э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида, начинающейся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».
Из
истории преобразований.
Преобразование подобия
Искусство изображать предметы на плоскости с древних времен привлекало к себе внимание человека. Попытки таких изображений появились значительно раньше, чем возникла письменность. Еще в глубокой древности люди рисовали на скалах, стенах, сосудах и прочих предметах быта различные орнаменты, растения, животных. При этом человек стремился к тому, чтобы изображение правильно отражало естественную форму предмета. Основное требование к изображению сводилось к соответствию точек натурального объекта с точками его изображения на плоскости или какой-либо другой поверхности.
Длительная практика подсказала людям, каким правилам надо следовать, чтобы правильно выразить на плоскости желаемый предмет. Так возникли зачатки учения о соответствии и преобразовании. Раньше других свойств при изображении различных предметов на плоскости были подмечены и изучены законы перспективы. Многие из этих законов были известны в Древней Греции. Как утверждает римский архитектор Витрувий (I в. до н. э.), уже Демокрит (ок. 460–370 гг. до н. э.) и Анаксагор (ок. 500–428 гг. до д. э.) соблюдали некоторые правила перспективы при подготовке декорации для постановки трагедий Эсхила (525–456 гг. до н. э.) «Прикованный Прометей» и др.
Теорема косинусов и теорема синусов
Начиная с древних времен и примерно ло XVII в. в тригонометрии рассматривали почти исключительно «решение треугольников», то есть вычисление одних элементов треугольника (или многоугольника, разбитого на треугольники) по другим его элементам. Такие вычисления были вызваны запросами астрономии, географии, мореплавания, геодезии и архитектуры. Лишь в XVII в. содержание тригонометрии значительно расширяется.
Для решения треугольника, то есть для нахождения трех его элементов, когда известны другие три его элемента (среди которых по крайней мере одна сторона), необходимо иметь три независимых соотношения между шестью его элементами. В евклидовой геометрии одно из них выражается равенством
![]() , где
, где ![]() (1)
(1)
В случае прямоугольного треугольника, помимо теоремы Пифагора, можно пользоваться, например, соотношением
b = с · sinB. (2)
В случае косоугольного треугольника, помимо (1), можно использовать теорему косинусов или теорему синусов.
Теорема косинусов была по существу доказана, конечно, геометрически, еще в «Началах» Евклида, а именно в 12-м и 13-м предложениях II книги, в которой обобщается теорема Пифагора и выводятся формулы, выражающие квадрат стороны, лежащей против острого или тупого угла треугольника. Это положение, доказанное Евклидом, эквивалентно теореме косинусов:
а2 = b2 + с2 – 2bс · cosA,
b2 = с2 + а2 – 2са · cosВ, (3)
с2 = а2 + b2 – 2аb · cosC.
Александрийские математики Герон (I в.) и Папп (III в.), ученые Индии (Брахмагупта, Бхаскара) и стран Ближнего и Среднего Востока (ал-Бируни), как и некоторые европейские математики XII–XV вв. (Л. Фибоначчи, И. Неморарий), пользовались формулами, близкими к (3), однако впервые теорема косинусов была явно сформулирована (словесно) в XVI в. французским математиком Франсуа Виетом, автором известных «Математических таблиц», появившихся в 1579 г. В современных обозначениях можно так записать соответствующую формулу Виета:
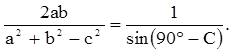
Современный вид теорема косинусов (3) принимает в 1801 г. у французского математика Лазара Карно (1753–1823). Ж.-Л. Лагранж вывел в 1799 г. теорему синусов из теоремы косинусов. Другой французский математик, О. Коши, выводит теорему косинусов из теоремы синусов в своем «Курсе анализа» (1821).
Ученые Индии, как и ученые стран ислама IX–X вв., сводили решение любых треугольников к решению прямоугольных треугольников и поэтому не нуждались в теореме синусов и ее не знали. Эта теорема была доказана лишь в XI в. уроженцем Хорезма, выдающимся астрономом ал-Бируни.
Вместе с соотношением (1) теорема синусов
![]() ,
(4)
,
(4)
представляющая два независимых уравнения, позволяет решать любой треугольник. Теоремой синусов пользовались, начиная с XVI в., и европейские математики.
О
построении подобных фигур.
Пропорциональный циркуль. Галилей
Свойства подобных фигур издавна применяются на практике при составлении географических карт, планов и чертежей, при землемерных работах на местности (так называемой мензульной съемке) и т. п.
Для практики всегда имели большее значение сравнительно простые и общедоступные методы построения подобных фигур. Одним из них является «способ палетки», который обычно применяется при копировании рисунков, картин и портретов. Желая сделать копию рисунка, мы накрываем его палеткой (от французского palette), то есть прозрачной пластинкой или бумагой с нанесенной на нее сеткой квадратов. На месте, предназначенном для копии, чертится временная квадратная сетка, которая по окончании работы стирается. Сторона квадрата временной сетки больше, меньше или равна стороне квадрата палеточной сетки в зависимости от того, требуется ли увеличить, уменьшить или оставить рисунок без изменений. Отношение стороны квадрата временной сетки к стороне квадрата палеточной сетки будет коэффициентом подобия. Пусть некоторая точка (деталь) рисунка находится в вершине (или в центре) одного из квадратов палеточной сетки. Отмечаем на копии соответствующую точку в вершине (или в центре) соответствующего квадрата временной сетки и т. д. Этот метод копирования при помощи квадратной сетки был известен еще древним египтянам. Палетку применяют также для вычисления площадей на планах и картах.
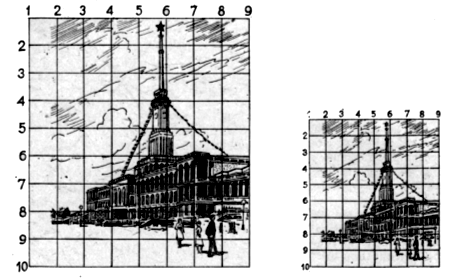
Уменьшение рисунка в отношении 3 : 5 способом палетки
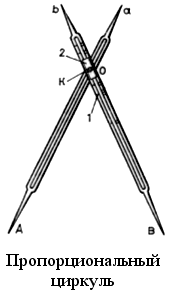
Для уменьшения или увеличения чертежа в произвольном
отношении служит также пропорциональный циркуль. Это простой инструмент, в
котором шарнир 2 устанавливается так, чтобы черта, нанесенная на нём, совпала с
определенным делением К шкалы 1 на одной из ножек. Тогда отношение расстояний ![]() тоже
будет равно К. Этот циркуль, который особенно широко используется в
картографии, был изобретен великим итальянским ученым Галилео Галилеем
(1564–1642), тем самым, который открыл закон инерции, законы падения тел,
колебаний маятника и др. Галилей впервые в истории астрономии с помощью им же
изготовленной зрительной трубы наблюдал набесные светила. Он открыл горы на
Луне, 4 спутника Юпитера, фазы Венеры, пятна на Солнце. За то, что Галилей
блестяще развил учение Коперника о движении Земли, католическая церковь его
жестоко преследовала, в 1633 г. римским католическим судом он был осужден.
тоже
будет равно К. Этот циркуль, который особенно широко используется в
картографии, был изобретен великим итальянским ученым Галилео Галилеем
(1564–1642), тем самым, который открыл закон инерции, законы падения тел,
колебаний маятника и др. Галилей впервые в истории астрономии с помощью им же
изготовленной зрительной трубы наблюдал набесные светила. Он открыл горы на
Луне, 4 спутника Юпитера, фазы Венеры, пятна на Солнце. За то, что Галилей
блестяще развил учение Коперника о движении Земли, католическая церковь его
жестоко преследовала, в 1633 г. римским католическим судом он был осужден.
Опубликованное Галилеем описание пропорционального циркуля («Построения геометрическим и военным циркулем». Падова, 1606) дало возможность ученым и техникам использовать новый инструмент для быстрого производства различных построений и расчетов. Еще в юношестве Галилей увлекался геометрией. Архимед стал его подлинным учителем. Галилей утверждал, что настоящая философия «написана в величайшей книге, которая постоянно открыта нашим глазам». Эта книга – сама Вселенная, природа, которую нужно научиться читать. «Написана же она на языке математики...»
О вписанных углах. Гиппократ Хиосский
Изложенное в современных учебниках доказательство того, что вписанный угол измеряется половиной дуги, на которую он опирается, дано в «Началах» Евклида. На это предложение ссылается, однако, еще Гиппократ Хиосский (V в. до н. э.) в своем труде о «луночках». Труды Гиппократа свидетельствуют о том, что уже во второй половине V в. до н. э. было известно большое число теорем, изложенных в «Началах» Евклида, и геометрия достигла высокого развития.
Тот факт, что опирающийся на диаметр вписанный угол – прямой, был известен вавилонянам еще 4000 лет назад. Первое его доказательство приписывается Памфилией, римской писательницей времен Нерона, Фалесу Милетскому. Некоторые комментаторы Евклида полагают, что доказательство Фалеса, основанное на предложении, что сумма углов треугольника равна 2d, было следующее: обозначив углы при диаметре через 1, 2, а части угла ABC, на которые он рассекается радиусом ОС, через 3, 4, получаем, с одной стороны: Ð1 = Ð3, Ð2 = Ð4; с другой стороны: Ð1+ Ð2 + Ð3 + Ð4 = 2d, откуда 2(Ð3 + Ð4) = 2d, Ð3 + Ð4 = d, то есть ÐACB = d.
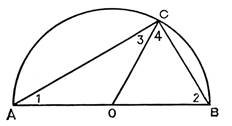
О правильных многоугольниках
В египетских и вавилонских старинных памятниках встречаются правильные четырехугольники, шестиугольники и восьмиугольники в виде изображений на стенах и украшений, высеченных из камня.
Древнегреческие ученые стали проявлять большой интерес
к правильным фигурам еще со времен Пифагора. Деление окружности на некоторое
число равных частей для построения правильных многоугольников имело важное
значение для пифагорейцев, которые утверждали, что числа лежат в основе всех
явлений мира. Учение о правильных многоугольниках, начатое в школе Пифагора,
продолженное и развитое в V–IV вв. до н. э., было систематизировано Евклидом и
изложено в IV книге «Начал». Кроме построения правильного треугольника, четырехугольника,
пятиугольника и шестиугольника, Евклид решает и задачу построения правильного
пятнадцатиугольника при помощи только циркуля и линейки. Эта фигура привлекала
внимание древних, так как было замечено, что дуга угла наклонения эклиптики к экватору
представляет собой ![]() всей окружности, то есть
стягивается стороной правильного пятнадцатиугольника.
всей окружности, то есть
стягивается стороной правильного пятнадцатиугольника.
Зная, как построить правильный n-угольник, легко можно построить правильный 2n-угольник. Долгое время математики тщетно искали способы построения правильного семиугольника, девятиугольника, одиннадцатиугольника и т. д., не зная даже, возможно ли вообще построение таких многоугольников с помощью только циркуля и линейки. Эта проблема была решена лишь в конце XVIII в. 19-летним К. Ф. Гауссом, великим немецким математиком, доказавшим, что с помощью циркуля и линейки можно разделить окружность на такое простое число N равных частей, которое выражается формулой N = 22n + 1, где n – натуральное число или нуль. Вот несколько примеров:
1) n = 0, N = 3; 2) n = 1, N = 5; 3) n = 2, N = 17; 4) n = 3, N = 257; 5) n = 4, N = 65537 и т. д.
После открытия Гаусса стало ясно, что, помимо ранее известных правильных многоугольников с 3; 4; 5; 6; 8; 10; 12; 15; 16; 20; 24; 30; 32; 40... сторонами, можно построить с помощью циркуля и линейки правильные многоугольники с 17; 34; 68; 126; 252; 257... сторонами. С другой стороны, невозможно циркулем и линейкой построить правильные многоугольники со следующим числом сторон: 7; 9; 11; 13; 14; 18; 19; 21; 22; 23; 25; 27; 28...
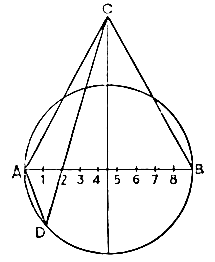
Еще в древности практиковалось для разных нужд приближенное построение любого правильного многоугольника. Так, например, Герон Александрийский находит приближенное значение стороны правильного девятиугольника.
Задача построения правильного n-угольника сводится к делению окружности на n равных частей. Один практический прием такого деления предложил математик Н. Бион. Прием этот состоит в следующем: пусть требуется разделить окружность, например, на 9 равных частей.
На диаметре окружности строится равносторонний треугольник ABC. Диаметр АВ делим на 9 равных частей. Соединяя вторую точку деления с вершиной треугольника С, продолжим прямую до пересечения с окружностью в точке D. Дуга АD является девятой частью окружности, хорда AD – стороной правильного девятиугольника.
О длине окружности и площади круга. Архимед
Задача вычисления длины окружности и площади круга возникла еще в глубокой древности. В папирусе Ахмеса указывается, что за площадь круга S следует принимать площадь квадрата, сторона которого равна 8/9 диаметра, то есть
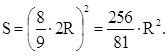
Это значит, что для
отношения длины окружности к диаметру (p) берется значение ![]() »
3,1605.
»
3,1605.
Однако в других древнеегипетских текстах встречается значение p = 3, которое вполне удовлетворяло потребности землемеров того времени. Позже римляне принимали p = 3,12. Эти и другие приближенные значения были получены эмпирическими способами, например путем прямого измерения длины окружности с помощью веревки и т. п.
Вопрос о вычислении отношения длины окружности к своему диаметру, то есть числа p, занимал лучшие умы человечества на протяжении тысячелетий. Первое вычисление p на основе строгих теоретических рассуждений было предпринято величайшим математиком древности Архимедом. В своем произведении «Об измерении круга» он доказал, что
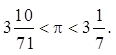
Выведенное Архимедом для p
приближенное значение 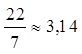 оказалось вполне
удовлетворительным для практики. На это значение ссылаются Герон
Александрийский, Папп, Прокл и другие ученые. Оно широко применяется и в
настоящее время.
оказалось вполне
удовлетворительным для практики. На это значение ссылаются Герон
Александрийский, Папп, Прокл и другие ученые. Оно широко применяется и в
настоящее время.
В произведениях Герона «Метрика» и «Геометрика» содержится много примеров на вычисление диаметра и длины окружности; площади круга, а также сегмента и сектора круга. Слово «сегмент» латинского происхождения (segmentum – отрезок) и является буквальным переводом соответствующего греческого термина, употребляемого Евклидом. То же можно сказать о термине «сектор» (по-латыни sector – резец).
О числе p
Известно, что отношение длины окружности к диаметру не может быть точно выражено ни целым числом, ни обыкновенной дробью, ни конечной десятичной дробью.
Приближенные с недостатком и избытком значения для p Архимед получил, рассматривая вписанные в круг и описанные около него многоугольники с достаточно большим числом сторон. Он последовательно определял стороны вписанных и описанных шестиугольника, двенадцатиугольника, двадцатичетырехугольника, сорокавосьмиугольника и девяностошестиугольника, выраженные через диаметр. Созданный Архимедом метод вычисления длины окружности посредством периметров вписанных и описанных многоугольников применялся многими видными математиками на протяжении почти 2000 лет.
В некоторых странах Азии встречается значение p
= ![]() то
есть 3,162. Астроном Ван Фань (229–267) утверждал, что p
=
то
есть 3,162. Астроном Ван Фань (229–267) утверждал, что p
= ![]() ,
то есть 3,155, а Цзу Чун-чжи (428–499) говорил о «неточном» значении
,
то есть 3,155, а Цзу Чун-чжи (428–499) говорил о «неточном» значении ![]() и
о «точном»
и
о «точном» ![]() , показав, что p
содержится между 3,1415926 и 3,1415927. Последнее значение записывалось в VII
в. в виде именованного числа: 3 чжана 1 чи 4 цуня 1 фень 5 ли 9 хао 2 мяо 7 хо.
, показав, что p
содержится между 3,1415926 и 3,1415927. Последнее значение записывалось в VII
в. в виде именованного числа: 3 чжана 1 чи 4 цуня 1 фень 5 ли 9 хао 2 мяо 7 хо.
В индийских «сутрах» (VII–V вв. до н. э.) имеются
правила: p = 3,008. Ариабхатта и Бхаскара брали значение 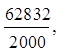 то
есть 3,1416, Брахмагупта, Магавира и Сриддхара брали p
=
то
есть 3,1416, Брахмагупта, Магавира и Сриддхара брали p
= ![]() .
.
В своей книге «Об измерении окружности» (1424) ал-Каши нашел для p значение, далеко превосходящее по точности все ранее известные. Рассмотрев вписанный и описанный многоугольники с 800 335 168 сторонами, он получает окончательный результат, выраженный в шестидесятеричных и в десятичных дробях в виде 2p » 6,2831853071795865, то есть p » 3,1415926535897932 – тут 16 верных знаков.
Однако труды ал-Каши в Европе долгое время не были
известны. Голландский профессор Адриан Меций вновь нашел в XVI в. значение ![]() для
p
независимо от Цзу Чун-чжи. В 1597 г. А. Ван Ромен из Лувена (Бельгия), применяя
метод Архимеда с помощью 230-угольников, получил 17 верных десятичных
знаков. Большое терпение и выдержку обнаружил голландский вычислитель Лудольф
ван-Цейлен (1540–1610), который, применяя метод Архимеда, дошел до
многоугольников с 60 · 202 степени сторонами, получив 35 верных
десятичных знаков для p. В его честь число p
было названо современниками «Лудольфово число». Согласно завещанию самого
Лудольфа, на его надгробном камне было высечено найденное им значение p.
для
p
независимо от Цзу Чун-чжи. В 1597 г. А. Ван Ромен из Лувена (Бельгия), применяя
метод Архимеда с помощью 230-угольников, получил 17 верных десятичных
знаков. Большое терпение и выдержку обнаружил голландский вычислитель Лудольф
ван-Цейлен (1540–1610), который, применяя метод Архимеда, дошел до
многоугольников с 60 · 202 степени сторонами, получив 35 верных
десятичных знаков для p. В его честь число p
было названо современниками «Лудольфово число». Согласно завещанию самого
Лудольфа, на его надгробном камне было высечено найденное им значение p.
Начиная с конца XVII в. для вычисления p применяются более эффективные методы высшей математики. Леонард Эйлер вычислил p с точностью до 153 десятичных знаков. После опубликования его работы (1736) стало общепринятым обозначение p (первая буква в греческом слове «периферия» – круг), которое встречается впервые в 1706 г. у английского математика У. Джонса. В 1873 г. англичанин В. Шенкс определил p с точностью до 707 десятичных знаков, усердно проработав для этой цели целых 15 лет. Однако, как выяснилось впоследствии, 527-й знак Шенкса оказался неверным. Ошибка была обнаружена Фергюссоном и Ренчем, которые в 1948 г. получили значение p с 808 знаками. С помощью электронных машин в 1949 г. получено значение p с 2035 знаками, а позднее – с 3089 знаками всего лишь за 13 с. К 1963 г. было найдено уже 100 265 десятичных знаков числа «пи». Вычисление такого большого числа знаков для p не имеет практического значения, а показывает лишь огромное преимущество и совершенство современных средств и методов вычисления по сравнению со старыми.
Вычисление площадей в древности
Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий. Еще 4–5 тысячелетий назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служил эталоном при измерении площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, ими можно заполнить плоскость без пробелов.
Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам и умножалось на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту. Для вычисления площади S четырехугольника со сторонами а, b, с, d применялась формула
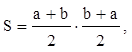
то есть умножались полусуммы противоположных сторон. Эта формула верна только для прямоугольника. С ее помощью можно вычислить приближенно площадь таких четырехугольников, у которых углы близки к прямым.
Для определения площади S равнобедренного треугольника ABC, в котором ½АВ½ = ½АС½, египтяне пользовались приближенной формулой:
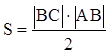 .
.
Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной ½АВ½ и высотой ½AD½ треугольника, иными словами, чем ближе вершины В и С к основанию высоты D. Вот почему приближенная формула (2) применима лишь для треугольников со сравнительно малым углом при вершине.
Измерение площадей в Древней Греции
В своих «Началах» Евклид не употребляет слово «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой.
Например, задача 16: «Параллелограммы, находящиеся на равных основаниях и между теми же параллельными, равны между собой, то есть равновелики. Докажите!»; задача 17: «Если параллелограмм ABCD имеет с треугольником ВСЕ одно и то же основание (ВС) и находится между теми же параллельными, то параллелограмм будет вдвое больше треугольника. Докажите!»
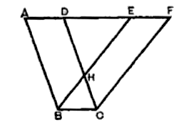
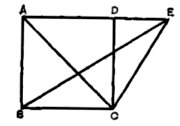
Как и другие ученые древности, Евклид занимается вопросами превращения одних фигур в другие, им равновеликие. Так, в «Началах» решается задача о построении квадрата, равновеликого любому данному многоугольнику. При этом Евклид оперирует самими площадями, а не числами, которые выражают эти площади. То, что мы получаем с помощью алгебры, Евклид получал геометрическим путем. Извлечение квадратного корня из числа означало для Евклида построение стороны квадрата, площадь которого равна площади данного многоугольника.
«О земном верстании, как земля верстать»
Потребность измерения расстояний и площадей привела к созданию на Руси рукописей геометрического содержания чисто практического характера. Первые сведения о таких рукописях относятся к XVI в. О промерах расстояний на Руси сохранились более древние памятники. В Государственном Эрмитаже хранится камень с надписью: «В лето 6576 Глеб князь мерил морем по льду от Тмутороканя до Корчева 14 тысяч сажен». Эта запись означает, что в XI в., точнее в 1068 г., было измерено расстояние между городами Таманью и Керчью через Керченский пролив по льду.
В старейшем русском памятнике XII в. – Русская Правда – говорится о межах, то есть о границах земельных владений.
Многие рукописи, существовавшие в Древней Руси, до нас не дошли. В высказываниях историков XVIII в. имеются заслуживающие доверия указания о том, что им были известны математические рукописи XVI в. Так, В. Н. Татищев (1686–1750) – автор «Истории Российской с древнейших времен...» – утверждал, что он читал наказ, данный в 1556 г. писцам о том, как следует измерять землю. К наказу, по его словам, прилагались «землемерные начертания» – чертежи. Однако этот наказ бесследно пропал.
Также бесследно исчезли математические рукописи XVII в., принадлежавшие писателю и известному историку Н. М. Карамзину (1766–1826). В настоящее время известны 2–3 рукописи XVII в., посвященные целиком арифметике или геометрии, и несколько сборников естественнонаучного содержания, в которые включены и арифметико-геометрические сведения.
В 1775 г. в Оружейной палате был найден «Устав ратных и других дел, касающихся до воинской науки», составленный в начале XVII в. (после того как он был перепечатан, подлинник устава также был утерян). В этом уставе имеются (правда, довольно туманные) правила рецептурного характера для определения расстояний между предметами.
В сохранившейся рукописи «Книга сошного письма», написанной в 1629 г., имеется глава «О земном верстании, как земля верстать». По-видимому, оригинал этой рукописи был создан значительно раньше, а сохранилась до наших дней одна из копий, переписанная с большим числом ошибок.
В главе «О земном верстании» собраны правила измерения площадей фигур различной конфигурации и приведен ряд примеров, как этими правилами пользоваться. Но выводов или обоснований указанных правил нет. В рукописи рекомендуется производить измерение и вычисление площадей различных фигур посредством измерения площадей простейших фигур: квадрата, прямоугольника, треугольника и трапеции.
Площадь прямоугольника согласно указаниям в этой рукописи следует вычислять путем выделения из прямоугольника наибольшего квадрата, а площадь оставшегося после отсечения квадрата прямоугольника вычислить, узнав, какую долю наибольшего квадрата составляет его площадь, посредством сравнения длины стороны квадрата и малого прямоугольника.
Для вычисления площади треугольника в рукописи рекомендуется произведение большей и меньшей сторон разделить на два. Это правило дает лишь приближенное значение истинного размера площади.
Площадь равносторонней трапеции в главе «О земном верстании» считается равной полусумме оснований, умноженной на большее основание. По-видимому, здесь вкралась ошибка при переписке рукописи. К этому заключению приводит сопоставление данного правила с аналогичным правилом в рукописях более поздних, в которых площадь трапеции выражается произведением полусуммы оснований на «хобот», то есть на боковую сторону, что тоже неверно, но значительно ближе к истинной величине.
Из сказанного можно заключить, что точного измерения и вычисления площадей треугольников и трапеций составители этой рукописи не знали.
В ряде более поздних геометрических рукописей правила измерения площадей даются также догматически и разъясняются рядом примеров. В них тоже встречается немало ошибочных утверждений. Например, при измерении площадей указано, что фигуры с равными периметрами имеют равные площади. Однако даже неглубокий анализ таких ошибочных утверждений показывает, что они получились в результате недостаточно обоснованного применения частного правила к более общим случаям.
Вопреки сохранившимся рукописям, создание «русскими мастерами каменных дел» различных грандиозных сооружений (кремлевских стен, башен, храмов) говорит о том, что эти мастера обладали довольно основательными знаниями в области геометрии, хотя возможно чисто рецептурного характера. Без этих знаний сооружение таких прекрасных зданий, как храм Василия Блаженного в Москве [1560 г., мастера Постник (Яковлев) и Барма], вряд ли можно было совершить.
Герон
Александрийский.
Формула площади треугольника
Одним из поздних греческих математиков-энциклопедистов, труды которого имели главный образом прикладной характер, был Герон Александрийский (годы его жизни точно не известны – одни историки предполагают, что он жил в III в. до н. э., а другие – в I в. н. э.). О жизни Герона до нас дошли лишь отрывочные сведения. Известно, что он был выдающимся ученым-механиком. Его даже называют «Герон-Механик». Он много внимания уделял вопросам геодезии и практическому применению геометрии.
В сочинении «Диоптры» Герон изложил правила съемки земельных участков на основе использования прямоугольных координат. В этом труде математик описал некоторые измерительные приборы и инструменты, в том числе и «диоптры» – приборы, которые служили для построения и измерения углов на местности.
Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников. О нахождении площади треугольника по его сторонам Герон пишет: «Пусть, например, одна сторона треугольника имеет в длину 13 мерных шнуров, вторая – 14 и третья – 15. Чтобы найти площадь, поступай вот как. Сложи 13, 14 и 15; получится 42. Половина этого будет 21. Вычти из этого три стороны одну за другой; сперва вычти 13 – останется 8, затем 14 – останется 7 и, наконец, 15 – останется 6. А теперь перемножь их: 21 раз по 8 даст 168, возьми это 7 раз – получится 1176, а это еще 6 раз – получится 7056. Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».
В своем наиболее важном геометрическом произведении «Метрика» Герон излагает доказательство примененной им выше формулы:
![]() ,
,
где a, b, с – стороны, р – полупериметр треугольника.
Эта формула носит название «формулы Герона». На самом деле она была установлена еще в III в. до н. э. величайшим математиком древности Архимедом.
Практические правила Герона для вычисления площадей применялись греческими, римскими и средневековыми землемерами и техниками.
Интересна задача Герона «Найти все треугольники с целочисленными сторонами, площади которых также выражаются целыми числами», то есть найти формулу, которая позволяла бы указать стороны и площадь треугольника в целых числах для определенного случая.
Среди прямоугольных треугольников – это все треугольники Пифагора, например со сторонами 3, 4, 5; 5, 12, 13; 7, 24, 25 и т. д. Сформулированная выше задача значительно шире – она является обобщением задачи Пифагора. Отличается же она от последней заменой в условии наличия прямого угла требованием выражения площади треугольника целым числом. Частные случаи решения известны, например: а = 7, b = 15, с = 20 или а = 9, b = 10, с = 17; а = 13, b = 14, с = 15 и др. Попробуйте проверить по известной формуле Герона, удовлетворяют ли треугольники с указанными сторонами требованиям, высказанным в условии задачи.
Для прямоугольного треугольника найдена формула, по которой можно найти решение для треугольника с одной заданной стороной. Для обобщенного же случая формулы, описывающей, как выразить стороны треугольника, нет.
Краткий обзор развития геометрии
Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако человек не только пассивно наблюдал природу, но практически осваивал и использовал ее богатства. В процессе практической деятельности он накапливал геометрические сведения. Материальные потребности побуждали людей изготовлять орудия труда, обтесывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук. Конечно, десятки и сотни тысяч раз натягивали люди свои луки, изготовляли разные предметы с прямыми ребрами и т. п., пока постепенно дошли до отвлеченного понятия прямой линии. Примерно то же можно сказать о других основных геометрических понятиях. Практическая деятельность человека служила основой длительного процесса выработки отвлеченных понятий, открытия простейших геометрических зависимостей и соотношений.
Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилась потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука. Примерно в VI–V вв. до н. э. в Древней Греции в геометрии начался новый этап развития, что объясняется высоким уровнем, которого достигла общественно-политическая и культурная жизнь в греческих государствах. Произведения, содержащие систематическое изложение геометрии, появились в Греции еще в V в. до н. э., но они были вытеснены «Началами» Евклида.
Геометрические знания примерно в объеме современного курса средней школы были изложены еще 2200 лет назад в «Началах» Евклида. Конечно, изложенная в «Началах» наука геометрия не могла быть создана одним ученым. Известно, что Евклид в своей работе опирался на труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евдокс и др. Ценой больших усилий, исходя из отдельных геометрических сведений, накопленных тысячелетиями в практической деятельности людей, эти великие ученые сумели на протяжении 3–4 столетий привести геометрическую науку к высокой ступени совершенства. Историческая заслуга Евклида состоит в том, что он, создавая свои «Начала», объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени. На протяжении двух тысячелетий геометрия изучалась в том объеме, порядке и стиле, как она была изложена в «Началах» Евклида. Многие учебники элементарной геометрии во всем мире представляли (а многие и поныне представляют) собой лишь переработку книги Евклида. «Начала» на протяжении веков были настольной книгой величайших ученых.
В XVII в. Декарт благодаря методу координат сделал возможным изучение свойств геометрических фигур с помощью алгебры. С этого времени начала развиваться аналитическая геометрия. В XVII–XVIII вв. зарождается и разрабатывается дифференциальная геометрия, изучающая свойства фигур с помощью методов математического анализа. В XVIII–XIX вв. развитие военного дела и архитектуры привело к разработке методов точного изображения пространственных фигур на плоском чертеже, в связи с чем появляются начертательная геометрия, научные основы которой заложил французский математик Г. Монж, и проективная геометрия, основы которой были созданы в трудах французских математиков Ж.Дезарга и Б. Паскаля (XVII в.). В ее создании важнейшую роль сыграл другой французский математик – Ж. В. Понселе (XIX в.).
Коренной перелом в геометрии впервые произвел в первой половине XIX в. великий русский математик Николай Иванович Лобачевский, который создал новую, неевклидову геометрию, называемую ныне геометрией Лобачевского.
Открытие Лобачевского было началом нового периода в развитии геометрии. За ним последовали новые открытия немецкого математика Б. Римана и др.
В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естестествознания, физики и техники.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.