Урок по теме "Свойство биссектрисы угла"

Тема: Свойство биссектрисы угла.

 Цели:

1. Рассмотреть  теорему  о  свойстве  биссектрисы  угла  и  её следствие.

2. Учить применять данные теоремы и следствие при решении задач.

3. Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.

4. Продолжать развивать познавательную активность, умение формулировать свои выводы и доказывать их.

 5. Воспитывать уверенность в себе, познавательный интерес.

Оборудование: ПК,  проектор, презентация, чертёжные инструменты, треугольные листы бумаги.

Ход урока

I. Организационный момент. Объявление темы и постановка целей урока совместно с учащимися.

II. Проверка домашнего задания.

- Сегодня на уроке мы повторим материал темы «Треугольники», проверим ещё раз ваши знания.

Для того, чтобы начать изучение нового материала, нам придётся опереться на уже изученный материал. Какие линии в треугольнике вам известны? К числу линий, изучаемых в школьном курсе геометрии, относятся:

• высоты треугольника;

• медианы треугольника;

• биссектрисы треугольника;

• серединные перпендикуляры к сторонам треугольника.

Повторение определений основных линий в треугольнике путём фронтальной беседы.

III. Мотивация изучения  материала (Слайд  3-10).

В старших классах каждый школьник

Изучает треугольник.

Три каких-то уголка,

А работы на века.

И опять треугольник! Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике.

Удивительно, но треугольник, несмотря на свою  простоту, является неисчерпаемым объектом изучения - никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника. (Слайд 3).

–А какие треугольники мы с вами рассматривали? (Слайд 4).

Ожидаемые ответы: равнобедренный, равносторонний, тупоугольный, прямоугольный, остроугольный.

–Сегодня мы с вами очень кратко ознакомимся с треугольниками, которые имеют своё собственное «имя», или носят имя того, кто их открыл или исследовал. (Слайд 4).

ü Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5. Египетский треугольник с соотношением сторон 3:4:5 применялся египтянами землемерами и архитекторами для построения прямых углов. Несмотря на возраст, это способ построения прямого угла активно используется строителями и теперь.  (Слайд 4, 6).

ü Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего.  (Слайды 4, 7).

ü Треугольник Рёло - это геометрическая фигура, образованная пересечением трёх равных кругов одинакового радиуса с центрами в вершинах равностороннего треугольника. Сверло, сделанное на основе треугольника Рёло, позволяет сверлить квадратные отверстия (с неточностью в 2%).  (Слайды  4, 8).

ü Один из самых загадочных и интересных треугольников – “Бермудский треугольник”. Еще это место называют аномальной зоной. На самом деле это место, которое традиционно считается самым ужасным, самым жутким местом планеты. Здесь бесследно исчезало множество кораблей и самолетов - большинство из них после 1945 года. Здесь погибло более тысячи человек. Однако при поисках никого и ничего не удалось обнаружить. Бермудский треугольник не имеет четких границ, нельзя найти на карте его точное обозначение. Разные ученые определяют его местоположение на свое усмотрение. Самое распространенное его определение - это область в Атлантическом океане между Бермудами, Пуэрто-Рико и Майами. Общая площадь - 1 млн. квадратных километров. Однако название этой области тоже условное, поэтому название “Бермудский треугольник” не является географическим.  (Слайды 4, 9).

ü Треугольник Пенроуза… Эта фигура –возможно, первый опубликованный в печати невозможный объект. Она появилась в 1958 году в журнале. в статье под заголовком "Удивительные фигуры, особый вид оптических иллюзий". Ее авторы, отец и сын Лайонелл и Роджер Пенроузы.  Невозможный» треугольник, треугольник Пенроуза, увековечен в виде статуи в городе Перт (Австралия). Созданный усилиями художника Брайна МакКея и архитектора Ахмада Абаса, он был воздвигнут в парке Клайзебрук в 1999 году и теперь все проезжающие мимо могут видеть «невозможную» фигуру.   (Слайды 4, 10).

ü Интересно! (Слайд 11).

–А теперь вернёмся к теме нашего урока. Итак, с каждым треугольником связаны 4 совершенно особые точки. Эти точки называются замечательными точками.   (Слайд 12).

IV. Изучение нового материала.

1.  Работа с чертёжными инструментами на доске (4 ученика):

построение биссектрисы, медианы, высоты, серединного перпендикуляра в треугольнике.

2.  Работа с бумагой (работа по рядам).

Каждый ряд получает задание (используя треугольный лист бумаги): построить сгибанием точку пересечения биссектрис.

Биссектриса треугольника - отрезок биссектрисы угла, соединяющий вершину треугольника с точкой противоположной стороны.

I ряд: с помощью сгибов постройте биссектрисы в остроугольном треугольнике.

II ряд: с помощью сгибов постройте биссектрисы в тупоугольном треугольнике. III ряд: с помощью сгибов постройте биссектрисы в прямоугольном треугольнике.

Вывод: Биссектрисы углов треугольника пересекаются в одной точке. (Слайд  13).

3.  Доказательство теоремы. (Слайд 14)

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

Обратно:

Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

4. Доказательство следствия из теоремы. (Слайд 15)

Биссектрисы треугольника пересекаются в одной точке.

V. Закрепление изученного материала.

Решить №№  676 (б). (Слайды 16,17)

Дано: стороны угла А, равного 90°, касаются окружности с центром О и радиусом r,  ОА = 14 дм.

Найдите: r.

Решение:  1) ( так как касательная перпендикулярна к радиусу, проведенному в точку касания)

2). АО – биссектриса угла А (так как точка О равноудалена от сторон угла).

3). ∆АОР – прямоугольный. По теореме Пифагора ОР² +АР² =АО².

r ² + r ² = 14²,       2r ² = 14²,         r = .     

  Ответ:  .

Дополнительно: № 678 (а), самопроверка. (Слайд  18).

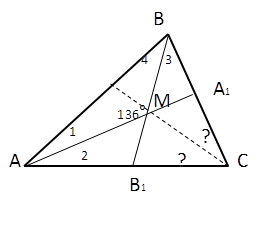
Дано: ∆АВС, АА₁ и ВВ₁  биссектрисы углов А и В .

Найти:

Решение: 1) СМ – биссектриса угла С, так как биссектрисы углов в треугольнике пересекаются в одной точке.

2) ∆АМВ,  

3)

Ответ:  46°.

VI. Итоги урока.   

 Рефлексия.  «Закрой глаза». (Слайд  19).

  Учащимся предлагается с закрытыми глазами мысленно ответить на три вопроса:

- Что нового я узнал сегодня на уроке?

- Что было особенно интересным и познавательным?

- Доволен ли я своей работой?

V. Домашнее задание: вопросы 15, 16, с. 187; №№ 676 (а), 678 (б). (Слайд  20).

Скачано с www.znanio.ru