
Урок 1. Десятичная система счисления
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: повторить особенности построения десятичной системы счисления, названия разрядов; способствовать формированию умений представлять числа в виде суммы разрядных слагаемых |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «десятичная система записи чисел»; научатся представлять трехзначное число в виде суммы разрядных слагаемых |
Метапредметные: |
Личностные: проявляют этические чувства, доброжелательность и эмоционально-нравственную отзывчивость, понимание и сопереживание чувствам других людей |
|
Познавательные: работают в информационной среде; владеют основными методами познания окружающего мира. Регулятивные: принимают и сохраняют учебную задачу; адекватно воспринимают оценку учителя и товарищей; планируют свое действие. Коммуникативные: умеют формировать коммуникативно-речевые действия, конструктивные способы взаимодействия с окружающими (учителем, сверстниками) |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||
|
I. Организация начала урока* |
Проверка готовности к уроку. Наличие общей установки на урок. Создание ситуации успеха. Приветствие обучающихся. Фиксирование отсутствующих. – Проверим готовность к уроку |
Сообщают о готовности к уроку. Определение самоготовности (настроен ли я слушать учителя, воспринимать материал урока). Один из учащихся читает стихотворение: Прибавляю, отнимаю – Математику я знаю, И поэтому с утра Я кричу: «Ура! Ура!» |
Слушать в соответствии с целевой установкой, принимать и сохранять организационные задачи |
|||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. 1) Определите порядок выполнения действий и вставьте соответствующие числа в «окошки». На доске: 45 : 15 + 39 : 13 + 85 : 17 + 48 : 16 = |
Отвечают на вопросы учителя, выполняют задания устного счета:
1) 45 : 15 + 39 : 13 + 85 : 17 + 48 : 16 = |
Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||
|
2) Запишите в каждом ряду пропущенные числа: а) 90 дес., 91 дес., … , 99 дес., 100 дес.;
б) 900, 910, … , 990, 1000. |
2) Записывают пропущенные числа: а) 92 дес., 93 дес., 94 дес., 95 дес., 96 дес., 97 дес., 98 дес. б) 920, 930, 940, 950, 960, 970, 980. |
|||||||||||||||||||
|
|
– Как узнать, сколько в числе десятков?
– Как можно прочитать число 1000? – Запишите любые числа, в которых 2 сотни. – Увеличьте любое из этих чисел на 4 сотни. – Сколько сотен в этом числе? – Увеличьте это число на 3 сотни. – Сколько сотен в этом числе? |
– Нужно закрыть разряд единиц и прочитать оставшееся число. Оно будет обозначать число десятков. – 1000 – это 100 десятков; 1000 – это 10 сотен. – 200, 201, 234, 258 и т. д. – 234 + 400 = 634. – 6 сотен. – 634 + 300 = 934. – 9 сотен. |
||||||||||||||||||
|
– Сколько сотен получим, если число 934 увеличим на 1 сотню? – Прочитайте данные числа, выделяя десятки.
– Прочитайте данные числа, выделяя сотни |
– 934 + 100 = 1034, получим 10 сотен и ещё 34.
– 234 – 23 дес., 932 – 93 дес., 975 – 97 дес., 1000 – 100 дес. – 234 – 2 сот., 932 – 9 сот., 975 – 9 сот., 1000 – 10 сот. |
|||||||||||||||||||
|
III. Сообщение темы урока. Определение целей урока** |
Выдвигает проблему. Организует формулирование темы урока учащимися, постановку учебной задачи. Уточняет понимание учащимися поставленной темы и целей урока. – Определите цели урока, используя опорные слова: • Мы познакомимся с… • Мы узнаем… • Мы вспомним… • Мы будем уметь… • Мы сможем поразмышлять… |
Формулируют тему урока, ставят учебную задачу. Обсуждают тему урока.
– Сегодня на уроке мы… |
Принимать и сохранять учебную цель и задачу. Анализировать, находить общее и различия, делать выводы |
|||||||||||||||||
|
IV. Открытие нового знания, нового способа действия. Работа по учебнику (I часть, с. 4‒5). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Прочитайте числа, которые держат ученики Лесной школы. Сколько сотен, десятков и единиц в каждом из чисел? – Какая цифра обозначает число сотен в записи числа 594? – А в записи чисел 451, 275 какая цифра обозначает число десятков, число единиц? – Итак, одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит. В записи числа значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому систему записи чисел, которой мы пользуемся, называют десятичной системой счисления. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– 594, 451, 275. – 594 – 5 сот. 9 дес. 4 ед.; 451 – 4 сот. 5 дес. 1 ед.; 275 – 2 сот. 7 дес. 5 ед. – В записи числа 594 цифра 5 обозначает число сотен. – В записи чисел 451, 275 цифра 5 обозначает число десятков, число единиц. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
|||||||||||||||||
|
Задание 2. |
– Что обозначает каждая цифра в записи чисел? |
|
||||||||||||||||||
|
Задание 3 |
– Запишите числа с помощью цифр |
– 448; 905; 950; 200 |
||||||||||||||||||
|
V. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 7‒8). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока. – Выполните устные вычисления. |
Отвечают на вопросы учителя. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Выполняют устные вычисления. Ответы: 31 240 40 110 4 60 48 81 300 3 100 25 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор |
|||||||||||||||||
|
Задание 12. |
– Чем похожи и чем различаются выражения? Выполните вычисления. |
– Выражения похожи числами и арифметическими действиями. Отличаются выражения порядком действий, поскольку во втором выражении есть скобки.
|
||||||||||||||||||
|
Задание 13. |
– Запишите выражения и вычислите их значения. |
Записывают выражения и вычисляют их значения.
|
||||||||||||||||||
|
Задание 15 |
– Вычислите значения буквенных выражений |
Вычисляют значения буквенных выражений (см. ресурсный материал к уроку) |
||||||||||||||||||
|
VI. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Какая система счисления называется десятичной? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально- нравственную отзывчивость |
Урок 2. Представление числа в виде суммы разрядных слагаемых
|
Тип урока: комбинированный |
||
|
Педагогические задачи: повторить особенности построения десятичной системы счисления, названия разрядов; способствовать формированию умений представлять числа в виде суммы разрядных слагаемых |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «десятичная система записи чисел»; научатся представлять трехзначное число в виде суммы разрядных слагаемых |
Метапредметные: |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
|
Познавательные: умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; активно используют математическую речь для решения разнообразных коммуникативных задач. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке. Коммуникативные: учатся слушать и понимать речь других; признают возможность существования различных точек зрения и право каждого иметь свою |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||
|
I–II. Организация начала урока. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет (задания пишутся на доске) с целью актуализации знаний. – Дополните каждую величину: 1 м2 = 26 дм2 + |
Отвечают на вопросы учителя. Выполняют задания устного счета. 1 м2 = 26 дм2 + 74 дм2 1 дм2 = 38 см2 + 62 см2 |
Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||
|
– Расставьте порядок выполнения действий и вставьте числа в «окошки»: 72 : 18 + 32 : 16 + 96 : 12 + 64 : 16 = |
72 : 18 + 32 : 16 + 96 : 12 + 64 : 16 =
|
||||||||||||
|
– Найдите лишнее выражение: 48 : 8 36 : 6 60 : 10 54 : 9 42 : 7 56 : 7 30 : 5 120 : 20 180 : 30 |
Ответ: лишнее выражение 56 : 7. |
||||||||||||
|
– Назовите пропущенные числа: а) б) 300000, |
а) 800998, 800999, 801000, 801001, 801002, 801003, 801004, 801005, 801006
б) 300000, 399999, 399998, 399997, 399996, 399995, 399994, 399993 |
||||||||||||
|
III– IV. Сообщение темы и целей урока. Открытие нового знания, нового способа действия. Работа по учебнику (с. 5‒6). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Запишите цифрами числа. – Что называют разрядным слагаемым? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Записывают цифрами числа: 448, 905, 950. – Каждое слагаемое суммы называют разрядным слагаемым. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи |
||||||||||
|
Задание 4. |
– Запишите числа в виде суммы разрядных слагаемых. |
Записывают числа в виде суммы разрядных слагаемых: 327 = 3 · 100 + 2 · 10 + 7 638 = 6 · 100 + 3 · 10 + 8 418 = 4 · 100 + 1 · 10 + 8 И т. д. |
|||||||||||
|
Задание 5. |
– Какие числа представлены в виде суммы разрядных слагаемых? |
6 · 100 + 9 · 10 + 2 = 692 1 · 10 + 8 = 18 1 · 100 + 3 · 10 = 130 7 · 100 + 5= 705 |
|||||||||||
|
Задание 6 |
– Запишите все трехзначные числа, используя цифры 8, 0 и 5 так, чтобы в записи каждого числа цифры не повторялись. – А теперь так, чтобы в записи каждого числа цифры повторялись |
Составляют и записывают числа: 805, 850, 508, 580.
Составляют и записывают числа: 855, 858, 885, 805, 850, 888, 588, 558, 585, 508, 580, 555 |
|||||||||||
|
V. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 8). Задание 16. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока. – Прочитайте условие задачи. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Доказывают, аргументируют свою точку зрения. Запись: Было – 85 л Долили – ? л Стало – 192 л Решение: Ответ: 107 л воды долили в бочку. |
Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок |
||||||||||
|
Задание 17. |
– Прочитайте задачу. Что известно? Каких тетрадей ученик купил больше и на сколько? – За какие тетради он заплатил больше денег? |
Решение: 9 – 5 = 4 (т.) – на столько больше в линейку. – За тетради в линейку он заплатил больше денег.
|
|||||||||||
|
Задание 18. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 12 : 4 = 3 (р.) – цена одной тетради. |
|||||||||||
|
Задание 19. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 9 – 5 = 4 (т.) – стоят 12 р. 2) 12 : 4 = 3 (р.) – цена одной тетради. 3) 9 · 3 = 27 (р.) – стоят тетради в линейку. 4) 5 · 3 = 15 (р.) – стоят тетради в клетку. |
|||||||||||
|
Задание 20 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Запись: 4 м – 320 р. 1 м – ? 7 м – ? Решение: 1) 320 : 4 = 80 (р.) 2) 80 · 7 = 560 (р.) |
|||||||||||
|
VI. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Какие слагаемые называют разрядными? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию, для чего проговаривают цель урока и определяют, достигнут или нет результат. Говорят о трудностях, с которыми встретились на уроке.
|
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Осуществлять итоговый контроль, оценивать результаты деятельности |
Урок 3. Сравнение десятичной системы с римской системой записи чисел.
Стартовая педагогическая диагностика № 1
|
Тип урока: комбинированный |
||
|
Педагогические задачи: повторить особенности построения десятичной системы счисления, названия разрядов; способствовать формированию умений представлять числа в виде суммы разрядных слагаемых |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с особенностями построения десятичной системы счисления; научатся: различать названия разрядов, читать и записывать римские цифры, использовать правила записи чисел в римской системе; представлять числа в виде суммы разрядных слагаемых; оценивать собственную работу, проводить анализ допущенных ошибок |
Метапредметные: |
Личностные: приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности |
|
Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; применяют методы информационного поиска, в том числе с помощью компьютерных средств. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке; адекватно оценивают результаты своей деятельности. Коммуникативные: высказывают свое мнение, прислушиваются к мнению других; аргументируют свою точку зрения и оценку событий |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. 1) Вставьте знак >, < или =. 10 дм … 10 см 1 м … 10 дм 1 дм2 … 10 см2 1 м2 … 10 дм2 1 дм2 … 100 см2 1 м2 … 100 дм2 5 см2 … 5 дм2 5 дм2 … 5 м2 6 дм2 … 60 см2 8 м2 … 80 дм2 6 дм2 … 600 см2 8 м2 … 800 дм2 |
Отвечают на вопросы учителя. Выполняют задания устного счета. 1) 10 дм > 10 см 1 м = 10 дм 1 дм2 > 10 см2 1 м2 > 10 дм2 1 дм2 = 100 см2 1 м2 … 100 дм2 5 см2 < 5 дм2 5 дм2 < 5 м2 6 дм2 … 60 см2 8 м2 > 80 дм2 6 дм2 = 600 см2 8 м2 = 800 дм2 |
Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||
|
|
2) Разгадайте правило, по которому записан каждый ряд величин, и продолжите ряды. а) 96 см2, 1 дм2, 104 см2, 1 дм2 8 см2, … б) 1 дм2, 90 см2, 80 см2, … в) 30 см2, 60 см2, 90 см2, 1 дм2 20 см2, … г) 100 см2, 2 дм2, 300 см2, 4 дм2, … |
Дополняют ряд величин: а) 1 дм2 12 см2 б) 70 см2 в) 1 дм2 50 см2 г) 500 см2 |
||||||||||||||||||||||||||
|
3) Таня начертила две прямые линии. На одной из них она отметила 3 точки, а на другой – 5 точек. Всего было отмечено 7 точек. Как она это сделала? |
Выполняют чертеж:
|
|||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 6‒7). Задание 7. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Запишите все двузначные числа, в которых число единиц в 2 раза меньше числа десятков. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– 21, 42, 63, 84. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия всоответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
|||||||||||||||||||||||||
|
Задание 8. |
– Кроме десятичной системы счисления часто используют римскую систему записи чисел. Римские цифры можно увидеть на циферблатах часов, на старинных зданиях; римскими цифрами иногда обозначают номер главы в книге, месяц, год, век. При записи чисел римскими цифрами используется семь цифр (букв). Какое число обозначает каждая римская цифра? |
I – 1 X – 10 С – 100 M – 1000 V – 5 L – 50 D – 500 |
||||||||||||||||||||||||||
|
Задание 9. |
– Для записи целых чисел в римской нумерации используются семь основных цифр:
– С их помощью можно записать любое целое число не более 4000, при этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трех раз. При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается так: CCLXXXIII, т. е. 200 + 50 + 30 + 3 = 283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза. Меньшая цифра может быть записана и слева от большей, тогда ее следует вычесть из большей. В этом случае повторения меньшей цифры не допускаются. Запишем по-римски число 94: XCIV = 100 – 10 + 5 – 1 = 94. Это так называемое «правило вычитания». Существует шесть вариантов использования «правила вычитания»:
– С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают класс тысяч, ставится одна черта, а над цифрами, которые обозначают класс миллионов, – двойная черта. Например, число 123 123 будет выглядеть так: ______ CXXIIICXXIII; число 123 123 123 так: 1______ CXXIIICXXIIICXXIII. |
|
||||||||||||||||||||||||||
|
Задание 10 |
– Прочитайте числа, записанные римскими цифрами. – В каком году построен замок? – Какое время показывают часы? |
– MDXIV = 1514.
– Замок построен в 1514 году. – Часы показывают 3 часа 23 минуты |
||||||||||||||||||||||||||
|
III. Включение нового вактивное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 9‒11). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу двумя способами. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Запись: 3 ящ. – 48 кг 6 ящ. – ? кг Решение:
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||
|
Задание 22. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись:
|
||||||||||||||||||||||||||
|
|
|
Решение: 1) 126 + 67 = 193 (р.) – перчатки. 2) 126 + 193 = 319 (р.) – футболка. |
||||||||||||||||||||||||||
|
Задание 23. |
– Составьте выражение для вычисления стоимости покупки.
– Узнайте цену одного глобуса и одной карты, если стоимость всех купленных глобусов 900 р., а карт – 861 р. |
Составляют выражение:
Решение: 1) 900 : 5 = 180 (р.) – цена глобуса. 2) 861 : 7 = 123 (р.) – цена карты. |
||||||||||||||||||||||||||
|
Задание 24. |
– Ломаная линия длиной 90 см состоит из шести одинаковых по длине звеньев. Найдите длину трех звеньев ломаной. |
Решение: 1) 90 : 6 = 15 (см) – длина 1 звена. 2) 15 · 3 = 45 (см) – длина трех звеньев. |
||||||||||||||||||||||||||
|
Задание 25. |
– Выполните построения. Начертите окружность, длина радиуса которой 5 см. Отметьте точку А на этой окружности. Постройте квадрат АВХМ так, чтобы все его вершины лежали на этой окружности. |
Выполняют чертеж:
|
||||||||||||||||||||||||||
|
Задание 26. |
– Площадь квадратной клумбы увеличили в 4 раза, сохранив ее форму. Во сколько раз увеличили длину стороны этой клумбы? |
– В 2 раза увеличили длину стороны этой клумбы. |
||||||||||||||||||||||||||
|
Задание 27. |
– Назовите пару отрезков, симметричных относительно оси ON. |
– Отрезки AB и СD. |
||||||||||||||||||||||||||
|
Задание 28. |
– Почему лучи АВ и CD не являются симметричными относительно оси ON? |
– Лучи АВ и CD не являются симметричными, так как они имеют разное направление. |
||||||||||||||||||||||||||
|
Задание 29. |
– Выполните практическую работу.
|
Выполняют практическую работу:
|
||||||||||||||||||||||||||
|
Задание 30 |
– Прочитайте верные высказывания |
Читают верные высказывания под номерами 1, 3, 4 |
||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Определяют, на какой ступеньке лестницы знаний они находятся: • Хочу знать больше. • Знаю хорошо, но могу лучше. • Пока испытываю трудности |
Способны к самооценке на ос-нове критерия успешности учебной деятельности |
Урок 4. Классы и разряды многозначного числа в пределах миллиарда
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: повторить особенности построения десятичной системы счисления, названия разрядов; способствовать формированию умений представлять числа в виде суммы разрядных слагаемых |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями классов и разрядов в записи многозначного числа; научатся: читать и записывать многозначные числа в пределах класса миллионов; выполнять запись многозначных чисел цифрами после предварительного определения числа цифр в каждом классе; сравнивать многозначные числа |
Метапредметные: |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
|
Познавательные: осуществляют анализ, сравнение, моделирование – преобразование объекта из чувственной формы в модель (пространственно-графическую или знаково-символическую), где выделены существенные характеристики объекта, и преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: излагают свое мнение и аргументируют свою точку зрения |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности учащегося |
|||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. 1) Игра «Цепочки».
|
Отвечают на вопросы учителя. Выполняют задания устного счета. 1) Восстанавливают цепочки:
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||
|
|
2) Поставьте знак >, < или = так, чтобы записи были верными. 54 сот. 7 ед. … 547 35 сот. 9 ед. … 3590 8 тыс. 12 дес. … 8012 7 тыс. 3 ед. … 7030 5021 … 5 дес. 21 ед. 89 сот. 89 ед. … 8999 |
2) Сравнивают числа:
54 сот. 7 ед. > 547 35 сот. 9 ед. < 3590 8 тыс. 12 дес. > 8012 7 тыс. 3 ед. < 7030 5021 > 5 дес. 21 ед. 89 сот. 89 ед. < 8999 |
||||||
|
|
3) Расположите карточки с числами в порядке возрастания.
|
Располагают карточки с числами в порядке возрастания. 3) 4400, 4409, 4423, 4499, 4506, 4573, 4601, 4708. |
||||||
|
|
4) Увеличьте каждое число на 30 десятков. 5) Решите задачу. Цена зимней шапки – 100 рублей. Сколько денег надо заплатить за три такие шапки? |
4) 4700, 4709, 4723, 4799, 4806, 4873, 4901, 5008. 5) Решают задачу. Ответ: 300 рублей |
|
|||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 13‒16). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Прочитайте число, которое держит Заяц. – Почему это число называют трехзначным?
– Какое число держит Волк? – Почему это число называют шестизначным? – Первые три цифры справа образуют класс единиц, а следующие три цифры – класс тысяч. В классе тысяч три разряда, которые называют так: единицы тысяч, десятки тысяч, сотни тысяч. В числе 625 347 цифра 6 обозначает шесть сотен тысяч (шестьсот тысяч), цифра 2 – два десятка тысяч (двадцать тысяч), цифра 5 – пять тысяч. Всего в этом числе 625 тысяч 347 единиц. Поэтому число 625 347 читают так: шестьсот двадцать пять тысяч триста сорок семь (слово «единиц» не произносят). – Какое число у Белки? – Почему это число называют девятизначным? – Итак, число 126 281 539 – девятизначное. Первые три цифры справа образуют класс единиц, следующие три цифры – класс тысяч, а последние три цифры – класс миллионов. В классе миллионов тоже три разряда, которые называют так: единицы миллионов, десятки миллионов, сотни миллионов. Десять единиц любого разряда в любом классе образуют единицу следующего (высшего) разряда. Так, 10 тысяч образуют единицу следующего разряда – десяток тысяч, 10 десятков тысяч – сотню тысяч, 10 сотен тысяч – миллион, 10 миллионов – десяток миллионов, 10 десятков миллионов – сотню миллионов. При этом значение каждой цифры от низшего разряда к высшему увеличивается в 10 раз. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. – Заяц держит число 328. – В записи трехзначного числа 328 цифры образуют три разряда – единицы, десятки, сотни. Эти разряды вместе называют классом единиц. В числе 328 цифра 3 обозначает три сотни (триста), цифра 2 – два десятка (двадцать), цифра 8 – восемь единиц. Число 328 читают так: триста двадцать восемь. – Волк держит число 625 347. – Число 625 347 – шестизначное, потому что оно содержит шесть цифр (знаков).
– У Белки число 126 281 539. – В нем 9 знаков. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия всоответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально- нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль дей- ствий по их результатам |
|||||
|
Задание 2. |
– Прочитайте числа в таблице. Что обозначает каждая цифра в записи чисел? – Прочитайте каждое число. – Сформулируйте правило чтения многозначного числа. |
Формулируют правило чтения многозначного числа: – Чтобы прочитать многозначное число, его запись разбивают справа налево на классы по три разряда в каждом. В последнем (слева) классе могут оказаться один или два разряда, в которых отсутствует цифра. Затем называют число единиц каждого класса. |
||||||
|
Задания 3, 4 |
– Прочитайте многозначные числа |
Читают многозначные числа |
||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 19‒20). Задание 18. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока. – При выполнении нижеследующих заданий воспользуйтесь карточкой-помощницей. – Запишите в виде суммы разрядных слагаемых числа. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. 12164 = 10000 + 2000 + 100 + 60 + 4 798053 = 700000 + 90000 + 8000 + 50 + 3 80070 = 80000 + 70 70190 = 70000 + 100 + 90 606060 = 600000 + 6000 + 60 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||
|
Задание 19. |
– Сравните выражения в столбиках. Чем они похожи? Чем отличаются? Выполните действия и сравните результаты. |
Выполняют действия в выражениях и сравнивают результаты.
2) (630 + 270 : 9) : 2 = 330 (630 + 270) : 9 : 2 = 50
|
||||||
|
Задание 20. |
– Проверьте, верны ли равенства и неравенства. |
706 + 43 = 749 – верно. 270 · 2 : 10 > 54 – неверно. 769 – 45 = 724 – верно. 880 : 44 · 10 > 100 – верно. 45 + 432 = 477 – верно. 488 – 135 < 353 – неверно. |
||||||
|
Задание 21. |
– Выполните вычисления. |
15 · 18 : 9 + 361 – 954 : 3 = 73
64 · (8 + 2) – 549 + 36 · 9 = 415 |
||||||
|
Задание 22 |
– Выполните деление с остатком и сделайте проверку |
327 : 5 = 65 (ост. 2) 800 : 24 = 33 (ост. 8) Проверка: Проверка: 65 · 5 + 2 = 327 33 · 24 + 8 = 800 |
||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Назовите классы и разряды девятизначного числа. – Назовите классы и разряды многозначного числа в пределах миллиарда. – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Продолжают высказывания: • Сегодня я узнал… • Было интересно… • Было трудно… • Я выполнял задания… • Я понял, что… • Теперь я могу… |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 5. Чтение многозначных чисел в пределах миллиарда
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «классы» и «разряды», названием, последовательностью и записью чисел от 0 до 1 000 000; способствовать развитию умений читать многозначное число путем разбивки его записи на классы, записывать многозначное число цифрами после предварительного определения числа цифр в каждом классе, сравнивать многозначные числа |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями классов и разрядов в записи многозначного числа; научатся: читать и записывать многозначные числа в пределах класса миллионов; выполнять запись многозначных чисел цифрами после предварительного определения числа цифр в каждом классе; сравнивать многозначные числа |
Метапредметные: |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
|
Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний. 1) Записаны три числа в порядке возрастания. Какую цифру можно поставить в «окошко»? а)
6249, 62 в)
9346, 735 |
Отвечают на вопросы учителя. Выполняют задания устного счета. 1) Вставляют пропущенные цифры:
а) 6249, 6251, 6262; б) 7687, 7787, 7790; в) 9346, 7350, 7352. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||
|
2) Догадайтесь, какие числа здесь записаны: а) 4000 + 3 · 100 + 5 · 10 + 2; б) 5 · 100 + 1 · 10 + 4; в) 2 · 100 + 2; г) 5000 + 0 · 100 + 2 · 10 + 1. |
2) Составляют числа: а) 4352; б) 514; в) 202; г) 5021. |
|||||||||||||||
|
3) Решите задачи. а) Ребята посадили 400 семян гороха. Из каждой сотни не взошло 2 семени. Сколько семян взошло? б) В одной пачке 15 книг. Сколько книг в 10 таких пачках? В 100 пачках? |
3) Решают задачи: а) 400 – 4 · 2 = 392 (семени).
б) 15 · 10 = 150 (книг) – в 10 пачках. 15 · 100 = 1500 (книг) – в 100 пачках. |
|||||||||||||||
|
4) Разгадайте правило, по которому записан каждый ряд, и продолжите ряды: а) 4855, 4854, 4853, … б) 2099, 3099, 4099, … в) 7004, 7002, 7000, … г) 5010, 5020, 5030, … д) 3904, 3907, 3910, … е) 8691, 7691, 6691, … |
4) Продолжают ряды чисел: а) 4855, 4854, 4853, 4852, 4851, 4850 б) 2099, 3099, 4099, 5099, 6099, 7099 в) 7004, 7002, 7000, 6998, 6996, 6994 г) 5010, 5020, 5030, 5040, 5050, 5060 д) 3904, 3907, 3910, 3913, 3916, 3919 е) 8691, 7691, 6691, 5691, 4691, 3691 |
|||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 17–18). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Прочитайте многозначные числа. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Читают многозначные числа. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
|||||||||||||
|
Задание 6. |
– Сколько цифр в каждом из классов в записях чисел? |
– При записи многозначного числа нужно следить за тем, чтобы в разрядах каждого класса (кроме первого слева) было по три цифры. Если в каком-нибудь классе отсутствуют единицы того или иного разряда, то в этих разрядах пишут нули. |
||||||||||||||
|
Задание 7. |
– Запишите многозначные числа цифрами. |
Записывают числа, осуществляют самопроверку по учебнику. |
||||||||||||||
|
Задание 8 |
– Запишите шесть четырехзначных чисел, используя цифры 5, 3, 4, 0. – В записи каждого числа цифры могут повторяться. – В записи каждого числа цифры не должны повторяться |
– 5340, 5304, 5403, 5555, 3333, 4444 и т. д.
– 5340, 5304, 5403, 5430, 3540, 3504, 3450, 3405 и т. д. |
||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 20–21). Задание 23. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 318 + 97 = 415 (м) – в 3-й день. 2) 318 + 415 + 227 = 960 (м) – по факту. 3) 1000 м > 960 м Ответ: рабочие задание не выполнили. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии |
|||||||||||||
|
Задание 24. |
– При переработке 696 кг нефти керосин составляет третью часть этой массы. Сколько килограммов керосина получилось? |
Решение: 696 : 3 = 232 (кг) |
||||||||||||||
|
Задание 25. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 11 – 7 = 4 (к.) – стоят 12 р. 2) 12 : 4 = 3 (р.) – цена. 3) 3 · 7 = 21 (р.) – заплатил мальчик. 4) 3 · 11 = 33 (р.) – заплатила девочка. |
||||||||||||||
|
Задание 26. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: Купили – 64 т. и 40 т. Учеников – 12 д. и 14 м. Раздали – по ? т. Решение: 1) 64 + 40 = 104 (т.) – купили. 2) 12 + 14 = 26 (т.) – было. 3) 104 : 26 = 4 (т.) – получил каждый ученик. |
||||||||||||||
|
Задание 27. |
Составьте задачу, решением которой является выражение х – 4.
а) Решите задачу, если х = 20. б) Решите задачу, если х = 15. |
Составьте задачу, решением которой является выражение х – 4. Запись: Было – х л Раздали – 4 л Осталось – ? л а) 20 – 4 = 16 (л) б) 15 – 4 = 11 (л) |
||||||||||||||
|
Задание 28 |
– Прочитайте задачу. Что известно? Что требуется узнать? Запишите решение задачи выражением |
Решение: 8 · а + 13 (р.) – стоимость покупки |
||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Сформулируйте правило чтения и записи многозначного числа. – Оцените свои достижения на уроке: кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Оценивать результаты своей деятельности на уроке |
|||||||||||||
Урок 6. Запись многозначных чисел в пределах миллиарда
|
Тип урока: развитие знаний и способов действий |
||
|
Педагогические задачи: содействовать развитию умений читать многозначное число путем разбивки его записи на классы, записывать многозначное число цифрами после предварительного определения числа цифр в каждом классе, сравнивать многозначные числа; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями, последовательностью и записью чисел от 0 до 1 000 000; научатся: читать многозначные числа путем раз-бивки их записи на классы; записывать многозначные числа цифрами после предварительного определения числа цифр в каждом классе |
Метапредметные: |
Личностные: приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности |
|
Познавательные: осуществляют анализ и сравнение объектов; проводят аналогии между изучаемым материалом и собственным опытом. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя. Выполняют задания устного счета. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||
|
1) Решите примеры-цепочки.
|
1) Решают цепочки: 32 · 2 = 64 24 · 4 = 96 15 · 5 = 75 64 : 4 = 16 96 : 2 =4 8 75 : 3 = 25 16 + 4 = 20 48 + 2 = 50 25 + 3 = 28 20 · 4 = 80 50 · 2 = 100 28 · 3 = 84 |
|||||||||
|
2) Найдите ошибку, которую допустил ученик. а) 2640, 2660, 2680, 2720, 2740. б) 3111, 3222, 3333, 3400, 3444, 3555. в) 5429, 5426, 5423, 5420, 5418, 5414. |
2) Находят и исправляют ошибки: а) 2640, 2660, 2680, 2700, 2720, 2740. б) 3111, 3222, 3333, 3444, 3555. в) 5429, 5426, 5423, 5420, 5417, 5414. |
|||||||||
|
3) Вставьте пропущенные цифры так, чтобы каждое следующее число уменьшалось на 21 десяток. 7 7 |
3) Вставляют цифры: 7845, 7635, 7425, 7215, 7005. |
|||||||||
|
4) Дополните каждое число до 1000. 999 + 800 + 550 + |
4) Вставляют числа: 999 + 1 = 1000 300 + 700 = 1000 800 + 200 = 1000 820 + 180 = 1000 550 + 450 = 1000 650 + 350 = 1000 |
|||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 18–19). Задания 10, 11. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Назовите числа по порядку. – Запишите числа. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Называют числа по порядку. Записывают три числа, которые при счете следуют за числом 3997, и три числа, которые предшествуют ему. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|||||||
|
Задание 12. |
– Составьте равенства. |
99 999 + 1 = 100 000 999 999 + 1 = 1 000 000 |
||||||||
|
Задание 13. |
– Из какого четырехзначного числа надо вычесть 1, чтобы получилось трехзначное число? |
1000 – 1 = 999 |
||||||||
|
Задание 14. |
– Запишите какое-нибудь трехзначное число. Поменяйте в нем местами цифры в разрядах единиц и сотен. Запишите получившееся число. Какое число больше и на сколько? |
Пример: 589 < 985; 985 – 589 = 356 |
||||||||
|
Задание 15. |
– Составьте равенства.
|
30000 + 5000 = 35000 6020 + 100 = 6120 30000 + 500 = 30500 100800 + 2000 = 102800 30000 + 50 = 300050 76400 + 30 = 76430 30000 + 5 = 30005 1000000 + 900000 = 1900000 |
||||||||
|
Задание 16. |
– Вычислите устно. |
3600 – 600 = 3000 1275 – 1000 – 200 – 70 = 5 28000 – 20000 = 8000 1999 – 999 = 1000 |
||||||||
|
Задание 17 |
– Выразите длины в километрах и метрах.
– Выразите величины в метрах |
124568 м = 124 км 568 м 70031 м = 70 км 31 м 504040 м = 504 км 40 м 72 км 275 м = 72275 м 8 км 64 м = 8064 м 10 км 740 м = 10740 м |
||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 22–23). Задание 29.
|
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните построения. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Развивать чувство доброжелательности. Приводить убедительные доказательства в диалоге. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|||||||
|
Задание 30. |
– Сколько всего треугольников на каждом рисунке? |
Ответ: 5. Ответ: 4. |
||||||||
|
Задание 31. |
– Как можно вычислить площадь первой фигуры? – Как можно вычислить площадь второй фигуры? |
Вычисляют площади первой и второй фигур (см. Ресурсный материал к уроку). |
||||||||
|
Задание 32. |
– Сколько копеек в 1 рубле? – Вычислите устно. |
– В 1 рубле 100 копеек. Работают самостоятельно. |
||||||||
|
Задание 33. |
– Клоун жонглирует шестью одинаковыми по виду кольцами. Одно из колец легче каждого из остальных. Как найти это кольцо, выполнив только два взвешивания колец на чашечных весах без гирь? |
– Делим по три кольца. Кладем на весы. Выбираем те три кольца, что легче. Берем из них два. Кладем на весы по одному. Если веса равные, то легкое то, что осталось; если неодинаковые, то легкое то, что легче. |
||||||||
|
Задание 34. |
– Подсчитайте стоимость покупки по чеку. – На какую сумму покупатель получит скидку по дисконтной карте? – Сколько денег покупатель должен заплатить за свою покупку с учетом скидки? |
– 369 рублей 50 копеек – стоимость покупки по чеку. – 36950 коп. : 10 = 3695 к. = 36 руб. 95 коп. – на – 36950 коп. – 3695 коп. = 33255 коп. = = 332 руб. 55 коп. 322 рубля 55 копеек покупатель должен заплатить за свою покупку с учетом скидки. |
||||||||
|
Задание 35 |
– Какая фигура изображена? – Увеличьте размеры данного прямоугольника в 3 раза. Постройте прямоугольник с новыми размерами |
– Изображен прямоугольник. Запись: 15 мм · 3 = 45 мм – ширина; 25 мм · 3 = 75 мм – длина. Строят прямоугольник |
||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Прием «Цветные карточки». У учащихся две карточки: синяя и красная. Они показывают карточку в соответствии с их настроением в начале и в конце урока. В данном случае можно проследить, как меняется эмоциональное состояние ученика в процессе урока |
Способны проводить самооценку на основе критерия успешности учебной деятельности |
Урок 7. Поразрядное сравнение многозначных чисел
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для развития навыка читать многозначное число путем разбивки его записи на классы; содействовать развитию умений записывать многозначное число цифрами после предварительного определения числа цифр в каждом классе, сравнивать многозначные числа |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями, последовательностью и записью чисел от 0 до 1 000 000; научатся: читать многозначные числа путем разбивки их записи на классы; записывать многозначные числа цифрами после предварительного определения числа цифр в каждом классе |
Метапредметные: |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
|
Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; строят логическую цепь рассуждений. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: умеют устанавливать, с какими учебными задачами могут справиться самостоятельно |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. 1) Математический диктант. а) Запишите самое большое трехзначное число. б) Запишите соседей числа 1005. в) Увеличьте число 2004 на 4 тысячи. г) Запишите самое маленькое четырехзначное число. д) Запишите цифрами: 23 сот., 46 дес., 21 сот. 7 ед., 8 тыс. 54 дес., 60 сот. 4 ед., 70 дес. 2 ед., 603 дес. |
Отвечают на вопросы учителя. Выполняют задания устного счета. 1) Выполняют математический диктант. а) 999 б) 1004, 1006 в) 6004 г) 1000 д) 2300, 460, 2100, 7 , 8540, 6004, 702, 6030 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||
|
|
2) Вставьте пропущенные цифры так, чтобы каждое следующее число увеличивалось на 12 сотен:
|
2) Вставляют пропущенные цифры: 1237, 2437, 3637, 3837, 4037 |
||||||||||||||
|
|
3) Сравните величины: 7 км 560 м … 756 м 450 см … 44 дм 543 м … 5430 дм 3 км 48 м … 3480 м |
3) Сравнивают величины: 7 км 560 м > 756 м 450 см > 44 дм 543 м = 5430 дм 3 км 48 м < 3480 м |
||||||||||||||
|
|
4) Решите задачу. Длина одной улицы 1200 м. Когда вторую улицу продолжили на 200 м, то она стала вдвое длиннее, чем первая. Какова была длина второй улицы первоначально? |
4) Решают задачу (устно). Ответ: 2200 м |
||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 24–25). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Сформулируйте способ поразрядного сравнения чисел. Выполните сравнение чисел. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
416 > 316 275 > 245 367 > 360 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Применять правила делового сотрудничества. Осуществлять контроль деятельности по результату |
|||||||||||||
|
Задание 2. |
– Выполните сравнение чисел. |
361 < 613 90652 < 91003 2976 > 2859 26578 < 26758 1999 < 2000 194057 < 194107 4503 < 4518 68341 > 6843 |
||||||||||||||
|
Задание 3. |
– Назовите высоту каждого из вулканов. Какой вулкан самый высокий? – Назовите вулканы в порядке уменьшения их высот. |
– Ключевская Сопка – 4750 м.
– Ключевская Сопка, Острый Толбачик, Кроноцкая Сопка, Корякская Сопка, Шивелуч, Авачинская Сопка. |
||||||||||||||
|
Задание 4 |
– Какая из рек России имеет наибольшую длину? – Какая из приведенных здесь рек – наименьшую? – Назовите реки в порядке увеличения их длин |
– Река Лена имеет наибольшую длину – 4400 м. – Река Индигирка – 1726 м. – Индигирка, Печора, Дон, Колыма, Амур, Енисей, Волга, Обь, Лена |
||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 26–27). Задание 9. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Запишите цифрами многозначные числа, встречающиеся в данных предложениях. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: 9 219 м, 230 000 м2, 1957 г. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Развивать чувство доброжелательности, эмоционально-нравст-венной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии |
|||||||||||||
|
Задание 10. |
– Выполните устные вычисления. |
15 · 4 = 60 1250 – 50 = 1200 609 + 1 = 610 150 · 4 = 600 6084 + 200 = 6284 690 – 1 = 689 |
||||||||||||||
|
Задание 11. |
– Выразите время в минутах.
– Выразите время в часах.
– Выразите время в секундах. |
6 ч = 360 мин 1 ч 12 мин = 72 мин 120 с = 2 мин 720 с = 12 мин 360 мин = 6 ч 5 сут. = 120 ч 3 мин = 180 с 4 мин 40 с = 280 с 9 мин 9 с = 549 с |
||||||||||||||
|
Задание 12. |
– Выполните деление с остатком. |
36 : 5 = 7 (ост. 1) 100 : 16 = 6 (ост. 4) |
||||||||||||||
|
Задание 13. |
– При делении 100 на неизвестное число частное равно 7, а остаток – 2. Как найти неизвестное число? |
100 : х = 7 (ост. 2) (100 – 2) : 7 = 98 : 7 = 14 х = 14 |
||||||||||||||
|
Задание 14. |
– Увеличьте на 4 сотни каждое из чисел. |
12058 + 400 = 12458 100 000 + 400 = 100 400 9030 + 400 = 9430 |
||||||||||||||
|
Задание 15. |
– Уменьшите на 5 тысяч каждое из чисел. |
855 000 – 5000 = 850 000 305 100 – 5000 = 300 100 4 995 000 – 5000 = 4 990 000 |
||||||||||||||
|
Задание 16. |
– Каждое из равенств верно. Какие числа написаны на перевернутых карточках? |
См. Ресурсный материал к уроку. |
||||||||||||||
|
Задание 17. |
– Купили банан массой 250 г. Масса кожуры составляет две пятых этой массы. Вычислите массу съедобной части банана. |
Решение: 1) 250 : 5 · 2 = 100 (г) – масса кожуры банана. 2) 250 – 100 = 150 (г) – масса съедобной части банана. |
||||||||||||||
|
Задание 18 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Решение: 1) 250 : 10 = 25 (п.) – производительность по плану. 2) 25 + 2 = 27 (п.) – производительность по факту. 3) 27 · 10 = 270 (п.) – сшили |
||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности
|
|||||||||||||
|
Ресурсный материал к уроку
|
||||||||||||||||
Урок 8. Запись результатов сравнения с помощью знаков < или >
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений выполнять запись результатов сравнения с помощью знаков < или >; содействовать развитию умения решать текстовые задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся выполнять поразрядное сравнение многозначных чисел, записывать результаты сравнения |
Метапредметные: Познавательные: осуществляют выбор оснований и критериев для сравнения, сериации, классификации объектов; овладевают умением подводить под понятия, выводить следствия. Регулятивные: умеют работать по предложенному учителем плану. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: расширяют познавательные интересы и учебные мотивы |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Соедините равные величины. 700 см2 7 м2 700 см 7 м 700 дм2 7 дм2 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
– Решите задачу. Верблюд с грузом 100 кг пробежал рысью за день 80 км, а другой верблюд с грузом 250 кг прошел за день 35 км. На сколько больше километров в день пробежал первый верблюд, чем прошел второй? – Что обозначает выражение 250 – 100? |
Ответ: 80 – 35 = 55 (км) (это задача с лишними данными). – Оно означает, на сколько груз первого верблюда легче, чем груз второго. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Догадайтесь, как составлен каждый ряд чисел, и продолжите его (назовите в каждом ряду еще 4 числа): а) 588, 590, 592, 594, … б) 909, 808, 707, 606, … в) 1000, 950, 900, 850, … |
а) 588, 590, 592, 594, 596, 598, 600, 602, 604 б) 909, 808, 707, 606, 608, 610, 612, 614, 616 в) 1000, 950, 900, 850, 800, 750, 700, 650, 600, 550 |
||||||||||||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль деятельности по результату |
|||||||||||||||||||||||||||||||||||||||||||||
|
Работа по учебнику (с. 25). Задание 5. |
– Прочитайте неравенства. Какие из них верные? |
– Верные неравенства: 2001 > 1002 90603 < 90613 777 < 7777 5200 < 42000 |
||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 6. |
– Назовите самое большое шестизначное число. Назовите самое маленькое семизначное число. |
– 999999 – самое большое шестизначное число. – 1000000 – самое маленькое семизначное число. |
||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 7. |
– Назовите самое большое четырехзначное число, в записи которого все цифры различны. |
– 9876. |
||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 8 |
– Назовите самое маленькое пятизначное число, записанное различными цифрами |
– 10234 |
||||||||||||||||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 28–30). Задание 19. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Проанализируйте форму фигур. Как называется каждая из этих фигур? – Начертите в тетради таблицу и расставьте в ее клетках знаки «+» так, чтобы название каждой фигуры соответствовало ее номеру.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Заполняют таблицу:
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально- нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||||||||||||||||||||||
|
Задание 20. |
– Какое свойство не является общим для данных чисел? Выберите верный ответ. |
– Высказывание под номером 4. |
||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 21. |
– Составьте и заполните таблицу по образцу. Ответьте на вопросы, используя данные таблицы. 1) Сколько детей отмечают свой день рождения в апреле? в сентябре? в июле? 2) Кто родился зимой? весной? летом? осенью? 3) В каком месяце (месяцах) родилось больше всего учеников? меньше всего учеников? 4) Сколько девочек отмечают свой день рождения в сентябре? 5) Кто из мальчиков родился в июле? |
Заполняют таблицу:
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1) Один ребенок отмечает свой день рождения в апреле, в сентябре – 3 детей, в июле – 3 детей. 2) Оля, Аня, Дима, Валя, Ася родились зимой; Коля, Саша, Юра, Катя – весной; Света, Федя, Толя, Маша, Петя, Таня – летом; Сережа, Даша, Юля – осенью. 3) В июле и сентябре родилось больше всего учеников; в апреле, июне, декабре – меньше всего учеников. 4) Две девочки отмечают свой день рождения в сентябре. 5) Федя и Толя родились в июле. |
||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 22 |
– Выполните необходимые измерения и вычислите периметр четырехугольника двумя способами. – Сравните стороны четырехугольника. Какие стороны равны по длине? – Можно ли назвать этот четырехугольник прямоугольником? Почему? |
– Противоположные стороны равны по длине. – Нет, нельзя назвать этот четырехугольник прямоугольником, так как его углы не прямые |
||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как выполнить поразрядное сравнение многозначных чисел? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать результаты деятельности, уровень владения учебным действием |
Урок 9. Многозначные числа.
Проверочная работа по теме «Чтение, запись и сравнение многозначных чисел»
|
Тип урока: контроль и оценка знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений читать многозначные числа путем разбивки их записи на классы, записывать многозначного числа цифрами после предварительного определения числа цифр в каждом классе, выполнять поразрядное сравнение многозначных чисел, записывать результаты сравнения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями, последовательностью и записью чисел от 0 до 1 000 000; научатся: читать многозначные числа путем разбивки их записи на классы; записывать многозначные числа цифрами после предварительного определения числа цифр в каждом классе; выполнять поразрядное сравнение многозначных чисел, записывать результаты сравнения |
Метапредметные: |
Личностные: осознают необходимость самосовершенствования; понимают причину успеха/неуспеха учебной деятельности и конструктивно действуют в ситуации неуспеха |
|
Познавательные: осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи. Регулятивные: осваивают начальные формы познавательной и личностной рефлексии. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками: определяют цели сотрудничества, функции участников, способы взаимодействия |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Вставьте пропущенные числа так, чтобы равенства были верными. 3025 = 3000 + 3250 = 3000 + 3205 = 3000 + |
Отвечают на вопросы учителя. Выполняют задания устного счета. Вставляют пропущенные числа:
3025 = 3000 + 20 + 5 3520 = 3000 + 500 + 20 3250 = 3000 + 200 + 50 3502 = 3000 + 500 + 2 3205 = 3000 + 200 + 5 3052 = 3000 + 50 + 2 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||||||||||||||||||||||||||||
|
|
– Поставьте знак >, < или =. 41 сот. … 410 36 дес. 3 ед. … 362 82 дес. 1 ед. … 8201 7 сот. 25 дес. … 7250 79 сот. 5 ед. … 7905 91 сот. 3 ед. … 9103 |
Проводят сравнение: 41 сот. > 410 36 дес. 3 ед. > 362 82 дес. 1 ед. < 8201 7 сот. 25 дес. < 7250 79 сот. 5 ед. = 7905 91 сот. 3 ед. = 9103 |
||||||||||||||||||||||||||||||||||
|
|
– Решите задачу. Масса автомашины «Волга» 1250 кг, а «Чайка» на 550 кг тяжелее. Какова масса автомашины «Чайка»? |
Решают задачу.
Ответ: 1800 кг |
||||||||||||||||||||||||||||||||||
|
II. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 30). Задание 23. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор |
|||||||||||||||||||||||||||||||||
|
– В словах пропущены гласные буквы. Какие это слова? Запишите их правильно. |
ТРГЛЬНК – треугольник, ВСМНДЦТЬ – восемнадцать, РВНСТВ – равенство, КВДРТ – квадрат. |
|||||||||||||||||||||||||||||||||||
|
Задание 24. |
– Сколько лампочек в гирлянде? |
Запись: 15 · 4 = 60. |
||||||||||||||||||||||||||||||||||
|
Задание 25 |
– Согласны ли вы с Петей? Почему? Найдите периметр каждого квадрата |
– Нет, не согласны.
Решение: 5 · 4 = 20 (см) Ответ: Р каждого квадрата 20 см |
||||||||||||||||||||||||||||||||||
|
III. Проверочная работа |
Проводит тест по теме урока.
I вариант 1. В записи числа 6 708 цифра 0 обозначает отсутствие:
2. Найди наименьшее пятизначное число:
3. Сколько разрядов в классе единиц?
4. Какое число можно представить в виде суммы чисел 560 000 и 21?
5. Найди наибольшее число:
6. Во сколько раз 1 дм больше 1 см?
7. Если уменьшаемое равно 12 000, а вычитаемое – 4 000, то разность равна:
8. Частное от деления чисел 36 000 и 9 равно:
9. Число 13 000 больше 7 000 на:
10. Чему равно произведение чисел 7 000 и 4?
11*. На сколько надо увеличить число 7 000, чтобы получить произведение чисел 3 000 и 3?
|
Выполняют тест по вариантам (выбирают верный ответ). I вариант Ключ: 1 – а 2 – в 3 – в 4 – б 5 – б 6 – б 7 – а 8 – в 9 – а 10 – б 11 – в |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательно- |
|||||||||||||||||||||||||||||||||
|
|
II вариант 1. В записи числа 7 503 цифра 0 обозначает отсутствие:
2. Найди наименьшее пятизначное число:
3. Сколько разрядов в классе тысяч?
4. Какое число можно представить в виде суммы чисел 350 000 и 87?
5. Найди наибольшее число:
6. Во сколько раз 1 дм больше 1 см?
7. Если уменьшаемое равно 13 000, а вычитаемое – 6 000, то разность равна:
8. Частное от деления чисел 27 000 и 9 равно:
9. Число 15 000 больше 8 000 на:
10. Чему равно произведение чисел 4 000 и 3?
11*. На сколько надо увеличить число 5 000, чтобы получить произведение чисел 4 000 и 2?
|
II вариант Ключ: 1 – а 2 – а 3 – в 4 – б 5 – а 6 – б 7 – в 8 – а 9 – в 10 – б 11 – в |
||||||||||||||||||||||||||||||||||
|
VI. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 10. Письменный прием сложения многозначных чисел
(поразрядное сложение).
Письменные приемы сложения многозначных чисел
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений применять алгоритм письменного сложения многозначных чисел, переносить умение складывать числа в пределах 1000 на область многозначных чисел до миллиарда; содействовать развитию умения выполнять проверку сложения перестановкой слагаемых |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного сложения многозначных чисел; научатся применять алгоритм письменного сложения многозначных чисел; выполнять перенос алгоритма сложения чисел в пределах 1000 на область многозначных чисел до миллиарда; выполнять проверку сложения перестановкой слагаемых |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера. Регулятивные: осуществляют коррекцию, вносят необходимые дополнения и коррективы в план и способ действия в случае расхождения эталона, реального действия и его результата, с учетом оценки этого результата самим обучающимся, учителем, товарищами. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения, считаются с мнением другого человека, проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности) |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. Запись на доске: 1398, 2398, 3398, 4398, … – Прочитайте данные числа. Разгадайте правило, по которому составлен ряд чисел. Продолжите ряд по тому же правилу, запишите еще 5 чисел. – Как называются эти числа? Сколько цифр требуется для их записи? |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Записывают числа. – Это четырехзначные числа: 1398, 2398, 3398, 4398, 5398, 6398, 7398, 8398, 9398. Требуется четыре цифры. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||
|
– Увеличьте последнее число на 1 тысячу. Какое число вы получили? Сколько цифр требуется для его записи? Как называется это число? – Как прочитать пятизначное число? Какой новый разряд появляется в пятизначных числах? – Что обозначает в пятизначном числе цифра, стоящая на четвертом месте справа? На пятом месте справа? |
– 10398 – пятизначное число. – 10398 – десять тысяч триста девяносто восемь. В пятизначном числе добавился новый разряд – десятки тысяч. – Единицы тысяч. – Десятки тысяч. |
|||||||
|
– Составьте задачу, используя данную схему:
|
Составляют задачу: Баобаб живет 4000 лет, лиственница – 400 лет. На сколько лет дольше живет баобаб, чем лиственница? 4000 – 400 = 3600 (лет). |
|||||||
|
– На какой вопрос вы ответите, выполнив действие 4000 : 400? |
– На вопрос «Во сколько раз дольше живет баобаб, чем лиственница?» |
|||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 31–32). Задания 1, 2. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Объясните алгоритм письменного сложения трехзначных и четырехзначных чисел. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют алгоритм письменного сложения трехзначных и четырехзначных чисел. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества |
|||||
|
Задание 3. |
– Найдите сумму чисел. |
|
||||||
|
Задание 4. |
– Прочитайте высказывание. Верно ли оно? |
– При любом значении а верны равенства: а + 0 = а, 0 + а = а. |
||||||
|
Задание 5. |
– Вычислите значения буквенных выражений. |
а) 3685 + а, если а = 0, то 3685 + 0 = 3685 б) а + 5001, если а = 0, то 0 + 5001 = 5001 |
||||||
|
Задание 6 |
– Выполните вычисления |
70616 + 19796 + 217 · 3 = 91063 56380 + 325478 + 130 · 6 + 714 : 7 = 382740 |
||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 33–34). Задание 16. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Какое из чисел больше? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
12540 > 3678 997054 > 874 309091 > 4444 10 000 000 > 1 000 000 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок |
|||||
|
Задание 17. |
– Какое из чисел меньше? |
605 < 6050 1000 < 10000 8150 < 815007 10100 < 101010 |
||||||
|
Задание 18. |
– Сравните значение величин. |
2006 м = 2 км 6 м 15 ч 20 мин < 16 ч 40 мин 9 м > 90 см 7 мин 45 с = 465 с 3000 см > 3 м 12 ч < 725 мин |
||||||
|
Задание 19. |
– Вычислите прибытие автобуса на 2-ю остановку. |
Решение: 9 ч + 25 мин + 35 мин + 2 мин + 18 мин = = 10 ч 20 мин. |
||||||
|
Задание 20 |
– Сравните тексты задач. Чем они похожи? Чем различаются? – Составьте выражение для решения первой задачи. – Решите задачу при п = 5. – Составьте выражение для решения второй задачи. – Решите задачу при п = 5 |
Задача 1. 9 · п. 9 · 5 = 45 (чел.). Задача 2. п · 3. 5 · 3 = 15 (чел.) |
||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Как выполнить сложение многозначных чисел? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного ряда на доске (на экране): • сегодня я узнал… • было интересно… • было трудно… • я выполнял задания… |
Способны проводить самооценку на основе критерия успешности учебной деятельности |
Урок 11. Алгоритм письменного сложения многозначных чисел
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений применять алгоритм письменного сложения многозначных чисел, складывать числа в пределах 1000 с переносом на область многозначных чисел до миллиарда; содействовать развитию умения выполнять проверку сложения перестановкой слагаемых |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного сложения многозначных чисел; научатся применять алгоритм письменного сложения многозначных чисел; выполнять перенос алгоритма сложения чисел в пределах 1000 на область многозначных чисел до миллиарда; выполнять проверку сложения перестановкой слагаемых |
Метапредметные: |
Личностные: имеют желание учиться; осваивают начальные формы познавательной и личностной рефлексии |
|
Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; используют знаково-символические средства для решения учебной задачи. Регулятивные: осуществляют саморегуляцию как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта и преодолению препятствий); принимают и сохраняют учебную задачу, соответствующую этапу обучения. Коммуникативные: умеют работать коллективно, контролируют действия партнера; допускают существование различных точек зрения; договариваются, приходят к общему решению |
||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Разгадайте правило, по которому записан каждый ряд, дополните каждую строку. 13872, 13871, 13870, … , … , … , … 25097, 26097, 27097, … , … , … , … 31254, 41254, 51254, … , … , … , … 22119, 33120, 44121, … , … , … , … |
Отвечают на вопросы учителя. Выполняют задания устного счета.
13872, 13871, 13870, 13868, 13866, 13864, 13862 25097, 26097, 27097, 28097, 29097, 30097, 31097 31254, 41254, 51254, 61254, 71254, 81254, 91254 22119, 33120, 44121, 55121, 66121, 77121, 88121 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой уста- новкой, принимать и сохранять учебную цель и задачу |
||||||||||||||||||||||||||||||
|
|
– Поставьте знак >, < или =. 38464 … 38465 78100 … 87100 38099 … 38990 78001 … 78010 38199 … 38200 78010 … 78111 |
38464 < 38465 78100 < 87100 38099 < 38990 78001 < 78010 38199 < 38200 78010 < 78111 |
|||||||||||||||||||||||||||||||
|
|
– Решите задачу. Масса бурого медведя 350 кг; он легче, чем белый медведь, на 150 кг. Чему равна масса белого медведя? – Выберите выражение, которое является решением данной задачи. а) 350 + 150 б) 350 – 150 |
Решение: 350 + 150 = 500 (кг).
– Вариант а) |
|||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 32–33). Задание 7. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, отзывчивости. Приводить убедительные доказательства в диалоге |
||||||||||||||||||||||||||||||
|
– Подставьте вместо звездочки число 70 000. Запишите полученное выражение и вычислите его значение. – Можно ли узнать значение второго выражения, не выполняя вычислений? – Составьте выражения, подставляя вместо звездочки число 16504 и число 89. Найдите значения выражений. |
3507 + (70 000 + 9) = 3507 + 70009 = 73516
– Можно, используя закон перестановки слагаемых, или сочетательный закон. 3507 + (16504 + 9) = 3507 + 16513 = 20020 3507 + (89 + 9) = 3507 + 98 = 3605 |
||||||||||||||||||||||||||||||||
|
Задание 8. |
– Увеличьте на 264308 каждое из чисел. |
|
|||||||||||||||||||||||||||||||
|
Задание 9. |
– Чему равна высота вулкана Этна над уровнем моря? |
|
|||||||||||||||||||||||||||||||
|
Задание 10. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение:
|
|||||||||||||||||||||||||||||||
|
Задание 11 |
– Сколько денег было в кассе? |
|
|||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 35–36). Задание 22. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Представьте каждое из чисел в виде суммы разрядных слагаемых. |
Отвечают на вопросы учителя, высказывают свои мнения
12305 = 10000 + 2000 + 300 + 5 1300254 = 1000000 + 300000 + 200 + 50 + 4 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||||||||||||
|
Задание 23 |
– Какое число представлено в виде суммы разрядных слагаемых? Прочитайте это число и запишите его. |
2000000 + 800000 + 5000 + 7 = 2805007 60000 + 4000 + 800 + 60 + 3 = 64863 |
|||||||||||||||||||||||||||||||
|
Задание 24. |
– Продолжите ряд чисел. |
1375, 1380, 1385, 1390, 1400, 1405, 1410, 1415, 1420. |
|||||||||||||||||||||||||||||||
|
Задание 25. |
– Замените число суммой. |
218507 = 218000 + 507 50086 = 50000 + 86 999413 = 999000 + 413 11010 = 11000 + 10 |
|||||||||||||||||||||||||||||||
|
Задание 26. |
– Сколько квадратных керамических плиток площадью 1 дм2 нужно для облицовки части стены площадью 1 м2? |
Решение: 1 м2 = 100 дм2 100 : 1 = 100 (пл.) – потребуется. |
|||||||||||||||||||||||||||||||
|
Задание 27. |
– Выразите в метрах, дециметрах и сантиметрах. |
642 см = 6 м 4 дм 2 см 510 см = 5 м 1 дм 604 см = 6 м 4 см 700 см = 7 м 39 дм 2 см = 3 м 9 дм 2 см 47 дм 6 см = 4 м 7 дм 6 см |
|||||||||||||||||||||||||||||||
|
Задание 28. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: Длина – 18 м Ширина – 9 м Р – ? см Шагов – ? по 75 см Решение: 1) (18 + 9 ) · 2 = 54 (м) – периметр. 2) 54 м = 5400 см 3) 5400 : 75 = 72 (ш.) |
|||||||||||||||||||||||||||||||
|
Задание 29. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
См. Ресурсный материал к уроку. |
|||||||||||||||||||||||||||||||
|
Задание 30 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
См. Ресурсный материал к уроку |
|||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как выполнить сложение многозначных чисел в столбик? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
Продолжают высказывания: • сегодня я узнал… • было интересно… • было трудно… |
Оценивать результаты деятельности, уровень владения учебным действием
|
||||||||||||||||||||||||||||||
|
Ресурсный материал к уроку
|
|||||||||||||||||||||||||||||||||
Урок 12. Отработка умений письменного сложения многозначных чисел
|
Тип урока: повторение и систематизации знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений применять алгоритм письменного сложения многозначных чисел, складывать числа в пределах 1000 с переносом на область многозначных чисел до миллиарда; содействовать развитию умения выполнять проверку сложения перестановкой слагаемых |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного сложения многозначных чисел; научатся: применять алгоритм письменного сложения многозначных чисел; выполнять перенос алгоритма сложения чисел в пределах 1000 на область многозначных чисел до миллиарда; выполнять проверку сложения перестановкой слагаемых |
Метапредметные: Познавательные: умеют ориентироваться в учебнике (на развороте, в оглавлении, в условных обозначениях); находят ответы на вопросы в тексте, иллюстрациях; делают выводы в результате совместной работы класса и учителя. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: имеют желание учиться; осознают необходимость самосовершенствования; понимают границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Вставьте пропущенные слагаемые:
237115 = 200000 + 468252 = 389021 = |
Отвечают на вопросы учителя. Выполняют задания устного счета.
237115 = 200000 + 30000 + 7000 + 100 + 10 + 5 468252 = 400000 + 60000 + 8000 + 200 + 50 + 2 389021 = 300000 + 80000 + 9000 + 20 + 1 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||||||||||||||||||||||||
|
|
– Расположите карточки с числами в порядке убывания:
Увеличьте каждое число на 32 десятка. |
200010, 138200, 99245, 58410, 38020, 9643 200330, 138520, 99565, 58730, 38340, 9963 |
||||||||||||||||||||||||||||||
|
|
– Решите задачу. За 1 секунду вычислительная машина может складывать и вычитать 5000 чисел. Сколько таких вычислений может сделать вычислительная машина за 2 с; 3 с; 10 с? |
Решение: 5000 · 2 = 10000 (вычислений) 5000 · 3 = 15000 (вычислений) 5000 · 10 = 50000 (вычислений) |
||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 33). Задание 12. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Измените вопрос задачи так, чтобы она решалась в два действия. Решите новую задачу. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
|
Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества |
|||||||||||||||||||||||||||||
|
Задание 13. |
– В каком году произошло Бородинское сражение? |
|
||||||||||||||||||||||||||||||
|
Задание 14. |
– Выполните вычисления. |
1) 367 м + 687 м = 1 км 54 м 2) 53 дм – 3 м 9 дм = 53 дм – 39 дм = 14 дм 3) 12 кг 581 г + 13419 г = 26 кг |
||||||||||||||||||||||||||||||
|
Задание 15 |
– Каков периметр поля? |
Решение: (850 + 625) · 2 = 2950 (м) – периметр поля |
||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 36–37). Задание 31. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 48 + 22 = 70 (дет./ч) – совместная производительность. 2) 280 : 70 = 4 (ч) – время работы. Ответ: 280 деталей они изготовят за 4 ч, работая вместе. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания. Осуществлять взаимный контроль, планировать способы взаимодействия. |
|||||||||||||||||||||||||||||
|
Задание 32. |
– Заполните таблицу.
|
Заполняют таблицу:
|
||||||||||||||||||||||||||||||
|
Задание 33. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: Было – 45 р. Картофель – ? р., девятая часть 200 г сыра – ? р. 1 кг сыра – ? р. Решение: 1) 45 : 9 = 5 (р.) – цена картофеля. 2) 45 – 5 = 40 (р.) – стоят 200 г сыра. 3) 1000 : 200 = 5 (раз) – по 200 г сыра. 4) 40 · 5 = 200 (р.) – цена сыра. |
||||||||||||||||||||||||||||||
|
Задание 34. |
– Выполните работу с таблицей «Разряды и классы». |
Работают с таблицей «Разряды и классы». |
||||||||||||||||||||||||||||||
|
Задание 35. |
– Какие числа соответствуют этим точкам? |
1) 2) |
||||||||||||||||||||||||||||||
|
Задание 36. |
– Выполните построения. |
1) 2) |
||||||||||||||||||||||||||||||
|
Задание 37 |
– Выполните построения. Вычислите периметр треугольника |
|
||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как выполнить сложение в столбик многозначных чисел? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
|||||||||||||||||||||||||||||
Урок 13. Письменный прием вычитания многозначных чисел
(поразрядное вычитание)
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений применять алгоритм письменного вычитания многозначных чисел; содействовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного вычитания многозначных чисел; научатся: применять алгоритм письменного вычитания многозначных чисел; выполнять перенос алгоритма поразрядного вычитания в пределах 1000 на область чисел до миллиарда; выполнять проверку вычитания с помощью сложения разности с вычитаемым и с помощью вычитания разности из уменьшаемого |
Метапредметные: Познавательные: применяют методы информационного поиска, в том числе с помощью компьютерных средств; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи; строят логическую цепь рассуждений. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации; осуществляют саморегуляцию как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта и преодолению препятствий). Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: определяют границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности учащегося |
|||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. Математический диктант. а) Запишите цифрами: 2 тыс. 740 ед., 56 тыс. 12 ед., 548 тыс., 16 тыс. 3 ед., 230 тыс. 750 ед., 43 тыс. 43 ед., 850 сот., 730 дес. б) Расположите данные числа в порядке убывания. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) Записывают числа цифрами: 2740, 56012, 548 000, 16003, 230750, 43043, 85000, 7300.
б) Располагают в порядке убывания: 548 000, 230 750, 85 000, 56 012, 43 043, 16 003, 7 300, 2740. |
Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||
|
|
– Решите задачи. а) Масса африканских слонов достигает 7000 кг, что на 2000 кг больше, чем масса, которой достигают индийские слоны. Какой массы достигают индийские слоны? б) Мост через реку находится между деревнями Аксеновка и Поливаново: от Аксеновки на рас-стоянии 1 км 500 м, а от Поливаново – на рас-стоянии 1 км 5 м. К какой деревне мост ближе и насколько? |
Решают задачи: а) Решение: 7000 – 2000 = 5000 (кг) – достигают индийские слоны.
б) Решение: 1500 – 1005 = 495 (м) – на столько ближе к деревне Поливаново. |
||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 39–40). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Объясните алгоритм письменного вычитания трехзначного числа. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют алгоритм письменного вычитания трехзначного числа. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|||||||||||
|
Задание 2. |
– Составьте алгоритм письменного вычитания многозначных чисел. |
Составляют алгоритм письменного вычитания многозначных чисел. |
||||||||||||
|
Задание 3. |
– Выполните вычитание и проверьте результаты с помощью калькулятора. |
|
||||||||||||
|
Задание 4. |
– Вычислите значение буквенного выражения. |
1) 10204 – а Если а = 964, то 10204 – 964 = 9240; если а = 1050, то 10204 – 1050 = 9154; если а = 9204, то 10204 – 9204 = 1000; если а = 10000, то 10204 – 10000 = 204; 2) b – 697 Если b = 1000, то 1000 – 697 = 303; если b = 2030, то 2030 – 697 = 1333; если b = 192697, то 192697 – 697 = 192000. |
||||||||||||
|
Задание 5 |
– Выполните задание |
1) 5789 < 5987 2) 5789 < 8759 5987 – 5789 = 198 8759 – 5789 = 2970 |
||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 2–43). Задание 15. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните устные вычисления. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осущест-влять взаимный контроль, планировать способы взаимодействия |
|||||||||||
|
Задание 16. |
– Запишите цифрами числа. |
Запись: 206008; 500060; 30001; 900000. |
||||||||||||
|
Задание 17. |
– Запишите наибольшее семизначное число, в записи которого все цифры различные. |
Запись: 9876543. |
||||||||||||
|
Задание 18. |
– Сравните значения выражений. |
324 + 68 = 68 + 324 960 : 2 > 960 : 3 409 + 48 > 409 – 48 15 · 8 < 15 · 12 1020 – 68 > 1020 – 72 1000 : 25 > 800 : 25 |
||||||||||||
|
Задание 19. |
– Выполните деление самостоятельно. Проведите взаимопроверку в парах. |
Работают самостоятельно и в парах. |
||||||||||||
|
Задание 20. |
– Найдите число, которое в 4 раза меньше суммы чисел 22 и 14. – Найдите число, которое в 5 раз меньше разности чисел 87 и 42. – Найдите число, которое в 3 раза меньше частного 24 и 4. |
(22 + 14) : 4 = 36 : 4 = 9
(87 – 42) : 5 = 45 : 5 = 9
24 : 4 : 3 = 6 : 3 = 2 |
||||||||||||
|
Задание 21. |
– Что означает цифра 3 в записях чисел 13, 234, 1369, 38 210? |
13 – 3 единицы 234 – 3 десятка 1369 – 3 сотни 38210 – 3 десятка тысяч |
||||||||||||
|
Задание 22. |
– Во сколько раз увеличится число 842, если к нему справа приписать нуль? На сколько единиц оно увеличится? |
– В 10 раз увеличится число 842, если к нему справа приписать нуль. На 7578 единиц число увеличится. |
||||||||||||
|
Задание 23. |
– Каждое равенство верно. Вычислите неизвестные числа. |
507 + 714 – 507 = 207 1000 – 96 = 904 |
||||||||||||
|
Задание 24. |
– Выполните самостоятельно умножение в столбик. Проведите взаимопроверку в парах. |
Работают в парах. |
||||||||||||
|
Задание 25. |
Задача. Спортсмен сделал 50 выстрелов по мишеням. Три пятых числа пуль попали в цель. Сколько раз спортсмен промахнулся? |
Решение: 1) 50 : 5 · 3 = 30 (раз) – попал в цель. 2) 50 – 30 = 20 (раз) – промахнулся. |
||||||||||||
|
Задание 26. |
– Прочитайте задачу. Что известно? Что требуется узнать? Выполните краткую запись условия в виде таблицы и решите задачу. Поясните каждое действие в решении задачи. |
См. Ресурсный материал к уроку. |
||||||||||||
|
Задание 27. |
– Прочитайте задачу. Что известно? Что требуется узнать? Выполните краткую запись условия в виде таблицы и решите задачу. |
См. Ресурсный материал к уроку. |
||||||||||||
|
Задание 28 |
– Прочитайте задачу. Что известно? Что требуется узнать? Выполните краткую запись в виде таблицы и решите задачу |
См. Ресурсный материал к уроку |
||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Как выполнить вычитание многозначных чисел в столбик? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Продолжают высказывания: • Я узнал… • Я повторил… • Я запомнил… |
Способны проводить самооценку на основе критериев успешности учебной деятельности
|
|||||||||||
|
Ресурсный материал к уроку
|
||||||||||||||
Урок 14. Алгоритм письменного вычитания многозначных чисел.
Проверочная работа по теме «Сложение и вычитание многозначных чисел»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: содействовать развитию умения переносить алгоритм поразрядного вычитания в пределах 1000 на область чисел до миллиарда; способствовать формированию умения выполнять проверку вычитания с помощью сложения разности с вычитаемым и с помощью вычитания разности из уменьшаемого |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного вычитания многозначных чисел; научатся: применять алгоритм письменного вычитания многозначных чисел; выполнять перенос алгоритма поразрядного вычитания в пределах 1000 на область чисел до миллиарда; выполнять проверку вычитания с помощью сложения разности с вычитаемым и с помощью вычитания разности из уменьшаемого |
Метапредметные: Познавательные: моделируют содержащиеся в задаче зависимости; планируют ход решения задачи. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Расположите выражения в порядке увеличения их значений, не вычисляя их. 7340 + 3; 7340 + 300; 7340 + 30; 7340 + 1; 7340 + 10; 7340 + 100; 7340 + 103. Проверьте свой ответ, вычислив значения выражений. |
Отвечают на вопросы учителя. Выполняют задания устного счета. Располагают выражения: 7340 + 1; 7340 + 3; 7340 + 10; 7340 + 30; 7340 + 100; 7340 + 103; 7340 + 300 Проверяют вычислением. |
Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||
|
– Вставьте пропущенные множители: 4 · 2 · 3 · 5 · 9 · 2 · 7 · |
4 · 2 · 100 = 2 · 800 6 · 9 · 100 = 5400 3 · 4 · 100 = 3 · 400 7 · 8 · 100 = 5600 5 · 9 · 100 = 4500 9 · 4 · 100 = 3600 2 · 7 · 10 = 2 · 70 5 · 100 · 6 = 3000 |
|||||||
|
– Выполните действия: 64 · 10 50000 : 5 100 · 100 · 10 70 · 10 16000 : 100 3000 · 1 100 · 100 3001 : 3001 1 : 1 + 0 · 0 100 : 100 1000 : 10 1 · 0 – 0 : 1 |
Выполняют вычисления. |
|||||||
|
– Вставьте пропущенные цифры так, чтобы каждое следующее число увеличилось на 12 сотен:
|
Вставляют цифры: 1287, 2487, 3687, 4887, 6087 |
|||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 40–41, 50). Задание 6. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Составьте записи. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|||||
|
Задание 7. |
– Какое число задумано? |
Решение: 1408 – 504 = 904 |
||||||
|
Задание 8. |
– Найдите значения выражений. |
8065 + 35124 – 2637 = 40552 900100 – 80400 + 504 = 820204 100000 – (248730 – 199006) = 50276 (5 + 77896) – (89107 – 82164) = 70958 3500 – 184 – (71203 – 69350) = 1463 9004 – 687 + 13 + 12501 = 20831 |
||||||
|
Задание 9 |
– Найдите устно значения выражений.
– Какие знания вам помогли выполнить это задание? |
(7356 + 506) – 506 = 7356 (10863 – 9524) + 9524 = 10863 |
||||||
|
III. Проверочная работа |
Проводит тест по теме урока. – Выберите верный ответ. 1. Найди сумму чисел 5 424 и 3 837. а) 9 251; б) 8 261; в) 9 261. 2. Найди разность чисел 40 109 и 36 327. а) 4 782; б) 3 782; в) 4 882. 3. На сколько число 52 301 больше числа 37 489? а) на 15 913; б) на 14 812; в) на 14 822. 4. На сколько число 28 719 меньше числа 340 000? а) на 312 291; б) на 321 281; в) на 311 281. 5. Увеличь число 89 389 на 978. а) 90 357; б) 89 411; в) 90 367. 6. Уменьши число 801 002 на 97 384. а) 703 728; б) 703 618; в) 703 718. 7. Сумма двух чисел равна 100 000. Одно из слагаемых 90 803. Найди, чему равно другое слагаемое. а) 9 207; б) 9 197; в) 9 297 8. Уменьшаемое 520, разность 17. Чему равно вычитаемое? а) 507; б) 503; в) 513. 9. Вычитаемое 807, разность 5 049. Найди уменьшаемое. а) 4 242; б) 5 847; в) 5 856. 10. Найди значение выражения: 10 038 – 8 541 + 238 а) 1 259; б) 1 735; в) 2 835 |
Выполняют тест (выбирают верный ответ). Ключ: 1 – в 2 – б 3 – б 4 – б 5 – в 6 – б 7 – б 8 – б 9 – в 10 – б |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Планировать способы взаимо-действия |
|||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как выполнить вычитание многозначных чисел в столбик? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Продолжают высказывания:
|
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Оценивать результаты деятельности |
Урок 15. Отработка умений письменного вычитания многозначных чисел
|
Тип урока: повторение и систематизации знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умения переносить алгоритм поразрядного вычитания в пределах 1000 на область чисел до миллиарда; содействовать развитию умения выполнять проверку вычитания с помощью сложения разности с вычитаемым и с помощью вычитания разности из уменьшаемого |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного вычитания многозначных чисел; научатся: применять алгоритм письменного вычитания многозначных чисел; выполнять перенос алгоритма поразрядного вычитания в пределах 1000 на область чисел до миллиарда; выполнять проверку вычитания с помощью сложения разности с вычитаемым и с помощью вычитания разности из уменьшаемого |
Метапредметные: Познавательные: осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; овладевают навыками смыслового чтения (осмысление цели чтения и выбор вида чтения в зависимости от цели); осуществляют анализ объектов с целью выделения признаков (существенных, несущественных). Регулятивные: определяют и формулируют цель деятельности на уроке; умеют прогнозировать, предвосхищать результат и уровень усвоения, его временные характеристики. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве |
Личностные: приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. – Составьте и расставьте в порядке возрастания шестизначные числа, записанные с помощью цифр 8 и 0. – Назовите самое большое и самое маленькое шестизначные числа, записанные с помощью цифр 9, 3 и 0. – Как рассуждали, записывая самое большое число?
– Назовите самое большое и самое маленькое шестизначные числа, записанные с помощью цифр 9, 5, 4 и 3. – Назовите самое большое и самое маленькое шестизначные числа, записанные с помощью цифр 0, 7, 2, 1. |
Отвечают на вопросы учителя. Выполняют задания устного счета. Составляют числа, расставляют в заданном порядке: 800000, 800008, 8000088, 800888, 808888, 888880, 888888.
– Самое большое – 999930. Самое маленькое – 300009.
– Чтобы записать самое большое число из данных цифр, надо в высший разряд – сотни тысяч – записать цифру, которой соответствует наибольшее количество единиц. А чтобы получить самое маленькое шестизначное число из цифр 9, 3 и 0, в высший разряд надо поставить цифру 3, а в разряд единиц – цифру 9. – 999543 и 333459.
– 777210 и 100027. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Поставьте знак >, < или = так, чтобы записи были верными. 6999 + 1 … 7000 – 1 9000 – 1 … 9000 – 100 6099 + 10 … 6100 + 9 1399 + 1 … 13 сот. 5110 – 100 … 5009 + 1 1700 – 100 … 16 сот. |
6999 + 1 > 7000 – 1 9000 – 1 > 9000 – 100 6099 + 10 = 6100 + 9 1399 + 1 > 13 сот. 5110 – 100 = 5009 + 1 1700 – 100 = 16 сот. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Вставьте пропущенные слагаемые. 6498 = 6000 + 4827 = 4000 + 5294 = 9891 = 7351 = |
6498 = 6000 + 400 + 90 + 8 4827 = 4000 + 800 + 20 + 7 5294 = 5000 + 200 + 90 + 4 9891 = 9000 + 800 + 90 + 1 7351 = 7000 + 300 + 50 + 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Назовите действие, которое пришлось выполнить, чтобы получить число в каждом следующем прямоугольнике:
|
– 3000 увеличили на 900; 3900 уменьшили на 1 тысячу (и т. д.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 41). Задание 10. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Составьте выражения и найдите их значения. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
80000 – (5308 – 906) = 80000 – 4402 = 75598 (2396 + 814) – 36 · 9 = 3210 – 324 = 2886 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 11. |
– Вычислите площадь Каспийского моря. |
Запись: 17700 + 353000 = 370700 (км2) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 12. |
– Прочитайте задачу. Что известно? Что требуется узнать? Составьте выражение и найдите его значение. |
Решение: 120 кг 500 г + (120 кг 500 г – – 17 кг 800 г) = 223 кг 200 г – собрали всего. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 13. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 4000 + 2000 = 6000 (т.) – было всего тетрадей. 2) 1350 + 2968 = 4318 (т.) – продали всего тетрадей. 3) 6000 – 4318 = 1682 (т.) – осталось. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 14 |
– Выполните задание |
– Наименьшее трехзначное число – 100, наибольшее двузначное число – 99. Значит: 100 + 99 + 199 +
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 44–46). Задания 29, 30. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль действий, планировать способы взаимодействия |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Решите обе задачи. Чем они похожи? Чем отличаются? – Как называются эти задачи? |
См. ресурсный материал к уроку. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 31. |
– Кто из детей шел быстрее? |
– Митя шел быстрее. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 32. |
– Какая машина раньше прибыла в Москву? |
– «Газель» раньше прибыла в Москву. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 33. |
– Найдите закономерность и назовите следующие три числа в ряду. |
– 340, 390, 440, 490, 540, 590. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 34. |
– На подносе 12 стаканов с тремя напитками: какао, соком и молоком. Дети выпили весь сок. Определите число пустых стаканов. Сколько осталось стаканов с другими напитками? |
– 4 пустых стакана. Осталось 8 стаканов с другими напитками. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 35. |
– Прочитайте условие задачи. Запишите на математическом языке «стоимость 3 кг яблок и 2 кг винограда равна 195 рублей». – Запишите на математическом языке «2 кг яблок дешевле 1 кг винограда на 10 рублей». – Запишите на математическом языке «если купить по 1 кг яблок и винограда, то нужно заплатить 85 рублей». |
Запись: 25 · 3 + 60 · 2 = 195 (р.)
60 – 25 · 2 = 10 (р.)
25 + 60 = 85 (р.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 36. |
– Начертите круг любого радиуса и разделите его на четыре одинаковые части; на шесть одинаковых частей. |
См. ресурсный материал к уроку. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 37. |
– Сколько треугольников на каждом рисунке? |
См. ресурсный материал к уроку. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 38. |
– Как можно начертить окружность, проходящую через все вершины квадрата? |
См. ресурсный материал к уроку. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 39. |
– Не выполняя указанного действия, определите, каким будет старший разряд суммы 5267 + 3928. |
– Старший разряд: 9 тысяч. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 40. |
– Постройте прямой угол с помощью угольника. |
См. ресурсный материал к уроку. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 41. |
– Выполните построения. – Как называются полученные четырехугольники? |
См. ресурсный материал к уроку. – Полученные четырехугольники называются прямоугольниками. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 42. |
– Выполните чертеж. |
См. ресурсный материал к уроку. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 43. |
– В каких отделах торгового центра и по какой цене Даша сможет сделать покупку? В каком отделе стоимость покупки будет наименьшей? Сколько денег останется у Даши в этом случае? |
Заполняют таблицу (см. ресурсный материал к уроку). – Если купить один утюг за 585 рублей, а другой – за 625 рублей, то стоимость покупки будет наименьшей. 290 рублей останется у Даши в этом случае. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 44 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
См. ресурсный материал к уроку |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ресурсный материал к уроку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Урок 16. Контрольная работа № 1
по теме «Письменные приемы сложения и вычитания многозначных чисел»
|
Тип урока: контроль и оценивание знаний и способов действий |
||
|
Педагогические задачи: проверить усвоение нумерации многозначных чисел, алгоритмов сложения и вычитания многозначных чисел, правил порядка выполнения действий в выражениях, взаимосвязи компонентов и результатов действий, умножения и деления на 10, 100 |
||
|
Планируемые результаты |
||
|
Предметные: научатся: применять алгоритм письменного сложения и вычитания многозначных чисел; выполнять перенос алгоритма поразрядного сложения и вычитания в пределах 1000 на область чисел до миллиарда; выполнять проверку вычитания с помощью сложения разности с вычитаемым и с помощью вычитания разности из уменьшаемого |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель (пространственно-графическую или знаково-символическую), где выделены существенные характеристики объекта, преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: в совместной работе определяют цели и функции участников, способы взаимодействия |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Выполнение контрольной работы |
Знакомит с содержанием контрольной работы, комментирует задания.
Вариант I 1. Запиши числа: 75 сот., 758 сот., 785 дес., 75 тыс. Расположи их в порядке возрастания. 2. Найди значения выражений: 24 · 3 + 68 : 17 – 25 86 – 90 : 6 + 9 |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы. Вариант I 1. 7500, 75800, 7850, 75000; 7500, 7850, 75000, 75800. 2. 51; 80. |
Принимать и сохранять учебную цель и задачу. Анализировать, объекты, находить общее и различия, делать выводы. Осознанно и произвольно строить речевые высказывания в устной форме |
|
|
3. Запиши выражения и найди их значения: а) 7987 увеличить на 2427; б) найти разность чисел 120 406 и 72 848; в) 30 270 уменьшить на 16 987. 4. Сравни выражения: 42: 14 ... 42 : (7 · 2) 270 : 10 : 3 ... 270 : 30 96 : 16 ... 96 : 8 : 2 510 : 170 ... 510 : 10 : 17 5. Вставь пропущенные числа:
3200 : Вариант II 1. Запиши числа: 84 сот., 845 сот., 854 дес., 85 тыс. Расположи их в порядке возрастания. 2. Найди значения выражений: 24 · 4 + 80 : 16 – 18 74 – 72 : 6 + 5 3. Запиши выражения и найди их значения: а) 4387 увеличить на 1368; б) найти разность чисел 125 733 и 36 118; в) 75642 уменьшить на 12369. 4. Сравни выражения: 72 : 18 ... 72 : (9 · 2) 540 : 10 : 6 ... 540 : 60 90 : 15 ... 90 : 3 : 5 810 : 270 ... 810 : 10 : 27 5. Вставь пропущенные числа:
2400 : Вариант III 1. Запиши числа: 57 сот., 578 сот., 587 дес, 57 тыс. Расположи их в порядке возрастания. 2. Найди значения выражений: 23 · 4 + 84 : 28 – 27 83 – 70 : 2 + 8 3. Запиши выражения и найди их значения: а) 5467 увеличить на 1236; б) найти разность чисел 189 121 и 62 432; в) 32 306 уменьшить на 15 664. 4. Сравни выражения: 84 : 14 ... 84 : (7 · 2) 480 : 10 : 6 ... 480 : 60 96 : 12 ... 96 : 6 : 2 750 : 150 ... 750 : 10: 15 |
3. а) 7987 + 2427 = 10414 б) 120 406 ‒ 72 848 = 47 558 в) 30 270 ‒ 16 987 = 13 283 4. 42: 14 = 42 : (7 · 2) 270 : 10 : 3 = 270 : 30 96 : 16 = 96 : 8 : 2 510 : 170 = 510 : 10 : 17 5. 5600 : 80 = 70 64000 : 8000 = 8 3200 : 40 = 80 40 · 9000 = 360000 Вариант II 1. 8400, 84500, 8540, 85000; 8400, 8540, 84500, 85000. 2. 83; 67. 3. а) 4387 + 1368 = 5755 б) 125 733 ‒ 36 118 = 89 615 в) 75 642 ‒ 12 369 = 63 273 4. 72 : 18 = 72 : (9 · 2) 540 : 10 : 6 = 540 : 60 90 : 15 = 90 : 3 : 5 810 : 270 = 810 : 10 : 27 5. 5600 : 70 = 80 21000 : 3000 = 7 2400 : 80 = 30 40 · 8000 = 320000 Вариант III 5700, 57800, 5870, 57000; 5700, 5870, 57000, 57800.
2. 68; 56. 3. а) 5467 + 1236 = 6703 б) 189 121 ‒ 62 432 = 126 689 в) 32 306 ‒ 15 664 = 16 642 4. 84 : 14 = 84 : (7 · 2) 480 : 10 : 6 = 480 : 60 96 : 12 = 96 : 6 : 2 750 : 150 = 750 : 10: 15 |
|
|
|
5. Вставь пропущенные числа:
2700 : Вариант IV 1. Запиши числа: 69 сот., 694 сот., 649 дес, 69 тыс. Расположи их в порядке возрастания. 2. Найди значения выражений: 23 · 3 + 85 : 17 – 17 78 – 80 : 5 + 7 3. Запиши выражения и найди их значения: а) 4784 увеличить на 5672; б) найти разность чисел 184025 и 68543; в) 27670 уменьшить на 24954. 4. Сравни выражения: 80 : 16 ... 80 : (8 · 2) 920 : 10 : 4 ... 920 : 4 75 : 15 ... 75 : 5 : 3 480 : 160 ... 480 : 10 : 16 5. Вставь пропущенные числа:
3500 : |
5. 5400 : 60 = 90 42000 : 7000 = 6 2700 : 90 = 30 7 · 7000 = 49000 Вариант IV 6900, 69400, 6490, 69000; 6490, 6900, 69000, 69400.
2. 57; 69 3. а) 4784 + 5672 = 10456 б) 184025 ‒ 68543 = 115482 в) 27670 ‒ 24954 = 2716 4. 80 : 16 = 80 : (8 · 2) 920 : 10 : 4 = 920 : 4 75 : 15 = 75 : 5 : 3 480 : 160 = 480 : 10 : 16 5. 3600 : 90 = 40 36000 : 4000 = 9 3500 : 70 = 50 70 · 6000 = 420000 |
|
|
II. Итог урока. Рефлексия |
Предлагает учащимся оценить свою работу на уроке. – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Проводить самооценку |
Урок 17. Построение прямоугольника на нелинованной бумаге.
Контрольный устный счет № 1
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений выполнять построение прямоугольника с заданными длинами сторон |
||
|
Планируемые результаты |
||
|
Предметные: научатся выполнять построение прямоугольника с заданными длинами сторон с помощью линейки и угольника на нелинованной бумаге |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: принимают и сохраняют учебную задачу; адекватно воспринимают оценку учителя и товарищей; планируют свое действие. Коммуникативные: умеют формировать коммуникативно-речевые действия, конструктивные способы взаимодействия с окружающими (учителем, сверстниками) |
Личностные: проявляют этические чувства, доброжелательность и эмоционально-нравственную отзывчивость, понимание и сопереживание чувствам других людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний. – Запишите числа цифрами: а) 5 единиц первого класса и 5 единиц второго класса; б) 23 единицы второго класса и 1 единица первого класса; в) 148 единиц первого класса; г) 256 единиц второго класса; д) сорок две тысячи тринадцать; е) сто восемнадцать тысяч один; ж) одна тысяча девятьсот девять; з) триста три тысячи три. |
Отвечают на вопросы учителя. Выполняют задания устного счета. Запись: а) 5005
б) 23001
в) 148 г) 256000 д) 42013 е) 118001 ж) 1909 з) 303003 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Поставьте знак >, < или = так, чтобы записи были верными: 9000 · 8 ... 9 · 8000 9 · 50 ... 5 · 900 800 · 6 ... 8 · 6000 700 · 3 ... 3 · 7000 6 · 7000 ... 600 · 7 5 · 600 ... 6 · 500 |
9000 · 8 = 9 · 8000 9 · 50 < 5 · 900 800 · 6 < 8 · 6000 700 · 3 < 3 · 7000 6 · 7000 > 600 · 7 5 · 600 = 6 · 500 |
|
|
|
– Вставьте пропущенные числа: 2900 + 2900 + 2900 + |
2900 + 100 = 3000 5100 – 100 = 5000 2900 + 10 = 2910 5100 – 10 = 5090 2900 + 1 = 2901 5100 – 1 = 5099 |
|
|
|
– Решите задачу. Ель может жить 1200 лет, а сосна – в 2 раза меньше, чем ель. Рябина живет на 520 лет меньше, чем сосна. Сколько лет живет рябина? |
Решение: 1200 : 2 – 520 = 80 (лет) ‒ живет рябина |
|
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 47–48). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Выполните построения по алгоритму. Какие инструменты вы использовали? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Мы использовали угольник и линейку. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
|
Задание 2. |
– Постройте прямоугольник с длинами сторон 4 см 5 мм и 3 см. |
Выполняют построение. |
|
|
Задание 3 |
– Постройте план участка с учетом того, что одному сантиметру на плане будут соответствоватьт 8 м на местности |
Решение: 120 : 8 = 15 (см) – длина; 96 : 8 = 12 (см) – ширина. Выполняют построение |
|
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 49–51). Задание 9. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
а) Чему равна сумма чисел в каждой строке? б) Чему равна сумма чисел в каждом столбце? в) Чему равна сумма чисел по диагоналям? г) Какие три числа из таблицы надо сложить, чтобы получить 1000? д) Разность каких двух чисел из этой таблицы равна 1000? Найдите все варианты ответов. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Доказывают, аргументируют свою точку зрения.
а, б, в) – отвечают на вопросы, выполняя вычисления.
г) 200 + 300 + 500 = 1000
д) 1300 – 300 = 1000; 1200 – 200 = 1000; 1100 – 100 = 1000 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости |
|
Задание 10. |
– Выполните устные вычисления. |
Выполняют устные вычисления. |
|
|
Задание 11. |
– Сравните данные числа. |
220 445 > 219 445 302 007 < 320 070 190 006 > 19 006 800 050 > 800 005 |
|
|
Задание 12. |
– Назовите результаты действий. |
85 450 – 400 = 85 050 199 999 + 1 = 200 000 70 000 – 30 000 = 40 000 900 000 – 1 = 899 999 |
|
|
Задание 13. |
– Составьте равенства. |
200 000 = 199 999 + 1 1 000 000 = 999 999 + 1 450 000 = 449 999 + 1 |
|
|
Задание 14. |
– Прочитайте задание. Как, по-вашему, его можно решить? Составьте уравнение и решите его. |
х – 3058 = 3058 х = 3058 + 3058 х = 6116 |
|
|
Задание 15. |
– Найдите значения выражений.
– Какие математические правила вы использовали? |
3685 + 200481 + 958 = 205124 101030 – 98104 – 56 = 2870 100000 – (586 + 49503) = 49911 7510 + (301296 – 4098) = 304708 Перечисляют правила. |
|
|
Задание 16. |
– Запишите равенство. |
(9999 – 999) : 100 = 9000 : 100 = 90 |
|
|
Задание 17. |
– Выполните вычисления. |
6 + 12 : 3 – 1 = 6 + 4 – 1 = 9 (851 – 763) + 198 = 286 |
|
|
|
|
56 : 7 · 3 : 4 = 8 · 3 : 4 = 24 : 4 = 6 625 : 125 = 5 48 : 6 + 36 : 9 = 8 + 4 = 12 832 : 208 = 4 (6 + 12) : (3 – 1) = 18 : 2 = 9 450 : 150 = 3 16 : (15 – 11) = 16 : 4 = 4 693 : 99 = 7 |
|
|
Задание 18. |
– Выразите в секундах. |
1 мин 20 с = 80 с 2 мин 16 с = 136 с 3 мин 10 с = 190 с 4 ч 12 мин = 15120 с 2 ч 30 мин = 9000 с 56 мин = 3360 с |
|
|
Задание 19 |
– Как должен был звучать приказ капитана? |
– «Прийти в 9 часов, или в 21 час» |
|
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Назовите свойства прямоугольника. – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
Урок 18. Построение квадрата на нелинованной бумаге
(практическая работа)
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений строить прямоугольник; содействовать развитию умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся выполнять построение прямоугольника с заданными длинами сторон с помощью линейки и угольника на нелинованной бумаге; выполнять построение квадрата с заданной длиной стороны |
Метапредметные: Познавательные: осуществляют выбор оснований и критериев для сравнения и классификации объектов; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи; строят логическую цепь рассуждений. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке. Коммуникативные: учатся слушать и понимать речь других; признают возможность существования различных точек зрения и право каждого иметь свою |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Разгадайте правило, по которому записан каждый столбик чисел, и продолжите его на два числа: 543000 999102 918273 544000 999012 928374 545000 999203 938475 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
543000 999102 918273 544000 999012 928374 545000 999203 938475 546000 999023 948576 547000 999304 958677 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Расположите карточки с числами в порядке убывания.
– Уменьшите каждое из этих чисел на 39 десятков. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Расположите карточки с выражениями в порядке увеличения их значений, не производя вычислений:
Вычислите значения этих выражений |
Располагают карточки, не производя вычислений, затем вычисляют и проверяют себя |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 48–49). Задание 4. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Составьте алгоритм построения квадрата. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Составляют алгоритм построения квадрата. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 5. |
– Постройте квадрат с длиной стороны 5 см. |
Выполняют построение. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 6. |
– Предложите способ построения квадрата, используя умение делить окружность на 4 равные части. |
Выполняют построение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 7. |
– Начертите квадрат, периметр которого равен 14 см. |
Решение: 14 см = 140 мм 140 : 4 = 35 (мм) – длина стороны квадрата. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 8 |
– Начертите прямоугольник, ширина которого 4 см, а периметр равен 24 см |
Решение: 1) 24 : 2 = 12 (см) – длина и ширина. 2) 12 – 4 = 8 (см) – длина |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 51–53). Задание 20. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Сколько плиток потребовалось, если площадь одной плитки 1 дм2? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 2 · 5 = 10 (м2) – площадь коридора. 10 м2 = 1000 дм2 2) 1000 : 1 = 1000 (шт.) – плиток. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 21. |
– Катя сложила из палочек прямоугольник, длина которого 25 см, а ширина 10 см. Сколько палочек использовала Катя, если длина одной палочки 50 мм? |
Решение: 1) 250 : 50 = 5 (п.) – длина прямоугольника в палочках. 2) 100 : 50 = 2 (п.) – ширина прямоугольника в палочках. 3) (5 + 2) · 2 = 14 (п.) – понадобилось палочек всего.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 22. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу разными способами. |
Решение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задания 23‒28. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
См. Ресурсный материал к уроку. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 29. |
– Какая машина раньше отправилась от автовокзала? |
– Автобус раньше отправился от автовокзала. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 30. |
– Кто из мальчиков шел быстрее? |
– Юра шел быстрее. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 31. |
– Прочитайте задание и дайте ответ. |
– Можно. Длина стороны квадрата может оканчиваться одной из десяти цифр. Площадь квадрата может оканчиваться только цифрами 0, 1, 4, 5, 6, 9, но не цифрой 3, так как: 1 · 1 = 1 4 · 4 = 16 7 · 7 = 49 2 · 2 = 4 5 · 5 = 25 8 · 8 = 64 3 · 3 = 9 6 · 6 = 36 9 · 9 = 81 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 32. |
– Поясните решение в задании. |
Решение: 1) 32 – 24 = 8 (ящ.) – больше ящиков с желтыми яблоками. 2) 15 · 8 = 120 (кг) – масса желтых яблок больше. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 33. |
– Полкило сыра стоит 17 р. По какой цене продается сыр? ‒ Сколько надо заплатить за полтора килограмма этого сыра? ‒ За два с половиной килограмма сыра? |
Решение: 17 · 2 = 34 (р.) – стоит килограмм сыра. 17 · 3 = 51 (р.) – стоят полтора килограмма сыра. 17 · 5 = 85 (р.) – стоят два с половиной килограмма сыра. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 34 |
– Прочитайте ряд чисел. Верны ли высказывания о них? |
«В ряду пять чисел» – верно. «Число 65217 – наибольшее в ряду» – неверно. «Все числа записаны одними и теми же цифрами» – верно. «Предпоследнее число в ряду – 56712» – неверно. «В записи числа 65217 старшим разрядом является разряд десятков тысяч» – верно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Что такое прямоугольник? Как можно построить прямоугольник? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Упражнение «Плюс-минус-интересно» (устно и письменно). Для письменного выполнения учащиеся заполняют таблицу из трех граф. В графу «Плюс» записывают все, что понравилось на уроке, информацию и формы работы, которые вызвали положительные эмоции, либо, по мнению ученика, могут быть ему полезны для достижения каких-то целей. В графу «Минус» записывают то, что осталось непонятным, или информацию, которая, по мнению ученика, оказалась для него ненужной, бесполезной. В графу «Интересно» вписывают все любопытные факты, о которых узнали на уроке, а также пишут о том, что еще хотелось бы узнать по данной проблеме, задают вопросы учителю. Способны проводить самооценку на основе критериев успешности учебной деятельности (оценивать свои достижения, степень самостоятельности, инициативности, анализировать
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 23. Запись: Было – 396 т. по 18 шт. в ? кор. Увезли – ? т. Осталось – 15 кор. Решение: Задание 25. Решение: Задание 27. Запись: Красные – 1 гирл., ? шар. Синие – 3 гирл., ? шар. Всего – 48 шар. Решение: 1) 1 + 3 = 4 (г.) – всего. 2) 48 : 4 = 12 (шар.) – в одной гирлянде, а также число красных. 3) 12 · 3 = 36 (шар.) – число синих.
|
Задание 24. Запись: 1-й день – 8700 кн. 2-й день – ?, на 1800 кн. м. 3-й день – ? кн. Всего – 24 500 кн. Решение: Задание 26. Запись: 2 кг ягод – 3 кг сахара. ? кг ягод – 12 кг сахара. Решение: 1) 12 : 3 = 4 (раз) – столько раз нужно взять по 3 кг сахара. 2) 2 · 4 = 8 (кг) – ягод. Задание 28. Запись: Синих – ?, в 3 раза б. Красных – Всего – 48 ш. Решение: 1) 1 + 3 = 4 (частей) 2) 48 : 4 = 12 (ш.) – составляет одна часть, а также число красных шариков. 3) 12 · 3 = 36 (ш.) – число синих шариков.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Урок 19. Понятие скорости. Единицы измерения скорости
Организационная структура урока
Ресурсный материал к уроку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Урок 19. Понятие скорости. Единицы измерения скорости
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для формирования представления о понятии «скорость» как характеристике быстроты движения тела; способствовать развитию умений обозначать единицы скорости |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся: с понятием «скорость равномерного прямолинейного движения», с единицами скорости: километром в час, километром в минуту, километром в секунду, метром в минуту, метром в секунду и их обозначениями: км/ч, км/мин, км/с, м/мин, м/с; с прибором для измерения скорости – спидометром; со шкалой спидометра |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта, и преобразование модели с целью выявления общих законов, определяющих данную предметную область; осуществляют анализ, сравнение; делают выводы. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: излагают свое мнение и аргументируют свою точку зрения |
Личностные: проявляют интерес к учебному материалу; знают основные моральные нормы поведения; осознают роль языка и речи в жизни людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Поставьте знак >, < или = так, чтобы записи были верными: 125 тыс. 1 … 125010 70 тыс. 250 … 70250 300 тыс. 300 … 30030 186015 … 186150 28045 … 280 тыс. 45 200 тыс. 3 ед. … 2003 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
125 тыс. 1 < 125010 70 тыс. 250 = 70250 300 тыс. 300 > 30030 186015 < 186150 28045 < 280 тыс. 45 200 тыс. 3 ед. > 2003 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Выберите равные величины: 573 см 125000 см2 2935 г 125 дм 125 дм2 2 кг 935 г 561 см 5 м 73 см 1250 см 56 дм 1см |
573 см = 5 м 73 см 125000 см2 = 125 дм2 2935 г =2 кг 935 г 125 дм =1250 см 561 см =56 дм 1 см |
|
|
|
Задача. Для посадки приготовили луковицы цветов: 800 тюльпанов, гладиолусов – в 20 раз меньше, чем тюльпанов, а нарциссов – в 9 раз больше, чем гладиолусов. Не решая задачу, объясните, что обозначают выражения: 800 : 20; 800 : 20 · 9? |
Ответ: 800 : 20 – столько гладиолусов. 800 : 20 · 9 – столько нарциссов |
|
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 54–56). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Какова длина дистанции? За какое время пробежал эту дистанцию Волк? За какое время пробежал Заяц? – Сколько метров за одну секунду пробегал Волк? – Сколько метров за одну секунду пробегал Заяц? – Кто из них бежал быстрее? – Итак, быстроту движения характеризует величина, которая называется «скорость». Скорость показывает, какое расстояние преодолевается за единицу времени (секунду, минуту, час). |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Длина дистанции – 150 м. За 15 секунд пробежал эту дистанцию Волк. За 10 секунд пробежал Заяц. 150 : 15 = 10 (м/с) – 10 метров за одну секунду пробегал Волк. 150 : 10 = 15 (м/с) – 15 метров за одну секунду пробегал Заяц. – Заяц бежал быстрее. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия всоответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества |
|
Задание 2. |
– Как узнать, кто шел с большей скоростью: Волк или Заяц? |
120 : 12 = 10 (м/с) – скорость Волка. 150 : 10 = 15 (м/с) – скорость Зайца. |
|
|
Задание 3. |
– Прибор, которым измеряют скорость, называется спидометром. Рассмотрите рисунок. С какой скоростью движется автомобиль? |
– Автомобиль движется со скоростью 110 км/ч. |
|
|
Задание 4 |
– Прочитайте значения скорости. В каких единицах измеряют скорость? |
– Метры в секунду, метры в минуту, километры в минуту, метры в час, километры в секунду, сантиметры в минуту и другие |
|
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 57–58). Задание 12. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Начертите и вырежите прямоугольник и квадрат. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Выполняют построение, вырезают фигуры. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным дейст-вием, уметь вносить необходимые коррективы в действие после завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|
Задание 13. |
– Выполните действия и сравните значения выражений. |
3 · 8 – 20 : 4 > (3 · 8 – 20) : 4
73 – 17 + 29 > 73 – (17 + 29)
48 + 36 + 14 = 48 + (36 + 14) 12 : 6 · 2 > 12 : (6 · 2)
|
|
|
Задание 14. |
– Вычислите значения выражений. |
11111 – 3939 + 2121 = 9293 86009 – 6009 + 3030303 = 3110303 1928 ‒ 630 : 126 · 156 = 1148 12 · 15 + 2000 : 100 + 87654 = 87854 |
|
|
Задание 15. |
– Продолжите ряд чисел. |
а) 2000, 2500, 3000, 3500, 4000, 4500, 5000, 5500, 6000, 6500, 7000, 7500, 8000. б) 8160, 8140, 8120, 8100, 8080, 8060, 8040, 8020, 8000. |
|
|
Задание 16 |
– Каждое равенство верно. Какие числа закрыты карточками? |
а) 426 : 426 : 213 = 2 288 : 8 = 36 |
|
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Что такое скорость? Назовите единицы измерения скорости. – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 20. Нахождение скорости
|
Тип урока: комбинированный |
||
|
Педагогические задачи: продолжить формировать знания о скорости; практиковать в обозначении единиц скорости |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся: с понятием «скорость равномерного прямолинейного движения», с единицами скорости и их обозначениями: км/ч, км/мин, км/с, м/мин, м/с; с прибором для измерения скорости – спидометром; со шкалой спидометра; научатся вычислять скорость по данным пути и времени движения |
Метапредметные: Познавательные: осуществляют моделирование, анализ, сравнение; делают выводы. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Вычислите значения выражений: 500 – 10 · 3 400 + 10 · 6 500 – 100 · 3 400 + 100 · 6 600 – 10 · 5 800 + 10 · 7 600 – 100 · 5 800 + 100 · 7 |
Отвечают на вопросы учителя. Выполняют задания устного счета. 500 – 10 · 3 = 470 400 + 10 · 6 = 460 500 – 100 · 3 = 200 400 + 100 · 6 = 1000 600 – 10 · 5 = 550 800 + 10 · 7 = 870 600 – 100 · 5 = 100 800 + 100 · 7 = 1500 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по су-ществу полученного задания |
|||||||||||||
|
|
– Дополните каждую величину до четырех килограммов. 3 кг 50 г + 1 кг 900 г + 2 кг 260 г + 100 г + |
3 кг 50 г + 950г = 4 кг 1 кг 900 г + 2 кг 100 г = 4 кг 2 кг 260 г + 1 кг 740г = 4 кг 100 г + 3 кг 900 г = 4 кг |
||||||||||||||
|
|
– Какое число пропущено при счете? а) 238, 239, 241, 242, 243; б) 897, 898, 901; в) 1208, 1209, 1211, 1212, 1213; г) 56769, 56771, 56772, 56773. |
а) 240 б) 899, 900 в) 1210 г) 56770 |
||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 56–57). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Сравните скорости. Какое расстояние преодолевается за еди- ницу времени в каждом случае?
– У кого или чего самая большая скорость? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Мышь пробегает 3 метра в секунду. Лыжник идет со скоростью 12 километров в час. Караван верблюдов движется со скоростью 80 километров в день. Собака – со скоростью 310 метров в минуту, ракета – 13 километров в секунду.
– Самая большая скорость у ракеты. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи |
|||||||||||||
|
Задание 6. |
– За 3 часа поезд прошел 240 км. С какой скоростью шел поезд? |
Запись: 240 : 3 = 80 (км/ч) |
||||||||||||||
|
Задание 7. |
– Плот проплыл 20 км за 5 ч. Какова скорость движения плота? |
Запись: 20 : 5 = 4 (км/ч) |
||||||||||||||
|
Задание 8 |
– За 5 с орел пролетел 150 м. Найдите скорость полета орла |
Запись: 150 : 5 = 30 (м/с) |
||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 58). Задание 17. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Запишите выражение, которое показывает, на сколько красных яблок больше, чем желтых. – Подставьте вместо х число 15, а вместо у – число 9. Прочитайте задачу с этими числами и решите ее. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
х – у – выражение, которое показывает, на сколько красных яблок больше, чем желтых. 15 – 9 = 6 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||
|
Задание 18. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись:
Решение: 1-й участок – 28 меш., ? кг 2-й участок – 23 меш., ? кг, на 250 кг м.
1) 28 – 23 = 5 (меш.) – весят 250 кг. 2) 250 : 5 = 50 (кг) – весит 1 мешок.
|
||||||||||||||
|
Задание 19. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 220 – 40 = 180 (ябл.) – посадили, работая вместе. 2) 40 + 50 = 90 (ябл. в день) – совместная производительность. 3) 180 : 90 = 2 (д.) – время работы 2-й бригады. 4) 2 + 1 = 3 (д.) – время работы 1-й бригады. 5) 40 · 3 = 120 (ябл.) – посадила 1-я бригада. 6) 50 · 2 = 100 (ябл.) – посадила 2-я бригада. |
||||||||||||||
|
Задание 20 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу разными способами |
Решение: I способ 1) 135 : 9 = 15 (кг) – масса одной коробки. 2) 15 · 7 = 105 (кг) – весят 7 коробок. 3) 135 – 105 = 30 (кг) – на столько кг печенья меньше привезли во 2-й магазин. II способ 1) 135 : 9 = 15 (кг) – масса одной коробки. 2) 9 – 7 = 2 (кор.) – на столько коробок меньше привезли во 2-й магазин. 3) 15 · 2 = 30 (кг) – на столько кг печенья меньше привезли во 2-й магазин |
||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как найти скорость движения? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и отзывчивость. Оценивать результаты своей деятельности |
|||||||||||||
Урок 21. Упражнение в решении задач на нахождение скорости
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений вычислять скорость, сравнивать скорости |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами нахождения скорости, пути и времени движения тела; научатся решать арифметические задачи разных видов, связанные с движением, применяя формулы: υ = s : t, s = υ· t, t = s : υ |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; осуществляют анализ, устанавливают причинно-следственные связи; строят логическую цепь рассуждений. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. Игра «Цепочки». а) б) |
Отвечают на вопросы учителя. Выполняют задания устного счета. Восстанавливают цепочки: а) б) |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||
|
|
– Поставьте знак >, < или =. 3 · 7 + 30000 … 9 · 2 + 300000 9 · 6 + 20000 … 9 · 6 + 200000 7 · 2 + 400 … 2 · 7 + 40000 8 · 6 + 60000 … 8 · 6 + 6000 5 · 3 + 4000 … 4 · 4 + 40000 6 · 5 + 70000 … 5 · 6 + 70000 |
3 · 7 + 30000 > 9 · 2 + 300000 9 · 6 + 20000 = 9 · 6 + 200000 7 · 2 + 400 < 2 · 7 + 40000 8 · 6 + 60000 > 8 · 6 + 6000 5 · 3 + 4000 < 4 · 4 + 40000 6 · 5 + 70000 = 5 · 6 + 70000 |
|||||||||||||
|
|
– Расположите карточки с выражениями в порядке увеличения их значений, не выполняя вычислений.
– Вычислите значения выражений |
Располагают карточки:
– 127; 129; 131 |
|||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 57). Задание 9. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Лошадь пробежала 406 м за 2 мин. Вычислите скорость движения лошади. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 406 : 2 = 203 (м/мин) |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия всоответствии с поставленной задачей |
||||||||||||
|
Задание 10. |
– Прочитайте задачу и решите ее. |
Решение: 12 : 6 = 2 (раза) |
|||||||||||||
|
Задание 11 |
– Прочитайте задачу и решите ее |
Решение: 58 + 12 = 70 (км/ч) |
|||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 59). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 60 : 10 = 6 (стр./ч) – производительность Ирины. 2) 60 : 15 = 4 (стр./ч) – производительность Ольги. 3) 6 + 4 = 10 (стр./ч) – общая производительность. 4) 60 : 10 = 6 (ч) – время работы при совместном труде. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||
|
Задание 22. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 70 – 15 = 55 (км) – проехал после обеда. 2) 70 + 55 = 125 (км) – весь путь. 3) 125 · 200 = 25 000 (г) 25 000 г = 25 кг 500 г Ответ: 25 кг 500 г топлива израсходовал. |
|||||||||||||
|
Задание 23. |
– Отдыхающий приехал в санаторий утром 28 августа, а выехал обратно вечером 20 сентября. Сколько дней он провел в санатории? |
– Отдыхающий провел в санатории 24 дня. |
|||||||||||||
|
Задание 24. |
– Площадь одного квадрата 1 дм2, а другого – 1 м2. Во сколько раз площадь первого квадрата меньше площади второго? |
Решение: 1 м2 = 100 дм2; 100 : 1 = 100 (раз) Ответ: в 100 раз. |
|||||||||||||
|
Задание 25. |
– Сколько прямоугольников на каждом рисунке? |
а) 9 прямоугольников. б) 18 прямоугольников. |
|||||||||||||
|
Рубрика «Путешествие в прошлое» (с. 60). |
– Прочитайте статью рубрики «Путешествие в прошлое». Что обозначает слово «дюйм»? – Выразите в сантиметрах длину: 4 дюйма; 8 дюймов; 20 дюймов. |
– Слово «дюйм» введено в русский язык Петром I в самом начале XVIII века. Сегодня под дюймом чаще всего понимают английский дюйм, равный 25 мм. Запись: 4 дюйма = 25 мм · 4 = 100 мм = 10 см 8 дюймов = 25 мм · 8 = 200 мм = 20 см 20 дюймов = 25 мм · 20 = 500 мм = 50 см |
|||||||||||||
|
Задание 26. |
АВ = 16 см, АВ = ВС. В него вписан квадрат NFKM. Какова площадь квадрата NFKM?
|
Решение. I способ S = 8 · 8 · 2 = 128 (см2) II способ S = 16 · 16 : 2 = 128 (см2) |
|||||||||||||
|
Задание 27 |
АС = 8 см, ВD = 6 см. Как вычислить площадь четырехугольника АВСD?
|
– Чтобы вычислить площадь четырехугольника АВСD, надо из треугольников сложить прямоугольник. Решение: 1) SΔ = 4 · 3 : 2 = 6 (см2) 2) Таких треугольников четыре. Þ SАВСD = 6 · 4 = 24 (см2) |
|||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как найти скорость движения? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 22. Задачи на движение. Нахождение скорости
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с зависимостью между величинами скорость, время, расстояние; способствовать формированию умения пользоваться изученной терминологией |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами нахождения скорости, пути и времени движения тела; научатся решать арифметические задачи разных видов, связанные с движением, применяя формулы: u = s : t, s = u · t, t = s : u |
Метапредметные: Познавательные: преобразуют информацию из одной формы в другую; применяют методы информационного поиска, в том числе с помощью компьютерных средств. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: проявляют инициативное сотрудничество в поиске и сборе информации |
Личностные: устанавливают, с какими учебными задачами могут справиться самостоятельно; проявляют интерес к учебному материалу; владеют основными моральными нормами |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Прочитайте на доске сведения о реках нашей планеты: • Самая длинная река в мире – Нил, ее длина – 6671 км. • Самая длинная река Южной Америки – Амазонка – 6480 км. • Самая длинная река Северной Америки – Миссисипи (вместе с притоком Миссури) – 6420 км. • Самая длинная река Азии – Янцзы – 5800 км. • Самая длинная река Европы – Волга – 3690 км. • Дунай имеет длину 2850 км. • Эльба имеет длину 1165 км. • Самая короткая река в мире находится в Америке. Ее длина 134 м. На какие вопросы вы сможете ответить, выполнив следующие действия: 6671 – 134, 6671 – 6480, 6420 – 1165, 6420 – 2850, 1165 – 134, 3690 – 2850, 6671 – 3690? – Какие еще можно составить выражения? |
Отвечают на вопросы учителя. Выполняют задания устного счета.
– На вопросы типа «На сколько километров больше (на сколько километров меньше) одна река, чем другая?».
Составляют выражения. Вычисляют значения данных и составленных выражений |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу |
||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 61–62). |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Для того чтобы найти скорость, нужно знать путь и время движения. Обычно скорость обозначают буквой u, путь – буквой s, а время – буквой t. Чтобы найти скорость, надо путь разделить на время, то есть u = s : t |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
||||
|
Задание 1. |
– Прочитайте задачу. С какой скоростью шел Заяц? |
Запись: s = 6 км t = 2 ч u – ? Решение: 6 : 2 = 3 (км/ч) |
|||||
|
Задание 2. |
– С какой скоростью плыла Катя? |
Запись: s = 50 м t = 25 с u – ? Решение: 50 : 25 = 2 (м/с) |
|||||
|
Задание 3. |
– Вычислите скорость машины. |
Запись: s = 30 км t = 15 мин u – ? Решение: 30 : 15 = 2 (км/мин) |
|||||
|
Задание 4 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Запись: s = 36 км Вышел – в 10 ч Прибыл – в 13 ч t – ? u – ? Решение: 1) 13 – 10 = 3 (ч) 2) 36 : 3 = 12 (км/ч) |
|||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 65–66). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните вычисления устно. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Выполняют вычисления устно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок |
||||
|
Задание 22. |
– Выполните деление. |
|
|||||
|
Задание 24. |
– Разделите с остатком. |
158 : 7 = 22 (ост. 4) 605 : 8 = 75 (ост. 5) 527 : 28 = 18 (ост. 23) 675 : 31 = 21 (ост. 24) 904 : 68 = 13 (ост. 20) 396 : 89 = 4 (ост. 40) |
|||||
|
Самостоятельная работа |
Организует самостоятельную работу по карточкам |
Выполняют самостоятельную работу (см. ресурсный материал к уроку) |
|||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как найти скорость движения? время? расстояние? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
||||
|
Ресурсный материал к уроку Самостоятельная работа по карточкам
|
|||||||
Урок 23. Задачи на движение. Нахождение расстояния
|
Тип урока: открытие новых знаний и способов действий |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами нахождения скорости, пути и времени движения тела; научатся решать арифметические задачи разных видов, связанные с движением, применяя формулы: u = s : t, s = u · t, t = s : u |
Метапредметные: Познавательные: осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: умеют работать по предложенному учителем плану. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: расширяют познавательные интересы и учебные мотивы; владеют основными моральными нормами поведения |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Вставьте пропущенные числа. 1 р. = 1 р. 20 к. = 5 р. 40 к. = 7 р. 30 к. = |
Отвечают на вопросы учителя. Выполняют задания устного счета.
1 р. = 100 к. 9 р. 10 к. = 910 к. 1 р. 20 к. = 120 к. 7 р. 60 к. = 760 к. 5 р. 40 к. = 540 к. 4 р. 40 к. = 440 к. 7 р. 30 к. = 730 к. 8 р. 50 к. = 850 к. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||
|
|
– Заполните таблицу.
– Так как же найти стоимость покупки? |
Заполняют таблицу:
– Чтобы найти стоимость покупки, надо цену умножить на количество |
||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 62–63). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– За полчаса лыжник прошел 6 км. С какой скоростью шел лыжник? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 1) 60 : 30 = 2 (раза) 2) 6 · 2 = 12 (км/ч) |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости |
|||||||||||||||||||||||||||||||||||
|
Задание 6. |
– Заяц шел к Волку 2 ч со скоростью 3 км/ч. Какой путь прошел Заяц? |
– Чтобы найти путь, надо скорость умножить на время: s = u · t. Решение: 3 · 2 = 6 (км) |
||||||||||||||||||||||||||||||||||||
|
Задание 7. |
– Найдите путь, который прошел поезд. |
Запись: u = 56 км/ч t = 12 ч s – ? Решение: 56 · 12 = 672 (км) |
||||||||||||||||||||||||||||||||||||
|
Задание 8. |
– Сколько метров пролетела муха со скоростью 5 м/с за полминуты? |
Запись: 5 · 30 = 150 (м) |
||||||||||||||||||||||||||||||||||||
|
Задание 9. |
– Дачник отъехал от дома на автомобиле со скоростью 60 км/ч и через полчаса приехал на дачу. На каком расстоянии от дома находится дача? |
– Дача находится на расстоянии 30 км от дома.
|
||||||||||||||||||||||||||||||||||||
|
Задание 10 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Решение: 1) 23 · 2 = 46 (км) – проплыли. 2) 55 · 3 = 165 (км) – проехали. 3) 165 + 46 = 211 (км) – весь путь |
||||||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 66–67). Задание 25. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: 4 апельсина – 800 г 3 апельсина, 1 грейпфрут – 1100 г Решение: 1) 800 : 4 = 200 (г) – весит 1 апельсин. 2) 200 · 3 = 600 (г) – весят 3 апельсина. 3) 1100 – 600 = 500 (г) – масса грейпфрута. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок |
|||||||||||||||||||||||||||||||||||
|
Задание 26. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 16 : 4 = 4 (кг) – масса дыни. |
||||||||||||||||||||||||||||||||||||
|
Задание 27. |
– Выполните задание. |
– В первом случае две восьмых всех фишек закрашено. – Во втором случае три девятых всех фишек закрашено. |
||||||||||||||||||||||||||||||||||||
|
Задание 28. |
– Запишите пять различных двузначных чисел так, чтобы ни одна цифра в записях этих чисел не повторялась. |
Запись: 98, 76, 54, 32, 10. |
||||||||||||||||||||||||||||||||||||
|
Задание 29 |
– Выполните задание |
Запись: 23 · 75 · 36 · 129 = … 0 |
||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как найти расстояние, зная время и скорость движения? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке: кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Оценивать результаты деятельности |
Урок 24. Задачи на движение. Нахождение времени
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с зависимостью между величинами скорость, время, расстояние; способствовать формированию умений пользоваться изученной терминологией, решать текстовые задачи на движение |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами нахождения скорости, пути и времени движения тела; научатся решать арифметические задачи разных видов, связанные с движением, применяя формулы: u = s : t, s = u · t, t = s : u |
Метапредметные: Познавательные: устанавливают зависимость между данными и искомыми величинами при решении разнообразных учебных задач. Регулятивные: осуществляют саморегуляцию как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта и преодолению препятствий). Коммуникативные: полно и точно выражают свои мысли в соответствии с задачами и условиями коммуникации; владеют монологической и диалогической формами речи в соответствии с нормами родного языка и современных средств коммуникации |
Личностные: осознают необходимость самосовершенствования; осваивают начальные формы познавательной и личностной рефлексии |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности учащегося |
||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Решите задачи. а) Стрекоза летит со скоростью 10 м/с. Какое расстояние пролетит стрекоза за полчаса? б) Лебедь летит со скоростью 88 км/ч. Какое расстояние пролетит лебедь за 15 минут? |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) Ответ: 18 км.
б) Ответ: 22 км. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||
|
|
в) Из двух сёл одновременно навстречу друг другу вышли два товарища – Миша и Коля. Миша шел со скоростью 3 км/ч, а Коля – 5 км/ч. Одновременно с Мишей к Коле побежала собака со скоростью 8 км/ч. Добежав до Коли, она повернула назад, к Мише, так и бегала между ребятами, пока они не встретились. Сколько километров пробежала собака, если расстояние между селами 16 км? |
в) Ответ: 16 км. |
|||||||||||
|
|
– Решите ребусы. Вместо букв поставьте цифры так, чтобы получилась верная запись (одинаковые цифры обозначены одинаковыми буквами):
|
|
|||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 63–64). Задание 11. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Заяц прошел 6 км со скоростью 3 км/ч. Сколько часов он шел? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. – Чтобы найти время, надо путь разделить на скорость: t = s : u. Запись: s = 6 км u = 3 км/ч t – ? Решение: 6 : 3 = 2 (ч) |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
||||||||||
|
Задание 12. |
– Сколько времени вертолет был в полете? |
Запись: s = 900 км u = 300 км/ч t – ? Решение: 900 : 300 = 3 (ч) |
|||||||||||
|
Задание 13. |
– Вычислите время движения плота. |
Запись: s = 630 м u = 90 м/мин t – ? Решение: 630 : 90 = 7 (ч) |
|||||||||||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: s = 630 км u = 90 км/ч Вышел – 23 ч 50 мин Прибыл – ? Решение: 1) 630 : 90 = 7 (ч) – время движения. 2) 23 ч 50 мин + 7 ч = 6 ч 50 мин следующего дня. |
|||||||||||
|
Задание 15. |
– Сколько часов бежали лошади? |
– 2 часа бежали лошади. |
|||||||||||
|
Задание 16 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 6 · 5 = 30 (км) – путь. 2) 30 : 15 = 2 (ч) – плыли на катере |
|||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 67–68). Задание 30. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Покупатель просит продавца взвесить ему 4 кг винограда. Сможет ли продавец это сделать, используя чашечные весы и гири массой 5 кг и 3 кг? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– На одну чашу весов надо положить гирю в 5 кг, а на другую – гирю в 3 кг и 2 кг винограда. Процедуру повторить 2 раза. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||
|
Задание 31. |
– Выполните практическую работу. |
Выполняют практическую работу (см. Ресурсный материал к уроку). |
|||||||||||
|
Задание 32. |
– Выполните чертеж. |
Выполняют чертеж (см. Ресурсный материал к уроку). |
|||||||||||
|
Задание 33. |
– Как достроить полукруг до целого круга? Объясните способ построения. |
Алгоритм построения. 1. Измерить диаметр (4 см). 2. Вычислить радиус, разделив диаметр пополам (2 см). 3. Отметить центр круга. 4. Достроить полукруг радиусом 2 см. |
|||||||||||
|
Задание 34. |
– Проверьте с помощью угольника, является ли угол А прямым. |
Рис. 1. Ð А = 90° Рис. 2. Ð А = 90° |
|||||||||||
|
Задание 35. |
– Вырежите из бумаги квадрат площадью 81 см2. Чему равна длина стороны квадрата? |
– 9 см. |
|||||||||||
|
Задание 36. |
– Выполните чертеж. |
Выполняют чертеж (см. Ресурсный материал к уроку). |
|||||||||||
|
Задание 37. |
– Рассмотрите рисунок в учебнике и ответьте на вопросы: а) Кто из детей живет в одной и той же квартире? б) В одном ли доме живут Аня и Митя? в) В одной ли квартире живут Аня и Петя? г) Назовите номер дома и квартиры Коли. д) Кто из детей живет в доме 18? е) У кого из детей квартира с номером 18? |
а) Петя и Коля живут в одной и той же квартире.
б) Да, в одном доме. в) Нет, не в одной квартире. г) У Коли номер дома – 18, номер квартиры – 12. д) Петя и Коля живут в доме 18. е) У Мити и Сережи квартира с номером 18. |
|||||||||||
|
Задание 38 |
– Проанализируйте ряд чисел. Выберите правило, с помощью которого составлен этот числовой ряд |
– Каждое следующее число, начиная с третьего, равно сумме двух предыдущих чисел |
|||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как найти время, зная расстояние и скорость движения? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
||||||||||
|
Ресурсный материал к уроку
|
|||||||||||||
Урок 25. Упражнение в решении задач на движение.
Проверочная работа по теме «Задачи на движение»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений решать задачи на движение |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами нахождения скорости, пути и времени движения тела; научатся решать арифметические задачи разных видов, связанные с движением, применяя формулы: u = s : t, s = u · t, t = s : u |
Метапредметные: Познавательные: осознанно и произвольно строят речевые высказывания в устной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: определяют последовательность промежуточных целей с учетом конечного результата. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения, считаются с мнением другого человека, проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности); понимают причину успеха/неуспеха учебной деятельности и конструктивно действуют в ситуации неуспеха |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Дополните каждую величину до 4 часов: 3 ч 15 мин 239 мин 2 ч 59 мин 219 мин 1 ч 1 мин 2 ч 30 мин |
Отвечают на вопросы учителя. Выполняют задания устного счета.
3 ч 15 мин + 45 мин = 4 ч 239 мин + 1 мин = 4 ч 2 ч 59 мин + 1 ч 1 мин = 4 ч 219 мин + 21 мин = 240 мин = 4 ч 1 ч 1 мин + 2 ч 59 мин = 4 ч 2 ч 30 мин + 1 ч 30 мин = 4 ч Составляют и решают задачи: |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||
|
|
– Соедините условие с вопросом так, чтобы получилась задача, и решите ее.
– Ответьте на вопросы задач
|
а) За 30 минут Наташа прошла 2 км 400 м. Какое расстояние Наташа пройдет за 1 час? Решение: 2 км 400 м · 2 = 4 км 800 м б) Скорость Наташи 80 м/мин. За какое время Наташа пройдет расстояние в 1 км 600 м? Решение: 1600 м : 80 м/мин = 20 мин в) Расстояние в 800 м Наташа проходит за 10 минут. На каком расстоянии от школы будет Наташа через 30 минут? Решение: 800 м : 10 мин = 80 м/мин 80 м/мин · 30 мин = 2400 м = 2 км 400 м г) Расстояние от дома до середины пути 1 км 600 м. На каком расстоянии от дома Наташа будет через 5 минут? Ответ: эта задача не имеет решения, так как чтобы найти путь (s), нужно знать скорость (u) и время (t), а в данном условии не указана скорость |
|||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 64–65).
Задание 17. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Запись: u = 62 км/ч t = 5 ч Прошел – ? км Осталось – ? км, в 2 раза б. s – ? Решение: 1) 62 · 5 = 310 (км) – прошел. 2) 310 · 2 = 620 (км) – осталось. 3) 310 + 620 = 930 (км) – весь путь.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимо-действии. Осуществлять контроль действий по результату |
||||||||||||||||||||
|
Задание 18. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 432 : 9 = 48 (км/ч) – первоначальная скорость. 2) 432 : 6 = 72 (км/ч) – новая скорость. 3) 72 – 48 = 24 (км/ч) – на столько новая скорость больше. |
|||||||||||||||||||||
|
Задание 19. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: t = 6 ч s = 432 км Проехал – ? км Осталось – 144 км u – ? км/ч Решение: 1) 432 – 144 = 288 (км) – проехал. 2) 288 : 6 = 48 (км/ч) – скорость. |
|||||||||||||||||||||
|
Задание 20 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Решение: 1) 18 · 3 = 54 (км) – первый путь. 2) 54 + 9 = 63 (км) – обратный путь. 3) 18 + 3 = 21 (км/ч) – скорость на обратном пути. 4) 63 : 21 = 3 (ч) – время на обратный путь |
|||||||||||||||||||||
|
III. Самостоятельная работа: решение задач |
Организует самостоятельную работу учащихся. Задача 1. Из двух поселков одновременно навстречу друг другу выехали автобус и мотоцикл. Скорость автобуса 45 км/ч, а скорость мотоцикла – 38 км/ч. Чему равно расстояние между поселками, если встреча произошла через 2 часа после выхода? Задача 2. Автотуристы за 3 дня наметили проехать 1520 км. В первый день они ехали 8 часов со скоростью 85 км/ч, во второй день они уменьшили скорость на 9 км/ч и ехали 4 часа. С какой скоростью должны ехать автотуристы в третий день, чтобы проехать оставшееся расстояние за 8 часов? |
Работают самостоятельно.
Задача 1. Решение: (45 + 38) · 2 = 166 (км)
Задача 2. Ответ: 67 км/ч.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||
|
|
Задача 3. От одной пристани одновременно в противоположных направлениях отплыли два катера. Через 2 часа расстояние между ними стало 114 км. Какова скорость первого катера, если скорость второго 28 км/ч? Задача 4. Расстояние в 270 км мотоциклист проезжает за 3 часа, а велосипедист – за 15 часов. Во сколько раз скорость мотоциклиста больше скорости велосипедиста? Задача 5. Автомобиль, скорость которого 95 км/ч, догоняет автобус, движущийся со скоростью 60 км/ч. Сейчас между ними расстояние 245 км. Через сколько времени автомобиль догонит автобус? Задача 6. Катер за 4 часа прошел 140 км. Его скорость на 15 км/ч больше скорости плота. Какое расстояние плот пройдет за это же время? Задача 7. Катер плыл по реке сначала 3 часа, а потом еще 5 часов с той же скоростью. Всего он проплыл 288 км. С какой скоростью он плыл? Задача 8. Всадник скачет на лошади со скоростью 15 км/ч. Какое расстояние преодолеет всадник за 20 минут? Задача 9. Поезд за 9 часов должен пройти 540 км. Сначала 3 часа он шел со скоростью 50 км/ч, а затем увеличил скорость на 5 км/ч и двигался с такой скоростью 2 часа. С какой скоростью поезд должен идти оставшийся путь, чтобы прибыть в пункт назначения вовремя? Задача 10. Сокол за 13 секунд пролетает 273 м, а орел за это же время пролетает 390 м. На сколько метров в секунду скорость орла больше скорости сокола? |
Задача 3. Решение: 114 : 2 – 28 = 29 (км/ч)
Задача 4. Решение: 270 : 3 – 270 : 15 = 72 (км/ч)
Задача 5. Решение: 245 : (95 – 60) = 7 (ч)
Задача 6. Решение: 140 : 4 – 15) · 4 = (80 км)
Задача 7. Решение: 288 : (5 + 3) = 36 (км/ч)
Задача 8. Ответ: 5 км.
Задача 9. Ответ: 70 км/ч.
Задача 10. (390 – 273) : 13 = 9 (м/с) |
|||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Запишите формулу зависимости между скоростью, временем и расстоянием. – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя по следующей методике: 1) Если урок прошел плодотворно и вы многое из него усвоили и остались довольны, то прикрепите к дереву яблоко. 2) Если урок прошел хорошо, но могло быть и лучше, то прикрепите к дереву цветок. 3) Если урок ничего нового вам не принес, прикрепите зеленый листочек. 4) А если совсем напрасно было потрачено время на уроке, то прикрепите желтый листок |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Методика «Дерево». На доске – силуэт дерева, на столе учителя – вырезанные из бумаги яблоки, листья и цветы. Учащиеся по очереди подходят и выбирают яблоко, цветок или листочек зеленого или желтого цвета, а затем прикрепляют его на дерево |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 26. Координатный угол, координатные точки.
Контрольный устный счет № 2
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для формирования понятия «координатный угол»; способствовать развитию умений решать арифметические задачи, строить точки с указанными координатами |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «координатный угол», «оси координат ОХ и ОУ», «начало координат», «координаты точки»; научатся: читать координаты данной точки; выполнять построение точки с указанными координатами |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера. Регулятивные: оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы; осваивают начальные формы познавательной и личностной рефлексии. Коммуникативные: контролируют действия партнера |
Личностные: имеют желание учиться, понимают границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Заполните пропуски. 560 = 250 : 5 + 271 – |
Отвечают на вопросы учителя. Выполняют задания устного счета.
560 = 250 : 5 + 510 570 + 150 – 410 = 310 271 – 71 + 106 = 306 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||
|
– Найдите выражения, значение которых равно 150. 135 + 15 17 · 4 + 82 94 + 56 400 – 350 396 – 246 8 · 7 + 93 81 + 79 10 + 20 · 5 182 – 4 · 8 |
135 + 15 = 150 396 – 246 = 150 17 · 4 + 82 = 150 182 – 4 · 8 = 150 |
|||||||
|
– Прочитайте условие задачи. Один велосипедист за 4 часа проехал 56 км, а другой за 5 часов проехал 60 км. Объясните, что обозначают выражения: а) 60 – 56 б) 56 : 4 в) 60 : 5 г) 56 : 4 – 60 : 5 д) 56 : 4 · 2 е) 60 : 5 · 3 |
Ответ: а) на сколько километров больше проедет один из велосипедистов; б) скорость первого велосипедиста; в) скорость второго велосипедиста; г) на сколько скорость одного велосипедиста больше, чем скорость другого; д) расстояние, которое проехал первый велосипедист за 2 часа; е) расстояние, которое проехал второй велосипедист за 3 часа |
|||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 69–71). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Волк и Заяц купили билеты на футбольный матч. В каком ряду и на каком месте будет сидеть Волк? – В каком ряду и на каком месте будет сидеть Заяц? – Между кем из зрителей сядет Заяц? – Между кем сядет Волк? – Кто будет правее Зайца? – Кто будет левее Волка? – Какой билет у Удава? – Какой билет у Мартышки? – Какой билет у Жирафа? – Итак, для того чтобы точно описать расположение какого-нибудь предмета, его обозначают точкой и указывают координаты на координатной сетке. Сетку строят так. Выбирают точку О (начало координат) и из нее проводят под прямым углом два числовых луча – ОХ и ОУ. (Чертит.) Эти лучи образуют координатный угол. Положение любой точки определяется двумя числами: первое указывается по горизонтальной оси ОХ, а второе – по вертикальной оси ОУ. Так, расположение точки А можно описать парой чисел – 2 и 4. (Показывает.) – Опишите парами чисел расположение остальных отмеченных точек. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Во 2-м ряду на 5-м месте будет сидеть Волк.
– В 4-м ряду на 6-м месте будет сидеть Заяц.
– Между Белкой и Ежиком сядет Заяц. – Между Лисой и Львом сядет Волк. – Белка будет правее Зайца. – Лев будет левее Волка. – У Удава – 1-й ряд, 1-е место. – У Мартышки – 1-й ряд, 3-е место. – У Жирафа – 3-й ряд, 6-е место.
Называют координаты точек: В (4; 7), К (3; 0), С (6; 1), Е (9; 0) М (0; 6), D (0; 3), Х (5; 5), У (8; 8) |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|||||
|
Задание 2. |
– Назовите пары чисел, соответствующие вершинам каждой фигуры. |
Рис. 1. А (2; 7), В (6; 7), С (6; 3), D (2; 3). Рис. 2. К (4; 7), Е (7; 4), М (1; 0). |
||||||
|
Задание 3 |
– Какое слово зашифровано на рисунке? |
– На рисунке зашифровано слово «умница» |
||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 71–74). Задание 4. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните действия. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
420 – 5 · (36 + 9) + 632 : 8 = 274 9345 + 100755 = 110100 532 : 4 + 6 · (42 – 8) – 237 = 100 10845 – 2699 = 8146 512384 – 95326 = 417058 4028 + 172 = 4200 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||
|
Задание 5. |
– Выполните задание, работая в парах. |
Выполняют задание, работая в парах. |
||||||
|
Задание 6. |
– На сколько наименьшее четырехзначное число меньше наибольшего четырехзначного числа? |
Решение: 9999 – 1000 = 8999. |
||||||
|
Задание 7. |
– Составьте выражения и найдите их значения. |
(948 – 36) : 8 = 114 (135 + 108) · 4 = 972 |
||||||
|
Задание 8. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 864 : 27 = 32 (ч) |
||||||
|
Задание 9. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
См. ресурсный материал к уроку. |
||||||
|
Задание 10. |
– Уменьшите на 7 десятков тысяч каждое число. |
989705 – 70000 = 919705 100000 – 70000 = 30000 97509 – 70000 = 27509 70025 – 70000 = 25 |
||||||
|
Задание 11. |
– Увеличьте на 8 десятков тысяч каждое число. |
635 + 80000 = 80635 98451 + 80000 = 178451 1287 + 80000 = 81287 538104 + 80000 = 618104 |
||||||
|
Задания 12, 13. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
См. Ресурсный материал к уроку. |
||||||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
– Если отец и сын будут работать вместе, то им потребуется больше 15 минут, но меньше 20 минут. |
||||||
|
Задание 15. |
– На ели сидели 8 ворон и 5 сорок. Улетели 6 птиц. Можно ли утверждать, что на ели осталась хотя бы одна ворона? Можно ли утверждать, что на ели осталась хотя бы одна сорока? |
– Да, можно утверждать, что на ели осталась хотя бы одна ворона. Нельзя утверждать, что на ели осталась хотя бы одна сорока. |
||||||
|
Задание 16. |
– Разделите отрезок АВ на две равные части с помощью циркуля. |
См. Ресурсный материал к уроку. |
||||||
|
Задание 17. |
– Как называются отрезки ОА и ОВ? Измерьте длину радиуса окружности и длину ее диаметра. – Во сколько раз длина диаметра больше длины радиуса? |
– Отрезки ОА и ОВ – радиусы окружности. Рис. 1. АВ = 2 см Рис. 2. АВ = 30 мм АО = ОВ = 1 см АО = ОВ = 15 мм – В 2 раза длина диаметра больше длины радиуса. |
||||||
|
Задание 18. |
– Назовите планеты Солнечной системы в порядке увеличения их диаметра. |
– Меркурий, Марс, Венера, Земля, Нептун, Уран, Сатурн, Юпитер. |
||||||
|
Задание 19. |
– Пете 18 лет. Катя на t лет моложе Пети. Запишите выражение для вычисления возраста Кати. Выполните вычисления при t, равном 3. |
– Выражение для вычисления возраста Кати: 18 – t.
Решение: 18 – 3 = 15 (лет). |
||||||
|
Задание 20. |
– Выполните построение. |
См. ресурсный материал к уроку. |
||||||
|
Задание 21 |
– Какие части круга закрашены каждым цветом на первом рисунке?
– Какие части круга закрашены каждым цветом на втором рисунке? |
– На первом рисунке синим цветом закрашена половина круга, красным цветом – четвертая часть, зеленым и коричневым цветами – по одной восьмой части круга. – На втором рисунке зеленым цветом закрашена четвертая часть круга, желтым цветом – три четвертых |
||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Что называют координатным углом? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Оценивать уровень владения учебным действием |
Ресурсный материал к уроку
|
Задание 9. Запись: Было – 500 чел. На велосипедах – 20 чел. В ? колоннах – ? чел. по 24 чел. Решение: 1) 500 – 20 = 480 (чел.) – в колоннах. 2) 480 : 24 = 20 (к.) – было. |
Задание 12. Запись: 1-я бригада – 5 км 600 м 2-я бригада – ? на 1 км 170 м б. 3-я бригада – ? на 1 км 900 м м. Всего – ? км Решение: 1) 5 км 600 м + 1 км 170 м = 6 км 770 м – 2-я бригада. 2) 6 км 770 м – 1 км 900 м = 4 км 870 м – 3-я бригада. 3) 5 км 600 м
|
||
|
Задание 13. Запись: 1-й день – 128 р. 60 к. 2-й день –?, на 42 р. 40 к. б. Всего – ? Решение: 1) 1128 р. 60 к. + 42 р. 40 к. = 171 (р.) – во 2-й день. 2) 128 р. 60 к. + 171 р. = 299 р. 60 к. – за два дня. |
Задание 16.
|
Задание 20. Ð K = 90°, Ð М = 90°
|
|
Урок 27. Графики, диаграммы, таблицы (Чтение)
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «график», «диаграмма», «таблица», объяснить их значение для передачи информации; способствовать формированию умений строить простейшие графики и диаграммы |
||
|
Планируемые результаты |
||
|
Предметные: научатся читать и выполнять построение простейших диаграмм и графиков |
Метапредметные: Познавательные: умеют ориентироваться в учебнике (на развороте, в оглавлении, в условных обозначениях); находят ответы на вопросы в тексте, иллюстрациях; делают выводы в результате совместной работы класса и учителя. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: умеют задавать вопросы; формулируют собственное мнение и позицию |
Личностные: имеют желание учиться; осознают необходимость самосовершенствования; понимают границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности учащегося |
||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Решите математические ребусы.
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
3886 + 8207 = 12093 308924 – 305211 = 3713 12618 – 5949 = 6669 3157 + 8420 = 11577 |
Осуществлять актуализацию личного жизненного опыта. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||
|
|
– Решите задачу. Самая высокая точка на земном шаре – 8 км 848 м над уровнем океана, а самая низкая – на глубине 11 км 022 м. Каково расстояние между самой высокой и самой низкой точками Земли? Выполните схему, она поможет вам решить задачу |
Решение:
|
|||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 75–76). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Рассмотрите график роста Волка. Что означают числа по оси Ох? – Что означают числа по оси Оу? – Какого роста был Волк, когда ему исполнился 1 год? – А в 3 года? В 4 года? В 6 лет?
– Вырос ли Волк за последний год? – Сколько лет было Волку, когда его рост был равен 40 см? Когда рост был 45 см? А когда 50 см? 70 см? 75 см?
– На сколько сантиметров вырос Волк от года до 3 лет? – На сколько сантиметров вырос Волк от 3 лет до 7 лет? – За какой год Волк вырос больше всего? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Числа по оси Ох означают возраст.
– Числа по оси Оу означают рост. – Волк был ростом 20 см, когда ему исполнился 1 год. – Рост Волка в 3 года – 50 см. В 4 года – 55 см. В 6 лет – 75 см. – Волк за последний год не вырос. – 2 года было Волку, когда его рост был равен 40 см; 2 года 6 месяцев было Волку, когда его рост был 45 см; 3 года было Волку, когда его рост был 50 см; 5 лет было Волку, когда его рост был 70 см; 6–7 лет было Волку, когда его рост был 75 см. – 50 –20 = 30 (см). На 30 сантиметров вырос Волк от года до 3 лет. – 75 – 50 = 25 (см). На 25 сантиметров вырос Волк от 3 лет до 7 лет. – За первый год Волк вырос больше всего. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
||||
|
Задание 2 |
– Рассмотрите график движения Волка и Зайца. Сколько секунд бежал Заяц? – Сколько секунд бежал Волк? – Сколько метров Волк не добежал до финиша? – Можно ли по графику определить, кто из них бежал быстрее? – За сколько секунд пробежал 300 м Волк? – За сколько секунд пробежал 300 м Заяц? – Какое расстояние пробежал за первые 10 секунд Волк? А Заяц? |
– 80 секунд бежал Заяц. – 70 секунд бежал Волк. – 200 метров Волк не добежал до финиша. – Да, можно по графику определить, кто из них бежал быстрее. – За 60 секунд пробежал 300 м Волк. – За 20 секунд пробежал 300 м Заяц. – 100 метров пробежал за первые 10 секунд Волк; 150 метров пробежал за первые 10 секунд Заяц |
|||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 78–79). Задание 4. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните вычисления устно. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают фронтально. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||
|
Задание 5. |
– Сравните длины. |
9 км 303 м < 9 км 330 м 280004 см > 280 м 405 м 85 см > 485 см 36 см 5 мм < 400 мм |
|||||
|
Задание 6. |
– Выполните действия. Какие математические законы вы использовали? |
875 : 35 · 5 = 125 18 · 7 + 124 · 6 = 870 3 · (991 – 661) : 45 = 22 180 : 36 + 58 · (30 – 17) = 759 28750 + 1250 = 30000 888 + 999 = 1887 |
|||||
|
Задание 7. |
– Сформулируйте алгоритм сложения и вычитания многозначных чисел в столбик. Выполните вычисления. |
37024 + 22465 = 59489 78879 – 45307 = 33572 44307 + 55572 = 99879 58956 – 20343 = 38618 |
|||||
|
Задание 8. |
– Найдите значения выражений. Если вы все решили верно, то сумма значений всех выражений должна быть равна числу 422. |
72 : 24 + 38 = 41 41 · 4 + 81 : 27 = 75 360 – 120 · (192 – 189) = 0 108 – 31 · 2 = 46 100 + 25 · 4 = 200 15 · 12 : 3 = 60 Проверка: 41 + 0 + 200 + 75 + 46 + 60 = 422 (Все решено верно.) |
|||||
|
Задание 9. |
– Вычислите значение буквенного выражения. |
Запись: 2 · у – х а) если х = 580, у = 450, то 2 · 450 – 580 = 320; б) если х = 91, у = 168, то 2 · 91 – 168 = 14. |
|||||
|
Задание 10 |
– Вычислите значение буквенного выражения |
Запись: b – 256 : 4 а) если b = 1000, то 1000 – 256 : 4 = 936; б) если b = 2563, то 2563 – 256 : 4 = 2499 |
|||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как в математике можно передавать информацию? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 28. Построение простейших графиков, таблиц
(практическая работа)
|
Тип урока: комбинированный |
||
|
Педагогические задачи: продолжать знакомить с понятиями «график», «диаграмма», «таблица», с их значением для передачи информации; способствовать формированию умений строить простейшие графики и диаграммы |
||
|
Планируемые результаты |
||
|
Предметные: научатся читать и выполнять построение простейших диаграмм и графиков |
Метапредметные: Познавательные: ориентируются на возможное разнообразие способов решения учебной задачи; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи, строят логическую цепь рассуждений. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: имеют желание учиться; владеют основными моральными нормами поведения |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Перед вами чертеж:
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
|
– На чертеже найдите 3 четырехугольника.
– Сколько треугольников на чертеже? – Решите головоломку. а) Рассмотрите рисунок: из 13 палочек сложили 4 квадрата. Как убрать 1 палочку, чтобы осталось 3 квадрата?
|
– На чертеже 3 четырехугольника: DKCE, DBCE, KCAD. – 7 треугольников на чертеже. Ответы: а)
|
||
|
|
б) Как убрать 2 палочки, чтобы осталось 4 одинаковых квадрата?
в) Уберите 3 палочки так, чтобы осталось 3 квадрата.
|
б)
в)
|
||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 76). Задание 3 |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Рассмотрите диаграмму. Что обозначают зеленые столбики на диаграмме? – Что обозначают красные столбики? – В каком классе больше учеников увлекаются театром? – В каком классе больше учеников увлекаются спортом? чтением? танцами?
– В каком классе нет ни одного ученика, который увлекался бы рисованием? – Сколько учеников увлекаются музыкой в каждом классе? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. – Зеленые столбики на диаграмме обозначают число учеников 4 «А» класса. – Красные столбики обозначают число учеников 4 «Б» класса. – В 4 «Б» классе больше учеников увлекаются театром. – В 4 «А» классе больше учеников увлекаются спортом. Чтением – также в 4 «А». А танцами – в 4 «Б». – В 4 «Б» классе нет ни одного ученика, который увлекался бы рисованием. – В 4 «А» – 5 чел., в 4 «Б» – тоже 5 чел. увлекаются музыкой |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей |
|
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 79). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: Было – 75 м Продали – ?, пятую часть Осталось – ? м |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
|
|
|
|
Решение: 1) 75 : 5 = 15 (м) – продали. 2) 75 – 15 = 60 (м) – осталось. |
||
|
Задание 12. |
– Какова цена плаща? Запишите выражение. Найдите его значение при а, равном 120. |
Запись: а · 5. Если а = 120, то 120 · 5 = 600 (р.). |
||
|
Задание 13. |
– Сколько орехов мальчик принес из леса? |
Решение: 1) 4 · 2 = 8 (ор.) – отдал сестре. 2) 8 · 2 = 16 (ор.) – принес из леса. |
||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: 69 л молока – 3 кг масла 92 л молока – ? кг масла Решение: 1) 69 : 3 = 23 (л) – на 1 кг масла. 2) 92 : 23 = 4 (кг) – масла можно получить. |
||
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: Было – 330 ящ. Увезли – ? ящ. поровну на 12 маш. Осталось – 126 ящ. На каждой маш. – ? ящ. Решение: 1) 330 – 126 = 204 (ящ.) – увезли. 2) 204 : 12 = 17 (ящ.) – на каждой машине. |
||
|
Задание 17 |
– Выполните чертеж |
|
||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как в математике можно передавать знания? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, анализировать причины неудачи |
Урок 29. Переместительное свойство сложения
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с переместительным свойством сложения; способствовать формированию умений выполнять сложение, используя свойства арифметических действий и правила вычисления с нулем |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названием и формулировкой переместительного свойства сложения; научатся записывать переместительное свойство сложения с помощью букв |
Метапредметные: Познавательные: моделируют содержащиеся в задаче зависимости; планируют ход решения задачи. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности учащегося |
|||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Метр шелка в 2 раза дороже метра сатина. Что дороже: 8 м сатина или 4 м шелка? |
Отвечают на вопросы учителя. Выполняют задания устного счета.
– Стоимость одинакова. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||||||
|
– В каких случаях достаточно переставить цифры, чтобы получились верные равенства? 36 – 82 = 8 58 + 63 = 94 28 + 18 = 100 71 – 37 = 43 |
Ответ: в трех первых выражениях: 36 – 28 = 8 58 + 36 = 94 82 + 18 = 100 |
|||||||||||||
|
– Перед вами четырехугольник и пятиугольник. Какие получатся новые фигуры, если стороны АВ и CD продолжить так, чтобы они пересеклись?
|
– Треугольник, четырехугольник |
|||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 80–81). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Почему Заяц, не выполняя вычислений, сразу показал сумму? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– От перестановки слагаемых значение суммы не меняется. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль действий по результату |
|||||||||||
|
– Выполните вычисления. |
|
|||||||||||||
|
Задание 2 |
– Выполните сложение и сравните результаты. Сделайте вывод |
80008 + 27681 = 107689 27681 + 80008 = 107689 302998 + 563 = 303561 563 + 302998 = 303561 651295 + 246116 = 897411 246116 + 651295 = 897411 – От перестановки слагаемых значение суммы не меняется. Это свойство называют переместительным свойством сложения |
||||||||||||
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 82–86). Задание 10. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– На рис. 1, 2 назовите пары чисел, соответствующие каждой из вершин четырехугольника. Как называется на каждом из рисунков четырехугольник АВСD? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Рис. 1. А (2; 3), В (2; 7), С (6; 7), D (6; 3). Квадрат. Рис. 2. А. (2; 2), В (6; 2), С (6; 8), D (2; 8). Прямоугольник. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||
|
Задание 11. |
– Как называется первый многоугольник? – Назовите его вершины. – Назовите его стороны. – Как называется второй многоугольник? – Назовите его вершины. – Назовите его стороны. – Как называется третий многоугольник? – Назовите его вершины. – Назовите его стороны. |
– Первый многоугольник – четырехугольник. – Его вершины: А, В, С, М. – Его стороны: АВ, ВС, СМ, МА. – Второй многоугольник – пятиугольник. – Его вершины: В, D, Е, К, О. – Его стороны: ВD, DЕ, ЕК, КО, ОВ. – Третий многоугольник – треугольник. – Его вершины: D, К, Р. – Его стороны: DК, КР, РD. |
||||||||||||
|
Задание 12. |
– Не выполняя вычисления, определите, сколько цифр в частном 375 : 5. |
– Две цифры в частном, так как первое неполное делимое – 37. |
||||||||||||
|
Задание 13. |
– Какое число надо прибавить к данным числам, чтобы получилось 10 000? |
10 000 – 3000 = 7000 10 000 – 9000 = 1000 10 000 – 2500 = 7500 10 000 – 9997 = 3 10 000 – 8800 = 1200 10 000 – 5000 = 5000 |
||||||||||||
|
Задание 14. |
– Четырехзначное число увеличили на 10 и получили пятизначное число. Назовите четырехзначное число. |
9990 + 10 = 10000 9995 + 10 = 10005 9991 + 10 = 10001 9996 + 10 = 10006 9992 + 10 = 10002 9997 + 10 = 10007 9993 + 10 = 10003 9998 + 10 = 10008 9994 + 10 = 10004 9999 + 10 = 10009 |
||||||||||||
|
Задание 15. |
– Какое время показывают часы? – Какое время они показывали полтора часа назад? Какое время покажут часы через четверть часа? |
– 11 ч 45 мин. показывают часы. – 10 ч 15 мин. часы показывали полтора часа назад. – 12 часов покажут часы через четверть часа. |
||||||||||||
|
Задание 16. |
– В каком году было построено каждое здание? |
Запись: МСМLIX = 1959, MCDVI = 1406. |
||||||||||||
|
Задание 17. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 70 · 5 = 350 (км) – по асфальту. 2) 40 · 3 = 120 (км) – по грунту. 3) 350 + 120 = 470 (км) – всего. |
||||||||||||
|
Задание 18. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: 2 ч – 18 км 3 ч – ? км Решение: 1) 18 : 2 = 9 (км/ч) – скорость. 2) 9 · 3 = 27 (км) – за 3 часа. |
||||||||||||
|
Задание 19. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: s = 120 км u = 48 км/ч s через 2 ч – ? км Осталось – ? км Решение: 1) 48 · 2 = 96 (км) – проехал за 2 часа. 2) 120 – 96 = 24 (км) – осталось. |
||||||||||||
|
Задание 20 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Запись: Было 28 см Прополз – ? (четвертую часть) Осталось – ? см Решение: 1) 28 : 4 = 7 (см) – прополз. 2) 28 – 7 = 21 (см) – осталось |
||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Сформулируйте переместительный закон сложения. – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
Урок 30. Переместительное свойство умножения.
Текущая проверочная работа по теме «Координатный угол»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с переместительным свойством умножения; способствовать формированию умения выполнять умножение, используя свойства арифметических действий и правила вычисления с нулем |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями и формулировкой переместительных свойств сложения и умножения; научатся выполнять запись этих свойств с помощью букв |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве |
Личностные: проявляют интерес к учебному материалу; владеют основными моральными нормами поведения; осознают роль языка в межличностном взаимодействии |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. Математический диктант. а) Запишите число, в котором 3 сотни и 2 десятка. Уменьшите его на 100. б) Сколько часов в трех сутках? в) Во сколько раз 14 меньше, чем 84? г) Запишите выражение и вычислите его значение: число 320 увеличить на произведение чисел 120 и 3. д) Запишите и вычислите разность чисел 72 и 4; частное тех же чисел. На сколько разность чисел больше, чем частное? е) Какое число надо увеличить в 7 раз, чтобы получилось 56? ж) На сколько надо увеличить 16, чтобы получить 96? з) Запишите все числа от 374 до 407, у которых в разряде единиц стоит цифра 6. и) Какое число надо взять слагаемым два раза, чтобы получить 260? к*) Найдите сумму, разность, частное и произведение наибольшего трехзначного числа и числа 1. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) 320; 220.
б) 72 ч. в) В 6 раз. г) 680.
д) 68; 18; на 50.
е) 8.
ж) 6.
з) 376; 386; 396; 406.
и) 130.
к*) 1000; 998; 999; 999. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Вставьте пропущенные числа: 5 м2 =
4 дм2 =
8 м2 = |
5 м2 = 500 дм2 36 м = 360 дм 1000 см2 = 10 дм2 940 см = 94 дм 4 дм2 = 400 см2 300 дм2 = 3 м2 7 дм = 70 м 19 дм2 = 1900 см2 8 м2 = 800 дм2 2500 дм2 = 25 м2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 81–82). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Обладает ли умножение переместительным свойством? Приведите примеры. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Да, обладает. Пример: 5 · 2 = 10, 2 · 5 = 10. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Осуществлять контроль действий по результату |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4. |
– Используя буквы а и b, попробуйте записать переместительное свойство умножения в обобщенном виде. |
Запись: а · b = b · а |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 5. |
– Выполните вычисления. ‒ Сделайте вывод. |
5 · 120 = 120 · 5 12 · х = х · 12 60 · 7 = 7 · 60 р · 8 = 8 · р – От перестановки множителей значение произведения не изменяется. Это свойство называют переместительным свойством умножения. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 6. |
– Сравните значения выражений, не выполняя вычислений. |
269 + 1050 = 1050 + 269 124 · 5 > 5 · 94 460 + 580 > 380 + 460 13 · 16 = 16 · 13 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 7. |
– Используя равенство 936 + 1504 = 2440, выполните вычисления. |
367 + (1504 + 936) = 367 + 2440 = 2807 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 8. |
– Используя равенство 13 · 15 = 195, выполните вычисления. |
4 · (15 · 13) = 4 · 195 = 780 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 9 |
– Верны ли равенства? – Какие законы вы применяли? |
– Равенства верны. – Переместительный закон сложения, переместительный закон умножения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 86–87). |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Сколько раз спортсмен попал в цель? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: Всего – 20 в. Промахи – ? (четвертая часть) В цель – ? в. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 21. |
|
Решение: 1) 20 : 4 = 5 (в.) – промахи. 2) 20 – 5 = 15 (в.) – в цель. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 22. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 360 : 30 = 12 (дн.) – по плану. 2) 360 : 40 = 9 (дн.) – по факту. 3) 12 – 9 = 3 (дн.) – меньше. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 23. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: Привезли – 12 ящ. по ? кг Продали – 69 кг Осталось – 27 кг Решение: 1) 69 + 27 = 96 (кг) – привезли. 2) 96 : 12 = 8 (кг) – в 1 ящике. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 24. |
– В коробке лежат 10 красных и 15 желтых бусин. Из нее наугад взяли 12 бусин. Обязательно ли среди взятых бусин окажется хотя бы одна бусина красного цвета? желтого цвета? |
– Красных бусин может и не быть, а желтая будет обязательно. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 25. |
– У Кати, Тани и Ани билеты в кинотеатр на места под номерами 24, 25 и 26. Кто на каком месте может сидеть? Рассмотрите все варианты. |
Рассматривают варианты:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 26. |
– Какие числа написаны на перевернутых карточках? |
а) (4009 – 3086 = 923.) (13092 – 891 = 12201.) в) (12112 + 6203 = 18315.) (82053 + 947 = 83000.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 27. |
– Ответьте на вопросы. • Во сколько раз а больше b, если а = 60, b = 30?
• Во сколько раз х меньше у, если у = 280, х = 10? |
– В 2 раза а больше b, если а = 60, b = 30, так как 60 : 30 = 2 (раза). – В 28 раз х меньше у, если у = 280, х = 10, так как 280 : 10 = 28 (раз). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 28. |
– Какая последовательность цифр соответствует записи числа пятьсот четыре тысячи сто шестнадцать? |
Запись: 504116 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 29. |
– В записи какого числа нет трех одинаковых цифр? – В записях каких чисел есть все три цифры: 4, 1 и 9? |
– В записи числа 30805 нет трех одинаковых цифр. – В записях чисел 84091, 91754 есть все три цифры: 4, 1 и 9. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Самостоятельная работа |
– Определите координаты точек на рисунке (см. ресурсный материал к уроку) |
Выполняют самостоятельную работу |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Сформулируйте переместительный закон умножения. – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Ресурсный материал к уроку
Самостоятельная работа
|
|
Ответ: А1 (3; 1); А2 (4; 2); А3 (4; 4); А4 (2; 7); А5 (3; 8); А6 (2; 9); А7 (2; 12); А8 (3; 11); А9 (4;11); А10 (5; 12); А11 (5; 9); А12 (7; 5); А13 (7; 1); А14 (9; 3); А15 (13; 3); А16 (11;1) |
Урок 31. Контрольная работа № 2 по темам «Задачи на движение»,
«Переместительное свойство сложения и умножения»
|
Тип урока: контроль и оценка знаний и сформированности способов действий |
||
|
Педагогические задачи: проверить усвоение знаний и умений по теме «Переместительное свойство сложения и умножения», умение решать задачи на движение |
||
|
Планируемые результаты |
||
|
Предметные: научатся использовать переместительный закон сложения и умножения, решать задачи на движение |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель (пространственно-графическую или знаково-символическую), где выделены существенные характеристики объекта, и преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: в совместной деятельности определяют цели и функции участников, способы взаимодействия |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Проведение контрольной работы |
Знакомит с содержанием контрольной работы, комментирует задания.
Вариант I 1. Запиши цифрами числа: шесть тысяч; тридцать восемь тысяч сто двадцать пять; один миллион сто десять тысяч триста. 2. Реши задачу. Поезд шел 2 ч со скоростью 75 км/ч и 3 ч со скоростью 80 км/ч. Какой путь прошел поезд за все время движения? 3. Выполни действия: 6 274 + 1 957 18 367 – 2 458 4. Начерти координатный угол, отметь точки с координатами: А (7; 7), В (0; 6), С (2; 5). Соедини эти точки. Какая фигура получилась?
|
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы. Вариант I 1. 6000; 38125; 1 110 300.
2. 75 · 2 + 80 · 3 = 390 (км) ‒ прошел поезд.
3. 8231; 15909. 4.
АВС – треугольник. |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу по-лученного зада-ния. Анализировать, находить общее и различия, делать выводы. Осознанно и произвольно строить речевые высказывания в устной форме |
|
5. Выпиши выражение, с помощью которого можно вычислить периметр прямоугольника: а + b 2 ∙ а + b (а + b) ∙ 2 а ∙ b 6*. Площадь квадрата равна 36 см2. Чему равна длина стороны? Вариант II 1. Запиши цифрами числа: восемь тысяч; пятьдесят две тысячи двести сорок три; два миллиона двести двадцать тысяч четыреста. 2. Реши задачу. За 3 ч поезд прошел 210 км, а затем с той же скоростью шел ещё 5 ч. Какой путь прошел поезд за все время движения? 3. Выполни действия: 5107 + 3 954 70 452 – 1 274 4. Начерти координатный угол, отметь точки с координатами: D (9; 2), Е (4; 0), Х (5; 5). Соедини эти точки. Какая фигура получилась?
5. Выпиши выражение, с помощью которого можно вычислить площадь квадрата: у ∙ 4 у + 4 у ∙ 2 у ∙ у 6*. Площадь квадрата равна 100 дм2. Чему равна длина стороны? |
5. (а + b) ∙ 2
6*. 6 · 6 = 36 (см2). Длина стороны – 6 см.
Вариант II 1. 8000; 52243; 2 220 400.
2. 210 + (210 : 3 · 5) = 460 (км) ‒ все расстояние.
3. 9061; 69178. 4.
ЕХD – треугольник. 5. у ∙ у
6*. 10 · 10 = 100 (дм2). Длина стороны – 10 см |
||
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 32. Сочетательное свойство сложения
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с сочетательным свойством сложения; способствовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названием и формулировкой сочетательного свойства сложения; научатся использовать сочетательное свойство сложения при выполнении вычислений |
Метапредметные: Познавательные: определяют основную и второстепенную информацию; выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Урок 33. Сочетательное свойство умножения
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с сочетательным свойством умножения; способствовать развитию умений решать задачи, выполнять сложение и умножение, используя свойства арифметических действий и правила вычисления с нулем |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями и формулировками сочетательных свойств сложения и умножения; научатся использовать сочетательное свойство сложения и умножения при выполнении вычислений |
Метапредметные: Познавательные: овладевают логическими действиями сравнения, анализа, синтеза, обобщения, классификации, установления аналогий и причинно-следственных связей. Регулятивные: принимают и сохраняют учебную задачу; адекватно воспринимают оценку учителя и товарищей; планируют свое действие. Коммуникативные: осуществляют коммуникативно-речевые действия, конструктивные способы взаимодействия с окружающими (учителем, сверстниками) |
Личностные: проявляют этические чувства, доброжелательность и эмоционально-нравственную отзывчивость, понимание и сопереживание чувствам других людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний. – Разгадайте правило и продолжите ряд чисел: а) 2, 4, 8, 16, 3, 9, 18, 36, 4, 8, 16, 32, 5, 10, 20, 40, ... б) 17, 170, 1700, 19, 190, 1900, 21, 210, 2100, ... |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) 2, 4, 8, 16, 3, 6, 12, 24, 4, 8, 16, 32, 5, 10, 20, 40, 6, 12, 24, 48; б) 17, 170, 1700, 19, 190, 1900, 21, 210, 2100, 23, 230, 2300. |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу |
|||||||||||||||||||||||||||||||
|
Интеллектуальная разминка |
– Работа по таблице:
– Назовите значение суммы чисел в каждом столбце. – Найдите сумму чисел в каждой строке. – Сложите числа в самой нижней строке. – Сложите числа в правом столбце. – Почему получили одинаковые результаты? |
Результаты записывают в свободных клетках нижней строки и в правом столбце:
Отвечают на вопросы.
– Потому что сложение обладает сочетательным свойством. |
||||||||||||||||||||||||||||||||
|
|
– Поставьте знак >, < или =. Объясните свой выбор.
|
|
||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 89–91). Задание 6. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Обладает ли умножение сочетательным свойством? – Сформулируйте это свойство и приведите примеры. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
(14 · 5) · 2 = 70 · 2 = 140 14 · (5 · 2) = 14 · 10 = 140 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
|||||||||||||||||||||||||||||||
|
Задание 7. |
– Используя буквы a, b, c, запишите сочетательное свойство умножения в обобщенном виде. Сравните свою запись с записью в учебнике. |
Запись: (а · b) · с = а · (b · с) |
||||||||||||||||||||||||||||||||
|
Задание 8. |
– Используя сочетательное свойство умножения, запишите выражения, равные данным. |
(12·4) · 5 = 12 · (4 · 5) (8 · х) · 3 = х · (8 · 3) 25 · (8 · 3) = (25 · 8) · 3 (100 · 7) · m = 100 · (7 · m) |
||||||||||||||||||||||||||||||||
|
Задание 9. |
– Не переставляя множители, вычислите значения 8 · 7 · 10 двумя способами.
– Как можно произведение двух чисел умножить на третье число? |
Запись: I способ: 8 · 7 · 10 = 57 · 10 = 560 II способ: 8 · 7 · 10 = 8 · 70 = 560 – Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. Это свойство называют сочетательным свойством умножения. |
||||||||||||||||||||||||||||||||
|
Задание 10. |
– Группируя множители удобным способом, вычислите произведения. |
9 · (15 · 2) = 9 · 30 = 270 (50 · 4) · 3 = 200 · 3 = 600 |
||||||||||||||||||||||||||||||||
|
Задание 11. |
– Сравните значения выражений, не выполняя вычислений. |
(248 + 622) + 1927 = 248 + (622 + 1927) (10 · 8) · 7 > 10 · (8 · 5) (700 + 300) + 50 > 700 + (290 + 50) (20 · 3) · 9 = 20 · (3 · 9) |
||||||||||||||||||||||||||||||||
|
Задание 12. |
– Вычислите значение выражения, используя равенство 518 + 409 = 927. |
(320 + 518) + 409 = 320 + (518 + 409) = = 320 + 927 = 1247 |
||||||||||||||||||||||||||||||||
|
Задание 13. |
– Выполните действия, используя сочетательное свойство сложения. |
(77 + 19) + 51 = 77 + (19 + 51) = 77 + 70 = 147 (623 + 1200) + 800 = 623 + (1200 + 800) = = 623 + 2000 = 2623 18 + (32 + 7) = (18 + 32) + 7 = 50 + 7 = 57 327 + (33 + 589) = (327 + 33) + 589 = = 360 + 589 = 949 |
||||||||||||||||||||||||||||||||
|
Задание 14. |
– Выполните действия, используя сочетательное свойство умножения. |
(4 · 5) · 2 = 4 · (5 · 2) = 4 · 10 = 40 (10 · 10) · 7 = 10 · (10 · 7) = 10 · 70 = 700 (14 · 12) · 5 = 14 · (12 · 5) = 14 · 60 = 840 (8 · 4) · 25 = 8 · (4 · 25) = 8 · 100 = 800 |
||||||||||||||||||||||||||||||||
|
Задание 15. |
– Найдите значение выражения, используя равенство 9 · 5 = 45. |
(11 · 9) · 5 = 11 · (9 · 5) = 11 · 45 = 495 |
||||||||||||||||||||||||||||||||
|
Задание 16 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу двумя способами. |
Запись: 5 ящ. – по 8 короб. В 1 коробке – 16 п. Пачек – ? шт. Решение: I способ 1) 5 · 8 = 40 (шт.) – коробок. 2) 40 · 16 = 640 (шт.) – всего пачек. II способ 1) 16 · 8 = 128 (шт.) – пачек в 1 ящике. 2) 128 · 5 = 640 (шт.) – пачек в 5 ящиках |
||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 92). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Имеет ли она решение? Что нужно изменить в тексте задачи, чтобы она имела решение? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Данная задача решения не имеет. Нужно слово «меньше» заменить на слово «больше», чтобы задача имела решение.
Решение: 1) 120 : 3 = 40 (гр.) – Коля. 2) 120 + 40 = 160 (гр.) – всего. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала |
|||||||||||||||||||||||||||||||
|
Задание 22. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 35 · 2 = 70 (км) – пройдет легковая машина. 2) 35 · 1 = 35 (км)– пройдет грузовая машина. |
||||||||||||||||||||||||||||||||
|
Задание 23 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Решение: 1) 4 · 5 = 20 (км) – пешком. 2) 189 – 20 = 169 (км) – на автобусе |
||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Сформулируйте сочетательный закон умножения. – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Работают с сигнальными карточками. Зеленая карточка. Я удовлетворен уроком. Урок был полезен для меня. Я с пользой и хорошо работал на уроке. Я понимал все, о чем говорилось и что делалось на уроке. Желтая карточка. Урок был интересен. Я принимал в нем участие. Урок был в определенной степени полезен для меня. Я отвечал с места, выполнил ряд заданий. Мне было на уроке достаточно комфортно. Красная карточка. Я не очень понимал, о чем идет речь. К ответу на уроке я был не готов |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
|||||||||||||||||||||||||||||||
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Запишите цифрами. 56 дес. 2 ед. 9 тыс. 33 сот. 18 сот. 3 ед. 200 дес. 3 тыс. 3 ед. 276 дес. 8 тыс. 8 ед. 399 дес. |
Отвечают на вопросы учителя. Выполняют задания устного счета. Запись: 562 9000 3300 1803 2000 3003 2760 8008 3990 |
Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||
|
|
– Запишите верные равенства, вставив пропущенные множители. 60 ·
30 · 40 · |
60 · 2 + 50 = 230 70 · 9 – 60 = 570 80 · 4 + 80 =360 70 · 8 + 90 = 650 30 · 2 – 90 = 150 90 · 9 – 40 = 770 40 · 8 + 90 = 410 50 · 7 + 80 = 430 |
||||||||||||||||||||||||
|
|
– Поставьте знак >, < или =, чтобы равенства были верными: 17 сот. 4дес. 1ед ... 171 21 дес. 4 ед. ... 214 1 тыс. 12 дес. ... 112 6280 ... 62 сот. 8 ед. 5030 … 503 дес. 10 сот. 10 дес. 1 ед. …1001 |
17 сот. 4дес. 1ед > 171 21 дес. 4 ед. = 214 1 тыс. 12 дес. > 112 6280 > 62 сот. 8 ед. 5030 = 503 дес. 10 сот. 10 дес. 1 ед. > 1001 |
||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 88–89). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Одинаковые ли результаты получат Волк и Заяц, когда выполнят вычисления? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
(400 + 80) + 20 = 480 + 20 = 500 400 + (80 + 20) = 400 + 100 = 500. Да, одинаковые. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|||||||||||||||||||||||
|
Задание 2. |
‒ Как можно к сумме двух чисел прибавить третье число? Сделайте вывод – сформулируйте сочетательное свойство сложения. |
– Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел. Это свойство называют сочетательным свойством сложения. |
||||||||||||||||||||||||
|
Задание 3. |
– Используя сочетательное свойство сложения, запишите выражение, равное данному. |
(265 + 405) + 2603 = 265 + (405 + 2603) 472 + (38 + 691) = (472 + 38) + 691 (12 + х) + 96 = х + (12 + 96) (54 + 158) + а = 54 + (158 + а) |
||||||||||||||||||||||||
|
Задание 4. |
– Не переставляя слагаемые, вычислите значение выражения двумя способами. |
Запись: I способ: 189 + 11 + 9 = 189 + (11 + 9) = = 189 + 20 = 209 II способ: 189 + 11 + 9 = (189 + 11) + 9 = = 200 + 9 =209 |
||||||||||||||||||||||||
|
Задание 5 |
– Группируя слагаемые удобным способом, вычислите сумму |
Запись: 3608 + 402 + 9054 + 46 = (3608 + 402) + (9054 + + 46) = 4100 + 9100 = 13200 2000 + 315 + 685 = 2000 + (315 + 685) = 2000 + + 1000 = 4000 |
||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 91–92). Задание 17. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните вычисления и сделайте проверку двумя способами: вычитанием и перестановкой чисел.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок |
|||||||||||||||||||||||
|
Задание 18. |
– Заполните таблицу.
|
Заполняют таблицу:
|
||||||||||||||||||||||||
|
Задание 19. |
– Выполните вычисления и сделайте проверку двумя способами: перестановкой чисел и делением. |
1) 15 · 18 = 270 2) 4 · 204 = 816 18 · 15 = 270 204 · 4 = 816 270 : 15 = 18 816 : 4 = 204 |
||||||||||||||||||||||||
|
Задание 20 |
– На каком берегу оказался Петя? На каком берегу оказался Вася? |
– На правом берегу оказался Петя. На левом берегу оказался Вася |
||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Сформулируйте сочетательное свойство сложения. – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать результаты деятельности, уровень владения учебным действием |
Урок 34. План и масштаб
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «план», «масштаб»; способствовать формированию умений записывать и читать масштаб, выполнять построение отрезка в заданном масштабе |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «план», «масштаб», с видами масштаба 1 : 10, 10 : 1; научатся определять на плане масштаб, выполнять построение отрезка в заданном масштабе |
Метапредметные: Познавательные: осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке; адекватно оценивают результаты своей деятельности. Коммуникативные: слушают и понимают речь других, признают возможность существования различных точек зрения и право каждого иметь свою; высказывают свое мнение и аргументируют свою точку зрения, дают свою оценку событий |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Какую цифру можно поставить вместо квадратиков, чтобы получить верное неравенство? Прочитайте полученные неравенства. 203 > 20 32540 < 3 11111 < 1111 |
Отвечают на вопросы учителя . Выполняют задания устного счета.
203 > 202 372 > 363 146 > 137 32540 < 33540 1725 < 1735 11111 < 11112 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Какова масса тыквы, если ее уравновешивают такие гири: а) 2 кг, 2 кг, 1 кг, 500 г. б) 2 кг, 1 кг, 500 г, 250 г. |
а) 5 кг 500 г. б) 3 кг 750 г. |
|
|
|
– Какие знаки действий можно поставить вместо звездочек и какие цифры вместо квадратиков так, чтобы получились верные равенства? 39 ¶ 16 = 5 9 ¶ 4 : 4 ¶ |
39 + 16 = 55 56 – 18 = 38 9 · 4 : 6 = 6 (63 + 27) : 9 = 10 4 · 15 – 60 = 0 75 : 5 + 85 = 100 |
|
|
|
– Выразите высоту, на которую могут подниматься птицы и насекомые, в километрах и метрах. Орлы поднимаются на высоту 7000 м. Журавли поднимаются на высоту 5000 м. Бабочки и пчелы – на высоту 6600 м. Дикие гуси – на высоту 9500 м |
7000 м = 7 км 5000 м = 5 км 6600 м = 6 км 600 м 9500 м = 9 км 500 м |
|
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 93–95). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – На прямоугольной грядке Маша решила посеять морковь и редис. На каждый квадратный метр грядки расходуется один пакетик семян. Сколько пакетиков семян каждой овощной культуры нужно Маше? Рассмотрите рисунок и выполните необходимые расчёты. – На листе бумаги Маша начертила план своей грядки. Во сколько раз все размеры на плане меньше соответствующих размеров грядки? – Отрезок на местности, равный ширине грядки (1 м), Маша изобразила на плане отрезком длиной 1 см, то есть уменьшила его в 100 раз (1 м = 100 см). Так же в 100 раз она уменьшила и остальные размеры грядки. На практике часто приходится изображать план квартиры, земельного участка, улицы. В этих случаях на плане все действительные размеры уменьшают в одно и то же число раз. Таким образом, Маша выполнила план грядки в масштабе один к ста. Записывают это так: Масштаб 1 : 100. Эта запись означает, что одному сантиметру на плане соответствует 100 см на местности, то есть первое число масштаба всегда относится к длине на плане, второе – к реальному размеру. Задание. Начертите в тетради план грядки, как у Маши. Проставьте на нем размеры в метрах и укажите масштаб плана. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Запись: 2 · 1 = 2 (кв. м); 3 · 1 = 3 (кв. м) – Необходимо 2 пакетика семян моркови и 3 пакетика семян редиса.
– В 100 раз меньше размеры на плане, чем на грядке.
Выполняют задание. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|
Задание 2. |
– Объясните, что означает следующий масштаб: а) 1 : 10 в) 1 : 1 000 б) 1 : 5 г) 1 : 2 000 000 |
– Масштаб 1 : 10 означает, что в 1 см содержится 10 см, или 1 дм. – Масштаб 1 : 5 означает, что в 1 см содержится 5 см. – Масштаб 1 : 1000 означает, что в 1 см содержится 1000 см, или 10 м. – Масштаб 1 : 2 000 000 означает, что в 1 см содержится 2 000 000 см, или 20 км. |
|
|
Задание 3. |
– Запишите масштаб плана, если 1 см на плане соответствует в действительности: 10 000 см; 50 см; 10 м; 1 км. |
Запись: Масштаб 1 : 10000 Масштаб 1 : 1000 Масштаб 1 : 50 Масштаб 1 : 100000 |
|
|
Задание 4. |
– Измерьте длину ключа, изображенного на рисунке. Какую длину имеет ключ, если рисунок выполнен в масштабе 1 : 2? – Начертите отрезок, длина которого соответствует действительной длине ключа. |
– Длина ключа на рисунке 4 см. Значит, если М 1 : 2, то ключ имеет длину 8 см.
Выполняют задание. |
|
|
Задание 5. |
– Чему равна длина каждой стороны клумбы в действительности? |
‒ Длина стороны клумбы равна 400 см, или 4 м. |
|
|
Задание 6 |
– Определите масштаб плана детской площадки, выполнив необходимые измерения и вычисления |
– На плане длина детской площадки равна 4 см. В действительности длина – 20 м. 20 м = 2000 см 2000 : 4 = 500 (раз) – уменьшение. Ответ: масштаб 1 : 500 |
|
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 97–98). Задание 13. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Соотнесите величину скорости и движущийся объект. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
6 км/ч – скорость пешехода. 13 км/ч, 24 км/ч – скорости велосипедиста. 70 км/ч – скорость поезда. 850 км/ч – скорость самолета. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок |
|
Задание 14. |
– Сколько стоит покупка?
– Какими купюрами без сдачи Петя может расплатиться? |
Запись: 15 + 85 + 25 = 125 (р.) – стоит покупка. – Петя может расплатиться следующими купюрами: 100 р. + 10 р. + 10 р. + 5 р. = 125 р. |
|
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: АВ = АС = 28 мм Р = 72 см ВС – ? см Решение: 72 – 28 – 28 = 16 (см) – сторона ВС. |
|
|
Задание 16. |
– Какая фигура нарушает признак, по которому отобраны остальные фигуры? |
– Четвертая фигура «лишняя». |
|
|
Задание 17 |
– Вычислите неизвестное число |
а) 50505 – 4949 = 45556 б) 128 · 6 = 768 |
|
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как определить расстояние на плане? – Что такое масштаб? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 35. План и масштаб. Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «план», «масштаб»; способствовать формированию умений записывать и читать масштаб |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «план», «масштаб», с различными видами масштаба; научатся определять на плане масштаб, выполнять построение отрезка в заданном масштабе |
Метапредметные: Познавательные: определяют наиболее эффективный способ достижения результата. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: излагают свое мнение и аргументируют свою точку зрения |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Рассмотрите таблицу и выполните задания. На доске:
а) Каждое число первого столбца увеличьте в 2 раза. б) Найдите сумму всех чисел второго столбца. в) Из каждого числа первого столбца вычтите первое число второго столбца. г) Каждое число второго столбца увеличьте в 4 раза. д) Каждое число третьего столбца уменьшите на 9 единиц. е) Каждое число четвертого столбца уменьшите в 100 раз, а затем увеличьте на 6. ж) Найдите сумму всех чисел четвертого столбца. з) Каждое число пятого столбца дополните до тысячи. и) Каждое число первой строки уменьшите на 2 десятка. к) Назовите числа второй строки, которые можно разделить на 100. л) Каждое число третьей строки дополните до 2 тысяч. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) 1400, 1600, 100, 1200, 1800.
б) 227. в) 610, 740, 492, 591, 820.
г) 360, 160, 32, 36, 320.
д) 381, 731, 899, 100, 871.
е) 8, 7, 11, 10, 9.
ж) 1500. з) 580, 230, 550, 690, 340.
и) 680, 70, 370, 180, 400.
к) 800, 100.
л) 500, 992, 92, 600, 690. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||||||||||||
|
|
– Выберите из данных величин – 75 г, 5 кг, 25 кг – наиболее подходящую для указания примерной массы одной моркови, одного арбуза, мешка картофеля |
– Масса одной моркови – 75 г, одного арбуза – 5 кг, мешка картофеля – 25 кг |
|||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 95–96). Задание 7. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Измерьте длину гусеницы на рисунке. Чему равна длина этой гусеницы в природе, если ее размеры на рисунке увеличены в 2 раза? – Говорят, что рисунок гусеницы сделан в масштабе 2 : 1. Объясните, что означает этот масштаб. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Длина гусеницы на рисунке 6 см, значит длина гусеницы в жизни – 3 см. Масштаб 2 : 1 означает, что 2 см на плане соответствует 1 см в действительности. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, Применять правила делового сотрудничества. Приводить
убедительные доказательства |
||||||||||||||||||||||||||||||||||||
|
Задание 8. |
– Что означает данный масштаб? |
– Масштаб 10 : 1 означает, что 10 см на плане соответствует 1 см в действительности, то есть все размеры на плане в 10 раз больше, чем в действительности. – Масштаб 3 : 1 означает, что 3 см на плане соответствует 1 см в действительности, то есть все размеры на плане в 3 раза больше, чем в действительности. – Масштаб 5 : 1 означает, что 5 см на плане соответствует 1 см в действительности, то есть все размеры на плане в 5 раз больше, чем в действительности. – Масштаб 4 : 1 означает, что 4 см на плане соответствует 1 см в действительности, то есть все размеры на плане в 4 раза больше, чем в действительности. |
|||||||||||||||||||||||||||||||||||||
|
Задание 9. |
– Запишите масштаб плана, если одному сантиметру на плане соответствует в действительности: а) 5 мм; б) 10 мм. |
Запись: а) Масштаб 2 : 1; б) Масштаб 1 : 1. |
|||||||||||||||||||||||||||||||||||||
|
Задание 10. |
– Измерьте длину радиуса колесика часов, изображенного на рисунке в масштабе 10 : 1. Вычислите настоящую длину радиуса этого колесика. |
– На рисунке радиус колесика – 3 см. Так как масштаб 10 : 1, то в реальности радиус этого колесика в 10 раз меньше, чем на плане, то есть 3 мм. |
|||||||||||||||||||||||||||||||||||||
|
Задание 11. |
– Определите масштаб рисунка, если на нем каждому отрезку длиной 3 см соответствует в действительности отрезок длиной 3 мм. |
Запись: Масштаб 10 : 1. |
|||||||||||||||||||||||||||||||||||||
|
Задание 12 |
– Начертите план в масштабе 1 : 100: а) своей классной комнаты; б) одной из комнат своей квартиры |
Выполняют измерения и чертят план |
|||||||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 98–99). Задание 18. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Решите логическую задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Толя родился 3 сентября, Алеша – 6 мая. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||||||||||||||||||
|
Задание 19. |
– Вычислите значения выражений. |
(43 · 14 – 602 : 301) : 50 = (602 – 2) : 50 = = 600 : 50 = 12 (55 + 45) · 7 : 35 + 35 = 100 · 7 : 35 + 35 = = 700 : 35 + 35 = 20 + 35 = 55 2700 – 700 : 50 = 2700 – 14 = 2686 500 + 500 : 25 = 500 + 20 = 520 |
|||||||||||||||||||||||||||||||||||||
|
Задание 20. |
– Запишите каждое из предложений в виде равенства или неравенства. Определите, верное оно или неверное. |
2768 + 604 > 3000 – верно 203 · 4 = 802 – неверно 30087 – 29672 = 315 – неверно 1260 < 18 · 55 – неверно 965 : 5 = 193 – верно |
|||||||||||||||||||||||||||||||||||||
|
Задание 21. |
– Решите задачу. |
Решение: 1) 60 : 5 = 12 (мин) – рассказ об уходе за черепахами. 2) 60 : 5 · 3 = 36 (мин) – фильм о природе. 3) 60 : 2 = 30 (мин) – рассказ детей. 4) 12 + 36 + 30 = 78 (мин) = 1 ч 18 мин – занятие кружка. |
|||||||||||||||||||||||||||||||||||||
|
Задание 22 |
– Рассмотрите график зависимости массы Юры от его возраста. Какой была масса Юры в 2 года, 5 лет, 7 лет, 9 лет? – На сколько килограммов его масса увеличилась за 3 года (от 2 до 5 лет), за 2 года (от 7 до 9 лет)?
– В каком возрасте масса Юры стала равной 25 кг, 45 кг? – За сколько лет масса Юры увеличилась от 25 кг до 40 кг? |
– В 2 года Юра весил 10 кг, в 5 лет – 15 кг, в 7 лет – 20 кг, в 9 лет – 35 кг. 15 кг – 10 кг = 5 кг – на 5 килограммов его масса увеличилась за 3 года (от 2 до 5 лет). 35 кг – 20 кг = 15 кг – на 15 килограммов его масса увеличилась за 2 года (от 7 до 9 лет). – В 8 лет масса Юры стала равной 25 кг, в 14 лет масса Юры стала равной 45 кг. 10 – 8 = 2 (лет) – за 2 года масса Юры увеличилась от 25 кг до 40 кг |
|||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
Урок 36. Понятие о многогранниках
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для формирования представления о многограннике; способствовать формированию умения определять и называть элементы многогранника – грани, вершины, ребра |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «многогранник» (пространственная фигура), «грани», «вершины», «ребра многогранника»; научатся определять видимые и невидимые элементы многогранника, изображенного на чертеже, выполнять обозначение элементов многогранника буквами латинского алфавита, моделировать различные многогранники |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта; осуществляют классификацию. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Вместо точек подставьте такие числа, чтобы выполнялись следующие условия:
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||
|
|
– Как, не разбирая составленную из конструктора деталь, узнать, сколько всего в ней «бугорков»?
Для каждой фигуры выберите выражение: а) 3 · 6 · 3; б) 4 · 6 · 5. Вычислите значения данных выражений. |
а) 3 · 6 · 3 = 54 б) 4 · 6 · 5 = 120 |
|||||||||||||||||
|
|
– Составьте задачу, используя следующие данные: ласточка может подняться на высоту 3 км, а коршун – на высоту 6 км |
– Ласточка может подняться на высоту 3 км, а коршун – на высоту 6 км. На сколько метров выше может подняться коршун? Решение: 6000 – 3000 = 3000 (м) |
|||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 100–101). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Из скольких и каких многоугольников состоит поверхность каждой фигуры? – Фигура, поверхность которой состоит из многоугольников, называется многогранником. Каждый из этих многоугольников называют гранью многогранника. Стороны многоугольников называют ребрами многогранника, а вершины многоугольников – вершинами многогранника. – Сколько у каждого многогранника вершин, ребер, граней? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Поверхность 1-й фигуры – из 6 прямоугольников; поверхность 2-й фигуры – из 4 треугольников; поверхность 3-й фигуры – из 6 прямоугольников.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
||||||||||||||||
|
Задание 2. |
– Из предметов, предложенных в задании, выберите те, которые по форме похожи на многогранник. Назовите их. |
– Карандаши (незаточенные) и коробки из-под молока, карандашей и печенья по форме похожи на многогранники. |
|||||||||||||||||
|
Задание 3. |
– Назовите вершины многогранника. Назовите ребра. Назовите грани. |
– А, В, С, D, Е, М, К, Р – вершины многогранника. АВ, ВС, СD, DА, ЕК, КР, РМ, МЕ, АЕ, ВМ, СР, DК – ребра. АВСD, ЕМРК, DСРК, АВМЕ, АDКЕ, ВСРМ – грани. |
|||||||||||||||||
|
Задание 4 |
– Рассмотрите модель куба. Ответьте на вопросы: является ли куб многогранником? – Сколько у него ребер? – Сколько граней? Сколько вершин? – Какую форму имеет каждая грань куба? – Сколько ребер выходит из каждой вершины? |
– Куб является многогранником. – У куба 12 ребер. – 6 граней; 8 вершин. – Каждая грань куба имеет форму квадрата. – По три ребра выходит из каждой вершины |
|||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 102–103). Задание 8. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните нижеследующие задания самостоятельно, с взаимопроверкой в парах. – Вычислите устно. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. Проверяют друг друга. Вычисляют. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
||||||||||||||||
|
Задание 9. |
– Не вычисляя, сравните значения выражений. |
230 + 280 < 250 + 280 405 – 25 > 405 – 65 640 – 130 > 600 – 130 125 + 274 = 274 + 125 |
|||||||||||||||||
|
Задание 10. |
– Вычислите значения выражений. |
(327392 – 326528) + 160 · 5 = 864 + 800 = 1664 (204293 – 203321) + 58 : 2 = 972 + 29 = 1001 324 : 2 + 243 : 27 = 162 + 9 = 171 (25 + 125) : 5 · 8 = 240 |
|||||||||||||||||
|
Задание 11. |
– Отцу и сыну вместе 60 лет. Сын моложе отца в 4 раза. Каковы возраст отца и возраст сына? |
Решение: 1) 60 : 5 = 12 (л.) – сыну; 2) 60 – 12 = 48 (л.) – отцу. |
|||||||||||||||||
|
Задание 12. |
– Миша утверждает, что если сумма двух чисел делится без остатка на 5, то и каждое слагаемое также без остатка делится на 5. Докажите, что Миша неправ. Приведите примеры. |
40 : 5 = 8; 24 + 16 = 40, но 24 : 5 = 4 (ост. 4), 16 : 5 = 3 (ост. 1) |
|||||||||||||||||
|
Задание 13. |
– Составьте выражения с данными величинами. |
а) 15 кг 700 г – 8 кг 250 г = 7 кг 450 г 24 см 5 мм – 19 см 9 мм = 4 см 6 мм б) 120 р. 40 к. – 56 р. 56 к. = 63 р. 84 к. в) 124 м 36 см + 45 м 8 см = 169 м 44 см |
|||||||||||||||||
|
Задание 14 |
– Выразите время в минутах.
– Выразите время в секундах.
– Выразите время в сутках |
2 ч 16 мин = 136 мин 10 ч = 600 мин 8 ч 1 мин = 481 мин 9 мин = 540 с 3 мин 58 с = 238 с 6 мин = 360 с 4 мин 1 с = 241 с 72 ч = 3 сут. 192 ч = 8 сут. 144 ч = 6 сут. 120 ч = 5 сут. |
|||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какое тело называют кубом? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 37. Вершины, ребра и грани многогранника.
Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для формирования представления о многограннике; способствовать формированию умения определять и называть элементы многогранника – грани, вершины, ребра; содействовать развитию умения решать арифметические задачи |
||
|
Предметные: познакомятся с понятиями «многогранник» (пространственная фигура), «грани», «вершины», «ребра многогранника»; научатся определять видимые и невидимые элементы многогранника, изображенного на чертеже, выполнять обозначение элементов многогранника буквами латинского алфавита, моделировать различные многогранники |
Метапредметные: Познавательные: осуществляют моделирование; структурируют знания; осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: формируют внутреннюю позицию школьника на уровне положительного отношения к школе |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Сколько треугольников на чертеже?
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
– На чертеже 10 треугольников. |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||
|
|
Решение комбинаторных задач (задание на доске). – Из цифр 1, 2, 3, 4, 5 составьте все двузначные числа, которые: а) начинаются цифрой 4; б) оканчиваются цифрой 3; в) содержат одинаковые цифры; г) начинаются цифрой 3; д) оканчиваются цифрой 5; е) начинаются цифрой 1 и оканчиваются цифрой 2; ж) начинаются цифрой 5 и оканчиваются цифрой 4; з) начинаются цифрой 5 или цифрой 1. |
Ответы: а) 41, 42, 43, 44, 45; б) 13, 23, 33, 43, 53; в) 11, 22, 33, 44, 55; г) 31, 32, 33, 34, 35; д) 15, 25, 35, 45, 55; е) 12;
ж) 54;
з) 51, 52, 53, 54, 55, 11, 12, 13, 14, 15. |
||||||||||||||||||||||||
|
|
– Вычислите устно, запишите только ответы. Прочитайте значения выражений в порядке возрастания.
|
|
||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 101–102). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Как попасть из вершины А в вершину К куба, двигаясь по его ребрам? Укажите несколько вариантов. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
1) AD ® DP ® PK 4) AB ® DC ® CK 2) AB ® BM ® MK 5) AD ® DC ® CK 3) AE ® EP ® PK 6) AE ® EM ® MK |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей |
|||||||||||||||||||||||
|
Задание 6. |
– Найдите среди окружающих вас предметов те, которые имеют форму разных многогранников. |
– Книга, тумба, коробка имеют форму многогранников. |
||||||||||||||||||||||||
|
Задание 7 |
– Используя спички и пластилин, выполните модели многогранников |
Выполняют модели многогранников, используя спички и пластилин |
||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 103–104). Задание 15. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Неизвестное число увеличили на 3562 и получили 14017. Найдите неизвестное число. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
14017 – 3562 = 10455 |
Выбирать действия в соответствии с поставленной
задачей, оценивать уровень владения тем или иным учебным действием, уметь
вносить необходимые коррективы в действие после его завершения на основе
оценки и учета характера сделанных ошибок. Приводить убедительные
доказательства в диалоге, проявлять активность во взаимодействии.
Преобразовывать модели |
|||||||||||||||||||||||
|
Задание 16. |
– Если из 170200 вычесть задуманное число, то получится 2345. Какое число задумано? |
170200 – 170200 – 2345 = 167855 |
||||||||||||||||||||||||
|
Задание 17. |
– К какому числу надо прибавить разность чисел 1903 и 618, чтобы получить 8040? |
8040 – 1285 = 6755 |
||||||||||||||||||||||||
|
Задание 18. |
– Рассмотрите таблицу и ответьте на вопросы: – При каких значениях а и b значение выражения а · b равно 400? равно 1000? меньше 400?
– При каких значениях а и b значение выражения а : b равно 40? меньше 50? больше 25? |
– Если а = 100 и b = 4, то значение выражения а · b равно 400. Если а = 200 и b = 5, то значение выражения а · b равно 1000. Если а = 0 и b = 36 или а = 50 и b = 1, то значение выражения а · b меньше 400. – Если а = 200 и b= 5, то значение выражения а : b равно 40. Если а = 100 и b = 4 или а = 0 и b = 36, то значение выражения а : b меньше 50. Если а = 200 и b = 5 или а = 50 и b = 1, то значение выражения а : b больше 25. |
||||||||||||||||||||||||
|
|
– Назовите значения а и b, при которых значения выражений а · b и а : b равны. |
– При всех значениях, когда или а, или b равны 1 или когда а = 0. Например: 50 · 1 = 50 : 1 0 · 36 = 0 : 36 |
||||||||||||||||||||||||
|
Задание 19. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 3 + 1 = 4 (части) 2) 24 : 4 = 6 (д.) – тополей. 3) 6 · 3 = 18 (д.) – лип. |
||||||||||||||||||||||||
|
Задание 20. |
– Килограмм конфет стоит 280 р. Сколько рублей надо заплатить за 250 г этих конфет? |
Решение: 1) 1 кг = 1000 г 1000 : 250 = 4 (раза) – во столько раз меньше. 2) 280 : 4 = 70 (р.) – стоят 250 г конфет. |
||||||||||||||||||||||||
|
Задание 21 |
– Составьте таблицу для выражений х + y и x – y, если х = 2036, 12800, 3000, 850, а y = 936, 2800, 50, 850. Выполните вычисления и заполните таблицу. – При каких значениях х и y выражение х – y равно нулю? – При каких значениях х и y выражение х + y принимает наибольшее значение? – При каких значениях х и y выражение х – y принимает наименьшее значение? |
Составляют и заполняют таблицу:
Отвечают на вопросы по таблице |
||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Какое тело называют многогранником? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности, выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 38. Распределительное свойство умножения относительно сложения
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства со свойствами арифметических действий (перестановка множителей в произведении, группировка множителей в произведении); способствовать формированию умений использовать свойства арифметических действий при выполнении вычислений |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями и формулировками распределительных свойств умножения относительно сложения и относительно вычитания и их использованием при вычислениях; научатся применять распределительное свойство умножения относительно сложения и относительно вычитания и использовать его при вычислениях |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: активно используют математическую речь для решения разнообразных коммуникативных задач |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Урок 39. Распределительное свойство умножения относительно вычитания
|
Тип урока: повторение и систематизации знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства со свойствами арифметических действий (перестановка множителей в произведении, группировка множителей в произведении); способствовать формированию умений использовать свойства арифметических действий при выполнении вычислений |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с названиями и формулировками распределительных свойств умножения относительно сложения и относительно вычитания и их использованием при вычислениях; научатся применять распределительное свойство умножения относительно сложения и относительно вычитания и использовать его при вычислениях |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; ориентируются на возможное разнообразие способов решения учебной задачи. Регулятивные: умеют работать по предложенному учителем плану. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: расширяют познавательные интересы и учебные мотивы, понимают границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Назовите выражения со значением 1000. 8754 – 7931 399 + 601 572 + 427 2371 + 7629 80124 – 79124 763 + 247 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
399 + 601 = 1000
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||
|
|
– Соедините выражения с одинаковыми значениями. 3 · (6 · 100) (3 · 60) · 10 (3 · 6) · 100 3 · 600 3 · (60 · 100) 6000 · 3 (6 · 3) ·10 3 · 60 |
|
|||
|
|
– Составьте фигуры из квадратов и треугольников. а) в) |
Составляют фигуры. |
|||
|
|
– Известно, что 25 · 12 = 300. Найдите значения выражений: 300 : 25 3 · 4 · 25 25 · (35 – 23) 300 : 12 25 · 11 2 · 25 · 6 25 · 7 + 25 · 5 12 · 25 25 · 13 |
300 : 25 = 12 3 · 4 · 25 = 300 25 · (35 – 23) = 300 300 : 12 = 25 25 · 11 = 275 2 · 25 · 6 = 300 25 · 7 + 25 · 5 = 200 12 · 25 = 300 25 · 13 = 225 |
|||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 106–108). Задание 4. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Ответьте на вопросы : как выполнял вычисления Слон? – Как Мышка умножала разность чисел 90 и 25 на число 4? – Сравните способы вычислений Слона и Мышки. Чей способ вычисления удобнее? – Чтобы разность умножить на какое-нибудь число, можно умножить на это число уменьшаемое, затем вычитаемое и из первого произведения вычесть второе. Это свойство называют распределительным свойством умножения относительно вычитания. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Объясняют, как выполнял вычисления Слон. 1) 90 – 25 = 65; 2) 65 · 4 = 260 Объясняют, как выполняла вычисления Мышка. 1) 90 · 4 = 360; 2) 25 · 4 = 100; 3) 360 – 100 = 260 – Мышкин способ вычисления удобнее. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
||
|
Задание 5. |
– Выполните вычисления. |
(42 – 15) · 2 = 42 · 2 – 15 · 2 = 84 – 30 = 54 (31 – 8) · 5 = 31 · 5 – 8 · 5 = 155 – 40 = 115 |
|||
|
Задание 6. |
– Используя распределительное свойство умножения относительно вычитания, запишите выражения, равные данным. |
(135 – 84) · 3 = 135 · 3 – 84 · 3 (90 – 43) · 10 = 90 · 10 – 43 · 10 (60 – 15) · 12 = 60 · 12 – 15 · 12 (164 – 97) · 9 = 164 · 9 – 97 · 9 |
|||
|
Задание 7. |
– Применяя распределительное свойство умножения относительно вычитания, найдите значения выражений. |
(30 – 5) · 6 = 30 · 6 – 5 · 6 = 150 (65 – 56) · 10 = 65 · 10 – 56 · 10 = 90 (200 – 106) · 5 = 200 · 5 – 106 · 5 = 470 (300 – 299) · 0 = 300 · 0 – 299 · 0 = 0 |
|||
|
Задание 8. |
– Выполните действия, используя распределительное свойство умножения относительно вычитания. |
(400 – 20) · 2 = 400 · 2 – 20 · 2 = 800 – 40 = 760 (80 – 1) · 5 = 80 · 5 – 1 · 5 = 400 – 5 = 395 (25 – 9) · 4 = 25 · 4 – 9 · 4 = 100 – 36 = 64 (20 – 1) · 7 = 20 · 7 – 1 · 7 = 140 – 7 = 133 |
|||
|
Задание 9. |
– Выполните вычисления устно, применяя, где это удобно, распределительное свойство умножения. |
(60 + 1) · 7 = 60 · 7 + 1 · 7 = 420 + 7 = 427 (17 – 13) · 5 = 4 · 5 = 20 (67 – 17) · 4 = 50 · 4 = 200 (30 – 2) · 5 = 30 · 5 – 2 · 5 = 150 – 10 = 140 |
|||
|
Задание 10 |
– Выполните задание в парах |
Работают самостоятельно, проверяют друг друга |
|||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 110–111). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Рассмотрите план квартиры. Вычислите действительные размеры гостиной и спальни. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Размеры гостиной: 3 · 6 = 18 (кв. м). – Размеры спальни: 3 · 3 = 9 (кв. м). |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
||
|
Задание 22. |
– Рассмотрите диаграмму в учебнике. Какой вариант ответа надо выбрать Волкову, чтобы выиграть? |
– Надо выбрать вариант ответа под буквой В. |
|||
|
Задание 23. |
– В двух корзинах грибов поровну. Сколько грибов надо переложить из одной корзины в другую, чтобы во второй стало на 4 гриба больше? |
– Два гриба надо переложить из одной корзины в другую, чтобы во второй стало на 4 гриба больше. |
|||
|
Задание 24. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: Длина – 22 дм Ширина – ? дм (половина) S – ? дм2 S пяти стекол – ? дм2 Решение: 1) 22 : 2 = 11 (дм) – ширина. 2) 22 · 11 = 242 (дм2) – площадь стекла. 3) 242 · 5 = 1210 (дм2) – площадь пяти стекол. |
|||
|
Задание 25. |
– Выполните вычисления и построение в масштабе 1 : 100. |
Решение: 36 : 4 = 9 (м) |
|||
|
Задание 26. |
– Вычислите периметр четырехугольника АВСD. – Сравните длины сторон четырехугольника АВСD. Докажите, что он не является квадратом. |
Р = 25 · 4 = 100 (мм); 100 мм = 10 см – Стороны четырехугольника АВСD равны, но он не является квадратом, так как его углы не прямые.
|
|||
|
Задание 27. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: 1 пачка – 350 г, ? п. по 14 г. 40 упаковок – ? п. Решение: 1) 350 : 14 = 25 (п.) – в 1 пачке. 2) 25 · 40 = 1000 (п.) – в 40 упаковках.
|
|||
|
Задание 28. |
– За какое время можно пройти 1 км, идя со скоростью 6 км/ч? |
– Так как 6 км можно пройти за 1 час (60 мин.), то 1 км можно пройти за 10 мин (60 мин : 6 = 10 мин). |
|||
|
Задание 29 |
– Выразите скорость 120 км/ч в километрах в минуту |
120 км/ч = 2 км/мин |
|||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Сформулируйте распределительное свойство умножения относительно вычитания. – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят само-оценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Разгадайте правило, по которому составлена первая схема, и вставьте пропущенные числа в другие схемы.
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
Заполняют схемы:
|
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||
|
|
– Вычислите площадь данных фигур с помощью мерок: а) |
Ответы: а) 8, 6, 12, 28; б) 4, 3, 6, 14 |
||||||||||||||
|
|
|
|
||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 105–106). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Как ученики выполнили умножение суммы на число? (90 + 25) · 4 = 460 – Чтобы сумму двух чисел умножить на какое-нибудь число, можно каждое из них умножить на это число и резуль-таты сложить. Это свойство называют распределительным свойством умножения относительно сложения. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Решение: 1) 90 · 4 = 360 2) 25 · 4 = 100 3) 360 + 100 = 460
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль действий по результату |
|||||||||||||
|
Задание 2. |
– Используя распределительное свойство умножения относительно сложения, запишите выражения, равные данным. |
(112 + 44) · 3 = 112 · 3 + 44 · 3 (7 + 4) · 132 = 7 · 132 + 4 · 132 (16 + 18) · 25 = 16 · 25 + 18 · 25 (36 + 24) · 9 = 36 · 9 + 24 · 9 |
||||||||||||||
|
Задание 3 |
– Найдите значение выражений двумя способами.
– В каком случае пользоваться при вычислении распределительным свойством было неудобно? Почему? |
1) (50 + 19) · 2 = 69 · 2 = 138 50 · 2 + 19 · 2 = 100 + 38 = 138 2) (72 + 28) · 7 = 100 · 7 = 700 72 · 7 + 28 · 7 = 504 + 196 = 700 – Во втором случае пользоваться распределительным свойством было неудобно, так как проще было 100 умножить на 7, чем умножать на 7 числа 72 и 28 |
||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 108–109). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Назовите невидимые ребра многогранников.
– Назовите невидимые грани многогранников. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Невидимые ребра многогранников: 1) КС, СD, BC; 2) BC, СD, КС. – Невидимые грани многогранников: 1) АВСD, BCK, CKD; 2) ABCDE, BCK, CDK. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль |
|||||||||||||
|
Задание 12. |
– Выполните вычисления. |
27 · 3 = 81 700 : 14 = 50 35600 : 100 · 0 = 0 141 · 6 = 846 78 : 6 = 13 57 : 7 = 8 (ост. 1) 5 · 170 = 850 24 · (3 · 10) = 720 57 : 19 = 3 98 : 14 = 7 90 : (5 · 2) = 9 570 : 57 = 10 |
||||||||||||||
|
Задание 13. |
– Чему равна разность произведений 40 · 4 и 14 · 6? |
40 · 4 – 14 · 6 = 160 – 84 = 76 |
||||||||||||||
|
Задание 14. |
– Найдите сумму частных 420 : 6 и 700 : 5. |
420 : 6 + 700 : 5 = 70 + 140 = 210 |
||||||||||||||
|
Задание 15. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
5730 + 70787 + 59724 = 136241 10091 – 9842 + 67991 = 68240 183018 – 10056 – 2088 = 170874 40009 + 52700 – 4176 = 88533 |
||||||||||||||
|
Задание 16. |
– Составьте выражение. Вычислите его значения при с = 480; 960. |
800 – с : 12 а) если с = 480, то 800 – 480 : 12 = 800 – 40 = 760 б) если с = 960, то 800 – 960 : 12 = 800 – 80 = 720 |
||||||||||||||
|
Задание 17. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: 6 ящ. – 72 кг ? ящ. – 96 кг Решение: 1) 72 : 6 = 12 (кг) – 1 ящик. 2) 96 : 12 = 8 (ящ.) – потребуется. |
||||||||||||||
|
Задание 18. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 4 – 2 = 2 (пл.) – на столько платков больше у Нины. 2) 1 м = 100 см; 100 : 2 = 50 (см) – на 1 платок. 3) 50 · 2 = 100 (см) – истратила Оля. 4) 50 · 4 = 200 (см) – истратила Нина. |
||||||||||||||
|
Задание 19. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 4 · 2 = 8 (км) – на плоту. 2) 6 · 3 = 18 (км) – пешком. 3) 8 + 18 = 26 (км) – всего. |
||||||||||||||
|
Задание 20 |
– Купили 48 конфет и часть из них раздали поровну пятерым детям. Верно ли, что осталось 4 конфеты? |
– 48 : 5 = 9 (ост. 3). Неверно. Осталось 3 конфеты; по 9 конфет получил каждый ребенок |
||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Сформулируйте распределительное свойство умножения относительно сложения. – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Оценивать результаты деятельности |
|||||||||||||
Урок 40. Умножение на 1000, 10 000, 100 000
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: помочь сформулировать и способствовать формированию умений применять правила умножения на 1000, 10 000, 100 000 |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами умножения на 1000, 10 000, 100 000; научатся применять правила умножения на 1000, 10 000, 100 000 |
Метапредметные: Познавательные: осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: осваивают начальные формы познавательной и личностной рефлексии. Коммуникативные: управляют поведением партнера, осуществляют контроль, коррекцию и оценку его действий; полно и точно выражают свои мысли в соответствии с задачами и условиями коммуникации |
Личностные: осознают необходимость самосовершенствования, повышают мотивацию к учению |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Какие цифры можно поставить вместо пропущенных? Почему? 5 3987 – 564 > 3987 – 8876 – 1574 > 175 + 645 + 89 < 89 + 64 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||
|
|
– Восстановите пропущенные цифры.
|
9486 – 3287 = 6199 8389 – 4845 = 3544 12300 – 5998 = 6302 |
|||||||||||||||||||||||||||
|
|
– Решите задание на смекалку. Крышка стола имеет четыре угла. Один из них отпилили. Сколько углов стало у крышки? |
Ответ: пять углов |
|||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 112–113). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Как умножать число на 10? – Как умножать число на 100? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
5 · 10 = 50 17 · 10 = 170 5 · 100 = 500 17 · 100 = 1700 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
||||||||||||||||||||||||||
|
Задание 2. |
– Сформулируйте правило умножения числа на 1000, 10 000, 100 000 и выполните умножение. |
Формулируют правило умножения числа на 1000, 10 000, 100 000 и выполняют умножение. |
|||||||||||||||||||||||||||
|
Задание 3. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно, проверяют друг друга. |
|||||||||||||||||||||||||||
|
Задание 4. |
– Вычислите значение буквенного выражения 15 · а при а = 100; 1000; 10 000. |
15 · а а) если а = 100, то 15 · 100 = 1500; б) если а = 1000, то 15 · 1000 = 15000; в) если а = 10 000, то 15 · 10 000 = 150 000. |
|||||||||||||||||||||||||||
|
Задание 5. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 15 + 23 = 38 (шт.) 2) 38 · 1000 = 38 000 (р.) |
|||||||||||||||||||||||||||
|
Задание 6. |
– Какая единица длины в 1000 раз больше метра? Выразите длину в метрах. |
6 км = 6000 м 125 км = 125000 м 11 км = 11000 м 5 км 300 м = 5300 м 42 км 50 м = 42050 м |
|||||||||||||||||||||||||||
|
Задание 7 |
– Какая единица массы в 1000 раз больше грамма? Выразите массу в граммах |
8 кг = 8000 г 3 г 200 г = 3200 г 12 кг = 12000 г 20 кг 7 г = 20007 г 150 кг = 150000 г |
|||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 114–115). Задание 13. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Найдите сумму чисел. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
6458 + 872 = 7330 5245 + 3270 = 8515 35700 + 16300 = 52000 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодейст-вии. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||||||||
|
Задание 14. |
– Найдите разность чисел. |
70635 – 8240 = 62395 2514 – 1664 = 850 9531 – 1230 = 8301 |
|||||||||||||||||||||||||||
|
Задание 15. |
– Составьте выражения. |
1) 7 · 8 – 36 : 6 = 56 – 6 = 50 2) 126 – 87 + 208 = 39 + 208 = 247 3) 6 · 4 + 6 · 4 + 6 · 4 = 24 + 24 + 2 4 = 72 4) 6 · (12 – 8) + 18 : (4 + 5) = 6 · 4 + 18 : 9 = = 24 + 2 = 26 |
|||||||||||||||||||||||||||
|
Задание 16. |
– Вычислите устно. Какие свойства вы использовали? |
130 · 3 – 130 · 2 = 130 · (3 – 2) = 130 · 1 = 130 25 · 3 + 45 · 3 = 3 · (25 + 45) = 3 · 70 = 210 – Распределительное свойство умножения. |
|||||||||||||||||||||||||||
|
Задание 17. |
– Сравните выражения. |
– Значение второго выражения в каждом столбике в 10 раз больше. |
|||||||||||||||||||||||||||
|
Задание 18. |
– Сравните величины. |
5 кг 250 г < 6 кг 120 г 4108 г < 5 кг 12 кг 470 г > 10 кг 220651 г > 220561 г |
|||||||||||||||||||||||||||
|
Задание 19. |
Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: 3 дня – 48 с. 6 дней – ? с. Решение:
|
|||||||||||||||||||||||||||
|
Задание 20. |
– Назовите ребра многогранника, которые выходят из вершины А. – Назовите ребра, которые выходят из вершины K. – Назовите видимые ребра. – Назовите невидимые ребра. – Какие грани видны на рисунке? – Какие грани не видны? |
– АВ, АD, АЕ – ребра многогранника, которые выходят из вершины А. – KD, KP, KE.– ребра, которые выходят из вершины K. – AD, AB, AE, BC, CD, CP, BM, EM – видимые ребра. – EK, KP, DK – невидимые ребра. – ABCD, BCPM, ABME – грани, которые видны на рисунке. – EKPM, KDCP, ADKE – грани, которые не видны. |
|||||||||||||||||||||||||||
|
Задание 21 |
– Составьте три задачи и решите их |
Решение: 1000 – 320 · 3 = 40 (р.)
Решение: (500 – 50) : 150 = 3 (м)
Решение: 80 · 2 + 40 = 200 (р.) |
|||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как выполнить умножение на 10, 100, 1000, 10 000? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, анализировать причины неудачи. Выражать доброжелательность |
Урок 41. Упражнения в умножении на 1000, 10 000, 100 000.
Контрольный устный счет № 3
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений применять правила умножения на 1000, 10 000, 100 000; содействовать развитию умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом умножения на 1000, 10 000, 100 000; научатся применять правила умножения на 1000, 10 000, 100 000 |
Метапредметные: Познавательные: осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи, строят логическую цепь рассуждений. Регулятивные: умеют работать по предложенному учителем плану. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: расширяют познавательные интересы и учебные мотивы |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Придумайте примеры по этим схемам. Найдите «ловушку».
|
Отвечают на вопросы учителя. Выполняют задания устного счета. а) 9302 + 1415 = 10717 б) 87654 – 87621 = 33 в) «ловушка» г) 9999 + 1 = 10000 д) 999207 + 101 = 999308 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||
|
|
– Подумайте: >, < или = ? 1) 2 · 37 + 5 · 37 … 7 · 37 2) 7 · 2674 … 3 · 2674 + 2674 · 4 3) 5 · 4312 + 4312 … 6 · 4312 4) 8 · 46 – 2 · 46 … 6 · 46 |
1) 2 · 37 + 5 · 37 = 7 · 37 2) 7 · 2674 = 3 · 2674 + 2674 · 4 3) 5 · 4312 + 4312 = 6 · 4312 4) 8 · 46 – 2 · 46 = 6 · 46 |
|||||||||||
|
|
– Выполните умножение. 1375 · 1 1375 · 10 1375 · 100 2039 · 10 2039 · 100 700 · 1 700 · 100 352 · 1000 62 · 1000 974 · 0 52936 · 1 79251 · 0 1 · 62 10 · 364 1000 · 27 |
Выполняют умножение |
|||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 113). Задание 8. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Запись: u = 1000 км/ч t – 3 ч s – ? Осталось – 787 км Весь путь – ? Решение: 1) 3 · 1000 = 3000 (км) – пролетел. 2) 3000 км + 787 км = 3787 км |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
||||||||||
|
Задание 9. |
– Найдите значения выражений. |
100000 · 9 – (3828 + 14963) = 881209 758 : 108 · 1000000 – 6995308 = 232105 358 · 10000 – (970 : 10) · 1000 = 3483000 1039 · 10 + 1039 · 100 + 1039 · 1000 = 1153290 |
|||||||||||
|
Задание 10. |
– Каждое из данных чисел увеличьте в десять тысяч раз и в сто тысяч раз. |
25 · 10000 = 250000 25 · 100000 = 2500000 609 · 10000 = 6090000 609 · 100000 = 60900000 5050 · 10000 = 50500000 5050 · 100000 = 505000000 |
|||||||||||
|
Задание 11. |
– Выполните вычисления. |
Запись: а = 23 м b = 10 м S – ? Решение: 23 · 1000 = 23000 (м2) |
|||||||||||
|
Задание 12 |
– Верно ли, что в одном километре содержится миллион миллиметров? Выполните вычисления |
– Верно, в одном километре содержится миллион миллиметров. 1 км = 1000 м 1 м = 100 см 1 см = 10 мм 1 км = 1000 · 100 · 10 = 1 000 000 мм |
|||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 115–116). Задание 22. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: I способ 1) 30 · 4 = 120 (км) – расстояние. 2) 120 : 2 = 60 (км/ч) – скорость. II способ 1) 4 : 2 = 2 (раза) – во столько раз меньше времени. 2) 30 · 2 = 60 (км/ч) – скорость. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||
|
Задание 23. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 60 : 30 = 2 (раза). 2) 32 · 2 = 64 (км/ч) – скорость автомобиля. 3) 64 : 4 · 3 = 48 (км/ч) – скорость мотоцикла. 4) 48 : 2 = 24 (км) – проедет мотоциклист за 30 мин. |
|||||||||||
|
Задание 24. |
– Проведите оси симметрии в каждой фигуре. |
См. Ресурсный материал к уроку. |
|||||||||||
|
Задание 25. |
– Выполните построение симметричных фигур относительно данной прямой. |
Выполняют построение. |
|||||||||||
|
Задание 26. |
– Выполните построение и проведите пять осей симметрии. |
См. Ресурсный материал к уроку. |
|||||||||||
|
Задание 27 |
– Какое расстояние пробежит гепард за 5 минут? |
Решение: 1) 60 : 5 = 12 (раз) – во столько раз меньше. 2) 120 : 12 = 10 (км) – за 5 мин |
|||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Как выполнить умножение на 10, 100, 1000, 10 000? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Продолжают высказывания: • сегодня я… • было интересно… • было трудно… |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Ресурсный материал к уроку
|
Задание 24.
|
Задание 26.
|
Урок 42. Прямоугольный параллелепипед. Куб
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «прямоугольный параллелепипед» и «куб»; способствовать формированию умений различать объемные тела, показывать грани, вершины, ребра прямоугольного параллелепипеда (куба), изображение прямоугольного параллелепипеда и куба на чертеже; выполнять развертку прямоугольного параллелепипеда (куба) |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «прямоугольный параллелепипед» и «куб»; научатся: показывать грани, вершины, ребра прямоугольного параллелепипеда (куба), изображение прямоугольного параллелепипеда и куба на чертеже; выполнять развертку прямоугольного параллелепипеда (куба) |
Метапредметные: Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи. Регулятивные: проговаривают вслух последовательность производимых действий, составляющих основу осваиваемой деятельности. Коммуникативные: допускают существование различных точек зрения; договариваются, приходят к общему решению; используют в общении правила вежливости |
Личностные: приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. – Игра «Найди пару» (задание на доске). Соедините стрелками каждое выражение с его значением: 700 : (14 · 10) 50 57000 : (10 · 19) 3 850000 : (17 · 100) 300 750 : (10 · 25) 5 5500 : (11 · 100) 30 81000 : (27 · 10) 500 210 : (7 · 10) 5 4200 : (10 · 6) 3 63000 : (9 · 1000) 70 3600 : (10 · 9) 80 35000 : (7 · 1000) 7 48000 : (100 · 6) 40 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
700 : (14 · 10) = 5 57000 : (10 · 19) = 300 850000 : (17 · 100) = 500 750 : (10 · 25) = 3 5500 : (11 · 100) = 5 81000 : (27 · 10) = 300 210 : (7 · 10) = 3 4200 : (10 · 6) = 70 63000 : (9 · 1000) = 7 3600 : (10 · 9) = 40 35000 : (7 · 1000) = 5 48000 : (100 · 6) = 80 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Найдите произведение: а) самого большого двузначного числа и самого маленького трехзначного; б) самого маленького трехзначного числа и самого большого однозначного; в) самого маленького четырехзначного числа и самого маленького двузначного. – Запишите число, в котором: а) 3 сотни, 9 десятков, 3 единицы; б) 18 сотен, 3 десятка; в) 15 сотен, 2 единицы |
Находят произведения: а) 9900;
б) 900;
в) 10000.
Записывают числа: а) 393; б) 1830; в) 1502 |
|
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 117–118). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Рассмотрите рисунок. Предметы, изображенные на рисунке, имеют форму многогранника. Каждый такой многогранник называют прямоугольным параллелепипедом. Есть ли в классной комнате предметы или части предметов, имеющие форму прямоугольного параллелепипеда? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Телевизор, аквариум, шкаф, сама комната. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества |
|
Задание 2. |
– Произнесите несколько раз слово «параллелепипед», запишите его два раза в тетрадь и запомните, как оно пишется. |
Произносят и записывают слово. |
|
|
Задание 3. |
– Рассмотрите модель прямоугольного параллелепипеда и ответьте на вопросы: сколько граней имеет прямоугольный параллелепипед? (6 граней.) – Почему такой параллелепипед называют прямоугольным? Какую форму имеет каждая грань? – Сколько вершин и сколько ребер у прямоугольного параллелепипеда? (Вершин – 8, ребер – 12.) – Есть ли у него равные грани, ребра? Покажите их. – Сколько ребер выходит из каждой вершины? (По 3 ребра.) |
Отвечают на вопросы.
|
|
|
Задание 4 |
– Рассмотрите модель куба. Объясните, почему куб тоже является прямоугольным параллелепипедом? |
– Грани куба – прямоугольники (у которых все стороны равны), поэтому куб – тоже параллелепипед |
|
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 119–120). Задание 9. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Запишите цифрами данные числа. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: 302006, 520000, 480050, 2070010. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Осуществлять взаимный контроль, планировать способы взаимодействия |
|
Задание 10. |
– Спортсмен сделал 50 выстрелов по мишени. Промахи составили десятую часть всех выстрелов. Сколько раз спорт-смен попал в цель? |
Решение: 50 : 10 = 5 (раз) – промахнулся; 50 – 5 = 45 (раз) – попал. |
|
|
Задание 11. |
– Вычислите устно. |
Работают самостоятельно. |
|
|
Задание 12 |
– За всю игру баскетболист 12 раз забросил мяч в корзину соперника. Попадания составили восьмую часть всех бросков мяча в эту корзину. Сколько всего бросков было сделано? |
Решение: 12 · 8 = 96 (бросков) – всего было сделано |
|
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какие тела называют кубом и параллелепипедом? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 43. Прямоугольный параллелепипед. Куб.
Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «прямоугольный параллелепипед» и «куб»; способствовать формированию умений различать объемные тела, показывать грани, вершины, ребра прямоугольного параллелепипеда (куба), изображение прямоугольного параллелепипеда и куба на чертеже; выполнять развертку прямоугольного параллелепипеда (куба) |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «прямоугольный параллелепипед» и «куб»; научатся: показывать грани, вершины, ребра прямоугольного параллелепипеда (куба), изображение прямоугольного параллелепипеда и куба на чертеже; выполнять развертку прямоугольного параллелепипеда (куба) |
Метапредметные: Познавательные: умеют ориентироваться в учебнике (на развороте, в оглавлении, в условных обозначениях); находят ответы на вопросы в тексте, иллюстрациях; делают выводы в результате совместной работы класса и учителя. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: умеют задавать вопросы; формулируют собственное мнение и позицию |
Личностные: имеют желание учиться, осознают необходимость самосовершенствования; понимают границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Запишите «соседей» чисел: а) … 283 …; в) … 531 …; б) … 90 …; г) … 499 … |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) 281, 283, 284; в) 530, 531, 532; б) 89, 90, 91; г) 498, 499, 500 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
– Назовите компоненты действий сложения, вычитания, умножения, деления. Как найти неизвестное слагаемое? неизвестное вычитаемое, уменьшаемое? неизвестный множитель? неизвестное делимое, неизвестный делитель?
– Какое действие следует выполнить на калькуляторе, чтобы на экране появилось число, которое нужно вставить в «окошко», в результате чего получится верное равенство? а) б) в) 83 – |
– Слагаемые, сумма. Чтобы найти неизвестное слагаемое, надо из значения суммы вычесть известное слагаемое. – Уменьшаемое, вычитаемое, разность. Чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить разность. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность. – Множители, произведение. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. – Делимое, делитель, частное. Чтобы найти неизвестное делимое, надо делитель умножить на частное. Чтобы найти неизвестный делитель, надо делимое разделить на частное. а) Умножение. б) Сложение. в) Вычитание. г) Деление. д) Вычитание. е) Деление.
– Получатся равенства: 90 : 30 = 3 3 · 15 = 45 77 – 50 = 27 200 + 32 = 232 83 – 23 = 60 700 : 100 = 7 |
||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 118–119). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Рассмотрите чертеж прямоугольного параллелепипеда. Назовите ребра, которые выходят из вершины А; из вершины К. – Назовите каждое видимое и каждое невидимое ребро. – Какие грани видны на рисунке и какие не видны?
– Назовите пары равных ребер, равных граней. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– АЕ, АВ, АD – ребра, которые выходят из вершины А; КD, КР, КЕ – ребра, которые выходят из вершины К. – Видимые ребра: АЕ, АВ, ВМ, ВС, СР, МР, DC, DА, ЕМ. Невидимые ребра: DК, КР, ЕК. – АВМЕ, АВСD, МВСР – грани, которые видны на рисунке, ЕМРК, АЕКD, КРСD – грани, которые не видны. – Пары равных ребер: АЕ = ВМ = СР = DК, АD = ВС = МР = ЕК. – Пары равных граней: АВСD = ЕМРК, АВЕМ = DКРС. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|
Задание 6. |
– Найдите площадь поверхности (площадь всех граней) куба, длина ребра которого равна: а) 8 см; б) 5 дм; в) 4 м. |
Решение: а) 8 · 8 = 64 (см2) 64 · 6 = 384 (см2) б) 5 · 5 = 25 (дм2) 25 · 6 = 150 (дм2) в) 4 · 4 = 16 (м2) 16 · 6 = 96 (м2) |
|
|
Задание 7. |
– Сколько проволоки пошло на изготовление каркаса данного куба? |
Решение: 2 дм · 12 = 24 дм |
|
|
Задание 8 |
– Назовите длину каждого ребра многогранника. |
АО = РВ = SC = TD = 3 см DC = TS = OP = AB = 2 см AD = BC = OT = PS = 4 см |
|
|
– Вычислите площадь каждой грани. |
SABCD = SOPST = 4 · 2 = 8 (см2) SAOPB = SDTSC = 3 · 2 = 6 (см2) SAOTD = SPBCS = 4 · 3 = 12 (см2) |
||
|
– Вычислите площадь всех граней многогранника |
8 см2 · 2 + 6 см2 · 2 + 12 см2 · 2 = 52 см2 |
||
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 120). Задание 13. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Сравните значения выражений, не выполняя указанных вычислений. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
8000 – 1500 >8000 – 2500 3650 – 380 < 4650 – 380 560 : 28<560:14 145 · 9 > 145 · 7 |
Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|
Задание 14. |
– Сколько лет составляют 5 веков, 13 веков, 18 веков, 25 веков? |
5 веков = 500 лет; 13 веков = 1300 лет; 18 веков = 1800 лет; 25 веков = 2500 лет |
|
|
Задание 15 |
– Рассмотрите схему линий московского метро. Как проехать от станции «Севастопольская» до станции «Третьяковская»? От станции «Алтуфьево» до станции «Тургеневская»? |
Работают с картой |
|
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 44. Контрольная работа № 3 по теме «Свойства арифметических действий»
|
Тип урока: контроль и оценка знаний и сформированности способов действий |
||
|
Педагогические задачи: проверить усвоение знаний и умений по теме «Свойства арифметических действий», умение решать составные задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся находить удобные способы решения задач, использовать алгоритм умножения трехзначных чисел |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель (пространственно-графическую или знаково-символическую), где выделены существенные характеристики объекта, и преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: в совместной деятельности определяют цели и функции участников, способы взаимодействия |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Проведение контрольной работы |
Знакомит с содержанием контрольной работы, комментирует задания.
Вариант I 1. Запишите результаты действий. 3685 + 0 = 532 · 1 = 0 · 54 108 = 98 – 0 = 0 : 15 687 = 1 698 : 1 = 213 · 100 = 7005 · 1000 = 2. Используя переместительное свойство сложения, запишите выражение, равное данному: 52 · а. 3. При каком числовом значении х значение выражения 8 · х равно 0? 4. Вычислите: 325 + 7 084 + 675 = 936 · 20 · 5 = (40 + 1) · 8 = 5. Выполните умножение в столбик: 5034 · 7 = 6. Выразите в килограммах: 8 т; 19 ц; 5 т 6 ц; 12 т 50 кг.
Вариант II 1. Запишите результаты действий. 4 125 – 0 = 2 726 · 0 = 0 : 9 670 = 0 + 91 238 = 2378 · 1 = 1 861 : 1 = 421 · 100 = 5 007 · 1000 = 2. Используя переместительное свойство умножения, запишите выражение, равное данному: у · 537. 3. При каком числовом значении а значение выражения 54 · а равно 54? 4. Вычислите. 410 + 8 996 + 590 = 738 · 25 · 4 = (30 + 1) · 7 = 5. Выполните умножение в столбик: 4082 · 9 = 6. Выразите в килограммах: 7 т; 15 ц; 2 т 3 ц ; 17 т 60 кг |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы Вариант I 1. 3685 + 0 = 3685 532 · 1= 532 0 · 54 108 = 0 98 – 0 = 98 0 : 15 687 = 0 1 698 :1 =1698 213 · 100= 21300 7005 · 1000= 7005000 2. 52 · а = а · 52
3. 8 · 0 = 0 4. 325 + 7 084 + 675 = 8084 936 · 20 · 5 = 93600 (40 + 1) · 8 = 328 5. 5034 · 7 = 35238 6. 8 т = 8000 кг 19 ц = 1900 кг 5 т 6 ц = 5600 кг 12 т 50 кг = 12050 кг Вариант II 1. 4 125 – 0 = 4125 2 726 · 0 = 0 0 : 9 670 = 0 0 + 91 238 = 91238 2378 · 1 = 2378 1 861 : 1 = 1861 421 · 100 = 42100 5 007 · 1000 = 5007000 2. у · 537 = 537 · у
3. 54 · 1 = 54 4. 410 + 8 996 + 590 = 9996 738 · 25 · 4 = 73800 (30 + 1) · 7 = 217 5. 4082 · 9 = 36738 6. 7 т = 7000 кг 15 ц = 1500 кг 2 т 3 ц = 2300 кг 17 т 60 кг = 17060 кг |
Принимать и сохранять учебную цель и задачу. Анализировать, находить общее и различия, делать выводы. Осознанно и произвольно строить речевые высказывания в устной форме |
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке. – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способны проводить самооценку |
Урок 45. Работа над ошибками. Тема: Единицы массы: тонна, центнер.
их обозначение
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для повторения соотношений между единицами массы: тонной, центнером и килограммом; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с единицами массы (тонной, центнером), их обозначениями, соотношениями: 1 т = 1 000 кг, 1 т = 10 ц; научатся: решать арифметические задачи; устанавливать соотношения между величинами массы |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: умеют формулировать учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще не известно; определяют последовательность промежуточных целей с учетом конечного результата. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками: определяют цели и функции участников, способы взаимодействия |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения, считаются с мнением другого человека, проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности); понимают причину успеха/неуспеха учебной деятельности и конструктивно действуют в ситуации неуспеха |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||
|
I. Работа над ошибками II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Рассматривает наиболее типичные ошибки, дает тренировочные задания |
Разбирают ошибки, выполняют задания |
Находить и исправлять ошибки. Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||
|
Организует устный счет с целью актуализации знаний. 1) Математический диктант: а) Чему равно произведение чисел 7 и 9? б) Найдите частное чисел 72 и 8. в) Чему равна сумма чисел 72 и 8? г) Найдите разность чисел 72 и 8. д) Число 6 увеличьте на 8. е) Число 36 увеличьте в 2 раза. 2) Вставьте пропущенный делитель: 49000 : 4800 : 54000 : 2700 : 3) Сравните: 0 · 3 и 3 · 0 0 · 3 и 0 : 3 0 : 3 и 3 – 0 0 + 3 и 0 · 3 0 + 3 и 3 – 0 0 + 3 и 3 · 0 – Из каких чисел составлены эти примеры? – Какие еще примеры в одно действие вы могли бы составить с этими же числами? Почему? 4) Помогите Волку и Зайцу расставить арифметические знаки: 752 360 – Назовите в каждом выражении компоненты. – Какие выражения взаимосвязаны? – Можете ли вы объяснить, почему? |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) 63. б) 9. в) 80. г) 64. д) 14. е) 72. 2) 49000 : 7 = 7000 81000 : 9 = 9000 4800 : 8 = 600 20000 : 4 = 5000 54000 : 6 = 9000 2400 : 6 = 400 2700 : 9 = 300 18000 : 6 = 3000 3) 0 · 3 = 3 · 0 0 · 3 = 0 : 3 0 : 3 < 3 – 0 0 + 3 > 0 · 3 0 + 3 = 3 – 0 0 + 3 > 3 · 0 Отвечают на вопросы.
4) 752 – 52 = 700 90 · 4 = 360 360 : 9 = 40 700 + 52 = 752
Отвечают на вопросы |
|||||||||||||
|
III. Открытие нового знания, нового способа действия. Работа по учебнику (с. 122–123). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Сколько килограммов муки каждого сорта отправили в магазины? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Пшеничной муки – 1000 кг, ржаной муки – 100 кг. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии |
|||||||||||
|
Задание 2. |
– Верно ли, что 1 тонна содержит 10 центнеров? |
|
||||||||||||
|
Задание 3. |
– Выразите величины в килограммах.
– Выразите величины в центнерах. |
|
||||||||||||
|
Задание 4. |
– Во сколько раз 15 т больше 5 ц?
– На сколько 15 т больше 5 ц? – На сколько 160 кг меньше 2 ц?
– На сколько 4 т больше 4 ц? – На сколько 500 г меньше 4 кг? |
– 15 т = 150 ц, 150 : 5 = 30 (раз). В 30 раз 15 т больше 5 ц. – 150 – 5 = 145 (ц). На 145 ц 15 т больше 5 ц. – 2 ц = 200 кг, 200 – 160 = 40 (кг). На 40 кг 160 кг меньше 2 ц. – 4 т = 40 ц, 40 – 4 = 36 (ц). На 36 ц 4 т больше 4 ц. – 4 кг = 4000 г, 4000 – 500 = 3500 (г). На 3500 г 500 г меньше 4 кг. |
||||||||||||
|
Задание 5. |
– Во сколько раз 1 т больше 1 ц? – Во сколько раз 1 кг меньше 1 ц? – На сколько 4 т больше 4 кг? |
– В 10 раз. – В 100 раз. – 4 т = 4000 кг, 4000 – 4 = 3996 (кг). На 3996 кг 4 т больше 4 кг. |
||||||||||||
|
Задание 6 |
– Решите задачу |
Решение: 5 · 2 = 10 (т) 10 т = 10000 кг |
||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 123–125). Задание 10. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Запишите наибольшее шестизначное число и три следующих за ним при счете числа. – Запишите наименьшее семизначное число и три предшествующих ему при счете числа. – Прочитайте число 1 010 000. Вычтите из него число 1 и запишите результат. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: 999999, 1000000, 1000001, 1000002
Запись: 1000000, 999999, 999998, 999997
1 010 000 – 1 = 1 009 999 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
|||||||||||
|
Задание 11. |
– Какие числа нужно записать в пустых клетках таблицы? |
Заполняют таблицу:
|
||||||||||||
|
Задание 12. |
– Выполните вычисления, записывая сложение и вычитание в столбик. |
Работают самостоятельно. |
||||||||||||
|
Задание 13. |
– Найдите значения выражения х · 42 + y · 107, если х = 14, y = 8. – Найдите значения выражения а · m + х, если х = 360, а = 60, m = 9. |
Запись: 14 · 42 + 8 · 107 = 588 + 856 = 1444
60 · 9 + 360 = 540 + 360 = 900 |
||||||||||||
|
Задание 14. |
– Проверьте равенство 64 · 7 + 1692 = 64 · 8 + 1692, не выполняя вычислений. |
– Равенство неверно. Так как в обеих его частях первое слагаемое представлено произведениями, где 64 · 7 меньше чем 64 · 8, то и вся левая часть равенства меньше, чем правая. |
||||||||||||
|
Задание 15. |
– Выполните вычисления. Какие математические правила вы использовали? |
Работают самостоятельно. |
||||||||||||
|
Задание 16. |
– Запишите данные числа в порядке убывания. |
Запись: 13954380, 13954270, 1522448, 1385361, 1325337 |
||||||||||||
|
Задания 17, 18 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу 17 двумя способами. – Каким способом быстрее получается результат? |
См. Ресурсный материал к уроку |
||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Назовите единицы массы. – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Продолжают высказывания: • Сегодняшний урок – это… • Сегодня на уроке я…
|
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Ресурсный материал к уроку
|
Задание 17.
Решение: I способ 1) 300 : 2 = 150 (см) – расход на одно изделие. 2) 600 : 150 = 4 (п.) – можно сшить из 6 метров. II способ 1) 6 : 3 = 2 (раза) – больше ткани. 2) 2 · 2 = 4 (п.) – можно сшить из 6 метров. |
Задание 18.
Решение: 1) 6 + 10 + 8 = 24 (нав.) – всего сшили. 2) 72 : 24 = 3 (м) – идет на 1 наволочку. 3) 3 · 6 = 18 (м) – израсходовала 1-я швея. 4) 3 · 10 = 30 (м) – израсходовала 2-я швея. 5) 3 · 8 = 24 (м) – израсходовала 3-я швея. |
||||||||||||||||||||||||||
Урок 46. Соотношение единиц массы. Решение задач с использованием единиц массы
|
Тип урока: комбинированный |
||
|
Педагогические задачи: повторить единицы массы (килограмм, тонна и центнер); способствовать формированию умений использовать соотношения между единицами массы при сравнении величин, сравнивать величины по их числовым значениям; создать условия для формирования навыка выражать данные величины в различных единицах |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с единицами массы (тонной, центнером), их обозначениями, соотношениями: 1 т = 1 000 кг, 1 т = 10 ц; научатся: решать арифметические задачи; устанавливать соотношения между величинами массы |
Метапредметные: Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях; осуществляют анализ, делают выводы. Регулятивные: осуществляют рефлексию способов и условий действия, контроль и оценку процесса и результатов деятельности. Коммуникативные: контролируют действия партнера |
Личностные: имеют желание учиться, применяют правила делового сотрудничества |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Вставьте пропущенный делитель. |
Отвечают на вопросы учителя. Выполняют задания устного счета. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, дополнять высказанные мнения по существу полученного задания |
|||
|
440 : 4400 : 44000 : 440000 : 4400000 : |
440 : 10 = 44 330 : 10 = 3 4400 : 100 = 44 33000 : 1000 = 33 44000 : 100 = 440 330000 : 1000 = 330 440000 : 1000 = 440 3300000 : 10000 = 330 4400000 : 10000 = 440 33000000 : 100000 = 330 |
|||||
|
– Расположите числа в порядке убывания. а) 3751, 3571, 3157, 1573 б) 1375, 1753, 5713, 7513 |
а) 3751, 3571, 3157, 1573 б) 7513, 5713, 1753, 1375 |
|||||
|
– Даны числа: 21, 30, 19, 2, 25, 15, 16, 27. Выберите из них три числа, сумма которых равна: а) 50; б) 70; в) 60 |
а) 15 + 16 + 19 = 50; 21 + 27 + 2 = 50 б) 25 + 15 + 30 = 70; 21 + 19 + 30 = 70 в) 25 + 16 + 19 = 60 |
|||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 123). Задание 7. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Сколько всего центнеров картофеля привезли? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
3 т · 3 = 9 т, 9 т = 90 ц. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Осуществлять контроль действий по результату |
|||
|
Задание 8. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение:
3) 4 т = 4000 кг 4000 – 2905 = 1095 (кг) – осталось. |
||||
|
Задание 9 |
– Составьте по рисунку задачу и решите ее |
Запись: Было – 10 т. Отгрузили – 35 ц и 4280 кг. Осталось – ? Решение: 1) 35 ц = 3500 кг 3500 + 4280 = 7780 (кг) – отгрузили. 2) 10 т = 10000 кг 10000 – 7780 = 2220 (кг) – осталось |
||||
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 125–128). Задание 19. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Назовите координаты центра каждой из окружностей. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Центр синей окружности имеет координаты (4; 4). Центр красной окружности имеет координаты (7; 4). |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
|||
|
Задание 20. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
См. Ресурсный материал к уроку. |
||||
|
Задание 21. |
– Изобразите в тетради такие многогранники. ‒ Как называется каждый из них? |
Выполняют практическую работу. – Это куб и параллелепипед. |
||||
|
Задание 22. |
– Составьте задачи и решите их. |
См. Ресурсный материал к уроку. |
||||
|
Задание 23. |
– Рассмотрите многогранник. Назовите невидимые ребра нижней грани; задней грани. – Какие грани видимые и какие невидимые?
|
– Невидимые ребра нижней грани – АВ, BC. Невидимые ребра задней грани – KB, ВС. – Видимые грани: передняя AMED, верхняя MKOE и правая боковая EOCD. Невидимые грани: нижняя ABCD, задняя BKOC и левая боковая AMKB. |
||||
|
Рубрика «Путешествие в прошлое». |
‒ Решите старинную задачу. Какие нитки обошлись Марфе дороже и на сколько? |
Решение: 1) 2 + 1 = 3 (к.) – столько катушек черных ниток. 2) 3 руб. 50 коп. – 50 коп. = 3 (р.) – стоит 1 катушка черных ниток. 3) 2 · 350 = 700 (коп.) = 7 (р.) – стоят красные нитки. 4) 3 · 300 = 900 (коп.) = 9 (р.) – стоят все черные нитки. 5) 9 р. – 7 р. = 2 р. Ответ: черные обошлись дороже на 2 рубля. |
||||
|
Задание 24. |
– Вычислите площадь четырехугольника АВСD. |
См. Ресурсный материал к уроку. |
||||
|
Задание 25. |
– Как должна выглядеть новая надпись на этикетке? |
Решение: 1) 1350 – 900 = 450 (г) – масса банки. 2) 650 + 450 = 1100 (г) – брутто. Новая надпись: НЕТТО – 650 г БРУТТО – 1100 г. |
||||
|
Задание 26. |
– На сколько меньше попаданий было у Петрова, чем у Васильева, если при каждом броске мяч попадал в корзину? |
Решение: 1) 24 : 2 = 12 (п.) – у Петрова. 2) 36 : 2 = 18 (п.) – у Васильева. 3) 18 – 12 = 6 (п.) – на столько меньше. |
||||
|
Задание 27. |
– Выполните построение (см. Ресурсный материал к уроку). |
|
||||
|
Задание 28. |
– Начертите в тетради прямоугольник. Сколькими способами можно разделить построенный прямоугольник отрезком на два равных прямоугольника? – Вычислите периметр каждого прямоугольника. Сколько решений имеет задача? |
Выполняют построение. – Это можно сделать двумя способами. Решение при первом способе деления: Р = (3 + 2) · 2 = 10 (см) Решение при втором способе деления: Р = (6 + 1) · 2 = 14 (см) |
||||
|
Задание 29 |
– В питомник для посадки привезли 480 кустов ягодных кустарников. На круговой диаграмме показано, какую часть числа всех кустов занимает каждый из этих видов кустарников. Подсчитайте число кустов смородины, малины, крыжовника и голубики, используя диаграмму |
Запись: Всего – 480 к. Смородины – ?, одна вторая Крыжовник – ?, одна восьмая Малина – ?, одна четвертая Голубика – ?, одна восьмая Решение: 480 : 8 = 60 (к.) – по стольку кустов голубики и крыжовника. 480 : 4 = 120 (к.) – кустов малины. 480 : 2 = 240 (к.) – кустов смородины |
||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Сколько килограмм в 1 тонне? – Сколько килограмм в 1 центнере? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
|||
Ресурсный материал к уроку
|
Задание 20.
Решение: 1) 150 : 5 = 30 (км/ч) – скорость по течению. 2) 30 – 12 = 18 (км/ч) – скорость против течения. 3) 18 · 3 = 54 (км) – путь против течения. Задание 22.
Решение: 24 · 5 = 120 (км)
Решение: 120 : 60 = 2 (ч)
Решение: 180 : 5 = 36 (км/ч) |
Задание 24. АВ = СЕ = 2 см АЕ = ВС = 4 см SСЕD = 6 см2 SАВСD – ?
Решение: SАВСЕ = 2 · 4 = 8 (см2) SАВСD = SАВСЕ + SСЕD SАВСD = 8 + 6 = 14 (см2) |
||||||||||||||||||||||||||||||||
|
Задание 27. 1) Начертите два треугольника так, чтобы их общей частью был треугольник. |
|
||||||||||||||||||||||||||||||||
|
2) Начертите два треугольника так, чтобы их общей частью был четырехугольник. |
|
||||||||||||||||||||||||||||||||
|
3) Начертите два треугольника так, чтобы их общей частью был пятиугольник. |
|
||||||||||||||||||||||||||||||||
|
4) Начертите два треугольника так, чтобы их общей частью был шестиугольник. |
|
Урок 47. Задачи на движение в противоположных направлениях из одной точки
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений решать текстовые задачи на движение в противоположных направлениях; побудить использовать приобретенные знания и умения в практической деятельности и повседневной жизни, при решении задач, связанных с бытовыми жизненными ситуациями (измерение) |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с движением двух тел в противоположных направлениях из одной точки, с понятием «скорость удаления»; научатся: вычислять расстояния между движущимися телами через данные промежутки времени; решать задачи на движение в противоположных направлениях из одной точки |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: определяют границы собственного знания и «незнания»; имеют мотивацию к учению |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Решите задачу. Лена сделала уроки за 1 ч 30 мин, Наташа – за 2 ч, а Валя – за 1 ч 45 мин. Кто быстрее всех сделал уроки? Кто дольше всех делал уроки? |
Отвечают на вопросы учителя. Выполняют задания устного счета.
– Лена быстрее всех сделала уроки. Наташа дольше всех делала уроки. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Запишите верные равенства: 3 мин 3 с =
5 ч 2 с = |
3 мин 3 с = 183 с 3606 с = 1 ч 6 с 76 мин = 1 ч 16 мин 2 ч 2 мин = 122 мин 5 ч 2 с = 18002 с 5 мин 5 с = 305 с |
|
|
|
– Решите задачу на смекалку. «Вот вам 3 таблетки, – сказал доктор. – Принимайте по одной через каждые 2 часа». Через сколько времени будет принята последняя таблетка? |
– Через 4 часа. |
|
|
|
– Прочитайте, вставляя пропущенные названия единиц времени. а) Урок и перемена вместе длились 60 мин, или 1 ... б) Поезд был в пути 24 ч, или 1 ... в) Геологи работали в горах 12 месяцев, или 1 ...
г) Спортсмен пробежал дистанцию за 60 с, или 1 ... |
а) Урок и перемена вместе длились 60 мин, или 1 час. б) Поезд был в пути 24 ч, или 1 сутки. в) Геологи работали в горах 12 месяцев, или 1 год. г) Спортсмен пробежал дистанцию за 60 с, или 1 минуту |
|
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 129). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Рассмотрите рисунки. В каких случаях машины движутся в одном направлении? В каких случаях – в противоположных направлениях? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– На рисунках 2 и 3 машины движутся в одном направлении. – На рисунках 1, 4, 5 машины движутся в противоположных направлениях. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Осуществлять контроль действий по результату |
|
Задание 2 |
– Прочитайте задачу. Что нам известно? На какое расстояние от палатки удалился каждый из туристов за 1 час? – Какое расстояние стало между туристами через час после начала движения? – На какое расстояние от палатки удалился каждый из туристов за 2 часа? – Какое расстояние стало между туристами через 2 часа после начала движения? – На какое расстояние от палатки удалился каждый из туристов за 3 часа? – Какое расстояние стало между туристами через 3 часа после начала движения? – Рассмотрите два способа вычисления расстояния от озера до водопада. Объясните, что означает каждая запись |
– На расстояние 6 км и 4 км от палатки удалился каждый из туристов за 1 час.
– 10 км стало между туристами через час после начала движения. – На расстояние 12 км и 8 км от палатки удалился каждый из туристов за 2 часа. – 20 км стало между туристами через 2 часа после начала движения. – На 18 км и 12 км от палатки удалился каждый из туристов за 3 часа. – 30 км стало между туристами через 3 часа после начала движения. Рассматривают разные способы вычисления, выбирают лучший (с их точки зрения) |
|
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 132–134).
Задание 5. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Найдите устно значения выражений.
– Каким свойством умножения вы пользовались? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
286 · 82 + 286 · 18 = 286 · (82 + 18) = = 286 · 100 = 28600 348 · 67 + 33 · 348 = 348 · (67 + 33) = = 348 · 100 = 34800 – Мы пользовались распределительным свойством умножения. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
|
Задание 6. |
– Выполните вычисления, используя известные вам свойства умножения. 468 · 2 · 5 = 5 · 19 · 20 = 25 · 34 · 4 = |
468 · 2 · 5 = 468 · 10 = 4680 5 · 19 · 20 = 19 · 5 · 20 = 19 · 100 = 1900 25 · 34 · 4 = 34 · 25 · 4 = 34 · 100 = 3400 |
|
|
Задание 7. |
– Прочитайте и решите задачу. Какова цена карандаша? Сколько стоит тетрадь? |
Решение: 1) 23 – 20 = 3 (р.) – цена карандаша. 2) 20 – 3 = 17 (р.) – стоит тетрадь. |
|
|
Задание 8. |
– Увеличьте на 3 десятка каждое из чисел. |
1330 + 30 = 1360 2048 + 30 = 2078 10470 + 30 = 10500 2408 + 30 = 2438 |
|
|
Задание 9. |
– Ответьте на вопросы: какая из планет наиболее удалена от Солнца? – Какая из планет находится ближе всех к Солнцу? – Какая из планет находится ближе к Солнцу: Сатурн или Марс? – Какая планета ближе к Солнцу: Земля или Венера? – Какая ближе к Солнцу: Меркурий или Юпитер? |
– Планета Нептун наиболее удалена от Солнца.
– Меркурий находится ближе всех к Солнцу.
– Марс находится ближе к Солнцу, чем Сатурн.
– Венера ближе к Солнцу, чем Земля.
– Меркурий ближе к Солнцу, чем Юпитер.
|
|
|
Задание 10. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно. |
|
|
Задание 11. |
– Каждое из чисел представьте в виде суммы двух равных слагаемых. |
48 = 24 + 24; 104 = 52 + 52; 116 = 58 + 58 |
|
|
Задание 12. |
– Каждое из чисел представьте в виде суммы двух слагаемых, разность которых равна 3. |
49 = 26 + 23 107 = 55 + 52 Число 116 нельзя представить в виде суммы двух слагаемых, разность которых равна 3. |
|
|
Задание 13. |
– Выполните действия. |
820 – 5 · 12 = 820 – 60 = 760 13 · 11 + 77 · 11 = 11 · (13 + 77) = 11 · 90 = 990 (630 + 270 : 9) : 2 = (630 + 30): 2 = 690 : 2 = 345 465102 + 559 – 10299 = 455362 240 : 3 + 150 · 3 = 80 + 450 = 530 3 · 120 – 200 : 5 = 360 – 40 = 320 730 – (170 + 290) = 730 – 460 = 270 1010101 – (782 + 18927) = 990392 |
|
|
Задание 14. |
– Сравните значения величин. |
9 км 720 м > 972 м 4520 см = 45 м 2 дм 8420 ц > 84 т 2 ц 12 т 250 кг < 12350 кг 180 мин > 2450 мин 306 кг 820 г > 36820 г |
|
|
Задание 15 |
– Сравните числа попарно |
2870 < 12600 43000 > 34000 403000 > 34000 12600 > 709 43000 < 3040 403000 > 3040 709 < 2870 403000 > 43000 34000 > 3040 |
|
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Выполняют упражнение «Волшебная палочка». Продолжают высказывание: – Если я найду волшебную палочку, я попрошу ее помочь… (кому? в чем?) |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 48. Задачи на движение в противоположных направлениях из двух точек.
Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умения решать текстовые задачи на движение в противоположных направлениях; побудить использовать приобретенные знания и умения в практической деятельности и повседневной жизни, при решении задач, связанных с бытовыми жизненными ситуациями (измерение) |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с движением двух тел в противоположных направлениях из двух точек (в случаях, когда тела удаляются друг от друга), с понятием «скорость удаления»; научатся: вычислять расстояния между движущимися телами через данные промежутки времени; решать задачи на движение в противоположных направлениях из одной точки, из двух точек |
Метапредметные: Познавательные: осуществляют моделирование; структурируют знания; осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Какие числа пропущены?
– Как найти неизвестный множитель, неизвестное слагаемое? |
Отвечают на вопросы учителя. Выполняют задания устного счета.
– Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||
|
|
– Восстановите примеры. Найдите «ловушку».
|
а) 2222 + 1034 = 3256 г) 4502 + 5201 = 9703 б) «ловушка» д) 9999 – 1036 = 8963 в) «ловушка» |
|||||||||||
|
|
‒ Выполните задание на смекалку. Сколько понадобится различных цифр, чтобы пронумеровать 200 страниц; 1222 страницы? Какие это цифры? Что интересного в этом задании? |
Ответ: 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то есть все цифры |
|||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 131). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу двумя способами.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: I способ 1) 100 · 5 = 500 (м) – прошел Антон. 2) 85 · 5 = 425 (м) – прошел Олег. 3) 500 + 425 = 925 (м) – расстояние. II способ 1) 100 + 85 = 185 (м/мин) – скорость удаления. 2) 185 · 5 = 925 (м) – расстояние. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль деятельности по результату |
||||||||||
|
Задание 4 |
– Составьте задачу по схеме. Ответьте на вопросы: На сколько километров за 3 ч удалился от села Лесное пешеход, который шел со скоростью 5 км/ч?
– На сколько километров за 3 часа удалился от села Дубки пешеход, который шел со скоростью 6 км/ч? – Какое расстояние будет между пешеходами через 3 часа? – Можно ли эту задачу решить другим способом? – На сколько километров удалятся пешеходы друг от друга за 1 час? за 3 часа?
– Какое расстояние будет между ними через 3 часа? |
– 5 · 3 = 15 (км) – на 15 километров за 3 ч удалился от села Лесное пешеход, который шел со скоростью 5 км/ч. – 6 · 3 = 18 (км) – на 18 километров за 3 часа удалился от села Дубки пешеход, который шел со скоростью 6 км/ч. – 15 + 18 + 75 = 108 (км) – 108 километров будет между пешеходами через 3 часа. – Да, эту задачу можно решить другим способом. – 5 + 6 = 11 (км) – на 11 километров удалятся пешеходы друг от друга за 1 час. – 11 · 3 = 33 (км) – на 33 километра удалятся пешеходы друг от друга за 3 часа. – 33 + 75 = 108 (км) – 108 километров будет между ними через 3 часа |
|||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 134–137). Задание 16. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Сколько костюмов можно сшить из 180 м ткани? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 120 : 30 = 4 (м) – на 1 костюм. 2) 180 : 4 = 45 (к.) – из 180 м. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
||||||||||
|
Задание 17. |
– Какую фигуру называют квадратом? Вырежите 4 такие фигуры и сложите из них квадрат. |
Выполняют практическую работу (см. Ресурсный материал к уроку). |
|||||||||||
|
Задание 18. |
– Вырежите квадрат, разрежьте по диагоналям и сложите из четырех частей два квадрата. |
См. Ресурсный материал к уроку. |
|||||||||||
|
Задание 19. |
– Почему четырехугольник, изображенный на рисунке, не является квадратом? |
– У данного четырехугольника стороны не равны. |
|||||||||||
|
Задание 20. |
– Многоугольник имеет 12 вершин. Как он называется? |
– Двенадцатиугольник. |
|||||||||||
|
Задание 21. |
– Измените порядок выполнения действий так, чтобы равенства были верными. |
Ответ: (630 + 270) : 90 : 2 = 5; 3 · (12 – 20 : 4) = 21 |
|||||||||||
|
Задание 22. |
– Одинаковые фигуры заменяют в записях одинаковые числа. Что должно быть нарисовано вместо вопросительного знака? |
1) ( (Ответ: 2) ( |
|||||||||||
|
Задание 23. |
– Какая из фигур является многогранником? |
– Фигуры 2 и 3 являются многогранниками. |
|||||||||||
|
Задание 24. |
– Вычислите длину отрезка ВС, если АМ = 8 дм, АВ = 2 дм 5 см, СМ = 1 дм 5 см. |
8 дм – 2 дм 5 см – 1 дм 5 см = 4 дм
|
|||||||||||
|
Задание 25. |
– Одинаковые ли фигуры заменяют в записях одинаковые числа? Что должно быть нарисовано вместо вопросительного знака? |
1)
Ответ: |
|||||||||||
|
Задание 26. |
– В каких случаях завяжется узел, если потянуть за концы веревочки? |
– У красной и синей нити завяжется узел, если потянуть за концы веревочки. |
|||||||||||
|
Задание 27. |
– Укажите несколько маршрутов проезда от Белорусской до Третьяковской. Называйте промежуточные станции. |
Называют варианты: 1) Белорусская – Новослободская – Цветной бульвар – Тургеневская – Театральная – Третьяковская. 2) Белорусская – Тверская – Пушкинская – Охотный ряд – Театральная – Третьяковская. 3) Белорусская – Краснопресненская – Киевская – Парк культуры – Октябрьская – Третьяковская. И т. д. |
|||||||||||
|
Задание 28 |
– Выразите массу самого большого дерева в мире в тоннах, а высоту – в метрах |
2 145 000 кг = 2145 т 8300 см = 83 м |
|||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Ресурсный материал к уроку
Задание 17. Задание 18.
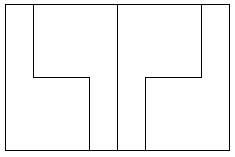
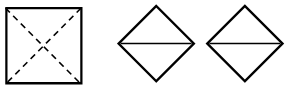
Урок 49. Пирамида
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятием «пирамида»; способствовать формированию умений различать пирамиду как пространственную фигуру, показывать вершину, основание, грани и ребра пирамиды; содействовать развитию умения выполнять изображение пирамиды на чертеже |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «пирамида как пространственная фигура»; научатся: различать пирамиду как пространственную фигуру, показывать вершину, основание, грани и ребра пирамиды; выполнять изображение пирамиды на чертеже |
Метапредметные: Познавательные: осуществляют анализ, овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи, строят логическую цепь рассуждений. Регулятивные: определяют и формулируют цель деятельности на уроке; определяют последовательность промежуточных целей с учетом конечного результата; составляют план и последовательность действий. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
Математический диктант. – Запишите числа цифрами: 25 тыс., 148 дес., 13 сот., 245 сот., 1108 дес. – Увеличьте каждое число на 2 десятка и запишите результат. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
25000, 1480, 1300, 24500, 11080 25020, 1500, 1320, 24520, 11100 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||
|
|
– Вставьте пропущенные цифры: 324 · 7 = 226 5738 · 3 = 1721 30256 · 9 = 27230 |
324 · 7 = 2268 3405 · 9 = 30645 5738 · 3 = 17214 69007 · 8 = 552056 30256 · 9 = 272304 43009 · 9 = 387081 |
|||||||||||||||
|
|
– Не вычисляя, поставьте знак >, < или = так, чтобы записи были верными: 52720 · 4 ... 52740 · 2 3604 · 60 ... 3603 · 70 42360 · 7 ... 42370 · 7 340700 · 80 ... 340900 · 60 1270 · 5 ... 1270 · 7 3705 · 30 ... 3706 · 5 · 6 |
52720 · 4 = 52740 · 2 3604 · 60 > 3603 · 70 42360 · 7 < 42370 · 7 340700 · 80 > 340900 · 60 1270 · 5 < 1270 · 7 3705 · 30 < 3706 · 5 · 6 |
|||||||||||||||
|
|
– Не выполняя умножения, расположите карточки с выражениями в порядке возрастания их значений:
|
4169 · 4, 41196 · 4, 41286 · 4, 41296 · 4, 41298 · 4, 43298 · 4 |
|||||||||||||||
|
II. Открытие нового знания, нового способа действия. Рассказ учителя.
Работа по учебнику (с. 138‒139). |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Одним из семи чудес света по праву считается пирамида Хеопса, построенная в Древнем Египте в первой половине III тысячелетия до н. э. В те времена она была самым высоким сооружением в мире: изначальная высота пирамиды равна 146 м 60 см, сторона квадратного основания – около 230 м. Пирамида Хеопса сложена более чем из 2 млн 300 тыс. каменных блоков общей массой свыше 6 млн т. В сооружении великой пирамиды и ведущей к ней дороги участвовали 100 тыс. человек. Форма пирамиды часто используется и в современном строительстве. Например, в виде пирамиды оформляются крыши башен, кафе, беседок, дачных домов. Форму пирамиды имеют и некоторые предметы быта. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества |
||||||||||||||
|
Задание 1. |
– Возьмите модель пирамиды и рассмотрите ее поверхность. Объясните, почему пирамида является многогранником. |
Читают определение в толковом словаре: – Пирами́да – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырехугольные и т. д. |
|||||||||||||||
|
Задание 2 |
– Рассмотрите чертеж пирамиды. Назовите ее основание, боковые грани, ребра, вершину. От чего зависит название пирамиды? |
Называют. – У любой пирамиды боковые грани – треугольники, а основание – многоугольник. Название пирамиды зависит от формы основания. Если основание – треугольник, то пирамиду называют треугольной, если основание четырехугольник – то четырехугольной, и так далее |
|||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 140–141). Задание 5. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– В таблице приведены данные о пяти самых больших по площади странах мира. Найдите эти страны на карте. – Ответьте на вопросы, используя данные таблицы: – Какая из этих стран имеет самую большую и какая – самую маленькую площадь?
– На сколько квадратных километров площадь России больше площади Канады? – Какую площадь имеет Китай? На сколько она меньше площади США? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Находят.
– Россия имеет самую большую, а Китай – самую маленькую площадь из пяти самых больших стран. – На 7 104 790 квадратных километров площадь России больше площади Канады. – Площадь Китая – 5 536 720 кв. км. На 3 826 480 кв. км она меньше площади США. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
||||||||||||||
|
Задание 6. |
– Проверьте результаты действий. Есть ли в вычислениях ошибки? |
1 400 м – 967 м = 433 м – верно 3 км – 305 м = 2 км 595 м – неверно 5 т – 3 т 178 кг = 822 кг – неверно 25 ц 30 кг + 5 ц 70 кг = 31 ц – верно |
|||||||||||||||
|
Задание 7. |
– Цена рамы составляет шестую часть цены картины. Рама стоит 150 р. Какова стоимость картины в раме? |
Запись:
Решение: 150 · 6 = 900 (р.) – цена картины. 900 + 150 = 1050 (р.) – стоит картина в раме. |
|||||||||||||||
|
Задание 8. |
– Расставьте скобки так, чтобы равенства стали верными. |
1) 240 : (6 · 5 – 20) = 24 2) (480 – 200) : 4 · 5 = 350 |
|||||||||||||||
|
Задание 9 |
– Понаблюдайте, как изменяются числа в выражениях. Запишите еще по три выражения в каждом столбце и выполните вычисления |
100 + 10 · 1 = 110 260 – (10+10) = 240 100 + 20 · 2 = 140 360 – (20 +20) = 320 100 + 30 · 3 = 190 460 – (30 + 30) = 400 100 + 40 · 4 = 260 560 – (40 + 40) = 480 100 + 50 · 5 = 350 660 – (50 +50) = 560 100 + 60 · 6 = 460 760 – (60 + 60) = 640 100 + 70 · 7 = 590 860 – (70 + 70) = 720 |
|||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что нового вы узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности; анализировать причины неудачи |
Урок 50. Пирамида. Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием «пирамида»; способствовать формированию умений различать пирамиду как пространственную фигуру, показывать вершину, основание, грани и ребра пирамиды; содействовать развитию умения выполнять изображение пирамиды на чертеже |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «пирамида как пространственная фигура»; научатся: различать пирамиду как пространственную фигуру, показывать вершину, основание, грани и ребра пирамиды; выполнять изображение пирамиды на чертеже |
Метапредметные: Познавательные: понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи; осуществляют анализ объектов с целью выделения их признаков (существенных, несущественных). Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: умеют задавать вопросы; формулируют собственное мнение и позицию |
Личностные: в совместной деятельности определяют цели и функции участников, способы взаимодействия |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Решите задачу. Сосна может прожить 600 лет, ель – вдвое дольше, чем сосна, а дуб – на 800 лет больше ели. Сколько лет может прожить дуб? Выберите выражение, которое является решением задачи: а) 600 : 2 + 800 б) 600 · 2 + 800 в) 600 · 2 – 800 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
– Это выражение 600 · 2 + 800. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||
|
|
– Вычислите значения произведений. а) 41 сот. · 2 в) 9 дес. · 8 д) 13 дес. · 5 б) 4 · 12 сот. г) 8 · 7 дес. е) 3 тыс. · 3 |
а) 82 сот. в) 72 дес. д) 65 дес. б) 48 сот. г) 56 дес. е) 9 тыс. |
|||
|
|
– Вычислите: а) На сколько сотен 9 тысяч больше 3 тысяч? б) На сколько десятков 1 сотня меньше 6 сотен? в) На сколько единиц 2 сотни больше 1 десятка? г) На сколько единиц 3 сотни больше 1 единицы? д) Увеличьте 9 десятков в 8 раз. е) Увеличьте 3 тысячи на 3 единицы. ж) Увеличьте 3 тысячи в 3 раза. з) Во сколько раз 9 тысяч больше 3 тысяч? и) Увеличьте 41 сотню в 2 раза. |
а) На 60 сотен 9 тысяч больше 3 тысяч. б) На 50 десятков 1 сотня меньше 6 сотен. в) На 190 единиц 2 сотни больше 1 десятка. г) На 299 единиц 3 сотни больше 1 единицы. д) 720. е) 3003. ж) 9000. з) В 3 раза 9 тысяч больше 3 тысяч. и) 8200. |
|||
|
|
– Соедините равные величины: 126 г 4830 м 5 м2 3005 г 4 км 83 м 3500 г 3 кг 5 г 126 кг 4 км 830 м 500 дм2 4083 м |
|
|||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 139–140). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– В чем отличие пирамиды от прямоугольного параллелепипеда? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Прямоугольный параллелепипед – объемная фигура, у которой шесть граней и каждая из них является прямоугольником. У пирамиды же боковые грани являются треугольниками, а основание может быть треугольником, четырехугольником, пятиугольником и т. д. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей, обосновывать свой выбор |
||
|
Задание 4 |
– Используя палочки и пластилин, сделайте такие же модели пирамиды. Какой фигурой является основание каждой из пирамид? Как называется каждая из этих пирамид? |
Выполняют построение. – Основанием первой пирамиды является пятиугольник. Это пятиугольная пирамида. Основанием второй пирамиды является шестиугольник. Это шестиугольная пирамида |
|||
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 142). Задание 10. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Вычислите и проверьте умножение делением, а деление умножением. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
954 : 9 = 106 106 · 9 = 954 920 : 4 = 230 230 · 4 = 920 864 : 12 = 72 72 · 12 = 864 205 · 3 = 615 615 : 3 = 205 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
||
|
Задание 11. |
– Охарактеризуйте фигуру (название, число звеньев, число вершин). |
– Первая ломанная имеет 5 звеньев, 6 вершин. – Вторая ломаная имеет 4 звена, 5 вершин. |
|||
|
Задание 12. |
– Вырежите прямоугольник с длинами сторон 8 см и 4 см. Отрежьте от прямоугольника полоску шириной 1 см. Вычислите площадь оставшейся части. Сколько решений имеет задача? Обсудите с соседом по парте варианты выполнения задания. Пусть каждый из вас выберет свой вариант и выполнит работу. Затем проверьте работу друг друга. |
– Задача имеет два решения: Решение 1. (8 – 1) · 4 = 28 (см2) Решение 2. 8 · (4 – 1) = 24 (см2) |
|||
|
Задание 13. |
– Какая единица не является единицей массы: грамм, тонна, метр, центнер? – Какая единица не является единицей скорости: км/ч, м/с, м/мин, км, см/с? |
– Метр не является единицей массы.
– Километр не является единицей скорости. |
|||
|
Задание 14 |
– Выразите скорость: 180 м/мин в метрах в секунду; 4 м/с в метрах в минуту; 5 км/мин в километрах в час |
Запись: 180 м/мин = 3 м/с 4 м/с = 240 м/мин 5 км/мин = 300 км/ч |
|||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель предлагает оценить свою работу на уроке: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Продолжают высказывания: • теперь я могу… • я научился… • у меня получилось… • я смог… |
Выражать доброжелательность и отзывчивость. Оценивать результаты деятельности |
Урок 51. Задачи на встречное движение в противоположных направлениях
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «встречное движение» и «скорость сближения»; способствовать формированию умений решать текстовые задачи на встречное движение в противоположных направлениях; побудить использовать приобретенные знания и умения в практической деятельности и повседневной жизни, при решении задач, связанных с бытовыми жизненными ситуациями (измерение) |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «встречное движение» и «скорость сближения»; научатся решать задачи на встречное движение в противоположных направлениях |
Метапредметные: Познавательные: ориентируются на возможное разнообразие способов решения учебной задачи; формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. – Решите задачу. Две морские черепахи одновременно начали движение по берегу навстречу друг другу и встретились через 15 минут. Скорость одной была 7 м/мин, а скорость другой – 8 м/мин. На каком расстоянии находились черепахи до начала движения? |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
7 · 15 + 8 · 15 = 105 + 120 = 225 (м) Ответ: 225 м. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта |
||||||
|
|
– Поставьте знак >, < или =. 17 м ... 170 см 112 см ... 112 дм 250 см ... 25 дм 7 км 50 м ... 75000 м 12 м2 ... 1200 дм2 12 см 3 мм ... 1 дм 23 см |
17 м > 170 см 112 см < 112 дм 250 см = 25 дм 7 км 50 м < 75000 м 12 м2 = 1200 дм2 12 см 3 мм <1 дм 23 см |
|||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 143). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Прочитайте задачу. Рассмотрите схему движения мальчиков. Как называется этот вид движения? – Сколько времени до встречи был в пути Миша? – А сколько был в пути до встречи Петя? – С какой скоростью шел Миша?
– С какой скоростью шел Петя?
– Какое расстояние между поселками? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Это встречное движение.
– 15 минут до встречи был в пути Миша.
– 15 минут был в пути до встречи Петя. – 900 : 15 = 60 (км/ч) – со скоростью 60 км/ч шел Миша. – 870 : 15 = 58 (км/ч) – со скоростью 58 км/ч шел Петя. – 900 + 870 = 1770 (м) – 1770 метров между поселками. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Осуществлять контроль действий по результату |
||||||
|
Задание 2 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу разными способами |
Решение: I способ 1) 60 · 2 = 120 (км) – проехал 1-й мотоциклист. 2) 75 · 2 = 150 (км) – проехал 2-й мотоциклист. 3) 120 + 150 = 270 (км) – расстояние. II способ 1) 60 + 75 = 135 (км/ч) – скорость сближения. 2) 135 · 2 = 270 (км) – расстояние |
|||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 146). Задание 5. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
||||||
|
Задание 6. |
– Запишите все числа в порядке уменьшения, начиная с самого большого. |
77 777 777, 1 002 615, 500 880, 400 004, 90 909, 32 323, 20 057, 13 837. |
|||||||
|
Задание 7. |
– Уменьшите на 4 сотни каждое из чисел. |
80 523 – 400 = 80 123 12 400 – 400 = 12 000 1000 – 400 = 600 |
|||||||
|
Задание 8. |
– Вычислите значение выражения х · у. |
а) если х = 50, у = 20, то 50 · 20 = 1000; б) если х = 15, у = 8, то 15 · 8 = 120; в) если х = 7, у = 120, то 7 · 120 = 840; г) если х = 250, у = 4, то 250 · 4 = 1000. |
|||||||
|
Задание 9 |
– Запишите выражения для определения площади каждого из участков. – Выполните вычисления, подставляя вместо х число 20, а вместо у – число 32 |
Запись: а) х · 35 б) 30 · у Выполняют вычисления, подставляя вместо х число 20, а вместо у – число 32. а) 20 · 35 = 700 (м2) б) 30 · 32 = 960 (м2) |
|||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Объясните понятия «встречное движение» и «скорость сближения». – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий. – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
Прием «Солнышко». На доске прикреплен круг – это солнышко. Детям раздаются лучики желтого и голубого цветов. Лучики нужно прикрепить к солнышку: желтого цвета – мне очень понравилось занятие, я получил(а) много интересной информации; голубого цвета – занятие неинтересное, не было никакой полезной информации
|
Способны проводить самооценку на основе критериев успешности учебной деятельности, выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 52. Упражнение в решении задач на встречное движение
в противоположных направлениях.
Контрольный устный счет № 4
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений решать текстовые задачи на встречное движение в противоположных направлениях |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «встречное движение» и «скорость сближения»; научатся решать задачи на встречное движение в противоположных направлениях |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: излагают свое мнение и аргументируют свою точку зрения |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Расставьте скобки так, чтобы выражение 60 – 24 : 3 + 1 имело значение: а) 54; б) 9; в) 53; г) 13; д) 51. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. а) 60 – 24 : (3 + 1) = 54 б) (60 – 24) : (3 + 1) = 9 в) 60 – (24 : 3) + 1 =53 г) (60 – 24) : 3 + 1 = 13 д) 60 – (24 : 3 + 1) = 51 |
Выделять существенную информациюиз текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения о существу полученного задания |
||||||||||||||||||||
|
|
– Решите задачу. Заяц в лесу столкнулся с медведем, и от неожиданности они бросились бежать в разные стороны. Заяц побежал со скоростью 18 м/с, а медведь – со скоростью 6 м/с. На каком расстоянии они оказались друг от друга через полминуты? |
Ответ: 720 м. |
|||||||||||||||||||||
|
|
– Используя данные таблицы о скоростях, с которыми летают птицы, составьте задачи на движение.
|
Пример задачи: Орел летит со скорость 160 км/ч. Какое расстояние он пролетит за 3 часа? И т. д. |
|||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 144). Задание 3 |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Прочитайте задачу. Рассмотрите схему движения теплоходов. Ответьте на вопросы: сколько часов до встречи был в пути каждый теплоход? – Сколько километров до встречи прошел теплоход, скорость которого 34 км/ч? – Сколько километров до встречи прошел другой теплоход? – С какой скоростью шел другой теплоход? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– 11 – 8 = 3 (ч) – 3 часа до встречи был в пути каждый теплоход. – 34 · 3 = 102 (км) – 102 километра до встречи прошел теплоход, скорость которого 34 км/ч. – 210 – 102 = 108 (км) – 108 километров до встречи прошел другой теплоход. – 108 : 3 = 36 (км/ч) – со скоростью 36 км/ч шел другой теплоход |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль действий по результату |
||||||||||||||||||||
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 147–148). Задание 10. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните вычисления. Какие математические правила
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Находят значение выражения: 1189. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
||||||||||||||||||||
|
Задание 11. |
– Выполните действия. |
26 · 9 = 234 616 : 11 = 56 125 · 5 = 625 18 · 15 = 270 300 : 150 = 2 230 · 4 = 920 927 : 3 = 309 870 : 435 = 2 |
|||||||||||||||||||||
|
Задание 12. |
– Заполните таблицу и ответьте на вопросы: сколько раз выпало по 3 очка? – Какое число очков выпадало чаще всех остальных? – Сколько очков выпало наименьшее число раз? – Повторите действия Кати. Запишите получившиеся результаты и занесите их в таблицу. Сравните. |
– Три раза выпало по 3 очка. – Четыре очка выпадало чаще всех остальных. – Три очка выпало наименьшее число раз. |
|||||||||||||||||||||
|
Задание 13 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Запись: Было – 3 р. по 60 м. Продали – ? м (пятую часть) Осталось – ? м Решение: 1) 60 · 3 = 180 (м.) – было. 2) 180 : 5 = 36 (м.) – продали. 3) 180 – 36 = 144 (м.) – осталось |
|||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
Прием «Мордашки». Данный прием рефлексии эмоционального состояния может использоваться на различных этапах урока. Учащиеся рисуют или выбирают из имеющихся те «мордашки», которые соответствуют их настроению |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Оценивать результаты деятельности |
Урок 53. Упражнение в решении задач на движение
в противоположных направлениях
Проверочная работа по теме «Задачи на движение в противоположных направлениях»
|
Тип урока: контроль и оценка знаний и умений |
||
|
Педагогические задачи: способствовать формированию умений решать текстовые задачи на движение в противоположных направлениях; совершенствовать вычислительные навыки |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «встречное движение» и «скорость сближения»; научатся решать задачи на движение в противоположных направлениях (в том числе встречное движение) |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; строят логическую цепь рассуждений. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: умеют устанавливать, с какими учебными задачами могут справиться самостоятельно |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. – Запишите ответ выражением, найдите его значение. а) За один прыжок кенгуру продвигается на 12 м. На сколько метров продвигается кенгуру за 3 прыжка? б) Масса булочки 75 г, масса куска сыра 25 г. Какова масса бутерброда? в) Длина тела кита 26 м, а тюленя – 2 м. Во сколько раз тюлень короче кита? г) От Москвы до нашей станции по шоссе 400 км, а по железной дороге на 30 км меньше. Сколько километров от Москвы до нашей станции по железной дороге? д) Синица может пролететь за день 100 км, а скворец – 75 км. На сколько километров больше может пролететь синица, чем скворец? е) Электропоезд из Москвы отправляется в 18 ч 4 мин и прибывает во Владимир в 20 ч 34 мин, не делая ни одной остановки. Сколько времени электропоезд находится в пути? |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
а) 12 · 3 = 36 (м)
б) 75 + 25 = 100 (г)
в) 26 : 2 = 13 (раз)
г) 400 – 30 = 370 (км)
д) 100 – 75 = 25 (км)
е) 20 ч 34 мин – 18 ч 4 мин = 2 ч 30 мин |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||
|
|
– Выполните задание на смекалку. Два мальчика играли в шахматы 40 минут. Сколько времени играл каждый из них? |
Ответ: 40 минут. |
||||||||
|
|
– Проверьте, верны ли равенства: 7 км 080 м = 70800 м 4 ч 30 мин = 430 мин 10 т 300 кг = 10300 г 8 мин 20 с = 500 с |
7 км 080 м = 70800 м – неверно 4 ч 30 мин = 430 мин – неверно 10 т 300 кг = 10300 г – верно 8 мин 20 с = 500 с – верно |
||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 145). Задание 4 |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Прочитайте задачу. Рассмотрите схему движения поездов. Решите задачу. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 1) 50 + 40 = 90 (км/ч) – скорость сближения. 2) 720 : 90 = 8 (ч) – через столько времени встретятся |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей |
|||||||
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 148–150). Задание 14. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 9 · 5 = 45 (шт.) – шаров. 2) 45 · 2 = 90 (шт.) – колокольчиков. 3) 90 : 6 = 15 (шт.) – колокольчиков в 1 коробке. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять взаимный контроль действий, планировать способы взаимодействия |
|||||||
|
Задание 15. |
– Чему равна масса портфеля? |
Решение: 20 кг – 10 кг 250 г – 6кг 130 г = = 3 кг 620 г |
||||||||
|
Задание 16. |
– Докажите, что прямая АВ не является осью симметрии семиугольника. |
– Точки удалены на разное расстояние относительно прямой АВ, поэтому она не является осью симметрии. |
||||||||
|
Задание 17. |
– Назовите два четырехугольника, у которых общей является вершина А. – Назовите два четырехугольника, у которых общей является сторона МО. – Назовите два четырехугольника, у которых общей является сторона СD. |
– Два четырехугольника, у которых общей является вершина А, это АВСD и ABOM. – Два четырехугольника, у которых общей является сторона МО, это ABOM и OMСD. – Два четырехугольника, у которых общей является сторона СD, это АВСD и OMСD. |
||||||||
|
Задание 18. |
– Вычислите периметр фигуры. |
Р = 3 · 2 + 6 · 2 = 18 (см)
|
||||||||
|
Задание 19. |
– Масса бублика 80 г. Ватрушка на 40 г тяжелее бублика. Какова масса пяти ватрушек? |
Решение: 80 + 40 = 120 (г) – масса 1 ватрушки. 120 · 5 = 600 (г) – масса 5 ватрушек. |
||||||||
|
Задание 20. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 750 – 250 = 500 (г) – маленький пакет. 2) 500 · 10 = 5000 (г) = 5 кг – в 10 маленьких пакетах. |
||||||||
|
Задание 21 |
– Рассмотрите рисунок и ответьте на вопросы: в какое время катер отошел от пристани? – Вычислите, с какой скоростью он шел. – На каком расстоянии от пристани катер был в 13 часов; в 14 часов; в 11 часов 30 минут; в 13 часов 30 минут? – В какое время катер находился от пристани на расстоянии 30 км; 45 км; 105 км? |
– В 11 часов катер отошел от пристани. – Скорость катера 30 км/ч. – На расстоянии 60 км от пристани катер был в 13 часов; в 14 часов – 90 км; в 11 часов 30 минут – 15 км; в 13 часов 30 минут – 75 км. – В 12 часов катер находился от пристани на рас-стоянии 30 км; в 12 часов 30 минут – 45 км; в 14 часов 30 минут – 105 км |
||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий. – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
Прием «Светофор». Учащимся в начале урока раздают по три кружочка: красный, желтый и зеленый. После урока или выполненной работы ребята должны высказать свое мнение по вопросу об этом уроке: красный – нет (что не понравилось, какие были ошибки), желтый – не совсем (сомнения, трудности) и зеленый – да (что понравилось, что получилось) |
Способны проводить самооценку на основе критериев успешности учебной деятельности (оценивать свои достижения, степень самостоятельности, инициативности) |
Урок 54. Умножение многозначного числа на однозначное
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с алгоритмом письменного умножения многозначного числа на однозначное; способствовать формированию умений выполнять устные и письменные вычисления с натуральными числами; содействовать развитию умения выполнять проверку с помощью калькулятора |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на однозначное; научатся: применять алгоритм письменного умножения многозначного числа на однозначное; выполнять устные и письменные вычисления с натуральными числами |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учета интересов сторон и сотрудничества |
Личностные: формируют внутреннюю позицию школьника на уровне положительного отношения к школе; приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Найдите ошибки, которые допустил ученик, составляя ряды чисел: а) 640, 660, 680, 720, 740, ... б) 987, 876, 765, 655, 543, ... в) 111, 222, 333, 455, 444, 555, ... |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
а) 640, 660, 680, 700, 720, 740, ... б) 987, 876, 765, 654, 543, ... в) 111, 222, 333, 455, 444, 555, ... |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Дополнять высказанные мнения |
|||||||||||||||||
|
|
– Вычислите: 700 · 3 37500 · 26 – 37500 · 25 8000 · 3 90 · 4 83 · 61 + 83 · 39 76800 · 6 + 76800 · 4 578 · 193 + 578 · 807 80 · 70 |
700 · 3 =2100 37500 · 26 – 37500 · 25 = 37500 8000 · 3 = 24000 90 · 4 = 360 83 · 61 + 83 · 39 = 8300 76800 · 6 + 76800 · 4 =768000 578 · 193 + 578 · 807 = 578000 80 · 70 = 5600 |
||||||||||||||||||
|
|
Задача. Дети вырезали на уроках труда геометрические фигуры. Их оказалось 32000. Сколько нужно пакетиков, если в каждый положить по одному десятку фигур; по одной сотне; по одной тысяче? |
Ответ: 3200; 320; 32 пакетика |
||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 151–152). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Составьте алгоритм умножения многозначного числа на однозначное. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Составляют алгоритм умножения многозначного числа на однозначное. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
|||||||||||||||||
|
Задание 2. |
– Выполните умножение. |
126 · 4 = 504 596 · 4 = 2384 205 · 9 = 1845 480 · 9 = 4320 675 · 9 = 6075 706 · 8 = 5648 608 · 5 = 3040 903 · 8 = 7224 284 · 5 = 1420 404 · 7 = 2828 290 · 7 = 3040 560 · 8 = 4480 338 · 7 = 2366 208 · 4 = 832 210 · 4 = 840 408 · 2 = 816 |
||||||||||||||||||
|
Задание 3. |
– Верно ли высказывание: «Если один из множителей равен 1, то произведение равно другому множителю»? Приведите примеры. – Сформулируйте правило об умножении любого числа на число 0. |
Запись: а · 1 = а, 1 · а = а Приводят примеры.
а · 0 = 0, 0 · а = 0 |
||||||||||||||||||
|
Задание 4. |
– Заполните таблицу. |
|
||||||||||||||||||
|
Задание 5. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 820 · 4 = 3280 (кг) – увезли со 2-го склада. 2) 3280 + 820 = 4100 (кг) – увезли всего. 3) 6080 – 4100 = 1980 (кг) – осталось на 1-м складе. |
||||||||||||||||||
|
Задание 6. |
– Выполните задание в парах. |
Работают в парах. |
||||||||||||||||||
|
Задание 7 |
– Найдите значение выражения 630 · х + 125 · у |
а) Если х = 3, у = 5, то 630 · 3 + 125 · 5 = = 1890 + 625 = 2515 б) если х = 5, у = 3, то 630 · 5 + 125 · 3 = = 3150 + 375 = 3525 в) если х = 4, у = 4, то 630 · 4 + 125 · 4 = = 4 · (630 + 125) = 4 · 755 = 3020 |
||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 155–156). Задание 19. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Сравните значения величин. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
18 ц 20 кг < 1 т 82 ц 125 кг 60 г < 125 кг 600 г 400 т 560 кг < 401 т 32 кг 156 г > 31 кг 900 г |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
|||||||||||||||||
|
Задание 20. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно. |
||||||||||||||||||
|
Задание 21. |
– Какое расстояние между сорокой и галкой? Найдите два решения этой задачи. |
Решение: Если ворона сидит посередине, то 32 метра между сорокой и галкой. Если галка сидит посередине, то 8 метров между сорокой и галкой. |
||||||||||||||||||
|
Задание 22. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 20 · 3 = 60 (км) – расстояние между пристанями. 2) 60 : 30 = 2 (ч) – на теплоходе. 3) 3 – 2 = 1 (ч) – на столько часов меньше. |
||||||||||||||||||
|
Задание 23. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись:
Решение: 1) 300 : 4 = 75 (км) – прошел автобус. 2) 300 : 6 = 50 (км) – прошла машина. 3) 75 – 50 = 25 (км) – на столько меньше идти автобусу. |
||||||||||||||||||
|
Задание 24 |
– Подставьте в каждое неравенство вместо х число 285. Верно или неверно каждое из неравенств при этом значении х? |
1000 – 285 < 700 – неверно 650 + 285 > 936 – неверно |
||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? ‒ Как выполнить умножение в столбик? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности, выражать доброжелательность, отзывчивость |
Урок 55. Умножение вида 1258 · 7, 4040 · 9
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного умножения многозначного числа на однозначное; способствовать формированию умений выполнять устные и письменные вычисления с натуральными числами, делать проверку с помощью калькулятора |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на однозначное; научатся: применять алгоритм письменного умножения многозначного числа на однозначное; выполнять устные и письменные вычисления с натуральными числами вида 1258 · 7, 4040 · 9 |
Метапредметные: Познавательные: осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: составляют план и последовательность действий; умеют прогнозировать, предвосхищать результат своих действий и уровень усвоения материала, его временные характеристики; осуществляют контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона. Коммуникативные: полно и точно выражают свои мысли в соответствии с задачами и условиями коммуникации; владеют монологической и диалогической формами речи в соответствии с нормами родного языка и современных средств коммуникации; принимают участие в работе парами и группами |
Личностные: владеют основными моральными нормами поведения; осознают роль языка и речи в жизни людей; приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. – Разгадайте правило, по которому составлены схемы, и вставьте числа в «окошки»:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. 8000 = 8 · 1000 9000 = 30 · 300 2000 = 2 · 1000 4000 = 100 · 40 900 = 9 · 1000 7000 = 100 · 70
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||
|
|
– Вычислите длину забора вокруг сада (периметр) разными способами: а) б)
|
Решение: а) Р = (62 + 38) · 2 = 100 · 2 = 200 Р = 62 · 2 + 38 · 2 = 200 б) Р = (25 + 75) · 2 = 100 · 2 = 200 Р = 25 · 2 + 75 · 2 = 200
|
||||||||||||||
|
|
– Вычислите площади фигур, используя мерку:
– Почему одни из вас решили эту задачу быстро, а другие – медленно? Как легче вычислить площадь второй фигуры? |
Вычисляют площади фигур, при этом часть детей решают эту задачу быстрее, часть – медленнее.
– Вторую фигуру можно «превратить» в прямоугольник, переложив квадраты |
||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 153). Задание 8. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 1) 2532 · 3 = 7596 (дет.) – в 1 большом ящике. 2) 2532 · 7 = 17724 (дет.) – в 7 маленьких ящиках. 3) 7596 · 10 = 75960 (дет.) – в 10 больших ящиках. 4) 75960 + 17724 = 93684 (дет.) – всего. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
|||||||||||||
|
Задание 9. |
– Выполните умножение. Какие знания вам помогли? |
1258 · 7 = 8806 110084 · 4 = 440336 5072 · 4 = 20288 41005 · 3 = 123015 60005 · 3 = 180015 973 · 5 = 4865 12587 · 6 = 75522 40003 · 8 = 320024 1364 · 2 = 2728 |
||||||||||||||
|
Задание 10. |
– Выполните действия. |
8 · 24372 – (12143 + 11778) · 7 = 27529 100 · (11372 – 10599) · 6 – (19060 – 15367) · 4 = = 449028 42178 · 4 – (24375 – 3979) · 8 + 90 · 10 : 5 = 5724 180 : 12 · 1000 – 906 : 3 + 3007 · 2 = 35747 |
||||||||||||||
|
Задание 11 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Решение: 1) 950 · 3 = 2850 (км) – за 3 часа. 2) 650 · 2 = 1300 (км) – за 2 часа. 3) 2850 + 1300 = 4150 (км) – всего |
||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 156–157). Задание 25. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 750 : 25 = 30 (мин) – на 1-м станке. 2) 750 : 30 = 25 (мин) – на 2-м станке. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
|||||||||||||
|
Задания 26, 27. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
См. ресурсный материал к уроку. |
||||||||||||||
|
Задание 28. |
– Достаточно ли купить 15 м ткани, чтобы сшить шторы на 3 окна, если на каждое окно нужно две полосы этой ткани длиной 2 м 60 см каждая? |
Решение: 1) 260 · 2 = 520 (см) – на одно окно. 2) 520 · 3 = 1560 (см) – на три окна. 1560 см = 15 м 60 см Ответ: 15 м не хватит. |
||||||||||||||
|
Задание 29. |
– Сколько звеньев у ломаной? Какова длина этой ломаной? – Изобразите ломаную такой же длины, но состоящую из трех звеньев. |
– Два звена у ломаной. 7 см – длина ломаной.
|
||||||||||||||
|
Задание 30. |
– Решите задачу на встречное движение. |
Решение: 1) 65 + 70 = 135 (км/ч) – скорость сближения. 2) 135 км + 8 км 500 м = 143 км 500 м. |
||||||||||||||
|
Задание 31 |
– У какого из многоугольников все вершины лежат на окружности? |
1) У треугольника; 2) у красного четырехугольника |
||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что нового вы узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию
|
Оценивать результаты деятельности, уровень владения учебным действием, формировать адекватную самооценку |
|||||||||||||
Ресурсный материал к уроку
|
Задание 26.
Решение: 1) 40 · 7 = 280 (дет.) – объем работы. 2) 280 : 10 = 28 (дет./мин) – производительность 2-го станка. |
Задание 27.
Решение: 1) 240 : 3 = 80 (км/ч) – скорость 1-го катера. 3) 80 : 4 = 20 (км/ч) – скорость 2-го катера. 2) 80 : 20 = 4 (раза) – во столько раз скорость 1-го катера больше. |
Урок 56. Упражнение в умножении многозначного числа на однозначное число
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного умножения многозначного числа на однозначное; способствовать формированию умений выполнять устные и письменные вычисления с натуральными числами, делать проверку с помощью калькулятора |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на однозначное; научатся: применять алгоритм письменного умножения многозначного числа на однозначное; выполнять устные и письменные вычисления с натуральными числами |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: умеют формулировать учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще не известно; контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками: определяют цели и функции участников, способы взаимодействия; проявляют инициативное сотрудничество в поиске и сборе информации |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Подберите такой второй множитель, чтобы выполнялись следующие условия:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу |
||||||||||||
|
|
– Используя данные равенства, найдите значения произведений. 327 · 5 = 1635 3007 · 4 = 12028 327 · 4 = 327 · 6 = |
327 · 5 = 1635 3007 · 4 = 12028 327 · 4 = 1308 3008 · 4 = 12032 327 · 6 = 1962 3007 · 3 = 9021 |
|||||||||||||
|
|
– Подумайте: >, < или = ? 97 · 9 … 97 · 90 970 · 90 … 9700 · 90 56 · 8 … 506 · 8 5060 · 8 … 5060 · 80 |
97 · 9 < 97 · 90 970 · 90 < 9700 · 90 56 · 8 < 506 · 8 5060 · 8 < 5060 · 80 |
|||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 153–154). Задание 12. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Выполните умножение. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
1700 · 8 = 13600 303800 · 2 = 607600 4050 · 5 = 20250 180400 · 8 = 1443200 20300 · 6 = 121800 345090 · 5 = 1725450 44500 · 3 = 133500 810000 · 9 = 7290000 12100 · 4 = 48400 1000200 · 5 = 5001000 25040 · 7 = 175280 2120000 · 4 = 8480000 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль деятельности по результату |
||||||||||||
|
Задание 13. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
См. ресурсный материал к уроку. |
|||||||||||||
|
Задание 14. |
– Длина каждой стороны девятиугольника 12 дм 8 см. Вычислите его периметр. |
12 дм 8 см = 128 см 128 · 9 = 1152 (см) = 11 м 52 см ‒ периметр девятиугольника. |
|||||||||||||
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 75 + 82 = 157 (км/ч) – скорость сближения. 2) 157 · 4 = 628 (км) – расстояние. |
|||||||||||||
|
Задание 16. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу двумя способами. |
См. ресурсный материал к уроку. |
|||||||||||||
|
Задание 17. |
– Прочитайте и решите задачу. |
Решение: 1) 124 р. 50 к. + 96 р. = 220 р. 50 к. – стоит 1 кг конфет и 1 кг пряников. 2) 220 р. 50 к. · 8 = 1764 р. – стоимость покупки. |
|||||||||||||
|
Задание 18 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Решение: 1) 850 + 850 = 1700 (км/ч) – скорость удаления друг от друга. 2) 1700 · 3 = 5100 (км) – расстояние через 3 часа |
|||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 157–158). |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу двумя способами.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись:
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль деятельности, планировать способы взаимодействия |
||||||||||||
|
Задание 32. |
|
Решение:
3) 37 + 29 = 66 (ящ.) – потребуется |
|||||||||||||
|
Задание 33. |
– Вычислите периметр двадцатиугольника, длина каждой стороны которого равна 3 см 5 мм. Выразите результат в сантиметрах. |
Решение: 3 см 5 мм · 20 = 70 см ‒ периметр двадцатиугольника. |
|||||||||||||
|
Задание 34. |
– Начертите отрезок АВ в масштабе 5 : 1. |
Чертят отрезок длиной 10 см. |
|||||||||||||
|
Задание 35. |
– Прочитайте и решите задачу. |
Решение: 1) 60 : 12 = 5 (раз) – во столько раз меньше. 2) 35 : 5 = 7 (км) – за 12 мин. |
|||||||||||||
|
Задание 36. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 1 т = 1000 кг 1000 : 15 = 200 (кг) – отходы. 2) 1000 – 200 = 800 (кг) – пшено. 3) 800 : 50 = 16 (меш.) – пшена. |
|||||||||||||
|
Задание 37. |
– Решите задачу на движение в противоположных направлениях. |
Решение: 1) 950 + 850 = 1800 (км/ч) – скорость удаления. 2) 60 : 30 = 2 (раза). 3) 1800 : 2 = 900 (км) – будет между ними через 30 минут. |
|||||||||||||
|
Задание 38 |
– Как быстрее доехать на метро от станции «Дмитровская» до станции «Автозаводская»? |
Работают со схемой метро |
|||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Прием «Карта настроения». Ученики заполняют карточки эмоционального состояния, в которых отмечают свое самочувствие, указывают свое отношение к уроку, вписывая то, что понравилось (не понравилось) во время урока |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Ресурсный материал к уроку
|
Задание 13.
Решение: 1) 8 т 200 кг · 4 = 32 т 800 кг – вывезли со 2-й базы. 2) 32 т 800 кг + 8 т 200 кг = 41 (т) – всего вывезли. 3) 45 т – 41 т = 4 (т) – осталось на 1-й базе. 4) 4 т + 8 т 200 кг = 12 т 200 кг – было на 1-й базе. |
Задание 16.
|
Урок 57. Алгоритм умножения многозначного числа на двузначное
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с алгоритмом письменного умножения многозначного числа на двузначное в пределах миллиарда; способствовать формированию умений выполнять развернутые и упрощенные записи алгоритма умножения, решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на двузначное; научатся: применять алгоритм письменного умножения многозначного числа на двузначное; переносить умение выполнять умножение на двузначное число в пределах 1000 на область чисел в пределах миллиарда; выполнять развернутые и упрощенные записи алгоритма умножения |
Метапредметные: Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи. Регулятивные: осваивают начальные формы познавательной и личностной рефлексии. Коммуникативные: полно и точно выражают свои мысли в соответствии с задачами и условиями коммуникации; владеют монологической и диалогической формами речи в соответствии с нормами родного языка и современных средств коммуникации |
Личностные: осознают необходимость самосовершенствования, понимают границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. Работа с таблицей:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Выполняют действия по таблице с числами.
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
а) Найдите сумму чисел первой строки. б) Умножьте каждое число первой строки на 4; 5; 6; 7; 8; 9. в) Разделите первое число второй строки на первое число первой строки (и т. д.). г) Из первого числа третьей строки вычтите первое число второй строки. Из второго числа третьей строки вычтите второе число второй строки (и т. д.). д) Первое число третьей строки разделите на первое число первой строки. Второе число третьей строки разделите на второе число первой строки (и т. д.). е) Найдите в четвертой строке пары чисел, сумма которых равна 1000. ж) Каждое число третьего столбца умножьте на 100. з) Найдите в пятой строке пары чисел, сумма которых равна 140. |
а) 36 б) 5 · 4 = 20; 6 · 4 = 24 и т. д.
в) 35 : 5 = 7; 54 : 6 = 9 и т. д.
г) 75 – 35 = 40; 72 – 54 = 18 и т. д.
д) 75 : 5 = 15; 72 : 6 = 12 и т. д.
е) 600 и 400, 300 и 700.
ж) 7 · 100 = 700; 42 · 100 = 4200 и т. д.
з) 90 и 50, 60 и 80 и т. д. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Какие цифры ученик заменил точками?
|
103 · 8 = 824 575 – 248 = 327 130 + 303 = 433 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Объяснение учителя. Работа по учебнику |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Рассмотрите математические записи.
(1-я запись) (2-я запись) – Почему получили разные результаты? Какой результат должны получить? Почему? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственной отзывчивости. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль действий по результату |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Рассмотрите опорные таблицы. Что делаем сначала? – Это окончательный результат?
– Как можно назвать такое произведение?
– Что делаем затем? – Что получаем? |
Рассматривают опорные таблицы: – Умножаем первый множитель на число единиц второго множителя. Получаем первое неполное произведение. – Умножаем первый множитель на число десятков второго множителя. Получаем второе неполное произведение. – Подписываем второе число под первым, смещая на одну цифру влево, складываем по разрядам. Получаем конечный результат. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Какое свойство умножения мы использовали? |
– Мы использовали распределительное свойство умножения. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Так какая же запись, на ваш взгляд, верна? Почему? |
– Верна первая запись. Умножали на 4 десятка, значит, получили 652 десятка, а во второй записи – 652 единицы, что неверно. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Из чего видно, что записано 652 десятка? |
– Первое место справа оставлено для разрядных единиц. 652 десятка – 6520 единицы. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 1. |
– Можно ли 0 не писать и оставить так, как было? Почему?
– Почему в другом случае получили ошибочный результат? – Смогли бы вы перемножить эти числа, не записав их в столбик? – Умножение в столбик – это действительно удобно, легко, просто при условии, что мы четко знаем алгоритм и действуем в соответствии с ним. Составьте алгоритм умножения в столбик на двузначное число. |
– При сложении числа единиц первого неполного произведения с нулем это число не изменится, поэтому 0 на конце второго неполного произведения не пишут, но всегда оставляют для него место. – Неверно подписали второе неполное произведение. Его нужно записывать левее, оставляя место для единиц.
– Нет, не смогли бы.
Составляют алгоритм. 1) Умножу 1-й множитель на число разрядных единиц 2-го мно-жителя. Получу 1-е неполное произведение. 2) Умножу 1-й множитель на число разрядных десятков 2-го множителя. Получу 2-е неполное произведение. 3) Сложу неполные произведения. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Что вы должны помнить при записи второго неполного произведения? |
– Его нужно записывать на одну цифру левее. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 2. |
– Выполните задание в парах |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 8). Задание 22. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Длина каждой стороны многоугольника 9 см. Периметр этого многоугольника равен 108 см. Как называется этот многоугольник? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
108 : 9 = 12 (сторон) Ответ: двенадцатиугольник. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 23. |
– Вычислите значения выражений. |
512 · 7 + 488 · 7 = 3584 + 3416 = 7000 960 · 8 + 140 · 8 = 7680 + 1120 = 8800 800 · 4 – 450 · 4 = 3200 + 1800 = 5000 3 · 315 – 3 · 150 = 945 – 450 = 495 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 24. |
– Если неизвестное число увеличить на 248 и результат уменьшить на 362, то получится 567. Вычислите неизвестное число. |
567 + 362 – 248 = 681 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 25 |
– Если неизвестное число уменьшить в 7 раз, а затем результат увеличить в 9 раз, то получится 810. Какое это число? |
810 : 9 · 7 = 90 · 7 = 630 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Какое задание понравилось вам больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 58. Умножение вида 516 · 52; 407 · 25
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для закрепления алгоритма письменного умножения многозначного числа на двузначное; содействовать формированию умения умножать многозначное число на двузначное в пределах миллиарда; совершенствовать умение выполнять развернутые и упрощенные записи алгоритма умножения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на двузначное; научатся: применять алгоритм письменного умножения многозначного числа на двузначное; переносить алгоритм умножения многозначного числа на двузначное в пределах 1000 на область чисел в пределах миллиарда; выполнять развернутые и упрощенные записи алгоритма умножения вида 516 · 52; 407 · 25 |
Метапредметные: Познавательные: устанавливают причинно-следственные связи, строят логическую цепь рассуждений, используя доказательство. Регулятивные: оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы; владеют первоначальным умением выполнять учебные действия в устной, письменной речи, в уме. Коммуникативные: умеют задавать вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения, считаются с мнением другого человека, проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности); понимают причину успеха/неуспеха учебной деятельности и конструктивно действуют в ситуации неуспеха |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Подберите пропущенные цифры:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решают математические ребусы: 354 · 2 = 708 761 · 9 = 6848 999 · 2 = 1998 621 · 9 = 5589 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Поставьте знак >, < или = так, чтобы записи были верными: 42 · 13 ... 402 · 13 85 · 29 ... 19 · 83 506 · 21 ... 21 · 56 190 · 14 ... 140 · 19 |
42 · 13 < 402 · 13 85 · 29 > 19 · 83 506 · 21 > 21 · 56 190 · 14 > 140 · 19 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Из данного ряда выберите числа, при делении которых на 9 в остатке получается 3: 75, 32, 48, 62, 84, 19, 30. |
Ответ: 75, 48, 84, 30. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Игра «Отгадай число». а) Я задумала число, умножила его на 5 и получила: 10; 20; 35; 40; 45; 30. Какое число я задумала? б) Я задумала число, разделила его на 5 и получила: 7; 9; 4; 6; 3; 8. Какое число я задумала? |
а) Ответ: 2, 4, 7, 8, 9, 6.
б) Ответ: 35, 45, 20, 30, 15, 40. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Заполните таблицу:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 4). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Выполните умножение. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
244 · 75 = 18300 307 · 76 = 23332 532 · 31 = 16492 168 · 27 = 4536 401 · 29 = 11629 702 · 48 = 33696 859 · 96 = 82464 509 · 95 = 48355 303 · 55 = 16665 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи. Осуществлять контроль действий по результату |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4. |
– Докажите, что равенство верно. |
108 · 26 = 234 · 12 – верно |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 5 |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. |
Запись: а1 = 65 см а2 = 52 см b1 = 76 см b2 = 37 см S1 – ? см2 S2 – ? см2 Sост. – ? см2 Решение: 1) 65 · 76 = 4940 (см2) – S1. 2) 52 · 37 = 1924 (см2) – S2. 3) 4940 – 1924 = 3016 (см2) – осталось |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 9). Задание 26 |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Прочитайте задачу. Сближаются лыжники или удаляются друг от друга и с какой скоростью, если они двигаются в противоположных направлениях? – Сближаются лыжники или удаляются друг от друга, если они идут навстречу друг другу? – Сближаются лыжники или удаляются друг от друга, если они идут от базы в одном направлении и Борис идет за Андреем?
– Сближаются лыжники или удаляются друг от друга, если они идут от базы в одном направлении и Андрей идет за Борисом |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. – Удаляются. 18 + 15 = 33 (км/ч) – скорость удаления.
– Сближаются. 18 + 15 = 33 (км/ч) – скорость сближения. – Лыжники удаляются, если они идут от базы в одном направлении и Борис идет за Андреем:
18 – 15 = 3 (км/ч) – скорость удаления. – Лыжники сближаются, если они идут от базы в одном направлении и Андрей идет за Борисом:
18 – 15 = 3 (км/ч) – скорость сближения |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Применять правила делового сотрудничества |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что нового вы узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий. – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Осуществлять итоговый контроль, оценивать результаты деятельности |
Урок 59. Умножение вида 358 · 90
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для закрепления алгоритма письменного умножения многозначного числа на двузначное; содействовать формированию умения умножать многозначное число на двузначное в пределах миллиарда; совершенствовать умение выполнять развернутые и упрощенные записи алгоритма умножения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на двузначное; научатся: применять алгоритм письменного умножения многозначного числа на двузначное; переносить алгоритм умножения многозначного числа на двузначное в пределах 1000 на область чисел в пределах миллиарда; выполнять развернутые и упрощенные записи алгоритма умножения вида 358 · 90 |
Метапредметные: Познавательные: устанавливают причинно-следственные связи, строят логическую цепь рассуждений, используя доказательство. Регулятивные: оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы; владеют первоначальным умением выполнять учебные действия в устной, письменной речи, в уме. Коммуникативные: умеют задавать вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения, считаются с мнением другого человека, проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности); понимают причину успеха/ неуспеха учебной деятельности и конструктивно действуют в ситуации неуспеха |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
Игра «Цепочка» (см. ресурсный материал к уроку). |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
См. ресурсный материал к уроку. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||
|
|
– Посмотрите на числа в столбиках: 530 504 720 406 930 708 Чем похожи числа первого столбика?
– Чем похожи числа второго столбика? |
– У всех чисел первого столбика отсутствуют разрядные единицы. – У всех чисел второго столбика отсутствуют разрядные десятки. |
|||||||||||
|
|
– Вставьте пропущенные числа: 351= 300 + 50 + 25367 = 20000 + 469 = 5491 = 5000 + |
351 = 300 + 50 + 1 25367 = 20000 + 5000 + 300 + 60 + 7 469 = 400 + 60 + 9 5491 = 5000 + 400 + 90 + 1 |
|||||||||||
|
|
– Подберите к каждому выражению из 1-го столбика значение из 2-го столбика. 73 + 6 50500 730 + 60 90 210 + 7 790 930 – 60 79 120 + 150 870 580 – 490 217 50000 + 500 20100 29100 – 9000 270 |
73 + 6 = 79 730 + 60 = 790 210 + 7 217 930 – 60 = 870 120 + 150 = 270 580 – 490 = 80 50000 + 500 = 50500 29100 – 9000 = 20100 |
|||||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 5–6). Задание 6. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Сравните записи. Какой способ записи умножения удобнее? Объясните ответ. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Составляют алгоритм умножения многозначного числа на круг-лое двузначное число. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Осуществлять контроль действий по результату |
||||||||||
|
Задание 7. |
– Выполните умножение, используя удобный способ записи. |
516 · 50 = 25800 140 · 20 = 2800 209 · 40 = 8360 274 · 80 = 21920 920 · 80 = 73600 960 · 96 = 92160 407 · 30 = 32560 570 · 70 = 39900 210 · 80 = 16800 |
|||||||||||
|
Задание 8. |
– Выполните задание в парах. |
Выполняют устные вычисления в парах по цепочке. |
|||||||||||
|
Задание 9. |
– Выразите время в минутах.
– Выразите время в секундах. |
12 ч = 720 мин 150 ч = 9000 мин 400 ч = 24000 мин 9 мин = 540 с 45 мин = 2700 с 128 мин = 7680 с |
|||||||||||
|
Задание 10 |
– Докажите, что равенство неверно |
276 · 70 = 512 · 35 – неверно
|
|||||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 9–10). Задание 27. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните действия, используя распределительное свойство умножения. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
(362 + 458) · 7 = 362 · 7 + 458 · 7 = = 2534 + 3206 = 5740 (2864 + 936) · 5 = 2864 · 5 + 936 · 5 = = 14320 + 4680 = 19000 (2924 – 1824) · 6 = 2924 · 6 – 1824 · 6 = = 17544 – 10944 = 6600 (5600 – 1480) · 4 = 5600 · 4 – 1480 · 4 = = 22400 – 5920 = 16480 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
||||||||||
|
Задание 28. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 85 · 5 = 425 (р.) – стоят 5 простыней. 2) 425 – 200 = 225 (р.) – стоят 5 наволочек. 3) 225 : 5 = 45 (р.) – цена наволочки. |
|||||||||||
|
Задание 29 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Решение: 1) 24 · 5 = 120 (р.) – цена фотоальбома. 2) 120 · 3 = 360 (р.) – цена словаря. 3) 120 + 360 = 480 (р.) – стоят вместе фотоальбом и словарь |
|||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что нового вы узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, анализировать причины неудачи |
Ресурсный материал к уроку
1.
Игра «Цепочка»: 
Решение: 
Урок 60. Упражнение в умножении многозначного числа на двузначное
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для закрепления алгоритма письменного умножения многозначного числа на двузначное; способствовать формированию умения умножать многозначное число на двузначное число в пределах миллиарда; совершенствовать умение выполнять развернутые и упрощенные записи алгоритма умножения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на двузначное; научатся: применять алгоритм письменного умножения многозначного числа на двузначное; переносить алгоритм умножения многозначного числа на двузначное в пределах 1000 на область чисел в пределах миллиарда; выполнять развернутые и упрощенные записи алгоритма умножения |
Метапредметные: Познавательные: устанавливают причинно-следственные связи, строят логическую цепь рассуждений, используя доказательство. Регулятивные: оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы; владеют первоначальным умением выполнять учебные действия в устной, письменной речи, в уме. Коммуникативные: умеют задавать вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения, считаются с мнением другого человека, проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности); понимают причину успеха/ неуспеха учебной деятельности и конструктивно действуют в ситуации неуспеха |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||
|
– Используя данные равенства, найдите значения выражений: а) 15504 : 19 = 816 б) 65484 : 306 = 214 15504 : 816 = 816 · 19 = 816 · 190 = 8160 · 19 = |
а) 15504 : 19 = 816 б) 65484 : 306 = 214 15504 : 816 = 19 214 · 306 = 65484 816 · 19 = 15504 2140 · 306 = 654840 816 · 190 = 155040 65484 : 214 = 306 8160 · 19 = 155040 214 · 3060 = 654840 |
||||
|
– Вставьте пропущенные цифры: 3709 · 26 = 9643 374 · 560 = 2094 30700 · 56 = 17192 38 · 2070 = 786 |
3709 · 26 = 96434 374 · 560 = 209440 30700 · 56 = 1719200 38 · 2070 = 78660 |
||||
|
– Поставьте знаки >, < или = так, чтобы записи были верными: 8050 · 84 ... 8050 · (80 + 4) 259 · (8 + 7) ... 259 · 8+ 259 · 6 606 · (37 · 8) ... (606 · 37) · 9 |
8050 · 84 = 8050 · (80 + 4) 259 · (8 + 7) > 259 · 8+ 259 · 6 606 · (37 · 8) < (606 · 37) · 9 |
||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 6–7). Задание 11. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 1) 235 · 15 = 3525 (р.) – стоят 15 столов. 2) 235 : 5 = 47 (р.) – цена табуретки. 3) 47 · 20 = 940 (р.) – стоят 20 табуреток. 4) 3525 + 940 = 4465 (р.) – стоимость покупки. 5) 3525 – 940 = 2585 (р.) – на столько дороже столы. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
||
|
Задание 12. |
Учитель раздает карточки: – Найдите значения буквенных выражений: 1) х · 38, если х = 96; если х = 108; если х = 517. 2) 156 · а – 42 · у, если а = 16, у = 53. 3) 304 : х + 94 · у, если х = 38, у = 80. |
1) Если х = 96, то 96 · 38 = 3648; если х = 108, то 108 · 38 = 4104; если х = 517, то 517 · 38 = 19646
2) Если а = 16, у = 53, то 156 · 16 – 42 · 53 = = 2496 – 2226 = 270
3) Если х = 38, у = 80, то 304 : 38 + 94 · 80 = = 8 + 7520 = 7528 |
|||
|
Задание 13. |
– Вычислите значения выражений и проверьте результаты с помощью калькулятора. 1804 · 25 = 111 111 · 99 = 30 941 · 72 = 404 040 · 80 = |
1804 · 25 = 45100 111 111 · 99 = 10 999 989 30941 · 72 = 2227752 404 040 · 80 = 32 323 200 |
|||
|
Задание 14. |
– Объясните, как выполнено умножение в столбик. |
Объясняют, как выполнено умножение в столбик. |
|||
|
Задание 15. |
– Найдите значения выражений: (107 + 96) · 43 + 480 : 12 · 54 = (890 – 36 · 4) · 37 – 106 · 8 = 23146 · 33 – 12146 · 33 – 3174 · 72 = |
(107 + 96) · 43 + 480 : 12 · 54 = 8729 + 2160 = 10889 (890 – 36 · 4) · 37 – 106 · 8 = 27602 – 848 = 26754 23146 · 33 – 12146 · 33 – 3174 · 72 = 134472 |
|||
|
Задание 16 |
– Прочитайте и решите задачу. Сколько винограда собрали? Выразите результаты в тоннах и килограммах. – Какое данное в задаче лишнее? |
Решение: 84 · 14 = 1176 (кг) 1176 кг = 1 т 176 кг – Лишнее данное – «15 человек в бригаде» |
|||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 10–11). Задание 30. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– По какому правилу записаны числа? Назовите следующее число. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Осуществлять взаимный контроль действий, планировать способы взаимодействия |
||
|
Задание 31. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 6 – 1 = 5 (лет) – Анечке. 2) 5 · 5 = 25 (лет) – Алексею. 3) 25 + 20 = 45 (лет) – тете Вале. 4) 45 : 3 = 15 (лет) – Оле. 5) 15 · 2 = 30 (лет) – дяде. |
|||
|
Задание 32. |
– Решите задачу. Какова масса покупки? – Сколько стоит покупка? |
– Масса покупки: 500 г · 3 = 1500 г. Решение: 1) 78 : 2 = 39 (р.) – стоят полкилограмма конфет. 2) 78 + 39 = 117 (р.) – стоят 1 кг 500 г конфет. |
|||
|
Задание 33 |
– Не выполняя вычислений, определите, сколько нулей в записи числа, которое является произведением чисел 78320 и 5 |
– Два нуля |
|||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Как выполнить умножение многозначного числа на двузначное? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Закрашивают ту часть круга, которая соответствует впечатлению от урока:
|
Способны проводить самооценку на основе критериев успешности учебной деятельности (оценивать свои достижения, степень самостоятельности, инициативности, анализировать причины неудачи) |
Урок 61. Закрепление умножения многозначного числа на двузначное число
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для закрепления алгоритма письменного умножения многозначного числа на двузначное; способствовать формированию умения умножать многозначное число на двузначное число в пределах миллиарда; совершенствовать умение выполнять развернутые и упрощенные записи алгоритма умножения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на двузначное; научатся: применять алгоритм письменного умножения многозначного числа на двузначное; переносить алгоритм умножения многозначного числа на двузначное в пределах 1000 на область чисел в пределах миллиарда; выполнять развернутые и упрощенные записи алгоритма умножения |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель (пространственно-графическую или знаково-символическую), где выделены существенные характеристики объекта , и преобразование модели с целью выявления общих законов, определяющих данную предметную область; структурируют знания. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологические высказывания, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. |
Выделять существенную информацию из текста задачи. Уметь слушать в соответствии с целевой установкой, дополнять, уточнять высказанные мнения по существу полученного задания |
||||||
|
– Используя данные равенства, найдите значения выражений: 63 · 15 = 945 45 · 6 = 270 63 · 150 = 45 · 60 = 63 · 1500 = 45 · 600 = 63 · 1501 = 45 · 602 = |
63 · 15 = 945 45 · 6 = 270 63 · 150 = 9450 45 · 60 = 2700 63 · 1500 = 94500 45 · 600 = 27000 63 · 1501 = 94563 45 · 602 = 27090 |
||||||||
|
– Вместо точек подставьте нужные цифры, найдите «ловушки»:
|
Решают математические ребусы. 264 · 9 = 2376 254 · 2 = 528 – Третья и четвертая запись являются «ловушками»: при умножении трехзначного числа на однозначное нельзя получить пятизначное или двузначное числа. |
||||||||
|
Задание на смекалку. – Я задумала число, умножила его на 9 и к произведению прибавила 8. Получилось 71. Какое число я задумала? |
– Задумали число 7 |
||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 7–8). Задание 17. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий. – Сколько асфальта потребовалось?
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Запись: а = 672 м b = 13 м S – ? м2 1 м2 – 39 кг асф. Всего асф. – ? кг Решение: 1) 672 · 13 = 8736 (м2) – S. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять контроль действий по результату |
||||||
|
|
|
2) 8736 · 39 = 340 704 (кг) – асфальта. Ответ: 340 т 704 кг асфальта. |
|||||||
|
Задание 18. |
– Восстановите записи. Вместо звездочек вставьте пропущенные числа. |
|
|||||||
|
Задание 19. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 200 + 167 = 367 (м/мин) – скорость удаления. 2) 367 · 45 = 16515 (м) – расстояние. |
|||||||
|
Задание 20. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Решение: 1) 65 + 78 = 143 (км/ч) – скорость сближения. 2) 572 : 143 = 4 (ч) – через столько произойдет встреча. |
|||||||
|
Задание 21 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу |
Запись: Было – 430 п. по 50 шт. Продали – 7494 шт. Осталось – ? шт. Решение: 1) 50 · 430 = 21500 (шт.) – было. 2) 21500 – 7494 = 14006 (шт.) – осталось |
|||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 11–12). Задание «Путешествие в прошлое». |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
Задача 1. На сколько лет одна лошадь моложе другой?
Задача 2. Во сколько кузнец оценит новую подкову? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Доказывают, аргументируют свою точку зрения. Решают старинные задачи. Задача 1. 8 + 4 = 12 (лет) – 1-й лошади. 5 + 3 = 8 (лет) – 2-й лошади. 12 – 8 = 4 (года) – на столько моложе 2-я лошадь. Задача 2. 80 – 10 = 70 (к.) |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||
|
Задание 34. |
– Выполните узоры, используя циркуль. |
Выполняют узоры, используя циркуль. |
|||||||
|
Задание 35. |
– Деталь какой формы вырезали из доски? |
– Деталь под номером 3 вырезали из доски. |
|||||||
|
Самостоятельная работа |
Проводит самостоятельную работу по вариантам. – Не выполняя умножения в столбик, соедините каждое выражение с его значением
|
Выполняют самостоятельную работу |
|||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что нового вы узнали на уроке? – Как выполнить умножение многозначного числа на двузначное? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность. Оценивать результаты деятельности |
Урок 62. Контрольная работа № 4 по темам
«Задачи на движение», «Умножение многозначного числа
на однозначное и двузначное»
|
Тип урока: контроль и оценка знаний и умений |
||
|
Педагогические задачи: проверить усвоение алгоритма письменного умножения многозначного числа на однозначное и двузначное, умение решать задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на двузначное; научатся: применять алгоритм письменного умножения многозначного числа на двузначное; переносить алгоритм умножения многозначного числа на двузначное в пределах 1000 на область чисел в пределах миллиарда; выполнять развернутые и упрощенные записи алгоритма умножения |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; строят логическую цепь рассуждений. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера, стараются их исправить. Коммуникативные: умеют устанавливать, с какими учебными задачами могут справиться самостоятельно |
Личностные: понимают границы собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Проведение контрольной работы |
Знакомит с содержанием контрольной работы, комментирует задания.
Вариант I 1. Найди значения выражений: 5764 · 9 = 3405 · 300 = 63458 · 4 = 500 · (2357 – 2000) = 534 · 600 = 3008 · 60 = 2380 · 40 = 82400 · 30 = 2. Реши задачу. Две черепахи начали двигаться одновременно навстречу друг другу, когда находились на расстоянии 66 м. Скорость одной черепахи 5 м/мин, а другой – 6 м/мин. Через сколько минут черепахи встретятся? 3. Реши задачу. В походе дети шли 15 км со скоростью 5 км/час и 12 км со скоростью 4 км/час. Сколько часов были в пути дети? |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы. Вариант I 1. 5764 · 9 = 51876 3405 · 300 = 1021500 63458 · 4 = 253832 500 · (2357 – 2000) = 178500 534 · 600 = 320400 3008 · 60 = 180480 2380 · 40 = 95200 82400 · 30 = 2472000 2. Решение: 1) 5 + 6 = 11 (м/мин) – скорость сближения; 2) 66 : 11 = 6 (мин) – время встречи.
3. Решение: 1) 15 : 5 = 3 (ч) – со скоростью 5 км/ч. 2) 12 : 4 = 3 (ч) – со скоростью 4 км/ч. 3) 3 + 3 = 6 (ч) ‒ были в пути дети. |
Принимать и сохранять учебную цель и задачу. Анализировать, находить общее и различия, делать выводы. Осознанно и произвольно строить речевые высказывания в устной форме |
|
Вариант II 1. Найди значения выражений: 9352 · 6 = 2608 · 400 = 75314 · 8 = 15400 + 600 · 1358 = 475 · 500 = 7004 · 70 = 3160 · 30 = 83200 · 40 = 2. Реши задачу. Слон и слоненок начали двигаться одновременно навстречу друг другу. Скорость слона 60 м/мин, скорость слоненка 20 м/мин. Слоны встретились через 10 мин. Какое расстояние было между ними сначала? 3. Реши задачу. За 3 часа Петя проехал на велосипеде 36 км, а Коля за то же время проехал 45 км. У кого скорость движения была больше и на сколько? |
Вариант II 1. 9352 · 6 = 56112 2608 · 400 = 1043200 75314 · 8 = 602512 15400 + 600 · 1358 = 830200 475 · 500 = 237500 7004 · 70 = 490280 3160 · 30 = 94800 83200 · 40 = 3328000 2. Решение: 60 + 20 = 80 (м/мин) – скорость сближения. 80 · 10 = 800 (м) ‒ расстояние было между ними сначала.
3. Решение: 36 : 3 = 12 (км/ч) – скорость Пети. 45 : 3 = 15 (км/ч) – скорость Коли. 15 – 12 = 3 (км/ч) – больше скорость Коли |
||
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способны проводить самооценку на основе критериев успешности учебной деятельности |
Урок 63. Алгоритм умножения многозначного числа на трехзначное
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с алгоритмом письменного умножения многозначного числа на трехзначное, способствовать формированию умения выполнять письменное умножение многозначного числа на трехзначное; содействовать развитию умения выполнять развернутые и упрощенные записи алгоритма умножения; совершенствовать умение решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на трехзначное; научатся: применять алгоритм письменного умножения многозначного числа на трехзначное, выполнять письменное умножение многозначного числа на трехзначное; объяснять выполнение развернутых и упрощенных записей алгоритма умножения |
Метапредметные: Познавательные: определяют основную и второстепенную информацию; осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются в учебнике (на развороте, в оглавлении, в условных обозначениях). Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве |
Личностные: проявляют интерес к учебному материалу; владеют основными моральными нормами поведения; осознают роль языка и речи в жизни людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|||||||
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. Игра «Распутай клубок».
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||
|
|
– Найдите среди данных решений правильное:
|
Ответ: 5034 · 7 = 35238. |
||||||||
|
|
– Подберите второй множитель и решите полученный пример:
|
|
||||||||
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 13). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Составьте алгоритм умножения в столбик многозначного числа на трехзначное. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Составляют алгоритм умножения в столбик многозначного числа на трехзначное. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Принимать и сохранять учебную цель и задачу. Применять правила делового сотрудничества |
|||||||
|
Задание 2. |
– Какие числа сложили при выполнении умножения чисел 324 и 123? |
972 + 6480 + 32400 = 39852 |
||||||||
|
Задание 3. |
– Выполните умножение, записывая числа столбиком. |
115 · 163 = 18745 94 · 216 = 279504 236 · 374 = 98736 2139 · 151 = 322989 563 · 113 = 63619 6431 · 333 = 2141523 264 · 856 = 225984 9075 · 152 = 1379400 64 · 952 = 60928 160 · 270 = 43200 650 · 125 = 81250 900 · 420 = 378000 |
||||||||
|
Задание 4 |
– Выполните задание в парах |
Выполняют задание и взаимопроверку в парах |
||||||||
|
III. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 17–18). Задание 25. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Выполните деление. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
846 : 2 = 423 380 : 5 = 76 420 : 210 = 2 112 : 4 = 28 891 : 9 = 99 84 : 42 = 2 623 : 7 = 89 320 : 8 = 40 100 : 20 = 5 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|||||||
|
Задание «Старинная задача». |
Всего – ? возов Перевозили – ? дн. по 10 раз |
Решение: 1) 30 – 10 = 20 (в.) – во 2-м стоге. 2) 30 + 20 = 50 (в.) – всего. 3) 50 : 10 = 5 (дн.) – перевозили сено. |
||||||||
|
Задание 27 |
– Назовите пару чисел, которые указывают расположение центра окружности. – Определите, где находится каждая точка, которой соответствует пара чисел |
– Центр окружности – точка О (3; 4).
Точка (2; 2) – вне окружности. Точка (6; 6) – вне окружности. Точка (4; 4) – внутри окружности. Точка (1; 4) – на окружности. Точка (5; 4) – на окружности. Точка (3; 5) – внутри окружности |
||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового вы узнали на уроке? – Как выполнить умножение многозначного числа на трехзначное? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик; те, у кого некоторые вопросы вызвали затруднения, – синий |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способны проводить самооценку на основе критериев успешности учебной деятельности (оценивать свои достижения, степень самостоятельности) |
Урок 64. Умножение многозначного числа на трехзначное.
Алгоритм умножения многозначного числа на трехзначное
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с алгоритмом письменного умножения многозначного числа на трехзначное; способствовать формированию умения выполнять письменное умножение многозначного числа на трехзначное; содействовать развитию умения выполнять развернутые и упрощенные записи алгоритма умножения; совершенствовать умение решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на трехзначное; научатся: применять алгоритм письменного умножения многозначного числа на трехзначное, выполнять письменное умножение многозначного числа на трехзначное; объяснять выполнение развернутых и упрощенных записей алгоритма умножения |
Метапредметные: Познавательные: осуществляют моделирование; структурируют знания; осознанно и произвольно строят речевые высказывания в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: в совместной деятельности определяют цели и функции участников, способы взаимодействия |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности учащихся (осуществляемые действия) |
Формируемые способы деятельности учащихся |
|
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Разгадайте правило, по которому составлены схемы, и вставьте числа в «окошки».
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой, дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Расставьте скобки так, чтобы выражение 60 – 24 : 3 + 1 имело значение: а) 54; б) 9; в) 53; г) 51 |
а) 60 – 24 : (3 + 1) = 54 в) 60 – (24 : 3) + 1 = 53 б) (60 – 24) : (3+ 1) = 9 г) 60 – (24 : 3 + 1) = 51 |
|
|
II. Открытие нового знания, нового способа действия. Работа по учебнику (с. 14). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением заданий.
– Проанализируйте и сравните полную и сокращенную записи умножения в столбик. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Сравнивают и анализируют полную и сокращенную записи умножения в столбик. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать ее выбор. Применять правила делового сотрудничества. Осуществлять контроль действий по результату |
|
Задание 6. |
– Выполните умножение на трехзначное число. |
207 · 503 = 104121 308 · 803 = 247324 609 · 305 = 185745 706 · 706 = 498436 708 · 504 = 356832 3570 · 602 = 2149140 909 · 808 = 734472 21250 · 307 = 6523750 107 · 208 = 22256 12609 · 800 = 10087200 409 · 907 = 370963 10920 · 203 = 2216760 |
|
|
Задание 7. |
– Найдите значение выражения. |
1) 506 · х + 207 · у Если х = 205, у = 70, то 506 · 205 + 207 · 70 = = 103730 + 14490 = 118220 2) 1290 + х · у Если х = 306, у = 405, то 1290 + 306 · 405 = = 125220 3) (217 + 583) · а = 800 · а Если а = 217, то 800 · 214 = 171200; если а = 387, то 800 · 387 = 309600; если а = 902, то 800 · 902 = 721600 4) (t + l) · 250 Если t = 499, l = 201, то (499 + 201) · 250 = = 175000 |
|
|
Задание 8 |
– Найдите произведения чисел |
2222 · 444 = 986568 1008 · 905 = 912240 1007 · 106 = 106742 10080 · 950 = 9576000 |
|
|
III. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 19). Задание 28. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания учащихся по теме урока.
– Вычислите расстояние между станциями. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 80 + 90 = 170 (км/ч) – скорость удаления. 2) 170 · 5 = 850 (км) – проехали. 3) 970 – 850 = 120 (км) – расстояние между станциями. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, уметь вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок |
|
Задание 29. |
– Какова масса обоих китов? |
Решение: 1) 150 : 5 · 2 = 60 (т) – масса детеныша. 2) 150 + 60 = 210 (т) – масса обоих китов. |
|
|
Задание 30 |
– Прочитайте и решите задачу |
Решение: 1 кг = 1000 г; 1000 г : 4 · 3 = 750 г |
|
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Учитель проводит беседу по вопросам: – Что нового вы узнали на уроке? – Как выполнить умножение многозначного числа на трехзначное число? – Какое задание вам понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам ваша работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты своей деятельности, уровень владения учебным действием |
Урок 65. Развёрнутые и упрощённые записи умножения
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного умножения многозначного числа на трехзначное; способствовать формированию умений выполнять письменное умножение многозначного числа на трехзначное; содействовать развитию умений выполнять развернутые и упрощенные записи алгоритма умножения; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на трехзначное; научатся применять алгоритм письменного умножения многозначного числа на трехзначное; выполнять письменное умножение многозначного числа на трехзначное; объяснять выполнение развёрнутых и упрощённых записей алгоритма умножения |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||||||||
|
II. Актуализация опорных знаний. Игра «Распутай клубок».
|
Организует устный счет с целью актуализации знаний. – какие числа зашифрованы?
|
Отвечают на вопросы учителя. Выполняют задания устного счета. Решение:
|
Осуществлять актуализацию личного жизненного опыта. Уметь слу-шать в соответствии с целевой установкой |
||||||||||||||||||
|
Устный счет |
– Вычислите значения выражений: (6400 – 800) : 8 8100 : 90 – 60 6400 – 800 : 8 8100 : (90 – 60) |
в) 786 – 726 = 60 60 – 30 = 30 30 · 15 = 450 Решение: (6400 – 800) : 8 = 700 8100 : 90 – 60 = 30 6400 – 800 : 8 = 6300 8100 : (90 – 60) = 270 |
|||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 14–15). |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Найдите значения выражений. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
125 · 2304 + 653 · 1000 – 851 · 106 = 850794 457100 + 1423 · (6123 – 5941) – 11007 = 705079 382 · 905 + 618 · 905 = 905000 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи. Применять правила делового сотрудничества |
||||||||||||||||||
|
Задание 9. |
|
749 · 709 + 251 · 709 = 709000. 1027 · 378 – 72 : 36 · 905 – 628 : 4 = 386239. (650 · 15 + 350 · 15) · 0 + 800 : 32 – 25 = 0. |
|||||||||||||||||||
|
Задание 10. |
– Выполните умножение величин. – Поменяйтесь тетрадями, проверьте работу друг у друга. |
216 м · 320 м = 69120 м2. 420 км · 170 км = 71400 км2. 51 см · 6 м = 51 см · 600 см = 30600 см2. 65 мм · 84 см = 65 мм · 840 мм = 54600 мм2. |
|||||||||||||||||||
|
Задание 11. |
– Какое расстояние пролетела ракета?
– Выразите результат в километрах и метрах. |
Запись: t = 102 с u = 8250 м/с s – ? Решение: 8250 · 102 = 841500 (м); 841500 м = 841 км 500 м. |
|||||||||||||||||||
|
Задание 12 |
– Сколько денег выручил магазин за проданные магнитофоны? – Сколько стоят 4 магнитофона? – Сколько стоят 20 магнитофонов? – Сколько стоят 100 магнитофонов? – Сколько стоят 124 магнитофона? |
– 107260 рублей выручил магазин за проданные магнитофоны. – 3460 рублей стоят 4 магнитофона. – 17300 рублей стоят 20 магнитофонов. – 86500 рублей стоят 100 магнитофонов. – 107260 рублей стоят 124 магнитофона |
|||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 19). Задание 31. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – чему равна масса 15 ящиков с изюмом? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись:
Решение: 1) 18 · 4 = 72 (кг) – масса 6 ящиков. 2) 72 : 6 = 12 (кг) – масса 1 ящика с изюмом. 3) 12 · 15 = 180 (кг) – масса 15 ящиков с изюмом. |
Выбирать действия в соответствии Планировать способы взаимодействия |
||||||||||||||||||
|
Задание 32*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какое расстояние проехала машина? |
Запись:
Решение: 1) 90 : 2 = 45 (км) – проехали за 30 мин. 2) 80 : 2 = 40 (км) – проехали за 30 мин со скоростью 80 км/ч. 3) 80 + 40 = 120 (км) – проехали за 1 ч 30 мин. 4) 120 + 45 = 165 (км) – весь путь. |
|||||||||||||||||||
|
Задание 33 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько времени занял весь путь? |
Запись: Шел – ? ч, 20 км, 5 км/ч. Остановки – 45 мин. Решение: 1) 20 : 5 = 4 (ч) – шел. 2) 4 ч + 45 мин = 4 ч 45 мин – занял весь путь |
|||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи |
||||||||||||||||||
Урок 66. Упражнение в умножении многозначного числа на трЁхзначное.
Решение задач
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного умножения многозначного числа на трехзначное; способствовать формированию умений выполнять письменное умножение многозначного числа на трехзначное; содействовать развитию умений выполнять развернутые и упрощенные записи алгоритма умножения; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на трехзначное; научатся применять алгоритм письменного умножения многозначного числа на трехзначное; выполнять письменное умножение многозначного числа на трехзначное; объяснять выполнение развёрнутых и упрощённых записей алгоритма умножения |
Метапредметные: Познавательные: формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера; используют знаково-символические средства для решения учебной задачи. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий. Коммуникативные: слушают и понимают речь других; признают возможность существования различных точек зрения и права каждого иметь свою |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Догадайтесь, как можно устно найти значения выражений: 999 + 2345 255 – 99 604 + 396 537 – 99 1153 + 498 420 – 98 71012 + 188 676 – 98 |
Отвечают на вопросы учителя . Выполняют задания устного счета.
Ответ: 999 + 2345 = 2345 + 1000 – 1 = 3345 – 1 = 3344. 255 – 99 = 255 – 100 + 1 = 155 + 1 = 156 и т. д. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||
|
Игра «Цепочка». |
– Решите числовые цепочки:
|
Решение:
|
||||||||||||||||||
|
Интеллектуальная разминка |
– Не производя вычислений, найдите самую большую сумму и самую маленькую разность: 999 + 999 6803 + 1576 9000 – 999 875 + 9003 5003 – 4999 1000 – 110 |
Решение: 875 + 9003 5003 – 4999 |
||||||||||||||||||
|
|
– Вставьте числа в «окошки»:
|
Решение: 25 : 5 = 5 49 : 7 = 7 17 : 4 = 4 (ост. 1) 36 : 6 = 6 64 : 8 = 8 83 : 9 = 9 (ост. 2) |
||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 15–16). Задание 13. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Найдите площадь грядки. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 1) 1 м 12 см = 112 см 112 · 3 = 336 (см) – длина грядки. 2) 112 · 336 = 37632 (см2) – площадь грядки. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
|||||||||||||||||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – На какую сумму привезли мебель в этот магазин? Составьте выражение.
– Найдите его значение, если а = 105, х = 210. |
Решение: 2375 · а + 5400 · х. Если а = 105, х = 210, то получим 2375 · 105 + 5400 · 210 = 249375 + 1134000 = = 1383375. |
||||||||||||||||||
|
Задание 15. |
– Чему равно произведение? |
1) 4000 · 298 = 1192000 2) 125 · 125 = 15625 |
||||||||||||||||||
|
Задание 16* |
– Назовите такое число а, при умножении которого на 196 получится а |
Ответ: 0 · 196 = 0. а = 0 |
||||||||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 20). Задание 34. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько бензина нужно для того, чтобы проехать 200 км? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: 50 км – 6 л бензина 200 км – ? л бензина Решение: 1) 200 : 50 = 4 (раза) – больше. 2) 6 · 4 = 24 (л) – бензина на 200 км. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок |
|||||||||||||||||
|
Задание 35 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько времени было затрачено на весь путь? |
Запись:
Решение: 1) 420 : 70 = 6 (ч) – 1-й путь. 2) 300 : 75 = 4 (ч) – 2-й путь. 3) 6 ч + 4 ч + 14 мин = 10 ч 14 мин |
||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Как выполнить умножение многозначного числа на трехзначное число? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
|||||||||||||||||
Урок 67. Закрепление навыка умножения многозначного числа на двузначное и трёхзначное
|
Тип урока: повторение и систематизации знаний и способов действий |
||
|
Педагогические задачи: продолжить тренировать в выполнении письменного умножения многозначного числа на трехзначное, развернутых и упрощенных записей алгоритма умножения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на трехзначное; научатся применять алгоритм письменного умножения многозначного числа на трехзначное; выполнять письменное умножение многозначного числа на трехзначное; объяснять выполнение развёрнутых и упрощённых записей алгоритма умножения |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; используют знаково-символические средства для решения учебной задачи; осуществляют моделирование и выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера; осуществляют контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона. Коммуникативные: излагают своё мнение и аргументируют свою точку зрения |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Найдите значения выражений, записанных на доске: 395448 · 9 – 395448 · 8 0 : (394126 – 127239) 872456 · 0 + 872456 · 1 89: 1 + 11 : 1 + 56 : 56 |
Отвечают на вопросы учителя. Выполняют задания устного счета. Решение: 395448 · 9 – 395448 · 8 = 395448 0 : (394126 – 127239) = 0 872456 · 0 + 872456 · 1 = 872456 89: 1 + 11 : 1 + 56 : 56 = 101 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||
|
|
– В каждой из этих записей есть ошибка. Найдите ее:
|
Решение:
|
||||||
|
Ребусы. |
– Какие цифры спрятаны?
|
Решение:
|
||||||
|
задача |
– Найдите периметр и площадь данного прямоугольника.
|
Решение: 1) (6 + 3) · 2 = 18 (см) – периметр прямоугольника. 2) 6 · 3 = 18 (кв. см) – площадь прямоугольника |
||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 16–17). Задание 17. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Сколькими нулями оканчивается произведение?
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Решение:
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества |
|||||
|
Задание 18. |
– К какому пятизначному числу надо прибавить 1, чтобы получить шестизначное число? – Из какого числа надо вычесть 3, чтобы получить 3597? – Какое число получится, если к наименьшему четырехзначному числу прибавить 50? |
– К 99999 надо прибавить 1, чтобы получить шестизначное число. – Из 3600 надо вычесть 3, чтобы получить 3597. – Получится число 1050, если к наименьшему четырехзначному числу прибавить 50. |
||||||
|
Задание 19. |
– Решите задачу устно. – Нужно узнать стоимость 100 г творога. |
Решение: 1) 24 : 4 = 6 (р.) – стоят 100 г. 2) 6 · 10 = 60 (р.) – цена творога. |
||||||
|
Задание 20* |
– Сумма трех чисел, следующих при счете одно за другим, равна 40. Какие это числа? |
Решение: 12 + 13 + 14 = 39 13 + 14 + 15 = 42 – Задача не имеет решения |
||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 20). Задание 36. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Постройте фигуры из кубиков. – Сколько всего кубиков в первой фигуре? – Сколько всего кубиков во второй фигуре? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 4 · 2 · 2 = 16 (кубиков) в первой фигуре. 2) 3 · 3 · 2 = 18 (кубиков) во второй фигуре. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок |
|||||
|
Задание 38 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – На каком расстоянии от станции будет машина через 3 часа после выезда? |
Запись:
Решение: 1) 65 · 3 = 195 (км) – проехали. 2) 210 – 195 = 15 (км) – осталось проехать до станции |
||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность. Оценивать результаты деятельности |
Урок 68. Закрепление навыка умножения многозначного числа на двузначное и трёхзначное
|
Тип урока: повторение и систематизации знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений выполнять письменное умножение многозначного числа на трёхзначное, развернутые и упрощенные записи алгоритма умножения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного умножения многозначного числа на трёхзначное; научатся применять алгоритм письменного умножения многозначного числа на трёхзначное; выполнять письменное умножение многозначного числа на трёхзначное; объяснять выполнение развёрнутых и упрощённых записей алгоритма умножения |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование и выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учёта интересов сторон и сотрудничества |
Личностные: устанавливают связь между целью учебной деятельности и ее мотивом (между результатом учения и тем, что побуждает деятельность, ради чего она осуществляется); задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Ответьте на вопросы по таблице:
|
Отвечают на вопросы учителя. Выполняют задания устного счета. Выполняют действия с числами по таблице. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||
|
|
а) Первое число первой строки разделите па первое число второй строки. Второе число первой строки разделите на второе число второй строки и т. д. б) Каждое число второй строки увеличьте в 2 раза; в 20 раз; в 200 раз.
в) Из числа 48 вычтите каждое число второй строки. Из числа 64 вычтите каждое число второй строки. г) Каждое число второй строки дополните до 100.
д) Каждое число первой строки представьте в виде произведения двух однозначных чисел. е) Разделите каждое число третьей строки на 10. ж) Каждое число третьей строки умножьте на 10, на 100. и) Найдите сумму чисел четвертой строки. |
а) 2, 3, 4, 3, 3, 2.
б) 48, 30, 32, 48, 42, 54; 480, 300, 320, 480, 420, 540; 4800, 3000, 3200, 4800, 4200, 5400. в) 24, 33, 32, 24, 27, 21; 40, 49, 48, 40, 43, 37.
г) 24 + 76; 15 + 85; 16 + 84; 24 + 76; 21 + 79; 27 + 73. д) 6 · 8; 5 · 9; 8 · 8; 9 · 8; 7 · 9; 9 · 6.
е) 48, 9, 72, 63; 128 и 108 делятся с остатком. ж) 4800, 900, 1280, 7200, 6300, 1080; 48000, 9000, 12800, 72000, 63000, 10800. и) 2500. |
||||||||||||||||||||||||||||||||||||
|
|
– Какой цифрой оканчивается произведение? 13 · 14 · 15 · 16 · 17 |
Ответ: произведение оканчивается цифрой 0 |
||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 17). Задание 21. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько меда можно получить с двух сибирских пасек? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Запись:
Решение: 1) 175 + 15 = 190 (ул.) – на 2-й пасеке. 2) 175 + 190 = 365 (ул.) – всего. 3) 365 · 160 = 58400 (кг) – всего. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Осуществлять контроль по результату |
|||||||||||||||||||||||||||||||||||
|
Задание 22. |
– Прочитайте и решите задачу.
Выразите площадь в квадратных метрах. |
Запись: Ширина – 15 м 2 дм = 152 дм. Длина – 22 м 5 дм = 225 дм. Площадь – ? Решение: 152 · 225 = 34200 (дм2). 34200 дм2 = 342 м2. |
||||||||||||||||||||||||||||||||||||
|
Задание 23*. |
– Восстановите математические записи. |
Ответ:
|
||||||||||||||||||||||||||||||||||||
|
Задание 24 |
– Выполните вычисления. – Какие математические знания вам помогли выполнить задание? – Поменяйтесь тетрадями, проверьте работу друг у друга |
38 · 1000 – 13496 – (495 · 17 + 136 · 104) = 1945 |
||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока. – Каждая буква обозначает цифру. Одинаковыми буквами обозначена одна и та же цифра. Угадайте, какие цифры обозначены буквами в записи:
– Объясните, как будете рассуждать
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. рассуждения: – Рассмотрим первое задание, так как два других выполняются аналогично.
В = 1 Г = 0 а) В = 1, так как есть переполнение разряда и образовалась новая мерка. б) Г = 0, так как сумма Г + Г может быть либо однозначным числом (0 + 0 + 0), либо двузначным с такой же цифрой в единицах, как и число Г, при условии, что из предыдущего разряда добавилась единица. Например:
Таким образом, Г+ Г = Г может быть либо при Г = 0, либо при Г = 9. В нашем примере предыдущего разряда нет, следовательно, Г = 0.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 69. Конус
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятием конуса как пространственной фигуры; способствовать формированию умений находить отличия конуса от пирамиды; показывать на фигуре, чертеже вершину, основание и боковую поверхность конуса; выполнять изображение конуса на чертеже; выполнять развертку конуса |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием конуса как пространственной фигуры; научатся находить отличия конуса от пирамиды; показывать на фигуре, чертеже вершину, основание и боковую поверхность конуса; выполнять изображение конуса на чертеже; выполнять развертку конуса |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; используют знаково-символические средства для решения учебной задачи; осуществляют моделирование; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: осуществляют саморегуляцию как способность к мобилизации сил и энергии; к волевому усилию (к выбору в ситуации мотивационного конфликта) и преодолению препятствий. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками; определяют цели, функции участников, способы взаимодействия |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя. Выполняют задания устного счета. |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Применять правила делового сотрудничества. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
Загадки о геометрических фигурах |
– Отгадайте загадки: Вроде круг, но дело в том, Что иначе мы зовем Нарисованный кружок. В чем секрет? Скажи, дружок! Эта странная наружность Называется… (окружность). *** По фигуре пролегла Очень тонкая игла: Не черта и не прямая, Что ж за линия такая? В математике живуч Этот очень ровный… (луч). *** Шесть тупых углов внутри На фигуре рассмотри И представь, что из квадрата Получили его брата. Слишком много здесь углов, Ты назвать его готов? (Многоугольник.)
Растянули мы квадрат И представили на взгляд, На кого он стал похожим Или с чем-то очень схожим? Не кирпич, не треугольник – Стал квадрат… (прямоугольник). *** Под линейку я рисую Очень ровную, простую Всем заметную черту. Как фигуру назову? Не спеши, а рассуждай И ответ скорее дай. (Линия.) |
Отгадывают загадки и показывают фигуры на чертеже.
|
|
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 21–22). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Учительница завязала Пете глаза, дала в руки одну из фигур и попросила её охарактеризовать. Вот что сказал Петя: «В ней нет ни одного угла. В основании фигуры – круг. Боковая поверхность без рёбер. Есть вершина». – Знаете ли вы, как называется эта фигура? – Проверьте себя. Найдите название данной фигуры среди слов: куб, пирамида, конус, шар. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Заранее подготовленный ученик читает стихотворение «Конус»*. |
Планировать решение учебной задачи. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
|
Задание 2. |
– Возьмите модель конуса и рассмотрите её. Какой фигурой является основание, вершина конуса? |
– Основание конуса – круг. – Вершина – точка. |
|
|
Задание 3 |
– Рассмотрите чертёж конуса. Назовите его вершину и центр основания конуса |
– Основанием любого конуса является круг |
|
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения. Осуществлять взаимный контроль |
|
Работа по учебнику (с. 23). Задание 6. |
– От рулона ткани продавец отрезал одну пятую часть, что составило 3 м. Сколько метров ткани было в рулоне первоначально? |
Решение: 3 · 5 = 15 (м) – ткани было в рулоне. |
|
|
Задание 7. |
– От деревни до города 32 км. Проехав четвертую часть пути, велосипедист остановился отдохнуть. Сколько километров ему осталось проехать до города? |
Решение: 32 : 4 = 8 (км) – осталось проехать велосипедисту. |
|
|
Задание 8 |
– Выполните действия с величинами. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга |
Ответы: 12 км – 7 км 60 м = 4 км 40 м 126 км : 3 = 42 км 10 т 160 кг + 840 кг = 11 т 304 м · 50 = 15200 м 85 ц – 2 кг = 84 ц 98 кг 17 р. 20 к. · 6 = 103 р. 20 к. 2 ч 30 мин – 45 мин = 1 ч 45 мин 3 р. : 4 = 75 к. |
|
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Назовите признаки конуса. – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 70. Конус. Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием конуса как пространственной фигуры; способствовать формированию умений находить отличия конуса от пирамиды; показывать на фигуре, чертеже вершину, основание и боковую поверхность конуса; выполнять изображение конуса на чертеже; выполнять развертку конуса |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием конуса как пространственной фигуры; научатся находить отличия конуса от пирамиды; показывать на фигуре, чертеже вершину, основание и боковую поверхность конуса; выполнять изображение конуса на чертеже; выполнять развертку конуса |
Метапредметные: Познавательные: осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; используют знаково-символические средства для решения учебной задачи. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: слушают и понимают речь других; договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Личностные: проявляют интерес к учебному материалу; владеют знаниями основных моральных норм поведения; осознают роль языка и речи в жизни людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
|
II. Актуализация опорных знаний. Устный счет.
|
Организует устный счет с целью актуализации знаний.
– Вычислите площади данных фигур:
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
Вычисляют площади данных фигур. Ответы: а) первую фигуру «перекраиваем» в прямоугольник со сторонами 3 см и 9 см. S1 = 3 · 9 = 27 (см2); б) площадь большого прямоугольника S = 10 · 5 = 50 (см2). Площадь вырезанного прямоугольника S = 3 · 2 = 6 (см2). Отсюда площадь фигуры: 50 – 6 = 44 (см2). |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
Интеллектуальная разминка |
– Задание на смекалку.
|
Решение:
|
||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 22–23). Задание 4. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Какие предметы или их части по форме похожи на боковую поверхность конуса? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Колпак, шляпка гриба, крыша башни. |
Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
|
|
Задание 5 |
– Начертите круг радиусом 5 см. Отметьте его центр. Надрежьте круг по его радиусу до центра круга. Наложите края один на другой так, чтобы получилась фигура конической формы. Склейте края |
Выполняют практическую работу |
||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 24). Задание 9. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок |
|
|
– Как изменяется второй множитель в произведениях? – Вычислите значение первого выражения. Вычисляйте значение каждого следующего выражения, используя значение предыдущего выражения. |
– Второй множитель увеличивается на 1. 250 · 2 = 500 250 · 6 = 1500 250 · 3 = 750 250 · 7 = 1750 250 · 4 = 1000 250 · 8 = 2000 250 · 5 = 1250 250 · 9 = 2250 |
|||
|
Задание 10. |
– Запишите номер своего дома или квартиры и выполните следующие действия: умножьте это число на 2, затем прибавьте 3, полученное число умножьте на 50, к произведению прибавьте свой возраст и число 65, вычтите из результата 215. – Проверьте себя: получится число, две последние цифры которого обозначают возраст, а оставшиеся – номер дома или квартиры. |
Выполняют задания математического фокуса. Решение: 32 · 2 = 64 64 + 3 = 67 67 · 50 = 3350 3350 + 10 + 65 – 215 = 3210. |
||
|
Задание 11 |
– Закончите предложения так, чтобы получились неверные высказывания |
Ответы: Если сложить 25 и 35, то получится 70. Частное чисел 24 и 8 равно 4. Разность чисел 100 и 70 не равна 30. Число 30 меньше числа 28 на 3. Произведение чисел 400 и 5 не равно 2000 |
||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 70. Конус. Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием конуса как пространственной фигуры; способствовать формированию умений находить отличия конуса от пирамиды; показывать на фигуре, чертеже вершину, основание и боковую поверхность конуса; выполнять изображение конуса на чертеже; выполнять развертку конуса |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием конуса как пространственной фигуры; научатся находить отличия конуса от пирамиды; показывать на фигуре, чертеже вершину, основание и боковую поверхность конуса; выполнять изображение конуса на чертеже; выполнять развертку конуса |
Метапредметные: Познавательные: осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; используют знаково-символические средства для решения учебной задачи. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: слушают и понимают речь других; договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Личностные: проявляют интерес к учебному материалу; владеют знаниями основных моральных норм поведения; осознают роль языка и речи в жизни людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
|
II. Актуализация опорных знаний. Устный счет.
|
Организует устный счет с целью актуализации знаний.
– Вычислите площади данных фигур:
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
Вычисляют площади данных фигур. Ответы: а) первую фигуру «перекраиваем» в прямоугольник со сторонами 3 см и 9 см. S1 = 3 · 9 = 27 (см2); б) площадь большого прямоугольника S = 10 · 5 = 50 (см2). Площадь вырезанного прямоугольника S = 3 · 2 = 6 (см2). Отсюда площадь фигуры: 50 – 6 = 44 (см2). |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
Интеллектуальная разминка |
– Задание на смекалку.
|
Решение:
|
||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 22–23). Задание 4. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Какие предметы или их части по форме похожи на боковую поверхность конуса? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Колпак, шляпка гриба, крыша башни. |
Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
|
|
Задание 5 |
– Начертите круг радиусом 5 см. Отметьте его центр. Надрежьте круг по его радиусу до центра круга. Наложите края один на другой так, чтобы получилась фигура конической формы. Склейте края |
Выполняют практическую работу |
||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 24). Задание 9. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок |
|
|
– Как изменяется второй множитель в произведениях? – Вычислите значение первого выражения. Вычисляйте значение каждого следующего выражения, используя значение предыдущего выражения. |
– Второй множитель увеличивается на 1. 250 · 2 = 500 250 · 6 = 1500 250 · 3 = 750 250 · 7 = 1750 250 · 4 = 1000 250 · 8 = 2000 250 · 5 = 1250 250 · 9 = 2250 |
|||
|
Задание 10. |
– Запишите номер своего дома или квартиры и выполните следующие действия: умножьте это число на 2, затем прибавьте 3, полученное число умножьте на 50, к произведению прибавьте свой возраст и число 65, вычтите из результата 215. – Проверьте себя: получится число, две последние цифры которого обозначают возраст, а оставшиеся – номер дома или квартиры. |
Выполняют задания математического фокуса. Решение: 32 · 2 = 64 64 + 3 = 67 67 · 50 = 3350 3350 + 10 + 65 – 215 = 3210. |
||
|
Задание 11 |
– Закончите предложения так, чтобы получились неверные высказывания |
Ответы: Если сложить 25 и 35, то получится 70. Частное чисел 24 и 8 равно 4. Разность чисел 100 и 70 не равна 30. Число 30 меньше числа 28 на 3. Произведение чисел 400 и 5 не равно 2000 |
||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 72. Упражнение в решении задач на движение в одном направлении
из одной точки.
Педагогическая диагностика № 2
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений решать текстовые задачи на движение в одном направлении; побудить использовать приобретенные знания и умения в практической деятельности и повседневной жизни, при решении задач, связанных с бытовыми жизненными ситуациями (направление движения) |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями о движении двух тел в одном направлении: «из одной точки», «из двух точек»; научатся различать виды движения двух тел в одном направлении: из одной точки, из двух точек; решать задачи на движение в одном направлении |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая), и преобразование модели с целью выявления общих законов, определяющих данную предметную область; осуществляют анализ; проводят аналогии между изучаемым материалом и собственным опытом. Регулятивные: осваивают начальные формы познавательной и личностной рефлексии. Коммуникативные: принимают участие в работе парами и группами; допускают существование различных точек зрения; договариваются, приходят к общему решению |
Личностные: осознают необходимость самосовершенствования |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Найдите значения выражений: 70 · 8 270 – 60 90 · 3 360 : 4 210 : 3 560 – 200 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Ответы: 70 · 8 = 560 270 – 60 = 210 90 · 3 = 30 360 : 4 = 90 210 : 3 = 70 560 – 200 = 360 |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Интеллектуальная разминка. |
– Заполните таблицу:
– Как найти неизвестный делитель? – Как найти неизвестное делимое? |
Заполняют таблицу:
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задачи |
– Решите задачи. а) Голубь улетел из голубятни на расстояние, равное 420 км. Через сколько времени он вернется, если будет лететь со скоростью 60 км/ч? б) Сайгак может бежать со скоростью 70 км/ч, это на 30 км/ч больше, чем скорость индийского носорога. Какова скорость носорога? |
Решения. а) 420 : 60 = 7 (ч) – вернется голубь.
б) 70 – 30 = 40 (км/ч) – скорость носорога. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
в) Почтовый голубь должен доставить донесение на расстояние 130 км. Скорость голубя 50 км/ч. Успеет ли голубь доставить это донесение за 3 ч? |
в) 50 · 3 = 150 (км.) – голубь успеет доставить донесение: 150 км > 130 км |
||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 26). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте задачу. Что известно? Что требуется узнать? – Догонит ли собака кошку?
– На сколько метров уменьшается расстояние между собакой и кошкой каждую минуту? – Через сколько минут собака догонит кошку? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Ответ: – Собака догонит кошку, так как у собаки скорость больше, чем у кошки. – На 30 метров уменьшается расстояние между собакой и кошкой каждую минуту: 350 – 320 = 30 (м). – Через 9 минут собака догонит кошку: 270 : 30 = 9 (мин). |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4. |
– Прочитайте и решите задачу. – Сколько километров проехал 1-й поезд за 2 часа? – На сколько километров уменьшается расстояние между поездами каждый час? – На сколько километров уменьшится расстояние через 3 часа?
– Какое расстояние будет между поездами через 3 часа? |
Решение. – проехал 1-й поезд за 2 часа: 70 · 2 = 140 (км).
– На 20 километров уменьшается расстояние между поездами каждый час: 90 – 70 = 20 (км). – На 60 километров уменьшится расстояние через 3 часа: 20 · 3 = 60 (км). – 80 километров будет между поездами через 3 часа: 140 – 60 = 80 (км). |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Проводит самостоятельную работу по карточкам (15 минут). Карточка 1. |
1. Какое расстояние пройдет автобус за 6 часов, если движется со скоростью 45 км/ч? 2. Сколько времени потребуется велосипедисту, чтобы проехать 252 км со скоростью 18 км/ч? 3. С какой скоростью должен идти катер, чтобы преодолеть 162 км за 9 часов? |
Ответы: 1. 270 км. 2. 14 ч.
3. 18 км/ч. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Карточка 2. |
1. Расстояние от деревни до станции 35 км. Успеет ли Сережа на электричку, которая отправляется в 13 часов, если он выезжает из деревни на велосипеде в 10 часов и будет ехать со скоростью 12 км/ч? 2. Миша ехал полем на велосипеде 27 км, а лесом – 15 км. На весь путь он затратил 3 часа. С какой скоростью ехал Миша? |
1. 35 : 12 = 2 (ост. 11). Успеет.
2. (27 + 15) : 3 = 14 км/ч. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Карточка 3 |
1. Из деревни к автобусной остановке Катя идет со скоростью 50 м/мин. На каком расстоянии от деревни находится автобусная остановка, если на весь путь Катя тратит 2 часа? 2. Автобус проходит 312 км за 6 часов. Какое рас-стояние пройдет автобус за 8 часов, если будет двигаться с той же скоростью? |
1. 6 км.
2. 416 км. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 27–28). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выполните умножение. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Решение: 205 · 603 = 123615 384 · 209 = 80256 405 · 504 = 204120 422 · 508 = 214376 108 · 207 = 22356 105 · 106 = 11130 704 · 101 = 71104 207 · 124 = 25668 607 · 702 = 426114 302 · 167 = 50434 408 · 902 = 368016 606 · 333 = 201798 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 12. |
– Выполните деление с остатком. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга. |
Решение: 46 : 8 = 5 (ост. 6) 361 : 9 = 40 (ост. 1) 60 : 9 = 6 (ост. 6) 276 : 8 = 34 (ост. 4) 85 : 4 = 21 (ост. 1) 418 : 7 = 59 (ост. 5) 78 : 19 = 4 (ост. 2) 425 : 21 = 20 (ост. 5) 124 : 5 = 24 (ост. 4) 836 : 17 = 49 (ост. 3) 56 : 13 = 4 (ост. 4) 526 : 15 = 35 (ост. 1) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 13. |
– Какие числа надо записать в «окошках», чтобы равенства были верными? |
1023 + 257 = 1280 9701 + 369 = 10070 3869 – 3091 = 778 8913 – 157 = 8756 12 · 8 = 96 625 : 25 = 25 675 : 15 = 45 48 · 2 = 96 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 14. |
– Подойдет ли эта коробка для торта по размеру? |
– эта коробка для торта по размеру подойдет. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 15. |
– Сколько кубиков в зеленой фигуре? – Сколько кубиков в синей фигуре? |
4 · 2 · 2 = 16 (кубиков) – в зеленой фигуре. 5 · 2 · 2 = 20 (кубиков) – в синей фигуре. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 16 |
– Какой стала площадь грядки? |
Решение: 20 дм = 2 м 2 · (5 + 1) = 2 · 6 = 12 (м2) – площадь 2-й грядки |
||||||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи |
Урок 73. Упражнение в решении задач на движение в одном направлении
из двух точек
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений решать текстовые задачи на движение в одном направлении; совершенствовать умения использовать приобретенные знания и умения в практической деятельности и повседневной жизни, при решении задач, связанных с бытовыми жизненными ситуациями (направление движения) |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями о движении двух тел в одном направлении: «из одной точки», «из двух точек»; научатся различать виды движения двух тел в одном направлении: из одной точки, из двух точек; решать задачи на движение в одном направлении |
Метапредметные: Познавательные: осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи; ориентируются в учебнике (на развороте, в оглавлении, в условных обозначениях). Регулятивные: умеют формулировать учебную задачу на основе соотнесения того, что уже известно и усвоено обучающимся, и того, что еще неизвестно; определяют последовательность промежуточных целей с учетом конечного результата; составляют план и последовательность действий. Коммуникативные: умеют задавать вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения; считаются с мнением другого человека; проявляют терпение и доброжелательность в споре, доверие к собеседнику |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. – Знаете ли вы? · Скорость кабана равна 8 м/с, а зайца-русака – 11 м/с. На сколько заяц быстрее кабана? Выразите данные скорости в метрах в минуту. · Пчела летит со скоростью 18 км/ч. Выразите данную скорость в метрах в час. Какое расстояние пчела пролетит за 5 часов? |
Отвечают на вопросы учителя. Выполняют задания устного счета. Ответы: 8 м/с = 480 м/мин ‒ скорость кабана; 11 м/с = 660 м/мин ‒ скорость зайца-русака.
18 км/ч = 18000 м/ч; 18 · 5 = 90 (км) – пролетит пчела за 5 часов. |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||
|
– Выразите данные скорости в метрах в час: · Сайгаки населяют полупустыни и сухие степи Евразии. По гладкой равнине эти стремительные антилопы могут мчаться со скоростью 80 км/ч. · Самая крупная птица – африканский страус. В случае опасности страусы бегут со скоростью 70 км/ч. · Самое быстроногое животное на Земле – гепард. В погоне за копытными на коротких дистанциях гепард мчится со скоростью 110 км/ч. · Земляная кукушка населяет сухие равнины США и Мексики. Живет на земле и летать не любит. Зато бегает быстрее всех других летающих птиц, развивая скорость до 25 км/ч |
Ответы: 80 км/ч = 80000 м/ч.
70 км/ч = 70000 м/ч. 110 км/ч = 110000 м/ч.
25 км/ч = 25000 м/ч |
|||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 26–27). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Через сколько секунд первая стрекоза догонит вторую?
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Запись:
Решение: 1) 12 – 10 = 2 (м/с) – скорость изменения расстояния. 2) 6 : 2 = 3 (с) – догонит. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Осуществлять контроль по результату |
|||||||||
|
Задание 6. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Через сколько минут собака догнала хозяина? |
Запись:
Решение: 1) 150 – 70 = 80 (м/мин) – скорость изменения рас-стояния. 2) 400 : 80 = 5 (мин) – догонит. |
||||||||||
|
Задание 7 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько времени Таня догоняла Колю? |
Запись:
Решение: 1) 160 – 80 = 80 (м/мин) – скорость изменения рас-стояния. 2) 240 : 80 = 3 (мин) – догонит |
||||||||||
|
IV. Включение нового в актив-ное использо- вание в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 29). Задание 17. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Вычислите площадь поля, размеры которого указаны на рисунке. Решите задачу двумя способами. Чертеж:
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Решение: I способ 1) 430 · 560 = 240800 (м2). 2) (850 – 560) · 180 = 52200 (м2). 3) 240800 + 52200 = 293000 (м2). II способ 1) 430 · 850 = 365500 (м2). 2) (430 – 180) · (850 – 560) = 250 · 290 = 72500 (м2). 3) 365500 – 72500 = 293000 (м2). |
Выбирать действия в соответствии с постав- ленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||
|
Задание 18. |
– От рулона ткани длиной 20 м отрезали полтора метра ткани. Сколько ткани осталось в рулоне? |
Ответ: 18 м 50 см. |
||||||||||
|
Задание 19. |
– Верно ли каждое утверждение? Поясните свой ответ на примерах. |
– Высказывание «Есть такие числа, сумма которых больше 20» верно, так как 15 + 17 = 32, 25 + 20 = 45. – Высказывание «Не существует верных неравенств» неверно, так как 5 + 6 > 10 – верно, 100 – 20 < 90 – верно. – Высказывание «Любое трехзначное число записывается тремя разными цифрами» неверно, так как есть числа 222, 555, 777 и др. |
||||||||||
|
Задание 20*. |
– За 20 минут поезд проходит 18 км. Чему равна скорость поезда? |
Решение: 1) 18 км = 18000 м; 18000 : 20 = 900 (м/мин) – скорость. 2) 60 : 20 = 3 (часть) – составляют 20 минут от часа. 3) 18 · 3 = 54 (км/ч) – скорость поезда. |
||||||||||
|
Задание 21 |
– Сколько минут в одном часу? Сколько секунд в одной минуте? – Выполните действия с величинами. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга |
Ответы: 1 ч = 60 мин; 1 мин = 60 с. 18 ч 46 мин – 13 ч 29 мин = 5 ч 17 мин. 8 ч 15 мин – 35 мин = 7 ч 40 мин. 40 мин 35 с – 20 мин 48 с = 19 мин 47 с. 14 ч 38 мин + 18 ч 46 мин = 33 ч 24 мин. 1 ч – 29 мин = 31 мин. 11 ч – 29 мин = 10 ч 31 мин |
||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, формировать адекватную самооценку |
Урок 74. Контрольная работа № 5 по теме «Письменные приёмы умножения чисел»
|
Тип урока: контроль и оценивание знаний и способов действий |
||
|
Педагогические задачи: проверить усвоение алгоритма письменного умножения многозначного числа на однозначное, умение решать задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями о движении двух тел в одном направлении: «из одной точки», «из двух точек»; научатся различать виды движения двух тел в одном направлении: из одной точки, из двух точек; решать задачи на движение в одном направлении |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; строят логическую цепь рассуждений. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: умеют устанавливать, с какими учебными задачами могут справиться самостоятельно |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
I. Содержание контрольной работы. Вариант 1
|
Знакомит с содержанием контрольной работы, комментирует задания.
1. Выполни вычисления. 406 · 307 808 · 444 469 · 208 307 · 147 108 · 107
2. Найди значение выражения. 618 : 6 + 804 · 7 = 3. Реши задачу. Из двух городов навстречу друг другу выехали два автобуса. Первый ехал со скоростью 58 км/ч, а скорость второго на 6 км/ч больше. Найди рас-стояние между городами, если автобусы встретились через 7 часов. 4. Реши задачу. Самолёт летел 3 ч со скоростью 950 км /ч, сделал посадку, а затем пролетел ещё 300 км. Какова длина маршрута самолёта? |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы.
1. Ответы: 124642 358752 97552 45129 11556 2. Ответ: 5731. 3. 854 км – расстояние между городами.
4. 3150 км – длина маршрута самолета.
|
Принимать и сохранять учебную цель и задачу. Анализировать, находить общее и различия, делать выводы. Осознанно и произвольно строить речевое высказывание в устной форме |
|
Вариант 2 |
1. Выполни вычисления. 306 · 407 707 · 333 347 · 306 402 · 168 104 · 109 |
1. Ответы: 124542 235431 106182 67536 11336 |
|
|
|
2. Найди значение выражения. 903 · 8 – 906 : 3 = 3. Реши задачу. Из двух городов навстречу друг другу одновременно выехали две машины. Одна двигалась со скоростью 68 км/ч, другая двигалась со скоростью 80 км/ч и проехала до встречи 320 км. Найди расстояние между городами. 4. Реши задачу. После того как самолёт летел 2 ч со скоростью 850 км/ч, до места назначения ему оставалось пролететь 630 км. На какое расстояние самолёт совершает перелёт? |
2. Ответ: 6922. 3. 592 км – расстояние между городами.
4. 2330 км – должен пролететь самолет |
|
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность |
Урок 75. Высказывания. Истинные и ложные высказывания
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «истинные» и «ложные» высказывания; рассмотреть область применения элементов математической логики, значение высказываний истины, лжи, отрицания; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «истинные» и «ложные» высказывания; научатся определять значения высказываний: И (истина), Л (ложь); анализировать образование составного высказывания с помощью логических связок «неверно, что…» и определять его истинность |
Метапредметные: Познавательные: умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: оценивают результат работы, определяют, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения; осуществляют саморегуляцию как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта) и преодолению препятствий. Коммуникативные: контролируют действия партнера |
Личностные: проявляют желание учиться; формируют внутреннюю позицию школьника на уровне положительного отношения к школе |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Сравните выражения, записанные на доске, не выполняя вычислений: 425 · 3 ... 4250 · 3 630 : 3 … (600 + 3) : 3 172560 · 9 ... 172500 · 9 609 : 3 … (300 + 300 + 9) : 3 3207 · 8 ... 3207000 · 8 720 : 6 … (600 + 12) : 6 |
Отвечают на вопросы учителя. Выполняют задания устного счета. Решение:
425 · 3 < 4250 · 3 630 : 3 > (600 + 3) : 3 172560 · 9 > 172500 · 9 609 : 3 = (300 + 300 + 9) : 3 3207 · 8 < 3207000 · 8 720 : 6 < (600 + 12) : 6 |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
||||||
|
|
– Назовите выражения, записанные в первой строке, и их значения, записанные во второй строке:
|
|
|||||||
|
|
– Запишите число, ответив на вопросы: а) Какое число надо прибавить к 150, чтобы получить 200? б) Какое число нужно вычесть из 620, чтобы получить 600? в) Какое число нужно прибавить к 200, чтобы получить частное 800 : 2? г) Какое число нужно вычесть из 900, чтобы получить 100 · 3? д) Из какого числа нужно вычесть 200, чтобы получить произведение 80 · 10? |
Ответы: а) 50.
б) 20.
в) 200.
г) 600.
д) 1000 |
|||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 30). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – В математике верные высказывания называются истинными, а неверные – ложными. – Прочитайте высказывания. Какие из них истинные и какие ложные? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. – Высказывание «В июле 30 дней» – истинное. – Высказывание «112 и 113 – двузначные числа» – ложное. – Высказывание «47 – 39 = 8» – истинное. – Высказывание «324 < 305» – ложное. – Высказывание «185 > 97» – истинное. – Высказывание «Любой квадрат является прямоугольником» – истинное. |
Планировать решение учебной задачи: выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
||||||
|
Задание 2 |
– Из данных высказываний выберите и прочитайте истинные высказывания |
– Истинные высказывания: В русском алфавите 33 буквы. 1 ч = 60 мин. 20 делится на 5 и на 4 |
|||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 31–32). Задание 6. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль |
||||||
|
Задание 7. |
– Выполните умножение. – Проверьте результаты умножения с помощью калькулятора. |
Решение: 1250 · 35 = 43750 405 · 270 = 109350 810 · 630 = 510300 108 · 502 = 54216 |
|||||||
|
Задание 8. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какое расстояние будет между мотоциклистом и велосипедистом через 3 часа, если расстояние от города до села 220 км? |
Запись:
Было – 220 км Проехали – ? км Осталось – ? км Решение: 1) 53 + 18 = 71 (км/ч) – скорость сближения. 2) 71 · 3 = 213 (км) – проехали. 3) 220 – 213 = 7 (км) – между. |
|||||||
|
Задание 9 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Через какое время расстояние между катером и теплоходом будет 76 км? |
Запись:
Решение: 1) 64 – 26 = 38 (км/ч) – скорость удаления. 2) 76 : 38 = 2 (ч) ‒ время |
|||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какие высказывания называют истинными? – А какие – ложными? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи |
Урок 76. Истинные и ложные высказывания. Высказывания
со словами «неверно, что»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «истинные» и «ложные» высказывания; рассмотреть область применения элементов математической логики, значение высказываний истины, лжи, отрицания; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «истинные» и «ложные» высказывания; научатся определять значения высказываний: И (истина), Л (ложь); анализировать образование составного высказывания с помощью логических связок «неверно, что…» и определять его истинность |
Метапредметные: Познавательные: умеют ориентироваться в учебнике (на развороте, в оглавлении, в условных обозначениях); находят ответы на вопросы в тексте, иллюстрациях; делают выводы в результате совместной работы класса и учителя. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: осознают необходимость самосовершенствования; понимают значение границ собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний.
– Разгадайте правило, по которому оставлены схемы, и вставьте числа в «окошки»:
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение:
|
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||
|
|
– Вставьте числа в «окошки»: 5 ·
96 :
|
Решение: 5 · 11 = 55 54 : 9 = 6 72 : 6 = 12 9 · 9 = 81 96 : 6 = 16 700 : 7 = 100 7 · 8 = 56 5 ·50 = 250 |
||||||||
|
Игра «Распутай клубок» |
– Какие числа пропущены?
|
Решение: а) 40+ 180 = 220 б) 0 + 1 = 1 в) 26 + 24 =50 220 · 3 = 660 0 + 25 = 25 50 – 32 = 18 900 – 660 = 240 25 : 1 = 25 74 – 24 = 50 |
||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 31). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Даны истинные высказывания. Каждое из этих высказываний замените другим высказыванием так, чтобы оно начиналось словами «неверно, что». Какое высказывание получилось: истинное или ложное? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Составляют высказывания: «Неверно, что орел – птица» – ложное. «Неверно, что в неделе 7 дней» – ложное. «Неверно, что февраль – зимний месяц» – ложное. «Неверно, что слово “нос” – существительное» – ложное. |
Планировать решение учебной задачи. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
|||||||
|
Задание 4. |
– Даны ложные высказывания. Каждое из этих высказываний замените другим высказыванием так, чтобы оно начиналось словами «неверно, что». Какое высказывание получилось: истинное или ложное? |
Составляют высказывания: «Неверно, что в любом четырехугольнике три вершины». «Неверно, что тонна – единица длины». «Неверно, что сумма 45 и 10 равна 54». – Это истинные высказывания. |
||||||||
|
Задание 5 |
– Сравните два высказывания. Чем они отличаются? |
– Высказывания отличаются истинностью. – В каждой паре одно высказывание истинное, другое – ложное |
||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 32–33). Задание 10. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – С какой скоростью ехала легковая машина?
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись:
Решение: 1) 60 · 2 = 120 (км) – проехала грузовая машина. 2) 120 + 40 = 160 (км) – проехала легковая машина. 3) 160 : 2 = 80 (км/ч) – скорость легковой машины. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|||||||
|
Задание 11. |
– Какое число надо записать в окошке, чтобы равенство было верным? |
а) 3672 + 12000 – 3672 = 8328 121 : 11 = 11 в) 260 : 13 = 20 401 – 96 = 305 |
||||||||
|
Задание 12. |
– Какое число задумала Лариса?
|
10 · 72 = 720 720 : 6 = 120 120 – 80 = 40 40 · 5 = 200 Ответ: 200. |
||||||||
|
Задание 13 |
– Какое число задумал Саша? |
2 · 90 = 180 180 : 18 = 10 10 · 15 = 150 150 – 60 = 90 Ответ: 90 |
||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 77. Истинные и ложные высказывания. Высказывания со словами
«неверно, что»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: рассмотреть область применения элементов математической логики, значение высказываний истины, лжи, отрицания; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «истинные» и «ложные» высказывания; научатся определять значения высказываний: И (истина), Л (ложь); анализировать образование составного высказывания с помощью логических связок «неверно, что…» и определять его истинность |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; используют знаково-символические средства для решения учебной задачи. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями её реализации. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: устанавливают связь между целью учебной деятельности и ее мотивом (между результатом учения и тем, что побуждает деятельность, ради чего она осуществляется) |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Расположите величины в порядке возрастания: 2 сут. 15 ч; 49 ч; 3 сут.; 2 сут. 5 ч; 64 ч; 4 сут. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение: 49 ч; 2 сут. 5 ч; 2 сут. 15 ч; 64 ч; 3 сут.; 4 сут. |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||||
|
Задача. |
– Решите задачу. а) Один велосипедист прошел дистанцию за 89 мин, а другой – за 1 ч 30 мин. Кто из них раньше пришел к финишу и на сколько минут опередил соперника? б) Урок закончился в 9 ч 50 мин. Когда начался урок, если он длился 40 минут? |
Решение: а) 1 ч 30 мин = 90 мин; 90 мин – 89 мин = 1 мин.
б) 9 ч 50 мин – 40 мин = 9 ч 10 мин. |
||||||||||
|
Задания на смекалку |
– Учащиеся измерили отрезок, данный в учебнике. Учительница записала правильный ответ: 1 дм 5 см 3 мм. У Светы получилось 1 дм 53 мм, у Коли – 15 см 3 мм, у Тани – 153 мм. Ошиблись эти ученики или нет? |
– Учащиеся не ошиблись. |
||||||||||
|
|
– В каких мерах удобнее выразить записанные на доске данные: а) длина реки – 30520 м; б) масса арбуза – 4830 г; в) возраст девочки – 49 месяцев; г) продолжительность каникул – 168 ч? |
Ответы: а) длина реки – 30 км 520 м; б) масса арбуза – 4 кг 830 г; в) возраст девочки – 2 года 1 месяц; г) продолжительность каникул –7 дней |
||||||||||
|
III. Открытие нового знания, способа действия. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Один мальчик говорит другому: 1. «Я такой сильный, что могу поднять живого слона». 2. «Самое большое животное на Земле – кит». 3. «Заяц съел на обед целого волка». 4. «Яблоки растут на деревьях». 5. «Банан – травянистое растение». – Какие из высказываний мальчика истинные? Какие ложные? – Под высказыванием понимают любое утверждение, о котором имеет смысл говорить, что оно истинно или ложно. Решение большинства задач этой темы основано на том простом факте, что каждое высказывание или истинно, или ложно; одновременно быть истинным и ложным высказывание не может. Примеры высказываний: 1. Минск – столичный город. 2. 33 – четное число. 3. Миша на большой перемене съел настоящего льва. 4. 25 умножить на 3 равно 75. Но, например, утверждения «х > 0» и «у него в кошельке нет денег» высказываниями не являются, так как судить об их истинности или ложности невозможно. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Определяют истинные и ложные высказывания.
– Высказывания 1 и 4 – истинны, 2 и 3 – ложны.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять контроль по результату |
|||||||||
|
Задача
|
Решите задачу. В велогонках приняли участие пятеро школьников. После гонок пятеро болельщиков заявили: «Коля занял 1-е место, а Ваня – 4-е». «Сережа занял 2-е место, а Ваня – 4-е». «Сережа занял 2-е место, а Коля – 3-е». «Толя занял 1-е место, а Надя – 2-е». «Надя заняла 3-е место, а Толя – 5-е». Зная, что одно из показаний каждого болельщика верное, а другое – неверное, найдите правильное распределение мест |
Составляют таблицу, отражающую высказывания всех болельщиков: Решение.
Фиксируют любую строку таблицы, например первую. Дальнейшие рассуждения будут основаны на том, что в каждой строке одно из высказываний – верное, а другое – нет. Допустим, что в выбранной 1–й строке высказывание «Коля – 1» – верное. Тогда по условию «Ваня – 4» – неверное высказывание. Например, поскольку «Коля – 1» – истинное предположение, то «Толя – 1» уже не может быть истинным высказыванием, значит, истинным будет «Надя – 2». Но тогда «Надя – 3» – неверное, а потому «Толя – 5» – верное высказывание. В итоге замечаем, что 2-е место заняли 2 человека – Сережа и Надя, что невозможно. Значит, первоначальное допущение оказалось неверным. Поэтому в той же 1-й строке делаем другое предположение «Ва-ня – 4», считая теперь высказывание «Ваня – 4» – истинным. Рассмотрев первые 3 строки, замечаем, что высказывания «Коля – 3» и «Надя – 3» не могут быть истинными одновременно. Поэтому «Надя – 3» – ложь. Тогда «Толя – 5» – истинно, «Надя – 2» – истинно, «Толя – 1» – ложно. При этом замечаем, что никаких противоречий со сделанным во второй раз допущением нет. Поэтому ответ будет следующим: Надя – 2, Коля – 3, Ваня – 4, Толя – 5, тогда Сережа – 1-е место |
||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 33–35). Задание 14. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Сколько кубиков в зеленой фигуре – Сколько кубиков в синей фигуре? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Ответы: 5 · 3 · 4 = 60 (кубиков) в зеленой фигуре. 3 · 3 · 3 = 27 (кубиков) в синей фигуре. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. |
Запись: 1 шарфик – 75 г 27 шарфиков – ? г Решение: 27 · 75 = 2025 (г) – можно связать из 75 г пуха. Ответ: 2025 г > 2000 г. |
||||||||||
|
Задание 16. |
– Купили 200 г кофе и заплатили за покупку 36 р. 80 к. Вычислите цену килограмма кофе. – Сколько стоит 100 г кофе? |
Решение: 1) 36 р. 80 к. : 2 = 18 р. 40 к. – стоит 100 г кофе. 2) 18 р. 40 к. · 10 = 184 р. – стоит 1 кг кофе. |
||||||||||
|
Задание 17. |
– Рассмотрите таблицу. Узнайте в магазине цены на данные в ней продукты. Внесите собранные данные в таблицу. Затем рассчитайте стоимость двух разных наборов из этих продуктов. |
Выполняют практическое задание. |
||||||||||
|
Задание 18. |
– Назовите координаты вершин ломаной АСВМК. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга. |
– Точка А (3;1), точка С (5; 4), точка В (6; 7), точка М (10; 11), точка К (13; 7). |
||||||||||
|
Задание 19 |
– Если вырезать из бумаги такую фигуру, как на рисунке, то можно сделать модель треугольной пирамиды с основанием АВС. – Используя кальку, скопируйте эту фигуру и сделайте модель пирамиды |
Выполняют практическое задание |
||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 78. Составные высказывания. Логическая связка «или».
Контрольный устный счёт № 5
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: рассмотреть область применения элементов математической логики, значение высказываний истины, лжи, отрицания; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами образования составных высказываний; научатся образовывать составные высказывания с помощью логических связок «и», «или», «если…то…» и определять их истинность |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Найдите значения выражений: 48 : 4 36 : 3 72 : 6 46 : 2 96 : 3 90 : 5 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Ответы: 48 : 4 = 12 36 : 3 = 12 72 : 6 = 12 46 : 2 = 23 96 : 3 = 32 90 : 5 = 18 |
Выделять существенную информацию |
|
– Вставьте пропущенные числа, чтобы равенства были верными: 7203 = 31015 = 99099 = 90000 + 9000 + 843001 = 11001 = |
Решение:
7203 = 7000 + 200 + 3 31015 = 30000 + 1000 +10 + 5 99099 = 90000 + 9000 + 90 + 9 843001 = 800000 + 40000 + 3000 + 1 11001 = 10000 + 1000 + 1 |
||
|
– Какие ошибки допущены при делении с остатком? 17 : 4 = 3 (ост. 5) 30 : 7 = 3 (ост. 2) 6 : 8 = 0 (ост. 8) 30 : 12 = 2 (ост. 7) |
Решение: 17 : 4 = 4 (ост. 1) 30 : 7 = 4 (ост. 2) 6 : 8 = 0 (ост. 6) 30 : 12 = 2 (ост. 6) |
||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 36–37). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте каждое высказывание и определите, истинно оно или ложно. џ Составное высказывание с союзом «или» истинно, если истинно хотя бы одно из двух составляющих его высказываний. В остальных случаях оно ложно. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Высказывание «Ель – лиственное дерево» – ложное. – Высказывание «Ель – хвойное дерево» – истинное. – Высказывание «Ель – лиственное или хвойное дерево» – истинное. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|
Задание 2. |
– Определите, истинно или ложно составное
высказывание |
1) Первое высказывание истинно, а второе ложно. (Истинно.) 2) Первое высказывание ложно, а второе истинно. (Истинно.) 3) Оба высказывания истинные. (Истинно.) 4) Оба высказывания ложные. (Ложно.) |
|
|
Задание 3. |
– Прочитайте простые высказывания и укажите, истинны они или ложны. Соедините каждое из двух высказываний союзом «или». Какое высказывание получилось: истинное или ложное? |
1) Высказывание «Буква э – гласная или буква э – согласная» – истинное. 2) Высказывание «Тринадцать больше тридцати или тринадцать меньше тридцати» – истинное. 3) Высказывание «В сутках 12 часов или в сутках 36 часов» – ложное. 4) Высказывание «Число 6 делится на 2 или число 6 делится на 3» – истинное. |
|
|
Задание 4. |
– Из каких двух высказываний образовано каждое составное высказывание? – Истинно или ложно каждое из составных высказываний? |
1) Высказывание «В одном часе 100 минут или 60 минут» – истинное. 2) Высказывание «Март – первый месяц весны или лета» – истинное. 3) Высказывание «Слоны обитают на северном или на южном полюсе» – ложное. 4) Высказывание «Разность чисел 960 и 180 равна 780 или 880» – истинное. 5) Высказывание «В одном метре 100 см или 10 дм» – истинное. 6) Высказывание «Основанием пирамиды может быть квадрат или семиугольник» – истинное. |
|
|
Задание 5* |
– Приведите примеры истинных и ложных составных высказываний, образованных с помощью союза «или» |
Примеры высказываний: – Осина – лиственное или хвойное дерево. – В одном километре 1000 метров или 100 дециметров. – Январь – весенний или летний месяц |
|
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 41–42). Задание 17. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Вычислите. Проверьте сложение вычитанием, вычитание –сложением. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Ответы: 263127 + 736452 = 999579 728326 – 607314 = 121012 32736 + 398585 = 431321 900076 – 704977 = 195099 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала |
|
Задание 18. |
– Найдите значения выражений. |
Ответы: (15 · (178 + 5) + 90) · 7 = 19845 486 : 9 · (46 + 54) : 10 = 540 624268 – 13965 + 190008 = 800311 105 · (6 + 203) – 300 : 5 = 21885 (6275 – 1829) · 0 + 3500 = 3500 0 : (17068 + 91374) + 10000 = 10000 |
|
|
Задание 19. |
– Выполните вычисления. – Какие математические знания помогли вам выполнить это задание? |
Ответы: 1) 35 · 104 – (320 : 80 + 156) : 160 = 3639. 2) 25 · (146 + 254) : 100 = 100. |
|
|
Задание 20* |
– Сумма трех чисел равна 30217. Первое слагаемое – наименьшее пятизначное число, второе – наибольшее четырехзначное. Чему равно каждое из слагаемых суммы? |
10000 + 9999 + 19999 +
|
|
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Понравилась ли вам работа на уроке? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию, продолжают фразы |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 79. Составные высказывания. Логическая связка «и»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений определять ложные и истинные высказывания; содействовать развитию умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами образования составных высказываний; научатся образовывать составные высказывания с помощью логических связок «и», «или», «если… то…» и определять их истинность |
Метапредметные: Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: учитывают разные мнения и стремятся к координации разных позиций в сотрудничестве |
Личностные: проявляют интерес к учебному материалу; владеют знаниями основных моральных норм поведения; осознают роль языка и речи в жизни людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний. – Какие цифры должны стоять на месте точек?
|
Отвечают на вопросы учителя . Выполняют задания устного счета.
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||
|
Задача |
– Решите задачу. Длина реки Лены 4320 км, а Волги – 3690 км. На сколько километров река Лена длиннее Волги?
|
Решение:
Ответ: 630 км |
|||||||||||||
|
III. Открытие нового знания, способа действия. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте каждое высказывание и определите, истинно оно или ложно. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге |
||||||||||||
|
Работа по учебнику (с. 38–39). Задание 6. |
– Соедините эти два высказывания союзом «и». – Истинное или ложное высказывание с союзом «и» получилось? • Составное высказывание с союзом «и» истинно, если истинны оба составляющих его высказывания. В остальных случаях оно ложно. |
– «Береза – лиственное и хвойное дерево». – Получилось ложное высказывание с союзом «и». |
|||||||||||||
|
Задание 7. |
– Определите, истинно или ложно составное
высказывание |
Определяют, истинно или ложно составное высказывание с союзом «и», если: 1) Первое высказывание истинно, а второе ложно. (Ложно.) 2) Первое высказывание ложно, а второе истинно. (Ложно.) 3) Оба высказывания ложные. (Ложно.) 4) Оба высказывания истинные. (Истинно.) |
|||||||||||||
|
Задание 8. |
– Прочитайте пары высказываний. Истинно или ложно каждое простое высказывание? Соедините каждое из двух высказываний союзом «и». Какое высказывание получилось: истинное или ложное? |
1) Высказывание «Буква ж – гласная и буква ж – согласная» – ложно. 2) Высказывание «Килограмм – единица массы и единица длины» – ложно. 3) Высказывание «В одном дециметре 100 сантиметров и в одном дециметре 10 миллиметров» – ложно. 4) Высказывание «Число 100 делится на 10 и делится на 5» – истинно. |
|||||||||||||
|
Задание 9. |
– Из каких двух высказываний образовано каждое составное высказывание? Истинно или ложно каждое из составных высказываний? |
1) Истинно. 2) Ложно. 3) Ложно. |
|||||||||||||
|
Задание 10* |
– Приведите примеры истинных и ложных составных высказываний, образованных с помощью союза «и» |
Приводят примеры высказываний: – У прямоугольника все углы прямые и противоположные стороны равны. – У треугольника три угла и четыре стороны |
|||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 42). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Найдите значения выражений. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
3687 · 5 = 18435 502 · 61 = 30622 12070 · 8 = 96560 390 · 84 = 32760 5002 · 6 = 30012 203 · 509 = 103327 9100 · 7 = 63700 615 · 301 = 185115 96 · 53 = 5088 1217 · 108 = 131436 77 · 77 = 5929 4050 · 204 = 826200 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
||||||||||||
|
Задание 22. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько времени потратил пешеход на обратный путь? |
Запись:
Решение: 1) 16 : 4 = 4 (км/ч) – скорость. 2) 4 – 2 = 2 (км/ч) – скорость на обратном пути. 3) 16 : 2 = 8 (ч) – время на обратный путь. |
|||||||||||||
|
Задание 23. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Через сколько часов машины встретятся? |
Запись:
Решение: 1) 43 + 56 = 99 (км/ч) – скорость сближения. 2) 198 : 99 = 2 (ч) – встретятся. |
|||||||||||||
|
Задание 24* |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – какое расстояние пробежала собака? |
Решение: 1) 24 : 8 = 3 (ч) – время движения. 2) 12 · 3 = 36 (км) – пробежала собака |
|||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
Урок 80. Составные высказывания. Логическая связка «если, то»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений определять ложные и истинные высказывания; содействовать развитию умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами образования составных высказываний; |
Метапредметные: Познавательные: понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное |
Личностные: определяют цели, функции участников, способы взаимодействия |
|
научатся образовывать составные высказывания с помощью логических связок «и», «или», «если…то…» и определять их истинность |
разнообразие способов решения учебной задачи. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями её реализации. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
|
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний. – Сравните величины: 72 ч ... 3 сут. 1 сут. ... 24 ч 2 сут. 5 ч ... 52 ч 300 мин ... 5 ч 120 мин ... 3 ч 48 ч ... 2 сут. 4 ч |
Отвечают на вопросы учителя. Выполняют задания устного счета. Решение: 72 ч = 3 сут. 1 сут. = 24 ч 2 сут. 5 ч > 52 ч 300 мин = 5 ч 120 мин < 3 ч 48 ч < 2 сут. 4 ч |
Выделять существенную информацию из текста задачи. Выдвигать гипотезу и обосновывать ее. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу |
|||||||||
|
Задача. |
– Решите задачу. Рабочий день длится 7 часов. Сколько рабочих часов в 2 (4, 5, 7) днях? |
Решение: 7 · 2 = 14 (ч) 7 · 5 = 35 (ч) 7 · 4 = 28 (ч) 7 · 7 = 49 (ч) |
||||||||||
|
Задание на смекалку. |
Старший брат идет от дома до школы 30 минут, а младший –40 минут. Через сколько минут старший брат догонит младшего, если тот вышел на 5 мин раньше? |
Ответ: через 15 минут. |
||||||||||
|
Интеллектуальная разминка |
– Найдите ошибку в записи:
– Объясните, почему так не может быть |
џ При умножении трехзначного числа на однозначное может получиться трехзначное или четырехзначное число, но не пятизначное число. џ При умножении четырехзначного числа на однозначное может получиться четырехзначное или пятизначное число, но не шестизначное или семизначное |
||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 39–40). Задание 11. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Истинное ли высказывание: «Если А. С. Пушкин жил с 1799 по 1837 год, то он прожил 48 лет»? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Ложно. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи |
|||||||||
|
Задание 12. |
– Прочитайте два высказывания. Выясните, истинные они или ложные. Соедините эти два высказывания с помощью слов «если, то». Какое высказывание получилось? |
1) Высказывание «Если ворона – птица, то она летает» – истинно. 2) Высказывание «Если число 4720 – четырехзначное, то после зачеркивания нуля в числе 4720 получится двузначное число» – ложно. |
||||||||||
|
Задание 13 |
– Составьте высказывание, образованное с помощью слов «если, то», если первая часть высказывания является истинной, а вторая ложной. Оцените высказывание «Если Петя отвечал на уроке математики, то он получил пятерку»? |
– Ложно. |
||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 43–44). Задание 25. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – Объясните решение задачи. – каково расстояние между станциями? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Объясняют решение задачи: 1) 10 минут – это шестая часть часа. 2) 60 : 6 = 10 (км) – проехал за 10 минут. 3) 60 – 20 = 40 (км/ч) – скорость из-за ремонтных работ. 4) 15 минут – это четвертая часть часа. 5) 40 : 4 = 10 (км) – проехал за 15 минут. 6) 10 + 10 = 20 (км) – расстояние между станциями. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль |
|||||||||
|
Задание 26. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какое расстояние будет между ними через полчаса? через час? |
Запись:
Решение: 1) 90 – 78 = 12 (км/ч) – скорость удаления. 2) 12 · 1 = 12 (км) – через 1 час. 3) 12 : 2 = 6 (км) – через 30 минут. |
||||||||||
|
Задание 27*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько килограммов ягод потребуется для варки варенья? |
Запись: 2 кг ягод – 3 кг сахара ? кг – 12 кг сахара Решение: 1) 12 : 3 = 4 (раза) – больше. 2) 2 · 4 = 8 (кг) – ягод. |
||||||||||
|
Задание 28*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько зерна осталось в первом амбаре? |
Запись:
Решение: 1) 470 · 4 = 1880 (кг) – взяли из второго амбара. 2) 1880 + 470 = 2350 (кг) – взяли всего. 3) 3090 – 2350 = 740 (кг) – осталось в первом амбаре. |
||||||||||
|
Задание 29 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько километров прошел поезд до остановки? |
Запись:
Решение: 1) 24 – 21 + 3 = 6 (ч) – время в пути. 2) 72 · 6 = 432 (км) – прошел поезд до остановки |
||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения. – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
|
Способность к самооценке на основе критерия успешности учебной деятельности (оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи) |
Урок 81. Упражнение в составлении сложных высказываний
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений определять ложные и истинные высказывания; содействовать развитию умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами образования составных высказываний; научатся образовывать составные высказывания с помощью логических связок «и», «или», «если…то…» и определять их истинность |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи; строят логическую цепь рассуждений. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний. – Вставьте пропущенные числа, найдите «ловушки»: 6 : 745 :
6 · 745 · 6 + 745 · |
Отвечают на вопросы учителя. Выполняют задания устного счета.
6 : 745 : 1 = 745 0 + 745 = 745 0+ 6 = 6 0 : 6 = 0 0 : 754 = 0 745 – 0 = 745 6 · 0 = 0 6 – 0 = 6 745 · 1 = 745 745 – 745 = 0 6 + 2 = 8 0 · 745 · 0 = 0 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу |
|||||||||||||||||||||||||||||||||||||
|
Таблица умножения и деления. |
а) В какой таблице умножения есть произведение, равное 36, 35, 40, 81, 72, 45, 14, 20, 16, 30? б) Какие из чисел 30, 27, 25, 36, 35, 40, 48, 72, 45 делятся на 5? На 9? в) Придумайте числа, которые делятся на 2; на 9; на 5. |
Называют результаты умножения и деления.
– Числа 30, 25, 35, 40, 45 делятся на 5. Числа 27, 36, 72, 45 делятся на 9. |
||||||||||||||||||||||||||||||||||||||
|
«Магический квадрат» |
‒ Выполните устные вычисления:
|
Решение:
|
||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 40–41). Задание 14. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Из каких высказываний образовано составное высказывание? Определите, истинно или ложно каждое из них. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
1) Ложно. 2) Истинно. 3) Ложно. 4) Истинно. |
Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|||||||||||||||||||||||||||||||||||||
|
Задание 15. |
– Образуйте из этих высказываний составное высказывание с помощью слов «если, то» и определите, истинно оно или ложно. |
– Высказывание «Если АВСМ – прямоугольник, то АВСМ – квадрат» ‒ ложно. – Высказывание «Если АВСМ – квадрат, то АВСМ – прямоугольник» ‒ истинно. |
||||||||||||||||||||||||||||||||||||||
|
Задание 16* |
– Приведите примеры истинных и ложных составных высказываний, образованных с помощью слов «если, то» |
– Если АВС – прямоугольный треугольник, то угол С – прямой. – Если АВСD – квадрат, то АВ = ВС = СD = DА |
||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 44–45). Задание 30. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Какая часть первой фигуры закрашена? – Какая часть второй фигуры закрашена? – Какая часть закрашена третьей фигуры? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Ответы: – Половина первой фигуры закрашена. – Четыре седьмых второй фигуры закрашено. – Одна четвертая часть закрашена третьей фигуры. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||||||||||||||
|
Задание 31*. |
– Выполните построения. |
а) ОА = 2 см ОА = 2 см ОВ = 3 см ОВ = 3 см в) О1А = 2 см О2В = 3 см г) О1А = 2 см О2В = 3 см АВ = 2 см |
||||||||||||||||||||||||||||||||||||||
|
Задание 32*. |
– Вычислите площадь прямоугольника. – Постройте два других прямоугольника, каждый из которых имеет такую же площадь. |
Решение: 6 · 3 = 18 (см2) ‒ площадь прямоугольника. |
||||||||||||||||||||||||||||||||||||||
|
Задание 33 |
– Выполните практическую работу. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга
|
Выполняют практическую работу.
|
||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи |
Урок 82. Проверочная работа по теме «Высказывания».
Знакомство с задачами на перебор вариантов
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: уточнить понятие «логические возможности»; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами и способами решения комбинаторных задач; научатся различать комбинаторные задачи, выполнять их решение способом перебора возможных вариантов расстановки или расположения предметов в соответствии с условиями задач; составлять таблицы |
Метапредметные: Познавательные: осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: принимают и сохраняют учебную задачу; адекватно воспринимают оценку учителя и товарищей; планируют свое действие. Коммуникативные: умеют формировать коммуникативно-речевые действия, конструктивные способы взаимодействия с окружающими (учителем, сверстниками) |
Личностные: проявляют этические чувства, доброжелательность и эмоционально-нравственную отзывчивость, понимание и сопереживание чувствам других людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний. – Назовите числа, которые без остатка делятся: а) на 5: 25, 28, 30, 38, 40, 49, 50, 55, 61, 67; б) на 8: 11, 15, 16, 18, 24, 27, 32, 34, 36, 40; в) на 7: 8, 14, 15, 20, 21, 25, 28, 32, 35, 42. |
Отвечают на вопросы учителя. Выполняют задания устного счета. – Делятся без остатка а) на 5: 25, 30, 40, 50, 55; б) на 8: 16, 24, 32, 40; в) на 7: 14, 21, 28, 35, 42. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Интеллектуальная разминка. |
– Заполните таблицу:
|
Заполняют таблицу:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задачи |
– Запишите ответ выражением и найдите его значение. а) Сова съедает в день 13 мышей. Сколько мышей съест сова за неделю? б) Кустик черники растет 300 лет, а плодоносит только 5 лет. На сколько лет больше кустик черники растет, чем плодоносит? в) Большая синица за летний день подлетает с кормом к гнезду 400 раз. Сколько раз прилетит синица с кормом к гнезду за неделю? г) Можжевельник живет 2000 лет, а сосна – 600 лет. На сколько лет больше живет можжевельник, чем сосна? д) Стрекоза за час съедает 20 мух. Сколько мух съест стрекоза за сутки? за двое суток? |
Ответы:
а) 91.
б) 295.
в) 2800.
г) 1400.
д) 480, 960 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 46). Задание 1 |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Папа купил три книги. В каком порядке эти книги можно поставить на книжную полку? – Чтобы перебрать все возможные варианты, не пропустить ни одного и не назвать один и тот же вариант дважды, обычно придумывают определенный способ перебора.
– Прочитайте высказывания. Используя таблицу, определите, в каких случаях каждое высказывание истинно и в каких – ложно |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 48). Задание 3. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Подтвердите или опровергните каждое высказывание, приведя примеры. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. 1) Высказывание «Среди трехзначных чисел есть такие, которые делятся на 10» может быть истинно и ложно.
2) Высказывание «Среди натуральных чисел нет наибольшего» истинно. 1000000, 1000001, 1000002 и т. д. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4*. |
– Используя скобки, измените порядок действий, чтобы выражение было верным. |
(630 + 270) : 90 : 2 = 5 3 · (120 – 200 : 4) = 210 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 5. |
– Произведение двух чисел равно 207. Чему равно новое произведение, если один из множителей увеличить в 3 раза, оставив другой без изменений? – Как надо изменить один из множителей, чтобы произведение уменьшилось в 3 раза? |
Запись: 207 · 3 = 621.
– Надо уменьшить в 3 раза. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Самостоятельная работа по карточкам. Вариант 1. |
1. Подчеркните истинные высказывания. 25 · 4 > 100 42 : 7 = 6 1 ч = 100 мин 3 дм 5 см = 35 см 2. Дано высказывание: «1 дм = 100 см». Используя это высказывание и слова «неверно, что…», запишите новое высказывание и определите, истинно оно или ложно. 3. Определите истинность сложных высказываний. Впишите в «окошки» буквы И (истина) или Л (ложь). 25 > 9 или 25 = 9 0 · 7 = 0 и 0 · 7 = 7 Если 5 + 12 = 19, то 19 > 5 |
Выполняют самостоятельную работу. 1. Ответы: 42 : 7 = 6 3 дм 5 см = 35 см.
2. Неверно, что 1 дм равен 100 см – ложно.
3. Ответы:
25 > 9 или 25 = 9 0 · 7 = 0 и 0 · 7 = 7 Если 5 + 12 = 19, то 10 > 5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 2 |
1. Подчеркните ложные высказывания. 18 · 0 = 18 1 м = 10 дм 2 ч = 120 мин 64 + 36 < 100 2. Дано высказывание: «0 < 1 ». Используя это высказывание и слова «неверно, что…», запишите новое высказывание и определите, истинно оно или ложно. 3. Определите истинность сложных высказываний. Впишите в «окошки» буквы И (истина) или Л (ложь). 5 > 2 или 5 < 2 0 : 4 = 4 и 0 · 4 = 4 Если 1 ч = 60 мин, то 3 ч = 120
мин |
1. Ответы: 18 · 0 = 18 (л). 1 м = 10 дм (И). 2 ч = 120 мин (И). 64 + 36 < 100 (Л). 2. Неверно, что 0 меньше 1 – ложно.
3. Ответы:
5 > 2 или 5 < 2 0 : 4 = 4 и 0 · 4 = 4 Если 1 ч = 60 мин, то 3 ч = 120 мин |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 83. Составление таблицы возможностей
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием «логические возможности»; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами и способами решения комбинаторных задач; научатся различать комбинаторные задачи, выполнять их решение способом перебора возможных вариантов расстановки или расположения предметов в соответствии с условиями задач; составлять таблицы |
Метапредметные: Познавательные: самостоятельно создают алгоритмы деятельности при решении проблем; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке. Коммуникативные: слушают и понимают речь других; признают возможность существования различных точек зрения и права каждого иметь свою |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– На доске записаны числа 8, 6, 9. а) К сумме первых двух чисел прибавьте 9. б) Сумму двух первых чисел умножьте на третье. в) Из суммы второго и третьего чисел отнимите первое число. г) Произведение первого и третьего чисел разделите на второе. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение: а) 23. б) 126. в) 7.
г) 12. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Назовите частное и остаток: а) 600 : 400 б) 65 : 30 500 : 300 250 : 80 800 : 300 630 : 80 900 : 200 750 : 90 1000 : 800 550 : 50 900 : 800 630 : 200 |
а) 600 : 400 = 1 (ост. 200) б) 65 : 30 = 2 (ост. 5) 500 : 300 = 1 (ост. 200) 250 : 80 = 3 (ост. 10) 800 : 300 = 2 (ост. 200) 630 : 80 = 7 (ост. 70) 900 : 200 = 4 (ост. 100) 750 : 90 = 8 (ост. 30) 1000 : 800 = 1 (ост. 200) 550 : 50 = 11 (ост. 0) 900 : 800 = 1 (ост. 100) 630 : 200 = 3 (ост. 30) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Выполните действия: 64 · 10 5000 : 5 100 · 100 · 10 100 : 100 70 · 10 16000 : 1000 3000 · 1 · 3000 1000 : 10 100 · 100 3001 : 3001 1 : 1 + 0 · 0 1 · 0 – 0 : 1 |
Решение: 64 · 10 = 640 5000 : 5 = 1000 100 · 100 · 10 = 100000 100 : 100 = 1 70 · 10 = 700 16000 : 1000 = 16 3000 · 1 · 3000 = 9000000 1000 : 10 = 100 100 · 100 = 10000 3001 : 3001 = 1 1 : 1 + 0 · 0 = 1 1 · 0 – 0 : 1 = 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 47–48). Задание 2. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Составьте таблицу для решения.
– Используя любую таблицу, определите, в каких случаях истинно каждое высказывание. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Решение:
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Игра «Раскрась флаги» |
– Флаг раскрашен в 2 красные и 3 зеленые полоски. Последовательность цветов раскраски обозначена цепочкой букв, записанных внизу в рамке. Сколько других способов раскраски флага этими цветами вы сможете найти? |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 48–50). Задание 6. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись:
Решение: 1) 23 · 2 = 46 (м) – отрезали. 2) 46 + 32 = 78 (м) – было. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 7. |
– Рассмотрите график движения грибника. – Что обозначают числа на оси OУ? – Что обозначают числа на оси OХ? – Сколько километров прошел грибник за первый час движения? – Сколько километров прошел через 2 часа после выхода из дома? – За сколько часов грибник прошел 10 км? – Как время отдыха обозначено на графике? Сколько времени он отдыхал? – С какой скоростью шел грибник до остановки на отдых? – С какой скоростью он шел после отдыха? |
– Числа на оси OУ обозначают расстояние. – Числа на оси OХ обозначают время. – 4 километра прошел грибник за первый час движения. – 8 километров прошел через 2 часа после выхода из дома. – За 5 часов грибник прошел 10 км. – 2 часа он отдыхал.
– 4 км/ч шел грибник до остановки на отдых. S = 8 км, t = 2 ч; 8 : 2 = 4 (км/ч). – 2 км/ч он шел после отдыха. S = 2 км, t = 1 ч; 2 : 1 = 2 (км/ч). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 8. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Запись: Длина участка – 85 м. Ширина участка – 64 м. Площадь участка – ? м2. Площадь дома – 160 м2. Осталось – ? м2. Площадь сада – ?, половина. Решение: 1) 85 · 64 = 5440 (м2) – площадь участка. 2) 5440 – 160 = 5280 (м2) – площадь участка без площади дома. 3) 5280 : 2 = 2640 (м2) – площадь сада. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 9. |
– Составьте высказывания со словами «неверно, что». |
1) Высказывание «Неверно, что в слове “корова” шесть букв» – ложно. 2) Высказывание «Неверно, что март, апрель и май – весенние месяцы» – ложно. 3) Высказывание «Неверно, что 1 – самое маленькое число» – истинно. 4) Высказывание «Неверно, что А. С. Пушкин был врачом» – истинно. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 10 |
– Образуйте новые высказывания без слов «неверно, что» |
– Высказывание «Белые медведи живут на севере» – истинно. – Высказывание «Любой прямоугольник является квадратом» – ложно. – Высказывание «В неделе 7 дней» – истинно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности (оценивать свои достижения, степень самостоятельности) |
Урок 84. Практическое решение задач способом перебора вариантов
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием «логические возможности»; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилами и способами решения комбинаторных задач; научатся различать комбинаторные задачи, выполнять их решение способом перебора возможных вариантов расстановки или расположения предметов в соответствии с условиями задач; составлять таблицы |
Метапредметные: Познавательные: умеют осознанно и произвольно строить речевое высказывание в устной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: проговаривают вслух последовательность производимых действий, составляющих основу осваиваемой деятельности; оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы. Коммуникативные: управляют поведением партнера, осуществляют контроль, коррекцию и оценку его действий; полно и точно выражают свои мысли в соответствии с задачами и условиями коммуникации |
Личностные: формируют внутреннюю позицию школьника на уровне положительного отношения к школе; приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности учебной деятельности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний. – Найдите задачи с «ловушками»: а) Папа купил на рынке 2 кг яблок, 1 кг груш, 5 кг картофеля и 3 кг огурцов. Сколько всего килограммов фруктов и овощей принес папа? б) Папа купил на рынке 2 кг яблок, 1 кг груш, 5 кг картофеля и 3 кг огурцов и разложил все купленное в две сумки, чтобы удобнее было нести. Сколько всего овощей и фруктов купил папа? в) Папа пошел в магазин и купил морковь, капусту и баклажаны. Сколько всего килограммов овощей купил папа? Измените задачу так, чтобы «ловушки» не стало, а вопрос задачи оставьте тем же. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
а) Решение: 2 + 1 + 5 + 3 = 11 (кг).
б) Решение: (2 + 1 + 5 + 3) : 2 = 5 кг 500 г.
в) Папа пошел в магазин и купил 3 кг моркови, 2 кг капусты и 4 кг баклажан. Сколько всего килограммов овощей купил папа? Решение: 3 + 2 + 4 = 9 (кг). |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||
|
Сравнение величин |
– Соедините равные величины:
|
Решение: а) 5 км 89 м = 5089 м б) 349 кг = 3 ц 49 кг 5890 м = 58900 дм 3 т 490 кг = 3490 кг 589 м = 5890 дм 34049 кг = 34 т 49 кг в) 40 т 70 кг = 40070 кг 40700 кг = 407 ц 407 т = 407000 кг |
|||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Наблюдение. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Перебирая варианты, всегда удобно действовать не случайно, «наобум», а системно, по определённому правилу. Например, все трёхзначные числа из цифр 2, 4, 5 лучше составить так: сначала поставить на место сотен 2 и перебрать все возможности, потом так же 4, а потом – 5: 245 425 524 254 452 542 Все эти варианты можно показать на «дереве»:
Каждый путь по этому «дереву» соответствует одному из вариантов решения. Общее число вариантов всегда равно числу «веток дерева» или числу точек в последнем ряду. Дерево возможностей помогает отыскать все варианты решения, не пропуская ни одного. Например, красным цветом на нашем «дереве» выделен вариант 524. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
||||||||||||||||||||||||||
|
Задача 1. |
– решите задачу. На полке в магазине стоят два медвежонка – жёлтый и коричневый, две машинки – чёрная и белая и три мяча – красный, зелёный и голубой. Васе надо купить 3 игрушки: одного медвежонка, одну машинку и один мяч. Определите с помощью «дерева», сколькими способами он может это сделать. – Отметьте красным карандашом вариант выбора жёлтого медвежонка, белой машинки и красного мяча. |
|
|||||||||||||||||||||||||||
|
Задача 2. |
– решите задачу. У Даши 4 кофты (красная, желтая, голубая и зеленая) и 2 юбки (синяя и белая). Сколькими способами она может составить себе костюм? |
|
|||||||||||||||||||||||||||
|
Задача 3 |
– решите задачу. В школьной столовой на первое можно заказать щи, суп и борщ, на второе – котлету и рыбу, на третье – чай и морс. Сколько различных обедов можно составить из указанных блюд? – Составьте «дерево» и покажите путь, который соответствует тройке «суп, котлета, морс» |
|
|||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 50–52). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Образуйте составное высказывание с союзом «и». |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Километр – единица массы и единица длины. (Ложно.) |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||||||||
|
Задание 12. |
– Верно ли высказывание: «Если периметр квадрата на рисунке равен 12 см, то его площадь равна 6 см2»? |
– Ложно. Решение: 1) 12 : 4 = 3 (см) – сторона квадрата. 2) 3 · 3 = 9 (см2) – площадь квадрата. |
|||||||||||||||||||||||||||
|
Задание 13. |
– Рассмотрите чертеж. Как называются данные фигуры? – Вырежьте такие треугольники и сложите из них один треугольник. |
Выполняют практическое задание. |
|||||||||||||||||||||||||||
|
Задание 14. |
– На какие три группы можно разделить данные фигуры? |
Решение: 1-я группа: параллелепипеды; 2-я группа: пирамиды; 3-я группа: конусы. |
|||||||||||||||||||||||||||
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – какова площадь такой взлетной полосы? |
Запись: длина – 5 км Ширина – 360 м Площадь – ? Решение: 360 · 5000 = 1800000 (м2) – площадь взлетной полосы. |
|||||||||||||||||||||||||||
|
Задание 16. |
– Используя справочник или энциклопедию, найдите данные о площадях самых крупных островов Европы. – Назовите эти острова в порядке увеличения площадей. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга. |
Запись:
|
|||||||||||||||||||||||||||
|
Задание 17 |
– Какую форму имеют сооружения, изображенные на фотоснимке? |
– На снимке египетские пирамиды |
|||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Прием «Солнышко». Рефлексия эмоционального состояния может использоваться на различных этапах урока. Обучающимся предлагается выбрать «солнышко», которое соответствует их настроению |
Оценивать свои достижения. Выражать доброжелательность и эиоционально-нравст-венную отзывчивость |
Урок 85. Деление суммы на число
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с правилом деления суммы на число; способствовать формированию умений использовать свойства арифметических действий при выполнении вычислений |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом деления суммы на число; научатся применять правило деления суммы на число; использовать свойства арифметических действий при выполнении вычислений |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; используют знаково-символические средства для решения учебной задачи; осуществляют моделирование. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: излагают своё мнение и аргументируют свою точку зрения; используют в общении правила вежливости |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Разгадайте правило, по которому записаны числа в каждом ряду: а) 2300, 2030, 2003, 3200, 3020, 3002 б) 5600, 5060, 5006, 6500, 6050, 6005 – Составьте по этому же правилу ряды для чисел: 8600, 9300. |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение:
а) 8600, 8060, 8006, 6800, 6080, 6008 б) 9300, 9030, 9003, 3900, 3090, 3009 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||
|
– Расположите выражения в порядке увеличения их значений, не вычисляя. 60 · 9 40 · 9 80 · 9 9 · 20 9 · 50 30 · 9 50 · 9 ; 10 · 9 |
Ответ:
10 · 9 9 · 20 30 · 9 40 · 9 9 · 50 50 · 9 60 · 9 80 · 9 |
||||||||||
|
– Закончите составление примеров. Где «ловушка»? (а, д.)
|
Решение: – В примерах а и д «ловушки».
|
||||||||||
|
Задача |
– Решите задачу. Ворона летит со скоростью 50 км/ч, а стриж в – 2 раза быстрее. Какова скорость стрижа? – Выразите скорость вороны и скорость стрижа в метрах в час? |
Решение: 1) 50 км/ч = 50000 м/ч. 2) 100 км/ч = 100000 м/ч |
|||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 53–54). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте задачу. Решая эту задачу, Волк и Заяц составили два разных выражения. Как рассуждал каждый из них? Вычислите значения выражений и сравните полученные результаты. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Решение: (30 + 60) : 3 = 30 30 : 3 + 60 : 3 = 30
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти Проявлять |
||||||||
|
Задание 2. |
– Сравните значения выражений. – Сделайте вывод. Объясните, как можно разделить сумму двух чисел на какое-нибудь число, если каждое слагаемое делится на это число. |
Решение: (14 + 28) : 7 = 14 : 7 + 28 : 7 (40 + 16) : 8 = 40 : 8 + 16 : 8 (250 + 150) : 5 = 250 : 5 + 150 : 5 џ Чтобы разделить сумму на число, можно каждое слагаемое разделить на это число и сложить полученные результаты. |
|||||||||
|
Задание 3. |
– Проверьте правило деления суммы на число. |
Решение: (14 + 28) : 7 = 42 : 7 = 6 (14 + 28) : 7 = 14 : 7 + 28 : 7 = 2 + 4 = 6 (320 + 160) : 8 = 480 : 8 = 60 (320 + 160) : 8 = 320 : 8 + 160 : 8 = 40 + 20 = 60 |
|||||||||
|
Задание 4 |
– Запишите выражения, равные данным, используя правило деления суммы на число. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга |
Решение: (16 + 24) : 8 = 16 : 8 + 24 : 8 (49 + 14) : 7 = 49 : 7 + 14 : 7 (180 + 540) : 90 = 180 : 90 + 540 : 90 (32 + 8) : 4 = 32 : 4 + 8 : 4 |
|||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 55–56). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
1) Приведите примеры истинного высказывания. 2) Приведите примеры ложного высказывания. 3) Приведите примеры предложения, которое не является высказыванием. 4) Приведите примеры истинного высказывания со словами «неверно, что». |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Приводят примеры: 1) В году 12 месяцев. 2) Январь – весенний месяц. 3) 135 + 249.
4) Неверно, что январь – первый зимний месяц. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения |
||||||||
|
Задание 12. |
– Назовите соседей данных чисел. |
Запись: а) 565998, 565999, 566000; б) 79999, 80000, 80001; в) 7508, 7509, 7510. |
|||||||||
|
Задание 13 |
– Вычислите значения выражений |
Решение: 690 : 3 · 205 – 47150 + 850 = 850 (238145 – 237776) : 41 + 327 : 3 · 7 = 772 10000 – 120 · 80 + (900 – 750 : 25) · 7 = 6490 |
|||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
Урок 86. Решение задач с применением правила деления суммы на число
|
Тип урока: комбинированный |
||
|
Педагогические задачи: повторить правило деления суммы на число; способствовать формированию умений использовать свойства арифметических действий при выполнении вычислений |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом деления суммы на число; научатся применять правило деления суммы на число; использовать свойства арифметических действий при выполнении вычислений |
Метапредметные: Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; устанавливают причинно-следственные связи; строят логическую цепь рассуждений. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учёта интересов сторон и сотрудничества |
Личностные: знают моральные нормы и умеют выделять нравственный аспект поведения; устанавливают связь между целью учебной деятельности и ее мотивом (между результатом учения и тем, что побуждает деятельность, ради чего она осуществляется) |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний.
– Соедините равные величины.
|
Отвечают на вопросы учителя. Выполняют задания устного счета. Ответ: а) 35 дм 8 мм = 3508 мм б) 340 км = 340000 м 358 см = 3580 мм 34000 м = 340000 дм 35 см 8 мм = 358 мм 340000 см = 3400 м
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||
|
Задача. |
– Решите задачу. Миша лег спать в 21 час, а проснулся в 8 часов. Сколько времени он спал? |
Решение: 3 + 8 = 11 (ч) – спал Миша. |
||||||||
|
Рубрика «Знаете ли вы?» |
– Знаете ли вы? · В воде наибольшую скорость развивает рыба-меч до 100–130 км/ч. · Летучие рыбы населяют все моря и океаны с температурой воды не ниже 20 °С. В воде рыба увеличивает скорость до 30 км/ч, а у поверхности доводит ее до 60 км/ч. – Выразите данные скорости в метрах в час. – На сколько меньше скорость акулы, чем скорость рыбы-меч, если акула плывет со скоростью 30 км/ч? – Во сколько раз меньше скорость акулы, чем скорость летучей рыбы у поверхности воды? |
Решение: 100 км/ч = 100000 м/ч. 130 км/ч = 130000 м/ч. Решение: 30 км/ч = 30000 м/ч. 60 км/ч = 60000 м/ч.
– На 100 км/ч меньше скорость акулы, чем скорость рыбы-меч.
– В 2 раза меньше скорость акулы, чем скорость летучей рыбы у поверхности воды |
||||||||
|
III. Открытие нового знания, способа действия. Работа по учеб- нику (с. 54–55). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Используя правило деления суммы на число, найдите значения выражений. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Решение: (56 + 12) : 2 = 56 : 2 + 12 : 2 = 28 + 6 = 34 (170 + 560) : 10 = 170 : 10 + 560 : 10 = 17 + 56 = 73 (72 + 96) : 12 = 72 : 12 + 96 : 12 = 6 + 8 = 14 (148 + 280) : 4 = 148 : 4 + 280 : 4 = 37 + 70 = 107 (360 + 80) : 40 = 360 : 40 + 80 : 40 = 9 + 2 = 11 (120 + 300) : 60 = 120 : 60 + 300 : 60 = 2 + 5 = 7 (280 + 280) : 70 = 280 : 70 + 280 : 70 = 4 + 4 = 8 (150 + 450) : 50 = 150 : 50 + 450 : 50 = 3 + 9 = 12 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи |
|||||||
|
Задание 6. |
– Сумму каких двух чисел разделили на данное число? |
Решение: 8 : 2 + 6 : 2 = (8 + 6) : 2 15 : 5 + 25 : 5 = (15 + 25) : 5 21 : 7 + 28 : 7 = (21 + 28) : 7 276 : 23 + 184 : 23 = (276 + 184) : 23 15 : 3 + 9 : 3 = (15 + 9) : 3 116 : 29 + 609 : 29 = (116 + 609) : 29 |
||||||||
|
Задание 7 |
– Верно ли высказывание: «Если одно из двух слагаемых суммы делится на данное число, а другое не делится, то и сумма не разделится на это число»? Приведите примеры |
– Истинно. (15 + 14) : 5 = 29 : 5 15 : 5 + 14 : 5 |
||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 56). Задание 14. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Сравните пары выражений. Найдите значение первого выражения. Найдите значение второго выражения, используя значение первого. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: а) 25 · 4 < 25000 · 4 б) 13 · 5 < 130000 · 5 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||
|
Задание 15. |
– Найдите значение второго выражения, используя значение первого. – Какие свойства умножения вы использовали? |
Решение: 2 · 360 = 720 (39 · 25) · 4 = 3900 360 · 2 = 720 39 · (25 · 4) = 3900 – Перестановка множителей, сочетательное свойство умножения. |
||||||||
|
Задание 16. |
– Выполните действия, применяя распределительное свойство умножения. |
Решение: (90 + 30) · 4 = 90 · 4 + 30 · 4 = 360 + 120 = 480. (25 + 50) · 4 = 25 · 4 + 50 · 4 = 100 + 200 = 300. |
||||||||
|
Задание 17. |
– Составьте выражения и найдите их значения. |
Решение: (58 + 7) · 11 = 715 309 : 3 – 33 = 70 (87 – 23) : 8 = 8 124 · 70 + 300 = 8980 |
||||||||
|
Задание 18* |
– Прочитайте задачу. Что известно? Что требуется узнать? – Объясните, как составлено выражение. – Закончите решение задачи. |
Запись:
Решение: 1) 48 : 4 = 12 (км/ч) – первоначальная скорость. 2) 12 + 4 = 16 (км/ч) – скорость на обратном пути. 3) 48 : 16 = 3 (ч) – обратный путь |
||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 87. Деление на 1000, 10000
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для повторения правила деления суммы на число; способствовать формированию умений использовать свойства арифметических действий при выполнении вычислений |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом деления суммы на 1000, 10000, 100000; научатся применять правило деления на 1000, 10000, 100000 |
Метапредметные: Познавательные: умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: определяют последовательность промежуточных целей с учетом конечного результата; составляют план и последовательность действий. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками; определяют цели, функции участников, способы взаимодействия |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Запишите верные равенства, вставив пропущенные цифры. 20750 · 32 = 6640 1999 · 250 = 4997 209 · 306 = 639 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение:
20750 · 32 = 664000 870 · 300 = 261000 1999 · 250 = 499750 506 · 600 = 303600 209 · 306 = 63954 2200 · 140 = 308000 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения |
|||||||||||||||||||||||||||||||
|
Задание на смекалку. |
– Можете ли вы поднять 1 000 000 граммов? |
Ответ: нет. 1 000 000 г = 1 т. |
||||||||||||||||||||||||||||||||
|
Задачи |
– Решите задачи. а) Черепаха двигалась со скоростью 5 м/мин. Какое расстояние прошла она за 3 мин? б) Слон двигался со скоростью 100 м/мин. Какое расстояние он прошел за 10 мин? – Рассмотрите таблицу и объясните, как можно найти расстояние, если известны скорость и время движения:
|
Ответы: а) Черепаха прошла 15 м.
б) Слон прошел 1 км.
Запись:
|
||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 57–58). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Как разделить число на 10? Приведите примеры. Как разделить число на 100? Приведите примеры. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 30 : 10 = 3 1000 : 100 = 10 и т. п. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость |
|||||||||||||||||||||||||||||||
|
Задание 2. |
– Составьте правило деления числа на 1000, 10000, 100000. |
Решение: 5000 : 1000 = 5; 5460000 : 10000 = 546; 1000000
: 100000 = 10 |
||||||||||||||||||||||||||||||||
|
Задание 3. |
– Назовите тысячную долю каждого из чисел. |
Решение: 6000 : 1000 = 6 280000 : 1000 = 280 13000 : 1000 = 13 700000 : 1000 = 700 4000000 : 1000 = 4000 |
||||||||||||||||||||||||||||||||
|
Задание 4. |
– Как называется тысячная доля килограмма? – Как называется тысячная доля тонны? – Как называется тысячная доля километра? – Как называется тысячная доля метра? |
– Тысячная доля килограмма – грамм. – Тысячная доля тонны – килограмм. – Тысячная доля километра – метр. – Тысячная доля метра – миллиметр. |
||||||||||||||||||||||||||||||||
|
Задание 5. |
– Сколько граммов в 1 тонне? – Какую часть тонны составляет 1 грамм? |
– В 1 тонне 1000000 грамм. ‒ 1 г составляет 1000000 часть тонны. |
||||||||||||||||||||||||||||||||
|
Задание 6. |
– Прочитайте записи. – Тысячную долю грамма называют миллиграммом. В миллиграммах обычно выражают дозы лекарств. |
Читают записи. |
||||||||||||||||||||||||||||||||
|
Задание 7. |
– Во сколько раз 1 мг меньше 1 г? – Во сколько раз 1мг меньше 1 кг? |
Решение: 1000 : 1 = 1000 1000000 : 1 = 1000000 |
||||||||||||||||||||||||||||||||
|
Задание 8 |
– Рассмотрите набор гирь-разновесок. Определите с помощью гирек и чашечных весов массу некоторых мелких предметов |
Выполняют практическую работу |
||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 61). Задание 19. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Истинно или ложно составное высказывание? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) – истинно; 2) – ложно; 3) – истинно; 4) – ложно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок |
|||||||||||||||||||||||||||||||
|
Задание 20 |
– Составьте задачи на движение. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга |
Записи: а)
б)
в)
|
||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 88. Деление на 1000, 10000
|
Тип урока: комбинированный |
||
|
Педагогические задачи: составить и учить применять правила деления на 1000, 10000, 100000; рассмотреть правило невозможности деления на нуль |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом деления суммы на 1000, 10000, 100000; научатся применять правило деления на 1000, 10000, 100000 |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: принимают участие в работе парами и группами; допускают существование различных точек зрения; договариваются, приходят к общему решению; используют в общении правила вежливости |
Личностные: проявляют интерес к учебному материалу; владеют знаниями основных моральных норм поведения |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний. – Заполните пропуски: 3 ц = ... кг 1 т = ... ц 200 кг = ... ц 1 т 5 ц = ... ц 8 ц = ... кг 2 т = ... кг 10 т = ... кг |
Отвечают на вопросы учителя. Выполняют задания устного счета. Решение: 3 ц = 300 кг 1 т = 10 ц 200 кг = 2 ц 1 т 5 ц = 15 ц 8 ц = 800 кг 2 т =2000 кг 10 т =10000 кг |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||
|
Задачи. |
– Решите задачу: а) В мешке 50 кг картофеля. Сколько мешков потребуется, чтобы положить в них 1 ц картофеля? Выразите 1 ц в килограммах. б) Масса нагруженного автомобиля 1275 кг, а масса самого автомобиля – 1 т. Чему равна масса груза? |
Решение: а) 1 ц = 100 кг. 100 : 50 = 2 (м.) – потребуется.
б) 1275 кг – 1000 кг = 275 кг – масса груза. |
||||||
|
Числовые записи |
а) Запишите число, в котором 9 единиц первого класса и столько же единиц второго класса. б) Сколько всего сотен в числе 4705; 14803? в) Сколько всего десятков в числе 3007; 52320? г) Запишите все пятизначные числа больше данного числа 99997. д) Уменьшите в три раза сумму чисел 80 и 40. е) Запишите число, которое содержит 26 тысяч и 26 единиц. ж) Сколько метров в 7 км? и) Сколько секунд в 20 минутах? к) Во сколько раз 2 часа больше 10 минут? л) Представьте число 180 в виде суммы двух слагаемых, одно из которых больше второго в 2 раза |
Решение: а) 9009. б) 47 сотен, 148 сотен. в) 300 десятков, 5232 десятка. г) 99999, 99998.
д) 40. е) 26026.
ж) 7000 м. и) 1200 с. к) 12. л) 120 + 60 |
||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 58–59). Задание 9. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Решите пары примеров и сравните результаты. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 800 : 400 = 8 : 4 1000 : 50 = 100 : 5 240 : 80 = 24 : 8 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|||||
|
Задание 10. |
– Разделите 1200 на 600.
– Разделите 1200 на 100 и 600 на 100. Найдите частное полученных чисел. Какое число получилось? – Сравните это число с частным чисел 1200 и 600. – Сделайте вывод. |
Решение: 1200 : 600 = 12 : 6 Вывод. При нахождении частного иногда удобно сначала разделить, если это возможно, делимое и делитель на одно и то же число, а затем найти частное полученных чисел. Результат не изменится. |
||||||
|
Задание 11. |
– На какое наибольшее число можно разделить делимое и делитель? |
Решение: 110 : 10 (на 10) 26500 : 100 (на 100) 360 : 120 (на 120) 12800 : 400 (на 400) 840 : 280 (на 280) 2060 : 10 (на 10) 100000 : 5000 (на 5000) 8000 : 2000 (на 2000) 25000 : 500 (на 500) 1000 : 100 (на 100) |
||||||
|
Задание 12. |
– Составьте и запишите равенства по образцу. – Какие математические знания помогли вам выполнить это задание? |
Составляют равенства по образцу. 400 : 25 = 80 : 5 175 : 35 = 35 : 7 315 : 45 = 63 : 9 495 : 55 = 99 : 11 |
||||||
|
Задание 13. |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – Сколько тонн капусты осталось? |
Запись:
Решение: 1) 2 · 7 = 14 (т) – увезли. 2) 25000 кг = 25 т. 25 – 14 = 11 (т) – осталось. |
||||||
|
Задание 14 |
– Может ли человек иметь массу 82000 грамма? – Может ли человек иметь рост 1920 мм? |
– Может. 82000 г = 82 кг. – Может. 1920 мм = 1 м 92 см |
||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 62). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выполните действия. – Проверьте результаты с помощью калькулятора.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. 309 · 706 = 218154 6385 + 27681 = 34066 255 · 538 = 137190 90000 – 14683 = 75317 470 · 250 = 117500 724008 – 697093 = 26915 504 · 504 = 254016 99999 + 6781 = 106780 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Осуществлять взаимный контроль |
|||||
|
Задание 22 |
– Сколько времени показывают часы? – Сколько минут прошло с того момента, как часы показывали 1 час?
– Сколько секунд прошло с того момента, как часы показывали 1 час 20 минут? |
– Часы показывают 4 часа 10 минут. – Прошло 3 часа 10 минут или 190 минут. 4 ч 10 мин – 1 ч = 3 ч 10 мин; 3 ч 10 мин = 180 мин + 10 мин = 190 мин. – Прошло 2 часа 50 минут или 10200 секунд. 4 ч 10 мин – 1 ч 20 мин = 2 ч 50 мин; 2 ч 50 мин = 120 мин + 50 мин = 170 мин; 170 мин = 170 · 60 с =10200 с |
||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность. Осуществлять итоговый контроль, оценивать результаты деятельности |
Урок 89. Тема: Деление на 1000, 10000
|
Тип урока: комбинированный |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом деления суммы на 1000, 10000, 100000; научатся применять правило деления на 1000, 10000, 100000 |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; ориентируются на возможное разнообразие способов решения учебной задачи. Регулятивные: умеют работать по предложенному учителем плану. Коммуникативные: учатся конструктивно разрешать конфликты посредством учёта интересов сторон и сотрудничества |
Личностные: проявляют положительное отношение к школе и учебной деятельности; имеют представление о причинах успеха в учебе; расширяют познавательные интересы и учебные мотивы |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Найдите в каждой строке «лишнюю» величину: а) 4 ч, 3 мин, 4 мм, 4 сут., 4 с; б) 6 кг, 6 т, 6 мин, 6 г, 6 ц; в) 8 см, 8 мм, 8 км, 8 дм, 8 сут. |
Отвечают на вопросы учителя. Выполняют задания устного счета. Ответ: а) 4 мм; б) 6 мин; в) 8 сут. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||
|
|
– Вставьте пропущенные числа: 1000 г = ... кг 24 ч = ... сут. 60 мин = ... ч 100 кг = ... ц 3600 с = ... ч 1 мин = ... с |
Ответ: 1000 г = 1 кг 24 ч = 1 сут. 60 мин = 1 ч 100 кг = 1 ц 3600 с = 1 ч 1 мин = 60 с |
||||||||||||||||||||||||||
|
Задача. |
– Решите задачу. Солнце взошло в 6 ч и зашло в 19 ч. Узнайте продолжительность дня. |
Решение: 19 – 6 = 13 (ч) ‒ продолжительность дня. |
||||||||||||||||||||||||||
|
Задание на смекалку |
– Из Чайковского в Пермь самолет летит 1 час 20 мин, а обратно – 80 мин. Чем объяснить такую разницу? |
Ответ: 1 ч 20 мин = 80 мин |
||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 60). Задание 15. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Чему равно значение выражения 52000 : а, если а = 10, а = 100, а = 1000? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Если а = 10, то 52000 : 10 = 5200. Если а = 100, то 52000 : 100 = 520. Если а = 1000, то 52000 : 1000 = 52. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
|||||||||||||||||||||||||
|
Задание 16. |
– Чему равно частное? Как проверить результат с помощью умножения? |
– Надо частное умножить на делитель. |
||||||||||||||||||||||||||
|
Задание 17. |
– Почему нельзя делить на 0? Объясните. |
Ответ: 1) 12 : 0. Частное – это число, при умножении которого на 0 должно получиться 12. такого числа нет. 2) 0 : 0. Частное – любое число. Какое бы число мы ни взяли, при умножении его на 0 получится 0. |
||||||||||||||||||||||||||
|
Задание 18 |
– Оцените (верно, неверно) утверждение: «Частное нуля и любого числа равно 0». – Как надо исправить его, чтобы оно стало верным? |
– Утверждение неверно.
џ Частное нуля и любого другого числа равно 0 |
||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 62–63). Задание 23. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Какие фигуры вы видите на рисунке? – Заполните таблицу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. – На рисунке изображены окружности, треугольники, квадраты, пятиугольник.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|||||||||||||||||||||||||
|
Задание 24 |
– Рассмотрите диаграмму. Перенесите данные из диаграммы в таблицу. |
Запись:
|
||||||||||||||||||||||||||
|
|
– Каких деревьев больше: дубов или сосен, елей или рябин? – Каких деревьев поровну? Каких меньше всего? – На сколько берез больше, чем елей? Берез больше, чем сосен? – Сколько всего хвойных деревьев? Сколько всего лиственных деревьев? |
– Больше дубов, чем сосен. Больше рябин, чем елей. – Рябин и дубов поровну. Сосен меньше всего. – На 150 берез больше, чем елей. На 175 берез больше, чем сосен. – 175 хвойных деревьев. 600 всего лиственных деревьев |
||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи |
Урок 90. Карта
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятием «масштаб»; способствовать формированию умений определять масштабы географических карт; выполнять решение задач, связанных с масштабом |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «масштаб»; научатся определять масштабы географических карт; выполнять решение задач, связанных с масштабом |
Метапредметные: Познавательные: умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; осуществляют анализ, сравнение. Регулятивные: оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками; определяют цели, функции участников, способы взаимодействия |
Личностные: осознают необходимость самосовершенствования |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. Каждому ученику предлагает карточку с заданиями.
|
Выполняют задания устного счета.
Проверка:
|
Выделять существенную информацию из текста загадки. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Вам предлагается 7 высказываний. Определите, истинные они или ложные, и в нужной графе таблицы поставьте «+» или другой какой-то знак. Предлагает обучающимся выполнить эту работу на карточках.
|
Проверяется выполнение задания с использованием карточек «И» (истина), «Л» (ложь). Одновременно открываются карточки. За правильными ответами открываются буквы слова «масштаб».
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 64–65). |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Как вы понимаете слово «масштаб»? – Мы увидели, что использование масштаба позволяет создавать модели реальных предметов. Ответы учеников можно дополнить демонстрацией реальных моделей предметов (глобус земли, географическая карта, показ моделей машинок, сделанных в масштабе 1 : 43). |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 1. |
– План города, области, государства, континента Земли называют картой. На карте имеется координатная сетка из параллелей и меридианов. Карта всегда одинаково ориентирована по отношению к сторонам света: сверху – север, снизу – юг, справа – восток, слева – запад. – Рассмотрите карту. В каком масштабе выполнена эта карта? Что означает этот масштаб? (См. ресурсный материал к уроку.) |
– Масштаб 1 : 140 000 000 означает, что в 1 см – 1400 км. Заранее подготовленные обучающиеся рассказывают о создании карты (см. ресурсный материал к уроку). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 2 |
– Запишите масштаб карты, если: а) 1 см на карте соответствует 10 000 000 см на местности; б) 1 см на карте соответствует 200 км на местности |
Запись: Масштаб 1 : 10000000
Масштаб 1 : 20000000 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 66). Задание 5. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Смешали по 1 кг конфет четырех сортов по цене 75 р., 72 р., 80 р. и 85 р. за килограмм. Какова цена 1 кг полученного набора? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 75 + 72 + 80 + 85 = 312 (руб.) – стоимость 4 килограммов конфет. 2) 312 : 4 = 78 (р.) – цена 1 килограмма набора. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 6. |
– Цена 1 кг кофе – 600 р.; 5 кг кофе стоят столько же, сколько 10 кг чая. Какова цена 1 кг чая? Решите задачу двумя способами. |
Решение (см. ресурсный материал к уроку). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 7. |
– Стоимость девяти мотков пряжи на 450 р. больше, чем стоимость шести мотков этой пряжи. На костюм нужно 30 мотков пряжи. Сколько это будет стоить? |
Решение (см. ресурсный материал к уроку). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 8. |
– При сушке из 10 кг свежих яблок получается 1 кг 500 г сушеных. Сколько сушеных яблок получится из тонны свежих? |
Решение: 1 т = 1000 кг. 1000 : 10 = 100 (раз) – больше 1 тонна, чем 10 кг. 1500 · 100 = 150000 (г) – получится сушеных яблок из 1 тонны свежих яблок. 150000 г = 150 кг. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 9. |
– Перелетные птицы за сутки преодолевают рас- стояние 200–300 км. Сколько километров пролетит стая птиц за 12 часов? |
Решение: 24 : 12 = 2 (раза) – меньше. 200 : 2 =100 (км) ‒ пролетит стая птиц за 12 часов. 300 : 2 = 150 (км) ‒ пролетит стая птиц за 12 часов. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 10. |
– На две стройки отправили 8 одинаковых ящиков с гвоздями. Когда на обеих стройках израсходовали 60 кг гвоздей, то на одной стройке осталось 3 полных ящика, а на другой – 2. Сколько гвоздей было в каждом ящике? |
Запись:
1 ящ. – ? гв. Решение: 3 + 2 = 5 (ящ.) – осталось; 8 – 5 = 3 (ящ.) – израсходовали; 60 : 3 = 20 (гв.) – в 1 ящике. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 11 |
– Автомат заворачивает шоколадные конфеты в обертки. Производительность автомата 45 конфет в минуту. Сколько конфет он завернет за час? За какое время автомат завернет 8775 конфет? |
Запись:
Решение: 45 · 60 = 2700 (к.) – за 1 час. 8775 : 45 = 195 (мин) – потребуется, чтобы завернуть 8775 конфет; 195 минут = 3 часа 15 минут |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ресурсный материал к уроку
Рассказ учителя о масштабе
– Само слово «масштаб» пришло к нам из немецкого языка. «Maс» означает «мера», «штаб» означает «размер», что уже говорит о связи с математикой. Слово «масштаб», придя из немецкого языка, хорошо прижилось в нашей речи. Какие родственные слова к нему вы можете назвать? (масштабный, крупномасштабный.) Реже используется слово «масштабировать», что означает «изменять все размеры в определенное количество раз». Это слово сегодня нам понадобится. Полное определение слова «масштаб» звучит так: Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом. А еще на уроке мы попрактикуемся: с помощью масштаба можно решать задачи и выполнять геометрические построения, например, при составлении плана квартиры, усадьбы, нахождении площади полной поверхности куба.
Рассказ учеников о создании карты
– Географическая карта – это земная поверхность или ее участок, изображенный на плоскости: на бумаге, материи, картоне. Географическая карта не бывает точной по очень простой причине: на плоскости отображается искривленная поверхность земного шара. Эта поверхность переводится на плоскость методом проецирования.
В картографии существуют различные его способы в зависимости от предназначения карты. Автор самого известного способа проецирования – фламандский географ Меркатор. Его метод восходит к 1568 году. На основе такого способа и сегодня составляют карты для атласов. Но здесь существуют серьезные недостатки: у полюсов получается такая же широта, как и у экватора, а некоторые страны расползаются до размеров континентов.
Самые древние карты составили египтяне в 1400 году до нашей эры, уже более совершенные карты рисовали греки. Греческий астроном Клавдий Птолемей, родившийся в Египте во II веке нашей эры, пересмотрел географию. Землю он поместил в центре мира и пользовался при составлении карт специальными линиями, что применяется и по сей день, а ведь тогда была известна очень маленькая часть Земли.
Решения к заданиям 6, 7
|
Задание 6. Запись:
Решение:
|
Задание 7. Запись:
Решение: 9 – 6 = 3 (м.) – они стоят 450 рублей. 450 : 3 = 150 (р.) – цена 1 мотка пряжи. 150 · 30 = 4500 (р.) – стоят 30 мотков пряжи. |
Урок 91. Карта.
Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием «масштаб»; способствовать формированию умений определять масштабы географических карт; выполнять решение задач, связанных с масштабом |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «масштаб»; научатся определять масштабы географических карт; выполнять решение задач, связанных с масштабом |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; понимают знаки, символы, модели, схемы. Регулятивные: умеют формулировать учебную задачу на основе соотнесения того, что уже известно и усвоено обучающимся, и того, что еще неизвестно. Коммуникативные: умеют работать коллективно; контролируют действия партнера |
Личностные: имеют желание учиться; знают моральные нормы и умеют выделять нравственный аспект поведения |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Каждое из данных чисел представьте в виде произведения двух одинаковых множителей: 9 = 25 = 640000 = |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение:
9 = 3 · 3 4900 = 70 · 70 25 = 5 · 5 8100 = 90 · 90 640000 = 800 · 800 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||
|
|
– Расставьте скобки так, чтобы выражение 60 – 24 : 3 + 1 имело значение: а) 13; б) 51; в) 54; г) 9. |
Решение: а) (60 – 24) : 3 + 1 = 13 в) 60 – 24 : (3 + 1) = 54 б) 60 – (24 : 3 + 1) = 51 г) (60 – 24) : (3 + 1) = 9 |
|||||||||||||||
|
Геометрический материал |
– Как можно узнать, сколько всего клеточек было в прямоугольнике, если от него осталась такая часть:
|
Решение: 7 · 10 = 70 4 · 10 = 40 2 · 8 = 16 |
|||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 65). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Что означает масштаб карты? 1 : 6 000 000 1: 7 500 000 1 : 300 000 000 |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Масштаб 1 : 6 000 000 обозначает, что в 1 см – 60 км. Масштаб 1: 7 500 000 обозначает, что в 1 см – 75 км. Масштаб 1 : 300 000 000 обозначает, что в 1 см – 3000 км. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти ин-формацию, необходимую для решения учебной задачи, обосновывать выбор |
||||||||||||||
|
Задание 4 |
– Рассмотрите карту Подмосковья, выполненную в масштабе 1 : 1 000 000. Измерьте по карте и вычислите расстояние между городами: а) Звенигород и Химки; б) Пушкино и Бронницы; в) Красногорск и Щёлково |
– В 1 см 10 км.
|
|||||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учеб-нику (с. 67). Задание 12*. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выразите длину лука в метрах и сантиметрах, а длину стрелы – в сантиметрах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: Длина спортивного лука 1 м 58 см – 1 м 77 см. Длина стрелы 60 см – 80 см. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Планировать способы взаимодействия |
||||||||||||||
|
Задание 13. |
– Длина комнаты равна 4 м 20 см, а ширина – 3 м 50 см. В магазине продаются ковры таких размеров. – Выберите для этой комнаты ковер наиболее подходящих размеров. |
Запись:
– Наиболее подходит ковер под номером 3. |
|||||||||||||||
|
Задание 14*. |
– Полкилограмма колбасы стоит 160 р. Какова стоимость 250 г, 750 г, 1 кг колбасы? |
Запись:
Решение: 1) 1000 : 500 = 2 (раза) больше стоит 1 кг, чем 500 г. 2) 160 · 2 = 320 (р.) – цена колбасы за 1 кг. 3) 500 : 250 = 2 (раза) – меньше стоит 250 г, чем 500 г. 4) 160 : 2 = 80 (р.) – стоят 250 г; 160 + 80 = 2 40 (р.) – стоят 750 г. |
|||||||||||||||
|
Задание 15. |
– От одной овцы тонкорунной породы настригают в год примерно 5 кг 200 г шерсти. Сколько шерсти можно получить при той же норме от отары овец, в которой 465 животных? |
Запись: 1 овца – 5 кг 200 г 465 овец – ? Решение: 5200 г · 465 = 2418000 (г) – шерсти получают от 465 животных. 2418000 г = 2418 кг. |
|||||||||||||||
|
Задание 16. |
– Для изготовления канцелярских скрепок длиной 4 см 5 мм проволоку разрезают на куски длиной 15 см. Сколько проволоки потребуется для изготовления 100 коробок таких скрепок, если в одну коробку кладут 75 штук? |
Решение: 1) 15 · 75 = 1125 (см) проволоки потребуется для изготовления 1 коробки. 2) 1125 · 100 = 112500 (см) – проволоки потребуется для изготовления 100 коробок. |
|||||||||||||||
|
Задание 17* |
– Вагончик подвесной канатной дороги проехал 1 км 200 м за 10 мин. Вычислите скорость движения вагончика в метрах в секунду. – Какие математические знания помогли вам выполнить это задание? |
Запись: 1200 : 10 = 120 м/мин = 2 м/с |
|||||||||||||||
|
V. Работа в группах. |
Делит класс на 2 группы. Объясняет задание. |
Выполняют практическое задание в группах. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества |
||||||||||||||
|
1-я группа работает с глобусами. |
Необходимый материал для выполнения задания: глобус, справочная литература для определения длины экватора, портновский метр. – В каком масштабе выполнен глобус? Как получить необходимые данные? Длину экватора найти из справочной литературы. Длину экватора на глобусе измерить подручными средствами, например, линейкой, портновским метром, ниткой. Вычислить масштаб глобуса. Решение записать в таблице:
|
Решение:
40 000 км = 4 000 000 000 см 4 000 000 000 : 80 = 50 000 000 Ответ: масштаб глобуса 1 : 50 000 000. (Это означает: 1 см на глобусе соответствует 50 000 000 см на земном шаре, то есть 500 км). |
|||||||||||||||
|
2-я группа работает с моделями геометрических тел |
Необходимый материал для выполнения задания: модели геометрических тел, развертки в первоначальных измерениях геометрических тел, линейка. – Сторона квадрата 3 см. Как изменится площадь полной поверхности куба и объем куба, если сторона увеличится в 2 раза; в 3 раза? |
Ответ: площадь увеличится в 4 раза, а объем – в 8 раз; площадь увеличится в 9 раз, а объем – в 27 раз |
|||||||||||||||
|
VI. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
||||||||||||||
Урок 92. Цилиндр
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятием «цилиндр» как пространственной фигуры; способствовать формированию умений показывать основания и боковую поверхность цилиндра; выполнять изображение цилиндра на плоскости |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «цилиндр» как пространственной фигуры; научатся показывать основания и боковую поверхность цилиндра; выполнять изображение цилиндра на плоскости |
Метапредметные: Познавательные: умеют ориентироваться в учебнике (на развороте, в оглавлении, в условных обозначениях); находят ответы на вопросы в тексте, иллюстрациях; делают выводы в результате совместной работы класса и учителя. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию, прислушиваются к мнению других |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения; считаются с мнением другого человека; проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности) |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Отгадайте загадки о геометрических фигурах (см. ресурсный материал к уроку). |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Отгадывают загадки о геометрических фигурах и показывают их на чертеже. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
Интеллектуальная разминка |
– Какая фигура «лишняя»? |
Рассматривают чертеж и называют «лишнюю» фигуру.
|
|
|
III. Открытие нового знания, способа действия. Работа по учеб-нику (с. 68). Задание 1 |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Рассмотрите фигуры. Названия каких фигур вы уже знаете? Назовите эти фигуры. – Знаете ли вы, как называется фигура под номером пять? Найдите ее название среди слов: конус, шар, цилиндр, куб. Запишите в тетради два раза слово «цилиндр» и запомните его написание. џ Цилиндр имеет два основания и боковую поверхность. Каждое из оснований представляет собой круг |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Рассматривают цилиндр.
Записывают в тетради два раза слово «цилиндр».
– Многие окружающие нас предметы по форме похожи на цилиндр: банки, вазы, детали машин, бидоны. В прошлом были в моде мужские шляпы, которые так и назывались – цилиндр |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей |
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учеб-нику (с. 69–70). Задание 5. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Перемножьте устно числа. 99 · 4 39 · 7 199 · 5 69 · 6 49 · 4 79 · 3 |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Решение: 99 · 4 = (100 – 1) · 4 = 400 – 4 = 396 69 · 6 = (70 – 1) · 6 = 420 – 6 = 414 39 · 7 = (40 – 1) · 7 = 280 – 7 = 273 49 · 4 = (50 – 1) · 4 = 200 – 4 = 196 199 · 5 = (200 – 1) · 5 = 1000 – 5 = 995 79 · 3 = (80 – 1) · 3 = 240 – 3 = 237 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|
Задание 6 (по вариантам). |
– Решите задачу. Вариант 1. В бассейне длина дорожки равна 200 м. Пловец уже проплыл три четвертых этой дорожки. Сколько метров ему осталось проплыть? |
Решение: 1) 200 : 4 · 3 = 150 (м) – проплыл пловец. 2) 200 – 150 = 50 (м) – осталось проплыть пловцу. |
|
|
|
Вариант 2. Длина лыжной трассы – 25 км. Лыжник прошел четыре пятых пути. Сколько километров ему осталось пройти? – Обменяйтесь тетрадями и проверьте работу друг друга. |
Решение: 1) 25 : 5 · 4 = 20 (км) – прошел лыжник. 2) 25 – 20 = 5 (км) – осталось пройти лыжнику. |
|
|
Задание 7. |
– Вычислите значения выражений. |
Решение: (260 : 40 + 540 : 40) · 6 + 184 = 304 750 : (50 · 3 – 25 · 3) · 30 + 70 = 370 |
|
|
Задание 8*. |
– Из 30 учащихся пятерки за контрольную работу по математике получили 5 человек, четверок было поставлено вдвое больше. Какая часть всех учащихся класса получила отличные и хорошие отметки? |
Решение: 1) 5 · 2 = 10 (чел.) – получили четверки. 2) 10 + 5 = 15 (чел.) – получили отличные и хорошие отметки. 3) 30 : 15 = 2 (части) ‒ полкласса получили отличные и хорошие отметки. |
|
|
Задание 9 |
1) На сколько 96 т больше 96 ц? 2) Какую часть часа составляют 6 мин, 10 мин, 15 мин, 20 мин, 30 мин?
3) Какую часть рубля составляют 1 к., 20 к., 50 к.?
4) Сколько копеек в 50 р., в 100 р.? 5) Сколько метров в 20 км, в 1 000 км? 6) Сколько центнеров в 40 т, в 100 т? |
Решение: 1) 960 ц – 96 ц = 864 ц 2) 60 мин : 6 мин = 10-я часть 60 мин : 10 мин = 6-я часть 60 мин : 15 мин = 4-я часть 60 мин : 20 мин = 3-я часть 60 мин : 30 мин = 2-я часть 3) 100 к. : 1 к. = 100-я часть 100 к. : 20 к. = 5-я часть 100 к. : 50 к. = 2-я часть 4) 50 р. = 5000 к. 100 р. – 10000 к. 5) 20 км = 20000 м 1000 км = 1000000 м 6) 40 т = 400 ц 100 т = 1000 ц |
|
|
V. Работа |
Организует работу в группах по карточкам. – Определите по техническим рисункам название геометрической фигуры, дайте максимальные сведения о ней и её применении. |
Работают в группах, готовят сообщения. |
Планировать учебное сотруд-ничество с учителем и сверстниками – определение цели, функций участников, способов взаимодействия, постановка вопросов – инициативное сотрудничество в поиске и сборе информации. Осуществлять управление поведением партнера – контроль, коррекцию, оценку его действий; уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Владеть монологической и диалогической формами речи |
|
Карточка 1. |
|
1-я группа: Цилиндром называется тело, которое состоит из двух кругов. Круги называются основаниями цилиндра. Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. |
|
|
Карточка 2. |
|
2-я группа: Куб – это геометрическое тело. Квадрат является гранью куба. Поверхность каждого куба состоит из квадратов, которые называются гранями. Куб называется правильным шестиугольником, так как у него 6 граней. Две соседние грани квадрата (многогранника) называются ребрами. У куба 12 ребер, равных по длине. Куб имеет вершины. Три ребра пересекаются (сходятся) к одной вершине. У куба 8 вершин. |
|
|
Карточка 3 |
|
3-я группа: Конус – это геометрическое тело. Основание конуса – круг. Высота конуса – это перпендикуляр, опущенный из вершины конуса на плоскость основания. Часть конической поверхности, расположенная между вершиной и плоскостью основания, называется боковой поверхностью конуса |
|
|
VI. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи |
Ресурсный материал к уроку
|
Чуть приплюснутый квадрат Приглашает опознать: Острый угол и тупой Вечно связаны судьбой. Догадались, дело в чем? Как фигуру назовем? (Ромб.) Прикатилось колесо, Ведь похожее оно, Как наглядная натура Лишь на круглую фигуру. Догадался, милый друг? Ну, конечно, это… (круг). *** На фигуру посмотри И в альбоме начерти Три угла. Три стороны Меж собой соедини. Получился не угольник, А красивый… (треугольник). |
Я фигура – хоть куда, Очень ровная всегда, Все углы во мне равны И четыре стороны. Кубик – мой любимый брат, Потому что я… (квадрат). Он похожий на яйцо Или на твое лицо. Вот такая есть окружность – Очень странная наружность: Круг приплюснутым стал. Получился вдруг… (овал). *** Треугольник подпилили И фигуру получили: Два тупых угла внутри И два острых – посмотри. Не квадрат, не треугольник, А похож на многоугольник. (Трапеция.) |
Часть от линии возьмем И фигуру назовем Не куском – уж слишком резко, А, наверное, … (отрезком).
В математике она Пригождается всегда: Без хвоста от запятой Всем нам кажется простой. И в конце, закончив строчку, Мы поставим, братцы, … (точку). |
Урок 93. Цилиндр.
Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием «цилиндр» как пространственной фигуры; способствовать формированию умений показывать основания и боковую поверхность цилиндра; выполнять изображение цилиндра на плоскости |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием «цилиндр» как пространственной фигуры; научатся показывать основания и боковую поверхность цилиндра; выполнять изображение цилиндра на плоскости |
Метапредметные: Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями её реализации. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: определяют границы собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний. – Сумма двух чисел равна 22. Одно из них оканчивается нулём. Если этот нуль отбросить, то получится другое число. |
Отвечают на вопросы учителя. Выполняют задания устного счета. Ответ: 20 и 2. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Интеллектуальная разминка. Задачи на логику. |
Догадайтесь, какие это числа? – В корзине 6 яблок. Как разделить их между тремя мальчиками, чтобы каждому досталось по 2 яблока и чтобы 2 яблока осталось в корзине? – Два ученика договорились сесть в четвёртый вагон электрички. Но один ученик сел в четвертый вагон от начала электрички, а другой – в четвёртый вагон от конца. В одном ли вагоне едут ученики, если всего в поезде 8 вагонов? |
– Один мальчик берёт яблоки вместе с корзиной.
– В соседних. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Геометрический материал |
– Утром проснулась белочка, позавтракать решила она. На березке – грибочки, на сосне – шишки. Собрала запасы, вернулась в дупло. – Найдите весь путь белочки, если от ели до березки 15 м, от березы до сосны 4 м, а от сосны до ели – 20 м.– Как называется фигура? – Докажите, что это треугольник. – Что нужно найти? – Как по-другому сказать, что нужно найти? – Что такое периметр? |
– У треугольника 3 угла, 3 стороны. – Весь путь белочки – это периметр треугольника. – Периметр – сумма длин всех сторон. Р = 15 + 4 + 20 = 39 (м). Ответ: Р = 39 м.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 69). Задание 2. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Какие предметы или их части имеют форму цилиндра? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Бревно, стакан, ведро, бидон, консервная банка имеют форму цилиндра. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 3. |
– Возьмите модель цилиндра и рассмотрите её основания, боковую поверхность. Какую фигуру представляет каждое из двух оснований цилиндра? |
– Каждое из двух оснований цилиндра представляет круг. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4 |
– Возьмите стакан, в основании которого круг (см. задание 2), и налейте в него воду. Какую форму принимает вода в стакане? – Развёртка конуса состоит из круга (основание конуса) и сектора (боковая поверхность). Длина окружности и длина дуги сектора равны. Выкройка модели конуса дополняется выступами для склейки. Развёртка цилиндра состоит из двух кругов (основания цилиндра) и прямоугольника (боковая поверхность). Длины окружностей равны длине прямоугольника. Выкройка модели цилиндра дополняется выступами для склейки |
– Форму стакана (цилиндра) принимает вода в стакане.
Выполняют модель цилиндра и конуса. Конус
Цилиндр
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 71–72). Задание 10. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Масса курантов, установленных на Спас-ской башне Московского Кремля, равна 25000000 г, диаметр каждого из четырех циферблатов – 6120 мм, длина часовой стрелки – 2970 мм, а минутной – 3280 мм. Выразите массу в тоннах, а длины – в метрах и сантиметрах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Решение: 25 000 000 г = 25 т 6120 мм = 612 см = 6 м 12 см 2 970 мм = 297 см = 2 м 97 см 3 280 мм = 328 см = 3 м 28 см |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным дейст вием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 11. |
– Найдите и объясните ошибки, которые допустил Миша при умножении чисел. |
– В первом произведении Миша допустил ошибки в переходе через разряд, в третьем – при записи третьего неполного произведения. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 12. |
– Какие из утверждений неверны? |
– Неверно утверждение «Это не конус». |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 13. |
– Запишите в таблицу значения данных выражений, подставляя вместо буквы t числа: 10, 20, 30, 60, 150.
|
Заполняют таблицу:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 14. |
– Изобразите от руки кривые линии. |
Чертят кривые линии от руки. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 15 |
– Определите и назовите координаты центра окружности и точек А, С, М. – В какой точке окружность касается оси х? Назовите координаты этой точки |
– Точка К (3; 2); точка А (1; 2); точка С (3; 4); точка М (5; 2). – В точке В окружность касается оси х. Точка В имеет координаты (3; 0) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 94. Деление на однозначное число. Алгоритм деления
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для уточнения способов проверки правильности вычислений; способствовать формированию умений выполнять деление многозначных чисел на однозначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с письменным алгоритмом деления многозначного числа на однозначное; научатся выполнять письменный алгоритм деления многозначного числа на однозначное |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование; структурируют знания; умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Запишите величины в порядке их возрастания. 6000 г, 4 кг, 5 кг 20 г, 5 кг 2 г; 5 кг 200 г, 28000 г, 39 кг. – Увеличьте каждую величину на 15 кг. |
Отвечают на вопросы учителя. Выполняют задания устного счета. Запись: 4 кг, 5 кг 2 г; 5 кг 20 г, 5 кг 200 г, 6000 г, 28000 г, 39 кг. 19 кг, 20 кг 2 г, 20 кг 20 г, 20 кг 200 г, 21 кг, 43 кг, 54 кг. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||
|
|
– Лыжные соревнования проводятся на дистанциях в 3 км; 5 км; 10 км. Вырази эти расстояния в метрах. |
Запись: 3 км = 3000 м 5 км = 5000 м 10 км = 10000 м |
||||||||||||||||||||||||||||||
|
|
– Рассмотрите таблицу и ответьте на вопросы.
|
Заполняют таблицу:
|
||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учеб-нику (с. 73–74). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Составьте алгоритм деления столбиком многозначного числа на однозначное.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Алгоритм деления многозначного числа на однозначное число: 1. Нахожу первое неполное делимое. 2. Определяю первую цифру частного. 3. Нахожу второе неполное делимое. 4. Определяю вторую цифру частного… 5. Проверяю, правильно ли найдено частное (умножением). |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
|||||||||||||||||||||||||||||
|
Задание 2 |
– Выполните деление столбиком. – Проверьте результаты с помощью калькулятора |
Решение: 62785 : 5 = 12557 52278 : 3 = 17426 236270 : 5 = 47254 638145 : 9 = 70905 16971 : 3 = 5657 123716 : 4 = 30929 22936 : 8 = 2867 229327 : 7 = 32761 |
||||||||||||||||||||||||||||||
|
IV. Включение нового в активное использо- вание в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 76). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||||||
|
– Разделите делимое 800 и делитель 160 на 10, затем на 2, на 4 и на 8. – Разделите делимое 128000 и делитель 64000 на 1000, затем на 2, на 4 и на 8. |
Ответы: 1) 800 : 160 2) 128000 : 64000 80 : 16 128 : 64 400 : 80 64000 : 32000 200 : 40 16000 : 8000 100 : 20 |
|||||||||||||||||||||||||||||||
|
Задание 12. |
– Верно ли высказывание: «Если сумма двух чисел делится без остатка на 2, то и каждое слагаемое делится на 2». Приведите примеры. |
– Верно высказывание. (10 + 14) : 2 = 24 : 2 = 12 (10 + 14) : 2 = 10 : 2 + 14 : 2 = 2 = 5 + 7 |
||||||||||||||||||||||||||||||
|
Задание 13. |
– Верно ли высказывание: «Если каждое из двух чисел делится на 2, то и сумма этих чисел делится на 2»? Приведите примеры. |
– Верно высказывание. (28 + 12) : 2 = 40 : 2 = 20 (28 + 12) : 2 = 28 : 2 + 12 : 2 = 14 + 6 = 20 |
||||||||||||||||||||||||||||||
|
Задание 14. |
– Прочитайте высказывания и определите, какие из них истинные и какие ложные. |
Решение: 1) истинно; 2) истинно; 3) ложно; 4) ложно. |
||||||||||||||||||||||||||||||
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу способом подбора. Сколько решений имеет задача? |
Решение:
|
||||||||||||||||||||||||||||||
|
Задание 16 |
– Постройте квадрат с длиной стороны 4 см 8 мм в масштабе 1 : 2, 2 : 1. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга |
Решение:
|
||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения. – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
Метод «Цветограмма» эффективен в конце урока, он может сочетать в себе рефлексию содержания учебного материала и рефлексию деятельности ребенка на каждом этапе урока. Для проведения этого приема понадобятся наборы цветных карточек по количеству обучающихся и демонстрационная схема. Инструкция учителя: «Составьте цветограмму урока по данной схеме» |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Осуществлять итоговый контроль, оценивать результаты деятельности, формировать адекватную самооценку |
Урок 95. Автоматизация навыка деления на однозначное число
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: создать условия для уточнения способов проверки правильности вычислений; способствовать формированию умений выполнять деление многозначных чисел на однозначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с письменным алгоритмом деления многозначного числа на однозначное; научатся выполнять письменный алгоритм деления многозначного числа на однозначное; использовать и объяснять способы проверки правильности вычислений; анализировать выполнение деления многозначных чисел на однозначное число |
Метапредметные: Познавательные: осуществляют анализ, сравнение; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи; строят логическую цепь рассуждений. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: учитывают разные мнения и стремятся к координации разных позиций в сотрудничестве |
Личностные: выражают этические чувства (стыда, вины, совести) на основе анализа простых ситуаций; проявляют интерес к учебному материалу |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя. Выполняют задания устного счета. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||
|
– Знаете ли вы? · Самое глубокое озеро в мире – Байкал. Его глубина 1940 м. · Самая высокая горная вершина на Земле – Джомолунгма (Эверест) в Гималаях – 8848 м. · Самый высокий из действующих вулканов в мире – Льюль-яйльяко в чилийско-аргентинских Андах – 6723 м. · Самый высокий водопад в мире – Анхель (Чурун-Мерун) в верховьях реки Чурун на Гвианском плоскогорье в Венесуэле. Он падает с высоты 1054 м. – Выразите данные величины в километрах и метрах. |
Решение: 1940 м = 1 км 940 м 6723 м = 6 км 723 м 8848 м = 8 км 848 м 1054 м = 1 км 54 м |
|||||||||||
|
– Разгадайте правило, по которому составлены схемы, и вставьте пропущенные величины.
|
Решение: 100 см = 5 дм + 50 см 3 м = 30 см + 27 дм 5 м = 6 см + 494 см 8 дм = 40 мм + 76 см
|
|||||||||||
|
III. Открытие нового знания, способа действия. Работа по учеб-нику (с. 74). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Выполните действия. Проверьте умножение делением, а деление умножением. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 3687 · 8 = 29496 12345 · 7 = 86415 529671 : 3 = 176557 92808 : 4 = 23202 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
|||||||||
|
Задание 4. |
– Вычислите значения выражений. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга. |
Решение: 632702 : 7 + 303804 : 6 – 882910 : 7 = 14890 (240328 : 8 + 654084 + 20) : 7 = 97735 (2118 · 105 : 3 – 654084 : 9) · 607 = 882578. |
||||||||||
|
Задание 5 |
– Докажите, что неравенства верны. |
Решение: а) 29765 : 5 > 9248 : 8 – верно б) 20841 · 3 < 6208200 : 9 – верно |
||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учеб-нику (с. 77–78). Задание 17. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Сравните четвертую часть часа и 15 минут. – Сравните пятую часть минуты и 27 секунд. – Сравните восьмую часть килограмма и 250 граммов. – Сравните тысячную часть километра и 10 дециметров. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Решение: 1) 15 мин = 15 мин; 60 мин : 4 = 15 мин. 2) 60 с : 5 = 12 с.; 12 с < 27 с. 3) 1000 г : 8 = 125 г; 125 г < 250 г. 4) 1 м = 10 дм; 10 дм = 1 м. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять взаимный контроль |
|||||||||
|
Задание 18. |
– Прочитайте задачу. Что известно? Что требуется узнать? – сколько золота нужно для изготовления пяти таких же цепочек? |
Решение: 1) 1 кг = 1000 грамм; 1000 : 1000 = 1 (грамм) – на одну цепочку. 2) 1 · 5 = 5 (грамм) – на 5 цепочек. |
||||||||||
|
Задание 19*. |
– Прочитайте задачу. Что известно? Что требуется узнать? – Сколько и какие упаковки порошка сможет купить мама? |
Решение: 650 г · 3 = 1950 г. |
||||||||||
|
Задание 20. |
– Выполните необходимые измерения и начертите такие прямоугольники, используя угольник и линейку. |
Решение:
|
||||||||||
|
Задание 21. |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – Сколько килограммов картофеля положили в каждый мешок? |
Запись: Собрали – 1 ц Большой мешок – 46 кг 2 маленьких мешка – по ? кг Решение: 1) 1 ц = 100 кг; 100 – 46 = 54 (кг) – в 2 маленьких мешках. 2) 54 : 2 = 27 (кг) – в 1 маленьком мешке. |
||||||||||
|
Задание 22*. |
– С какой скоростью шел человек, если за 20 минут он прошел 2 км? |
Решение: 1) 60 : 20 = 3 (так как 20 минут – третья часть часа). 2) 2 · 3 = 6 (км/ч). |
||||||||||
|
Задание 23. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – С какой скоростью шел другой поезд? |
Запись:
Решение: 1) 652 : 4 = 163 (км/ч) – скорость сближения. 2) 163 – 85 = 78 (км/ч) – скорость 2-го поезда. |
||||||||||
|
Работа по учебнику (с. 74). Задание 6. |
– Является ли число 3 значением буквы х в каждом равенстве? |
Решение: а) 712020 : х = 237340 б) 12228 : х = 3 712020 : 3 = 237340 – верно 12228 : 3 = 4076 – неверно. |
||||||||||
|
Задание 7 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какая площадь занята зерновыми культурами? |
Решение: 1) 247840 : 5 = 49568 (м2) – овощи. 2) 49568 : 4 = 12392 (м2) – фрукты. 3) 49568 + 12392 = 61960 (м2) – овощи и фрукты. 4) 247840 – 61960 = 185876 (м2) – зерновые |
||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 96. Закрепление навыка деления на однозначное число
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для уточнения способов проверки правильности вычислений; способствовать формированию умений выполнять деление многозначных чисел на однозначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с письменным алгоритмом деления многозначного числа на однозначное; научатся выполнять письменный алгоритм деления многозначного числа на однозначное; использовать и объяснять способы проверки правильности вычислений; анализировать выполнение деления многозначных чисел на однозначное число |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной форме. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями её реализации. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: определяют цели, функции участников, способы взаимодействия |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Найдите частное. 63 : 21 96 : 6 6000 : 2000 46 : 23 72 : 6 5600 : 800 88 : 22 75 : 5 420000 : 700 |
Отвечают на вопросы учителя. Выполняют задания устного счета. Решение: 63 : 21 = 3 96 : 6 = 16 6000 : 2000 = 3 46 : 23 = 2 72 : 6 = 12 5600 : 800 = 7 88 : 22 = 4 75 : 5 = 15 420000 : 700 = 600 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу |
|||||||||||
|
|
– В данных выражениях выделите первое неполное делимое и определите количество цифр в частном.
|
Решение: 18330 : 705 – две цифры в частном. 219618 : 249– три цифры в частном. 46935 : 63 – три цифры в частном. 4680 : 3 – четыре цифры в частном. 432 : 4 – три цифры в частном. 140448 : 456 – три цифры в частном. |
||||||||||||
|
|
– Можно ли разложить: а) 3724; б) 5252 карандаша в коробки по 4 штуки в каждую? |
Решение: а) 3724 : 4 = 931 б) 5214 : 4 = 1313 |
||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учеб-нику (с. 75). Задание 8*. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Чему равна длина прямоугольника? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Запись:
Решение: 1) 2133 : 3 = 711 (м2) – площадь 2-го прямоугольника. 2) 711 : 9 = 79 (м) – длина 2-го прямоугольника. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
|||||||||||
|
Задание 9. |
– По какой цене стали продавать диван, если его первоначальная цена была 4560 р.? |
Решение: 1) 4560 : 10 = 456 (р.) – на столько снизилась цена в первый раз. 2) 4560 – 456 = 4104 (р.) – цена дивана после первого снижения. 3) 4104 : 4 = 1026 (р.) – на столько снизилась цена второй раз. 4) 4104 – 1026 = 3078 (р.) – цена дивана после второго снижения |
||||||||||||
|
Задание 10 |
– Чему равно частное? Как проверить результат с помощью умножения? џ Если делитель равен 1, то частное равно делимому. В математике это предложение записывают так: при любом значении а верно равенство а : 1 = а |
Решение: 268 : 1 = 268; 1254 : 1 = 1254. 268 · 1 = 268; 1254 · 1 = 1254. |
||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 78–79). Задание 24. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Через сколько минут Петя догонит Сережу? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись:
Решение: 1) 160 – 100 = 60 (м/мин) – скорость изменения расстояния. 2) 300 : 60 = 5 (мин) – догонит. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Дополнять, уточнять высказанные мнения по существу полученного задания. Планировать способы взаимодействия |
|||||||||||
|
Задание 25. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько свёклы осталось на базе? |
Запись: Было – 30 т 1-й грузовик – 2 т 500 кг 2-й грузовик – 3 т 3-й грузовик – 4 т 800 кг Осталось – ? Решение:
|
||||||||||||
|
Задание 26. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – За сколько минут ученик делает одну деталь? |
Запись:
Решение: I способ 1) 1 ч 40 мин = 100 мин; 100 : 50 = 2 (мин) – 1 деталь делает мастер. 2) 2 · 2 = 4 (мин) – 1 деталь делает ученик. II способ 1) 1 ч 40 мин · 2 = 3 ч 20 мин; 3 ч 20 мин = 200 мин – работает ученик. 2) 200 : 50 = 4 (мин) – 1 деталь делает ученик. |
||||||||||||
|
Задание 27*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – какое расстояние будет между самолетами через 30 минут после вылета? |
Запись:
Решение: 1) 850 + 950 = 1800 (км/ч) – скорость удаления. 2) 60 : 30 = 2 (раза) – меньше. 3) 1800 : 2 = 900 (км) – расстояние через 30 мин. |
||||||||||||
|
Задание 28. |
– Назовите пары чисел, которые соответствуют вершинам четырехугольника АВСМ. |
Решение: А (1; 4); В (5; 9); С (9; 6); М (6; 1). |
||||||||||||
|
Задание 29. |
– Какую форму имеют предметы или их части? |
– Форму шара имеют глобус, мяч. – Форму цилиндра имеет термос. – Форму конуса имеет сачок. – Форму пирамиды имеет крыша. – Форму параллелепипеда имеет аквариум. |
||||||||||||
|
Задание 30 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – какова цена шубы? |
Решение: 30000 : 10 = 3000 (р.) – снизили цену. 30000 – 3000 = 27000 (р.) – новая цена шубы |
||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Рефлексивный прием «Смайлики»: ученикам раздаются размноженные листы с упрощённым изображением человека, у которого не нарисовано лицо. Ребята сами рисуют те эмоции, что свойственны им сейчас. Они могут дополнить изображение деталями (воздушным шаром, букетом или же тяжёлой сумкой в руке), что будет дополнять общее впечатление: «Понравился ли мне урок? Остались ли у меня вопросы? Доволен ли я своей работой?» |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 97. Контрольная работа № 6 по теме «Деление многозначного числа
на однозначное.
Деление на 10, 100, 1000…»
|
Тип урока: контроль и оценивание знаний и способов действий |
||
|
Педагогические задачи: проверить усвоение алгоритмов деления многозначного числа на однозначное и умножения многозначных чисел, умение решать задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с письменным алгоритмом деления многозначного числа на однозначное; научатся выполнять письменный алгоритм деления многозначного числа на однозначное; использовать и объяснять способы проверки правильности вычислений; анализировать выполнение деления многозначных чисел на однозначное число |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; строят логическую цепь рассуждений. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: умеют устанавливать, с какими учебными задачами могут справиться самостоятельно |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
I. Содержание контрольной работы. Вариант 1 |
Знакомит с содержанием контрольной работы, комментирует задания.
1. Найди значения выражений: 4780 · 26 53 084 : 4 255 681 : 9 935 · 607 272 580 : 3 10 735 : 5 2. Запиши выражения и найди их значения: 8407 уменьшить на 3312. Во сколько раз 57 000 больше 19? 7264 увеличить в 100 раз. Сумму чисел 375 и 927 уменьшить в 6 раз. На сколько произведение 534 · 803 больше 28 189? 3. За 4 пакета молока заплатили 32 р. Сколько стоят 5 таких пакетов? |
Задают вопросы по содержанию контрольной работы. Самостоятельное выполнение заданий контрольной работы. 1. Ответы: 124280 13271 28409 567545 90860 2147 2. Ответы: 8407 – 3312 = 5095 57000 : 19 = 3000 7264 · 100 = 726400 (375 + 927) : 6 = 217 534 · 803 – 28189 = 400613
3. Решение: 1) 32 : 4 = 8 (р.) – стоит 1 пакет молока. 2) 8 · 5 = 40 (р.) – стоят 5 пакетов молока |
Принимать и сохранять учебную цель и задачу. Анализировать, находить общее и различия, делать выводы. Осознанно и произвольно строить речевое высказывание в устной форме |
|
Вариант 2 |
1. Найди значения выражений: 9340 · 27 80 118 : 9 422 814 : 7 578 · 406 281 890 : 5 16 824 : 3 2. Запиши выражения и найди их значения: 5309 уменьшить на 2429. Во сколько раз 52 000 больше 13? 8423 увеличить в 100 раз. Сумму чисел 729 и 1584 уменьшить в 9 раз. На сколько произведение чисел 247 и 509 больше 32 964? 3. За 4 порции мороженого заплатили 28 р. Сколько нужно заплатить за 3 такие же порции мороженого? |
1. Ответы: 252180 8902 60402 234668 56378 5608 2. Ответы: 5309 – 2429 = 2880 52000 : 13 = 4000 8423 · 100 = 842300 (729 + 1584) : 9 = 257 247 · 509 – 32964 = 92759
3. Решение: 1) 28 : 4 = 7 (р.) – стоит 1 мороженое. 2) 7 · 3 = 21 (р.) – стоят 3 мороженых |
|
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 98. Деление на двузначное число. Алгоритм деления
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений делить многозначное число на двузначное и трехзначное число; создать условия для составления алгоритма письменного деления на трехзначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на двузначное число; научатся применять алгоритм письменного деления на двузначное число; объяснять выполнение деления многозначного числа на двузначное |
Метапредметные: Познавательные: осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; овладевают навыками смыслового чтения (осмысление цели чтения и выбор вида чтения в ависимости от цели); определяют основную и второстепенную информацию. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: договариваются с одноклассниками, совместно с учителем о правилах поведения и общения и следуют им |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. Задача |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя. Выполняют задания устного счета. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу |
|||||||
|
– Определите, каким может быть первое неполное делимое:
|
Возможные ответы: 41368 : 4137 137501 : 1376 97653 : 977 61138 : 6114 15784 : 1579 3070815 : 307082 |
|||||||||
|
– Найдите значения выражений: 6633 : 11 8899 : 11 4455 : 11 7766: 11 |
Ответы: 6633 : 11 = 603 8899 : 11 = 809 4455 : 11 =405 7766: 11 = 706 |
|||||||||
|
– Поставьте в «окошко» цифры так, чтобы число делилось на 4: 97281 36373 |
Ответы: 972812 : 4 387928 : 4 363732 : 4 7281544 : 4 |
|||||||||
|
– Отцу и сыну 52 года. Отец старше сына на 32 года. Сколько лет каждому? |
Ответ: сыну – 10 лет, отцу – 42 года |
|||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 80–81). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Составьте алгоритм деления многозначного числа на двузначное.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Составляют алгоритм деления многозначного числа на двузначное.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Осуществлять контроль по результату |
|||||||
|
Задание 2. |
– Выполните деление. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга. |
Решение: 10455 : 85 = 123 8357 : 61 = 137 8508 : 12 = 709 78273 : 39 = 2007 27090 : 45 = 602 33684 : 12 = 2807 |
||||||||
|
Задание 3. |
– Выполните действия. Проверьте результаты с помощью калькулятора. |
Решение: 82320 : 28 : 14 : 7 = 30 990 : 55 · 16 : 72 = 4 |
||||||||
|
Задание 4 |
– Выполните деление. – Какие математические знания помогли вам выполнить это задание? |
Решение: 268800 : 84 = 3200 196196 : 14 = 14014 121000 : 11 = 11000 144144 : 12 = 12012 |
||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учеб-нику (с. 83–84). Задание 19. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выполните задание самостоятельно, запишите только результаты. проведите взаимопроверку в парах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||
|
Задание 20. |
– Подтвердите или опровергните каждое высказывание, приводя примеры.
|
1) Высказывание «В любом многоугольнике вершин и сторон поровну» истинно.
2) Высказывание «Любая незамкнутая ломаная линия имеет столько же вершин, сколько звеньев» ложно.
3) Высказывание «Среди прямоугольников нет таких, у которых длина равна ширине» ложно.
4) Высказывание «Среди квадратов нет ни одного прямоугольника» ложно.
|
||||||||
|
Задание 21. |
– Во сколько раз число в верхнем ряду меньше числа, записанного под ним? |
Решение: 10000 : 1000 = 10 8400 : 100 = 84 60000 : 10 = 6000 50000 : 10000 = 5 4000 : 1000 = 4 |
||||||||
|
Задание 22 |
– Выполните деление. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга |
Решение: 10170 : 5 = 2034 242432 : 8 = 30304 406630 : 7 = 58090 960038 : 2 = 480019 480270 : 6 = 80045 6013200 : 3 = 2004400 1010097 : 9 = 112233 89991 : 9 = 9999 |
||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Как выполнить деление на двузначное число? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 99. Упражнение в делении на двузначное число.
Контрольный устный счёт № 6
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: создать условия для составления алгоритма письменного деления на трехзначное число; способствовать формированию умений выполнять деление многозначного числа на двузначное и трехзначное число; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на двузначное число; научатся применять алгоритм письменного деления на двузначное число; объяснять выполнение деления многозначного числа на двузначное |
Метапредметные: Познавательные: выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера; осуществляют поиск нужной информации в учебнике и учебных пособиях; понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях. Регулятивные: принимают и сохраняют учебную задачу; адекватно воспринимают оценку учителя и товарищей; планируют свое действие. Коммуникативные: умеют формировать коммуникативно-речевые действия, конструктивные способы взаимодействия с окружающими (учителем, сверстниками) |
Личностные: проявляют этические чувства, доброжелательность и эмоционально-нравственную отзывчивость, понимание и сопереживание чувствам других людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
‒ Решите задачу.
|
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение: 1) 130 – 10 = 120 (м) – две длины. 2) 120 : 2 = 60 (м) – длина участка. 3) 60 · 10 = 600 (м2) – площадь участка. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||
|
|
– В данных примерах восстановите цифры вместо знака «*»:
– Где «ловушка»? |
Решение:
– В первом и последнем ребусе «ловушка». |
||||||||||||||||||||||||
|
|
По заготовке определите количество цифр в частном:
|
Решение:
|
||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учеб-нику (с. 81–82). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Вычислите частное. – Сложите результаты деления. Если получится число 11531, то деление выполнено верно. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 238266 : 61 = 3906 238266 : 62 = 3843 238266 : 63 = 3782 Проверка: 3906 + 3843 + 3782 = 11531. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|||||||||||||||||||||||
|
Задание 6*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Чему равна площадь прямоугольника? |
Запись:
Решение: 1) 4225 : 65 = 65 (дм) – длина 1-го прямоугольника. 2) 65 : 5 = 13 (дм) – длина 2-го прямоугольника. 3) 65 : 13 = 5 (дм) – ширина 2-го прямоугольника. 4) 13 · 5 = 65 (дм2) – площадь 2-го прямоугольника. |
||||||||||||||||||||||||
|
Задание 7. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько имеется килограммов винограда каждого сорта? |
Запись:
Решение: 1) 35 + 48 = 83 (ящ.) – всего. 2) 1162 : 83 = 14 (кг) – 1 ящ. 3) 35 · 14 = 490 (кг) – сорт «Изабелла». 4) 48 · 14 = 672 (кг) – сорт «Мускат». |
||||||||||||||||||||||||
|
Задание 8. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу разными способами. – Сколько килограммов моркови в 32 мешках? |
Запись: 16 м. – 768 кг 32 м. – ? кг Решение: I способ 1) 768 : 16 = 48 (кг) – 1 мешок. 2) 48 · 32 = 1536 (кг) – 32 мешка. II способ 1) 32 : 16 = 2 (раза) – больше. 2) 768 · 2 = 1536 (кг) в 32 мешках.
|
||||||||||||||||||||||||
|
Задание 9* |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько картофеля собрали с каждого поля? |
Запись:
Решение: 1) 84 – 56 = 28 (м.) – весят 1 т 400 кг. 2) 1400 : 28 = 50 (кг) – 1 мешок. 3) 50 · 56 = 2800 (кг) – с 1-го поля. 4) 50 · 84 = 4200 (кг) – со 2-го поля |
||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учеб-нику (с. 84). Задание 23. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Найдите значение выражений. 0 : 2412 + 456 · 1 – 78 : 1 + 354 · 0 = 451 – 78 = = 373 |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 0 : 2412 + 456 · 1 – 78 : 1 + 354 · 0 = 456 – 78 = = 378. (678 – 125 · 5 + 781 · 0) · 1 = 53. 1000 – (456 · 104 + 8907) · 0 = 1000. 0 : (4567 – 4399 + 56 · 42) = 0. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||
|
Задание 24. |
– Рассчитайте количество продуктов на 1 кг муки. |
Запись:
|
||||||||||||||||||||||||
|
Задание 25. |
– Рассчитайте количество продуктов на 2 кг мяса. |
Запись:
|
||||||||||||||||||||||||
|
Задание 26* |
– Площадь прямоугольника 24 см2. Можно ли из этого прямоугольника вырезать квадрат с длиной стороны 4 см? – Какие математические знания помогли вам выполнить это задание? |
– Можно, если прямоугольник имеет длины сторон 4 см и 6 см |
||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
|||||||||||||||||||||||
Урок 100. Закрепление навыка деления на двузначное число.
Проверочная работа по теме «Деление на двузначное число»
|
Тип урока: контроль и оценивание знаний и способов действий |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного деления на трехзначное число; способствовать формированию умений выполнять деление многозначного числа на двузначное и трехзначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на двузначное число; научатся применять алгоритм письменного деления на двузначное число; объяснять выполнение деления многозначного числа на двузначное |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной форме. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке. Коммуникативные: слушают и понимают речь других; признают возможность существования различных точек зрения и права каждого иметь свою |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Найдите частное: 68 : 34 34 : 17 72 : 18 96 : 32 84 : 21 52 : 13 |
Отвечают на вопросы учителя. Выполняют задания устного счета.
Решение: 68 : 34 = 2 34 : 17 = 2 72 : 18 = 4 96 : 32 = 3 84 : 21 = 4 52 : 13 = 4 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||||||
|
|
– Зная первое неполное делимое, определите количество цифр в частном:
Для каждого примера запишите по одному числу, которое могло быть делителем. |
Решение:
|
||||||||||||
|
Задача |
– Решите задачу. По дороге в школу мальчик считал свои шаги. Сначала он считал шаги парами и насчитал 55 пар, потом – тройками и насчитал 30 троек. Сколько всего шагов он насчитал? |
Решение: 55 · 2 + 30 · 3 = 200 (ш.) – насчитал мальчик |
||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учеб-нику (с. 82). Задание 10. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Вычислите значения выражений. – Какие математические знания помогли вам выполнить это задание? – Поменяйтесь тетрадями, проверьте работу друг у друга. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: (4826 : 38 + 62 · 11 – 2398 : 22) : 35 = 20 (59937 – 304752 : 21 – 1117 · 17) : 12 = 2203 (25287 + 48 589) : 92 – 92 · 10 : 2 = 343 397370 : 79 – (327 · 84 – 5295) : 57 = 4641. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге. Осуществлять контроль |
|||||||||||
|
Задание 11. |
– Лыжник идет по лыжне со скоростью 18 км/ч. – Сколько метров в час проходит лыжник? – Сколько метров в минуту проходит лыжник? – Сколько метров в секунду проходит лыжник? |
Решение: 18000 метров в час проходит лыжник. 300 метров в минуту проходит лыжник. 5 метров в секунду проходит лыжник. |
||||||||||||
|
Задание 12. |
– Пешеход идет со скоростью 6 км/ч. Выразите его скорость в метрах в минуту. |
Решение: 6 км/ч = 6000 м/ч = 100 м/мин. |
||||||||||||
|
Задание 13. |
– Самолет летит со скоростью 960 км/ч. Выразите его скорость в километрах в минуту. |
Решение: 960 км/ч = 16 км/мин. |
||||||||||||
|
Задание 14. |
– Автомобиль едет со скоростью 120 км/ч. Какова его скорость в метрах в минуту? |
Решение: 120 км/ч = 2 км/мин = 2000 м/мин. |
||||||||||||
|
Задание 15 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Выполнил ли токарь дневную норму? |
Запись:
Решение: 1) 1755 : 27 = 65 (дет.) – производительность. 2) 68 · 27 = 1836 (дет.) – выполнил с новой производительностью |
||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учеб-нику (с. 85). Задание 27. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись:
Решение: 1) 66 + 18 = 84 (км/ч) – скорость сближения. 2) 84 · 3 = 252 (км) – проехали. 3) 252 + 46 = 298 (км) – расстояние между селами. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок |
|||||||||||
|
Задание 28. |
– Какие числа можно записать в «окошках», чтобы неравенства были верными? |
Решение: 4 < 5 0 < 1 36 : 9 < 5 8 > 5 12 + 3 < 16 8 · 4 < 40 |
||||||||||||
|
Задание 29 |
– Через сколько минут после встречи друг охотника
дойдет до шалаша по той же дороге, если он идет со скоростью |
Запись:
Решение: 1) 96 · 30 = 2880 (м) – расстояние. 2) 2880 : 80 = 36 (мин) – идет друг |
||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 101. Автоматизация навыка деления многозначного числа на двузначное
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного деления на трехзначное число; способствовать формированию умений выполнять деление многозначного числа на двузначное и трехзначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на двузначное число; научатся применять алгоритм письменного деления на двузначное число; объяснять выполнение деления многозначного числа на двузначное |
Метапредметные: Познавательные: устанавливают причинно-следственные связи; строят логическую цепь рассуждений; используют доказательство. Регулятивные: оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы; адекватно оценивают результаты своей деятельности. Коммуникативные: учатся разрешать конфликт: выявляют, идентифицируют проблемы, осуществляют поиск и оценку альтернативных способов разрешения конфликта, принимают решение и реализуют его |
Личностные: проявляют интерес к учебному материалу; владеют знаниями основных моральных норм поведения; осознают роль языка и речи в жизни людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – На доске записаны две строки чисел. Найдите сумму чисел верхней строки. Найдите сумму чисел нижней строки, не складывая их между собой: а) 320 540 160 120 300 520 140 100 б) 320 540 160 120 300 560 140 140 |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
Решение: а) 320 + 540 + 160 + 120 = 1140 300 + 520 + 140 + 100 = 1060 б) 320 + 540 + 160 + 120 = 1140 300 + 560 + 140 + 140 = 1140 |
Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. |
||||||||
|
– Найдите «лишнюю» величину: а) км, дм, ч, мм, см; б) мин, с, сут., век, ч, см; в) кг, т, ц, ч, г. |
Решение: а) ч; б) см; в) ч. |
||||||||||
|
– Зная первое неполное делимое, определите количество цифр в частном:
Для каждого выражения запишите по одному числу, которое могло быть делителем |
Решение:
Четыре цифры Три цифры Четыре цифры
Пять цифр Три цифры Четыре цифры
34075 : 32; 62394 : 600; 173928 : 170; 260817 : 25; 574025 : 5730; 9752 : 8 |
||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 83). Задание 16. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Во сколько раз ответ Вани меньше правильного ответа? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 108 : 18 = 6 (раз) ‒ ответ Вани меньше. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять контроль по результату |
||||||||
|
Задание 17. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – сколько километров проедет автомобиль с той же скоростью? |
Запись:
Решение: 1) 1148 : 14 = 82 (км/ч) – скорость. 2) 19 · 82 = 1558 (км) – проехал за 19 ч. |
|||||||||
|
Задание 18 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Через сколько часов машины встретятся? |
Запись:
Решение: 1) 43 + 56 = 99 (км/ч) – скорость сближения. 2) 693 : 99 = 7 (ч) – встретятся |
|||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 85–87). Задание 30. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько стоит 1 кг масла? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 1 кг = 1000 г. 2) 1000 : 250 = 4 (раза) – больше. 3) 32 · 4 = 128 (р.). |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||
|
Задание 31. |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – Чему равна масса ртути в пятилитровом баллоне? |
Запись: 1 л ртути – 13 кг 600 г 5 л ртути – ? кг Решение: 13 кг 600 г · 5 = 68 кг. |
|||||||||
|
Задание 32. |
– Рассмотрите диаграмму. Назовите рост каждого из детей.
– Кто из детей самый высокий? – Кто по росту ниже Оли? – Есть ли дети одинакового роста? – Кто по росту выше Оли, но ниже Юры? – На сколько сантиметров Ира ниже Зои? – Кто из девочек выше всех других девочек? – Верно ли, что из мальчиков самый высокий Яша? – На сколько сантиметров Тая выше Иры? |
Решение: Оля – 128 см. Юра – 140 см. Зоя – 125 см. Ира – 123 см. Яша – 134 см. Тая – 125 см. – Юра самый высокий. – Ира, Зоя, Тая по росту ниже Оли. – Зоя и Тая одинакового роста. – Яша по росту выше Оли, но ниже Юры. – На 2 сантиметра Ира ниже Зои. – Оля выше всех других девочек. – Неверно, что из мальчиков самый высокий Яша.
– На 2 сантиметра Тая выше Иры. |
|||||||||
|
Задание 33. |
– Предложите способ устного вычисления данной суммы. |
– Надо разбить все слагаемые на удобные пары для сложения: 50 + 60 = 110 53 + 57 = 110 51 + 59 = 110 54 + 56 = 110 52 + 58 = 110 – Получили пять раз сумму 110. Это будет 550. |
|||||||||
|
Задание 34. |
– Начертите и вырежьте данные фигуры. – Составьте из всех четырех фигур прямоугольник. |
Выполняют практическое задание. |
|||||||||
|
Задание 35. |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – На сколько дороже обойдется покупателю покупка телевизора? |
Решение: 1) 8500 : 10 = 850 (руб.) – надо заплатить сразу. 2) 750 · 11 = 8250 (руб.) – оплата за 11 месяцев. 3) 8250 + 850 = 9100 (руб.) – стоимость телевизора. 4) 9100 – 8500 = 600 (руб.) – переплата. |
|||||||||
|
Задание 36 |
– Выразите массу самого большого золотого самородка в килограммах и граммах |
Решение: 36200 грамм = 36 кг 200 грамм |
|||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Оценивают работу, выбирая символ-фигуру: – Я работал…
|
Проявлять способность к самооценке на основе критерия успешности учебной деятельности. Выражать доброжелательность |
Урок 102. Деление на трёхзначное число. Алгоритм деления
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного деления на трехзначное число; способствовать формированию умений выполнять деление многозначного числа на двузначное и трехзначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на трехзначное число; научатся применять алгоритм письменного деления на трехзначное число; объяснять выполнение деления многозначного числа на двузначное и трехзначное число |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; используют знаково-символические средства для решения учебной задачи; осуществляют моделирование. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: излагают своё мнение и аргументируют свою точку зрения |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Решите задачу. а) За 1 час поезд проходит 60 км. Сколько километров он пройдет за 1 минуту? б) За 1 минуту девочка проходит 60 м. Сколько метров она проходит за 1 секунду? |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Ответы: а) 1 километр он пройдет за 1 минуту.
б) 1 метр девочка проходит за 1 секунду. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу |
|
– Определите количество цифр в частном. 3704 : 8 24030 : 6 3236 : 4 10035 : 5 5184 : 9 22400 : 400 35042 : 7 7528 : 8 20036 : 4 |
Решение: 3704 : 8 – три цифры 24030 : 6 – четыре цифры 3236 : 4 – три цифры 10035 : 5 – четыре цифры 5184 : 9 – три цифры 22400 : 400 – две цифры 35042 : 7 – четыре цифры 7528 : 8 – три цифры 20036 : 4 – четыре цифры |
||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 88). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Составьте алгоритм деления на трехзначное число. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Составляют алгоритм деления на трехзначное число. |
Планировать решение учебной задачи: выстраивать алгоритм действий. Воспроизводить по памяти информацию, необходимую для решения учебной задачи. Осуществлять контроль |
|
Задание 2. |
– Найдите частное. |
23166 : 429 = 54 20412 : 378 = 54 64980 : 684 = 95 20319 : 521 = 39 19536 : 444 = 44 36261 : 153 = 237 69471 : 837 = 83 19869 : 537 = 37 957220 : 209 = 4580 |
|
|
Задание 3 |
– Проверьте умножением, правильно ли выполнено деление |
Решение: 162409 : 403 = 403 403 · 403 = 162409 – верно 27336 : 402 = 608 – неверно 608 · 402 = 244416 |
|
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 90–92). Задание 13. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Проверьте, верны ли равенства и неравенства.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 706 + 43 = 749 – верно 270 · 2 : 10 > 54 – неверно 769 – 45 = 724 – верно 880 : 44 · 10 > 100 – верно 45 + 432 = 477 – верно 488 – 135 < 353 – неверно |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
|
Задание 14. |
– Назовите результаты действий. – Какие математические правила вы использовали? |
Выполняют вычисления по цепочке. |
|
|
Задание 15. |
– Приведите пример, опровергающий или подтверждающий высказывание. |
1) Высказывание «Среди ломаных есть замкнутые ломаные» истинно.
|
|
|
|
|
2) Высказывание «Нельзя начертить два пересекающихся луча» ложно.
3) Высказывание «Существуют треугольники с равными сторонами» истинно.
4) Высказывание «Существуют два числа, произведение которых равно 70» истинно. 35 · 2 = 70; 7 · 10 = 70. |
|
|
Задание 16*. |
– В пакете 9 кг крупы. Как с помощью чашечных весов и гирь массой 50 г и 200 г развесить всю крупу в два пакета так, чтобы в одном было 2 кг, а в другом 7 кг, при условии, что можно сделать только три взвешивания? |
1-е взвешивание: 9 кг крупы разложить в 2 пакета по 4 кг 500 г с помощью весов. 2-е взвешивание: 4 кг 500 г крупы разложить в 2 пакета по 2 кг 250 г с помощью весов. 3-е взвешивание: от 2 кг 250 кг крупы отмерить 250 г с помощью гирь массой 50 г и 200 г. И т. д. |
|
|
Задание 17. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно. |
|
|
Задание 18. |
– Найдите значения выражений. |
Решение: 1070 + 86 · 101 – 2008 – 2116 : 46 = 7702 123 · 60 + 1356 : 12 + 5041 : 71 · 15 · 5 = 12818 190 · 50 – 3283 : 49 + 69046 : 23 = 12435 2491 : 47 + 8364 : 82 – 3094 : 91 = 121 |
|
|
Задание 19 |
– Выполните вычисления. Сделайте записи по образцу |
Решение: 71 – 9 = 71 – 10 + 1 = 61 + 1 = 62 327 + 99 = 327 + 100 – 1 = 427 – 1 = 426 5263 – 999 = 5263 – 1000 + 1 = 4263 + 1 = 4264 |
|
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Осуществлять итоговый контроль |
Урок 103. Порядок действий. Деление на трёхзначное число
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного деления на трехзначное число; способствовать формированию умений выполнять деление многозначного числа на двузначное и трехзначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на трехзначное число; научатся применять алгоритм письменного деления на трехзначное число; объяснять выполнение деления многозначного числа на двузначное и трехзначное число |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной форме. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учёта интересов сторон и сотрудничества |
Личностные: проявляют положительное отношение к школе и учебной деятельности; имеют представление о причинах успеха в учебе; выражают этические чувства (стыда, вины, совести) на основе анализа простых ситуаций |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Подчеркните первое неполное делимое и количество цифр в частном:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: 64218 : 36 – четыре цифры в частном 783104 : 608 – четыре цифры в частном 5931027 : 8691 – три цифры в частном 40075 : 86 – три цифры в частном |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 89). Задание 4. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Найдите значения выражений. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Решение: 1) (1494 + 1854) : (1104 – 1077) · 378 = 46872 2) 27463 · 0 + 37400 : 136 = 275 3) (76114 : 19 – 3928) · 751 + 60521 = 119099 4) 166842 : 207 · 207 = 166842 5) 203 · 604 – 140904 : 456 + 0 : 33987 = = 122303 6) (87147 : 207 – 87527 : 803) · 312 = 97344 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
|||||||||||||||||||||||||||||||
|
Задание 5. |
– Составьте выражения и найдите их значения. |
Решение: 1) (13479 + 16397) : (1276 – 968) = 97 2) (14374 – 13389) · (9300 : 372) = 24625 |
||||||||||||||||||||||||||||||||
|
Задание 6 |
– Повторите алгоритм деления многозначного числа на трехзначное число. – Выполните деление |
Решение: 230202 : 378 = 609 84854 : 406 = 209 32922 : 279 = 118 460756 : 508 = 907 2231100 : 670 = 3330 4087140 : 102 = 40070 631350 : 305 = 2070 529156 : 503 = 1052 |
||||||||||||||||||||||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 91–93). Задание 17. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Применять правила делового сотрудничества. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||||||||||
|
– По какому правилу расположены числа? – Назовите следующие три числа. |
– Каждое следующее число уменьшают на 100. – 15300, 15200, 15100, 15000, 14900, 14800. |
|||||||||||||||||||||||||||||||||
|
Задание 18. |
– Найдите значения выражений. |
Выполняют вычисления. |
||||||||||||||||||||||||||||||||
|
Задание 19. |
– Выполните устные вычисления. |
Работают самостоятельно. |
||||||||||||||||||||||||||||||||
|
Задание 20. |
– Выполните «подъем в гору», работая в парах. |
Работают в парах. |
||||||||||||||||||||||||||||||||
|
Задание 21*. |
– Сколько путей ведут от озера к лесу, если идти по указанным тропинкам через деревню? |
– Рис. 1 – 3 дороги; рис. 2 – 6 дорог; рис. 3 – 6 дорог; рис. 4 – 9 дорог. |
||||||||||||||||||||||||||||||||
|
Задание 22*. |
– Решите задачу с помощью таблицы.
|
Решение:
|
||||||||||||||||||||||||||||||||
|
Задание 23*. |
– Решите задачу с помощью таблицы.
|
Решение.
|
||||||||||||||||||||||||||||||||
|
Задание 24* |
– Решите задачу с помощью таблицы.
|
Решение.
|
||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Методика «Оценочная лесенка».
|
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 104. Автоматизация навыка деления на трёхзначное число
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного деления на трехзначное число; способствовать формированию умений выполнять деление многозначного числа на двузначное и трехзначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на трехзначное число; научатся применять алгоритм письменного деления на трехзначное число; объяснять выполнение деления многозначного числа на двузначное и трехзначное число |
Метапредметные: Познавательные: осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: умеют прогнозировать, предвосхищать результат и уровень усвоения, его временные характеристики; осуществляют контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона. Коммуникативные: владеют монологической и диалогической формами речи в соответствии с нормами родного языка и современных средств коммуникации |
Личностные: формируют внутреннюю позицию школьника на уровне положительного отношения к школе |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание
деятельности обучающегося |
Формируемые способы деятельности обучающегося |
||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний. – Узнайте, каким мог быть делитель. Помните о «ловушках»:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Определяют делитель:
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||
|
Задачи. |
‒ Решите задачу. а) За сутки из неисправного крана утекает 27 л воды. За сколько суток из крана утечет 108 л воды? Сколько литров воды утечет за сутки из 20 неисправных кранов? б) В двух бочках было 60 л воды. Когда из одной бочки взяли 12 л, то воды в бочках осталось поровну. Сколько литров воды было в каждой бочке сначала? |
Решение: а) За 4 дня из крана утечет 108 л воды. 540 литров воды утечет за сутки из 20 неисправных кранов.
б) 24 литра и 36 литров было в бочке сначала.
|
|||||||||||||
|
Геометрический материал |
– Из кубиков составлены две фигуры. Объем кубика – 1 дм3. – Чему равен объем каждой фигуры?
|
Ответ: 14 дм3, 90 дм3 |
|||||||||||||
|
III. Открытие нового знания, способа действия. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
||||||||||||
|
Работа по учебнику (с. 89). Задание 7. |
– Найдите значение выражения 17940 : у. |
Решение: Если у = 115, то 17940 : 115 = 156. Если у = 345, то 17940 : 345 = 52. Если у = 690, то 17940 : 690 = 26. |
|||||||||||||
|
Задание 8. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько часов самолет был в пути? |
Запись: s = 1900 км u = 950 км/ч t – ? ч Решение: t = s : u t = 1900 : 950 = 2 (ч). |
|||||||||||||
|
Задание 9 |
– Прочитайте задачу. – Составьте выражение для решения этой задачи. – Выполните вычисления, если а = 2479 |
Решение: а – 160 · 7. Если а = 2479, то 2479 – 160 · 7 |
|||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 93–94). Задание 25. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Как называются числа и результаты действий при сложении, вычитании, умножении и делении? Прочитайте равенства и скажите, как называется каждое из чисел. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Читают равенства и называют каждое из чисел. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||
|
Задание 26. |
– Как называются неизвестные числа в равенствах? – Выполните вычисления. Сделайте проверку. |
Решение: 1) 200 – 127 = 73 760 + 53 = 813 73 + 127 = 200 813 – 53 = 760 3) 480 : 6 = 80 120 · 5 = 600 80 · 6 = 480 600 : 5 = 120 5) 92 + 350 – 92 = 258 79 – 6 = 73 92 + 258 = 350 79 – 73 = 6 7) 150 · 900 : 150 = 6 300 : 50 = 6 150 · 6 = 900 300 : 6 = 50 |
|||||||||||||
|
Задание 27. |
– Запишите предложение в виде равенства. Вычислите неизвестное число, обозначенное буквой. |
Решение: 1) 86 + b = 109 2) 250 – у = 7 b = 109 – 86 у = 250 – 7 b = 23 у = 143 3) х – 9 = 999 4) п : 10 = 10 х = 999 + 9 п = 10 · 10 х = 1018 п = 100 |
|||||||||||||
|
Задание 28. |
– Сумму чисел 4000 и 1000 уменьшите в 100 раз и результат увеличьте на 200. Сколько получилось? |
Решение: (4000 + 1000) : 100 + 200 = 5000 : 100 + 200 = 250. |
|||||||||||||
|
Задание 29 |
– Выполните задание самостоятельно. Запишите результат. проведите взаимопроверку в парах |
Работают самостоятельно, проводят взаимопроверку в парах |
|||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Знаковая символика:
|
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 105. Закрепление навыка деления на трёхзначное число
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: создать условия для повторения алгоритма письменного деления на трехзначное число; способствовать формированию умений выполнять деление многозначного числа на двузначное и трехзначное число |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом письменного деления на трехзначное число; научатся применять алгоритм письменного деления на трехзначное число; объяснять выполнение деления многозначного числа на двузначное и трехзначное число |
Метапредметные: Познавательные: осуществляют анализ, сравнение, классификацию объектов; воспроизводят по памяти информацию, необходимую для решения учебной задачи. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: формулируют собственное мнение и позицию; строят понятные для партнера высказывания; умеют задавать вопросы |
Личностные: приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности учебной |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя по материалу прошлого урока. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||
|
– Решите «математические цепочки»:
|
Выполняют задания устного счета.
|
|||||||||
|
– Запишите в тетради получившиеся ответы. – На какие группы можно разделить полученные числа?
– Запишите числа в порядке убывания. |
Запись: 52, 36, 4, 54, 47, 160. – 1-й вариант: четные и нечетные числа. – 2-й вариант: однозначные, двузначные и трехзначные числа. Запись: 160, 54, 52, 47, 36, 4. |
|||||||||
|
Задача |
– Решите задачу. Чемпионом по бегу среди животных является гепард. Его скорость равна 112 км/ч. На втором месте – черный олень. Его скорость равна 104 км/ч. Сколько километров пробежит гепард за 30 минут? Сколько метров пробежит черный олень за полчаса? |
Решение: 56 километров пробежит гепард за 30 минут. 52 метра пробежит черный олень за полчаса |
||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 90). Задание 10. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу.
– На сколько метров сатина меньше, чем ситца? Во сколько раз ситца больше, чем сатина? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Запись:
Решение: 1) 135 · 5 = 675 (м) – ситца. 2) 25 · 9 = 225 (м) – сатина. 3) 675 – 225 = 450 (м) – меньше сатина. 4) 675 : 225 = 3 (раза) – больше ситца. Ответ: на 450 м меньше; в 3 раза больше. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
|||||||
|
Задание 11 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько времени затратил самолет на весь рейс? |
Запись:
Решение: 1) 3820 : 955 = 4 (ч) – пролетел 3820 км. 2) 1900 : 950 = 2 (ч) – пролетел 1900 км. 3) 4 + 2 = 6 (ч) – время полета |
||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 94–95). Задание 30. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– В котором часу автобус отошел от места остановки? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 8 ч 48 мин + 35 мин + 8 мин = 9 ч 31 мин. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять актив-ность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||
|
Задание 31*. |
– Какую скорость набрал поезд в пути? Выразите её в километрах в час. |
Решение: 80 · 15 = 1200 (м/мин); 1200 м/мин = 72 км/ч |
||||||||
|
Задание 32*. |
– За какое время вагонетка проедет путь? |
Запись: u = 10 м/с s = 3 км t – ? Решение: 3 км = 3000 м; 3000 : 10 = 300 с; 300 с = 5 мин. |
||||||||
|
Задание 33*. |
– Какое из двух облаков движется быстрее? |
Решение: 1) 120 м/мин = 12000 см/мин. 2) 12000 : 60 = 200 (см/с) – скорость первого облака. 200 см/с > 120 см/с. Ответ: скорость первого облака больше. |
||||||||
|
Задание 34. |
– Рассмотрите таблицу. Ответьте на вопросы. – Сколько игроков в команде? – Сколько игроков носит спортивную форму 44 размера? 46 размера? 48 размера? – Кто из игроков носит обувь 40 размера? 39 размера?
– Есть ли футболисты, которые носят обувь 38 размера? 41 размера? – У кого из игроков самый большой размер обуви? – Какой размер формы и обуви у Цветкова, Смирнова, Ершова?
– Кто носит форму 48 размера и обувь 40 размера?
– У кого размер формы 46, а обуви 42? – У кого из игроков одинаковый размер обуви?
– У кого из игроков одинаковый размер формы? |
Решение: – 11 игроков в команде. – 3 игрока носят спортивную форму 44 размера, 4 игрока – 46 размера, 4 игрока – 48 размера. – Иванов, Петров, Рыбкин, Крылов носят обувь 40 размера. Цветков, Сорокин, Белов – 39 размера. – Нет футболистов, которые носят обувь 38 размера. Степанов носит обувь 41 размера. – У Скворцова и Смирнова самый большой размер обуви. – У Цветкова размер формы 48, обуви – 39; у Смирнова размер формы 48, обуви – 42; у Ершова размер формы 44, обуви – 39. – Рыбкин носит форму 48 размера и обувь 40 размера. – У Скворцова размер формы 46, а обуви – 42. – У Цветкова, Сорокина, Ершова, Белова размер обуви 39. У Иванова, петрова, Рыбкина, Крылова – размер обуви 40. У Скворцова, Смирнова – размер обуви 42. – У Иванова, Сорокина, Ершова – размер формы 44. У Скворцова, Петрова, Белова, Крылова – размер формы 46. У Цветкова, Степанова, Рыбкина, Смирнова – размер формы 48. |
||||||||
|
Задание 35. |
– Рассмотрите рисунок в учебнике. На какие две группы можно разделить данные фигуры? |
1-я группа: конусы. 2-я группа: пирамиды. |
||||||||
|
Задание 36 |
– Вычислите площадь футбольного поля, указав ее наибольшее и наименьшее значения |
Решение: Наименьшая площадь: 100 · 69 = 6900 (м2). Наибольшая площадь: 110 · 75 = 8258 (м2) |
||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 106. Деление отрезка на 2, 4, 8 равных частей с помощью циркуля и линейки
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений измерять длину отрезка и строить отрезки заданной длины; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся выполнять решение практических задач, связанных с делением отрезка на равные части, с использованием циркуля и линейки |
Метапредметные: Познавательные: осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: излагают своё мнение и аргументируют свою точку зрения |
Личностные: осознают необходимость самосовершенствования |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения |
|
|
– Выполните сравнение величин, поставьте знаки: >, < или =. 18 кг 25 г … 18250 г 4 ч 5 мин … 240 мин 18 т 25 кг ... 18025 кг 4 ч 50 мин ... 450 мин 18 ц 25 кг ... 1825 кг 4 ч 3 мин ... 240 мин 18 ц 25 кг ... 18250 кг 4 мин 3 с ... 270 с 18 ц 250г ... 1825 г 4 мин 30 с ... 270 с |
Решение: 18 кг 25 г < 18250 г 4 ч 5 мин > 240 мин 18 т 25 кг = 18025 кг 4 ч 50 мин < 450 мин 18 ц 25 кг = 1825 кг 4 ч 3 мин > 240 мин 18 ц 25 кг < 18250 кг 4 мин 3 с < 270 с 18 ц 250 г > 1825 г 4 мин 30 с = 270 с |
|||
|
– Из следующих математических записей выберите уравнения: а) х · 7 = 63 г) а + 15 = 40 б) у + 3 · 8 д) у – 20 > 60 в) 25 · (653 – 299) е) 15 + 16 · 2 – Устно вычислите корни данных уравнений. |
Решение:
Ответ: а) |
|||
|
– Запишите верные равенства, вставив пропущенные цифры. 3636 4540 |
Решение: 36365 : 5 = 7273 80309 · 9 = 722781 45400 : 5 = 9080 30027 · 5 = 150135 |
|||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 97). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Как выполнил задание каждый из учеников? – Кто выполнил задание правильно? Проверьте, используя циркуль. – Какую ошибку допустила Катя? Какую ошибку допустил Саша? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Маша выполнила задание правильно.
– Катя допустила ошибку: радиусы окружностей должны быть больше половины отрезка. Саша допустил ошибку: радиусы окружностей должны быть равны. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Применять правила делового сотрудничества. Осуществлять контроль по результату |
|
|
Задание 2 |
|
Алгоритм деления отрезка на 2 равные части: – Из концов отрезка А и В при помощи циркуля проведите две ду-ги окружности радиуса R. Радиус окружности сделайте несколь-ко большим половины отрезка АВ. Доведите дуги до взаимного пересечения. Таким образом вы получите точки C и D, равноудаленные от отрезка АВ. Проведите через точки С и D прямую линию, пересекающую отрезок АВ. Точка пересечения этой линии и отрезка будет искомой точкой О, в которой отрезок АВ разделяется на две равные части |
||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
|
|
Работа по учебнику (с. 98–100). Задание 6. |
– Не выполняя указанных вычислений, определите, больше или меньше числа 100 результаты действий. |
Решение: 2475 – 876 больше 1000 903 · 20 больше 1000 603 + 495 больше 1000 427 : 70 меньше 1000 |
||
|
Задание 7. |
– Ответьте на вопросы. – Во сколько раз 1 кг больше 100 г?
– Во сколько раз 1 ц меньше 1 т?
– Во сколько раз 1 ц больше 10 кг? |
Ответы: – В 10 раз 1 кг больше 100 г. 1 кг = 1000 г, 1000 г : 100 г = 10 (раз). – В 10 раз 1 ц меньше 1 т. 1 т = 10 ц; 10 ц : 1 ц = 10 (раз). – В 10 раз 1 ц больше 10 кг. 1 ц = 100 кг; 100 кг : 10 кг = 10 (раз). |
||
|
Задание 8. |
– Какое свойство умножения выражает каждое равенство? – Сформулируйте каждое свойство. |
Объясняют каждое равенство: 1) 324 · 17 = 17 · 324. џ От перестановки множителей значение произведения не изменяется. 2) (12 · 8) · 30 = 12 · (8 · 30). џ Сочетательный закон умножения относительно сложения. 3) (165 + 38) · 70 = 165 · 70 + 38 · 70. Чтобы умножить сумму на число, надо каждое слагаемое умножить на это число, полученные результаты сложить. Это распределительное свойство умножения относительно сложения. |
||
|
Задание 9. |
– Составьте задачу и решите её двумя способами. |
Запись: Всего – 3600 пар Детская обувь – ? пар, три четверти Женская – ? пар Решение: I способ 1) 3600 : 4 · 3 = 27000 (пар) – детской обуви. 2) 3600 – 2700 = 900 (пар) – женской обуви. II способ 1) Какую часть составляет женская обувь? (Одну четвертую часть.) 2) 3600 : 4 · 1 = 900 (пар) – женской обуви. |
||
|
Задание 10. |
– Сколько рублей стоит книга? |
Решение: 36 + 36 : 3 · 2 = 36 + 24 = 60 (р.) – стоит книга. |
||
|
Задание 11. |
– Ответьте на вопросы, используя данные таблицы. – На сколько граммов литр нефти тяжелее литра керосина?
– Чему равна масса 2 л ртути? |
– На 40 граммов литр нефти легче литра керосина. 840 – 800 = 40 (г). – 27 кг 200 граммов весят 2 л ртути. 13 кг 600 г · 2 = 27 кг 200 г. |
||
|
|
– Что легче: 2 л бензина или 1 л ртути?
– Во сколько раз масса 80 л морской воды больше массы 1 л керосина? |
– Легче 1 л ртути. 690 г · 2 = 1380 г = 13 кг 800 г; 13 кг 800 г > 13 кг 600 г. – В 125 раз масса 80 л морской воды больше массы 1 л керосина. 1 кг 250 г · 80 = 100000 г, 100000 г : 800 г = 125 (раз). |
||
|
Задание 12 |
– Составьте выражения и найдите их значения |
Решение: 1) 3407 + 19007856 = 19011263 2) 1010203 – 998877 = 11326 3) 196 · 408 = 79968 4) 123140 : 524 = 235 |
||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Как разделить отрезок на 2 равные части? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 107. Решение практических задач, связанных с делением
отрезка на две части. Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений измерять длину отрезка и строить отрезки заданной длины; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся выполнять решение практических задач, связанных с делением отрезка на равные части, с использованием циркуля и линейки |
Метапредметные: Познавательные: понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи. Регулятивные: умеют прогнозировать, предвосхищать результат и уровень усвоения, его временные характеристики; осуществляют контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения; считаются с мнением другого человека; проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности) |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний. – Вставьте пропущенные числа, чтобы равенства были верными. 420 · 840 : 290 + 666 – |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: 420 · 2 = 840 333 · 3 = 999 840 : 4 = 210 5000 : 5 = 1000 290 + 210 = 500 224 + 376 = 600 666 – 427 = 239 827 – 127 = 700 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|||||||||
|
Интеллектуальная разминка. |
Задание на смекалку. Поросята Ниф-Ниф и Нуф-Нуф бежали от волка к домику Наф-Нафа. Волку бежать до поросят (если бы они стояли на месте) 4 минуты. Поросятам бежать до домика Наф-Нафа 6 минут. Волк бежит в 2 раза быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа? |
Ответ: волк будет бежать 7 минут. Поросята успеют. |
||||||||||
|
Геометрический материал |
– Сколько отрезков на чертеже?
|
Решение: 12 отрезков на чертеже
|
||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 98). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Разделите произвольный отрезок на 2 равные части с помощью циркуля и линейки. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Делят произвольный отрезок на 2 равные части с помощью циркуля и линейки. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость |
|||||||||
|
Задание 4. |
– Составьте алгоритм деления отрезка на 4 части и на 8 равных частей с помощью циркуля и линейки. |
Делят отрезок на 4 части и на 8 равных частей с помощью циркуля и линейки.
|
||||||||||
|
Задание 5 |
– Выполните задание самостоятельно, проведите взаимопроверку в парах |
Работают самостоятельно в парах |
||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 100–102). Задание 13. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Найдите значения выражений. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Выполняют задание (см. ресурсный материал к уроку). |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||
|
Задание 14. |
– Вычислите неизвестное число. а) 605 : в) |
Решение: а) 605 : 5 = 121 б) 19056 – 7056 = 12000 в) 12 · 75 = 900 г) 30010 – 29921 = 89 |
||||||||||
|
Задание 15. |
– Истинно или ложно высказывание? |
Решение: 1) истинно; 2) истинно; 3) ложно; 4) истинно; 5) ложно; 6) истинно. |
||||||||||
|
Задание 16. |
– Не выполняя вычислений, запишите выражения в порядке увеличения их значения. |
Запись: 2 · 1100; 1100 · 4; 6 · 1100; 8 · 1100; 1100 · 9; 10 · 1100. |
||||||||||
|
Задание 17. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Выполните вычисления. – С какой скоростью бежал Петя? |
Запись:
Решение: 1) 540 : 2 = 270 (м/мин) – скорость сближения. 2) 270 – 150 = 120 (м/мин) – скорость Пети. |
||||||||||
|
Задание 18. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно. 8 · 10000 = 80000 1000 : 1000 = 1 50 · 10000 = 500000 85000 : 1000 = 85 32 · 10000 = 320000 124000 : 1000 = 124 100 · 10000 = 1000000 2400000 : 1000 = 24000 |
||||||||||
|
Задание 19. |
– Петя съел несколько порций мороженого и заболел. Врач выписал ему лекарство от кашля: в упаковке 20 таблеток по 50 мг лекарства в каждой. Сколько граммов лекарства в этой упаковке? |
Решение: 50 · 20 = 1000 (мг) ‒ в упаковке. 1000 мг = 1 г. |
||||||||||
|
Задание 20. |
– Дима, Коля и Таня по очереди помогают маме убирать квартиру. Рассмотрите таблицу и ответьте на вопросы. – В какие дни дежурит каждый из детей?
– Кто убирает квартиру в среду, кто – во вторник?
– В какой день все дети отдыхают? – В какие дни помогают маме мальчики? |
– Дима дежурит в понедельник, четверг. Коля – во вторник, пятницу. Таня – в среду, субботу. – Таня убирает квартиру в среду, Коля – во вторник. – В воскресенье все дети отдыхают. – В понедельник, вторник, четверг, пятницу маме помогают мальчики. |
||||||||||
|
Задание 21. |
– Рассмотрите частные. Прежде чем вычислять, прикиньте, сколько цифр будет в частном. |
Решение: 1384 : 4 = три цифры 48006 : 6 = четыре цифры 9306 : 9 = четыре цифры 50250 : 5 = пять цифр |
||||||||||
|
Задание 22 |
– Рассмотрите умножение в столбик. Объясните ошибки в записях |
– В первой записи – неверно выполнено умножение; во второй записи – неверно записано второе неполное произведение, в третьей записи – нет второго неполного произведения, в четвертой записи – потеряли ноль |
||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
|
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи |
Ресурсный материал к уроку
Задание 13.
|
2912 : 8 + 1200 : 300 – 1 · 144 : 12 = 356 |
(207 · 304 – 12967 + 3072 : 24) · 0 = 0 102867 – 867 · 90 + 57000 : 380 = 24987 |
(51855 + 9857) : 532 : 58 : 2 · 10000 = 10000 |
Урок 108. Контрольная работа № 7 по теме «Деление на двузначное число»
|
Тип урока: контроль знаний и способов действий |
||
|
Педагогические задачи: проверить умения делить многозначное число на двузначное, решать задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять правило деления суммы на число; объяснять использование свойств арифметических действий при выполнении вычислений; выполнять деление многозначного числа на однозначное, двузначное и трехзначное число; решать арифметические задачи |
Метапредметные: Познавательные: строят логическую цепь рассуждений; проводят аналогии между изучаемым материалом и собственным опытом; формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера. Регулятивные: осуществляют коррекцию, вносят необходимые дополнения и коррективы в план и способ действия в случае расхождения эталона, реального действия и его результата, с учетом оценки этого результата самим обучающимся, учителем, товарищами. Коммуникативные: контролируют действия партнера |
Личностные: имеют желание учиться; понимают причину успеха/неуспеха учебной деятельности и конструктивно действуют в ситуации неуспеха |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
I. Содержание контрольной работы. |
Знакомит с содержанием контрольной работы, комментирует задания. |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
|
Вариант 1 |
1. Решите задачу: Три дня ученик читал по 45 страниц в день, а потом ещё 50 страниц. Сколько страниц осталось ему прочитать, если в книге 300 страниц? |
1. Решение: 1) 45 · 3 = 135 (с.) – прочитал за 3 дня. 2) 135 + 50 = 185 (с.) – прочитал всего. 3) 300 – 185 = 115 (с.) – осталось прочитать. |
|
|
2. Выполни действия: 11016 : 27 481 : 13 2052 : 19 12096 : 56 16533 : 33 3. Вычисли значение выражения: 2603 · 58 + (1000000 –19975): 75 4. Площадь участка 156 м2. Ширина участка – 12 м. Чему равна длина этого участка? 5. Реши уравнение: 204 · 500 – х = 390 |
2. Ответы: 408 37 108 216 501
3. Ответ: 164041. 4. Ответ: длина участка 13 м.
5. Ответ: х = 101610 |
||
|
Вариант 2 |
1. Решите задачу: Пять дней магазин продавал по 65 м шёлка, а потом продал ещё 300 м. Сколько метров осталось продать, если всего было 1000 м шёлка? 2. Выполни действия: 5070 : 78 12502 : 14 15652 : 26 529 : 23 26334 :19 3. Вычисли значение выражения: 16095 : 15 + (940 · 70 – 7948) 4. Площадь участка 224 м². Длина участка 16 м. Чему равна ширина этого участка? 5. Реши уравнение: 701 · 200 – х = 920 |
1. Решение: 1) 65 · 5 = 325 (м) – шелка продал за 5 дней. 2) 325 + 300 = 625 (м) – продал всего. 3) 1000 – 625 = 375 (м) – осталось продать. 2. Ответы: 65 893 602 23 1386 3. Ответ: 58925. 4. Ответ: ширина участка 14 м.
5. Ответ: х = 139280 |
|
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 109. Нахождение неизвестного числа в равенствах вида: х + 5 = 7
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для развития умений решать равенства вида: х + 5 = 7, х · 5 = 15, х – 5 = 7, х : 5 = 15; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с алгоритмом решения уравнения: разбивкой выражения, записанного в одной или обеих частях уравнения, на части; научатся применять алгоритм решения уравнения: разбивка выражения, записанного в одной или обеих частях уравнения, на части; выполнять упрощение выражений; находить неизвестный компонент арифметических действий |
Метапредметные: Познавательные: умеют ориентироваться в тексте задачи, находят ответы на вопросы в тексте, иллюстрациях; делают выводы в результате совместной работы класса и учителя. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: имеют желание учиться; осознают необходимость самосовершенствования; понимают значение границ собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Подчеркните первое неполное делимое и определите количество цифр в частном.
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение:
318 : 3 = три цифры 816 : 8 = три цифры 675 : 5 = три цифры 927 : 9 = три цифры 1804 : 4 = три цифры 2121 : 7 = три цифры |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу |
|||||||||
|
Задание на смекалку |
а) Написано 99 чисел: 1, 2, 3, ... , 98, 99. Сколько раз в записи встречается цифра 5? б) Сколько всего двузначных чисел? |
Решение: а) 5, 15, 25, 35, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 65, 75, 85, 95. Получается 19 раз. б) Всего 90 двузначных чисел |
||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 103–104). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Как можно вычислить неизвестное первое слагаемое? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно вычислить неизвестное первое слагаемое. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии |
|||||||||
|
Задание 2. |
– Какое действие надо выполнить, чтобы найти неизвестное первое слагаемое в каждом из равенств? – Сформулируйте правило для нахождения неизвестного первого слагаемого. |
– Надо выполнить вычитание, чтобы найти неизвестное первое слагаемое в каждом из равенств. џ Чтобы найти неизвестное первое слагаемое, надо из суммы вычесть второе слагаемое. |
||||||||||
|
Задание 3. |
– Пользуясь правилом, найдите неизвестное первое слагаемое. |
Решение: х + 7006 = 89400 у + 12345 = 31006 х = 89400 – 7006 у = 31006 – 12345 х = 82394 у = 18661 |
||||||||||
|
Задание 4. |
– Запишите каждое предложение в виде равенства. Найдите неизвестное число. |
1) х + 7050 = 7153 2) а + 316 = 2004 х = 7153 – 7050 а = 2004 – 316 х = 103 а = 1688 |
||||||||||
|
Задание 5. |
– Какое число задумал Дима? |
Решение: х + 1217 = 1500 х = 1500 – 1217 х = 283 |
||||||||||
|
Задание 6. |
– Какое число задумала Катя? |
Решение: х + 75 = 1500 х = 1500 – 75 х = 1425 |
||||||||||
|
Задание 7 |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – сколько рыбок было в аквариуме? |
Запись: Было – х р. Пустили – 8 р. Стало – 15 р. Решение: х + 8 = 15 х = 15 – 8 х = 7 (р.) – было в аквариуме |
||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 108). Задание 26. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием. Преобразовывать модели |
|||||||||
|
Задание 27. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – сколько часов самолет был в пути? |
Запись: s = 3800 км u = 950 км/ч t – ? Решение: 3800 : 950 = 4 (ч) – был в пути. |
||||||||||
|
Задание 28 |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – Какой из участков имеет бо́льшую площадь и на сколько? |
Запись:
Решение: 1) 32 : 2 = 16 (м) – ширина 2-го участка. 2) 20 · 3 = 60 (м) – длина 2-го участка. 3) 60 · 16 = 360 (м2) – площадь 2-го участка. 4) 32 · 20 = 640 (м2) – площадь 1-го участка. 5) 640 – 360 = 280 (м2) – больше площадь 1-го участка |
||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 110. Тема: Нахождение неизвестного числа в равенствах вида: х · 5 = 15
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: создать условия для развития умений решать равенства вида: х + 5 = 7, х · 5 = 15, х – 5 = 7, х : 5 = 15; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять правила нахождения неизвестных компонентов арифметических действий (первого слагаемого, первого множителя, уменьшаемого и делимого); находить неизвестный компонент арифметических действий |
Метапредметные: Познавательные: строят логическую цепь рассуждений; проводят аналогии между изучаемым материалом и собственным опытом; формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями её реализации. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: устанавливают связь между целью учебной деятельности и ее мотивом (между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется); задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Найдите значения выражений: 21147 : 7 48168 : 8 15550 : 5 565656 : 56 727272 : 72 818181 : 81 |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
Решение: 21147 : 7 = 3021 48168 : 8 = 6021 15550 : 5 = 3110 565656 : 56 = 10101 727272 : 72 = 10101 818181 : 81 = 10101 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой |
|
Интеллектуальная разминка. |
– Вставьте пропущенные цифры. 1748 : 23 = 9522 : 46 = 65088 : 72 = |
Решение: 1748 : 23 = 76 7147 : 7 = 1021 9522 : 46 = 207 812 : 4 = 203 65088 : 72 = 904 9018: 9 = 1002 |
|
|
Геометрический материал |
– В квадрате проведены два отрезка, соеди- няющих противоположные вершины. Сколько всего получилось треугольников?
|
Запись: Получилось 8 треугольников |
|
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 104–105). Задание 8. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Объясните, как можно найти неизвестный первый множитель. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно найти неизвестный первый множитель. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Осуществлять контроль по результату |
|
Задание 9. |
– Какое действие надо выполнить, чтобы найти неизвестный первый множитель? – Сформулируйте правило для нахождения неизвестного первого множителя. |
– Надо выполнить деление, чтобы найти неизвестный первый множитель. џ Чтобы найти неизвестный первый множитель, надо произведение разделить на второй множитель. |
|
|
Задание 10. |
– Используя правило, найдите неизвестный первый множитель. |
Решение: х · 38 = 36480 у · 4 = 8060 х = 36480 : 38 у = 8060 : 4 х = 960 у = 2015 |
|
|
Задание 11. |
– Запишите предложение в виде равенства. |
Решение: 1) t · 107 = 22042 2) т · 50 = 18200 t = 22042 : 107 т = 18200 : 50 t = 206 т = 364 |
|
|
Задание 12. |
– Какое число задумал Юра? |
Решение: х · 365 = 44530 х = 44530 : 365 х = 122 |
|
|
Задание 13. |
– Какое число задумал Коля? |
Решение: х · 25 = 625000 х = 625000 : 25 х = 25000 |
|
|
Задание 14 |
– Выполните задание самостоятельно, проведите взаимопроверку в парах |
Работают самостоятельно |
|
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 108–109). Задание 29. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Сколько деталей должен изготовить токарь за месяц? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) 23 · 8 = 184 (дет.) – изготовил токарь за 8 дней. 2) 184 · 3 = 552 (дет.) – должен изготовить токарь за месяц. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Осуществлять взаимный контроль, планировать способы взаимодействия |
|
Задание 30. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько зерна отправили на мельницу? |
Запись: Было – 18234 кг зерна Разгрузили – 3 дня по ? кг Отправили – ? кг, половину Решение: 1) 18234 : 3 = 6078 (кг) – разгружали каждый день. 2) 6078 : 2 = 3039 (кг) – отправили на мельницу. |
|
|
Задание 31. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какое расстояние будет между поездами за 1 ч до встречи? |
Решение: 65 + 55 = 120 (км) – расстояние между поездами за час до встречи. |
|
|
Задание 32 |
– Вычислите четверть данных чисел.
– Вычислите пятую часть данных чисел.
– Вычислите сотую часть данных чисел.
– Вычислите тысячную часть данных чисел |
Вычисляют четверть числа: 80 : 4 = 20 164 : 4 = 41 160 : 4 = 40 200 : 4 = 50 Вычисляют пятую часть числа. 500 : 5 = 100 60 : 5 = 12 150 : 5 = 30 25 : 5 = 5 Вычисляют сотую часть числа. 300 : 100 = 3 1800 : 100 = 18 66000 : 100 = 660 Вычисляют тысячную часть числа. 24000 : 1000 = 24 240000 : 1000 = 240 |
|
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 111. Нахождение неизвестного числа в равенствах вида: х – 5 = 7
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для развития умений решать равенства вида: х + 5 = 7, х · 5 = 15, х – 5 = 7, х : 5 = 15; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять правила нахождения неизвестных компонентов арифметических действий (первого слагаемого, первого множителя, уменьшаемого и делимого); объяснять нахождение неизвестного компонента арифметических действий |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая), и преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний. – Найдите первое неполное делимое; определите количество цифр в частном.
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: 37545 : 5 = четыре цифры в частном 67248 : 12 = четыре цифры в частном 13876 : 43 = три цифры в частном 5976405 : 128 = пять цифр в частном |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения |
||||
|
Интеллектуальная разминка. |
– Вставьте пропущенные цифры, чтобы равенства были верными. 1326 : 13 = 2515 : 5 = 5656 : 7 = 515 : 5 = |
Решение:
1326 : 13 = 102 7280 : 14 = 520 2515 : 5 = 503 5656 : 7 = 808 728 : 14 = 52 515 : 5 = 103 |
|||||
|
Задание на смекалку |
Геологи нашли 7 камней, массы которых 1, 2, 3, 4, 5, 6 и 7 кг. Эти камни разложили в четыре рюкзака так, что в каждом рюкзаке масса камней была одинаковая. Как это сделали? |
Решение: Рюкзак № 1 – камень 7 кг; рюкзак № 2 – камень 6 кг и камень 1 кг; рюкзак № 3 – камень 5 кг и камень 2 кг; рюкзак № 4 – камень 4 кг и камень 3 кг |
|||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 106–107). Задание 15. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Объясните, как можно найти неизвестное уменьшаемое. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно найти неизвестное уменьшаемое |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Осуществлять контроль по результату |
||||
|
Задание 16. |
– Какое действие надо выполнить, чтобы найти неизвестное уменьшаемое? – Сформулируйте правило для нахождения неизвестного уменьшаемого. |
– Надо выполнить сложение.
џ Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. |
|||||
|
Задание 17. |
– Используя правило, вычислите уменьшаемое. |
Решение: а) а – 24056 = 100000 в) т – 3356 = 476 а = 100000 + 24056 т = 3356 + 476 а = 124056 т = 3832 б) у – 339 = 18 г) п – 12758 = 6907 у = 339 + 18 п = 12758 + 6907 у = 357 п = 19665 |
|||||
|
Задание 18. |
– Запишите предложения в виде равенства. – Выполните взаимопроверку в парах. |
Решение: 1) п – 7777 = 896 2) у – 509871 = 18059 п = 7777 + 896 у = 509871 + 18059 п = 8673 у = 527930 |
|||||
|
Задание 19. |
– Найдите задуманное число. |
Решение: х – 5627 = 12996 х = 12996 + 5627 х = 18623 |
|||||
|
Задание 20 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько воды было в бочке? |
Запись: Было – х л. Взяли – 75 л Осталось – 125 л Решение: х – 75 = 125 х = 125 + 75 х = 200 (л) |
|||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 109). Задание 33. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Составьте выражения и найдите их значения. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 328 + 414 : 46 = 328 + 9 = 337 901 – 16 · 15 = 901 – 240 = 661 30 · 9 – (68 + 127) = 270 – 195 = 75 (627 + 373) : (250 : 50) = 1000 : 5 = 200 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Планировать способы взаимодействия |
||||
|
Задание 34. |
– Не выполняя вычислений, объясните, почему верно неравенство 2568 – 395 > 2568 – 593. |
– Уменьшаемое в левой и правой части неравенства одинаковое и равно числу 2568. Вычитаемое в левой части меньше, чем вычитаемое в правой части, значит, левая часть неравенства будет больше, так как при вычитании меньшего числа разность получается больше. |
|||||
|
Задание 35 |
– Докажите, что при а, равном числу 315, верно равенство (3685 + а) : 200 = 20. |
Решение: (3685 + 315) : 200 = 20 – верно. |
|||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Как найти неизвестное уменьшаемое? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Осуществлять итоговый контроль, оценивать результаты деятельности |
Урок 112. Нахождение неизвестного числа в равенствах вида: х : 5 = 15
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для развития умений решать равенства вида: х + 5 = 7, х · 5 = 15, х – 5 = 7, х : 5 = 15; способствовать формированию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять правила нахождения неизвестных компонентов арифметических действий (первого слагаемого, первого множителя, уменьшаемого и делимого); объяснять нахождение неизвестного компонента арифметических действий |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: планируют, контролируют и оценивают учебные действия в соответствии с поставленной задачей и условиями её реализации. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: определяют цели, функции участников, способы взаимодействия |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Найдите «лишнюю» величину в каждой строке. а) 91 см, 85 дм, 73 м, 39 м2, 736 мм. б) 36 км, 5 м2, 7 м2, 9 см2, 89 дм2. в) 38 см, 47 дм, 105 м, 13 кг, 608 мм. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: а) 39 м2. б) 36 км. в) 13 кг. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения |
|||||||||||||||||||||||
|
Интеллектуальная разминка |
– Увеличьте каждую величину в 3 раза и заполните таблицу:
|
Запись:
|
||||||||||||||||||||||||
|
|
– Дополните каждую величину до 1 метра: 23 см + 5 дм + |
Решение: 23 см + 77 см = 1 м 15 мм + 985 мм = 1 м 5 дм + 5 дм = 1 м 115 мм + 885 мм = 1 м |
||||||||||||||||||||||||
|
|
– Выразите в километрах и метрах высоту полета самолета ТУ-154: 12 300 м. – Размеры экранов телевизоров указаны в миллиметрах. Выразите их в сантиметрах.
|
Решение: 12 300 м = 12 км 300 м. Ответы: 650 мм = 65 см 230 мм = 23 см 100 мм = 10 см |
||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 107–108). Задание 21. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Объясните, как можно найти неизвестное делимое. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно найти неизвестное делимое. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
|||||||||||||||||||||||
|
Задание 22. |
– Какое действие надо выполнить, чтобы найти неизвестное делимое? – Сформулируйте правило для нахождения неизвестного делимого. |
– Надо выполнить умножение, чтобы найти неизвестное делимое. џ Чтобы найти неизвестное делимое, надо частное умножить на делитель. |
||||||||||||||||||||||||
|
Задание 23. |
– Запишите предложения в виде равенства. Найдите неизвестное число. |
Решение: 1) а : 309 = 309 2) t : 104 = 52 а = 309 · 309 t = 104 · 52 а = 95481 t = 5408 |
||||||||||||||||||||||||
|
Задание 24. |
– Какое число было задумано? |
Решение: х : 65 = 7020 х = 7020 · 65 х = 456300 |
||||||||||||||||||||||||
|
Задание 25 |
– Найдите неизвестное число. |
Решение: х : 4500 = 90 х = 4500 · 90 х = 405000 |
||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 110–112). Задание 36*. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выразите в квадратных сантиметрах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Выполняют задание (см. ресурсный материал к уроку). |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||||||
|
Задание 37*. |
– Выразите в квадратных дециметрах. |
Выполняют задание (см. ресурсный материал к уроку). |
||||||||||||||||||||||||
|
Задание 38. |
– Для каждого из данных чисел назовите ближайшее к нему число, состоящее только из сотен. |
Запись: 597 – 600 899 – 900 305 – 300 112 – 100 489 – 500 999 – 1000 |
||||||||||||||||||||||||
|
Задание 39. |
– Вычислите площадь детали в квадратных сантиметрах. |
Решение (см. ресурсный материал к уроку). |
||||||||||||||||||||||||
|
Задание 40. |
– Рассмотрите построенную диаграмму и ответьте на вопросы. – На сколько минут длиннее стал день 17 февраля по сравнению с 15 февраля?
– На сколько минут длиннее стал день 17 февраля по сравнению с 14 февраля?
– На сколько минут длиннее стал день 17 февраля по сравнению с 12 февраля? |
– На 9 минут длиннее стал день 17 февраля по сравнению с 15 февраля. 9 ч 47 мин – 9 ч 38 мин = 9 мин. – На 14 минут длиннее стал день 17 февраля по сравнению с 14 февраля. 9 ч 47 мин – 9 ч 33 мин = 14 мин. – На 23 минуты длиннее стал день 17 февраля по сравнению с 12 февраля. 9 ч 47 мин – 9 ч 24 мин = 23 мин. |
||||||||||||||||||||||||
|
Задание 41. |
– Прочитайте слова. Что они обозначают? – Прочитайте высказывания. Какое высказывание истинно,а какое – ложно? |
Выполняют задание (см. ресурсный материал к уроку). |
||||||||||||||||||||||||
|
Задание 42. |
– Какова цена шарфика? – Какова стоимость куртки и шарфика? |
Запись:
Решение: 1) 5200 : 100 = 52 (р.) – цена шарфика. 2) 5200 + 52 = 5252 (р.) – стоимость покупки. |
||||||||||||||||||||||||
|
Задание 43 |
– Прежде чем выполнять деление, прикиньте, сколько цифр должно быть в частном |
Решение: 690 : 46 – две цифры в частном. 3040 : 76 – две цифры в частном. 90000 : 45 – четыре цифры в частном. 203700 : 9 – пять цифр в частном |
||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Как найти неизвестный делитель? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Ресурсный материал к уроку
|
Задание 36*. Ответы: 7 дм2 = 700 см2 2 м2 3 дм2 = 20300 см2 21 дм2 = 2100 см2 15 дм2 8 см2 = 1508 см2 6 м2 = 60000 см2 2500 мм2 = 25 см2 9 м2 = 90000 см2 80000 мм2 = 800 см2 Задание 37*. Ответы: 70000 мм2 = 7 дм2 65000 см2 = 650 дм2 90000 мм2 = 9 дм2 60 м2 = 6000 дм2 5200 см2 = 52 дм2 13 м2 = 1300 дм2 |
Задание 39. Решение: 1) 36 · 20 = 720 (см2). 2) 12 · 8 = 96 (см2). 3) 720 – 96 = 624 (см2). |
Задание 41. 1) Высказывание «В словах зима и лето по 4 буквы» – истинно. 2) Высказывание «Нет слов, состоящих из 7 букв» – истинно. 3) Высказывание «Нет слов с буквой в» – ложно. 4) Высказывание «В некоторых словах есть буква с» – истинно. 5) Высказывание «Каждое слово начинается с согласной буквы» – ложно. 6) Высказывание «В слове зима первый звук – мягкий» – истинно. 7) Высказывание «Есть два слова с буквой т» – ложно. 8) Высказывание «В каждом из слов 4 или 5 букв» – истинно. 9) Высказывание «В каждом из слов 5 или 6 букв» – ложно. 10 Высказывание «Каждое слово обозначает время года» – истинно. |
Урок 113. Контрольная работа № 8 по теме «Деление на трёхзначное число»
|
Тип урока: контроль знаний и способов действий |
||
|
Педагогические задачи: проверить знания, умения, навыки обучающихся по теме «Деление на двузначное и трехзначное число» |
||
|
Планируемые результаты |
||
|
Предметные: научатся объяснять выполнение деления многозначного числа на трехзначное число; решать арифметические задачи |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке; прогнозируют результат решения. Коммуникативные: учатся слушать и понимать речь других; признают возможность существования различных точек зрения и права каждого иметь свою |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
I. Содержание контрольной работы. Вариант 1 |
Знакомит с содержанием контрольной работы, комментирует задания.
1. Запиши верные равенства, вставив пропущенные цифры:
2. Используя числа 9, 85146, 766314, составь три верных равенства.
3. Запиши равенство, в котором значение частного – трехзначное число, а делимое в 74 раза больше значения частного. 4. Найди значения частных. 21624 : 8 4168 : 521 1539 : 19 8692 : 164 6912 : 216 123360 : 257 223554 : 318 5. Вычисли неизвестный множитель в равенстве 364 · х = 3640 |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы. 1. Ответы: 2198 : 7 = 314 1442 : 7 = 206 4572 : 9 = 508 4024 : 8 = 503 2157 : 3 = 719 4266 : 6 = 711
2. Ответы: 766314 : 85146 = 9 85146 · 9 = 766314 766314 : 9 = 85146 3. Ответ: 9102 : 74 = 123.
4. Ответы: 2703 8 81 53 32 480 703
5. Ответ: х = 10 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Осуществлять контроль по результату |
|
Вариант 2 |
1. Запиши верные равенства, вставив пропущенные цифры:
2. Используя числа 695184, 99312, 7, запиши три верных равенства.
3. Запиши равенство, в котором значение частного – двузначное число, а делимое в 217 раз больше значения частного. |
1. Ответы: 2848 : 4 = 712 2472 : 8 = 309 2763 : 9 = 307 2184 : 7 = 312 2075 : 5 = 415 3678 : 6 = 613
2. Ответы: 695184 : 99312 = 7 7 · 99312 = 695184 695184 : 7 = 99312 3. Ответ: 2821 : 217 = 13. |
|
|
|
4. Найди значения частных. 351708 : 7 3304 : 472 23278 : 113 37800 : 315 52780 : 26 10682 : 218 171270 : 519 5. Вычисли неизвестный множитель в равенстве 587 · у = 5870 |
4. Ответы: 50244 7 206 120 2030 49 330 5. Ответ: у = 10 |
|
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 114. Угол и его обозначение
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений распознавать и изображать угол; создать условия для совершенствования умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «виды углов», «вершина» и «стороны» угла; научатся определять виды углов, вершину и стороны угла; распознавать и изображать углы, обозначать буквами латинского алфавита; читать обозначения углов |
Метапредметные: Познавательные: осуществляют анализ; устанавливают причинно-следственные связи; строят логическую цепь рассуждений; структурируют знания. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: выстраивают коммуникативно-речевые действия, направленные на учет позиции собеседника, конструктивные способы взаимодействия с окружающими |
Личностные: договариваются с одноклассниками, совместно с учителем о правилах поведения и общения и следуют им |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Соотносить модель и текст задачи |
||||||||
|
– Соедините условия с соответствующими схемами:
|
Запись:
|
||||||||||
|
– Найдите «лишнюю» величину: а) 10 км/ч, 20 км/ч, 30 м/ч, 40 км/ч; б) 8 ч, 9 ч, 12 мин, 10 кг, 11 сут.; в) 77 км, 107 см, 27 т, 97 дм, 57 мм |
Решение: а) 30 м/ч; б) 10 кг; в) 27 т |
||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 113–114). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Рассмотрите рисунок. Какие фигуры здесь изображены? џ Сторонами угла являются два луча, исходящие из одной точки. Эту точку называют вершиной. – Назовите вершину каждого угла. – Назовите стороны каждого угла. – Прочитайте и запишите обозначение каждого угла. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Вершины углов: О; М. – Стороны углов: ОА, ОВ; МК, МС. Читают обозначение каждого угла: 1) Ð АОВ, Ð ВОА; 2) Ð КМС, Ð СМК. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
||||||||
|
Задание 2. |
– Величину угла можно показать, вращая луч на плоскости так, как стрелка часов вращается на циферблате. – Покажите вращением карандаша величину каждого из углов. |
Показывают вращением карандаша величину каждого из углов. |
|||||||||
|
Задание 3 |
– Запишите обозначение каждого угла двумя способами и прочитайте эти обозначения.
– Назовите стороны углов |
Читают обозначение каждого угла двумя способами: 1) Ð АОВ, Ð ВОА; 2) Ð МКС, Ð СКМ; 3) Ð EDР, Ð РDE. – Стороны углов: 1) АО, ВО; 2) МК, СК; 3) ED, PD |
|||||||||
|
IV. Включение нового знания. Работа по учебнику (с. 116–117). Задание 8. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Работают самостоятельно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
||||||||
|
Задание 9. |
– Найдите неизвестное число. |
Решение: а) а – 986 = 3974 д) т · 8 = 50800 а = 3974 + 986 т = 50800 : 8 а = 4960 т = 6350 б) у + 1138 = 4000 е) а · 4 = 4100 у = 4000 – 1138 а = 4100 : 4 у = 2862 а = 1025 в) х – 2765 = 7081 ж) х · 90 = 34200 х = 7081 + 2765 х = 34200 : 90 х = 9846 х = 380 г) k + 40521 = 50521 з) y · 208 = 13936 k = 50521 – 40521 y = 13936 : 208 k = 10000 y = 67 |
|||||||||
|
Задание 10. |
– Найдите значения выражений. |
Решение: 9480 : (300 – 285) · 1000 – 109 · 197 = 610527 85625 : 25 – 1104 : (73992 – 804 · 92) = 3379 (16316 + 10774) : 45 · 100 + 878 · 607 = 593146 94 · 768 – (63782 + 10998 : 9) = 7188 |
|||||||||
|
Задание 11. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – сколько времени затратил турист на весь путь? |
Запись: u = 18 км/ч s = 30 км и 60 км t – ? Решение: (30 + 60) : 18 = 5 (ч) – затратил турист. |
|||||||||
|
Задание 12 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – сколько времени затратил автомобиль на весь путь? |
Запись:
Решение: 1) 108 : 54 = 2 (ч) – проехал 1-й участок. 2) 180 : 60 = 3 (ч) – проехал 2-й участок. 3) 2 + 3 = 5 (ч) – затратил автомобиль на весь путь |
|||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность. Оценивать результаты деятельности, уровень владения учебным действием |
Урок 115. Единицы величины угла. Измерение величины угла.
Практическая работа. Контрольный устный счёт № 7
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений распознавать и изображать угол; создать условия для совершенствования умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся показывать вершину и стороны угла; распознавать и изображать углы, обозначать буквами латинского алфавита; читать обозначения углов |
Метапредметные: Познавательные: строят логическую цепь рассуждений; проводят аналогии между изучаемым материалом и собственным опытом; формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера. Регулятивные: принимают и сохраняют учебную задачу; адекватно воспринимают оценку учителя и товарищей; планируют свое действие. Коммуникативные: учатся разрешать конфликт: выявляют, идентифицируют проблемы, осуществляют поиск и оценку альтернативных способов разрешения конфликта, принимают решение и реализуют его |
Личностные: проявляют этические чувства, доброжелательность и эмоционально-нравственную отзывчивость, понимание и сопереживание чувствам других людей |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Рассмотрите таблицу и объясните, что обозначают выражения: а) 30 : 5 в) 100 : 5 д) 30 : 5 + 400 : 100 б) 400 : 100 г) 100 – 5 е) 30 : 5 – 400: 100
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: а) 30 : 5 – время движения велосипедиста. б) 400 : 100 – время движения автомобилиста. в) 100 : 5 – во сколько раз больше скорость автомобилиста. г) 100 – 5 – на сколько меньше скорость велосипедиста. д) 30 : 5 + 400 : 100 – время движения на велосипеде и на автомобиле. е) 30 : 5 – 400 : 100 – на сколько больше время движения на велосипеде. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения |
|||||||||
|
|
– Вставьте пропущенные числа. 35000 : 18000 : |
Решение: 35000 : 7 = 5000 81000 : 9 = 9000 500 · 5 = 2500 4200 : 6 = 700 4000 : 8 = 500 70 · 7 = 490 18000 : 90 = 200 2400 : 4 = 600 800 · 8 = 6400 3600 : 6 = 600 14000 : 2 = 7000 64000 · 4 = 16000 |
||||||||||
|
Задача |
‒ Решите задачу. Джип ехал 3 часа со скоростью 120 км/ч. Какое расстояние пройдет джип за то же время, если его скорость уменьшится в 2 раза? – Догадайтесь, как ответить на вопрос задачи, используя схему |
Схема: Решение: 120 · 3 : 2 = 360 : 2 = 180 (км) |
||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 114–115). Задание 4*. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Имеют ли общую вершину пары углов? – Назовите эту вершину. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Запись: 1) Ð АКО и Ð ВКМ – вершина К. 2) Ð АВС и Ð DBC – вершина В. 3) Ð ОАМ и Ð КВС – нет общей вершины. 4) Ð CDO и Ð ODC – вершина D. |
Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
|||||||||
|
Задание 5*. |
– Назовите общую сторону углов. |
Запись: 1) Ð КМВ и Ð КМО – сторона КМ. 2) Ð ВАС и Ð МАС – сторона АС. 3) Ð АВС и Ð СВА – стороны АВ и ВС. |
||||||||||
|
Задание 6. |
– Сравните углы способом наложения. |
Сравнивают углы способом наложения. |
||||||||||
|
Задание 7 |
– Используя угольник, найдите среди углов на рисунке прямой угол. – Какие из углов больше прямого угла? – Какие меньше прямого угла? |
Ответ: – Прямой угол – Ð ХОУ. – Ð CDK, Ð AMB – больше прямого угла. – Ð АВС – меньше прямого угла |
||||||||||
|
IV. Включение нового в актив-ное использо- вание в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 117–118). Задание 13. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и постав- ленной учебной целью |
|||||||||
|
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – С какой скоростью ехала машина? |
Запись:
Решение: 1) 17 – 11 – 1 = 5 (ч) – время движения. 2) 345 : 5 = 69 (км/ч) – скорость. |
|||||||||||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – сколько потребуется асфальта, чтобы покрыть весь участок? |
Запись: Длина – 600 м Ширина – 13 м 100 м2 – 3 т 850 кг Решение: 1) 13 · 600 = 7800 (м2) – площадь дороги. 2) 7800 : 100 = 78 (раз) – по 3 т 850 кг. 3) 3850 кг · 78 = 300300 (кг) – потребуется на весь участок. |
||||||||||
|
Задание 15. |
– Истинно или ложно высказывание? |
Решение: 1) истинно; 2) ложно. |
||||||||||
|
Задание 16. |
– Расстояние между двумя населенными пунктами на карте равно 3 см 2 мм. Масштаб карты 1 : 2500000. Какое расстояние между этими пунктами на местности? – Выразите результат в километрах. |
– Масштаб 1:2500000 – это обозначает, что 1 см на карте составляет 2500000 см на местности. Решение: 1) 2500000 см = 25 км; 3 см 2 мм = 32 мм. 2) 3 см · 25 км = 75 км; 2 мм – это пятая часть 1 см, значит, 25 км : 5 = 5 км. 3) 75 км + 5 км = 80 км. |
||||||||||
|
Задание 17. |
– Истинно или ложно высказывание: «Если в выражении 120 – 5 · (4 + 3) есть скобки, то действия выполняются слева направо по порядку»? |
– Высказывание ложно. |
||||||||||
|
Задание 18. |
– Какое расстояние преодолеет жук? |
Решение: 10 см + 25 см + 5 см = 40 (см) ‒ преодолеет жук. |
||||||||||
|
Задание 19. |
– Перед выполнением деления прикиньте, сколько цифр будет в частном. |
Решение: 43680 : 840 = две цифры в частном. 509040 : 126 = четыре цифры в частном. 1241240 : 124 = пять цифр в частном. 67488 : 888 = две цифры в частном. |
||||||||||
|
Задание 20 |
– Найдите и объясните ошибки в каждой из записей |
– В первой записи деления в значении частного не записали ноль в разряде единиц. – Во второй записи деления в значении частного не записали ноль в разряде десятков. – В третьей записи деления получили остаток больше делителя |
||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 116. Виды углов
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «острый», «тупой», «прямой» угол; способствовать формированию умений распознавать и изображать угол; содействовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «острый», «тупой», «прямой» угол; научатся выполнять классификацию углов: острый, тупой, прямой; распознавать и изображать углы |
Метапредметные: Познавательные: понимают знаки, символы, модели, схемы, приведенные в учебнике и учебных пособиях; ориентируются на возможное разнообразие способов решения учебной задачи; овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи. Регулятивные: определяют и формулируют цель деятельности на уроке; проговаривают последовательность действий на уроке. Коммуникативные: слушают и понимают речь других; признают возможность существования различных точек зрения и права каждого иметь свою |
Личностные: задаются вопросом о том, «какое значение, смысл имеет для меня учение», и умеют находить ответ на него |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу |
||||
|
– Найдите первое неполное делимое и определите, сколько цифр будет в результате деления:
|
Решение: 5270 : 5 – четыре цифры в частном 6472 : 23 – три цифры в частном 1524 : 82 – две цифры в частном 371204 : 548 – три цифры в частном 783245 : 1364 – три цифры в частном 2870632 : 1236 – четыре цифры в частном |
||||||
|
|
– Выразите скорость в других единицах: 750 м/мин = 70 м/мин = 90 м/мин = |
Ответы: 750 м/мин = 45000 м/ч = 45 км/ч 70 м/мин = 4200 м/ч 90 м/мин = 5400 м/ч |
|||||
|
Геометрический материал |
– Сколько углов в каждом многоугольнике?
|
– В треугольнике три угла. В шестиугольнике – шесть. В четырехугольнике – четыре. В пяти-угольнике – пять
|
|||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 119). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Найдите с помощью угольника прямой угол. – Какой из остальных углов меньше прямого угла? џ Угол, который меньше прямого угла, называют острым. – Какой из остальных углов больше прямого угла? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Под номером 2 прямой угол. – Под номером 1 угол меньше прямого угла.
– Под номером 3 угол больше прямого угла. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Осуществлять контроль по результату |
||||
|
Задание 2. |
– Назовите острые углы. – Назовите прямые углы. – Назовите тупые углы. |
Ответы: – Острые углы – 1, 4, 5. Прямые углы – 3, 6. Тупой угол – 2. |
|||||
|
Практическая работа. Задание 1. |
Отметьте на листе бумаги точку А и проведите лучи АВ и АС. На сколько частей они делят плоскость? Раскрасьте меньшую часть цветными карандашами и вырежьте из бумаги. |
– Два луча с общим началом разбивают плоскость на две части. Меньшая из этих частей называется углом.
Точка А – вершина угла. Лучи АВ и АС – стороны угла. Записывают: Ð ВАС или Ð А. |
|||||
|
Задание 2 |
Запишите различные обозначения углов. Назовите их вершины и стороны.
– Прямые углы удобно находить и строить с помощью угольника |
– Если сложить лист бумаги пополам, а потом ещё раз пополам, то получится прямой угол. џ Если две прямые образуют прямой угол, то их называют перпендикулярными.
|
|||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 120). Задание 5. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Найдите неизвестное число. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: х · 65 = 24700 х : 17 = 17340 х = 24700 : 65 х = 17340 · 17 х = 380 х = 294780 |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||
|
Задание 6. |
– Выполните действия. |
Выполняют задание (см. ресурсный материал к уроку). |
|||||
|
Задание 7. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. |
Выполняют задание (см. ресурсный материал к уроку). |
|||||
|
Задание 8. |
– Может ли один человек быть старше другого в 600 раз? – Проверьте, используя данные: внуку 1 месяц, а дедушке 50 лет. |
– Может один человек быть старше другого в 600 раз. 50 лет = 600 мес.; 600 мес. : 1 мес. = 600 раз. |
|||||
|
Задание 9. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Чему равен периметр прямоугольника? |
Выполняют задание (см. ресурсный материал к уроку). |
|||||
|
Задание 10. |
– Вычислите площадь квадрата, если длина его стороны равна 12 см 5 мм.
– Вычислите площадь квадрата, если длина его стороны равна 1 дм 5 см 6 мм. |
Решение: 1) 12 см 5 мм = 125 мм; S = 125 · 125 = 15625 (мм2). 2) 1 дм 5 см 6 мм = 156 мм; S = 156 · 156 = 24336 (мм2). |
|||||
|
Задание 11. |
– Не выполняя вычислений, определите неизвестное число в каждом из равенств. |
Решение: а) х – 125 = 625 – 125 б) х + 254 = 254 + 85 х = 625 х = 85 |
|||||
|
Задание 12. |
– Каждое из чисел увеличьте в 4 раза. – Каждое из чисел уменьшите в 100 раз. |
Решение: 600 · 4 = 2400 600 : 100 = 6 8000 · 4 = 32000 8000 : 100 = 80 10000 · 4 = 40000 10000 : 100 = 100 |
|||||
|
Задание 13. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какое расстояние будет между грузовиком и мопедом? |
Решение (см. ресурсный материал к уроку). |
|||||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какое расстояние будет между машиной и автобусом? |
Решение (см. ресурсный материал к уроку). |
|||||
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько килограммов гвоздей в каждом ящике? |
Решение (см. ресурсный материал к уроку). |
|||||
|
Самостоятельная работа. Задание 1. |
– Среди углов, образованных звеньями ломаной линии, найдите острые, прямые и тупые углы.
|
Решение: Угол В и угол Е – острые. Угол С и угол К – прямые. Угол D и угол F – тупые. |
|||||
|
Задание 2 |
Определите величину угла между минутной и часовой стрелкой.
|
Решение: а) 60 градусов; г) 100 градусов; б) 165 градусов; д) 120 градусов в) 24 градуса; |
|||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Ресурсный материал к уроку
|
Задание 6. Решение:
Задание 7. Запись:
Решение: 1) 12 – 7 = 5 (р.) – 50 метров. 2) 50 : 5 = 10 (м) – в 1 рулоне. 3) 10 · 7 = 70 (м) – 1-я комната. 4) 10 · 12 = 120 (м) – 2-я комната.
Задание 9.
Решение: 1) 860 : 10 = 86 (дм) – длина прямоугольника. 2) (86 + 10) · 2 = 192 (дм) – периметр прямоугольника. |
Задание 13. Запись:
Решение: 1) 47 + 33 = 80 (км/ч) – скорость сближения. 2) 80 · 1 = 80 (км) – через 1 час. 3) 80 · 6 = 480 (км) – через 6 часов.
Задание 14. Запись:
Решение: 1) 75 – 65 = 10 (км/ч) – скорость изменения расстояния. 2) 10 · 1 = 10 (км) – через 1 час. 3) 10 · 6 = 60 (км) – через 6 часов.
Задание 15. Запись:
Решение: 1) 5 + 2 = 7 (ящ.) – осталось. 2) 10 – 7 = 3 (ящ.) – использовали. 3) 60 : 3 = 20 (кг) – в 1 ящике. |
Урок 117. Нахождение на чертеже каждого вида угла.
Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятиями «острый», «тупой», «прямой» угол; способствовать формированию умений распознавать и изображать угол; содействовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятиями «острый», «тупой», «прямой» угол; научатся выполнять классификацию углов: острый, тупой, прямой; распознавать и изображать углы |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; структурируют знания. Регулятивные: умеют формулировать учебную задачу на основе соотнесения того, что уже известно и усвоено обучающимся, и того, что еще неизвестно. Коммуникативные: полно и точно выражают свои мысли в соответствии с задачами и условиями коммуникации; владеют монологической и диалогической формами речи в соответствии с нормами родного языка и современных средств коммуникации |
Личностные: проявляют интерес к учебному материалу; владеют знаниями основных моральных норм поведения |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Заполните таблицу.
– Как найти неизвестное делимое? Неизвестный делитель? |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Заполняют таблицу.
|
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Интеллектуальная разминка. |
– Используя первую запись в каждом столбике, вставьте пропущенные числа. а) 362 : 15 = 24 (ост. 2) б) 603 : 81 = 7 (ост. 36)
|
Решение: а) 362 : 15 = 24 (ост. 2) б) 603 : 81 = 7 (ост. 36) 364 : 15 = 24 (ост. 4) 612 : 81 = 7 (ост. 45) 366 : 15 = 24 (ост. 6) 621 : 81 = 7 (ост. 54) 368 : 15 = 24 (ост. 8) 630 : 81 =7 (ост. 63) 370 : 15 = 24 (ост. 10) 639 : 81 = 7 (ост. 72) 372 : 15 = 24 (ост. 12) 648 : 81 = 8 (ост. 0) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Геометрический материал |
– Найдите прямые углы в каждой фигуре |
Решение:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 120). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Начертите в тетради прямой угол, два острых и три тупых угла. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Выполняют построения в тетради. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4 |
– Как называется первый многоугольник? – Назовите прямой угол. – Назовите острый угол. – Назовите тупые углы. – Как называется второй многоугольник? – Назовите прямой угол. – Как называются остальные углы? – Как называется третий многоугольник?
– Есть у этой фигуры прямой угол?
– Дайте характеристику всем углам |
– Четырехугольник ADCO. – Прямой угол – Ð АОС. – Острый угол – Ð ADC. – Тупые углы – Ð OAD, Ð OCD. – Второй многоугольник – треугольник ВМК. – Прямой угол – Ð КВМ. – Остальные углы острые – Ð ВМК, Ð ВКМ. – Третий многоугольник – четырехугольник ЕХРУ. – У этой фигуры нет прямого угла. Ð ЕХР, Ð ХЕУ, Ð ХРУ – тупые; Ð ЕУР – острый угол |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 122–124). Задание 16. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Расстояние между двумя городами на плане равно 7 см. Масштаб плана 1 : 1000000. Каково рас-стояние между этими городами на местности? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 7 см · 1 000 000 = 7 000 000 (см). 7 000 000 см = 70 км. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 17. |
– Прямое шоссе длиной 12 км изображено на плане отрезком длиной 4 см. В каком масштабе выполнен план? |
Решение: Масштаб 1 : 300 000. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 18. |
– От села до города 1500 м. Каким будет это расстояние на плане, сделанном в масштабе 1: 30000? |
Решение: 1500 м = 150000 см. 150000 : 30000 = 5 см. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 19. |
– На рисунке дан график изменения температуры воздуха в разное время суток. Сколько градусов показывал термометр в 8 ч утра? в полдень? в 15 часов? – Когда температура была максимальной? – В какой промежуток времени температура не изменялась? |
Ответы: – 10 градусов показывал термометр в 9 часов утра; в полдень – 20 градусов; в 15 часов – 15 градусов. – В 14 часов температура была максимальной. – С 8 до 9 часов и с 15 до 16 часов температура не изменялась. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 20. |
– Ответьте на вопросы. – У каких растений сроки цветения совпадают?
– Какие цветы цветут только один месяц?
– Какие цветы цветут в мае? Какие – в июле? Какие – в сентябре?
– У каких цветов сроки цветения больше: лилии или настурции? У настурции или хризантемы? – Какие цветы отцветают последними? – Какие цветы зацветают раньше всех? – Какие цветы зацветают позже: гиацинт или крокус? нарцисс или незабудка? – Сколько месяцев цветет: пион? ландыш? гвоздика? купальница? – Назовите сроки цветения бархатцев, календулы, пиона. |
Ответы: – Сроки цветения совпадают у нескольких растений: лилия – гвоздика китайская; крокус – незабудка; календула – настур-ция – бархатцы; гиацинт – тюльпан – ландыш. – Гиацинт, ландыш, пион, тюльпан цветут только один месяц. – Гиацинт, крокус, купальница, ландыш, нарцисс, незабудка, тюльпан цветут в мае. Бархатцы, гвоздика китайская, календула, купальница, лилия, настурция – в июле. Астра, бархатцы, гвоздика китайская, календула, лилия, настурция, хризантема – в сентябре. – У лилии сроки цветения больше, чем у настурции. У настурции больше, чем у хризантемы. – Астры отцветают последними. – Крокус, незабудка зацветают раньше всех. – Гиацинт зацветает позже, чем крокус. Нарцисс – позже, чем незабудка. – Один месяц цветет пион и ландыш; гвоздика – 4 месяца; купальница – 3 месяца. – Сроки цветения бархатцев: июнь, август, сентябрь. У календулы: июль, август, сентябрь. У пиона: июнь. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 21. |
– Расположите значения величин в порядке увеличения. |
Решение: 1) 30 м 8 дм; 1250 дм; 999 м; 1250 м; 2 км. 2) 280 г; 1600 г; 5300 г ; 16 кг; 6 ц; 1 т. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 22. |
– Выразите время в минутах.
– Выразите время в сутках. – Выразите время в часах.
– Выразите время в секундах. |
Решение: 28800 с = 480 мин; 40 ч = 2400 мин; 6 ч 12 мин = 372 мин. 96 ч = 4 сут.; 168 ч = 7 сут.; 192 ч = 8 сут. 420 мин = 7 ч; 600 мин = 10 ч; 540 мин = 9 ч; 1020 мин = 17 ч. 9 мин 15 с = 555 с; 2 ч 30 мин 15 с = 9015 с. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 23* |
– Скорость движения лодки в стоячей воде 3752 м/ч, скорость течения реки – 1976 м/ч. Найдите скорость движения лодки по течению реки и против течения |
Решение: 1) 3752 + 1976 = 5728 (м/ч) – скорость движения лодки по течению реки. 2) 3752 – 1976 = 1776 (м/ч) – скорость движения лодки против течения реки |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. Методика «Дерево успеха». Выбирают лист и прикрепляют на дерево успеха: зелёный лист – нет ошибок, жёлтый лист – 1 ошибка, красный лист – 2–3 ошибки |
Выражать доброжелательность и эмоционально-нравственную отзывчивость. Осуществлять итоговый контроль |
Урок 118. Нахождение неизвестного числа в равенствах вида: 8 + х = 16
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений решать равенства вида 8 + х = 16; содействовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом нахождения второго слагаемого; научатся применять правила нахождения неизвестных компонентов арифметических действий (второго слагаемого) |
Метапредметные: Познавательные: осуществляют анализ; устанавливают причинно-следственные связи; строят логическую цепь рассуждений; структурируют знания; осуществляют моделирование. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера; адекватно оценивают результаты своей деятельности. Коммуникативные: излагают своё мнение и аргументируют свою точку зрения |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Подберите первый множитель и решите полученные числовые выражения, найдите выражения с «ловушками».
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: Выражение г) с «ловушкой».
|
Осуществлять актуализацию личного жизненного опыта |
|||||||||||||
|
– Вставьте знаки арифметических действий, чтобы записи были верными: 40 … 40 … 40 = 40 3 … 8 … 2 = 12 |
Решение: 40 + 40 – 40 = 40 3 · 8 : 2 = 12 |
|||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 125–126). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Объясните, как можно вычислить неизвестное второе слагаемое. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно вычислить неизвестное второе слагаемое. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества |
|||||||||||||
|
Задание 2. |
– Какое действие надо выполнить, чтобы найти неизвестное второе слагаемое в каждом из равенств? – Сформулируйте правило для нахождения неизвестного второго слагаемого. |
– Надо выполнить вычитание, чтобы найти неизвестное второе слагаемое в каждом из равенств. џ Чтобы найти неизвестное второе слагаемое, надо из суммы вычесть первое слагаемое. |
||||||||||||||
|
Задание 3. |
– Пользуясь правилом, вычислите неизвестное второе слагаемое. |
Решение: 12800 + т = 40213 893 + k = 2000 m = 40213 – 12800 k = 2000 – 893 m = 27413 k = 1107 |
||||||||||||||
|
Задание 4. |
– Запишите предложение в виде неравенства. Найдите неизвестное число. |
Решение: 1) 678 + т = 101200 2) 5080 + t = 6117 т = 101200 – 678 t = 6117 – 5080 т = 100522 t = 1037 |
||||||||||||||
|
Задание 5. |
– Какое число задумала Оля? |
Решение: 968 + х = 1000 х = 1000 – 968 х = 32 |
||||||||||||||
|
Задание 6 |
– Прочитайте задачу. Что известно? Что требуется узнать? – Решите задачу. – Сколько капусты привезли на базу? |
Запись: Было – 3450 кг Привезли – х кг Стало – 8700 кг Решение: 3450 + х = 8700 х = 8700 – 3450 х = 5250 (кг) – привезли |
||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 129–130). Задание 21. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|||||||||||||
|
– Выполните действия. |
Решение: 409801 – 586 = 409215 258 · 137 = 35346 50728 + 6183 = 56911 830605 : 5 = 166121 867 + 995540 = 996407 17280 : 36 = 480 50308 · 4 = 201232 109296 : 297 = 368 320 · 406 = 129920 |
|||||||||||||||
|
Задание 22. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно. |
||||||||||||||
|
Задание 23. |
– Найдите значения выражений.
|
Решение: 64 · 35 + 106 · 402 – 128 : 64 = 44850 (8000 – 3988) · 105 – 945 : 5 · 100 = 402360 46839 – (322060 – 64 · 150) : 20 – 31216 (753 · 486 – 82 · 105 – 37048) : 100 = 3203 (12460 + 760 · 112) : 41 – 1791 = 589 (34 · 28 – 952) · 161829 + 5463 · 60 = 327600
|
||||||||||||||
|
Задание 24 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – За сколько дней мастера выполнят заказ? |
Запись:
Решение: 1) 18 + 20 + 16 = 54 (м./дн.) – совместная производительность. 2) 324 : 54 = 6 (дн.) – время выполнения заказа |
||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. предлагает каждому оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
Заполните таблицу самооценки:
|
Способность к самооценке на основе критерия успешности учебной деятельности |
|||||||||||||
Урок 119. Нахождение неизвестного числа в равенствах вида: 8 · х = 16.
Текущая проверочная работа по теме «Угол и его обозначение»
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений решать равенства вида 8 · х = 16; содействовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом нахождения второго множителя; научатся применять правила нахождения неизвестных компонентов арифметических действии (второго множителя) |
Метапредметные: Познавательные: строят логическую цепь рассуждений; проводят аналогии между изучаемым материалом и собственным опытом; формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учёта интересов сторон и сотрудничества |
Личностные: формируют внутреннюю позицию школьника на уровне положительного отношения к школе; приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности учебной деятельности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
– Вместо точек подберите цифры и решите полученные числовые выражения. Где «ловушка»?
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: Выражение б) с «ловушкой».
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения |
||||||||||||
|
Задачи |
– Прочитайте задачи, найдите задачи с «ловушками»: а) В альбоме собраны марки. Узнай, сколько всего марок в альбоме, если в нем 16 страниц и на каждой странице по 4 марки. б) В альбоме собраны марки. Узнай, сколько всего марок в альбоме, если коллекционеру 10 лет, страниц в альбоме 16, марок на каждой странице 4. в) В альбоме собраны марки. Узнай, сколько всего марок в альбоме, если на каждую страницу мальчик помещал их по 15 штук. – Решите задачу а). |
Ответ: Задача б) с избыточными данными; в) с недостающими данными.
Решение: 16 · 4 = 64 (м.) – всего в альбоме. |
|||||||||||||
|
|
– Найдите частное и остаток. 38 : 54 126 : 100 543 : 789 124 : 282 126 : 10 1267 : 1000 |
Решение: 38 : 54 = 0 (ост. 38) 126 : 10 = 12 (ост. 6) 124 : 282 = 0 (ост. 124) 543 : 789 = 0 (ост. 543) 126 : 100 = 1 (ост. 26) 1267 : 1000 = 1 (ост. 267) |
|||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 126–127). Задание 7. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Объясните, как можно вычислить неизвестный второй множитель. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно вычислить неизвестный второй множитель. |
Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
||||||||||||
|
Задание 8. |
– Какое действие надо выполнить, чтобы найти неизвестный второй множитель в каждом из равенств? – Сформулируйте правило для нахождения неизвестного второго множителя. |
– Надо выполнить деление, чтобы найти неизвестный второй множитель в каждом из равенств? џ Чтобы найти неизвестный второй множитель, надо произведение разделить на первый множитель. |
|||||||||||||
|
Задание 9. |
– Запишите предложения в виде равенства. Найдите неизвестное число. |
Решение: 1) 28 · а = 103432 2) 312 · п = 4992 а = 103432 : 28 п = 4992 : 312 а = 3694 п = 16 |
|||||||||||||
|
Задание 10 |
– Какое число задумал Митя? |
Решение: 960 · х = 336000 х = 336000 : 960 х =350 |
|||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 130–131). Задание 25. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока. – Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – За сколько часов, работая вместе, повара испекут все пирожки? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись:
Решение: 1) 30 + 28 = 58 (п./ч) – совместная производительность. 2) 174 : 58 = 3 (ч) – время работы. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии Осуществлять взаимный контроль, планировать способы взаимодействия. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
||||||||||||
|
Задание 26. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько черной смородины приготовили для варки варенья? |
– Прочитайте и решите задачу. Запись:
Решение: 1) 6 кг 500 г · 3 = 19 кг 500 г – было малины. 2) 19 кг 500 г + 6 кг 500 г = 26 кг – было крыжовника и малины. 3) 45 кг – 26 кг = 19 кг – сварили смородины. |
|||||||||||||
|
Задание 27. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько нефти было в каждом резервуаре первоначально? |
Запись:
Решение: 1) 35 т 600 кг + 46 т 400 кг = 82 т – взяли. 2) 120 – 82 = 38 (т) – осталось в двух цистернах. 3) 38 : 2 = 19 (т) – осталось в каждой цистерне. |
|||||||||||||
|
Задание 28*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – На каком расстоянии вдоль шоссе будут находиться машина и мотоцикл друг от друга в 10 ч утра? |
Решение: 1) Какое расстояние проедет машина за 1 час? 72 км/ч · 1 ч = 72 (км). 2) Какое расстояние проедет мотоцикл за 30 минут? 60 км/ч : 2 = 30 (км). 3) На сколько больше километров проедет машина, чем мотоцикл? 72 – 30 = 42 (км). |
|||||||||||||
|
Задание 29. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какова масса четырех упаковок котлет? |
Решение: 1) 120 · 5 = 600 (г) – масса 1 упаковки. 2) 600 · 4 = 2400 (г) – масса 4 упаковок. |
|||||||||||||
|
Задание 30. |
– Выполните действия. |
Выполняют вычисления. Взаимопроверка в парах. |
|||||||||||||
|
Задание 31. |
– Выразите длину в километрах и метрах. |
Решение: 50321 км = 50 км 321 м 800000 м = 800 км 8111 м = 8 км 111 м 123005 м = 123 км 5 м 34780 м = 34 км 780 м |
|||||||||||||
|
Задание 32 |
– Выразите длину в метрах |
Решение: 42 км 120 м = 42120 м 49 км = 49000 м 179 км 500 м = 179500 м 5 км 6 м = 5006 м 86 км 35 м = 86035 м |
|||||||||||||
|
V. Проверочная работа |
Проводит проверочную работу (см. ресурсный материал) |
Работают самостоятельно |
|||||||||||||
|
VI. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Как найти неизвестный второй множитель? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
||||||||||||
Ресурсный материал к уроку
Проверочная работа
|
Вариант 1 Пронумеруй углы. Напиши номера углов в порядке возрастания.
Измерь углы, запиши их величину в порядке убывания |
Вариант 2 Пронумеруй углы. Напиши номера углов в порядке убывания.
Измерь углы, запиши их величину в порядке увеличения |
Урок 120. Нахождение неизвестного числа в равенствах вида: 8 – х = 2
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений решать равенства вида 8 – х = 2; содействовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом нахождения вычитаемого; научатся применять правила нахождения неизвестных компонентов арифметических действий (вычитаемого) |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая), и преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний.
– Вместо точек подставьте нужные цифры. Найдите «ловушки».
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. – Примеры в), г) с «ловушками».
|
Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Выберите из чисел 0, 5, 7, 9, 14, 19, 21, 33, 42, 49, 54, 57, 63 те, которые: а) делятся на 7 без остатка; б) делятся на 7 с остатком 5. |
Решение:
а) 7, 14, 21, 42, 49, 63 делятся на 7 без остатка; б) 19, 33, 54 делятся на 7 с остатком 5. |
|
|
|
– Найдите «лишнее» выражение: 720 : 9 540 : 6 480 : 8 360 : 6 930 : 3 810 : 9 |
Ответ: 930 : 3 |
|
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 127–128). Задание 11. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Объясните, как можно найти неизвестное вычитаемое. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно найти неизвестное вычитаемое. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Осуществлять контроль по результату |
|
Задание 12. |
– Какое действие надо выполнить, чтобы найти неизвестное вычитаемое в каждом из равенств? – Сформулируйте правило для нахождения неизвестного вычитаемого. |
– Надо выполнить вычитание, чтобы найти неизвестное вычитаемое в каждом из равенств. џ Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность. |
|
|
Задание 13. |
– Запишите предложение в виде равенства. |
Ответы: 1) 10120 – а = 983 2) 40308 – у = 409 а = 10120 – 983 у = 40308 – 409 а = 9137 у = 39899 |
|
|
Задание 14. |
– Чему равно неизвестное число? |
Решение: 5555 – х = 3939 х = 5555 – 3939 х = 1616 |
|
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какова цена магнитофона? |
Запись: Было – 12000 р. Заплатили – х р. Осталось – 8440 р. Решение: 12000 – х = 8440 х = 12000 – 8440 х = 3560 (р.) – цена магнитофона. |
|
|
Задание 16 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько пшеницы смололи? |
Запись: Было – 15450 кг. Заплатили – х кг. Осталось – 8600 кг. Решение: 15450 – х = 8600 х = 15450 – 8600 х = 6850 (кг) – пшеницы смололи |
|
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 131–132). Задание 33. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Верно или неверно высказывание? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Решение: 1) ложно; 2) истинно; 3) ложно; 4) истинно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Осуществлять взаимный контроль, планировать способы взаимодействия |
|
Задание 34. |
– Назовите число, которое при делении на 5 дает в остатке 2. – Назовите число, которое при делении на 5 дает в остатке 3; дает в остатке 4. |
– Число 7 при делении на 5 дает в остатке 2.
– Число 8 при делении на 5 дает в остатке 3; число 9 при делении на 5 дает в остатке 4. |
|
|
Задание 35. |
– Какие числа на числовом луче соответствуют отмеченным точкам? |
Решение:
|
|
|
Задание 36. |
– На каком участке числового луча находятся числа? |
Решение: 267500 – участок Г 184000 – участок Б 102800 – участок А 212999 – участок В 396125 – участок Е |
|
|
Задание 37*. |
– Какая из этих фигур является пирамидой? прямоугольным параллелепипедом? – Какая из этих фигур может быть кубом? |
– Куб – это 2-я и 3-я фигуры. |
|
|
Задание 38 |
– Оля начертила квадрат. Зоя посмотрела на него и сказала, что это прямоугольник. Не ошиблась ли Зоя? |
– Зоя не ошиблась, так как квадрат – это прямоугольник, у которого все стороны равны |
|
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Как найти неизвестное вычитаемое? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность. Осуществлять итоговый контроль, оценивать результаты деятельности |
Урок 121. Нахождение неизвестного числа в равенствах вида: 8 : х = 2
Текущая проверочная работа по теме «Применение правил нахождения
неизвестных компонентов арифметических действий»
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений решать равенства вида 8 : х = 2; содействовать развитию умений решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с правилом нахождения делителя; научатся применять правила нахождения неизвестных компонентов арифметических действий (делителя) |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; структурируют знания. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: слушают и понимают речь других; договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний. – Подчеркните первое неполное делимое и определите количество цифр в значении частного: 47736 : 9 5436 : 3 6549 : 3 5216 : 2 48538 : 7 30087 : 9 816 : 4 520 : 5 107124 : 6 96072 : 8 |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: 47736 : 9 – четыре цифры в частном 5436 : 3 – четыре цифры в частном 6549 : 3 – четыре цифры в частном 5216 : 2 – четыре цифры в частном 48538 : 7 – четыре цифры в частном 30087 : 9 – четыре цифры в частном 816 : 4 – три цифры в частном 520 : 5 – три цифры в частном 107124 : 6 – пять цифр в частном 96072 : 8 – пять цифр в частном |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
Игра «Не подведи свой ряд». |
1-й ряд 2-й ряд 3-й ряд 20 : 5 40 : 8 30 : 6 36 : 12 48 : 12 36 : 18 810 : 10 : 9 640 : 10 : 8 540 : 10 : 9 6001 : 10 900 : 1 : 10 700 : 10 · 1 540 · 0 : 10 630 : 10 · 0 560 · 0 : 10 – Какое правило вы использовали при умножении на единицу? При делении на единицу? ‒ При умножении на нуль? |
џ При умножении 1 на любое число получается это же число. џ При делении 1 на любое число получается это же число. џ При умножении 0 на любое число получается 0. |
|
|
Числа и цифры |
– Запишите числа цифрами и подчеркните наименьшее: а) 3 тыс., 8 ед.; д) 53 тыс. 12 ед.; б) 562 тыс. 4 ед.; е) 57 тыс.; в) 1 тыс. 100 ед.; ж) 100 тыс. 10 ед.; г) 51 тыс. 163 ед.; и) 11 тыс. 11 ед. |
Решение: а) 3008; д) 53012; б) 562004; е) 57000; в) 1100; ж) 100010; г) 51163; и) 11011 |
|
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 128–129). Задание 17. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Объясните, как можно найти неизвестный делитель. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Объясняют, как можно найти неизвестный делитель. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
|
Задание 18. |
– Какое действие надо выполнить, чтобы найти неизвестный делитель в каждом из равенств? – Сформулируйте правило для нахождения неизвестного делителя. |
– Надо выполнить деление, чтобы найти неизвестный делитель в каждом из равенств. џ Чтобы найти неизвестный делитель, надо делимое разделить на частное. |
|
|
Задание 19. |
– Запишите предложение в виде равенства. |
Решение: 1) 920 : а = 46 2) 2100 : b = 35 a = 920 : 46 b = 2100 : 35 a = 20 b = 60 |
|
|
Задание 20 |
– Найдите неизвестное число |
Решение: 14168 : х = 92 х = 14168 : 92 х = 154 |
|
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 133–134). Задание 39. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Какие из высказываний истинны? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Решение: 1) Ð АОВ – не прямой – истинно. 2) Ð АОВ – не острый – истинно. 3) Ð АОВ – острый – ложно. 4) Ð АОВ – не тупой – ложно. 5) Ð АОВ – тупой – истинно. 6) Ð АОВ – острый или прямой – ложно. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|
Задание 40. |
– В каком треугольнике есть прямой угол? тупой угол? – В каком треугольнике все углы острые? – В каком треугольнике есть не только острый угол, но и прямой? |
– В зеленом треугольнике есть прямой угол. В розовом – тупой угол. – В желтом треугольнике все углы острые. – В зеленом треугольнике есть не только острый угол, но и прямой. |
|
|
Задание 41. |
– В каком треугольнике нет прямого угла?
– У какого из треугольников все стороны разной длины? одной и той же длины?
– У какого из треугольников только две стороны имеют одинаковую длину? |
– В желтом и розовом треугольниках нет прямого угла. – У оранжевого треугольника все стороны разной длины. У зеленого треугольника все стороны одной и той же длины. – У синего треугольника две стороны имеют одинаковую длину. |
|
|
Задание 42. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно в парах. |
|
|
Задание 43 |
– В конкурсе детской песни участвовали шестеро четвероклассников – Андреев, Серова, Павлов, Васильев, Белов и Галкина. На диаграмме показано, сколько баллов получил каждый из них. |
|
|
|
|
– Кто из участников конкурса получил наибольшее число баллов и кто – наименьшее? – Сколько баллов получила каждая из девочек? Сколько баллов получил Павлов? – Кто получил больше баллов: Галкина или Васильев и на сколько? |
– Андреев получил наибольшее число баллов, Белов – наименьшее. – Галкина получила 4 балла, Серова – 6 баллов. Павлов получил 8 баллов. – Васильев получил больше баллов, чем Галкина, на 1 балл |
|
|
V. Проверочная работа |
Проводит проверочную работу по вариантам. Вариант 1 Реши уравнения: 72 : х = 4 х · 12= 24 Вариант 2 Реши уравнения: х : 6 = 11 75 : х = 25 |
Работают самостоятельно.
Ответы: х = 18 х = 2
Ответы: х = 66 х = 3 |
Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
|
VI. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Как найти неизвестный делитель? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 122. Виды треугольников
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с классификацией треугольников по величинам их углов и по длинам их сторон; способствовать формированию умений распознавать и изображать треугольники; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с классификацией треугольников по величинам их углов и по длинам их сторон; научатся классифицировать треугольники по величинам их углов (остроугольный, прямоугольный, тупоугольный); по длинам их сторон (разносторонний, равнобедренный, равносторонний) |
Метапредметные: Познавательные: овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи; строят логическую цепь рассуждений; используют доказательство. Регулятивные: умеют работать по предложенному учителем плану. Коммуникативные: учатся конструктивно разрешать конфликты посредством учёта интересов сторон и сотрудничества |
Личностные: расширяют познавательные интересы и учебные мотивы; умеют устанавливать, с какими учебными задачами могут справиться самостоятельно |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка.
|
Организует устный счет с целью актуализации знаний.
– Поставьте знак «>», «<» или «=», чтобы записи были верными: 14088 : (3 · 8) ... 14088 : 8 · 3 30492 : 36 ... 30492 : 9 : 4 80919 : 9 · 9 ... 80919 : 81 19915 : 35 ... 19915 : 7 : 5 |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
Решение: 14088 : (3 · 8) < 14088 : 8 · 3 30492 : 36 = 30492 : 9 : 4 80919 : 9 · 9 > 80919 : 81 19915 : 35 = 19915 : 7 : 5 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||
|
Геометрический материал. |
– Сколько треугольников на рисунке?
|
Ответ: 4 треугольника. |
||||||||||||||||
|
Задача |
– Таня живет на II этаже. Ваня – в том же
подъезде, но ему приходится подниматься по лестнице, в которой в 2 раза
больше ступенек. Ступенек до подъезда и до I этажа нет. |
Ответ. на III этаже живет Ваня |
||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 135–136). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Определите вид углов в каждом треугольнике. – Почему красный треугольник называют остроугольным? – Почему синий треугольник считается прямоугольным? – Почему зеленый треугольник тупоугольный? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Красный треугольник называют остроугольным, потому что все углы острые. – Синий треугольник считается прямоугольным, потому что есть прямой угол. – Зеленый треугольник тупоугольный, так как есть тупой угол. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять контроль по результату |
|||||||||||||||
|
Задание 2. |
– Определите вид каждого треугольника, используя угольник. |
– 1-й треугольник – тупоугольный; 2-й треугольник – прямоугольный; 3-й треугольник – остро-угольный. |
||||||||||||||||
|
Задание 3. |
– Измерьте длины сторон каждого треугольника. – Почему красный треугольник называют разносторонним? – Почему синий треугольник называют равнобедренным?
– Почему зеленый треугольник называют равносторонним? |
– Красный треугольник называют разносторонним, так как все стороны разной длины.
– Синий треугольник называют равнобедренным, так как две стороны равны по длине.
– Зеленый треугольник называют равносторонним, так как все стороны равны по длине. Заполняют таблицу в тетради.
|
||||||||||||||||
|
Задание 4. |
– Можно ли равносторонний треугольник назвать равнобедренным? – Можно ли равнобедренный треугольник назвать равносторонним? |
– Можно равносторонний треугольник назвать равнобедренным. – Нельзя равнобедренный треугольник назвать равносторонним, так как только две стороны имеют равную длину. |
||||||||||||||||
|
Задание 5 |
– Верно или неверно высказывание? |
– Высказывание «Разносторонний треугольник не может быть прямоугольным» – ложно. – Высказывание «Равнобедренный треугольник не может быть тупоугольным» – ложно. – Высказывание «В треугольнике могут быть только два острых угла» – истинно |
||||||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 138–139). Задание 11. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько денег было у мамы? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись:
Решение: 1) 26 · 2 + 32 = 84 (р.) – потратила. 2) 84 · 5 = 420 (р.) – осталось. 3) 420 + 84 = 504 (р.) – было. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||
|
Задание 12*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какое расстояние человек пройдет: за 30 мин; за 20 мин; за 5 мин? |
Решение (см. ресурсный материал к уроку). |
||||||||||||||||
|
Задание 13. |
– Составьте выражения. |
Выполняют задание (см. ресурсный материал к уроку). |
||||||||||||||||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько секунд пройдет с момента встречи машинистов до момента встречи проводников, стоящих у последних дверей последних вагонов? |
Решение: 1) 45 + 45 = 90 (км/ч) – скорость, с которой приближаются поезда. 2) 250 + 250 = 500 (м) расстояние между последними дверями последних вагонов, когда встретятся машинисты. 90 км/ч = 90000 м/ч = 25 м /с. 3) 500 : 25 = 20 (с) – пройдет с момента встречи машинистов до встречи проводников. |
||||||||||||||||
|
Задание 15. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – С какой скоростью шел другой агроном? |
Запись:
Решение: 1) 80 м/мин · 40 мин = 3200 м – пройдет первый за 40 мин. 2) 6000 м – 3200 м = 2800 м – пройдет второй за 40 мин. 3) 2800 м : 40 мин = 70 м/мин – скорость второго. |
||||||||||||||||
|
Задание 16. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – На каком расстоянии от шалаша находится озеро? |
Решение: 5 км/ч = 5000 м/ч. 1) 5000 : 2 = 2500 (км) – прошёл охотник за полчаса. 2) 2500 · 3 = 7500 (км) – озеро находится от шалаша. |
||||||||||||||||
|
Задание 17 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько было пятитонных грузовиков? |
Запись: Пятитонных – ? м. Трехтонных – 8 м. Всего – 54000 кг. Решение: 1) 3 · 8 = 24 (т) – погрузили в трехтонные машины. 2) 54000 кг = 54 т; 54 – 24 = 30 (т) – погрузили в пятитонные машины. 3) 30 : 5 = 6 (м.) – было пятитонных |
||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи. Выражать доброжелательность и эмоционально-нравственную отзывчивость |
|||||||||||||||
Ресурсный материал к уроку
|
Задание 12*.
Решение: 1) 30 минут – половина часа. 6 : 2 = 3 (км) – пройдет за 30 мин. 2) 20 минут – третья часть часа. 6 : 3 = 2 (км) – пройдет за 20 мин. 3) 6 км/ч = 6000 м/ч = 100 м/мин. 100 · 5 = 500 (м). |
Задание 13. 1) 226 · 41 + 3120 : 390 = 9274
2) 27 · 307 – 4685 : 937 = 8284
|
Урок 123. Определение вида треугольника. Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с классификацией треугольников по величинам их углов и по длинам их сторон; способствовать формированию умений распознавать и изображать треугольники; совершенствовать умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с классификацией треугольников по величинам их углов и по длинам их сторон; научатся классифицировать треугольники по величинам их углов (остроугольный, прямоугольный, тупоугольный); по длинам их сторон (разносторонний, равнобедренный, равносторонний) |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы. Регулятивные: принимают и сохраняют учебную задачу, соответствующую этапу обучения; проговаривают вслух последовательность производимых действий, составляющих основу осваиваемой деятельности. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками; определяют цели, функции участников, способы взаимодействия; проявляют инициативное сотрудничество в поиске и сборе информации |
Личностные: осознают необходимость самосовершенствования |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний. Игра «Распутай клубок».
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: а) 7 · 8 = 56 б) 30 + 38 = 68 56 : 4 = 14 68 – 18 = 50 14 · 6 = 84 38 + 30 = 68 |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||
|
|
– Запишите верные равенства, вставив пропущенные цифры. 3636 4540 |
Решение: 36365 : 5 = 7273 2184 : 3 = 728 45400 : 5 = 9080 5142 : 3 = 1714 |
||||||||||||
|
|
– Выполните деление: 65 : 8 61 : 7 37 : 9 29 : 4 43 : 7 47 : 5 52 : 8 55 : 6 31 : 3 39 : 6 10 : 9 6 : 9 7 : 8 1 : 6 3 : 8 |
Решение: 65 : 8 = 8 (ост. 1) 61 : 7 = 8 (ост. 5) 29 : 4 = 7 (ост. 1) 43 : 7 = 6 (ост. 1) 52 : 8 = 6 (ост. 4) 55 : 6 = 9 (ост. 1) 39 : 6 = 6 (ост. 3) 10 : 9 = 1 (ост. 1) 7 : 8 = 0 (ост. 7) 1 : 6 = 0 (ост. 1)
37 : 9 = 4 (ост. 1) 47 : 5 = 9 (ост. 2) 31 : 3 = 10 (ост. 1) 6 : 9 = 0 (ост. 6) 3 : 8 = 0 (ост. 3) |
||||||||||||
|
Геометрический материал |
– Сколько всего квадратов на рисунке 1 и на рисунке 2? |
– Всего 5 квадратов на рисунке 1 и 14 квадратов на рисунке 2. Рис. 1 Рис. 2 |
||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 137). Задание 6. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Определите вид треугольника, измерив длины его сторон. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
1-й треугольник – равносторонний. 2-й треугольник – равнобедренный. 3-й треугольник – разносторонний. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|||||||||||
|
Задание 7. |
– Периметр равнобедренного треугольника равен 25 см. Длина наибольшей из сторон равна 9 см. найдите длины остальных сторон. |
Решение:
|
||||||||||||
|
Задание 8. |
– Приведите пример, подтверждающий или опровергающий высказывание. 1) Среди прямоугольных треугольников есть равнобедренные.
2) Если треугольник тупоугольный, то он разносторонний.
3) Любой остроугольный треугольник является равносторонним. |
Ответы:
1) Истинно. АВ = АС FD ¹ DE
|
||||||||||||
|
Задание 9. |
– Периметр равностороннего треугольника равен 609000 мм. Вычислите длину стороны треугольника в метрах. |
Решение: 1) 609000 мм = 609 м. 2) 609 : 3 = 203 (м) – длина стороны. |
||||||||||||
|
Задание 10 |
– Начертите в тетради прямоугольный равнобедренный треугольник. Длина каждой из равных сторон – 4 см 6 мм |
|
||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 139–141). Задание 18. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько пуха израсходуют для изготовления пяти больших подушек?
|
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись:
Решение: 1) 800 · 3 = 2400 (г) – на 1 большую подушку. 2) 2400 · 5 = 12000 (г) – 5 больших подушек. 12000 г = 12 кг |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||
|
Задание 19. |
– Выполните действия. |
Выполняют задание (см. ресурсный материал к уроку). |
||||||||||||
|
Задание 20. |
– Найдите значения выражений. |
Выполняют задание (см. ресурсный материал к уроку). |
||||||||||||
|
Задание 21. |
– Найдите неизвестное число. |
Выполняют задание (см. ресурсный материал к уроку). |
||||||||||||
|
Задание 22. |
– Вычислите периметр и площадь прямоугольника АВСD. – Вычислите периметр и площадь прямоугольника ADEM. |
Выполняют задание (см. ресурсный материал к уроку). |
||||||||||||
|
Задание 23. |
– Какие из высказываний истинны? |
– 2 и 4 высказывания истинны. |
||||||||||||
|
Задание 24*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какова цена 1 кг орехов? – Какова стоимость 400 г орехов? |
Запись: 100 г орехов – 24 р. 1 кг – ? р. 400 г – ? р. Решение: 1) 1000 : 100 = 10 (раз) – больше. 2) 24 · 10 = 240 (р.) – стоит 1 кг орехов. 3) 24 · 4 = 96 (р.) – стоимость 400 г орехов. |
||||||||||||
|
Задание 25*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какова стоимость 100 г кофе? |
Решение (см. ресурсный материал к уроку). |
||||||||||||
|
Задание 26*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько денег у Андрея? |
Решение: 1) 2500 : 5 = 500 (р.) – 1/5 часть денег Олега и 1/10 часть денег Андрея. 2) 500 · 10 = 5000 (р.) – у Андрея. |
||||||||||||
|
Задание 27. |
– Прочитайте определения понятий. – Выполните от руки рисунки, иллюстрирующие эти определения. |
|
||||||||||||
|
Задание 28 |
– Постройте первый треугольник в масштабе 1 : 2 (вариант 1). – Постройте второй треугольник в масштабе 2 : 1 (вариант 2) |
– Стороны первого треугольника: 15 мм, 30 мм, 33 мм. – Стороны второго треугольника: 5 см, 4 см, 6 см 6 мм |
||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности |
Ресурсный материал к уроку
|
Задание 19. 639 · 185 = 118215 302 · 408 = 123216 4308 + 28765 = 33073 148431 – 139648 = 8783 45494 : 43 = 1058 35042 : 7 = 5006 9408 : 98 = 96 25578 : 63 = 406 1008 · 206 = 207648 67266 : 222 = 303
Задание 20. 413 · 302 – 54203 : 67 + 67591 · 0 = 123917 26433 : 33 + 507 · 418 – 0 : 9235 = 212727 2547 · 8 – 25 · 78 · 4 + 355 · 404 = 155996
Задание 21. а) 4350 – х = 2874 б) 180 · у = 9000 х = 4350 – 2874 у = 9000 : 180 х = 1476 у = 50 в) а : 208 = 67 г) т + 3008 = 14873 а = 67 · 208 т = 14873 – 3008 а = 13936 т = 11865 |
Задание 22.
Задание 25*. Решение: 1) Какую часть составляет 250 г от 1 кг? 1000 : 25 = 4 (ч.). 2) Сколько стоит 1 кг кофе? 150 · 4 = 600 (р.). 3) Какую часть составляет 100 г от 1 кг? 1000 : 100 = 10 (ч). 4) Сколько стоит 100 г кофе? 600 : 10 = 60 (р.). |
Урок 124. Контрольная работа № 9 по теме «Письменные приёмы вычислений.
Решение задач»
|
Тип урока: контроль знаний и способов действий |
||
|
Педагогические задачи: проверить знания, умения, навыки обучающихся по теме «Письменные приемы вычислений. Решение задач» |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять правила нахождения неизвестных компонентов арифметических действий (второго слагаемого, второго множителя, вычитаемого, делителя); решать задачи |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи. Регулятивные: определяют и формулируют цель деятельности на уроке; составляют план и последовательность действий; оценивают результат работы, определяют, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения |
Личностные: имеют желание учиться; осознают необходимость самосовершенствования; понимают значение границ собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
|
I. Содержание контрольной работы. Вариант 1 |
Знакомит с содержанием контрольной работы, комментирует задания. |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять контроль по результату |
|
|
1. Выполни действие.
|
1. Ответы: 311311 56172 59099 6832 1529 270 21640 13 365180 1234321 |
|||
|
2. Вычисли значение выражения. (45576 : 27 – 1600) · 251 + 49 = |
2. Ответ: 22137. |
|||
|
3. Начерти отрезок длиной 5 см 5 мм и раздели его пополам с помощью циркуля и линейки. |
|
|||
|
4. Запиши обозначение угла и определи его вид.
|
4. Ответ: ВОА – прямой угол. |
|||
|
5. Какой треугольник изображён на рисунке – прямоугольный, остроугольный или тупоугольный?
|
5. Ответ: АВС – тупоугольный треугольник. |
|||
|
6*. Сколько часов и минут составляют полтора часа? |
6*. Ответ: 1 ч 30 мин |
|||
|
Вариант 2 |
1. Выполни действие.
2. Вычисли значение выражения. (105 · 24 + 480 ) : 150 · 20 = |
1. Ответы: 411380 80592 46909 9598 1821 330 33320 15 409840 4937284 2. Ответ: 400. |
||
|
3. Начерти отрезок длиной 4 см 5 мм и раздели его пополам с помощью циркуля и линейки. |
|
|||
|
4. Запиши обозначение угла и определи его вид.
|
4. Ответ: ВОА – острый угол. |
|||
|
5. Какой треугольник изображён на рисунке – прямоугольный, остроугольный или тупоугольный?
|
5. Ответ: АВС – остроугольный треугольник. |
|||
|
6*. Сколько тонн и килограммов составляют полторы тонны? |
6*. Ответ: 1 т 500 кг |
|||
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 125. Точное и приближённое значение величины
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: создать условия для знакомства с понятием о точности измерений и её оценке, с понятием о приближенных значениях величины (с недостатком, с избытком); повторить единицы длины, массы, вместимости, времени; способствовать формированию умений соотносить между собой единицы измерения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием о точности измерений и её оценке, с понятием о приближенных значениях величины (с недостатком, с избытком); научатся определять источники ошибок при измерении величин; выполнять запись результатов измерения с использованием знака |
Метапредметные: Познавательные: умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: применяют правила делового сотрудничества: сравнивают разные точки зрения; считаются с мнением другого человека; проявляют терпение и доброжелательность в споре, доверие к собеседнику (соучастнику деятельности) |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
Выполните деление:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Ответ: 7 треугольников. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||
|
Интеллектуальная разминка. |
– Найдите и исправьте ошибки, если они есть:
|
Решение:
|
||||||
|
Задача |
– Решите задачу. Масса гуся 5 кг, что на 3 кг больше, чем масса курицы. Сколько весят гусь и курица вместе? |
Решение: (5 – 3) + 5 = 7 (кг) – масса гуся и курицы |
||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 142). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Какое время показывают каждые часы? – Какие часы наиболее точно показывают время в данный момент? По каким часам можно определить время с точностью до часа? – А с точностью до минуты? – А с точностью до секунды? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– По первым часам можно определить время с точностью до часа.
– По вторым часам – с точностью до минуты. – По третьим часам – с точностью до секунды. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей |
|||||
|
Задание 2 |
– С помощью каких весов можно точнее определить массу апельсина? |
– С помощью третьих весов можно точнее определить массу апельсина |
||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 144–145). Задание 7. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько листов фанеры потребуется для того, чтобы вырезать 90 таких квадратов? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Ответ: 6 листов фанеры потребуется для того, чтобы вырезать 90 таких квадратов. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью |
|||||
|
Задание 8. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно. |
||||||
|
Задание 9. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько муки получилось из всей пшеницы? |
Запись: 5 кг пшеницы – 4 кг муки. 7500 кг пшеницы – ? кг муки. Решение: 1) 7500 : 5 = 1500 (раз) – по 4 кг муки. 2) 1500 · 4 = 6000 (кг) – муки из всей пшеницы. |
||||||
|
Задание 10. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько сена собрали со всего луга? |
Запись: Длина – 150 м. Ширина – 60 м. Площадь – ? м2, ? кг. 100 м2 – 180 кг. Решение: 1) 150 · 60 = 9000 (м2) – площадь луга. 2) 9000 : 100 = 90 (раз) – по 180 кг. 3) 180 · 90 = 16200 (кг) – собрали со всего луга. |
||||||
|
Задание 11 |
– Определите вид треугольников по длинам сторон. – Определите вид треугольников по видам углов. – Проверьте, выполнив необходимые измерения, что прямая XY является осью симметрии каждого из указанных треугольников |
D АХС – равнобедренный. D ВХК – равнобедренный. D РХМ – равносторонний. D АХС – тупоугольный. D ВХК – остроугольный. D РХМ – остроугольный |
||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 126. Приближённое значение величины. Контрольный устный счёт № 8
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием о точности измерений и её оценке, с понятием о приближенных значениях величины (с недостатком, с избытком); повторить единицы длины, массы, вместимости, времени; способствовать формированию умений соотносить между собой единицы измерения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием о точности измерений и её оценке, с понятием о приближенных значениях величины (с недостатком, с избытком); научатся определять источники ошибок при измерении величин; выполнять запись результатов измерения с использованием знака |
Метапредметные: Познавательные: используют знаково-символические средства для решения учебной задачи; выдвигают и формулируют проблему, самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера. Регулятивные: адекватно воспринимают оценку своей работы учителем, товарищами; осуществляют рефлексию способов и условий действия, контроль и оценку процесса и результатов деятельности. Коммуникативные: умеют работать в паре; контролируют действия партнера |
Личностные: имеют желание учиться |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Разложите карточки с выражениями в порядке возрастания их значений:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
Решение:
|
Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||||||
|
|
– Соедините выражения, значения которых содержат одинаковое количество цифр: 5426 : 6 87045 : 9 39505 : 5 4971 : 5 148444 : 6 5392 : 4 8291 : 3 269743 : 5 |
Решение:
|
|||||||||||||||||||||||||||||||
|
|
– Дети решали пример 707 : 7. У Маши получилось 11, у Оли – 110, у Коли – 101. Кто из них прав? |
– Прав Коля |
|||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 143). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания. – Кто из учеников точнее указал длину отрезка АВ? – На сколько миллиметров ошибся Миша? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. – Маша точнее указала длину отрезка АВ.
– На 6 миллиметров ошибся Миша. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Осуществлять контроль по результату |
||||||||||||||||||||||||||||||
|
– На сколько миллиметров ошиблась Маша? – Говорят, что длина отрезка АВ, измеренная с точностью до сантиметра, равна 5 см. Записывают это так: АВ » 5 см. |
– На 4 миллиметра ошиблась Маша. |
||||||||||||||||||||||||||||||||
|
Задание 4 |
– Прочитайте записи. Какая запись выражает точное значение величины, а какая – приближенное? – На сколько они отличаются друг от друга? |
Запись:
|
|||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 145–147). Задание 12. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Вычислите периметр и площадь участка. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
Запись: а = 40 м b = 50 м Периметр – ? Площадь – ? Решение: 1) (40 + 50) · 2 = 180 (м) – периметр участка. 2) 40 · 50 = 2000 (м2) – площадь участка. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии |
||||||||||||||||||||||||||||||
|
Задание 13. |
– Составьте три задачи. |
Задача 1) u = 70 км/ч t = 3 ч s = u · t s – ? s = 70 · 3 = 210 (км) Задача 2) u = 50 км/ч t – ? ч t = s : u s = 350 км t = 350 : 50 = 7 (ч) Задача 3) u – ? км/ч t = 2 ч u = s : t s = 1900 км u = 1900 : 2 = 950 (км/ч) |
|||||||||||||||||||||||||||||||
|
Задание 14. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько платков получится? |
Запись: Ширина – ?, 2 пл. с длиной стороны 30 см Длина – 1 м 20 см Платков – ? шт. Решение: 1) 1 м 20 см = 120 см; 120 : 30 = 4 (раза) – по 30 см в длине. 2) 4 · 2 = 8 (пл.) – можно выкроить из куска ткани. |
|||||||||||||||||||||||||||||||
|
Задание 15*. |
– Произведение двух чисел равно 705. Чему равно новое произведение, если один из множителей уменьшить в 5 раз, а другой оставить без изменения? |
Решение: 141 · 5 = 705 5 : 5 = 1 141 : 1 = 141 Вывод: произведение уменьшится в 5 раз. |
|||||||||||||||||||||||||||||||
|
Задание 16*. |
– Частное двух чисел равно 180. Чему равно новое частное, если делитель увеличить в 2 раза? |
Решение: 720 : 4 = 180 4 · 2 = 8 720 : 8 = 90 Вывод: частное уменьшится в 2 раза. |
|||||||||||||||||||||||||||||||
|
Задание 17 |
– Рассмотрите диаграмму и ответьте на вопросы. – Сколько в доме квартир, в которых живут попугаи, кошки, хомяки? – Каких животных больше всего? Меньше всего? – Назовите животных в порядке увеличения их численности в доме.
– На сколько собак больше, чем кошек? – На сколько попугаев меньше, чем кошек и собак?
– Во сколько раз черепах меньше, чем собак? – Верно ли, что хомяков на 5 больше, чем черепах? – Сколько всего животных живет в доме? |
– 30 в доме квартир, в которых живут попугаи. 35 квартир, в которых живут кошки. 25 квартир, в которых живут хомяки. – Собак больше всего. Черепах меньше всего. Называют животных в порядке увеличения их численности в доме: черепахи, хомяки, попугаи, кошки, собаки. – На 5 собак больше, чем кошек. – На 5 попугаев меньше, чем кошек. – На 10 попугаев меньше, чем собак. – В 2 раза черепах меньше, чем собак. – Верно, что хомяков на 5 больше, чем черепах.
– Всего 150 животных живет в доме. 20 + 35 + 25 + 40 + 30 = 150 |
|||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
Урок 127. Решение задач на нахождение приближённой величины
|
Тип урока: комбинированный |
||
|
Педагогические задачи: создать условия для знакомства с понятием о точности измерений и её оценке, с понятием о приближенных значениях величины (с недостатком, с избытком); повторить единицы длины, массы, вместимости, времени; способствовать формированию умений соотносить между собой единицы измерения |
||
|
Планируемые результаты |
||
|
Предметные: познакомятся с понятием о точности измерений и её оценке, с понятием о приближенных значениях величины (с недостатком, с избытком); научатся определять источники ошибок при измерении величин; выполнять запись результатов измерения с использованием знака |
Метапредметные: Познавательные: умеют ориентироваться в учебнике (на развороте, в оглавлении, в условных обозначениях); находят ответы на вопросы в тексте, иллюстрациях; делают выводы в результате совместной работы класса и учителя. Регулятивные: определяют и формулируют цель деятельности на уроке. Коммуникативные: задают вопросы; формулируют собственное мнение и позицию |
Личностные: имеют желание учиться; осознают необходимость самосовершенствования; понимают значение границ собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка. |
Организует устный счет с целью актуализации знаний.
Решите ребусы:
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
Решение:
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||
|
Задачи. |
– Решите задачи: а) Надя отдыхала на даче с 3 по 21 июля. Сколько дней Надя была на даче? б) Кинофестиваль начал работу 14 марта и закончил 19 марта. Сколько дней проходил кинофестиваль? |
Решение: а) 19 дней Надя была на даче.
б) 6 дней проходил кинофестиваль. |
||||||||||||||||||||||
|
Игра «Угадай число». |
– Задумано число. При умножении его на 5 получилось 10; 40; 20; 45; 35; 30; 5; 0; 15; 25. Какое число было задумано? |
|
||||||||||||||||||||||
|
Задача |
– Решите задачу. На одной чаше весов, которые находятся в равновесии, лежат одна морковка и две одинаковые редиски, на другой – такие же две морковки и 1 редиска. Что легче: морковка или редиска? |
Ответ: массы морковки и редиски одинаковые |
||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 144). Задание 5. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Определите массу тыквы с помощью изображенных на рисунке весов. – Определите ошибку измерения. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Решение: 5 кг + 2 кг + 1 кг + 500 г + 200 г = 8 кг 700 г. 8 кг 700 г – 8 кг 657 г = 43 г. |
Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор |
|||||||||||||||||||||
|
Задание 6 |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Укажите приближенное значение длины каждого шнура с точностью до метра |
Решение: 12 м 6 см » 12 м 12 м 95 см » 13 м |
||||||||||||||||||||||
|
IV. Включение нового в активное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 147–148). Задание 18. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Определите вид треугольника по заданным параметрам. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– Первый треугольник равнобедренный, второй треугольник – равносторонний. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок |
|||||||||||||||||||||
|
Задание 19. |
– Запишите в тетради названия фигур. |
Запись: конус, куб, цилиндр, пирамида. |
||||||||||||||||||||||
|
Задание 20. |
– У кого из мальчиков равносторонний треугольник? – Как называется другой треугольник? |
– У Коли равносторонний треугольник. – Дима начертил равнобедренный треугольник. |
||||||||||||||||||||||
|
Задание 21 |
– Определите вид каждого из углов. Запишите в соответст-вующей графе таблицы его номер |
Запись:
|
||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 128. Построение отрезка, равного данному, с помощью циркуля и линейки
|
Тип урока: открытие новых знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений распознавать и изображать отрезки с помощью циркуля и линейки; содействовать развитию умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся выполнять построение отрезка, равного данному, с помощью циркуля и линейки |
Метапредметные: Познавательные: умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Регулятивные: проговаривают последовательность действий на уроке; оценивают совместно с учителем или одноклассниками результат своих действий, вносят соответствующие коррективы. Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками; определяют цели, функции участников, способы взаимодействия |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. – Выполните деление: 150 : 3 240 : 6 420 : 7 210 : 7 350 : 5 2800 : 4 7200 : 9 3600 : 9 5400 : 6 2700 : 3 – Какие знания вам пригодились? |
Отвечают на вопросы учителя.
Выполняют задания устного счета. 50 40 60 30 70 700 800 400 900 900 – Пригодились знания таблицы умножения и деления. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Найдите делимое:
– Как найти неизвестное делимое? |
Решение: 240 : 3 = 80 280 : 7 = 40 540 : 9 = 60 200 : 5 = 40 560 : 8 = 70 160 : 4 = 40
џ Чтобы найти неизвестное делимое, надо значение частного умножить на делитель. |
|
|
|
– Положите 3 палочки так, чтобы получились 3 разных угла: прямой, острый и тупой. – Положите три палочки так, чтобы получилось три острых угла |
Решение: |
|
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 149–150). Задание 1. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Составьте алгоритм построения отрезка, равного данному, с помощью циркуля и линейки.
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Составляют алгоритм построения отрезка, равного данному, с помощью циркуля и линейки. 1. Начертить луч, отметить на нем точку С. 2. Циркулем измерить длину отрезка АВ. 3. Провести окружность радиуса, который равен отрезку АВ, с центром в точке С. 4. Отметить точку пересечения луча и дуги окружности. Обозначить ее буквой К. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость |
|
Задание 2. |
– Выполните задание самостоятельно, проведите взаимопроверку в парах. |
Работают самостоятельно. |
|
|
Дополнительный материал |
Построение прямого угла и деление отрезка пополам. Отложим на прямой отрезок АВ (рис. 1). Одним и тем же радиусом, равным длине отрезка, проведём две окружности с центрами в точках А и В. Окружности пересекутся в двух точках С и D. Проведём прямую через точки С и D. Обозначим точку пересечения прямых буквой О. Вместо окружностей можно проводить дуги (части окружностей) любого одинакового радиуса, лишь бы он был больше, чем половина отрезка КЕ. – Сделаем такой чертёж, как на рисунке 2, и убедимся, что построенные прямые при пересечении образуют прямые углы, а точка их пересечения делит отрезок пополам |
|
|
|
IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным. Работа по учебнику (с. 151–152). Задание 5. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– На сколько приближенный результат, который получила Даша, отличается от точного значения длины рукава? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– На 3 мм приближенный результат отличается от точного значения длины рукава. 54 см 3 мм – 54 см = 3 мм. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий |
|
Задание 6. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Сколько денег могло остаться у Кати? |
Решение: 1) 15 · 6 = 90 (р.) – стоят 6 пирожных. 2) 15 · 7 = 105 (р.) – стоят 7 пирожных. Ответ: у Кати осталось от 90 до 104 рублей. |
|
|
Задание 7. |
– За какое время в действительности Алеша проплыл дистанцию? |
– За 1 минуту 20 секунд в действительности Алеша проплыл дистанцию. |
|
|
Задание 8*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Как изменяется масса воды в трюме – увеличивается или уменьшается и как быстро? |
– Масса воды в трюме уменьшается. 8 т 500 кг – 5 т = 3 т 500 кг. |
|
|
Задание 9. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какова масса Ванечки? |
Решение: 1) 1 т = 1000 кг; 1000 : 100 = 10 (кг) – вес Тани. 2) 1000 : 1000 = 1 (кг) – разница в весе; 10 – 1 = 9 (кг) – вес Вани. |
|
|
Задание 10. |
– Найдите значения выражений. |
Выполняют задание (см. ресурсный материал к уроку). |
|
|
Задание 11. |
– Составьте равенства. |
Выполняют задание (см. ресурсный материал к уроку). |
|
|
Задание 12. |
– Приведите пример, подтверждающий или опровергающий высказывание. 1) Среди равнобедренных треугольников есть равносторонние.
2) Существуют углы, которые больше прямого угла. 3) Из двух чисел одно всегда больше или меньше другого. 4) Не существует равнобедренных прямоугольных треугольников. |
– Первое высказывание ложно, так как у равнобедренных треугольников только две стороны имеют одинаковую длину. – Второе высказывание истинно. Это тупые углы. – Третье высказывание истинно. Например, 6 > 3. – Четвертое высказывание ложно. АС = АВ; Ð А – прямой.
|
|
|
Задание 13 |
– Вычислите неизвестное число |
Выполняют задание (см. ресурсный материал к уроку) |
|
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Ресурсный материал к уроку
|
Задание 10. (484260 – 1020 · 34) : (133350 : 105) = 354 22680 : 54 : (12873 – 112 · 114) = 4 3640 : 28 · 2 + 8 · 2010 = 16340 (26908 : 124 + 74370 : 74) · 20 = 24440 |
Задание 11. 1) 8000 : 20 : 4 = 100 2) (9500 – 2500) : 7 = 1000 3) 1400 : 700 : 2 = 1 4) (12000 + 15000) : 1000 = 27 |
Задание 13. а) 381 · х = 1524 х = 1524 : 381 х = 4 б) 1010 – у = 304 у = 1010 – 304 у = 706 в) х : 88 = 102 х = 102 · 88 х = 8976 г) 629 + у = 1258 у = 1258 – 629 у = 629 |
Урок 129. Упражнения в построениИ отрезков. Практическая работа
|
Тип урока: комбинированный |
||
|
Педагогические задачи: способствовать формированию умений распознавать и изображать отрезки с помощью циркуля и линейки; содействовать развитию умения решать арифметические задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся выполнять построение отрезка, равного данному, с помощью циркуля и линейки |
Метапредметные: Познавательные: строят логическую цепь рассуждений; проводят аналогии между изучаемым материалом и собственным опытом; формулируют проблемы; самостоятельно создают способы решения проблем творческого и поискового характера. Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации. Коммуникативные: учатся конструктивно разрешать конфликты посредством учёта интересов сторон и сотрудничества |
Личностные: формируют внутреннюю позицию школьника на уровне положительного отношения к школе; приобретают первичные умения оценки работ, ответов одноклассников на основе заданных критериев успешности учебной деятельности |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний. – Заполните таблицу.
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Запись:
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– Разгадайте правило, по которому составлен первый столбик. Составьте по тому же правилу второй и третий столбики выражений: а) 24 : 8 = 3 128 : 8 = 16 144 : 6 = 24 24 : 3 = 8 … … 3 · 8 = 24 … … 8 · 3 = 24 … … |
Решение:
а) 24 : 8 = 3 128 : 8 = 16 144 : 6 = 24 24 : 3 = 8 128 : 16 = 8 144 : 24 = 6 3 · 8 = 24 16 · 8 = 128 24 · 6 = 124 8 · 3 = 24 8 · 16 = 128 6 · 24 = 124 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– Решите задачу. Масса куска дерева 3 кг. Чему равна масса 3 кусков железа таких же размеров, как кусок дерева, если дерево в 12 раз легче железа? |
Решение: 3 · 3 · 12 = 108 (кг). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
– На какое число надо умножить 285714, чтобы получить шестизначное число, записанное теми же цифрами? Вторая цифра этого числа равна 5 |
Решение: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 150). Задание 3. |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
– Найдите длину каждой ломаной, выполняя только одно измерение. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
– Длина ломаной АВС составляет 5 см. Длина ломаной MCAD составляет 11 см. |
Планировать решение учебной задачи. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4. |
– Найдите периметр фигуры, выполняя только одно измерение. |
Решение: 1) РАВС = 50 мм + 20 мм + 35 мм = 105 мм. 2) PEMAD = 20 мм + 30 мм + 55 мм + 25 мм = =130 мм. 3) PABCD = (60 мм + 20 мм) · 2 = 160 мм. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Дополнительный материал |
Построение треугольника с двумя равными сторонами. Выполнив чертёж, показанный на рисунке 1, легко получить треугольник с двумя равными сторонами. Достаточно любую точку прямой МВ соединить отрезками с точками К и Е. На рисунке 1 показаны 3 таких треугольника: КМЕ, КВЕ и КСЕ. Сделайте чертёж. Построение прямоугольника (квадрата). – Чтобы построить прямоугольник, легче всего начертить любую окружность, провести в ней два любых диаметра и соединить их концы отрезками (рис. 2). Чтобы построить квадрат, надо провести диаметры, которые образуют прямые углы |
а) б) в) Рис. 2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
IV. Включение нового в актив-ное использо- вание в сочетании с ранее изученным, освоенным. Работа по учеб- нику (с. 153–157). |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Рассмотрите схему движения двух поездов. – На сколько километров за 6 ч удалится от пункта А поезд, который шел со скоростью 50 км/ч?
– На сколько километров за 6 ч удалится от пункта В поезд, который шел со скоростью 60 км/ч? |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.
– На 300 километров за 6 ч удалился от пункта А поезд, который шел со скоростью 50 км/ч. 50 · 6 = 300 (км). – На 360 километров за 6 ч удалился от пункта В поезд, который шел со скоростью 60 км/ч. 60 · 6 = 360 (км). |
Выбирать действия в соответствии с постав- ленной задачей, оценивать уровень владения тем или иным учебным дейст- вием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять взаимный контроль, планировать способы взаимодействия |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 14. |
– Какое расстояние будет между поездами через 6 ч после начала движения? |
– 835 км – расстояние между поездами через 6 ч. 50 · 6 + 60 · 6 + 175 = 835 (км). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 15. |
– Кто выполнил точнее измерение? – Кто допустил ошибку? – Какую ошибку? |
– Саша выполнил точнее измерение. – Лена допустила ошибку. Ошибка: 9 дм – 8 дм 6 см 3 мм = 3 см 7 мм. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 16. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – сколько времени необходимо автобусу на обратный путь? |
Решение (см. ресурсный материал к уроку). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 17. |
– Сколько денег положила Маша в копилку на пятнадцатый день? |
Запись: 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + + 512 + 1024 + 2048 + 4096 + 8192 + 16384 = = 32767 (к.); 32767 к. = 327 р. 67 к. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 18. |
– Выполните вычисления. – Проверьте свои вычисления с помощью калькулятора. |
Работают самостоятельно в парах. Осуществляют взаимоконтроль. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 19*. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – Какова стоимость 50 г смеси? |
Решение (см. ресурсный материал к уроку). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 20*. |
– Определите число пустых стаканов. |
– Пустых стаканов – 4. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 21*. |
– С какой скоростью катер будет плыть на обратном пути? |
Решение: 1) 24 – 2 = 22 (км/ч) – собственная скорость катера. 2) 22 – 2 = 20 (км/ч) скорость катера на обратном пути. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 23. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – С какой скоростью ехала «Газель»? |
Решение (см. ресурсный материал к уроку). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 24*. |
– Какова масса одной дыни? |
Решение: 16 : 4 = 4 (кг) – масса одной дыни. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 25. |
– Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. – В чем ошибка Пети? |
– Ошибка в том, что длина и ширина взята в самом широком месте, так озеро не прямоугольное, поэтому и площадь отличается. А Петя посчитал так, если бы озеро было прямоугольным. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 26. |
– Какие числа надо записать в «окошках», чтобы равенства были верными? |
Выполняют задание (см. ресурсный материал к уроку). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 27. |
– Составьте выражение и решите задачу. – Найдите значение выражения, если р = 17 км/ч. |
Запись: 90 – р · 3. 90 – 17 · 3 = 90 – 51 = 39 (км). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 28 |
– Вычислите неизвестное число |
Выполняют задание (см. ресурсный материал к уроку) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность. Осуществлять итоговый контроль, формиро-вать адекватную самооценку |
Ресурсный материал к уроку
|
Задание 16.
Решение: 1) 64 : 2 = 32 (км) – проехал за 30 мин. 2) 32 + 28 = 60 (км) – весь путь. 3) 64 – 4 = 60 (км/ч) – скорость на обратном пути. 4) 60 : 60 = 1 (ч) – время на обратный путь.
Задание 19*.
Решение: 1) 28 · 10 = 280 (р.) – стоит 1 кг цейлонского чая. 2) 280 · 5 = 1400 (р.) – стоят 5 кг цейлонского чая. 3) 30 · 10 = 300 (р.) – стоит 1 кг индийского чая. 4) 300 · 5 = 1500 (р.) – стоят 5 кг индийского чая. 5) 1400 + 1500 = 2900 (р.) – стоят 10 кг смеси. 6) 10 кг = 10000 г 10000 : 50 = 200 (раз) – меньше стоимость 50 г смеси. 7) 2900 р. : 200 = 14 р. 50 к. – стоимость 50 г смеси. |
Задание 23. Решение: 1) 40 : 4 = 10 (км/ч) – скорость изменения. 2) 50 + 10 = 60 (км/ч) – скорость «Газели».
Задание 26. а)
944 : 8 = 118 1020 – 874 = 146 в)
9116 – 3075 = 6041 365 : 5 = 73
Задание 28. а) т : 8 = 134924 б) с : 306 = 409 т = 134924 · 8 с = 306 · 409 т = 1079392 с = 125154 в) b : 29 = 1060 г) k : 108 = 706 b = 1060 · 29 k = 706 · 108 b = 30740 k = 76248 |
|||||||||||||||||||||||||||
Урок 130. Повторение по теме «Многозначное число.
Устные и письменные приёмы сложения и вычитания многозначных чисел»
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: способствовать формированию умений читать и записывать многозначное число; выполнять устные и письменные приёмы сложения и вычитания многозначных чисел; применять полученные знания при выполнении заданий |
||
|
Планируемые результаты |
||
|
Предметные: научатся читать и записывать многозначное число; выполнять устные и письменные приёмы сложения и вычитания многозначных чисел; применять полученные знания при выполнении заданий |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая), и преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Найдите значения выражений: 46 : 2 63 : 3 4246 : 2 36 : 3 96 : 3 9636 : 3 48 : 2 82 : 2 4848 : 4 |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: 46 : 2 = 23 63 : 3 = 21 4246 : 2 = 2123 36 : 3 = 12 96 : 3 = 32 9636 : 3 = 3212 48 : 2 = 24 82 : 2 = 41 4848 : 4 = 1212 |
Выделять существенную информацию из текста задачи. Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||
|
Интеллектуальная разминка. |
– Расположите выражения в порядке возрастания их значений:
– Объясните, как рассуждали. |
Решение:
|
||||||||||||||||||||
|
|
– Найдите задачи с «ловушками»: а) На овощной базе расфасовывали картофель в контейнеры. Сколько всего килограммов картофеля расфасовали, если получилось 14 контейнеров по 876 кг в каждом? |
Ответ: б) «ловушка»; в) «ловушка». |
||||||||||||||||||||
|
|
б) В магазин привезли 16 ящиков лимонада по 20 бутылок в каждом. Ящики разгрузили за 15 минут. Сколько бутылок лимонада привезли в магазин? в) Для детского сада купили 10 одинаковых наборов кубиков. Сколько всего кубиков привезли в детский сад? – Выберите выражение, которое является решением задачи а):
|
Решение: 876 · 14 = 12264 (кг) – масса картофеля. |
||||||||||||||||||||
|
Задание на смекалку |
– Напишите число 100 с помощью пяти единиц и знаков действий |
Решение: 111 – 11 = 100 |
||||||||||||||||||||
|
III. Открытие нового знания, способа действия. Работа по учебнику (с. 157). Задание 29*. |
Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.
– Выразите скорость в метрах в минуту. |
Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения. Запись: 90 км/ч = 90000 м/ч = 1500 м/мин. 960 км/ч = 960000 м/ч = 16000 м/мин. 18 км/ч = 18000 м/ч = 300 м/мин. 120 км/ч = 120000 м/ч = 2000 м/мин. |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью. Осуществлять взаимный контроль, планировать способы взаимодействия |
|||||||||||||||||||
|
Задание 30. |
– Вычислите неизвестные числа. |
Решение: а) х + 4078 = 12106 д) 91356 + х = 100000 х = 12106 – 4078 х = 100000 – 91356 х = 8028 х = 8644 б) а – 9999 = 101010 е) 60015 – а = 4326 а = 101010 + 9999 а = 60015 – 4326 а = 111009 а = 55689 в) с · 6 = 3864 ж) 15 · с = 153075 с = 3864 : 6 с = 153075 : 15 с = 644 с = 10205 г) у : 9 = 81810 и) 10800 : у = 40 у = 81810 · 9 у = 10800 : 40 у = 736290 у = 270 |
||||||||||||||||||||
|
Задание 31*. |
– Заполните таблицу.
|
Заполняют таблицу.
|
||||||||||||||||||||
|
Задание 32 |
– Изобразите расстояние от дома до школы отрезком в масштабе 1 : 4000 |
– Масштаб 1 : 4000 означает, что 1 см плана содержит 40 метров местности. Ведь 100 см это один метр. Если 4000 см поделить на 100 см, то получим 40 метров. Теперь 200 метров делим на 40 метров, получаем 5, то есть 200 м на местности изображаются на плане отрезком в 5 см |
||||||||||||||||||||
|
IV. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Выражать доброжелательность и эмоционально-нравственную отзывчивость |
Урок 131. Контрольная работа № 10
по теме «Сложение и вычитание многозначных чисел»
|
Тип урока: контроль знаний и способов действий |
||
|
Педагогические задачи: проверить сформированность знаний о нумерации многозначных чисел и умений решать задачи на движение, сравнивать величины, вычислять значения выражений с многозначными числами, находить площадь и периметр прямоугольника |
||
|
Планируемые результаты |
||
|
Предметные: научатся читать и записывать многозначное число; выполнять устные и письменные приёмы сложения и вычитания многозначных чисел; применять полученные знания при выполнении заданий |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи. Регулятивные: определяют и формулируют цель деятельности на уроке; составляют план и последовательность действий; оценивают результат работы, определяют, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения |
Личностные: имеют желание учиться; осознают необходимость самосовершенствования; понимают значение границ собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
I. Содержание контрольной работы. Вариант 1 |
Знакомит с содержанием контрольной работы, комментирует задания. |
Задают вопросы по содержанию контрольной работы. Самостоятельно выполняют задания контрольной работы. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осуществлять контроль по результату |
|
1. Выполни сложение и вычитание. 72 304 + 9 658 = 30 745 – 21 839 = 2. Выполни умножение и деление. 3 458 · 6 = 906 · 58 = 6 132 : 14 = 59 472 : 236 = 3. В магазин привезли 126 пакетов картофеля по 3 кг и столько же кг моркови в сетках по 2 кг. Сколько было сеток с морковью? 4. Измерь длину и ширину прямоугольника и вычисли его периметр и площадь.
|
1. Ответы: 81962 8906 2. Ответы: 20748 52548 438 252
3. Решение: 1) 126 · 3 = 378 (кг) – масса картофеля. 2) 378 : 2 = 189 (сеток) – с морковью. 4. Решение: 1) (7 + 2) · 2 = 18 (см) – периметр прямоугольника. 2) 7 · 2 = 14 (см2) – площадь прямоугольника.
|
||
|
5. Скорый поезд прошёл 1 080 км за 12 ч. Вычисли скорость поезда. 6. Обозначь цифрами 1, 2, 3, 4 порядок выполнения действий в выражении. 1054 + 32 · 280 – 30 450 : 15 7*. Длина одной стороны треугольника равна 2 дм 5 см, другой – 25 см, а третьей – 250 мм. Определи вид треугольника |
5. Решение: 1080 : 12 = 90 (км/ч) – скорость поезда. 6. Решение: 3 1 4 2 1054 + 32 · 280 – 30 450 : 15 7*. Ответ: равносторонний треугольник |
||
|
Вариант 2 |
1. Выполни сложение и вычитание. 82 139 + 7 951= 40 253 – 31 349 = 2. Выполни умножение и деление. 2 613 · 8 = 702 · 49 = 5 505 : 15 = 42 000 : 175 = 3. Имеется 168 трехлитровых банок с томатным соком и столько же литров морковного сока в двухлитровых банках. Сколько имеется банок с морковным соком? 4. Измерь длину и ширину прямоугольника и вычисли его периметр и площадь.
|
1. Ответы: 90090 8904 2. Ответы: 20904 34398 367 240
3. Решение: 1) 168 · 3 = 504 (л) – томатного сока. 2) 504 : 2 = 252 (б.) – с морковным соком.
4. Решение: 1) (4 + 2) · 2 = 12 (см) – периметр прямоугольника. 2) 4 · 2 = 8 (см2) – площадь прямоугольника. |
|
|
5. Самолёт летел 2 580 км за 3 ч. Вычисли скорость самолёта. |
5. Решение: 2 580 : 3 = 860 (км/ч) – скорость самолета |
||
|
6. Обозначь цифрами 1, 2, 3, 4 порядок выполнения действий в выражении. 14 · 250 – 32 800 : 16 + 1078 7*. Катя и Оля живут в одном доме. Катя ходит в школу со скоростью 4 км/ч, а Оля по той же дороге – со скоростью 6 км/ч. Кто из девочек тратит на дорогу больше времени? |
6. Решение: 1 3 2 4 14 · 250 – 32 800 : 16 + 1078 7*. Ответ: Катя тратит на дорогу больше времени |
||
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 132. Анализ контрольной работы. Работа над ошибками.
Повторение по теме «Многозначное число.
Устные и письменные приёмы сложения и вычитания многозначных чисел»
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: учить выполнять работу над ошибками; повторить единицы массы длины площади; совершенствовать вычислительные навыки |
||
|
Планируемые результаты |
||
|
Предметные: научатся читать и записывать многозначное число; выполнять устные и письменные приёмы сложения и вычитания многозначных чисел; применять полученные знания при выполнении заданий |
Метапредметные: Познавательные: осуществляют моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая), и преобразование модели с целью выявления общих законов, определяющих данную предметную область. Регулятивные: проговаривают последовательность действий на уроке; учатся высказывать свое предположение (версию) на основе работы с материалом учебника. Коммуникативные: умеют строить монологическое высказывание, владеют диалогической формой речи |
Личностные: планируют учебное сотрудничество с учителем и сверстниками |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний.
Устный счет. Интеллектуальная разминка |
Организует устный счет с целью актуализации знаний. |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
– Расставьте числа в порядке возрастания. 98, 4295, 3 846, 20 000, 34 295, 45 348, 1 309 400, 923 527, 500 004 – Назовите семизначное число. Назовите число, которое стоит после числа 20 000. Назовите число, в котором 295 единиц первого класса. Назовите число, в котором 3 единицы класса тысяч. Назовите соседей числа 923 527. Назовите чётные числа. – Что нужно сделать, чтобы легче прочитать многозначное число? |
Ответ: 98, 3846, 4 295, 20 000, 34 295, 45 348, 500 004, 923 527, 1 309 400.
• Многозначное число надо разбить на классы, начиная справа налево. А затем прочитать слева направо, называя количество единиц и название класса. |
||
|
– Вычислите разницу между глубиной океана и самой высокой точкой на Земле, если высота самой высокой горы в мире (Эверест) равна 8 848 м над уровнем моря. Максимальная глубина океана 11 022 м. |
Решение: 11022 – 8848 = 2174 (м). |
||
|
– Сорное растение василек дает 6680 семян в год, а такое растение, как ржаной костер, на 5260 меньше, полевой осот –на 12 920 больше, чем василек. Сколько семян в год дают все вместе эти растения? |
Решение: 1) 6680 – 5260 = 1420 (с.) – ржаной костер. 2) 6680 + 12920 = 19600 (с.) – полевой осот. 3) 6680 + 1420 + 19600 = 27700 (с.) – в год |
||
|
III. Повторение по теме урока. |
Организует работу по закреплению знаний, обеспечивает контроль за выполнением задания. |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. |
|
Задание 1. |
– На какой планете мы живём? – Выполнив сложение, определите диаметр планет. – Диаметр какой планеты больше ? – Диаметр какой планеты меньше? – Как сравнивать многозначные числа? |
Запись: 6 000 + 700 + 90 = 6790 км – диаметр Марса. 10 000 + 2 000 + 100 = 12 100 км – диаметр Венеры. 10 000 + 2 000 + 700 + 40 + 2 = 12 742 км – диаметр Земли. 50 000 + 1000 + 100 + 10 + 8 = 51118 км – диаметр Урана. 40 000 + 9 000 + 500 + 20 + 8 = 49 528 км – диаметр Нептуна. 100 000 + 40 000 + 3000 + 800 + 80 + 4 = 143884 км – диаметр Юпитера. |
|
|
Задание 2. |
– Решите задачу. Температура поверхности солнца 6000 градусов, температура солнечной короны в 250 раз больше температуры поверхности, а температура ядра в 9 раз больше температуры солнечной короны. Чему равна температура солнечного ядра? |
Работают в парах, составляют схему.
Решение: 6000 · 250 = 1500000 (гр.) – температура солнечной короны 1500000 · 9 = 13500000 (гр.) – температура ядра |
|
|
Задание 3. |
– Решите задачу. Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время дали другую цифру – 40 075. На сколько километров ошиблись древние учёные? |
Анализ задачи, решение самостоятельное. Решение: 40 075 – 39 690 = 385 (км). Проверка: 385 + 39 690 = 40 075 (км). |
Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|
Задание 4 |
Организует работу в парах. – Запишите многозначные числа: – Расстояние от Земли до Луны сорок тысяч семьсот километров. – Возраст нашего Солнца около пять миллиардов лет. – Расстояние от Земли до Солнца сто пятьдесят миллионов километров. – Толщина слоя воздуха над поверхностью Земли составляет 1 000 километров. – Длина Земли по экватору сорок тысяч семьдесят пять километров. – Подчеркните одной чертой самое маленькое число, подчеркните двумя чертами самое большое число. – Увеличьте числа на 100. – Представьте число 34 981 в виде суммы разрядных слагаемых |
Работают в парах. Запись: 40 700, 5 000 000 000, 150 000 000, 1 000, 40 075.
40 800, 5 000 000 100, 150 000 100, 1 100, 40 175. 34 981 = 30 000 + 4000 + 900 + 80 + 1 |
|
|
IV. Самостоятельная работа |
Проводит тест по теме урока. – Выберите верный ответ.
1. Укажи правильную запись числа: девять тысяч пятнадцать. а) 9 015 б) 90 015 в) 9 150 г) 915 2. Какое число следует за числом 24 567? а) 24 667 б) 24 568 в) 25 567 г) 24 566 3. Какое число представлено в виде суммы разрядных слагаемых: 40 000 + 5 000 + 600 + 50 + 4 а) 405 654 б) 4 565 в) 45 654 г) 54 654 4. Какая цифра стоит в разряде сотен в записи числа 432 567? а) 4 б) 3 в) 2 г) 5 5. Какое число содержит 572 единицы первого класса и 400 единиц второго класса. а) 572 400 б) 400 572 в) 400 г) 572 |
Выполняют тест. Работают самостоятельно. Выбирают верный ответ. Ответы: 1 – а
2 – б
3 – в
4 – г
5 – б |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения |
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию
|
Осуществлять итоговый контроль, оценивать результаты деятельности, уровень владения учебным действием |
Урок 133. Итоговая годовая контрольная работа № 11 по тексту администрации
|
Тип урока: контроль знаний и способов действий |
||
|
Педагогические задачи: проверить сформированность знаний о нумерации многозначных чисел и умений решать задачи на движение, задачи с величинами «цена», «количество», «стоимость», уравнения, сравнивать величины, вычислять значения выражений с многозначными числами, находить площадь и периметр прямоугольника |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять полученные знания при выполнении контрольной работы |
Метапредметные: Познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи. Регулятивные: определяют и формулируют цель деятельности на уроке; составляют план и последовательность действий; оценивают результат работы, определяют, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения |
Личностные: имеют желание учиться; осознают необходимость самосовершенствования; понимают значение границ собственного знания и «незнания» |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
I. Содержание контрольной работы. Вариант 1 |
Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.
1. Расположи числа в порядке возрастания: 7864, 7564, 795, 7964, 7664, 74645. Увеличь трёхзначное число в 5 раз. Уменьши пятизначное число на 1823. 2. Вычисли значения выражений: 18848 : 38 + (260 – 4) · 20 (7594 – 2129) : 5 + 707 |
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
1. Ответы: 795, 7564, 7664, 7864, 7964, 74645. 795 · 5 = 3975. 74645 – 1823 = 72822. 2. Ответы: 5616 1800 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий. Осуществлять контроль по результату |
|
|
3. Сравни величины: 6 км 64 м ... 665 м 4т 8 ц... 408 кг 2 ч 50 мин ... 200 мин 4. Реши уравнения: 171 : х = 3 85 · х = 600 + 335 Задачи. 1. Поезд прошёл 280 км за 4 часа. Сколько времени ему потребуется, чтобы пройти 630 км, если он будет идти с той же скоростью? 2. Длина прямоугольника 18 см, а ширина в 6 раз меньше. Вычисли периметр и площадь прямоугольника. 3. У Иры было 40 р. Она купила 4 открытки по 5 р. и 3 конверта по 2 р. Хватит ли ей денег на покупку тетради, если она стоит 3 рубля? |
3. Ответы: 6 км 64 м < 665 м 4 т 8 ц > 408 км 2 ч 50 мин < 200 мин. 4. Ответы: х = 57 х = 11. Решения: 1. 1) 280 : 4 = 70 (км/ч) – скорость поезда. 2) 630 : 70 = 9 (ч) – потребуется.
2. 1) (18 + 3) · 2 = 42 (см) – периметр прямоугольника. 2) 18 · 3 = 54 (см2) – площадь прямоугольника. 3. 1) 5 · 4 = 20 (р.) – стоят открытки. 2) 2 · 3 = 6 (р.) – стоят конверты. 3) 20 + 6 + 3 = 29 (р.) – стоит покупка. 4) 40 – 29 = 11 (р.) – сдача |
|
|
Вариант 2 |
1. Расположи числа в порядке возрастания: 9576, 9876, 946, 9976, 9676, 97764. Увеличь трёхзначное число в 4 раза. Уменьши пятизначное число на 8516. 2. Вычисли значения выражений: 35082 : 18 + (360 – 7) · 30 (7592 – 2468) : 4 + 909 3. Сравни величины: 5 км 63 м ... 564 м 2 т 8 ц ... 208 кг 4 ч 20 мин ... 400 мин 4. Реши уравнения: 920 : х = 4 63 · х = 500 + 256 Задачи. 1. Турист проехал 48 км за 3 часа. Сколько времени ему потребуется, чтобы проехать 64 км, если он будет ехать с той же скоростью? 2. Длина прямоугольника 15 см, а ширина в 3 раза меньше. Вычисли периметр и площадь прямоугольника. 3. У Коли было 40 р. Он купил 3 солдатика по 5 р. и две ручки по 4 р. Хватит ли ему денег на покупку машинки, если она стоит 14 рублей? предлагает обучающимся, выполнившим верно только одно или два задания, варианты уровня стандарта (см. далее). |
1. Ответы: 946, 9576, 9676, 9876, 9976, 97764. 946 · 4 = 3784. 97764 – 8516 = 89248. 2. Ответы: 12539 2190 3. Ответы: 5 км 63 м < 564 м 2 т 8 ц < 208 кг 4 ч 20 мин < 400 мин 4. Ответы: х = 230 х = 12. Решения: 1. 1) 48 : 3 = 16 (км/ч) – скорость туриста. 2) 64 : 16 = 4 (ч) – потребуется.
2. 1) (15 + 5) · 2 = 40 (см) – периметр прямоугольника. 2) 15 · 5 = 75 (см2) – площадь прямоугольника. 3. 1) 5 · 3 = 15 (р.) – стоят солдатики. 2) 4 · 2 = 8 (р.) – стоят ручки. 3) 15 + 8 + 14 = 37 (р.) – стоит покупка. 4) 40 – 37 = 3 (р.) – сдача. |
|
|
Вариант 1 |
1. Сравни числа: 7439 ... 7349 28764 ... 27864 346500 ... 65900 2. Найди значения выражений: 7592 + 92468 4210 · 53 800 – 240 · 3 600100 – 92015 234 · 407 320 : (400 – 360) 3. Сравни величины: 35 см ... 12 дм 2 т... 15 ц 4 ч ... 240 мин Задачи. 1. Длина прямоугольника 12 см, а ширина 7 см. Вычисли периметр и площадь прямоугольника.
2. В четырёх одинаковых коробках 28 карандашей. Сколько карандашей в одной коробке? 3. У Светы 4 открытки, а у Маши в 3 раза больше. Сколько открыток у Маши? 4. В саду 12 яблонь, а вишен на 6 меньше. Сколько вишен в саду? |
1. Ответы: 7439 < 7349 28764 > 27864 346500 > 65900 2. Ответы: 100060 223130 80 508085 95238 8 3. Ответы: 35 см < 12 дм 2 т > 15 ц 4 ч = 240 мин. Решения: 1. 1) (12 + 7) · 2 = 38 (см) – периметр прямоугольника. 2) 12 · 7 = 84 (см2) – площадь прямоугольника. 2. 28 : 4 = 7 (кар.) – в одной коробке.
3. 4 · 3 = 12 (откр.) – у Маши.
4. 12 – 6 = 6 (дер.) – вишен в саду |
|
|
Вариант 2 |
1. Сравни числа: 7638 ... 7368 43296 ... 42396 842600 ... 94950 2. Найди значения выражений: 42507 + 97478 246 · 38 700 – 270 · 2 700200 – 13265 421 · 609 350 : (500 – 450) 3. Сравни величины: 73 см ... 39 дм 3 т... 24 ц 5 ч ... 300 мин Задачи. 1. Длина прямоугольника 13 см, а ширина 4 см. Вычисли периметр и площадь прямоугольника.
2. В трёх одинаковых корзинах 21 кг яблок. Сколько килограммов яблок в одной корзине? 3. В вазе лежат 5 апельсинов, а конфет в 3 раза больше. Сколько конфет в вазе? 4. В конструкторе 16 зелёных деталей, а синих на 7 больше. Сколько синих деталей в конструкторе? |
1. Ответы: 7638 < 7368 43296 < 42396 842600 > 94950 2. Ответы: 139985 9348 160 686935 256389 7 3. Ответы: 73 см < 39 дм 3 т > 24 ц 5 ч = 300 мин. Решения: 1. 1) (13 + 4) · 2 = 34 (см) – периметр прямоугольника. 2) 13 · 4 = 52 (см2) – площадь прямоугольника. 2. 21 : 3 = 7 (кг) – яблок в одной корзине.
3. 5 · 3 = 15 (шт.) – конфет.
4. 16 + 7 = 27 (дет.) – синих деталей |
|
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 134. Анализ контрольной работы. Работа над ошибками
|
Тип урока: повторение и систематизация знаний и способов действий |
||
|
Педагогические задачи: учить выполнять работу над ошибками; совершенствовать вычислительные навыки, умения решать текстовые задачи |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять полученные знания при выполнении заданий |
Метапредметные: Познавательные: умеют самостоятельно выделять и формулировать познавательную цель; осуществляют поиск и выделение необходимой информации для выполнения учебных заданий с использованием учебной литературы; структурируют знания. Регулятивные: контролируют свою деятельность: обнаруживают ошибки логического характера и ошибки вычислительного характера. Коммуникативные: слушают и понимают речь других; договариваются с одноклассниками совместно с учителем о правилах поведения и общения и следуют им |
Личностные: понимают значение границ собственного знания и «незнания»; осознают необходимость самосовершенствования; адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|
II. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Выполните задание на смекалку. а) Расположите 10 точек на 5 отрезках так, чтобы на каждом отрезке было 4 точки.
б) Как записать число 100 шестью цифрами 4? в) Как записать число 100 семью цифрами 4? |
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. Решение: а) б) 100 = (444 – 44) : 4. в) 100 = (4 · 4 + 4) · (4 · 4 + 4) : 4. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|
|
– Вставьте пропущенные числа в «окошки»: 237 = 200 + 5629 = 8934 = 12395 = 34897 = 126237 = |
Запись: 237 = 200 + 30 + 7 5629 = 5000 + 600 + 20 + 9 8934 = 8000 + 900 + 30 + 4 12395 = 10000 + 2000 + 300 + 90 + 5 34897 = 30000 + 4000 + 800 + 90 + 7 126237 = 100000 + 20000 + 6000 + 200 + 30 + 7 |
|
|
III. Повторение по теме урока |
Организует работу по закреплению знаний, обеспечивает контроль за выполнением задания. – Сейчас я буду читать интересные факты. Используя многозначные числа, вы должны записать в тетрадь все, которые состоят более чем из трех разрядов единиц. – Когда мы смотрим на самую дальнюю из видимых звезд, мы смотрим на 4 миллиарда лет в прошлое. Свет от нее, путешествующий со скоростью почти в 300 000 км/секунду достигает нас только через много лет. – Автомобилю, движущемуся со средней скоростью 60 миль в час, потребовалось бы примерно 48 миллионов лет, чтобы достичь ближайшей к нам звезды (после Солнца) Проксимы Центавра. – На борту станции «Мир» находится более 14 000 кг различной исследовательской аппаратуры. – Общая масса станции «Мир» с двумя пристыковаными кораблями составляет более 36 000 кг. – Если наполнить чайную ложку веществом, из которого состоят нейтронные звезды, то ее вес будет равняться примерно 110 миллионам тонн. – Самый большой лунный кратер, видимый с Земли, называется Бэйли или «поле гибели». Он имеет площадь примерно в 26 000 квадратных миль. – Первые карты Луны изготовил в 1609 году Томас Харриот. – Самая высокая гора на Луне имеет высоту 11 500 метров. – Горы на Марсе достигают высоты 25 000 м. – Каждый день на Землю из космоса падает около 210 тысяч метеоритов. Правда, все они настолько малы, что сгорают в атмосфере. – Если протянуть паутину до ближайшей к нам звезды в созвездии Центавра, то она весила бы 500 000 тонн. – Около 27 тонн космической пыли падает на Землю каждый день. За год более 10 000 тонн пыли приземляется на Землю. – Площадь солнечной поверхности размером с почтовую марку светит с такой же энергией, как и 1 500 000 свечей. – Ганимед, самый большой из спутников планеты Юпитер, по своим размерам превосходит планету Меркурий. Диаметр Ганимеда составляет примерно 5269 километров. – Диаметр Луны – 3476 километров. – Назовите самое большое число. – Назовите самое маленькое число. – Сколько единиц 1-го класса в самом маленьком числе? – Сколько единиц 2-го класса в самом маленьком числе? |
Выполняют задания, отвечают на вопросы, высказывают свое мнение. Записывают многозначные числа.
– Самое большое число – 4 000 000 000. – Самое маленькое число – 1 609. – 609 единиц 1-го класса в самом маленьком числе. – 1 единица 2-го класса в самом маленьком числе |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату |
|
IV. Самостоятельная работа |
Организует работу в группах по карточкам. – Найдите сумму самого большого и самого маленького числа. |
Работают в группах. Ответ: |
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием |
|
|
– Найдите разность 2 чисел: уменьшаемое содержит 11 единиц 2-го класса, а вычитаемое число содержит 5 единиц 2-го класса. |
Ответ: 11500 – 5269 = 6231 |
|
|
|
– Увеличьте число, в котором 4 единицы тысяч, 1 сотня, 4 десятка, 7 единиц в 100 раз. |
Ответ: 4147 · 100 = 414700. |
|
|
|
– Уменьшите, число, в котором 36 тыс. единиц (36.000), в 10 раз. |
Ответ: 36000 : 10 = 3600. |
|
|
|
– Уменьшите число, которое на 1 больше, чем 4149, на 100. |
Ответ: 4150 – 100 = 4050 |
|
|
|
– Увеличьте число, которое составляет половину миллиона (500000) на 1000 |
Ответ: 500000 + 1000 = 501000 |
|
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 135. Педагогическая диагностика № 3
|
Тип урока: решение учебной задачи, контроль знаний |
||
|
Педагогические задачи: создать условия для проверки знаний по математике за курс начальной школы |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять полученные знания при выполнении заданий |
Метапредметные: Познавательные: овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи; строят логическую цепь рассуждений; используют доказательство. Регулятивные: умеют работать по предложенному учителем плану |
Личностные: расширяют познавательные интересы и учебные мотивы; умеют устанавливать, с какими учебными задачами могут справиться самостоятельно |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||
|
I. Диагностическая работа. Вариант 1 |
Знакомит с содержанием диагностической работы, комментирует задания.
1. Как записать цифрами число двести тысяч сорок восемь? 1) 20 048; 2) 2 000 048; 3) 200 048; 4) 2 048. 2. Найди значение суммы чисел 3589 и 10645. 3. Найди значение разности чисел 4092 и 2368. 4. Найди значение частного чисел 8276 и 4. 1) 269; 2) 2069; 3) 2079; 4) 20069. 5. На мосту расположен знак, указывающий, что по мосту можно провезти груз весом не более 2 т 300 кг. Выбери вес груза, который можно провезти по этому мосту: 1) 2220 кг; 2) 3200 кг; 3) 2 т 301 кг; 4) 3 т. 6. Найди значение выражения: 720 : 90 + 13 ∙ 4 + 219. 1) 247; 2) 191; 3) 415; 4) 279. 7. В комнату с площадью пола 20 м2 постелили квадратный коврик со стороной 2 метра. Какая площадь комнаты осталась не занятой ковром? 1) 16 м; 2) 44 м2; 3) 16 м2; 4) 72 дм2. 8. На молочном комбинате «Кубанская Бурёнка» изготовили 4700 л молочной продукции. Молока изготовили 2700 л, кефира – в три раза меньше, чем молока, остальная продукция – ряженка. Какой молочной продукции изготовили больше – ряженки или кефира и на сколько? 9. В таблице изображены четыре фигуры. Укажи, в какой клетке неверная фигура:
Ответ: ___________. |
Задают вопросы по содержанию диагностической работы. Самостоятельно выполняют задания работы по вариантам. Ответы: 1. 3) 200 048.
2. 14243. 3. 1724. 4. 2) 2069.
5. 1) 2220 кг.
6. 4) 279.
7. Решение: 1) 2 · 2 = 4 (м2) – площадь коврика. 2) 20 – 4 = 16 (м2) – остальная площадь комнаты. Ответ: 3) 16 м2. 8. 1) 2700 : 3 = 900 (л) – кефира. 2) 2700 + 900 = 3600 (л) – молока и кефира. 3) 4700 – 3600 = 1100 (л) – ряженка. 4) 1100 – 900 = 200 (л) – больше ряженки.
9. 2 – 1 |
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор. Выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий. Осуществлять контроль по результату |
|||||||||
|
Вариант 2 |
1. Как записать цифрами число триста восемь тысяч три? 1) 380 003; 2) 308 003; 3) 308 030; 4) 3 008 003. 2. Найди значение суммы чисел 4583 и 30759. 3. Найди значение разности чисел 5028 и 3899. 4. Найди значение частного чисел 35075 и 5. 1) 7510; 2) 7015; 3) 7115; 4) 5751. 5. Знак на весах указывает, что на них можно взвешивать груз не более 2 т 500 кг. Укажи вес груза, который можно взвесить на этих весах: 1) 2490 кг; 2) 3 т; 3) 3 т 230 кг; 4) 2590 кг. 6. Найди значение выражения (98 : 14 + 70 : 2) ∙ 60. 1) 2025; 2) 1078; 3) 2520; 4) 987. 7. В комнату, длина которой 8 м, а ширина 6 м, постелили ковёр площадью 12 м2. Какая площадь комнаты осталась не занятой ковром? 1) 48 м2; 2) 36 м; 3) 20 м2; 4) 36 м2. 8. В компьютерной игре надо набрать 500 очков. Саша на первом этапе набрал в 2 раза меньше очков, чем на третьем этапе, на втором этапе набрал 130 очков. Выиграл ли Саша, если на третьем этапе он набрал 250 очков? 9. В таблице изображены четыре фигуры. Укажи, в какой клетке неверная фигура:
|
Ответы: 1. 2) 308 003.
2. 35342. 3. 1129. 4. 2) 7015.
5. 1) 2490 кг.
6. 3) 2520.
7. Решение: 1) 6 · 8 = 48 (м2) – площадь комнаты. 2) 48 – 12 = 36 (м2) – свободная площадь. Ответ: 2) 36 м2. 8. Решение: 1) 250 : 2 = 125 (очков) – на 1-м этапе. 2) 125 + 130 + 250 = 505 (очков) – набрал Саша. Ответ: Саша выиграл.
9. 3 – 4 |
||||||||||
|
II. Итог урока. Рефлексия |
Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что было трудным в контрольной работе? – Кто успешно справился со всеми заданиями? |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке |
Способность к самооценке на основе критерия успешности учебной деятельности |
Урок 136. Портфолио ученика
|
Тип урока: демонстрация личных достижений обучающихся |
||
|
Педагогические задачи: сформировать умения словесно оценивать свою работу, сравнивать с образцом или результатами предыдущей работы; дать представление о конкретных умениях и навыках, способах деятельности, которые должны быть сформированы; выработать потребность в организации своего труда |
||
|
Планируемые результаты |
||
|
Предметные: научатся применять полученные знания при выполнении заданий; употреблять понятия «портфолио», «копилка результатов деятельности», «самооценка» |
Метапредметные: Познавательные: осознанно и произвольно строят речевое высказывание в устной форме. Коммуникативные: используют речь для регуляции своего действия; адекватно используют речевые средства для решения различных коммуникативных задач; строят монологическое высказывание |
Личностные: вырабатывают «Я-концепцию» и самооценку личности (самоидентификация, адекватная позитивная самооценка, самоуважение, самовосприятие); углубляют познавательный интерес; вырабатывают мотивы достижения и социального признания; оценивают свою деятельность |
Организационная структура урока
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности обучающегося |
|||||||||||||||||||||||||||||||||||||||||||||
|
II. Актуализация опорных знаний. Устный счет. |
Организует устный счет с целью актуализации знаний.
– Как быстро посчитать количество квадратов в фигурах? – Для каждой фигуры выберите соответствующее выражение: 7 · 4; 5 · 5.
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета. – Надо переложить квадраты так, чтобы получились прямоугольники. 7 · 4 – площадь второй фигуры. 5 · 5 – площадь первой фигуры. |
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой. Принимать и сохранять учебную цель и задачу. Дополнять, уточнять высказанные мнения по существу полученного задания |
|||||||||||||||||||||||||||||||||||||||||||||
|
Интеллектуальная разминка |
– Разгадайте правило, по которому составлена первая схема, и вставьте пропущенные числа в других схемах.
|
Ответы:
|
||||||||||||||||||||||||||||||||||||||||||||||
|
III. Заполнение «карты успеха» в портфолио |
Организует работу по заполнению «карты успеха». «Карта успеха» работает на успех ученика, позволяет дифференцированно подойти к оцениванию, формирует самостоятельность и ответственность. Процедура составления и работы с «картой». На начальном этапе в первом классе вводится словесная оценка за содержательный ответ, интересное высказывание, «умный» вопрос или творческое проявление. По мере того как у ребят накапливаются учебный опыт, определенные знания и умения, им становится мало словесных оценок. Постепенно учителя первых классов вводят разбор ошибок, допущенных учениками класса, выписывают их на доску и предлагают создать игровую ситуацию. Затем ребенок ищет ошибки в работе соседа по парте, но не ограничивается их исправлением, а обязательно дает совет, о чем нужно вспомнить ученику, допустившему ошибку, какое правило повторить. Далее школьник самостоятельно ищет это правило в учебнике или справочнике. Работа усложняется. Ученик, допустивший ошибку, сам называет правило, которое он не знает, объясняет свою ошибку. Подобная работа завершается самооценкой и рекомендациями – «советами самому себе». Особое внимание при этом уделяется совместному определению критериев оценивания различных видов работ. Совместными усилиями разрабатываются и вводятся «карты успеха», которые по окончании четверти вручаются их авторам. На каждую четверть создается отдельная «карта», неусвоенные вопросы и неотработанные умения переносятся в «карту» на следующую четверть |
Заполняют «карту успеха» по математике на конец учебного года
|
Планировать учебное сотрудничество с учителем и сверстниками – определение цели, функций участников, способов взаимодействия. Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость |
|||||||||||||||||||||||||||||||||||||||||||||
|
IV. Работа
|
Организует работу с «рефлексивной картой». «Рефлексивная карта» представляет собой листы плотной бумаги, которые вклеиваются в дневник ученика. В ней отмечены предметные умения и навыки, которые ученики должны приобрести в процессе обучения, а также коммуникативные умения и личностное развитие ребенка. Набор рубрик, вносимых в «карту», составляется учителем. Чтобы он стал понятным и осмысленным для детей, необходима специальная работа. Так, в начале изучения каждой темы учитель совместно с учениками определяет, что дети должны усвоить и уметь в результате работы над темой. При проверке выполненных заданий акцент делается на том, на развитие каких умений они направлены. На уроке выделяется специальное время для взаимопроверки разных типов заданий в форме работы в парах. В конце урока, подводя итоги работы, учитель вовлекает учеников в процесс анализа и оценки своих успехов. Еженедельно, ежемесячно или по четвертям ученик и учитель в соответствующих графах ставят условные знаки |
Самооценка ученика предшествует оценке учителя. Учитель либо соглашается с ней, либо вносит коррективы. Отметки первоначально делаются карандашом, затем выделяются ярким цветом (особенно успех).
В конце учебного года «рефлексивная карта» вкладывается в «портфолио» ученика в раздел «Мои достижения по предметам»
|
Умеют устанавливать связи между целью учебной деятельности и ее мотивом, другими словами, между результатом учения и тем, что побуждает деятельность, ради чего она осуществляется |
|||||||||||||||||||||||||||||||||||||||||||||
|
V. Итог урока. Рефлексия |
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися. предлагает каждому оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что особенно заинтересовало вас во время урока? – Что нового узнали на уроке? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – Какое задание понравилось больше всего? – Что вызвало затруднение? – Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий – если некоторые вопросы вызвали затруднения. – Понравилась ли вам работа на уроке? Оцените себя |
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию.
Заполните таблицу самооценки:
|
Способность к самооценке на основе критерия успешности учебной деятельности (оценивать свои достижения, степень самостоятельности, инициативности, причины неудачи) |
Литература
1. Агеева, С. И. Обучение с увлечением. Ч. 1 / С. И. Агеева. – М. : ВО «Совэкспорткнига», ИГ «Истоки», 1991.
2. Арутюнян, Е. Б. Занимательная математика : кн. для учащихся, учителей и родителей. 1–5 класс / Е. Б. Арутюнян, Г. Г. Левитас. – М. : АСТ-ПРЕСС, 1999.
3. Афонькин, С. Ю. Учимся мыслить логически. Увлекательные задачи для развития логического мышления / С. Ю. Афонькин. – СПб. : Литера, 2002.
4. Веселая математика : наглядное пособие для детей дошкольного возраста. – М. : Град-Пресс : АСТ-Пресс, 1994.
5. Волина, В. В. Праздник числа : книга для учителей и родителей / В. В. Волина. – М. : Знание, 1993.
6. Кочурова, Е. С. Дружим с математикой. 4 класс. Рабочая тетрадь для учащихся общеобразоват. организаций / Е. С. Кочурова. – М. : Вентана-Граф, 2014.
7. Математика. 4 класс : поурочные планы по учебнику Н. Б. Истоминой. I полугодие / авт.-сост. Н. В. Лободина. – Волгоград : Учитель, 2010.
8. Математика. 4 класс : поурочные планы по учебнику Н. Б. Истоминой. II полугодие / авт.-сост. Н. В. Лободина. – Волгоград : Учитель, 2010.
9. Перельман, Я. И. Живая математика. Математические рассказы и головоломки / Я. И. Перельман. – М. : Наука, 1978.
10. Петраков, И. С. Математические олимпиады школьников : пособие для учителей / И. С. Петраков. – М. : Просвещение, 1982.
11. Рудницкая, В. Н. Математика. Устные вычисления. 1–4 классы : метод. пособие / В. Н. Рудницкая, Т. В. Юдачева. – М. : Вентана-Граф, 2014.
12. Рудницкая, В. Н. Математика : проверочные и контрольные работы / В. Н. Рудницкая, Т. В. Юдачева. – М. : Вентана-Граф, 2013.
13. Рудницкая, В. Н. Математика : 4 класс : метод. пособие / В. Н. Рудницкая, Т. В. Юдачева. – М. : Вентана-Граф, 2015.
14. Рудницкая, В. Н. Математика : 4 класс : дидактические материалы : пособие для учащихся общеобразовательных организаций : в 2 ч. / В. Н. Рудницкая, Т. В. Юдачева. – М. : Вентана-Граф, 2014.
15. Рудницкая, В. Н. Математика : 4 класс : рабочая тетрадь для учащихся общеобразоват. организаций / В. Н. Рудницкая, Т. В. Юдачева. – М. : Вентана-Граф, 2015.
16. Рудницкая, В. Н. Математика : 4 класс : учеб. для учащихся общеобразовательных организаций : в 2 ч. / В. Н. Рудницкая, Т. В. Юдачева. – М. : Вентана-Граф, 2015.
17. Шадрина, И. В. Решаем геометрические задачи. 4 класс / И. В. Шадрина. – М. : Школьная пресса, 2003.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.