
Публикация является частью публикации:
Урок №1 Числовые выражения
Цели: ввести понятия числового выражения, значения числового выражения; формировать умение находить значение числового выражения, выполняя действия над числами и используя скобки.
Ход урока
I. Организационный момент
Устная работа.
Вычислите.
а) 13 – 18,5; б) –19 + 21,3; в) –14 – 71,03;
г) 17 – (–21,3); д) – (–3 – 2,8); е) 3 · 15 – 7;
ж) 12 – 16 : 4; з) (15 – 2) · (–3); и) (–2)
∙ ![]() ;
к) 7 :
;
к) 7 : ![]() .
.
II. Объяснение нового материала.
При решении многих задач приходится над заданными числами производить арифметические действия: сложение, вычитание, умножение и деление. Но часто, прежде чем доводить до конца каждое из этих действий, удобно заранее указать порядок (план), следуя которому надо производить эти действия. Этот план сводится к тому, что по данным задачи с помощью чисел, знаков действий и скобок составляется числовое выражение.
2. Разбираем задачу со с. 3 учебника и показываем на примере полученное числовое выражение.
следует привести достаточное число различных числовых выражений:
43 : 5; 9,6 – 3 · 1,2; 5 · (7,4 – 6,1);
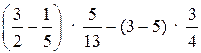 ; (39
– 15) : 23 +
; (39
– 15) : 23 + 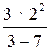 .
.
3. Если в числовом выражении выполнить все указанные в нем действия, то в результате получим действительное число, про которое говорят, что оно равно данному числовому выражению и называется значением выражения.
Подчеркнем, что числовое выражение дает указание, какие арифметические действия и в каком порядке мы должны произвести над данными числами. Скобки помогают установить порядок действий.
Задание. расставить над знаками арифметических действий порядковые номера их выполнения.
3,5 – 8 · 2,7 + 2,5 : 3 – 112 · 5;
(3,5 – 8) · 2,7 + 2,5 : (3 – 112) · 5;
3,5 – 8 · (2,7 + 2,5 : 3) – 112 · 5;
3,5 – 8 · (2,7 + 2,5 : (3 – 112)) · 5.
4. № 1 (а, г, ж).
Решение:
а) 6,965 + 23,3 = 30, 265;
г) 6,5 · 1,22 = 7,93;
ж) 53,4 : 15 = 3,56.
5. Мы, конечно, предполагаем, что все действия возможно осуществить. Поясним эти слова. Всегда возможно произвести сложение, вычитание и умножение любых чисел. А вот делить числа одно на другое возможно, только если делитель не равен нулю: на нуль делить нельзя. Если в данном выражении на некотором его этапе требуется делить на нуль, то это требование неосуществимо. Такое выражение не имеет смысла.
Например, выражения 35 : (4 · 2 – 8) и 0,37 – 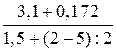 не имеют смысла, потому что при
выполнении указанных в них действий появляется необходимость делить на нуль.
не имеют смысла, потому что при
выполнении указанных в них действий появляется необходимость делить на нуль.
6. Замечаем, что числовое выражение может состоять и из одного числа.
III. Формирование умений и навыков.
1. № 1 (б; д; з). Самостоятельно.
2. Найдите сумму или разность.
а) ![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г) ![]() ; д)
; д)
![]() ; е)
; е) ![]() ;
;
ж) ![]() ; з)
; з) ![]() ; и)
; и) ![]() .
.
3. Найдите значение выражения.
а) 7 + 5,31 + 9 + 13,49;
б) 62,7 + 8,31 + 5,79 + 0,07.
4. № 4 (д, е, ж, з); № 5 (а, г, ж); № 6 (а, г, ж).
2-я группа
1. № 3 (а, б).
2. Найдите значение выражения.
а) ![]() ; б)
; б)
![]() ;
;
в) 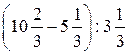 ; г)
; г)
![]() .
.
3. Вычислите.
а) (0,008 + 0,992) : (5 · 0,6 – 1,4);
б) 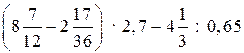 .
.
3-я группа
1. № 13.
2. Записать несколько числовых выражений, значение которых равно:
а) 8; б) 0; в) –14; г) 3,76.
3. Придумать два примера числовых выражений, где бы участвовали все арифметические действия, причем одно из них имело бы смысл, а второе нет.
IV. Итоги урока.
– Что называется значением числового выражения?
– Для чего в записи числового выражения присутствуют скобки?
– Когда числовое выражение имеет смысл? Приведите пример такого выражения.
– Когда числовое выражение не имеет смысла? Приведите пример такого выражения.
Домашнее задание.
1. № 1 (в, е, и); № 2; № 4 (а, б, в, г); № 5 (б, в, д, е, з, и) (устно); № 6 (б, д, з).
Урок №2 Выражения с переменными
Цели: ввести понятия «переменная», «выражение с переменной», «числовое значение выражения с переменной»; формировать умение находить значение выражения с переменной, используя различные формы записи («если … , то …», таблица).
Ход урока
I. Организационный момент
Устная работа.
1. Назовите числовые выражения, не имеющие смысла.
а) ![]() + 8 : 4
– 2 ∙ 2; б)
+ 8 : 4
– 2 ∙ 2; б) 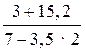 ; в)
; в) ![]() ;
;
г) 3,4 : 8 ∙ (–2) + 16; д) 3 : (3 ∙ 0,9 – 2,7)
+ 2; е) 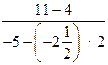 .
.
2. Найдите значение числового выражения.
а) ![]() ∙
(–9); б)
∙
(–9); б) 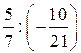 ;
в)
;
в) ![]() ; г)
; г)
![]() ;
;
д) 33; е) (–8)2;
ж) ![]() ; з)
(–0,2)2.
; з)
(–0,2)2.
II. Объяснение нового материала.
1. Мотивация изучения.
При решении многих практических задач удобно для обозначения различных чисел использовать буквы.
Например, если а и b – длины сторон прямоугольника, то выражение а · b показывает способ вычисления его площади. Это утверждение носит общий характер, оно относится к любому прямоугольнику, имеющему любые значения длин сторон; а и b – переменные, входящие в запись выражения.
Затем рассматриваем задачу со с. 5 учебника. Выражение 60t обозначает путь, пройденный автомобилем за некоторый промежуток времени. Подчеркиваем, что в этом выражении t является переменной, подставляя вместо t различные значения, мы можем находить путь, пройденный автомобилем за различные промежутки времени.
2. Определение 1. Если в числовом выражении некоторые (или все) входящие в него числа заменить буквами, то получим выражение с переменными (переменной).
Определение 2. Если в выражение с переменными подставить вместо каждой переменной какое-либо её значение, то получится числовое выражение. Его называют значением выражения с переменными при выбранных значениях переменных.
3. Необходимо ввести понятие допустимых значений переменных, входящих в выражения с переменными. Рассматриваем различные примеры выражений с переменными, имеющих смысл при любых значениях переменных (всех значениях) и не имеющих смысла при некоторых значениях переменной.
III. Формирование умений и навыков.
На этом уроке отрабатываются умения выполнять в буквенных выражениях числовые подстановки и производить соответствующие вычисления.
1. Найдите значение выражения.
а) х + 3,2 при х = –6,8; –3,2; 1![]() ; б) –5у при у = –2,6; 0; 1;
2
; б) –5у при у = –2,6; 0; 1;
2![]() ;
;
в) 12а – 7 при а = –1; 0; –7,6; 0,05; г) 3 – 1,5т
при т = 4; –2; –![]() ; 0,8.
; 0,8.
При выполнении задания обращаем внимание учащихся на запись решения.
Решение:
а) если х = –6,8, то х + 3,2 = –6,8 + 3,2 = –3,6;
б) если х = –3,2, то х + 3,2 = –3,2 + 3,2 = 0;
в) если х = 1![]() , то x + 3,2 = 1
, то x + 3,2 = 1![]() + 3,2 =
+ 3,2 = ![]() + 3
+ 3![]() =
= ![]() =
=
= ![]() .
.
2. № 21.
Решение:
|
у |
–3 |
–1 |
0 |
2 |
3 |
4 |
6 |
|
10 – 2у |
16 |
12 |
10 |
6 |
4 |
2 |
–2 |
|
10 + 2у |
4 |
8 |
10 |
14 |
16 |
18 |
22 |
Данное задание можно вынести на доску. Каждый ученик самостоятельно выполняет все задания в тетради, а затем «по цепочке» ученики выходят к доске и заполняют соответствующую ячейку таблицы. Также данное задание можно выполнить устно.
3. Заполните таблицу.
|
|
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
х (3 – 5х) |
–54 |
–26 |
–8 |
0 |
–2 |
–14 |
–36 |
1. № 22 (устно); № 23.
2. Найдите значение выражения.
а) 8т + 3п + 1, при т = –4 и п = 10; т
= –6,5 и n = 4![]() .
.
б) (а + b) · (а – b), при а = 1,7 и b = –1,3; в) 2 – 0,3 · (b + 3а), при а = –0,2 и b = 0,6;
г) ![]() , при а
= 2,8 и b = 0.
, при а
= 2,8 и b = 0.
1. Пусть х + у = 5 и z = –8. Найдите:
а) х + у – z; в) x – 5z
+ y; д) 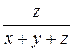 ;
;
б) 2z – (х + у); г) 3 (х + у) + 2z; е) z (х + у + 5z).
2. № 27.
IV. Проверочная работа.
Вариант 1
1. Заполните таблицу:
|
р |
0 |
–1 |
2 |
–3 |
3 |
|
t |
–7 |
–2 |
3 |
0 |
9 |
|
p (3t – p) |
|
|
|
|
|
2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.
Вариант 2
1. Заполните таблицу:
|
т |
0 |
–1 |
3 |
2 |
–2 |
|
п |
–2 |
–3 |
6 |
0 |
1 |
|
т (п – 2т) |
|
|
|
|
|
2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.
V. Итоги урока.
Домашнее задание: № 19, № 20, № 24 (а; в), № 26 (а; в), № 28.
Вариант 1
1. Заполните таблицу:
|
р |
0 |
–1 |
2 |
–3 |
3 |
|
t |
–7 |
–2 |
3 |
0 |
9 |
|
p (3t – p) |
|
|
|
|
|
2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.
Вариант 2
1. Заполните таблицу:
|
т |
0 |
–1 |
3 |
2 |
–2 |
|
п |
–2 |
–3 |
6 |
0 |
1 |
|
т (п – 2т) |
|
|
|
|
|
2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.
Вариант 1
1. Заполните таблицу:
|
р |
0 |
–1 |
2 |
–3 |
3 |
|
t |
–7 |
–2 |
3 |
0 |
9 |
|
p (3t – p) |
|
|
|
|
|
2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.
Вариант 2
1. Заполните таблицу:
|
т |
0 |
–1 |
3 |
2 |
–2 |
|
п |
–2 |
–3 |
6 |
0 |
1 |
|
т (п – 2т) |
|
|
|
|
|
2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.
Вариант 1
1. Заполните таблицу:
|
р |
0 |
–1 |
2 |
–3 |
3 |
|
t |
–7 |
–2 |
3 |
0 |
9 |
|
p (3t – p) |
|
|
|
|
|
2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.
Вариант 2
1. Заполните таблицу:
|
т |
0 |
–1 |
3 |
2 |
–2 |
|
п |
–2 |
–3 |
6 |
0 |
1 |
|
т (п – 2т) |
|
|
|
|
|
2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.
Вариант 1
1. Заполните таблицу:
|
р |
0 |
–1 |
2 |
–3 |
3 |
|
t |
–7 |
–2 |
3 |
0 |
9 |
|
p (3t – p) |
|
|
|
|
|
2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.
Урок №3 Выражения с переменными
Цели: продолжить формировать умение находить значение выражения с переменными; формировать умение составлять выражение с переменными по условию задачи, в том числе формулы, и находить их значение.
Ход урока
I. Устная работа.
1. Назовите выражения, не имеющие смысла.
а) 2 · 4 – 8; б) 3 · 2 : (6 – 1,5 · 4); в) 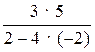 ;
;
г) 3 : 3 – 7 · 2; д) 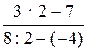 ; е)
; е) 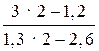 ;
;
ж) 2 : 4 – 2; з) 3 : 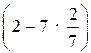 .
.
2. Найдите значение выражения 3а – b, если:
а) а = 2 и b = –4; б) а = 0 и b
= ![]() ;
;
в) а = –4 и b = 5; г) а = –![]() и b =
и b = ![]() .
.
3. Сколько процентов составляет:
а) 50 от 200; б) 13 от 260;
в) 1,5 от 20; г) 240 от 80?
II. Объяснение нового материала.
Вводится понятие формулы.Приведу примеры различных формул, применяемых на практике (вычисление площадей, объемов, числовые формулы и т. п.). Также следует объясняю что есть стабильные формулы, которые уже выведены и могут использоваться для расчетов. А есть задачи, для решения которых необходимо самостоятельно выявить закономерности (зависимости), описанные в условии, ввести переменные, составить выражение с переменными (формулу) и использовать его для вычисления искомого задачи при конкретных исходных данных.
III. Формирование умений и навыков.
1. № 29.
Решение:
Если площадь первого участка а га, а с каждого га собрали 32 ц пшеницы, то со всего участка собрали 32а ц пшеницы. Аналогично получаем для второго участка урожай 40b ц пшеницы. Тогда с обоих участков был собран урожай 32а + 40b (ц). Если а = 120 и b = 80, то 32а + + 40b = 32 · 120 + 40 · 80 = 3840 + 3200 = 7040.
Ответ: 32а + 40b (ц); 7040 ц.
2. № 31.
Решение:
Фигура состоит из отдельных частей. её площадь можно найти двумя способами:
1-й способ. «Разбить» фигуру на отдельные фигуры, для которых можно легко найти площадь, и, сложив полученные результаты, получить общую площадь.
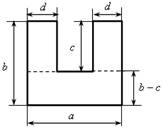
Площадь состоит из суммы площадей трех прямоугольников со сторонами: d и с; d и с; а и b – с. Их площади соответственно равны: сd; сd; а (b – с). Значит, площадь искомой фигуры составляет:
сd + сd + а (b – с) или 2сd + а (b – с).
2-й способ. Представить фигуру в виде прямоугольника со сторонами а и b с «вырезанным» прямоугольником со сторонами с и а – 2d. Их площади соответственно равны аb и с (а – 2d). Значит, площадь искомой фигуры составляет аb – с (а – 2d).
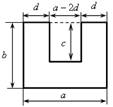
Ответ: 2сd + а (b – с) (см2) или аb – с (а – 2d) (см2).
3. № 33.
Решение:
После добавления 5 г соли в раствор масса его стала равна 255
г. Масса чистой соли в растворе также увеличилась на 5
г и стала составлять (х + 5) г. Концентрация соли, таким
образом, составляет ![]() ∙ 100 %.
∙ 100 %.
Ответ: ![]() ∙ 100 %.
∙ 100 %.
4. № 35 (устно); № 36 (устно).
2-я группа
1. № 37 (устно); № 38.
2. № 39 (устно); № 40 (устно).
3. № 41 (устно); № 42.
iV. Проверочная работа.
Вариант 1
Составьте выражение для вычисления площади пола, уложенного п квадратными плитками со стороной а см. Вычислите эту площадь, если а = 20 и п = 500.
Вариант 2
Составьте выражение для вычисления пути, пройденного велосипедистом за время t ч со скоростью υ км/ч. Вычислите путь велосипедиста, если υ = 25, t = 1,2.
V. Итоги урока.
– Что называется значением выражения с переменными?
– В каком случае выражение с переменными не имеет смысла? Назовите выражение, которое содержит переменную х и которое не имеет смысла при х = –3,5.
– Назовите выражение, имеющее смысл при любых значениях входящей в него переменной у.
– Что представляет собой формула? Назовите формулу четного числа, нечетного числа.
Домашнее задание: 1. № 30, № 32, № 34, № 43.
Урок №4
Сравнение значений числовых
выражений
и выражений с переменными
Цели: формировать умение сравнивать значения числовых выражений, а также буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений; ввести понятие двойного неравенства; формировать умение записывать результат сравнения выражений в виде двойного неравенства.
Ход урока
I. Организационный момент
Устная работа.
1. Проанализируйте порядок выполнения действий в каждом из данных выражений и объясните, как оно читается:
а) а + b; б) а · b; в) 2аb; г) а
+ (b – с); д) ![]() ; е) 2х – 3у; ж) ak
+ p; з)
; е) 2х – 3у; ж) ak
+ p; з) ![]() .
.
2. От куска проволоки длиной а м первый раз отрезали b м, а второй раз – с м проволоки. Какой смысл имеют следующие выражения:
а) b + с; б) а – (b + с); в) а – b; г) а – b – с?
3. Поставьте вместо звездочек такое число, чтобы получилось верное равенство.
а) –(–12) = *; б) 1,5 = –(*); в) = –8 = –(*); г) 0 = –(*).
II. Объяснение нового материала.
Рассмотрим задачу со с. 10 учебника. Она носит чисто практический характер, и её решение служит мотивацией изучения темы. Показываем учащимся, что при записи неравенства слева или справа (или в обеих частях) может стоять числовое выражение. Просим назвать неравенства.
Здесь следует напомнить, что неравенства бывают верные или неверные.
Задание. Определите, верно ли неравенство.
а) 3 · 15 > 8 : 2; б) 14 : 2 < –3 · 2;
в) 1,7 · 10 > 7 : 10; г) ![]() < –2,5 ∙ 2.
< –2,5 ∙ 2.
Показываем на конкретных примерах, что если выражения содержат переменные, то для разных значений переменных результат сравнения значений этих выражений может оказаться различным.
Рассматриваем пример со с. 10 учебника. Также целесообразно попросить учащихся подобрать несколько значений переменной а, при которых будут верны либо не верны неравенства 2а > а + 4 и 2а < а + 4.
Вводим понятие двойного неравенства. Обращаем внимание на различные формулировки прочтения двойного неравенства.
III. Формирование умений и навыков.
1. Сравните значение выражений:
а) ![]() и
и ![]() ; б)
; б)
![]() и
и ![]() ;
;
в) 0,5 и ![]() ; г)
; г)
![]() и –1,6;
и –1,6;
д) 3,2 · 6,01 и 77,2 : 4; е) 38,4 : 6 и 12 – 5,6.
2. № 50.
3. № 48 (а; в); № 49 (а; б).
1. № 51; № 52 (устно).
2. Сравните значения выражений:
а) 2х + 5 при х = 0 и х = –1![]() ;
;
б) 3 – 3а при а = 1 и а = –1;
в) 3х + 5у при х = –0,3, у = 0,6 и х = 1,2, у = –0,3;
г) 7а + b – 2c при а = 2, b = –4, с = 3 и а = –1,2, b = 0,4, с = 1.
3. Для выражений 25х + 1 и 800 : х – 99 составьте таблицу значений при х = 1; 2; 4; 5; 8. При каких из этих значений х:
а) первое выражение меньше второго;
б) первое выражение равно второму;
в) первое выражение больше второго?
Решение:
|
х |
1 |
2 |
4 |
5 |
8 |
|
25х + 1 |
26 |
51 |
101 |
126 |
201 |
|
800 : х – 99 |
701 |
301 |
101 |
61 |
1 |
Ответ: а) 1; 2; б) 4; в) 5; 8.
1. № 56, № 57.
2. Какие числа, кратные 5, удовлетворяют неравенству:
а) 64 < х < 78; б) 405 < у < 450?
3. Запишите все числа х, у которых знаменатель дробной части 10,
если ![]() .
.
4. № 59.
IV. Итоги урока.
– В каком отношении могут находиться числовые выражения?
– Каким образом сравниваются выражения, содержащие переменные?
– Верны ли неравенства:
а) 3х + 5 > –7х + 11 при х = –1; х = 2?
б) 3х – 2 = – 5х + 6 при х = –2; х = 1?
в) –2х – 1,4 > х + 5 при х = 1; х = 0?
– Прочитайте неравенство:
а) –5 < х < –8; б) 15,7 < 15,9 <
16,2; в) –1 < 3![]() < 5,85.
< 5,85.
Домашнее задание: № 47; № 48 (б; г); № 49 (в; г); № 53; № 54; № 58.
Урок №5
Сравнение значений выражений
Цели: продолжить формировать умение сравнивать значения числовых выражений, а также выражений с переменными при заданных значениях входящих в них переменных; ввести понятие строгого и нестрогого неравенства; формировать умение составлять выражения по условию задачи и сравнивать их значения.
Ход урока
I. Организационный момент
Устная работа.
1. Сколько процентов составляет: а) число 8 от числа 200; б) число 15 от
числа 1500; в) число 24 от числа 12; г) число ![]() от
от ![]() ?
?
2. Замените звездочку знаком: >, < или =.
а) ![]() * 3; г)
32,5 – 12 * 4,01; б)
* 3; г)
32,5 – 12 * 4,01; б) ![]() * 5 – 2,5; д) (5 – 2) · 7,5 * 5 – 2 ·
7,5;
* 5 – 2,5; д) (5 – 2) · 7,5 * 5 – 2 ·
7,5;
в) (–2) ∙ ![]() ∙ 7 * – 3,5; е)
–3,7 – 2,4 * –6,2.
∙ 7 * – 3,5; е)
–3,7 – 2,4 * –6,2.
3. Прочитайте неравенство:
а) 3,7 < 3,8 < 3,95; в) –b < –a < – c; б)
k < p < 2k; г) ![]() .
.
II. Проверочная работа.
Вариант 1
1. Сравните значения выражений:
1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;
2) 2a – 3b и 3a – 2b при а = –2 и b = 3.
2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2
1. Сравните значения выражений:
1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;
2) 3a + 2b и 2a – 3b при а = –2 и b = 4.
2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
III. Объяснение нового материала.
Вводится понятие строгого и нестрогого неравенства на конкретных примерах (число дней в месяце, количество пассажиров в автобусе, предельные температуры и т. п.).
Определение. Неравенства, составленные с помощью знаков > и <, называют строгими неравенствами, а неравенства, составленные с помощью знаков ≥ и ≤, называют нестрогими.
Необходимо подчеркнуть, что нестрогое неравенство является верным, если выполняется хотя бы одно соотношение:
18 ≥ 14 – верно (выполняется 18 > 14);
–35 ≤ –35 – верно (выполняется –35 = –35).
Если не выполняется ни одно из соотношений, то неравенство является неверным:
–35 ≥ –34.
Двойные неравенства также могут быть записаны с помощью знаков ≥ и ≤:
18 ≤ х ≤ 19; 1,7 < п ≤ 1,8; ![]() .
.
IV. Формирование умений и навыков.
1. № 60 (устно); № 61 (устно).
2. Задание по вариантам.
Запишите каждое предложение с помощью знаков неравенства. Подберите три значения переменной, при которых данное неравенство верно, и три, при которых неверно.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
1) а) t больше 7;
б) υ меньше или равно –1,17;
в) р – неположительное число;
2) а) b меньше 8 и больше или равно –7;
б) а меньше 0,07 и больше 0,06;
в) q меньше или равно 0,1 и положительно.
3. Расположите числа в порядке возрастания.
![]() .
.
4. Расположите числа в порядке убывания.
(0,3)2; 0,3; (0,3)3.
1. Один сплав состоит из 5 кг олова и 15 кг меди, другой – из 3 кг олова и 7 кг меди. В каком из сплавов процентное содержание меди больше?
При решении задач на проценты нужно использовать наглядное изображение данных, что в дальнейшем позволит учащимся грамотно выполнять анализ условия текстовых задач, решаемых алгебраическим методом.
Решение:
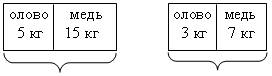
20 кг 10 кг
1) Масса первого сплава равна 20 кг, второго – 10 кг.
2) Выразим процентное содержание меди в первом и во втором сплавах:
![]() ∙
100 % = 75 % и
∙
100 % = 75 % и ![]() ∙
100 % = 70 %.
∙
100 % = 70 %.
3) 75 > 70, значит, в первом сплаве процентное содержание меди больше.
Ответ: в первом сплаве.
2. № 65.
Решение:
Средняя скорость автомобиля «Жигули» равна ![]() км/ч, а автомобиля «Москвич» –
км/ч, а автомобиля «Москвич» – ![]() км/ч. Сравним средние
скорости автомобилей:
км/ч. Сравним средние
скорости автомобилей:
а) Если х = 12,5, у =10,5, то ![]() = 56, а
= 56, а ![]() = 60. То есть при данных значениях
переменных верно неравенство
= 60. То есть при данных значениях
переменных верно неравенство ![]() <
< ![]() .
.
б) Если х = у = 14, то ![]() = 50, а
= 50, а ![]() = 45. То есть при данных значениях
переменных верно неравенство
= 45. То есть при данных значениях
переменных верно неравенство ![]() >
> ![]() .
.
Ответ: а) Средняя скорость автомобиля «Жигули» меньше. б) Средняя скорость автомобиля «Жигули» больше.
V. Итоги урока.
– Какое неравенство называется строгим? Приведите примеры.
– Какое неравенство называется нестрогим? Приведите примеры.
– Когда верно нестрогое неравенство? Когда оно не верно? Приведите примеры.
Домашнее задание: 1. № 62, № 63, № 64.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
1) а) t больше 7;
б) υ меньше или равно –1,17;
в) р – неположительное число;
2) а) b меньше 8 и больше или равно –7;
б) а меньше 0,07 и больше 0,06;
в) q меньше или равно 0,1 и положительно.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
1) а) t больше 7;
б) υ меньше или равно –1,17;
в) р – неположительное число;
2) а) b меньше 8 и больше или равно –7;
б) а меньше 0,07 и больше 0,06;
в) q меньше или равно 0,1 и положительно.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
1) а) t больше 7;
б) υ меньше или равно –1,17;
в) р – неположительное число;
2) а) b меньше 8 и больше или равно –7;
б) а меньше 0,07 и больше 0,06;
в) q меньше или равно 0,1 и положительно.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
1) а) t больше 7;
б) υ меньше или равно –1,17;
в) р – неположительное число;
2) а) b меньше 8 и больше или равно –7;
б) а меньше 0,07 и больше 0,06;
в) q меньше или равно 0,1 и положительно.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
1) а) t больше 7;
б) υ меньше или равно –1,17;
в) р – неположительное число;
2) а) b меньше 8 и больше или равно –7;
б) а меньше 0,07 и больше 0,06;
в) q меньше или равно 0,1 и положительно.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
1) а) t больше 7;
б) υ меньше или равно –1,17;
в) р – неположительное число;
2) а) b меньше 8 и больше или равно –7;
б) а меньше 0,07 и больше 0,06;
в) q меньше или равно 0,1 и положительно.
Вариант 1
1. Сравните значения выражений:
1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;
2) 2a – 3b и 3a – 2b при а = –2 и b = 3.
2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2
1. Сравните значения выражений:
1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;
2) 3a + 2b и 2a – 3b при а = –2 и b = 4.
2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
Вариант 1
1. Сравните значения выражений:
1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;
2) 2a – 3b и 3a – 2b при а = –2 и b = 3.
2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2
1. Сравните значения выражений:
1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;
2) 3a + 2b и 2a – 3b при а = –2 и b = 4.
2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
Вариант 1
1. Сравните значения выражений:
1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;
2) 2a – 3b и 3a – 2b при а = –2 и b = 3.
2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2
1. Сравните значения выражений:
1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;
2) 3a + 2b и 2a – 3b при а = –2 и b = 4.
2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
Вариант 1
1. Сравните значения выражений:
1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;
2) 2a – 3b и 3a – 2b при а = –2 и b = 3.
2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2
1. Сравните значения выражений:
1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;
2) 3a + 2b и 2a – 3b при а = –2 и b = 4.
2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
Вариант 1
1. Сравните значения выражений:
1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;
2) 2a – 3b и 3a – 2b при а = –2 и b = 3.
2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2
1. Сравните значения выражений:
1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;
2) 3a + 2b и 2a – 3b при а = –2 и b = 4.
2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
Урок №6
основные свойства сложения и умножения чисел
Цели: актуализировать знания основных свойств сложения и умножения чисел (переместительное, сочетательное и распределительное свойства); формировать умение применять свойства действий над числами при нахождении значений числовых выражений.
Ход урока
I. Организационный момент
Устная работа.
1. Объясните следующие записи:
а) +(2x – 3y + 5) = 2x – 3y + 5; б) –(2x – 3y + 5) = –2x + 3y – 5.
2. Раскройте скобки.
а) a ∙ (–b + c); г) 2 ∙ (a + b – c); ж) (2x + 4y – 5z – 3) ∙ 7;
б) (–a + b) ∙ c; д) –5 ∙ (a – b + c); з) –0,5 ∙ (4a – 3b – 2c + 7).
в) (1 + b) ∙ (–4); е) (a + b – 4) ∙ (–5);
3. Следующие выражения заключите в скобки двумя способами:
1) поставив перед скобкой знак «плюс»;
2) поставив перед скобкой знак «минус»:
а) а + b; б) 1 – b; в) 0,5 – 2х; г) –1,3х + 2,4;
д) –2 + а – b; е) –х – у + 5; ж) 6 – 5а + b; з) –15 – 7х – 2у.
4. Вынесите за скобки общий множитель.
а) ax + bx + cx; б) 10a – 5b – 15c; в) ay – by + 3y;
г) 6xy – 12x + 9xz; д) –8ab – 29ac + 16a; е) 8abc – 24abd – 6ab.
II. Актуализация знаний.
Выполнение устной работы позволит вспомнить основные свойства сложения и умножения чисел, которые целесообразно записать в буквенной форме для любых чисел и оформить в виде плаката.
|
Переместительное свойство Для любых чисел а и b верны равенства: а + b = b + а; а · b = b · а. Сочетательное свойство Для любых чисел а, b и с верны равенства: (а + b) + с = а + (b + с); (аb) с = а (bс). Распределительное свойство Для любых чисел а, b и с верно равенство: а (b + с) = аb + ас. |
Например:
1. Найдите значение выражения 928 · 36 + 72 · 36.
Для нахождения значения выражения целесообразно преобразовать его, применив распределительное свойство:
928 · 36 + 72 · 36 = (928 + 72) · 36 = 1000 · 36 = 36 000.
2. Вычислите сумму 1,23 + 13,5 + 4,27.
В учебнике указано, что «удобно объединить первое слагаемое с третьим». Учащиеся должны объяснить, в чем это удобство (в сумме получается десятичная дробь с одним разрядом после запятой):
1,23 + 13,5 + 4,27 = (1,23 + 4,27) + 13,5 = 5,5 + 13,5 = 19.
3. 1,8 · 0,25 · 64 · 0,5 = (1,8 · 0,5) · (64 · 0,25).
Такое распределение целесообразно потому, что 0,5 = ![]() и 0,25 =
и 0,25 = ![]() . То есть следует понимать, что,
умножая число на
. То есть следует понимать, что,
умножая число на ![]() ,
мы получаем половину, а умножая на
,
мы получаем половину, а умножая на ![]() , – четверть. Поэтому удобно найти
половину от 1,8 и четверть от 64.
, – четверть. Поэтому удобно найти
половину от 1,8 и четверть от 64.
Аналогично комментируем все примеры со с. 15 учебника.
III. Формирование умений и навыков.
1. № 70 (устно).
2. № 71.
Решение:
а) 3,17 + 10,2 + 0,83 + 9,8 = (3,17 + 0,83) + (10,2 + 9,8) = 4 + 20 = 24;
б) 4,11 + 15,5 + 0,89 + 4,4 = (4,11 + 0,89) + (15,5 + 4,4) = 5 + 19,9 = 24,9;
в) 15,21 – 3,9 – 4,7 + 6,79 = (15,21 + 6,79 + (–3,9 – 4,7) = 22 + (–8,6)
=
= 13,4;
г) –4,27 + 3,8 – 5,73 – 3,3 = (–4,27 – 5,73) + (3,8 – 3,3) = –10 + 0,5 = –9,5.
3. Вычислите наиболее рациональным способом.
а) 527 – 825 + 925;
б) –5,37 + 9,27 + 4,37.
Решение:
а) 527 – 825 + 925 = 527 + (925 – 825) = 527 + 100 = 627;
б) –5,37 + 9,27 + 4,37 = (4,37 – 5,37) + 9,27 = –1 + 9,27 = 8,27.
4. № 73.
5. № 75 (а; в); № 76 (а; в); № 77.
IV. Итоги урока.
– Сформулируйте переместительное свойство сложения и умножения. Приведите примеры.
– Сформулируйте сочетательное свойство сложения и умножения. Приведите примеры.
– Сформулируйте распределительное свойство умножения. Приведите примеры.
– Какие свойства действий позволяют, не выполняя вычислений, утверждать, что верно равенство:
а) 3 · 17,8 = 17,8 · 3; б) 35 + 73 = 73 + 35;
в) 32 + (14 + 3) = (32 + 14) + 3; г) 13 · (5 + 11) = 13 · 5 + 13 · 11?
Домашнее задание: № 72; № 74; № 75 (б; г); № 76 (б; г); № 78.
Урок №7 Свойства действий над числами
Цель: продолжить формирование умений применять основные свойства действий над числами (переместительное, сочетательное, распределительное) при нахождении значений числовых выражений.
Ход урока
I. Организационный момент
Устная работа.
1. Вычислите:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ;
;
2. Вычислите:
а) ![]() ∙
2; б)
∙
2; б) ![]() : 3;в)
: 3;в) ![]() ;г) 5 :
;г) 5 : ![]() ;д)
;д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
II. Актуализация знаний.
Вычислить значение каждого выражения наиболее простым способом, проговорив при этом используемое свойство действий над числами:
а) 405 · 82 + 405 · 18;
б) 707 · 13 + х · 13 при х = 293;
в) 417р – 217 · 163 при р = 163;
г) 24а – 48 · 15 при а = 33;
д) (64 · 37 + 64 · 23) : 5.
III. Формирование умений и навыков.
На этом уроке решаются задания более высокого уровня сложности.
1. № 79.
Решение:
а) 24 · 17 + 17 · 6 = 17 · (24 + 6) = 17 · 30 = 17 · 6 · 5, значит, выражение делится на 5.
б) 34 · 85 + 34 · 36 = 34 · (85 + 36) = 34 · 121 = 34 · 11 · 11, значит, выражение делится на 11.
2. № 223.
Решение:
а) 5,9 · 2,6 + 5,9 · 3,2 + 5,8 · 4,1 = 5,9 (2,6 + 3,2) + 5,8 · 4,1 = 5,9
· 5,8 +
+ 5,8 · 4,1 = 5,8 (5,9 + 4,1) = 5,8 · 10 = 58;
б) 6,8 · 8,4 – 1,6 · 8,4 + 5,2 · 1,6 = 8,4 (6,8 – 1,6) + 5,2 · 1,6 = 8,4
· 5,2 +
+ 5,2 · 1,6 = 5,2 (8,4 + 1,6) = 5,2 · 10 = 52.
3. Вычислите наиболее рациональным способом.
а) ![]() ; б)
; б) ![]() .
.
Решение:
а) Выполняем сперва умножение первой дроби на вторую, затем полученный
результат – на третью дробь и т. д. Получим ![]() .
.
б) ![]()
![]() .
.
4. Найдите последовательно значение каждой из разностей:
![]() , а затем
значение суммы
, а затем
значение суммы ![]() .
.
Решение:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() .
.
![]()
![]()
![]() .
.
5. Разберите, как выполнено умножение.
5 · 424 = 5 · 2 · 212 = 10 · 212 = 2120.
Используя данный прием, выполните вычисления устно.
а) 5 · 822; б) 5 · 412; в) 5 · (–724);
г) 822,2 · 5; д) 43,6 · 5; е) (–0,626) · 5.
Решение:
Суть приема заключается в том, чтобы разложить четный сомножитель на произведение 2 · х, тогда выражение примет вид 5 · 2 · х = 10 · х, что позволит выполнить действие устно.
а) 5 · 822 = 5 · 2 · 411 = 10 · 411 = 4110;
б) 5 · 412 = 5 · 2 · 206 = 10 · 206 = 2060;
в) 5 · (–724) = 5 · 2 · (–362) = 10 · (–362) = –3620;
г) 822,2 · 5 = 411,1 · 2 · 5 = 411,1 · 10 = 4111;
д) 43,6 · 5 = 21,8 · 2 · 5 = 21,8 · 10 = 218;
е) (–0,626) · 5 = (–0,313) · 2 · 5 = (–0,313) · 10 = –3,13.
6. № 224*.
Решение:
а) (1,25 ∙ 1,7 ∙ 0,8 – 1,7) ∙ 3,45 = 1,7 ∙
(1,25 ∙ 0,8 – 1) ∙ 3,45 =
= 1,7 ∙ ![]() ∙
3,45 = 1,7 ∙ (1 – 1) ∙ 3,45 = 0;
∙
3,45 = 1,7 ∙ (1 – 1) ∙ 3,45 = 0;
б) 3,947 : (3,6 – 2,6 · 4 · 0,25) = 3,947 : (3,6 – 2,6 · 1) =
= 3,947 : (3,6 – 2,6) = 3,947 : 1 = 3,947.
IV. Проверочная работа.
Вариант 1
Вычислите наиболее рациональным способом:
1. ![]() .
.
2. 28 · 3,9 · ![]() . 3.
5 ·
. 3.
5 · ![]() .
.
Вариант 2
Вычислите наиболее рациональным способом:
1. ![]() .
.
2. 36 · 2,7 · ![]() . 3.
8 ·
. 3.
8 · ![]() .
.
V. Итоги урока.
Домашнее задание: № 80, № 82.
Урок №8 тождества
Цели: ввести понятия тождественно равных выражений и тождества; формировать умение определять тождественное равенство выражений на основе выражения основных свойств действий над числами.
Ход урока
I. Организационный момент
Устная работа.
1. Найдите значение числового выражения.
а) 3 + 15 : (–5);г) 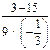 ;б) (–18 – 2) : (–4); ) 9 · 0,1 –
0,1;в) 7 · 2 + (–4) : 2;
;б) (–18 – 2) : (–4); ) 9 · 0,1 –
0,1;в) 7 · 2 + (–4) : 2;
2. Какие свойства действий позволяют, не выполняя вычислений, утверждать, что верно равенство?
а) –368 + 2,54 = 2,54 – 368; г) (1,5 · 3) · 10 = 1,5 · (3 · 10);
б) ![]() ; д)
; д) ![]() ; в) 3 ·
; в) 3 · ![]() – 3 · 2; е) (2,8 – 10) · 5 =
2,8 · 5 – 10 · 5.
– 3 · 2; е) (2,8 – 10) · 5 =
2,8 · 5 – 10 · 5.
II. Объяснение нового материала.
|
х |
1 |
1 |
2 |
–3 |
|
у |
2 |
–2 |
0 |
2 |
|
2 (х + у) |
6 |
–2 |
4 |
–2 |
|
2х + 2у |
6 |
–2 |
4 |
–2 |
|
х – (2 + у) |
–3 |
1 |
0 |
–7 |
|
(х – 2) + у |
1 |
–3 |
0 |
–3 |
|
(х – 2) – у |
–3 |
1 |
0 |
–7 |
Задания:
1) Назовите выражения, равные при всех наборах значений х и у.
2) Назовите выражения, равные при одних наборах х и у и не равные при других наборах значений х и у.
3) Из каких свойств действий над числами следует равенство этих выражений (или не следует)?
3. Введение определений.
Определение 1. Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Определение 2. Равенство, верное при любых значениях переменных, называется тождеством.
Следует помнить, что в 8 классе с введением дробно-рациональных выражений авторы учебника вернутся к понятию тождества и определят тождество как равенство, верное при всех допустимых значениях входящих в него переменных.
4. Рассматриваем примеры тождеств со с. 18 учебника. Подчеркиваем, что равенства, выражающие основные свойства действий над числами, являются тождествами.
Отмечаем, что замена выражения тождественно равным позволяет часто упростить вычисление значения исходного выражения.
III. Формирование умений и навыков.
все упражнения, решаемые на этом уроке, направлены на усвоение определений тождества и тождественно равных выражений, а также на закрепление навыка применения основных свойств действий над числами для преобразования выражений в тождественно равные.
1. № 85 (устно).
При выполнении этого упражнения ученики должны четко проговаривать свойство действий, которое позволило им сделать соответствующий вывод.
2. № 86, № 87.
3. № 88, № 89.
4. Упростите выражение.
а) 2,8 · 5а; в) 3,6 · 0,8а; д) 8х · (–3а); ж) –0,25у · 8b;
б) –3,5а · 4; г) –8а · (–12); е) 3,5х
· 2у; з) ![]() .
.
5. № 92, № 94.
IV. Проверочная работа.
Вариант 1
1. Упростите сумму.
а) –8 + х + (–22); б) –10 + а + 34.
2. Выполните вычисления, выбирая удобный порядок действий:
–25 · 123,7 · 4.
3. Представьте выражение в виде произведения.
а) 27 · 41 + 41 · х; б) 31а + 14а.
Вариант 2
1. Упростите сумму.
а) –17 + с + 47; б) –16 + р + (–21).
2. Выполните вычисления, выбирая удобный порядок действий:
–50 · 12,1 · 4.
3. Представьте выражение в виде произведения.
а) 38 · 54 + 54у; б) 34х + 15х.
Решение заданий проверочной работы
Вариант 1
1. а) –8 + х + (–22) = (–8 + (–22)) + х = –30 + х = х – 30;
б) –10 + а + 34 = (–10 + 34) + а = 24 + а = а + 24.
2. –25 · 123,7 · 4 = (–25 · 4) · 123,7 = –100 · 123,7 = –12370.
3. а) 27 · 41 + 41 · х = 41 · (27 + х);
б) 31а + 14а = (31 + 14) · а = 45а.
Вариант 2
1. а) –17 + с + 47 = (–17 + 47) + с = 30 + с = с + 30;
б) –16 + р + (–21) = (–16 + (–21)) + р = –37 +р = р – 37.
2. –50 · 12,1 · 4 = (–50 · 4) · 12,1 = –100 · 12,1 = –1210.
3. а) 38 · 54 + 54у = 54 · (38 + у);
б) 34х + 15х = (34 + 15) · х = 49х.
V. Итоги урока.
– Какие выражения называются тождественно равными? Приведите пример тождественно равных выражений.
– Какое равенство называется тождеством? Приведите пример тождества.
– Для чего необходимо заменять выражения тождественно равными?
Домашнее задание: № 90, № 91, № 93, № 108
Урок
№9
Тождественные преобразования выражений
Цели: закрепить усвоение понятий тождественно равных выражений и тождества; ввести понятие тождественного преобразования выражения; формировать умения выполнять основные тождественные преобразования (приведение подобных слагаемых, раскрытие скобок).
Ход урока
I. Устная работа.
1. Сравните значения выражений, не вычисляя их:
а) 35,8 + ![]() и
35,8 +
и
35,8 + ![]() ; г)
–2,8 +
; г)
–2,8 + ![]() и
и ![]() – 2,8;б)
– 2,8;б) ![]() и
и ![]() ; д) 19,7 ·
; д) 19,7 · ![]()
2. Является ли тождеством равенство:
а) х + 4 = (3 + х) + 1; г) 3а – 4 = (2а – 4) – а;
б) 5у – 35 = 5 (у – 7); д) –2 (b – 3) = –2b – 6;
в) 7х – 42 = (х – 6) · 7; е) 25 (а – а) = 25?
II. Объяснение нового материала.
1. Объяснение проводить согласно пункту 5 учебника.
III. Формирование умений и навыков.
1. № 95.
Образец оформления:
в) 6х – 14 – 13х + 26 = (6х – 13х) + (–14 +
26) = (6 – 13) х + 12 =
= –7х + 12.
2. № 96 (в; г); № 97 (в; г).
3. № 98, № 100.
1. № 102 (б; г).
Образец оформления:
г) 37 – (х – 16) + (11х – 53) = 37 – х + 16 + 11х
– 53 = (–х + 11х) +
+ (37 + 16 – 53) = (–1 + 11) х + 0 = 10х.
Если х = –0,03, то 10х = 10 · (–0,03) = –0,3.
Ответ: –0,3.
2. № 103 (а; б; в) (самостоятельно).
3. № 104, № 105, № 106.
1. № 107 (а).
Решение:
В первом альбоме а марок, тогда во втором – (а + 15) марок, а в третьем – 3 · (а + 15) марок.
Всего марок у Игоря: а + (а + 15) + 3 · (а + 15). Упростим данное выражение:
а + (а + 15) + 3 · (а + 15) = а + а +
15 + 3а + 45 = (1 + 1 + 3) а +
+ (15 + 45) = 5а + 60.
Ответ: всего 5а + 60 марок.
Напоминаем учащимся, что удобно отмечать подобные слагаемые подчеркиванием их одинаковыми линиями:
а + а + 15 + 3а + 45.
2. В магазине товар стоит а рублей. На распродаже его цена упала на 30 %. На сколько полученная прибыль магазина меньше предполагаемой первоначальной прибыли, если закупочная цена товара составляет 0,6а?
Решение:
Предполагаемая прибыль: а – 0,6а.
Новая цена: 0,7а.
Полученная прибыль: 0,7а – 0,6а.
Составим разность:
(а – 0,6а) – (0,7а – 0,6а) = а – 0,6а – 0,7а + 0,6а = а – 0,7а = 0,3а.
Ответ: 0,3а.
На этом примере показываем, что если подобные слагаемые имеют противоположные коэффициенты, то их сумма равна нулю и такие слагаемые можно «сокращать».
– 0,6а + 0,6а = (–0,6 + 0,6) а = 0 · а = 0.
IV. Итоги урока.
– Какие выражения называются тождественно равными?
– Какие преобразования выражений называются тождественными? Приведите примеры.
– Каким способом приводятся подобные слагаемые?
– Назовите правило раскрытия скобок, перед которыми стоит знак «плюс». На каком свойстве действий основывается это правило?
– Назовите правило раскрытия скобок, перед которыми стоит знак «минус». На каком свойстве действий основывается это правило?
Домашнее задание: № 96 (а; б); № 97 (а; б); № 99; № 101; № 102 (а; в).
Урок №10 Выражения. тождества
Цели: обобщить и систематизировать знания: свойства действий над числами, термины «числовое выражение», «выражение с переменными», «значение выражения», «тождество», «тождественные преобразования»; актуализировать умения: выполнять в буквенных выражениях числовые подстановки и производить соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами.
Ход урока
I. Организационный момент
Проверочная работа.
Вариант 1
1. Приведите подобные слагаемые.
а) 8b + 12b – 21b + b; б) 1,2c + 1 – 0,6y – 0,8 – 0,2c.
2. Раскройте скобки и приведите подобные слагаемые.
(1 – 9y) – (22y – 4) – 5.
Вариант 2
1. Приведите подобные слагаемые.
а) 9a + 17a – 30a + 4a; б) 1,8y + 3 – 2,8c – 0,2 – 2y.
2. Раскройте скобки и приведите подобные слагаемые.
(2 – 4b) – (31b – 6) – 11.
II. Повторение материала.
Повторение целесообразно организовать в форме практикума по решению задач. Все задания можно разбить на три группы.
1-я группа. Нахождение значения числового выражения и выражения с переменными.
1. Устная работа.
1) Используя термины «сумма», «разность», «произведение» и «частное», прочитайте выражение:
а) ![]() ; г)
3,72 · 8,02; ж) 3,12 · (5,3 + 2,7);
; г)
3,72 · 8,02; ж) 3,12 · (5,3 + 2,7);
б) 6,8 : 34; д) ![]() ; з)
; з) ![]() + 11;
+ 11;
в) 5,3 + 7,2; е) (10 – 18) : 3,4; и) 3,11 · (12 : 3,5).
2) Из данных выражений выберите выражение, не имеющее смысла:
а) 32 : (7 · 2 – 3,5 · 3); в) ![]() ;
;
б) ![]() ; г)
(3,8 · 2 – 7,6) : 4.
; г)
(3,8 · 2 – 7,6) : 4.
2. Письменная работа.
1) Найдите значение выражения.
а) 13 + 27,13 + 40 + 50,07; в) 4,24 – 17,05 : 12,5;
б) 5,47 – (8,32 – 5,311); г) (0,018 + 0,982) : (8 · 0,5 – 0,8).
При выполнении этих упражнение учащиеся должны обосновывать, почему они выбирают тот или иной порядок действий.
2) Найдите значение данного выражения:
а) 2m + 6n – 11 при т = –12 и п = 4; т
= –3,5 и п = 3![]() ;
;
б) 8 – 0,7 (3b – 5a) при а = –3,3 и b = 5,5;
в) ![]() при а
= 0 и b = 2,3;
при а
= 0 и b = 2,3;
г) пусть х – у = 3 и z = –5. Найдите 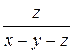 .
.
2-я группа. Сравнение значений выражений.
1. Устная работа.
Не выполняя вычислений, сравните значения выражений:
а) 3,5 · 0,24 и 3,5; г) 0,57 : 6 и 0,57
: ![]() ;
;
б) 3,5 · 0,24 и 0,24; д) –0,57 : ![]() и –0,57;
и –0,57;
в) –3,5 · 0,24 и –3,5; е) 94 : (–2,1) и 64 : (–2,1).
2. Письменная работа.
1) Сравните значения выражений:
а) ![]() и
и ![]() ; б)
0,5 и
; б)
0,5 и ![]() ;
;
в) 5 – 2х при х = 2 и х = –2;
г) 4х + 10у при х = –0,7, у = 0,9 и х = 1,4, у = –1,37.
2) Расположите числа в порядке убывания:
2,07; 2,007; –1,65; –1,66; 0.
3-я группа. Преобразование выражений на основе свойств действий, приведение подобных слагаемых и раскрытие скобок.
1. Устная работа.
Какие свойства действий позволяют, не выполняя вычислений, утверждать, что верно равенство?
а) ![]() + 354 =
354 +
+ 354 =
354 + ![]() ; в)
; в)
![]() ;
;
б) 85 · 11 = 11 · 85; г) ![]() .
.
2. Письменная работа.
1) Вычислите наиболее рациональным способом.
а) 6,83 + 7,81 + 3,17 + 8,19; в) ![]() ;
;
б) ![]() ∙
13,5 ∙ 19; г) –4,83 + 3,99 + 2,83.
∙
13,5 ∙ 19; г) –4,83 + 3,99 + 2,83.
2) Раскройте скобки и приведите подобные слагаемые.
а) 2a + (3a – 8b); в) 9x + 3 (15 – 8x);
б) (2a – 7y) – (5a – 7y); г) 33 – 8 (11b – 1) – 2b.
3) Найдите значение данного выражения:
а) 1,7 (а – 11) – 16,3 при а = 3,8;
б) 0,6 (4х – 14) – 0,4 (5х – 1) при x = 4![]() .
.
III. Итоги урока.
Домашнее задание: повторить п. 1–5; № 210; № 109, № 217 (а; г), № 230 (а).
Урок
№11
Контрольная работа № 1 «Выражения»
Вариант 1
1. Найдите значение выражения 6х –
8у при x = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений –0,8х – 1 и 0,8х – 1 при х = 6.
3. Упростите выражение.
а) 2х – 3у – 11х + 8у;
б) 5(2а + 1) – 3;
в) 14х – (х – 1) + (2х + 6).
4. Упростите выражение и найдите его значение.
–4 (2,5a – 1,5) + 5,5a – 8
при a = –![]() .
.
5. Раскройте скобки: 3x – (5x – (3x – 1)).
Вариант 2
1. Найдите значение выражения 16а +
2у при a = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений 2 + 0,3а и 2 – 0,3а при а = –9.
3. Упростите выражение.
а) 5a + 7b – 2a – 8b;
б) 3 (4х + 2) – 5;
в) 20b – (b – 3) + (3b – 10).
4. Упростите выражение и найдите его значение.
–6 (0,5x – 1,5) – 4,5x – 8
при x = ![]() .
.
5. Раскройте скобки: 2p – (3p – (2p – c)).
Вариант 1
1. Найдите значение выражения 6х – 8у при x = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений –0,8х – 1 и 0,8х – 1 при х = 6.
3. Упростите выражение.а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6).
4. Упростите выражение и найдите его значение. –4 (2,5a – 1,5)
+ 5,5a – 8 при a = –![]() .
.
5. Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля υ км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если s = 200, t = 2, υ = 60.
6. Раскройте скобки: 3x – (5x – (3x – 1)).
Вариант 2
1. Найдите значение выражения 16а + 2у при a = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений 2 + 0,3а и 2 – 0,3а при а = –9.
3. Упростите выражение. а) 5a + 7b – 2a – 8b; б) 3 (4х + 2) – 5; в) 20b – (b – 3) + (3b – 10).
4. Упростите выражение и найдите его значение. –6 (0,5x – 1,5) –
4,5x – 8 при x = ![]() .
.
5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля υ1 км/ч, а скорость мотоцикла υ2 км/ч. Ответьте на вопрос задачи, если t = 3, υ1 = 80, υ2 = 60.
6. Раскройте скобки: 2p – (3p – (2p – c)).
Вариант 1
1. Найдите значение выражения 6х – 8у при x = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений –0,8х – 1 и 0,8х – 1 при х = 6.
3. Упростите выражение.а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6).
4. Упростите выражение и найдите его значение. –4 (2,5a – 1,5)
+ 5,5a – 8 при a = –![]() .
.
5. Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля υ км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если s = 200, t = 2, υ = 60.
6. Раскройте скобки: 3x – (5x – (3x – 1)).
Вариант 2
1. Найдите значение выражения 16а + 2у при a = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений 2 + 0,3а и 2 – 0,3а при а = –9.
3. Упростите выражение. а) 5a + 7b – 2a – 8b; б) 3 (4х + 2) – 5; в) 20b – (b – 3) + (3b – 10).
4. Упростите выражение и найдите его значение. –6 (0,5x – 1,5) –
4,5x – 8 при x = ![]() .
.
5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля υ1 км/ч, а скорость мотоцикла υ2 км/ч. Ответьте на вопрос задачи, если t = 3, υ1 = 80, υ2 = 60.
6. Раскройте скобки: 2p – (3p – (2p – c)).
Вариант 1
1. Найдите значение выражения 6х – 8у при x = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений –0,8х – 1 и 0,8х – 1 при х = 6.
3. Упростите выражение.а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6).
4. Упростите выражение и найдите его значение. –4 (2,5a – 1,5)
+ 5,5a – 8 при a = –![]() .
.
5. Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля υ км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если s = 200, t = 2, υ = 60.
6. Раскройте скобки: 3x – (5x – (3x – 1)).
Вариант 2
1. Найдите значение выражения 16а + 2у при a = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений 2 + 0,3а и 2 – 0,3а при а = –9.
3. Упростите выражение. а) 5a + 7b – 2a – 8b; б) 3 (4х + 2) – 5; в) 20b – (b – 3) + (3b – 10).
4. Упростите выражение и найдите его значение. –6 (0,5x – 1,5) –
4,5x – 8 при x = ![]() .
.
5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля υ1 км/ч, а скорость мотоцикла υ2 км/ч. Ответьте на вопрос задачи, если t = 3, υ1 = 80, υ2 = 60.
6. Раскройте скобки: 2p – (3p – (2p – c)).
Вариант 1
1. Найдите значение выражения 6х – 8у при x = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений –0,8х – 1 и 0,8х – 1 при х = 6.
3. Упростите выражение.а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6).
4. Упростите выражение и найдите его значение. –4 (2,5a – 1,5)
+ 5,5a – 8 при a = –![]() .
.
5. Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля υ км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если s = 200, t = 2, υ = 60.
6. Раскройте скобки: 3x – (5x – (3x – 1)).
Вариант 2
1. Найдите значение выражения 16а + 2у при a = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений 2 + 0,3а и 2 – 0,3а при а = –9.
3. Упростите выражение. а) 5a + 7b – 2a – 8b; б) 3 (4х + 2) – 5; в) 20b – (b – 3) + (3b – 10).
4. Упростите выражение и найдите его значение. –6 (0,5x – 1,5) –
4,5x – 8 при x = ![]() .
.
5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля υ1 км/ч, а скорость мотоцикла υ2 км/ч. Ответьте на вопрос задачи, если t = 3, υ1 = 80, υ2 = 60.
Урок №13
линейное уравнениес одной переменной
Цели: ввести определение линейного уравнения с одной переменной (общий вид); выяснить, сколько корней может иметь линейное уравнение; формировать умение решать линейное уравнение переходом к равносильному уравнению, применяя свойства уравнений и выполняя тождественные преобразования.
Ход урока
I. Организационный момент
Устная работа.
1. Какие из чисел 3; –2; 2 являются корнями следующих уравнений:
а) 3х = –6; г) 4х – 4 = х + 5;
б) 3х + 2 = 10 – х; д) 10х = 5(2х + 3);
в) х + 3 = 6; е) 10 + х = 13?
2. Являются ли уравнения равносильными? Если да, то сформулируйте, по какому свойству уравнений.
а) 3х + 4 = 2 и 3х = –2;
б) –3х + 12 + 2х = 4 и 2х + 12 = 3х + 4;
в) 3х + 15 = 0 и 3х = 15;
г) 0,5х = 0,08 и 50х = 8;
д) 120х = –10 и 12х = 1;
е) ![]() x
= 11 и 3х = 44.
x
= 11 и 3х = 44.
II. Объяснение нового материала.
Рассмотрим уравнение 9х – 23 = 5х – 11. Применим известные свойства уравнений и получим равносильные уравнения:
9х – 5х = – 11 + 23;
4х = 12;
х = 3.
Уравнение, равносильное исходному, имеет единственный корень 3, значит, исходное уравнение также имеет единственный корень 3.
Используя свойства уравнений, многие из них всегда можно привести к виду ax = b, где х – переменная, а a и b – некоторые числа. Уравнения такого вида называются линейными.
Важно подчеркнуть учащимся, что, используя буквенные обозначения, мы записали целый класс уравнений.
3. Организация исследовательской деятельности учащихся.
На этом этапе востребуется логический прием мышления – обобщение.
Задание. Привести уравнение к линейному виду, используя свойства уравнений:
а) 3х – 11 = 5х + 7;
б) 2 (х + 1) = 2х + 2;
в) –8х + 11 = 8 (3 – х).
Решение:
а) 3х – 11 = 5х + 7; б) 2 (х + 1) = 2х + 2;
3х – 5х = 7 + 11; 2х + 2 = 2х + 2;
–2х = 18. 2х – 2х = 2 – 2;
0 · х = 0.
в) –8х + 11 = 8 (3 – х);
–8х + 11 = 24 – 8х;
–8х + 8х = 24 – 11;
0 · х = 13.
Теперь, глядя на линейное уравнение, записать, чему равны коэффициенты a и b и сколько корней имеет уравнение. как это определили?
а) a = –2; b = 18 – один корень х = –9, определили, разделив обе части на (–2).
б) a = 0; b = 0 – бесконечно много корней, так как равенство 0 · х = 0 верно при любом значении х.
в) a = 0; b = 13 – нет корней, так как равенство 0 · х = 13 неверно ни при каком значении х.
Обобщая полученные данные, заполняем таблицу решения линейного уравнения в общем виде:
|
Линейное уравнение ax = b, где х – переменная, a, b – любое число. Если
a ¹ 0, то x
= если а = 0 и b = 0, то х – любое; если а = 0 и b ¹ 0, то нет корней. |
4. Создание алгоритма решения уравнений, сводящихся к линейным.
Анализируя решенные примеры, приходим к выводу, что решение многих уравнений сводится к решению линейных.
Учащиеся могут сами создать алгоритм:
1-й шаг. Если выражения, стоящие в левой или правой части уравнения, содержат скобки, то раскрываем их по правилам.
2-й шаг. Переносим слагаемые с переменными в левую часть уравнения, а без переменных в правую.
3-й шаг. Приводим подобные слагаемые в обеих частях уравнения, приводя его к виду ax = b.
4-й шаг. Решаем получившееся линейное уравнение, равносильное исходному, в зависимости от значений коэффициентов a и b.
III. Формирование умений и навыков.
Задания, решаемые на этом уроке, направлены на усвоение определения линейного уравнения и решение линейных уравнений в зависимости от значений коэффициентов a и b.
1. (Устно.) Назовите коэффициенты a и b линейного уравнения ax = b. Сколько корней имеет уравнение:
а) 3х = 12; в) 1![]() x = –14; д) 0 · х = 0;б) –3х
= 18;г) 0 ∙ x =
x = –14; д) 0 · х = 0;б) –3х
= 18;г) 0 ∙ x = ![]() ;е) –18х = –2?
;е) –18х = –2?
2. Решите уравнение.
а) –8х = 24;г) –3x = ![]() ; ж) –6 =
; ж) –6 = ![]() x;б) 50х = –5; д) –x
= –1
x;б) 50х = –5; д) –x
= –1![]() ; з)
; з) ![]() ;
;
в) –18х = 1;е) ![]() = –5x; и) –0,81х = 72,9.
= –5x; и) –0,81х = 72,9.
3. Определите значение х, при котором значение выражения –3х равно:
а) 0; б) 6; в) –12; г) ![]() ; д)
; д) ![]() ; е) 2
; е) 2![]() .
.
IV. Итоги урока.
Домашнее задание: № 126, № 127, № 245, № 142.
Урок №14
Линейное
уравнение с одной переменной
Цель: формировать умение решать по алгоритму уравнения, сводящиеся к линейным.
Ход урока
I. Организационный момент
II. Проверочная работа.
Вариант 1
1. Сколько корней имеет уравнение: а) –2х = 17; б) 0 · х = –6; в) 0 · х = 0?
2. Найдите корень уравнения. а) 26х = –78; б) 0,2х
= 2,8; в) ![]() x
= 24; г) –3x =
x
= 24; г) –3x = ![]() .
.
Вариант 2
1. Сколько корней имеет уравнение: а) 0 · х = –72; б)
![]() x = 11; в)
0 · х = 0?
x = 11; в)
0 · х = 0?
2. Найдите корень уравнения. а) 21х = 84; б) –1,2х
= 0,36; в) ![]() x
= 21; г) –2x =
x
= 21; г) –2x = ![]() .
.
III. Формирование умений и навыков.
№ 128 (а; б; е; ж; и); № 129; № 131.
3. № 131, № 132.
№ 131.
Решение:
|
а) (у + 4) – (у – 1) = 6у; у + 4 – у + 1 = 6у; у – у – 6у = –4 – 1; – 6у = –5; у = (–5) : (–6); у
= |
б) 3р – 1 – (р + 3) = 1; 3р – 1 – р – 3 = 1; 3р – р = 1 + 1 + 3; 2р = 5; р = 5 : 2; р = 2,5; |
|
в) 6х – (7х – 12) = 101; 6х – 7х + 12 = 101; 6х – 7х = 101 – 12; –х = 89; х = –89. |
г) 20х = 19 – (3 + 12х); 20х = 19 – 3 – 12х; 20х + 12х = 19 – 3; 32х = 16; х = 16 : 32; х = 0,5. |
№ 132.
Решение:
а) (13х – 15) – (9 + 6х) = –3х;
13х – 15 – 9 – 6х = –3х;
13х – 6х + 3х = 15 + 9;
10х = 24;
х = 24 : 10;
х = 2,4.
б) 12 – (4х – 18) = (36 + 4х) + (18 – 6х);
12 – 4х + 18 = 36 + 4х + 18 – 6х;
– 4х – 4х + 6х = 36 + 18 – 12 – 18;
– 2х = 24;
х = 24 : (–2);
х = –12.
в) 1,6х – (х – 2,8) = (0,2х + 1,5) – 0,7;
1,6х – х + 2,8 = 0,2х + 1,5 – 0,7;
1,6х – х – 0,2х = 1,5 – 0,7 – 2,8;
0,4х = –2;
х = (–2) : 0,4;
х = –5.
г) (0,5х + 1,2) – (3,6 – 4,5х) = (4,8 – 0,3х) + (10,5х + 0,6);
0,5х + 1,2 – 3,6 + 4,5х = 4,8 – 0,3х + 10,5х + 0,6;
0,5х + 4,5х + 0,3х – 10,5х = 4,8 + 0,6 – 1,2 + 3,6;
–5,2х = 7,8;
х = 7,8 : (–5,2);
х = –1,5.
4. № 134.
Решение:
|
а) 8b – 27 = 5; 8b = 5 + 27; 8b = 32; b = 32 : 8; b = 4. |
б) 8b – 27 = –11; 8b = –11 + 27; 8b = 16; b = 16 : 8; b = 2. |
|
в) 8b – 27 = 1,8; 8b = 1,8 + 27; 8b = 28,8; b = 28,8 : 8; b = 3,6. |
г) 8b – 27 = –1; 8b = –1 + 27; 8b = 26; b = 26 : 8; b = 3,25. |
5. При каком значении t:
а) значение выражения 5t + 11 равно значению выражения 7t + 31;
б) значение выражения 8t + 3 в три раза больше значения выражения 5t – 6;
в) значение выражения 5t + 1 в два раза меньше значения выражения 10t + 18;
г) значение выражения 0,25t – 31 на 5 больше значения
выражения ![]() t
– 18;
t
– 18;
д) значение выражения 13t – 7 на 8 меньше значения
выражения
12t + 11;
е) разность выражений 1,5t – 37 и 1,5t – 73 равна 36?
Основную трудность при составлении равенств у учащихся вызывают задания б) – д). Следует разобрать принцип составления равенства с использованием наглядности.
Решение:
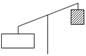
б) 8t + 3 5t – 6 8t + 3 3 (5t – 6)
![]()
(8t + 3) = 3 (5t – 6);
8t + 3 = 15t – 18;
8t – 15t = – 18 – 3;
–7t = –21;
t = 3.
в) 5t + 1 10t + 18 5t + 1 (10t + 18) : 2
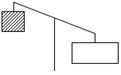
5t + 1 = (10t + 18) : 2;
5t + 1 = 5t + 9;
5t – 5t = 9 – 1;
0 · t = 8 – нет решений.
г) 0,25t – 31 ![]() t – 18 0,25t
– 31
t – 18 0,25t
– 31 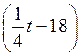 + 5
+ 5
0,25t – 31 = ![]() t – 18 + 5;
t – 18 + 5;
0,25t – ![]() t = – 18 + 5 + 31;
t = – 18 + 5 + 31;
0 · t = 18 – нет решений.
д) 13t – 7 = (12t + 11) – 8 или (13t – 7) + 8 = 12t + 11.
е) (1,5t – 37) – (1,5t – 73) = 36;
1,5t – 37 – 1,5t + 73 = 36;
1,5t – 1,5t = 36 + 37 – 73;
0 · t = 0 – t – любое число.
IV. Итоги урока.
Домашнее задание: № 128 (в; г; д; з); № 130; № 133; № 135.
Урок
№15
Линейное уравнение с одной переменной
Цели: продолжить формировать умение решать уравнения, сводящиеся к линейным.
Ход урока
I. Организационный момент
Устная работа.
1. Показать, что следующие уравнения не имеют решений, и объяснить почему:
а) х + 3 = х; в) 2х = 2(х + 1); д) (–х)2 + 1 = 0.
б) х – 1 = х + 1; г) х2 + 4 = 0;
2. Определить, равносильны ли уравнения и почему:
а) 5х + 1 = 2 и 10х + 2 = 4;
б) 2х – 1 = 4 и 2х = 6;
в) 3х + 1 = 10 и х = 3;
г) 2х + 3 = 2х – 4 и х + 5 = х;
д) ![]() и 21х
= –6.
и 21х
= –6.
II. Математический диктант.
Вариант 1
1. Придумайте и запишите какое-нибудь линейное уравнение с одним неизвестным х.
2. Как называется уравнение –2х = 17?
3. При каком условии уравнение сх = 5 имеет единственный корень? Запишите этот корень.
4. Решите уравнение 0,2х = –1.
5. К обеим частям уравнения прибавили число –3. Какими являются полученное и исходное уравнения?
6. Решите уравнение 2х + 1 = 3х – х.
7. Решите уравнение 5 – х = 2х + 2.
Вариант 2
1. Придумайте и запишите какое-нибудь линейное уравнение с одним неизвестным у.
2. Как называется уравнение 17х = –2?
3. При каком условии уравнение ау = 3 не имеет корней?
4. Решите уравнение –0,3х = 1.
5. Обе части уравнения умножим на число –7. Какими являются полученное и исходное уравнения?
6. Решите уравнение х + 3 = 5 + х – 2.
7. Решите уравнение 2 – 2х = –2х + 3.
III. Формирование умений и навыков.
1. Решите уравнение.
а) (5х – 3) + (7х – 4) = 8 – (15 – 11х);
б) (4х + 3) – (10х + 11) = 7 + (13 – 4х);
в) (7 – 5х) – (8 – 4х) + (5х + 6) = 8;
г) (3 – 2х) + (4 – 3х) + (5 – 5х) = 12 + 7х.
Решение:
а) (5х – 3) + (7х – 4) = 8 – (15 – 11х);
5х – 3 + 7х – 4 = 8 – 15 + 11х;
5х + 7х – 11х = 8 – 15 + 3 + 4;
х = 0.
б) (4х + 3) – (10х + 11) = 7 + (13 – 4х);
4х + 3 – 10х – 11 = 7 + 13 – 4х;
4х – 10х + 4х = 7 + 13 – 3 + 11;
–2х = 28;
х = 28 : (–2);
х = –14.
в) (7 – 5х) – (8 – 4х) + (5х + 6) = 8;
7 – 5х – 8 + 4х + 5х + 6 = 8;
– 5х + 4х + 5х = 8 – 7 + 8 – 6;
4х = 3;
х = ![]() .
.
г) (3 – 2х) + (4 – 3х) + (5 – 5х) = 12 + 7х;
3 – 2х + 4 – 3х + 5 – 5х = 12 + 7х;
– 2х – 3х – 5х – 7х = 12 – 3 – 4 – 5;
–17х = 0;
х = 0.
2. Среди данных уравнений выберите те, которые имеют тот же корень, что и уравнение 2х – 3 = 5х + 6:
а) 19 (2х – 3) = 19 (5х + 6);
б) 5х – 2х = 6 – 3;
в) ![]() .
.
Решение:
2х – 3 = 5х + 6;
2х – 5х = 6 + 3;
–3х = 9;
х = –3.
а) 19 (2х – 3) = 19 (5х + 6); | : 19
2х – 3 = 5х + 6;
х = –3, так как уравнение равносильно исходному.
При решении данного уравнения важно заметить, что разделить обе части уравнения на 19 рационально, а выполнить умножение числа на скобку – нет.
б) 5х – 2х = 6 – 3; в) ![]() | · 11;
| · 11;
3х = 3; 2х – 3 = 5х + 6;
х = 1. 2х – 5х = 6 + 3;
х = –3,
так как уравнение равносильно исходному.
Ответ: а); в); х = –3.
3. Среди данных уравнений укажите те, которые не имеют корней:
а) 5х – 10 = 4х; в) 5 – х = 6 – х; д) | x | + 1 = 0.
б) 3х + 7 = 3х + 11; г) | x | = 8;
Решение:
а) 5х – 10 = 4х; б) 3х + 7 = 3х + 11;
5х – 4х = 10; 3х – 3х = 11 – 7;
х = 10. 0 · х = 4 – нет корней.
в) 5 – х = 6 – х; г) | x | = 8; д) | x | + 1 = 0.
–х + х = 6 – 5; х = 8 или х = –8. | x | = –1 –
0 · х = 1 – нет корней. нет решений,
так как | x | ≥ 0.
№ 238. Решение:
Если т ¹ 0, то тх = 5 имеет единственный корень х = 5 : т.
Если т = 0, то уравнение примет вид 0 · х = 5, оно не имеет корней.
Не существует такое значение т, чтобы уравнение имело бесконечно много корней.
№ 239. Решение:
Если х = –5, то р · (–5) = 10 – верное равенство.
Найдем р: р = 10 : (–5);
р = –2.
Если х = 1, то р · (–1) = 10;
р = 10 : (–1);
р = –10.
Если х = 20, то р · 20 = 10;
р = 10 : 20;
р = 0,5.
Ответ: –2; –10; 0,5.
Обращаем внимание учащихся, что это уравнение с параметром р.
№ 242. Решение:
а) (х + 5) (х + 6) + 9 = 0;
х2 + 6х + 5х + 30 + 9 = 0;
х2 + 11х + 39 = 0;
х2 = –11х – 39.
Слева стоит выражение, значение которого не отрицательно. если х – положительное число, то –11х < 0 и –11х – 39 < 0, значит, х2 = –11х – 39 – неверно для любого положительного х, значит, уравнение не может иметь положительный корень.
б) х2 + 3х + 1 = 0.
Если х > 0, то каждое слагаемое в левой части уравнения положительно, значит, и вся сумма положительна, следовательно, х > 0 не может являться корнем данного уравнения.
IV. Итоги урока.
Домашнее задание: № 136, № 137, № 138
Урок №16
Решение задач с помощью уравнений
Цели: обеспечить понимание уравнения в качестве математической модели некоторой жизненной ситуации, описанной в текстовой задаче; выделить этапы решения задач алгебраическим методом; формировать умение составлять уравнение по условию задачи и решать его.
Ход урока
I. Организационный момент
II. Объяснение нового материала.
1. Объяснение начать с решения конкретной (приведенной в учебнике) задачи № 1.
Можно воспользоваться таблицей:
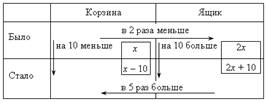
Сперва в таблице стрелками обозначаем и подписываем все зависимости, затем видим, что неизвестны все четыре клеточки, значит, обозначить переменной удобно главный вопрос задачи, например, количество яблок в корзине первоначально. Затем, по стрелкам, заполняем все клеточки. Последняя стрелка даст уравнение: 5(х – 10) = 2х + 10.
Аналогичную таблицу можно составить для задачи № 2:
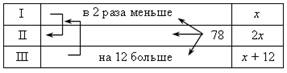
х + 2х + (х + 12) = 78.
При решении второй задачи особое внимание уделяется последнему этапу – интерпретации полученного результата.
III. Формирование умений и навыков.
1. № 143.
Решение:
Пусть в одной кассе было х билетов, тогда во второй – (х + 36) билетов. Зная, что всего было продано 392 билета, составим уравнение:
х + (х + 36) = 392;
х + х + 36 = 392;
2х = 356;
х = 178.
Следовательно, в первой кассе было продано 178 билетов.
Так как х + 36 = 178 + 36 = 214, то во второй кассе было продано 214 билетов.
Ответ: 178 и 214 билетов.
2. № 146.
Решение:
Анализ условия:
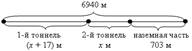
Пусть х м – длина одного тоннеля, тогда (х + 17) м – длина другого. Так как наземная часть составляет 703 м, а вся трасса – 6940 м, то длина тоннелей в сумме составляет (6940 – 703) м. Зная, что длина тоннелей равна х + (х + 17) м, составим уравнение:
х + (х + 17) = 6940 – 703;
х + х + 17 = 6237;
х + х = 6237 – 17;
2х = 6220;
х = 3110.
Значит, длина одного тоннеля равна 3110 м. Так как х + 17 = = 3110 + 17 = 3127, то длина другого тоннеля равна 3127 м.
Ответ: 3110 м и 3127 м.
3. № 147.
Анализ условия:
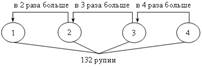
Пусть первый жертвователь дал х рупий, тогда второй дал 2х рупий, третий – 3 · 2х рупий, четвертый – 4 · (3 · 2х) рупий. Зная, что все вместе они дали 132 рупии, составим уравнение:
х + 2х + 3 · 2х + 4 · (3 · 2х) = 132;
х + 2х + 6х + 24х = 132;
33х = 132;
х = 132 : 33;
х = 4.
Значит, первый жертвователь дал 4 рупии. Так как 2х = 2 · 4 = 8, то второй дал 8 рупий. Так как 3 · 2х = 3 · 8 = 24, то третий дал 24 рупии. Так как 4 · (3 · 2х) = 4 · 24 = 96, то четвертый дал 96 рупий.
Ответ: 4; 8; 24 и 96 рупий.
4. № 148.
Анализ условия:
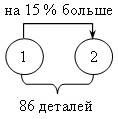
Пусть х деталей изготовил второй рабочий, тогда первый изготовил (х + 0,15х) деталей. Зная, что вместе они изготовили 86 деталей, составим уравнение:
х + (х + 0,15х) = 86;
х + х + 0,15х = 86;
2,15х = 86;
х = 86 : 2,15;
х = 40.
Значит, второй рабочий изготовил 40 деталей. Так как х + 0,15х
= 40 +
+ 0,15 · 40 = 40 + 6 = 46, то первый рабочий изготовил 46 деталей.
Ответ: 46 деталей и 40 деталей.
IV. Итоги урока.
Домашнее задание: № 144; № 145; № 149; № 165.
Урок 18
Решение задач с помощью уравнений
Цели: продолжить формировать умение решать текстовые задачи алгебраическим методом – с помощью составления уравнений, сводящихся к линейным.
Ход урока
I. Устная работа.
1. Вычислите.
а) 0,35 · 0,2 + 0,35 · 0,8; в) ![]() ; д)
; д) ![]() ;б)
;б) ![]() · 0,5 · 8; г)
· 0,5 · 8; г) ![]() ; е) (–3)2 – 9,2.
; е) (–3)2 – 9,2.
2. Выразите:
а) t из s = υ · t; в) y из υ = 2a – y;
б) p из N = p : t; г)
x из y = ![]() .
.
II. Проверочная работа.
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
III. Формирование умений и навыков.
При решении задач замечаем, что неизвестную величину не обязательно обозначаем за х. Наоборот, если в задаче используется формула, например, s = υ · t, то и переменную удобно обозначать соответствующей буквой.
1. № 151.
Решение:
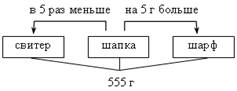
Пусть х г шерсти ушло на шапку, тогда на свитер ушло 5х г, а на шарф – (х – 5) г шерсти. Зная, что на все изделия ушло 555 г шерсти, составим уравнение:
х + 5х + (х – 5) = 555;
х + 5х + х – 5 = 555;
7х = 560;
х = 80.
Значит, на шапку ушло 80 г шерсти. Так как 5х = 5 · 80 = 400, то на свитер ушло 400 г шерсти.
Так как х – 5 = 80 – 5 = 75, то на шарф ушло 75 г шерсти.
Ответ: 400 г; 80 г; 75 г.
2. № 152.
Решение:
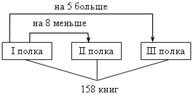
Пусть на первой полке расположено п книг, тогда на второй полке – (п + 8), а на третьей – (п – 5) книг. Зная, что на трех полках необходимо расположить всего 158 книг, составим уравнение:
п + (п + 8) + (п – 5) = 158;
п + п + 8 + п – 5 = 158;
3п + 3 = 158;
3п = 155;
п = 51![]() .
.
Интерпретация результата: так как п – число книг, то п
дол-жно быть натуральным числом. 51![]() – дробное, значит, указанным способом
нельзя разместить книги на полках.
– дробное, значит, указанным способом
нельзя разместить книги на полках.
Ответ: нельзя.
На примере этой задачи видно, что важен этап интерпретации полученного решения.
3. № 154.
Решение:
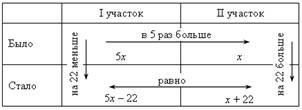
Пусть х кустов малины было на втором садовом участке, тогда на первом было 5х кустов. После пересадки на первом участке осталось (5х – 22) кустов малины, а на втором стало (х + 22) куста малины. Зная, что после пересадки на обоих участках стало кустов малины поровну, составим уравнение:
5х – 22 = х + 22;
5х – х = 22 + 22;
4х = 44;
х = 11.
Значит, на втором участке было 11 кустов малины. Так как 5х
=
= 5 · 11 = 55, то на первом участке было 55 кустов малины.
Ответ: 55 и 11 кустов малины.
4. № 155.
Решение:
Анализ условия:
|
|
υ (км/ч) |
t (ч) |
s (км) |
|
|
По течению |
υc + 2 |
9 |
9 · (υc + 2) |
|
|
Против течения |
υc – 2 |
11 |
11 · (υc – 2) |
|
Пусть υc км/ч – собственная скорость теплохода, тогда по течению он шел со скоростью (υc + 2) км/ч и за 9 часов прошел 9 · (υc + 2) км. Против течения он шел со скоростью (υc – 2) км/ч и прошел 11 · (υc – 2) км. Зная, что он прошел по течению и против одинаковое расстояние, составим уравнение:
9 · (υc + 2) = 11 · (υc – 2);
9 υc + 18 = 11 υc – 22;
9 υc – 11 υc = – 22 – 18;
–2 υc = –40;
υc = 20.
Значит, собственная скорость теплохода равна 20 км/ч.
Ответ: 20 км/ч.
При обозначении переменной можно не ставить индекс υc, а просто обозначить υ. Не возбраняется использовать любую букву латинского алфавита.
5. № 157.
Решение:
|
|
υ (верст/день) |
t (день) |
s (верст) |
||
|
I |
40 |
|
п + 1 |
|
40 (п + 1) |
|
II |
45 |
п |
45п |
||
Пусть второй человек догонит первого через п дней, тогда за эти дни он пройдет 45п верст. Первый человек, так как он шел на день дольше, пройдет 40 (п + 1) верст. Зная, что они пройдут одинаковое расстояние, составим уравнение:
45п = 40 (п + 1);
45п = 40п + 40;
45п – 40п = 40;
5п = 40;
п = 8 Значит, через 8 дней второй догонит первого.
IV. Итоги урока.
Домашнее задание: № 150, № 153, № 156, № 248.
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Вариант 1
1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?
2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
Вариант 2
1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?
Урок №19
Решение задач с помощью уравнений
Цель: продолжить формировать умение решать текстовые задачи алгебраическим методом – с помощью составления уравнений, сводящихся к линейным.
Ход урока
I. Организационный момент
II. Формирование умений и навыков.
1. № 158.
Решение:
Анализ условия:
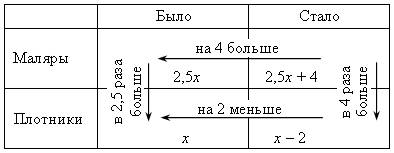
Пусть х плотников было в бригаде, тогда маляров было 2,5х. После переводов в бригаде стало (2,5х + 4) маляров и (х – 2) плотников. Зная, что маляров стало в 4 раза больше плотников, составим уравнение:
(2,5х + 4) = 4 · (х – 2);
2,5х + 4 = 4х – 8;
2,5х – 4х = –8 – 4;
–1,5х = –12;
х = (–12) : (–1,5);
х = 8.
Значит, в бригаде было 8 плотников. Так как 2,5х = 2,5 · 8 = 20, то в бригаде было 20 маляров.
Ответ: 20 маляров и 8 плотников.
В таблице основную зависимость, по которой формируем равенство, можно выделить другим цветом или более жирной линией.
2. № 161.
Решение:
Анализ условия:
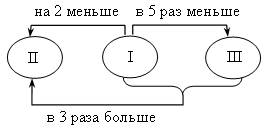
Пусть х кг – масса первого арбуза, тогда второй арбуз весит (х + 2) кг, а третий – 5х кг. Первый и третий арбуз вместе весят х + 5х, то есть 6х кг. Зная, что в сумме они весят в 3 раза больше второго арбуза, составим уравнение:
3 · (х + 2) = 6х;
3х + 6 = 6х;
3х – 6х = –6;
–3х = –6;
х = 2.
Значит, первый арбуз весит 2 кг. Так как х + 2 = 2 + 2 = 4, то второй арбуз весит 4 кг. Так как 5 · х = 5 · 2 = 10, то третий арбуз весит 10 кг.
Ответ: 2 кг, 4 кг, 10 кг.
3. № 162.
Решение:
Анализ условия:
|
|
было |
взяли |
осталось |
|
в 2 раза меньше |
|
I |
50 |
х |
50 – х |
||
|
II |
50 |
3х |
50 – 3х |
Пусть х кг сахара взяли из первого мешка, тогда из второго мешка взяли 3х кг сахара. В первом мешке осталось (50 – х) кг сахара, а во втором – (50 – 3х) кг. Зная, что во втором мешке осталось в 2 раза меньше сахара, чем в первом, составим уравнение:
2 · (50 – 3х) = 50 – х;
100 – 6х = 50 – х;
–6х + х = 50 – 100;
–5х = –50;
х = (–50) : (–5);
х = 10.
Значит, из первого мешка взяли 10 кг сахара. Так как 50 – х
=
= 50 – 10 = 40, то в первом мешке осталось 40
кг сахара. Так как 50 – 3х =
= 50 – 3 · 10 = 50 – 30 = 20, то во втором мешке осталось 20
кг сахара.
Ответ: 40 кг и 20 кг.
4. Федя на 7 лет старше Пети, а их папе в 3 раза больше лет, чем им обоим вместе. Сколько лет каждому из них, если папе было 36 лет, когда родился Петя?
Решение:
Анализ условия:
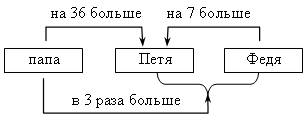
Пусть х лет Пете, тогда Феде (х + 7) лет, а папе (х + 36) лет. Пете и Феде вместе х + (х + 7) лет или 2х + 7 лет. Зная, что папе лет в 3 раза больше, чем им обоим вместе, составим уравнение:
(2х + 7) · 3 = х + 36;
6х + 21 = х + 36;
6х – х = 36 – 21;
5х = 15;
х = 3.
Значит, Пете 3 года. Так как х + 7 = 3 + 7 = 10, то Феде 10 лет.
Ответ: Пете 3 года, Феде 10 лет.
III. Проверочная работа.
Вариант 1
Стоимость изделия третьего сорта в 3 раза меньше стоимости изделия первого сорта. Сколько стоит каждое изделие, если изделие первого сорта на 5000 р. дороже изделия третьего сорта?
Вариант 2
Мама весит в 5 раз больше дочери, а дочь на 40 кг легче мамы. Сколько весят мама и дочь в отдельности?
IV. Итоги урока. Домашнее задание: 1. № 159, № 160, № 252.
Урок 20
Среднее арифметическое, размах и мода
Цели: ввести понятия таких статистических характеристик, как среднее арифметическое, размах и мода; формировать умение находить средние статистические характеристики различных рядов.
Ход урока
I. Организационный момент
II. Объяснение нового материала.
Объяснение следует проводить согласно пункту 9 учебника.
Особое внимание следует уделить целесообразности использования различных средних статистических характеристик в зависимости от ситуации.
Необходимо подытожить, какие статистические характеристики теперь могут находить учащиеся. Для этого на доску можно вынести пример.
|
Упорядоченный ряд чисел: 1; 2; 2; 3; 4; 4; 5; 5; 5 1) Среднее
арифметическое: 2) Размах: 5 – 1 = 4 3) Мода: 5 |
III. Формирование умений и навыков.
1. № 167, № 168.
Необходимо, чтобы учащиеся четко мотивировали свои ответы.
а) сложили все члены ряда и полученную сумму разделили на их количество. Значит, искали среднее арифметическое.
б) Нашли разность между наибольшим и наименьшим числом в ряду, то есть размах ряда.
в) Число … встречается наибольшее количество раз, значит, это мода ряда.
2. Даны упорядоченные ряды чисел:
а) 1; 1; 2; 3; 4; 5; 6; б) ![]() .
.
Для каждого из них найти среднее арифметическое, размах и моду.
3. Найти среднее арифметическое, размах и моду рядов чисел:
а) 1; 2; 5; 2; 3; 4; 2;
б) 1; 2; 0; 2; 0; 1; 2; 1; 3; 1.
4. № 170.
5. № 171.
Решение:
Средний ежемесячный расход электроэнергии находим по формуле среднего арифметического:
x = ![]() =
63.
=
63.
Ответ: 63 кВт · ч.
IV. Итоги урока.
– Какие существуют средние статистические характеристики ряда?
– Какой ряд называется упорядоченным?
– Что называется размахом ряда? Приведите пример.
– Что такое мода ряда? Приведите пример.
– Как найти среднее арифметическое ряда?
Урок 21
Использование средних статистических
характеристик при решении различных задач
Цель: продолжить формировать умения находить среднестатистические характеристики ряда (среднее арифметическое, размах, мода) при решении различных задач.
Ход урока
I. Устная работа.
Для упорядоченных рядов:
а) 0; 0; 1; 2; 3; б) 1; 2; 2; 2; 3; 3; в) 1; 2; 3; 4; 5; 5
найдите размах, среднее арифметическое, моду.
II. Проверочная работа.
Вариант 1
1. В таблице приведен возраст сотрудников одного из отделов:
|
Фамилия |
Возраст |
|
1. Башмачкин |
42 |
|
2. Галошев |
24 |
|
3. Каблуков |
30 |
|
4. Сапогов |
24 |
|
5. Тапочкин |
40 |
Найдите среднее арифметическое, размах и моду этого ряда.
2*. Постройте ряд из четырех чисел, у которого размах равен 2, а среднее арифметическое равно моде.
Вариант 2
1. В таблице приведено количество очков, набранных в чемпионате некоторыми баскетболистами.
|
Фамилия |
Количество очков |
|
1. Дождева |
48 |
|
2. Градова |
26 |
|
3. Лунева |
20 |
|
4. Метелева |
40 |
|
5. Снежкова |
26 |
Найдите среднее арифметическое, размах и моду этого ряда.
2*. Постройте ряд из четырех чисел, у которого размах равен 2, а среднее арифметическое в два раза больше моды.
III. Формирование умений и навыков.
1. № 177.
Решение:
Среднее арифметическое равно:
X = ![]() 42,45.
42,45.
Размах A = xmax – xmin = 48 – 36 = 12.
Мода М = 45 (встречается 3 раза).
Среднее арифметическое – это условная величина (она не целая, хотя число деталей может быть только «целым»); она показывает центр «рассеивания» наблюдаемых величин (сумма отклонений от неё равна нулю); также это можно назвать средней выработкой рабочими деталей.
Размах характеризует разброс наблюдаемых значений, а мода показывает, какое число изготовленных деталей встречается чаще всего в данной смене рабочих.
Ответ: » 42,45; 12; 45.
2. № 179.
Решение:
Найдем средний балл каждого выпускника по формуле среднего арифметического:
Ильин: X = ![]() = 4,4;
= 4,4;
Семенов: X = ![]() 3,5;
3,5;
Романов: X = ![]() = 3,8;
= 3,8;
Попов: X = ![]() 4,7.
4,7.
Чтобы выявить наиболее типичную оценку для каждого выпускника, найдем для каждой совокупности моду, то есть оценку, встречающуюся чаще других:
Ильин: М = 4 (9 раз из 15);
Семенов: М = 3 (9 раз из 15);
Романов: М = 4 (10 раз из 15);
Попов: М = 5 (10 раз из 15).
Использованы среднее арифметическое и мода.
Ответ: 4,4 и 4; 3,5 и 3; 3,8 и 4; 4,7 и 5.
3. № 180.
Решение:
Средняя урожайность пшеницы в хозяйстве равна общему сбору зерна,
деленному на общую площадь полей; общий сбор зерна равен 18 ц/га · 12
га + 19 ц/га · 8 га + 23 ц/га · 6га = 506 ц, а общая площадь участков равна 12
га + 8 га + 6 га = 26 га. Средняя урожайность в хозяйстве ![]() 19,5 ц/га.
19,5 ц/га.
Нельзя находить среднюю урожайность как ![]() = 20 (ц/га), так как значения 18, 19 и 23
характеризуют участки разной величины и их «вклад» в общую урожайность зависит от
площади каждого участка.
= 20 (ц/га), так как значения 18, 19 и 23
характеризуют участки разной величины и их «вклад» в общую урожайность зависит от
площади каждого участка.
Ответ: » 19,5 ц/га.
4. № 181.
Решение:
Среднее арифметическое равно: X = ![]() = 1,7.
= 1,7.
Размах равен: A = xmax – xmin = 3 – 0 = 3.
Мода равна: М = 4 (встречается 4 раза из 10).
Среднее арифметическое показывает среднее количество бракованных деталей.
Размах показывает разброс количества бракованных деталей в ящиках.
Мода показывает наиболее часто встречающееся количество бракованных деталей.
Ответ: 1,7; 3; 4.
5. № 183.
Решение:
Среднее значение находим по формуле среднего арифметического:
X = ![]() =
0,9.
=
0,9.
Составим таблицу отклонений от средней температуры воздуха в полдень в каждый из дней декады:
|
Число месяца |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отклонение |
–2,9 |
–1,9 |
–3,9 |
–0,9 |
0,1 |
1,1 |
1,1 |
2,1 |
3,1 |
2,1 |
Обращаем внимание, что сумма всех отклонений (вторая строка таблицы) равна нулю.
Ответ: 0,9 °С; таблица отклонений.
IV. Итоги урока.
– Какие существуют средние статистические характеристики ряда?
– Как найти среднее арифметическое ряда?
– Что такое размах ряда? Что он характеризует?
– Что такое мода ряда? Что она характеризует?
Домашнее задание: № 178, № 182
Урок 22
Медиана упорядоченного ряда
Цели: ввести понятие медианы как статистической характеристики упорядоченного ряда; формировать умение находить медиану для упорядоченных рядов с четным и нечетным числом членов; формировать умение интерпретировать значения медианы в зависимости от практической ситуации.
Ход урока
I. Устная работа.
Даны ряды:
1) 4; 1; 8; 5; 1; 7.
2) ![]() ; 9; 3;
0,5;
; 9; 3;
0,5; ![]() .
.
3) 6; 0,2; ![]() ;
4; 6; 7,3; 6.
;
4; 6; 7,3; 6.
Найдите:
а) наибольшее и наименьшее значения каждого ряда;
б) размах каждого ряда;
в) моду каждого ряда.
II. Объяснение нового материала.
Объяснение проводить согласно пункту 10 учебника. Следует подчеркнуть, что перед нахождением медианы нужно всегда упорядочить ряд данных.
На доску следует вынести правила нахождения медианы для рядов с четным и нечетным числом членов:
|
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посредине. Медианой произвольного ряда называется медиана соответствующего упорядоченного ряда. |
Особое внимание следует уделить интерпретации значений медианы для различных задач. Учитель должен прививать критическое отношение к статистическим выводам и обобщениям.
III. Формирование умений и навыков.
1-я группа. Упражнения на применение формул нахождения медианы упорядоченного и неупорядоченного ряда.
1. № 186.
Решение:
а) число членов ряда п = 9; медиана есть среднее в упорядоченном ряду значение варианта Ме = 41;
б) п = 7, ряд упорядочен, Ме = 207;
в) п = 6, ряд упорядочен, Ме = ![]() = 21;
= 21;
г) п = 8, ряд упорядочен, Ме = ![]() = 2,9.
= 2,9.
Ответ: а) 41; б) 207; в) 21; г) 2,9.
3. № 188 (устно).
Решение:
а) Может, если сумма членов не кратна числу членов.
б) Не может, так как разность двух натуральных чисел,
из которых уменьшаемое больше вычитаемого, есть натуральное число.
в) Не может, так как мода – один из членов ряда, а все члены ряда – натуральные числа.
г) Может, если число членов ряда четное и числа ![]() и
и ![]() не равны между собой.
не равны между собой.
Ответ: да; б) нет; в) нет; г) да.
4. Зная, что в упорядоченном ряду содержится т чисел, где т – нечетное число, укажите номер члена, являющегося медианой, если т равно:
а) 5; б) 17; в) 47; г) 201.
Решение:
Номер находим как ![]() + 1, где
+ 1, где ![]() – целая часть числа.
– целая часть числа.
а) ![]() + 1 = 2
+ 1 = 3; в)
+ 1 = 2
+ 1 = 3; в) ![]() + 1 = 23 + 1 = 24;
+ 1 = 23 + 1 = 24;
б) ![]() + 1 = 8
+ 1 = 9; г)
+ 1 = 8
+ 1 = 9; г) 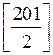 + 1 = 100 + 1 = 101.
+ 1 = 100 + 1 = 101.
Ответ: а) 3; б) 9; в) 24; г) 101.
2-я группа. Практические задачи на нахождение медианы соответствующего ряда и интерпретацию полученного результата.
1. № 189.
Решение:
Число членов ряда п = 12. Для нахождения медианы ряд нужно упорядочить:
136, 149, 156, 158, 168, 174, 178, 179, 185, 185, 185, 194.
Медиана ряда Ме = ![]() = 176.
= 176.
Выработка за месяц была больше медианы у следующих членов артели:
1) Квитко; 4) Бобков;
2) Баранов; 5) Рылов;
3) Антонов; 6) Астафьев.
Ответ: 176.
2. № 192.
Решение:
Упорядочим ряд данных:
30, 31, 32, 32, 32, 32, 32, 32, 33, 35,
35, 36, 36, 36, 38, 38, 38, 40, 40, 42;
число членов ряда п = 20.
Размах A = xmax – xmin = 42 – 30 = 12.
Мода Мо = 32 (это значение встречается 6 раз – чаще других).
Медиана Ме = ![]() = 35.
= 35.
Размах показывает наибольший разброс времени на обработку детали; мода показывает наиболее типическое значение времени обработки; медиана – время обработки, которое не превысили половина токарей.
Ответ: 12; 32; 35.
IV. Итоги урока.
– Что называется медианой ряда чисел?
– Может ли медиана ряда чисел не совпадать ни с одним из чисел ряда?
– Какое число является медианой упорядоченного ряда, содержащего 2п чисел? 2п – 1 чисел?
– Как найти медиану неупорядоченного ряда?
Домашнее задание: № 187, № 190, № 191, № 254.
Урок
23
Использование средних статистических
характеристик при решении различных задач
Цели: продолжить формировать умение использовать средние статистические характеристики (размах, мода, среднее арифметическое, медиана) при решении различных задач (вычисление и интерпретация).
Ход урока
I. Устная работа.
1. Педагогический стаж восьми учителей школы, работающих в старших классах одной школы, следующий:
5 лет, 8 лет, 15 лет, 12 лет, 8 лет, 14 лет, 18 лет, 9 лет.
Найдите моду и медиану этой выборки.
2. Найдите среднее арифметическое и размах ряда:
2; 3; 5; 6; 14; 15; 17; 18.
II. Проверочная работа.
Вариант 1
1. Найдите медиану упорядоченного ряда:
а) ![]() ;
;
б) 11, 12, 18, 23, 29, 31, 37, 42.
2. Найдите медиану неупорядоченного ряда:
8, 11, 4, 17, 35, 21, 19, 50.
Вариант 2
1. Найдите медиану упорядоченного ряда:
а) ![]() ;
;
б) 0,5; 1,2; 1,8; 2,5; 3,5; 4,8; 5,1; 5,9.
2. Найдите медиану неупорядоченного ряда:
21, 13, 18, 11, 27, 32, 23, 41.
III. Формирование умений и навыков.
На данном уроке обобщаются знания по теме «Статистические характеристики» и учащимся предлагаются задания на нахождение всех характеристик и их интерпретацию в зависимости от условия задачи.
Кроме того, сильным учащимся можно предложить для решения задачи повышенной сложности. В конце занятия целесообразно привести пример, показывающий необходимость критического отношения к полученным результатам.
1. В таблице показано число посетителей выставки в разные дни недели:
|
День недели |
Пн |
Вт |
Ср |
Чт |
Пт |
Сб |
Вс |
|
Число посетителей |
604 |
638 |
615 |
636 |
625 |
710 |
724 |
Найдите медиану указанного ряда данных. В какие дни недели число посетителей выставки было больше медианы?
Решение:
Число членов в ряду п = 7. Для нахождения медианы упорядочим ряд: 604, 615, 625, 636, 638, 710, 724.
Медиана Ме = 636. Число посетителей было больше медианы во вторник, субботу и воскресенье.
Ответ: 636; вторник, суббота, воскресенье.
2. Ниже указана среднесуточная переработка сахара (в тыс. ц) заводами сахарной промышленности некоторого региона:
12,2; 13,2; 13,7; 18,0; 18,6; 12,2; 18,5; 12,4; 14,2; 17,8.
Для представленного ряда данных найдите среднее арифметическое, моду, размах и медиану. Что характеризует каждый из этих показателей?
Решение:
Число членов ряда п = 10. Упорядочим ряд:
12,2; 12,2; 12,4; 13,2; 13,7; 14,2; 17,8; 18,0; 18,5; 18,6.
Среднее арифметическое характеризует средний уровень значений и общую сумму всех значений:
х = 15,08.
Мода Мо = 12,2 показывает значение, встречающееся чаще других (в данном случае слабо выражена, значение 12,2 встречается только 2 раза).
Размах A = xmax – xmin = 18,6 – 12,2 = 6,4 характеризует величину разброса наблюдаемых значений.
Медиана Me = ![]() = 13,95 показывает, что половина членов
ряда не превосходит по величине 13,95.
= 13,95 показывает, что половина членов
ряда не превосходит по величине 13,95.
Ответ: 15,08; 12,2; 6,4; 13,95.
3. Девочки седьмого класса на уроке физкультуры при прыжках взяли высоты, величины которых (в см) учитель записал в журнал:
90; 125; 125; 130; 130; 135; 135; 135; 140; 140; 140.
Какая высота прыжка наилучшим образом характеризует спортивную подготовку девочек класса?
Решение:
Ряд наблюдений упорядочен: п = 11.
Ряд имеет две моды: Мо1 = 135, Мо2 = 140.
Среднее арифметическое ряда равно х » 129,5.
Медиана Ме = 135.
Наилучшей характеристикой спортивной подготовки девочек следует признать медиану: мода неоднозначна (135 и 140), а среднее значение занижено за счет одного очень плохого результата 90 см (если этот результат отбросить, то х = 133,5 см).
Ответ: 135 см.
5. Владелец одного частного предприятия уволил бльшую часть рабочих, а оставшимся снизил зарплату на 20 %. После этого он заявил, что средний заработок его рабочих повысился. Так ли это?
|
|
Заработок |
Заработок |
||
|
1000 р. |
400 р. |
800 р. |
320 р. |
|
|
Число рабочих |
200 |
800 |
200 |
120 |
Решение:
Вычисляем средние статистические характеристики:
мода до увольнения Мо = 400;
мода после увольнения Мо = 800;
медиана до увольнения Ме = 400;
медиана после увольнения Ме = 800;
среднее арифметическое
до увольнения X = ![]() = 520;после увольнения X =
= 520;после увольнения X = ![]() = 620.
= 620.
Вычисления подтверждают, что средние характеристики действительно увеличились. Однако простой взгляд на таблицу подтверждает, что жизнь рабочих не улучшилась, а, наоборот, ухудшилась! Не говоря уже о тех, кто потерял работу. Здесь итоги решения математической задачи противоречат здравому смыслу. Математическая модель не всегда адекватна практической ситуации. В данном случае средние характеристики не являются типичными представителями статистических данных, поэтому их использование приводит к ложному выводу.
На примере этой задачи показываем учащимся, что необходимо не только формально вычислять средние характеристики, но и уметь правильно истолковывать статистическую информацию.
IV. Итоги урока.
Домашнее задание:
1. Найдите размах, моду и медиану ряда:
а) 1; 3; –2; 4; –2; 0; 2; 3; 1; –2; 4;
б) 0,2; 0,4; 0,1; 0,5; 0,1; 0,2; 0,3; 0,5; 0,4; 0,6.
2. В вашем (или соседнем) классе соберите данные о месяцах рождения учеников. Месяцы удобнее перечислять не по названиям, а по номерам.
Найдите: а) размах; б) моду; в) среднее арифметическое для экспериментальной выборки.
3. Для упорядоченного ряда, содержащего т чисел, где т – четное число, укажите номера двух последовательных членов, между которыми заключена медиана, если т равно:
а) 6; б) 18; в) 56; г) 240.
Урок
25
Контрольная работа № 2
«Уравнение с одной переменной»
Вариант 1
1. Решите уравнение.
а) ![]() x
= 12; в) 5x – 4,5 = 3x + 2,5;
x
= 12; в) 5x – 4,5 = 3x + 2,5;
б) 6x – 10,2 = 0; г) 2x – (6x – 5) = 45.
2. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у неё занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
3. В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально?
4. Решите уравнение 7x – (x + 3) = 3(2x – 1).
Вариант 2
1. Решите уравнение.
а) ![]() x
= 18; в) 6x – 0,8 = 3x + 2,2;
x
= 18; в) 6x – 0,8 = 3x + 2,2;
б) 7x + 11,9 = 0; г) 5x – (7x + 7) = 9.
2. Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально?
4. Решите уравнение 6x – (2x – 5) = 2(2x + 4).
Урок №25
Что такое функция?
Цели: ввести понятие функциональной зависимости; дать определения независимой переменной (аргумента), зависимой переменной, области определения функции, области значений функции.
Ход урока
Организационный момент
I. Устная работа.
1. Найдите значение выражения.
а) 3x – (2 + 3x) при х = 7,862; б) 2a – (a – 0,3) при а = 0,7;
2. Решите уравнение.
а) 3х = –9; б) ![]() ; в)
5а – 15 = 0;
; в)
5а – 15 = 0;
г) 3х = 3х + 11; д) ![]() (x – 8); е) 3y
+
(x – 8); е) 3y
+ ![]() = 0.
= 0.
II. Объяснение нового материала.
1. Основная задача первого занятия: показать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.
Функция имеет общекультурное, мировоззренческое значение. При её изучении учащиеся знакомятся с идеей всеобщей связи, идеей непрерывности, бесконечности, интерполяции.
2. Объяснение проводить согласно пункту 12 учебника. Необходимо привести достаточно примеров функциональной зависимости (учебник, с. 51–53). Также нужно не только показывать зависимости, но и сразу обсуждать, в какой области человеческой деятельности применяются такие функциональные зависимости.
3. Вводим понятия независимой и зависимой переменных и определение функции как зависимости одной переменной от другой. На примерах показываем, что область определения функции может быть бесконечным и конечным множеством чисел.
III. Формирование умений и навыков.
Все задания, решаемые на этом уроке, направлены на усвоение как самого понятия функции, так и различных способов её задания (словесный, с помощью формулы, табличный, графический). Ученики должны уметь переходить от одного вида задания к другому и находить значения функции при каждом способе задания.
1. № 258, № 260.
2. Функция задана формулой у = 2 – 5х, верны ли равенства:
а) у = 12 при х = –2; б) у
= 3 при х = ![]() ;
;
в) у = 20 при х = 4; г) у
= –0,5 при х = ![]() ?
?
3. № 261.
4. Функция задана графиком:
а) Найти значения функции при х = 0; 2; 3,5; –1.
б) При каком значении х значение функции равно 1; 2; 0?
в) Назвать несколько значений х, при которых значение функции положительно.
г) Назвать несколько значений х, при которых значение функции отрицательно.
5. Устно.
Результаты измерений температуры воздуха за сутки даны в следующей таблице:
|
Время, ч |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
Температура, °С |
–1 |
+1 |
–3 |
–4 |
2 |
5 |
8 |
10 |
11 |
9 |
6 |
3 |
1 |
а) Назовите температуру в 6 ч, 8 ч, 24 ч.
б) В какое время температура была равна +1°, –4°, 11°?
в) Почему эту зависимость можно назвать функцией?
6. № 263.
Решение:
Если r – остаток от деления натурального числа п на 4, то можно записать n = 4 · x + r, где 0 ≤ r < 4.
Найдем соответствующие значения r:
а) Если п = 13, то 13 = 3 · 4 + 1, то есть r = 1;
б) если п = 34, то 34 = 8 · 4 + 2, то есть r = 2;
в) если п = 43, то 43 = 10 · 4 + 3, то есть r = 3;
г) если п = 100, то 100 = 25 · 4 + 0, то есть r = 0.
В рассматриваемой функциональной зависимости аргументом является переменная п.
Областью определения является множество чисел {13; 34; 43; 100}.
Значениями функции служат числа 0; 1; 2; 3.
IV. Итоги урока.
– Что называется функцией?
– Что называется аргументом?
– Какими способами можно задать функцию? Назовите преимущества каждого из них.
Домашнее задание: 1. № 259; № 262; № 264.
2. Функция задана графиком:
а) Найти значения функции при значениях аргумента 0; –2; 1; 3.
б) При каком значении х значение функции равно 2; 0; 1; –1?
в) Назвать несколько значений х, при которых значение функции положительно.
г) Назвать несколько значений х, при которых значение функции отрицательно.
Урок 26
Вычисление значений функции по формуле
Цели: продолжить работу по усвоению понятия функции и связанных с функцией понятий (область определения функции, область значений функции и др.); формировать умение находить значения функций, заданных аналитически (с помощью формулы).
Ход урока
I.Организационный момент
Устная работа.
1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа; сумму этого числа с числом 5.
2. Велосипедист едет со скоростью 15
км/ч и за t ч проходит расстояние s км (зависимость s от t).
Найдите значение функции, соответствующее значению аргумента, равному ![]() ; 2; 2
; 2; 2![]() .
.
II. Объяснение нового материала.
Цель этого и последующих занятий – в упорядочении имеющихся представлений о функции, развертывании системы понятий, характерных для функциональной линии. Значительное место должно быть отведено усвоению важного представления – однозначности соответствия аргумента и определенного по нему значения функции. Для рассмотрения этого вопроса привлекаются различные способы задания функции.
Чаще других в математике и её приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Однако сопоставление разных способов задания выполняет важную роль:
1) и таблицы, и графики служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи;
2) необходимо для усвоения всего многообразия аспектов понятия функции.
Объяснение проводить согласно пункту 13 учебника. Разбираем пример № 1 со с. 55 учебника. Показываем, что для того, чтобы найти значение функции, необходимо подставить некоторое значение аргумента в формулу.
Также объясняем, что в случае, когда область определения функции явно не задана, считают, что она состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
III. Формирование умений и навыков.
1. № 267. 2. Вычислить значение следующих функций при х, равном –2; –1; 0; 1; 2.
а) у = 3х; б) у = –2х; в) у = –х – 3; г) у = 20х + 4.
2-я группа.
1. № 270. 2. № 271.Решение:
у = х (х – 3,5)
|
х |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
у |
0 |
–1,5 |
–2,5 |
–3 |
–3 |
–2,5 |
–1,5 |
0 |
2 |
1. Найдите область определения функции, заданной формулой:
а) у = 3х + 2; б) у = ![]() ; в) у
= x7 + 2x – 3;
; в) у
= x7 + 2x – 3;
г) у = ![]() ; д)
у =
; д)
у = ![]() ; е)
у =
; е)
у = ![]() .
.
2. № 351.Решение:
а) у = ![]() .
.
Область определения функции – все числа, кроме тех, при которых х – 4 = 0, то есть х2 = 4. Значит, не входят в ООФ х = 2 и х = –2.
б) у = ![]() .
.
Область определения функции – все числа, кроме тех, при которых х2 + 4 = 0, то есть х2 = –4. Уравнение не имеет решения, значит, ООФ – любое число.
Ответ: а) любое число, кроме 2 и –2; б) любое число.
3. Дополнительные задания (для сильных учащихся).
3.1. Найдите область определения функции.
а) у = 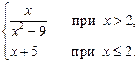
б) у = 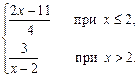
3.2. Задайте формулой какую-нибудь функцию, область определения которой:
а) все действительные числа;
б) все действительные числа, кроме –11;
в) все действительные числа, кроме 3 и 5;
г) все неотрицательные действительные числа;
д) все неположительные действительные числа.;
е) только одно число.
IV. Проверочная работа.
Вариант 1
1. Дана функция у = 2х2 – 4х. Найдите
значение функции при х = 0
и х = –1.
2. Найдите область определения функции.
а) у = 2х – 7; б) у =
![]() ;
;
Вариант 2
1. Дана функция у = 5х2 + х. Найдите
значение функции при х = 0
и х = 1.
2. Найдите область определения функции.
а) у = 3х + 6; б) у =
![]() ;
;
V. Итоги урока.
Домашнее задание: 1. № 268; № 269; № 272.
Урок 27
Вычисление значений функции по формуле
Цели: продолжить формировать умение находить значение функции по формуле, а также формировать умение находить значение аргумента, соответствующее заданному значению функцию, умение решать практические задачи с использованием функциональной терминологии.
Ход урока
I. Организационный момент
Устная работа.
1. Найдите значение функции у = 2х – 1 для значений аргумента, равного 0; 1; 2; –1.
2. Найдите область определения функции:
а) у = 3х – 7; б) у = ![]() ; в) у = x3
– 2x2 – 1; г) у =
; в) у = x3
– 2x2 – 1; г) у = ![]() ;
;
II. Формирование умений и навыков.
1. № 273, № 274.
2. Функция задана формулой у = 2х – 1.
а) Какое значение у соответствует х, равному 10; –4,5; 15; 251; 600?
б) При каком значении х соответствующее значение у равно:
–19; –57; 205; –3![]() ?
?
Решение:
а) Если х = 10, то у = 2 · 10 – 1 = 19;
если х = –4,5, то у = 2 · (–4,5) – 1 = –10;
если х = 15, то у = 2 · 15 – 1 = 29;
если х = 251, то у = 2 · 251 – 1 = 501;
если х = 600, то у = 2 · 600 – 1 = 1199.
б) Если у = –19, то 2х – 1 = –19;
2х = –19 + 1;
2х = –18;
х = –9; то есть у = –19, при х = –9.
Если у = –57, то 2х – 1 = –57;
2х = –57 + 1;
2х = –56;
х = – 28, то есть у = –57 при х = – 28.
Если у = 205, то 2х – 1 = 205;
2х = 205 + 1;
2х = 206;
х = 103, то есть у = 205 при х = 103.
Если у = –3![]() , то 2х – 1 = –3
, то 2х – 1 = –3![]() ;
;
2х = –3,5 + 1;
2х = –2,5;
х = –1,25,
то есть у = –3![]() при х = –1
при х = –1![]() .
.
1. Из формулы равномерного движения s = υt выразить скорость υ как функцию пути s и времени t. Вычислить по этой формуле среднюю скорость полета пули, если s = 3 км, t = 6 с.
2. № 276.Решение:
Обозначим за т массу пробки в граммах, а за V – объем в см3. Тогда зависимость массы куска пробки от объема можно выразить формулой т = 0,18 · V.
а) Если V = 240, то т = 0,18 · 240 = 43,2 (г);
б) если т = 64,8, то 0,18 · V = 64,18;
V = 64,18 : 0,18;
V = 360 (см3).
Ответ: а) 43,2 г; б) 360 см3.
3. № 278.Решение:
Анализ условия: 
s = 12 · t.
а) Если t = 3,5, то s = 12 · 3,5 = 42 (км);
б) если s = 30, то 12 · t = 30;
t = 30 : 12;
t = 2,5 (ч).
Ответ: а) 42 км; б) 2,5 ч.
4. № 352.Решение:
Анализ условия: ![]()
у = 1,5х + 150.
а) если х = 10, то у = 1,5 · 10 + 150 = 15 + 150 = 165;
б) если у = 180, то 1,5х + 150 = 180;
1,5х = 180 – 150;
1,5х = 30;
х = 30 : 1,5;
х = 20, значит, у = 180 при х = 20.
Ответ: а) у = 165; б) х = 20.
III. Проверочная работа.
Вариант 1
1. Функция задана формулой у = 3х – 7. Найдите значение аргумента, при котором значение функции равно нулю.
2. Найдите значение аргумента, при котором функция у = –3х – 2 принимает значение 0,3.
3. Запишите область определения функции, заданной формулой
у = ![]() .
.
Вариант 2
1. Функция задана формулой у = 5 + 2х. Найдите значение аргумента, при котором значение функции равно нулю.
2. Найдите значение аргумента, при котором функция у = –5х + 11 принимает значение 0,2.
3. Запишите область определения функции, заданной формулой
у = ![]() .
.
IV. Итоги урока.
– Дайте определение функции. Что называется аргументом, значением функции?
– Объясните на примере функции, заданной формулой у = 3х + 18
Домашнее задание: № 275; № 277; № 279; № 353.
Урок 28
График функции.
Цели: формировать понятие «график функции», умение строить график функции, заданной аналитически, а также с помощью графика находить значение функции, соответствующее заданному значению аргумента, и значения аргумента, которым соответствует данное значение функции.
Ход урока
I. Проверочная работа.
Вариант 1
1. Найдите значения функции, заданной формулой у = ![]() для значений аргумента, равных
–6; 1,5.
для значений аргумента, равных
–6; 1,5.
2. Найдите значение аргумента, при котором функция у = 4х +
3 принимает значение, равное ![]() .
.
Вариант 2
1. Найдите значения функции, заданной формулой у = ![]() – 6 для значений аргумента, равных
–8; 0,8.
– 6 для значений аргумента, равных
–8; 0,8.
2. Найдите значение аргумента, при котором функция у = 5х + 4 принимает значение, равное 1,5.
II. Устная работа.
На рисунке изображен график зависимости некоторой величины у от некоторой величины х.
Ответьте на вопросы:
а) Чему равное значение у, если х = –3; –1; 2; 5?
б) Чему равны значения х, если у = 3; 0; 1?
в) Какое минимальное и какое максимальное значения принимает величина у?
III. Объяснение нового материала.
На этом уроке наша задача – показать, что эти два способа тесно связаны с графическим, причем его особенность в том, что с помощью графика мы можем наглядно представлять функциональную зависимость не только для точечной, но и бесконечной области определения функции:
|
задание функциональной зависимости |
В соответствии с этими положениями объяснение нового материала проводится в несколько этапов:
1) Формирование представления о графике функции на основе связи аналитического, табличного и графического способов задания функции.
2) введение определения понятия графика функции.
3) Построение графика функции по точкам.
4) Работа по изображенному графику функции.
На рисунке изображены точки на координатной плоскости, выражающие результаты наблюдений за атмосферным давлением. Построить график зависимости давления от времени в промежутке 12 ≤ t ≤ 18, соединив эти точки плавной линией.
Затем рассматриваем пример со с. 58 учебника, в
котором показано, как по точкам строится график функции y = ![]() , где –2 ≤ х
≤ 3.
, где –2 ≤ х
≤ 3.
Необходимо сделать вывод: по точкам можно построить график любой функции, заданной таблично или аналитически (с помощью формулы).
Вводим определение:
|
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. |
На примере 2 со с. 60 учебника показываем работу по изображенному графику на нахождение значения функции по заданному значению аргумента и обратное задание.
IV. Формирование умений и навыков.
1. № 283.
Можно задать учащимся дополнительные вопросы:
а) Сколько точек пересечения с осью х имеет график? Каково значение у в этих точках?
б) Сколько точек пересечения с осью у имеет график? Каково значение х в этой точке?
в) Сравните значения функции в точках –2 и 1.
г) Назовите координаты какой-нибудь точки графика, у которой значения аргумента и функции положительны; значение аргумента положительно, а функции – отрицательно и т. д.
2. № 284, № 285.
3. Используя график функции, заполните таблицу значений функции для –2 ≤ х ≤ 3 с шагом 0,5.
V. Итоги урока.
– Что называется графиком функции?
– Как построить график функции, заданной формулой?
– Как по графику найти значение функции, соответствующее данному значению аргумента?
– Как по графику функции найти значение аргумента, которому соответствует данное значение функции?
– Как по графику зависимости определить, является ли она функцией?
Домашнее задание: 1. № 286; № 287; № 288.
Урок
29
График функции
Цели: продолжить формировать умения строить график функции и находить значение функции по заданному аргументу с помощью графика; формировать умение интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы практической задачи.
Ход урока
I. Организационный момент
Устная работа.
1. Какие из графиков, изображенных на рисунках, являются графиками функций?
а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)
2. По графику, изображенному на рисунке д), найдите:
а) значение функции, соответствующее значению аргумента, равному –3; –2; 1; 2;
б) значения аргумента, при которых значение функции равно –1; 2; 3;
в) координаты точек пересечения с осью х;
г) координаты точек пересечения с осью у.
II. Формирование умений и навыков.
1. № 289.
2. № 291, № 293.
3. На рисунке изображен график зависимости потребления районом электрической энергии р (%) от времени суток t (ч).
а) В какое время суток электрическая нагрузка была максимальной?
б) В какое время суток нагрузка не превосходила 20 % от максимума?
в) Какова была нагрузка в 18 ч?
г) Какое событие может отражать участок графика АВ?
д) Возрастала или убывала нагрузка с 4 до 8 ч; с 18 до 20 ч?
4. В таблице представлено население (млрд) земного шара в различные годы.
|
Год, t |
1900 |
1940 |
1950 |
1970 |
1990 |
2000 |
|
Население, Н |
1,63 |
2,25 |
2,53 |
3,64 |
5,3 |
6,1 |
По этим данным постройте график. Оцените приближенно по графику население земли в 1981, 1987, 2010 гг.
5. (Криминальная история.) В 11 ч вечера слуга зажег хозяину две свечи, а утром в 7 ч обнаружил его убитым. Одна свеча лежала на полу потухшая, а вторая догорала. В какое время произошло убийство, если длина целой свечи 21 см, опрокинутой во время убийства 16 см, а непотухшего огарка 1 см? Постройте график зависимости длины горения свечи от времени.
III. Итоги урока.
– Как по графику найти значение функции, соответствующее данному значению аргумента?
– Как по графику найти значения аргумента, которым соответствует данное значение функции?
– Как, не строя график, выявить принадлежность ему точки с данными координатами?
– Как, не строя график, определить, в каких точках он пересекает ось абсцисс; ось ординат?
Домашнее задание: № 290; № 292; № 355; № 356*.
Урок 33
прямая пропорциональность
Цели: ввести понятие прямой пропорциональности как функции определенного вида; формировать умение распознавать прямую пропорциональность и вычислять значение функции по формуле; повторить тему «Построение точек в координатной плоскости» для последующего изучения графика прямой пропорциональности.
Ход урока
I. Устная работа.
1. Найдите значение функции у = ![]() для следующих значений аргумента:
для следующих значений аргумента:
а) 0; б) 4; в) –4; г) –2.
2. Проверьте, принадлежат ли графику функции, заданной формулой у = 2х + 14, следующие точки:
а) А (0; 14); б) В (–2; 8); в) С (–7; 0); г) D (7; 0).
3. Решите уравнение.
а) 3х = 12; б) –2х + 14 = 0; в) х – 15 = 2; г) х + 2 = х.
II. Объяснение нового материала.
1. Введение понятия основывается на рассмотрении конкретных практических примеров. Желательно их привести несколько. Так, следует рассмотреть пример со с. 65 учебника. Кроме того, представить уже знакомую учащимся задачу: «Вычислить площадь прямоугольника, основание которого равно 3, а высота равна х». Если искомую площадь обозначить буквой у, то ответ можно записать формулой:
у = 3х.
Если основание прямоугольника равно k, то зависимость между высотой х и площадью у выразится формулой
у = kх.
Каждое заданное значение числа k определяет некоторую функцию у = kх.
Затем формулируем четкое определение:
|
Прямой пропорциональностью называется функция, которую можно задать формулой вида у = kх, где х – независимая переменная, k – не равное нулю число. |
2. Просим учащихся привести примеры прямой пропорциональности и примеры функций, не являющихся прямой пропорциональностью. Также рассматриваем примеры со с. 66 учебника. Показываем, что число k называется коэффициентом прямой пропорциональности, а само название функции связано со следующей пропорцией:
у = kх.
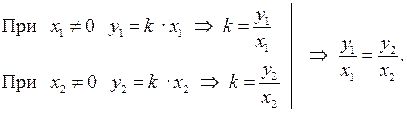
III. Формирование умений и навыков.
Задания, решаемые на этом уроке, можно разбить на 2 блока.
В первом блоке представлены упражнения на усвоение понятия прямой пропорциональности и выполнение основных действий по формуле.
Второй блок носит повторительный характер и направлен на актуализацию знаний по теме «Построение точек в координатной плоскости».
1-й блок
1. № 297, № 298 (устно).
2. Книга стоит 150 рублей. Выразите формулой зависимость между купленным количеством (п) данных книг и уплаченной суммой (у) в рублях.
3. Автомобиль «Лада» движется по шоссе со скоростью
80 км/ч. Записать формулу, выражающую зависимость длины пути s (в км) от
времени движения t (в ч). Чему равно s (3), s (5,4)?
4. Зависимость между переменными х и у выражена формулой у = kх. Определить k, если у = –5 при х = 2,5.
5. Дана таблица значений функции у = kх:
|
х |
0,5 |
|
1,4 |
2,1 |
3 |
|
|
у |
|
1 |
4,2 |
|
|
9,6 |
Найти k и заполнить пропущенные клетки.
2-й блок
Самостоятельная работа
Вариант 1
1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5).
2. Запишите координаты точек:
3. В каких координатных четвертях расположены точки:
А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)?
4. Постройте в координатной плоскости прямую проходящую через точки С (–4; 3) и D (3; –1). Найдите координаты точек, в которых эта прямая пересекает ось х и ось у.
Вариант 2
1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5).
2. Запишите координаты точек:
3. В каких координатных четвертях расположены точки:
А (25; 360); В (–2,5; –100); С 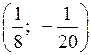 ?
?
4. Постройте в координатной плоскости прямую, проходящую через точки А (3; 4) и В (–5; –1). Найдите координаты точек, в которых эта прямая пересекает ось х и ось у.
IV. Итоги урока.
– Сформулируйте определение прямой пропорциональности.
– Приведите примеры прямой пропорциональности.
– Как называется число k в записи формулы прямой пропорциональности у = kх? Какое это число?
– Почему данная функция получила свое название?
Домашнее задание: 1. № 299.
. № 310; № 311.
Вариант 1
1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5).
2. Запишите координаты точек:
3. В каких координатных четвертях расположены точки:
А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)?
4. Постройте график функции y=-3x+5
Вариант 2
1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5).
2. Запишите координаты точек:
3. В каких координатных четвертях расположены точки:
А (25; 360); В (–2,5; –100); С ![]() ?
?
4 Постройте график функции y= 2x - 7
Вариант 1
1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5).
2. Запишите координаты точек:

3. В каких координатных четвертях расположены точки:
А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)?
4. Постройте график функции y=-3x+5
Вариант 2
1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5).
2. Запишите координаты точек:

3. В каких координатных четвертях расположены точки:
А (25; 360); В (–2,5; –100); С ![]() ?
?
4. Постройте график функции y= 2x - 7
Вариант 1
1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5).
2. Запишите координаты точек:

3. В каких координатных четвертях расположены точки:
А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)?
4. Постройте график функции y=-3x+5
Вариант 2
1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5).
2. Запишите координаты точек:

3. В каких координатных четвертях расположены точки:
А (25; 360); В (–2,5; –100); С ![]() ?
?
4 Постройте график функции y= 2x - 7
Урок 34
График прямой пропорциональности
Цели: определить график прямой пропорциональности как прямую, проходящую через начало координат; выявить расположение прямой в зависимости от знака коэффициента пропорциональности; формировать умение строить график прямой пропорциональности по формуле и выполнять обратное действие – записывать по графику формулу функции.
Ход урока
I. Устная работа.
1. Найдите область определения функции.
а) y = 3x + 2; б) y = ![]() ; в) y =
; в) y = 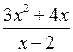 ;г) y =
;г) y = ![]() ; д) y =
; д) y = ![]() x; е) y
= 2x2 + 6x + 1.
x; е) y
= 2x2 + 6x + 1.
2. Является ли функция прямой пропорциональностью:
а) y = 182x;б) y = ![]() ;в) y =
;в) y = ![]() x;г) y = –17x2; д)
y =
x;г) y = –17x2; д)
y = ![]() ; е)
y = 3x + 11?
; е)
y = 3x + 11?
3. Функция задана формулой у = kх. Найдите коэффициент прямой пропорциональности k, если:
а) х = 2; у = 4; б) x = ![]() ; y = –4;в) х = 3;
у =
; y = –4;в) х = 3;
у = ![]() ; г) х
= 0; у = 0.
; г) х
= 0; у = 0.
II. Объяснение нового материала.
Начинаем с рассмотрения конкретной функции (см. учебник, с. 66). Можно предложить учащимся лабораторную работу: подобрать функции, заданные формулами:
у = 0,5х; у = –0,5х;
у = х; у = –х;
у = 1,5х; у = –1,5х;
у = 2х; у = –2х;
у = 2,5х; у = –2,5х;
у = 3х; у = –3х;
у = 3,5х; у = –3,5х;
у = 4х; у = –4х.
Затем заполнить таблицу значений функции при –4 ≤ х ≤ 4 с шагом 0,5.
выводы:
1) График прямой пропорциональности является прямой, проходящей через начало координат.
2) Если коэффициент пропорциональности k > 0, то график расположен в первой и третьей координатных четвертях.
3) Если коэффициент пропорциональности k < 0, то график расположен во второй и четвертой координатных четвертях.
На основе этих выводов учащиеся выводят простейший алгоритм построения графика прямой пропорциональности:
1-й шаг. Для х1 0 вычислить у1 по формуле у = kх.
2-й шаг. Отметить в координатной плоскости точки с координатами (0; 0) и (х1; у1).
3-й шаг. Провести прямую через построенные точки.
III. Формирование умений и навыков.
Упражнения, выполняемые на этом уроке, направлены на отработку алгоритма построения графика прямой пропорциональности и нахождения значений функции по графику.
1. № 300, № 302.
№ 302.
|
Решение: у = –0,5х |
|
Пусть х = 3, тогда у = –0,5 · 3 = –1,5. Проведем прямую, проходящую через начало координат и точку с координатами (3; –1,5).
а) Если х = –2, то у = 1; б) у = –1 при х = 2;
если х = 4, то у = –2; у = 0 при х = 0;
если х = 1, то у = –0,5. у = 2,5 при х = –5.
Если у = –150, то найдем х, решив уравнение:
–0,5х = –150;
х = –150 : (–0,5);
х = 300.
При выполнении этого задания повторяем с учащимися правило нахождения по графику значения функции по данному значению аргумента и наоборот (отмечаем точку на оси абсцисс; проводим прямую, перпендикулярную оси абсцисс, до пересечения с графиком функции; из полученной точки опускаем перпендикуляр на ось ординат и находим соответствующее числовое значение ординаты).
Также на этом примере показываем, что очень важен выбор правильной величины единичного отрезка. Если взять в качестве единицы измерения одну клеточку, то будет очень неудобно строить график, точки будут «слипаться», чертеж будет грязным и нефункциональным.
При больших значениях аргумента или функции (у = –150) удобнее работать с формулой и выполнять действия аналитически (решить уравнение; вычислить по формуле).
2. № 303 (устно).
Выполняем работу по предыдущему чертежу.
3. № 305, № 306.
|
№ 305. Решение: а) у = 1,7х; б) у = –3,1х; в) у = 0,9х; г) у = –2,3х; д) у = kх, где k > 0; е) у = kх, где k < 0. |
|
После выполнения этого задания обсудить с учащимися, почему график а) расположен в первой четверти выше графика в).
№ 306. Решение:
Все графики являются прямыми, проходящими через начало координат, значит, функции являются прямыми пропорциональностями и их можно задать формулой у = kх. Задача сводится к нахождению коэффициента k.
Выберем на каждом графике произвольную точку с целыми координатами:
I (2; 6), значит, 6 = k · 2; k = 3; у = 3х;
II (4; 1), значит, 1 = k · 4; k = 0,25; у = 0,25х;
III (2; –2), значит, –2 = k · 2; k = –1; у = –х;
IV (2; –6), значит, –6 = k · 2; k = –3; у = –3х.
Ответ: у = 3х; у = 0,25х; у = –х; у = –3х.
IV. Проверочная работа.
Вариант 1
1. График функции у = kх проходит через точку В (–30; 3). Найдите k.
2. Построить графики функций:
а) у = 5х; б) у = –5х.
В каждом случае указать координаты двух точек графика, лежащих выше оси абсцисс.
Вариант 2
1. График функции у = kх проходит через точку А (4; –80). Найдите k.
2. Построить графики функций:
а) у = 6х; б) у = –6х.
В каждом случае указать координаты двух точек графика, лежащих ниже оси абсцисс.
V. Итоги урока.
Домашнее задание: 1. № 301; № 304. № 357.
Урок 31
линейная функция и её график
Цели: ввести понятие линейной функции; формировать умение выделять линейную функцию из множества функций; определить график линейной функции и выявить роль параметров k и b в расположении графика линейной функции.
Ход урока
I. Устная работа.
1. Какие из функций являются прямой пропорциональностью:
а) у = 13х; б) у = ![]() ; в) у =
; в) у = ![]() ;г) у = 13(х
– 2); д) у = 13х2; е) у =
;г) у = 13(х
– 2); д) у = 13х2; е) у = 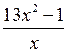 ?
?
2. Какая из точек принадлежит графику функции, заданной формулой у
= ![]() :
:
а) (0; –2); б) ![]() ; в) (4; –2);
; в) (4; –2);
г) (0; 0); д) ![]() ; е)
; е) ![]() ?
?
3. График линейной пропорциональности проходит через точку А. Найдите коэффициент пропорциональности, если:
а) А ![]() ; б)
А (2; –6); в) А
; б)
А (2; –6); в) А 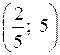 ;
;
г) А ![]() ; д)
А (0; 0); е) А (3; –0,3).
; д)
А (0; 0); е) А (3; –0,3).
II. Объяснение нового материала.
Весь материал целесообразно разбить на несколько логических частей и на каждом уроке изучать одну из них.
На этом уроке целесообразно рассмотреть два вопроса: понятие линейной функции и влияние параметров k и b на расположение графика линейной функции.
В соответствии с этим объяснение проводится в два этапа.
1. Введение понятия линейной функции.
Понятие линейной функции начинаем изучать с рассмотрения реальных процессов и реальных ситуаций.
Необходимо привести примеры из учебника и вынести полученные формулы на доску:
s = 50t + 20, где t ≥ 0;
y = 3x + 5, где x N.
Далее можно спросить учащихся: что общего во всех этих формулах? Затем сообщить им, что зависимости такого вида называются линейными функциями, и дать четкое определение.
На доску может быть вынесена запись:
|
Линейной функцией называется функция, которую можно задать формулой вида у = kx + b, где x – независимая переменная, k и b – некоторые числа. |
2. Определение прямой пропорциональности как частного случая линейной функции.
Обращаем внимание учащихся, что в отличие от определения прямой пропорциональности, где k 0, в формуле линейной функции коэффициенты k и b – любые числа, то есть могут равняться нулю. Причем как по отдельности, так и одновременно.
В случае если k 0 и b = 0, функция у = kx + b принимает вид у = kx, то есть является прямой пропорциональностью. Сразу делаем вывод: графиком линейной функции в этом случае является прямая, проходящая через начало координат, и для её построения необходимо вычислить по формуле координаты ещё одной точки.
3. График линейной функции и роль параметров k и b в её расположении.
а) Следующим шагом целесообразно рассмотреть случай k 0 и b 0. Заполняем таблицу со с. 71 учебника для функций у = 0,5х и у = 0,5х + 2. Анализируя полученные данные, учащиеся делают вывод: графиком функции у = 0,5х + 2 является прямая, параллельная прямой, являющейся графиком функции у = 0,5х, и любая точка графика получается сдвигом по оси у на 2 единицы вверх.
Устное упражнение.
Что является графиком функции у = 3х + 1; у = –1,5х + 2; у = 2х – 14; у = –3х – 1,5?
б) Рассматриваем случай k = 0, b 0. Функция у = kx + b принимает вид у = b. Получаем, что, независимо от значения х, у всегда равно b. Значит, графиком функции является прямая, параллельная оси х и проходящая через точку (0; b).
в) Рассматриваем случай k = 0, b = 0. Функция у = kx + b принимает вид у = 0, то есть графиком является сама ось х.
После этого на доску можно вынести запись:
|
Графиком линейной функции является прямая: а) при k
0 и b = 0, проходящая через начало
координат б) при k 0 и b 0, параллельная графику функции у = kx; в) при k = 0, b 0, параллельная оси х; г) при k = 0, b = 0, совпадающая с осью х. |
4. Последним шагом формулируем простейший алгоритм построения графика линейной функции:
1-й шаг. По формуле найти координаты двух точек графика.
2-й шаг. Отметить полученные точки на координатной плоскости.
3-й шаг. Провести через построенные точки прямую.
III. Формирование умений и навыков.
1. Рассматриваем примеры 3–5 со с. 72–73 учебника. Во время работы учащиеся должны называть значения коэффициентов k и b.
2. Определите, какие из следующих функций являются линейными. Назовите для них значения коэффициентов k и b.
а) у = 2,5x – 7; б) у = 4 – ![]() x; в)
у = 4x – 5x2;
x; в)
у = 4x – 5x2;
г) у = ![]() ;
д) у = –3х; е)
у =
;
д) у = –3х; е)
у = ![]() ;
;
ж) у = 3x2 + 2; з) у = –5; и) у = 0.
3. Что является графиком линейной функции и как он расположен?
а) у = –3x + 5; б) у = ![]() x; в)
у = –3;
x; в)
у = –3;
г) у = ![]() ; д)
у =
; д)
у = ![]() ; е)
у = 0.
; е)
у = 0.
4. На рисунках изображены графики функций. Какие из этих функций являются линейными?
а)  в)
в)
 б)
б)  г)
г)
5. № 313, 315.
6. № 319, 321.
IV. Итоги урока.
Домашнее задание: № 314; № 316 (устно); № 318; № 320.
Урок 35
Взаимное расположение графиков
линейных функций
Цели: продолжить формировать умение строить график линейной функции и определять по графику значение функции по данному аргументу и наоборот; ввести понятие углового коэффициента прямой и выявить случаи взаимного расположения графиков линейных функций в зависимости от значений угловых коэффициентов.
Ход урока
I. Организационный момент
II. Проверочная работа.
Вариант 1
1. Постройте график функции, заданной формулой у = –2х+ 0,5.
2. Линейная функция задана формулой у = 5х – 12. Найдите:
а) значение у, если х = 1,2; –3;
б) значение х, при котором у = 0; –1,5.
Вариант 2
1. Постройте график функции, заданной формулой у = –3х– 1,5.
2. Линейная функция задана формулой у = –4х + 7. Найдите:
а) значение у, если х = –1,3; 8;
б) значение х, при котором у = –2,8; 0.
III. Актуализация знаний.
1. Назовите координаты точек пересечения графиков функций с осями координат. Какие особенности этих точек?
а) б)
б) в)
в) г)
г)  д)
д) е)
е) 
2. № 322, № 324.
№ 322.
Решение:
а) у = –2,4х + 9,6.
Точка пересечения с осью х имеет ординату, равную нулю. Найдем её абсциссу, решив уравнение:
–2,4х + 9,6 = 0;
–2,4х = – 9,6;
х = – 9,6 : (–2,4);
х = 4.
(4; 0) – точка пересечения с осью х.
Точка пересечения с осью у имеет абсциссу, равную нулю. Найдем её ординату по формуле:
Если х = 0, то у = –2,4 · 0 + 9,6 = 9,6.
(0; 9,6) – точка пересечения с осью у.
б) у = –0,7х – 28.
Если у = 0, то –0,7х – 28 = 0;
–0,7х = 28;
х = 28 : (–0,7);
х = –40.
(–40; 0).
Если х = 0, то у = –0,7 · 0 – 28 = –28.
(0; –28).
в) у = 1,2х + 6.
Если у = 0, то 1,2х + 6 = 0;
1,2х = –6;
х = –6 : 1,2;
х = –5.
(–5; 0).
Если х = 0, то у = 1,2 · 0 + 6 = 6.
(0; 6).
г) у = –5х + 2.
Если у = 0, то –5х + 2 = 0;
–5х = –2;
х = –2 : (–5);
х = 0,4.
(0,4; 0).
Если х = 0, то у = –5 · 0 + 2 = 2.
(0; 2).
Ответ: а) (4; 0), (0; 9,6); б) (–40; 0), (0; –28); в) (–5; 0), (0; 6); г) (0,4; 0), (0; 2).
3. № 325.
При выполнении этого задания учащиеся замечают, что для построения графика линейной функции частного вида y = b достаточно построить точку с координатами (0; b) и провести прямую, параллельную оси х (если выполняем задание в тетради в клеточку), либо построить 2 точки с координатами (0; b) и (х0; b), где х0 – любое число, и провести через них прямую.
IV. Объяснение нового материала.
1. Напоминаем, что график прямой пропорциональности y = kx располагается в I и III или в II и IV координатных четвертях в зависимости от знака коэффициента k. Посмотрев в тетради выполненные ранее построения, замечаем, что графики линейных функций пересекают ось х либо под острым углом (с положительным направлением оси х), либо под тупым. Угол зависит от знака k. Если k = 0, то прямая параллельна оси х. Так как от k зависит угол, то k называют угловым коэффициентом прямой.
2. Затем рассматриваем и анализируем рис. 36, 37 со с. 73 учебника. Делаем вывод: если угловые коэффициенты прямых, являющихся графиками двух линейных функций, равны, то эти прямые параллельны, а если угловые коэффициенты различны, то прямые пересекаются.
3. Рассматриваем случай, когда у линейных функций k различны, а b – одинаковые. Во время актуализации знаний мы вспомнили, что графики этих функций все проходят через точку (0; b), значит, они все пересекаются в этой точке.
V. Формирование умений и навыков.
1. Постройте в одной системе координат графики функций:
у = ![]() x
+ 1; у =
x
+ 1; у = ![]() x
– 2; у =
x
– 2; у = ![]() x.
x.
Ответьте на вопросы:
1) Чему равен угловой коэффициент каждой прямой?
2) Каково взаимное расположение графиков функций?
3) Каковы координаты точек пересечения каждого графика с осями координат?
2. Пересекаются ли графики функций у = 2х – 4 и у = –4х + 2; у = 2х – 3 и у = 2х + 3?
В том случае, когда графики пересекаются, постройте их. Определите по графику координаты точки пересечения и проверьте результаты вычислением.
3. № 327.
4. Постройте прямую, если её угловой коэффициент равен –0,5 и она проходит через точку (–6; 4). Задайте формулой линейную функцию, график которой параллелен этой прямой и пересекает ось у в точке (0; 5).
VI. Итоги урока.
– Дайте определение линейной функции.
– Что является графиком линейной функции? Как его построить?
– Почему коэффициент k называется угловым? Как от k зависит расположение графика линейной функции?
– В каком случае графики двух линейных функций пересекаются и в каком случае они являются параллельными прямыми?
Домашнее задание: № 323; № 326; № 328; № 329.
Урок 36
Взаимное расположение графиков линейных функций
Цели: формировать умение использовать знания о линейной функции и её график при решении практических задач; интерпретировать полученные результаты.
Ход урока
I. Устная работа.
Тест.
1. Отметьте знаком «+» пары функций, графики которых пересекаются:
а) у = ![]() х
и у = 0,4x – 1; б) у = 4,2х + 2 и у
= –4,2х – 2;
х
и у = 0,4x – 1; б) у = 4,2х + 2 и у
= –4,2х – 2;
в) у = 3х + 1 и у = х + 1; г) у = 2х + 5 и у = 2х – 10.
2. Даны функции:
а) у = 0,75х;б) у = ![]() х – 5; в) у = х;г)
у = –4х + 3; д) у = –8х + 5; е)
у =
х – 5; в) у = х;г)
у = –4х + 3; д) у = –8х + 5; е)
у = ![]() ;
;
выпишите
функции, графики которых параллельны графику функции
у = 0,75х – 5.
3. Найдите координаты точки пересечения графиков функций
у = 37х – 8 и у = 25х + 4.
III. Формирование умений и навыков.
1. № 330, 332.
2. Дорожный просвет – это расстояние между днищем автомобиля и дорогой,
на которой он стоит. Для некоторого легкового автомобиля дорожный просвет можно
вычислить по формуле h = 40 – ![]() , где h – дорожный просвет (в см), т
– масса груза (в кг), погруженного в автомобиль.
, где h – дорожный просвет (в см), т
– масса груза (в кг), погруженного в автомобиль.
а) Вычислите дорожный просвет, если масса груза в автомобиле равна: 100 кг; 150 кг; 200 кг; 0 кг.
б) Является ли зависимость величины дорожного просвета от массы груза, погруженного в автомобиль, линейной функцией? Чему в этом случае равны коэффициенты k и b?
в) Начертите координатные оси, выбрав на них подходящий масштаб, и
постройте график функции h = 40 – ![]() , где 0 ≤ т ≤ 600.
, где 0 ≤ т ≤ 600.
г) С помощью построенного графика найдите, какой груз погружен в автомобиль, если дорожный просвет равен: 33 см; 38 см; 35 см; 40 см.
д) С помощью графика определите:
1) на сколько сантиметров уменьшится дорожный просвет, если к грузу в 50 кг добавить груз в 25 кг; к грузу в 100 кг добавить груз в 25 кг;
2) на сколько сантиметров увеличится дорожный просвет, если с машины с грузом в 150 кг снять груз в 50 кг.
3. № 1201*.
Решение:
а) y = | x | – 3. Данную функцию можно переписать в виде:
|
y = Функция «кусочная», на каждом промежутке области определения является линейной. |
|
б) y = 4 – | x |.
|
Если х ≥ 0, то 4 – | x | = 4 – x = –x + 4; если х < 0, то 4 – | x | = 4 – (–x) = 4 + x = x + 4. y = |
|
IV. Итоги урока.
– Какая функция является линейной?
– Что является графиком линейной функции?
– Как называется коэффициент k? Что он показывает в формуле линейной функции?
– Как расположен график функции y = x + 2; у = –3х;
y = ![]() ?
?
– Назовите признак параллельности графиков двух линейных функций.
Домашнее задание: № 332; 333; 335; 366.
Урок 37
Взаимное расположение графиков линейных функций
Цели: обобщить и систематизировать знания по теме «Линейная функция»; подготовиться к написанию контрольной работы.
Ход урока
I. Игра-слалом.
Класс разбивается на 3 команды. Игра состоит из теоретического и практического конкурсов. Задания выполняются на время. Побеждает команда, получившая наибольшее число правильных ответов за наименьшее время.
1. Теоретический конкурс
1. Какую зависимость называют функциональной или функцией?
2. Что такое аргумент и что такое функция?
3. Что называют областью определения функции?
4. Что такое график функции?
5. Какую функцию называют линейной?
6. Что является графиком линейной функции?
7. Что является графиком прямой пропорциональности?
8. В чём их сходство и различие?
9. От чего зависит расположение графика линейной функции?
10. Сколько точек необходимо для построения графика линейной функции?
11. А для графика прямой пропорциональности? Почему?
12. Что такое угловой коэффициент?
13. Как расположен график функции y = kx при k > 0 и k < 0?
14. Как найти координаты точки пересечения графиков двух линейных функций?
15. В каком случае графики двух линейных функций являются параллельными прямыми?
2. Практический конкурс
1. Заполните таблицу для функции, заданной формулой у = –0,5(8 – x).
|
х |
–1,4 |
|
2,6 |
|
8,8 |
|
|
у |
|
–3,4 |
|
–1,8 |
|
2,4 |
2. Какова область определения функции?
а) у = ![]() ; в)
у =
; в)
у = ![]() ;
;
б) у = 7х + 6; г) у =
![]() .
.
3. Является ли линейной функция:
а) у = ![]() ; в)
у = х(6 – х);
; в)
у = х(6 – х);
б) у = 3(х + 8); г) у = 2(1 – 3х)(х – 3)?
4. Постройте график функции, заданной формулой у = 2х + 3.
5. Постройте график функции, заданной формулой у = 0,5х + 3. С помощью графика найдите:
а) значение у, если х = –4;
б) значение х, если у = 6;
в) координаты точек пересечения графика с осями координат;
г) корень уравнения 0,5х + 3 = 0.
6. Не выполняя построения, выясните, проходит ли график функции, заданной формулой у = 1,25х – 5, через точку:
а) А (20; 20); б) В (20; 10).
7. Функция задана формулой у = 0,25х + 3, где х принадлежит промежутку от –4 до 8.
Постройте график этой функции и укажите все целые значения, которые может принимать эта функция.
8. Пересекает ли ось х график линейной функции, и если пересекает, то в какой точке? Функция задана формулой:
а) у = 7х + 49; б) у = 15.
9. График некоторой линейной функции вида y = kx + 1 параллелен графику функции у = –0,4х. Найдите значение коэффициента k и выясните, принадлежит ли этому графику точка М (50; –19).
10. Не выполняя построения, найдите координаты точки пересечения графиков линейных функций: у = 4х + 9 и у = 6х – 5.
11. Отметьте точки А (–4; 3) и В (2; –6). Проведите прямую АВ и найдите координаты точек пересечения этой прямой с осью х и осью у.
12. Постройте график функций:
а) у = –5; б) х = 3.
13. Какие из графиков функций параллельны, а какие пересекаются:
а) у = –3х + 4; в) у = –(2 + 3х);
б) у = –х + 3; г) у = х + 3?
14. В одной и той же координатной плоскости постройте графики функции: у = 5, у = х – 2, у = –2х + 4, у = 0.
15. В каких координатных четвертях расположен график прямой пропорциональности, параллельный графику линейной функции, заданной формулой:
а) у = 0,8х – 1,6; б) у = – 0,4х + 1?
II. Итоги урока.
Домашнее задание: повторить п. 15, п. 16. № 360; № 363; № 372.
Урок 40
Контрольная работа № 3
Вариант 1
1. Функция задана формулой у = 6х + 19. Определите:
а) значение у, если х = 0,5;
б) значение х, при котором у = 1;
в) проходит ли график функции через точку А (–2; 7).
2. а) Постройте график функции у = 2х – 4.
б) Укажите с помощью графика, чему равно значение у при х = 1,5.
3. В одной и той же системе координат постройте графики функций:
а) у = –2х; б) у = 3.
4. Найдите координаты точки пересечения графиков функций
у = 47х – 37 и у = –13х + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.
Вариант 2
1. Функция задана формулой у = 4х – 30. Определите:
а) значение у, если х = –2,5;
б) значение х, при котором у = –6;
в) проходит ли график функции через точку В (7; –3).
2. а) Постройте график функции у = –3х + 3.
б) Укажите с помощью графика, при каком значении х значение у равно 6.
3. В одной и той же системе координат постройте графики функций:
а) у = 0,5х; б) у = –4.
4. Найдите координаты точки пересечения графиков функций
у = –38х + 15 и у = –21х – 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = –5х + 8 и проходит через начало координат.
Вариант 3
1. Функция задана формулой у = 5х + 18. Определите:
а) значение у, если х = 0,4;
б) значение х, при котором у = 3;
в) проходит ли график функции через точку С (–6; –12).
2. а) Постройте график функции у = 2х + 4.
б) Укажите с помощью графика, чему равно значение у при х = –1,5.
3. В одной и той же системе координат постройте графики функций:
а) у = –0,5х; б) у = 5.
4. Найдите координаты точки пересечения графиков функций
у = –14х + 32 и у = 26х – 8.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 2х + 9 и проходит через начало координат.
Вариант 4
1. Функция задана формулой у = 2х – 15. Определите:
а) значение у, если х = –3,5;
б) значение х, при котором у = –5;
в) проходит ли график функции через точку K (10; –5).
2. а) Постройте график функции у = –3х – 3.
б) Укажите с помощью графика, при каком значении х значение у равно –6.
3. В одной и той же системе координат постройте график функций:
а) у = 2х; б) у = –4.
4. Найдите координаты точки пересечения графиков функций
у = –10х – 9 и у = –24х + 19.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = –8х + 11 и проходит через начало координат.
Рекомендации по оцениванию.
Задания 1–3 относятся к базовому уровню знаний по теме. Верное выполнение любых трех заданий оценивается отметкой «3». Для получения отметки «5» необходимо выполнить верно все пять заданий.
Решение заданий контрольной работы
Вариант 1
1. у = 6х + 19.
а) Если х = 0,5, то у = 6 · 0,5 + 19 = 3 + 19 = 22;
б) если у = 1, то 6х + 19 = 1;
6х = 1 – 19;
6х = –18;
х = –18 : 6;
х = –3;
в) 7 = 6 · (–2) + 19;
7 = –12 + 19;
7
= 7 – верно, значит, график функции проходит через точку
А (–2; 7).
Ответ: а) 22; б) –3; в) проходит.
|
2. а) у = 2х – 4. Построим две точки, принадлежащие графику. Если х = 0, то у = 2 · 0 – 4 = –4; если х = 2, то у = 2 · 2 – 4 = 0. (0; –4), (2; 0). б) При х = 1,5 у = –1. |
|
|
3. а) у = –2х. Графиком является прямая, проходящая через начало координат и точку (2; –4). б) у = 3. Графиком является прямая, проходящая через точку (0; 3) и параллельная оси х.
4. Решим уравнение: 47х – 37 = –13х + 23. 47х + 13х = 23 + 37; |
|
60х = 60;
х = 1, значит, абсцисса точки пересечения графиков функций равна 1. Найдем соответствующее значение ординаты:
если х = 1, то у = 47 · 1 – 37 = 10.
Точка пересечения имеет координаты (1; 10).
Ответ: (1; 10).
5. График параллелен прямой у = 3х – 7, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 3х.
Ответ: у = 3х.
Вариант 2
1. у = 4х – 30.
а) Если х = –2,5, то у = 4 · (–2,5) – 30 = –10 – 30 = –40;
б) если у = –6, то 4х – 30 = –6;
4х = –6 + 30;
4х = 24;
х = 24 : 4;
х = 6;
в) –3 = 4 · 7 – 30;
–3 = 28 – 30;
–3 = –2 – неверно, значит, график функции не проходит через точку В (7; –3).
Ответ: а) –40; б) 6; в) не проходит.
|
2. а) у = –3х + 3. Построим две точки, принадлежащие графику. Если х = 0, то у = –3 · 0 + 3 = 3; если х = 2, то у = –3 · 2 + 3 = –3; (0; 3), (2; –3)
б) Если у = 6, то х = –1. |
|
3. а) у = 0,5х. Графиком является прямая, проходящая через начало координат и точку (4; 2).
б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.
4. Решим уравнение:
–38х + 15 = –21х – 36;
–38х + 21х = –36 – 15;
–17х = –51;
х = (–51) : (–17);
х = 3, значит, абсцисса точки пересечения графиков функций равна 3.
Найдем соответствующее значение ординаты:
если х = 3, то у = –38 · 3 + 15 = –99.
Точка пересечения имеет координаты (3; –99).
Ответ: (3; –99).
5. График параллелен прямой у = –5х + 8, значит, угловые координаты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = –5х.
Ответ: у = –5х.
Вариант 3
1. у = 5х + 18.
а) Если х = 0,4, то у = 5 · 0,4 + 18 = 2 + 18 = 20;
б) если у = 3, то 5х + 18 = 3;
5х = 3 – 18;
5х = –15;
х = –15 : 5;
х = –3;
в) –12 = 5 · (–6) + 18;
–12 = –30 + 18;
–12 = –12 – верно, значит, график функции проходит через точку
С (–6; –12).
Ответ: а) 20; б) –3; в) проходит.
|
2. а) у = 2х + 4. Построим две точки, принадлежащие графику. Если х = 0, то у = 2 · 0 + 4 = 4; если х = –2, то 2 · (–2) + 4 = 0. (0; 4), (–2; 0) б) Если х = –1,5, то у = 1. |
|
3. а) у = –0,5х. Графиком является прямая, проходящая через начало координат и точку (4; –2).
б) у = 5. Графиком является прямая, проходящая через точку (0; 5) и параллельная оси х.
4. Решим уравнение:
–14х + 32 = 26х – 8;
–14х – 26х = –8 – 32;
–40х = –40;
х = 1, значит, абсцисса точки пересечения графиков равна 1. Найдем соответствующее значение ординаты:
если х = 1, то у = –14 · 1 + 32 = 18.
Точка пересечения имеет координаты (1; 18).
Ответ: (1; 18).
5. График параллелен прямой у = 2х + 9, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 2х.
Ответ: у = 2х.
Вариант 4
1. у = 2х – 15.
а) Если х = –3,5, то у = 2 · (–3,5) – 15 = –7 – 15 = –22;
б) если у = –5, то 2х – 15 = –5;
2х = –5 + 15;
2х = 10;
х = 5;
в) –5 = 2 · 10 – 15;
–5 = 20 – 15;
–5 = 5 – неверно, значит, график функции не проходит через точку
K (10; –5).
Ответ: а) –22; б) 5; в) не проходит.
|
2. а) у = –3х – 3. Построим две точки, принадлежащие графику: если х = 0, то у = –3 · 0 – 3 = –3; если х = –2, то у = (–3) · (–2) – 3 = 3. (0; –3), (–2; 3). б) Если у = –6, то х = 1. |
|
|
3. а) у = 2х. Графиком является прямая, проходящая через начало координат и точку (2; 4). б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х. |
|
4. Решим уравнение:
–10х – 9 = –24х + 19;
–10х + 24х = 19 + 9;
14х = 28;
х = 28 : 14;
х = 2, значит, абсцисса точки пересечения графиков равна 2. Найдем соответствующее значение ординаты:
если х = 2, то у = –10 · 2 – 9 = –29.
Точка пересечения имеет координаты (2; –29).
Ответ: (2; –29).
5. График параллелен прямой у = –8х + 11, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это – прямая пропорциональность. Значит, у = –8х.
Ответ: у = –8х.
Урок №39
Определение степени с натуральным показателем
Цели: ввести понятие степени числа а с натуральным показателем п; определить значение степени с натуральным показателем положительного и отрицательного числа в зависимости от четности / нечетности показателя степени; формировать умение вычислять значение степени и представлять число в виде степени с натуральным показателем.
Ход урока
I. Организационный момент
Устная работа.
Вычислите.
а) 3 · 45; б) ![]() · 120; в)
· 120; в)
![]() ;
;
г) ![]() ;
д)
;
д) ![]() · 49; е)
–3 · (–16);
· 49; е)
–3 · (–16);
ж) –(–3) · 12; з) –(2 · (–9)); и)
![]() ;
;
к) 18 · 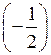 +
11; л)
+
11; л) ![]() · (11 – 6); м)
· (11 – 6); м) 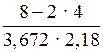 .
.
II. Объяснение нового материала.
1. Объяснение проводить согласно пункту 18 учебника. Напоминаем, что вместо длинной записи произведения 5 · 5 · 5 · 5 · 5 · 5 · 5 можно записать выражение 57, где 5 – основание степени (повторяющийся множитель), а 7 – показатель степени (число повторяющихся множителей).
Понятие степени определяем для любого числа а в качестве основания и любого натурального показателя (аналитическая запись).
На доску выносится запись:
|
Степенью числа а с натуральным показателем п, большим 1, называется выражение ап, равное произведению п множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а. |
Проговариваем с учащимися правило чтения степени, приводим примеры.
2. Мини-лабораторная работа.
Найдите значение степени.
33; 34; 35; 36; 01;
![]() ; 02;
; 02;
(0,1)2; (0,1)3; (0,1)4; (0,1)5; 03;
(–2)2; (–2)3; (–2)4; (–2)5; 04;
![]() ; 05;
; 05;
(–0,1)2; (–0,1)3; (–0,1)4; (–0,1)5; 06.
Задания разбиваем либо по группам, либо раздаем индивидуально. Затем «по цепочке» ученики выходят к доске и записывают результаты.
После анализа полученных результатов на доску выносятся следующие правила:
|
При возведении в степень положительного числа получается положительное число. |
|
При возведении в степень нуля получается нуль. |
|
Степень отрицательного числа с четным показателем – положительное число. |
|
Степень отрицательного числа с нечетным показателем – отрицательное число. |
Обособленно выносим правило для квадратов чисел (пропедевтика изучения решения квадратных уравнений):
|
Квадрат любого числа есть положительное число либо нуль (а2 ≥ 0 при любом а). |
3. Рассматриваем примеры 1–3 со с. 88–89 учебника.
III. Формирование умений и навыков.
Упражнения, решаемые на этом уроке, можно условно разбить на группы:
1-я группа. Задания на усвоение понятия степени.
2-я группа. Задания на вычисление значения степени числа с натуральным показателем.
3-я группа. Задания на вычисление значения числового выражения, содержащего степень.
1-я группа
№ 374, № 375 (устно), № 376, № 378, № 380.
При выполнении этих заданий учащиеся должны четко называть степень, можно просить назвать их основание и показатель степени.
2-я группа
1. № 382, № 381 (а, б).
2. Не выполняя вычислений, сравните значение данного выражения с нулем:
а) (–4,1) · (–5,6)6; б) (–3,3)3 : (–5,7);
в) –(4,8)2 · (–1,2)4; г) –(–2,7)4 · (–6,4)5.
3. Сравните значения выражений:
а) (–6,5)4 и (–2,4)3;
б) (–0,2)6 и (–0,2)10;
в) (–1,5)7 и (–1,5)9.
3-я группа
№ 384, 385 (а, в, г), 386 (а, в, д, ж), 387 (а, б, в).
IV. Итоги урока.
– Сформулируйте определение степени числа с натуральным показателем. Приведите примеры и назовите в каждом из них основание и показатель степени.
– Чему равна первая степень любого числа?
– Какой знак имеет результат возведения положительного числа в натуральную степень?
– Какой знак имеет значение степени отрицательного числа с четным показателем? С нечетным показателем?
– Каков порядок действий при нахождении значения выражения, содержащего степени с натуральным показателем?
Домашнее задание: № 377; 379; 381 (в, г); 383; 385 (б, г, е); 386 (б, г, е, з).
Урок 40
Определение степени с натуральным показателем
Цели: продолжить формировать умение вычислять значение числового выражения, содержащего степень; формировать умение вычислять значение буквенного выражения, содержащего степень, и решать практические задачи с использованием понятия степени с натуральным показателем.
Ход урока
I. Математический диктант.
Вариант 1
1. Запишите в виде произведения третью степень числа 4 и найдите её числовое значение.
2. Чему равна первая степень числа –5?
3. Вычислите значение выражения 23 · 0,5.
4. Чему равна сумма кубов чисел 5 и 3?
5. Вычислите значение выражения (–3)2 + (0,1)3.
Вариант 2
1. Запишите в виде произведения четвертую степень числа 3 и найдите её числовое значение.
2. Чему равна первая степень числа ![]() ?
?
3. Вычислите значение выражения 32 · 0,7.
4. Чему равен квадрат разности чисел 7 и 5?
5. вычислите значение выражения (–5)3 – (0,2)2.
II. Актуализация знаний.
№ 387 (г, д, е, ж, з, и), № 388.
№ 388.
Решение:
а) –13 + (–2)3 = –1 + (–8) = –9;
б) –62 – (–1)4 = –36 – 1 = –37;
в) –83 + (–3)3 = –512 + (–27) = –539;
г) 10 – 5 · 24 = 10 – 5 · 16 = 10 – 80 = –70;
д) 2 · 34 – 3 · 24 = 2 · 81 – 3 · 16 = 162 – 48 = 114;
е) 2 · 53 + 5 · 23 = 2 · 125 + 5 · 8 = 250 + 40 = 290;
ж) 34 – 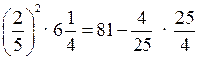 = 81 – 1 = 80;
= 81 – 1 = 80;
з) 0,2 · 32 – 0,4 · 24 = 0,2 · 32 – 0,2
· 2 · 24 = 0,2(32 – 2 · 24) =
= 0,2(9 – 2 · 16) = 0,2 · (9 – 32) = 0,2 · (–23) = –4,6;
и) 8 · 0,53 + 25 · 0,22 = 2 3 · 0,53
+ 52 · 0,22 = (2 · 0,5)3 + (5 · 0,2)2
=
= 13 + 12 = 1 + 1 = 2.
При выполнении этого упражнения учащиеся выводят правило:
|
an · bn = (a · b)n, для любых a и b. |
III. Формирование умений и навыков.
На этом уроке отрабатывается умение вычислять значение буквенного выражения, содержащего степень.
1-й блок
1. Найдите значения выражений х2; – х2; х2 – 4 для заданных значений х и заполните таблицу (используйте найденные значения выражения х2 для вычисления значений двух других выражений):
|
х |
–5 |
–2,5 |
0 |
0,3 |
1 |
12 |
|
х2 |
|
|
|
|
|
|
|
–х2 |
|
|
|
|
|
|
|
х2 – 4 |
|
|
|
|
|
|
2. Найдите значение выражений х3; 0,1х3; х3 + 10 для заданных значений х и заполните таблицу:
|
х |
–4 |
–0,3 |
–1 |
0 |
9 |
|
х3 |
|
|
|
|
|
|
0,1х3 |
|
|
|
|
|
|
х3 + 10 |
|
|
|
|
|
3. № 392 (устно).
2-й блок
1. Найдите значение выражения.
а) (ху)2 при х = 12 и у = –0,5; х = –14 и у = –1;
б) ![]() при х
= –6 и у = 1,5; х = 0 и у = –23;
при х
= –6 и у = 1,5; х = 0 и у = –23;
в) (х + у)4 при х = 0,7 и у = 0,3; х = –11 и у = 6;
г) (у – х)3 при х = –14 и у = –10; х = 0,9 и у = 1,1.
2. № 393.
3. Сравните значения выражений.
а) –а2 и (–а)2 при а = 3; –5; 0;
б) –а3 и (–а)3 при а = 10; –2; 0.
4. № 395.
Решение:
а) а3 · а = (а · а · а) · а = а4;
б) а4 · а2 = (а · а · а · а) · (а · а) = а6;
в) а3 · а6 = 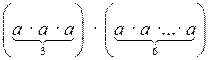 = а9;
= а9;
г) а20 · а12 = 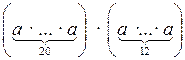 = а32.
= а32.
№ 396, № 397.
3-й блок
1. № 389.
2. Сколько биений сделает сердце человека за сутки, если за 1 мин оно делает в среднем 75 биений?
3. Может ли школьник поднять 1 м3 пробки? (Масса 1 см3 пробки 0,2 г.)
Решение:
Рассчитаем, сколько см3 в 1 м3:
1 м3 = 1 · 1 · 1 ( в м) = 100 · 100 · 100 (в см) = 1 000 000 = 106 см3.
Масса 1 м3 пробки равна 0,2 · 106 (г), что составляет 200 000 г или 200 кг. Значит, школьник не сможет поднять такую массу.
Ответ: нет.
4. Если разрезать кубический метр на кубические сантиметры и поставить их один на другой, то какой высоты получится столб?
При решении этой задачи следует использовать результаты предыдущей задачи.
IV. Итоги урока.
– Сформулируйте определение степени с натуральным показателем.
– Чему равна любая натуральная степень нуля?
– Каков порядок действий при нахождении числового и буквенного выражения, содержащего степень?
– Чему равно значение выражения 0,28 · 58? Как рационально вычислить? Каким правилом необходимо воспользоваться?
Домашнее задание: № 390; № 391; № 394; № 398.
Урок 41
Умножение и деление степеней с одинаковыми основаниями
Цели: вывести правила умножения и деления степеней с одинаковым основанием; дать определение нулевой степени числа, не равного нулю; формировать умение выполнять указанные действия со степенями.
Ход урока
I. Устная работа.
1. Вычислите.
а) 32; б) ![]() ; в) (0,1)3; г)
; в) (0,1)3; г) ![]() ; д)
; д) ![]() ; е) (–0,1)4; ж)
; е) (–0,1)4; ж)
![]() ; з) –(–7)2;
; з) –(–7)2;
и) –(–2)3; к) 016; л) (–1)18; м) –(–1)23.
2. Сравните значение двух выражений:
а) (–8,64)20 и 030; б) (–1)76 и (–1)70;
в) ![]() и (–3,82)13; г)
и (–3,82)13; г)
![]() и
и ![]() .
.
II. Проверочная работа.
Вариант 1
1. Найдите значение выражения. а) ![]() – (0,5)2; б) 3000 · (0,2)3
– (–2)6; в)
– (0,5)2; б) 3000 · (0,2)3
– (–2)6; в) ![]() – (–3)3.
– (–3)3.
2. Вычислите значение выражения х3 – х2 при: а) х = 0,3; б) х = –6.
Вариант 2
1. Найдите значение выражения.а) ![]() + (0,6)2; б)
2000 · (0,3)4 – (–2)4; в)
+ (0,6)2; б)
2000 · (0,3)4 – (–2)4; в) ![]() – (–4)3.
– (–4)3.
2. Вычислите значение выражения х2 + х3 при:а) х = –0,4; б) х = 10.
III. Объяснение нового материала.
На этом уроке изучаем два важных свойства степени: сложение и умножение степеней с одинаковыми основаниями.
|
Свойство 1. При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают. |
|
|
|
|
по сочетательному свойству умножения |
|
|
|
|
|
по определению степени с натуральным показателем |
|
|
= 25 Итак, 22 · 23 = 22 + 3 |
= am + n
|
|
Свойство 2. При делении степеней с одинаковыми основаниями, основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. |
|
5 > 3 35
: 33 = |
m > n, a ¹ 0 am : an =
|
|
запишем частное в виде дроби |
|
|
|
|
|
сократим дробь |
|
|
|
|
|
по определению степени с натуральным показателем |
|
|
= 32 Итак, 35 : 33 = 35 – 3 |
= am – n
|
Замечаем, что am : am = am – m = a0 = 1.
|
Определение. Степень числа а, не равного нулю, с нулевым показателем равна единице. |
IV. Формирование умений и навыков.
1. № 403.
Решение:
а) x5x8 = x5 + 8 = x13; е) yy12 = y1 + 12 = y13;
ж) 2624 = 26 + 4 + 210; з) 757 = 75 + 1 = 76.
2. № 405.
Решение:
а) a15 = a6 + 9 = a6 ∙ a9; б) a15 = a9 + 6 = a9 ∙ a6;
в) a15 = a2 + 13 = a2 ∙ a13; г) a15 = a14 + 1 = a14 ∙ a = a ∙ a14.
3. № 407.
Решение:
Представим число 6 в виде суммы двух натуральных чисел всеми возможными способами:
6 = 1 + 5; 6 = 2 + 4; 6 = 3 + 3.
Значит, a6 = a ∙ a5; a6 = a2 ∙ a4; a6 = a3 ∙ a3.
4. № 409.
Решение:
а) m3m2m8 = m3 + 2 + 8 = m13; в) xx4x4x = x1 + 4 + 4 + 1 = x10;
д) 78 ∙ 7 ∙ 74 = 78 + 1 + 4 = 713; е) 5 ∙ 52 ∙ 53 ∙ 55 = 51 + 2 + 3 + 4 = 511.
5. № 410.
Решение:
а) 58 ∙ 25 = 58 ∙ 52 = 58 + 2 = 510;
в) 615 ∙ 36 = 615 ∙ 62 = 615 + 2 = 617;
д) 0,45 ∙ 0,16 = 0,45 ∙ 0,42 = 0,45 + 2 = 0,47;
е) 0,001 ∙ 0,14 = 0,13 ∙ 0,14 = 0,13 + 4 = 0,17.
6. № 411.
Решение:
а) 24 ∙ 2 = 24 + 1 = 25 = 32;
б) 26 ∙ 4 = 26 ∙ 22 = 26 + 2 = 28 = 256;
в) 8 ∙ 27 = 23 ∙ 27 = 23 + 7 = 210 = 1024;
г) 16 ∙ 32 = 24 ∙ 25 = 24 + 5 = 29 = 512.
7. № 413.
Решение:
а) (c4)2 = c4 ∙ c4 = c4 + 4 = c8;
б) (c2)4 = c2 ∙ c2 ∙ c2 ∙ c2 = c2 + 2 + 2 + 2 = c8.
V. Итоги урока.
Домашнее задание: № 404; № 406; № 408; 412; № 533.
Вариант 1
1. Найдите значение выражения. а) ![]() – (0,5)2; б) 3000 · (0,2)3
– (–2)6; в)
– (0,5)2; б) 3000 · (0,2)3
– (–2)6; в) ![]() – (–3)3.
– (–3)3.
2. Вычислите значение выражения х3 – х2 при: а) х = 0,3; б) х = –6.
Вариант 2
1. Найдите значение выражения.а) ![]() + (0,6)2; б)
2000 · (0,3)4 – (–2)4; в)
+ (0,6)2; б)
2000 · (0,3)4 – (–2)4; в) ![]() – (–4)3.
– (–4)3.
2. Вычислите значение выражения х2 + х3 при:а) х = –0,4; б) х = 10.
Вариант 1
1. Найдите значение выражения. а) ![]() – (0,5)2; б) 3000 · (0,2)3
– (–2)6; в)
– (0,5)2; б) 3000 · (0,2)3
– (–2)6; в) ![]() – (–3)3.
– (–3)3.
2. Вычислите значение выражения х3 – х2 при: а) х = 0,3; б) х = –6.
Вариант 2
1. Найдите значение выражения.а) ![]() + (0,6)2; б)
2000 · (0,3)4 – (–2)4; в)
+ (0,6)2; б)
2000 · (0,3)4 – (–2)4; в) ![]() – (–4)3.
– (–4)3.
2. Вычислите значение выражения х2 + х3 при:а) х = –0,4; б) х = 10.
Вариант 1
1. Найдите значение выражения. а) ![]() – (0,5)2; б) 3000 · (0,2)3
– (–2)6; в)
– (0,5)2; б) 3000 · (0,2)3
– (–2)6; в) ![]() – (–3)3.
– (–3)3.
2. Вычислите значение выражения х3 – х2 при: а) х = 0,3; б) х = –6.
Вариант 2
1. Найдите значение выражения.а) ![]() + (0,6)2; б)
2000 · (0,3)4 – (–2)4; в)
+ (0,6)2; б)
2000 · (0,3)4 – (–2)4; в) ![]() – (–4)3.
– (–4)3.
2. Вычислите значение выражения х2 + х3 при:а) х = –0,4; б) х = 10.
Вариант 1
1. Найдите значение выражения. а) ![]() – (0,5)2; б) 3000 · (0,2)3
– (–2)6; в)
– (0,5)2; б) 3000 · (0,2)3
– (–2)6; в) ![]() – (–3)3.
– (–3)3.
2. Вычислите значение выражения х3 – х2 при: а) х = 0,3; б) х = –6.
Вариант 2
1. Найдите значение выражения.а) ![]() + (0,6)2; б)
2000 · (0,3)4 – (–2)4; в)
+ (0,6)2; б)
2000 · (0,3)4 – (–2)4; в) ![]() – (–4)3.
– (–4)3.
2. Вычислите значение выражения х2 + х3 при:а) х = –0,4; б) х = 10.
Вариант 1
1. Найдите значение выражения. а) ![]() – (0,5)2; б) 3000 · (0,2)3
– (–2)6; в)
– (0,5)2; б) 3000 · (0,2)3
– (–2)6; в) ![]() – (–3)3.
– (–3)3.
2. Вычислите значение выражения х3 – х2 при: а) х = 0,3; б) х = –6.
Вариант 2
1. Найдите значение выражения.а) ![]() + (0,6)2; б)
2000 · (0,3)4 – (–2)4; в)
+ (0,6)2; б)
2000 · (0,3)4 – (–2)4; в) ![]() – (–4)3.
– (–4)3.
2. Вычислите значение выражения х2 + х3 при:а) х = –0,4; б) х = 10.
Вариант 1
1. Найдите значение выражения. а) ![]() – (0,5)2; б) 3000 · (0,2)3
– (–2)6; в)
– (0,5)2; б) 3000 · (0,2)3
– (–2)6; в) ![]() – (–3)3.
– (–3)3.
2. Вычислите значение выражения х3 – х2 при: а) х = 0,3; б) х = –6.
Вариант 2
1. Найдите значение выражения.а) ![]() + (0,6)2; б)
2000 · (0,3)4 – (–2)4; в)
+ (0,6)2; б)
2000 · (0,3)4 – (–2)4; в) ![]() – (–4)3.
– (–4)3.
2. Вычислите значение выражения х2 + х3 при:а) х = –0,4; б) х = 10.
Урок 42 Умножение и деление степеней
Цели: продолжить формировать умение выполнять действия со степенями с одинаковыми основаниями.
Ход урока
I. Устная работа.
1. Найдите значение выражения.а) 43; б) (0,7)2; в)
![]() ; г) 012;
; г) 012;
д) (–6)2; е) (–0,3)4; ж)
(–1)8; з) ![]() .
.
2. Сравните с нулем значение выражения.а) (–25)12 · (–25)9;б) (–4)19 : (–4)7;в) (–12)13 · (–12)8.
3. Замените звездочку степенью с основанием а так, чтобы стало верным равенство:
а) а4 · * = а12; б) * · а = а4;в) а14 : * = а7; г) * : а9 = а10.
II. Формирование умений и навыков.
На этом занятии учащиеся отрабатывают умение делить степени с одинаковыми основаниями и решают комбинированные задачи.
1. № 414.
Решение:
а) x5 : x3 = x5 – 3 = x2; в) a21 : a = a21 – 1 = a20; з) 0,79 : 0,74 = 0,79 – 4 = 0,75.
2. № 416.
Решение:
а) 56 : 54 = 56 – 4 = 52 = 25; б) 1015 : 1012 = 1015 – 12 = 103 = 1000; в) 0,510 : 0,57 = 0,510 – 7 = 0,53 = 0,125;
г) ![]() ; д)
2,7313 : 2,7312 = 2,7313 – 12 = 2,73;
; д)
2,7313 : 2,7312 = 2,7313 – 12 = 2,73;
е) ![]() .
.
3. Используя правила умножения и деления степеней, упростите выражение.
а) x8 ∙ x3 : x5; б) x20 : x10 ∙ x; в) x7 : x3 : x3; г) x14 : x9 ∙ x5.
Решение:
а) x8 ∙ x3 : x5 = x8 + 3 : x5 = x11 : x5 = x11 – 5 = x6; б) x20 : x10 ∙ x = x20 – 10 ∙ x = x10 ∙ x = x10 + 1 = x11;
в) x7 : x3 : x3 = x7 – 3 : x3 = x4 : x3 = x4 – 3 = x; г) x14 : x9 ∙ x5 = x14 – 9 ∙ x5 = x5 ∙ x5 = x5 + 5 = x10.
4. № 417.
Решение:
а) ![]() = 86
: 84 = 86 – 4 = 82 = 64; б)
= 86
: 84 = 86 – 4 = 82 = 64; б) ![]() = 0,87 : 0,84
= 0,87 – 4 = 0,83 = 0,512;
= 0,87 : 0,84
= 0,87 – 4 = 0,83 = 0,512;
в) ![]() = (–0,3)5
: (–0,3)3 = (–0,3)5 – 3 = (–0,3)2 = 0,09; г)
= (–0,3)5
: (–0,3)3 = (–0,3)5 – 3 = (–0,3)2 = 0,09; г) 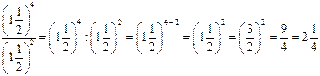 ;
;
д) 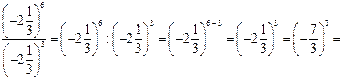
![]() .
.
5. Найдите значение выражения.
а) ![]() ; б)
; б)
![]() ;
;
в) ![]() ; г)
; г)
![]() .
.
При выполнении этого упражнения уже не обязательно переписывать дробь в виде частного.
Желательно, чтобы учащиеся проговаривали не только правила действий над степенями, но и правила возведения в степень отрицательного числа при четном нечетном показателях.
Решение:
а) 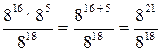 = 821
– 18 = 83 = 512;
= 821
– 18 = 83 = 512;
б) 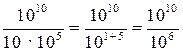 = 1010
– 6 = 104 = 10 000;
= 1010
– 6 = 104 = 10 000;
в) 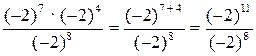 = (–2)11
– 8 = (–2)3 = –8;
= (–2)11
– 8 = (–2)3 = –8;
г) 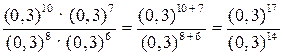 = (0,3)17
– 14 = (0,3)3 = 0,027.
= (0,3)17
– 14 = (0,3)3 = 0,027.
6. № 419 (а, в, д).
Решение:
а) xn ∙ x3 = xn + 3;
в) x ∙ xn = x1 + n = xn + 1;
д) c9 : cm = c9 – m.
7. Представьте данное выражение сначала в виде произведения степеней, а затем в виде частного степеней.
а) am – 2; б) a4n; в) an.
Решение:
а) am – 2 = am – 4 ∙ a2; am – 2 = am : a2;
б) a4n = a2n ∙ a2n; a4n = a5n : an;
в) an = an – 1 ∙ a; an = a2n : an.
Выполняя это упражнение, учащиеся могут предложить свои варианты разбиения на множители.
8. № 420 (а, в), № 421 (а, б).
№ 420.
Решение:
а) если х = 2,6, то 3х0 = 3 (при любом значении х);
в) 10a2b0 = 10a2, если а = 3, b = –8, то 10a2 = 10 · 32 = 10 · 9 = 90.
№ 421.
Решение:
а) b4 · b0 = b4 · 1 = b4; б) c5 : c0 = c5 : 1 = c5.
При выполнении этого упражнения учащиеся могут воспользоваться правилом умножения и деления степеней.
III. Итоги урока.
– Дайте определение степени с натуральным показателем.
– Сформулируйте правило возведения отрицательного числа в четную степень, в нечетную степень.
– Какой знак имеет результат возведения любого числа в квадрат?
– Сформулируйте правила сложения и умножения степеней с одинаковыми основаниями.
– Чему равно значение выражения 20; (–1)1; 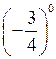 ?
?
Домашнее задание: № 415; № 418; № 419 (б, г, е); № 420 (б,
г);
№ 421 (в, г); № 422.
Урок 43
Умножение и деление степеней
Цель: формировать умение использовать правила умножения и деления степеней с одинаковыми основаниями при решении практических задач.
Ход урока
I. Проверочная работа.
Вариант 1
1. Представьте в виде степени произведение.
а) x6 ∙ x3 ∙ x7; б) (–7)3 ∙ (–7)2 ∙ (–7)9.
2. Представьте в виде степени частное.
а) x8 : x4; б) (–0,5)6 : (–0,5)8.
3. Найдите значение выражения.
а) 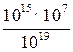 ; б)
; б)
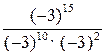 .
.
Вариант 2
1. Представьте в виде степени произведение.
а) y5 ∙ y9 ∙ y2; б) (–6)8 ∙ (–6)2 ∙ (–6)3.
2. Представьте в виде степени частное.
а) z10 : z7; б)
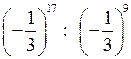 .
.
3. Найдите значение выражения.
а) 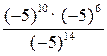 ; б)
; б)
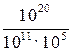 .
.
II. Мотивация изучения.
Данная тема предоставляет учителю возможность познакомить детей с числовыми величинами, которыми можно выразить количественные отношения реального мира. В этом плане особенно важны задачи, содержащие реальные величины, например задачи о Солнечной системе, планетах и других космических телах.
Полезно ознакомить учащихся с названиями классов принятой десятичной нумерации:
|
103 – тысяча 106 – миллион 109 – биллион (миллиард) 1012 – триллион 1015 – квадриллион 1018 – квинтиллион 1021 – секстиллион 1024 – септиллион 1027 – октиллион |
1030 – нониллион 1033 – дециллион 1036 – андециллион 1039 – дуодециллион 1042 – тредециллион 1045 – кваттордециллион 10100 – гугол |
Интересно для сравнения привести наименования классов старинной русской нумерации. Л. Магницкий в своей «Арифметике», изданной при Петре I, упоминает такие названия:
103 – тысяча
104 – тьма
105 – легион
106 – леодр
107 – вран
108 – колода.
Операции с числовыми великанами делают актуальными приближенные вычисления. Если исходные данные в задаче получены в результате измерений (например, астрономических) с точностью до 2–3 десятичных знаков, нет никакого смысла в последующих десятках цифр. Поэтому в этой теме уместно познакомить детей с правилами округления чисел.
III. Формирование умений и навыков.
1. Найдите отношение массы каждой из планет Солнечной системы к массе Земли.
Справка.
|
Планета |
Солнце |
Меркурий |
Венера |
Земля |
Марс |
|
масса, кг |
2 · 1030 |
3,4 · 1023 |
4,9 · 1024 |
6 · 1024 |
6,4 · 1023 |
|
Планета |
Юпитер |
Сатурн |
Уран |
Нептун |
Плутон |
|
масса, кг |
1,9 · 1027 |
5,7 · 1026 |
8,8 · 1025 |
1,0 · 1026 |
1,1 · 1021 |
2. В астрономии одной из единиц длины является световой год,
то есть расстояние, которое проходит за год луч света. Скорость света
с = 300 000 км/с. Вычислите:
а) за какое время луч света доходит от Земли до Луны, от Солнца до Земли; б) величину светового года в километрах; в) расстояние от Земли до звезды Сириус в световых годах.
Справка. Среднее расстояние от Земли до Луны 384 000 км, от Земли до звезды Сириус 8,2 · 1013 км.
3. Ежегодно прирост древесины на опытном участке составляет 10 %. Какое количество древесины будет на участке через 10 лет, если сейчас её 105 м3?
4. В сберегательном банке вкладчику начисляется 20 % в год от сданной на хранение суммы. Через сколько лет первоначальная сумма увеличится более чем в 2 раза; в 5 раз?
5. Найдите массу мотка медной проволоки сечением 2 мм и длиной 50 м.
Справка. Масса вычисляется по формуле m = ρ ∙ V, где ρ – плотность вещества. В частности, для меди ρ = 8,9 г/см3. А для вычисления объема цилиндра V нужно воспользоваться формулой V = πR2H.
6*. Какое наибольшее число абонентов может быть прикреплено к одной АТС при семизначной записи номеров телефона? Первые три цифры всех номеров данной АТС одинаковы.
IV. Итоги урока.
– Сформулируйте определение степени с натуральным показателем.
– В каких областях используются вычисления больших степеней числа 10?
Домашнее задание: 1. Во сколько раз число 4,8 · 1019 больше числа 1,2 · 1019?
2. Найдите расстояние от Солнца до планет Солнечной системы в астрономических единицах.
Справка.
|
Планета |
Меркурий |
Венера |
Земля |
Марс |
Юпитер |
Сатурн |
Уран |
Нептун |
Плутон |
|
Среднее
|
58 |
108 |
150 |
228 |
778 |
1430 |
2870 |
4500 |
5900 |
Астрономическая единица (а. е.) – среднее расстояние от Солнца до Земли.
3. № 542; № 543.
Вариант 1
1. Представьте в виде степени произведение. а) x6 ∙ x3 ∙ x7; б) (–7)3 ∙ (–7)2 ∙ (–7)9.
2. Представьте в виде степени частное. а) x8 : x4; б) (–0,5)6 : (–0,5)8.
3. Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Вариант 2
1. Представьте в виде степени произведение. а) y5 ∙ y9 ∙ y2; б) (–6)8 ∙ (–6)2 ∙ (–6)3.
2. Представьте в виде степени частное. а) z10 : z7;
б) ![]() .
.
3. Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Вариант 1
1. Представьте в виде степени произведение. а) x6 ∙ x3 ∙ x7; б) (–7)3 ∙ (–7)2 ∙ (–7)9.
2. Представьте в виде степени частное. а) x8 : x4; б) (–0,5)6 : (–0,5)8.
3. Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Вариант 2
1. Представьте в виде степени произведение. а) y5 ∙ y9 ∙ y2; б) (–6)8 ∙ (–6)2 ∙ (–6)3.
2. Представьте в виде степени частное. а) z10 : z7;
б) ![]() .
.
3.
Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Вариант 1
1. Представьте в виде степени произведение. а) x6 ∙ x3 ∙ x7; б) (–7)3 ∙ (–7)2 ∙ (–7)9.
2. Представьте в виде степени частное. а) x8 : x4; б) (–0,5)6 : (–0,5)8.
3. Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Вариант 2
1. Представьте в виде степени произведение. а) y5 ∙ y9 ∙ y2; б) (–6)8 ∙ (–6)2 ∙ (–6)3.
2. Представьте в виде степени частное. а) z10 : z7;
б) ![]() .
.
3.
Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Вариант 1
1. Представьте в виде степени произведение. а) x6 ∙ x3 ∙ x7; б) (–7)3 ∙ (–7)2 ∙ (–7)9.
2. Представьте в виде степени частное. а) x8 : x4; б) (–0,5)6 : (–0,5)8.
3. Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Вариант 2
1. Представьте в виде степени произведение. а) y5 ∙ y9 ∙ y2; б) (–6)8 ∙ (–6)2 ∙ (–6)3.
2. Представьте в виде степени частное. а) z10 : z7;
б) ![]() .
.
3.
Найдите значение выражения.а) ![]() ; б)
; б) ![]() .
.
Урок 44
Возведение в степень произведения и степени
Цели: вывести правило возведения в степень произведения двух и более сомножителей; формировать умение вычислять степень произведения, а также рационально преобразовывать выражения, содержащие степень произведения либо предполагающие использование данного свойства.
Ход урока
I. Организационный момент
Устная работа.
Вычислите.
а) 23 · 53; в) 122;
д) 53 · ![]() ; ж)
(bx)5;
; ж)
(bx)5;
б) 103; г) 32 · 42; е) (2а)3; з) (ab)n.
II. Объяснение нового материала.
|
(ab)n = anbn. |
|
|
Для любых а и b и произвольного натурального п верно равенство (ab)n = anbn. |
||
Доказательство:
(ab)n = (ab) · (ab) · ... · (ab) по определению степени п раз;
(ab) · (ab) · ... · (ab) = (aa...a)(bb...b) по свойствам умножения п раз п раз; (ab)n = anbn.
Вывод:
1) каждый множитель возводить в эту степень;
2) результаты перемножить.
Пример:
(abсd)4 = ...
Решение:
(abcd)4 = a4b4c4d4.
Рассмотреть пример 1 со с. 97 учебника.
III. Формирование умений и навыков.
1. № 428.
2. Выполните возведение в степень, представив предварительно основание степени в виде произведения множителей –1 и х:
а) (–х)2; б) (–х)8; в) (–х)100; г) (–х)2п;
д) (–х)3; е) (–х)9; ж) (–х)71; з) (–х)2п + 1.
Решение:
а) (–х)2 = ((–1) · х)2 = (–1)2 · х2 = 1 · х2 = х2;
е) (–х)9 = ((–1) · х)9 = (–1)9 · х9 = –1 · х9 = –х9;
г) (–х)2п = ((–1) · х)2п = (–1)2п · х2п = 1 · х2п = х2п;
з) (–х)2п + 1 = ((–1) · х)2п + 1 = (–1)2п + 1 · х2п + 1 = –1 · х2п + 1 = –х2п + 1.
3. № 431.
Решение:
а и –а – противоположные числа.
а2;
(–а)2 = ((–1) · а)2 = (–1)2 · а2 = 1 · а2 = а2,
значит, а2 = (–а2).
4. № 432.
Решение:
|
|
Пусть а – сторона квадрата, тогда площадь квадрата равна а2. Если сторона квадрата увеличится в 2 раза, то станет равна 2а, а
его площадь будет равна (2а) · (2а) = |
Аналогично рассуждаем для остальных случаев.
5. № 433.
Решение:
|
|
Пусть а – ребро куба, тогда его объем равен а3. Если ребро увеличить в 3 раза, то объем куба будет вычисляться по
формуле (3а) · (3а) · (3а) = (3а)3 = |
6. № 434.
Для решения используем данные задачи № 432.
Решение:
Поверхность куба состоит из 6 квадратов площадью а2, то есть равна 6а2.
Если ребро куба увеличить в 3 раза, то площадь боковой грани составит 9а2, а общая площадь поверхности равна 6 · 9а2 или 54а2.
Новая площадь больше в 9 раз, значит, и краски потребуется в 9 раз больше, то есть 40 · 9 = 360 г. Следовательно, 350 г краски на хватит.
Ответ: не хватит.
7. Представьте произведение в виде степени.
а) x5y5; б) 36a2b2; в) 0,001x3c3;
г) –х3; д) –8х3; е) –32a5b5;
ж) x5y5z5; з) 0,027a3b3c3; и) ![]() x3a3z3.
x3a3z3.
8. Вычислите значение выражения, используя свойство степени произведения.
а) 53 · 23; в) (0,5)3 · 603;
б) ![]() · 204; г)
(1,2)4 ·
· 204; г)
(1,2)4 · 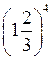 .
.
IV. Итоги урока.
– Сформулируйте определение степени с натуральным показателем.
– Сформулируйте правило возведения в степень произведения.
– Сколько сомножителей может стоять в формуле степени произведения?
– Чему равно значение выражения (3 · 5 · 78)0?
Домашнее задание: № 429; № 430; № 435; № 436; № 437.
Урок 45
Возведение в степень произведения и степени
Цели: вывести правило возведения степени в степень; формировать умение выполнять преобразование выражений, содержащих степень в степени.
Ход урока
I. Проверочная работа.
Вариант 1
1. Возведите в степень произведение. а) (xyz)8;
б) ![]() ; в) (–2а)3; г)
; в) (–2а)3; г)
![]() .
.
2. Вычислите значение выражения. а) 252 · 42;
б) ![]() · 93;
в) (–0,5)3 · 403.
· 93;
в) (–0,5)3 · 403.
Вариант 2
1. Возведите в степень произведение. а) (abc)10;
б) ![]() ; в) (–4а)3; г)
; в) (–4а)3; г)
![]() .
.
2. Вычислите значение выражения. а) 203 · 53;
б) ![]() · 252;
в) (–0,2)4 · 504.
· 252;
в) (–0,2)4 · 504.
II. Объяснение нового материала.
1. Устная работа.
Представьте в виде степени.
а) (а5)3 = а5 · а5 · а5 = … ; б) (у2)5 = … ;
в) (ат)7 = … ; г) (ат)п = … .
В результате появится запись:
|
(ат)п = ат п. |
2. Доказательство свойства можно оформить в виде таблицы.
Свойство. При возведении степени в степень основание оставляют тем же, а показатели перемножают.
|
(23)2 = 23 · 23 = |
|
|
по первому свойству степени |
|
|
= 23 + 3 = |
|
|
по определению умножения |
|
|
= 23 · 2 Итак, (23)2 = 23 · 2 |
= am · n
|
Подчеркиваем, что формулу можно применять в следующем виде:
|
(am)n = am n = an m = (an)m. |
III. Формирование умений и навыков.
1. № 438 (устно).
Решение:
а) (х3)2 = х3 · 2 = х6;
з) (b5)2 = b5 · 2 = b10.
2. № 440, № 441.
№ 441.
Решение:
а) ап · а3 = ап + 3;
г) (а2)т = а2т.
3. № 443, № 445, № 446.
№ 443.
Решение:
а) 220 = 22 · 10 = (22)10; б) 220 = 24 · 5 = (24)5;
в) 220 = 25 · 4 = (25)4; г) 220 = 210 · 2 = (210)2.
№ 445.
Решение:
12 = 1 · 12; а12 = (а1)12;
12 = 2 · 6; а12 = (а2)6;
12 = 3 · 4; а12 = (а3)4;
12 = 4 · 3; а12 = (а4)3;
12 = 6 · 2; а12 = (а6)2;
12 = 12 · 1; а12 = (а12)1.
№ 446. Решение:
а2 = т;
а6 = а2 · 3 = (а2)3 = т3.
4. Представьте выражение в виде квадрата числа.
а) а4; б) b6; в) d8; г) c10;
д) d20; е) ![]() ; ж) 1
; ж) 1![]() ; з)
; з)
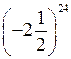 .
.
5. № 447, № 449 (а, б), № 450 (а, б).
№ 447.
Решение:
а) x3 · (x2)5 = x3 · x2 · 5 = x3 · x10 = x3 + 10 = x13;
б) (a3)2 · a5 = a3 · 2 · a5 = a6 · a5 = a6 + 5 = a11;
в) (a2)3 · (a4)2 = a2 · 3 · a4 · 2 = a6 · a8 = a6 + 8 = a14;
г) (x2)5 · (x5)2 = x2 · 5 · x5 · 2 = x10 · x10 = (x10)2 = x10 · 2 = x20;
д) (a3a3)2 = (a6)2 = a6 · 2 = a12;
е) (aa6)3 = a3 · (a6)3 = a3 · a6 · 3 = a3 · a18 = a3 + 18 = a21.
№ 449.
Решение:
а) x5 · (x2)3 = x5 · x6 = x11;
б) (x3)4 · x8 = x12 · x8 = x20.
№ 450.
Решение:
а) ![]() = 24
= 16;
= 24
= 16;
б) ![]() = 5.
= 5.
6. (Устно.) Найдите примеры, в которых допущена ошибка.
1) (ab)3 = a3b3; 5) (–32)3 = 36;
2) (–2bc)2 = –4b2c; 6) (c4)2c3 = c9;
3) (2 · 5)4 = 10000; 7) ![]() = a24;
= a24;
4) (–33)2 = 36; 8)
![]() = 26a6b14.
= 26a6b14.
IV. Итоги урока.
– Сформулируйте определение степени с натуральным показателем.
– Сформулируйте правило возведения степени в степень. приведите примеры.
– Каков алгоритм возведения степени в степень?
– Чему равно значение выражения: ![]() ; (x3)0?
; (x3)0?
Домашнее задание: № 439; № 442; № 444; № 448; № 449 (в, г);
№ 450 (в, г).
Вариант 1
1. Возведите в степень произведение. а) (xyz)8;
б) ![]() ; в)
(–2а)3; г)
; в)
(–2а)3; г) ![]() .
.
2. Вычислите значение выражения. а) 252
· 42; б) ![]() · 93; в) (–0,5)3
· 403.
· 93; в) (–0,5)3
· 403.
Вариант 2
1. Возведите в степень произведение. а)
(abc)10; б) ![]() ; в) (–4а)3; г)
; в) (–4а)3; г)
![]() .
.
2. Вычислите значение выражения. а) 203
· 53; б) ![]() · 252; в)
(–0,2)4 · 504.
· 252; в)
(–0,2)4 · 504.
Вариант 1
1. Возведите в степень произведение. а) (xyz)8;
б) ![]() ; в)
(–2а)3; г)
; в)
(–2а)3; г) ![]() .
.
2. Вычислите значение выражения. а) 252
· 42; б) ![]() · 93; в) (–0,5)3
· 403.
· 93; в) (–0,5)3
· 403.
Вариант 2
1. Возведите в степень произведение. а)
(abc)10; б) ![]() ; в) (–4а)3; г)
; в) (–4а)3; г)
![]() .
.
2. Вычислите значение выражения. а) 203
· 53; б) ![]() · 252; в)
(–0,2)4 · 504.
· 252; в)
(–0,2)4 · 504.
Вариант 1
1. Возведите в степень произведение. а) (xyz)8;
б) ![]() ; в)
(–2а)3; г)
; в)
(–2а)3; г) ![]() .
.
2. Вычислите значение выражения. а) 252
· 42; б) ![]() · 93; в) (–0,5)3
· 403.
· 93; в) (–0,5)3
· 403.
Вариант 2
1. Возведите в степень произведение. а)
(abc)10; б) ![]() ; в) (–4а)3; г)
; в) (–4а)3; г)
![]() .
.
2. Вычислите значение выражения. а) 203
· 53; б) ![]() · 252; в)
(–0,2)4 · 504.
· 252; в)
(–0,2)4 · 504.
Вариант 1
1. Возведите в степень произведение. а) (xyz)8;
б) ![]() ; в)
(–2а)3; г)
; в)
(–2а)3; г) ![]() .
.
2. Вычислите значение выражения. а) 252
· 42; б) ![]() · 93; в) (–0,5)3
· 403.
· 93; в) (–0,5)3
· 403.
Вариант 2
1. Возведите в степень произведение. а)
(abc)10; б) ![]() ; в) (–4а)3; г)
; в) (–4а)3; г)
![]() .
.
2. Вычислите значение выражения. а) 203
· 53; б) ![]() · 252; в)
(–0,2)4 · 504.
· 252; в)
(–0,2)4 · 504.
Вариант 1
1. Возведите в степень произведение. а) (xyz)8;
б) ![]() ; в)
(–2а)3; г)
; в)
(–2а)3; г) ![]() .
.
2. Вычислите значение выражения. а) 252
· 42; б) ![]() · 93; в) (–0,5)3
· 403.
· 93; в) (–0,5)3
· 403.
Вариант 2
1. Возведите в степень произведение. а)
(abc)10; б) ![]() ; в) (–4а)3; г)
; в) (–4а)3; г)
![]() .
.
2. Вычислите значение выражения. а) 203
· 53; б) ![]() · 252; в)
(–0,2)4 · 504.
· 252; в)
(–0,2)4 · 504.
Урок 46
Возведение в степень произведения и степени
Цели: обобщить знания по теме «Степень и её свойства»; закрепить умения преобразовывать числовые и буквенные выражения, содержащие степень.
Ход урока
I. Обобщение и систематизация материала.
Повторяем и систематизируем теоретический материал и практическую часть.
Дана таблица. В левом столбце заполнить пропущенные места, в правом – выполнить задания.
|
Степенью числа а с
натуральным Степень числа а с
показателем, |
1. Представьте в виде степени а) (–8) · (–8) · (–8) · (–8) · (–8)= б) (х – у) · (х – у) · (х – у) · (х – у)= 2. Возведите в степень: 34= (–0,2)5=
Назовите основание и показатель записанных степеней:
|
|
При умножении степеней с одина- |
Выполните действия: а4 · а12= b6 · b9 · b= 32 · 33= |
|
При делении степеней с
одинаковыми основаниями ________ оставляют |
Выполните действия: b8 : b2= n7 : n6= c9 : c= 57 : 54= |
|
При возведении степени в
степень |
Выполните действия: (m3)7= (k4)5= (22)3= |
|
При возведении в степень произведения возводят в эту степень _______________ и результаты перемножают |
Выполните возведение в степень: (–2a3b)5=
|
|
Степень числа а, не
равного нулю, |
Вычислите: при х = 2,6 3х0 = |
II. Закрепление умений и навыков.
Каждый учащийся выполняет задания, к ним прилагается ключ, в котором использован весь алфавит, чтобы исключить угадывание ответов по буквам. В случае правильного решения – правильное слово.
|
РОМАШКА
|
|
|
||||||
|
№ п/п |
Задание I ряд |
Ответ |
|
№ п/п |
Задания II ряд |
Ответ |
||
|
|
код |
|
|
код |
||||
|
1 |
т3 · т2 · т8 |
т13 |
У |
1 |
а4 · а3 · а2 |
а9 |
Г |
|
|
2 |
р20 : р17 |
р3 |
Н |
2 |
(24)5 : (27)2 |
64 |
Л |
|
|
3 |
с5 : с0 |
с5 |
И |
3 |
3 · 32 · 30 |
27 |
О |
|
|
4 |
(3а)3 |
27а3 |
К |
4 |
(2у)5 |
32у5 |
Б |
|
|
5 |
т · т5 · т3 · т0 |
т9 |
А |
5 |
(т2)4 · т |
т9 |
А |
|
|
6 |
214 : 28 |
64 |
Л |
6 |
(23)2 |
64 |
Л |
|
|
7 |
(–х)3 · х4 |
–х7 |
Ь |
7 |
(–х3) · (–х)4 |
–х7 |
Ь |
|
|
8 |
(р · р3)2 : р5 |
р3 |
Н |
8 |
(р2 · р5) · р0 : р4 |
р3 |
Н |
|
|
9 |
37 · (32)3 : 310 |
27 |
О |
9 |
(35)2 · 37 : 314 |
27 |
О |
|
|
№ п/п |
Задание III ряд |
Ответ |
|
|
|
код |
||
|
1 |
а4 · а · а3а |
а9 |
Г |
|
2 |
(7х)2 |
49х2 |
Е |
|
3 |
р · р2 · р0 |
р3 |
Н |
|
4 |
с · с3 · с |
с5 |
И |
|
5 |
т · т4 · (т2)2 · т0 |
т9 |
А |
|
6 |
(23)7 : (25)3 |
64 |
Л |
|
7 |
–х3 · (–х)4 |
–х7 |
Ь |
|
8 |
(р2)4 : р5 |
р3 |
Н |
|
9 |
(34)2 · (32)3 : 311 |
27 |
О |
Ключ
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Л |
|
т9 |
32у5 |
81 |
а9 |
х3 |
49х2 |
т5 |
р4 |
с5 |
27а3 |
64 |
|
|
||||||||||
|
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
|
34 |
р3 |
27 |
25 |
х7 |
р6 |
т3 |
т13 |
а8 |
81а3 |
с7 |
|
|
||||||||||
|
Ч |
Ш |
Щ |
Ъ |
Ь |
Ы |
Э |
Ю |
Я |
|
|
|
16а4 |
25 |
10у5 |
9у7 |
–х7 |
а2 |
32х5 |
49у3 |
х5 |
|
|
III. Итоги урока.
Домашнее задание: № 534; № 535; № 539; № 547; № 548.
Математика –это
|
№ п/п |
Задание
|
Ответ |
|
№ п/п |
Задания
|
Ответ |
||
|
|
код |
|
|
код |
||||
|
1 |
т3 · т2 · т8 |
|
|
1 |
а4 · а3 · а2 |
|
|
|
|
2 |
р20 : р17 |
|
|
2 |
(24)5 : (27)2 |
|
|
|
|
3 |
с5 : с0 |
|
|
3 |
3 · 32 · 30 |
|
|
|
|
4 |
(3а)3 |
|
|
4 |
(2у)5 |
|
|
|
|
5 |
т · т5 · т3 · т0 |
|
|
5 |
(т2)4 · т |
|
|
|
|
6 |
214 : 28 |
|
|
6 |
(23)2 |
|
|
|
|
7 |
(–х)3 · х4 |
|
|
7 |
(–х3) · (–х)4 |
|
|
|
|
8 |
(р · р3)2 : р5 |
|
|
8 |
(р2 · р5) · р0 : р4 |
|
|
|
|
9 |
37 · (32)3 : 310 |
|
|
9 |
(35)2 · 37 : 314 |
|
|
|
|
№ п/п |
Задание
|
Ответ |
|
|
|
код |
||
|
1 |
а4 · а · а3а |
|
|
|
2 |
(7х)2 |
|
|
|
3 |
р · р2 · р0 |
|
|
|
4 |
с · с3 · с |
|
|
|
5 |
т · т4 · (т2)2 · т0 |
|
|
|
6 |
(23)7 : (25)3 |
|
|
|
7 |
–х3 · (–х)4 |
|
|
|
8 |
(р2)4 : р5 |
|
|
|
9 |
(34)2 · (32)3 : 311 |
|
|
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Л |
|
т9 |
32у5 |
81 |
а9 |
х3 |
49х2 |
т5 |
р4 |
с5 |
27а3 |
64 |
|
|
||||||||||
|
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
|
34 |
р3 |
27 |
25 |
х7 |
р6 |
т3 |
т13 |
а8 |
81а3 |
с7 |
|
|
||||||||||
|
Ч |
Ш |
Щ |
Ъ |
Ь |
Ы |
Э |
Ю |
Я |
|
|
|
16а4 |
25 |
10у5 |
9у7 |
–х7 |
а2 |
32х5 |
49у3 |
х5 |
|
|
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Л |
|
т9 |
32у5 |
81 |
а9 |
х3 |
49х2 |
т5 |
р4 |
с5 |
27а3 |
64 |
|
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
|
34 |
р3 |
27 |
25 |
х7 |
р6 |
т3 |
т13 |
а8 |
81а3 |
с7 |
|
Ч |
Ш |
Щ |
Ъ |
Ь |
Ы |
Э |
Ю |
Я |
|
|
|
16а4 |
25 |
10у5 |
9у7 |
–х7 |
а2 |
32х5 |
49у3 |
х5 |
|
|
Математика –это
|
№
|
Задание
|
Ответ |
|
№
|
Задания |
Ответ |
||
|
|
код |
|
|
код |
||||
|
1 |
т3 · т2 · т8 |
|
|
1 |
а4 · а3 · а2 |
|
|
|
|
2 |
р20 : р17 |
|
|
2 |
(24)5 : (27)2 |
|
|
|
|
3 |
с5 : с0 |
|
|
3 |
3 · 32 · 30 |
|
|
|
|
4 |
(3а)3 |
|
|
4 |
(2у)5 |
|
|
|
|
5 |
т · т5 · т3 · т0 |
|
|
5 |
(т2)4 · т |
|
|
|
|
6 |
214 : 28 |
|
|
6 |
(23)2 |
|
|
|
|
7 |
(–х)3 · х4 |
|
|
7 |
(–х3) · (–х)4 |
|
|
|
|
8 |
(р · р3)2 : р5 |
|
|
8 |
(р2 · р5) · р0 : р4 |
|
|
|
|
9 |
37 · (32)3 : 310 |
|
|
9 |
(35)2 · 37 : 314 |
|
|
|
|
№ п/п |
Задание
|
Ответ |
|
|
|
код |
||
|
1 |
а4 · а · а3а |
|
|
|
2 |
(7х)2 |
|
|
|
3 |
р · р2 · р0 |
|
|
|
4 |
с · с3 · с |
|
|
|
5 |
т · т4 · (т2)2 · т0 |
|
|
|
6 |
(23)7 : (25)3 |
|
|
|
7 |
–х3 · (–х)4 |
|
|
|
8 |
(р2)4 : р5 |
|
|
|
9 |
(34)2 · (32)3 : 311 |
|
|
|
Степенью числа а с
натуральным Степень числа а с
показателем, |
1. Представьте в виде степени а) (–8) · (–8) · (–8) · (–8) · (–8)= б) (х – у) · (х – у) · (х – у) · (х – у)= 2. Возведите в степень: 34= (–0,2)5=
|
|
При умножении степеней с
одина- |
Выполните действия: а4 · а12= b6 · b9 · b= 32 · 33= |
|
При делении степеней с одинаковыми основаниями ________ оставляют прежним, а из ______ числителя _________________ знаменателя |
Выполните действия: b8 : b2= n7 : n6= c9 : c= 57 : 54= |
|
При возведении степени в
степень |
Выполните действия: (m3)7= (k4)5= (22)3= |
|
При возведении в степень произведения возводят в эту степень _______________ и результаты перемножают |
Выполните возведение в степень: (–2a3b)5=
|
|
Степень числа а, не
равного нулю, |
Вычислите: при х = 2,6 3х0 = |
|
Степенью числа а с
натуральным Степень числа а с
показателем, |
1. Представьте в виде степени а) (–8) · (–8) · (–8) · (–8) · (–8)= б) (х – у) · (х – у) · (х – у) · (х – у)= 2. Возведите в степень: 34= (–0,2)5=
|
|
При умножении степеней с
одина- |
Выполните действия: а4 · а12= b6 · b9 · b= 32 · 33= |
|
При делении степеней с одинаковыми основаниями ________ оставляют прежним, а из ______ числителя _________________ знаменателя |
Выполните действия: b8 : b2= n7 : n6= c9 : c= 57 : 54= |
|
При возведении степени в
степень |
Выполните действия: (m3)7= (k4)5= (22)3= |
|
При возведении в степень произведения возводят в эту степень _______________ и результаты перемножают |
Выполните возведение в степень: (–2a3b)5=
|
|
Степень числа а, не
равного нулю, |
Вычислите: при х = 2,6 3х0 = |
|
Степенью числа а с
натуральным Степень числа а с
показателем, |
1. Представьте в виде степени а) (–8) · (–8) · (–8) · (–8) · (–8)= б) (х – у) · (х – у) · (х – у) · (х – у)= 2. Возведите в степень: 34= (–0,2)5=
|
|
При умножении степеней с
одина- |
Выполните действия: а4 · а12= b6 · b9 · b= 32 · 33= |
|
При делении степеней с одинаковыми основаниями ________ оставляют прежним, а из ______ числителя _________________ знаменателя |
Выполните действия: b8 : b2= n7 : n6= c9 : c= 57 : 54= |
|
При возведении степени в
степень |
Выполните действия: (m3)7= (k4)5= (22)3= |
|
При возведении в степень произведения возводят в эту степень _______________ и результаты перемножают |
Выполните возведение в степень: (–2a3b)5=
|
|
Степень числа а, не
равного нулю, |
Вычислите: при х = 2,6 3х0 = |
|
Степенью числа а с
натуральным Степень числа а с
показателем, |
1. Представьте в виде степени а) (–8) · (–8) · (–8) · (–8) · (–8)= б) (х – у) · (х – у) · (х – у) · (х – у)= 2. Возведите в степень: 34= (–0,2)5=
|
|
При умножении степеней с
одина- |
Выполните действия: а4 · а12= b6 · b9 · b= 32 · 33= |
|
При делении степеней с одинаковыми основаниями ________ оставляют прежним, а из ______ числителя _________________ знаменателя |
Выполните действия: b8 : b2= n7 : n6= c9 : c= 57 : 54= |
|
При возведении степени в
степень |
Выполните действия: (m3)7= (k4)5= (22)3= |
|
При возведении в степень произведения возводят в эту степень _______________ и результаты перемножают |
Выполните возведение в степень: (–2a3b)5=
|
|
Степень числа а, не
равного нулю, |
Вычислите: при х = 2,6 3х0 = |
Урок 47
Одночлены и его стандартный вид
Цели: ввести понятие одночлена и его стандартного вида; формировать умение приводить одночлен к стандартному виду путем его упрощения; формировать умение определять коэффициент и степень одночлена.
Ход урока
I. Устная работа.
1. Упростите выражение.
а) х3 · (–х4); б) х3 · (–х)4; в) (–х)3 · х4;
г) (–х3) · (–х)4; д) (а2)5 · а5; е) (а2 · а5)2.
2. Выполняя задания на преобразование выражений, содержащих степени, ученик допустил следующие ошибки:
а) 5 · 5 · 5 · 5 = 45; б) (–3)2 = –3 · 3 = –9; в) 71 = 1;
г) 00 = 1; д) 23 · 27 = 221; е) 23 · 28 = 410;
ж) 23 + 27 = 210; з) 230 : 210 = 23; и) (2х)3 = 2х3;
к) (а3)2 = а9; л) (а2)3 · (а4)2 = (а6)5 = а30.
Какие определения, свойства, правила не знает ученик?
II. Объяснение нового материала.
1. При решении различных задач часто встречаются алгебраические выражения
вида a · b; ![]() · a · b · c; 3 · a2
· b. Для сокращения записи этих выражений знак умножения «точка» обычно
опускается, то есть пишут просто ab;
· a · b · c; 3 · a2
· b. Для сокращения записи этих выражений знак умножения «точка» обычно
опускается, то есть пишут просто ab; ![]() abc; 3a2b.
Каждое из этих произведений называют одночленом.
abc; 3a2b.
Каждое из этих произведений называют одночленом.
На доску выносится запись:
|
Произведение нескольких чисел, обозначенных цифрами или буквами, называют одночленом. |
Например, одночленами являются выражения:
abc; (–4)a3ab; ![]() a(–0,3)bab; 172; –
a(–0,3)bab; 172; –![]() .
.
Так как произведение равных множителей можно записать в виде степени с натуральным показателем, то степень числа и произведение степеней чисел также называют одночленами.
Например: ![]() ; (–7)3; c5;
4a2;
; (–7)3; c5;
4a2; ![]() a2b.
a2b.
Множители одночлена, записанные с помощью цифр, называют числовыми множителями одночлена, а множители, обозначенные буквами, называют буквенными множителями.
2. Одночлены можно упрощать, пользуясь переместительным и сочетательным законами умножения.
|
Стандартным видом одночлена называется его запись, когда на первом месте стоит числовой коэффициент, а затем степени различных переменных. |
Обращаем внимание учащихся, что коэффициент одночлена может быть равен единице, в этом случае мы его не пишем перед буквенной частью. Переменные принято записывать в алфавитном порядке, то есть не 3x2a4c, а 3a4cx2.
3. Вводим понятие степени одночлена.
|
Степенью одночлена называют сумму показателей степеней всех входящих в него переменных. Если одночлен не содержит переменных и является числом, отличным от нуля, то степень этого одночлена считают равной нулю. Число 0 является одночленом, степень которого не определена. |
III. Формирование умений и навыков.
На этом занятии необходимо отработать следующие умения:
1) выявлять одночлен, используя определения;
2) выделять элементы одночлена: числовой коэффициент и буквенную часть;
3) определять, записан ли одночлен в стандартном виде;
4) приводить одночлен к стандартному виду;
5) вычислять значение одночлена в стандартном виде;
6) определять степень одночлена стандартного вида.
1. (Устно). Назовите числовые и буквенные множители одночлена.
а) 6a(0,3)b2c; в) 3p(–0,1)q7r;
б) 0,5a![]() b3c; г)
2,5m
b3c; г)
2,5m![]() n4k.
n4k.
2. № 455 (устно).
3. Вместо словесной формулировки запишите алгебраическое выражение:
а) удвоенное произведение чисел a и b;
б) утроенное произведение чисел b и с;
в) произведение квадратов чисел х и у;
г) произведение числа а и квадрата числа b;
д) произведение куба числа т и числа р;
е) утроенное произведение квадрата числа а и числа b.
4. № 456 (устно).
При выполнении этого упражнения ученики должны мотивировать свой ответ.
5. Среди одночленов 10,2a2b2c;
–7,3ab2c; 17a2bca; –2,6ab2c;
–m; 3ab; –28a2b2c2;
3aabc; –2a![]() b; –m4m; m ∙ 2; 17a2b2c2:
b; –m4m; m ∙ 2; 17a2b2c2:
а) назвать одночлены стандартного вида;
б) указать одночлены, отличающиеся только коэффициентами.
6. № 457.
Решение:
а) 8x2x = 8x2 + 1 = 8x3; б) 1,2abc ∙ 5a = (1,2 ∙ 5) ∙ (a ∙ a) ∙ bc = 6a2bc;
в) 3xy(–1,7)y = 3 ∙ (–1,7) ∙ x ∙ y ∙ y = –5,1xy2; г) 6c2(–0,8)c = 6(–0,8)c2c = –4,8c3;
д) ![]() m2n
∙ 4,5n3 =
m2n
∙ 4,5n3 = ![]() ∙ m2
∙ n ∙ n3 = 3m2n4;
е)
∙ m2
∙ n ∙ n3 = 3m2n4;
е) 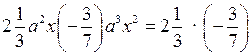 a2a3xx2 =
–a5x3.
a2a3xx2 =
–a5x3.
7. № 459.
Решение:
а) если у = –2, то –0,125у4 = –0,125 · (–2)4 = –0,125 · 16 = –2;
б) если х = –0,3, у = ![]() , то 12x2y = 12 ·
(–0,3)2 ·
, то 12x2y = 12 ·
(–0,3)2 · ![]() = 2 · 0,09 = 0,18.
= 2 · 0,09 = 0,18.
Ответ: а) –2; б) 0,18.
8. № 461.
Решение:
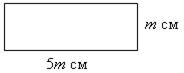 S
= 5m · m = 5m2 (см2).
S
= 5m · m = 5m2 (см2).
Ответ: 5m2 (см2).
9. Запишите одночлен в стандартном виде и определите его степень.
а) ac12c; г) ![]() · 4; б)
· 4; б) ![]() a8b2
a8b2![]() ba3; д)
–
ba3; д)
–![]() m3np;
m3np;
в) –0,5xy2![]() x3; е)
x3; е)
![]() a3d0x.
a3d0x.
IV. Итоги урока.
Домашнее задание: № 458; № 460; № 462; № 463; № 554; № 555.
Урок 48
Умножение одночленов
Цель: формировать умение умножать одночлен на одночлен, используя правило умножения степеней с одинаковыми основаниями.
Ход урока
I. Устная работа.
1. Назовите коэффициент одночлена.
а) 15a2b2c; б) 18a3b2c; в) –24ab2c3; г) –35ab3c2;д) nm2; е) n3m; ж) –pqr2; з) –pq2r.
2. Определите степень одночлена.
а) 37a2bx3; б) ![]() xyz; в)
xyz; в)
![]() x2y; г)
–862.
x2y; г)
–862.
III. Объяснение нового материала.
1. Решим следующую задачу.
Объем прямоугольного параллелепипеда вычисляется по формуле
V = abc, где а – длина, b – ширина и с –
высота этого параллелепипеда.
Каким будет объем нового параллелепипеда, если длину данного увеличить в 5 раз, ширину – в 2п раз, высоту в 3п раз?
Решение:
Найдем измерения нового параллелепипеда:
длина – 5а;
ширина – 2пb;
высота – 3пс.
Тогда его объем равен (5а) · (2пb) · (3пс). Данное выражение является произведением трех одночленов. По правилам умножения можно записать равенство:
(5а) · (2пb) · (3пс) = 5а · 2пb · 3пс
= (5 · 2 · 3) · (аппbс) = 30ап2bс =
= 30аbсп2.
2. В результате умножения одночленов снова получается одночлен, который можно упростить, записав в стандартном виде:
(3a2b3c) · (4ab2) = (3 · 4) · (a2a) · (b3b2) · c = 12a3b5c.
3. Аналогично находим произведение трех и более одночленов.
IV. Формирование умений и навыков.
На уроке отрабатываются умения перемножать одночлены и раскладывать одночлен в виде произведения двух и более одночленов.
1. Выполните умножение.
1) а) 12у · 0,5у; б) 8x · 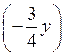 ; в) –b3
· 3b2;
; в) –b3
· 3b2;
2) а) ![]() xy2
· 16y; б) 1,6a2c · (–2ac2); в)
–x3y4 · 1,4x6y5.
xy2
· 16y; б) 1,6a2c · (–2ac2); в)
–x3y4 · 1,4x6y5.
Решение:
1) а) 12у · 0,5у = (12 · 0,5) (у · у) = 6у2;
б) 8x2 · ![]() (x2y) = –6x2y;
в) –b3 · 3b2 = (–1 · 3)(b3b2)
= –3b5;
(x2y) = –6x2y;
в) –b3 · 3b2 = (–1 · 3)(b3b2)
= –3b5;
2) а) ![]() xy2 · 16y =
xy2 · 16y = ![]() (xy2y)
= 12xy3; б) 1,6a2c
· (–2ac2) = (1,6 (–2))(a2cac2)
= –3,2a3c3;
(xy2y)
= 12xy3; б) 1,6a2c
· (–2ac2) = (1,6 (–2))(a2cac2)
= –3,2a3c3;
в) –x3y4 · 1,4x6y5 = (–1 · 1,4)(x3y4x6y5) = –1,4x9y9.
2. Перемножьте одночлены.
а) (–0,4x5y6z2) ·
(–1,2xyz3); б) (–2,5n4m5k2)
· (3nm2k5); в) ![]() ;г)
;г) ![]() .
.
Решение:
а) (–0,4x5y6z2) ·
(–1,2xyz3) = (–0,4 · (–1,2)) · (x5x)
· (y6y) · (z2z3) =
= 0,48x6y7z5;
б) (–2,5n4m5k2) · (3nm2k5) = (–2,5 · 3) · (n4n) · (m5m2) · (k2k5) = 7,5n5m7k7;
в) ![]() · (x2x)
· (y3y2) · (zz3) =
· (x2x)
· (y3y2) · (zz3) =
= 2x3y5z4;
г) ![]() · (a2a3)
· (b5b2) · (c3c4)
=
· (a2a3)
· (b5b2) · (c3c4)
=
= –7,5a5b7c7.
3. Перемножьте одночлены.
1) –20х4, 0,5ху2 и –0,3х2у3;
2) 12x2y2z, ![]() xy2z2
и –0,1x2yz2.
xy2z2
и –0,1x2yz2.
Решение:
1) (–20x4) · (0,5xy2)
· (–0,3x2y3) = (–20 · 0,5 · (–0,3)) · (x4xx2)
· (y2y3) =
= 3x7y5;
2) (12x2y2z)
· 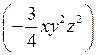 · (–0,1x2yz2) =
· (–0,1x2yz2) = 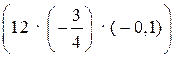 · (x2xx2)
×
· (x2xx2)
×
× (y2y2y)
· (zz2z2) = 0,9x5y5z5.
4. Выполните умножение.
а) (–a) · (3b) · (4a2b)
· (5ab2); б) (5a) · (a2b2)
· (–2b) · (–3a); в) (–1,5ab) · ![]() · (–2ac)
· (24ab).
· (–2ac)
· (24ab).
Решение:
а) (–a) · (3b) · (4a2b) · (5ab2) = (–1 · 3 · 4 · 5) · (aa2a) · (bbb2) = –60a4b4;
б) (5a) · (a2b2) · (–2b) · (–3a) = (5 · 1 · (–2) · (–3)) · (aa2a) · (b2b) = 30a4b3;
в) (–1,5ab) · ![]() · (–2ac) · (24ab)
=
· (–2ac) · (24ab)
= ![]() ×
×
× (aaa) · (bbb) · (cc) = 18a3b3c2.
V. Итоги урока.
Урок 49
Возведение одночлена в степень
Цели: формировать умение возводить одночлен в степень и приводить его к стандартному виду.
Ход урока
I. Организационный момент
II. Объяснение нового материала.
1. Актуализация знаний.
Выполните устно умножение одночленов.
а) a3 ∙ a4;б) a ∙ ![]() a2; в) –a
∙ a2 ∙ a4;г) a ∙ (–x); д) (–x)
∙ (–y); е) (–x) ∙
a2; в) –a
∙ a2 ∙ a4;г) a ∙ (–x); д) (–x)
∙ (–y); е) (–x) ∙ 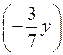 ;
;
ж) (–2a) ∙ a2; з) b2 ∙ (–3b3); и) ![]() ∙ 6y;к) (0,2a)
∙ (–5b);л)
∙ 6y;к) (0,2a)
∙ (–5b);л) 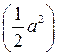 ∙ (–4ab); м) (–8m3) ∙ (–0,5n).
∙ (–4ab); м) (–8m3) ∙ (–0,5n).
2. Теперь рассмотрим произведение двух или нескольких одинаковых одночленов, то есть степень одночлена. Например, (5a3b2c)2. Так как этот одночлен является произведением чисел 5, a3, b2, c, то по свойству возведения в степень произведения имеем:
(5a3b2c)2 = 52(a3)2(b2)2c2 = 25a6b4c2.
В результате возведения одночлена в натуральную степень снова получается одночлен.
III. Формирование умений и навыков.
1. № 472.
Решение:
а) ![]() ;б)
;б) ![]() ;в)
;в) ![]() ;
;
г) ![]() ;д)
;д) ![]() ;
;
е) ![]() .
.
2. Выполните возведение одночлена в степень.
1) а) (6y)2; б) 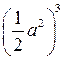 ; в) (0,1c5)4;
; в) (0,1c5)4;
2) а) (5ax)3; б) (4ac4)3; в) (5x5y3)3;
3) а) 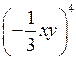 ; б)
(–10x2y6)3; в) (–a2b3c4)7;
; б)
(–10x2y6)3; в) (–a2b3c4)7;
4) а) –(3a2b)3; б) –(–2ab4)3; в) –(–a3b2c)4.
Решение:
1) а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() .
.
2) а) ![]() ;
б)
;
б) ![]() ;
;
в) ![]() .
.
3) а) 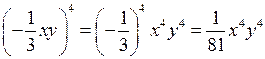 ;
б)
;
б) ![]() ;
;
в) ![]() .
.
4) а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
3. № 475, № 477.
№ 475.
Решение:
а) ![]() ;б)
;б)![]() ;
;
в) ![]() ;г)
;г) ![]() .
.
№ 477.
Решение:
а) ![]() ;
; ![]() ;
;
б) ![]() ;
; ![]() .
.
4. № 479.
Решение:
а) ![]() ;
; ![]() .
.
б) ![]() ;
; ![]() .
.
5. Упростите выражение.
1) а) 35a ∙ (2a)2; б) –4x3 ∙ (5x2)3; в) (–4y2)3 ∙ y5;
2) а) 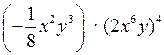 ; б)
; б)
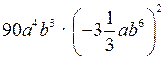 .
.
Решение:
1) а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
2) а) 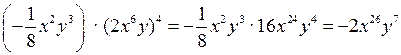 ;
;
б) 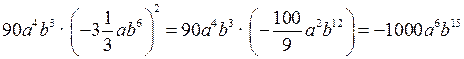 .
.
IV. Проверочная работа.
Вариант 1
Выполните действия.
1) ![]() ∙
(–24n) ∙ (4mn); 2)
∙
(–24n) ∙ (4mn); 2) ![]() ; 3) (0,1a3b3)3.
; 3) (0,1a3b3)3.
Вариант 2
Выполните действия.
1) (–18n) ∙ ![]() ∙ (–5mn); 2)
∙ (–5mn); 2) ![]() ; 3)
(0,4a3b2)2.
; 3)
(0,4a3b2)2.
V. Итоги урока.
– Дайте определение одночлена.
– В каком случае мы говорим, что одночлен задан в стандартном виде?
– Сформулируйте определение степени одночлена. Приведите пример.
– Каким образом можно умножить одночлен на одночлен? Что получится в результате?
– Как возвести одночлен в степень? На какое правило мы при этом опираемся?
Домашнее задание: № 473; № 474; № 476; № 478; № 480.
Вариант 1
Выполните действия.
1) ![]() ∙
(–24n) ∙ (4mn); 2)
∙
(–24n) ∙ (4mn); 2) ![]() ; 3) (0,1a3b3)3.
; 3) (0,1a3b3)3.
Вариант 2
Выполните действия.
1) (–18n) ∙ ![]() ∙ (–5mn); 2)
∙ (–5mn); 2) ![]() ; 3)
(0,4a3b2)2.
; 3)
(0,4a3b2)2.
Вариант 1
Выполните действия.
1) ![]() ∙
(–24n) ∙ (4mn); 2)
∙
(–24n) ∙ (4mn); 2) ![]() ; 3) (0,1a3b3)3.
; 3) (0,1a3b3)3.
Вариант 2
Выполните действия.
1) (–18n) ∙ ![]() ∙ (–5mn); 2)
∙ (–5mn); 2) ![]() ; 3)
(0,4a3b2)2.
; 3)
(0,4a3b2)2.
Вариант 1
Выполните действия.
1) ![]() ∙
(–24n) ∙ (4mn); 2)
∙
(–24n) ∙ (4mn); 2) ![]() ; 3) (0,1a3b3)3.
; 3) (0,1a3b3)3.
Вариант 2
Выполните действия.
1) (–18n) ∙ ![]() ∙ (–5mn); 2)
∙ (–5mn); 2) ![]() ; 3)
(0,4a3b2)2.
; 3)
(0,4a3b2)2.
Вариант 1
Выполните действия.
1) ![]() ∙
(–24n) ∙ (4mn); 2)
∙
(–24n) ∙ (4mn); 2) ![]() ; 3) (0,1a3b3)3.
; 3) (0,1a3b3)3.
Вариант 2 Выполните действия.
1) (–18n) ∙ ![]() ∙ (–5mn); 2)
∙ (–5mn); 2) ![]() ; 3)
(0,4a3b2)2.
; 3)
(0,4a3b2)2.
Вариант 1 Выполните действия.
1) ![]() ∙
(–24n) ∙ (4mn); 2)
∙
(–24n) ∙ (4mn); 2) ![]() ; 3) (0,1a3b3)3.
; 3) (0,1a3b3)3.
Вариант 2 Выполните действия.
1) (–18n) ∙ ![]() ∙ (–5mn); 2)
∙ (–5mn); 2) ![]() ; 3)
(0,4a3b2)2.
; 3)
(0,4a3b2)2.
Вариант 1 Выполните действия.
1) ![]() ∙
(–24n) ∙ (4mn); 2)
∙
(–24n) ∙ (4mn); 2) ![]() ; 3) (0,1a3b3)3.
; 3) (0,1a3b3)3.
Урок 55
Функции y = x2
и у = х3
и их графики
Цели: изучить функциональные зависимости y = x2 и у = х3; формировать умение строить графики данных функций и работать с ними.
Ход урока
I. Устная работа.
1. Назовите область определения функции.
а) y = 3x; г) y = 2x2;ж) y
= ![]() ;б) y =
;б) y = ![]() ; д) y
=
; д) y
= ![]() х3; з)
y =
х3; з)
y = ![]() ;
;
в) y = –3x2 + 11; е) y = ![]() ; и) y
= (3 – x)(x + 6).
; и) y
= (3 – x)(x + 6).
2. Найдите значение функции y = x2 – 11, если:
а) х = 3; в) х = ![]() ;
;
б) х = 0; г) х = 0.
II. Объяснение нового материала.
Организуем самостоятельную работу по учебнику в парах.
С помощью учебника (пункт 23, с. 105–108) ответить на вопросы, описанные в таблице (см. далее), и сравнить две функции: в чем схожи и в чем их отличие.
|
Вопросы |
y = x2 |
y = x3 |
||||||||||||||||||||||||
|
Заполните таблицу |
|
|
||||||||||||||||||||||||
|
По данным таблицы построить график |
|
|
||||||||||||||||||||||||
|
Свойства функции |
1. 2. 3. |
1. 2. 3. |
||||||||||||||||||||||||
|
Функция возрастает |
|
|
||||||||||||||||||||||||
|
Функция убывает |
|
|
||||||||||||||||||||||||
|
Название графика |
|
|
III. Формирование умений и навыков.
1. № 484, № 485.
2. № 487. Решение:
а) А (6; 36) 36 = 62;
36 = 36 – верно, значит, принадлежит;
б) В (–1,5; 2,25) 2, 25 = (–1,5)2;
2,25 = 2,25 – верно, значит, принадлежит;
в) С (4; –2) –2 = 42;
–2 = 16 – неверно, значит, не принадлежит;
г) D (1,2; 1,44) 1,44 = (1,2)2;
1,44 = 1,44 – верно, значит, принадлежит.
Ответ: а) да; б) да; в) нет; г) да.
3. № 489.
4. № 490. Решение:
а) А (–0,2; –0,008) –0,008 = (–0,2)3;
–0,008 = –0,008 – верно, значит, принадлежит;
б) B 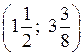
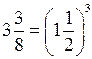 ;
;
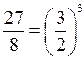 ;
;
![]() – верно, значит, принадлежит;
– верно, значит, принадлежит;
в) C 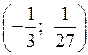
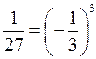 ;
;
![]() – неверно, значит, не принадлежит.
– неверно, значит, не принадлежит.
Ответ: а) да; б) да; в) нет.
5. № 491.
6. № 492. Решение:
а) Р (а; 64) 64 = а2;
82 = а2 – возможно в случае а = 8 или а = –8.
б) Р (а; 64) 64 = а3;
43 = а3 возможно в случае а = 4.
Ответ: а) 8; –8; б) 4.
IV. Итоги урока.
– Сформулируйте свойства функции y = x2. Как отражаются эти свойства на графике функции?
– Как называется график функции y = x2?
– Сформулируйте свойства графика функции y = x3. Как отражаются эти свойства на графике функции?
– Как называется график функции y = x3?
Домашнее задание: № 486; № 488; № 562; № 563.
Урок 51
Функции y = x2
и у = х3
и их графики
Цели: формировать понятие графического решения уравнения как нахождения абсциссы точек пересечения графиков двух функций; формировать умение решать графически уравнения вида у = х2 и у = х3.
Ход урока
I. Устная работа.
1. Заданы функции:
1) у = 2х; 4) у = 3х
+ 2; 7) у = ![]() ;
;
2) у = ![]() х; 5)
у = –3х + 2; 8) у = х2;
х; 5)
у = –3х + 2; 8) у = х2;
3) у = –3х; 6) у = –3х – 2; 9) у = х3.
На рисунках а) – и) изображены графики этих функций. Заполните таблицу соответствия:
|
Формула |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
График |
|
|
|
|
|
|
|
|
|
a) 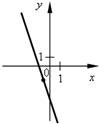 б)
б)
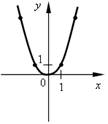 в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж)  з)
з)  и)
и) 
2. Как называется функция вида y = kx?
3. Как называется функция вида y = kx + b?
4. Как называется график функции y = x2?
5. Как называется график функции вида y = x3?
II. Актуализация знаний.
Решить уравнение.
а) x2 = 16; б) x3 = 8; в)
x2 = ![]() ;г) x3 =
;г) x3 = ![]() ; д) x2
= 0; е) x2 = –4.
; д) x2
= 0; е) x2 = –4.
III. Объяснение нового материала.
Необходимо разъяснить принцип графического решения уравнения.
Рассматриваем примеры 1, 2 со с. 109 учебника. Показываем, что равенство (аналитическое) x2 = x + 1 можно понимать как равенство значений двух функций y = x2 и y = x + 1. Графически, если графики этих функций пересекаются, то точка пересечения показывает значение х (абсцисса), при котором значения функций (ордината) равны.
алгоритм графического решения уравнения:
1-й шаг. Преобразовать уравнение к равенству двух функций известного вида (y = kx; y = kx + b; y = x2; y = x3).
2-й шаг. В одной системе координат построить графики этих функций.
3-й шаг. Определить наличие или отсутствие точки (точек) пересечения.
4-й шаг. Если точки пересечения есть, то найти по графику их абсциссы, которые и будут являться решениями уравнения. Если точек пересечения нет, то, значит, уравнение не имеет решений.
Проверить полученное значение можно, подставив в уравнение.
IV. Формирование умений и навыков.
1. № 493 (устно).
2. Решите графически уравнение.
а) x2 = 2x; б) x2
= ![]() x; в)
x2 = –2x.
x; в)
x2 = –2x.
3. № 566.
В следующем упражнении от учащихся требуется сначала преобразовать уравнение к «удобному» виду, а затем решить его графически.
|
4. № 494. Решение: б) x2 + 2x – 3 = 0; x2 = –2x + 3. Построим графики функций y = x2 и y = –2x + 3. Ответ: х = –3; х = 1. 5. № 495 (устно). 6. № 496. |
|
V. Итоги урока.
– В каком случае уравнение можно решить графически?
– Назовите алгоритм решения уравнения графическим способом.
– В каком случае уравнение не имеет корней?
– Как можно проверить точность корней уравнения, найденных графическим способом?
Домашнее задание:
1. Решите графически уравнение.
а) х = 3х; б) 2x = ![]() x + 2; в) 3x =
3x + 4.
x + 2; в) 3x =
3x + 4.
2. Решите графически уравнение.
а) x2 = 9; б) x2 =
![]() ; в)
x2 = –3; г) x3 = 8.
; в)
x2 = –3; г) x3 = 8.
3. Решите уравнение графически.
а) x2 = 6 – x; б) x2 + 4x = –3; в) x2 – 4x = 0; г) x3 + 2 = 3x.
Урок 52
Функции y = x2
и у = х3
и их графики
Цели: обобщить и систематизировать знания по теме «Степень с натуральным показателем»; оценить степень сформированности умений и навыков, провести коррекционную работу.
Ход урока
I. Устная работа.
1. Представьте в виде степени.
а) c7 ∙ c4; б) b ∙ b2 ∙ b3; в) (–7)3 ∙ (–7)8 ∙ (–7)9;
г) a10 : a8; д) 214 : 29; е) (x5)2;
ж) (–a3)3; з) 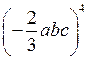 ; и) (a2)5
∙ a5.
; и) (a2)5
∙ a5.
2. Упростите.
а) (a5)2 ∙ (a2 ∙ a3)2; в) (4xy)2; д) 94 : 37;
б) (y4)5 : (y4)2; г) 20a3 ∙ (5a)2; е) 1012 : (24 ∙ 54).
3. Выполняя задания, ученик допустил ошибки. Какие свойства, правила не знает ученик?
35 ∙ 38 = 340; 81 = 1; 24 + 22 = 26;
(2a)5 = 2a5; (x2)3 = x8.
4. Представьте в виде степени.
(–3)8 ∙ (–3)4; (0,1)20 : (0,1)6; (xn)2.
5. Найдите значение выражения.
(1014 ∙ 107) : 1019; 53 ∙ 23.
6. Представьте произведение в виде степени.
x5y5;
36a2b2; ![]() a3b3c3.
a3b3c3.
II. Теоретический опрос.
1) Сформулируйте определение степени с натуральным показателем.
2) Каким числом является:
а) степень положительного числа;
б) степень отрицательного числа с четным показателем;
в) степень отрицательного числа с нечетным показателем?
3) Сформулируйте правило умножения степеней с одинаковыми показателями.
4) Сформулируйте правило деления степеней с одинаковыми показателями.
5) Дайте определение степени числа с нулевым показателем.
6) Сформулируйте правило возведения степени в степень.
7) Сформулируйте правило возведения в степень произведения.
III. Математический диктант.
Вариант 1
1. Упростите.
а) x2 ∙ x8 : x; б) a10 : a6 ∙ a4.
2. Найдите значение выражения.
94 : 37.
3. Представьте в виде квадрата одночлена.
0,25х4; 49т2п6.
4. Выполните умножение.
![]() x2y3
∙ 16yx.
x2y3
∙ 16yx.
5. Вычислите.
(516 · 316) : 1515.
Вариант 2
1. Упростите.
а) b3 ∙ b7 : b; б) y12 : y5 ∙ y2.
2. Найдите значение выражения.
44 : 26.
3. Представьте в виде квадрата одночлена.
0,36у6; 100с2а6.
4. Выполните умножение.
![]() a3b4
∙ 12ab2.
a3b4
∙ 12ab2.
5. Вычислите.
(310 · 710) : 219.
IV. Работа по карточкам.
Карточка № 1
1. Вычислите.
(494 · 75) : 712.
2. Упростите выражения.
а) 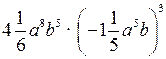 ; б)
am + 1 · a · a3 – m.
; б)
am + 1 · a · a3 – m.
Карточка № 2
1. Вычислите.
(56 · 125) : 254.
2. Упростите выражения.
а) 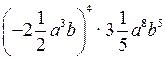 ; б)
x2n : (xn – 1)2.
; б)
x2n : (xn – 1)2.
V. Итоги урока.
Домашнее задание: 1. Повторить п. 18–23.
2. Ответьте на вопросы теста:
1) Выполните умножение: 0,5х2у · (–ху) =
а) –0,5х3у2; б) 0,5у2х3; в) –0,5х2у3.
2) Упростите: –0,4x4y3 · 2,5x2y7 =
а) x8y6; б) –10x6y7; в) –x6y7.
3) Преобразуйте выражение в одночлен стандартного вида:
20а3 · (–5а)2 =
а) 100а5; б) –500а6; в) 500а5.
4) Вычислите: (25 · (23)4) : 213 =
а) 23; б) 16; в) 32.
1. Представьте в виде степени.
а) c7 ∙ c4; б) b
∙ b2 ∙ b3; в)
(–7)3 ∙ (–7)8 ∙ (–7)9;г) a10
: a8; д) 214 : 29; е) (x5)2;
ж) (–a3)3;з) ![]() ;и) (a2)5 ∙ a5.
;и) (a2)5 ∙ a5.
2. Упростите. а) (a5)2 ∙ (a2 ∙ a3)2; в) (4xy)2; д) 94 : 37; б) (y4)5 : (y4)2; г) 20a3 ∙ (5a)2; е) 1012 : (24 ∙ 54).
3. Выполняя задания, ученик допустил ошибки. Какие свойства, правила не знает ученик?
35 ∙ 38 = 340; 81 = 1; 24 + 22 = 26; (2a)5 = 2a5; (x2)3 = x8.
4. Представьте в виде степени. (–3)8 ∙ (–3)4; (0,1)20 : (0,1)6; (xn)2.
5. Найдите значение выражения. (1014 ∙ 107) : 1019; 53 ∙ 23.
6. Представьте произведение в виде
степени. x5y5;
36a2b2; ![]() a3b3c3.
a3b3c3.
Математический диктант.
Вариант 1
1. Упростите. а) x2 ∙ x8 : x; б) a10 : a6 ∙ a4.
2. Найдите значение выражения. 94 : 37.
3. Представьте в виде квадрата одночлена. 0,25х4; 49т2п6.
4. Выполните умножение.![]() x2y3
∙ 16yx.
x2y3
∙ 16yx.
5. Вычислите. (516 · 316) : 1515.
Вариант 2
1. Упростите. а) b3 ∙ b7 : b; б) y12 : y5 ∙ y2.
2. Найдите значение выражения. 44 : 26.
3. Представьте в виде квадрата одночлена. 0,36у6; 100с2а6.
4. Выполните умножение. ![]() a3b4
∙ 12ab2.
a3b4
∙ 12ab2.
5. Вычислите. (310 · 710) : 219.
Работа по карточкам.
Карточка № 1
1. Вычислите. (494 · 75) : 712.
2. Упростите выражения. а) ![]() ; б) am
+ 1 · a · a3 – m.
; б) am
+ 1 · a · a3 – m.
Карточка № 2
1. Вычислите. (56 · 125) : 254.
2. Упростите выражения.а) ![]() ; б) x2n
: (xn – 1)2.
; б) x2n
: (xn – 1)2.
1. Представьте в виде степени.
а) c7 ∙ c4; б) b ∙ b2 ∙ b3; в) (–7)3
∙ (–7)8 ∙ (–7)9;г) a10 : a8; д) 214 : 29;
е) (x5)2;
ж) (–a3)3;з)
![]() ;и) (a2)5 ∙ a5.
;и) (a2)5 ∙ a5.
2. Упростите.
а) (a5)2 ∙ (a2 ∙ a3)2; в) (4xy)2; д) 94 : 37; б) (y4)5 : (y4)2; г) 20a3 ∙ (5a)2; е) 1012 : (24 ∙ 54).
3. Выполняя задания, ученик допустил ошибки. Какие свойства, правила не знает ученик?
35 ∙ 38 = 340; 81 = 1; 24 + 22 = 26; (2a)5 = 2a5; (x2)3 = x8.
4. Представьте в виде степени. (–3)8 ∙ (–3)4; (0,1)20 : (0,1)6; (xn)2.
5. Найдите значение выражения. (1014 ∙ 107) : 1019; 53 ∙ 23.
6. Представьте произведение в виде
степени. x5y5;
36a2b2; ![]() a3b3c3.
a3b3c3.
Математический диктант.
Вариант 1
1. Упростите. а) x2 ∙ x8 : x; б) a10 : a6 ∙ a4.
2. Найдите значение выражения. 94 : 37.
3. Представьте в виде квадрата одночлена. 0,25х4; 49т2п6.
4. Выполните умножение.![]() x2y3
∙ 16yx.
x2y3
∙ 16yx.
5. Вычислите. (516 · 316) : 1515.
Вариант 2
1. Упростите. а) b3 ∙ b7 : b; б) y12 : y5 ∙ y2.
2. Найдите значение выражения. 44 : 26.
3. Представьте в виде квадрата одночлена. 0,36у6; 100с2а6.
4. Выполните умножение. ![]() a3b4
∙ 12ab2.
a3b4
∙ 12ab2.
5. Вычислите. (310 · 710) : 219.
Работа по карточкам.
Карточка № 1
1. Вычислите. (494 · 75) : 712.
2. Упростите выражения. а) ![]() ; б) am
+ 1 · a · a3 – m.
; б) am
+ 1 · a · a3 – m.
Карточка № 2
1. Вычислите. (56 · 125) : 254.
2. Упростите выражения.а) ![]() ; б) x2n
: (xn – 1)2.
; б) x2n
: (xn – 1)2.
Урок 53
Контрольная работа № 4 «Степень с натуральным показателем»
Вариант 1
1. Найдите значение выражения 1 – 5х2 при х = –4.
2. Выполните действия.
а) y7 ∙ y12; б) y20 : y5; в) (y2)8; г) (2y)4.
3. Упростите выражение.
а) –2ab3 ∙ 3a2 ∙ b4; б) (–2a5b2)3.
4. Постройте график функции y = x2. С помощью графика определите значение у при х = 1,5; х = –1,5.
5. Вычислите: 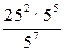 .
.
6. Упростите выражение.
а) 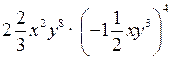 ; б)
xn – 2 ∙ x3 – n
∙ x.
; б)
xn – 2 ∙ x3 – n
∙ x.
Вариант 2
1. Найдите значение выражения –9р3 при p = ![]() .
.
2. Выполните действия.
а) c3 ∙ c22; б) c18 : c6; в) (c4)6; г) (3c)5.
3. Упростите выражение.
а) –4x5y2 ∙ 3xy4; б) (3x2y3)2.
4. Постройте график функции y = x2. С помощью графика определите, при каких значения х значение у равно 4.
5. Вычислите: 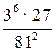 .
.
6. Упростите выражение.
а) 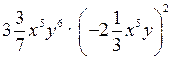 ; б)
(an + 1)2 : a2n.
; б)
(an + 1)2 : a2n.
Вариант 1
1. Найдите значение выражения 1 – 5х2 при х = –4.
2. Выполните действия. а) y7 ∙ y12; б) y20 : y5; в) (y2)8; г) (2y)4.
3. Упростите выражение. а) –2ab3 ∙ 3a2 ∙ b4; б) (–2a5b2)3.
4. Постройте график функции y = x2. С помощью графика определите значение у при х = 1,5; х = –1,5.
5. Вычислите: ![]() .
.
6. Упростите выражение. а) ![]() ; б) xn
– 2 ∙ x3 – n ∙ x.
; б) xn
– 2 ∙ x3 – n ∙ x.
Вариант 2
1. Найдите значение выражения –9р3 при p = ![]() .
.
2. Выполните действия. а) c3 ∙ c22; б) c18 : c6; в) (c4)6; г) (3c)5.
3. Упростите выражение. а) –4x5y2 ∙ 3xy4; б) (3x2y3)2.
4. Постройте график функции y = x2. С помощью графика определите, при каких значения х значение у равно 4.
5. Вычислите: ![]() .
.
6. Упростите выражение. а) ![]() ; б) (an
+ 1)2 : a2n.
; б) (an
+ 1)2 : a2n.
Вариант 1
1. Найдите значение выражения 1 – 5х2 при х = –4.
2. Выполните действия. а) y7 ∙ y12; б) y20 : y5; в) (y2)8; г) (2y)4.
3. Упростите выражение. а) –2ab3 ∙ 3a2 ∙ b4; б) (–2a5b2)3.
4. Постройте график функции y = x2. С помощью графика определите значение у при х = 1,5; х = –1,5.
5. Вычислите: ![]() .
.
6. Упростите выражение. а) ![]() ; б) xn
– 2 ∙ x3 – n ∙ x.
; б) xn
– 2 ∙ x3 – n ∙ x.
Вариант 2
1. Найдите значение выражения –9р3 при p = ![]() .
.
2. Выполните действия. а) c3 ∙ c22; б) c18 : c6; в) (c4)6; г) (3c)5.
3. Упростите выражение. а) –4x5y2 ∙ 3xy4; б) (3x2y3)2.
4. Постройте график функции y = x2. С помощью графика определите, при каких значения х значение у равно 4.
5. Вычислите: ![]() .
.
6. Упростите выражение. а) ![]() ; б) (an
+ 1)2 : a2n.
; б) (an
+ 1)2 : a2n.
Вариант 1
1. Найдите значение выражения 1 – 5х2 при х = –4.
2. Выполните действия. а) y7 ∙ y12; б) y20 : y5; в) (y2)8; г) (2y)4.
3. Упростите выражение. а) –2ab3 ∙ 3a2 ∙ b4; б) (–2a5b2)3.
4. Постройте график функции y = x2. С помощью графика определите значение у при х = 1,5; х = –1,5.
5. Вычислите: ![]() .
.
6. Упростите выражение. а) ![]() ; б) xn
– 2 ∙ x3 – n ∙ x.
; б) xn
– 2 ∙ x3 – n ∙ x.
Вариант 2
1. Найдите значение выражения –9р3 при p = ![]() .
.
2. Выполните действия. а) c3 ∙ c22; б) c18 : c6; в) (c4)6; г) (3c)5.
3. Упростите выражение. а) –4x5y2 ∙ 3xy4; б) (3x2y3)2.
4. Постройте график функции y = x2. С помощью графика определите, при каких значения х значение у равно 4.
5. Вычислите: ![]() .
.
6. Упростите выражение. а) ![]() ; б) (an
+ 1)2 : a2n.
; б) (an
+ 1)2 : a2n.
Урок 54 многочлен и его стандартный вид
Цели: ввести понятие многочлена, подобных членов многочлена, стандартного вида многочлена; формировать умение приводить многочлен к стандартному виду.
Ход урока
I. Устная работа.
1. Является ли одночленом выражение:
а) 7х2у2; в) у3 + у; д) 5(a + b)3;
б) a
∙ ![]() ; г)
; г)
![]() ; е)
; е)
![]() a2ba?
a2ba?
2. Представьте одночлен в стандартном виде и назовите его коэффициент:
а) 4х3х; в) 10х2 · (–0,1х2); д) –2р5 · 5р3;
б) –3![]() aba7; г)
aba7; г)
![]() ∙ 4c; е)
∙ 4c; е)
![]() xy2
∙ (–3x7).
xy2
∙ (–3x7).
II. Объяснение нового материала.
Объяснение материала проводится в несколько этапов, каждый из которых закрепляется примерами и устными заданиями.
1. Введение понятия многочлена.
При выполнении устной работы у учащихся была возможность вспомнить понятие одночлена, поэтому определение многочлена не должно вызывать у них затруднений.
Задание. Назовите каждый член многочлена и определите вид многочлена (одночлен, двучлен, трёхчлен).
а) –6a3 + 1,3b2; г) 4ab + 7ab2;
б) ![]() c8; д)
xyz + x2 – z;
c8; д)
xyz + x2 – z;
в) 5x2 + 7x – 8; е) 3a2b2c3.
2. Приведение подобных членов многочлена.
Можно предложить учащимся определить вид многочлена 3y4
+ 2y –
– 2y4. Некоторые из них скажут, что это трёхчлен. Тогда
следует обратить внимание на то, что слагаемые 3у4 и –2у4
являются подобными, и после их приведения получится многочлен у4
+ 2у, который является двучленом.
3. Стандартный вид многочлена.
Сначала необходимо вспомнить, что называется стандартным видом одночлена, а затем рассмотреть вопрос о приведении многочлена к стандартному виду.
Обратить внимание учащихся на то, что для приведения многочлена к стандартному виду нужно выполнить две операции:
– каждый член многочлена записать в стандартном виде;
– привести подобные члены многочлена.
Пример. Привести многочлен 3х5 – 2х2 + 3х · (–2) + 4х2 к стандартному виду.
3х5 – 2х2 + 3х · (–2) + 4х2 = 3х5 – 2х2 – 6х + 4х2 = 3х5 + 2х2 – 6х.
Как уже говорилось, вопрос о степени многочлена лучше рассмотреть на следующем уроке.
III. Формирование умений и навыков.
1. № 567.
2. Определите количество членов многочлена и назовите его (двучлен, трёхчлен).
а) ![]() x5
+ 2ab; в) 8ab + b5
– 9;
x5
+ 2ab; в) 8ab + b5
– 9;
б) xy2
+ x – 2y + 5; г) 5x3 – ![]() y2 –
5x3.
y2 –
5x3.
1. Приведите подобные члены многочлена.
а) 2a + 4ab – 6ab; в) 2x3 – 5x2 + 4x – x3 + 3x2;
б) 5x2 + 6x – 9x2; г) 4a5 – 7a3 + 2 – 2a3 – 10.
2. № 569.
1. Запишите в стандартном виде многочлен:
а) 3x7 + 2x ∙ (–5) + 5y; в) 5a4 – 2a ∙ a2 – a2 + 7a3;
б) 2p3 – p2 + 7p + 9p2; г) 2y2 ∙ (–4y3) + 5y ∙ y3 – 3y5.
2. № 571.
IV. Итоги урока.
– Что называется многочленом? членом многочлена?
– Приведите примеры двучленов, трёхчленов.
– Что такое подобные члены многочлена?
– Как записать многочлен в стандартном виде?
– Записан ли многочлен –3x7 + 2x3 + 4x ∙ (–x2) + x в стандартном виде? Почему?
Домашнее задание: № 568, № 570.
Урок 55
многочлен и его стандартный вид
Цели: ввести понятие степени многочлена; формировать умение определять степень многочлена и находить значения многочлена; продолжить формирование умения записывать многочлен в стандартном виде.
Ход урока
I. Устная работа.
Записаны ли многочлены в стандартном виде?
а) 3ab2 – 7y –
9; б) ![]() x5 + 2x2
– abc;
x5 + 2x2
– abc;
в) 3y5 – 7y2 + 2y
– 9y5; г) ![]() x4 – 3x ∙ x2
+ 5;
x4 – 3x ∙ x2
+ 5;
д) 4xy – 8x2y + 2xy2 – x2y2; е) 2a4 + 3a (–4) + a3 + 8a.
Приведите к стандартному виду все многочлены.
II. Формирование умений и навыков.
1. № 572.
Решение:
а) 5x6 – 3x2 + 7 – 2x6 – 3x6 + 4x2 = x2 + 7
при х = –10: х2 + 7 = (–10)2 + 7 = 107.
б) 4a2b – ab2 – 3a2b + ab2 – ab + 6 = a2b – ab + 6
при а = –3, b = 2: a2b – ab + 6 = 9 ∙ 2 + 3 ∙ 2 + 6 = 30.
2. № 574.
1. № 577 (а), № 578 (а).
2. Определите степень многочлена.
а) 3x2 – x5 + 8x3; г) 2a3b – 5b5 + 2a4b2;
б) 8 – 6а; д) 5t2 – 3t + 8 – 4t ∙ t2;
в) 5xy + 2y – 3xy2; е) 3a2x2 + 2ax – a2x2 + 5 – 2a2x2.
3. Вместо значка * запишите такой одночлен, чтобы получился многочлен четвертой степени.
а) 3x3 – 5x2 + 7 – *; б) 5a – 4a4 + 1 + *;
в) x5 + 2x4 – 3x2 + *; г) 4a3b2 + 3a2b2 + ab + *.
Решение:
а) Данный многочлен содержит одночлен второй и третьей степени. Чтобы многочлен был четвертой степени, вместо * нужно записать любой одночлен четвертой степени. Например, 7х4, 3а4, х2у2, ab3 и т. п.
б) Данный многочлен содержит одночлены первой и четвертой степени. Чтобы он был четвертой степени, вместо * достаточно записать любой одночлен не выше четвертой степени. Например, 2а2, xz2, 8у и т. п.
в) Данный многочлен содержит одночлены второй, четвертой и пятой степени. Чтобы он был четвертой степени, нужно вместо * записать такой одночлен, который взаимно уничтожиться с одночленом х5, то есть – х5.
г) Аналогично предыдущему заданию вместо * нужно записать одночлен –4a3b2.
III. Итоги урока.
– Что называется многочленом? Членом многочлена?
– Как записать многочлен в стандартном виде?
– Как найти значение многочлена при данных значениях переменных?
– Что называется степенью многочлена? Как определить степень произвольного многочлена?
Домашнее задание: № 573, № 577 (б); № 578 (б); № 579.
Урок 56 сложение и вычитание многочленов
Цели: рассмотреть вопрос о сложении и вычитании многочленов; формировать умение выполнять эти действия.
Ход урока
I. Проверочная работа.
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
II. Устная работа.
1. Назовите выражение, которое получится после раскрытия скобок.
а) x + (y – z); в) x – (a – b);
б) a – (b + c); г) 2p – (p + q).
2. Найдите значение выражения разными способами.
а) 17 + (2 – 10); в) 10 + (–3 + 8);
б) 4 – (5 + 2); г) 12 – (4 – 7).
III. Объяснение нового материала.
Достаточно актуализировать знания учащихся и рассмотреть примеры из учебника.
IV. Формирование умений и навыков.
1. № 585.
2. № 587 (а, в, д); № 589 (а, в).
3. № 588 (а, в).
4. № 591.
Решение:
а) Любое нечетное число можно записать в виде 2п + 1, тогда следующее за ним нечетное число будет равно 2п + 3.
Найдем сумму этих чисел:
2п + 1 + 2п + 3 = 4п + 4.
Первое слагаемое этой суммы делится на 4 и второе слагаемое делится на 4. Значит, вся сумма 4п + 4 делится на 4.
б) Пусть 2п + 1, 2п + 3, 2п + 5 и 2п + 7 – четыре последовательных нечетных числа. Найдем их сумму:
2п + 1 + 2п + 3 + 2п + 5 + 2п + 7 = 8п + 16.
Оба слагаемых этой суммы делятся на 8, значит, и вся сумма делится на 8.
V. Итоги урока.
– Что называется многочленом? степенью многочлена?
– Как привести многочлен к стандартному виду?
– Как раскрыть скобки, перед которыми стоит знак «+»? знак «–»?
– Как выполнить сложение или вычитание многочленов?
Домашнее задание: № 586; № 587 (б, г, е); № 588 (б, г); № 589 (б, г).
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
Вариант 1
1. Приведите многочлен к стандартному виду.
а) 5x ∙ 8y ∙ (–7x2) + (–6x) ∙ 3y2;
б) 5a2 + 3a – 7 – 5a3 – 3a2 + 7a – 11;
в) 6a2b – 5ab2 + 5a3 + 2ab2 – 8a3 – 3a2b.
2. Найдите значение многочлена.
а) –15a – b – 2 + 14a при а = –29, b = –2;
б) m4 – 3m3n + m2n2 – m3n – 4mn3 при т = –1, п = 1.
Вариант 2
1. Приведите многочлен к стандартному виду.
а) 8x ∙ 3y ∙ (–5y) – 7x2 ∙ (–4y);
б) 3t2 – 11t – 5t2 + 5t – 3t2 + 11;
в) 3a2x + 3ax2 + 5a3 + 3ax2 – 8a2x – 10a3.
2. Найдите значение многочлена.
а) –x – 3y – 4 + 2y при х = –15, у = –4;
б) 3uv3 + u2v2 – 2uv3 + u3v – u4 при u = 1, v = –1.
Урок 57
сложение и вычитание многочленов
Цели: продолжить формирование умения выполнять сложение и вычитание многочленов.
Ход урока
I. Устная работа.
Выполните сложение или вычитание многочленов.
а) (1 + a) + (3 + 2a); г) (5 – y) + (3y – 2);
б) (a – b) – (a + b); д) 4p2 – (p2 + 2);
в) 3x – (1 – 2x); е) (2 + x) – (x – 3).
II. Формирование умений и навыков.
1. № 590, № 592.
2. № 593.
Решение:
M + (5x2 – 2xy) = 6x2 + 9xy – y2.
Слева: Справа:
5х2 6х2
–2ху 9ху
0 –у2
Нужно найти такие одночлены, которые в сумме с одночленами из левой части дадут одночлены, равные стоящим в правой части. Получаем их: х2, 11ху, у2.
Значит, вместо М нужно записать многочлен х2 + 11ху + у2.
б) M – (4ab – 3b2) = a2 – 7ab + 8b2.
Сначала раскроем скобки: М – 4ab + 3b2 = a2 – 7ab + 8b2.
Слева: Справа:
–4ab –7ab
3b2 8b2
0 a2
Находим недостающие одночлены: –3ab, 5b2, –а2. Получаем многочлен: 5b2 – 3ab – а2.
Если задание не вызывает затруднений у учащихся, то они могут выполнять его устно.
3. Запишите во втором столбце многочлен, сумма которого с многочленом из первого столбца равна многочлену из третьего столбца.
|
1) 3х + 5 2) 7х + 3 3) a3 + 3a2b + b3 4) 2x2y – 3xy2 – 8 5) x2 + 2xy + y2 6) 3x + 2a |
|
8х – 11 х2 + 7х – 15 a3 + 3a2b + b3 0 x2 – 2xy + y2 2x + b |
4. № 605.
Решение:
Необходимо объяснить учащимся, что решение любого уравнения начинается с его преобразования.
в) (3,2у – 1,8) – (5,2у + 3,4) = –5,8;
3,2у – 1,8 – 5,2у – 3,4 = –5,8;
3,2у – 5,2у = 1,8 + 3,4 – 5,8;
–2у = –0,6;
у = –0,6 : (–2);
у = 0,3.
Ответ: 0,3.
д) 3,8 – 1,5у + (4,5у – 0,8) = 2,4у + 3;
3,8 – 1,5у + 4,5у – 0,8 = 2,4у + 3;
– 1,5у + 4,5у – 2,4у = 3 – 3,8 + 0,8;
0,6у = 0;
у = 0.
Ответ: 0.
III. Итоги урока.
– Что называется многочленом? степенью многочлена?
– Как раскрыть скобки, перед которыми стоит знак «+»? знак «–»?
– Как выполнить сложение или вычитание многочленов?
Домашнее задание: № 594; № 596; № 606.
1. Приведите подобные члены многочлена:
а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t
2. Раскройте скобки и приведите подобные слагаемые:
а) (12а + 3 b) + (7а - 4 b); б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)
3. Докажите, что при любом значении х значение выражения
(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1. Приведите подобные члены многочлена:
а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t
2. Раскройте скобки и приведите подобные слагаемые:
а) (12а + 3 b) + (7а - 4 b); б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)
3. Докажите, что при любом значении х значение выражения
(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1. Приведите подобные члены многочлена:
а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t
2. Раскройте скобки и приведите подобные слагаемые:
а) (12а + 3 b) + (7а - 4 b); б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)
3. Докажите, что при любом значении х значение выражения
(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1. Приведите подобные члены многочлена:
а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t
2. Раскройте скобки и приведите подобные слагаемые:
а) (12а + 3 b) + (7а - 4 b); б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)
3. Докажите, что при любом значении х значение выражения
(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1. Приведите подобные члены многочлена:
а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t
2. Раскройте скобки и приведите подобные слагаемые:
а) (12а + 3 b) + (7а - 4 b); б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)
3. Докажите, что при любом значении х значение выражения
(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1. Приведите подобные члены многочлена:
а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t
2. Раскройте скобки и приведите подобные слагаемые:
а) (12а + 3 b) + (7а - 4 b); б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)
3. Докажите, что при любом значении х значение выражения
(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1. Приведите подобные члены многочлена:
а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t
2. Раскройте скобки и приведите подобные слагаемые:
а) (12а + 3 b) + (7а - 4 b); б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)
3. Докажите, что при любом значении х значение выражения
(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
Урок 58 умножение одночлена на многочлен
Цели: изучить правило умножения одночлена на многочлен; формировать умение применять это правило при преобразовании выражений.
Ход урока
I. Устная работа.
1. Раскройте скобки.
а) 3 (2х – 5); в)
![]() (4 + 2y); д)
(4 + 2y); д)
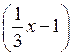 · (–3);
· (–3);
б) (5а – 1) 4; г) –5 (3р – 8); е) 0,7 (3а – 10).
2. Упростите выражение.
а) а5 · а7; в) аа2а3; д) (п3)2 п4;
б) х8 : х3; г) (х2)5; е) у2 у3(у4)2.
II. Объяснение нового материала.
При объяснении этого материала достаточно привести несколько примеров умножения одночлена на многочлен и сформулировать соответствующее правило.
III. Формирование умений и навыков.
1. № 614; № 615 (а, в, д).
2. № 616.
Решение:
(На первых порах желательно, чтобы учащиеся (особенно слабые) вели подробные записи, это позволит избежать ошибок в преобразованиях.)
в) ![]()
![]()
г) 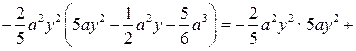
![]()
3. № 618 (а, в).
Решение:
(Здесь важно ещё раз напомнить учащимся о том, что перед нахождением значения любого выражения его сначала упрощают.)
в) 4у – 2 (10у – 1) + (8у – 24) = 4у – 20у + 2 + 8у – 24 = –8у – 22
при у = –0,1: –8у – 22 = –8 · (–0,1) – 22 = 0,8 – 22 = –21,2.
4. № 619.
IV. Итоги урока.
– Как выполнить умножение одночлена на одночлен?
– Перемножьте одночлены –2х2 и 5х4.
– Сформулируйте правило умножения одночлена на многочлен.
– Умножьте одночлен 4а3 на многочлен 2а – 3.
Домашнее задание: № 617; 618 (б, г); № 620.
Урок 59 Умножение одночлена на многочлен
Цели: продолжить формирование умения умножать одночлен на многочлен; формировать умение выполнять данное действие при решении уравнений.
Ход урока
I. Устная работа.
1. Выполните умножение одночленов.
а) 2х5 · 3х2; в) (–3b) · (–7b); д) (х2)3 · 5х;
б) –4a3
· ![]() a; г)
a; г)
![]() y7
· (–3y); е)
y7
· (–3y); е) 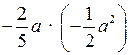 .
.
2. Упростите выражение.
а) 2x (x2 – 4x); в) 4y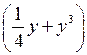 ;
;
б) –а2
(а + 8); г) ![]() p2(2p – 4).
p2(2p – 4).
II. Формирование умений и навыков.
1. № 630 (а, в, д, ж).
2. № 631 (а, в).
Решение:
а) 3х (2х – 1) – 6х (7 + х) = 90;
6х2 – 3х – 42х – 6х2 = 90;
–45х = 90;
х
=![]() ;
;
х = –2.
Ответ: –2.
в) 5x (12x – 7) – 4x (15x – 11) = 30 + 29x;
60x2 – 35x – 60x2 + 44x = 30 + 29x;
–35х + 44 х – 29х = 30;
–20х = 30;
х
= ![]() ;
;
х = –1,5.
Ответ: –1,5.
1. № 634 (а, в, д, и).
2. № 636.
3. № 637.
Решение:
б) ![]() .
.
Умножим обе части уравнения на 30:
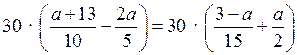 ;
;
3 (a + 13) – 6 · 2a = 2 (3 – a) + 15a;
3а + 39 – 12а = 6 – 2а + 15а;
–9а – 13а = 6 – 39;
–22а = –33;
а = ![]() ;
;
а = 1,5.
Ответ: 1,5.
г) ![]() .
.
Умножим обе части уравнения на 18:
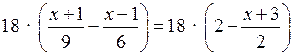 ;
;
2 (х + 1) – 3 (х – 1) = 36 – 9 (х + 3);
2х + 2 – 3х + 3 = 36 – 9х – 27;
–х + 9х = 9 – 5;
8х = 4;
х = ![]() .
.
Ответ: 0,5.
1. № 622.
2. № 629.
Решение:
Преобразуем данное выражение:
2x (x – 6) – 3 (x2 – 4x + 1) = 2x2 – 12x – 3x2 + 12x – 3 = – x2 – 3.
Очевидно, что при любом значении х значение выражения –х2 будет неположительным, тогда значение выражения –х2 – 3 будет отрицательным при любом значении х.
III. Итоги урока.
– Как выполнить умножение одночлена на одночлен?
– Сформулируйте правило умножения одночлена на многочлен.
– Как решить уравнение, в котором встречаются дроби?
Домашнее задание: № 632; № 634 (б, г, е, з); № 638; № 627.
Урок 60 Умножение одночлена на многочлен
Цели: формировать умение решать задачи с помощью уравнений; закрепить умение выполнять умножение одночлена на многочлен; проверить степень усвоения учащимися изученного материала.
Ход урока
I. Устная работа.
1. Выполните умножение одночленов.
а) 3а2 · (–2а); г) ![]() x6 · (–4x);
б) 7b3 ·
x6 · (–4x);
б) 7b3 · ![]() b2; д) (а2)4
· 2а; в) –4с · (–2с5); е)
b2; д) (а2)4
· 2а; в) –4с · (–2с5); е) ![]() .
.
2. Упростите выражение.
а) 3а (4 – а2); в) 2n ![]() ; б) –х3
(х + 2); г)
; б) –х3
(х + 2); г) ![]() y2(5 + 2y).
y2(5 + 2y).
II. Проверочная работа.
Вариант 1
1. Упростите выражение.а) 3p (8c + 1) – 8c (3p – 5); б) 5n2 (3n + 1) – 2n (5n2 – 3).
2. Решите уравнение.а) 6x – 5 (3x + 2) = 5 (x – 1) –
8; б) ![]() = 2.
= 2.
3. Преобразуйте в многочлен стандартного вида:–xt (x2t2 – xt – 3) · p.
Вариант 2
1. Упростите выражение.а) 5b (3a – b) – 3a (5b + a); б) a (2a2 – 3n) – n (2n2 + a).
2. Решите уравнение.а) 40 – 8 (11 – 2x) = 3 (5x – 4); б)
![]() .
.
3. Преобразуйте в многочлен стандартного вида:–ab (a2b – ab2 – a3b3) · p.
III. Формирование умений и навыков.
1. № 642.
Решение:
Составим таблицу:
|
|
Было |
Стало |
|
1-й сарай |
3х т |
(3х – 2) т |
|
2-й сарай |
х т |
(х + 2) т |
Составим и решим уравнение.
x + 2 = ![]() (3x – 2);
(3x – 2);
7 (х + 2) = 5 (3х – 2);
7х + 14 = 15х – 10;
–8х = –24;
х = 3.
Значит, во втором сарае было 3 т сена, а в первом 9 т сена.
Ответ: 9 т, 3 т.
2. № 643.
Решение:
Составим таблицу:
|
|
А |
k |
t |
|
По плану |
х га |
50 га/день |
|
|
Реально |
х га |
60 га/день |
|
Составим и решим уравнение:
![]() = 1;
= 1;
300![]() = 300;
= 300;
6х – 5х = 300;
х = 300.
Значит, площадь луга равна 300 га.
Ответ: 300 га.
3. № 646.
Решение:
Составим таблицу:
|
|
s |
υ |
t |
|
Велосипедист |
х км |
12 км/ч |
|
|
Мотоциклист |
(х + 60) км |
30 км/ч |
|
Составим и решим уравнение:
![]() ;
;
![]() ;
;
5х = 2 (х + 60);
5х = 2х + 120;
3х = 120;
х = 40.
Значит, велосипедист проехал 40 км до того, как его догнал мотоциклист.
Ответ: 40 км.
4. № 648.
Решение:
Представим наглядно описанную в задаче ситуацию.
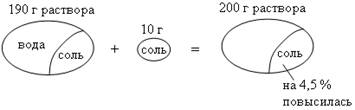
Пусть первоначально в растворе было х г соли, то есть её
концентрация была равна ![]() ∙ 100 % =
∙ 100 % = ![]() %.
%.
В новом растворе уже имеется (х + 10) г соли,
значит, её концентрация стала равна ![]() ∙ 100 % =
∙ 100 % = ![]() %. По условию концентрация соли
в новом растворе повысилась на 4,5 %.
%. По условию концентрация соли
в новом растворе повысилась на 4,5 %.
Составим и решим уравнение:
![]() = 4,5;
= 4,5;
19(х + 10) – 20х = 38 · 4,5;
19х + 190 – 20х = 171;
–х = –19;
х = 19.
Ответ: 19 г.
IV. Итоги урока.
– Сформулируйте правило умножения одночлена на многочлен.
– Умножьте одночлен –3х4 на многочлен 2х – 5.
– Как начать решение уравнения, в котором есть дроби?
– Как узнать концентрацию какого-либо вещества в растворе?
Домашнее задание: № 640; № 644; № 647; № 649.
задание 1
1. Выполните умножение одночленов.
а) 3а2 · (–2а); г) ![]() x6 · (–4x);
б) 7b3 ·
x6 · (–4x);
б) 7b3 · ![]() b2; д) (а2)4
· 2а; в) –4с · (–2с5); е)
b2; д) (а2)4
· 2а; в) –4с · (–2с5); е) ![]() .
.
2. Упростите выражение.
а) 3а (4 – а2); в) 2n ![]() ; б) –х3
(х + 2); г)
; б) –х3
(х + 2); г) ![]() y2(5 + 2y).
y2(5 + 2y).
Задание 2
1. Упростите выражение.а) 3p (8c + 1) – 8c (3p – 5); б) 5n2 (3n + 1) – 2n (5n2 – 3).
в) 5b (3a – b) – 3a (5b + a); г) a (2a2 – 3n) – n (2n2 + a).
2. Решите уравнение.а) 6x – 5 (3x + 2) = 5 (x – 1) –
8; б) ![]() = 2.
= 2.
в) 40 – 8 (11 – 2x) = 3 (5x – 4); г) ![]() .
.
3. Преобразуйте в многочлен стандартного вида:а) –xt (x2t2 – xt – 3) · p. б) –ab (a2b – ab2 – a3b3) · p
3. Выполните умножение.
а) 3x (2x2
– 5); в) 5y4
![]() ; б)
; б) ![]() a2 (a + 2); г) –ab (a2 – b).
a2 (a + 2); г) –ab (a2 – b).
4. Найдите наибольший общий делитель чисел.
а) 10, 15 и 25 в) 8, 12 и 16; б) 6, 9 и 21; г) 12, 18 и 30.
задание 1
1. Выполните умножение одночленов.
а) 3а2 · (–2а); г) ![]() x6 · (–4x);
б) 7b3 ·
x6 · (–4x);
б) 7b3 · ![]() b2; д) (а2)4
· 2а; в) –4с · (–2с5); е)
b2; д) (а2)4
· 2а; в) –4с · (–2с5); е) ![]() .
.
2. Упростите выражение.
а) 3а (4 – а2); в) 2n ![]() ; б) –х3
(х + 2); г)
; б) –х3
(х + 2); г) ![]() y2(5 + 2y).
y2(5 + 2y).
Задание 2
1. Упростите выражение.а) 3p (8c + 1) – 8c (3p – 5); б) 5n2 (3n + 1) – 2n (5n2 – 3).
в) 5b (3a – b) – 3a (5b + a); г) a (2a2 – 3n) – n (2n2 + a).
2. Решите уравнение.а) 6x – 5 (3x + 2) = 5 (x – 1) –
8; б) ![]() = 2.
= 2.
в) 40 – 8 (11 – 2x) = 3 (5x – 4); г) ![]() .
.
3. Преобразуйте в многочлен стандартного вида:а) –xt (x2t2 – xt – 3) · p. б) –ab (a2b – ab2 – a3b3) · p
3. Выполните умножение.
а) 3x (2x2
– 5); в) 5y4
![]() ; б)
; б) ![]() a2 (a + 2); г) –ab (a2 – b).
a2 (a + 2); г) –ab (a2 – b).
4. Найдите наибольший общий делитель чисел.
а) 10, 15 и 25 в) 8, 12 и 16; б) 6, 9 и 21; г) 12, 18 и 30.
Урок 61
вынесение общего множителя за скобки
Цели: ввести понятие разложения многочлена на множитель; изучить способ вынесения общего множителя за скобки и формировать умение его применять.
Ход урока
I. Устная работа.
1. Выполните умножение.
а) 3x (2x2 – 5); в) 5y4
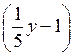 ;
;
б) ![]() a2 (a
+ 2); г) –ab (a2 – b).
a2 (a
+ 2); г) –ab (a2 – b).
2. Найдите наибольший общий делитель чисел.
а) 10, 15 и 25 в) 8, 12 и 16;
б) 6, 9 и 21; г) 12, 18 и 30.
II. Объяснение нового материала.
Вынесение общего множителя за скобки является обратной задачей к умножению одночлена на многочлен. Поэтому данный материал будет понят учащимися только в том случае, если они хорошо усвоили предыдущую тему.
Объяснение проводится в несколько этапов.
1. Начать лучше с постановки проблемной задачи.
Задача. После умножения некоторого одночлена на некоторый многочлен был получен многочлен 4х2 – 6х4. Какой одночлен на какой многочлен умножали?
2 (2х2 – 3х4), х (4х – 6х3), 2х2 (2 – 3х2) и т. п.
Можно рассмотреть ещё несколько подобных задач. Главное, что такие задачи всегда имеют решение и являются обратными к выполнению умножения одночлена на многочлен.
2.Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.
Данная операция является очень полезной при решении ряда задач, которые впоследствии будут рассмотрены.
3. Вернуться к разложенным на множители многочленам и обратить внимание учащихся, что для задач наиболее целесообразным является нахождение «наибольшего» общего множителя каждого члена много-члена. Поэтому в рассмотренном примере лучше записать следующее равенство:
4х2 – 6х4 = 2х2 (2 – 3х2).
Данный способ разложения многочлена на множители называется вынесением общего множителя за скобки.
4. Разобрать несколько примеров вынесения за скобки общего множителя:
а) 8х2у – 6х;
б) 3а4 + 9а2 – 6а;
в) пример 1 из учебника.
Сделать вывод: при вынесении общего множителя за скобки среди модулей коэффициентов берут их наибольший общий делитель, а переменные, выносимые за скобки, берут с наименьшим показателем.
III. Формирование умений и навыков.
1. № 654; № 655 (а, в, д, ж, и); № 656 (а, в, д).
В данных заданиях у многочленов общим множителем является либо только число, либо только буква. Необходимо, чтобы учащиеся сначала научились находить такие простые общие множители.
2. № 657 (а, в, д, и, л); № 659.
Здесь общие множители находить сложнее. Важно, чтобы учащиеся отыскивали правильно «наибольшие» общие множители.
№ 659.
Решение:
а) 14x + 21y = 7 (2x + 3y);
б) 15a + 10b = 5 (3a + 2b);
в) 8ab – 6ac = 2a (4b – 3c);
г) 9xa + 9xb = 9x (a + b);
д) 6ab – 3a = 3a (2b – 1);
е) 4x – 12x2 = 4x (1 – 3x);
ж) m4 – m2 = m2 (m2 – 1);
з) c3 + c4 = c3 (1 + c);
и) 7x – 14x3 = 7x (1 – 2x2);
к) 16y3 + 12y2 = 4y2 (4y + 3);
л) 18ab3 – 9b4 = 9b3 (2a – b);
м) 4x3y2 – 6x2y3 = 2x2y2 (2x – 3y).
IV. Итоги урока.
– Что называется разложением многочлена на множители?
– Какой способ разложения многочлена на множители мы узнали на этом уроке?
– В чём состоит способ вынесения общего множителя за скобки?
– Как отыскивать выносимый за скобки общий множитель?
Домашнее задание: № 655 (б, г, е, з); № 656 (б, г, е); № 657 (б, г, е, з, м); № 658.
Урок 62
Вынесение общего множителя за скобки
Цели: продолжить формирование умения выносить за скобки общий множитель; проверить степень усвоения учащимися изученного материала.
Ход урока
I. Устная работа.
Найдите общий множитель членов многочлена.
а) 3a + 6b; г) 5а4 – 10а2;
б) х3 – 2х; д) –3а2с – ас;
в) 4xy + 6xz; е) 12x – 16x2y.
Если его вынести за скобки, то какое выражение останется?
II. Объяснение нового материала.
Рассмотрим пример 4 из учебника и сделаем соответствующие выводы. После этого учащиеся должны проговорить своими словами, как решаются подобные уравнения.
III. Формирование умений и навыков.
№ 661.
Решение:
г) 3х2 – 1,2х = 0;
х (3х – 1,2) = 0;
х = 0 или 3х – 1,2 = 0;
3х = 1,2;
х = 0,4.
Ответ: 0; 0,4.
и) y2 + ![]() y = 0;
y = 0;
y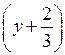 = 0;
= 0;
y
= 0 или y + ![]() = 0;
= 0;
y = ![]() .
.
Ответ: 0; ![]() .
.
№ 660 (а, г).
Решение:
а) 3,28х – х2 = х (3,28 – х)
при х = 2,28:
х (3,28 – х) = 2,28 (3,28 – 2,28) = 2,28 · 1 = 2,28;
г) –mb – m2 = –m (b + m)
при m = 3,48 и b = 96,52:
–m (b + m) = –3,48 (96,52 + 3,48) = –3,48 · 100 = –348.
3-я группа
№ 664 (а, г); № 666.
№ 666.
Решение:
а) x3 – 3x2 + x = x (x2 – 3x + 1);
б) m2 – 2m3 – m4 = m2 (1 – 2m – m2);
в) 4a5 – 2a3 + a = a (4a4 – 2a2 + 1);
г) 6x2 – 4x3 + 10x4 = 2x2 (3 – 2x + 5x2);
д) 15a3 – 9a2 + 6a = 3a (5a2 – 3a + 2);
е) –3m2 – 6m3 + 12m5 = –3m2 (1 + 2m – 4m3).
IV. Проверочная работа.
Вариант 1
1. Разложите на множители многочлен.
а) 5ab + 10a2;
б) 6x2 – 3x3 – 9x4;
в) 6c2x3 – 4c3x2 + 2c2x2.
2. Решите уравнение.
а) 2х2 + 4х = 0;
б) 3х – 5х2 = 0.
Вариант 2
1. Разложите на множители многочлен.
а) 7ab – 14a2;
б) 3a2 – 6a3 + 18a4;
в) 4a3c2 + 8a2c3 – 12a3c3.
2. Решите уравнение.
а) 3х2 – 12х = 0;
б) 4х + 7х2 = 0.
V. Итоги урока.
– Что называется разложением многочлена на множители?
– В чём состоит способ вынесения общего множителя за скобки?
– Как отыскать выносимый за скобки общий множитель?
– При решении каких заданий пригодится умение выносить за скобки общий множитель?
– Как решаются уравнения с помощью вынесения за скобки общего множителя?
Домашнее задание: № 660 (б, в); № 662; 664 (б, в); № 667.
Вариант 1
1. Разложите на множители многочлен.
а) 5ab + 10a2;
б) 6x2 – 3x3 – 9x4;
в) 6c2x3 – 4c3x2 + 2c2x2.
2. Решите уравнение.
а) 2х2 + 4х = 0;
б) 3х – 5х2 = 0.
Вариант 2
1. Разложите на множители многочлен.
а) 7ab – 14a2;
б) 3a2 – 6a3 + 18a4;
в) 4a3c2 + 8a2c3 – 12a3c3.
2. Решите уравнение.
а) 3х2 – 12х = 0;
б) 4х + 7х2 = 0.
Вариант 1
1. Разложите на множители многочлен.
а) 5ab + 10a2;
б) 6x2 – 3x3 – 9x4;
в) 6c2x3 – 4c3x2 + 2c2x2.
2. Решите уравнение.
а) 2х2 + 4х = 0;
б) 3х – 5х2 = 0.
Вариант 2
1. Разложите на множители многочлен.
а) 7ab – 14a2;
б) 3a2 – 6a3 + 18a4;
в) 4a3c2 + 8a2c3 – 12a3c3.
2. Решите уравнение.
а) 3х2 – 12х = 0;
б) 4х + 7х2 = 0.
Вариант 1
1. Разложите на множители многочлен.
а) 5ab + 10a2;
б) 6x2 – 3x3 – 9x4;
в) 6c2x3 – 4c3x2 + 2c2x2.
2. Решите уравнение.
а) 2х2 + 4х = 0;
б) 3х – 5х2 = 0.
Вариант 1
1. Разложите на множители многочлен.
а) 5ab + 10a2;
б) 6x2 – 3x3 – 9x4;
в) 6c2x3 – 4c3x2 + 2c2x2.
2. Решите уравнение.
а) 2х2 + 4х = 0;
б) 3х – 5х2 = 0.
Вариант 2
1. Разложите на множители многочлен.
а) 7ab – 14a2;
б) 3a2 – 6a3 + 18a4;
в) 4a3c2 + 8a2c3 – 12a3c3.
2. Решите уравнение.
а) 3х2 – 12х = 0;
б) 4х + 7х2 = 0.
Вариант 2
1. Разложите на множители многочлен.
а) 7ab – 14a2;
б) 3a2 – 6a3 + 18a4;
в) 4a3c2 + 8a2c3 – 12a3c3.
2. Решите уравнение.
а) 3х2 – 12х = 0;
б) 4х + 7х2 = 0.
Вариант 1
1. Разложите на множители многочлен.
а) 5ab + 10a2;
б) 6x2 – 3x3 – 9x4;
в) 6c2x3 – 4c3x2 + 2c2x2.
2. Решите уравнение.
а) 2х2 + 4х = 0;
б) 3х – 5х2 = 0.
Вариант 2
1. Разложите на множители многочлен.
а) 7ab – 14a2;
б) 3a2 – 6a3 + 18a4;
в) 4a3c2 + 8a2c3 – 12a3c3.
2. Решите уравнение.
а) 3х2 – 12х = 0;
б) 4х + 7х2 = 0.
Вариант 1
1. Разложите на множители многочлен.
а) 5ab + 10a2;
б) 6x2 – 3x3 – 9x4;
в) 6c2x3 – 4c3x2 + 2c2x2.
2. Решите уравнение.
а) 2х2 + 4х = 0;
б) 3х – 5х2 = 0.
Вариант 2
1. Разложите на множители многочлен.
а) 7ab – 14a2;
б) 3a2 – 6a3 + 18a4;
в) 4a3c2 + 8a2c3 – 12a3c3.
2. Решите уравнение.
а) 3х2 – 12х = 0;
б) 4х + 7х2 = 0.
Урок 63
Вынесение общего множителя за скобки
Цели: закрепить умение выносить за скобки общий множитель; рассмотреть, как используется это умение при решении вопроса о делимости и кратности чисел; формировать умение выносить за скобки двучлен.
Ход урока
I. Устная работа.
1. Вынесите за скобки общий множитель.
а) 5ab + 5ac; в) а3 + а5; д) 6х2 – 9х4;
б) х2 – ху; г) n2m + nm2; е) 8р3 – 12р.
2. Найдите корни уравнения:
а) (х + 1) (х – 1) = 0; в) х2 – 2х = 0;
б) (х – 3) (х + 2) = 0; в) х2 + 4х = 0.
II. Формирование умений и навыков.
1. № 663 (а, в).
Решение:
а) Вынесем в сумме 165 + 164 за скобки общий множитель:
165 + 164 = 164 (16 + 1) = 164 · 17.
Так как в произведении 164 · 17 встречается множитель 17, то данное произведение кратно 17.
в) Преобразуем выражение и вынесем за скобки общий множитель:
365 – 69 = (62)5 – 69 = 610 – 69 = 69 (6 – 1) = 69 · 5 = 68 · 30.
Очевидно, что полученное произведение кратно 30.
2. № 665 (а, в).
а) Вынесем за скобки общий множитель:
78 – 77 + 76 = 76 (72 – 7 + 1) = 76 · 43.
Так как один из множителей полученного произведения делится на 43, то и всё произведение делится на 43.
в) Преобразуем выражение и вынесем за скобки общий множитель:
274 – 95 + 39 = (33)4 – (32)5 + 39 = 312 – 310 + 39 = 39 (33 – 3 + 1) = 39 · 25.
Так как один из множителей полученного произведения делится на 25, то и все произведение делится на 25.
№ 668.
Решение:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
д) ![]()
е) ![]()
1. № 670.
Решение:
б) y (a – b) – (a – b) = (a – b) (y – 1);
г) ![]()
д) ![]()
= (b – 2) (–3b + 7b – 14) = (b – 2) (4b –
14).
2. № 671.
Решение:
б) x (y – 5) – y (5 – y) = x (y – 5) + y (y – 5) = (y – 5) (x + y);
г) ![]()
е) ![]() (3 – b) (2 + 5
(3 – b)) =
(3 – b) (2 + 5
(3 – b)) =
= (3 – b) (2 + 15 – 5b) = (3 – b) (17 – 5b).
III. Итоги урока.
– Что называется многочленом? Стандартным видом многочлена?
– Сформулируйте правило сложения и вычитания многочленов.
– Как умножить одночлен на многочлен?
– Какое преобразование называется разложением многочлена на множители?
– В чём состоит способ вынесения общего множителя за скобки?
–
Какой общий множитель имеют слагаемые суммы 3х (а – 3) +
+ 2 (3 – а)2?
Домашнее задание: № 663 (б, г); № 665 (б, г); № 669; № 672.
Урок 63
Контрольная работа № 5 «Сумма и разность многочленов. произведение многочленов»
Вариант 1
1. Выполните действия.
а) (3a – 4ax + 2) – (11a – 14ax);
б) 3y2 (y3 + 1).
2. Вынесите общий множитель за скобки.
а) 10ab – 15b2; б) 18а3 + 6а2.
3. Решите уравнение 9х – 6 (х – 1) = 5 (х + 2).
4. Пассажирский поезд за 4 ч прошёл такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
5. Решите уравнение ![]() .
.
6. Упростите выражение 2a (a + b – c) – 2b (a – b – c) + 2c (a – b + c).
Вариант 2
1. Выполните действия.
а) (2a2 – 3a + 1) – (7a2 – 5a);
б) 3х (4х2 – х).
2. Вынесите общий множитель за скобки.
а) 2ху – 3ху2; б) 8b4 + 2b3.
3. Решите уравнение 7 – 4 (3х – 1) = 5 (1–2х).
4. В трех шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе?
5. Решите уравнение ![]() .
.
6. Упростите выражение 3x (x + y + c) – 3y (x – y – c) – 3c (x + y – c).
Вариант 3
1. Выполните действия.
а) (12ab – 5a) – (ab + 6a);
б) 5х (3х2 – 2х – 4).
2. Вынесите общий множитель за скобки.
а) 3х2 + 9ху; б) 10х5 – 5х.
3. Решите уравнение 4 (х + 1) = 15х – 7 (2х + 5).
4. Ученик за 8 ч работы сделал столько же деталей, сколько мастер за 5 ч. Сколько деталей в час изготовил ученик, если известно, что мастер изготовлял в час на 6 деталей больше, чем ученик?
5. Решите уравнение ![]() .
.
6. Упростите выражение 4х (a + х + y) + 4a (a – х – y) – 4y (х – a – y).
Вариант 4
1. Выполните действия.
а) (4y3 + 15y) – (17y – y3);
б) 2a (3a – b + 4).
2. Вынесите общий множитель за скобки.
а) 2ab – ab2; б) 2х2 + 4х6.
3. Решите уравнение 5 (х – 3) = 14 – 2 (7 – 2х).
4. В трёх корзинах 56 кг яблок. Во второй корзине на 12 кг яблок больше, чем в первой, а в третьей – в 2 раза больше, чем в первой. Сколько килограммов яблок в каждой корзине?
5. Решите уравнение ![]() .
.
6. Упростите выражение 6a (a – х + c) + 6х (a + х – c) – 6c (a – х – c).
Решение заданий контрольной работы
Вариант 1
1. а) (3a – 4ax + 2) – (11a – 14ax) = 3a – 4ax + 2 – 11a + 14ax =
= 10ax – 8a + 2;
б) 3y2 (y3 + 1) = 3y5 + 3y2.
2. а) 10ab – 15b2 = 5b (2a – 3b);
б) 18а3 + 6а2 = 6а2 (3а + 1).
3. 9х – 6 (х – 1) = 5 (х + 2);
9х – 6х + 6 = 5х + 10;
3х – 5х = 10 – 6;
–2х = 4;
х = –2.
Ответ: –2.
4. Составим таблицу:
|
|
s |
υ |
t |
|
Пассажирский поезд |
4х км |
х км/ч |
4 ч |
|
Товарный поезд |
6 (х – 20) км |
(х – 20) км/ч |
6 ч |
Известно, что поезда прошли одинаковое расстояние. Получим уравнение:
4х = 6 (х – 20);
4х = 6х – 120;
–2х = –120;
х = 60.
Ответ: 60 км/ч.
5. ![]() .
.
Умножим обе части уравнения на 18:
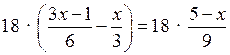 ;
;
3 (3х – 1) – 6х = 2 (5 – х);
9х – 3 – 6х = 10 – 2х;
3х + 2х = 10 + 3;
5х = 13;
х = ![]() ;
;
х = 2,6.
Ответ: 2,6.
6. ![]()
–2ac – 2ab + 2b2 + 2bc + 2ac – 2bc
+ 2c2 = 2a2 + 2b2 + 2c2.
Вариант 2
1. а) (2a2 – 3a + 1) – (7a2 – 5a) = 2a2 – 3a + 1 – 7a2 + 5a = –5a2 + 2a + 1;
б) 3х (4х2 – х) = 12х3 – 3х2.
2. а) 2ху – 3ху2 = ху (2 – 3у);
б) 8b4 + 2b3 = 2b3 (4b + 1).
3. 7 – 4 (3х – 1) = 5 (1–2х);
7 – 12х + 4 = 5 – 10х;
– 12х + 10х = 5 – 11;
–2х = –6;
х = 3.
Ответ: 3.
4. Пусть в 6 «Б» классе всего х учеников. Тогда в 6 «А» (х – 2) ученика, а в 6 «В» (х + 3) ученика.
По условию всего в трех классах 91 ученик. Составим и решим уравнение.
х + (х – 2) + (х + 3) = 91;
х + х – 2 + х + 3 = 91;
3х = 90;
х = 30.
Значит, в 6 «Б» классе 30 учеников. Тогда в 6 «А» 28 учеников, а в 6 «В» 33 ученика.
Ответ: 28, 30 и 33 ученика.
5. ![]() .
.
Умножим обе части уравнения на 20.
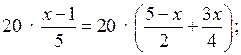
4 (х – 1) = 10 (5 – х) + 15х;
4х – 4 = 50 – 10х + 15х;
4х – 5х = 50 + 4;
–х = 54;
х = –54.
Ответ: –54.
6. ![]()
+ 3хc – 3хy + 3y2 + 3yc – 3хc – 3yc
+ 3c2 = 3х2 + 3y2 + 3c2.
Вариант 3
1. а) (12ab – 5a) – (ab + 6a) = 12ab – 5a – ab – 6a = 11ab – 11a;
б) 5х (3х2 – 2х – 4) = 15х3 – 10х2 – 20х.
2. а) 3х2 + 9ху = 3х (х + 3у);
б) 10х5 – 5х = 5х (2х4 – 1).
3. 4 (х + 1) = 15х – 7 (2х + 5);
4х + 4 = 15х – 14х – 35;
4х – х = –35 – 4;
3х = –39;
х = –13.
Ответ: –13.
4. Составим таблицу:
|
|
A |
k |
t |
|
Ученик |
8х дет. |
х дет./ч |
8 ч |
|
Мастер |
5 (х + 6) дет. |
(х + 6) дет./ч |
5 ч |
По условию мастер и ученик изготовили одинаковое количество деталей. Получим уравнение:
8х = 5 (х + 6);
8х = 5х + 30;
3х = 30;
х = 10.
Ответ: 10 деталей.
5. ![]() .
.
Умножим обе части уравнения на 12:
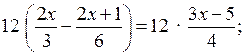
8х – 2 (2х + 1) = 3 (3х – 5);
8х – 4х – 2 = 9х – 15;
4х – 9х = – 15 + 2;
–5х = –13;
х = ![]() .
.
х = 2,6
Ответ: 2,6.
6. ![]()
+ 4хy + 4a2 – 4aх – 4ay – 4хy + 4ay + 4y2 = 4х2 + 4a2 + 4y2.
Вариант 4
1. а) (4y3 + 15y) – (17y – y3) = 4y3 + 15y – 17y + y3 = 5y3 – 2y;
б) 2a (3a – b + 4) = 6a2 – 2ab + 8a.
2. а) 2ab – ab2 = ab (2 – b);
б) 2х2 + 4х6 = 2х2 (1 + 2х4).
3. 5 (х – 3) = 14 – 2 (7 – 2х);
5х – 15 = 14 – 14 + 4х;
5х – 4х = 15;
х = 15.
Ответ: 15.
4. Пусть в первой корзине х кг яблок. Тогда во второй корзине (х + 12) кг яблок, а в третьей 2х кг яблок.
По условию всего в трёх корзинах 56 кг яблок. Составим и решим уравнение:
х + х + 12 + 2х = 56;
4х = 44;
х = 11.
Значит, в первой корзине 11 кг яблок. Тогда во второй корзине 23 кг яблок, а в третьей – 22 кг яблок.
Ответ: 11, 23 и 22 кг яблок.
5. ![]() .
.
Умножим обе части уравнения на 12:
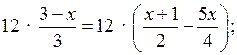
4 (3 – х) = 6 (х + 1) – 15х;
12 – 4х = 6х + 6 – 15х;
–4х + 9х = 6 – 12;
5х = –6;
х = ![]() ;
;
х = –1,2.
Ответ: –1,2.
6. ![]()
+ 6ac + 6ax + 6x2 – 6cx – 6ac + 6cx + 6c2 = 6a2 + 6x2 + 6c2.
Вариант 1
1. Выполните действия. а) (3a – 4ax + 2) – (11a – 14ax); б) 3y2 (y3 + 1).
2. Вынесите общий множитель за скобки. а) 10ab – 15b2; б) 18а3 + 6а2.
3. Решите уравнение 9х – 6 (х – 1) = 5 (х + 2).
4. Пассажирский поезд за 4 ч прошёл такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
5. Решите уравнение ![]() .
.
6. Упростите выражение 2a (a + b – c) – 2b (a – b – c) + 2c (a – b + c).
Вариант 2
1. Выполните действия. а) (2a2 – 3a + 1) – (7a2 – 5a); б) 3х (4х2 – х).
2. Вынесите общий множитель за скобки. а) 2ху – 3ху2; б) 8b4 + 2b3.
3. Решите уравнение 7 – 4 (3х – 1) = 5 (1–2х).
4. В трех шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе?
5. Решите уравнение ![]() .
.
6. Упростите выражение 3x (x + y + c) – 3y (x – y – c) – 3c (x + y – c).
Вариант 1
1. Выполните действия. а) (3a – 4ax + 2) – (11a – 14ax); б) 3y2 (y3 + 1).
2. Вынесите общий множитель за скобки. а) 10ab – 15b2; б) 18а3 + 6а2.
3. Решите уравнение 9х – 6 (х – 1) = 5 (х + 2).
4. Пассажирский поезд за 4 ч прошёл такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
5. Решите уравнение ![]() .
.
6. Упростите выражение 2a (a + b – c) – 2b (a – b – c) + 2c (a – b + c).
Вариант 2
1. Выполните действия. а) (2a2 – 3a + 1) – (7a2 – 5a); б) 3х (4х2 – х).
2. Вынесите общий множитель за скобки. а) 2ху – 3ху2; б) 8b4 + 2b3.
3. Решите уравнение 7 – 4 (3х – 1) = 5 (1–2х).
4. В трех шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе?
5. Решите уравнение ![]() .
.
6. Упростите выражение 3x (x + y + c) – 3y (x – y – c) – 3c (x + y – c).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.